Dimensional study of COVID-19 via fractal functions

Abstract

The present paper deals with the modeling of the COVID-19 via fractal interpolation function (FIF) and the estimation of the dimension of constructed FIF. Further, we determine the adjoint of the fractal operator defined on ${\mathcal{L}}^2$ space associated with the FIF.

Introduction

Several outbreaks have occurred in India over the last century, but none have been as deadly as the COVID-19 outbreaks. The first indication that the COVID-19 outbreak has spread to India is on January 27, 2020, when the first case of infection in Kerala, India, was reported. Since then, the entire country has been in a state of chaos and turbulence as a result of the virus’s increasing casualties. Coronavirus disease caused by the coronavirus strain, viz., Severe Acute Respiratory Syndrome Coronavirus 2 (SARS-CoV-2), mainly affects the respiratory system of the human body. The disease is highly contagious, which explains the high death toll. In the battle with this infectious disease, mankind has had to discover a strategy to survive. Active surveillance of the increase in the number of infected cases and deaths due to COVID-19 through a fractal interpolation polynomial provides a way to better understand the dynamical nature of the virus. In this attempt, several authors studied the dynamic nature of the COVID-19 virus via the fractal-based models [11, 14, 19, 28].

There are numerous real-world applications for functional interpolation from a given data set. In the classical approach, the interpolation has been accomplished by smooth functions, sometimes infinitely differentiable, but natural phenomena may occur with sudden changes. In 1986, Barnsley [6, 7] used the concept of an iterated function system (IFS) to introduce continuous interpolation functions called fractal interpolation functions (FIFs). For more details about these IFS and related concept, we refer the interested reader to, for instance, [12, 16, 22].

In advance of the classical approach, these FIFs possess a self-similar nature on small scales and are not essentially smooth. Due to advancements in its properties, this theory gained remarkable attention in mathematical modeling. Following that Navascués [25] introduced $\alpha$-fractal functions on a real compact interval. Motivated by Navascués work, bivariate [9, 21–23], multivariate [1, 29, 30], vector-valued [39], complex-valued [40], set-valued [31] $\alpha$-fractal functions as well as fractal functions on the fractal domains [2, 3, 32, 34] are constructed and studied recently. We also encourage to see some recent works [5, 10, 17, 18, 35, 36] on non-stationary fractal functions which are generalizations of fractal functions and fractal dimension of fractal functions. The fractal interpolation function has numerous applications in real life and medical science [13, 15, 28, 41].

Computation of the fractal dimension of a given set, the graph of a function and measure is an integral part of fractal analysis. Fractal dimension has a nice connection with some topological properties of a metric space. For example, if box dimension of a set is strictly less than 1,  then the set will be totally disconnected, for more details, see [12]. Liang [20] proved that for a continuous function of bounded variation on the unit interval [0, 1], its graph has box dimension 1. We can also note (see, for instance, [12]) that if a real-valued function is Hölder continuous with Hölder exponent $\sigma ,$ then the upper box dimension of its graph is less than $2-\sigma$. Some works related to the estimation and computation of fractal dimension of fractal sets and functions can be seen in [1, 2, 8, 10, 12, 18, 22, 29, 38].

The paper is organized as follows. In Sect. 2, we provide background related to the article where we discussed in detail the construction of the fractal interpolation function and the basic of fractal dimensions. In Sect. 3, we modeled COVID-19 using the data collected from the second wave in India and estimate the fractal dimension of the constructed FIFs. Further, we define the fractal operator on ${\mathcal{L}}^2$ space and determine the adjoint of the fractal operator using series expansions. In Sect. 4, we close the discussion of this paper by writing some concluding remarks and some possible future works.

Fractal functions

Let the interpolation data set be given as $\{(x_i,y_i)\in I\times \mathbb{R}:i=0,1,2,\cdots ,N\}$ such that $x_0<x_1<\cdots <x_N.$ Consider the intervals $I=[x_0,x_N]$ and $I_n=[x_{n-1},x_n],$ for $n\in \{1,2,\cdots ,N\}.$ Define a function $L_n:I\to I_n$ such that it is a contractive homeomorphism and satisfies

$$\begin{array}{c}\hfill L_n(x_0)=x_{n-1}\text{and}{L}_n(x_N)=x_n.\end{array}$$

Define a continuous function $F_n:I\times \mathbb{R}\to \mathbb{R}$ such that it is a contraction in second co-ordinate and satisfies the join-up condition, that is,

$$\begin{array}{c}\hfill |F_n(x,y)-F_n(x,y_{\ast })|\le c_n|y-y_{\ast }|,\\ \hfill \text{for}(x,y),(x,y_{\ast })\in I\times \mathbb{R},\end{array}$$

where $0<c_n<1$ and

$$\begin{array}{cc}& F_n(x_0,y_0)=y_{n-1}\text{and}\hfill \\ \hfill & F_n(x_N,y_N)=y_n,\text{for}n\in \{1,2,\cdots ,N\}.\hfill \end{array}$$

Define a function ${\mathcal{W}}_n:I\times \mathbb{R}\to I\times \mathbb{R}$ as

$$\begin{array}{c}\hfill {\mathcal{W}}_n(x,y)=(L_n(x),F_n(x,y)),\text{for}(x,y)\in I\times \mathbb{R}.\end{array}$$

Thus, $\{I\times \mathbb{R};{\mathcal{W}}_n:n=1,2,\cdots ,N\}$ is an iterated function system (IFS). Using Theorem 1 of [7], the IFS defined above has a unique attractor which is the graph of the continuous function $f:I\to \mathbb{R}$ satisfying the self-referential equation given as

$$\begin{array}{cc}\hfill f(x)=& F_n(L_n^{-1}(x),f(L_n^{-1}(x))),\text{for}x\in I_n,\text{and}n\in \{1,2,\cdots ,N\},\hfill \\ \hfill & \text{that is,}f(L_n(x))=F_n(x,f(x)),\text{for}x\in I.\hfill \end{array}$$

The functions $L_n:I\to I_n$ and $F_n:I\times \mathbb{R}\to \mathbb{R}$ mentioned above can be chosen as

$$\begin{array}{cc}\hfill L_n(x)=& a_{n}x+b_n,\text{for}x\in I\hfill \\ \hfill F_n(x,y)=& {\alpha }_{n}y+q_n(x),\text{for}(x,y)\in I\times \mathbb{R},\hfill \end{array}$$

where $a_n,b_n,{\alpha }_n\in \mathbb{R}$ such that $0<|{\alpha }_n|<1$ and $q_n:I\to \mathbb{R}$ is a continuous function given as

$$\begin{array}{c}\hfill q_n(x)=f(L_n(x))-{\alpha }_{n}b(x),\text{for}x\in I,\end{array}$$

where the continuous function $b:I\to \mathbb{R}$ is called a base function satisfying $b(x_0)=y_0\text{and}b(x_N)=y_N$ and $f:I\to \mathbb{R}$ is the original interpolating function satisfying the interpolation points, called the germ function. Since the function $F_n$ also satisfies the join-up conditions, we obtain,

$$\begin{array}{c}\hfill q_n(x_0)=f(L_n(x_0))-{\alpha }_{n}b(x_0)\text{and}{q}_n(x_N)=f(L_n(x_N))-{\alpha }_{n}b(x_N).\end{array}$$

Consequently, the IFS $\{I\times \mathbb{R};{\mathcal{W}}_n:n=1,2,\cdots ,N\}$ has a unique attractor given by the graph of the continuous function f, denoted by $f^{\alpha }$ and satisfies the self-referential equation given as

$$\begin{array}{c}\hfill f^{\alpha }(x)=f(x)+{\alpha }_n(f^{\alpha }-b)(L_n^{-1}(x)),\\ \hfill \text{for}x\in I_n\text{and}n\in \{1,2,\cdots ,N\}.\end{array}$$

Therefore, for any partition $\mathrm{\Delta }$ of the interval $I=[x_0,x_N]$, scaling vector $\alpha =({\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_N)$ and base function b, we get a fractal interpolation function $f_{\mathrm{\Delta },b}^{\alpha }$, called $\alpha$-fractal interpolation function. For box dimensions, we refer the reader to [12].

Definition 2.1

Let A be a non-empty bounded subset of the metric space (X, d). The box dimension of A is defined as

$$\begin{array}{c}\hfill {dim}_{B}A=\underset{\delta \to 0}{lim}\frac{log{N}_{\delta }(A)}{-log\delta },\end{array}$$

provided the limit exists, where $N_{\delta }(A)$ denotes the smallest number of sets of diameter at most $\delta$ that can cover A. If this limit does not exist, then the upper and the lower box dimension, respectively, are defined as

$$\begin{array}{cc}\hfill & {\overline{dim}}_{B}A=\underset{\delta \to 0}{lim\; sup}\frac{log{N}_{\delta }(A)}{-log\delta },\hfill \\ \hfill & {\underset{\_}{dim}}_{B}A=\underset{\delta \to 0}{lim\; inf}\frac{log{N}_{\delta }(A)}{-log\delta }.\hfill \end{array}$$

The following result is a special case of Theorem 3 in [8] applied to Lipschitz functions.

Theorem 2.2

Let $\mathrm{\Delta }=\left(x_0,,,x_1,,,\dots ,,,x_N\right)$ be a partition of $I=\left[x_0,,,x_N\right]$ satisfying $x_0<x_1<\cdots <x_N$ and let $\alpha =\left({\alpha }_1,,,{\alpha }_2,,,\dots ,,,{\alpha }_N\right)\in {(-1,1)}^N$. Assume that f and b are Lipschitz functions defined on I with $b\left(x_0\right)=f\left(x_0\right)$ and $b\left(x_N\right)=f\left(x_N\right)$. If the data points $\left\{\left(x_i,,,f,\left(x_i\right)\right),:,i,=,0,,,1,\dots ,,,N\right\}$ are not collinear, then

$$\begin{array}{c}\hfill {\text{dim}}_B(Gr(f_{\mathrm{\Delta },b}^{\alpha }))=\left\{\begin{array}{c}D,\text{if}{\sum }_{i=1}^N\left|{\alpha }_i\right|>1;\hfill \\ 1,\text{otherwise,}\hfill \end{array}\right)\end{array}$$

where $Gr(f_{\mathrm{\Delta },b}^{\alpha })$ denotes the graph of $f_{\mathrm{\Delta },b}^{\alpha }$ and D is the unique positive solution of the equation given as

$$\begin{array}{c}\hfill \sum _{i=1}^N\left|{\alpha }_i\right|a_i^{D-1}=1.\end{array}$$

COVID-19

Our objective is to understand the epidemic from a fractal point of view which will be a better method to analyze the growth of the virus. In that facet, we collected the data from India and constructed the $\alpha$-fractal interpolation function following the procedure mentioned before. The number of positive cases at a difference of forty days starting from 15th Nov 2021 is taken as shown in Table 1. All the data that is shown in Table 1 is gathered from ourworldindata.org [42].

Table 1.

Cases of Covid-19

S.No.	Date	$x_i$	$y_i$ (Number of positive cases)
0	15 Nov, 2021	0	8865
1	25 Dec, 2021	0.1	6987
2	3 Feb, 2022	0.2	149394
3	15 March, 2022	0.3	2876
4	24 April, 2022	0.4	2541
5	3 June, 2022	0.5	3962
6	13 July, 2022	0.6	20139
7	22 Aug, 2022	0.7	8586
8	1 Oct, 2022	0.8	3375
9	10 Nov, 2022	0.9	4517
10	20 Dec, 2022	1	132

Thus, the set of interpolation points is given by $\{(x_i,y_i):i=0,1,2,\cdots ,10\}$. In the first case base function b is taken to be line passing through $(x_0,y_0)$ and $(x_{10},y_{10})$, that is, $b(x)=-8733x+8865$ and germ function f is taken as

$$\begin{array}{c}\hfill f(x)=\left\{\begin{array}{ccc}-18780x+8865\hfill & \text{for}\hfill & 0\le x<0.1\hfill \\ 1424070x-135420\hfill & \text{for}\hfill & 0.1\le x<0.2\hfill \\ -1465180x+442430\hfill & \text{for}\hfill & 0.2\le x<0.3\hfill \\ -3350x+3881\hfill & \text{for}\hfill & 0.3\le x<0.4\hfill \\ 14210x-3143\hfill & \text{for}\hfill & 0.4\le x<0.5\hfill \\ 161770x-76923\hfill & \text{for}\hfill & 0.5\le x<0.6\hfill \\ -115530x+89457\hfill & \text{for}\hfill & 0.6\le x<0.7\hfill \\ -52110x+45063\hfill & \text{for}\hfill & 0.7\le x<0.8\hfill \\ 11420x-5761\hfill & \text{for}\hfill & 0.8\le x<0.9\hfill \\ -43850x+43982\hfill & \text{for}\hfill & 0.9\le x\le 1.\hfill \end{array}\right)\end{array}$$

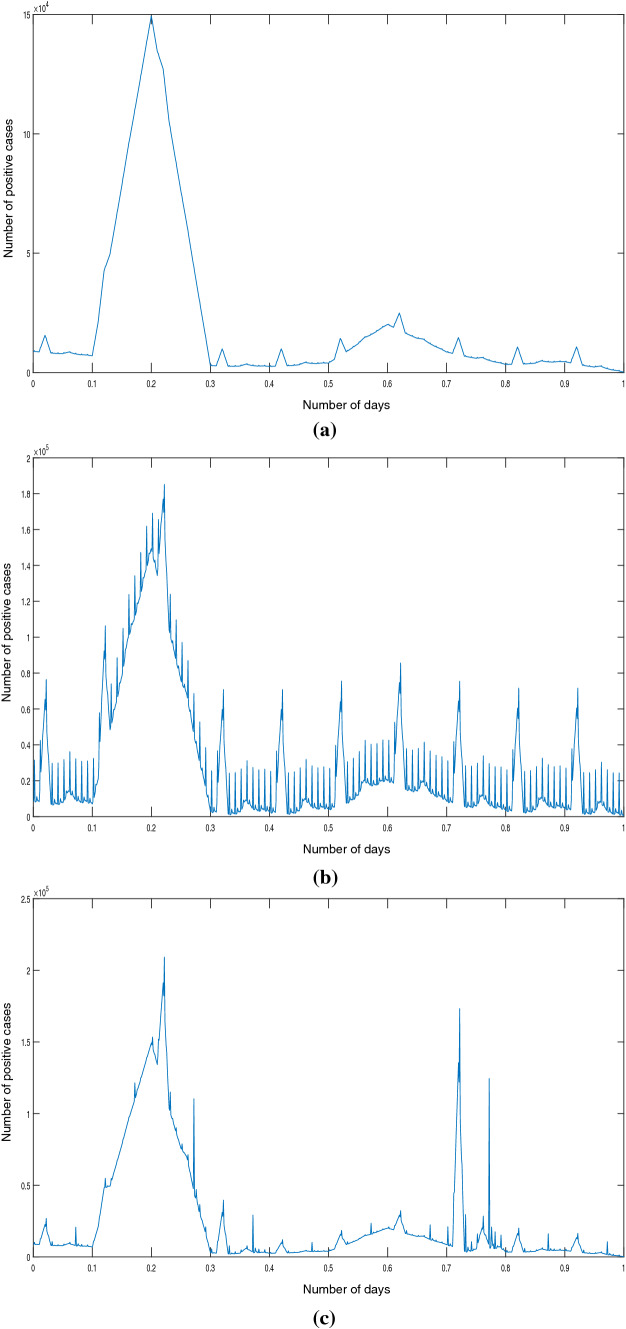
For $n\in \{1,2,\cdots ,10\}$, the function $L_n(x)=(0.1)x+x_{n-1},\text{where}x\in [0,1]$. Now by varying $\alpha ,$ the vector scale function, we get different fractal function represented in a graph. For $\alpha =0.05,$ its fractal function is represented in Fig. 1a. Again for $\alpha =0.4,$ its fractal function is represented in Fig. 1b. Now for $\alpha =(0.1,0.09,0.5,0.2,0.05,0.06,0.08,0.9,0.09,0.07),$ we get Fig. 1c.

Fig. 1.

a $f^{\alpha }$ when ${\alpha }_n=0.05\text{for}n\in \{1,2,\cdots ,10\}$ and ${\text{dim}}_B(Gr(f^{\alpha }))=1$. b $f^{\alpha }$ when ${\alpha }_n=0.4\text{for}n\in \{1,2,\cdots ,10\}$ and ${\text{dim}}_B(Gr(f^{\alpha }))=1.60$. c $f^{\alpha }$ when $\alpha =(0.1,0.09,0.5,0.2,0.05,0.06,0.08,0.9,0.09,0.07)$ and ${\text{dim}}_B(Gr(f^{\alpha }))=1.33$

Consider the germ function f given before and take base function b as a Bernstein polynomial $B_2(f)$ of order 2 written as

$$\begin{array}{c}\hfill b(x)=B_2(f)(x)={\mathrm{\Sigma }}_{k=0}^2\left(\begin{array}{c}2\\ k\end{array}\right)f(\frac{k}{2})x^k{(1-x)}^{2-k},\end{array}$$

that is,

$$\begin{array}{c}\hfill b(x)=1073x^2+(-9806)x+8865.\end{array}$$

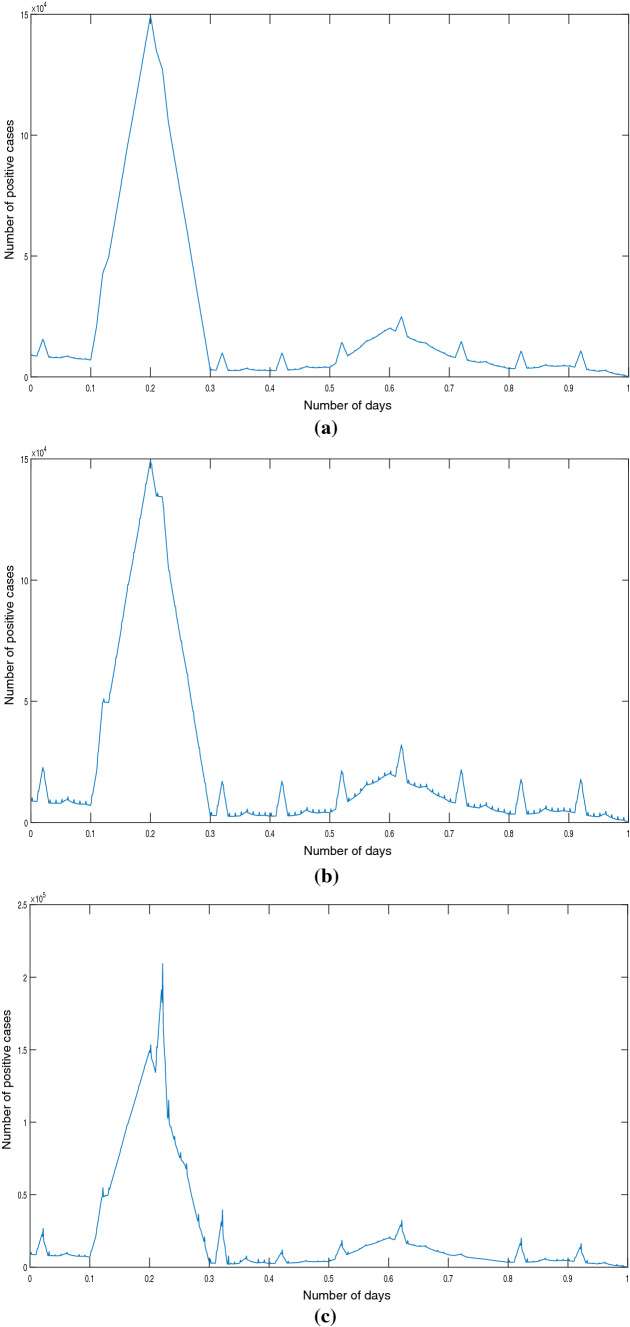
Now by varying $\alpha ,$ we get different fractal interpolations represented in a graph. As for $\alpha =0.05,$ we get Fig. 2a, and for $\alpha =0.1,$ we get Fig. 2b. Again for $\alpha =(0.1,0.09,0.5,0.2,0.05,0.06,0.08,0.01,0.09,0.07),$ the fractal function obtained is represented in Fig. 2c. Let us note the following:

• All functions $f_i$ and $b_i$ are Lipschitz functions for each $i=1,2,\cdots ,10.$

• The data set $\{(x_i,y_i):i=0,1,2,\cdots ,10\}$ are not collinear.

In view of the above, we can apply Theorem 2.2 to compute the fractal dimension of the graphs of the $\alpha$-fractal functions associated with these data set and considered functions to analyze fluctuation in the number of positive cases.

• In Fig. 1a, we have $a_i=0.1$ and ${\alpha }_i=0.05$. Since ${\sum }_{i=1}^{10}0.05=0.5\le 1,$ using Theorem 2.2, we get ${dim}_B(Gr(f_{\mathrm{\Delta },b}^{\alpha }))=1.$

• In Fig. 1b, we have $a_i=0.1$ and ${\alpha }_i=0.4$. Since ${\sum }_{i=1}^{10}0.4=4>1,$ using Theorem 2.2, we get ${dim}_B(Gr(f_{\mathrm{\Delta },b}^{\alpha }))=D,$ which is calculated as,

  $$\begin{array}{c}\hfill \sum _{i=1}^{10}(0.4)(\frac{1}{10}{)}^{D-1}=1\Rightarrow 4(\frac{1}{10}{)}^{D-1}=1\Rightarrow {10}^{D-1}=4.\end{array}$$

  After taking the log on both sides, we get

  $$D=1+2log2\approx 1.60.$$
• In Fig. 1c, we have $a_i=0.1$ and $\alpha =(0.1,0.09,0.5,0.2,0.05,0.06,0.08,0.9,0.09,0.07)$. Since ${\sum }_{i=1}^{10}|{\alpha }_i|=(0.1+0.09+0.5+0.2+0.05+0.06+0.08+0.9+0.09+0.07)=2.14>1,$ using Theorem 2.2, we get ${dim}_B(Gr(f_{\mathrm{\Delta },b}^{\alpha }))=D,$ which is calculated as,

  $$\begin{array}{cc}\hfill & (0.1+0.09+0.5+0.2+0.05+0.06+0.08+0.9\hfill \\ \hfill & +0.09+0.07)(\frac{1}{10}{)}^{D-1}=1\hfill \\ \hfill & \Rightarrow (2.14)(\frac{1}{10}{)}^{D-1}=1\Rightarrow {10}^{D-1}=2.14.\hfill \end{array}$$

  After taking the log on both sides, we get

  $$\begin{array}{c}\hfill D=1+log2.14\approx 1.33.\end{array}$$

• In Fig. 2a, we have $a_i=0.1$ and ${\alpha }_i=0.05$. Since ${\sum }_{i=1}^{10}0.05=0.5\le 1,$ using Theorem 2.2, we get ${dim}_B(Gr(f_{\mathrm{\Delta },b}^{\alpha }))=1.$

• In Fig. 2b, we have $a_i=0.1$ and ${\alpha }_i=0.1$. Since ${\sum }_{i=1}^{10}0.1=1\le 1,$ using Theorem 2.2, we get ${dim}_B(Gr(f_{\mathrm{\Delta },b}^{\alpha }))=1.$

• In Fig. 2c, we have $a_i=0.1$ and $\alpha =(0.1,0.09,0.5,0.2,0.05,0.06,0.08,0.01,0.09,0.07)$. Since ${\sum }_{i=1}^{10}|{\alpha }_i|=(0.1+0.09+0.5+0.2+0.05+0.06+0.08+0.01+0.09+0.07)=1.25>1,$ using Theorem 2.2, we get ${dim}_B(Gr(f_{\mathrm{\Delta },b}^{\alpha }))=D,$ which is calculated as,

  $$\begin{array}{cc}\hfill & (0.1+0.09+0.5+0.2+0.05+0.06\hfill \\ \hfill & +0.08+0.01+0.09+0.07)(\frac{1}{10}{)}^{D-1}=1\hfill \\ \hfill & \Rightarrow (1.25)(\frac{1}{10}{)}^{D-1}=1\Rightarrow {10}^{D-1}=1.25.\hfill \end{array}$$

  After taking the log on both sides, we get

  $$\begin{array}{c}\hfill D=1+log1.25\approx 1.10.\end{array}$$

Fig. 2.

a $f^{\alpha }$ when ${\alpha }_n=0.05\text{for}n\in \{1,2,\cdots ,10\}$ and ${\text{dim}}_B(Gr(f^{\alpha }))=1$. b $f^{\alpha }$ when ${\alpha }_n=0.1\text{for}n\in \{1,2,\cdots ,10\}$ and ${\text{dim}}_B(Gr(f^{\alpha }))=1$. c $f^{\alpha }$ when $\alpha =(0.1,0.09,0.5,0.2,0.05,0.06,0.08,0.01,0.09,0.07)$ and ${\text{dim}}_B(Gr(f^{\alpha }))=1.10$

A fractal operator

Let $f\in \mathcal{C}(I)$ be the germ function and let the base function $b=Lf$, where $L:\mathcal{C}(I)\to \mathcal{C}(I)$ be a bounded linear map such that $(Lf)(x_1)=x_1$, $(Lf)(x_N)=x_N$, and $Lf\ne f$. We shall denote the corresponding $\alpha$-fractal function by $f_{\mathrm{\Delta },L}^{\alpha }$. Let us fix the elements in the corresponding IFS, namely, the partition $\mathrm{\Delta }$, scale vector $\alpha$, and operator L. Let us note the following definition due to Navascués [24].

Definition 3.1

We refer to the transformation ${\mathcal{F}}_{\mathrm{\Delta },L}^{\alpha }={\mathcal{F}}^{\alpha }$ which assigns $f_{\mathrm{\Delta },L}^{\alpha }$ to f, as a $\alpha$-fractal operator or simply fractal operator with respect to $\mathrm{\Delta }$ and L.

Navascués [25, Theorem 3.3] proved the next theorem.

Theorem 3.2

Let ${|\alpha |}_{\infty }=max\{|{\alpha }_n|:n\in \{1,2,\cdots ,N\}\}$, and let Id be the identity operator on $\mathcal{C}(I)$.

1. For any $f\in \mathcal{C}(I)$, the perturbation error satisfies

   $$\Vert f^{\alpha }{-f\Vert }_{\infty }\le \frac{{|\alpha |}_{\infty }}{1-{|\alpha |}_{\infty }}{\Vert f-Lf\Vert }_{\infty }.$$
2. The fractal operator ${\mathcal{F}}^{\alpha }:\mathcal{C}(I)\to \mathcal{C}(I)$ is a bounded linear map. Further, the operator norm satisfies

   $$\Vert {\mathcal{F}}^{\alpha }||\le 1+\frac{{|\alpha |}_{\infty }}{1-{|\alpha |}_{\infty }}\Vert I_d-L\Vert .$$

3. For ${|\alpha |}_{\infty }<{\Vert L\Vert }^{-1}$, ${\mathcal{F}}^{\alpha }$ is bounded below. In particular, ${\mathcal{F}}^{\alpha }$ is an injective map.

4. ${|\alpha |}_{\infty }<(1+\Vert I_d-L\Vert {)}^{-1}$, then ${\mathcal{F}}^{\alpha }$ is a topological isomorphism (that is, bijective bounded map with bounded inverse). Moreover, $\Vert {({\mathcal{F}}^{\alpha })}^{-1}\Vert \le {\displaystyle \frac{1+{|\alpha |}_{\infty }}{1-{|\alpha |}_{\infty }\Vert L\Vert }}.$

5. For ${|\alpha |}_{\infty }<{\Vert L\Vert }^{-1}$, the fractal operator ${\mathcal{F}}^{\alpha }$ is not a compact operator.

Remark 3.3

According to item (1) of the previous theorem, the collection of maps $f_{\mathrm{\Delta },b}^{\alpha }$ constitutes continuous functions containing f as a particular case (for $\alpha =0$). Furthermore, the inequality therein reveals that by appropriate choice of the scale vector $\alpha$ or operator L, the fractal perturbation $f_{\mathrm{\Delta },b}^{\alpha }$ can be made close to the original function f. Thus, $f_{\mathrm{\Delta },b}^{\alpha }$ is a simultaneously interpolating and approximating fractal function to f.

Let $f\in \mathcal{C}(I).$ The Bernstein polynomial $B_n(f)$ of order n is defined as

$$\begin{array}{c}\hfill B_n(f)(x):=\sum _{k=0}^n\left(\begin{array}{c}n\\ k\end{array}\right)f(\frac{k}{n})x^k{(1-x)}^{n-k}.\end{array}$$

Note 1 Let us note the following:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill B_n(f)(x)=& \sum _{k=0}^n\left(\genfrac{}{}{0pt}{}{n}{k}\right)x^k{(1-x)}^{n-k}f(\frac{k}{n}).\hfill \end{array}\end{array}$$

Choosing $f=1,$ we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill B_{n}1(x)& =\sum _{k=0}^n\left(\genfrac{}{}{0pt}{}{n}{k}\right)x^k{(1-x)}^{n-k}=1.\hfill \end{array}\end{array}$$

This implies that $\Vert B_n\Vert \ge 1$ and $\Vert B_n^m\Vert \ge 1.$ Now, for every $f\in \mathcal{C}(I),$ we get

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill B_n(f)(x)& \le {\Vert f\Vert }_{\infty }\sum _{k=0}^n\left(\genfrac{}{}{0pt}{}{n}{k}\right)x^k{(1-x)}^{n-k}={\Vert f\Vert }_{\infty }.\hfill \end{array}\end{array}$$

Since the Bernstein operator $B_n$ is a linear positive operator, the previous inequality gives

$$\begin{array}{c}\hfill \begin{array}{c}\hfill B_n^m(f)(x)\le {\Vert f\Vert }_{\infty },\end{array}\end{array}$$

which produces $\Vert B_n^m\Vert \le 1.$ Therefore, we have $\Vert B_n^m\Vert =1$ for all $m\in \mathbb{N}.$ We know that for a bounded linear operator T and the operator norm $\Vert .\Vert$, the spectral radius $\rho (T)$ of T is given by

$$\begin{array}{c}\hfill \rho (T)=\underset{k\to \infty }{lim}{\Vert T^k\Vert }^{\frac{1}{k}}.\end{array}$$

Since $\Vert B_n^m\Vert =1,\forall m\in \mathbb{N},$ we have

$$\begin{array}{c}\hfill \rho (B_n)=\underset{m\to \infty }{lim}{\Vert B_n^m\Vert }^{\frac{1}{m}}=1.\end{array}$$

Adjoint of ${\mathcal{F}}^{\alpha }$ on ${\mathcal{L}}^2(I)$

We now consider the Banach space of functions with finite energy:

$$\begin{array}{c}\hfill {\mathcal{L}}^2{(I)=\{g:I\to \mathbb{R}:g\text{is}\text{measurable}\text{and}\Vert g\Vert }_2<\infty \},\end{array}$$

where the norm is defined by

$$\begin{array}{cc}\hfill {\Vert g\Vert }_2& ={\left({\int }_I,{|g(x)|}^2,,\text{d},x\right)}^{1/2}.\hfill \end{array}$$

Note that the space ${\mathcal{L}}^2(I)$ is in fact a Hilbert space with respect to the inner product

$$\begin{array}{c}\hfill ⟨g,h⟩={\int }_{I}g(x)h(x)\text{d}x,\text{for}g,h\in {\mathcal{L}}^2(I).\end{array}$$

It is worth to note that the construction of fractal functions in ${\mathcal{L}}^2(I)$ was initiated by Prof. Navascués in her work [25], wherein she also showed that every complex-valued square integrable function defined in a real bounded interval can be well approximated by a complex fractal function. Let $f\in {\mathcal{L}}^2(I)$. To construct the fractal function in ${\mathcal{L}}^2(I)$ corresponding to f, there are two approaches in the literature. One is to apply the density of $\mathcal{C}(I)$ in ${\mathcal{L}}^2(I)$ to obtain a fractal analog of $f\in {\mathcal{L}}^2(I)$ using $\alpha$-fractal functions corresponding to continuous functions; see, for instance, [25]. Though this approach is natural and elementary, the self-referentiality of the fractal analog of $f\in {\mathcal{L}}^2(I)$ is not evident in this case. Using another approach due to Massopust ([23, Theorem 2]), one may easily deduce the next theorem.

Theorem 3.4

Let $f\in {\mathcal{L}}^2(I)$ be chosen arbitrarily and held fixed. Suppose that $\mathrm{\Delta }=\{x_i:i=0,1,2,\cdots ,N\}$ is a partition of I satisfying $x_0<x_1<x_2<\cdots <x_N$, $I_i^{\ast }:=[x_i,x_{i+1})$ for $i=0,1,2,\cdots ,N-2$ and $I_{N-1}^{\ast }:=[x_{N-1},x_N]$. Let $L_i:[x_0,x_N)\to I_i^{\ast }$ be affine maps satisfying $L_i(x_0)=x_i$ and $L_i(x_N^{-})=x_{i+1}$ for $i\in \{0,1,2,\cdots ,N-2\}$. Further suppose that $L_{N-1}:I\to I_{N-1}^{\ast }$ is an affinity satisfying $L_{N-1}(x_0)=x_{N-1}$ and $L_{N-1}(x_N)=x_N$. Let the affinities be given by $L_i(x)=a_{i}x+b_i$ for $i\in J:=\{0,1,2,\cdots ,N-1\}$. Fix ${\alpha }_i\in (-1,1)$ for all $i\in J$ and $b\in {\mathcal{L}}^2(I)$. Define $T:{\mathcal{L}}^2(I)\to {\mathcal{L}}^2(I)$ by

$$\begin{array}{cc}\hfill Tg(x)& =f(x)+{\alpha }_i(L_i^{-1}(x))[g(L_i^{-1}(x))-b(L_i^{-1}(x))],\hfill \\ \hfill & x\in I_i^{\ast },i\in J.\hfill \end{array}$$

If the scaling factors ${\alpha }_i$, $i\in J$ satisfy $[{\sum }_{i\in J}{a}_i{\alpha }_i^2{]}^{1/2}<1$, then the operator T is a contraction on ${\mathcal{L}}^2(I)$. Furthermore, the corresponding unique fixed point $f_{\mathrm{\Delta },b}^{\alpha }$ (denoted for notational convenience by $f^{\alpha }$) in ${\mathcal{L}}^2(I)$ satisfies the self-referential equation:

$$f^{\alpha }(x)=f(x)+{\alpha }_i(f^{\alpha }-b)(L_i^{-1}(x)),x\in I_i^{\ast },i\in J.$$

Note 2 Let $L:{\mathcal{L}}^2(I)\to {\mathcal{L}}^2(I)$ be a bounded linear operator $L\ne I$. Taking $b=Lf$, in the previous theorem, one obtains fractal function $f^{\alpha }=f_{\mathrm{\Delta },L}^{\alpha }$ corresponding to the germ function $f\in {\mathcal{L}}^2(I)$. Further, a bounded linear operator ${\mathcal{F}}^{\alpha }:{\mathcal{L}}^2(I)\to {\mathcal{L}}^2(I)$, $f\mapsto f^{\alpha }$ arise.

Let ${\mathcal{F}}^{\alpha }:{\mathcal{L}}^2(I)\to {\mathcal{L}}^2(I)$ be the aforementioned fractal operator. The adjoint of the fractal operator is defined by

$$⟨{\mathcal{F}}^{\alpha }(f),g⟩=⟨f,{({\mathcal{F}}^{\alpha })}^{\ast }(g)⟩.$$

In what follows we attempt to obtain an expression for ${({\mathcal{F}}^{\alpha })}^{\ast }.$

$$\begin{array}{c}\hfill \begin{array}{cc}& ⟨{\mathcal{F}}^{\alpha }(f),g⟩=⟨f^{\alpha },g⟩\hfill \\ \hfill & ={\int }_I{f}^{\alpha }(x)g(x)\text{d}x\hfill \\ \hfill & =\sum _{n=0}^{N-1}{\int }_{I_n}[f(x)+{\alpha }_n(f^{\alpha }-Lf)\circ L_n^{-1}(x)]g(x)\text{d}x\hfill \\ \hfill & ={\int }_{I}f(x)g(x)\text{d}x+\sum _{n=0}^{N-1}{\alpha }_n{\int }_{I_n}(f^{\alpha }-Lf)\circ L_n^{-1}(x)g(x)\text{d}x.\hfill \end{array}\end{array}$$

With the change of variable $L_n^{-1}(x)=t$ for the second term on the right-hand side, we have

$$\begin{array}{c}\hfill \begin{array}{cc}& {\int }_{I_n}(f^{\alpha }-Lf)\circ L_n^{-1}(x)g(x)\text{d}x\hfill \\ \hfill & =a_n{\int }_I(f^{\alpha }-Lf)(t)g(L_n(t))\text{d}t.\hfill \\ \hfill & =a_n{\int }_I{f}^{\alpha }(t)g(L_n(t))\text{d}t-a_n{\int }_I(Lf)(t)g(L_n(t))\text{d}t.\hfill \end{array}\end{array}$$

From the previous equations

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill ⟨f^{\alpha },g⟩& =⟨f,g⟩+\sum _{n=1}^{N-1}{\alpha }_n{a}_n[⟨f^{\alpha },g\circ L_n⟩-⟨Lf,g\circ L_n⟩].\hfill \\ \hfill & =⟨f,g⟩+\sum _{n=0}^{N-1}{\alpha }_n{a}_n[⟨f,g\circ L_n⟩+\sum _{m=1}^{N-1}{\alpha }_m{a}_m\hfill \\ \hfill & \{⟨f^{\alpha },g\circ L_n\circ L_m⟩-⟨Lf,g\circ L_n\circ L_m⟩\}-⟨Lf,g\circ L_n⟩].\hfill \end{array}\end{array}$$

Expanding the terms to infinite times and writing $L^{\ast }$ as the adjoint operator of L we get

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill ⟨f^{\alpha },g⟩=& ⟨f,g⟩-\sum _{k_1=0}^{N-1}{\alpha }_{k_1}{a}_{k_1}\hfill \\ \hfill & [⟨f,L^{\ast }g\circ L_{k_1}⟩+\sum _{k_2=0}^{N-1}{\alpha }_{k_2}{a}_{k_2}\{⟨f,L^{\ast }g\circ L_{k_1}\circ L_{k_2}⟩\hfill \\ \hfill & +\sum _{k_3=0}^{N-1}{\alpha }_{k_3}{a}_{k_3}(⟨f,L^{\ast }g\circ L_{k_1}\circ L_{k_2}\circ L_{k_3}⟩+\cdots )\}]\hfill \\ \hfill & +\sum _{k_1=0}^{N-1}{\alpha }_{k_1}{a}_{k_1}[⟨f,g\circ L_{k_1}⟩\hfill \\ \hfill & +\sum _{k_2=0}^{N-1}{\alpha }_{k_2}{a}_{k_2}\{⟨f,g\circ L_{k_1}\circ L_{k_2}⟩\hfill \\ \hfill & +\sum _{k_3=0}^{N-1}{\alpha }_{k_3}{a}_{k_3}(⟨f,g\circ L_{k_1}\circ L_{k_2}\circ L_{k_3}⟩+\cdots )\}].\hfill \end{array}\end{array}$$

That is

$$\begin{array}{c}\hfill \begin{array}{cc}& ⟨f^{\alpha },g⟩\hfill \\ \hfill & =\langle f,g-\sum _{k_1=0}^{N-1}{\alpha }_{k_1}{a}_{k_1}[L^{\ast }g\circ L_{k_1}\hfill \\ \hfill & +\sum _{k_2=0}^{N-1}{\alpha }_{k_2}{a}_{k_2}\{L^{\ast }g\circ L_{k_1}\circ L_{k_2}\hfill \\ \hfill & +\sum _{k_3=0}^{N-1}{\alpha }_{k_3}{a}_{k_3}(L^{\ast }g\circ L_{k_1}\circ L_{k_2}\circ L_{k_3}+\cdots )\}]\hfill \\ \hfill & +\sum _{k_1=0}^{N-1}{\alpha }_{k_1}{a}_{k_1}[g\circ L_{k_1}+\sum _{k_2=0}^{N-1}{\alpha }_{k_2}{a}_{k_2}\{g\circ L_{k_1}\circ L_{k_2}\hfill \\ \hfill & +\sum _{k_3=0}^{N-1}{\alpha }_{k_3}{a}_{k_3}(g\circ L_{k_1}\circ L_{k_2}\circ L_{k_3}+\cdots )\}]\rangle \hfill \\ \hfill & =\langle f,{(F^{\alpha })}^{\ast }(g)\rangle .\hfill \end{array}\end{array}$$

Consequently, we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {({\mathcal{F}}^{\alpha })}^{\ast }(g)=& g-\sum _{k_1=0}^{N-1}{\alpha }_{k_1}{a}_{k_1}\hfill \\ \hfill & [L^{\ast }g\circ L_{k_1}+\sum _{k_2=0}^{N-1}{\alpha }_{k_2}{a}_{k_2}\{L^{\ast }g\circ L_{k_1}\circ L_{k_2}\hfill \\ \hfill & +\sum _{k_3=0}^{N-1}{\alpha }_{k_3}{a}_{k_3}(L^{\ast }g\circ L_{k_1}\circ L_{k_2}\circ L_{k_3}+\cdots )\}]\hfill \\ \hfill & +\sum _{k_1=0}^{N-1}{\alpha }_{k_1}{a}_{k_1}[g\circ L_{k_1}+\sum _{k_2=0}^{N-1}{\alpha }_{k_2}{a}_{k_2}\{g\circ L_{k_1}\circ L_{k_2}\hfill \\ \hfill & +\sum _{k_3=0}^{N-1}{\alpha }_{k_3}{a}_{k_3}(g\circ L_{k_1}\circ L_{k_2}\circ L_{k_3}+\cdots )\}].\hfill \end{array}\end{array}$$

Further simplification provides the following expression for ${({\mathcal{F}}^{\alpha })}^{\ast }(g)$

$$\begin{array}{c}\hfill g+(I-L^{\ast })(\sum _{m=1}^{\infty }(\sum _{k_1=0}^{N-1}\sum _{k_2=0}^{N-1}\cdots \sum _{k_m=0}^{N-1}{\alpha }_{k_1}{a}_{k_1}{\alpha }_{k_2}{a}_{k_2}\cdots {\alpha }_{k_m}{a}_{k_m}g\circ L_{k_1}\circ L_{k_2}\circ \cdots \circ L_{k_m})).\end{array}$$

Since ${(A+B)}^{\ast }=A^{\ast }+B^{\ast }$, we get the following expression for ${({\mathcal{F}}^{\alpha })}^{\ast }(g)$

$$\begin{array}{c}\hfill \begin{array}{cc}& g+{(I-L)}^{\ast }(\sum _{m=1}^{\infty }(\sum _{k_1=0}^{N-1}\sum _{k_2=0}^{N-1}\cdots \hfill \\ \hfill & \sum _{k_m=0}^{N-1}{\alpha }_{k_1}{a}_{k_1}{\alpha }_{k_2}{a}_{k_2}\cdots {\alpha }_{k_m}{a}_{k_m}g\circ L_{k_1}\circ L_{k_2}\circ \cdots \circ L_{k_m})).\hfill \end{array}\end{array}$$

Remark 3.5

Let us assume that the scaling vector is constant and the partition is equidistant. In this case, with the help of the above expression for the adjoint operator, we could deduce that the fractal operator turns out to be a topological isomorphism for a slightly wider range of values of the scaling factors than that prescribed in [25, Theorem 4.10]. It should also be noted that we may get better results for a fractal operator associated with non-stationary fractal functions [17, 27, 35] via the adjoint operator. To keep the article at a reasonable length we avoid the details.

Remark 3.6

Since fractal functions in ${\mathcal{L}}^2(I)$ can be discontinuous, we can use this space to model more natural phenomena with the help of fractal interpolation theory.

Concluding remarks and future directions

In this article, we computed the exact value of the box dimension of the graphs of the constructed $\alpha -$fractal functions generated by the COVID-19 data over some specific time period. We also provided an expression for the adjoint operator of the associated fractal operator in terms of an infinite series. Calculating the fractal dimension of the epidemic curve is a new approach for observing the epidemic and retrieving the missing information via fractal functions. The higher the dimension of the graph of the epidemic curve, the higher the complexity of the distribution of the COVID-19 virus and it is affected by the parameter in the surrounding. In the future, we will try to estimate other fractal dimensions such as the Hausdorff dimension and Assouad dimension of the $\alpha$-fractal functions. As the Assouad dimension gives more local information, estimating this dimension for fractal functions generated by COVID-19 data may help us to understand the spread of the virus in a better way. We believe that our method of using fractal dimension and $\alpha$-fractal functions can be used to study fluctuations or randomness in the stock market and heart rate.

Author contribution statement

All authors contributed equally to this manuscript.

Funding

The first author is financially supported by MHRD Fellowship at the Indian Institute of Information Technology (IIIT), Allahabad.

Data Availability

This manuscript has associated data in a data repository. [Author’s comment: We have taken COVID-19 data from https://ourworldindata.org/covid-cases.]

Declarations

Conflict of interest

We declare that we do not have any conflict of interest.