Accurate Prediction of Enzyme Thermostabilization with Rosetta Using AlphaFold Ensembles

Abstract

Thermostability enhancement is a fundamental aspect of protein engineering as a biocatalyst’s half-life is key for its industrial and biotechnological application, particularly at high temperatures and under harsh conditions. Thermostability changes upon mutation originate from modifications of the free energy of unfolding (ΔG_u), making thermostabilization extremely challenging to predict with computational methods. In this contribution, we combine global conformational sampling with energy prediction using AlphaFold and Rosetta to develop a new computational protocol for the quantitative prediction of thermostability changes upon laboratory evolution of acyltransferase LovD and lipase LipA. We highlight how using an ensemble of protein conformations rather than a single three-dimensional model is mandatory for accurate thermostability predictions. By comparing our approaches with existing ones, we show that ensembles based on AlphaFold models provide more accurate and robust calculated thermostability trends than ensembles based solely on crystallographic structures as the latter introduce a strong distortion (scaffold bias) in computed thermostabilities. Eliminating this bias is critical for computer-guided enzyme design and evaluating the effect of multiple mutations on protein stability.

1. Introduction

Enzymes’ thermostability is a fundamental property in the design and optimization of biocatalytic processes.¹ By increasing the thermostability of the enzyme, the target biocatalytic transformation can be carried out at higher temperatures, which entails a series of advantages in terms of substrate solubility and enzyme productivity under harsh conditions, ultimately translating into a commercial advantage.² The study of thermophilic enzymes has helped outlining structural factors that are key for determining protein thermostability, highlighting rigidity as a major player. Thermophilic enzymes show reduced flexibility and improved packing of the core regions over their mesophilic counterparts, which stabilize the native folded state and allow them to maintain their function at higher temperatures.^3,4 This observation has been corroborated by a number of successful thermostabilization campaigns carried out with different enzyme engineering strategies.⁵⁻¹²

Directed evolution is currently the most successful approach to enzyme engineering. It involves an iterative procedure wherein a large number of variants are screened at each round, followed by selection of the variant that optimizes the target property the most, which is then used as a starting point for the next iteration.¹³ This approach allows an effective exploration of the enzyme’s fitness landscape as selected variants at each round are increasingly more active, but it is resource-intensive as improved variants are identified at the price of exploring a large number of ineffective ones. A different approach to enzyme engineering is rational design, which uses structural information (X-ray, cryo-electron microscopy, and NMR structures) to restrict the number of explored variants to a smaller pool, thus reducing the number of ineffective variants. Despite several successes, rational design seldom produces as highly active variants as directed evolution.¹³

The screening/selection criterion used in directed evolution to quantify the catalytic activity of explored variants is usually based on monitoring substrate consumption or product formation by the enzymatic reaction. Catalytic activity is the result of not only thermostability but also several concurring factors, including the level of preorganization of the enzyme’s active site; the binding affinity toward substrates, intermediates, and products that can lead to inhibition; and the presence of competing reactions to cite a few. For this reason, the relationship between activity and thermostability is complex and enzyme-dependent. While in some cases thermostabilization comes at the cost of activity, particularly when thermostability and catalysis make opposite demands on enzyme flexibility, in other cases, the explicit evolutionary pressure for maximizing product yield results in thermostabilization.¹⁴⁻¹⁶

Several parameters can be used to quantify thermostability, including the free energy of unfolding ΔG_u, the melting temperature T_M, and the thermal inactivation temperature T₅₀.¹⁷⁻¹⁹ ΔG_u corresponds to the free-energy difference between the denatured and native states at a given temperature.²⁰ Of particular interest for protein engineering is measuring thermal unfolding, that is, the transition between native and denatured states as a function of the applied heat. This process is highly endothermic since the denatured state has inherently higher configurational entropy and less negative enthalpy than the native state and is commonly measured with differential scanning calorimetry by monitoring the heat capacity of the protein as it is heated through its melting transition. The melting temperature T_M is identified as the temperature corresponding to the maximum heat uptake, where ΔG_u is 0 and the folded and unfolded states are equally populated (eq 1)²⁰

1

Thus, T_M is the ratio of enthalpy and entropy of unfolding, providing a different measure of stability than ΔG_u. Considering thermostability changes between variants (ΔΔG_u,mut), mutations that induce a non-zero change in ΔG_f also produce a change in T_M, but the proportionality between the two quantities depends on both the protein and the identity of the mutations.¹⁹T₅₀ values provide a way to quantify enzymes’ stability as the temperature at which half of the protein irreversibly denatured after incubation for a fixed amount of time. Because denaturation is irreversible, T₅₀ values do not measure thermodynamic equilibrium properties and as such do not generally correlate with ΔG_u.²¹

Several structure-based computational approaches have been developed to estimate the ΔΔG_u,mut (unfolding) or ΔΔG_f,mut (folding) associated with mutations. Two popular approaches are Rosetta ddg(22−24) and FoldX.²⁵ In both cases, the effect of mutations on the folding free energy is evaluated locally, that is, assessing how the protein interaction network is changed at the mutated position and its close surroundings, leaving the rest of the system unperturbed. This is motivated by the assumption that taken individually, mutations generally exert only a local effect on the protein structure and have a very small impact on stability (|ΔΔG_f,mut| < 1 kcal mol^–1).²⁶ For single mutations, ΔΔG_f,mut values can be exceeded by energy changes elicited by differences in the global structures if the reference and mutant protein are obtained separately.^22,27 For this reason, ddg and FoldX are standard approaches for evaluating the thermostabilizing effect of single mutations.

However, when a variant accumulates multiple mutations, |ΔΔG_f,mut| increases and mutations cannot be assumed to act independently but rather cooperatively or anti-cooperatively and can alter the protein structure beyond the extent that can be predicted with local sampling.²⁸⁻³⁰ The Rosetta³¹ suite developed by Baker’s group offers a variety of Monte Carlo-based applications that by performing global optimization can refine the native structure of a given sequence. In this work, we used the relax application, which performs cycles of side chain repacking and gradient-based minimization, for evaluating energy differences between variants and hence their relative thermostability.³² Using relax, models derived from crystallographic structures or AlphaFold predictions are optimized under the Rosetta energy function ref15.

All the aforementioned approaches require a model of the protein’s structure as a starting point for the simulations, which is normally provided by crystallography. As crystallographic structures are not always complete, unresolved regions need to be modeled with high accuracy for analyzing mutation effects. This modeling can be critical to the success of the study as flexible loop conformations can play important roles in the overall proficiency of the enzyme, for instance, fine-tuning substrate binding and product release.³³⁻³⁶

The artificial intelligence-based AlphaFold algorithm³⁷ (AF) released by DeepMind in 2021 has rapidly revolutionized how the structural biology community confronts protein structure problems by providing an alternative route to crystallography for obtaining accurate protein structures at a fraction of the cost and infrastructure required by experimental methods. Despite this extraordinary advance, AF models share part of the weakness of crystallographic structures regarding flexible regions.^37,38 AF relies on the analysis of multiple sequence alignments to generate the three-dimensional models and evaluates the quality of the prediction using a local (residue-based) score. Flexible loops are often the least conserved and structured parts of a protein and as such accumulate the highest uncertainty.^39,40

With this background in mind, we set out to develop a computational method for predicting protein thermostabilization based on ensembles generated from AF models. We present this approach and compare its performance with Rosetta ddg for the Monacolin J acid acyltransferase LovD and Lipase A LipA. LovD, which has been the object of a number of studies from our group, has been evolved through directed evolution by Tang and co-workers in collaboration with Codexis, Inc. for maximizing the production of simvastatin, a blockbuster drug for controlling cholesterol levels in the blood.^16,34,41 The directed evolution campaign produced nine variants (LovD1-9), accumulating 29 mutations in total. We measured the T_M of each variant,¹⁶ shown in Table 1 along with the number of mutations introduced at each round (see Table S1 for further details). Thermostability increases monotonically along the first six rounds of directed evolution, with LovD6 being the most thermostable variant, and is slightly reduced over the three final rounds. These T_M values represent the reference for evaluating the performance of the tested computational approaches.

Table 1. Engineered LovD Variants.

name	number of mutations	TM (°C)
LovD		38.5
LovD1	1	39.5
LovD2	6	44.0
LovD3	7	44.3
LovD4	9	45.0
LovD5	15	46.0
LovD6	20	52.0
LovD7	23	49.0
LovD8	25	49.3
LovD9	29	50.8

2. Methods

2.1. Generation of Crystallographic Scaffolds from X-ray Structures

Variant models were built using the protocol outlined in Figure S1. When needed, missing residues were modeled so that all initial structures have the same number of amino acids. Coordinates for missing loops (in LovD variants) were grafted among different crystallographic structures (see the next section for details). When needed, structures were reverted to the wild-type sequence by removing the side chains of mutated residues and using Rosetta score_jd2 application to replace the side chain of the native residue. The resulting wild-type models were pre-relaxed using the minimize_with_cst application. This application performs a geometry optimization of the structure enforcing harmonic constraints between all pairs of α carbons whose distance is below 9 Å. This corrects suboptimal residue geometries in the X-ray structure to make it a local minimum under the Rosetta energy function while ensuring maximal fidelity to the parent crystallographic structure. The same side chain replacement approach with Rosetta score_jd2 application is used to generate initial structures of the variants from the wild-type models.

2.2. Modeling of Missing Loops and N-Terminus

Missing residues 1–9 of structure 3HLB (LovD) were grafted from the crystallographic structure 3HLC of S5, a variant outside the set considered in this paper.⁴² Missing residues 1–10 and 163–171 of structure 4LCL (LovD6) were grafted from structures 3HLC and 4LCM, respectively. Missing residues 1–11 and 257–265 of structure 4LCM were grafted from structures 3HLC and 4LCL, respectively.

2.3. Thermostability Evaluation

For evaluating thermostability, we evaluated variants’ relative energies with Rosetta⁴³ under the assumption that when comparing two variants, the one that shows the lower energy is more thermostable. We employed ref15, the default energy function in Rosetta since 2017. This is a combination of physics-based and statistical potentials parameterized on crystallographic structures to be minimal at the native folded state of a given sequence.⁴⁴ We chose this energy function as Rosetta is one of the most successful suites for protein design, spanning from antibodies⁴⁵ to enzymes⁴⁶ to new-to-Nature folds.⁴⁷

Benchmarking of the prediction accuracy was performed using Pearson’s correlation coefficient. To evaluate the stabilizing/destabilizing effect of mutations, we evaluated the folding free-energy difference ΔΔG_f,mut between each engineered variant and the wild-type. As the ref15 energy function provides an estimate of ΔG_f (folding free energy), we computed ΔΔG_f,mut values for each variant according to eq 2

2

ΔΔG_f,mut values were correlated with ΔT_M values, computed for each variant as the difference between its T_M and that of the wild-type. Within this framework, negative ΔΔG_f,mut values indicate a more thermostable variant, and positive ΔΔG_f,mut values indicate a less thermostable variant than the wild-type enzyme. It follows that the expected result is a negative correlation, with more thermostable variants showing negative ΔΔG_f,mut and positive ΔT_M with respect to the wild-type.

2.4. Rosetta Calculations

All Rosetta calculations were performed with version 3.13.

The following flags were used to perform Rosetta ddg calculations:

For each variant, 500 independent ddg runs were performed and, following the recommended protocol, ΔΔG_f,mut values were computed as the difference between the averages of the three top scoring decoys for each variant and the wild-type; since ddg always calculates the energy of the wild-type together with that of the requested mutant, a total of 500 runs × 9 variants = 4500 decoys were generated for the wild-type.

The following flags were used to perform Rosetta relax calculations:

The following flags were used to perform Rosetta minimize calculations:

2.5. AlphaFold Calculations

All AlphaFold (AF) calculations were performed with the 2.2.2 version and the following options for monomer predictions:

The following options were used for multimer predictions:

2.6. Kernel Density Estimates

Kernel density estimates (KDEs) were computed with Scikit-learn using a Gaussian kernel.⁴⁸ The optimal bandwidth (h) for each set of data was estimated according to eq 3, where n is the number of datapoints and σ is their standard deviation⁴⁹

3

KDEs were calculated and represented using the following code, where values_for_kernel is an array of Rosetta energy values:

3. Results and Discussion

3.1. Thermostabilization Prediction with Rosetta ddg

To set a baseline of thermostability trend prediction accuracy, we first predicted LovD variants’ thermostabilization using Rosetta ddg.²² As mentioned in the introduction, ddg relies on the use of a starting structure for the reference sequence—which in our case is the wild-type LovD enzyme—that is usually crystallographic. Among the available X-ray structures for LovD variants, we considered those deposited with PDB IDs 3HLB, 3HLF, 4LCL, and 4LCM corresponding to apo LovD,⁵⁰ simvastatin-bound LovD,⁵⁰apo LovD6,³⁴ and apo LovD9,³⁴ respectively (Figure 1).

Figure 1.

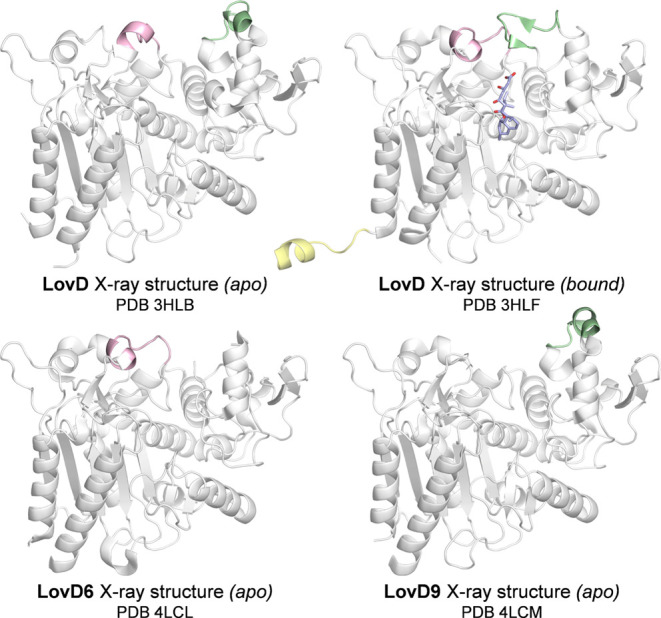
X-ray structures of LovD variants. Flexible loops encompassing residues 162–170 (in green) and 257–265 (in pink) and the 1–11 N-terminus (in yellow) are highlighted.

Analysis of these crystallographic structures reveals (i) that the evolved variants show only small structural differences from the wild-type (all-atom RMSD values of 1.84 and 1.19 Å with respect to the wild-type for LovD6 and LovD9, respectively) and (ii) the presence of highly flexible loops. Residues 162–170 form a loop that is not resolved in the LovD6 structure and that undergoes an important transition from an “open” conformation for LovD in the apo state to a “closed” conformation in the simvastatin-bound state, where this loop closes over the active site. In a similar manner, residues 257–265 are not resolved in the crystallographic structure of LovD9 and assume different conformations in the remaining structures. Additionally, the flexible N-terminus (residues 1–11) is solved only in the simvastatin-bound LovD structure.

In order to evaluate thermostability trends obtained with ddg from these four structures, unresolved regions were grafted among different PDBs, and the resulting complete models reverted to the wild-type sequence and pre-relaxed with Rosetta minimize_with_cst application (see Methods and Figure S1 for further details), yielding scaffolds 3HLB′, 3HLF′, 4LCL′, and 4LCM′.

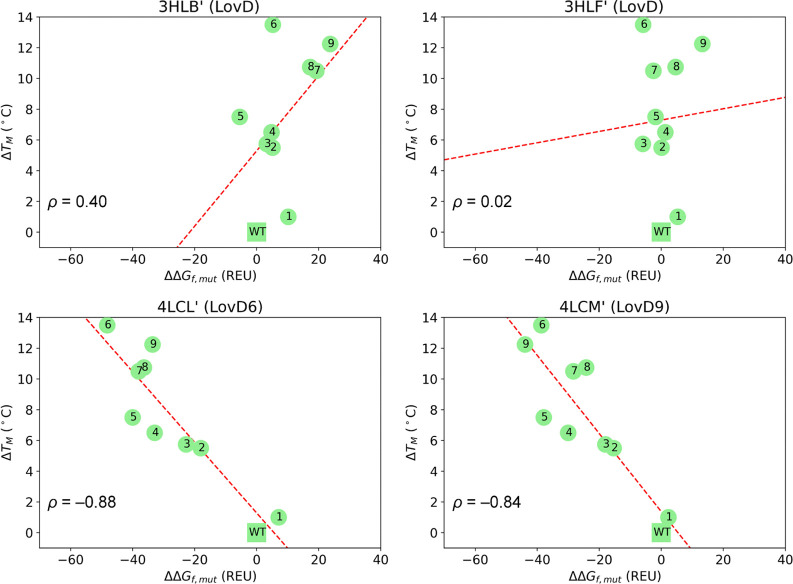
Figure 2 shows the thermostability trends computed for LovD1-9 with ddg (500 runs) using as starting scaffolds each of the four models derived from the crystallographic structures. The results clearly indicate that the choice of the reference structure imposes a large bias on the calculated thermostability trends. When either LovD structure is used (3HLB′, 3HLF′), we obtain no correlation between ΔΔG_f,mut values computed with ddg and ΔT_M values, while we obtain moderate to good negative correlation when the structures of LovD6 (4LCL′) and LovD9 (4LCM′) are used. Both ΔΔG_f,mut values and Pearson’s correlation coefficients are essentially converged after 200 runs (see Figure S2 and Table S2).

Figure 2.

Representation of ΔT_Mvs ΔΔG_f,mut for LovD1-9 variants computed with respect to the wild-type (WT) as the average of the three top scoring decoys from 500 ddg runs starting from crystallographic structures. ρ = Pearson’s correlation coefficient. Dashed red line: linear regression.

The lack of correlation for the model derived from the fully solved simvastatin-bound LovD structure rules out the possibility that the observed trends are an artifact deriving from the modeling of unresolved regions. Also, the (lack of) correlation is independent of the quality of the crystallographic coordinates (i.e., structure 3HLF is solved at 2.00 Å and provides no correlation, while structure 4LCM is solved at 3.19 Å and provides a good correlation). We use the term scaffold bias to describe this dependence of computed ΔΔG_f,mut trends on the reference structure used in the calculation, and attribute it to a sampling deficiency, that is, the inability of ddg to move the mutated structure away from the local free-energy minimum represented by each crystallographic scaffold. Thus, even if the four crystallographic structures look extremely similar to the human eye, their three-dimensional coordinates encode differences that translate into divergent computed thermostability trends.

3.2. Thermostabilization Prediction with Rosetta Relax on Crystallographic Structures

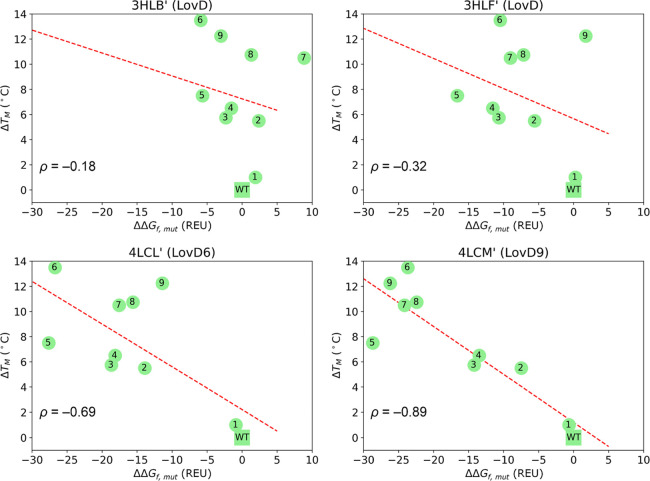
To assess whether a protocol involving global sampling could cure the scaffold bias and converge the thermostability trends calculated from the four crystallographic structures, we recomputed ΔΔG_f,mut values using Rosetta relax application. Starting from each scaffold, we generated initial models for all LovD variants by replacing the side chains of mutated residues and subjected each variant to 3000 relax runs (see Methods). We then averaged the Rosetta energies of the 25 top scoring decoys and computed ΔΔG_f,mut values as the difference of these averages. Correlation of ΔΔG_f,mut with T_M is shown in Figure 3. A similar trend is obtained when only the top scoring decoy was considered (Figure S3).

Figure 3.

Representation of ΔT_Mvs ΔΔG_f,mut for LovD1-9 variants computed with respect to the wild-type (WT) as the average of the 25 top scoring decoys from 3000 relax runs starting from crystallographic structures. ρ = Pearson’s correlation coefficient. Dashed red line: linear regression.

As can be deduced from these plots, global sampling through the relax application does not eliminate the scaffold bias as it does not converge the computed thermostability trends, which still show no correlation with ΔT_M values when LovD structures are used as the starting scaffolds and moderate or good negative correlations when starting from LovD6 and LovD9 structures.

We analyzed the distribution of Rosetta energies over the relax runs through kernel density estimates for the wild-type LovD, the most thermostable variant LovD6 and the most evolved variant LovD9 (Figure S4). Rosetta energy distributions are generally unimodal and skewed toward lower energy values. The relative position of the distribution centers is qualitatively conserved among different variants. Decoys originating from 3HLB′ (LovD “open”) always appear at high energy values, while decoys originating from 4LCL′ (LovD6 “open”) always appear at low energy values. The relative position of distributions originating from 3HLF′ (LovD “closed”) and 4LCM′ (LovD9 “open”, which are close in energy) depends on the variant. These results confirm that generating variant structures from a crystallographic scaffold with the relax application only provides limited conformational exploration.

3.3. Thermostabilization Prediction with Rosetta Relax on AlphaFold Structures

Having detected this strong dependence of the computed thermostability trend on the initial crystallographic scaffold, we set out to investigate whether AF structures can provide more robust computational predictions. AF calculations provide complete protein structures, eliminating the need to model missing parts, and virtually the same accuracy as experimental structures.³⁷ Each AF run yields not one but five 3D models, corresponding to five different training specifications for the neural network. These differ in a series of parameters including the number of templates (from the PDB70⁵¹ database) and sequences used, number of training samples, and the training time.³⁷ While the predicted structures of the core regions of the protein are nearly identical across the five models, we observed pronounced differences at the flexible loops of LovD. Particularly, we observed that in models 1 and 2, where training involves the use of templates, the loops corresponding to residues 162–170 and 257–265 are systematically predicted in a “closed” conformation; this is likely the consequence of using as templates the crystallographic structures of ligand–bound complexes, where interactions with the ligand stabilize this conformation (Figure 1). Models 3–5, which are trained without using templates, return a variety of loop conformations with low prediction confidence (pLDDT score), not corresponding to the “open” conformation of the apo state, but that can be rather attributed to the intrinsic difficulty of predicting unstructured regions.

We performed an independent structure prediction with AF for each LovD variant and subjected each model of each variant to 3000 relax runs (15,000 runs per variant in total). We then analyzed the correlation between ΔT_M and ΔΔG_f,mut values predicted for each of the five models as differences of the average 25 top scoring decoys of each variant with respect to the wild-type (Figure S5). While ΔΔG_f,mut values computed considering each of the models separately show no correlation or only moderate negative correlation with ΔT_M, ΔΔG_f,mut values computed taking the 25 top scoring decoys independent of the model of origin show a better negative correlation with experimental thermostability. A similar trend is obtained when only the top scoring decoy was considered (Figure S6).

Rosetta energy distributions for the relax runs are still mostly unimodal, but with large fluctuations on both distribution width and the position of its center without a clear trend associated to any AF model (Figure S7).

To assess whether this behavior is systematic and induced by structural differences between LovD variants, we repeated the same calculations (3000 relax runs per model) for four independent runs of AF structure prediction. These predictions differ in the starting geometry because AF calculations are not deterministic; that is, repetition of the exact same calculation does not yield exactly the same structure across any of the five models. This stochastic character is the consequence of the use of random seeds in the manipulation of PDB templates and multiple sequence alignment (MSA) data and in the inference process itself.³⁷ We then recomputed the kernel density estimates (Figure S7) for Rosetta energy distributions and the Pearson’s correlation coefficients ρ between ΔT_M and ΔΔG_f,mut values, shown in Table 2. The erratic behavior of ρ along different runs suggests that refining AF models with relax runs leads to random energy values, which do not allow to either (i) identify any significant difference in thermostabilization predictivity between AF models or (ii) affirm whether combining decoys from different models should entail and advantage over using a single model. Overall, the combination of the stochastic nature of AF and relax produces a high level of noise in the Rosetta energies that prevents any meaningful correlation with experimental T_M values.

Table 2. Pearson’s Correlation Coefficients (ρ) between ΔT_Mversus ΔΔG_f,mut for LovD1-9 Variants Computed with Respect to the Wild-Type from Five Independent AF Runs Averaging over the 25 Top Scoring Decoys for Each of the Five AF Models and All Models Combined.

	run 1	run 2	run 3	run 4	run 5
ρ model 1	–0.59	–0.77	–0.20	–0.56	–0.71
ρ model 2	–0.28	–0.60	–0.79	–0.60	–0.69
ρ model 3	–0.62	–0.25	–0.04	–0.26	–0.43
ρ model 4	–0.67	–0.78	–0.07	–0.91	–0.37
ρ model 5	–0.46	–0.86	–0.35	–0.49	–0.76
ρ combined	–0.84	–0.72	–0.04	–0.88	–0.68

3.4. Thermostabilization Prediction with Multiple AF Runs

As an alternative approach for ensemble generation with reduced noise, we explored the possibility of generating ensembles directly from accumulating multiple AF runs without further conformational sampling. For each variant, we ran 100 independent AF structure predictions, accumulating 500 structures (100 × 5 models). As AF does not provide an internal energy metric, we ranked the 500 structures of each variant according to their Rosetta energies. However, AF structures are not minima under the Rosetta energy function and often show high (unfavorable) energy values, which makes relative energies meaningless and precludes direct comparison of structures.

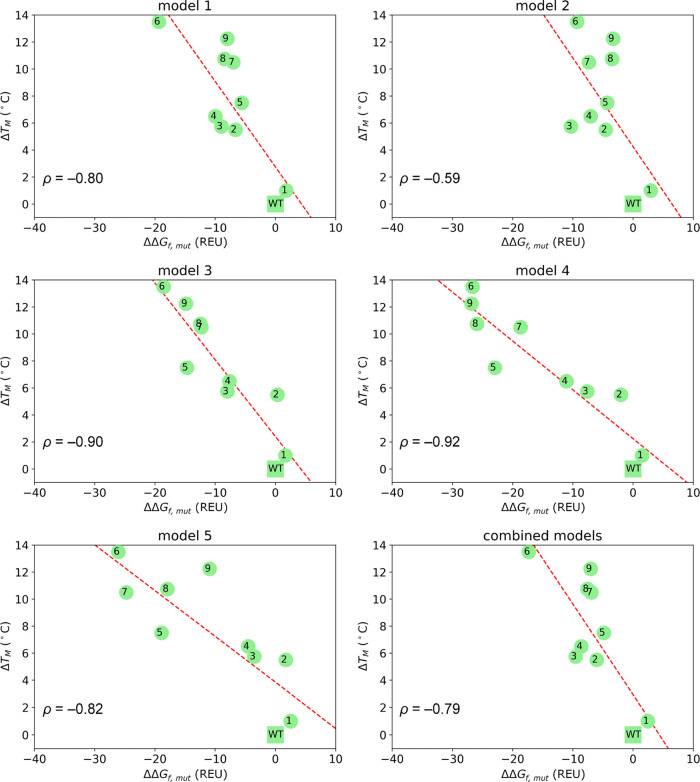
To cure this problem, we subjected each structure to Rosetta minimize protocol, which performs a simple gradient-based minimization (no repacking of side chains), in order to converge each AF structure to the closest local minimum under the Rosetta energy function while keeping the maximum fidelity to the original AF prediction (see Methods). We then analyzed the correlation between ΔT_M and ΔΔG_f,mut values predicted for each of the five models and considering all models at once (Figure 4).

Figure 4.

Representation of ΔT_Mvs ΔΔG_f,mut for LovD1-9 variants computed with respect to the wild-type (WT) from 100 AF runs averaging over the 25 top scoring decoys for each of the five AF models and all models combined. ρ = Pearson’s correlation coefficient. Dashed red line: linear regression.

With this approach, we obtained an excellent negative correlation for models 3 and 4 (ρ = −0.90 and ρ = −0.92, respectively). Slightly worse correlations were obtained when only the top scoring decoy was considered (Figure S8). These results prove that AF structures provide access to accurate calculated stability trends with limited conformational sampling and removing the scaffold bias imposed by crystallographic structures.

Analysis of the per-model kernel density estimates of Rosetta energies (Figure S9) shows a marked difference between distributions according to the model of origin. Models 1 and 2, which use templates, provide a sharper distribution than models 3–5 and also show lower (more favorable) Rosetta energies.

Of note, these more favorable energies and narrower distributions do not translate into better correlation with T_Mvalues. This is the reason why combining decoys from all models worsens correlation with experimental T_M over using decoys originating from model 3 or 4 only.

We analyzed the dependence of the correlation between ΔT_M and ΔΔG_f,mut on the number of AF runs for the most successful models 3 and 4 by computing ρ on the 25 top scoring decoys extracted from a number of runs n increasing from 25 to 100 (Figure S10). For model 4, ρ is already converged at n = 25 and is stable with respect to the number of accumulated runs. For model 3, ρ converges rapidly (n = 32) and remains equal or better than −0.88 along the whole explored span.

Thus, we propose that the computational protocol that combines multiple AF runs with Rosetta minimize, which we name mAF-min, affords robust thermostabilization estimation of evolved enzyme variants, providing an accurate approach to the in silico prediction of relative thermostabilities in the context of computational enzyme design and engineering.

3.5. Geometry Analysis of Conformational Ensembles

We analyzed the geometries of the 25 top scoring decoy ensembles used for ΔΔG_f,mut calculation in our mAF-min protocol. The ensembles for LovD, LovD6, and LovD9 obtained from AF models 1 (using templates) and 4 (not using templates) are shown in Figure 5. For model 1, highly consistent loop geometries are predicted for the three LovD variants, matching the conformations observed in the structure of LovD bound to simvastatin (PDB: 3HLF) for both the 162–170 (in “closed” conformation) and 257–265 loops. For model 4, we identified a varying range of loop geometries across different LovD variants. Moving from LovD to the most evolved LovD9 variant, the geometry of the two loops becomes progressively better defined and, for the 162–170 loop, more similar to the “open” conformation corresponding to the apo form (PDB 3HLB, Figure 1); this is likely the consequence of the mutations accumulated in the loop region (M157V, S164G, S172N, QL174F, see Table S1).

Figure 5.

Overlay of the 25 top scoring decoys obtained with the mAF-min method for LovD, LovD6, and LovD9 (AF models 1 and 4). The 162–170 loop is represented in green, and the 257–265 loop is represented in pink. RMSD = average root-mean-square deviation of loops computed on all heavy atoms of each ensemble.

The excellent agreement of T_M values with Rosetta energies computed on AF model 4 decoys highlights the importance of describing the native state of LovD variants as an ensemble of conformations rather than a single structure for recapitulating the effect of directed evolution, as recently discussed by Chica and co-workers.⁵²

For this reason, model 1, which systematically predicts a single conformation for the flexible loops (and typically obtains better pLDDT scores), provides only moderate correlation with the experimental thermostability trend.

3.6. Thermostabilization Prediction on a Rigid Enzyme Scaffold

If our hypothesis is correct—that is, the better correlation with experimental thermostabilities of model 4 over model 1 arises from the need to sample multiple conformations in enzymes with flexible regions—it follows that for a rigid enzyme scaffold, thermostabilization could be predicted with equal accuracy by all AF models using the mAF-min approach. To test this hypothesis, we computed the relative thermostability of a family of variants of Lipase A (LipA). LipA from Bacillus subtilis is a privileged scaffold for engineering efforts owing to its robustness and lack of flexible loops, which made it the object of several evolutionary campaigns.^{1,7,10,53−57} In this work, we considered the variants engineered by Rao and co-workers^7,54 through directed evolution, where a ΔT_M of over 20 °C is obtained in four evolution rounds. The number of mutations and T_M values of LipA variants are shown in Table 3 (see Table S3 for further details).

Table 3. Engineered LipA Variants.

name	number of mutations	TM (°C)
WT		56.0
TM	3	61.2
2D9	6	67.4
4D3	9	71.2
6B	12	78.2

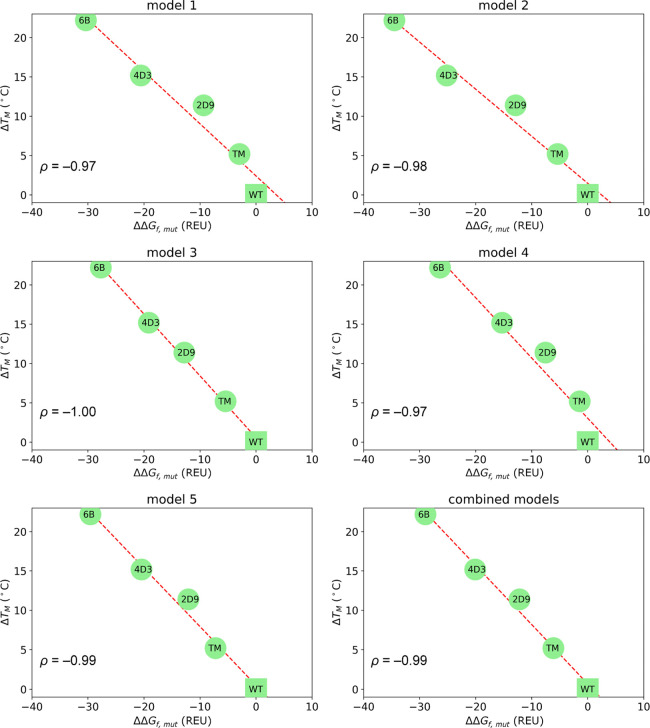
We applied the mAF-min protocol (100 AF runs) to these LipA variants and computed Pearson’s correlation coefficient between ΔT_M and ΔΔG_f,mut values (Figure 6). In this case, and corroborating our hypothesis, we obtained an essentially perfect correlation irrespective of the model used, suggesting that for rigid systems, all AF models have equivalent predictivity and that mAF-min provides highly accurate thermostabilization predictions. As expected, the conformational variability within the ensembles of 25 best scoring decoys used for energy evaluation (Figure S11) is extremely small for both models 1 and 4, describing a highly rigid enzyme. This similarity between conformational ensembles translates into similar Rosetta energy distributions (Figure S12), where we observed a high overlap between kernel density estimates for the five models.

Figure 6.

Representation of ΔT_Mvs ΔΔG_f,mut for LipA variants computed with respect to the wild-type (WT) from 100 AF runs averaging over the 25 top scoring decoys for each of the five AF models and all models combined. ρ = Pearson’s correlation coefficient. Dashed red line: linear regression.

3.7. Validation of mAF-min on a Diverse Pool of Evolved Enzymes

With the aim of exploring the general validity of the mAF-min approach, we turned to expanding the pool of analyzed enzyme families. To this end, we extensively searched the literature for enzyme evolution campaigns reporting T_M data on the engineered variants, identifying the three families presented in Table 4. The first is a family of p-nitrobenzyl esterases from B. subtilis engineered by Arnold and co-workers by directed evolution, comprising four variants spanning a ΔT_M range of 14 °C (see Table S4 for further details).⁵⁸ The second is a family of xylanases A from B. subtilis engineered by Ward and co-workers by directed evolution, comprising six variants spanning a ΔT_M range of 18 °C (see Table S5 for further details).⁵⁹ The third is a family of homodimeric tryptophan 6-halogenases from Streptomyces albogriseolus engineered by Sewald and co-workers by directed evolution, comprising six variants spanning a ΔT_M range of 24 °C (see Table S6 for further details).⁶⁰

Table 4. Selected Enzyme Families for the Validation of the mAF-min Method^a.

family	N. variants	N. mutations	sequence length	ρm3	ρm4
p-nitrobenzyl esterases	4	9	489	–0.59	–0.80
xylanases A	6	4	185	–0.85	–0.44
tryptophan 6-halogenases	6	5	531	–0.63	–0.79

^aN. mutations is the maximum number of mutations from the reference wild-type sequence occurring within the family of variants. For homodimeric halogenases, sequence length and N. mutations refer to a single chain. ρ_m3 and ρ_m4 are Pearson’s correlation coefficients computed using decoys obtained from AF models 3 and 4, respectively.

These three families were selected to test the general validity of our computational approach because their thermostabilization prediction is intrinsically more challenging than that of the LovD and LipA families discussed in the previous sections owing to the number of mutations accumulated in the evolution rounds. The most evolved LovD variant differs from its wild-type by 29 residues out of 413 amino acids, and the most evolved LipA variant differs by 12 out of 181 amino acids, with mutations affecting ∼7% of the sequence in both cases. In the esterase, xylanase, and halogenase families, mutations do not affect more than 2% of the sequence; more diluted mutations imply lower absolute shifts in the Rosetta energy distributions (ΔG_f) with a concomitant increase of the random noise arising from the ensemble averages.

Even under these conditions, Pearson’s correlation coefficients (Table 4) computed from 100 AF runs averaging over the 25 top scoring decoys provide strong negative correlations (equal or better than −0.79) with ΔT_M values for AF model 3 (xylanases family) and AF model 4 (esterase and halogenase families). These results confirm and generalize our previous observation that ensembles derived from AF models 3 and 4 provide good correlations with experimental thermostability values. The correlation plots for all AF models are shown in Figures S13–S18.

These three enzyme families differ in size, flexibility, and quaternary structure (Table 4); overlays of the 25 top scoring decoys from AF models 3 (xylanase A) and 4 (p-nitrobenzyl esterase and tryptophan 6-halogenase) for the wild-type enzymes are shown in Figure S19. The esterase ensemble is highly diverse, particularly at the level of the flexible C-terminal domain,⁵⁸ while the xylanase ensemble shows a unique conformation as already observed for LipA. The halogenase exists in solution as both a homodimer and a monomer, and the mutations introduced along the directed evolution campaign (Table S6) were shown to boost thermostability by enhancing the dimerization propensity, which in turn resulted in increased activity.⁶⁰ The calculations presented in Table 4 were performed on the dimeric form of the enzyme, and the overlay shows a narrow distribution of geometries. Overall, these results demonstrate the wide applicability of mAF-min for the prediction of the thermostabilizing effect of mutations over a wide range of sequence lengths and flexibility and including both monomeric and multimeric proteins, with the caveat that at high dilution of mutations, benchmarking is required to select the best AF model for ensemble generation.

4. Conclusions

Summarizing, we propose a new ensemble-based computational approach for predicting protein thermostabilization trends upon mutation (mAF-min) that combines AlphaFold structure prediction with the Rosetta energy function. Unlike currently available methods based on local sampling for evaluating thermostability changes induced by single mutations, the proposed approach performs global sampling and allows for the quantitative prediction of thermostability trends induced by multiple missense mutations. mAF-min outperforms traditional approaches based on crystallographic structures owing to its ability to escape local minima of the potential energy surface (scaffold bias) and highlights the need of using an ensemble of structures accounting for multiple conformations for accurate thermostabilization predictions of flexible enzymes.

5. Data and Software Availability

The following data are available through the Zenodo repository (https://doi.org/10.5281/zenodo.7497464):

ΔT_Mversus ΔΔG_f,mut values for top scoring LovD, LipA, p-nitrobenzyl esterase, xylanase A, and tryptophan 6-halogenase variants.

AlphaFold predicted structures in PDB and PyMOL session formats for top scoring LovD, LovD6, LovD9, LipA WT, LipA 6B, p-nitrobenzyl esterase WT, xylanase A WT, and tryptophan 6-halogenase WT decoys.

Rosetta energies for all calculations.

No restrictions on data availability apply.

The Rosetta Software Suite is freely available to academic and government laboratories from https://www.rosettacommons.org/software/license-and-download. A license must first be obtained through the University of Washington through the Express Licensing Program at https://els2.comotion.uw.edu/product/rosetta.

AlphaFold open source code can be downloaded from https://github.com/deepmind/alphafold.

PyMOL open source code can be downloaded from https://github.com/schrodinger/pymol-open-source.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jcim.2c01083.

• Mutations and melting temperatures (T_M) of the engineered variants of the five enzyme families considered in this work; model preparation pipeline from crystallographic structures; convergence of ddg calculations; ΔT_Mversus ΔΔG_f,mut correlation plots; kernel density estimates of Rosetta energy distributions; evolution of ΔT_M versus ΔΔG_f,mut correlation as a function of the number of AlphaFold decoys; and overlays of AlphaFold decoys (PDF)

Author Contributions

The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

The authors declare no competing financial interest.