Abstract
The drop-weight impact test is an experiment that has been used for nearly 80 years to evaluate handling sensitivity of high explosives. Although the results of this test are known to have large statistical uncertainties, it is one of the most common tests due to its accessibility and modest material requirements. In this paper, we compile a large data set of drop-weight impact sensitivity test results (mainly performed at Los Alamos National Laboratory), along with a compendium of molecular and chemical descriptors for the explosives under test. These data consist of over 500 unique explosives, over 1000 repeat tests, and over 100 descriptors, for a total of about 1500 observations. We use random forest methods to estimate a model of explosive handling sensitivity as a function of chemical and molecular properties of the explosives under test. Our model predicts well across a wide range of explosive types, spanning a broad range of explosive performance and sensitivity. We find that properties related to explosive performance, such as heat of explosion, oxygen balance, and functional group, are highly predictive of explosive handling sensitivity. Yet, models that omit many of these properties still perform well. Our results suggest that there is not one or even several factors that explain explosive handling sensitivity, but that there are many complex, interrelated effects at play.
Introduction
All high explosives (HE) react violently to external stimuli, although some do so more easily than others. The ability to understand, reliably predict, and manipulate the handling safety of new explosives would have a revolutionary effect on both basic explosives research and applied commercial systems. However, the handling safety of explosives can vary markedly, even between related compounds. The coupling between mechanics and chemistry in explosives is evidently complex and depends on properties that span the molecular scale through the mesoscale. Most explosives development is based on a costly trial-and-error approach, consisting of iterated rounds of synthesis and testing, in part because it has been difficult to predict the sensitivities of new HEs. Theory and simulation struggle to provide consistent guidance for the explosive design process, due to the multitude of factors that influence handling safety.
The handling safety of explosives is currently characterized by a suite of empirical tests that subject explosives to a range of stimuli.1 The most common method to evaluate material handling safety in the initial design stage is the use of a drop-weight impact test. In a typical drop-weight impact test, about 40 mg of HE is placed between two anvils, one of which is typically covered with fine grit paper. A weight (usually 2.5 kg) is dropped from a specified height onto the anvils and transducers detect the acoustic signature of a thermal explosion. This test is used routinely at the earliest stages of explosive development because of its simplicity and its use of modest quantities of material. The mechanism of initiation is not explicitly known,2 but has been debated for many decades, and is most often assumed to be thermal activation through friction.3−5 Results of the test are reported as an estimate of the H50 (or E50) value, the drop height (or drop energy) at which the HE will undergo a violent explosion in 50% of tests. Though the drop-weight impact test involves a somewhat simplified view of an explosive’s sensitivity, it is widely available and allows for rapid comparison to common explosives with well-defined properties.
Drop-weight impact tests measure, albeit indirectly, the activation enthalpy for an explosive to undergo a thermal explosion.6−10 Recent molecular dynamics simulations have confirmed the connection between the thermal stabilities of explosives and their sensitivities.11,12 Numerous researchers, dating back to the seminal works of Wenograd,6 Kamlet and co-workers,7,8 Bowden and Yoffe,9 and Storm, Stine, and Kramer,10 have sought to identify correlations between the physical and chemical properties of explosives and their impact sensitivities. Correlations between physically intuitive descriptors such as the oxygen balance of the molecule—as well as more esoteric properties like bond charge densities—have been investigated.13−27 Machine learning methods such as artificial neural networks have been applied to predicting impact sensitivities for well over 20 years.28−33 While these methods have been somewhat successful in predicting trends in impact sensitivities, they are strictly interpolative, and they provide limited insights or physical understanding. In fact, Brill and James34 have specifically cautioned against taking correlations of properties with impact sensitivity as the actual cause of the observed sensitivity trends, or only looking at one correlation and disregarding the importance of other effects. For example, as we see in this work, two neural networks that are trained on the same data by the same authors may give equally good predictions, but use different sets of descriptors with limited overlap.28
The lack of a coherent theory in this area is in part due to the fact that previous research has focused on correlations of a limited number of molecular properties (often less than 5) with a relatively small (<200–300) number of explosives, often of similar types. Analyzing a small number of explosives and descriptors inherently adds bias to the estimated model before the study even begins. Such studies are likely to find trends that are specific to the set of explosives considered and may not generalize outside the class of explosives analyzed.
This field is missing several critical areas of study: (1) analyses of how much variation to expect within a test of a single material at a single site or multiple sites (this has only occurred on single explosives in previous work35−37) and (2) data collected from more than a few hundred sources with more than a few molecular descriptors. A key contribution of our work is the compilation of a data set of over 1500 drop-weight impact tests from multiple institutions, including hundreds of repeat measurements collected from common explosives such as PETN, TNT, and RDX. We have collected data from common benchmark data sets10 and other historical tests at LANL,38 as well as more recent studies of new synthesized molecules from Chavez and co-workers,39,40, Klapotke et al.,41 Sabatini et al.,42 and Shreeve et al.43 We have measured and calculated over 100 descriptors for molecular properties, including energetic functional groups, heat of explosion, oxygen balance, specific heat, and hydrogen bonding. We hope that our data-driven approach to understanding which molecular properties matter in the drop-weight impact test will inform and direct future studies addressing these critical problems in the HE literature.
Data
We modeled logE50 (“drop energy”) as a function of the molecular descriptors. We used only observations that had complete data for all descriptors. These data consisted of 1533 observations with 156 descriptors. There were 25 molecules with repeat observations (which made up 1032 of the 1533 observations); the remaining 501 molecules had a single observation. The five most common explosives tested, and the number of observations per explosive, are given in Table 1. Unless otherwise noted, we use logE50 to represent sensitivity, where “log” is the base-10 logarithm, as in Kamlet,7 Nefati et al.,28 and Wang et al.44 The main source of data was legacy LANL tests; however, many of the data were obtained from the published scientific literature.11,45−170 Particularly sizable data sources are the works of Kamlet,7 Marrs et al.,36 and Keshavarz and Jaafari,29 the latter of which incorporates most of the data of Storm et al.10 More recent works of Rice and Hare14 and Mathieu171 draw on these same data sources.
Table 1. Five Most Common Explosives and Number of Observations of Each.
| PETN | HMX | RDX | NQ | TNT |
|---|---|---|---|---|
| 490 | 164 | 130 | 44 | 40 |
We considered both categorical and continuous descriptors; however, the majority of descriptors we considered were continuous or integer valued; see Table 3 for a summary of descriptors. In the simplest case, we included the stoichiometry of the molecule (C, H, N, O, etc.) in the molecular formula of each observation. We computed oxygen balance from the chemical formula of each molecule. Oxygen balance is a measure of the relative weight of oxygen in deficiency, or excess, of what is required to burn all carbon to carbon dioxide and all hydrogen to water.172,173 Explicitly, the oxygen balance is computed using
| 1 |
where MW is the molecular weight of the compound; nC, nH, and nO are the numbers of carbon, hydrogen, and oxygen atoms in the compound; and nM is the number of metallic atoms that form metallic oxides. The atomic connectivity within each molecule was evaluated using a condensed version of the classification scheme developed originally by Kober et al.4 Descriptors relating to energetic and electronic properties of the molecules were evaluated using semiempirical density functional tight binding (DFTB) theory with the lanl31 parametrization;174−176 see the following subsections for more details of the of the computed descriptors. Lastly, we considered descriptors that were outputs of the CHEETAH software from Lawrence Livermore National Laboratory software that predicts explosive performance properties, including mechanical energy of detonation, detonation velocity, and reaction products for over 100 unique molecules. The correlations observed with the properties calculated by CHEETAH were ultimately found to be encompassed by the correlations with heat of explosion and with oxygen balance.
Table 3. Summary of Descriptors.
| Predictor(s) | Description |
|---|---|
| Lab | Laboratory where drop-weight impact test was performed |
| Grit | Identifies whether the test series used a bare anvil or an anvil covered with grit paper |
| Method | Identifies the statistical method used to analyze the drop-weight impact series |
| Functional group | Most sensitive explosive group |
| C, . . ., Si | Number of atoms of each element in the molecule |
| C[C], . . ., C[NNNN] | Atomic connectivity |
| Q (per g) | Specific heat of explosion computed from the difference in the heat of formation of the reactant and products |
| N, O, and NO groups | Number of functional groups with an N (N group), O (O group), or an N and O (NO group) |
| Mol mass | Molecular mass of energetic molecule (amu) |
| Oxygen balance | Oxygen balance (1) |
| Heat of formation | Gas phase heat of formation of energetic molecule computed at the DFTB-lanl31 level of theory176 |
| Dipole | Molecular dipole (eA) |
| Max change | Maximum charge on any atom (e) |
| Min change | Minimum charge on any atom (e) |
| Atomization energy | Atomization energy (eV) computed at the DFTB/lanl31 level of theory |
| Normalized atomization energy | Normalized by number of atoms (eV/atom) |
| Band energy | DFTB band energy (eV) |
| Coulomb energy | DFTB Coulombic energy (eV) |
| HOMO–LUMO gap | DFTB HOMO–LUMO gap (eV) |
| Moment1, . . ., Moment4 | Moments of the DFTB electron densities of states |
| ZPE (kJ/g) | Vibrational zero point energy per g (kJ/g) |
| ZPE (kJ/mol) | Vibrational zero point energy per mole (kJ/mol) |
| Cv (J/mol K) | Heat capacity per mole (J/mol K) |
| Cv (J/g K) | Heat capacity per g (J/g K) |
| H donor | Number of hydrogen bond donors per molecule |
| H acceptor | Number of hydrogen acceptors per molecule |
Functional Group and Other Categorical Descriptors
To examine the effect of chemical composition on sensitivity, we sorted measured drop energies (logE50), by the presence of functional groups. The functional groups we considered were peroxides (O2), azides (N3), nitrate esters (ONO2), nitromines (NNO2), and nitros (CNO2). In this portion of the study, we allow sensitivities to be double counted; that is, if a sample had both CNO2 and NNO2 functional groups, we classified its sensitivity for both groups, CNO2 and NNO2. Table 2 shows the number of observations for each functional group, and/or pair of functional groups, as appropriate.
Table 2. Number of Observations for Each Functional Groupa.
| O2 | N3 | ONO2 | NNO2 | CNO2 | |
|---|---|---|---|---|---|
| O2 | 2 | 5 | 0 | 0 | 11 |
| N3 | 5 | 19 | 1 | 10 | 23 |
| ONO2 | 0 | 1 | 538 | 8 | 5 |
| NNO2 | 0 | 10 | 8 | 397 | 84 |
| CNO2 | 11 | 23 | 5 | 84 | 367 |
The diagonal shows the number with a single functional group, and off diagonal entries count those observations with multiple functional groups.
Previous studies have shown that the test setting, such as the test prescription method, the laboratory where the test was performed, and whether grit was used on the anvil or not, may be predictive of observed drop energies.36 So, in addition to the “functional group” variable, we included the test method,177,178 the laboratory, and the use of grit as categorical descriptors. The test prescriptions consisted of the Bruceton (746), Neyer (759), and BAM (28) methods. Drop energy measurements from tests with unspecified prescription methods were assumed to be Bruceton (for tests from before 1995) or Neyer (after 1995). We split the laboratories where the tests were performed into the two laboratories with the most tests (LANL and NRL, with 870 and 204 tests each, respectively) and an “other” laboratory category (440 tests). Finally, measurements that did not specify whether grit paper was used were assumed to be have used grit (1249 total tests), compared with 284 tests without grit (see Table 3).
Connectivity
The atomic connectivity within each molecule was evaluated using a condensed version of the classification scheme developed originally by Kober et al.4 Here, atoms are considered to be covalently bonded when their interatomic distance is less than 120% of the sum of their covalent radii. We then denote the coordination environments of atom X as X[A], X[AB], X[ABC], and X[ABCD], which count the number of instances where atoms of species X are directly bonded to between one and four atoms of species A–D, respectively. We do not report unphysical coordination environments, such as H[CCCC], which would correspond to a hydrogen atom that forms covalent bonds to four carbon atoms. By limiting the number of atoms in the coordination environments to one for H (i.e., H[A]), two for O (O[A] and O[AB]), three for N (N[A], N[AB], and N[ABC]), and four for C (C[A], C[AB], C[ABC], and C[ABCD]), we produce a set of 115 unique atomic coordination environments for up to four bonded atoms. Finally, we count only the number of unique environments and exclude those associated with trivial permutations of the atoms. Illustrative examples of the coordination environments for a handful of simple molecules are provided below:
Hydrogen dimer, H2: H[H] = 1, all other environments = 0
Water, H2O: H[O] = 2, O[HH] = 1, all others = 0
Methane, CH4: C[H] = 4, C[HH] = 6, C[HHH] = 4, C[HHHH] = 1, all others = 0
Aminomethanol, NH2CH2OH: C[H] = 2, C[N] = 1, C[O] = 1, H[N] = 2, H[O] = 1, C[HH] = 1, C[HN] = 2, C[HO] = 2, C[NO] = 1, N[CH] = 2, N[HH] = 1, O[CH] = 1, C[HHN] = 1, C[HHO] = 1, C[HNO] = 2, N[CHH] = 1, C[HHNO] = 1, all others = 0
DFTB-Calculated Properties
Descriptors relating to energetic and electronic properties of the molecules have been evaluated in the gas phase using semiempirical density functional tight binding (DFTB) theory with the lanl31 parametrization.174−176 The lanl31 DFTB parametrization for molecules containing C, H, N, and O was demonstrated to exhibit near DFT accuracy at a much smaller computational cost, which makes the combination of model and parameters ideal for rapidly computing the properties of large numbers of molecules containing tens of heavy atoms.
The total energy in DFTB theory is a sum of three contributions,
where Eband = 2 Tr((P – P0)H0) describes the cohesion arising from the overlap of valence orbitals on neighboring atoms. Here, Tr(X) denotes the trace of matrix X; H0 is the two-center, Slater-Koster tight binding Hamiltonian;179,180P0 is the density matrix for neutral, noninteracting atoms; and P is the self-consistent density matrix computed from the DFTB Hamiltonian,
where S is the overlap matrix; i labels atoms; and α labels orbitals. V are electrostatic potentials,
arising from the set of atom-centered Mulliken partial charges, where U(i) is the Hubbard U parameter for the species at site i; N is the total number of atoms; and γij is a screened Coulomb potential.174Eqq is the Coulombic energy arising from the set of Mulliken partial charges, that is,
where
and ni is the number of valence electrons assigned to neutral atom i. Finally, Erep is a sum of pairwise terms, Φ(Rij), that provide strong repulsion at short interatomic distances. We used the three terms in the total DFTB energy, Eband, Eqq, and Erep, as descriptors for the energetic molecules owing to their clear and unambiguous physical meanings. The atomization energy,
which is equal to the change in energy upon
completely separating all of the atoms in a molecule, was also computed
using DFTB/lanl31 and used as a descriptor. Here, 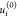 is the energy of noninteracting atom i in its ground state electronic configuration (which includes
spin multiplicity), and u is the total energy of
the molecule.
is the energy of noninteracting atom i in its ground state electronic configuration (which includes
spin multiplicity), and u is the total energy of
the molecule.
Heat of Formation
The gas-phase heat of formation, ΔHf°, of each molecule was computed using the total DFTB energy, u, at the self-consistent electronic ground state with the four parameter atom equivalent energy scheme described in Cawkwell et al.,181 that is,
where ηl is the number of atoms of species l in the molecule, and ϵl is the corresponding atom equivalent energy. The total energies, u, were obtained following a geometry optimization until the maximum force acting on any atom was less than 0.001 eV/Å.
Charge and Electrostatic Properties
The self-consistent charge DFTB formalism yields a set of atom-centered Mulliken partial charges, {q}. We have used the self-consistent Mulliken charges at the optimized geometry of each molecule to compute (i) the maximum and minimum Mulliken partial charges in the molecule, qmax and qmin, and the molecular dipole moment,
where N is the number of atoms in the molecules, and Ri are the Cartesian coordinates of atom i.
Properties of Electronic Eigenspectra
We have computed a series of descriptors of the ground state electronic structures of the molecules at the DFTB level of theory. The allowable electronic energy levels of a molecule are equal to the eigenvalues, ε, of the DFTB Hamiltonian, H. The band energy is equal to the sum of the occupied energy levels,
where electronic, or molecular orbital, energy levels are occupied sequentially with the available electrons, with two electrons per level, starting from the lowest eigenvalue. The separation in energy between the highest occupied eigenvalue and lowest unoccupied eigenvalue is known as the HOMO–LUMO gap. The HOMO–LUMO gaps of explosive molecules have been investigated heavily with respect to sensitivity because the rupture of bonds typically involves the closure of, or excitation of electrons across, the HOMO–LUMO gap (see, for example, refs (182 and 183)). Therefore, we might expect molecules with small HOMO–LUMO gaps to be relatively sensitive. Hence, the DFTB HOMO–LUMO gap has been included in our set of electronic descriptors.
The distribution of the eigenspectrum controls the structural stabilities of molecules and materials. While binding energy as a function of structure can be obtained numerically from the eigenspectrum, {ε}, directly, the first few moments of the eigenvalue spectrum,
provide deep insights into the origin of structural stability. The moments theorem, which showed how the electronic eigenspectrum can be connected to molecular topology via hopping paths of length p that start and finish on the same orbital, was first developed by Cyrot-Lackmann and Ducastelle184−186 and became the basis for subsequent major developments in linear scaling electronic structure theory.180,187−189 We have used moments of the DFTB eigenspectra up to and including p = 4 to construct descriptors to understand whether explosive sensitivity is connected to electronic structure and molecular topology in more profound ways than just through the relatively simple concept of the HOMO–LUMO gap.
The zeroth moment, μ0, returns the total number
of valence orbitals Norb. The normalized first moment, 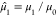 , gives the center of mass of the eigenspectrum.
The subsequent moments are calculated with respect to
, gives the center of mass of the eigenspectrum.
The subsequent moments are calculated with respect to 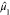 , that is, the eigenspectrum is shifted
so that
, that is, the eigenspectrum is shifted
so that 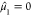 . The normalized second moment,
. The normalized second moment, 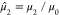 , gives the mean square width of the eigenspectrum,
and the dimensionless third moment,
, gives the mean square width of the eigenspectrum,
and the dimensionless third moment, 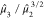 , measures the skewness of the distribution.
Finally, we use the normalized fourth moment,
, measures the skewness of the distribution.
Finally, we use the normalized fourth moment, 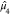 , to build the dimensionless shape parameter,
, to build the dimensionless shape parameter,
that measures whether the distribution is
bimodal (s < 1) or unimodal (s > 1).190 We refer to 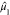 ,
, 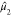 ,
, 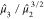 , and s as Moment1 through
Moment4 in our study. The applications of the moments theorem to the
electronic eigenspectra of PETN and 2,4,6-TNT are illustrated in Figure 1, which also serves
to highlight that the HOMO–LUMO gap is just one of numerous
possible descriptors of the electronic structures of organic molecules.
The four moments-based descriptors derived from the eigenspectra of
PETN and 2,4,6-TNT are given in Table 4. The eigenspectra of PETN and 2,4,6-TNT do not differ
markedly; the mean square width,
, and s as Moment1 through
Moment4 in our study. The applications of the moments theorem to the
electronic eigenspectra of PETN and 2,4,6-TNT are illustrated in Figure 1, which also serves
to highlight that the HOMO–LUMO gap is just one of numerous
possible descriptors of the electronic structures of organic molecules.
The four moments-based descriptors derived from the eigenspectra of
PETN and 2,4,6-TNT are given in Table 4. The eigenspectra of PETN and 2,4,6-TNT do not differ
markedly; the mean square width, 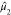 , of the spectrum of 2,4,6-TNT is slightly
larger than that of PETN, and both exhibit positive skewness
, of the spectrum of 2,4,6-TNT is slightly
larger than that of PETN, and both exhibit positive skewness 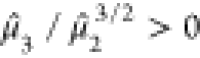 and a unimodal distribution, s ≈ 1. The vast majority of the explosive molecules in our
data set exhibit a unimodal eigenvalue distribution with s ≈ 1, which we attribute to the absence of four-membered rings
within their mostly flat 2D topologies that would promote a small s and a strong bimodal distribution.188 Indeed, the shape parameter, s, (Moment4),
was not ranked highly as a descriptor of explosive sensitivity, presumably
because of the structural similarities among the small organic molecules
sampled by our data set.
and a unimodal distribution, s ≈ 1. The vast majority of the explosive molecules in our
data set exhibit a unimodal eigenvalue distribution with s ≈ 1, which we attribute to the absence of four-membered rings
within their mostly flat 2D topologies that would promote a small s and a strong bimodal distribution.188 Indeed, the shape parameter, s, (Moment4),
was not ranked highly as a descriptor of explosive sensitivity, presumably
because of the structural similarities among the small organic molecules
sampled by our data set.
Figure 1.
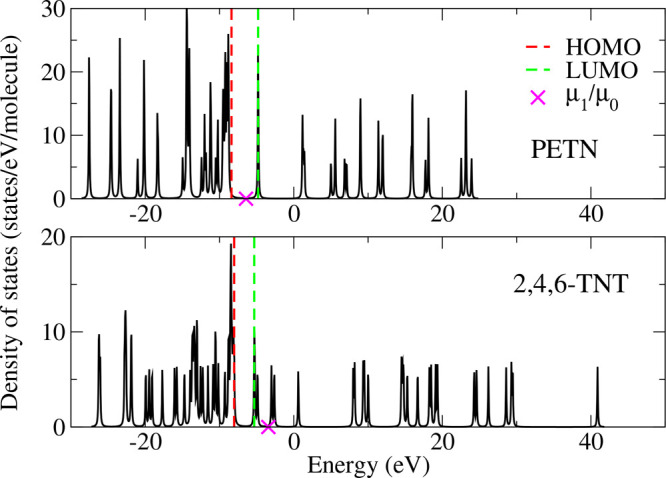
Electronic eigenspectra of PETN and 2,4,6-TNT
from the ground state
DFTB electronic structure. The energies of the HOMO, LUMO, and center
of mass, 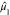 , are highlighted. 2,4,6-TNT has a slightly
wider eigenspectrum than PETN, which is measured by the normalized
second moment,
, are highlighted. 2,4,6-TNT has a slightly
wider eigenspectrum than PETN, which is measured by the normalized
second moment, 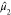 . Both eigenspectra exhibit positive skewness,
. Both eigenspectra exhibit positive skewness, 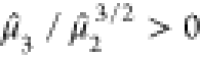 , which is larger for 2,4,6-TNT, and moderately
unimodal distributions, s ≈ 1.
, which is larger for 2,4,6-TNT, and moderately
unimodal distributions, s ≈ 1.
Table 4. Moments-Based Descriptors for PETN and 2,4,6-TNT.
| μ̂1 (eV) | μ̂2 (eV2) | μ̂3/μ̂23/2 | s | |
|---|---|---|---|---|
| PETN | –6.43 | 14.01 | 0.62 | 1.02 |
| 2,4,6-TNT | –3.42 | 16.48 | 0.76 | 0.96 |
Vibrational Modes
The vibrational normal modes, {ω}, were computed following a geometry optimization until the maximum force acting on any atom was less than 0.001 eV/Å by building and diagonalizing the force constant matrix.191 The vibrational zero point energy,
and heat capacity at T = 300 K,
on a per gram and per mole basis are computed from the sets of vibrational normal modes.
Numbers of H Bond Donors and Acceptors
The numbers of hydrogen bond donors and acceptors were obtained using the Chemical Identifier Resolver tool using the simplified molecular-input line-entry system (SMILES) string in the data, which is available from the U.S. National Institutes of Health at https://cactus.nci.nih.gov/chemical/structure.
Reaction Products
Reaction products were calculated according the oxidation priority established in the literature for detonation reactions.192 All nitrogen is assumed to be released as N2. Oxygen is assumed to first convert all hydrogen to water vapor. Further oxygen converts all carbon to carbon monoxide followed by full oxidation to carbon dioxide. Excess oxygen is released as molecular oxygen, O2. In oxygen deficient compounds, excess hydrogen and carbon are released in molecular form as H2 and soot (C). Heats of explosion (Q) were calculated through comparison of experimental gas phase heats of formation, ΔHf°, of the products,193 with heats of formation of the reactants, calculated by the DFTB method explained above.
Methods
Correlation Analysis
Before modeling impact sensitivity as a function of all descriptors, we evaluated the relationship of each descriptor with drop energy in isolation (and the relationship of each pair of descriptors). To evaluate the relationship of the continuous- and integer-valued descriptors with drop energy, we used the Spearman correlation. The Spearman correlation quantifies the ordinal correlation between two continuous quantities, allowing for strong correlation when one variable is a monotonic function of another (rather than exclusively linear functions as in the Pearson correlation). We used the coefficient of determination in a one-way analysis of variance (ANOVA) model to evaluate the relationship between continuous measurements and the categorical descriptors. We emphasize that the correlation analysis has no bearing on subsequent variable selection.
Predictive Modeling
We modeled drop energy as linear, and nonlinear, functions of the descriptors. Due to the large number of descriptors and drop-weight impact tests, we wish to employ methods that simultaneously estimate a model for drop energy and subset the descriptors to only the most useful descriptors. Models with fewer descriptors are not only easier to interpret but also are less likely to “overfit” by, for example, incorporating random variation present in the data into the learned model. The methods we employ estimate the following regression model:
| 2 |
where i refers to each observation; yi is the sensitivity of observation i; and xi is a vector of p descriptors for observation i. The function f(.) is the object of inference; the random errors ϵi are assumed to be mean zero and have constant variance. These assumptions imply that variation in drop-weight impact tests outside of the descriptors xi is not systematic, and departures from these assumptions will degrade performance, for example, if certain explosive materials have less variable drop-weight impact tests than others, or if certain methods of determining “Go” do not correlate with others.
LASSO
The least absolute shrinkage and selection operator (LASSO) is a method for estimating a linear function f(.) to represent the sensitivity function.194 Explicitly,
| 3 |
where β is a vector of coefficients to be estimated. The LASSO selects the coefficients β to trade off the number of nonzero values (and thus the complexity of f(.)) with model fit. It does so by minimizing the criterion
| 4 |
where |β|1 denotes the sum of absolute values of nonzero entries in β. The parameter λ > 0 controls the trade-off between model fit and model complexity and is selected using cross-validation. The λ that predicts best out-of-sample (or nearly the best) is chosen to guard against overfitting. The LASSO optimization problem is known to have a unique solution, so that it chooses the one best β value that minimizes the optimization criterion for a given λ. The LASSO is a fast method and is known (for sufficiently large λ) to set some entries in β to zero, effectively removing descriptors from the model. Drawbacks include that the function f(.) is constrained to be linear (although this type of model is easier to interpret) and, in the canonical setting, does not include interactions between the descriptors. We use the LASSO method as implemented in the R statistical programming language.195
Random Forest
The random forest method represents f(.) as a sum of decision tree models.196 Thus, f(.) is a highly flexible piecewise constant function. Each tree is trained on a random subset of the data with a random subset of the number of descriptors. The number of trees and number of variables are tuning parameters to be selected by the user, although the defaults often work well for a range of applications. We explore the choice of various hyperparameters for the random forest method(s) in the Supporting Information,197,198 finding that the defaults (p/3 descriptors and minimum number size of terminal node of 5) perform as well as any other settings examined. Trees are learned in an optimal way that controls the out-of-sample performance. That is, splits are added to the tree using the variable that reduces the out-of-sample mean-square error the most,
| 5 |
where Θ is the set of observations under consideration. The random forest optionally reports the typical decrease in this error as each descriptor is added to each tree, where large decreases in error suggest that the descriptor is useful in predicting the response yi. For more details on the random forest method, see Hastie et al.,199 for example.
Random forest models are quite flexible, where f(.) is inherently nonlinear and includes interactions. However, this flexibility makes interpretation of the estimated function f(.) challenging. Further, the random searching for the “best” function f(.) is not guaranteed to have a single solution, such that another function g(.) may perform just as well.
Unlike the LASSO method, canonical random forests do not automatically subset the descriptors to the most useful ones—although the random forest method does offer some notion of variable “importance”—and such subsetting may not be necessary for good performance.200 In hopes of improving interpretability, and possibly to improve predictive performance, we employ a method for reducing the descriptors to the most useful ones for random forests. This method, variable selection using random forests (VSURF),201 takes several passes through the data to select the smallest subset of descriptors that effectively represent the relationship between drop energy and the descriptors. We use the importance measure native to random forest methods to interpret the relative contribution of each (selected) descriptor to the prediction of drop energy. We use the random forest and VSURF methods as implemented in the R statistical programming language.202,203
Model Evaluation
Evaluation of predictive performance
on the drop-weight impact data is challenging due to the imbalance
of molecules represented in the data, and the stochastic nature of
estimating E50 from relatively few binary
measurements. In hopes of addressing these challenges, we compared
predicted values of drop energy 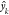 to the mean drop energy
to the mean drop energy 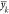 across observations of molecule k, for each of the unique molecules.
across observations of molecule k, for each of the unique molecules.
An additional
consideration in evaluating predictive performance is that we are
more certain of 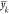 for molecules which we have large number
of observations, such as PETN, where the number of observations mk = 490. Hence, we should weight
errors of molecules for which mk is large higher than errors for those which have mk = 1. We introduce a weighted root-mean
square error,
for molecules which we have large number
of observations, such as PETN, where the number of observations mk = 490. Hence, we should weight
errors of molecules for which mk is large higher than errors for those which have mk = 1. We introduce a weighted root-mean
square error,
| 6 |
where wk is the weight for molecule k, and 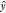 is the predicted drop energy for molecule k.
is the predicted drop energy for molecule k.
When wk = mk/∑kmk, each error is weighted by the number of times molecule k was observed, whereas when mk = 1/K, we ignore the multiplicity
of observations for each molecule. Generally, we seek a compromise
between these two extremes. The extreme unbalance in the data makes
weighting by wk = mk/∑kmk seem too strong: should roughly 1/3 of the error criterion
be generated by a single molecule (PETN)? Or should molecules with
two or three observations count double those with a single observation?
And yet, completely ignoring the multiplicity of each molecule does
not recognize the true structure of the data, nor the fact that we
are more certain about some values of 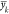 than others. Thus, we define η ∈
[0, 1] as a mixing parameter between the extremes wk = mk/∑kmk and mk = 1/K, so that the desired
predictive model should minimize the following RMSE over a broad range of η:
than others. Thus, we define η ∈
[0, 1] as a mixing parameter between the extremes wk = mk/∑kmk and mk = 1/K, so that the desired
predictive model should minimize the following RMSE over a broad range of η:
| 7 |
We evaluated the fit of each predictive model
using 10-fold cross-validation. Here, 10-fold cross-validation is
an approach that is meant to evaluate predictive performance of each
model on data outside of that used in estimating each model, thus
mimicking the use of the model to design new molecules, and is a canonical
machine learning technique.204 We randomly
partitioned the data set into 10 “folds” of roughly
equal numbers of unique molecules (no molecule was allowed to reside
in more than one fold). For each fold, we selected variables (LASSO
and VSURF) and estimated each predictive model (LASSO, random forest
without subsetting descriptors, and VSURF) using the data outside
the fold and generated the predictions from each model within the
fold. Repeating for each fold, we obtained an out-of-sample prediction
for each unique molecule in the data set. We fit models to the complete
data set (including repeat observations) and to a data set consisting
of each unique molecule and only its mean drop energy across repeat
observations. The former approach implicitly weights predictions toward
molecules for which we have more observations and are thus more certain
about the true drop-weight impact sensitivity; we allow predictive
performance to decide which approach is best for these data. We computed
the weighted RMSE in (eq 7) for 1000 equally spaced values of η
∈ [0, 1]. We repeated the entire procedure 10 times, with 10
different partitionings of the unique molecules. Averaging across
the 10 random partitions and 1000 values of η gave a final error
criterion, 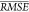 , which we used to compare predictive models.
, which we used to compare predictive models.
Results
Correlation Analysis
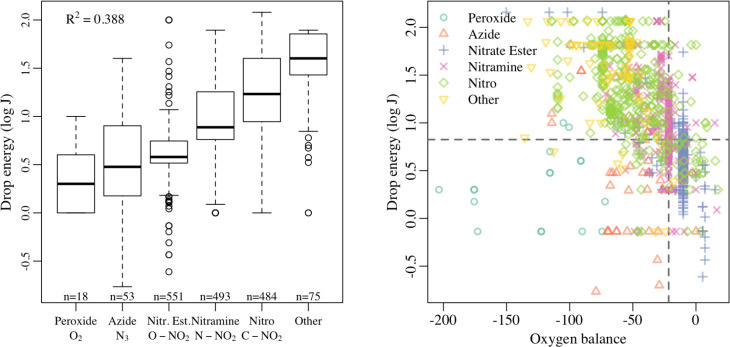
We studied five major functional groups: peroxides (O2), azides (N3), nitrate esters (ONO2), nitromines (NNO2), and nitros (CNO2). We found that about 86% of observations had exactly one major functional group, about 9% of observations had two or more of the major functional groups (see Table 2), and about 5% had none of the major functional groups. Following Mathieu,171 we labeled each observation with the most reactive functional group (where “reactivity” corresponds to the lowest median drop height by functional group). That is, in a hypothetical molecule with ONO2 and NNO2 functional groups, the “group” label for this molecule was “ONO2”. Figure 2 shows the estimated sensitivities separated by functional group. As expected, the functional group does appear to affect impact sensitivity, explaining about 40% of the variation in sensitivity (as measured using coefficient of determination, commonly denoted R2). Peroxides and azides were the most sensitive, and molecules with aromatic nitro groups (and/or none of the major functional groups) are the least sensitive.
Figure 2.
Drop energy trends with the strongest related categorical and continuous descriptors, functional groups, and oxygen balances, respectively.
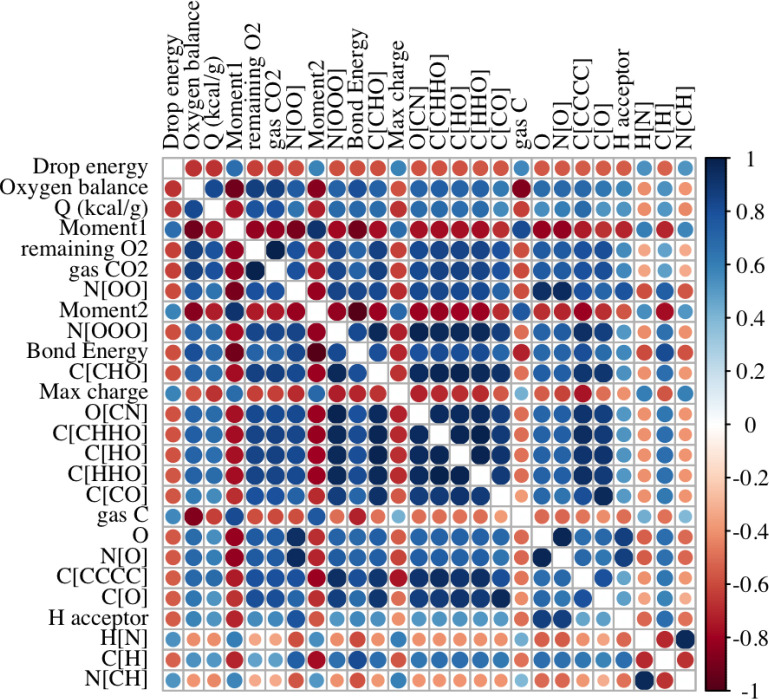
The Spearman correlations among continuous predictors are displayed in Figure 3, for the descriptors with the largest correlations with sensitivity. We observe that oxygen balance has the highest correlation with sensitivity, followed by the first moment of the distribution of electron states, and the heat of explosion, Q, has the third largest correlation with sensitivity. We notice that correlations between descriptors are often at least as large as the correlations between the descriptors and drop energy, logE50.
Figure 3.
Spearman correlations of descriptors most strongly correlated with logE50, ordered by the absolute value of this correlation.
In Figure 2, we plot drop energy against oxygen balance (separated by functional group), which is the descriptor with the strongest correlation with drop energy. We observe that the trend is negative for most functional groups and nonlinear in general. The general negative trend indicates that molecules with higher oxygen balance (more performant) have lower drop energies (and thus higher sensitivity). Moreover, the strength of the trend varies by functional group. Drop energies of peroxides have little trend with oxygen balance, while drop energies of nitro compounds have a much stronger trend. This fact suggests that an interaction between functional group and oxygen balance may be appropriate. Finally, we point out that the presence of vertical stacks of points indicates molecules with many repeat observations. These molecules have the same oxygen balance, but different measured drop energies.
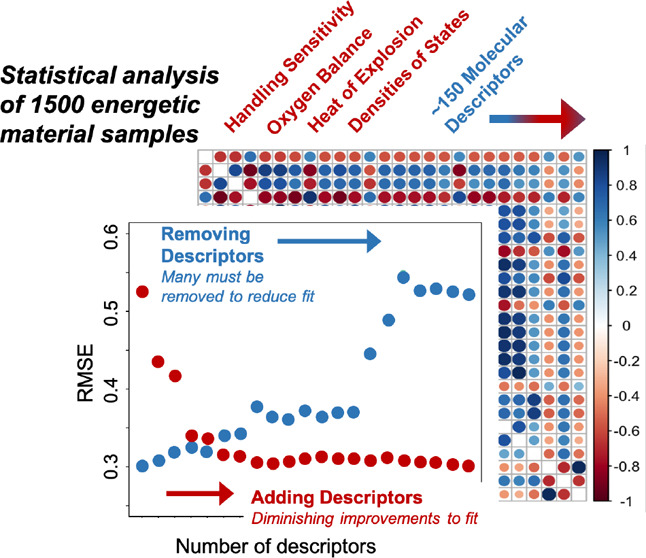
Predictive Performance
The estimated performance, measured
by 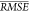 discussed in the previous section, of the
predictive models is given in Table 5. Both random forest and VSURF models outperform the
linear LASSO method by a substantial margin, suggesting that there
may be some nonlinearity in the true function relating the descriptors
and the observed drop energies. We also notice a slight improvement
in the VSURF method over the random forest method, especially when
training on all the data, including repeats. VSURF achieves this performance
improvement with far fewer descriptors as well (only 19 when selecting
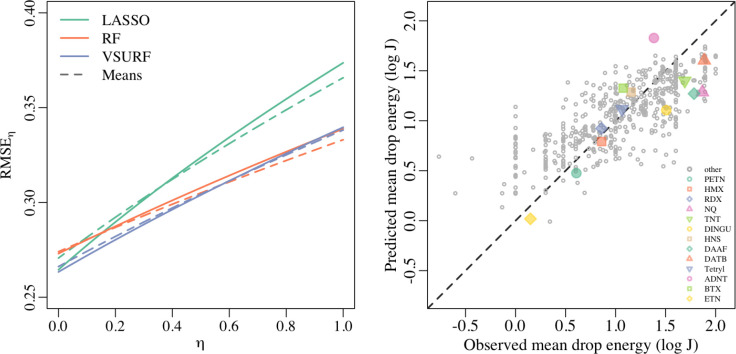
on the complete data set, compared to all 156). Finally, in Figure 4, we plot the mean RMSEη (see eq 7) across random partitions as a function of η
and see that the VSURF method trained on all data performs best for
the broadest range of η. The value of
discussed in the previous section, of the
predictive models is given in Table 5. Both random forest and VSURF models outperform the
linear LASSO method by a substantial margin, suggesting that there
may be some nonlinearity in the true function relating the descriptors
and the observed drop energies. We also notice a slight improvement
in the VSURF method over the random forest method, especially when
training on all the data, including repeats. VSURF achieves this performance
improvement with far fewer descriptors as well (only 19 when selecting
on the complete data set, compared to all 156). Finally, in Figure 4, we plot the mean RMSEη (see eq 7) across random partitions as a function of η
and see that the VSURF method trained on all data performs best for
the broadest range of η. The value of 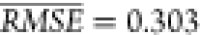 for the selected method corresponds to
an approximate coefficient of determination R2 ≈ 0.64 (see Supporting Information for computation of this value from
for the selected method corresponds to
an approximate coefficient of determination R2 ≈ 0.64 (see Supporting Information for computation of this value from 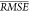 ). The performance of the VSURF method trained
on all data, along with the limited number of descriptors, leads us
to select this method for further study and interpretation.
). The performance of the VSURF method trained
on all data, along with the limited number of descriptors, leads us
to select this method for further study and interpretation.
Table 5. Performance of Predictive Models As
Measured by 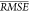 in 10 10-Fold Cross-Validationsa.
in 10 10-Fold Cross-Validationsa.
| Means data | All data | |
|---|---|---|
| LASSO | 0.321 | 0.322 |
| RF | 0.305 | 0.307 |
| VSURF | 0.304 | 0.303 |
The models were trained on data consisting only of mean drop energies of unique molecules (“Means data”) and on data including all repeat observations (“All data”).
Figure 4.
(Left) Average RMSEη across random cross validation partitions, as a function of η. Dashed lines denote models trained on data consisting only of mean drop energies of unique molecules (“Means data”), and solid lines denote models trained on data including all repeat observations (“All data”). (Right) Average predicted drop energy (logE50), across 10 random cross-validations, from VSURF method trained all data, compared to observed mean drop energy for all unique molecules. Molecules with five or more repeated observations are highlighted in color.
The observed mean values of drop energy, logE50, are compared to the predicted mean values (for the VSURF method trained on all data) in the right panel of Figure 4. We emphasize that the predictions represent out-of-sample predicted mean drop energies from the cross-validation study (averaged across random partitions). Generally, we see good agreement between the observations and the predictions from the model, especially for the molecules with several repeat observations.
We expect that the 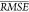 of about 0.30 to be roughly representative
of the accuracy of the selected VSURF predictive method. Concretely,
we expect to predict (mean) drop energy within a multiplicative factor
of 102(0.3) ≈ 4, where the factor of “2”
results from choosing error bounds two standard deviations from the
predicted value. Since the measurement error of the drop-weight impact
test (for a single test) has been reported to be accurate to a multiplicative
factor of 1.5–3 in Marrs et al.,36 the degree of error in the predictive model is not unexpected.
of about 0.30 to be roughly representative
of the accuracy of the selected VSURF predictive method. Concretely,
we expect to predict (mean) drop energy within a multiplicative factor
of 102(0.3) ≈ 4, where the factor of “2”
results from choosing error bounds two standard deviations from the
predicted value. Since the measurement error of the drop-weight impact
test (for a single test) has been reported to be accurate to a multiplicative
factor of 1.5–3 in Marrs et al.,36 the degree of error in the predictive model is not unexpected.
Important Descriptors
To determine which descriptors
are most influential in predicting drop-weight impact sensitivity,
we trained the best-performing method, VSURF, to the entire data set.
In Table 6, we report
the descriptors selected when using the VSURF method and their estimated
importance. To compute the importance, we used the permutation method
described in Fisher et al.205 Briefly,
we randomly permuted each descriptor and then recomputed 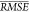 , for 1000 random permutations for each
descriptor. The mean increase in
, for 1000 random permutations for each
descriptor. The mean increase in 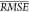 (see Table 6) for a given descriptor corresponds to how “important”
that descriptor is for the model, where large increases correspond
to higher importance.
(see Table 6) for a given descriptor corresponds to how “important”
that descriptor is for the model, where large increases correspond
to higher importance.
Table 6. Descriptor Importance of VSURF Regression Model, Ordered by Decreasing Importancea.
| VSURF | Spearman ρ | |
|---|---|---|
| Oxygen balance | 0.111 | –0.668 |
| Moment1 | 0.100 | 0.664 |
| Functional group | 0.095 | 0.659 |
| Q (kcal/g) | 0.081 | –0.668 |
| ZPE (kJ/g) | 0.054 | 0.280 |
| H acceptor | 0.054 | 0.589 |
| Moment3 | 0.054 | 0.193 |
| Max charge | 0.040 | 0.493 |
| Moment2 | 0.039 | –0.543 |
| Gas C | 0.039 | 0.085 |
| Band Energy | 0.033 | –0.582 |
| Lab | 0.033 | 0.560 |
| HOMO–LUMO gap | 0.031 | 0.577 |
| N[CO] | 0.024 | 0.178 |
| Min charge | 0.024 | 0.326 |
| N[CHH] | 0.021 | 0.141 |
| N[N] | 0.020 | 0.196 |
| Method | 0.005 | –0.432 |
| Grit | 0.005 | 0.415 |
Importance corresponds to the
expected decrease in 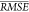 when each descriptor is randomly permuted.
The last column gives the Spearman correlation between the descriptor
and drop energy (in log J).
when each descriptor is randomly permuted.
The last column gives the Spearman correlation between the descriptor
and drop energy (in log J).
Discussion
One caveat of our analysis is that the data analyzed are observational and are not the result of designed experiments to examine the effect of particular descriptors on observed drop energy. Further, as discussed in the Results section, the descriptors are largely correlated. As a simple example, the count of oxygen atoms in a given molecule is related to the oxygen balance of that molecule (since the number of oxygen atoms is used to compute the oxygen balance). Thus, our results can be interpreted as primarily correlational. However, by analyzing a large data set of a broad range of explosives, and by restricting learning to the most parsimonious models, we are able to make conclusions regarding the most important chemical and physical factors (out of those available) for estimating drop energy.
To examine the effects of correlated descriptors on the importance
of said descriptors selected by VSURF in Table 6, we removed each descriptor in order of
importance and then refit and reevaluated the selected model. Hence,
we fit the model corresponding to Table 6 with all descriptors except oxygen balance,
then with all descriptors except oxygen balance and Moment1, and so
on. We also worked from the other direction, removing Method, then
Method and NCO, and so on. We used each submodel in the 10 10-fold
cross validations to determine 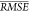 , as in the model selection study. The
, as in the model selection study. The 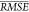 for the submodels is plotted for each model
in Figure 5. We notice
immediately that the inclusion of the first four descriptors (oxygen
balance, Moment1, Q, and functional group) account
for most of the predictive performance of the model. The inclusion
of further descriptors does improve performance, but only slightly.
On the other hand, the removal of oxygen balance, Moment1, Q, and functional group leaves model performance largely
unchanged. Although at first these facts may appear contradictory,
they suggest that, although oxygen balance, Moment1, Q, and functional group succinctly describe the influence of chemical
structure on impact sensitivity, all the information contained within
these descriptors is also contained within other descriptors. This
result may have been expected, since oxygen balance, Moment1, Q, and functional group are all computed from descriptors
that are present in the set of descriptors considered. However, this
study does illustrate the challenge in interpreting importance of
the descriptors. For example, it is unclear whether heat of formation
is selected for the model because it may be correlated with oxygen
balance and Q, or because it affects sensitivity
directly.
for the submodels is plotted for each model
in Figure 5. We notice
immediately that the inclusion of the first four descriptors (oxygen
balance, Moment1, Q, and functional group) account
for most of the predictive performance of the model. The inclusion
of further descriptors does improve performance, but only slightly.
On the other hand, the removal of oxygen balance, Moment1, Q, and functional group leaves model performance largely
unchanged. Although at first these facts may appear contradictory,
they suggest that, although oxygen balance, Moment1, Q, and functional group succinctly describe the influence of chemical
structure on impact sensitivity, all the information contained within
these descriptors is also contained within other descriptors. This
result may have been expected, since oxygen balance, Moment1, Q, and functional group are all computed from descriptors
that are present in the set of descriptors considered. However, this
study does illustrate the challenge in interpreting importance of
the descriptors. For example, it is unclear whether heat of formation
is selected for the model because it may be correlated with oxygen
balance and Q, or because it affects sensitivity
directly.
Figure 5.
Mean cross-validation performance  of the selected model when adding each
descriptor in turn (“forward”) and removing each descriptor
in turn (“backwards”).
of the selected model when adding each
descriptor in turn (“forward”) and removing each descriptor
in turn (“backwards”).
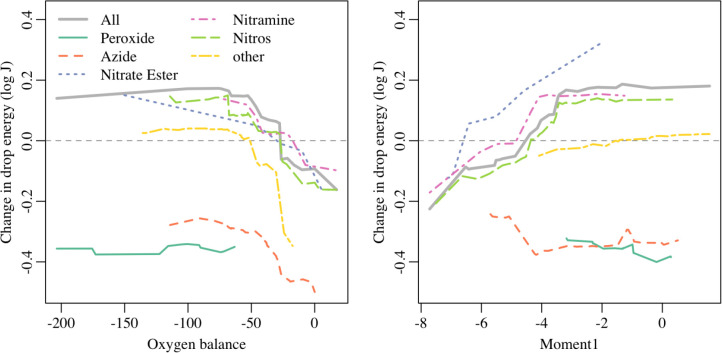
The estimated mean drop energy from the selected VSURF model is, in general, a nonlinear function that allows many interactions of the descriptors. One way to envision the average effect of each descriptor on the estimated drop energy, as predicted by the selected model, is to use the accumulated local effects.205,206 The estimated average effects of oxygen balance and Moment1, separated by functional group, on drop energy are shown in Figure 6 (it is challenging to interpret plots that include the effect of more than two descriptors on drop energy). The general trends across all the data agree with what we expect: drop energy decreases (sensitivity increases) with increasing oxygen balance and with decreasing Moment1. However, these trends are different for each functional group. For example, the peroxides show little trend of drop energy with either oxygen balance or Moment1. The effect of oxygen balance appears stronger for molecules with nitro groups than the trend for molecules with nitrate esters. Finally, we note that both Moment1 and oxygen balance show saturation effects for large drop energies (low sensitivities). We cannot determine whether this is a real physical phenomenon—that insensitive molecules perform the same beyond a certain sensitivity threshold—or an artifact of limitations in drop-weight testing, where there is some maximum drop height (320 cm at LANL), and hence maximum drop energy that can be measured.
Figure 6.
Estimated average effects of oxygen balance (left) and Moment1 (right), separated by functional group.
We examined the residuals to see where the model might predict incorrectly. In general, there is little trend of any of the selected descriptors with residuals. The exception is functional group, where the model estimates peroxide and azide groups as more sensitive than they truly are, and slightly underestimates sensitivity for “other” molecules (see Figure 7). The model most likely favors functional groups with many observations—nitros, nitromines, and nitrate esters—over those with few observations. Although the fact that the model performs less well on azide, peroxide, and other functional groups is not unexpected, one should take care in using predictions for molecules with these functional groups. Performance of the model could be improved by collecting more data for these underrepresented functional groups.
Figure 7.
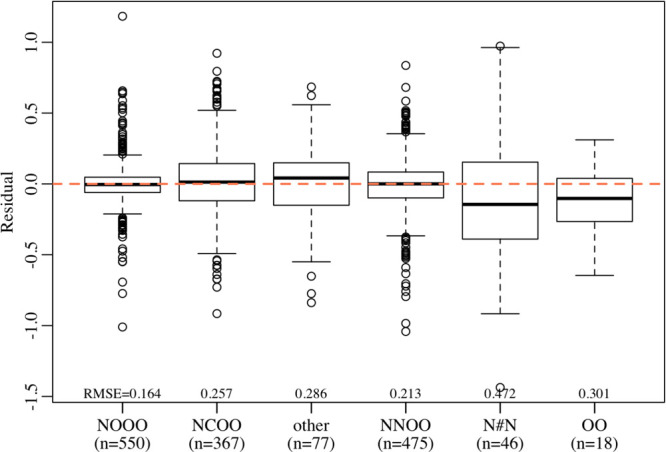
Residuals (observed drop energy less predicted drop energy) for each functional group.
Conclusions
We have collected and analyzed a large and diverse data set of drop-weight impact tests available in the literature. To mitigate the variability inherent in the drop-weight impact test, we have collected as many replications of drop-weight impact tests on the same molecules as were available. We illustrated that, despite the variability of the drop-weight impact test, we can predict drop energy relatively well across a broad range of explosives. We estimate that the predictions from the model come within a multiplicative factor of 4 of the mean drop energy for a hypothesized, unobserved molecule, corresponding to an out-of-sample coefficient of determination of about R2 ≈ 0.64. Our data set includes hundreds of repeat molecules on a variety of explosives, and we find that the variation of values for each individual explosive is substantial. This study also indicates that caution must be taken when drawing conclusions about important molecular properties when analyzing drop-weight impact test results, because many of the important variables appear to be interrelated.
We have illustrated the difficulty in interpreting the structure of the estimated random forest model. However, the model selects several descriptors convincingly: oxygen balance, Moment1, Q, and functional group; oxygen balance and Q are known to be predictive of explosive performance. We feel confident in concluding that, generally, more performant explosives are more sensitive, which confirms reports elsewhere.8,10,171,207,208 We postulate that the functional group descriptor likely relates to the ease of initiating reaction in the material.12 Although it has been hypothesized that the HOMO–LUMO gap is important in determining molecular properties, the moments of the electronic eigenspectrum, especially Moment1, which gives a more complete picture of the electronic structure, appear to correlate much better with drop-weight impact sensitivity.
The interpretation of other descriptors may be even more challenging. For example, band energy (the sum of occupied molecular orbital energies) is selected by the VSURF method. However, band energy is also highly correlated with oxygen balance and Moment1. It is unclear whether band energy is selected because of these correlations, because band energy influences sensitivity in some other way, or because all are calculated from similar inputs. Although we can only learn an interpolative model from this large data set, we know how each descriptor is computed from other data streams. Future work should explicitly encode these relationships. For example, encoding that the number of oxygen atoms feeds into the oxygen balance calculation can allow one to test whether the number of oxygen atoms influences sensitivity only through oxygen balance, or if there is additional influence. A model with the known physical hierarchy encoded should improve our ability to be confident in drawing conclusions regarding the chemical descriptors of sensitivity based on the best predictive model fit to observational data.
Acknowledgments
The authors thank the LANL High Explosives Science and Technology group and it is analytical team, who were gracious in sharing over 60 years of drop-weight impact test data for this study. This work was supported by the Laboratory Directed Research and Development program of Los Alamos National Laboratory under project numbers 20200234ER and 20220068DR. Los Alamos National Laboratory is operated by Triad National Security, LLC, for the National Nuclear Security Administration of U.S. Department of Energy (Contract No. 89233218CNA000001). This research used resources provided by the Los Alamos National Laboratory Institutional Computing Program, which is supported by the U.S. Department of Energy National Nuclear Security Administration under Contract No. 89233218CNA000001. This work as been cleared for unlimited release by Los Alamos National Laboratory (LANL), LA-UR-22-25745.
Data Availability Statement
The data used in this article are publicly available as Supporting Information. All methods are existing and available in open source software, and thus, we do not provide reproduction software. All statistical analysis was performed using the programming language R, version 4.1.3, available at https://cran.r-project.org/src/base/R-4/. Key packages for reproduction, and their versions, are randomForest (4.6-14), VSURF (1.1.0), glmnet (4.1-3), ALEPlot (1.1), and mltools (0.3.5). All packages are available online at https://cran.r-project.org/. All of the density functional tight binding calculations were performed using the open-source code LATTE, which is available for download from https://github.com/lanl/LATTE. The lanl31 parametrization is supplied with the LATTE source via the GitHub repository and in Cawkwell and Perriot.176 Open Babel version 3.1.0 was used to convert SMILES to three-dimensional geometries in the standard .xyz format.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jcim.2c01154.
The authors declare no competing financial interest.
Supplementary Material
References
- DOE Explosive Safety Standard; DOE-STD-1212-2012; U.S. Department of Energy, 2012.
- Rae P. J.; Dickson P. M. Some Observations About the Drop-weight Explosive Sensitivity Test. J. Dyn. Behav. Mater. 2021, 7, 414–424. 10.1007/s40870-020-00276-2. [DOI] [Google Scholar]
- Davis W. C. High Explosives: The Interaction of Chemistry and Mechanics. Los Alamos Science 1981, 2, 48. [Google Scholar]
- Manner V.; Cawkwell M.; Kober E.; Myers T.; Brown G.; Tian H.; Snyder C.; Perriot R.; Preston D. Examining the Chemical and Structural Properties that Influence the Sensitivity of Energetic Nitrate Esters. Chem. Sci. 2018, 9, 3649–3663. 10.1039/C8SC00903A. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng R.; Zecevic M.; Moore J.; Cawkwell M.; Manner V. W.. Large Deformation GNARLYX Hydrocode Simulations of the Drop Weight Impact Experiment. In Review, 2022.
- Wenograd J. Behaviour of Explosives at Very High Temperatures. Trans. Faraday Soc. 1961, 57, 1612–1620. 10.1039/tf9615701612. [DOI] [Google Scholar]
- Kamlet M.The Relationship of Impact Sensitivity with Structure of Organic High Explosives. II. Polynitroaliphatic Explosives. Sixth Symposium (International) on Detonation, Coronads, CA, 1976; pp 69–72.
- Kamlet M. J.; Adolph H. G. Relationship of Impact Sensitivity with Structure of Organic High Explosives 0.2. Polynitroaromatic Explosives. Propellants, Explos. Pyrotech. 1979, 4, 30–34. 10.1002/prep.19790040204. [DOI] [Google Scholar]
- Bowden F. P.; Yoffe A.. Initiation and Growth of Explosion in Liquids and Solids; Cambridge University Press, 1952. [Google Scholar]
- Storm C.; Stine J.; Kramer J.. Chemistry and Physics of Energetic Materials; Springer, 1990; pp 605–639. [Google Scholar]
- Cawkwell M. J.; Manner V. W. Ranking the Drop-Weight Impact Sensitivity of Common Explosives Using Arrhenius Chemical Rates Computed from Quantum Molecular Dynamics Simulations. J. Phys. Chem. A 2020, 124, 74–81. 10.1021/acs.jpca.9b10808. [DOI] [PubMed] [Google Scholar]
- Cawkwell M. J.; Davis J.; Lease N.; Marrs F. W.; Burch A.; Ferreira S.; Manner V. W. Understanding Explosive Sensitivity with Effective Trigger Linkage Kinetics. ACS Phys. Chem. Au 2022, 2, 448. 10.1021/acsphyschemau.2c00022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cady H. H.; Larson A. C. Crystal Structure of 1,3,5-Triamino-2,4,6-Trinitrobenzene. Acta Crystallogr. 1965, 18, 485–496. 10.1107/S0365110X6500107X. [DOI] [Google Scholar]
- Rice B. M.; Hare J. J. A Quantum Mechanical Investigation of the Relation Between Impact Sensitivity and the Charge Distribution in Energetic Molecules. J. Phys. Chem. A 2002, 106, 1770–1783. 10.1021/jp012602q. [DOI] [Google Scholar]
- Rice B. M.; Sahu S.; Owens F. J. Density Functional Calculations of Bond Dissociation Energies for NO2 Scission in Some Nitroaromatic Molecules. J. Mol. Struct. THEOCHEM 2002, 583, 69–72. 10.1016/S0166-1280(01)00782-5. [DOI] [Google Scholar]
- Zhurova E. A.; Stash A. I.; Tsirelson V. G.; Zhurov V. V.; Bartashevich E. V.; Potemkin V. A.; Pinkerton A. A. Atoms-in-molecules Study of Intra- and Intermolecular Bonding in the Pentaerythritol Tetranitrate Crystal. J. Am. Chem. Soc. 2006, 128, 14728–14734. 10.1021/ja0658620. [DOI] [PubMed] [Google Scholar]
- Kimmel A. V.; Sushko P. V.; Shluger A. L.; Kuklja M. M. Effect of Molecular and Lattice Structure on Hydrogen Transfer in Molecular Crystals of Diamino-Dinitroethylene and Triamino-Trinitrobenzene. J. Phys. Chem. A 2008, 112, 4496–4500. 10.1021/jp800930d. [DOI] [PubMed] [Google Scholar]
- Klapotke T. M.; Sabate C. M. Bistetrazoles: Nitrogen-rich, High-performing, Insensitive Energetic Compounds. Chem. Mater. 2008, 20, 3629–3637. 10.1021/cm703657k. [DOI] [Google Scholar]
- Dattelbaum D.; Sheffield S.; Stahl D.; Dattelbaum A. Influence of Hot Spot Features on the Shock Initiation of Heterogeneous Nitromethane. AIP Conf. Proc. 2009, 263–266. 10.1063/1.3295119. [DOI] [Google Scholar]
- Landerville A. C.; Oleynik I. I.; White C. T. Reactive Molecular Dynamics of Hypervelocity Collisions of PETN Molecules. J. Phys. Chem. A 2009, 113, 12094–12104. 10.1021/jp905969y. [DOI] [PubMed] [Google Scholar]
- Yau A. D.; Byrd E. F. C.; Rice B. M. An Investigation of KS-DFT Electron Densities used in Atoms-in-Molecules Studies of Energetic Molecules. J. Phys. Chem. A 2009, 113, 6166–6171. 10.1021/jp9010845. [DOI] [PubMed] [Google Scholar]
- Dippold A. A.; Klapotke T. M. A Study of Dinitro-bis-1,2,4-triazole-1,1 ’-diol and Derivatives: Design of High-Performance Insensitive Energetic Materials by the Introduction of N-Oxides. J. Am. Chem. Soc. 2013, 135, 9931–9938. 10.1021/ja404164j. [DOI] [PubMed] [Google Scholar]
- Evers J.; Gobel M.; Krumm B.; Martin F.; Medvedyev S.; Oehlinger G.; Steemann F. X.; Troyan I.; Klapotke T. M.; Eremets M. I. Molecular Structure of Hydrazoic Acid with Hydrogen-Bonded Tetramers in Nearly Planar Layers. J. Am. Chem. Soc. 2011, 133, 12100–12105. 10.1021/ja2027053. [DOI] [PubMed] [Google Scholar]
- Chellappa R. S.; Dattelbaum D. M.; Coe J. D.; Velisavljevic N.; Stevens L. L.; Liu Z. X. Intermolecular Stabilization of 3,3 ’-Diamino-4,4 ’-azoxyfurazan (DAAF) Compressed to 20 GPa. J. Phys. Chem. A 2014, 118, 5969–5982. 10.1021/jp504935g. [DOI] [PubMed] [Google Scholar]
- Bennion J. C.; McBain A.; Son S. F.; Matzger A. J. Design and Synthesis of a Series of Nitrogen-Rich Energetic Cocrystals of 5,5 ’-Dinitro-2H,2H ’-3,3 ’-bi-1,2,4-triazole (DNBT). Cryst. Growth Des. 2015, 15, 2545–2549. 10.1021/acs.cgd.5b00336. [DOI] [Google Scholar]
- Rice B. M.; Larentzos J. P.; Byrd E. F. C.; Weingarten N. S. Parameterizing Complex Reactive Force Fields Using Multiple Objective Evolutionary Strategies (MOES): Part 2: Transferability of ReaxFF Models to C-H-N-O Energetic Materials. J. Chem. Theory Comput. 2015, 11, 392–405. 10.1021/ct5007899. [DOI] [PubMed] [Google Scholar]
- Zeman S.; Jungova M. Sensitivity and Performance of Energetic Materials. Propellants, Explos. Pyrotech. 2016, 41, 426–451. 10.1002/prep.201500351. [DOI] [Google Scholar]
- Nefati H.; Cense J. M.; Legendre J. J. Prediction of the Impact Sensitivity by Neural Networks. J. Chem. Inf. Comput. Sci. 1996, 36, 804–810. 10.1021/ci950223m. [DOI] [Google Scholar]
- Keshavarz M. H.; Jaafari M. Investigation of the Various Structure Parameters for Predicting Impact Sensitivity of Energetic Molecules via Artificial Neural Network. Propellants, Explos. Pyrotech. 2006, 31, 216–225. 10.1002/prep.200600030. [DOI] [Google Scholar]
- Keshavarz M. H.; Pouretedal H. R.; Semnani A. Novel Correlation for Predicting Impact Sensitivity of Nitroheterocyclic Energetic Molecules. J. Hazard. Mater. 2007, 141, 803–807. 10.1016/j.jhazmat.2006.07.046. [DOI] [PubMed] [Google Scholar]
- Wang R.; Jiang J. C.; Pan Y.; Cao H. Y.; Cui Y. Prediction of Impact Sensitivity of Nitro Energetic Compounds by Neural Network Based on Electrotopological-state Indices. J. Hazard. Mater. 2009, 166, 155–186. 10.1016/j.jhazmat.2008.11.005. [DOI] [PubMed] [Google Scholar]
- Wang R.; Jiang J. C.; Pan Y. Prediction of Impact Sensitivity of Nonheterocyclic Nitroenergetic Compounds Using Genetic Algorithm and Artificial Neural Network. J. Energy Mater. 2012, 30, 135–155. 10.1080/07370652.2010.550598. [DOI] [Google Scholar]
- Elton D. C.; Boukouvalas Z.; Butrico M. S.; Fuge M. D.; Chung P. W. Applying Machine Learning Techniques to Predict the Properties of Energetic Materials. Sci. Rep. 2018, 8, 9059. 10.1038/s41598-018-27344-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brill T. B.; James K. J. Thermal-Decomposition of Energetic Materials. 61. Perfidy in the Amino-2,4,6-Trinitrobenzene Series of Explosives. J. Phys. Chem. 1993, 97, 8752–8758. 10.1021/j100136a017. [DOI] [Google Scholar]
- Doherty R. M.; Watt D. S. Relationship Between RDX Properties and Sensitivity. Propellants, Explos. Pyrotech. 2008, 33, 4–13. 10.1002/prep.200800201. [DOI] [Google Scholar]
- Marrs F. W.; Manner V. W.; Burch A. C.; Yeager J. D.; Brown G. W.; Kay L. M.; Buckley R. T.; Anderson-Cook C. M.; Cawkwell M. J. Sources of Variation in Drop-weight Impact Sensitivity Testing of the Explosive Pentaerythritol Tetranitrate. Ind. Eng. Chem. Res. 2021, 60, 5024–5033. 10.1021/acs.iecr.0c06294. [DOI] [Google Scholar]
- Burch A. C.; Kay L. M.; Yeager J. D.; Brown G. W.; Tappan B. C.; Cawkwell M. J.; Manner V. W. The Effect of Hardness on Polymer-bonded Pentaerythritol Tetranitrate (PETN) Explosive Impact Sensitivity. J. Appl. Phys. 2022, 131, 015102. 10.1063/5.0073867. [DOI] [Google Scholar]
- Gibbs T.; Popolato A.. LASL Explosive Property Data; University of California Press, 1980. [Google Scholar]
- Lease N.; Kay L. M.; Brown G. W.; Chavez D. E.; Robbins D.; Byrd E. F. C.; Imler G. H.; Parrish D. A.; Manner V. W. Synthesis of Erythritol Tetranitrate Derivatives: Functional Group Tuning of Explosive Sensitivity. J. Org. Chem. 2020, 85, 4619–4626. 10.1021/acs.joc.9b03344. [DOI] [PubMed] [Google Scholar]
- Chavez D. E.; Parrish D. A.; Mitchell L.; Imler G. H. Azido and Tetrazolo 1,2,4,5-Tetrazine N-Oxides. Angew. Chem., Int. Ed. 2017, 56, 3575–3578. 10.1002/anie.201612496. [DOI] [PubMed] [Google Scholar]
- Klapotke T. M.; Martin F. A.; Stierstorfer J. C2N14: An Energetic and Highly Sensitive Binary Azidotetrazole. Angew. Chem., Int. Ed. 2011, 50, 4227–4229. 10.1002/anie.201100300. [DOI] [PubMed] [Google Scholar]
- Barton L. M.; Edwards J. T.; Johnson E. C.; Bukowski E. J.; Sausa R. C.; Byrd E. F. C.; Orlicki J. A.; Sabatini J. J.; Baran P. S. Impact of Stereo- and Regiochemistry on Energetic Materials. J. Am. Chem. Soc. 2019, 141, 12531–12535. 10.1021/jacs.9b06961. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dharavath S.; Mitchell L. A.; Parrish D. A.; Shreeve J. M. From FOX-7 to H-FOX to Insensitive Energetic Materials with Hypergolic Properties. Chem. Commun. 2016, 52, 8168–8168. 10.1039/C6CC90263D. [DOI] [PubMed] [Google Scholar]
- Wang R.; Jiang J.; Pan Y.; Cao H.; Cui Y. Prediction of Impact Sensitivity of Nitro Energetic Compounds by Neural Network Based on Electrotopological-State Indices. J. Hazard. Mater. 2009, 166, 155–186. 10.1016/j.jhazmat.2008.11.005. [DOI] [PubMed] [Google Scholar]
- Chavez D. E.; Schulze M. C.; Parrish D. A. Synthesis and Characterization of N 3 -(2,2,2-Trinitroethyl)-1,2,4-Oxadiazole-3,5-Diamine. Chem. Heterocycl. Compd. 2017, 53, 737–739. 10.1007/s10593-017-2119-4. [DOI] [Google Scholar]
- Chavez D. E.; Bottaro J. C.; Petrie M.; Parrish D. A. Synthesis and Thermal Behavior of a Fused, Tricyclic 1,2,3,4-Tetrazine Ring System. Angew. Chem., Int. Ed. 2015, 54, 12973–12975. 10.1002/anie.201506744. [DOI] [PubMed] [Google Scholar]
- Chavez D. E.; Parrish D. A.; Leonard P. The Synthesis and Characterization of a New Furazan Heterocyclic System. Synlett 2012, 23, 2126–2128. 10.1055/s-0032-1316704. [DOI] [Google Scholar]
- Leonard P. W.; Pollard C. J.; Chavez D. E.; Rice B. M.; Parrish D. A. 3,6-Bis(4-nitro-1,2,5-oxadiazol-3-yl)-1,4,2,5-dioxadiazene (BNDD): A Powerful Sensitive Explosive. Synlett 2011, 2011, 2097–2099. 10.1055/s-0030-1261169. [DOI] [Google Scholar]
- Schulze M. C.; Scott B. L.; Chavez D. E. A High Density Pyrazolo-triazine Explosive (PTX). J. Mater. Chem. A 2015, 3, 17963–17965. 10.1039/C5TA05291B. [DOI] [Google Scholar]
- Mitchell L. A.; Imler G. H.; Parrish D. A.; Deschamps J. R.; Leonard P. W.; Chavez D. E. Crystal Structures of the Three Closely Related Compounds: Bis-[(1H-tetra-zol-5-yl)meth-yl]nitramide, Tri-amino-guanidinium 5-([(1H-tetra-zol-5-yl)meth-yl](nitro)-amino-meth-yl)tetra-zol-1-ide, and Di-ammonium bis-[(tetra-zol-1-id-5-yl)meth-yl]nitramide Monohydrate. Acta Crystallogr. E: Crystallogr. Commun. 2017, 73, 1056–1061. 10.1107/S2056989017008817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lease N.; Kay L. M.; Brown G. W.; Chavez D. E.; Leonard P. W.; Robbins D.; Manner V. W. Modifying Nitrate Ester Sensitivity Properties Using Explosive Isomers. Cryst. Growth Des. 2019, 19, 6708–6714. 10.1021/acs.cgd.9b01062. [DOI] [Google Scholar]
- Manner V. W.; Tiemann C. G.; Yeager J. D.; Kay L. M.; Lease N.; Cawkwell M. J.; Brown G. W.; Anthony S. P.; Montanari D. Examining Explosives Handling Sensitivity of Trinitrotoluene (TNT) with Different Particle Sizes. AIP Conf. Proc. 2020, 2272, 050015. 10.1063/12.0001125. [DOI] [Google Scholar]
- Manner V. W.; Cawkwell M. J.; Brown G. W.; Yeager J.; Kay L. M.; Shorty M.; Leonard P.; Tappan B. C.; Veauthier J.. Examining the Effects of Crystal Structure and Bonding on Explosive Impact Sensitivity. Sixteenth International Detonation Symposium, 2019; pp 1384–1393.
- Tang Y. X.; He C. L.; Mitchell L. A.; Parrish D. A.; Shreeve J. M. Small Cation-Based High-Performance Energetic Nitraminofurazanates. Chem.—Eur. J. 2016, 22, 11846–11853. 10.1002/chem.201602171. [DOI] [PubMed] [Google Scholar]
- Tang Y. X.; Ma J. C.; Imler G. H.; Parrish D. A.; Shreeve J. M. Versatile Functionalization of 3,5-Diamino-4-nitropyrazole for Promising Insensitive Energetic Compounds. Dalton Trans 2019, 48, 14490–14496. 10.1039/C9DT03138C. [DOI] [PubMed] [Google Scholar]
- Tang Y.; Imler G. H.; Parrish D. A.; Shreeve J. M. Energetic and Fluorescent Azole-Fused 4-Amino-1,2,3-triazine-3-N-oxides. ACS Appl. Energy Mater. 2019, 2, 8871–8877. 10.1021/acsaem.9b01889. [DOI] [Google Scholar]
- Liu Y. L.; Zhao G.; Yu Q.; Tang Y. X.; Imler G. H.; Parrish D. A.; Shreeve J. M. Intermolecular Weak Hydrogen Bonding (Het-H-N/O): An Effective Strategy for the Synthesis of Monosubstituted 1,2,4,5-Tetrazine-Based Energetic Materials with Excellent Sensitivity. J. Org. Chem. 2019, 84, 16019–16026. 10.1021/acs.joc.9b02484. [DOI] [PubMed] [Google Scholar]
- Liu Y. L.; He C. L.; Tang Y. X.; Imler G. H.; Parrish D. A.; Shreeve J. M. Asymmetric Nitrogen-rich Energetic Materials Resulting from the Combination of Tetrazolyl, Dinitromethyl and (1,2,4-Oxadiazol-5-yl)nitroamino Groups with Furoxan. Dalton Trans 2018, 47, 16558–16566. 10.1039/C8DT03616K. [DOI] [PubMed] [Google Scholar]
- Zhang J. C.; Yin P.; Pan G. X.; Wang Z. Y.; Zhang J. H.; Mitchell L. A.; Parrish D. A.; Shreeve J. M. 5-(4-Azidofurazan-3-yl)-1-hydroxytetrazole and Its Derivatives: From Green Primary to Secondary Explosives. New J. Chem. 2019, 43, 12684–12689. 10.1039/C9NJ03306H. [DOI] [Google Scholar]
- He C.; Imler G. H.; Parrish D. A.; Shreeve J. M. Energetic Salts of 4-Nitramino-3-(5-dinitromethyl-1,2,4-oxadiazolyl)-furazan: Powerful Alliance Towards Good Thermal Stability and High Performance. J. Mater. Chem. A 2018, 6, 16833–16837. 10.1039/C8TA06199H. [DOI] [Google Scholar]
- Zhang J.; Zhang J.; Imler G. H.; Parrish D. A.; Shreeve J. M. Sodium and Potassium 3,5-Dinitro-4-hydropyrazolate: Three-Dimensional Metal-Organic Frameworks as Promising Super-heat-resistant Explosives. ACS Appl. Energy Mater. 2019, 2, 7628–7634. 10.1021/acsaem.9b01608. [DOI] [Google Scholar]
- Gospodinov I.; Singer J.; Klapotke T. M.; Stierstorfer J. The Pyridazine Scaffold as a Building Block for Energetic Materials: Synthesis, Characterization, and Properties. Z. Anorg. Allg. Chem. 2019, 645, 1247–1254. 10.1002/zaac.201900146. [DOI] [Google Scholar]
- Claßen M.; Heimsch S. B.; Klapotke T. M. Synthesis and Characterization of New Azido Esters Derived from Malonic Acid. Propellants, Explos. Pyrotech. 2019, 44, 1515–1520. 10.1002/prep.201900285. [DOI] [Google Scholar]
- Hermann T. S.; Klapotke T. M.; Krumm B.; Stierstorfer J. Synthesis, Characterization and Properties of Ureido-Furazan Derivatives. J. Heterocycl. Chem. 2018, 55, 852–862. 10.1002/jhet.3109. [DOI] [Google Scholar]
- Klapotke T. M.; Krumm B.; Reith T. Polyfunctional Energetic Nitrates Derived from Tris(hydroxymethyl) Aminomethane (Tris). Eur. J. Org. Chem. 2017, 2017, 3666–3673. 10.1002/ejoc.201700434. [DOI] [Google Scholar]
- Klapotke T. M.; Krumm B.; Widera A. Synthesis and Properties of Tetranitro-Substituted Adamantane Derivatives. ChemPlusChem. 2018, 83, 61–69. 10.1002/cplu.201700542. [DOI] [PubMed] [Google Scholar]
- Hermann T. S.; Karaghiosoff K.; Klapotke T. M.; Stierstorfer J. Synthesis and Characterization of 2,2 ’-Dinitramino-5,5 ’-bi(1-oxa-3,4-diazole) and Derivatives as Economic and Highly Dense Energetic Materials. Chem.—Eur. J. 2017, 23, 12087–12091. 10.1002/chem.201702191. [DOI] [PubMed] [Google Scholar]
- Klapotke T. M.; Stiasny B.; Stierstorfer J. Energetic Materials - Nitrated Phenyl Peroxy Anhydrides as Peroxide Based Explosives with Relatively High Densities and Thermal Stabilities. ChemistrySelect 2016, 1, 4057–4061. 10.1002/slct.201601114. [DOI] [Google Scholar]
- Klapotke T. M.; Rotariu T.; Stiasny B.; Stierstorfer J.; Wiegmann S.; Zecheru T. Azido(tert-butylperoxy)methyl Compounds - An Exceptional Class of Energetic Materials. Eur. J. Org. Chem. 2016, 2016, 4382–4386. 10.1002/ejoc.201600717. [DOI] [Google Scholar]
- Klapotke T. M.; Krumm B.; Scharf R. From Amino Acids to High-Energy Dense Oxidizers: Polynitro Materials Derived from beta-Alanine and L-Aspartic Acid. Z. Anorg. Allg. Chem. 2016, 642, 887–895. 10.1002/zaac.201600223. [DOI] [Google Scholar]
- Axthammer Q. J.; Klapotke T. M.; Krumm B. Studies on the Synthesis and Properties of 1,1,1-trinitroprop-2-yl Urea, Carbamate and Nitrocarbamate. Z. fur Naturforsch. B, J. Chem. Sci. 2016, 71, 811–820. 10.1515/znb-2016-0022. [DOI] [Google Scholar]
- Klapotke T. M.; Krumm B.; Scharf R. Oxalyl Chloride and Hydrazide Based Energetic Polynitro Derivatives. Eur. J. Inorg. Chem. 2016, 2016, 3086–3093. 10.1002/ejic.201600357. [DOI] [Google Scholar]
- Klapotke T. M.; Witkowski T. G. 5,5-Bis(2,4,6-trinitrophenyl)-2,2-bi(1,3,4-oxadiazole) (TKX-55): Thermally Stable Explosive with Outstanding Properties. ChemPlusChem. 2016, 81, 357–360. 10.1002/cplu.201600078. [DOI] [PubMed] [Google Scholar]
- Izsak D.; Klapotke T. M.; Pfluger C. Energetic Derivatives of 5-(5-amino-2H-1,2,3-triazol-4-yl)-1H-tetrazole. Dalton Trans 2015, 44, 17054–17063. 10.1039/C5DT03044G. [DOI] [PubMed] [Google Scholar]
- Klapotke T. M.; Penger A.; Pfluger C.; Stierstorfer J. Melt-cast Materials: Combining the Advantages of Highly Nitrated Azoles and Open-chain Nitramines. New J. Chem. 2016, 40, 6059–6069. 10.1039/C6NJ00202A. [DOI] [Google Scholar]
- Gamage N. D. H.; Stiasny B.; Stierstorfer J.; Martin P. D.; Klapotke T. M.; Winter C. H. Highly Energetic, Low Sensitivity Aromatic Peroxy Acids. Chem.—Eur. J. 2016, 22, 2582–2585. 10.1002/chem.201502989. [DOI] [PubMed] [Google Scholar]
- Klapotke T. M.; Krumm B.; Rest S. F.; Suceska M. Polynitro Containing Energetic Materials based on Carbonyldiisocyanate and 2,2-Dinitropropane-1,3-diol. Z. Anorg. Allg. Chem. 2014, 640, 84–92. 10.1002/zaac.201300563. [DOI] [Google Scholar]
- Aas B.; Kettner M. A.; Klapotke T. M.; Suceska M.; Zoller C. Asymmetric Carbamate Derivatives Containing Secondary Nitramine, 2,2,2-Trinitroethyl, and 2-Fluoro-2,2-dinitroethyl Moieties. Eur. J. Inorg. Chem. 2013, 2013, 6028–6036. 10.1002/ejic.201301114. [DOI] [Google Scholar]
- Kettner M. A.; Karaghiosoff K.; Klapotke T. M.; Suceska M.; Wunder S. 3,3 ’-Bi(1,2,4-oxadiazoles) Featuring the Fluorodinitromethyl and Trinitromethyl Groups. Chem.—Eur. J. 2014, 20, 7622–7631. 10.1002/chem.201402291. [DOI] [PubMed] [Google Scholar]
- Klapotke T. M.; Krumm B.; Moll R.; Rest S. F.; Schnick W.; Seibald M. Asymmetric Fluorodinitromethyl Derivatives of 2,2,2-Trinitroethyl N-(2,2,2-trinitroethyl)carbamate. J. Fluor. Chem. 2013, 156, 253–261. 10.1016/j.jfluchem.2013.06.019. [DOI] [Google Scholar]
- Klapotke T. M.; Preimesser A.; Stierstorfer J. Energetic Derivatives of 4, 4 ’,5, 5 ’-Tetranitro-2, 2 ’-bisimidazole (TNBI). Z. Anorg. Allg. Chem. 2012, 638, 1278–1286. 10.1002/zaac.201200188. [DOI] [Google Scholar]
- Dippold A. A.; Klapotke T. M. Nitrogen-Rich Bis-1,2,4-triazoles-A Comparative Study of Structural and Energetic Properties. Chem.—Eur. J. 2012, 18, 16742–16753. 10.1002/chem.201202483. [DOI] [PubMed] [Google Scholar]
- Klapotke T. M.; Krumm B.; Steemann F. X.; Umland K. D. Bis(1,3-dinitratoprop-2-yl) Nitramine, a New Sensitive Explosive Combining a Nitrate Ester with a Nitramine. Z. Anorg. Allg. Chem. 2010, 636, 2343–2346. 10.1002/zaac.201000229. [DOI] [Google Scholar]
- Klapotke T. M.; Piercey D. G.; Stierstorfer J.; Weyrauther M. The Synthesis and Energetic Properties of 5,7-Dinitrobenzo-1,2,3,4-tetrazine-1,3-dioxide (DNBTDO). Propellants, Explos. Pyrotech 2012, 37, 527–535. 10.1002/prep.201100151. [DOI] [Google Scholar]
- Klapotke T. M.; Piercey D. G.; Stierstorfer J. The Facile Synthesis and Energetic Properties of an Energetic Furoxan Lacking Traditional “Explosophore” Moieties: (E,E)-3,4-bis(oximomethyl)furoxan (DPX1). Propellants, Explos. Pyrotech 2011, 36, 160–167. 10.1002/prep.201000057. [DOI] [Google Scholar]
- Evangelisti C.; Klapotke T. M.; Krumm B.; Nieder A.; Berger R. J. F.; Hayes S. A.; Mitzel N. W.; Troegel D.; Tacke R. Si la-Substitution of Alkyl Nitrates: Synthesis, Structural Characterization, and Sensitivity Studies of Highly Explosive (Nitratomethyl)-, Bis(nitratomethyl)-, and Tris(nitratomethyl)silanes and Their Corresponding Carbon Analogues. Inorg. Chem. 2010, 49, 4865–4880. 10.1021/ic902387y. [DOI] [PubMed] [Google Scholar]
- Dippold A. A.; Klapotke T. M.; Martin F. A.; Wiedbrauk S. Nitraminoazoles Based on ANTA - A Comprehensive Study of Structural and Energetic Properties. Eur. J. Inorg. Chem. 2012, 2012, 2429–2443. 10.1002/ejic.201101416. [DOI] [Google Scholar]
- Fischer D.; Klapotke T. M.; Piercey D. G.; Stierstorfer J. Synthesis of 5-Aminotetrazole-1N-oxide and Its Azo Derivative: A Key Step in the Development of New Energetic Materials. Chem.—Eur. J. 2013, 19, 4602–4613. 10.1002/chem.201203493. [DOI] [PubMed] [Google Scholar]
- Klapotke T. M.; Nordheider A.; Stierstorfer J. Synthesis and reactivity of an unexpected highly sensitive 1-carboxymethyl-3-diazonio-5-nitrimino-1,2,4-triazole. New J. Chem. 2012, 36, 1463–1468. 10.1039/c2nj40044h. [DOI] [Google Scholar]
- Dippold A. A.; Klapotke T. M. Synthesis and Characterization of 5-(1,2,4-Triazol-3-yl)tetrazoles with Various Energetic Functionalities. Chem.—Asian J. 2013, 8, 1463–1471. 10.1002/asia.201300063. [DOI] [PubMed] [Google Scholar]
- Klapotke T. M.; Krumm B.; Steemann F. X. Preparation, Characterization, and Sensitivity Data of Some Azidomethyl Nitramines. Propellants, Explos. Pyrotech. 2009, 34, 13–23. 10.1002/prep.200700261. [DOI] [Google Scholar]
- Heppekausen J.; Klapotke T. M.; Sproll S. A. Synthesis of Functionalized Tetrazenes as Energetic Compounds. J. Org. Chem. 2009, 74, 2460–2466. 10.1021/jo802738c. [DOI] [PubMed] [Google Scholar]
- Klapotke T. M.; Sabate C. M.; Stierstorfer J. Neutral 5-nitrotetrazoles: Easy Initiation with Low Pollution. New J. Chem. 2009, 33, 136–147. 10.1039/B812529E. [DOI] [Google Scholar]
- Stepanov V.; Anglade V.; Bezmelnitsyn A.; Krasnoperov L. N.. Production and Characterization of Nanocrystalline Explosive RDX. AIChE Annual Meeting, San Francisco, CA, USA, 2006.
- Balzer J.; Field J.; Gifford M.; Proud W.; Walley S. High-speed Photographic Study of the Drop-Weight Impact Response of Ultrafine and Conventional PETN and RDX. Combust. Flame 2002, 130, 298–306. 10.1016/S0010-2180(02)00373-5. [DOI] [Google Scholar]
- Klapotke T. M.; Mayer P.; Stierstorfer J.; Weigand J. J. Bistetrazolylamines – Synthesis and Characterization. J. Mater. Chem. 2008, 18, 5248–5258. 10.1039/b811273h. [DOI] [Google Scholar]
- Snyder C. J.; Wells L. A.; Chavez D. E.; Imler G. H.; Parrish D. A. Polycyclic N-oxides: high performing, low sensitivity energetic materials. Chem. Commun. 2019, 55, 2461–2464. 10.1039/C8CC09653H. [DOI] [PubMed] [Google Scholar]
- Ma Q.; Zhang G. J.; Li J.; Zhang Z. Q.; Lu H. C.; Liao L. Y.; Fan G. J.; Nie F. D. Pyrazol-triazole Energetic Hybrid with High Thermal Stability and Decreased Sensitivity: Facile Synthesis, Characterization and Promising Performance. Chem. Eng. J. 2020, 379, 122331. 10.1016/j.cej.2019.122331. [DOI] [Google Scholar]
- Zhao G.; Yin P.; Kumar D.; Imler G. H.; Parrish D. A.; Shreeve J. M. Bis(3-nitro-1-(trinitromethyl)-1H-1,2,4-triazol-5-yl)methanone: An Applicable and Very Dense Green Oxidizer. J. Am. Chem. Soc. 2019, 141, 19581–19584. 10.1021/jacs.9b11326. [DOI] [PubMed] [Google Scholar]
- Yu Q.; Imler G. H.; Parrish D. A.; Shreeve J. M. Challenging the Limits of Nitro Groups Associated with a Tetrazole Ring. Org. Lett. 2019, 21, 4684–4688. 10.1021/acs.orglett.9b01565. [DOI] [PubMed] [Google Scholar]
- Ma J. C.; Tang Y. X.; Cheng G. B.; Imler G. H.; Parrish D. A.; Shreeve J. M. Energetic Derivatives of 8-Nitropyrazolo[1,5-a][1,3,5]triazine-2,4,7-triamine: Achieving Balanced Explosives by Fusing Pyrazole with Triazine. Org. Lett. 2020, 22, 1321–1325. 10.1021/acs.orglett.9b04642. [DOI] [PubMed] [Google Scholar]
- Hu L.; Yin P.; Imler G. H.; Parrish D. A.; Gao H. X.; Shreeve J. M. Fused Rings with N-oxide and -NH2: Good Combination for High Density and Low Sensitivity Energetic Materials. Chem. Commun. 2019, 55, 8979–8982. 10.1039/C9CC04496E. [DOI] [PubMed] [Google Scholar]
- Leonard P. W.; Chavez D. E.; Pagoria P. F.; Parrish D. L. Azotetrazolylfurazan and Nitrogenous Salt Derivatives. Propellants, Explos. Pyrotech. 2011, 36, 233–239. 10.1002/prep.201000093. [DOI] [Google Scholar]
- Pagoria P. F.; Zhang M. X.; Zuckerman N. B.; DeHope A. J.; Parrish D. A. Synthesis and Characterization of Multicyclic Oxadiazoles and 1-Hydroxytetrazoles as Energetic Materials. Chem. Heterocycl. Compd. 2017, 53, 760–778. 10.1007/s10593-017-2122-9. [DOI] [Google Scholar]
- Zhang M. X.; Pagoria P. F.; Imler G. H.; Parrish D. Trimerization of 4-Amino-3,5-dinitropyrazole: Formation, Preparation, and Characterization of 4-Diazo-3,5-bis(4-amino-3,5-dinitropyrazol-1-yl) Pyrazole (LLM-226). J. Heterocycl. Chem. 2019, 56, 781–787. 10.1002/jhet.3434. [DOI] [Google Scholar]
- Guzman P. E.; Sausa R. C.; Wingard L. A.; Pesce-Rodriguez R. A.; Sabatini J. J. Synthesis and Characterization of Isoxazole-Based Energetic Plasticizer Candidates EEIN and IDN. Eur. J. Org. Chem. 2018, 2018, 6724–6728. 10.1002/ejoc.201801285. [DOI] [Google Scholar]
- Wingard L. A.; Johnson E. C.; Guzman P. E.; Sabatini J. J.; Drake G. W.; Byrd E. F. C.; Sausa R. C. Synthesis of Biisoxazoletetrakis(methyl nitrate): A Potential Nitrate Plasticizer and Highly Explosive Material. Eur. J. Org. Chem. 2017, 2017, 1765–1768. 10.1002/ejoc.201700280. [DOI] [Google Scholar]
- Johnson E. C.; Sabatini J. J.; Chavez D. E.; Wells L. A.; Banning J. E.; Sausa R. C.; Byrd E. F. C.; Orlicki J. A. Bis(Nitroxymethylisoxazolyl) Furoxan: A Promising Standalone Melt-Castable Explosive. ChemPlusChem. 2020, 85, 237–239. 10.1002/cplu.201900710. [DOI] [PubMed] [Google Scholar]
- Johnson E. C.; Sabatini J. J.; Chavez D. E.; Sausa R. C.; Byrd E. F. C.; Wingard L. A.; Guzman P. E. Bis(1,2,4-oxadiazole)bis(methylene) Dinitrate: A High-Energy Melt-Castable Explosive and Energetic Propellant Plasticizing Ingredient. Org. Process Res. Dev. 2018, 22, 736–740. 10.1021/acs.oprd.8b00076. [DOI] [Google Scholar]
- Miller C. W.; Johnson E. C.; Sausa R. C.; Orlicki J. A.; Sabatini J. J. A Safer Synthesis of the Explosive Precursors 4-Aminofurazan-3-Carboxylic Acid and its Ethyl Ester Derivative. Org. Process Res. Dev. 2020, 24, 599–603. 10.1021/acs.oprd.0c00068. [DOI] [Google Scholar]
- Tang Y. X.; He C. L.; Imler G. H.; Parrish D. A.; Shreeve J. M. A C-C bonded 5,6-fused Bicyclic Energetic Molecule: Exploring an Advanced Energetic Compound with Improved Performance. Chem. Commun. 2018, 54, 10566–10569. 10.1039/C8CC05987J. [DOI] [PubMed] [Google Scholar]
- Kumar D.; Imler G. H.; Parrish D. A.; Shreeve J. M. Aminoacetonitrile as Precursor for Nitrogen Rich Stable and Insensitive Asymmetric N-methylene-C linked Tetrazole-based Energetic Compounds. J. Mater. Chem. A 2017, 5, 16767–16775. 10.1039/C7TA05394K. [DOI] [Google Scholar]
- Tang Y. X.; He C. L.; Imler G. H.; Parrish D. A.; Shreeve J. M. Aminonitro Groups Surrounding a Fused Pyrazolotriazine Ring: A Superior Thermally Stable and Insensitive Energetic Material. ACS Appl. Energy Mater. 2019, 2, 2263–2267. 10.1021/acsaem.9b00049. [DOI] [Google Scholar]
- Kumar D.; Mitchell L. A.; Parrish D. A.; Shreeve J. M. Asymmetric N,N ’-ethylene-bridged Azole-based Compounds: Two Way Control of the Energetic Properties of Compounds. J. Mater. Chem. A 2016, 4, 9931–9940. 10.1039/C6TA03536A. [DOI] [Google Scholar]
- Yin P.; Parrish D. A.; Shreeve J. M. Bis(nitroamino-1,2,4-triazolates): N-Bridging Strategy Toward Insensitive Energetic Materials. Angew. Chem., Int. Ed. 2014, 53, 12889–12892. 10.1002/anie.201408127. [DOI] [PubMed] [Google Scholar]
- He C. L.; Gao H. X.; Imler G. H.; Parrish D. A.; Shreeve J. M. Boosting Energetic Performance by Trimerizing Furoxan. J. Mater. Chem. A 2018, 6, 9391–9396. 10.1039/C8TA02274G. [DOI] [Google Scholar]
- Zhang J. H.; Dharavath S.; Mitchell L. A.; Parrish D. A.; Shreeve J. M. Bridged Bisnitramide-substituted Furazan-based Energetic Materials. J. Mater. Chem. A 2016, 4, 16961–16967. 10.1039/C6TA08055C. [DOI] [Google Scholar]
- Tang Y. X.; He C. L.; Mitchell L. A.; Parrish D. A.; Shreeve J. M. C-N Bonded Energetic Biheterocyclic Compounds with Good Detonation Performance and High Thermal Stability. J. Mater. Chem. A 2016, 4, 3879–3885. 10.1039/C5TA09803C. [DOI] [Google Scholar]
- Tang Y. X.; Imler G. H.; Parrish D. A.; Shreeve J. M. C6N10O4: Thermally Stable Nitrogen-Rich Inner Bis(diazonium) Zwitterions. Org. Lett. 2019, 21, 8201–8204. 10.1021/acs.orglett.9b02875. [DOI] [PubMed] [Google Scholar]
- Kumar D.; He C. L.; Mitchell L. A.; Parrish D. A.; Shreeve J. M. Connecting Energetic Nitropyrazole and Aminotetrazole Moieties with N,N ’-ethylene Bridges: A Promising Approach for Fine Tuning Energetic Properties. J. Mater. Chem. A 2016, 4, 9220–9228. 10.1039/C6TA02387H. [DOI] [Google Scholar]
- Zhao G.; Kumar D.; Yin P.; He C. L.; Imler G. H.; Parrish D. A.; Shreeve J. M. Construction of Polynitro Compounds as High-performance Oxidizers via a Two-step Nitration of Various Functional Groups. Org. Lett. 2019, 21, 1073–1077. 10.1021/acs.orglett.8b04114. [DOI] [PubMed] [Google Scholar]
- Chand D.; Parrish D. A.; Shreeve J. M. Di(1H-tetrazol-5-yl) methanone oxime and 5,5 ’-(hydrazonomethylene) bis(1H-tetrazole) and Their Salts: A Family of Highly Useful New Tetrazoles and Energetic Materials. J. Mater. Chem. A 2013, 1, 15383–15389. 10.1039/c3ta13425c. [DOI] [Google Scholar]
- Chand D.; He C. L.; Mitchell L. A.; Parrish D. A.; Shreeve J. M. Electrophilic Iodination: A Gateway to High Iodine Compounds and Energetic Materials. Dalton Trans 2016, 45, 13827–13833. 10.1039/C6DT02438F. [DOI] [PubMed] [Google Scholar]
- He C. L.; Yin P.; Mitchell L. A.; Parrish D. A.; Shreeve J. M. Energetic Aminated-azole Assemblies from Intramolecular and Intermolecular N-H ··· O and N-H ··· N Hydrogen Bonds. Chem. Commun. 2016, 52, 8123–8126. 10.1039/C6CC03833F. [DOI] [PubMed] [Google Scholar]
- Tang Y. X.; He C. L.; Mitchell L. A.; Parrish D. A.; Shreeve J. M. Energetic Compounds Consisting of 1,2,5-and 1,3,4-Oxadiazole Rings. J. Mater. Chem. A 2015, 3, 23143–23148. 10.1039/C5TA06898C. [DOI] [Google Scholar]
- Wang K.; Parrish D. A.; Shreeve J. M. 3-Azido-N-nitro-1H-1,2,4-triazol-5-amine-based Energetic Salts. Chem.—Eur. J. 2011, 17, 14485–14492. 10.1002/chem.201102901. [DOI] [PubMed] [Google Scholar]
- Zhang Y. Q.; Parrish D. A.; Shreeve J. M. Synthesis and Properties of 3,4,5-Trinitropyrazole-1-ol and Its Energetic Salts. J. Mater. Chem. 2012, 22, 12659–12665. 10.1039/c2jm31535a. [DOI] [Google Scholar]
- Thottempudi V.; Forohor F.; Parrish D. A.; Shreeve J. M. Tris(triazolo)benzene and Its Derivatives: High-density Energetic Materials. Angew. Chem., Int. Ed. 2012, 51, 9881–9885. 10.1002/anie.201205134. [DOI] [PubMed] [Google Scholar]
- He C. L.; Zhang J. H.; Parrish D. A.; Shreeve J. M. 4-Chloro-3,5-dinitropyrazole: A Precursor for Promising Insensitive Energetic Compounds. J. Mater. Chem. A 2013, 1, 2863–2868. 10.1039/c2ta01359b. [DOI] [Google Scholar]
- Zhang Q. H.; Zhang J. H.; Parrish D. A.; Shreeve J. M. Energetic N-Trinitroethyl-Substituted Mono-, Di-, and Triaminotetrazoles. Chem.—Eur. J. 2013, 19, 11000–11006. 10.1002/chem.201300994. [DOI] [PubMed] [Google Scholar]
- Yin P.; Zhang Q. H.; Zhang J. H.; Parrish D. A.; Shreeve J. M. N-Trinitroethylamino Functionalization of Nitroimidazoles: A New Strategy for High Performance Energetic Materials. J. Mater. Chem. A 2013, 1, 7500–7510. 10.1039/c3ta11356f. [DOI] [Google Scholar]
- Yin P.; Zhang J. H.; Parrish D. A.; Shreeve J. M. Energetic N,N’-Ethylene-bridged bis(nitropyrazoles): Diversified Functionalities and Properties. Chem.—Eur. J. 2014, 20, 16529–16536. 10.1002/chem.201404991. [DOI] [PubMed] [Google Scholar]
- Zhang J. H.; Parrish D. A.; Shreeve J. M. Thermally Stable 3,6-Dinitropyrazolo[4,3-c]pyrazole-based Energetic Materials. Chem.—Asian J. 2014, 9, 2953–2960. 10.1002/asia.201402538. [DOI] [PubMed] [Google Scholar]
- Thottempudi V.; Yin P.; Zhang J. H.; Parrish D. A.; Shreeve J. M. 1,2,3-Triazolo[4,5,-e]furazano[3,4,-b]pyrazine 6-Oxide-A Fused Heterocycle with a Roving Hydrogen Forms a New Class of Insensitive Energetic Materials. Chem.—Eur. J. 2014, 20, 542–548. 10.1002/chem.201303469. [DOI] [PubMed] [Google Scholar]
- Tang Y. X.; Gao H. X.; Parrish D. A.; Shreeve J. M. 1,2,4-Triazole Links and N-Azo Bridges Yield Energetic Compounds. Chem.—Eur. J. 2015, 21, 11401–11407. 10.1002/chem.201501612. [DOI] [PubMed] [Google Scholar]
- Vo T. T.; Zhang J. H.; Parrish D. A.; Twamley B.; Shreeve J. M. New Roles for 1,1-Diamino-2,2-dinitroethene (FOX-7): Halogenated FOX-7 and Azo-bis(diahaloFOX) as Energetic Materials and Oxidizers. J. Am. Chem. Soc. 2013, 135, 11787–11790. 10.1021/ja406629g. [DOI] [PubMed] [Google Scholar]
- Yin P.; Zhang J. H.; Mitchell L. A.; Parrish D. A.; Shreeve J. M. 3,6-Dinitropyrazolo[4,3-c]pyrazole-based Multipurpose Energetic Materials through Versatile N-Functionalization Strategies. Angew. Chem., Int. Ed. 2016, 55, 12895–12897. 10.1002/anie.201606894. [DOI] [PubMed] [Google Scholar]
- Zhang J. H.; Yin P.; Mitchell L. A.; Parrish D. A.; Shreeve J. M. N-functionalized Nitroxy/azido Fused-ring Azoles as High-performance Energetic Materials. J. Mater. Chem. A 2016, 4, 7430–7436. 10.1039/C6TA02384C. [DOI] [Google Scholar]
- Tang Y. X.; Gao H. X.; Mitchell L. A.; Parrish D. A.; Shreeve J. M. Syntheses and promising properties of Dense Energetic 5,5-Dinitramino-3,3-azo-1,2,4-oxadiazole and Its Salts. Angew. Chem., Int. Ed. 2016, 55, 3200–3203. 10.1002/anie.201600068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yin P.; Mitchell L. A.; Parrish D. A.; Shreeve J. M. Comparative Study of Various Pyrazole-based Anions: A Promising Family of Ionic Derivatives as Insensitive Energetic Materials. Chem.—Asian J. 2017, 12, 378–384. 10.1002/asia.201601615. [DOI] [PubMed] [Google Scholar]
- Tang Y. X.; He C. L.; Imler G. H.; Parrish D. A.; Shreeve J. M. Dinitromethyl-3(5)-1,2,4-oxadiazole Derivatives from Controllable Cyclization Strategies. Chem.—Eur. J. 2017, 23, 16401–16407. 10.1002/chem.201704446. [DOI] [PubMed] [Google Scholar]
- Dharavath S.; Zhang J. H.; Imler G. H.; Parrish D. A.; Shreeve J. M. 5-(Dinitromethyl)-3-(trinitromethyl)-1,2,4-triazole and Its Derivatives: A New Application of Oxidative Nitration Towards Gem-trinitro-based Energetic Materials. J. Mater. Chem. A 2017, 5, 4785–4790. 10.1039/C7TA00730B. [DOI] [Google Scholar]
- Tang Y. X.; He C. L.; Imler G. H.; Parrish D. A.; Shreeve J. M. Energetic 1,2,5-Oxadiazolo-Pyridazine and its N-Oxide. Chem.—Eur. J. 2017, 23, 15022–15025. 10.1002/chem.201703930. [DOI] [PubMed] [Google Scholar]
- Tang Y. X.; He C. L.; Imler G. H.; Parrish D. A.; Shreeve J. M. High-performing and Thermally Stable Energetic 3,7-diamino-7H-[1,2,4]triazolo[4,3-b][1,2,4]triazole derivatives. J. Mater. Chem. A 2017, 5, 6100–6105. 10.1039/C7TA01111C. [DOI] [Google Scholar]
- Kumar D.; Imler G. H.; Parrish D. A.; Shreeve J. M. N-Acetonitrile Functionalized Nitropyrazoles: Precursors to Insensitive Asymmetric N-Methylene-C Linked Azoles. Chem.—Eur. J. 2017, 23, 7876–7881. 10.1002/chem.201700786. [DOI] [PubMed] [Google Scholar]
- Yu Q.; Imler G. H.; Parrish D. A.; Shreeve J. M. Nitromethane Bridged Bis(1,3,4-oxadiazoles): Trianionic Energetic Salts with Low Sensitivities. Chem.—Eur. J. 2017, 23, 17682–17686. 10.1002/chem.201704939. [DOI] [PubMed] [Google Scholar]
- Yin P.; Zhang J. H.; Imler G. H.; Parrish D. A.; Shreeve J. M. Polynitro-Functionalized Dipyrazolo-1,3,5-triazinanes: Energetic Polycyclization toward High Density and Excellent Molecular Stability. Angew. Chem., Int. Ed. 2017, 56, 8834–8838. 10.1002/anie.201704687. [DOI] [PubMed] [Google Scholar]
- Yu Q.; Yin P.; Zhang J. H.; He C. L.; Imler G. H.; Parrish D. A.; Shreeve J. M. Pushing the Limits of Oxygen Balance in 1,3,4-Oxadiazoles. J. Am. Chem. Soc. 2017, 139, 8816–8819. 10.1021/jacs.7b05158. [DOI] [PubMed] [Google Scholar]
- Kumar D.; Imler G. H.; Parrish D. A.; Shreeve J. M. Resolving Synthetic Challenges Faced in the Syntheses of Asymmetric N,N ’-ethylene-bridged Energetic Compounds. New J. Chem. 2017, 41, 4040–4047. 10.1039/C7NJ00327G. [DOI] [Google Scholar]
- Snyder C. J.; Myers T. W.; Imler G. H.; Chavez D. E.; Parrish D. A.; Veauthier J. M.; Scharff R. J. Tetrazolyl Triazolotriazine: A New Insensitive High Explosive. Propellants, Explos. Pyrotech. 2017, 42, 238–242. 10.1002/prep.201600294. [DOI] [Google Scholar]
- Tang Y. X.; He C. L.; Yin P.; Imler G. H.; Parrish D. A.; Shreeve J. M. Energetic Functionalized Azido/Nitro Imidazole Fused 1,2,3,4-Tetrazine. Eur. J. Org. Chem. 2018, 2018, 2273–2276. 10.1002/ejoc.201800347. [DOI] [Google Scholar]
- Zhao G.; He C. L.; Gao H. X.; Imler G. H.; Parrish D. A.; Shreeve J. M. Improving the Density and Properties of Nitrogen-rich Scaffolds by the Introduction of a C-NO2 Group. New J. Chem. 2018, 42, 16162–16166. 10.1039/C8NJ03472A. [DOI] [Google Scholar]
- Kumar D.; Tang Y. X.; He C. L.; Imler G. H.; Parrish D. A.; Shreeve J. M. Multipurpose Energetic Materials by Shuffling Nitro Groups on a 3,3 ’-Bipyrazole Moiety. Chem.—Eur. J. 2018, 24, 17220–17224. 10.1002/chem.201804418. [DOI] [PubMed] [Google Scholar]
- Tang Y. X.; Imler G. H.; Parrish D. A.; Shreeve J. M. Oxidative Cyclization Protocol for the Preparation of Energetic 3-Amino-5-R-1,2,4-oxadiazoles. Org. Lett. 2018, 20, 8039–8042. 10.1021/acs.orglett.8b03639. [DOI] [PubMed] [Google Scholar]
- Tang Y. X.; He C. L.; Imler G. H.; Parrish D. A.; Shreeve J. M. Ring Closure of Polynitroazoles via an N, N ’-alkylene Bridge: Towards High Thermally Stable Energetic Compounds. J. Mater. Chem. A 2018, 6, 8382–8387. 10.1039/C8TA02704H. [DOI] [Google Scholar]
- Dharavath S.; Tang Y. X.; Kumar D.; Mitchell L. A.; Parrish D. A.; Shreeve J. M. A Halogen-Free Green High Energy Density Oxidizer from H-FOX. Eur. J. Org. Chem. 2019, 2019, 3142–3145. 10.1002/ejoc.201900415. [DOI] [Google Scholar]
- Liu Y. L.; Zhao G.; Tang Y. X.; Zhang J. C.; Hu L.; Imler G. H.; Parrish D. A.; Shreeve J. M. Multipurpose [1,2,4]triazolo[4,3-b][1,2,4,5] Tetrazine-based Energetic Materials. J. Mater. Chem. A 2019, 7, 7875–7884. 10.1039/C9TA01717H. [DOI] [Google Scholar]
- Zhang J. H.; He C. L.; Parrish D. A.; Shreeve J. M. Nitramines with Varying Sensitivities: Functionalized Dipyrazolyl- N-nitromethanamines as Energetic Materials. Chem.—Eur. J. 2013, 19, 8929–8936. 10.1002/chem.201300747. [DOI] [PubMed] [Google Scholar]
- Rhein R. A.; Reed R.; Vu N. Q. Impact Sensitivity Reduction Via Exo-Electron Control. Propellants, Explos. Pyrotech. 1993, 18, 184–187. 10.1002/prep.199300003. [DOI] [Google Scholar]
- Phillips J. J. A Modified Type-12 Impact Sensitivity Test Apparatus for Explosives. Propellants, Explos. Pyrotech. 2012, 37, 223–229. 10.1002/prep.201100074. [DOI] [Google Scholar]
- Bowers R. C.; Romans J. B.; Zisman W. A. Mechanisms Involved in Impact Sensitivity and Desensitization of RDX. Ind. Eng. Chem. Prod. Res. Dev. 1973, 12, 2–13. 10.1021/i360045a002. [DOI] [Google Scholar]
- Wang D. X.; Chen S. S.; Li Y. Y.; Yang J. Y.; Wei T. Y.; Jin S. H. An Investigation into the Effects of Additives on Crystal Characteristics and Impact Sensitivity of RDX. J. Energy Mater. 2014, 32, 184–198. 10.1080/07370652.2013.812160. [DOI] [Google Scholar]
- Zhang G. X.; Weeks B. L. A Device for Testing Thermal Impact Sensitivity of High Explosives. Propellants, Explos. Pyrotech. 2010, 35, 440–445. 10.1002/prep.201000030. [DOI] [Google Scholar]
- Paul W.; Cooper S. R. K.. Introduction to the Technology of Explosives; Wiley-VCH, 1997. [Google Scholar]
- Lease N.; Holmes M. D.; Englert-Erickson M. A.; Kay L. M.; Francois E. G.; Manner V. W. Analysis of Ignition Sites for the Explosives 3,3′-Diamino-4,4’-azoxyfurazan (DAAF) and 1,3,5,7-Tetranitro-1,3,5,7-tetrazoctane (HMX) Using Crush Gun Impact Testing. ACS Mater. Au 2021, 1, 116–129. 10.1021/acsmaterialsau.1c00013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oxley J. C.; Smith J. L.; Brady J. E.; Brown A. C. Characterization and Analysis of Tetranitrate Esters. Propellants, Explos. Pyrotech. 2012, 37, 24–39. 10.1002/prep.201100059. [DOI] [Google Scholar]
- Licht H. H. Performance and Sensitivity of Explosives. Propellants, Explos. Pyrotech. 2000, 25, 126–132. . [DOI] [Google Scholar]
- Afanas’Ev G. T.; Pivina T. S.; Sukhachev D. V. Comparative Characteristics of Some Experimental and Computational Methods for Estimating Impact Sensitivity Parameters of Explosives. Propellants, Explos. Pyrotech. 1993, 18, 309–316. 10.1002/prep.19930180602. [DOI] [Google Scholar]
- Zeman S.; Krupka M. New Aspects of Impact Reactivity of Polynitro Compounds, part III. Impact Sensitivity as a Function of the Intermolecular Interactions. Propellants, Explos. Pyrotech. 2003, 28, 301–307. 10.1002/prep.200300018. [DOI] [Google Scholar]
- Ritter H.; Braun S. High Explosives Containing Ultrafine Aluminum ALEX. Propellants, Explos. Pyrotech. 2001, 26, 311–314. . [DOI] [Google Scholar]
- Mathieu D. Sensitivity of Energetic Materials: Theoretical Relationships to Detonation Performance and Molecular Structure. Ind. Eng. Chem. Res. 2017, 56, 8191–8201. 10.1021/acs.iecr.7b02021. [DOI] [Google Scholar]
- Alster J.A Statistical Correlation of Impact Sensitivity with Oxygen Balance for Secondary Explosives. Proceedings of the 3rd Symposium on Detonation, 1960; pp 693–705.
- Cooper P. W.Explosives Engineering; John Wiley & Sons, 2018. [Google Scholar]
- Elstner M.; Porezag D.; Jungnickel G.; Elsner J.; Haugk M.; Frauenheim T.; Suhai S.; Seifert G. Self-consistent-charge Density-functional Tight-binding Method for Simulations of Complex Materials Properties. Phys. Rev. B 1998, 58, 7260. 10.1103/PhysRevB.58.7260. [DOI] [Google Scholar]
- Frauenheim T.; Seifert G.; Elsterner M.; Hajnal Z.; Jungnickel G.; Porezag D.; Suhai S.; Scholz R. A Self-consistent Charge Density-functional Based Tight-binding Method for Predictive Materials Simulations in Physics, Chemistry and Biology. Phys. Status Solidi B 2000, 217, 41–62. . [DOI] [Google Scholar]
- Cawkwell M. J.; Perriot R. Transferable Density Functional Tight Binding for Carbon, Hydrogen, Nitrogen, and Oxygen: Application to Shock Compression. J. Chem. Phys. 2019, 150, 024107. 10.1063/1.5063385. [DOI] [PubMed] [Google Scholar]
- Tukey J. W. .Statistical Analysis for A New Procedure in Sensitivity Experiments. Applied Mathematics Panel National Defense Research Committee Report, 1944, Vol. 101.
- Neyer B. T. A D-optimality-based Sensitivity Test. Technometrics 1994, 36, 61–70. 10.2307/1269199. [DOI] [Google Scholar]
- Slater J. C.; Koster G. F. Simplified LCAO Method for the Periodic Potential Problem. Phys. Rev. 1954, 94, 1498. 10.1103/PhysRev.94.1498. [DOI] [Google Scholar]
- Finnis M.Interatomic Forces in Condensed Matter; Oxford Series on Materials Modelling, 2003. [Google Scholar]
- Cawkwell M. J.; Burch A. C.; Ferreira S. R.; Lease N.; Manner V. W. Atom Equivalent Energies for the Rapid Estimation of the Heat of Formation of Explosive Molecules from Density Functional Tight Binding Theory. J. Chem. Inf. Model. 2021, 61, 3337–3347. 10.1021/acs.jcim.1c00312. [DOI] [PubMed] [Google Scholar]
- Politzer P.; Murray J. S. Are HOMO-LUMO gaps reliable indicators of explosive impact sensitivity?. J. Mol. Model. 2021, 27, 327. 10.1007/s00894-021-04956-1. [DOI] [PubMed] [Google Scholar]
- Zhang H.; Cheung F.; Zhao F.; Cheng X.-L. Band gaps and the possible effect on impact sensitivity for some nitro aromatic explosive materials. Int. J. Quantum Chem. 2009, 109, 1547–1552. 10.1002/qua.21990. [DOI] [Google Scholar]
- Cyrot-Lackmann F. On the Electronic Structure of Liquid Transitional Metals. Adv. Phys. 1967, 16, 393–400. 10.1080/00018736700101495. [DOI] [Google Scholar]
- Ducastelle F.; Cyrot-Lackmann F. Moments Developments and Their Application to the Electronic Charge Distribution of d-bands. J. Phys. Chem. Solids 1970, 31, 1295–1306. 10.1016/0022-3697(70)90134-4. [DOI] [Google Scholar]
- Ducastelle F.; Cyrot-Lackmann F. Moments Developments: II. Application to the Crystalline Structures and the Stacking Fault Energies of Transition Metals. J. Phys. Chem. Solids 1971, 32, 285–301. 10.1016/S0022-3697(71)80031-8. [DOI] [Google Scholar]
- Pettifor D. G.; Aoki M. Bonding and structure of intermetallics: a new bond order potential. Philos. Trans. R. Soc. London A 1992, 334, 47. 10.1007/978-1-4615-3394-8_5. [DOI] [Google Scholar]
- Pettifor D. G.Bonding and Structure of Molecules and Solids; Oxford University Press, 1995. [Google Scholar]
- Hammerschmidt T.; Drautz R. In Multiscale Simulation Methods in Molecular Sciences; Grotendorst J., Attig N., Blügel S., Marx D., Eds.; Jülich Supercomputing Centre: Forschungzentrum Jülich, Jülich, Germany, 2009; p 229. [Google Scholar]
- Aoki M.; Nguyen-Manh D.; Pettifor D. G.; Vitek V. Atom-based bond-order potentials for modelling mechanical properties of metals. Prog. Mater. Sci. 2007, 52, 154–195. 10.1016/j.pmatsci.2006.10.004. [DOI] [Google Scholar]
- Ashcroft N. W.; Mermin N. D.. Solid State Physics; Saunders College Publishing, 1976. [Google Scholar]
- Kinney G. F.; Graham K. J.. Explosive Shocks in Air; Springer Science & Business Media, 2013. [Google Scholar]
- Burgess D. In NIST Chemistry WebBook, NIST Standard Reference Database Number 69; Linstrom P., Mallard W., Eds.; National Institute of Standards and Technology, 2022. [Google Scholar]
- Tibshirani R. Regression Shrinkage and Selection via the Lasso. J. R. Stat. Soc. Ser. B Stat. Methodol. 1996, 58, 267–288. 10.1111/j.2517-6161.1996.tb02080.x. [DOI] [Google Scholar]
- Zou H.; Hastie T.. elasticnet: Elastic-Net for Sparse Estimation and Sparse PCA, 2020; R package version 1.3.
- Breiman L. Random Forests. Mach. Learn. 2001, 45, 5–32. 10.1023/A:1010933404324. [DOI] [Google Scholar]
- Scornet E. Tuning Parameters in Random Forests. ESAIM: Proceedings and Surveys 2017, 60, 144–162. 10.1051/proc/201760144. [DOI] [Google Scholar]
- Probst P.; Boulesteix A.-L. To Tune or Not to Tune the Number of Trees in Random Forest. J. Mach. Learn. Res. 2017, 18, 6673–6690. [Google Scholar]
- Hastie T.; Tibshirani R.; Friedman J. H.. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer, 2009; Vol. 2. [Google Scholar]
- Mentch L.; Zhou S.. Randomization as Regularization: A Degrees of Freedom Explanation for Random Forest Success. J. Mach. Learn. Res. 2020, 21.1–36.34305477 [Google Scholar]
- Genuer R.; Poggi J.-M.; Tuleau-Malot C. Variable Selection Using Random Forests. Pattern Recognition Letters 2010, 31, 2225–2236. 10.1016/j.patrec.2010.03.014. [DOI] [Google Scholar]
- Liaw A.; Wiener M. Classification and Regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Genuer R.; Poggi J.-M.; Tuleau-Malot C.. VSURF: Variable Selection Using Random Forests, 2019; R package version 1.1.0.
- Stone M. Cross-Validatory Choice and Assessment of Statistical Predictions. J. R. Stat. Soc. Series B Stat. Methodol. 1974, 36, 111–133. 10.1111/j.2517-6161.1974.tb00994.x. [DOI] [Google Scholar]
- Fisher A.; Rudin C.; Dominici F. All Models are Wrong, but Many are Useful: Learning a Variable’s Importance by Studying an Entire Class of Prediction Models Simultaneously. J. Mach. Learn. Res. 2019, 20, 1–81. [PMC free article] [PubMed] [Google Scholar]
- Apley D. W.; Zhu J. Visualizing the Effects of Predictor Variables in Black Box Supervised Learning Models. J. R. Stat. Soc. Ser. B Stat. Methodol. 2020, 82, 1059–1086. 10.1111/rssb.12377. [DOI] [Google Scholar]
- Politzer P.; Seminario J. M.. Modern Density Functional Theory: A Tool for Chemistry; Elsevier, 1995. [Google Scholar]
- Bennion J. C.; McBain A.; Son S. F.; Matzger A. J. Design and Synthesis of a Series of Nitrogen-Rich Energetic Cocrystals of 5,5 ’-Dinitro-2H,2H ’-3,3 ’-bi-1,2,4-triazole (DNBT). Cryst. Growth Des. 2015, 15, 2545–2549. 10.1021/acs.cgd.5b00336. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data used in this article are publicly available as Supporting Information. All methods are existing and available in open source software, and thus, we do not provide reproduction software. All statistical analysis was performed using the programming language R, version 4.1.3, available at https://cran.r-project.org/src/base/R-4/. Key packages for reproduction, and their versions, are randomForest (4.6-14), VSURF (1.1.0), glmnet (4.1-3), ALEPlot (1.1), and mltools (0.3.5). All packages are available online at https://cran.r-project.org/. All of the density functional tight binding calculations were performed using the open-source code LATTE, which is available for download from https://github.com/lanl/LATTE. The lanl31 parametrization is supplied with the LATTE source via the GitHub repository and in Cawkwell and Perriot.176 Open Babel version 3.1.0 was used to convert SMILES to three-dimensional geometries in the standard .xyz format.