Adaptive and pathological connectivity responses in Parkinson’s disease brain networks

Abstract

Functional imaging has been used extensively to identify and validate disease-specific networks as biomarkers in neurodegenerative disorders. It is not known, however, whether the connectivity patterns in these networks differ with disease progression compared to the beneficial adaptations that may also occur over time. To distinguish the 2 responses, we focused on assortativity, the tendency for network connections to link nodes with similar properties. High assortativity is associated with unstable, inefficient flow through the network. Low assortativity, by contrast, involves more diverse connections that are also more robust and efficient. We found that in Parkinson’s disease (PD), network assortativity increased over time. Assoratitivty was high in clinically aggressive genetic variants but was low for genes associated with slow progression. Dopaminergic treatment increased assortativity despite improving motor symptoms, but subthalamic gene therapy, which remodels PD networks, reduced this measure compared to sham surgery. Stereotyped changes in connectivity patterns underlie disease progression and treatment responses in PD networks.

Introduction

Disease-related network patterns identified with functional brain imaging are increasingly being used to gain insight into neurodegenerative disorders and to track disease progression and treatment responses in patient populations (Meyer et al. 2017; Woo et al. 2017; Niethammer et al. 2018; Schindlbeck and Eidelberg 2018; Wilson et al. 2020). Given the brain’s enormous capacity to compensate for dysfunction—network changes are apparent on imaging long before the onset of symptoms—it is difficult to determine whether the novel connections that arise reflect underlying pathology or an adaptive response to the disease. Such studies are particularly challenging in neurodegenerative disorders, such as Parkinson’s and Alzheimer’s, where it is difficult to identify individuals decades before they develop symptoms unless they have a rare, inherited form of the disorder.

In the case of Parkinson’s disease (PD), crosscomparisons have begun to provide insight into the connectivity patterns that are associated with more aggressive or more benign disease courses. The dominant disease network, termed the PD-related covariance pattern (PDRP), consists of nodes that are either more or less metabolically active than in healthy subjects, and these differences from baseline intensify so that pattern expression increases with disease progression (Spetsieris and Eidelberg 2011; Vo et al. 2017; Schindlbeck and Eidelberg 2018). Although PDRP (which correlates primarily with motor dysfunction) and its cognition-related counterpart network, the PD-related cognitive pattern (PDCP) (Schindlbeck and Eidelberg 2018; Schindlbeck et al. 2020), were identified in patients with idiopathic PD, we recently found that patients with PD caused by the LRRK2 G2019S mutation or GBA1 variants express the same disease networks (Schindlbeck et al. 2020). Although this makes sense (after all, the patients have clinical and pathological features of sporadic PD regardless of genotype), we speculated that a deeper analysis of functional connectivity within the PDRP and PDCP spaces might provide clues as to why LRRK2-associated PD tends to progress more slowly, and GBA1-associated PD tends to progress more rapidly, than sporadic disease. This turned out to be the case: Both genotypes were associated with abnormal increases in connectivity compared to idiopathic PD, but the pattern was quite different. LRRK2 mutation led to the formation of additional connections within the network core, particularly between the cerebellum and putamen, which may represent protective adaptations (Schindlbeck et al. 2020). GBA1 variants, on the other hand, were associated with gain in connections outside the core, involving mainly cortico-cortical projections (Schindlbeck et al. 2020). Of note, conventional network metrics, such as degree centrality, clustering coefficient, and characteristic path length, did not distinguish the slow and rapidly progressive PD genotypes.

This led us to ask whether other descriptors of functional connectivity within PD networks or subgraphs would be more informative. Specifically, we hypothesized that pathological connectivity patterns would be distinguished by their assortativity. Defined as the link-averaged correlation coefficient of degree centrality across pairs of connected nodes, assortativity can be thought of as an index of connectional diversity within a network (Peel et al. 2018). When a network is dominated by links between nodes of different degree centrality (negative degree pair correlation), it is termed dissortative. Such networks are robust and transfer information efficiently along the graph. When connections predominate between nodes of similar degree centrality, the network is termed assortative (positive degree pair correlation). Assortative networks are more vulnerable to random attack than their disassortative counterparts (Zhou et al. 2012) and information transfer is comparatively less efficient (Newman 2003; Noldus and Van Mieghem 2015; Barabasi 2016; Murakami et al. 2017). Given these properties, we hypothesized that pathological responses, such as those observed over time in patient populations, would be associated with increasing assortativity of disease networks. Adaptive responses, on the other hand, would be accompanied by lower assortativity or disassortativity in the disease network space. To test this hypothesis, we measured assortativity for the PDRP and PDCP as a function of disease progression, genotype, and response to 2 different treatments: intravenous levodopa infusion, which acutely improves motor symptoms, and subthalamic AAV2-GAD gene therapy, which remodels motor networks over time (Niethammer et al. 2018).

Materials and methods

Study samples

Network metrics were computed for previously validated motor and cognition-related PD topographies described elsewhere (Woo et al. 2017; Schindlbeck and Eidelberg 2018). Group differences in the measures, as well as the effects of disease progression, genotype, and treatment were explored in previously published datasets referenced below (Supplementary Tables S1A and S2E). PD patients in each sample were diagnosed according to UK Parkinson Disease Society Brain Bank criteria (Hughes et al. 1992). The subjects were evaluated at the time of imaging according to the Unified Parkinson’s Disease Rating Scale (Fahn and Elton 1987) at least 12 h after the last medication dose. Ethical permission for these studies was obtained from the Institutional Review Boards of the participating institutions. Written consent was obtained from each subject following detailed explanation of the procedures.

Study cohorts

Comparison of network metrics in PD and healthy control subjects

We studied 96 PD patients and 22 age- and gender-matched healthy control (HC) subjects (HC1, n = 22) who were scanned with [¹⁸F]-fluorodeoxyglucose (FDG) PET at North Shore University Hospital as part of a long-term diagnostic project (Tang, Poston, Eckert, et al. 2010) (Supplementary Table S1A). For validation, we studied an independent cohort of 146 PD and 39 HC subjects who were scanned with FDG PET as part of 2 subsequently published ascertainment studies (Tripathi et al. 2016; Rus et al. 2020) (Supplementary Table S1B).

Change in network metrics with disease progression

Longitudinal progression

We studied a longitudinal cohort of early PD patients (n = 15) who were scanned with FDG PET at baseline, 24 months and 48 months, and a matched group of HC subjects (HC3; n = 15) (see Supplementary Table S2A). Limited metabolic data from these subjects have appeared previously (Huang et al. 2007).

Comparison of groups with increasing symptom duration

We compared 3 age- and gender-matched groups of PD patients with motor symptoms of short (0–4 years; n = 20), intermediate (5–9 years; n = 20), and long (≥10 years; n = 20) duration, and age- and gender-matched HC subjects (HC4; n = 20) (see Supplementary Table S2B).

Effects of PD genotype on network metrics

We studied patients with PD associated with either the LRRK2-G2019S mutation (PD-LRRK2; n = 14) or GBA1 variants (PD-GBA; n = 12), and matched HC subjects (HC5; n = 14) (Supplementary Table S2C). Clinical details and limited network data from these patients have appeared previously (Schindlbeck et al. 2020).

Effects of levodopa infusion on network metrics

We studied PD subjects (n = 14), who underwent metabolic imaging in the unmedicated state (“off”) and during intravenous levodopa infusion (“on”), and a matched group of HC subjects (HC6; n = 14) (Supplementary Table S2D). In each patient, the levodopa dose was titrated to achieve maximal clinical benefit, without eliciting involuntary movements. Experimental details and limited metabolic data from these patients have appeared previously (Jourdain et al. 2016).

Effects of subthalamic gene therapy and sham surgery on network metrics

We analyzed baseline and 12-month FDG PET data from PD patients, who were randomized to either subthalamic AAV2-GAD (n = 16) or sham surgery (n = 21) as part of a double-blind surgical trial, and a matched group of HC subjects (HC7; n = 22) (Niethammer et al. 2017) (Supplementary Table S2E). The results of graph analysis of the gene therapy-induced network topography have appeared previously (Niethammer et al. 2018).

Imaging

FDG PET imaging

Study participants at North Shore underwent metabolic imaging with FDG PET on a GE Advance tomograph (General Electric, Milwaukee, WI) at The Feinstein Institutes for Medical Research (Manhasset, NY) as described in detail elsewhere (Spetsieris and Eidelberg 2011; Mattis et al. 2016). Study participants from other centers underwent metabolic imaging on their respective FDG PET platforms (Tripathi et al. 2016; Niethammer et al. 2017; Rus et al. 2020). In all centers, subjects fasted overnight prior to PET imaging; antiparkinsonian medications were withheld for at least 12 h before the scanning session. Scans from each subject were realigned and spatially normalized to a standard Montreal Neurological Institute (MNI)-based PET template and were smoothed with an isotropic Gaussian kernel (10 mm) in all directions to improve the signal-to-noise ratio. Image processing was performed using Statistical Parametric Mapping (SPM5) software (Wellcome Trust Centre for Neuroimaging, Institute of Neurology).

Network analysis

PD-related networks

We used previously validated PD-related metabolic patterns associated with motor and cognitive dysfunction (PDRP and PDCP, respectively) (Niethammer and Eidelberg 2012; Schindlbeck and Eidelberg 2018).

These patterns were identified using spatial covariance analysis of FDG PET data from PD patients and HC subjects as described previously (Spetsieris and Eidelberg 2011; Spetsieris et al. 2015; Schindlbeck et al. 2021). Based on prior graphical analysis, we used nodal valence (region weight sign) to partition both networks into core and periphery subgraphs (Ko et al. 2018). For the PDRP (38 nodes according to the AAL atlas (Tzourio-Mazoyer et al. 2002) (see below; Supplementary Table S3A), the 20 nodes with positive metabolic valence (i.e. those with region weights ≥ 1.0) were found to form a discrete topological core zone (Ko et al. 2018; Schindlbeck et al. 2020), whereas the remaining 18 nodes had negative valence (i.e. region weights ≤ −1.0) and comprised the network periphery (Schindlbeck et al. 2020). For PDCP (35 nodes; Supplementary Table S3B), the core was composed of the 16 nodes with negative valence (Schindlbeck et al. 2020), which corresponded to the cortical core of the default mode network (Spetsieris et al. 2015; Betzel et al. 2017; Schindlbeck and Eidelberg 2018). The assignment of each PDRP and PDCP node to the core or periphery of the respective network is given in Supplementary Table S3A and B. For both networks, assignments based on metabolic valence agreed well with the results of modularity maximization and information theoretic community detection algorithms (Schindlbeck et al. 2020).

A‌AV2-GAD-related pattern

We utilized the previously reported AAV2-GAD-related metabolic pattern (GADRP) identified in trial participants scanned with FDG PET at baseline and after subthalamic gene therapy (Niethammer et al. 2017, 2018). This network was extracted from the metabolic data using ordinal trends canonical variates analysis, a form of supervised principal component analysis (Habeck et al. 2005). The details of this analysis and its results are provided elsewhere (Niethammer et al. 2018). The GADRP was composed of 14 nodes according to the AAL atlas (Supplementary Table S3C). Because of its relatively small size, this network could not be reliably partitioned; graphical analysis was therefore performed on the network as a whole. Preliminary graph theory analysis of the GADRP has appeared previously (Niethammer et al. 2018). In the current study, we extended the analysis to the PDRP and additionally measured graphical metrics for this space in the various groups and time points.

Graph theory and network metrics

Defining nodes and edges

As noted above, for each network, nodes were defined based on the AAL atlas (Tzourio-Mazoyer et al. 2002) in which we parcellated the 3D image of the whole brain, normalized to MNI space. This produced 95 standardized anatomical regions-of-interest (ROIs) as described previously (Ko et al. 2018; Niethammer et al. 2018; Schindlbeck et al. 2020). For the significant clusters identified by voxel-wise network analysis, we identified corresponding AAL nodes (see Supplementary Table S3A–C for listings). For each node, we computed normalized metabolic activity for FDG PET scans.

Different network spaces were used in the various analyses. Most of the studies were analyzed in PDRP space for FDG PET (Spetsieris and Eidelberg 2011). As mentioned above, comparison of PD genotypes (PD-LRRK2 vs. PD-GBA) relied on prespecified subnetworks of the PDRP and PDCP (i.e. network core and periphery) defined in an earlier study (Schindlbeck et al. 2020). Lastly, in addition to the PDRP, we used the treatment-induced AAV2-GAD gene therapy network (GADRP) reported previously (Niethammer et al. 2018) to assess the changes in graph metrics that occurred with this intervention and with sham surgery in this network space and in the PDRP. The details of each of these networks are provided in Supplementary Table S3A–C.

In this study, we used AAL ROI data from FDG PET (globally normalized regional metabolic activity) to construct matrices of pairwise correlations. We used bootstrap methods (in-house Matlab script; MATLAB R2020a) to generate 100 samples for each group. For each iteration, we computed pairwise nodal correlation coefficients (Pearson correlations). The median values of the iterates (100 bootstrap correlation estimates) were used to create an adjacency matrix for the network/subgraph in each group. These calculations were performed using the Machine Learning Toolbox in MATLAB R2020a.

Network metrics

To assess group differences in connectivity parameters within the relevant network spaces, we used undirected graphs for simplicity in hypothesis testing and computational ease. The following metrics were computed on weighted graphical links:

1. Assortativity coefficient: The correlation coefficient between the degrees of all nodes on two opposite ends of a link (Newman 2003; Noldus and Van Mieghem 2015; Barabasi 2016). The details of calculating the assortativity coefficient are described elsewhere (Barabasi 2016). For a given network, we consider assortativity in a group of subjects to be increased if the assortativity coefficient, which is described as assortative for positive values, neutral for ≈0, or disassortative for negative values, is significantly elevated compared to values for the same network computed in a different group. Analogously, assortativity is considered to be reduced when the coefficient computed for the same network is lower than in a comparison group.

2. Degree centrality: The number of connections (edges), within the network or subgraph, divided by the total number of nodes in the same space.

3. Clustering coefficient: A measure of the likelihood that the nearest neighbors of a node will also be connected.

4. Characteristic path length: The shortest path length between 2 nodes averaged over all pairs of nodes in a given network. High characteristic path length implies less efficient information transfer through the network (Newman 2010; Rubinov and Sporns 2010).

5. Small-worldness: The ratio of clustering coefficient to characteristic path length, which is normalized to corresponding parameters from an equivalent random graph (Betzel et al. 2017). This measure quantifies the ratio of segregation to integration of information sources in the network space.

These parameters were computed using the Brain Connectivity Toolbox (Rubinov and Sporns 2010) and an in-house Matlab script (MATLAB R2020a). We present assortativity and the other network metrics over a range of connectivity thresholds as described previously (Niethammer et al. 2018; Schindlbeck et al. 2020). In the current study, thresholds ranged from r = 0.3–0.6, at 0.05 increments, corresponding to graph densities between 25% and 60% (Niethammer et al. 2018; Schindlbeck et al. 2020). At lower thresholds (r < 0.3, graph density > 60%), however, group differences may be difficult to discern because of the inclusion of random, nonspecific links. At higher thresholds (r > 0.6, graph density < 25%), graphs may disconnect and distort group comparisons. By plotting the results over a range of thresholds, we demonstrated that group differences in a given metric were robust beyond 2 or 3 adjacent levels.

Visualization

To visualize assortativity effects along a graph, we generated 2D displays of the joint probability distribution of remaining degree (i.e. the total degree centrality for each node minus the connected edge) for random pairs of nodes in the network space (Newman 2003; Barabasi 2016). This was done using the bivariate Gaussian copula with the correlation matrix 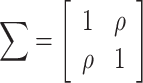. Poisson marginal distributions (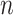=1,000 random numbers, mean = λ) were computed for each variable, where 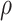is the degree–degree correlation coefficient and λ is the average degree of the network (Newman 2003; Barabasi 2016). These 2 parameters were estimated from the empiric data from each group and network. The simulation steps were performed using an in-house Matlab script (Statistics and Machine Learning Toolbox, MATLAB R2020a).

To visualize differences in connectivity patterns across groups or conditions, graphs were displayed at the minimum threshold (level 1, r = 0.30) for a given network. For assortative configurations (mean ρ > 0), an exemplar with assortativity coefficient between the mean value and the mean + 0.5 standard deviation (SD) was selected from the bootstrap samples described above. For disassortative configurations (mean ρ < 0), an exemplar was selected with assortativity coefficient between the mean value and the mean − 0.5 SD. Graphical configurations were constructed using an in-house Matlab script (mathematics/graph and network algorithms toolbox, MATLAB R2020a).

Lastly, to assess differences in nodal organization between groups and/or conditions, we ordered the nodes hierarchically according to degree centrality. For each configuration, we computed the Spearman rank-order correlation coefficient for the median graph at minimum threshold (r = 0.30). Significant correlations (P ≤ 0.05) reflected similar nodal hierarchy across groups or conditions. Uncorrelated rank order implied the presence of structural differences in the 2 graphs.

Statistical analysis

Network expression values were compared across groups using Student's t-test or 1-way analysis of variance with Tukey–Kramer HSD post hoc tests for multiple comparison correction. For the graph analysis, the bootstrapped data or subject data were used to assess group differences in the network parameters for the relevant subgraphs. Group differences in each of the parameters were evaluated using the general linear model with post hoc Bonferroni tests across graph thresholds. These analyses were performed using IBM SPSS Statistics for Windows, version 21 (IBM Corp., Armonk, NY, USA) or GraphPad Software (Version 7.0, La Jolla California, USA). Results were considered to be significant for P < 0.05, with Bonferroni correction for multiple independent comparisons.

Results

Network assortativity is higher in PD than in HCs

We measured PDRP assortativity, degree centrality, clustering coefficient, characteristic path length, and small-worldness in FDG PET scans previously taken from 96 PD patients and 22 HC subjects (Supplementary Table S1A) (Tang, Poston, Eckert, et al. 2010). We evaluated the same metrics in FDG PET scans from an independent group of 146 PD and 39 HC subjects (Supplementary Table S1B) studied under similar conditions (Tripathi et al. 2016; Rus et al. 2020). Group-level analysis showed that PDRP assortativity was greater in PD than in HCs (P_CORR < 0.001 when compared to HC in both populations) (Fig. 1, Supplementary Fig. S1A and B, Supplementary Table S4A and G). Analysis of the other network metrics revealed only inconsistent differences between the patient and control samples (Table 1).

Fig. 1.

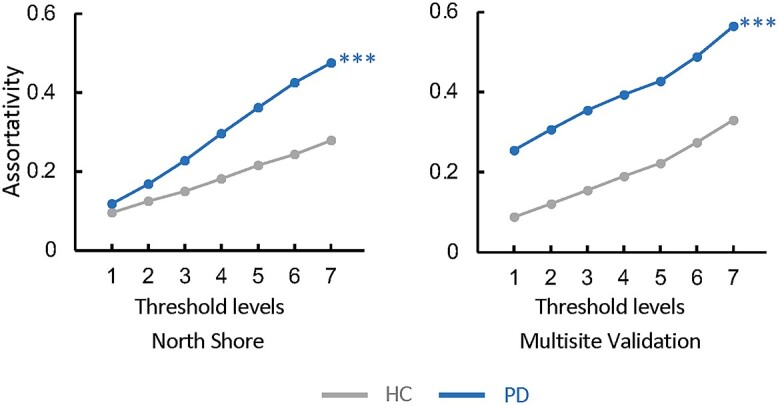
PDRP assortativity is increased in PD patients. Assortativity measurements in the PDRP space are elevated in FDG PET scans from 96 clinically ascertained PD patients compared to 22 HC subjects scanned at the North Shore site (Tang, Poston, Eckert, et al. 2010) (Supplementary Table S1A). PDRP assortativity was likewise increased in FDG PET scans from a combined validation cohort comprising 146 PD and 39 HC subjects from 2 other sites (Supplementary Table S1B, Supplementary Fig. S1). Consistent group differences were not seen for the other PDRP network metrics (Table 1). (Levels 1–7 correspond to cutoff graph thresholds of r = 0.3–0.6 in increments of 0.05. ^***P < 0.001, compared to HC, corrected for multiple comparisons (see Materials and methods)).

Table 1.

Group differences in PDRP network metrics.

Cohort (PD/HC)a	Assortativity coefficient	Degree centrality	Clustering coefficient	Characteristic path length	Small-worldness
North Shore (96/22)	+++	+++	0	+++	0
Multisite (146/39)	+++	+++	−−	+++	−−−

Increase: +++ = P < 0.001 (PD > HC) for comparison of PD with HC (see text).

Decrease: −− and −−− = P < 0.01 and P < 0.001 (PD < HC).

No difference = 0 (PD = HC).

^aSee Supplementary Table S1A and B.

Network assortativity increases with disease progression

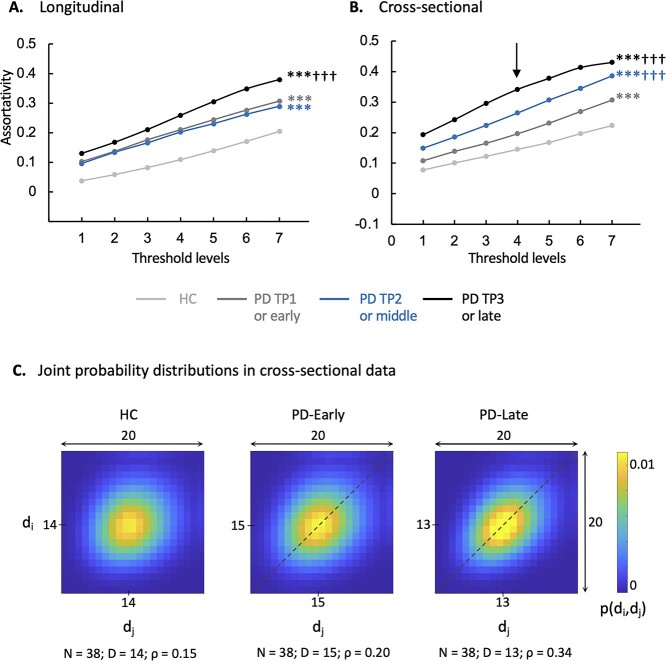
If high assortativity in disease networks, such as PDRP, indicates pathological patterns of connectivity, we would expect to see steady increases in this measure over time. We therefore measured PDRP assortativity in a group of 15 early-stage PD patients who underwent longitudinal metabolic imaging at baseline, 24 months, and 48 months (Huang et al. 2007; Tang, Poston, Dhawan, et al. 2010) (Supplementary Table S2A). Assortativity (Fig. 2A, Supplementary Table S4B) was elevated in the PDRP space at baseline and 24 months (P_CORR < 0.001 at both time points when compared to HC subjects), with further increases at 48 months (P_CORR < 0.001 when compared to baseline and 24 months as well as HC). We next performed a cross-sectional comparison of age- and gender-matched groups of PD patients with early (0–4 years), intermediate (5–9 years), and long (>10 years) duration of symptoms, along with HC subjects (n = 20 in each group; Supplementary Table S2B). PDRP assortativity (Fig. 2B, Supplementary Table S4B) was elevated in all 3 PD groups (P_CORR < 0.001); values were higher (P_CORR < 0.001) with each successive increment in disease duration.

Fig. 2.

PDRP assortativity increases with disease progression. A) Longitudinal PD cohort: Assortativity in the PDRP space rose over time in PD patients (Supplementary Table S2A). B) Cross-sectional PD cohort: PDRP assortativity was elevated in the 3 PD groups compared to HC (Supplementary Table S2B). Values were higher with each successive 4-year increment in disease duration. (Levels 1–7 correspond to cutoff graph thresholds of r = 0.3–0.6 in increments of 0.05. ^***P < 0.001 compared to HC; †††P < 0.001 compared to PD-TP1 A) or PD-early B).) C) 2D displays of the joint probability distribution of degree–degree correlations in the PDRP space for the groups in B). Whereas the HC group showed a relatively symmetrical distribution of probability (P) values around the mean (center), the PD-early and PD-late groups exhibited an assortative connectivity patterns: The density of high P values along the main diagonal (“dashed lines”) represents a tendency for PDRP connections to link nodes with similar degree centrality. (The joint probability distribution for degree–degree correlations in the PDRP space was generated at threshold level 4 [“vertical arrow” in B)]. The color scale represents the computed probability that a randomly selected link connects nodes with degrees d_i and d_j (see Materials and methods). Because mean degree centrality differed for the 3 groups, the centers of the joint distributions also varied. For comparable visualization, the x- and y-axes were shifted so that the mean value for each group was at or near the center of the corresponding display. N = number of nodes; D = mean degree centrality; ρ = assortativity coefficient.)

To visualize the changes in PDRP assortativity seen with advancing disease, we constructed 2D matrix displays of degree–degree correlations in the PDRP space (Fig. 2C) for the early and late PD groups and the HC subjects. Each of the patient groups exhibited an assortative connectivity pattern; this relationship, demonstrated by an elliptical joint probability distribution (see Materials and methods), was more pronounced in late than in early PD patients but was not present in healthy subjects.

Genotypic differences in assortativity parallel the rate of clinical progression

We next asked whether disease network assortativity differed for clinically matched PD patients carrying genetic variants for slower (LRRK2) or faster (GBA1) disease progression (Davis et al. 2016; Saunders-Pullman et al. 2018; Schindlbeck et al. 2020). As noted in the introduction, we recently found that although both genotypes express the same disease networks as sporadic PD, the 3 groups differ in the pattern of connectivity within the disease network spaces (Schindlbeck et al. 2020). We therefore measured assortativity in the PDRP and PDCP networks in these patient groups, which were carefully matched so that the observed network effects were unlikely to have been caused by differences in age or motor symptoms (Supplementary Table S2C).

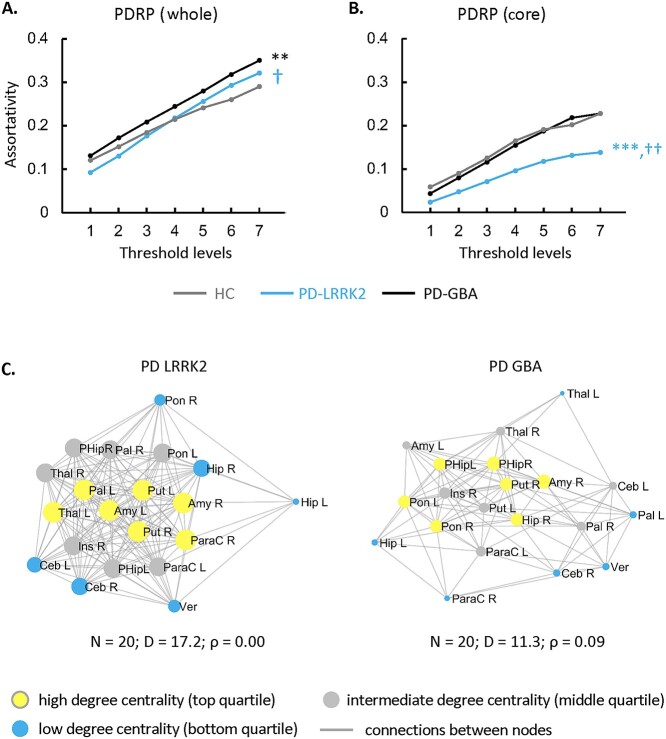
Assortativity in the PDRP space (Fig. 3A, Supplementary Table S4C) was elevated for PD-GBA (P_CORR < 0.05 when compared to HC as well as PD-LRRK2) but did not differ from normal for PD-LRRK2 (P_CORR = 1.00). Given our recent findings that genotypic differences in PD network connectivity were more pronounced at the subnetwork level (Schindlbeck et al. 2020), we partitioned the PDRP space into core and periphery zones (Supplementary Table S3A) based on metabolic valence as described elsewhere (Ko et al. 2018) (see Materials and methods). Assortativity in the PD-LRRK2 PDRP core was lower than in the other groups (P_CORR < 0.01 when compared to PD-GBA and HC) (Fig. 3B, Supplementary Table S4C) even though degree centrality was elevated (Schindlbeck et al. 2020).

Fig. 3.

Influence of genotype on PDRP assortativity. A) PD-GBA patients showed higher assortativity than PD-LRRK2 or HC subjects in the PDRP space as a whole. B) In the PDRP core zone (see text), PD-LRRK2 patients showed lower assortativity than HC or PD-GBA subjects. (Levels 1–7 correspond to cutoff graph thresholds of r = 0.3–0.6 in increments of 0.05, corrected for multiple comparisons [see Materials and methods]. ^**P < 0.01, ^***P < 0.001 for PD-LRRK2 or PD-GBA relative to HC. †P < 0.05, ††P < 0.01 for PD-LRRK2 relative to PD-GBA.) C) Connectivity patterns in the PDRP core zone for the genotypic patient groups in B). PD-LRRK2 (“left”) exhibited a neutral pattern, with a combination of assortative and disassortative connections linking subgraph nodes. By contrast, in PD-GBA (“right”), the connectivity pattern for the subgraph was assortatitve at the same threshold (|r| ≥ 0.3). (Core nodes are represented by disks, with radius proportional to the corresponding degree centrality. Yellow = high degree (top quartile); blue = low degree (bottom quartile); gray = intermediate degree (middle quartile). Connections were thresholded at |r| ≥ 0.3 and displayed as gray lines. N = number of nodes; D = degree centrality; ρ = assortativity.)

To examine connectivity patterns in the PDRP core in greater detail, we reconstructed corresponding subgraphs for the 2 PD genotypes. PD-LRRK2 showed a dense cluster of interconnected high-degree nodes (Fig. 3C, “left”) at the center of the core zone, involving the putamen, globus pallidus, thalamus, and supplementary motor area (SMA) as well as the amygdala, parahippocampal gyrus, and insula. These were connected to an outer rim of low-degree nodes in the pons, cerebellum, and hippocampus, which were also linked to each other. This configuration was therefore characterized by a neutral connectivity pattern, i.e. a combination of assortative and disassortative connections, for the subgraph as a whole. By contrast, for PD-GBA (Fig. 3C, “right”), a set of interconnected low-degree nodes in the globus pallidus, thalamus, and SMA formed the rim of the subgraph. Sparse connections linked these to a cluster of interconnected high-degree nodes in the interior of the core zone.

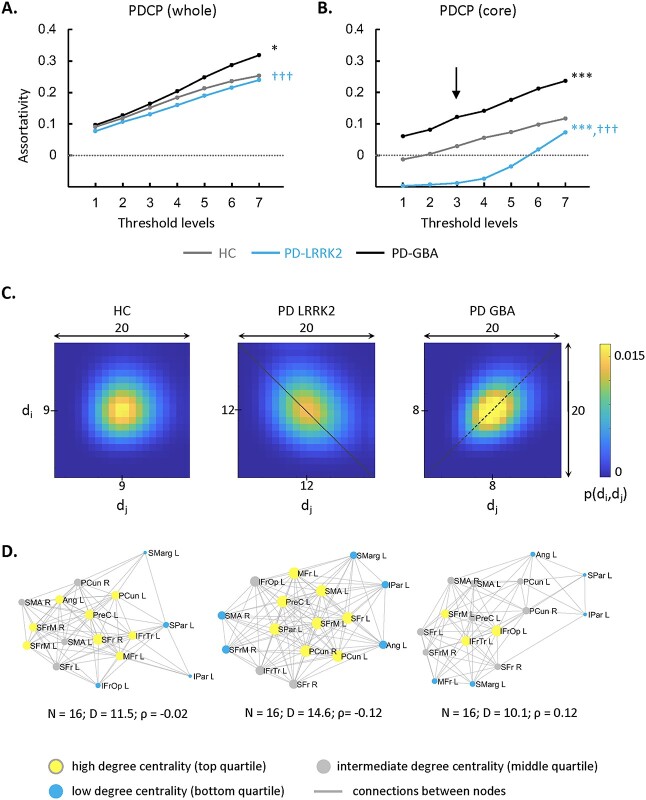
Analogous group differences were seen in the PDCP space (Fig. 4A, Supplementary Table S4D): Network assortativity was higher in PD-GBA than in the other groups (P_CORR < 0.05 when compared to HC; P_CORR < 0.001 when compared to PD-LRRK2), but PD-LRRK2 assortativity did not differ from HC (P_CORR > 0.34). This is consistent with the general lack of cognitive decline in PD-LRRK2. Genotypic differences were also more pronounced in the PDCP core zone (Supplementary Table S2B) when compared to the whole network. As in the PDRP core, the PDCP core was least assortative in PD-LRRK2 (Fig. 4B, Supplementary Table S4D) (P_CORR < 0.001 when compared to HC and PD-GBA) but most assortative in PD-GBA (P_CORR < 0.001 when compared to HC and PD-LRRK2).

Fig. 4.

Influence of genotype on PDCP assortativity. A) PDCP assortativity was elevated in PD-GBA patients compared to PD-LRRK2 and the control group (HC). B) In the PDCP core zone, PD-GBA again showed the highest assortativity and LRRK2 showed the lowest. ^*P < 0.05, ^***P < 0.001 for PD-LRRK2 or PD-GBA relative to HC. †††P < 0.001 for PD-LRRK2 relative to PD-GBA. C) 2D displays of the joint degree–degree probability distribution in the PDCP core for the three groups. PD-LRRK2 exhibited disassortativity, as evident by the density of high P values along the secondary diagonal (“dotted line”). PD-GBA, by contrast, showed high P values along the main diagonal (“dashed line”). The joint probability distribution was spherical for HC subjects in the same subgraph. The joint degree probability distribution was generated at threshold level 3 (“vertical arrow” in B)) for each group. (The color scale represents the probability that a randomly selected link connects nodes with degrees d_i and d_j. Because mean degree centrality differed for the 3 groups, the centers of the joint distributions also varied. For comparable visualization, the x- and y-axes were shifted so that the mean value for each group was at or near the center of the corresponding display.) D) Connectivity patterns in the PDCP core zone for the groups in C). In PD-LRRK2, the subgraph exhibited a disassortative configuration, whereas the pattern was assortative in PD-GBA and neutral in HC (see text). (Core nodes are represented by disks, with radius proportional to the corresponding degree centrality. Yellow = high degree (top quartile); blue = low degree (bottom quartile); gray = intermediate degree (middle quartile). Connections were thresholded at |r| ≥ 0.3 and displayed as gray lines. N = number of nodes; D = degree centrality; ρ = assortativity.)

The genotypic differences in PDCP core assortativity are highlighted in the corresponding correlation matrix displays and subgraph reconstructions (Fig. 4C and D). For PD-LRRK2, the connectivity pattern in this subgraph was disassortative on average, with prominent connections linking high- and low-degree nodes in frontal and parietal association regions. For PD-GBA, the PDCP core was assortative. In contrast to the PD groups, HC subjects exhibited a balance of assortative and disassortative connections in the same subgraph.

Dopaminergic treatment increases PDRP assortativity

Given that PDRP assortativity rises with disease progression, we were particularly interested in whether treatment would affect this measure. On the one hand, dopaminergic therapy improves symptoms; on the other hand, the disease continues to progress, as indicated by rising expression of PDRP (Schindlbeck and Eidelberg 2018).

We first examined changes in network assortativity in 14 PD subjects who underwent metabolic imaging in the unmedicated baseline state (“off”) state and during intravenous levodopa infusion (“on”), which was titrated to maximal clinical benefit without abnormal involuntary movements (Jourdain et al. 2016). The clinical and demographic features of these subjects are provided in Supplementary Table S2D. In the PDRP space, assortativity (Fig. 5A, Supplementary Table S4E) was elevated in the off state (P_CORR = 0.001 when compared to HC). Values increased further during levodopa infusion (P_CORR < 0.05, “on” compared to “off”), reaching even more abnormal levels (P_CORR < 0.001, “on” compared to HC). Interestingly, this increase (worsening) in network assortativity was not accompanied by changes in degree centrality (Table 2) or nodal hierarchy (see Materials and methods), given that the rank order of degree centrality in the network space was similar for the 2 treatment conditions (r_s = 0.69 [0.57–0.78, 95% confidence interval {CI}], P < 0.001; Spearman correlation).

Fig. 5.

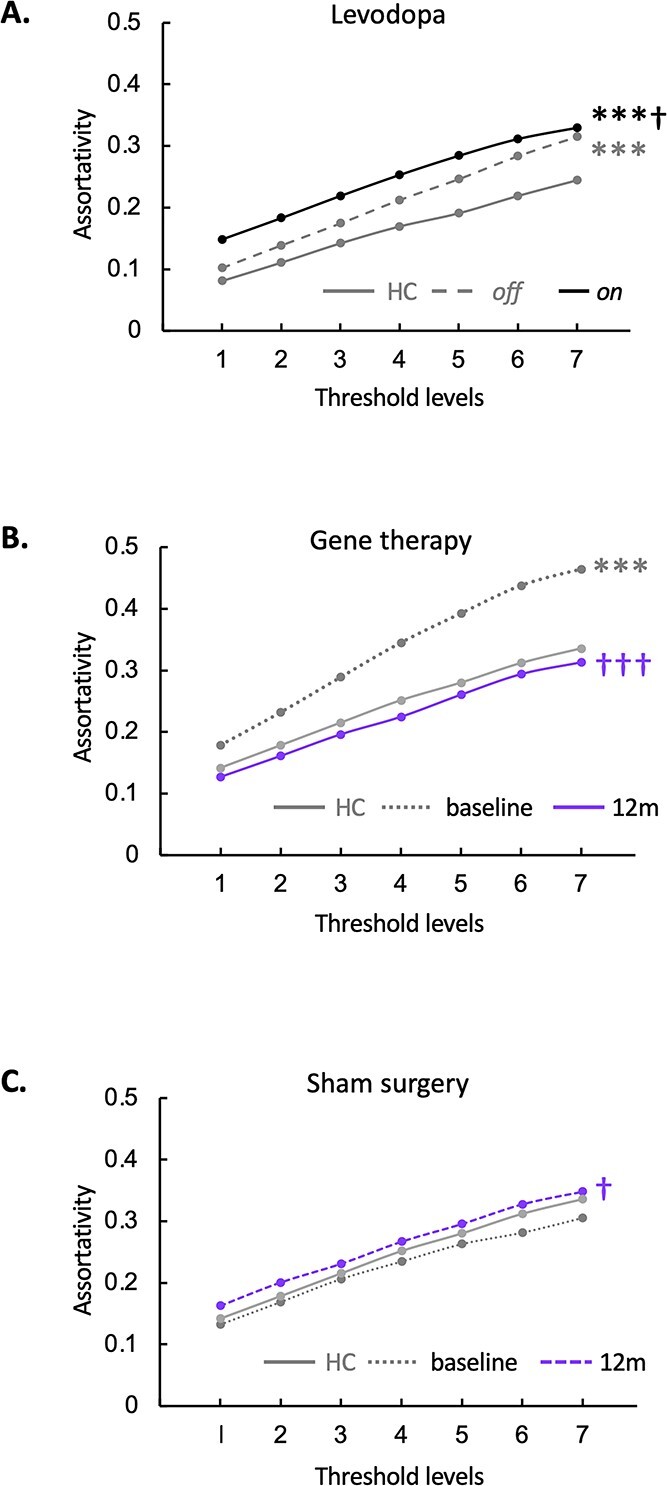
PDRP network assortativity: Changes with treatment. A) Levodopa infusion: In the PDRP space, assortativity was elevated in the unmedicated (“off”) state compared to the HC group (Supplementary Table S2D) but rose even higher during intravenous levodopa infusion (“on”). (^***P < 0.001, “off” or “on” compared to HC. †P < 0.05, “on” compared to “off.”) B) STN AAV2-GAD: PDRP assortativity was elevated at baseline in the gene therapy group (Supplementary Table S2E) compared to HC subjects but declined by 12 months after gene therapy. C) Sham surgery: In this group (Supplementary Table S2E), PDRP assortativity increased relative to baseline at 12 months but did not differ significantly from HC at either time point. (Levels 1–7 correspond to cutoff graph thresholds of r = 0.3–0.6 in increments of 0.05. ^***P < 0.001 for baseline or 12 months vs. HC. †P < 0.05 †††P < 0.001 for baseline vs. 12 months.)

Table 2.

Treatment-mediated changes in PDRP network metrics.

Interventiona (number of subjects)	Assortativity coefficient	Degree centrality	Clustering coefficient	Characteristic path length	Small-worldness
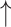
Levodopa infusion (14) (“on” vs. “off” medication)		0	0
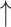
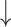
STN AAV2-GAD (16) (12 months vs. baseline)
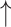
Sham surgery (21) (12 months vs. baseline)		0		0	0

Increase: 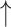and = P < 0.05 and P < 0.001 versus baseline (see text), for comparison of treatment with baseline.

Decrease: 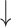and = P < 0.05 and P < 0.001 versus baseline (see text), for comparison of treatment with baseline.

No change = 0.

^aSee Supplementary Table S2D and E.

Subthalamic gene therapy reduces PDRP assortativity

We previously found that AAV2-GAD gene therapy induces therapeutic remodeling of brain networks (Niethammer et al. 2018), which gives rise to what we called the GADRP. An important test of our hypothesis was therefore to determine whether this disease-modifying treatment also diminishes assortativity. We analyzed metabolic imaging data from PD patients scanned at baseline before randomization to either gene therapy or sham surgery, as part of a double-blind randomized clinical trial, and again 12 months after surgery (Niethammer et al. 2017) (for demographic information, see Supplementary Table S2E).

For each group and time point, we measured assortativity for both PDRP and GADRP (Supplementary Table S3C) (Niethammer et al. 2018). PDRP assortativity (Fig. 5B, Supplementary Table S4E) was elevated at baseline in the gene therapy group (P_CORR < 0.001 when compared to HC) but fell to normal levels 12 months after treatment (P_CORR < 0.001 when compared to baseline). Nodal hierarchy in the PDRP space was not appreciably altered by the gene therapy (r_s = 0.63 [0.49–0.74, 95% CI], P < 0.05; Spearman correlation).

In the sham group (Fig. 5C, Supplementary Table S4E), PDRP assortativity increased somewhat at 12 months (P_CORR < 0.05 when compared to baseline) but did not differ from HC at either time point (P_CORR > 0.50). At baseline, the rank order of nodal degree in the PDRP space was similar for the sham surgery and gene therapy groups (r_s = 0.57 [0.42–0.69, 95% CI], P < 0.001; Spearman correlation), and nodal hierarchy for this network remained the same 12 months after sham surgery (r_s = 0.84 [0.77–0.89, 95% CI], P < 0.001; Spearman correlation).

The independent GADRP network (Supplementary Table S3C) (Niethammer et al. 2018) showed lower assortativity (Fig. 6A, “top,” Supplementary Table S4F) 12 months after gene therapy compared to baseline and HC (P_CORR < 0.05). GADRP assortativity was higher 12 months after sham surgery compared to baseline (P_CORR < 0.01; Fig. 6B, “top,” Supplementary Table S4F), which reached abnormally elevated levels at endpoint compared to HC (P_CORR < 0.001). The divergence of the GADRP assortativity responses in the gene therapy and sham groups can be seen in the graphical displays of the treatment-induced network. In the gene therapy group, GADRP exhibited an assortative baseline configuration (Fig. 6A, “middle”), with a cluster of high-degree nodes, representing the caudate nuclei, thalamus, and frontal regions, which linked to pairs of interconnected lower-degree nodes in the putamen and supramarginal gyrus bilaterally. Twelve months after treatment (Fig. 6A, “bottom,” Supplementary Table S4F), degree centrality increased in most GADRP nodes, with a concurrent decline in network assortativity. In the sham surgery group, the baseline configuration (Fig. 6B, “middle”) was also assortative, with nodal degree in similar rank order to that observed at baseline in the gene therapy group (r_s = 0.53 [0.37–0.66, 95% CI], P < 0.05; Spearman correlation). The network configuration seen after sham surgery (Fig. 6B, “bottom,” Supplementary Table S4F), however, was strikingly different, with an overall reduction in degree and an increase in network assortativity. Despite these changes, GADRP nodal hierarchy was not appreciably altered after sham surgery (r_s = 0.54 [0.38–0.67, 95% CI], P < 0.05; Spearman correlation). This contrasted with the substantial network remodeling following gene therapy, given the revision of nodal hierarchy that took place over the same time period (r_s = 0.13 [−0.7–0.32, 95% CI], P = 0.67).

Fig. 6.

Changes in the GADRP connectivity pattern with treatment versus sham surgery. A) The GADRP connectivity pattern was assortative at baseline but transitioned to a less assortative, neutral configuration 12 months after treatment (Supplementary Table S2E). B) In the sham surgery group, the baseline pattern was assortative and remained so 12 months later. (“Top”: Threshold levels 1–7 correspond to cutoff thresholds of r = 0.3–0.6 in increments of 0.05. ^*P < 0.05, ^**P < 0.01, ^***P < 0.001 for baseline or 12 months vs. HC. †P < 0.05, ††P < 0.01 for baseline vs. 12 months. “Middle, bottom”: Core nodes are represented by disks, with radius proportional to the corresponding degree centrality. High, low, and intermediate degree nodes [top, bottom, and middle quartile] are depicted in yellow, blue, and gray, respectively. Connections were thresholded at |r| ≥ 0.3 and displayed as gray lines. N = number of nodes; D = degree centrality; ρ = assortativity.)

Increase in module-to-module bridging connections in the PDRP core

In previous work, we reported an increase in GADRP connections following STN AAV2-GAD gene therapy (Niethammer et al. 2018). We now observed parallel connectivity changes in the PDRP space of these subjects, which were similar to those seen in PD-LRRK2 (Schindlbeck et al. 2020). Compared to baseline, 8 new PDRP connections developed in the 12 months following gene therapy (Supplementary Table S5). It is worth noting that 3 of these overlapped with the novel connections observed in PD-LRRK2 (Schindlbeck et al. 2020). In both groups (Fig. 7A), these connections linked basal ganglia and limbic nodes, which are located in separate modules within the PDRP core (Ko et al. 2018).

Fig. 7.

Increase in connections linking PDRP core modules: A shared adaptive response. A) Map of functional connections between PDRP core nodes in low-assortativity configurations associated with genotype (PD-LRRK2; Schindlbeck et al. 2020) or treatment (12 months after subthalamic [STN] AAV2-GAD; Niethammer et al. 2018). In both groups, novel connections were observed between 2 previously identified modules (“dashed circles”) in the PDRP core zone (Ko et al. 2018). The PDRP network is composed of 38 nodes (Supplementary Table S3A) (Ko et al. 2018), which are represented by circles with radius proportional to the corresponding degree centrality. The core zone is composed of 20 metabolically active regions (“red circles”) and 18 relatively underactive nodes (“blue circles”) which form the network periphery. PDRP node-to-node connections were displayed at minimum threshold (|r| = 0.3) and were represented by thin gray lines for PD-LRRK2. B) In the PDRP core, both PD-LRRK2 and STN AAV2-GAD patients 12 months after gene therapy showed lower modularity than HC subjects and PD patients scanned at baseline. (^***P < 0.001 for the PD groups [gene therapy or PD-LRRK2] relative to HC. †††P < 0.001 for gene therapy baseline vs. 12 months or for gene therapy baseline vs. PD-LRRK2.)

As previously reported in PD-LRRK2 (Schindlbeck et al. 2020), such connections reduce the modularity of the PDRP core (P_CORR < 0.001, relative to HC; Fig. 7B), and indeed, comparable modularity reductions were also seen after gene therapy (P_CORR < 0.001 when compared to baseline and HC; Fig. 7B). Thus, low PDRP assortativity, as occurs intrinsically in PD-LRRK2 and following STN AAV2-GAD in sporadic PD, was accompanied by reductions in subgraph modularity linked to increases in bridging connections between core modules.

Discussion

Elevated assortativity has been observed in neurodegenerative disorders, including Alzheimer’s disease (Luo et al. 2021) and frontotemporal dementia (Agosta et al. 2013). Here, we quantify this graph metric in specific, previously validated disease networks identified in the resting state with FDG PET (Schindlbeck and Eidelberg 2018; Schindlbeck et al. 2020). Furthermore, to date, assortativity has not been used to discern the effects of specific interventions on connectivity patterns in these networks. In this study, we found that PDRP assortativity is elevated in the course of PD, indicating overreliance on connections between nodes of similar degree centrality, which is associated with unstable network configurations and inefficient information (Newman 2003; Zhou et al. 2012; Murakami et al. 2017). Disease network assortativity was diminished by subthalamic AAV2-GAD, but not by levodopa, suggesting a shift toward a more stable connectivity pattern after the former intervention. In functional brain networks, assortativity is only minimally correlated with other graph metrics (Li et al. 2011)—indeed, we observed no consistent changes in degree centrality or characteristic path length—which underscores the unique information this metric provides about the architecture and dynamic properties of the underlying circuitry (Noldus and Van Mieghem 2015; Peel et al. 2018).

Assortativity increases with disease progression

Network assortativity increases with disease progression and is also influenced by intrinsic factors such as genotype. Disease progression is relatively fast in PD patients with GBA1 variants (Davis et al. 2016), and indeed, assortativity in the PDRP/PDCP core zones was greater than in clinically matched carriers of the more benign LRRK2-G2019S mutation (Saunders-Pullman et al. 2018). In the latter genotype, assortativity was reduced in the core subgraphs of both networks, suggesting more efficient information transfer (Noldus and Van Mieghem 2015; Murakami et al. 2017). The current findings extend our previous observation that the gain in functional connections in PD-LRRK2 occurred primarily in the core zone of the 2 PD networks (Schindlbeck et al. 2020). The relatively benign clinical course seen with this mutation can be attributed to the enhanced integration of signal across these subgraphs, as implied by the observed reduction in core assortativity as well as the relatively low modularity and increased synchronization reported previously in these patients (Schindlbeck et al. 2020). In aggregate, the altered pattern of functional connectivity seen in PD-LRRK2 may represent a previously unrecognized adaptation to the disease process. The pattern in PD-GBA was quite different, however, in that connectional gain was not centralized to the PDRP/PDCP core zones as it was in PD-LRRK2 (Schindlbeck et al. 2020). Genotypic differences in assortativity were particularly striking in the core zones of both networks, with significant increases in the measure for PD-GBA compared to PD-LRRK2. This is consistent with fragmentation of information transfer in the former genotype, as expected in a pathological connectivity pattern (Ko et al. 2018). By contrast, the lower assortativity seen in PD-LRRK2 is consistent with a more integrated response, as might be expected in a beneficial adaptation. That said, given the small numbers of genotypic patients, the current findings need to be substantiated in larger samples. It will also be important to determine the degree to which comparable changes are evident in asymptomatic carriers of these mutations.

In this vein, we note that while cognitive functioning was grossly preserved in both patient groups (Schindlbeck et al. 2020), genotypic differences in core assortativity were greater for the PDCP compared to PDRP. The propensity for neocortical Lewy body formation is also greater in PD-GBA patients (Neumann et al. 2009; Shiner et al. 2016). Thus, the increases in PDCP core assortativity seen in these patients suggest that pathological connectivity changes develop in this subgraph before clinically identifiable cognitive decline. In this regard, the disassortativity observed in the PDCP core zone in PD-LRRK2 patients may be compatible with an adaptive response that slows the transition to dementia in patients with this mutation. Prospective imaging studies will be needed to determine whether increased baseline assortativity in the PDCP core predicts future cognitive deterioration in individual PD patients.

Changes in assortativity distinguish treatment responses

Mean PDRP expression increases with disease progression, paralleling the changes in network assortativity seen over time in the same groups of patients. While these measurements relate to a fixed PDRP, it is also possible to identify similar yet topographically more extensive disease patterns at each successive time point (Spetsieris and Eidelberg 2011; Spetsieris et al. 2015). In this context, the magnitude of the corresponding eigenvalue would rise, leading potentially to parallel increases in network assortativity (Van Mieghem 2010; Noldus and Van Mieghem 2015). It is therefore not surprising that for PDRP, assortativity and mean pattern expression both increase with advancing disease.

That said, the 2 network measures exhibit divergent responses to treatment. Levodopa administration consistently improves motor symptoms in PD patients by repleting nigrostriatal dopamine. Although levodopa lowers PDRP expression levels (Niethammer and Eidelberg 2012; Vo et al. 2017), network assortativity increased in these individuals during treatment. It is conceivable that transient increases in PDRP assortativity occur with each levodopa dose. Under such circumstances, repeated daily administration of the drug may lead over time to development of a maladaptive connectivity pattern in the network space (Picconi et al. 2018). It would be interesting to see whether changes in PDRP assortativity appear with chronic treatment and, if so, how they relate to the appearance of levodopa-induced dyskinesia.

A much different set of network changes follow subthalamic AAV2-GAD gene therapy: PDRP expression levels increase over time, consistent with disease progression (Niethammer et al. 2018), yet PDRP assortativity substantially declined in the treatment group. Treatment reduced assortativity in the GADRP space to subnormal levels and extensively reorganized network structure, as indicated by treatment-mediated changes in nodal hierarchy for this network but not for PDRP.

Thus, assortativity provides complementary information not obtained by routine network expression measurements. In this context, it is worth noting that treatment-mediated modulation in PDRP assortativity (Table 2) was not associated with parallel changes in degree centrality or the other connectivity metrics. The response of PDRP small-worldness to treatment is interesting in this regard. Assortativity in this network increased with levodopa and sham surgery and declined with gene therapy. PDRP small-worldness, by contrast, declined toward normal after either levodopa or gene therapy. Given that significant clinical improvement occurred with both treatments, it is possible that normalization of PDRP small-worldness is a feature of the symptomatic benefit seen with both interventions (Ko et al. 2018; Niethammer et al. 2018). The reductions in PDRP assortativity, on the other hand, may reflect longer-term adaptive responses that occur with gene therapy but not with acute levodopa treatment.

As mentioned above, symptomatic PD treatments are generally associated with suppression of PDRP activity (Niethammer and Eidelberg 2012; Vo et al. 2017). By contrast, the network changes that occur with disease modification are likely to be more complex, with remodeling of disease networks, treatment-induced regional patterns, or both. In this regard, graphical analysis of network connectivity patterns becomes a useful means of documenting such longer term treatment effects. In the current FDG PET study, network metrics were necessarily quantified at the group level. However, to evaluate treatment, these changes should optimally be determined for individual patients. Resting-state functional magnetic resonance imaging (MRI) (rs-fMRI) provides a useful alternative in that regard. PDRP and PDCP networks closely related to their FDG PET counterparts have already been characterized by this method (Vo et al. 2017; Rommal et al. 2021; Schindlbeck et al. 2021). Moreover, unlike FDG PET, rs-fMRI time series data can be used to assess connectivity patterns in individual subjects. Whether network metrics such as assortativity can be reliably quantified in single cases using this method is a topic of ongoing investigation. If successful, the results will support the use of functional networks for the evaluation of new treatments for PD and other brain disorders.

Conflict of interest statement

D.E. has received consultant fees from MeiraGTx and has received research support from the NIH (NINDS, NIDCD, and NIAID) and The Michael J. Fox Foundation for Parkinson’s Research. All other authors declare no relevant competing interests.

Authors’ contributions

A.V., K.A.S., and D.E. contributed to the conception and design of the study; M.N. and V.D. acquired the data; A.V., K.A.S, C.C.T., Y.Y.C. and D.E. performed voxel-based network analysis; N.N., A.V., K.A.S., P.G.S., and D.E. performed graph theory analysis and quantitative network measurements; A.V., K.A.S, N.N., A.R., and D.E. prepared the figures; and A.V., K.A.S., and D.E. drafted the article. All authors revised the article for intellectual content.

Funding

Aspects of this work were supported by the National Institute of Neurological Disorders and Stroke (P50 NS 071675 [Morris K. Udall Center of Excellence for Parkinson’s Disease Research at The Feinstein Institute for Medical Research] to D.E.), The Michael J. Fox Foundation for Parkinson’s Research, and Neurologix, Inc. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health or the National Institute of Neurological Disorders and Stroke. K.A.S. is the recipient of a Research Fellowship for Clinical Neurologists (PF-FBS-1929) from the Parkinson’s Foundation and the Leopoldina Fellowship Program of the German National Academy of Sciences Leopoldina (LDS 2016-08).

Data availability

Deidentified data will be made available on reasonable request from interested investigators for the purpose of replicating results.