Anisotropic superconductivity at KTaO₃(111) interfaces

Abstract

A two-dimensional, anisotropic superconductivity was recently found at the KTaO₃(111) interfaces. The nature of the anisotropic superconducting transition remains a subject of debate. To investigate the origins of the observed behavior, we grew epitaxial KTaO₃(111)-based heterostructures. We show that the superconductivity is robust against the in-plane magnetic field and violates the Pauli limit. We also show that the Cooper pairs are more resilient when the bias is along [11$\overline{2}$] (I ∥ [11$\overline{2}$]) and the magnetic field is along [1$\overline{1}$0] (B ∥ [1$\overline{1}$0]). We discuss the anisotropic nature of superconductivity in the context of electronic structure, orbital character, and spin texture at the KTaO₃(111) interfaces. The results point to future opportunities to enhance superconducting transition temperatures and critical fields in crystalline, two-dimensional superconductors with strong spin-orbit coupling.

Revealing anisotropic nature of 2D superconductivity in the context of electronic structure, orbital character, and spin texture.

INTRODUCTION

Two-dimensional (2D) superconductivity is a fertile landscape for exotic quantum phenomena. Earlier studies were focused on understanding the quantum phase transitions in 2D disordered systems (1–3). Recently, highly crystalline 2D superconductors have allowed observation of intrinsic quantum phenomena, such as violation of paramagnetic Pauli limit (4–6) and quantum Griffiths singularity (7). Spin-orbit coupling (SOC) in crystalline 2D superconductors gives rise to a robust superconducting state, surviving anomalous applied magnetic fields (8). For example, SOC combined with out-of-plane inversion symmetry breaking elements, i.e., Rashba SOC, creates a distinctive in-plane spin configuration and enhances the in-plane critical magnetic field (9). Zeeman-like spin splitting also competes with in-plane magnetic field in Ising superconductors, stabilizing 2D superconductivity beyond Pauli limit (4, 5, 10). In real systems, however, Rashba- and Zeeman-like SOCs could coexist (6, 11, 12). Furthermore, symmetry-restricted spin configuration and orbital arrangements give rise to anisotropic superconducting transition in crystalline 2D superconductors.

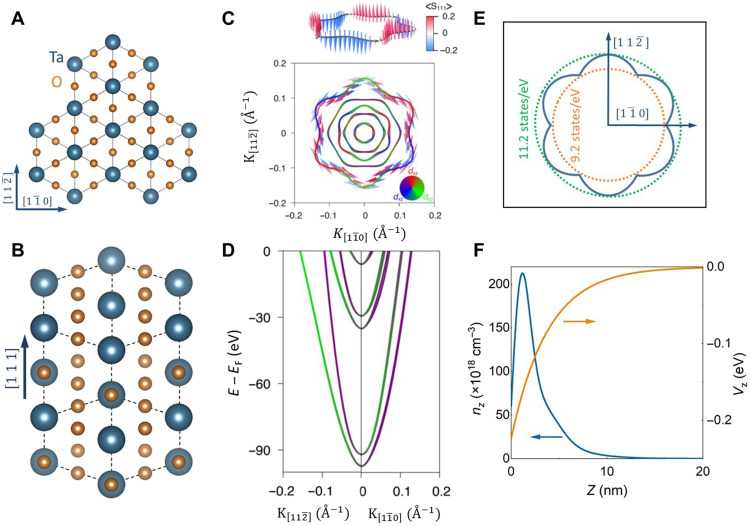
KTaO₃ is a cubic perovskite and an incipient ferroelectric (13, 14). Figure 1 (A and B) shows the schematic crystal structure of the KTaO₃(111) surface. Itinerant electrons occupy the tantalum 5d-derived t_2g states in electron-doped samples (15, 16). Figure 1 (C and D) illustrates the calculated Fermi surface and band structure, demonstrating the anisotropy of the orbital character and spin texture in a KTaO₃(111) 2D electron gas. Figure 1C shows a substantial out-of-plane canting of the otherwise helically polarized spin texture of carriers in the momentum space. The out-of-plane spin canting is maximal along [1$\overline{1}$0] and completely quenched along [11$\overline{2}$] direction. Conduction electrons reside in the J = 3/2 states at low-temperature limit, due to the large SOC gap [0.4 eV at gamma point (17)]. The trigonal warping of the Fermi pockets, arising from the spatial polarization of the d_xy, d_yz, and d_xz orbitals, gives rise to a momentum-dependent density of states. Figure 1E shows the calculated density of states at various Fermi momenta in a KTaO₃(111) 2D electron gas (n = 6 × 10¹³ cm⁻²). Figure 1F shows the Poisson-Schrödinger calculation of the carrier density distribution and electric potential, suggesting that the conduction states are confined near the KTaO₃(111) interface (d_FWHM ∼ 3 nm).

Fig. 1. Anisotropic electronic structure and spin texture in a KTaO₃(111) 2D electron system.

(A and B) Lattice structure of the KTaO₃(111) surface (tantalum and oxygen atoms are depicted). (C) Calculated Fermi surface, demonstrating the anisotropy of the orbital character (blue, red, and green represent d_xz, d_xy, and d_yz orbitals, respectively) and spin texture for a KTaO₃(111) 2D electron gas (n = 6 × 10¹³ cm⁻²). The out-of-plane canting of the spin texture peaks along [1$\overline{1}$0] and is quenched along [11$\overline{2}$] direction. (D) Electronic band structure of the KTaO₃ along [11$\overline{2}$] and [1$\overline{1}$0]. (E) Anisotropy of the density of states in a KTaO₃(111) 2D electron gas (n = 6 × 10¹³ cm⁻²). (F) Poisson-Schrödinger calculations of carrier density distribution and electric potential, demonstrating that the states are confined within 15 nm below the KTaO₃(111) interface with d_FWHM ∼ 3 nm.

An anisotropic 2D superconductivity was recently found in KTaO₃(111) interfaces (18). The superconducting order parameter is sensitive to the interface orientation with critical superconducting temperatures of 2 K (18), 1 K (19), and 0.05 K (20) for (111), (110), and (100) interfaces, respectively. Furthermore, KTaO₃(111) interfaces show an anisotropic superconducting transition that is sensitive to the bias directions (18). The nature of superconductivity and its anisotropic behavior are not clearly understood in KTaO₃(111) heterostructures.

Here, we report on emergence of an anisotropic superconductivity in molecular beam epitaxy (MBE) grown KTaO₃(111) epitaxial interfaces. The in-plane critical field (H_c2) exceeds the Pauli limit and is highly sensitive to current and magnetic field orientations. To understand the sensitivity of the superconducting order parameter to bias and magnetic field orientations, we examined the electronic, spin, and orbital structures at the KTaO₃(111) interfaces.

RESULTS

Epitaxial LaSrMnO₃/KTaO₃(111) heterostructures were grown in an oxide MBE system. Figure 2A shows the resistance with temperature, confirming a metallic behavior, dR/dT > 0, extending to 3 K. The Hall carrier density is ∼6 × 10¹³ cm⁻² at 3 K, resolving a carrier mobility of ∼176 cm²/Vs. The carrier mobility is in agreement with high quality KTaO₃(111) two-dimensional electron gases (2DEGs) (18). Similar heterostructures, grown on sapphire substrate instead of KTaO₃, show insulating behavior. The 2D carrier density falls in the range that a superconducting transition is expected (21). High-angle annular dark-field scanning transmission electron microscope (HAADF-STEM) was used to investigate the grown heterostructures. Figure 2B shows the HAADF-STEM image of the LaSrMnO₃ grown on a KTaO₃(111) substrate along the [1$\overline{1}$0] zone axis. The HAADF-STEM image confirms epitaxial growth of LaSrMnO₃ on KTaO₃(111). The zoomed-in region at the interface shows a continuous bright contrast at the interface. The intensity line profile and EDX elemental map (figs. S1 and S2), respectively, suggest formation of an intermixed region over a few atomic layers at the interface. Interfacial steps in (111) heterostructures of the other perovskite oxides also demonstrate similar features (22).

Fig. 2. Two-dimensional electron system at the LaSrMnO₃/KTaO₃(111) interface.

(A) Sheet resistant with temperature, suggesting a metallic behavior. Inset shows Hall 2D carrier density with temperature. (B) Cross-sectional HAADF-STEM image of the LaSrMnO₃ film grown on KTaO₃(111) substrate. (C) Higher-magnification HAADF-STEM image of the LaSrMnO₃/KTaO₃ interface.

To measure the superconducting transition, we cooled the device to the base temperature in a dilution refrigerator. Below 1.5 K, we observe a transition to a zero-resistance state, which we attribute to the onset of superconductivity at the LaSrMnO₃/KTaO₃ interface. This transition temperature is comparable to those found on EuO/KTaO₃(111) and LaAlO₃/ KTaO₃(111) interfaces (18, 23). We estimate the Bardeen-Cooper-Schrieffer (BCS) superconducting gap to be Δ ≈ 1.76k_BT_c ≈ 200 μeV.

We compare the current bias and temperature dependencies along both the [1$\overline{1}$0] and the [11$\overline{2}$] directions (Fig. 3, A and B). Notably, there is a pronounced peak in $R_{[1\overline{1}0]}$ near the zero-bias superconducting transition that is absent in the [11$\overline{2}$] direction (Fig. 3C). A similar feature was previously reported at the interface between polycrystalline EuO and KTaO₃(111) (18). The apparent difference between $R_{[1\overline{1}0]}$ and $R_{[11\overline{2}]}$ near the superconducting transition could be due to a granular superconductivity in which two directions have different coherent coupling strength (24). The observed behavior, however, can be explained by considering the anisotropic nature of band structure (Fig. 1C). The anisotropic band structure also gives rise to different density of states and effective mass along [1$\overline{1}$0] and [11$\overline{2}$] directions (Fig. 1, D and E). Furthermore, the superconductivity is more robust along the $R_{[11\overline{2}]}$ direction. This is also consistent with previous results in high mobility EuO/KTaO₃ samples (18).

Fig. 3. Anisotropic superconducting transition at the LaSrMnO₃/KTaO₃(111) interface.

(A to C) Superconducting transition with temperature and bias direction. Cooper pairs are more resilient when the bias is along the [11$\overline{2}$] ($T_{\mathrm{c},[11\overline{2}]}/T_{\mathrm{c},[1\overline{1}0]}=1.25$). (D to F) Superconducting transition with out-of-plane magnetic field and bias direction. H_c2 results, similar to T_c, confirm that superconductivity is more resilient when the bias is along the [11$\overline{2}$] ($H_{c2,[11\overline{2}]}/H_{\mathrm{c}2,[1\overline{1}0]}=1.65$). Cuts corresponding to (A) and (B) and (D) and (E) can be found in fig. S4.

We further study this transport anisotropy by measuring the two directions under an out-of-plane magnetic field (Fig. 3, D and F). We find that the critical fields (H_c2 defined at 0.8R_n) are also anisotropic with critical values $H_{\mathrm{c}2[1\overline{1}0]}$ = 310 mT and $H_{\mathrm{c}2[11\overline{2}]}=510$ mT. Superconductivity is again more robust along $R_{[11\overline{2}]}$ direction, and we see a peak at zero bias in $R_{[1\overline{1}0]}$ exceeding the normal resistance near the superconducting transition.

We now compare the critical values when the magnetic field is oriented in-plane and along either [1$\overline{1}$0] (B ∥ [1$\overline{1}$0]) or [11$\overline{2}$] (B ∥ [11$\overline{2}$]) directions. The out-of-plane spin canting and Rashba spin splitting are maximal along [1$\overline{1}$0] and suppressed along [11$\overline{2}$] direction (17). We note, regardless of the bias direction or the direction of the magnetic field, the critical fields exceed the Pauli limit, which we estimate to be $H_{\mathrm{p}}\approx \frac{\text{Δ}}{\sqrt{2}{\mathrm{\mu }}_{\mathrm{B}}}\sim 2.6$ T, assuming a g-factor of 2 [close to measured value (25)] and weakly coupled superconductivity. In addition, there is a significant asymmetry between out-of-plane and in-plane H_c2 results, an effect commonly observed in 2D superconductors (26). This asymmetry, however, varies depending on the bias direction with $\frac{H_{\mathrm{c}2,\mathrm{ip}}}{H_{\mathrm{c}2,\mathrm{oop}}}=\frac{6}{0.31}\sim 20$ along [1$\overline{1}$0] and $\frac{H_{\mathrm{c}2,\mathrm{ip}}}{H_{\mathrm{c}2,\mathrm{oop}}}=\frac{7.5}{0.51}\sim 15$ along the [11$\overline{2}$] direction.

Figure 4 also shows that the in-plane H_c2 depends on the directions of both bias and magnetic field. The superconductivity, in line with Fig. 3, is more robust when bias is along the [11$\overline{2}$] direction. In addition, the in-plane H_c2, regardless of the bias direction, increases ∼1.8 T when the magnetic field is rotated from [11$\overline{2}$] to [1$\overline{1}$0]. This shows that Cooper pairs are more resilient when the magnetic field is applied along [1$\overline{1}$0]. Next, we measured the in-plane H_c2 with temperature while magnetic field was along [1$\overline{1}$0] (B ∥ [1$\overline{1}$0]). Figure 4E shows a monotonic increase of in-plane H_c2 upon cooling, in line with a modified Ginzburg-Landau model.

Fig. 4. Anisotropic in-plane H_c2 at the LaSrMnO₃/KTaO₃(111) interface.

(A to D) Superconducting transition with in-plane magnetic field and bias direction at base temperature. H_c2 peaks with bias along [11$\overline{2}$] (I ∥ [11$\overline{2}$]) and magnetic field along [1$\overline{1}$0] (B ∥ [1$\overline{1}$0]). (E) H_c2 with temperature and B ∥ [1$\overline{1}$0] for $R_{[1\overline{1}0]}$ and $R_{[11\overline{2}]}$. The data are in agreement with a modified Ginzburg-Landau model H_c2(T) = H_c2(0)(1 − T/T_c)^α, where H_c2(0) is the upper critical field at the zero Kelvin and α is a constant accounting for dimensionality. The α = 0.5 and α = 1 correspond to 2D and 3D limits, respectively. The resolved α values suggest that the system might be at the verge of a dimensional crossover. Cuts corresponding to (A) to (D) can be found in fig. S5.

DISCUSSION

To briefly summarize the results, our main findings are as follows: (i) An anisotropic superconductivity emerges at KTaO₃(111) interfaces in which the superconducting state is resilient against the in-plane magnetic field (H_{c2, ip}/H_{c2, oop} as high as 20); (ii) Cooper pairs are more robust when the bias is along the [11$\overline{2}$] direction ($T_{c,[11\overline{2}]}/T_{c,[1\overline{1}0]}=1.25$); and (iii) the in-plane H_c2 is sensitive to the magnetic field orientation and is enhanced when B ∥ [1$\overline{1}$0].

First, we discuss the resilience of the superconducting state against in-plane magnetic field and violation of Pauli limit. One possible explanation could be emergence of an Fulde-Ferrell-Larkin-Ovchinnikov (FFLO) state (27). In the presence of finite Rashba-type SOC, an FFLO state, where Cooper pairs have nonzero momentum, is likely to be realized. The FFLO state, however, only emerges in clean regime (l_mfp >> ζ_∥). Here, the in-plane coherence length is ≈33 nm, ${\mathrm{\zeta }}_{\parallel }=\sqrt{{\text{Φ}}_0/2\mathrm{\pi }{H}_{c2,\perp }}$, where Φ₀ is the flux quantum. The mean free path of charge carriers at 3 K is ≈22 nm (see the Supplementary Materials), suggesting that the system is not in the clean limit. Another potential explanation could be emergence of triplet Cooper pairs. The Pauli limit does not apply to p-wave superconductors, and emergence of the mixed-parity superconductivity could explain the violation of the Pauli limit. Second harmonic transport measurements near the superconducting transition are sensitive to the presence of mixed parity superconductivity in noncentrosymmetric superconductors (28–30). Inversion symmetry is broken at the KTaO₃ interface, and we conducted the second harmonic transport measurements, which were predicted to show the signs of mixed parity superconductivity (31, 32). The second harmonic transport measurements, however, do not show a detectable signal in our samples (fig. S6).

Rashba-type spin splitting was reported at the KTaO₃(111) surface (17). Rashba SOC is expected to enhance the Pauli limit by a factor of $\sqrt{2}$ ($\sqrt{2}{H}_{\mathrm{p}}\approx 3.7$ T) (9). All the measured critical fields at base temperature, however, exceed this limit. The Pauli limit (H_p ≈ 1.86T_c) is calculated on the basis of the assumption of weakly coupled superconductivity and g-factor of 2, which is close to the value measured in bulk KTaO₃ samples (25). The deviation from these assumptions could account for the discrepancy. The Rashba-type spin splitting, however, does not explain the highly anisotropic nature of superconducting transition.

To explain the remarkable robustness of superconductivity against the in-plane magnetic field and its anisotropy, one must thoroughly examine the electronic structure of the KTaO₃(111) surface. The charge accumulation at the interface between KTaO₃ and LaSrMnO₃ forms a negative band-bending potential that can effectively quantize Ta-t_2g conduction bands into a set of subbands, electronically and spatially separated from the rest of the system. Our Poisson-Schrödinger calculations show that the resulting quantized states are confined within a region about 15 nm below the KTaO₃(111) surface with an effective full width at half maximum of d_FWHM ∼ 3 nm, roughly nine times larger than the spacing between TaO₂ layers (Fig. 1B). This is a significant penetration depth, although expected as all three components {d_xy, d_yz, d_xz} of the t_2g manifold share a strong electron-hopping along the [111] direction [17]. We should thus treat this as a quasi-2D electron gas, showing a subtle violation of the pure 2D limit. To verify this, we have fitted our H_c2 data for both $B_{[1\overline{1}0]}$ and $B_{[11\overline{2}]}$ directions using a modified Ginzburg-Landau model (33) H_c2(T) = H_c2(0)(1 − T/T_c)^α, where H_c2(0) is the upper critical field at the zero Kelvin and α is a constant accounting for dimensionality with lower α = 0.5 and upper α = 1 bound corresponding to 2D and 3D limits, respectively (Fig. 4E). On the basis of our fits, we find ${\mathrm{\alpha }}_{[11\overline{2}]}=0.61$ and ${\mathrm{\alpha }}_{[1\overline{1}0]}=0.68$, suggesting a noticeable crossover from 2D to 3D superconductivity, in agreement with our calculations. We have also calculated the thickness of superconducting layer using $d_{\mathrm{sc}}=\sqrt{12}{\zeta }_{\parallel }{H}_{\mathrm{c}2,\perp }/H_{\mathrm{c}2,\parallel }$ (34–37). Thickness of the superconducting layer is ≈8 nm, which is larger than d_FWHM, further supporting the possibility that the observed superconductivity has a mixed-dimensional character. Such a crossover in the dimensionality of superconductivity has already been shown to drastically enhance H_c2 (38, 39, 40).

Another crucial factor is the strong trigonal warping of the Fermi pockets arising from the distinct spatial polarization of the d_xy, d_yz, and d_xz orbitals (41). The strong distortion of the energy pockets results from the projection of the ellipsoidally shaped Ta-t_2g orbitals onto the (111) surface. As each orbital is oriented along one of the cubic KTaO₃ bulk crystalline axes, this projection requires that these orbitals be mutually mixed along the [1$\overline{1}$0] direction while remaining isolated along the [11$\overline{2}$] direction, as shown in Fig. 1C. In the presence of SOC, this results in a Rashba spin texture with significant out-of-plane spin canting in the [1$\overline{1}$0] direction, where orbital mixing is maximal (17, 42). As mentioned earlier, the Rashba effect alone can enhance H_c2 by a factor of $\sqrt{2}$. The out-of-plane spin canting, σ, can further strengthen the cooper pairs through an Ising coupling between the electrons with wave functions ψ_σ↓(k) and ψ_−σ(−k) (5, 6, 43). As this term is maximal along [1$\overline{1}$0] and completely quenched along the [11$\overline{2}$] direction (Fig. 1C) (17), we expect H_c2 to reach its maximum whenever the field is along [1$\overline{1}$0]. In the Supplementary Materials (fig. S7), we estimate the strength of the Ising spin-orbit field (44) and find reasonable agreement with the calculated values (17). Therefore, supported by the magnetoresistance data in Fig. 4, we claim that this interplay between the trigonal warping and strong SOC is the origin of the observed anisotropy. This, combined with the strong SOC of tantalum and inversion asymmetry of the interface, leads to a significant out-of-plane canting of the otherwise helically polarized spin texture of the carriers in the momentum space.

The warping effect mentioned above also results in a momentum-dependent modulation of the density of states at the Fermi level, N_F, maximizing (minimizing) it along [11$\overline{2}$] ([1$\overline{1}$0]), as shown in Fig. 1E. Furthermore, a momentum-dependent density of states was theoretically observed at EuO/KTaO₃(111) interfaces and was attributed to a magnetic stripe instability (45). Within BCS theory (33), we know T_c ∝ exp(−1/V₀N_F), with V₀ being the interaction potential satisfying V₀N_F < 1. Accordingly

$$\frac{T_{\mathrm{c},[11\overline{2}]}}{T_{\mathrm{c},[1\overline{1}0]}}=\exp \left(\frac{N_{\mathrm{F},[11\overline{2}]}-N_{\mathrm{F},[1\overline{1}0]}}{V_0{N}_{\mathrm{F},[11\overline{2}]}{N}_{\mathrm{F},[1\overline{1}0]}}\right)$$ (1)

Using the density functional theory (DFT) results, $N_{\mathrm{F},[11\overline{2}]}$ = 11.2 states/eV and $N_{F,[1\overline{1}0]}$ = 9.2 states/eV, we find that $V_0{N}_{\mathrm{F},[1\overline{1}0]}$ should be near unity to reproduce $T_{\mathrm{c},[11\overline{2}]}/T_{\mathrm{c},[1\overline{1}0]}=1.25$. This, accordingly, suggests that the observed superconductivity at the KTaO₃(111) interface might be on the verge of violating the weakly coupled regime.

In summary, our experimental results highlight a large degree of anisotropy of H_c2 and T_c between the [1$\overline{1}$0] and [11$\overline{2}$] directions. This anisotropy is born from the interplay between strong trigonal warping and strong SOC effects. Therefore, KTaO₃ interfaces such as these should be an interesting testbed for a variety of proposed theoretical models, which relate superconductivity in low-dimensional crystalline systems to anisotropic SOC and orbital character (46–48). These results point to opportunities to enhance T_c and H_c2 by tuning the electronic structure and spin texture in crystalline 2D superconductors with strong SOC. Further, it would also be interesting to explore whether similar anisotropic behavior could be obtained in other crystalline 2D systems such as transition metal dichalcogenides.

MATERIALS AND METHODS

Mobile charge carriers were introduced to the KTaO₃ surface in TiO_x/La _2/3Sr_1/3MnO₃/KTaO₃(111) heterostructures, grown in an oxide MBE chamber with base pressure of 2 × 10⁻¹⁰ torr. LaSrMnO₃ (10 unit cells.) was grown followed by TiO _x (3 nm) on KTaO₃(111) substrate. Pure elements were evaporated from effusion cells. The elemental fluxes were calibrated using a quartz crystal microbalance.

Substrate was annealed at 600°C in an oxygen partial pressure of 3 × 10⁻⁶ torr for 30 min before the growth. Sample was then heated to 800°C and growth started immediately to minimize the potassium loss. Oxygen partial pressure was kept at 3 × 10⁻⁶ torr during the growth of LaSrMnO₃. The growth was monitored by reflection high-energy electron diffraction (RHEED) that shows diffraction streaks, suggesting 2D growth of LaSrMnO₃ (fig. S3). After the growth of LaSrMnO₃, the sample was cooled to 550°C, followed by the growth of the titanium capping layer (∼3 nm). The RHEED streaks fade during the growth of titanium layer, suggesting an amorphous cap layer (fig. S3). The thin titanium layer oxidizes upon exposure to atmosphere and acts as a buffer, protecting the 2DEG. The growth (TiO_x/LaSrMnO₃) was replicated on a sapphire substrate, which resulted in insulating films (∼1 to 10 MOhm).

STEM was performed to study the film and interface structures. Cross-sectional samples were prepared using a Thermo Fisher Scientific Helios G4UX focused ion beam. HAADF images were obtained using a Thermo Fisher Scientific Spectra 300 X-CFEG operating at 200 kV with a convergence angle of 30 mrad and a HAADF detector with an angular range of 60 to 200 mrad. STEM energy-dispersive x-ray (EDX) spectroscopy data were collected on a steradian Dual-X EDX detector with a probe current of 60 pA. The STEM-EDX spectrum’s noise was reduced by applying the principal components analysis.

Transport measurements were carried out in van der Pauw geometry with square-shaped samples (5 mm by 5 mm). The contacts (400-nm Au) were deposited on the sample corners using a sputtering system through a shadow mask. The magnetoelectric measurements (300 to 3 K) were carried out in a Quantum Design Physical Property Measurement System. The Hall carrier density was extracted from the Hall experiments, n_2D = −1/(eR_H), where R_H is the Hall coefficient and e is the electron charge. The Hall coefficient was calculated from a linear fit to the transverse resistance with the magnetic field (R_H = dR _xy/dB).

The sub-Kelvin magnetoelectric measurements were carried out in a Leiden Cryogenics dilution refrigerator with a base temperature of 30 mK (100 mK with the application of high field). The lines were filtered to avoid spurious microwave frequency radiation from heating the sample. The superconductivity measurements were carried out using signals generated by NI-6363 I/O board. Differential resistance was measured with a digital 10-μA, 23.7-Hz square-wave. Only the last half of the square-wave pulse is measured and averaged—this ensures that the large capacitors used in the filtering have discharged and the transient of the discharge is not incorporated in our reported resistance values. The signal was measured using homemade circuitry. The critical field was measured by setting the magnetic field and measuring the longitudinal resistance after several minutes (which allows the temperature to settle and ensures the sample is appropriately thermalized).

Electronic structure calculations were performed within the DFT using Perdew-Burke-Ernzerhof exchange-correlation functional (49) as implemented in the WIEN2K program (50). All relativistic effects, including SOC, were included. The Brillouin zone was sampled by a 10 × 10 × 10 k-mesh. For all the atoms, the muffin-tin radius R_MT was chosen such that its product with the maximum modulus of reciprocal vectors K_max becomes R_MTK_max = 7.0. To describe the quantum confinement at the surface, we downfolded the bulk DFT Hamiltonian using maximally localized Wannier functions (51) made of Ta-t_2g orbitals, and the resulting six-band tight-binding transfer integrals were implemented within a 30-U (90-Ta layers) supercell, with an additional on-site potential term, accounting for the electrostatic band bending potential. This was solved self-consistently with the Poisson’s equation (17, 52) assuming an electric field–dependent dielectric constant (53). The only adjustable parameter was the potential that was varied until the experimental surface carrier density 6 × 10¹³ cm⁻² was reproduced.

Supplementary Materials

This PDF file includes:

Sections 1 to V

Figs. S1 to S7

Table S1