Using Metadynamics to Explore the Free Energy of Dewetting in Biologically Relevant Nanopores

Abstract

Water confined within hydrophobic spaces can undergo cooperative dewetting transitions due to slight changes in water density and pressure that push water toward the vapor phase. Many transmembrane protein ion channels contain nanoscale hydrophobic pores that could undergo dewetting transitions, sometimes blocking the flow of ions without physical blockages. Standard molecular dynamics (MD) simulations have been extensively applied to study the behavior of water in nanoscale pores, but the large free energy barriers of dewetting often prevent direct sampling of both wet and dry states and quantitative studies of the hydration thermodynamics of biologically relevant pores. Here, we describe a metadynamics protocol that uses the number of waters within the pore as the collective variable to drive many reversible transitions between relevant hydration states and calculate well-converged free energy profiles of pore hydration. By creating model nanopore systems and changing their radius and morphology and including various cosolvents, we quantify how these pore properties and cosolvents affect the dewetting transition. The results reveal that the dewetting free energy of nanoscale pores is determined by two key thermodynamic parameters, namely, the effective surface tension coefficients of water-air and water-pore interfaces. Importantly, while the effect of salt can be fully captured in the water activity dependence, amphipathic cosolvents such as alcohols modify both dry and wet states of the pore and dramatically shift the wet-dry equilibrium. The metadynamics approach could be applied to studies of for dewetting transitions within nanoscale pores of proteins and provide new insight into why different pore properties evolved in biological systems.

Graphical Abstract

Introduction

Water is a complex liquid with distinct thermodynamic properties that make it a vital component of the cells and not merely a passive solvent.¹ Under physiological conditions, the free energy difference between the liquid and vapor phases of water is quite modest, such that water can readily move between these phases due to slight changes in density and pressure.² The cell is extremely crowded, with an average distance of about 1 nm between macromolecules, resulting in many regions of confined or constrained water that exhibit unique behavior compared to bulk liquid water.¹ This is especially true when water is confined between hydrophobic surfaces, which exert a repulsive force on water molecules.^3,4 Between two extended hydrophobic surfaces or inside of a cylindrical hydrophobic surface, there is a critical radius, ~1 nanometer (nm), under which a pressure imbalance is created within the confined water,⁵ leading to a cooperative dewetting transition where liquid water completely exits the confined region. Importantly, the stability of confined liquid water is sensitive to the confined region’s size and hydrophobicity.^6,7

Significant evidence has accumulated to suggest that transmembrane protein ion channels can use dewetting transitions as a gating mechanism, which is referred to as hydrophobic gating.⁸ The ion permeation pathway of ion channels often contains hydrophobic inner cavities with radii on the nm scale, where confined water properties discussed above become relevant. In particular, a small change in the size or hydrophobicity of the wall can drastically shift the water liquid-vapor equilibrium within the pore. Hydrophobic gating is being recognized for a growing list of channels that are activated by voltage, mechanical force, and/or ligand binding.^9-22 Some ion channels appear to have even evolved to utilize small conformational changes to generate a vapor barrier preventing ion permeation without the need for a physical barrier.^7,8 As such, studying the properties that control the dewetting transition in nanoscale pores will give insight into the important emerging hydrophobic gating mechanism in ion channels.

Molecular dynamics (MD) simulations of hydrophobic surfaces and model nanopores have previously been used to study the behavior of water in confinement.^5,23-35 However, existing studies rely on direct MD simulations of dewetting transitions, which generally cannot be used to sample reversible dewetting transitions in biologically relevant nanoscale pores that favor either the hydrated or dry state. For example, the dewetting transitions take several hundred nanoseconds (ns) and are largely irreversible for the deactivated state of BK channels, whereas in the activated state, the pore remains fully hydrated throughout μs MD simulations.¹⁶ There is thus a need for a method that can sample these reversible dewetting transitions within a relatively short simulation, which would allow quantitative analysis of how the thermodynamics of dewetting depends on various pore properties.

Metadynamics (MetaD) is an enhanced sampling technique designed for overcoming the challenges of sampling rare transitions with direct MD.^36-41 In MetaD simulations, one or more collective variables (CVs) are first defined, which should capture the rate-limiting degrees of freedom of a given system. During the simulation, Gaussian bias potentials are periodically deposited along the CV. As the bias builds up, the system can be driven to cross energy barriers and sample new conformational space. MetaD has been widely and successfully used to across physical chemistry,^42-44 solid state physics^45-48 and biophysics.^49-53 In this work, we developed a MetaD protocol that biases the number of waters within the pore and can readily sample multiple dewetting transitions and generate well-converged free energy profiles of dewetting within short simulations (e.g., 50-100 ns). We then applied this protocol to quantify how key pore properties as well as the presence of salt and cosolvents affect water dewetting transitions in biologically relevant model nanopores. We show that dewetting free energies can be described using a simple thermodynamic model with two effective water-air and water-wall surface tension coefficients. Our results also show that the effects of amphipathic cosolvents such as alcohols can preferentially interact with the hydrophobic wall and affect hydrophobic dewetting in a complex fashion. The MetaD protocol can be applied to quantify dewetting free energy profiles in protein ion channel systems and will allow future studies to shed light on the specific properties that are crucial for hydrophobic gating in these channels.

Methods

Model nanopores and simulation systems

Model nanopores in this work are comprised of rings of carbon-like atoms with a van der Waals (vdW) radius, R_min, of 4.0 Å and interaction strength ε of −0.140 kcal/mol, unless otherwise stated. The value of ε was selected to reflect that of a methyl group in the CHARMM36m force field,⁵⁴ slightly adjusted to achieve near liquid-vapor equilibrium for a nanopore of radius ~7 Å and height of 16 Å. The pore atoms are arranged with 3 Å spacing, which roughly mimic the density of methyl groups in a hydrophobic protein pore. Three model nanopores are investigated in this work. The straight-wall pores are characterized by the height (h) and inner radius (r), as illustrated in Figure 1A and B. Slanted-wall pores are defined with two inner radii (R and r) and a wall length (s) (see Figure S1). The pores may have a lid on one end of the pore, to mimic the presence of selectivity filter above the inner pore of many ion channels. Water, salt and cosolvent molecules are described using the CHARMM36m force field⁵⁴ with the TIP3P model.⁵⁵ We used a box size of (70 Å)³, which each contain about 35 thousand atoms. The salt and cosolvent molecules were added using the gromacs tools genion⁵⁶ and insert-molecules,⁵⁷ respectively. Figure S2 contains example snapshots of the solvent boxes.

Figure 1. Model nanopores and reversible dewetting transitions.

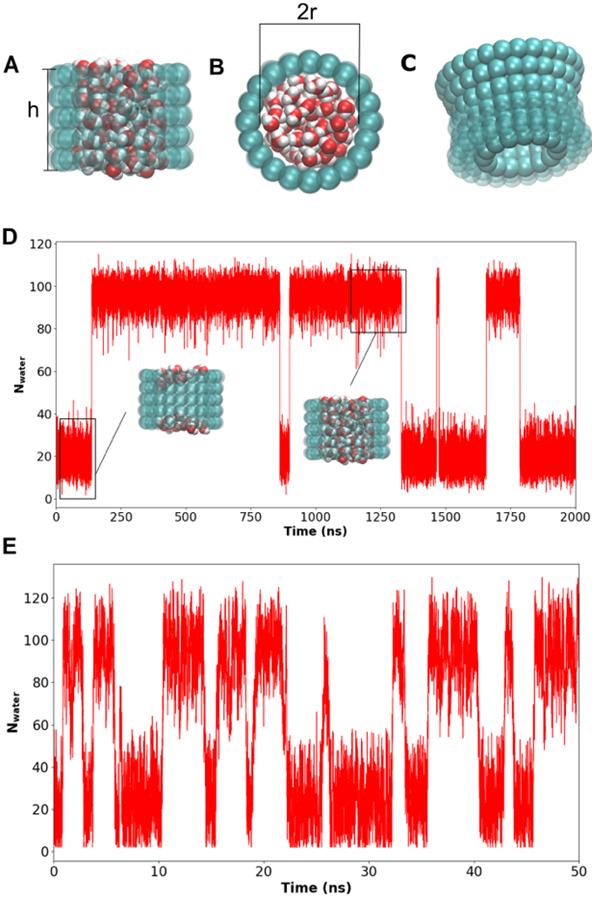
A) The side view of a hydrated cylindrical nanopore with the pore height labeled. B) The top view with the (inner) pore diameter labeled. C) A side view of a nanopore with a 20° wall slanting angle. D) Pore water count as a function of time during a 2-μs unbiased simulation of a pore of radius 7.5 Å and height 16 Å. Representative structures of the wet and dry states of the pore are also shown. E) Pore water count as a function of time from a 50-ns MetaD simulation of the same pore as in panel D.

Metadynamics simulation of reversible dewetting of nanopores

For a dewetting transition, the most relevant degree of freedom is the number of water molecules, N_water, which is the chosen CV for MetaD in this work. The counting region is defined using the function INCYLINDER in Plumed 2.7.^58-60 The occupancy of a water molecule is 1 within the user-defined cylindrical region and smoothly approaches 0 using a Gaussian switching function beyond the region,

$$O(r)=e^{-\frac{(r-d_0{)}^2}{2r_0^2}},\text{for}d>d_0,$$ (1)

where r is the radial distance to the cylinder central axis (z-axis in this work), d₀ is the corresponding boundary, and r₀ controls the width of the switching region.⁶¹ N_water is then calculated as the sum of the occupancies of all water molecules. Because the switching function only applies in the x-y plane, a water crossing into the cylinder experiences no biasing force along z.⁶⁰ To address this using the existing code, we defined the counting region to be slightly larger than the actual pore along the z axis, with a 1.0 Å buffer region added on either end of the cylindrical pore region in the z-direction. This buffer region effectively shifts the dry state to N_water ~ 5 – 10 (see Results). The buffer region has an additional benefit because N_water is strictly non-negative, which may lead to excessive accumulation of bias potentials (see below) at exactly N_water = 0 whenever the pore becomes fully dehydrated. In addition, we added an one-sided harmonic wall potential with a force constant of 50 kcal/mol for N_water < 2 to further prevent reaching N_water = 0.

During MetaD simulations, Gaussian bias potentials (or “hills”) are periodically added to the original energy function along selected CVs.³⁶ Key parameters of MetaD include the height and width of the Gaussians (given by two parameters, “hill height” and “sigma” in Plumed, respectively) and the rate at which they are deposited (i.e., “pace”). A key consideration in developing effective MetaD protocols is to have the appropriate combination of Gaussian height and deposition rate. Small Gaussians and slow deposition rates increase the simulation time required for convergence. Conversely, depositing large Gaussians at a rate exceeding how quickly the system could fluctuate along the CV can drive the system too far out of equilibrium, causing the calculated free energy surface to oscillate and not converge.⁴⁰ In the well-tempered MetaD protocol, the hill height is attenuated as the bias potential accumulates along the CV. Specifically in Plumed 2.7⁵⁹, the bias factor (bf) controls how quickly the hill height is attenuated,

$$w(s,t)\propto w_0{e}^{-\frac{V(s,t^{\prime })}{T(bf-1)}},$$ (2)

where w₀ is the original height, T is the simulation temperature, and V(s,t′) is the total bias potential previously deposited at the current CV value s. To optimize the protocol for efficient simulation of dewetting transitions of the nanopore, we will determine the optimal combination of the above key parameters, by considering the inherent timescale of water dynamics in these nanopores and examining the convergence of the calculated free energy profiles.

MD simulation and analysis

All simulations were run with GROMACS 2019.4^62-68 with Plumed 2.7.⁵⁹ All nanopore beads were harmonically restrained with a force constant of 50 kcal/mol/Ų. The solvated nanopore systems were first equilibrated for 5 ns under constant temperature and pressure (NPT) conditions at 300 K and 1.0 atmospheric pressure. Berendsen barostat with tau_p of 20 ps and compressibility of 10⁻⁶ bar⁻¹ was used in the equilibrium simulations. We note that the use of the Parrinello-Rahman barostat could result in large pressure and volume box oscillations in the current systems when paired with our desired harmonic restraints.⁶⁹ All production MetaD simulations presented in this work were run with a timestep of 2 fs and the Berendsen barostat with tau_p of 10 ps, and compressibility of 10⁻⁵ bar⁻¹. The lengths of all MetaD simulations were 50 ns except for the system with 5% glycerol volume fraction, which lasted 100 ns to better sample the glycerol distribution.

The accumulated bias from each MetaD run was converted into a potential of mean force (PMF) using Plumed. In the cases involving nanopores with lids, the free energy minima of the hydrated state were not well-defined. The hydration free energies were estimated by first determining the number of waters expected to constitute the state from a pore of the same volume, then taking the free energy with that number of waters as the corresponding minimum. The presence of a lid on the nanopores exacerbated the need for a buffer region in the Plumed counting cylinder (as the water can enter or leave the pore only from one end). Therefore, we used a larger buffer of 3 Å as opposed to the standard 1 Å. This results in a slightly greater degeneracy in the N_water CV, which in turn affects how pores with different lids could be compared. For this, we shifted all PMFs such that the vapor-state minima were aligned at the origin. To derive 2D PMFs as a function of both water and cosolvent occupancies, we first reweighed each MetaD frame according to the cumulated bias potential and then calculated the 2D histograms. PMFs from unbiased simulations were calculated directly from the corresponding histograms of water occupancy. All plots were made with matplotlib,⁷⁰ and molecular representations were rendered in VMD.⁷¹

Results & Discussion

Optimizing metadynamics protocol for sampling reversible dewetting transitions

Given the nature of the CV N_water, we set the hill height and sigma to 1.2 kcal/mol (two units of RT) and 1.0 (one water), respectively. The remaining key MetaD parameters are the pace and bias factor. In principle, the pace is limited by the inherent timescale of fluctuation of the CV, beyond which the system may be driven too far out of equilibrium for generating a stably converged free energy profiles. We performed a 100 ns unbiased MD simulation of a radius 7.5 Å, height 16 Å pore to calculate the mean-squared-displacement function and the effective diffusion constant. The result, shown in Figure S3, shows that water within the pore fluctuates rapidly with a rate greater than a few waters per ps, suggesting that very fast pace could be used. Indeed, we tested the convergence of the free energy profile with the pace ranging from 100 to 10,000, and the results (Figure S4) show that stable free energies can be generated using pace as aggressive as 100. In our final protocol, we set pace to 500 (i.e., 1 ps⁻¹) to provide a compromise which allows fast deposition while reducing the risk of overdriving the system. A pace of 500 also appears to drive the largest number of reversible transitions (Figure S4).

Given the choice of hill height, sigma and pace, the bias factor determines how quickly the hill height is attenuated during MetaD simulations as the bias potential accumulates at a given CV value (Eq. 2). The optimal choice in principle depends on the nature of the free energy profile to be explored. Larger bias factors should be used for cases with larger free energy barriers, and vice versa. For the nanopore systems studied in this work, the free energy barriers are expected to be ~10 kcal/mol or less. As such, one may directly estimate the optimal bias factor to be about 10 / 0.6 = 20 or less. We compared the ability of MetaD to drive reversible dewetting transitions and generate converged free energy profiles with the bias factor ranging from 2 to 20. The tests suggest bias factor of 10 or 20 may be too aggressive for nanopores with small free energy barriers, leading to larger errors in the final PMFs (Figure S5, green and red traces). Therefore, we set bias factor to 5 in the final protocol as a good compromise for simulating of various nanopores with large differences in free energy barriers. An additional parameter could affect the rate of convergence is the switching width r₀ in Eq. 1. A large switching with would blue the CV, and a small switching region would result in large forces at the boundary, Given the water radius (~1.4 Å), we tested r₀ = 0.5, 1.0 and 2.0 Å. the results suggest that r₀ does significantly affect the convergence of the PMF within this range (Figure S6), even though the number of reversible transition sampled appears to slightly higher with r₀ = 1.0 Å.

The final MetaD protocol for all the nanopore simulations shown in this work has a pace of 500 MD steps, r₀ = 1.0 Å, a sigma of 1.0, a hill height of 1.2 kcal/mol, and a bias factor of 5. Figure 1 illustrates the ability of the protocol to significantly accelerate the sampling of reversible dewetting transitions in nanopores. For example, only four reversible dewetting transitions were observed in the 2-μs of unbiased MD simulation (Figure 1D), while nine were generated in only 50 ns of MetaD simulation (Figure 1E). This reflects a ~100-fold increase in sampling efficiency, greatly facilitating quantitative free energy studies of dewetting of biologically relevant nanopores. Note that, even with 2-μs simulation time, the free energy profile derived from the unbiased MD remains poorly converged because a lack of sampling of high energy transition states, in contrast to the smooth and continuous profile derived from the 50-ns MetaD run (Figure S7).

We further evaluate the convergence of MetaD simulations using a smaller pore with a radius of 6 Å and a height of 12 Å, where a converged free energy profile could also be generated using unbiased MD due to the smaller free energy barrier. As shown in Figure 2A, the free energy profiles for the system stabilize rapidly during MetaD simulations, within 30 ns of simulation. Comparing the results from two independent 50 ns MetaD runs suggests that the convergence is 0.5 kcal/mol or less for the final free energy profile. (Figure 2B). Importantly, the free energy profile from MetaD is highly consistent with the result from a direct 500-ns unbiased MD simulation of the same system (Figure 2B), further validating the MetaD protocol for quantitative studies of dewetting free energy of biologically relevant nanopores.

Figure 2. Convergence of MetaD free energy profiles of pore hydration.

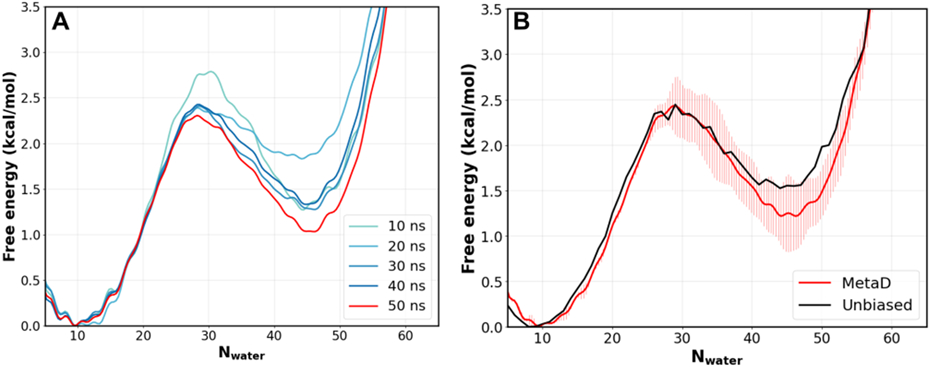
A) Free energy profiles of pore hydration as a function of MetaD simulation time, for a pore with radius 6 Å and height of 12 Å. B) Comparison of free energy profiles calculated from 50-ns MetaD simulations and a 500-ns unbiased MD simulation of the same pore. The error bars for the MetaD result reflect the difference between two independent 50 ns runs, and the final trace was plotted using the average of the two runs.

Effects of pore radius and geometry on dewetting free energy

The hydrophobic inner pore region below the selectivity filter in protein ion channels is typically ~ 15 Å in length, but can vary substantially in the pore radius and tilt angle of the wall.⁶ Here, we examine the dependence of dewetting free energy on these two key pore properties. Figure 3 compares the free energy profiles of dewetting in a set of model nanopores with a height of 16 Å and radius ranging from 5 to 10 Å. The MetaD protocol as discussed above was able to calculate well converged free energy profiles for all these pores, including the largest 10 Å pore with a dewetting free energy greater than 10 kcal/mol (see Figure 2B for representative uncertainties of the final free energy profile). The result show that, lined with methyl-like hydrophobic beads and at a height of 16 Å, the critical radius of hydrophobic dewetting is as large as 7.5 Å, at which the free energy of the dry and wet states is nearly equal. Below the critical radius, the nanopore can readily dewet, with relatively low free energy barriers. The dewetting and rehydration transitions are highly cooperative, manifested as two well-defined free energy minima separated by a single barrier. Note that the apparent shift of the location of the dry state with respect to radius is due to the inclusion of 1 Å in calculation of N_water (see Methods).

Figure 3. Free energy profile of pore hydration as a function of the pore radius.

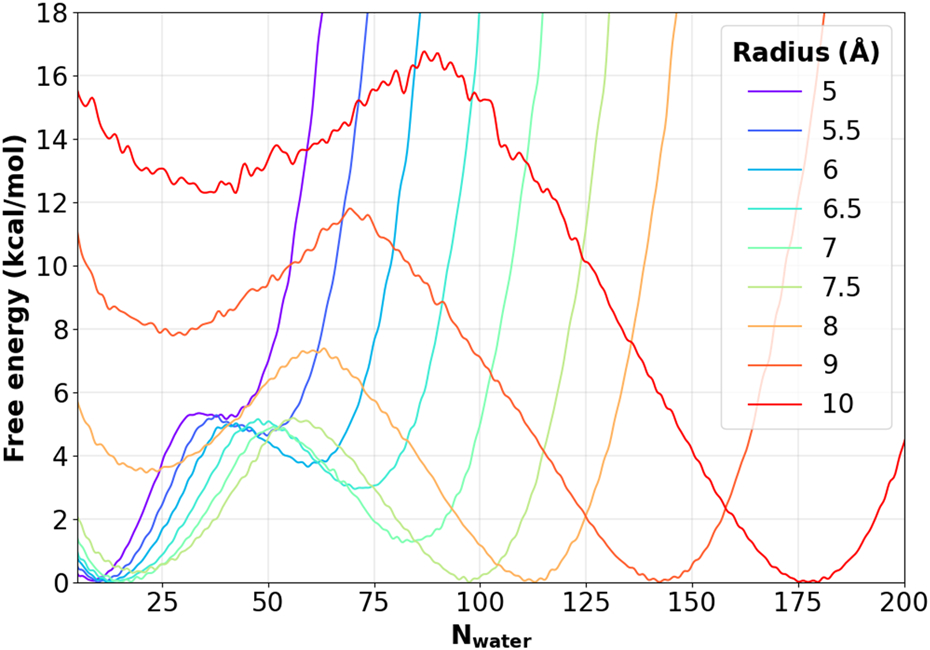
All profiles were calculated from 50 ns MetaD simulations and the height of all nanopores is 16 Å.

The free energy cost of pore dewetting can be attributed to the competition between the costs of creating two different types of water interfaces. The dry state contains two water-air interfaces between bulk water and vapor at both ends of the cylindrical region, whereas the wet state contains an interface between liquid water and the confining pore surface. Therefore, the free energy of dewetting can be described using two effective surface tension coefficients as,

$$\Delta {\mathrm{G}}_{\text{dewet}}=\Delta {\sigma }_{air}{\gamma }_{air}+\Delta {\sigma }_{pore}{\gamma }_{pore}+P\Delta V,$$ (3)

where Δσ is the change in the water-air or water-pore interface surface area, γ is the corresponding surface tension coefficient, and PΔV is the work for creating a cavity of volume ΔV against external pressure P. Note that the PΔV term is negligible for nanoscale cavities (~ 0.06 kcal/mol for a spherical cavity of 1 nm radius under the atmospheric pressure). Assuming that the water-air interface is flat, Δσ_air = 2πr² and Δσ_pore = −2πrh. Indeed, the calculated dewetting free energies can be fit very well to Eq. 3, yielding γ_air = 0.076 kcal/mol Å⁻² and γ_pore = 0.035 kcal/mol/Ų with a Pearson correlation coefficient R > 0.99 (Figure 4A). We note that γ_air from the fitting is highly consistent with the reported value of the TIP3P water model of 0.073 kcal/mol/Ų at 298 K.⁷² The result that γ_pore is about half of γ_air is also in general agreement with reported values for water-oil interfaces.^73,74 It is notable that both γ_air and γ_pore show minimal dependence on the pore radius, even though hydrophobic solvation is known to have a length-scale dependence for sub-nanometer spherical cavities.² Clearly, the dependence is much weaker for cylindrical cavities within the range of radius 5 to 10 Å.

Figure 4. Parametric fitting of free energy cost of dewetting.

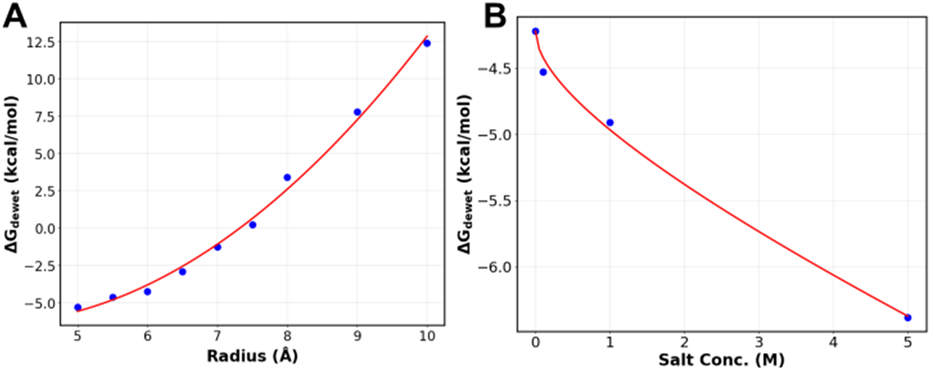
A) Free energy of dewetting for pores with a height of 16 Å and radii between 5-10 Å fit to Eq. 3. B) Free energy of dewetting at different NaCl concentrations fitted to Eq. 5. The nanopore used has a height of 16 Å and a radius of 6 Å. The values of the coefficients are as follows: A = −0.570, B = −0.175. The R values for both fits are greater than 0.99.

We further study how the tilt of the wall and/or the presence of a lid affect the dewetting free energy. The latter is to mimic the fact that the inner pore of a biological ion channel is usually capped by the selectivity filter. In Figure 5, we examine the effects of these pore modifications on the free energy of dewetting. Clearly, adding the lid significantly destabilize the hydrated states (e.g., Figure 5A, blue vs orange traces), apparently due to an increase in the hydrophobic surface that needs to be solvated in the hydrated state. The effects of tilting of the wall also seem to be well captured by consideration of water-air vs water-pore interface surface areas. As such, the free energy costs of dewetting in pores with tilted walls and lids obtained from MetaD simulations is in excellent agreement with theoretical values calculated from Eq. 3 using the same two surface tension coefficients, γ_air = 0.076 kcal/mol/Ų and γ_pore = 0.035 kcal/mol/Ų (Figure 5B). Note that the 50 ns MetaD simulation did not sample a fully hydrated state for the tilted pore with the lid on the wide end (Figure 5A purple trace). Nonetheless, the theoretical value based on Eq. 5 clearly over-estimates the dewetting free energy from the MetaD simulation (Figure 5A and B, open purple circle). The reason is that water never fully filled the volume nearest to the lid due to the sharp corner (Figure S1D), reducing the accessible hydrophobic pore surface area. Taken together, the pore shape does not contribute to the dewetting free energy cost, but rather the cost is largely determined by the hydrophobic pore surface area and the area of the water-air interface at the mouth of the pore. Therefore, the dewetting cost of biological pores, such as those of ion channels, will likely be well approximated using solvent-accessible surface area-based models, regardless of the pore’s shape.

Figure 5. Free energy profiles of hydration of nanopores with different geometries and lid configurations.

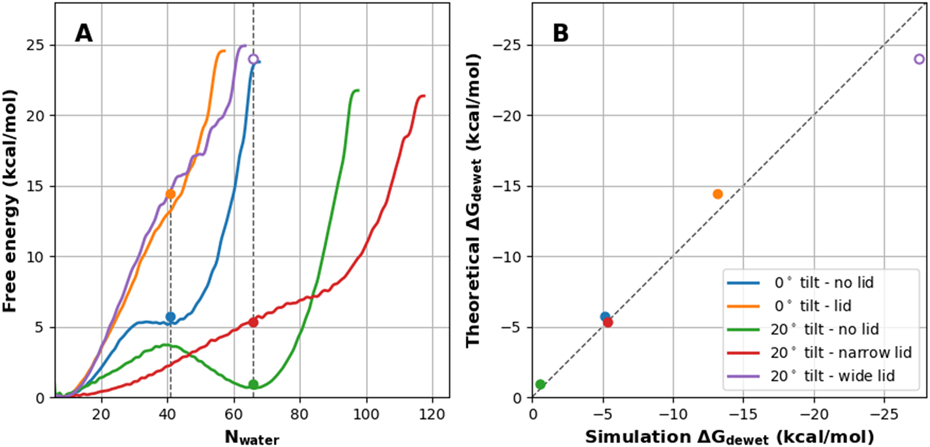
A) PMFs of hydration for a set of nanopores with and without a lid and/or tilt (see Figure S1). The circles mark the theoretical ΔG_dewet as calculated using Eq. 3. The pores with 0° tilt - lid (orange), 20° tilt - narrow lid (red), and 20° tilt - wide lid (purple) did not have well-defined hydrated minima, so their locations were estimated by using the N_water of the corresponding pore without the lid, denoted with a vertical dashed line (see Methods for details). B) Correlation of dewetting ΔGs calculated using Eq. 3 (theoretical) with those derived from the PMFs (simulation). The dashed line marks the ideal diagonal line. Note that the PMF for 20° tilt - wide lid (purple) never reached a fully hydrated state with the same N_water as in the no lid pore. The simulation ΔG_dewet was estimated to be greater than 25 kcal/mol.

Effects of salts on nanopore dewetting thermodynamics

Ionic strength is a key environmental factor that can affect ion channel function. In addition to directly modulate the stability of various states of the protein,^75-78 salt could also directly modulate the water activity and thus the liquid-vapor equilibrium of confined water.^79,80 We applied MetaD simulations to calculate additional free energy profiles of dewetting of a pore with a height of 16 Å and a radius of 6 Å in the presence of 0.1 M, 1.0 M, and 5.0 M NaCl (Figure S8). A duplicated simulation was performed for the representative 1.0 M solution and the results show that 50 ns MetaD is sufficient to achieve convergence well within 0.5 kcal/mol (Figure S9). As shown in Figure S8, the dewetting free energy cost decreases with increasing salt concentration, as expected. Based on the Debye-Hückel limiting law,⁸¹ the salt-induced change of the effective surface tension coefficients can be approximated as

$$\Delta \gamma =a\sqrt{c}+bc,$$ (4)

where a and b are coefficients related to properties of the solvated ions, and c is ionic strength of cosolvents (zero for pure water). Combining Eqs. 3 and 4, the salt-induced change of the dewetting free energy can be expressed as

$$\Delta \Delta {\mathrm{G}}_{\text{dewet}}=A\sqrt{c}+Bc,$$ (5)

where A = a (Δσ_air + Δσ_pore), and B = b (Δσ_air + Δσ_pore). The dewetting free energy derived from MetaD calculations can be fit to Eq. 6 with a Pearson’s correlation coefficient R > 0.99 (Figure 4B). Importantly, coefficients a and b in Eq. 4 depend on the ion type alone. Therefore, Eq. 5 is an important result, and parameters derived from free energy studies of model nanopores can be directly applied to predict the salt dependence of hydrophobic dewetting of protein ion channels.

Complex effects of amphipathic cosolvents on hydrophobic nanopores

Amphipathic molecules, like alcohols and sugars, are also often used as cosolvents in functional studies of protein ion channels.^82-89 For example, addition of glycerol or sucrose to the intracellular solution can enhance Ca²⁺-dependent activation of the big potassium (BK) channel.⁹⁰ The molecular basis of how these cosolvents modulate channel function is not yet fully understood, even though it has been proposed to impact the protein rigidity.⁹⁰ To examine how these cosolvents affect hydrophobic dewetting, we analyzed the free energy landscapes of pore hydration with increasing ethanol and glycerol concentrations. We applied the same MetaD protocol with N_water as the CV in all simulations, and then derived 2D PMFs as a function of both pore ethanol/glycerol and water numbers.

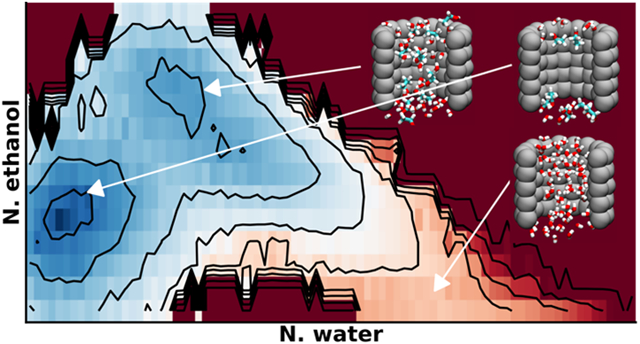
As summarized in Figure 6, the effects of even simple ethanol are much more complex compared to those of salt. The presence of ethanol not only changes the ability of the pore to dewet, but also shifts the location of the hydrated state significantly. This may be directly attributed to the amphipathic nature of ethanol molecules. As illustrated in Figure S10, ethanol tends to coat the both the inner and outer surfaces of the pore wall with the hydrophobic methyl group facing the wall and the hydroxyl group facing the bulk and (hydrated) center. Similar observations have been made in previous studies of hydration properties of carbon nanotubes²⁸ and hydrophobic plates.²⁷ Hydrophobicity of the wall is clearly central to the observed preferential surface adsorption of ethanol. For example, ethanol was found to absorb preferentially to the water-air interface but not the calcite solid-water interface.³⁵ Even with 5% ethanol, this mixed-solvent “wet” state is only about 1 kcal/mol less stable than the dry state. In comparison, the hydrated state is about 4 kcal/mol less stable than the dry state in pure water (Figure 3). In the presence of ethanol, there is no longer a local minimum for a wet state of the pore hydrated largely by water (N_water ~ 60, see Figure 3). Even in the dry state, the pore remains partially solvated by a few ethanol molecules. As the ethanol concentration increases, the mixed solvent wet state becomes the most dominant state (Figure 6B-D). Furthermore, the wet state shifts from consisting of a mixture to consisting of mostly ethanol as the ethanol concentration increases (Figure 6). At 40% ethanol, the free energy cost of desolvating the nanopore is ~3 kcal/mol from the ethanol solvated state, while the cost of solvating the pore with water is >10 kcal/mol (Figure 6D).

Figure 6. Ethanol effects on hydration property of nanopores.

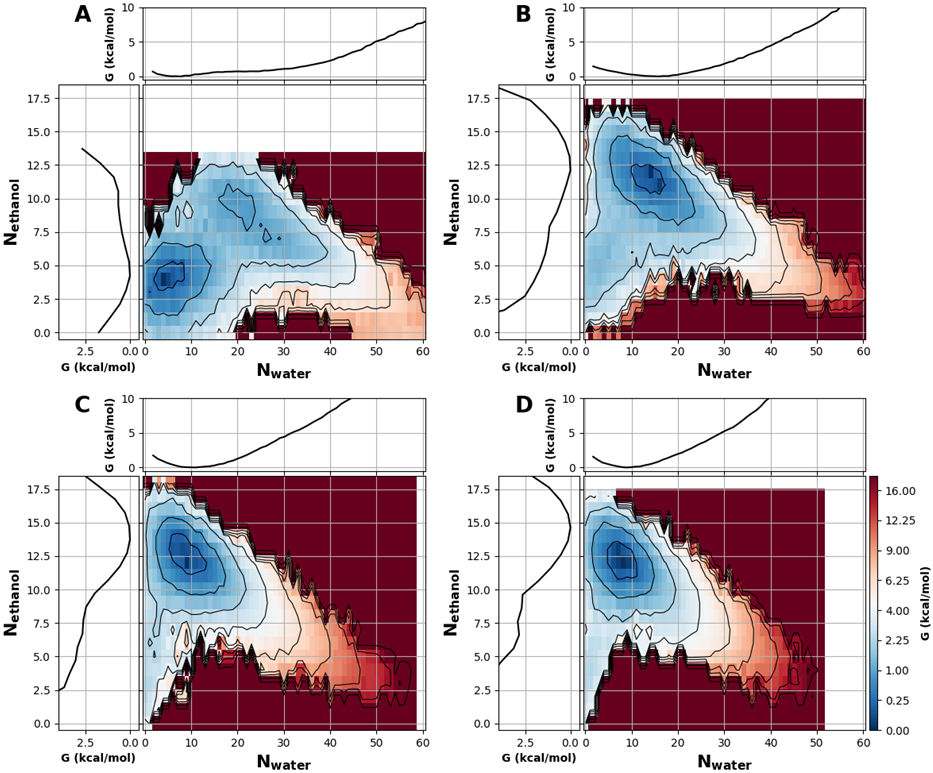
All 2D PMFs were calculated as a function of pore ethanol and water numbers for a nanopore with a radius 6 Å and height of 16 Å. The ethanol volume fraction is A) 5%, B) 13%, C) 23%, and D) 40%. Black contour lines and color bar ticks are drawn at the same energy levels and are distributed quadratically. In each panel, the marginal projections are the 1D PMFs along N_water (top) and N_ethanol (left). The convergence of these free energy surfaces is illustrated in Figure S11.

The impact of glycerol on hydrophobic dewetting of the model nanopores are summarized in Figure 7 and are similarly complex to those of ethanol. Previous studies has shown that carbon nanotubes dewet in the presence of organic cosolvents like guanidinium and urea.^91,92 As previously discussed, glycerol is of particular interest for effecting the gating mechanism of some ion channels.⁹⁰ To quantify the effect glycerol has on hydrophobic dewetting, we solvated the pore of radius 6 Å and height 16 Å with various glycerol concentrations. We found that increasing glycerol concentration also destabilizes the pure water hydrated state (Figure 7). Below 5% we saw no interesting effect beyond simply drying the nanopore as expected (data not shown). At a glycerol concentration of 5%, the hydrated state is still essentially pure water and has a ΔG_dewet of ~−4 kcal/mol (Figure 7A), comparable to that of dehydrating the same pore in pure water (Figure. 3). At a higher glycerol concentration of 23%, the mixed glycerol and water state ΔG_dewet is reduced to about −2.5 kcal/mol (Figure 7B). Glycerol is likely more sterically hindered than ethanol in a 6 Å-radius pore, which would explain why the mixed solvent state is only achieved at relatively high concentration. Clearly, a sufficiently high concentration of amphipathic cosolvent can induce a mixed-solvent state that solvates a hydrophobic pore that would otherwise remain dehydrated in pure water. The prediction that glycerol (and ethanol) can stabilize the hydrated state of the pore is important, because such direct effects of glycerol on hydrophobic dewetting may contribute to the experimental observation that glycerol promotes the activation of BK channels.⁹⁰

Figure 7. Glycerol effects on hydration property of nanopores.

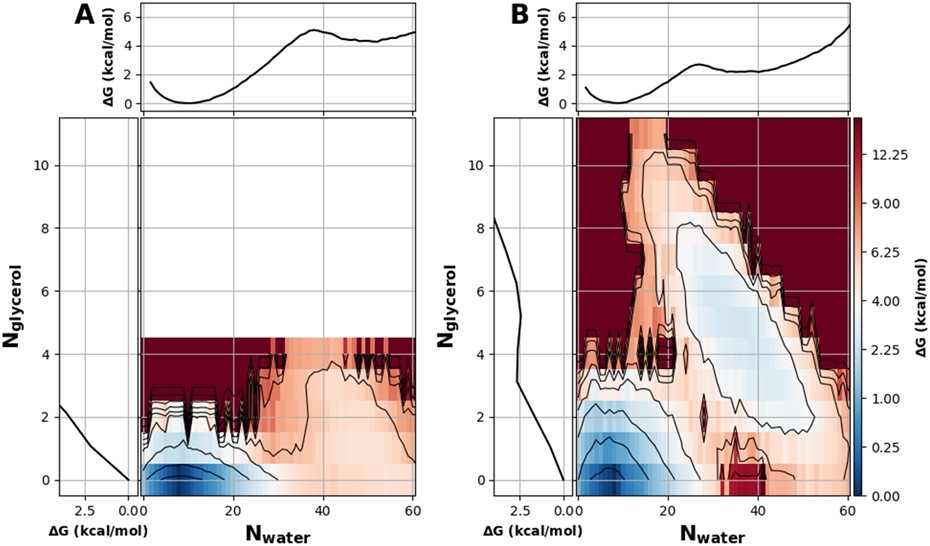
All free energy profiles were calculated for a pore with a radius 6 Å and height of 16 Å and in a solution with A) 5%, and B) 23% glycerol by volume. The black contour lines and color bar ticks are drawn at the same energy levels and are distributed quadratically. In each panel, the marginal projections are the 1D PMFs along N_water (top) and N_glycerol (left). The convergence of these free energy surfaces is illustrated in Figure S12.

Conclusions

The delicate balance of water’s liquid-vapor equilibrium in nanoscale confinement is vital to cellular functions, including as a gating mechanism in ion channels. We developed a MetaD enhanced sampling protocol to sample reversible liquid-vapor transitions in nanopores and quantify the energetic effects of changing biologically-relevant properties of the pore. We carefully selected key MetaD parameters, particularly the pace and bias factor, to balance the computational cost and achievable convergence, and identified a single protocol that was able to achieve converged free energy profiles within 50 ns for a wide variety of nanopores and solution conditions. Importantly, the MetaD protocol provides sufficient sampling even for capturing the complex effects of amphipathic cosolvents without needing to bias both the water and cosolvent, demonstrating its robustness to accelerate the sampling of dewetting transitions in a wide array of biologically-relevant settings. We expect that the protocol can be used in simulations of protein ion channels to quantify the effects of ions, surfactants, or even channel-activating drugs on hydrophobic dewetting, as well as the effects of mutations and protein conformational changes. The general protocol will also be useful to study confined water properties in any system where the liquid-vapor transition lies beyond what’s accessible to conventional all-atom MD simulations.

Using a set of nanopores of various sizes and geometries, we found that the dewetting free energy was insensitive to curvature and shape. Instead, it can be fully determined by two key thermodynamic parameters, namely, the effective surface tension coefficients of the water-air and water-pore surfaces (Eq. 3). Furthermore, the effects of salts can be fully captured in the ion-specific salt dependence of surface tension coefficients, such as using a Debye-Hückel limiting law (Eqs. 4 and 5). Therefore, results from studies of model nanopores can be used to quantitatively predict the salt dependence of hydrophobic gating of complex protein. Our simulations further showed that amphipathic molecules such as ethanol and glycerol had complex effects on the hydration properties of nanopores, shifting both the location of hydrated state and the free energy equilibrium. In particularly, amphipathic molecules such as glycerol can directly perturb the liquid-vapor equilibrium of water in nanopores to enhance the activation of ion channels. This may provide a general probe for detecting and studying hydrophobic gating in protein ion channels.

Statement of significance.

Life has evolved to take full advantage of the complex properties of water, its primary solvent. One such important property is the delicate balance between the liquid and vapor phases, which some protein ion channels utilize to assist in the gating mechanism. We describe an enhanced stimulation protocol that helps sample many reversible dewetting events in biologically relevant model nanopores. We used this protocol to analyze how key properties of the nanopore and solvent affect dewetting thermodynamics, including the effects of cosolvents like salt and alcohols. Our method will be useful to study systems such as protein nanopores and ion channels where confined water dynamics are of great biological interest.