Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2023 Feb 3;8(6):5426–5436. doi: 10.1021/acsomega.2c06582

Effect of Spiral Inlet Geometric Parameters on the Performance of Hydrocyclones Used for In Situ Desanding and Natural Gas Hydrate Recovery in the Subsea

Shunzuo Qiu †,*, Teng Wang ‡, Guorong Wang §, Lin Zhong §, Xing Fang §
PMCID: PMC9933186  PMID: 36816650

Abstract

graphic file with name ao2c06582_0012.jpg

The inlet structure of hydrocyclones has great impact on performance. In this paper, the effects of spiral inlet geometric parameters on the flow field characteristics and separation performance were investigated by CFD. Numerical results show that the pitch has the largest influence, followed by the heads, the turns, and the steady flow cone. With the increase of the steady flow cone angle, the turbulence intensity increases. The efficiency, pressure drop, tangential velocity, sand volume fraction at the spigot, and natural gas hydrate (NGH) volume fraction at the vortex finder decrease, when the pitch increases. With the increase of the number of heads and turns, the efficiency, pressure drop, tangential velocity, the NGH volume fraction at the vortex finder, and the sand volume fraction at the spigot increase. The efficiency and pressure drop of hydrocyclones with the optimal parameters are 90% and 0.05 MPa, respectively. Therefore, the performance of the NGH hydrocyclone can be improved by increasing the inlet pitch and the number of spiral heads and inlet spiral turns. The results provide theoretical guidance for the engineering design of NGH in situ separators.

1. Introduction

Hydrocyclone is one of the most important liquid–solid separation devices that is widely used in many industrial fields. Due to the comprehensive force field in the hydrocyclone, the particles can be classified. With higher centrifugal force, the larger or heavier particles are collected by the underflow, while the smaller or lighter particles are separated from most of the fluid by overflow. As efficient centrifugal separation equipment, hydrocyclones are characterized by large capacity, a small physical size, low production, maintenance costs, and strong adaptability to harsh conditions.1 So far, the accurate classification of continuous liquid–solid suspension particles has been greatly concerned in the development of different industries. Natural gas hydrate (NGH) has been proven to be one of the most promising clean energy sources.2,3 Trial production shows that the sand production is serious during mining, resulting in a high sand content of NGH slurry.4−6 Therefore, the new separation and desanding technology and equipment are urgently needed. Hydrocyclone is selected as the most potential separation equipment in the in situ separation and desanding technology, presented in Figure 1. The research on desanding and NGH recovery using hydrocyclones gradually becomes a potential field of high research interest.

Figure 1.

Figure 1

Open in a new tab

Technology and process of exploitation of NGH.

Research has been carried out to evaluate the impact on the internal flow behavior of the hydrocyclone applied in other fields. Accordingly, many suggestions for optimizing the structural parameters of hydrocyclones are put forward.7,8 For example, the performance of hydrocyclones can be improved by changing the overflow pipe,9−11 the cone section,12 and the column section.13 Since the inlet structure is the key point affecting the separation behavior of hydrocyclones, more attention is paid to the optimization of the inlet structure. Some results show that the classification sharpness of hydrocyclones is improved by the symmetrical inlet.14,15 Li et al.16,17 studied the influence of linear, arc, and spiral inlet pipes on the separation performance, which showed that the vortex involute inlet can improve the performance. Ren et al.18−20 presented that tangential inlets have the highest separation sharpness among different types of inlets. At the same time, Zhang et al.21 concluded that the separation efficiency can be improved by optimizing the tangential inlet angle. Celis et al.22,23 studied the influence of the spiral inlet structure on the performance of hydrocyclones and showed that better spiral inlet structure parameters can improve the separation performance. Some research on the effect of structure on the performance of NGH hydrocyclone has been carried out. Wang et al.24−26 studied the influence of the structural parameters of a tangential inlet on the separation performance and showed that the separation performance can be improved by optimizing the parameters of the overflow pipe, underflow pipe, column section, and cone section. Chang et al.27,28 designed two types of axial-flow NGH hydrocyclones, analyzed the influence of geometric parameters such as inlet and outlet, and spiral separation section on the separation performance, and then obtained a better parameter combination. However, the mechanism between the spiral inlet structure and the performance of NGH hydrocyclone is not fully understood. To further improve the performance of NGH hydrocyclone, it is of great practical significance to understand the mechanism of the spiral inlet structure affecting separation efficiency and sharpness.

The purpose of the present work is to investigate the effect of spiral inlet geometric parameters on the performance of NGH hydrocyclone by the numerical method. An axial spiral inlet hydrocyclone was proposed for the in situ desanding of NGH. The effect of spiral inlet pitch, the heads, the turns, and the steady flow cone on the flow field characteristics, separation efficiency, and pressure drop were studied. These results are used to understand the mechanism that affects the turbulence intensity, tangential velocity, discrete phase, and separation efficiency with the change of inlet steady flow cone, pitch, number of turns, and number of heads. In addition, hydrocyclones with optimized inlet structure parameters are used for in situ desanding and NGH recovery.

2. Materials and Methods

2.1. Geometry and Mesh Generation

Figure 2 presents the geometrical model and the mesh of the novel hydrocyclone. To better understand the movement of NGH and sand in hydrocyclone, a simplified novel hydrocyclone geometry is built by Solidworks software. Different from the traditional hydrocyclone and spiral separator, the novel hydrocyclone is mainly divided into two parts: spiral inlet and cyclone body. The spiral inlet plays the role of preseparation and produces a swirling flow. The cyclone body plays the main role of separation. The main structural parameters of the parts are shown in Table 1. To improve the computational accuracy, the grids were refined in the key section. The grid was divided by the mesh software in the Workbench. The whole computational domain was represented by tetrahedral and hexahedral mesh.

Figure 2.

Figure 2

Open in a new tab

Geometry and meshing.

Table 1. Main Structural Parameters of Novel Hydrocyclone.

structural parameters size
dominant diameter D (mm) 100
pitch of inlet B (mm) 24
number of inlet spiral circles n 2
number of inlet spiral heads m 2
cone angle of steady flow cone (°) 10
diameter of vortex finder d0 (mm) 32
insertion depth of vortex finder h0 (mm) 50
length of cylindrical section H (mm) 65
diameter of spigot ds (mm) 26
length of spiral inlet H1 (mm) 125
cone angle (°) 10
Open in a new tab

2.2. Model Description

2.2.1. Multiphase Model

DPM is only applicable to simulate hydrocyclones processing the feed with a low solid concentration. The mixture model which can be regarded as a simplified two-fluid model has been proven to be valid for hydrocyclones with a high feed solid concentration.21 In this paper, to represent the multiphase characteristic, the mixture model was used, because the mixed slurry concentration is 25%. The mixture model is a simplified multiphase model with the advantages of both calculation precision and speed compared with the full Eulerian multiphase model and Lagrangian model.

The continuity equation can be written as:

2.2.1. 1

The momentum equation of the mixture model can be written as:

2.2.1. 2

where udr is the drift velocity, g is gravitational acceleration, and −ρ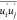Inline graphic is the Reynolds stress term. uj, ui, and ρ are velocity and the density of the mixture phase fluid, respectively, which are written as equations:

2.2.1. 3

where μk, αk, ρk, and uk are viscosity, the volume fraction, density, and velocity the kth phase fluid, respectively.

2.2.2. Turbulence Model

The RSM model has the advantages of both calculation time and accuracy compared with the RANS (Reynolds Average Navier–Stokes) models and LES (Large eddy) model, which also are great advantages for predicting behavior of complex flows such as swirling flow in the cyclone accurately. The RSM model uses the partial differential transport equation to calculate the single component of the turbulent stress tensor. Therefore, the Reynolds stress model was used in this paper.

The RSM model transport equation can be written as:

2.2.2. 4

where DL, ij is molecular viscous diffusion, DT, ij is the turbulent diffusion, Gij is the buoyancy generation, Φij is the pressure strain, εij is viscous dissipation, Fij is the system rotation generation, and Pij is shear stress generation.

2.3. Boundary Conditions and Solver

The hydrate dissociation is very little in the downhole in situ environment. The temperature of the hydrate reservoir in the South China Sea is about 278 K, and the pressure is about 12 MPa. From the phase equilibrium curve of the hydrate, when the temperature is 278 K, the minimum pressure to keep the hydrate stable is about 8 MPa.29,30 In this paper, the maximum pressure drop from the inlet to the outlet of hydrocyclone is not more than 0.6 MPa. Judging from the pressure drop, the probability of hydrate decomposition is small. The second reason is that the decomposition of hydrate takes time. Generally, it takes 30 min for the hydrate to decompose. The residence time of mixed slurry in the hydrocyclone is generally second. Before entering the hydrocyclone, the hydrate will be decomposed to a certain extent affected by factors such as temperature and other collisions. Due to the decomposition of hydrate, there will be a small amount of gas phase in the mixed slurry. Therefore, based on the ideas of solid fluidization mining of NGH, it was supposed that the mixture slurry of NGH contained only three phases, namely, seawater, NGH solid, and sand. NGH has no phase change. The size distributions of NGH and sand particles are the same and spherical. The fluid is incompressible. The physical parameters of the media used in this study are shown in Table 2. The specific simulation parameters are set as follows: the particle diameter was 30 μm, the sand volume fraction was 15%, the NGH volume fraction was 10%, and the inlet velocity was 0.63 m/s, that is, the flow rate is 15 m3/h. The density of NGH is 910 kg/m3, and the density of sand is 2600 kg/m3.

Table 2. Physical Parameters of Various Media.

media density (kg/m3) viscosity (kg/m/s) volume fraction (%)
seawater 1025 0.0017 75
sand 2600   15
NGH 910   10
Open in a new tab

The particle simulation is based on the Euler method, assuming that it is a continuous phase, and the particle size is set. The distribution plot of the NGH sediment particle diameter measured by a BT-9300LD dry wet laser particle size analyzer in South China is shown in Figure 3. The particle median diameter of sediment is about 30 μm and mainly less than 100 μm. Therefore, in this paper, the particle diameter was used as 30 μm.

Figure 3.

Figure 3

Open in a new tab

BT-9300LD dry wet laser particle size analyzer and diagram of sediment particle size distribution.

In this paper, Fluent 18.0 software, a 3-D model, steady state, and double precision implicit solver were used. The SIMPLE (semi-implicit pressure linked equations) algorithm scheme combined with continuity and momentum equations to derive an equation for pressure was carried out. Interpolation of field variables from cell centers to faces of the control volumes was opted with a higher-order quadratic upwind interpolation (QUICK) spatial discretization scheme as it was reported to be useful for swirling flows. The inlet, outlets, and no-slip boundary conditions were set as velocity, pressure, and wall boundary, respectively.

2.4. Calculation Method of Separation Efficiency and Pressure Drop

The separation efficiency is an important index of the separation performance of spiral separator. The sand discharge amount and NGH recovery amount are considered at the outlet section in this device. Separation efficiency is generally defined as the ratio of outlet phase mass to inlet phase mass.

2.4. 5

where E1 is NGH recovery efficiency %, Mo1 is the NGH mass flow rate at vortex finder (NGH recovery) outlet kg/s, Mi1 is the NGH mass flow rate at inlet kg/s, E2 is desanding efficiency %, Mo2 is the sand mass flow rate at spigot (desanding) outlet kg/s, and Mi2 is the sand mass flow rate at the inlet, kg/s.

As we know, the low pressure drop of the separator represents its low energy consumption. Thus, the pressure drop is also one of the most important indexes to evaluate the performance of the separator.

The pressure drop is shown in equation

2.4. 6

where Δp1 is NGH pressure drop Pa, p0 is inlet pressure Pa, p1 is pressure at vortex finder (NGH recovery) outlet Pa, Δp2 is sand pressure drop Pa, and p2 is pressure at spigot(desanding) outlet Pa.

2.5. Experimental Materials and Setup

The separation experiment is shown in Figure 4. The amount of sand added to the mixing tank was calculated according to the proportion of the solid volume concentration. The particle size was prepared according to the particle size distribution obtained from the South China Sea trial mining. The sand particles with the required particle size are selected with a standard screen, and then the BT-9300LD dry and wet laser particle size analyzer shown in Figure 3 is used to measure the sand particle size.

Figure 4.

Figure 4

Open in a new tab

Experimental equipment for NGH separation (1. Mixing tank. 2. Mixing device. 3. Flowmeter. 4. Stop valve. 5. Pressure sensor. 6. Sampling place at overflow port. 7. At the inlet sampling point. 8. Sampling place at underflow port. 9. Variable frequency controller. 10. Pump. 11. NGH separator).

Experiment Steps

According to different proportions, the required materials are added to the mixing tank, and the mixing mechanism is started to mix the materials until it is observed that the materials are mixed evenly. The pump is used to pump the mixed slurry to the inlet of the hydrocyclone. After the mixed slurry enters the separator, the high-concentration mortar is discharged from the spigot outlet and finally enters the mixing tank. The frequency of the frequency converter is adjusted to make the flow reach a specific value within the range. Then the flow meter and pressure sensor at the inlet and overflow port of the separator are observed, and samples are taken at the sampling port after the flow rate and pressure are stabilized. Finally, the above steps are repeated. In this paper, only the water-phase experiment is carried out. By calculating the flow value and pressure value obtained, the split ratio and pressure drop are obtained respectively.

3. Results and Discussion

3.1. Meshing Independence Test and Model Validation

The grid independence verification is shown in Table 3 and Figure 5, with the increase of the number of meshes, the maximum velocity decreases first and then increases, and then remains basically unchanged, while the maximum pressure increases first and then remains stable. The maximum velocity and maximum pressure remain basically unchanged after the number of grids exceeds 150,000. Therefore, about 150,000 grids are selected as the final grid scheme. The water was used as the research medium. The numerical results of the split ratio and pressure drop are compared with the experimental results. The comparison results are shown in Figure 6. With the increase of inlet velocity, the split ratio is basically unchanged, and the pressure drop increases. It can be seen that the split ratio and pressure drop predicted by the numerical simulation are basically consistent with the experimental data, which verifies the simulation results of this paper.

Table 3. Relationship between Computational Cells and Maximum Velocity, Maximum Static Pressure.

no number of grids max velocity (m/s) max pressure (Pa)
1 50,451 13.14 210986.3
2 100,278 12.07 233682.4
3 150,370 13.97 255192.8
4 200,468 13.87 252825.9
Open in a new tab

Figure 5.

Figure 5

Open in a new tab

Relationship between pressure, velocity, and mesh number.

Figure 6.

Figure 6

Open in a new tab

Comparison between the measured and simulated split ratio and pressure drop.

3.2. Effect of Spiral Inlet Geometric Parameters on Separation Performance

The spiral inlet is mainly composed of a cylinder, a steady flow cone, and a spiral deflector. The important main structural parameters are the cone angle of the steady flow cone, the pitch of the spiral deflector, the number of turns of the spiral deflector, the number of spiral heads, and the internal and external diameter of the cylinder. The inner and outer diameters of the cylinder are closely related to the overflow pipe and the main diameter of the separator. Thus, these structural parameters are ignored when the influence of the spiral inlet on the separation performance is studied. Therefore, in this paper, several structural parameters, such as the cone angle of the steady flow cone, the pitch of the spiral deflector, the number of turns of the spiral deflector, and the number of spiral heads, are selected to study the effect of the spiral inlet on the separation performance.

3.2.1. Effect of Inlet Steady Flow Cone

The cone angle of the inlet steady flow cone determines the smoothness of the steady flow cone and thus determines its steady flow effect. Therefore, the effect of the inlet steady flow cone angle on separation performance was studied in this study. The cone angles of 5°, 10°, 15°, and 20° and the structure without a steady flow cone are selected, as shown in Figure 7a. The effect of the inlet steady flow cone on the performance was studied from tangential velocity, turbulence intensity, pressure drop, and separation efficiency.

Figure 7.

Figure 7

Open in a new tab

Effect of the cone angle of steady flow cone on separation performance: (a) structure of NGH hydrocyclone; (b) cloud diagram of turbulence intensity distribution; (c) cloud diagram of tangential velocity distribution; (d) NGH recovery efficiency and desanding efficiency; (e) pressure drop.

Figure 7d,e shows the comparison of the separation efficiency and pressure drop with different inlet steady flow cone angles. It can be seen that although the separation efficiency is somewhat different, the overall change is not big. The NGH recovery efficiency is distributed in the range of 82∼84%. The desanding efficiency is distributed in the range of 84.5∼87%. The separation efficiency decreases with the increase of the cone angle. With the increase of the cone angle, the pressure drop increases, and the pressure drop basically changes within the range of 0.17∼0.19 MPa. The pressure drop without the steady flow cone structure is greater than that with the steady flow cone structure. The pressure drop at the vortex finder is slightly smaller than that at the spigot. The main reason is that as shown in Figure 7b,c, as the cone angle increases, the tangential velocity decreases. The larger the amplitude of the velocity change is, the greater the turbulence intensity is in the separator. The turbulence intensity with the steady flow cone is significantly lower than that without the steady flow cone. The increase of tangential velocity is helpful to increase the centrifugal force required for particle separation, but the increase of turbulence intensity increases the probability of particle displacement. The change of the inlet steady flow cone structure has a great influence on the inlet flow field, especially turbulence intensity. Therefore, proper consideration should be given to the design of NGH hydrocyclone, and the optimal cone angle of steady flow is 5° in this research scope.

3.2.2. Effect of Spiral Deflector Pitch

Five different structures with inlet spiral pitch structural parameters of 14, 24, 34, 44, and 54 mm were respectively modeled and compared with the simulation results. The five different spiral pitch structures are shown in Figure 8a. It presents that the change of the spiral pitch changes the length of the spiral inlet section and the area of the inlet flow section.

Figure 8.

Figure 8

Open in a new tab

Effect of spiral pitch on separation performance: (a) structure of NGH hydrocyclone; (b) cloud diagram of tangential velocity distribution; (c) cloud diagram of NGH distribution; (d) cloud diagram of sand distribution; (e) NGH recovery efficiency and desanding efficiency; (f) pressure drop.

The comparison of the distribution cloud diagram of the tangential velocity in the NGH hydrocyclone with the change of the screw pitch is shown in Figure 8b. It presents that the tangential velocity decreases with the increase of the screw pitch. The main reason is that when the inlet velocity and other structural parameters are determined, the smaller the pitch is, the larger the tangential velocity component is. It indicates that the smaller the screw pitch is, the larger the centrifugal force can be generated, but the smaller the flow area is. Reducing the screw pitch within a certain range is conducive to the separation of particles.

The distribution clouds of NGH and sand phase with different spiral pitch are shown in Figure 8c,d. It can be seen that when the spiral pitch decreases, the more the NGH is concentrated in the center of the hydrocyclone, the more the sand phase concentrates on the wall. From the volume fraction distribution of the outlet, the smaller the pitch is, the higher the NGH volume fraction at the vortex finder and the higher the sand volume fraction at the spigot. The main reason can be obtained from the analysis of the influence of spiral pitch on tangential velocity in the previous of this paper. Specifically, the smaller the spiral pitch is, the greater the tangential velocity is, and the greater the centrifugal force is generated. Therefore, the smaller the spiral pitch, the greater the centrifugal force received by the discrete phase.

The separation efficiency and pressure drop curves of hydrocyclone with different spiral pitches are presented in Figure 8e,f. It shows that the change of spiral pitch has a significant impact on the separation efficiency. With the increase of spiral pitch, the NGH recovery efficiency and desanding efficiency are significantly reduced, and the maximum value of efficiency is above 90%, which is consistent with the prediction of tangential velocity and phase distribution. It is presented that the inlet spiral pitch is one of the key structural parameters that determine the separation efficiency of the NGH hydrocyclone. With the increase of the spiral pitch, the pressure drop decreases, which is about 0.5 MPa. The main reason is that the increase of the spiral pitch reduces the speed at the spiral inlet when the flow is determined, resulting in the reduction of local pressure loss.

The inlet spiral pitch has obvious effects on the velocity, discrete phase distribution, pressure drop, and separation efficiency. Within the research range, the separation efficiency changes by about 30%, and the pressure drop changes by about 0.5 MPa. This structural parameter should be considered emphatically, and the optimal value of spiral pitch is 15 mm in this research scope.

3.2.3. Effect of the Turns Number of the Spiral Deflector

A comparative study was conducted on five different NGH hydrocyclone structures with 1, 2, 3, 4, and 5 spiral turns, respectively. The NGH hydrocyclones with five different spiral turns are shown in Figure 9a. It can be seen that the more the number of turns is, the longer the inlet spiral section is.

Figure 9.

Figure 9

Open in a new tab

Effect of the number of spiral turns on the separation performance: (a) structure of NGH hydrocyclone; (b) cloud diagram of tangential velocity distribution; (c) cloud diagram of NGH distribution; (d) cloud diagram of sand distribution; (e) NGH recovery efficiency and desanding efficiency; (f) pressure drop.

The cloud diagram of tangential velocity distribution with different numbers of turns is presented in Figure 9b. It shows that the distribution laws of tangential velocities are not changed with the increase of the spiral turns number, and it still increases first and then decreases from the wall to the center. The increase of the number of spiral turns increases the preseparation section of the spiral inlet and prolongs the tangential velocity range, but the value of the tangential velocity does not change much.

The volume fraction distribution cloud diagram of sand and NGH in the NGH hydrocyclone with different spiral turns is shown in Figure 9c,d. With the increase of the spiral turns number, the sand volume fraction near the wall and spigot increases, and the NGH volume fraction near the center and vortex finder increases. The main reason is that the increase of spiral turns prolongs the pre-separation section. At the same time, the residence time of the particles in the separator is prolonged. Increasing the number of spiral turns is helpful to the NGH recovery and desanding.

The separation efficiency and pressure drop curves with different numbers of spiral turns are shown in Figure 9e,f. It presents that the NGH recovery efficiency and desanding efficiency first increase and then tend to be stable with the increase of the spiral turns number. The NGH recovery efficiency and desanding efficiency tend to be relatively stable when the number of spiral turns is greater than 2. All separation efficiencies are above 80%. When the number of the spiral turns increases from 1 to 2, the NGH recovery efficiency increases by 2%, and the desanding efficiency increases by 3%, indicating that the number of spiral turns has a great impact on the separation efficiency. With the increase of the number of turns, the pressure drop increases. The pressure drop at the spigot is close to that at the vortex finder. Within the research range, the pressure drop variation amplitude is about 0.06 MPa. The main reason is that the increase of the number of turns increases the energy loss of the resistance along the way. In order to ensure low energy consumption, the number of spiral turns should not be too many. It is suggested that the number of spiral turns can be appropriately increased to improve the separation performance.

The number of spiral turns has a great influence on the velocity, discrete phase distribution, pressure drop, and separation efficiency of the NGH hydrocyclone. Within the research range, the maximum change of separation efficiency is within 10%, and the change of pressure drop is about 0.06 MPa. The optimal number of spiral turns is 5 in this research scope.

3.2.4. Effect of the Spiral Heads Number of Spiral Deflector

Four different structures with the number of spiral heads of 1, 2, 3, and 4 were studied respectively. The structures are shown in Figure 10a. It can be seen that with the increase of the number of spiral heads, structural parameters will divide the cross-section of the screw inlet into more screw channels, resulting that the cross-sectional area of a single screw channel is reduced. In this way, when the inlet flow is constant, the velocity in the single screw channel will increase.

Figure 10.

Figure 10

Open in a new tab

Effect of the number of spiral heads on the separation performance: (a) Structure of NGH hydrocyclone; (b) cloud diagram of tangential velocity distribution; (c) cloud diagram of NGH distribution; (d) cloud diagram of sand distribution; (e) NGH recovery efficiency and desanding efficiency; (f) pressure drop.

The distribution cloud diagram of tangential velocity in the NGH hydrocyclone with different numbers of screw heads is shown in Figure 10b. It obtained that with the increase of the number of spiral heads, the distribution law of tangential velocity remains unchanged and its value keeps increasing. The above results indicate that increasing the number of screw heads at the inlet can increase the centrifugal force on discrete phase particles, which is conducive to the NGH recovery and desanding.

As shown in Figure 10c,d, with the increase of the number of spiral heads, the sand volume fraction near the wall and spigot increases, and the volume fraction of the NGH near the center and vortex finder increases, indicating that increasing the number of spiral heads increases the probability of sand flowing out from the spigot. The possibility of NGH approaching the center and being recovered from the vortex finder increases.

Figure 10e,f presents the separation efficiency and pressure drop curves with different numbers of spiral heads. It can be seen that the number of spiral heads has a more obvious impact on the separation efficiency. With the increase of the number of spiral heads, the NGH recovery efficiency and desanding efficiency increase. The main reason is that the increase of the number of spiral heads leads to a decrease in the cross-section of the spiral channel and increases the velocity in the spiral channel. With the increase of the number of spiral heads, the pressure drop increases. Within the research range, the pressure drop variation amplitude is about 0.1 MPa. Therefore, the appropriate number of spiral heads can be selected to improve the separation performance of the NGH hydrocyclone. The optimal number of spiral heads is 4 in this research scope.

4. Conclusions

The spiral inlet geometric parameters have a great impact on the performance of NGH hydrocyclone; the largest impact is the inlet pitch, followed by the number of inlet spiral heads, the number of inlet spiral turns, and the inlet steady flow cone. With the optimal combination of inlet structural parameters, the separation efficiency is above 90%, and the lowest pressure drop is within 0.05 MPa.

With the increase of the inlet steady flow cone angle, the separation efficiency decreases, the pressure drop and turbulence intensity increase, and the tangential velocity changes little. With the increase of the pitch, the separation efficiency, pressure drop, and tangential velocity decrease, the NGH volume fraction at the vortex finder and the sand fraction at the spigot decrease. The separation efficiency and pressure drop increase, and the tangential velocity value changes little, the NGH volume fraction at the vortex finder and the sand fraction at the spigot increase, when the number of turns increases. With the increase of the number of spiral heads, the separation efficiency, pressure drop, tangential velocity increase, and the NGH volume fraction at the vortex finder, and the sand fraction at the spigot increase.

Therefore, when designing the spiral inlet structure and determining the parameters of the NGH in situ separator, it is recommended to focus on the spiral pitch, the number of heads, the number of turns, and the steady flow cone. If conditions permit, the pitch is reduced, the number of heads is increased, the cone angle of the steady flow cone is reduced, and the number of turns is increased.

Acknowledgments

The authors are grateful to Science and Technology Innovation in Sichuan Province (Seedling Project) [2022074]; “Sailing” project of Yibin University [2021QH020]; National Key R&D Program of China [2019YFC0312305].

The authors declare no competing financial interest.

References

  1. Ni L.; Tian J.; Song T.; Jong Y.; Zhao J. Optimizing geometric parameters in hydrocyclones for enhanced separations: a review and perspective. Sep. Purif. Rev. 2019, 48, 30–51. 10.1080/15422119.2017.1421558. [DOI] [Google Scholar]
  2. Li X.; Xu C.; Zhang Y.; Ruan X.; Li G.; Wang Y. Investigation into gas production from natural gas hydrate: a review. Appl. Energy 2016, 172, 286–322. 10.1016/j.apenergy.2016.03.101. [DOI] [Google Scholar]
  3. Huang L.; Yin Z.; Wan Y.; Sun J.; Wu N.; Veluswamy H. P. Evaluation and comparison of gas production potential of the typical four gas hydrate deposits in shenhu area, south china sea. Energy 2020, 204, 117955 10.1016/j.energy.2020.117955. [DOI] [Google Scholar]
  4. Yang L.; Liu Y.; Zhang H.; Xiao B.; Guo X.; Wei R.; Xu L.; Sun L.; Yu B.; Leng S.; Li Y. The status of exploitation techniques of natural gas hydrate. Chin. J. Chem. Eng. 2019, 27, 2133–2147. 10.1016/j.cjche.2019.02.028. [DOI] [Google Scholar]
  5. Yamamoto K.; Boswell R.; Collett T. S.; Dallimore S. R.; Lu H. Review of past gas production attempts from subsurface gas hydrate deposits and necessity of long-term production testing. Energy Fuels 2022, 36, 5047–5062. 10.1021/acs.energyfuels.1c04119. [DOI] [Google Scholar]
  6. Yu T.; Guan G.; Abudula A. Production performance and numerical investigation of the 2017 offshore methane hydrate production test in the nankai trough of japan. Appl. Energy 2019, 251, 113338 10.1016/j.apenergy.2019.113338. [DOI] [Google Scholar]
  7. Hou D.; Zhao Q.; Cui B.; Wei D.; Song Z.; Feng Y. Geometrical configuration of hydrocyclone for improving the separation performance. Adv. Powder Technol. 2022, 33, 103419 10.1016/j.apt.2021.103419. [DOI] [Google Scholar]
  8. Venkatesh S.; Sivapirakasam S. P.; Sakthivel M.; Krishnaraj R.; Leta T. J. Investigation on hydrocyclone for increasing the performance by modification of geometrical parameters through cfd approach. Desalin. Water Treat. 2021, 244, 157–166. 10.5004/dwt.2021.27944. [DOI] [Google Scholar]
  9. Jiang L.; Liu P.; Yang X.; Zhang Y.; Li X.; Zhang Y.; Wang H. Effect of overflow pipe on the internal flow fields and separation performance of w-shaped hydrocyclones. Minerals 2020, 10, 329. 10.3390/min10040329. [DOI] [Google Scholar]
  10. Su T. L.; Zhang Y. Effect of the vortex finder and feed parameters on the short-circuit flow and separation performance of a hydrocyclone. Processes 2022, 10, 771. 10.3390/pr10040771. [DOI] [Google Scholar]
  11. Lai Y.; Wu R. Effect of the wall thickness of an overflow pipe on the short-circuit flow. Desalin. Water Treat. 2020, 185, 124–131. 10.5004/dwt.2020.25404. [DOI] [Google Scholar]
  12. Han T.; Liu H.; Xiao H.; Chen A.; Huang Q. Experimental study of the effects of apex section internals and conical section length on the performance of solid-liquid hydrocyclone. Chem. Eng. Res. Des. 2019, 145, 12–18. 10.1016/j.cherd.2019.02.040. [DOI] [Google Scholar]
  13. Hou D.; Cui B.; Zhao Q.; Wei D.; Song Z.; Feng Y. Research on the structure of the cylindrical hydrocyclone spigot to mitigate the misplacement of particles. Powder Technol. 2021, 387, 61–71. 10.1016/j.powtec.2021.04.013. [DOI] [Google Scholar]
  14. Nenu R. K. T.; Yoshida H. Comparison of separation performance between single and two inlets hydrocyclones. Adv. Powder Technol. 2009, 20, 195–202. 10.1016/j.apt.2008.08.004. [DOI] [Google Scholar]
  15. Al-Kayiem H. H.; Osei H.; Hashim F. M.; Hamza J. E. Flow structures and their impact on single and dual inlets hydrocyclone performance for oil-water separation. J. Pet. Explor. Prod. Technol. 2019, 9, 2943–2952. 10.1007/s13202-019-0690-1. [DOI] [Google Scholar]
  16. Li F.; Liu P.; Yang X.; Zhang Y.; Li X.; Jiang L.; Wang H.; Fu W. Enhancement on the separation precision of fine particles in a novel hydrocyclone with the vorticose involute-line diversion inlet head. Int. J. Coal Prep. Util. 2022, 43, 169. 10.1080/19392699.2022.2031174. [DOI] [Google Scholar]
  17. Li F.; Liu P.; Yang X.; Zhang Y. Numerical simulation on the effects of different inlet pipe structures on the flow field and seperation performance in a hydrocyclone. Powder Technol. 2020, 373, 254–266. 10.1016/j.powtec.2020.06.066. [DOI] [Google Scholar]
  18. Ren L.; Liang Z.; Meng J.; Yang L.; Tian J.. Contrast study on the radial velocity of the flow field of the hydrocyclones with different inlet structures. In Ai Z. J., Zhang X. D., Kim Y. H., Yarlagadda P., Eds.; Advanced Manufacturing Systems, 339, International Conference on Materials and Products Manufacturing Technology (ICMPMT 2011), 2011; p 624.
  19. Zhao Q.; Hou D.; Cui B.; Wei D.; Song T.; Feng Y. Development of an integrated multichannel inlet for improved particle classification in hydrocyclones. Adv. Powder Technol. 2021, 32, 4546–4561. 10.1016/j.apt.2021.10.003. [DOI] [Google Scholar]
  20. Tang B.; Xu Y.; Song X.; Sun Z.; Yu J. Effect of inlet configuration on hydrocyclone performance. Trans. Nonferrous Met. Soc. China 2017, 27, 1645–1655. 10.1016/S1003-6326(17)60187-0. [DOI] [Google Scholar]
  21. Zhang C.; Wei D.; Cui B.; Li T.; Luo N. Effects of curvature radius on separation behaviors of the hydrocyclone with a tangent-circle inlet. Powder Technol. 2017, 305, 156–165. 10.1016/j.powtec.2016.10.002. [DOI] [Google Scholar]
  22. Zhang Y.; Liu P.; Ge J.; Yang X.; Yang M.; Jiang L. Simulation analysis on the separation performance of spiral inlet hydrocyclone. Int. J. Coal Prep. Util. 2021, 41, 474–490. 10.1080/19392699.2021.1934828. [DOI] [Google Scholar]
  23. Celis G. E. O.; Loureiro J. B. R.; Lage P. L. C.; Silva Freire A. P. The effects of swirl vanes and a vortex stabilizer on the dynamic flow field in a cyclonic separator. Chem. Eng. Sci. 2022, 248, 117099 10.1016/j.ces.2021.117099. [DOI] [Google Scholar]
  24. Fang X.; Wang G. R.; Zhong L.; Qiu S. Z.; Wang D. F. A cfd-dem analysis of the de-cementation behavior of weakly cemented gas hydrate-bearing sediments in a hydrocyclone separator. Part. Sci. Technol. 2022, 40, 812–823. 10.1080/02726351.2021.2017087. [DOI] [Google Scholar]
  25. Qiu S. Z.; Wang G. R.; Wang L. Z.; Fang X. A downhole hydrocyclone for the recovery of natural gas hydrates and desanding: the cfd simulation of the flow field and separation performance. Energies 2019, 12, 3257. 10.3390/en12173257. [DOI] [Google Scholar]
  26. Qiu S. Z.; Wang G. R.; Zhou S. W.; Liu Q. Y.; Zhong L.; Wang L. Z. The downhole hydrocyclone separator for purifying natural gas hydrate: structure design, optimization, and performance. Sep. Sci. Technol. 2020, 55, 564–574. 10.1080/01496395.2019.1577264. [DOI] [Google Scholar]
  27. Chang Y. L.; Ti W. Q.; Wang H.; Zhou S. W.; Huang Y.; Li J.; Wang G. R.; Fu Q.; Lin H. T.; Wu J. W. Hydrocyclone used for in-situ sand removal of natural gas-hydrate in the subsea. Fuel 2021, 285, 119075 10.1016/j.fuel.2020.119075. [DOI] [Google Scholar]
  28. Lin H. T.; Huang Y.; Wang H. L.. Study on axial-flow hydrocyclone for in-situ sand removal of natural gas hydrate in the subsea. In Duan L., Abdullah A. Z., Eds.; 5th International Conference on Advances in Energy, Environment and Chemical Science (AEECS), 2021; p 24501050.
  29. Ruan X. K.; Li S. S.; Xu C. G. A review of numerical research on gas production from natural gas hydrates in China. J. Nat. Gas Sci. Eng. 2021, 85, 103713 10.1016/j.jngse.2020.103713. [DOI] [Google Scholar]
  30. Chen L.; Yamada H.; Kanda Y.; Okajima J.; Komiya A.; Maruyama S. Investigation on the dissociation flow of methane hydrate cores: numerical modeling and experimental verification. Chem. Eng. Sci. 2017, 163, 31–43. 10.1016/j.ces.2017.01.032. [DOI] [Google Scholar]

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES