Insights into the Reactivity of the Ring-Opening Reaction of Tetrahydrofuran by Intramolecular Group-13/P- and Al/Group-15-Based Frustrated Lewis Pairs

Abstract

A theoretical study concerning key factors affecting activation energies for ring-opening reactions of tetrahydrofuran (THF) by G13/P-based (G13 = B, Al, Ga, In, and Tl) and Al/G15-based (G15 = N, P, As, Sb, and Bi) frustrated Lewis pairs (FLPs) featuring the dimethylxanthene scaffold was performed using density functional theory. Our theoretical findings indicate that only dimethylxanthene backbone Al/P-Rea (Rea = reactant) FLP-type molecules can be energetically favorable to undergo the ring-opening reaction with THF. Our theoretical evidence reveals that the shorter the separating distance between Lewis acidic (LA) and Lewis basic (LB) centers of the dimethylxanthene backbone FLP-type molecules, the greater the orbital overlaps between the FLP and THF and the lower the activation barrier for such a ring-opening reaction. Energy decomposition analysis (EDA) evidence suggests that the bonding interaction for such a ring-opening reaction is predominated by the donor–acceptor interaction (singlet–singlet interaction) compared to the electron-sharing interaction (triplet–triplet interaction). In addition, the natural orbitals for chemical valence (NOCV) evidence demonstrate that the bonding situations of such ring-opening reactions can be best described as FLP-to-THF forward bonding (the lone pair (G15) → the empty σ*(C–O)) and THF-to-FLP back bonding (the empty σ*(G13) ← filled p-π(O)). The EDA-NOCV observations show that the former plays a predominant role and the latter plays a minor role in such bonding conditions. The activation strain model reveals that the deformation energy of THF is the key factor in determining the activation energy of their ring-opening reactions. Comparing the geometrical structures of the transition states with their corresponding reactants, a linear relationship between them can be rationally explained by the Hammond postulate combined with the respective activation barriers calculated in this work.

I. Introduction

Frustrated Lewis pairs (FLPs) are known for their steric bulks, which can sufficiently prevent adduct formation between the Lewis acid (LA) and Lewis base (LB) because of their sterically induced inability to quench one another.¹⁻³ Since the initial findings by Stephan and co-workers 15 years ago,¹ FLP chemistry has become a powerful strategy to activate small molecules²⁻¹⁹ and develop reactivity/reaction in laboratories.²⁰⁻²² In addition, FLP reactions are widely utilized in modern experiments because the activation of small molecules conventionally requires the participation of transition metals, which are usually expensive and environmentally harmful. By contrast, most FLP reactions do not involve transition-metal-catalyzed processes; thus, metal-free FLPs are suitable for catalysts and activation reactions used under nontoxic conditions.¹⁻²² After more than 10 years of effort, chemists have discovered that many novel and interesting FLP reactions can be exhibited by combining a variety of inter- and intramolecular LA and LB. Many theoretical studies on FLP-promoted small-molecule activation have been published elsewhere.²³⁻³⁴ Thus, the FLP chemistry has attracted considerable interest for their use in studying fundamental chemistry problems and for their widespread applications, particularly in heterogeneous catalysis, polymers, solid-state chemistry, and bioorganic and bioinorganic syntheses.¹⁻²²

Recently, Limberg and co-workers reported that the intramolecular P/Al-based FLP-type molecules featuring the dimethylxanthene backbone can be synthesized, crystallized, and used to activate tetrahydrofuran (THF) to undergo ring-opening reactions (Scheme 1).³⁵ The intramolecular FLP-type molecule featuring the dimethylxanthene scaffold, in which an LB phosphine center and an LA borane center are compelled with each other in a distance of 4.24 Å,³⁵ was reported and structurally characterized by Aldridge et al. in 2015. Although experimental examples of intermolecular LA-LB-mediated ring-opening reactions of THF have been published elsewhere,³⁶⁻⁴² to the best of our knowledge, only two papers concerning the THF ring-opening reaction by the intramolecular FLP-assisted molecule were reported by Limberg,³⁵ Wass,⁴³ and co-workers. Based on available mechanistic studies,³⁵ THF is initially activated at the LA aluminum element and then attacked by the basic phosphine function. Moreover, Limberg’s laboratory has observed that increasing the Lewis acidity of the Al center through C₆F₅ groups can increase the reaction rate by 10-fold compared with Mes substituents.³⁵ Based on the aforementioned findings, we aim to investigate the reactivity of the ring-opening reaction of THF via an intramolecular G13/G15-based (G13 = B, Al, Ga, In, Tl and G15 = N, P, As, Sb, Bi) FLP-assisted molecule possessing the dimethylxanthene backbone as schematically represented in eqs 1 and 2. In this work, we use density functional theory (DFT) and several sophisticated theoretical approaches to comprehend the key factors affecting activation barriers and the chemical reactivity trend for the element–substituent effect of the FLP molecule on the THF ring-opening reaction.

Scheme 1. Reactions of Dimethylxanthene Backbone Al/P-Based FLP-Type Molecules Containing (a) a (Mes)₂Al and (b) a (C₆F₅)₂Al Site with THF to produce ring-opened products.

II. Methodology

All of the structures reported in this work were fully optimized without symmetry constraints using the Gaussian 16 program package.⁴⁴ Geometry optimizations were conducted using the B3LYP functional.^45,46 The def2-TZVP⁴⁷ basis set was used for all atoms. Grimme’s dispersion-corrected functional (DFT-3D)⁴⁸ with BJ damping⁴⁹ was used to account for dispersion interactions. Thus, it was denoted as B3LYP-D3(BJ)/def2-TZVP. We have chosen B3LYP for this project because it gives the agreement of the calculated main-group chemistry and kinetics with the observed data.^50,51 Frequency analysis was performed to verify the characteristics of all optimized structures as minima (the number of imaginary frequencies is zero) or transition states (TSs; the number of imaginary frequencies is one). Transition states were submitted to intrinsic reaction coordinate (IRC)⁵² computations to check the energy profiles connecting each TS to two associated minima. Moreover, frequency calculations provide the thermal corrections of the Gibbs free energy (ΔG) at 298.15 K and 1 atm.

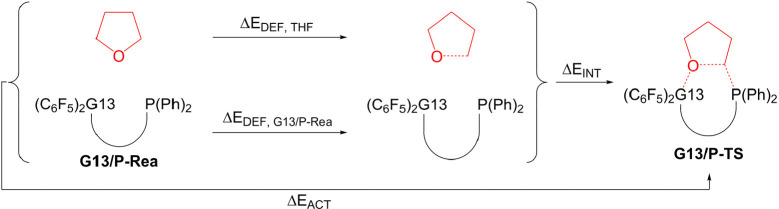
The activation strain model (ASM)⁵³⁻⁵⁵ (or distortion/interaction model)^56,57 was used with the Gaussian 16 program package to provide insights into the physical factors controlling the height of the activation barriers and reactivity trends upon changing the structure of the reactants. The activation energy (ΔE_ACT) was decomposed into the deformation energy (ΔE_def) and interaction energy (ΔE_INT) among the deformed reactants,

3

Furthermore, as shown in eq 4, ΔE_INT among reacting species was divided into the electrostatic interaction (ΔE_Elstat), Pauli repulsion (ΔE_Pauli), orbital interaction (ΔE_Orb), and dispersion effect (ΔE_Disp) by energy decomposition analysis (EDA)⁵⁸⁻⁶² based on the Kohn–Sham molecular orbitals.

4

Moreover, the bonding situations in the present FLP system were studied by EDA and the natural orbitals for chemical valence (NOCV)⁶³⁻⁶⁶ method, which can partition the total ΔE_Orb term into pairwise contributions of the orbital interactions. Details of the EDA-NOCV⁵⁸⁻⁶⁶ method, which decomposes the bond energy in several well-defined terms, can be found elsewhere.^67,68 This approach has been proven to be a highly efficient tool for describing the bonding conditions in different types of systems.^69,70 EDA-NOCV computations were thus carried out at the zeroth-order regular approximation ZORA⁷¹-B3LYP-D3(BJ)/TZ2P⁷²//B3LYP-D3(BJ)/def2-TZVP level, where the scalar relativistic effects were included by adopting the ZORA. All EDA-NOCV computations were performed using the Amsterdam density functional⁷³ program package.

III. Theoretical Model

Before discussing the computational results of the potential energy profile, the bonding models utilized in this work were explored. Based on previous theoretical analyses,⁵¹ two electronic interaction models can be used to understand the bonding conditions between THF and the G13/G15-assisted FLP-associated molecule. The first model is the donor–acceptor model, which is named the singlet–singlet (S–S) model. The other model is called the electron-sharing interaction model, which is viewed as the triplet–triplet (T-T) model. They are schematically presented in Figure 1(a) and (b), respectively. The former can be written as [G13/G15]¹ + [THF]¹ → [Prod]¹, and the latter can be described as [G13/G15]³ + [THF]³ → [Prod]¹. Notably, for the latter model, we propose its TS for the ring-opening reaction of THF by G13/G15-FLP, which is composed of the respective triplet states of reactants. Consequently, two individual triplets are coupled to an overall singlet state. The bonding characteristics for the singlet–singlet and triplet–triplet models are similar to those of the Fischer-type⁷⁴ and Schrock-type⁷⁵ metal carbenes, respectively, which are widely utilized in the field of organometallic chemistry (Figure 2).

Figure 1.

Schematic interaction diagram for (a) the donor–acceptor (or singlet–singlet) model and (b) the electron-sharing (or triplet–triplet) model.

Figure 2.

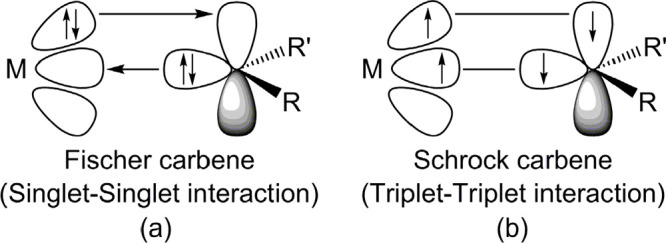
Schematic representations for (a) the Fischer-type metal carbene and (b) the Schrock-type metal carbene.

IV. Results and Discussion

IV.1. Ring-Opening Reactions of THF by G13/P-Based (G13 = Group 13 Element) and Al/G15-Based (G15 = Group 15 Element) FLPs

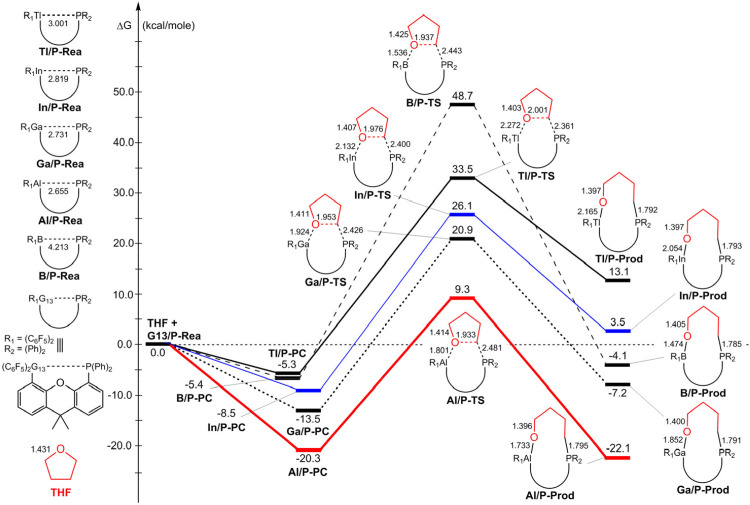
The calculated results for the four regions on the potential energy profiles of eq 1 are shown in Figure 3: G13/P-Rea (Rea = reactant) + THF → G13/P-PC (PC = precursor complex)⁷⁶ → G13/P-TS (TS = transition state) → G13/P-Prod (Prod = product). Our theoretical investigations collected in Figure 3 suggest that all five G13/P-Rea species have a separating G13(LA)···P(LB) distance (Å),⁷⁷ whose order increases in the order Al/P-Rea (2.655) < Ga/P-Rea (2.731) < In/P-Rea (2.819) < Tl/P-Rea (3.001) < B/P-Rea (4.213). It is noted that our B3LYP evidence reveals that B/P-Rea has the largest separating distance between LA and LB in all dimethylxanthene-based G13/P-Rea FLPs. Presumably, there may be two reasons for this. One possible reason is that the atomic radius of the B element is the smallest among the group 13 family.^78,79 The other possible reason is that atoms with more electrons have stronger dispersion forces. Hence, the heavy G13′ atom (= Al, Ga, In, and Tl) acting as LA and P acting as LB have a strong attraction so that the separating distance between G13′ and P in G13′/P-Rea is shorter than the separating distance between B(LA) and P(LB) in B/P-Rea. Surely, enough experimental evidence and theoretical calculation results are needed to comprehend the real reason behind it, but this is beyond the scope of this article.

Figure 3.

Computed reaction profiles for the ring-opening reaction of dimethylxanthene-based G13/P-Rea with THF at the B3LYP-D3(BJ)/def2-TZVP level. Relative free energies and bond lengths are given in kcal/mol and angstroms, respectively.

Our DFT results given in Figure 3 indicate that the PC (G13/P-PC) for each G13/P-Rea case should exist because their calculated free-energy values are relatively lower than those of the corresponding reactants ranging from −20.3 to −5.3 kcal/mol. Moreover, our DFT evidence reveals that all five G13/P-PC structures have a similar three-center (O–G13–C) pattern, in which the oxygen atom of THF is attached to the G13 element of G13/P-Rea. Based on the available experimental report,³⁵ before THF is activated by the Al/P-FLP with the dimethylxanthene scaffold, the presence of a PC, in which the O element of THF is connected to the Al center of the Mes-substituted Al/P-FLP, is confirmed by the NMR evidence but without isolation (Scheme 2(a)). Nevertheless, the same intermediate produced by the reaction of THF and the C₆F₅-substituted Al/P-FLP, in which the O atom of THF is attached to the Al element of the latter, has not been experimentally detected (Scheme 2 [b]).³⁵

Scheme 2. (a) Intermediate of the Mes-Substituted Al/P-FLP with THF and (b) Intermediate of the C₆F₅-Substituted Al/P-FLP with THF.

The reaction barrier (kcal/mol) relative to the corresponding PC was found to increase as follows: Al/P-TS (29.6) < Ga/P-TS (30.4) < In/P-TS (34.6) < Tl/P-TS (38.8) < B/P-TS (47.6). Nevertheless, the order of ΔG_RXN (kcal/mol) follows a different trend from that of the reaction barrier: Al/P-Prod (−22.1) < Ga/P-Prod (−7.2) < B/P-Prod (−4.1) < In/P-Prod (3.5) < Tl/P-Prod (13.1). Notably, the free energy of In/P-Prod and Tl/P-Prod is higher than that of their corresponding starting materials, which strongly implies that THF ring-opening products of In/P-Rea and Tl/P-Rea are endothermic. Accordingly, on the basis of our theoretical conclusions, only intramolecular Al/P-Rea FLP bearing the dimethylxanthene scaffold can be energetically favorable to undergo the ring-opening reaction of THF. Indeed, according to one experimental report (Scheme 1(b)), the intramolecular C₆F₅-substituted P/Al-FLP based on the dimethylxanthene backbone can interact with THF to first generate the intermediate (Al/P-PC), which can be converted to yield the final ring-opening product (Al/P-Prod) after being heated to 80 °C.³⁵

Furthermore, our computational evidence shown in Figure 3 reveals that the single-component G13/P-Rea FLP featuring a G13···P separation (Å) shows a distinct increasing trend: 2.655 (Al) < 2.731 (Ga) < 2.819 (In) < 3.001 (Tl) < 4.213 (B). This trend is similar to that of the activation barrier of the ring-opening reaction of THF by the corresponding G13/P-Rea FLP (Figure 3). Therefore, our theoretical finding indicates that the longer the separating distance between LA (G13) and LB (P) centers in the intramolecular G13/P-Rea FLP-type molecule bearing the dimethylxanthene scaffold, the higher the reaction barrier during its ring-opening reaction with THF.

Figure 4 exhibits relative energetic values of stationary points for the following mechanism: Al/G15-Rea + THF → Al/G15-PC → Al/G15-TS → Al/G15-Prod. The B3LYP results shown in Figure 4 indicate that the energies of Al/G15-PC are lower than those of the corresponding reactants by approximately −28.7 to −20.3 kcal/mol. As mentioned in Scheme 2, only experimental evidence about the PC for the Al/P-FLP with the LA Al center attached to the Mes group has been reported.³⁵

Figure 4.

Computed reaction profiles for the ring-opening reaction of dimethylxanthene-based Al/G15-Rea with THF at the B3LYP-D3(BJ)/def2-TZVP level. Relative free energies and bond lengths are given in kcal/mol and angstroms, respectively.

As shown in Figure 4, the separating Al···G15 distance (Å) of the reactant species (Al/G15-Rea) decreases in the following order: Al/N-Rea (4.913) > Al/Bi-Rea (3.544) > Al/Sb-Rea (2.934) > Al/As-Rea (2.787) > Al/P-Rea (2.655).⁸⁰ Moreover, our calculated free activation energy (kcal/mol), relative to its corresponding PC, for the ring-opening reaction of THF by Al/G15-Rea increases in the following order: 29.6 (P) < 33.8 (As) < 39.6 (Sb) < 47.7 (Bi) < 58.1 (N). Moreover, our theoretical computations collected in Figure 4 reveal that ΔG_RXN (kcal/mol) increases in the following order: Al/P-Prod (−22.1)⁸¹ < Al/As-Prod (−10.2) < Al/Sb-Prod (0.7) < Al/N-Prod (11.0) < Al/Bi-Prod (12.5). Therefore, the aforementioned computational evidence indicates that only the dimethylxanthene-based Al/P-Rea FLP-assisted molecule is energetically feasible to undergo a ring-opening reaction with THF rather than the other four Al/G15-based FLPs. To our knowledge, only one available experimental work has reported that the Al/P-based FLP-type molecules, which are linked by a dimethylxanthene spacer, can cleave THF.³⁵

Furthermore, a closer inspection of the optimized geometrical structure of Al/G15-Rea and the free activation barrier (ΔG_ACT) of its corresponding TS (Al/G15-TS) indicates that a good linear relationship (ΔG_ACT = 13.02r – 25.09, correlation coefficient of 0.97) could be found when plotting the computed free activation barriers versus the separating Al···G15 distance (r) in Al/G15-Rea FLP (Figure 5).⁸² Therefore, the C–O bond length must be stretched to gain the best orbital overlap between the Al···G15 centers of Al/G15-Rea FLP and the C···O elements of THF. Moreover, the separating Al···G15 distance in the dimethylxanthene scaffold Al/G15-based FLP-type molecule can be used as a reliable, quantitative measure of the barrier height for its ring-opening reaction with THF.

Figure 5.

Plot of the free activation energy (ΔG_ACT) vs the Al···G15 distance (r) in the corresponding transition state (Al/G15-TS) at the B3LYP-D3(BJ)/def2-TZVP level.

IV.2. FMO and EDA-NOCV

First, we explored the frontier molecular orbitals (FMOs)⁸³ of G13/P-containing FLP molecules featuring the dimethylxanthene scaffold and THF using the B3LYP-D3(BJ)/def2-TZVP level of theory, whose HOMO and LUMO along with the corresponding energetics were collected (Figure 6). Figure 6 reveals that the HOMO of G13/P-Rea is primarily located on the LB (P) site, whereas the LUMO of G13/P-Rea mostly resides on the LA (G13) site. We also calculated energy gaps between the FMOs of G13/P-Rea and THF, when both reactants react with each other to undergo the ring-opening reaction (eq 1). Table 1 shows the energy gap between the HOMO of G13/P-Rea and the LUMO of THF, which is smaller (113.3–136.9 kcal/mol) than that between the HOMO of THF and the LUMO of G13/P-Rea (116.5–148.5 kcal/mol). Consequently, our above theoretical observations indicate that the predominant interaction should take place between the HOMO of G13/P-Rea and the LUMO of THF. The EDA-NOCV results schematically shown below will again confirm the above FMO evidence.

Figure 6.

Frontier molecular orbitals (HOMOs and LUMOs) and calculated energy levels (in kcal/mol) for the dimethylxanthene scaffold G13/P-Rea FLP-type compounds and THF. Hydrogens are omitted for clarity.

Table 1. Calculated Energy Differences (in kcal/mol, B3LYP-D3(BJ)/def2-TZVP) of the HOMO and LUMO for G13/P-Rea FLPs and THF^a.

system	energy difference |FLP (HOMO) – THF (LUMO)|	energy difference |THF (HOMO) – FLP (LUMO)|
B/P-Rea + THF	113.3	116.5
Al/P-Rea + THF	136.9	148.5
Ga/P-Rea + THF	132.5	145.8
In/P-Rea + THF	133.4	147.4
Tl/P-Rea + THF	126.8	142.7

^aAlso see Figure 6.

The results of EDA-NOCV taking G13/P-Rea and THF as fragments are presented in Table 2 to gain more information of the bonding situations in G13/P-TS. As mentioned in Section III, two bonding interaction models (singlet–singlet interaction and triplet–triplet interaction) for the closed-shell and open-shell fragments, respectively, were utilized in this study. The results of EDA provided stronger FLP–THF interactions between triplet G13/P-Rea and triplet THF (ΔE_INT = −188.8 – −180.8 kcal/mol), whereas the weak bonding was calculated between the singlet fragment G13/P-Rea and singlet THF (ΔE_INT = −67.8 – −60.4 kcal/mol). Selecting the bonding model that could better represent the studied set of systems is challenging. However, previous studies have shown that a simple way to select the bonding model is to evaluate the ΔE_Orb value for each scheme.⁸⁴ In general, the bonding model that produces the smallest ΔE_Orb value can be used as an efficient indicator to describe the bonding situation because it requires the least alteration in the electronic charge distribution to generate the electronic structure of the system. Table 2 demonstrates that the fragments G13/P-Rea and THF for the singlet–singlet model have smaller ΔE_Orb values (−149.1 to −79.1 kcal/mol), whereas the corresponding fragments for the triplet–triplet model have higher ΔE_Orb values (−359.5 to −242.6 kcal/mol). Therefore, the former model is suitable for discussing the bonding situations between G13/P-Rea and THF.

Table 2. Results of EDA-NOCV at the ZORA-B3LYP-D3(BJ)/TZ2P//B3LYP-D3(BJ)/def2-TZVP Level of G13/P-TS^a.

	B/P-TS		Al/P-TS		Ga/P-TS		In/P-TS		Tl/P-TS
fragments	B/P-Rea (S)+ THF (S)	B/P-Rea (T)+ THF (T)	Al/P-Rea (S) +THF (S)	Al/P-Rea (T) +THF (T)	Ga/P-Rea (S) +THF (S)	Ga/P-Rea (T) +THF (T)	In/P-Rea (S) +THF (S)	In/P-Rea (T) +THF (T)	Tl/P-Rea (S) +THF (S)	Tl/P-Rea (T) +THF (T)
ΔEINTb	–66.6	–186.9	–67.8	–183.0	–61.8	–188.8	–62.1	–180.8	–60.4	–184.1
ΔEPauli	246.6	393.6	170.1	357.7	173.2	302.9	151.6	261.2	139.8	200.5
ΔEElstatc	–145.9 (46.6%)	–202.8 (34.9%)	–125.8 (52.9%)	–193.7 (35.8%)	–125.3 (53.3%)	–163.9 (33.3%)	–115.7 (54.2%)	–151.1 (34.2%)	–105.8 (52.8%)	–126.7 (32.9%)
ΔEOrbc	–149.1 (47.6%)	–359.5 (61.9%)	–96.3 (40.5%)	–331.2 (61.3%)	–93.7 (39.9%)	–311.8 (63.4%)	–83.2 (38.9%)	–276.1 (62.5%)	–79.1 (39.5%)	–242.6 (63.1%)
ΔEOrb(1)d	–64.6 (43.3%)	–289.1 (80.4%)	–39.1 (40.6%)	–288.1 (87.0%)	–39.7 (42.4%)	–256.5 (82.3%)	–40.6 (48.9%)	–234.7 (85.0%)	–41.1 (51.9%)	–208.7 (86.0%)
ΔEOrb(2)d	–50.2 (33.6%)	–36.9 (10.3%)	–28.5 (29.6%)	–19.0 (5.7%)	–31.7 (33.8%)	–22.4 (7.2%)	–23.9 (28.7%)	–17.9 (6.5%)	–21.5 (27.2%)	–17.6 (7.2%)
ΔERestd	–34.4 (23.0%)	–33.4 (9.3%)	–28.6 (29.8%)	–24.1 (7.3%)	–22.3 (23.8%)	–32.8 (10.5%)	–18.6 (22.4%)	–23.5 (8.5%)	–16.6 (20.9%)	–16.3 (6.7%)
ΔEDisperc	–18.2 (5.8%)	–18.2 (3.1%)	–15.8 (6.6%)	–15.8 (2.9%)	–16.0 (6.8%)	–16.0 (3.3%)	–14.8 (6.9%)	–14.8 (3.3%)	–15.3 (7.7%)	–15.3 (4.0%)

^aFragments are G13/P-Rea and THF in singlet (S) and triplet (T) electronic states. All energy values are in kcal/mol.

^bΔE_INT = ΔE_Elstat + ΔE_Pauli + ΔE_Orb + ΔE_Disper.

^cThe values in parentheses offer the percentage contribution to the total attractive interactions (ΔE_Elstat + ΔE_Orb + ΔE_Disper).

^dThe values in parentheses offer the percentage contribution to the total orbital interactions (ΔE_ORB)

More valuable information is obtained from the breakdown of the ΔE_Orb term into pairwise orbital contributions, which links the numerical results to the frontier orbital model (Figure 6). The EDA-NOCV results for G13/P-TS in the S–S model (Table 2) indicate that the strongest orbital interaction is dominated by ΔE_Orb(1), which may contribute to the total orbital interaction energy by 40.6–51.9%. However, the next smaller orbital interaction, namely, ΔE_Orb(2), contributes about 27.2–33.8% to ΔE_Orb. Consequently, they yield 70.2–79.1% of the total ΔE_Orb. The profile of deformation densities (Δρ_n) associated with ΔE_Orb(n) is schematically represented in Figure 7, in which the direction of the charge flow is from the red to blue area in the color code. Figure 7 reveals that for the donor–acceptor interaction, ΔE_Orb(1) is the principal contributor of the orbital interaction, which corresponds to the transfer of electronic density from the lone pair of phosphorus to the empty σ* orbital of THF, i.e., the lone pair (P) → the empty σ*(C–O). On the contrary, ΔE_Orb(2) is the next contributor of the orbital interaction, which corresponds to the transfer of electronic density from the filled p−π orbital of oxygen to the vacant σ* orbital on the G13 element, i.e., the empty σ*(G13) ← filled p-π(O).

Figure 7.

Plots of deformation densities, Δρ(r), of the pairwise orbital interactions in G13/P-TS at the ZORA-B3LYP-D3(BJ)/TZ2P//B3LYP-D3(BJ)/def2-TZVP level. Also see Table 2. Hydrogen atoms are omitted for clarity.

In understanding the relative reactivity for the ring-opening reaction of THF by Al/G15-based FLP-mediated molecules, we first investigated the FMOs of Al/G15-Rea and THF with the B3LYP-D3(BJ)/def2-TZVP method, whose calculated results are collected in Figure 8. Figure 8 revels that the HOMO of Al/G15-Rea primarily resides on the LB G15 element, whereas the LUMO of Al/G15-Rea is located on the LA aluminum element. Moreover, we calculated the energy gaps between the HOMO of Al/G15-Rea and the LUMO of THF as well as those between the HOMO of THF and the LUMO of Al/G15-Rea, whose computational data are shown in Table 3. The latter data (136.6–153.9 kcal/mol) are obviously larger than the former data (108.1–137.6 kcal/mol; Table 3). Again, the EDA-NOCV diagram shown below will confirm the above FMO observations.

Figure 8.

Frontier molecular orbitals (HOMOs and LUMOs) and calculated energy levels (in kcal/mol) for the dimethylxanthene scaffold Al/G15-Rea FLPs and THF. Hydrogens are omitted for clarity.

Table 3. Calculated Energy Differences (in kcal/mol, B3LYP-D3(BJ)/def2-TZVP) of the HOMOs and LUMOs for Al/G15-Rea FLPs and THF^a.

system	energy difference |FLP (HOMO) – THF (LUMO)|	energy difference |THF (HOMO) – FLP (LUMO)|
Al/N-Rea + THF	108.1	136.6
Al/P-Rea + THF	135.9	148.5
Al/As-Rea + THF	137.6	149.2
Al/Sb-Rea + THF	133.7	146.5
Al/Bi-Rea + THF	128.4	153.9

^aAlso see Figure 8.

In uncovering the bonding nature of the interaction between the dimethylxanthene-linked Al/G15-FLP molecule and THF, we performed EDA-NOCV on their electronic structures to provide a strong basis for the mechanistic understanding. Similar to previous EDA-NOCV analyses for G13/P-TS cases shown in Table 2, the S–S and T–T models were applied to explore the bonding nature of the electronic structures of TSs (Al/G15-TS). As previously mentioned,⁸⁴ the size of the total orbital interactions (ΔE_Orb) can be used as an efficient indicator to justify the correct partitioning scheme because a low absolute ΔE_Orb value requires the least alteration in the electronic charge distribution to generate the electronic structure of the system. As shown in Table 4, 10 different fragmentation patterns, concerning the S–S and T–T models, are considered for all 5 calculated TSs, Al/G15-TS. Examining the strength of orbital interactions (Table 5), the S–S interaction provides lower Al/G15-TS values for ΔE_Orb than the T–T interaction. For example, Table 4 demonstrates that the ΔE_Orb values of all Al/G15-TS for the S–S interaction range from −119.9 to −96.3 kcal/mol, while those for the T–T model range from −331.2 to −298.4 kcal/mol. Consequently, the data in Table 4 indicate that the best representation of the bonding situation in all five Al/G15-TS is obtained by the S–S interaction. Notably, this theoretical finding is consistent with that of the previous five G13/P-TS systems shown in Table 2.

Table 4. Results of EDA-NOCV at the ZORA-B3LYP-D3(BJ)/TZ2P//B3LYP-D3(BJ)/def2-TZVP Level of G13/P-TS^a.

	Al/N-TS		Al/P-TS		Al/As-TS		Al/Sb-TS		Al/Bi-TS
fragments	Al/N-Rea (S)+ THF (S)	Al/N-Rea (S) +THF (S)	Al/P-Rea (S) +THF (S)	Al/P-Rea (T) +THF (T)	Al/As-Rea (S) +THF (S)	Al/As-Rea (T) +THF (T)	Al/Sb-Rea (S) +THF (S)	Al/Sb-Rea (T) +THF (T)	Al/Bi-Rea (S) +THF (S)	Al/Bi-Rea (T) +THF (T)
ΔEINTb	–65.7	–162.3	–67.8	–183.0	–69.6	–195.4	–71.1	–184.8	–77.3	–172.2
ΔEPauli	193.3	333.8	170.1	357.7	174.1	341.3	181.5	347.4	195.9	367.6
ΔEElstatc	–126.5(48.9%)	–179.5(36.2%)	–125.8(52.9%)	–193.7(35.8%)	–128.1(52.6%)	–194.4(36.2%)	–132.7(52.5%)	–199.2(37.4%)	–140.5(51.4%)	–210.0(38.9%)
ΔEOrbc	–114.2(−114.2%)	–298.4(−298.4%)	–96.3(40.5%)	–331.2(61.3%)	–100.8(−100.8%)	–327.6(−327.6%)	–106.7(−106.7%)	–319.7(−319.7%)	–119.9(−119.9%)	–316.9(−316.9%)
ΔEOrb(1)d	–47.4(41.5%)	–256.5(86.0%)	–39.1(40.6%)	–288.1(87.0%)	–41.7(41.4%)	–282.2(86.1%)	–45.7(42.8%)	–272.0(85.1%)	–54.3(45.3%)	–263.6(83.2%)
ΔEOrb(2)d	–34.1(29.9%)	–17.3(5.8%)	–28.5(29.6%)	–19.0(5.7%)	–29.6(29.4%)	–20.2(6.2%)	–30.7(28.8%)	–21.3(6.7%)	–32.6(27.2%)	–24.3(7.7%)
ΔERestd	–32.7(28.6%)	–24.6(8.2%)	–28.6(29.8%)	–24.1(7.3%)	–29.5(29.3%)	–25.2(7.7%)	–30.2(28.3%)	–26.3(8.2%)	–33.0(27.5%)	–29.0(9.2%)
ΔEDisperc	–18.3(7.0%)	–18.3(3.7%)	–15.8(6.6%)	–15.8(2.9%)	–14.8(6.1%)	–14.8(2.8%)	–13.2(5.2%)	–13.2(2.5%)	–12.8(4.7%)	–12.8(2.4%)

^aFragments are Al/G15-Rea and THF in singlet (S) and triplet (T) electronic states. All energy values are in kcal/mol.

^bΔE_INT = ΔE_Elstat + ΔE_Pauli + ΔE_Orb + ΔE_Disper.

^cThe values in parentheses offer the percentage contribution to the total attractive interactions (ΔE_Elstat + ΔE_Orb + ΔE_Disper).

^dThe values in parentheses offer the percentage contribution to the total orbital interactions (ΔE_Orb).

Table 5. Energy Decomposition Analysis for the Ring-Opening Reaction of THF by Dimethylxanthene Backbone G13/P-TS^a,b.

entry	B/P-TS	Al/P-TS	Ga/P-TS	In/P-TS	Tl/P-TS
ΔEACTb,c	13.9	–3.9	14.6	17.8	25.0
ΔEDEF,THF	46.7	28.8	38.9	40.9	44.1
ΔEDEF,G13/P-Rea	34.8	35.1	37.5	39.0	41.3
ΔEINT	–66.6	–67.8	–61.8	–62.1	–60.4

^aAt the ZORA-B3LYP-D3(BJ)/TZ2P//B3LYP-D3(BJ)/def2-TZVP level.

^bAll in kcal mol^–1.

^cΔE_ACT = ΔE_DEF,THF + ΔE_{DEF,G13/P-Rea} + ΔE_INT.

Using the NOCV⁶¹⁻⁶⁴ method, the crucial information can be obtained from the further decomposition of ΔE_Orb into pairwise orbital interaction, ΔE_Orb(n). As shown in Table 4, in five Al/G15-TSs utilizing the S–S interaction, only two dominant contributions (ΔE_Orb(1) and ΔE_Orb(2)) are obtained, which provide at least 70% to ΔE_Orb. In addition, one intriguing feature for NOCV analyses is that the charge migration associated with pairwise orbital interactions can be schematically represented as deformation densities Δρ. Consequently, ΔE_Orb(1) and ΔE_Orb(2) can be identified using the associated deformation densities (Δρ₁ and Δρ₂, respectively) and the connected occupied and vacant fragment orbitals (Figure 9). Notably, the color code indicates that the charge flow is red → blue. Figure 9 shows that the strongest orbital contribution in Al/G15-TS is obtained from the donation of the HOMO of Al/G15-Rea (i.e., the LP of LB G15 center) to the LUMO of THF (i.e., the vacant C–O σ* orbital), with ΔE_Orb(1) ranging from −54.3 to −39.1 kcal/mol. Moreover, the second strongest orbital interaction ΔE_Orb(2) = −34.1 – −28.5 kcal/mol is obtained from the donation of the HOMO of THF (i.e., the filled p−π orbital on O) to the LUMO of Al/G15-Rea (i.e., the vacant σ* orbital on LA Al center). In other words, the EDA-NOCV result indicates that the FLP-to-THF forward bonding (i.e., ΔE_Orb(1)) plays a significant role in determining the contribution of the orbital interaction to the bonding conditions between Al/G15-Rea and THF, while the THE-to-FLP back bonding (i.e., ΔE_Orb(2)) plays a minor role in such bonding interactions. From the theoretical analyses for both G13/P-TS and Al/G15-TS cases, it is therefore known that the theoretical information based on EDA-NOCV can be used to comprehensively understand the bonding situations in the ring-opening reaction of THF by the dimethylxanthene backbone Al/G15-based FLP-related molecules.

Figure 9.

Plots of deformation densities, Δρ(r), of the pairwise orbital interactions in Al/G15-TS at the ZORA-B3LYP-D3(BJ)/TZ2P//B3LYP-D3(BJ)/def2-TZVP level. Also see Table 4. Hydrogen atoms are omitted for clarity.

IV.3. Origin of Activation Energies Investigated by ASM

In obtaining more information about the origin of activation barriers for the ring-opening reactions of THF by the G13/P-Rea FLP-associated molecule, ASM has been utilized in the present work. Notably, the ASM involves the decomposition of the electronic reaction barrier (ΔE_ACT) into the deformation energy (ΔE_DEF,THF and ΔE_{DEF,G13/P-Rea}; Scheme 3), which is associated with the rigidity of the reactants and the interaction energy (ΔE_INT) among deformed fragments, whose calculated results are presented in Table 5 and Figure 10. Figure 10 shows that the deformation energy of THF (ΔE_DEF,THF) is a decisive factor in determining the reactivity trend in such ring-opening reactions of THF by G13/P-Rea FLPs. This phenomenon can be understood when G13/P-Rea and THF approach each other. In obtaining good orbital overlaps between the carbon element of THF and the phosphorus element of G13/P-Rea and between the oxygen element of THF and the G13 element of G13/P-Rea, the C–O bond of THF must stretch to match the separating distance between G13 and P in G13/P-Rea. As shown in Scheme 3, the cleavage of the C–O bond in THF accompanies the formation of C–P and O–G13 chemical bonds. Our B3LYP results shown in Figure 3 demonstrate that G13/P-Rea has the longest separating B(LA)···P(LB) distance in the G13/P-Rea FLPs. Thus, the C–O bond in THF is elongated to perform effective orbital overlaps with the B/P-Rea FLP. Consequently, ΔE_DEF, THF of B/P-TS becomes the largest (Table 5 and Figure 10). This phenomenon leads to the highest activation barrier for B/P-TS when B/P-Rea undergoes the ring-opening reaction with THF.

Scheme 3. Schematic Representation of the Ring-Opening Reaction of Dimethylxanthene Backbone G13/P-Rea with THF.

Figure 10.

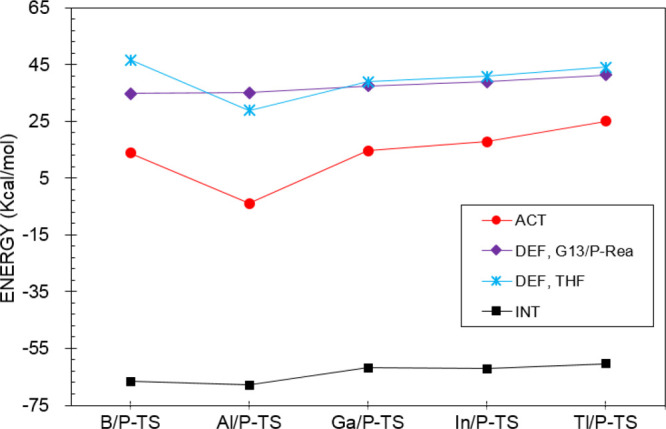
Plot of energy decomposition analysis of ΔE_ACT for the ring-opening reactions of G13/P-Rea with THF. Values are taken from Table 5.

Furthermore, our B3LYP computational results shown in Figure 3 indicate that there was an increasing trend in the calculated C–O bond of G13/P-TS: Al/P-TS (35.1%) < B/P-TS (35.4%) < Ga/P-TS (36.5%) < In/P-TS (38.1%) < Tl/P-TS (39.8%). This result is relative to that in the initial THF (1.431 Å). Notably, the trend for the elongated C–O bond length in the geometry of G13/P-TS indicates its corresponding barrier height. Our DFT results shown in Figure 3 and Table 5 demonstrate that the reaction barrier (kcal/mol) increases as follows: Al/P-TS (−3.9) < B/P-TS (13.9) < Ga/P-TS (14.6) < In/P-TS (17.8) < Tl/P-TS (35.0). The aforementioned theoretical evidence is consistent with the Hammond postulate,⁸⁵ which indicates that an early TS would be accompanied by a smaller barrier height. Accordingly, our theoretical evidence suggests that the key factor affecting the activation energy of G13/P-TS is highly dependent on the structural deformation energy of THF during its ring-opening reaction.

Again, the detailed ASM analyses of two representative cases (i.e., B/P-TS and Al/P-TS) were performed along the reaction profile to elucidate the different reactivity of G13/P-Rea toward the ring-opening reaction of THF.⁸⁶ The ASM results shown in Figure 11 reveal that a smaller ΔE_ACT for Al/P-TS can be attributed to the low deformation energy of the THF fragment (ΔE_DEF,THF). This finding is consistent with previous examinations shown in Table 5 and Figure 10. For example, Figure 11 shows that the ΔE_{DEF,G13/P-Rea} value (kcal/mol) of B/P-TS and Al/P-TS was 33.1 and 30.5 at the C–O distance of 1.822 Å, whereas the interaction energy (kcal/mol) of B/P-TS and Al/P-TS was −45.9 and −49.9, respectively. The two aforementioned energy parameters are similar to each other; therefore, ΔE_{DEF,G13/P-Rea} and ΔE_INT cannot influence the barrier height. The ΔE_DEF,THF (kcal/mol) value for Al/P-TS (14.8) and B/P-TS (25.6) can affect their respective activation energies, that is, Al/P-TS (−4.6) and B/P-TS (12.8).

Figure 11.

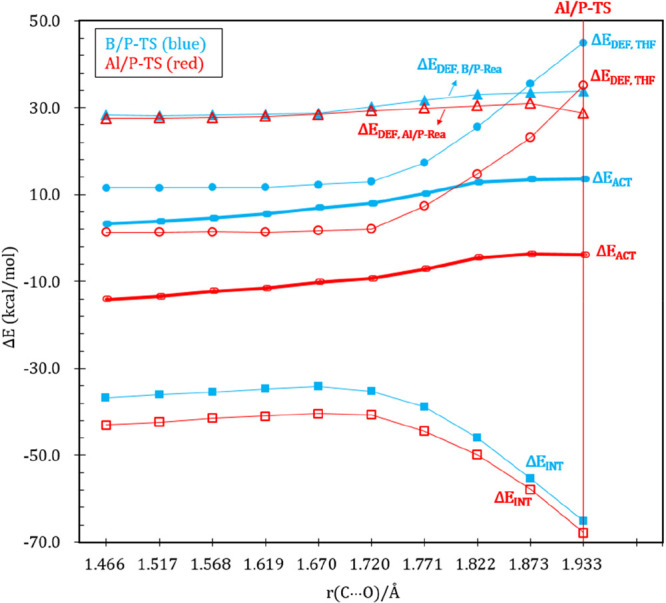
Comparative activation strain diagrams for the ring-opening reactions of THF involving dimethylxanthene backbone B/P-TS (blue lines) and Al/P-TS (red lines) along the reaction coordinate projected onto the C···O bond distance, calculated at the ZORA-B3LYP-D3(BJ)/TZ2P//B3LYP-D3(BJ)/def2-TZVP level.

We again applied the ASM approach to the ring-opening reaction of THF involving the Al/G15-based FLP-associated molecules bearing the dimethylxanthene scaffold to understand the reactivity trend (Scheme 4, Table 6, and Figure 12). Similar to the G13/P-TS cases discussed earlier, the activation energy (ΔE_ACT) can be composed of two deformation energies (ΔE_DEF, THF + ΔE_{DEF,Al/G15-Rea}) and the interaction energy (ΔE_INT). As shown in Figure 12, the deformation energy of THF could be a decisive factor in influencing the barrier heights for such ring-opening reactions. As shown in Figure 9, the separating Al(LA)···N(LB) distance in the Al/N-Rea FLP species is the largest (4.193 Å). In obtaining a better orbital overlap between THF and the Al/N-Rea FLP, a C–O bond of THF must be elongated, and the deformation energy of THF (ΔE_DEF,THF) must be increased. This technique, in turn, leads to the highest reaction barrier for the ring-opening reaction of THF by the Al/N-Rea FLP with a dimethylxanthene scaffold (Figure 4). Moreover, based on the calculated geometrical structure of Al/G15-TS shown in Figure 4, the broken C–O bond length of the THF fragment increases as Al/P-TS (35.1%) < Al/As-TS (39.9%) < Al/Sb-TS (45.7%) < Al/Bi-TS (56.1%) < Al/N-TS (74.4%), which is relative to that of the original THF (1.431 Å). This structural trend is consistent with the trend of free reaction barriers for Al/G15-TS as discussed earlier. Therefore, the aforementioned theoretical finding is consistent with the Hammond postulate,⁸⁵ which indicates that “the more reactant-like the TS, the smaller its activation barrier”.

Scheme 4. Schematic Representation of the Ring-Opening Reaction of Dimethylxanthene Backbone Al/G15-Rea with THF.

Table 6. Energy Decomposition Analysis of the Ring-Opening Reaction of THF by Dimethylxanthene Backbone Al/G15-Rea.

entry	Al/N-TS	Al/P-TS	Al/As-TS	Al/Sb-TS	Al/Bi-TS
ΔEACTa,b,c	14.9	–3.9	–1.7	–0.2	1.2
ΔEDEF,THF	54.4	28.8	40.7	47.0	57.6
ΔEDEF,Al/G15-Rea	26.2	35.1	27.3	23.8	20.9
ΔEINT	–65.7	–67.8	–69.6	–71.1	–77.3

^aAt the ZORA-B3LYP-D3(BJ)/TZ2P//B3LYP-D3(BJ)/def2-TZVP level.

^bAll in kcal mol^–1.

^cΔE_ACT = ΔE_DEF,THF + ΔE_{DEF, Al/G15-Rea} + ΔE_INT.

Figure 12.

Plot of energy decomposition analysis of ΔE_ACT for the ring-opening reactions of Al/G15-Rea with THF. Values are taken from Table 6.

Two representative systems, Al/N-TS and Al/P-TS, have been selected for theoretical analysis by using a detailed ASM approach, whose calculated results are collected in Figure 13.⁸⁶ Our B3LYP investigations clearly reveal that only the deformation energy of THF (ΔE_DEF,THF) plays a significant role in influencing barrier heights of the ring-opening reactions of THF by the Al/G15-based FLP-type molecules featuring a dimethylxanthene backbone. For example, Figure 13 indicates that at a C–O distance of 1.822 Å the ΔE_{DEF,G13/P-Rea} (kcal/mol) values of Al/N-TS and Al/P-TS are approximately 10.3 and 30.5, whereas the interaction energies (kcal/mol) of Al/N-TS and Al/P-TS are −30.6 and −49.9, respectively. The sums of the two aforementioned energy parameters (ΔE_{DEF,G13/P-Rea} + ΔE_INT) are similar to each other. Consequently, ΔE_{DEF,G13/P-Rea} and ΔE_INT cannot effectively control the reaction barrier. Only the ΔE_DEF,THF (kcal/mol) values for B/P-TS (24.3) and Al/P-TS (14.8) can affect their respective activation energies, that is, B/P-TS (4.1) and Al/P-TS (−4.6). Accordingly, the above theoretical observation is in good agreement with the findings shown in Table 6 and Figure 12.

Figure 13.

Comparative activation strain diagrams for the ring-opening reactions of THF involving the dimethylxanthene backbone Al/N-TS (black lines) and Al/P-TS (red lines) along the reaction coordinate projected onto the C···O bond distance, calculated at the ZORA-B3LYP-D3(BJ)/TZ2P//B3LYP-D3(BJ)/def2-TZVP level.

V. Conclusions

The present study reports on the theoretical investigations of the chemistry of the THF ring-opening reaction by intramolecular G13/G15-FLPs based on the dimethylxanthene scaffold. Several theoretically sophisticated methods, including the FMO theory, ASM, and the EDA–NOCV approach, have been utilized in this work to gain insights into the origin of activation barriers and reactivity trends. Several crucial conclusions can be drawn as follows:

• (1)Our theoretical examinations predict that in the intramolecular dimethylxanthene-linked G13/P-Rea FLP-assisted molecules, only Al/P-Rea FLP evidently is energetically favorable to undergo the ring-opening reaction of THF.
• (2)Our calculated evidence indicates that in Al-based and G15-based Al/G15-Rea FLP-related compounds featuring the dimethylxanthene scaffold, only Al/P-Rea FLP can be energetically feasible to cleave THF without difficulty.
• (3)By comparing all ring-opening reactions of THF studied in this work, our B3LYP analyses demonstrate that the dimethylxanthene backbone Al/G15-Rea FLPs can undergo the ring-opening reaction of THF more easily than the congener G13/P-Rea FLPs since the former has a lower reaction barrier and a larger exergonicity than the latter.
• (4)Our EDA analyses indicate that the donor–acceptor model rather than the electron-sharing model controls the bonding natures of their TSs. Furthermore, it is known with some certainty that both forward and backward donations, which are widely used to explain bonding scenarios in organometallic chemistry, will be important. In the past computational studies, this is a quantity that could be difficult to pin down. This work is the first theoretical study to prove quantitatively that the two donations contribute differently to chemical bonding. Our theoretical findings quantitatively demonstrate that the forward donation is the FLP-to-THF interaction (a LP(G15) → σ*(C–O)), which predominantly governs such ring-opening reactions of THF by the dimethylxanthene backbone G13/G15-based FLPs. On the other hand, the back-bonding component is the THF-to-FLP interaction (an empty σ*(G13) ← filled p−π(O)), which plays a minor role in such bonding situations.
• (5)It is already known that the size of THF is smaller than that of the dimethylxanthene-based G13/G15-based FLP. Our ASM study clearly indicates that when G13/G15-FLP and THF are close enough to each other to react, the C–O bond of THF must be elongated to effectively overlap with G13/G15-FLP. As a result, the longer the C–O bond is stretched, the more the structural deformation energy of THF will be increased. Namely, when they form a transition state, the geometric structure of THF would be greatly deformed, resulting in its deformation energy being larger. This, in turn, becomes the key factor in determining the whole activation energy. Accordingly, our B3LYP findings reveal that in the ring-opening reaction of THF by G13/P-Rea and Al/G15-Rea FLPs bearing the dimethylxanthene scaffold, the separating LA···LB distance in such FLP-type reactant species can be taken as a diagnostic tool to estimate the relative activation barriers.
• (6)Our DFT results shown in this work indicate that the ring-opening reaction of THF by the G13/G15-Rea FLPs is consistent with Hammond’s postulate. That is, the earlier the TS of the chemical reaction arrives, the smaller the activation energy.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.2c06194.

• Sums of electronic and thermal free energies (PDF)

Author Contributions

Z.-F.Z. conducted all of the theoretical computations and analyzed the results. M.-D.S. supervised the research activities and contributed to the manuscript preparation. Both authors regularly discussed the progress of the research, reviewed the manuscript, and gave approval for the final version.

The authors declare no competing financial interest.