Abstract
Identification of the most stable structure(s) of a system is a prerequisite for the calculation of any of its properties from first-principles. However, even for relatively small molecules, exhaustive explorations of the potential energy surface (PES) are severely hampered by the dimensionality bottleneck. In this work, we address the challenging task of efficiently sampling realistic low-lying peptide coordinates by resorting to a surrogate based genetic algorithm (GA)/density functional theory (DFT) approach (sGADFT) in which promising candidates provided by the GA are ultimately optimized with DFT. We provide a benchmark of several computational methods (GAFF, AMOEBApro13, PM6, PM7, DFTB3-D3(BJ)) as possible prescanning surrogates and apply sGADFT to two test case systems that are (i) two isomer families of the protonated Gly-Pro-Gly-Gly tetrapeptide (Masson A.; et al. J. Am. Soc. Mass Spectrom. 2015, 26, 1444−1454) and (ii) the doubly protonated cyclic decapeptide gramicidin S (Nagornova N. S.; et al. J. Am. Chem. Soc. 2010, 132, 4040−4041). We show that our GA procedure can correctly identify low-energy minima in as little as a few hours. Subsequent refinement of surrogate low-energy structures within a given energy threshold (≤10 kcal/mol (i), ≤5 kcal/mol (ii)) via DFT relaxation invariably led to the identification of the most stable structures as determined from high-resolution infrared (IR) spectroscopy at low temperature. The sGADFT method therefore constitutes a highly efficient route for the screening of realistic low-lying peptide structures in the gas phase as needed for instance for the interpretation and assignment of experimental IR spectra.
1. Introduction
Understanding the correlation between composition, structure, properties, and functional roles of biomolecules is at the very heart of biochemistry and biophysics. The first step in this hierarchy, i.e., the connection between composition and structure, has thus attracted enormous interest both in the case of, e.g., entire proteins3−6 and for smaller peptides.7−10 The latter are especially interesting in view of reducing the complexity of natural systems and studying smaller-size models under controlled conditions. Furthermore, peptides made of few amino acids have attracted much attention in recent years thanks to their promising and wide scope of applications, be it in the fabrication of biomaterials,11 in the engineering of biomimetic compounds for catalysis,12 or in drug design.13 Indeed, in addition to contributing to physiological health,14 peptides have brought about conclusive benefits as anti-infective drugs due to their antimicrobial activity,15−17 leading to intense efforts in therapeutics development with peptidomimetic systems.18,19
The study of gas-phase peptides alone or with a defined number of solvent molecules constitutes a first step toward the understanding of the in vivo properties and allows for a differential picture of well-controlled intramolecular interactions separated from their combination with condensed-phase and intermolecular effects. Moreover, in some cases, the experimentally produced gas-phase systems are able to retain solution-phase features so that scrutinizing native forms in the gas phase and at near zero temperature can provide valuable insight into remanent condensed-phase interactions.1,20,21
Experimentally, advances over the past decade have coupled laser desorption and supersonic molecular beam cooling to capture IR spectra of neutral biomolecules in the gas phase.22,23 Alternatively, combinations of electrospraying, ion-mobility selection, mass spectrometry, and cryogenic ion traps were reported to separate between conformational families of charged molecules prior to, e.g., IR measurements.1,22,24 In particular, such experiments performed at cryogenic temperatures have been able to produce vibrationally resolved and conformer-selective measurements, but due to the high intrinsic complexity, the identification of the underlying structures and the full assignment of the observed IR spectra can only be achieved with the support of computational methods. In turn, the experimental low-temperature data provide highly sensitive benchmarks for the assessment of the performance of computational methods for biorelevant systems where the availability of accurate quantitative data is often sparse and hard to obtain. Therefore, the present work also illustrates a sensitive test case of the complementarity between simulations and experiments.
At low temperature, conformers are expected to occupy the thermodynamically most stable configuration on the PES or at least some kinetically trapped low-lying metastable states. Therefore, from a computational perspective relevant local minima (LM) are usually searched on the rugged, high-dimensional PES and theoretical IR spectra, commonly computed with DFT including exact exchange at the hybrid level for sufficient accuracy, are compared to the experimentally observed spectra.1,25−30
The exploration of the PES is typically performed with molecular dynamics (MD), relying on classical force fields, semiempirical, or first-principles potentials in combination with replica-exchange and/or simulated annealing (SA) to enhance sampling.22−24,27,31−35 Though highly successful in many cases,1,29,30 this approach based on traditional quantum chemical tools suffers from severe drawbacks and limitations: On one hand, the quantitative identification of the lowest energy structures at low temperature poses stringent accuracy demands to provide a correct energetic ordering in the 0–2.5 kcal/mol observation range for biomolecules that are characterized by complex interatomic and noncovalent interactions.31 This imposes the use of higher level computational methods for the determination of realistic relative energetics,24,34,36 while force fields or semiempirical approaches often fail at providing the necessary accuracy.24,31,37,38 On the other hand, even small peptides contain of the order of tens to hundreds of atoms, making higher level first-principles calculations time-consuming for all but the smallest molecules. In particular, using first-principles MD requires long simulation times with ten thousands of energy and force evaluations for typical simulated annealing runs and, in spite of multiple runs with different starting geometries and varying simulated annealing protocols (in terms of highest temperature, simulation length at Tmax and subsequent cooling rate), can potentially fail to recover the most stable structures due to the presence of high-energy barriers on the PES.23,35 Even when successful, DFT-MD based identifications of the lowest-energy structures observed in experiments can take several months and might only be practicable for larger systems when introducing experimental information to guide the search.24,30
Here, we tackle the task of rapidly finding the global minimum (GM) as well as low-lying LM, with the help of surrogate based genetic algorithms (GA). By leveraging evolutionary mechanisms, GAs have shown efficiency in solving highly nonlinear and complex global optimization problems39−41 where deterministic or analytical methods fail at finding correct solutions or efficiently search enormous solution spaces. In particular, the capabilities of GAs were for instance found to surpass SA in the search for ground state fullerene clusters42 or perform better at protein structure predictions compared to Monte Carlo approaches on simplified energy models.43−45 GAs are also among the most CPU-/search-efficient methods to computationally identify low-energy conformations when applied to small organic molecules46−48 or peptides in the gas phase.37,49,50 For example, they outperformed systematic and random search methods for the mycophenolic acid drug-like ligand and were more efficient than replica-exchange MD for dipeptides in terms of low-energy conformational coverage (respectively within 5 and 10 kcal/mol from the GM).51
Despite this algorithmic gain, the predictive power of such evolutionary methods evidently depends on whether the energy function is able to faithfully describe the relevant physical interactions. For example, up to now, the lack of fast and sufficiently accurate (free) energy models52−56 explains why ab initio protein folding predictions have met little success in recovering secondary and tertiary structures in close agreement with native-like conformations.45,55,57,58 In that case, the enormous space defined by the number of structural degrees of freedom severely challenges search engines, so that protein folding approaches often privilege sequence homology5,59 or machine learning6,60 algorithms. However, in the mid-size range of peptidic systems, GA applications have a lot of potential if tractable energy models with sufficient accuracy exist.
Due to the large number of energy evaluations required, GAs for peptide folding are commonly used in conjunction with classical force fields37,46−49 or expedient semiempirical methods,50 at the price of loosing accuracy so that identified stable structures might correspond to false LM introduced by the energy function and relative energies between different conformers might be far off experimental observations.37,46,48 As a potential remedy, GA optimizations were recently combined with DFT local relaxations.51 However, this approach was rather limited to short GA instances of dipeptides and molecules up to ∼40 atoms so that applications of this fully DFT-based approach to larger systems are currently compromised even when resorting to massively parallel computational resources.
We rather explore here the possibility of using less accurate surrogate models for a faster (pre)evaluation of the PES and demonstrate that a judicious choice of surrogate level can provide satisfactory knowledge for establishing a pool of low-energy candidates, to be ultimately refined at a first-principles level. This seems also reasonable in view of the fact that relative energies and vibrational frequencies can differ markedly upon changing the level of theory, DFT functional, or basis set1,36,38,61 and that there exists a priori no exact, tractable and universal baseline for the PES to drive the optimization with.
To anticipate our results, it turns out that while the surrogate LM geometries are in general very close to their first-principles analogues for all lower-level methods considered here, the energy hierarchy varies significantly between PES approximations and can considerably deteriorate the search. Nevertheless, our results show that, in combination with a state-of-the-art polarizable force field, the approach is highly successful in generating surrogate low-lying minima that match experimental structures for the two test case systems including two isomers of the protonated Gly-Pro-Gly-Gly tetrapeptide (referred to as GPGG herein) and the doubly protonated gramicidin S cyclodecapeptide. This encourages the use of sGADFT as a straightforward, fast, and automatized way to identify the lowest energy structures of peptides in the gas phase.
In what follows, we first describe the reference test systems in Section 2, along with our GA implementation. After presenting the computational details and the investigated surrogate models in Section 3, we provide a quantitative assessment of their cost-accuracy performance on a test set of GPGG structures in Section 4.1. Respective GA results are then presented in Sections 4.2 and 4.3, and their computational footprint finally is reported in Section 4.4, before drawing conclusions in Section 5.
2. Methods
2.1. Reference Data
To test the performance of the sGADFT approach, we have chosen two reference systems of different size for which the lowest energy structures have previously been determined via a combination of high-resolution conformer-selective IR spectroscopy paired with electrospray ionization and cryo-cooled ion traps, supported by a traditional computational approach (as described above) to determine the most stable structures. The first test case system comes from the work of Masson et al., who leveraged ion-mobility techniques to identify and separate two conformational families of the protonated GPGG peptide (Figure 1) with different collisional cross-sections, and acquired respective spectroscopic data.1 Major conformers of each family were determined as involving either the cis or trans isomers of the proline residue.
Figure 1.
Schematic structure of the 39-atom protonated GPGG peptide in its cis (ω = 0) isomer, shown with the respective backbone dihedrals employed for GA optimization.
The 3D structure determination was previously established by running SA ab initio MD starting from random cis/trans structures extracted from the Protein Data Bank (PDB).62 The search was conducted at the DFT level with the B3LYP functional63 and a 6-31G basis set, with extensive trials of heating temperatures and annealing rates for total simulation times of several tens to hundreds of picoseconds. After this first exploration, isomers were structurally and energetically selected and locally relaxed at the B3LYP/6-31G(d,p) level of theory to provide a final set of 13 cis and 29 trans energetically low-lying candidate structures, which serve as the reference pool in this work. Comparison of theoretical harmonic vibrational frequencies (at B3LYP/6-311++G(d,p) level) including isotopic substitutions with the measured spectra clearly confirmed that the lowest-energy configuration of each family of these two sets corresponded indeed to the most abundant of the observed conformers.
Similarly, in 2010, Nagornova et al. published highly resolved IR spectra of the doubly protonated gramicidin S peptide (Figure 2) featuring a d rather than an l enantiomer of a phenylalanine.2 Since the experimental data indicated some symmetry (C2) for the major conformer, an SA exploration of the high-dimensional PES could be performed by imposing structural constraints over multiple FF99SB64 and FF02polEP65 force field trajectories.30 The 3D structure was finally determined by calculating B3LYP/6-31G(d,p) spectra of few candidates.
Figure 2.
Schematic structure of the 176-atom doubly protonated gramicidin S cyclic decapeptide, shown with respective backbone and side-chain dihedrals employed for optimization.
2.2. Genetic Algorithms
Genetic algorithms (GAs) are global optimizers that belong to the larger class of evolutionary algorithms rooted in the mechanisms of biological evolution. As metaheuristic search engines, GAs operate over populations of individuals that each represent a candidate solution of the optimization problem and are progressively modified toward (near-) optimal solutions. GAs are powerful tools when it comes to hard optimization problems for which the solution space is supposedly noisy, unsteady, and involves constraints or many LM as well as many degrees of freedom that do not allow simpler local optimizers or enumeration searches to perform efficiently.
Figure 3 depicts a schematic representation of the GA employed in this work built from conventional genetic operations. Generally, first individuals are randomly generated, if no other information or constraints are known, to ensure diversity and prevent any other bias in the solution space originating from the initialization. At each generation (iteration), GA evolves solution individuals with biologically inspired operators. Each individual is assigned a fitness that serves as a metric to drive the genetic evolution of the algorithm. Most of the time, this fitness function is nothing else than the objective function of the optimization problem.
Figure 3.
Schematic representation of the GA cycle as implemented in EVOLVE for this study.
Following the Darwinian principles of mate selection and survival of the fittest, individuals are stochastically selected based on relative fitnesses in the population and give birth to children individuals through crossover of genes. Genes are encoding fragments of a tentative solution that depend on the problem at hand and that must be carefully designed by the practitioner. Examples of such encodings or representations are bit strings, symbols, or vectors that contain relevant information to be transferred from one generation to the next. Children solutions are then randomly mutated to maintain diversity and possibly extend the search over yet uncovered regions of the solution space. Finally, elitism consists of replacing some of the current less-fit individuals with the best individuals of the previous generation, in order to maintain the best traits discovered so far over the generations. Such a selection-crossover-mutation-elitism cycle hence simulates an artificial evolution and propagates relevant and optimal features of the representations across GA iterations. The algorithm terminates after a fixed number of generations or when improvement of the fitness function stagnates over several iterations.
Due to the very nature of the initialization, selection, and mutation, GAs are intrinsically stochastic and provide statistical results that hopefully contain the GM of the optimization problem. In the following, our GA implementation toward the optimization and generation of low-lying peptide geometries is described.
2.3. Optimization of Peptide Conformations with EVOLVE
All of the work presented in this article was performed with the in-house implementation of a single-objective and multiobjective GA engine called EVOLVE.66,67 As a versatile and modular Python code for peptide and protein sequence optimization, EVOLVE was successful in the optimization of a biomimetic peptidic scaffold for the fixation of CO268 and in the engineering of a highly thermostable metalloprotein.69 It also served in the elaboration of training sets for enhanced machine learning models of molecular properties.70
For the compositional optimizations mentioned above, side chain rotamer libraries were used in order to restrict the search space to discrete sets of residue conformations. In contrast here, EVOLVE is extended into a complete in silico optimizer of a peptide structure (including both the backbone conformation and side chain dihedrals) with a fixed amino acid sequence whose degrees of freedom therefore cover a huge space. In the gas phase at near zero temperature, the objective function is nothing more than the potential energy as a function of atomic coordinates, meaning that the lower the energy (fitness), the better the structure. Such an “ab initio” peptide folder is capable of exploring the low-lying LM or reaching the GM of the PES, which is particularly relevant for assigning 3D structures to measured IR spectra.1,22,27,29,30 In addition, it also provides an exhaustive search that enables a quality test of the method used to describe the PES.
In practice, genetic operators have parameters that are fixed before execution, which strongly influence the efficiency and reliability of the algorithm. The optimal choice of these parameters is a multivariate problem in itself and depends on the forms of the operator, the problem to be solved, and the characteristics of the fitness function.71 We studied the effect of several parameters such as population size, crossover probability, or mutation rate and selected a set for which independent runs progress steadily toward the lowest energies in a small number of iterations. In what follows, we describe the specificities of the algorithm (Figure 3) and list the corresponding parameters in Section 3.1.
2.3.1. Representation
Each individual or tentative solution of the optimization problem is a peptide conformation. Translated in a GA framework, each geometry is represented by the backbone ϕ and ψ torsional angles as well as possible side chain torsional angles χ. The genes of one individual composed of N amino acids with respective k numbers of side chain dihedrals are therefore
| 1 |
encoded into a single numerical vector Θ that defines the internal coordinates of the optimizer. The specific torsional angles used for the optimization of the two test systems studied herein are indicated in Figures 1 and 2. This choice of representation, inspired by the underlying characteristics of the Ramachandran plot,72 was already exploited in previous evolutionary methods37,51 and has the advantage of easily defining genetic operators that preserve the peptide atomic connectivity.
2.3.2. Initialization
The information about the amino acid sequence, the atom types, and atomic connectivity are provided to EVOLVE in the form of a PDB file which serves as an initial template. From this, a Θi representation of size K is randomly generated in which each individual i of the first population has a uniform distribution of its torsional angles such that Θki ∈ [−180°,180°) for k = 1, ..., K. Technically, such modifications of the peptide structures are performed with the help of the Open Babel toolbox.73
2.3.3. Fitness Function
At each generation, the ability of an individual to be among the lowest energy configurations is assessed by calculating its potential energy. In order to avoid the exploration of highly improbable nonphysical structures, e.g., with too close distances or steric overlaps, initial local relaxations are performed before assigning the energy. Indeed, the individuals modified by the genetic operators can be very distorted and far from LM of the fitness function, which prevents the algorithm from progressing rapidly to low energies by stagnation or by bouncing off the PES,49 in a manner quite similar to a gradient descent with a high learning rate. To improve this, the search space is consequently focused on the physically more meaningful regions that involve LM.
The algorithm thus operates at two levels: a coarser (and wider) exploration of the configurational space driven by genetic operators acting on Θ, refined by local optimizations of the Cartesian coordinates R, as illustrated in the central graph of Figure 3. The relaxed structures R̃ and energies are stored to construct the pool of putative LM and corresponding fitnesses and are further translated back to their torsional representations Θ̃ that are updated before selection:
 |
2 |
The computational cost is determined by the number of fitness function calls (equal to the number of generations times the population size) times the cost for a single fitness evaluation. The latter depends crucially on the level of the surrogate method, while the choice of the PES model (and thus the fitness function) is critical in order to reliably reflect experimental results. Thus, compromises have to be made between cost and accuracy. EVOLVE is currently interfaced with several external software programs (Gaussian,74 Amber,75 OpenMM76) that can be used for local gradient based optimizations at different levels of theory. Note that the modular structure of EVOLVE and the use of the Atomic Simulation Environment (ASE) library77 to interface with external codes greatly facilitate the integration of new fitness evaluators. Finding an appropriate surrogate model for the PES in terms of speed and accuracy for the relative energetics is investigated in Section 4.1. For the GA applications envisioned here, it is not absolutely necessary to reproduce the PES in every detail but for a given surrogate model to be satisfactory, it has to be able to drive the GA optimizations toward regions with a promising set of candidates also likely to belong to low-energy regions at the higher-level reference method.
2.3.4. Sanity Checks and Constraints
The resulting geometries and energies are checked after each fitness evaluation to ensure that the local optimization was successful, as it may happen that the initial structures R generated by the GA operators have clashes or are so deformed that it becomes difficult for the local optimizer to converge to a stable (local) minimum, especially within the first few generations. In this uncommon case, individuals from nonconverged optimizations are simply ignored and replaced in the next generation by assigning them a very high (unfavorable) fitness value.
A similar procedure is applied to constrain the GA search. In particular, when running separate optimizations for the cis- and trans-GPGG manifolds, the geometries are checked on-the-fly to ensure that they belong to the chosen isomer class since the local optimizer can, although very rarely, alter the isomerization state of the proline (Figure S6).
For gramicidin, the cyclic structure is enforced by requiring the bond between the PRO1 nitrogen and PHE10 carbon atom not to exceed 2 Å, which again rarely occurs due to the definition of a cyclic topology in the force fields which imposes a bonding potential between these two atoms. If we were to use a surrogate at the electronic structure level, the ring structure would be constrained similarly by an additional penalty potential.
2.3.5. Selection
Individuals are selected with tournament selection: a subset of a given size s is randomly created from the population and a competition operates between individuals in this set. The solution with minimal (i.e., most optimal) fitness in the set is added to a pool of mates for crossing over. The process is repeated until the number of mates in the mating pool reaches the population size.
2.3.6. Crossover
The recombination of genetic material to be inherited by the offspring is achieved with the simulated binary crossover (SBX)78 operator, which is a real-valued analogue of the single-point crossover of binary strings that was used in early GAs with discrete degrees of freedom. This simple operator cuts and swaps at one random site in the bit representations. More specifically, SBX is designed to enhance the probability for two parents to give birth to an arbitrary child solution and better explore the fitness landscape. More details about the SBX implementation are provided in Appendix A.1. This operator demonstrated better performance in finding global optima of multivariable objective functions with numerous LM. To illustrate its enhanced search power, we report the number of LM visited along a GA run with SBX in Figure S1, compared to simple swaps of Θ components (genewise crossover) that cover less space on average.
2.3.7. Mutation
Mutations are random disturbances to ensure that all regions of the solution space are accessible during the search. A point in the solution space should in principle be reachable from any other point thanks to mutations (and their combination with crossover). However, in conventional GAs, mutations should not be too strong in order not to scatter promising features out of their optimal regions as long as the search improves. Mutations are therefore usually considered as rather local changes aimed at exploiting the vicinities of current solutions, whereas larger moves (explorations) are driven by crossovers.41,48
Dealing with a real-valued search space, an instinctive choice for mutations is the addition of Gaussian noise79 that mutates an individual Θi like
| 3 |
where ◦ denotes the element-wise multiplication
between vectors. P(pm, K) is a vector of size K filled with 0
or 1 that selects genes to be mutated with probability pm. For pm = 1, all genes are
mutated, while pm = 0 turns off the mutation.
Selected genes are consequently modified with independent samples
from the standard normal distribution 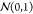 scaled with the parameter σ that
controls the mutation strength, along with pm.
scaled with the parameter σ that
controls the mutation strength, along with pm.
2.3.8. Elitism
The crossover and mutation operators mix and alter the tentative solutions that were among the best individuals in the previous generation. While the solutions are expected to improve along a GA run on average, there is no guarantee that the best fitness at a certain generation is lower than its previous counterpart and genes can drastically change in the case of genetic drift, escaping from a region where the GM actually sits. A way to counteract this is the application of an elitism operator which consists of replacing a fraction f of the worst solutions by the best individuals of the previous generation. This makes sure that the best fragments of information found so far are automatically transferred to the offspring generation, which thus always contains the overall best solution. Such a selective pressure can improve the convergence speed,71,80 though the efficiency of any GA is dictated by its ability to balance between exploration and exploitation and elitism introduces the risk of losing diversity and converging prematurely to less-fit LM.81
3. Computational Details
3.1. GA Parameters
We report in Table 1 the parameters optimized through a series of test runs and finally used in this study. The algorithm terminates after a fixed number of generations, for which we verified that no significant improvement in fitness was observed anymore.
Table 1. Input Parameters for EVOLVE.
| GA parametera | GPGG | Gramicidin |
|---|---|---|
| Population size | 40 | 48 |
| No. of generations | 60 | 80 |
| Tournament selection, s | 2 | |
| Mating probability | 1.0 | |
| Crossover, pc | 0.5 | |
| Crossover, n | 5 | |
| Mutation probability | 0.75 | |
| Mutation, pm | 1/3 | 1/10 |
| Mutation, σ | 60° | |
| Elitism, f (if applicable) | 4/40 | 5/48 |
s, set size; pc, genewise probability; n, SBX crossover order; pm, genewise probability; σ, mutation strength; f, elitism fraction.
The mating and mutation probabilities fix the fractions of the population that are respectively crossed or mutated. For a solution Θ, pc = 50% of its components are crossed with the SBX operator while the others remain unchanged. 75% of the population is mutated and the probability pm of mutating each gene is chosen so that one ϕ and one ψ backbone dihedral are modified on average. For gramicidin, the same probability applies to all 16 side chain dihedrals resulting in an average rate of 1.6 side chain mutants per individual. We choose a reasonable replacement of about 10% of the population by elites, unless otherwise specified, and also study the effect of no or stronger elitism in what follows.
3.2. Surrogate Fitness Function
Among the plethora of available methods, we focus our assessment of surrogate PES on some widely used force fields and semiempirical approaches that are expected to give fairly accurate results over a broad chemical and conformational space, as well as for charged or nonstandard residues.
The first chosen surrogate candidate is the General Amber Force Field (GAFF)82 as provided in the Amber 2018 suite.75 Fixed partial charges, atom types, and force field parameters have been assigned with the Antechamber and Leap tools. Atomic charges are derived from the default restrained electrostatic potential (RESP) fit83 at the HF/6-31(d) level of theory. For the purpose of comparison and to test the sensitivity with respect to the choice of fixed point charges, we also used charges derived with the faster Austin Model 1 with bond charge correction (AM1-BCC) scheme.84,85 For both cis- and trans-GPGG, charges are calculated from structures constructed with the amino acid sequence editor of Molden,86 while the X-ray-resolved crystal structure is used for gramicidin.87 van der Waals and electrostatic interactions are not truncated in the absence of periodic boundary conditions. Local geometry optimizations are performed using Sander single-core jobs consisting first of 4000 steepest descent steps followed by conjugate gradient optimization until convergence to the default 10–4 kcal/(mol Å) root-mean-square deviation of the Cartesian elements of the gradient.
Second, we examine the AMOEBA polarizable force field for proteins88 in its OpenMM implementation76 with the L-BFGS minimizer tolerance set to 10–4 kcal/mol. In our experience, the GPU-accelerated version significantly speeds up geometry optimizations by up to a factor of 80 compared to the CPU version.
Calculations with the self-consistent-charge (SCC) density functional tight binding method89 with full third order terms90 (DFTB3) are performed with the DFTB+91 code with the SCC tolerance set to 10–7 a.u. using the parameter set 3OB.92 Hydrogen interactions are corrected with a damping exponent of 4.2 in the SCC short-range contribution.90 DFTB3 is extended with the London dispersion correction D393 as parametrized for DFTB394 with the Becke–Johnson damping variant.95 The geometry optimizations are carried out with the L-BFGS algorithm and default convergence criteria.
We also evaluate the ability to rely on hybrid DFT with a small basis set (6-31G) as a possible surrogate. For this, we use the GPU-supported TeraChem software96,97 with L-BFGS optimizations98 at the B3LYP level of theory performed on 2 parallel GPU cards with default settings.
Finally, Gaussian1674 is used for the semi-empirical PM699 and PM7100 methods with the Berny optimizer101 and default convergence criteria. The same is true for the B3LYP/6-31G(d,p) reference calculations with the difference being that very tight (tight) convergence criteria with ultrafine grid were chosen for GPGG (gramicidin). The performances of all these alternative surrogates compared to the B3LYP/6-31G(d,p) reference are discussed in the next section.
4. Results and Discussion
4.1. Performance of Different Surrogate Fitness Functions
The success of the search for good candidate structures relies on the matching of the surrogate PES with the one of a reference method capable of reproducing the experimental results. Ideally, running the GA with the surrogate should lead to a similar coverage of the configurational space as well as a good match of the relative energetics between structures within an affordable computational cost. We therefore seek to establish here which approximation provides the best compromise between accuracy and computational expense.
However, a quantitative evaluation of the performance of a given fitness function is nontrivial due to the stochastic nature of GAs, in addition to the intractable cost of running multiple benchmark instances with, for example, hybrid DFT. Furthermore, assessing accuracy differences between various methods has been one of the major challenges in computational chemistry for decades. For this reason, we rather test the quality of the different PES approximations on a finite test set of GPGG geometries.
In order to maximize the coverage of different regions of the PES, the set was generated from 10 high mutation rate GA instances with the GAFF force field and with the structures that resulted from GA crossovers and mutations before local relaxations (and fitness evaluations). Therefore, these latter are not LM of the GAFF force field which is only used to drive the sampling. From all visited configurations (20000 in total), 200 diverse geometries were initially selected using a farthest-point sampling (FPS) algorithm102 in the space defined by the radius of gyration RG and the number of hydrogen bonds NH (see Appendix A.2) that turned out to be useful for differentiating polypeptide configurations.103 Among these, 146 geometries were successfully relaxed to distinct LM at the B3LYP/6-31G(d,p) reference level, which we augmented with 42 structures derived from ab initio SA (cf. Section 2.1) that we know correspond to low energy minima. Hence, the test set finally contains 69 cis and 119 trans nonrelaxed individuals that are representative of points potentially visited during GA runs.
As it would happen for a GA process, the different surrogates are employed to locally optimize the set and produce pools of respective LM. Therefore, the evaluation of a surrogate’s performance must be based on its ability to not only approximate the energy but also the coordinates of the reference LM; a satisfactory model should provide target structures with relative energies following the B3LYP/6-31G(d,p) ranking at best. Illustratively, the wells of the surrogate in Figure 4 must be as “close” as possible to the reference wells, in terms of both energy and structure. However, as also depicted in Figure 4, we note that a direct (one-to-one) comparison between surrogate and reference LM is not possible because similar initial points may relax into very different geometries depending on the method and optimizer used. Consequently, in the absence of side chains for GPGG, the backbone RMSD (bb-RMSD) was chosen as a metric to identify “closest” LM structures and rely on a more faithful measure of proximity than a direct comparison from the shared initial point.
Figure 4.

Illustration of the local relaxation of test structures on the surrogate and reference PES projected along two arbitrary reaction coordinates. The LM resulting from the same initial points are not necessarily close in energy and/or geometry.
We opted for a statistical analysis to mimic the various fitness evaluations during a GA run, which also informs about the performance of the surrogates for different population sizes: For a random subset of S initial structures taken from the test set, each reference B3LYP/6-31G(d,p) LM is associated with its closest (in terms of bb-RMSD) surrogate LM. Then, the relative energies within the subset are used to calculate the mean absolute error (MAE) of the surrogate energy:
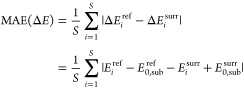 |
4 |
with E0,sub being the minimum energy in the respective subset. This represents the ranking on which the GA selection would operate and avoids giving too much importance to whether the surrogate was able to correctly find the GM of the entire set or not.
Figure 5a shows the MAE(ΔE) for different subset sizes and surrogates, and Figure 5b gives the average bb-RMSD between the closest reference and surrogate LM structures from which the ΔE were calculated. As could be expected, the B3LYP/6-31G(d,p) LM are best reproduced using the same method (B3LYP) but with the smaller (nonpolarized) 6-31G basis set, with structures showing on average 0.2–0.4 Å bb-RMSD and ∼4 kcal/mol energy differences. While all other surrogates show similar differences in geometries that saturate at best around 0.3 Å bb-RMSD for DFTB3, the relative energies between methods are more variable. The PM6 semi-empirical method appears to perform best with average energy deviations of 5 kcal/mol, followed by the GAFF(RESP) and AMOEBA force fields, as well as DFTB3, which all have energy differences of about 6 kcal/mol while these exceed 7 kcal/mol for the remaining surrogates. The worst approach is the GAFF force field with AM1-BCC charges, which were only used here to explicitly test the influence of the effective charge set but are indeed not recommended for common practice.75
Figure 5.
(a) MAE of relative energies between surrogate LM and their bb-RMSD closest B3LYP/6-31G(d,p) counterparts for the GPGG test set. (b) Average bb-RMSD between the surrogate LM and their closest B3LYP/6-31G(d,p) counterparts. Average values over max(S, 70) random subsets for each size S are plotted; standard deviations are of the order of 1 kcal/mol, respectively, 0.03 Å, and are provided in the Supporting Information (Figure S5a,b). The energies of the reference LM span 30 kcal/mol with two outliers around 40 and 60 kcal/mol.
Regarding the quality of the structural prediction, Figure S2 gives an illustration of some bb-RMSD between reference and surrogate LM. In general, structures with a bb-RMSD of less than 0.5 Å are very similar and thus more likely to relax to their B3LYP/6-31G(d,p) counterpart upon reoptimization. As for the energetic performance, the closest reproduction of the reference geometries is found for the smaller basis set B3LYP variant, but also all remaining surrogate methods perform relatively well in terms of geometric predictions, yielding LM geometries with a bb-RMSD around 0.5 Å from a subset size of 40, which is the population size of the GA chosen for GPGG. Therefore, we conclude that over a set of representative geometries encountered in a GA optimization, all non-DFT surrogates show a similar performance in terms of reproducing B3LYP/6-31G(d,p) structures. However, correct relative energies are more difficult to approximate and differ between methods, with PM6 slightly outperforming GAFF(RESP), AMOEBA and DFTB3 in terms of overall MAE.
Apart from the fact that the surrogate method should be able to generate a diverse set of structures, we are particularly interested in the performance for the low-energy regime, whose members will drive GAs to the most optimal regions of the PES. The pool of low-energy LM at the surrogate level also represents the candidates that will be selected for a reoptimization with a higher level reference. For all cis, respectively trans isomers, Table 2 presents the MAE of the relative energies of LM at less than 10 kcal/mol of the respective GM in the set. Again, the energies are compared between corresponding pairs of surrogate-reference geometries that exhibit the smallest bb-RMSD.
Table 2. Assessment of Surrogate Methods in the Low-Energy Regime ΔẼ ≤ 10 kcal/mola.
| cis |
trans |
|||||
|---|---|---|---|---|---|---|
| Surrogate | MAE
|
Av bb-RMSD | NLM | MAE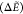
|
Av bb-RMSD | NLM |
| GAFF AM1-BCC | 7.1 ± 3.1 | 0.48 ± 0.25 | 10 | 5.9 ± 4.3 | 0.41 ± 0.12 | 15 |
| GAFF HF/6-31G(d) RESP | 6.1 ± 7.6 | 0.29 ± 0.25 | 10 | 6.1 ± 4.9 | 0.35 ± 0.17 | 29 |
| AMOEBApro13 | 3.6 ± 4.1 | 0.36 ± 0.11 | 23 | 4.8 ± 4.7 | 0.27 ± 0.16 | 49 |
| PM6 | 3.7 ± 4.6 | 0.37 ± 0.14 | 25 | 4.4 ± 3.4 | 0.23 ± 0.16 | 32 |
| PM7 | 5.5 ± 6.7 | 0.43 ± 0.18 | 31 | 2.6 ± 1.9 | 0.21 ± 0.06 | 13 |
| DFTB3-D3(BJ) | 6.9 ± 4.7 | 0.36 ± 0.21 | 34 | 6.0 ± 6.7 | 0.36 ± 0.22 | 45 |
| B3LYP/6-31G | 1.6 ± 2.8 | 0.16 ± 0.17 | 30 | 1.1 ± 0.9 | 0.13 ± 0.13 | 35 |
| B3LYP/6-31G(d,p), reference | 27 | 21 | ||||
NLM is the number of local minima within the
range.  in kcal/mol,
where
in kcal/mol,
where 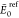 and
and 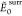 are
the respective cis or trans putative
GM found over the entire test set. The energies of the surrogate and
the reference are compared according to the smallest bb-RMSD match,
whose average value and standard deviation are reported in Å.
are
the respective cis or trans putative
GM found over the entire test set. The energies of the surrogate and
the reference are compared according to the smallest bb-RMSD match,
whose average value and standard deviation are reported in Å.
All methods provide on average satisfactory geometries with a difference in bb-RMSD of less than 0.5 Å with the reference LM. In addition to providing the closest structural match, the B3LYP/6-31G PES is the best surrogate with respect to relative energies in the low-energy realm. However, the performance of some of the other tested surrogates can markedly deviate from the overall energetic performance shown in Figure 5. Both GAFF(RESP) and DFTB3, are comparatively less accurate with MAEs between 6 and 7 kcal/mol for both cis and trans configurations. Although PM7 performs well for trans low-lying minima, it shows more weaknesses in ranking higher energy configurations (Figure 5a) as well as cis isomers in the low-energy range, which highlights the fact that the performance of surrogates can be system-dependent. Finally, AMOEBA and PM6 exhibit the smallest MAEs of all non-DFT methods with balanced accuracies for the two configurational classes.
While the previous analyses assessed the quality of the structural as well as energetic predictions of the different surrogate methods, their overall computational cost also plays a major role in the choice of the most appropriate fitness function. To give an overview of the different time scales involved we give estimates of the average time needed for a local geometry optimization for each surrogate method in Table 3. For the sake of comparison, running a GA search with the B3LYP/6-31G(d,p) reference would take more than 2.5 months on a desktop workstation for the 39-atom GPGG molecule, highlighting the need for more expedient approaches. Although it is found that resorting to a smaller basis set provides the best accuracy, a GPU-accelerated implementation only reduces the elapsed time to the order of a month, while other surrogates bring it down to less than a day for semi-empirical methods (PM6, PM7, DFTB3) and only few minutes for force fields (GAFF, AMOEBA).
Table 3. Average Elapsed Time t̅ for Local GPGG Geometry Optimization on Ncores Cores (or GPU) for Different Surrogate Methods Based on the GPGG Test Seta.
| Surrogate | t̅ (min) | Ncores | t̅GAb |
|---|---|---|---|
| GAFF AM1-BCC | 0.024 | 1b | 3 min |
| GAFF HF RESP | 0.028 | 1b | 3 min |
| AMOEBApro13 | 0.005 | 1 GPUc | 5 min |
| PM6 | 1.072 | 8b | 15 h |
| PM7 | 1.578 | 8b | 22 h |
| DFTB3-D3(BJ) | 1.331 | 1b | 2.7 h |
| B3LYP/6-31G | 19.508 | 2 GPUsc | 1 mth |
| B3LYP/6-31G(d,p) | 150.235 | 8b | 2.7 mths |
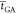 is an estimate of the average time spent
on fitness evaluations for a 60-generation 40-individual GA run if
executed on a 24-core 2-GPU workstationb.
The calculation details of each method are reported in Section 3.2.
is an estimate of the average time spent
on fitness evaluations for a 60-generation 40-individual GA run if
executed on a 24-core 2-GPU workstationb.
The calculation details of each method are reported in Section 3.2.
24-core Intel Xeon E5-2650 v4 @ 2.20 GHz CPU, 2 Nvidia GeForce GTX 1060 GPUs.
16-core Intel Xeon E5-2630 v3 @ 2.40 GHz CPU, 2 Nvidia GeForce GTX 970 GPUs.
The small improvement in accuracy of PM6 does not seem to justify its use over AMOEBA, which is about 180 times faster. From these tests on the GPGG tetrapeptide, AMOEBA is thus emerging as a promising surrogate for GA optimization of peptides in terms of cost and accuracy and it will therefore be our choice in the following sections along with the fast but presumably less accurate GAFF (HF/6-31G(d) RESP) force field for comparison.
4.2. GA Optimization of GPGG
4.2.1. Global Minimum Search
The results presented here are all based on a common pool of surrogate geometries generated after 10 GA runs, for which the minimum energy progressions are plotted in the Supporting Information (Figures S7 and S8). Without prior knowledge about structures and energies, the GM is assumed to be the lowest-energy individual found over all instances.
In terms of GA performance, it is worth mentioning that elitism markedly increases the chance of finding the GM as reported in Figure 6 that shows the cumulative success of reaching the GM at a given iteration. A 10% replacement of the current population with the best parent individuals substantially improves the GM search for all schemes but the cis-GPGG on the AMOEBA PES due to its rapid convergence (the energy decrease between the first and last generations is only 0.1/0.6 kcal/mol as shown in Figure S7) For the other cases, the GA might not always succeed in finding the GM but elitism allows enhancement of the convergence rate by 30%. Since the minimum energy will fix the overall ranking of surrogate LM, and consequently the selection of candidates to be reoptimized, it is essential for the GA to reach the surrogate GM or at least low-lying structures within a few kcal/mol from it.
Figure 6.
GPGG: cumulative success of finding the surrogate GM at each generation, averaged over 10 GA optimizations per surrogate/isomer combination.
Comparing the sampled structures of the cis isomer with the DFT-resolved GM, it is found that the putative GM of AMOEBA has a heavy-atom RMSD of only 0.5 Å (Figure 7a). However, this is not the most similar structure found, as the GA was able to provide an even closer structure with an RMSD of 0.4 Å about 0.6 kcal/mol higher in energy that better reproduces the configuration of the proline cycle (Figure 7b). At the GAFF level, although the lowest energy structure is more compact (Figure 7c) and therefore shows a larger RMSD from the reference, a geometry almost equal to the DFT GM is also discovered about 1 kcal/mol higher in energy (Figure 7d).
Figure 7.
cis-GPGG: putative GM and closest
LM found on
surrogate PES after 10 GA runs for (a, b) AMOEBA and (c, d) GAFF. 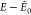 is the
relative energy of the LM with respect
to the putative GM. The B3LYP/6-31G(d,p) GM is depicted in green with
respective backbone/heavy-atom RMSD. Similar structures are obtained
with or without elitism.
is the
relative energy of the LM with respect
to the putative GM. The B3LYP/6-31G(d,p) GM is depicted in green with
respective backbone/heavy-atom RMSD. Similar structures are obtained
with or without elitism.
For the trans isomer, the AMOEBA GM is more distant from the DFT reference (Figure 8a) than it is with GAFF (Figure 8c) with respective RMSDs of 1.1 Å against 0.6 Å, but both force fields yield almost identical structures to the DFT GM within 2 kcal/mol above their putative GM (Figure 8b and 8d).
Figure 8.
trans-GPGG: putative GM and closest LM found on
surrogate PES after 10 GA runs for (a, b) AMOEBA and (c, d) GAFF. 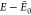 is the
relative energy of the LM with respect
to the putative GM. The B3LYP/6-31G(d,p) GM is depicted in green with
respective backbone/heavy-atom RMSD. Similar structures are obtained
with or without elitism.
is the
relative energy of the LM with respect
to the putative GM. The B3LYP/6-31G(d,p) GM is depicted in green with
respective backbone/heavy-atom RMSD. Similar structures are obtained
with or without elitism.
Hence, for both cis- and trans-GPGG, GAFF and AMOEBA are able to identify the DFT GM as a low-lying surrogate structure within a maximum of 2 kcal/mol above their (putative) GM demonstrating that a surrogate approach can indeed be beneficial before resorting to higher-level refinement as it is done in the next section.
4.2.2. Low-Lying Minima Search and Refinement
GA optimization offers the additional advantage that one can profit from all of the LM visited during evolution. Maximizing the number of low-energy structures is therefore important in order to capture all surrogate candidates likely to relax to the desired reference minimum. As an example, the progression of the number of new minima explored is shown in Figure 9 for a single GA as well as after several executions. The average number of minima found over the GA iterations is very similar with or without elitism and reaches a plateau after a certain number of GA generations (Figure 9a). Figure 9b shows that it is more efficient to perform independent runs in parallel to improve the search and sample more LM, rather than extending a single execution with more generations. In this case, however, the use of elitism can alter diversity and reduce the exploration of low-lying LM, which is observed for all schemes (Figure S9).
Figure 9.
trans-GPGG: number of low-lying minima found on the AMOEBA PES within 15, 10, and 5 kcal/mol with respect to the putative GM. (a) Per GA generation, averaged over 10 GA runs. (b) By running independent GAs. Distinct LM are taken to be at least separated by 10–4 kcal/mol and 0.2 heavy-atom RMSD.
The collection of thousands of structures provided by the GA is followed by their ultimate reoptimization at the reference level. For this purpose, only surrogate structures within 10 kcal/mol of their putative GM are selected and locally relaxed with DFT (B3LYP/6-31G(d,p)). To establish the actual accuracy of the surrogate, Figure 10 compares the energies and coordinates between the AMOEBA LM and their reoptimized counterparts and Table 4 reports respective MAE on energy and bb-RMSD for all schemes. As expected, relative energies are not perfectly reproduced and the largest errors (outliers) cannot be systematically attributed to larger RMSDs. However, AMOEBA provides a rather good MAE of only 1.9 kcal/mol for the cis isomers, while it increases to 4.4 kcal/mol for the trans structures. Surprisingly, the relative energies obtained for the GAFF (fixed point charge) force field are only slightly worse than the ones of AMOEBA for cis and even slightly better for trans isomers. In spite of the few kcal/mol error in the predictive power of the surrogates, LM are generally very close to their DFT counterparts with a small backbone (heavy-atom) RMSD around 0.3 (0.5) Å on average. Some of them relax into identical minima on the DFT PES, but the GA candidates still provide an extensive set of realistic low-lying minima: We note that all LM that were identified as closest to the DFT GM for AMOEBA (Figures 7b and 8b) and GAFF (Figures 7d and 8d) did indeed relax to the DFT GM. Therefore, the surrogate GA approach was overall successful in retrieving the target DFT GM structures that were assigned to experimental IR spectra.
Figure 10.

GPGG: predictive performance of AMOEBA in reproducing geometries and relative energies of LM at the B3LYP/6-31G(d,p) level for (a) cis isomers and (b) trans isomers. Backbone (bb) and heavy-atom (no-H) RMSDs are reported. Also indicated are the median and 75% quantile of absolute errors on energies. The 75% quantile outliers are marked in green with their respective RMSD. Corresponding plots for the GAFF force field are given in the Supporting Information (Figure S10).
Table 4. GPGG:  a in kcal/mol
and
Average Backbone RMSD in Å between the Surrogate LM and Their
Reoptimized Counterparts at B3LYP/6-31G(d,p).
a in kcal/mol
and
Average Backbone RMSD in Å between the Surrogate LM and Their
Reoptimized Counterparts at B3LYP/6-31G(d,p).
| Surrogate/isomer | MAE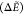
|
Av bb-RMSD | NLMb |
|---|---|---|---|
| AMOEBA/cis | 1.9 ± 1.5 | 0.28 ± 0.10 | 31 |
| GAFF/cis | 2.9 ± 1.9 | 0.29 ± 0.14 | 94 |
| AMOEBA/trans | 4.4 ± 2.9 | 0.31 ± 0.21 | 64 |
| GAFF/trans | 4.0 ± 2.5 | 0.38 ± 0.23 | 87 |
Compared to a previous SA search,1 the sGADFT found more (theoretical) LM on the B3LYP PES within the convergence criteria and basis set employed, as it is shown in Figure 11. In the cis subspace, the AMOEBA GA gave four similar lowest-energy geometries to SA within 2 kcal/mol and misses four of them within 5 kcal/mol. Nevertheless, it provides additional structures that were not found in the SA search. Ditto for the GAFF force field, except for some very low energies that are not recovered. For the trans-GPGG, the very low region is more sparse and a structure at 0.05 kcal/mol is missed with AMOEBA, as is another one close to 5 kcal/mol that was spotted with GAFF. Overall, this demonstrates that GA-sampled structures are indeed relevant for the low-energy resolution of the ab initio PES. Should the results not be satisfactory, there is always the possibility of running additional GAs and/or performing a higher number of reoptimizations.
Figure 11.
GPGG: zero point energy-corrected energies of B3LYP/6-31G(d,p) reoptimized structures obtained with ab initio simulated annealing (SA) at B3LYP/6-31G1 and GA with AMOEBA or GAFF force fields. The green and shorter red levels are respectively matches and misses compared to SA. The respective number of LM is indicated in parentheses.
The obtained ab initio LM can describe very similar structures that are chemically indistinguishable. To group essentially identical structures, a minimum RMSD can be imposed and the number of distinct LM becomes of the same order for both AMOEBA and GAFF (Figures S11 and S12). This shows that it is important to sample not only as many low-lying minima as possible at the surrogate level but also those that are farthest away and likely to relax into distinct DFT minima. An effective approach in this sense would be to select distant structures using clustering,104 FPS,102 or RMSD analysis prior to reoptimization and avoid irrelevant relaxations due to small numerical differences.
4.3. GA Optimization of Gramicidin
4.3.1. Global Minimum Search
An even harder performance test is represented by the larger gramicidin system with explicit side chain optimization. As reported in Figure S13 using the AMOEBA surrogate PES, the energy progression is clearly hampered or stagnates after a few tens of iterations in the absence of elitism. On the other hand, a (too) high fraction of elitism of 20% increases the variance and does not reach the lowest energies, whereas the putative GM is finally found in 3 over 10 GA runs using a medium 10% rate of elites. Astonishingly, the surrogate GM is also the closest geometry to the DFT-resolved structure, which are both reproduced in Figure 12. The agreement between the AMOEBA and the B3LYP geometries is remarkable with a backbone (heavy-atom) RMSD of only 0.2 (0.4) Å.
Figure 12.
Gramicidin: two views (a) and (b) of the AMOEBA putative GM that is also the closest LM found over 10 GA runs (with 10% elitism). The DFT B3LYP/6-31G(d,p) reference GM is depicted in green. Backbone/heavy-atom RMSDs are 0.2/0.4 Å.
In contrast, the GAFF putative GM is found with a 20% elitism rate (Figure S13), which highlights the fact that elitism is an essential factor in the search for GM on complicated PES, but its magnitude may be system- and method-dependent and remains a parameter to be assessed or adjusted in order to find an ideal exploration–exploitation trade-off. As opposed to AMOEBA, the GAFF putative GM is very far from the DFT GM with a large (2.1 Å) backbone RMSD (Figure S14a). Over 30 GA runs, the closest LM found is only located within 26 kcal/mol (!!) from the putative GM, has a 0.5 (1.5) Å backbone (heavy-atom) RMSD and does not relax to the DFT GM (Figure S14b). In order to assess if this poor performance originates from the limitation of the GA search or the quality of the surrogate PES, we relaxed the DFT GM with the GAFF force field and obtained a very similar structure (0.1 (0.3) RMSD) located 18 kcal/mol above the GAFF putative GM. Therefore, the DFT GM is indeed a LM on the GAFF PES but does not lie in the low-energy regime which definitely renders the GAFF force field unsuitable for the GM search, in particular because several hundreds of structures were found within 18 kcal/mol (Figure S15) and, in the absence of prior knowledge, reoptimizing all would be far from tractable.
4.3.2. Low-Lying Minima Search and Refinement
As seen previously, the number of explored minima depends on the ability of the GA to reach different low-energy regions and varies with the fraction of elitism and the choice of fitness function. Running multiple GA instances starting from different initial structures is again more efficient than extending a single run whose variance decreases with the number of iterations (Figure S16). Elitism reduces in principle the overall diversity of the LM (cf. Section 4.2.2) but becomes essential to explore the very low energy regions of more complex systems. Indeed, for gramicidin, the greater number of low-energy minima was obtained by the elitism fraction capable of identifying the putative GM (Figures S15 and S16). Therefore, mitigating elitism with other mutation-like operators could potentially improve the search power in the low-energy regime by providing a certain diversity of structures visited while maintaining low energies.
B3LYP/6-31G(d,p) reoptimizations of gramicidin candidates are much more CPU intense than those of the smaller GPGG peptides, so that only structures sampled with 10% elitism and located within 5 kcal/mol could be retained for subsequent optimizations. It is therefore crucial that the surrogate, although not optimal, provides relevant candidates located in a range of only a few kcal/mol, as the number of structures and their refinement cost increase considerably with the size of the system. Again, we plot relative energies and RMSDs against DFT reoptimized geometries in Figure 13 and report averages in Table 5.
Figure 13.

Gramicidin: predictive performance of AMOEBA and GAFF in reproducing geometries and relative energies of LM at the B3LYP/6-31G(d,p) level. Backbone (bb) and heavy-atom (no-H) RMSDs are reported. Also indicated are the median and 75% quantile of absolute errors on energies. The 75% quantile outliers are marked in green with their respective RMSD.
Table 5. Gramicidin: 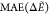 a in kcal/mol
and
Average Backbone RMSD in Å between the Surrogate LM and Their
Reoptimized Counterparts at B3LYP/6-31G(d,p).
a in kcal/mol
and
Average Backbone RMSD in Å between the Surrogate LM and Their
Reoptimized Counterparts at B3LYP/6-31G(d,p).
| Surrogate | MAE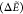
|
Av bb-RMSD | NLMb |
|---|---|---|---|
| AMOEBA | 4.3 ± 3.3 | 0.29 ± 0.11 | 48 |
| GAFF | 17.9 ± 2.0 | 0.25 ± 0.05 | 28 |
For gramicidin, AMOEBA performs as well as for GPGG with a MAE around 4 kcal/mol and small 0.3 Å average backbone RMSD. Successfully, the three lowest candidate structures relax to the DFT GM (Figure 13a). For GAFF, the geometries of the candidate structures are also very similar to their closest DFT minima, but relative energies are significantly off due to GAFF’s inability to correctly reproduce the lower regions of the DFT PES of this system (Figure 13b). By visualizing the LM in the RG-NH space in Figure 14, we notice that GAFF biases the search toward higher-energy DFT regions. In these, GAFF does rather well on relative energies despite a large energy offset (∼18 kcal/mol, Figure 13b). Hence, we conclude that GAFF cannot reliably approximate the energetics for screening low-energy gramicidin structures and sampling realistic regions of the PES, which the polarizable AMOEBA force field, on the other hand, seems to achieve surprisingly well.
Figure 14.

Gramicidin:
surrogate AMOEBA and GAFF LM candidates within 5 kcal/mol
in the RG (radius of gyration) and NH (number of hydrogen bonds) space, connected
by lines to their reoptimized structures at the B3LYP/6-31G(d,p) level
of theory. 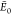 are the respective energies of the putative
GM for each PES, indicated by
are the respective energies of the putative
GM for each PES, indicated by 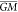 for the surrogates and
GM for B3LYP.
for the surrogates and
GM for B3LYP.
Figure 15 finally demonstrates that the straightforward GA approach with AMOEBA produces an extensive set of low-lying B3LYP/6-31G(d,p) structures with little effort, as opposed to the more technically involved restrained SA simulations that were used in the initial search for the experimentally observed structure30 (cf. Section 2.1). Although the overall sGADFT method did not find similar LM, its explored energy space is denser in the low-energy range and the experimental GM is retrieved, advocating the use of surrogate GAs for low-energy sampling with little setup management and cost, as discussed in the next section.
Figure 15.
Gramicidin: zero point energy-corrected energies of B3LYP/6-31G(d,p) reoptimized structures obtained with SA based on classical force fields (SA/FF),30 and GAs with AMOEBA and GAFF force fields. The green and shorter red levels are respectively matches and misses compared to SA/FF. The respective number of LM is indicated in parentheses. A similar plot restricted to clearly distinct structures (only LM differing by at least two side chain dihedrals) is provided in Figure S18.
4.4. Computational Performance
Thanks to the use of surrogates that allows one to bypass a direct exploration of the PES at the first-principles level, searching for GPGG conformers takes less than 15 min on a conventional workstation as indicated in Table 6, albeit requiring more than 2400 local relaxations per GA execution.
Table 6. Wall Time t̅ per GA Execution for the AMOEBApro13(OpenMM76) and GAFF(Amber75) Surrogatesa.
| System | t̅ AMOEBA (min) | t̅ GAFF (min) |
|---|---|---|
| cis GPGG | 13.9 ± 0.6 | 14.3 ± 1.6 |
| trans GPGG | 12.5 ± 0.1 | 7.5 ± 0.8 |
| Gramicidin | 43.7 ± 3.4 | 122.8 ± 11.2 |
For GAFF, benefits come from a parallel split of fitness evaluations over multiple cores. The timing difference between cis- and trans-GPGG originates from the longer initialization of a complete cis population that has the tendency to relax to trans structures. Apart from that, for the smaller GPGG system, GAFF is generally faster than the more sophisticated (polarizable) AMOEBA force field but the recent GPU-accelerated implementation76 of AMOEBA makes the optimizations significantly faster for the larger gramicidin peptide; thanks to a load split of EVOLVE over two parallel GPUs, the evaluation of more than 3800 fitness evaluations can be achieved in less than 45 min for this 176 atom molecule.
All in all, in the case of AMOEBA, the pools of low-energy candidate structures for GPGG and gramicidin were sampled in respectively 2.5 and 7 h on a single workstation for 10 serial GA runs, without monitoring or restart procedures, in contrast to the previously employed B3LYP/6-31G SA search for GPGG that took several days with multiple runs, with different heating temperatures and annealing rates and a postprocessing analysis of trajectories to extract promising candidates.1 Such an ab initio exploration is simply out of reach for gramicidin and only SA based on classical force fields employing additional experimentally observed constraints could provide the GM.30
Regardless of the search approach employed, a final ab initio refinement with a large basis set is necessary for calculating properties, e.g., reliably assigning IR frequencies to experimental spectra. DFT reoptimizations and (harmonic) vibrational analyses are far more demanding than the GA searches themselves; in fact, they required 6 days on two workstations for all AMOEBA/GAFF GPGG LM (276 structures) while 4 days on 8 16-core compute nodes were needed for the AMOEBA gramicidin (48 structures). However, similar to the previous SA searches, experimental information like ion-mobility cross-sections1 or symmetry constraints derived from typical vibrational fingerprints30 can be used as additional prefilter for GA applications, to further narrow down the pool of candidate geometries instead of retaining all structures within a given energy range. This would drastically reduce the computational demand when treating larger systems.
5. Conclusions and Outlook
In this work, we have presented a GA based search method to efficiently sample low-energy structures of peptides and its implementation in our in-house code EVOLVE.67 Rather than aiming for a full first-principles exploration, we argue that resorting to more expedient surrogates allows significant reduction of the computational expense in the screening of candidate structures to be later reoptimized at the ab initio level. This is motivated by the fact that coordinates of local minimum candidates are in general well-approximated by surrogates, while getting reliable energies is the main difficulty.
Among several approximate methods investigated, the AMOEBApro13 polarizable force field showed the best compromise between cost and accuracy. Tested on three systems that are the cis-, trans-proline protonated GPGG and the doubly protonated gramicidin S decapeptide, the approach was successful in identifying B3LYP DFT GM within a maximum 2 kcal/mol from the putative surrogate GM. The GAFF force field also succeeded for GPGG isomers but failed for gramicidin due to a large offset in the energy predictions. As opposed to the more cumbersome and expensive ab initio simulated annealing employed in earlier studies, GPGG local minima were generated over 10 serial GA runs in less than 3 h on a single workstation, and only 7 h were necessary for the larger gramicidin system. Obviously, these timings can be further improved by parallelizing between multiple GA instances.
Overall, this demonstrates that the AMOEBA based surrogate GA alternative can provide substantial advantages in the three-dimensional determination of trapped metastable or global minimum peptide structures, as observed in ultracold spectroscopy, because all resulting GM coordinates were indeed correctly identified.
Thinking ahead, such a comprehensive generation of low-energy minima can also be advantageous for a wider range of research studies: for example as starting points for MD simulations, free-energy sampling, transition state searches, and nudged elastic band methods, or as templates for protein–ligand complexes in the rational design of analogues, or finally as training data for a variety of machine learning approaches.105−107
Acknowledgments
U.R. acknowledges funding from the Swiss National Science Foundation via individual Grant No. 200020_185092.
Appendix
A.1. Simulated Binary Crossover
Let Θki be the kth real-coded gene (component)
of the parent individual i with representation of
size K (eq 1). For a two-to-two crossover between individuals i and j, the spread factor β is defined
as the ratio of the distance between children points 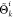 to that of the parent points:
to that of the parent points:
| 5 |
such that for β < 1 (β >
1),
the spread of the children points is smaller (larger) than that of
the parents and has a contracting (expanding) effect on the children
extent. Deb and Agrawal78 showed that the
probability distribution 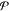 of having
a contracting or expanding single-point
binary crossover with spread β can be approximated by polynomial
functions, such that
of having
a contracting or expanding single-point
binary crossover with spread β can be approximated by polynomial
functions, such that
 |
6 |
is used to design a real-value crossover,
where n between 2 and 5 appeared to match closely
with single-point crossover results. It is easy to show that contracting
or expanding the distance between children genes is equiprobable (with
0.5 probability) by integrating 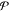 in the respective
ranges. Figure 16 shows
the probability distribution
of eq 6 for different n. Generally, the probability of creating children close
to their parents (β = 1) is higher than creating very different
children. Larger values of n accentuates this effect.
In practice, a fixed n is chosen although one could
broaden the initial search with small n and progressively
narrow the exploration over generations with larger n.
in the respective
ranges. Figure 16 shows
the probability distribution
of eq 6 for different n. Generally, the probability of creating children close
to their parents (β = 1) is higher than creating very different
children. Larger values of n accentuates this effect.
In practice, a fixed n is chosen although one could
broaden the initial search with small n and progressively
narrow the exploration over generations with larger n.
Figure 16.
Probability distributions  (eq 6) of contracting and expanding SBX crossover to mimic binary
single-point crossover distributions.
(eq 6) of contracting and expanding SBX crossover to mimic binary
single-point crossover distributions.
A sample from this probability distribution is
generated by choosing
the point β̅ for which the cumulative probability 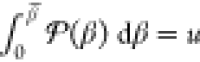 , where u is a
uniformly
generated random number in [0,1) and the change in contracting or
expanding
, where u is a
uniformly
generated random number in [0,1) and the change in contracting or
expanding 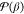 occurs at u = 1/2. For
such a β̅, the children’s genes are crossed according
to
occurs at u = 1/2. For
such a β̅, the children’s genes are crossed according
to
 |
7 |
Up to
now, the SBX operator has been presented for unbounded variables,
whereas peptide dihedrals are periodic. To restrict the search space
to specified lower (lb = −180°)
and upper (ub = 180°) bounds used
throughout the GA, the probability distributions are modified so that
the probability of creating dihedrals outside of the bounds is equal
to zero; without loss of generality in what follows, one can assign
the largest value to Θki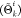 and the lowest to Θk
and the lowest to Θk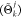 . It is straightforward to notice
from eq 5 that a maximum
spread
allowed for
. It is straightforward to notice
from eq 5 that a maximum
spread
allowed for  can be chosen as
can be chosen as
| 8 |
which provides a scaling factor α for the probability distribution in order to make the overall cumulative probability in the bounds equal to one.
| 9 |
Therefore, the bounded crossover operates
with eq 7 and β̅ is generated from the normalized cumulative
probability 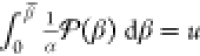 , where u is a
uniformly
sampled random number in [0,1). The normalized probability distribution
consequently changes at u = 1/(2α) such that
, where u is a
uniformly
sampled random number in [0,1). The normalized probability distribution
consequently changes at u = 1/(2α) such that
 |
10 |
The extension of the single-variable (Θki) SBX operator to the multivariate problem is straightforward: setting a probability pc of crossing over, pcK respective components of the solutions Θi and Θj are selected and crossed with the single-variable operator described above.
A.2. Radius of Gyration and Number of Hydrogen Bonds
The radius of gyration used in this work is the geometric radius rather than its mass-weighted analogue, defined as
| 11 |
where Nbb is the number of backbone heavy atoms located at positions ri, so that RG represents the RMSD of the backbone coordinates with respect to the average center of the backbone chain. It therefore differentiates between linear or more globular structures. For gramicidin, all heavy atoms are rather considered in eq 11 to establish a finer resolution of the side chains packing around the cyclic backbone.
The number of hydrogen bonds is evaluated as
 |
12 |
with d0 = 1.8 Å and i, j running over all oxygen and hydrogen atoms of the peptide, excluding their covalent bonds. This second quantity informs about the secondary structure and distinguishes between molten globular geometries or properly folded peptides. The RG and NH geometric descriptors are for example used as collective variables in the context of metadynamics.103
Data Availability Statement
A snapshot version of the EVOLVE code67 as used in this work is provided on Zenodo at 10.5281/zenodo.7251981, along with the data and analysis scripts needed to reproduce the results.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jctc.2c01078.
Effect of the SBX versus genewise crossover; examples of surrogate versus reference structures; relative energies and RMSD plots for the different surrogate fitness functions; minimum energy progression against GA iterations; number of local minima found along and for different GA instances; energy levels recovered by the sGADFT method when imposing a minimum RMSD between the resulting structures (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Whitford D.Proteins: Structure and Function, 1st ed.; John Wiley & Sons: New York, 2005. [Google Scholar]
- Lindorff-Larsen K.; Best R. B.; DePristo M. A.; Dobson C. M.; Vendruscolo M. Simultaneous determination of protein structure and dynamics. Nature 2005, 433, 128–132. 10.1038/nature03199. [DOI] [PubMed] [Google Scholar]
- Lee D.; Redfern O.; Orengo C. Predicting protein function from sequence and structure. Nat. Rev. Mol. Cell Biol. 2007, 8, 995–1005. 10.1038/nrm2281. [DOI] [PubMed] [Google Scholar]
- Jumper J.; et al. Highly accurate protein structure prediction with AlphaFold. Nature 2021, 596, 583–589. 10.1038/s41586-021-03819-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dyson H.; Wright P. E. Peptide conformation and protein folding. Curr. Opin. Struct. Biol. 1993, 3, 60–65. 10.1016/0959-440X(93)90203-W. [DOI] [Google Scholar]
- Daura X.; Gademann K.; Jaun B.; Seebach D.; van Gunsteren W. F.; Mark A. E. Peptide Folding: When Simulation Meets Experiment. Angew. Chem., Int. Ed. 1999, 38, 236–240. . [DOI] [Google Scholar]
- Venkatraman J.; Shankaramma S. C.; Balaram P. Design of Folded Peptides. Chem. Rev. 2001, 101, 3131–3152. 10.1021/cr000053z. [DOI] [PubMed] [Google Scholar]
- Thomas A.; Deshayes S.; Decaffmeyer M.; Van Eyck M. H.; Charloteaux B.; Brasseur R. Prediction of peptide structure: How far are we?. Proteins: Struct., Funct., Bioinf. 2006, 65, 889–897. 10.1002/prot.21151. [DOI] [PubMed] [Google Scholar]
- Zhang S. Fabrication of novel biomaterials through molecular self-assembly. Nat. Biotechnol. 2003, 21, 1171–1178. 10.1038/nbt874. [DOI] [PubMed] [Google Scholar]
- Maeda Y.; Makhlynets O. V.; Matsui H.; Korendovych I. V. Design of Catalytic Peptides and Proteins Through Rational and Combinatorial Approaches. Annu. Rev. Biomed. Eng. 2016, 18, 311–328. 10.1146/annurev-bioeng-111215-024421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fosgerau K.; Hoffmann T. Peptide therapeutics: current status and future directions. Drug Discovery Today 2015, 20, 122–128. 10.1016/j.drudis.2014.10.003. [DOI] [PubMed] [Google Scholar]
- Bhandari D.; Rafiq S.; Gat Y.; Gat P.; Waghmare R.; Kumar V. A Review on Bioactive Peptides: Physiological Functions, Bioavailability and Safety. International Journal of Peptide Research and Therapeutics 2020, 26, 139–150. 10.1007/s10989-019-09823-5. [DOI] [Google Scholar]
- Zasloff M. Antimicrobial peptides of multicellular organisms. Nature 2002, 415, 389–395. 10.1038/415389a. [DOI] [PubMed] [Google Scholar]
- Brogden K. A. Antimicrobial peptides: Pore formers or metabolic inhibitors in bacteria?. Nature Reviews Microbiology 2005, 3, 238–250. 10.1038/nrmicro1098. [DOI] [PubMed] [Google Scholar]
- Hancock R. E.; Sahl H. G. Antimicrobial and host-defense peptides as new anti-infective therapeutic strategies. Nat. Biotechnol. 2006, 24, 1551–1557. 10.1038/nbt1267. [DOI] [PubMed] [Google Scholar]
- Qvit N.; Rubin S. J.; Urban T. J.; Mochly-Rosen D.; Gross E. R. Peptidomimetic therapeutics: scientific approaches and opportunities. Drug Discov Today 2017, 22, 454–462. 10.1016/j.drudis.2016.11.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee A. C. L.; Harris J. L.; Khanna K. K.; Hong J. H. A comprehensive review on current advances in peptide drug development and design. Int. J. Mol. Sci. 2019, 20, 2383. 10.3390/ijms20102383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Masson A.; Kamrath M. Z.; Perez M. A.; Glover M. S.; Rothlisberger U.; Clemmer D. E.; Rizzo T. R. Infrared Spectroscopy of Mobility-Selected H+-Gly-Pro-Gly-Gly (GPGG). J. Am. Soc. Mass Spectrom. 2015, 26, 1444–1454. 10.1007/s13361-015-1172-4. [DOI] [PubMed] [Google Scholar]
- Hoaglund-Hyzer C. S.; Counterman A. E.; Clemmer D. E. Anhydrous Protein Ions. Chem. Rev. 1999, 99, 3037–3079. 10.1021/cr980139g. [DOI] [PubMed] [Google Scholar]
- Wyttenbach T.; Bowers M. T. Structural stability from solution to the gas phase: Native solution structure of ubiquitin survives analysis in a solvent-free ion mobility-mass spectrometry environment. J. Phys. Chem. B 2011, 115, 12266–12275. 10.1021/jp206867a. [DOI] [PubMed] [Google Scholar]
- Rijs Anouk M.; Oomens J.. Gas-Phase IR Spectroscopy and Structure of Biological Molecules, 1st ed.; Springer: Cham, Switzerland, 2015; Vol. 364, 10.1007/978-3-319-19204-8. [DOI] [Google Scholar]
- Bakels S.; Gaigeot M. P.; Rijs A. M. Gas-Phase Infrared Spectroscopy of Neutral Peptides: Insights from the Far-IR and THz Domain. Chem. Rev. 2020, 120, 3233–3260. 10.1021/acs.chemrev.9b00547. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scutelnic V.; Perez M. A.; Marianski M.; Warnke S.; Gregor A.; Rothlisberger U.; Bowers M. T.; Baldauf C.; Von Helden G.; Rizzo T. R.; Seo J. The Structure of the Protonated Serine Octamer. J. Am. Chem. Soc. 2018, 140, 7554–7560. 10.1021/jacs.8b02118. [DOI] [PubMed] [Google Scholar]
- Hünig I.; Kleinermanns K. Conformers of the peptides glycine-tryptophan, tryptophan-glycine and tryptophan-glycine-glycine as revealed by double resonance laser spectroscopy. Phys. Chem. Chem. Phys. 2004, 6, 2650–2658. 10.1039/B316295H. [DOI] [Google Scholar]
- Bakker J. M.; Plutzer C.; Hünig I.; Häber T.; Compagnon I.; Von Helden G.; Meijer G.; Kleinermanns K. Folding structures of isolated peptides as revealed by gas-phase mid-infrared spectroscopy. ChemPhysChem 2005, 6, 120–128. 10.1002/cphc.200400345. [DOI] [PubMed] [Google Scholar]
- Chin W.; Dognon J. P.; Piuzzi F.; Tardivel B.; Dimicoli I.; Mons M. Intrinsic folding of small peptide chains: Spectroscopic evidence for the formation of β-turns in the gas phase. J. Am. Chem. Soc. 2005, 127, 707–712. 10.1021/ja045251c. [DOI] [PubMed] [Google Scholar]
- Häber T.; Seefeld K.; Kleinermanns K. Mid- and near-infrared spectra of conformers of H-Pro-Trp-OH. J. Phys. Chem. A 2007, 111, 3038–3046. 10.1021/jp070571e. [DOI] [PubMed] [Google Scholar]
- Jaeqx S.; Du W.; Meijer E. J.; Oomens J.; Rijs A. M. Conformational study of Z-Glu-OH and Z-Arg-OH: Dispersion interactions versus conventional hydrogen bonding. J. Phys. Chem. A 2013, 117, 1216–1227. 10.1021/jp3053339. [DOI] [PubMed] [Google Scholar]
- Nagornova N. S.; Guglielmi M.; Doemer M.; Tavernelli I.; Rothlisberger U.; Rizzo T. R.; Boyarkin O. V. Cold-ion spectroscopy reveals the intrinsic structure of a decapeptide. Angewandte Chemie - International Edition 2011, 50, 5383–5386. 10.1002/anie.201100702. [DOI] [PubMed] [Google Scholar]
- Gloaguen E.; Mons M.; Schwing K.; Gerhards M. Neutral Peptides in the Gas Phase: Conformation and Aggregation Issues. Chem. Rev. 2020, 120, 12490–12562. 10.1021/acs.chemrev.0c00168. [DOI] [PubMed] [Google Scholar]
- Aseev O.; Perez M. A.; Rothlisberger U.; Rizzo T. R. Cryogenic Spectroscopy and Quantum Molecular Dynamics Determine the Structure of Cyclic Intermediates Involved in Peptide Sequence Scrambling. J. Phys. Chem. Lett. 2015, 6, 2524–2529. 10.1021/acs.jpclett.5b01088. [DOI] [PubMed] [Google Scholar]
- Loquais Y.; Gloaguen E.; Habka S.; Vaquero-Vara V.; Brenner V.; Tardivel B.; Mons M. Secondary Structures in Phe-Containing Isolated Dipeptide Chains: Laser Spectroscopy vs Quantum Chemistry. J. Phys. Chem. A 2015, 119, 5932–5941. 10.1021/jp509494c. [DOI] [PubMed] [Google Scholar]
- Schubert F.; Rossi M.; Baldauf C.; Pagel K.; Warnke S.; von Helden G.; Filsinger F.; Kupser P.; Meijer G.; Salwiczek M.; Koksch B.; Scheffler M.; Blum V. Exploring the conformational preferences of 20-residue peptides in isolation: Ac-Ala19-Lys + H+vs. Ac-Lys-Ala19 + H+ and the current reach of DFT. Phys. Chem. Chem. Phys. 2015, 17, 7373–7385. 10.1039/C4CP05541A. [DOI] [PubMed] [Google Scholar]
- Hao G. F.; Xu W. F.; Yang S. G.; Yang G. F. Multiple simulated annealing-molecular dynamics (MSA-MD) for conformational space search of peptide and miniprotein. Sci. Rep. 2015, 5, 15568. 10.1038/srep15568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rossi M.; Chutia S.; Scheffler M.; Blum V. Validation challenge of density-functional theory for peptides - Example of Ac-Phe-Ala5-LysH+. J. Phys. Chem. A 2014, 118, 7349–7359. 10.1021/jp412055r. [DOI] [PubMed] [Google Scholar]
- Damsbo M.; Kinnear B. S.; Hartings M. R.; Ruhoff P. T.; Jarrold M. F.; Ratner M. A. Application of evolutionary algorithm methods to polypeptide folding: Comparison with experimental results for unsolvated Ac-(Ala-Gly-Gly)5-LysH+. Proc. Natl. Acad. Sci. U. S. A. 2004, 101, 7215–7222. 10.1073/pnas.0401659101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doemer M.; Guglielmi M.; Athri P.; Nagornova N. S.; Rizzo T. R.; Boyarkin O. V.; Tavernelli I.; Rothlisberger U. Assessing the performance of computational methods for the prediction of the ground state structure of a cyclic decapeptide. Int. J. Quantum Chem. 2013, 113, 808–814. 10.1002/qua.24085. [DOI] [Google Scholar]
- Holland J. H.Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence, 1st ed.; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Mitchell M.An Introduction to Genetic Algorithms, 1st ed.; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Kramer O.Genetic Algorithm Essentials, 1st ed.; Springer: Cham, Switzerland, 2017, 10.1007/978-3-319-52156-5. [DOI] [Google Scholar]
- Deaven D. M.; Ho K. M. Molecular Geometry Optimization with a Genetic Algorithm. Phys. Rev. Lett. 1995, 75, 288–291. 10.1103/PhysRevLett.75.288. [DOI] [PubMed] [Google Scholar]
- Unger R.; Moult J. Genetic Algorithms for Protein Folding Simulations. J. Mol. Biol. 1993, 231, 75–81. 10.1006/jmbi.1993.1258. [DOI] [PubMed] [Google Scholar]
- Pedersen J. T.; Moult J. Genetic algorithms for protein structure prediction. Curr. Opin. Struct. Biol. 1996, 6, 227–231. 10.1016/S0959-440X(96)80079-0. [DOI] [PubMed] [Google Scholar]
- Unger R.Applications of Evolutionary Computation in Chemistry, 1st ed.; Springer: Berlin, 2004; Vol. 110, pp 153–175, 10.1007/b13936. [DOI] [Google Scholar]
- Judson R. S.; Jaeger E. P.; Treasurywala A. M.; Peterson M. L. Conformational searching methods for small molecules. II. Genetic algorithm approach. J. Comput. Chem. 1993, 14, 1407–1414. 10.1002/jcc.540141117. [DOI] [Google Scholar]
- Nair N.; Goodman J. M. Genetic Algorithms in Conformational Analysis. J. Chem. Inf. Comput. Sci. 1998, 38, 317–320. 10.1021/ci970433u. [DOI] [Google Scholar]
- Vainio M. J.; Johnson M. S. Generating Conformer Ensembles Using a Multiobjective Genetic Algorithm. J. Chem. Inf. Model. 2007, 47, 2462–2474. 10.1021/ci6005646. [DOI] [PubMed] [Google Scholar]
- Mcgarrah D. B.; Judson R. S. Analysis of the genetic algorithm method of molecular conformation determination. J. Comput. Chem. 1993, 14, 1385–1395. 10.1002/jcc.540141115. [DOI] [Google Scholar]
- Herrmann F.; Suhai S. Energy minimization of peptide analogues using genetic algorithms. J. Comput. Chem. 1995, 16, 1434–1444. 10.1002/jcc.540161112. [DOI] [Google Scholar]
- Supady A.; Blum V.; Baldauf C. First-Principles Molecular Structure Search with a Genetic Algorithm. J. Chem. Inf. Model. 2015, 55, 2338–2348. 10.1021/acs.jcim.5b00243. [DOI] [PubMed] [Google Scholar]
- Pedersen J. T.; Moult J. Ab initio structure prediction for small polypeptides and protein fragments using genetic algorithms. Proteins: Struct., Funct., Bioinf. 1995, 23, 454–460. 10.1002/prot.340230319. [DOI] [PubMed] [Google Scholar]
- Pedersen J. T.; Moult J. Ab initio protein folding simulations with genetic algorithms: Simulations on the complete sequence of small proteins. Proteins: Struct., Funct., Bioinf. 1997, 29, 179–184. . [DOI] [PubMed] [Google Scholar]
- Pedersen J. T.; Moult J. Protein folding simulations with genetic algorithms and a detailed molecular description. J. Mol. Biol. 1997, 269, 240–259. 10.1006/jmbi.1997.1010. [DOI] [PubMed] [Google Scholar]
- Le Grand S. M.; Merz K. M. The Genetic Algorithm and the Conformational Search of Polypeptides and Proteins. Mol. Simul. 1994, 13, 299–320. 10.1080/08927029408021995. [DOI] [Google Scholar]
- Le Grand S. M.; Merz K. M. The application of the genetic algorithm to the minimization of potential energy functions. Journal of Global Optimization 1993, 3, 49–66. 10.1007/BF01100239. [DOI] [Google Scholar]
- Schulze-Kremer S.Genetic Algorithms and Protein Folding. Protein Structure Prediction: Methods and Protocols; Methods in Molecular Biology, Vol. 143; Humana Press, 2000; pp 175–222, 10.1385/1-59259-368-2:175. [DOI] [PubMed] [Google Scholar]
- Mijajlovic M.; Biggs M. J.; Djurdjevic D. P. On Potential Energy Models for EA-based Ab Initio Protein Structure Prediction. Evolutionary Computation 2010, 18, 255–275. 10.1162/evco.2010.18.2.18204. [DOI] [PubMed] [Google Scholar]
- Steinegger M.; Meier M.; Mirdita M.; Vöhringer H.; Haunsberger S. J.; Söding J. HH-suite3 for fast remote homology detection and deep protein annotation. BMC bioinformatics 2019, 20, 473. 10.1186/s12859-019-3019-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dor O.; Zhou Y. Achieving 80% ten-fold cross-validated accuracy for secondary structure prediction by large-scale training. Proteins: Struct., Funct., Bioinf. 2007, 66, 838–845. 10.1002/prot.21298. [DOI] [PubMed] [Google Scholar]
- Sitkiewicz S. P.; Zaleśny R.; Ramos-Cordoba E.; Luis J. M.; Matito E. How Reliable Are Modern Density Functional Approximations to Simulate Vibrational Spectroscopies?. J. Phys. Chem. Lett. 2022, 13, 5963–5968. 10.1021/acs.jpclett.2c01278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berman H. M.; Westbrook J.; Feng Z.; Gilliland G.; Bhat T. N.; Weissig H.; Shindyalov I. N.; Bourne P. E. The Protein Data Bank. Nucleic Acids Res. 2000, 28, 235–242. 10.1093/nar/28.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stephens P. J.; Devlin F. J.; Chabalowski C. F.; Frisch M. J. Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields. J. Phys. Chem. 1994, 98, 11623–11627. 10.1021/j100096a001. [DOI] [Google Scholar]
- Nagornova N. S.; Rizzo T. R.; Boyarkin O. V. Highly resolved spectra of gas-phase gramicidin S: A benchmark for peptide structure calculations. J. Am. Chem. Soc. 2010, 132, 4040–4041. 10.1021/ja910118j. [DOI] [PubMed] [Google Scholar]
- Hornak V.; Abel R.; Okur A.; Strockbine B.; Roitberg A.; Simmerling C. Comparison of multiple Amber force fields and development of improved protein backbone parameters. Proteins: Struct., Funct., Bioinf. 2006, 65, 712–725. 10.1002/prot.21123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Z.-X.; Zhang W.; Wu C.; Lei H.; Cieplak P.; Duan Y. Strike a balance: Optimization of backbone torsion parameters of AMBER polarizable force field for simulations of proteins and peptides. J. Comput. Chem. 2006, 27, 781–790. 10.1002/jcc.20386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Browning N. J.Applications of Artificial Intelligence to Computational Chemistry. Ph.D. thesis, EPFL, Lausanne, 2019. [Google Scholar]
- (Releases of EVOLVE will be available on GitHub)
- Brunk E.; Perez M. A.; Athri P.; Rothlisberger U. Genetic-Algorithm-Based Optimization of a Peptidic Scaffold for Sequestration and Hydration of CO2. ChemPhysChem 2016, 17, 3831–3835. 10.1002/cphc.201601034. [DOI] [PubMed] [Google Scholar]
- Bozkurt E.; Perez M. A.; Hovius R.; Browning N. J.; Rothlisberger U. Genetic Algorithm Based Design and Experimental Characterization of a Highly Thermostable Metalloprotein. J. Am. Chem. Soc. 2018, 140, 4517–4521. 10.1021/jacs.7b10660. [DOI] [PubMed] [Google Scholar]
- Browning N. J.; Ramakrishnan R.; von Lilienfeld O. A.; Roethlisberger U. Genetic Optimization of Training Sets for Improved Machine Learning Models of Molecular Properties. J. Phys. Chem. Lett. 2017, 8, 1351–1359. 10.1021/acs.jpclett.7b00038. [DOI] [PubMed] [Google Scholar]
- Brain Z. E.; Addicoat M. A. Optimization of a genetic algorithm for searching molecular conformer space. J. Chem. Phys. 2011, 135, 174106. 10.1063/1.3656323. [DOI] [PubMed] [Google Scholar]
- Ramachandran G. N.; Ramakrishnan C.; Sasisekharan V. Stereochemistry of polypeptide chain configurations. J. Mol. Biol. 1963, 7, 95–99. 10.1016/S0022-2836(63)80023-6. [DOI] [PubMed] [Google Scholar]
- O’Boyle N. M.; Banck M.; James C. A.; Morley C.; Vandermeersch T.; Hutchison G. R. Open Babel: An open chemical toolbox. J. Cheminform. 2011, 3, 33. 10.1186/1758-2946-3-33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frisch M. J.; et al. Gaussian 16, Rev. A.03; 2016; https://gaussian.com (accessed 2022-10-13).
- Case D. A.; et al. AMBER 2018; University of California: San Francisco, 2018; https://ambermd.org (accessed 2022-10-13).
- Eastman P.; Swails J.; Chodera J. D.; McGibbon R. T.; Zhao Y.; Beauchamp K. A.; Wang L.-P.; Simmonett A. C.; Harrigan M. P.; Stern C. D.; Wiewiora R. P.; Brooks B. R.; Pande V. S. OpenMM 7: Rapid development of high performance algorithms for molecular dynamics. PLOS Comput. Biol. 2017, 13, e1005659. 10.1371/journal.pcbi.1005659. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hjorth Larsen A.; et al. The atomic simulation environment—a Python library for working with atoms. J. Phys.: Condens. Matter 2017, 29, 273002. 10.1088/1361-648X/aa680e. [DOI] [PubMed] [Google Scholar]
- Deb K.; Agrawal R. B. Simulated Binary Crossover for Continuous Search Space. Complex Syst. 1995, 9, 115–148. [Google Scholar]
- Beyer H.-G.; Schwefel H.-P. Evolution strategies – A comprehensive introduction. Natural Computing 2002, 1, 3–52. 10.1023/A:1015059928466. [DOI] [Google Scholar]
- Ahn C. W.; Ramakrishna R. S. Elitism-based compact genetic algorithms. IEEE Transa. Evol. Comput. 2003, 7, 367–385. 10.1109/TEVC.2003.814633. [DOI] [Google Scholar]
- Du H.; Wang Z.; Zhan W.; Guo J. Elitism and distance strategy for selection of evolutionary algorithms. IEEE Access 2018, 6, 44531–44541. 10.1109/ACCESS.2018.2861760. [DOI] [Google Scholar]
- Wang J.; Wolf R. M.; Caldwell J. W.; Kollman P. A.; Case D. A. Development and testing of a general Amber force field. J. Comput. Chem. 2004, 25, 1157–1174. 10.1002/jcc.20035. [DOI] [PubMed] [Google Scholar]
- Bayly C. I.; Cieplak P.; Cornell W. D.; Kollman P. A. A well-behaved electrostatic potential based method using charge restraints for deriving atomic charges: The RESP model. J. Phys. Chem. 1993, 97, 10269–10280. 10.1021/j100142a004. [DOI] [Google Scholar]
- Jakalian A.; Bush B. L.; Jack D. B.; Bayly C. I. Fast, Efficient Generation of High-Quality Atomic Charges. AM1-BCC Model: I. Method. J. Comput. Chem. 2000, 21, 132–146. . [DOI] [PubMed] [Google Scholar]
- Jakalian A.; Jack D. B.; Bayly C. I. Fast, efficient generation of high-quality atomic charges. AM1-BCC model: II. Parameterization and validation. J. Comput. Chem. 2002, 23, 1623–1641. 10.1002/jcc.10128. [DOI] [PubMed] [Google Scholar]
- Schaftenaar G.; Vlieg E.; Vriend G. Molden 2.0: quantum chemistry meets proteins. Journal of Computer-Aided Molecular Design 2017, 31, 789–800. 10.1007/s10822-017-0042-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Llamas-Saiz A. L.; Grotenbreg G. M.; Overhand M.; Van Raaij M. J. Double-stranded helical twisted β-sheet channels in crystals of gramicidin S grown in the presence of trifluoroacetic and hydrochloric acids. Acta Crystallographica Section D: Biological Crystallography 2007, 63, 401–407. 10.1107/S0907444906056435. [DOI] [PubMed] [Google Scholar]
- Shi Y.; Xia Z.; Zhang J.; Best R.; Wu C.; Ponder J. W.; Ren P. Polarizable atomic multipole-based AMOEBA force field for proteins. J. Chem. Theory Comput. 2013, 9, 4046–4063. 10.1021/ct4003702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elstner M.; Porezag D.; Jungnickel G.; Elsner J.; Haugk M.; Frauenheim T.; Suhai S.; Seifert G. Self-consistent-charge density-functional tight-binding method for simulations of complex materials properties. Phys. Rev. B 1998, 58, 7260–7268. 10.1103/PhysRevB.58.7260. [DOI] [Google Scholar]
- Gaus M.; Cui Q.; Elstner M. DFTB3: Extension of the Self-Consistent-Charge Density-Functional Tight-Binding Method (SCC-DFTB). J. Chem. Theory Comput. 2011, 7, 931–948. 10.1021/ct100684s. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hourahine B.; et al. DFTB+, a software package for efficient approximate density functional theory based atomistic simulations. J. Chem. Phys. 2020, 152, 124101. 10.1063/1.5143190. [DOI] [PubMed] [Google Scholar]
- Gaus M.; Goez A.; Elstner M. Parametrization and benchmark of DFTB3 for organic molecules. J. Chem. Theory Comput. 2013, 9, 338–354. 10.1021/ct300849w. [DOI] [PubMed] [Google Scholar]
- Grimme S.; Antony J.; Ehrlich S.; Krieg H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. 10.1063/1.3382344. [DOI] [PubMed] [Google Scholar]
- Brandenburg J. G.; Grimme S. Accurate modeling of organic molecular crystals by dispersion-corrected density functional tight binding (DFTB). J. Phys. Chem. Lett. 2014, 5, 1785–1789. 10.1021/jz500755u. [DOI] [PubMed] [Google Scholar]
- Grimme S.; Ehrlich S.; Goerigk L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32, 1456–1465. 10.1002/jcc.21759. [DOI] [PubMed] [Google Scholar]
- Ufimtsev I. S.; Martinez T. J. Quantum chemistry on graphical processing units. 3. Analytical energy gradients, geometry optimization, and first principles molecular dynamics. J. Chem. Theory Comput. 2009, 5, 2619–2628. 10.1021/ct9003004. [DOI] [PubMed] [Google Scholar]
- Titov A. V.; Ufimtsev I. S.; Luehr N.; Martinez T. J. Generating efficient quantum chemistry codes for novel architectures. J. Chem. Theory Comput. 2013, 9, 213–221. 10.1021/ct300321a. [DOI] [PubMed] [Google Scholar]
- Kästner J.; Carr J. M.; Keal T. W.; Thiel W.; Wander A.; Sherwood P. DL-FIND: An open-source geometry optimizer for atomistic simulations. J. Phys. Chem. A 2009, 113, 11856–11865. 10.1021/jp9028968. [DOI] [PubMed] [Google Scholar]
- Stewart J. J. Optimization of parameters for semiempirical methods V: Modification of NDDO approximations and application to 70 elements. J. Mol. Model. 2007, 13, 1173–1213. 10.1007/s00894-007-0233-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stewart J. J. Optimization of parameters for semiempirical methods VI: More modifications to the NDDO approximations and re-optimization of parameters. J. Mol. Model. 2013, 19, 1–32. 10.1007/s00894-012-1667-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li X.; Frisch M. J. Energy-Represented Direct Inversion in the Iterative Subspace within a Hybrid Geometry Optimization Method. J. Chem. Theory Comput. 2006, 2, 835–839. 10.1021/ct050275a. [DOI] [PubMed] [Google Scholar]
- Cersonsky R. K.; Helfrecht B. A.; Engel E. A.; Kliavinek S.; Ceriotti M. Improving sample and feature selection with principal covariates regression. Mach. Learn.: Sci. Technol. 2021, 2, 035038. 10.1088/2632-2153/abfe7c. [DOI] [Google Scholar]
- Bussi G.; Gervasio F. L.; Laio A.; Parrinello M. Free-energy landscape for β hairpin folding from combined parallel tempering and metadynamics. J. Am. Chem. Soc. 2006, 128, 13435–13441. 10.1021/ja062463w. [DOI] [PubMed] [Google Scholar]
- Mancini G.; Fusè M.; Lazzari F.; Barone V. Fast exploration of potential energy surfaces with a joint venture of quantum chemistry, evolutionary algorithms and unsupervised learning. Digital Discovery 2022, 1, 790–805. 10.1039/D2DD00070A. [DOI] [Google Scholar]
- Chmiela S.; Sauceda H. E.; Poltavsky I.; Müller K. R.; Tkatchenko A. sGDML: Constructing accurate and data efficient molecular force fields using machine learning. Comput. Phys. Commun. 2019, 240, 38–45. 10.1016/j.cpc.2019.02.007. [DOI] [Google Scholar]
- von Lilienfeld O. A.; Müller K. R.; Tkatchenko A. Exploring chemical compound space with quantum-based machine learning. Nature Reviews Chemistry 2020, 4, 347–358. 10.1038/s41570-020-0189-9. [DOI] [PubMed] [Google Scholar]
- Unke O. T.; Chmiela S.; Sauceda H. E.; Gastegger M.; Poltavsky I.; Schütt K. T.; Tkatchenko A.; Müller K.-R. R. Machine Learning Force Fields. Chem. Rev. 2021, 121, 10142–10186. 10.1021/acs.chemrev.0c01111. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
A snapshot version of the EVOLVE code67 as used in this work is provided on Zenodo at 10.5281/zenodo.7251981, along with the data and analysis scripts needed to reproduce the results.















