Locomotion of bovine spermatozoa during the transition from individual cells to bundles

Significance

Evolutionary selective pressures drive spermatozoa to assemble into bundles for increased fertilizing ability. To understand this type of collective behavior of spermatozoa, we investigate the underlying mechanisms that make spermatozoa form bundles. Here, we explore the dynamic processes during the bundle formation by characterizing the cell-to-cell interactions in three consecutive phases: far field–locking, rotational-oscillation, and steady-swimming phase. During these phases, the interactions are found to regulate flagellar beat and lead to three dynamic behaviors: hydrodynamic attraction/repulsion, alignment, and synchronization, whereby sperm cells can obtain enhanced swimming velocity. Our study not only reveals the efficient collective locomotion of spermatozoa at a low Reynolds number but also inspires the design of adaptive and powerful soft microrobots.

Abstract

Various locomotion strategies employed by microorganisms are observed in complex biological environments. Spermatozoa assemble into bundles to improve their swimming efficiency compared to individual cells. However, the dynamic mechanisms for the formation of sperm bundles have not been fully characterized. In this study, we numerically and experimentally investigate the locomotion of spermatozoa during the transition from individual cells to bundles of two cells. Three consecutive dynamic behaviors are found across the course of the transition: hydrodynamic attraction/repulsion, alignment, and synchronization. The hydrodynamic attraction/repulsion depends on the relative orientation and distance between spermatozoa as well as their flagellar wave patterns and phase shift. Once the heads are attached, we find a stable equilibrium of the rotational hydrodynamics resulting in the alignment of the heads. The synchronization results from the combined influence of hydrodynamic and mechanical cell-to-cell interactions. Additionally, we find that the flagellar beat is regulated by the interactions during the bundle formation, whereby spermatozoa can synchronize their beats to enhance their swimming velocity.

Collective locomotion emerges in multiscale biological systems ranging from cilia/flagella arrays (1), bacterial colonies (2), and insect swarms (3) to animal herds (4). These systems show interesting ordering phenomena (4). For instance, at the microscale, biological cilia/flagella arrays can spontaneously exhibit metachronal waves, resulting in enhanced fluid transport (5, 6). Facilitated by the collective locomotion of their cilia/flagella, some unicellular organisms exhibit high efficiency in spreading (2), feeding (7), or swimming (1). Collective locomotion also emerges in spermatozoa driven by flagella. In some higher organisms, e.g., bulls (8), rodents (9, 10), and insects (11), spermatozoa are found to assemble into bundles. The assembly is an efficient locomotion strategy at a low Reynolds number, which has been numerically (12–16) and experimentally (8–10) demonstrated to increase the swimming speed of spermatozoa, whereby their fertilizing ability is favored (10, 17).

The swimming velocity of sperm bundles comprising multiple cells results from complex cell-to-cell interactions. A mechanical model of sperm bundles suggests that the swimming speed of sperm bundles is subject to the bundle size and there exists an optimal sperm bundle size giving rise to a maximum rectilinear velocity (13). In addition, the performance of sperm bundles is significantly affected by the geometry of sperm heads, structure of the adhesive region of the heads, and the angle between the heads (14, 16).

However, as the minimal model of collective locomotion of sperm cells, the system of two spermatozoa already shows complex interactions. The interactions are found to cause flagellar synchronization (8, 18) and attraction/repulsion between two sperm cells (12, 18, 19). The emergence of flagellar synchronization is attributed to either only hydrodynamic interactions (12, 19, 20) or dominantly mechanical interactions (8, 21). The cell-to-cell attraction/repulsion as well as the swimming speeds of two sperm cells depend on their configuration, separation distance, and phase shift of flagellar waves (12, 19), which is consistent with the prediction of a numerical model of two three-sphere swimmers (22).

Although the collective locomotion of sperm cells has been preliminarily disclosed (8, 12–14, 18, 19), it is still not fully understood, especially the dynamic processes during the transition from individual cells to bundles. A recent study explains that the bundling of sperm cells is a result of hydrodynamic and adhesive interactions which occur frequently during prolonged incubation times. Mostly pairs of two motile sperm cells are formed (23). There are only a few studies of bundle formation for two key reasons. First, the momentary formation of sperm bundles occurs randomly, limiting our ability to observe and measure their motion characteristics. Second, the locomotion of spermatozoa during bundle formation is influenced by time-varying cell-to-cell interactions. The interactions and bundle formation are likely to be affected by intrinsic and external factors. The intrinsic factors that characterize the locomotion of sperm cells are represented by the time-dependent wave variables (i.e., the mean flagellar curvature K₀, bending amplitude A₀, wavelength λ, and angular frequency ω) of the actively propagating waves along flagella, the phase shift of the flagellar waves Δϕ, and the angle between the heads Δθ. The external factors denote the parameters that can influence the bundle formation through the environment, such as the geometry of the surrounding environment (24), chemoattractants (25), and the viscosity of fluids (26).

In this study, we investigate the dynamic formation of bundles of two sperm cells with regard to the intrinsic factors and the external factor, fluid viscosity μ. We divide the formation into three phases: far field–locking (FFL) phase, rotational-oscillation (RO) phase, and steady-swimming (SS) phase. These phases are experimentally observed during the bundle formation. We numerically investigate the hydrodynamic cell-to-cell interactions of the spermatozoa during the three consecutive phases. Further, time-dependent wave variables are measured to characterize the flagellar wave pattern across the whole course of the transition.

Results

Formation of Sperm Bundles.

Spermatozoa display a variety of three-dimensional (3D) swimming patterns (27–29). However, they tend to gather near the bottom surface and hence exhibit flagellar beats that consist mostly of planar waves due to hydrodynamic cell-to-surface interactions (30, 31). Therefore, we characterize the flagellar waves in the plane where sperm cells swim, neglecting the out-of-plane component (Fig. 1A). The time-varying flagellar wave pattern of the ith sperm cell is characterized in terms of the position vector of the centerline of the flagellum ⁱr(s_i, t) in the laboratory frame and in terms of the wave variables in the material frame spanned by the orthonormal unit vectors ${}^i{\mathbf{e}}_1$ and ${}^i{\mathbf{e}}_2$ (32, 33) (Materials and Methods). Here, ${}^i{\mathbf{e}}_1$ and ${}^i{\mathbf{e}}_2$ are the unit vectors oriented along the long axis and short axis of the projection of the head of the ith sperm cell in the swimming plane, respectively (Fig. 1B).

Fig. 1.

Locomotion and hydrodynamic interactions of sperm cells are modeled. (A) Sperm suspension is pipetted in a 20 µm-high chamber and recorded with an inverted microscope. Near the bottom surface of the chamber, the sperm cells exhibit primarily planar flagellar beats in the swimming plane with distance d from the bottom surface. (B, i) The locomotion of sperm cells is characterized in the swimming plane. The flagellar pattern at a time t can be characterized by the tangent angle ψ along the flagellum in the material frame spanned by orthonormal vector e${}_1$ and e${}_2$. The orientation θ${}_1$ is positive, and θ${}_2$ is negative. (B, ii) Each sperm cell is discretized with N points. The hydrodynamic force ⁱf${}_k$ on the kth points along the ith flagellum and fluid flow u(x) at the point x are contributed by every regularized Stokeslets on the surface of the sperm cells. Here, the force ⁱf${}_k$ is the discretization of ⁱf(s${}_i$,t). Further, the rotation of ith head leads to a hydrodynamic torque in the swimming plane ⁱM_h. The position vector ⁱr${}_k$ is used to determine the time-varying flagellar waveform. Note that the force f${}_k$, torque M_h, velocity of the fluid u, and position vector r${}_k$ and x are vectors in the three-dimensional space.

Flagellar beats are governed by the balance between the internal force generated by many active elements (e.g., dyneins) and passive elastic elements (e.g., nexins) and the external forces on the flagellum (32, 34). The external forces can result from either the fluid flow induced by other cells or mechanical coupling when the cells are in physical contact. Therefore, the flagellar beat as well as the movement of cells is regulated by hydrodynamic or mechanical cell-to-cell interactions during the bundle formation, which consists of three phases. In the FFL phase, two sperm cells approach each other until their heads come into contact. Hydrodynamic attraction between the cells is likely to facilitate the approach. Once the heads are attached, the mechanical interaction between the heads constrains the relative translational motion but allows the ith cell to rotate about the axis ${}^{\mathit{ij}}\mathbf{e}={}^i{\mathbf{e}}_1\times {}^j{\mathbf{e}}_1$, (i + j = 3) (Fig. 2A, iii and iv and B, iii–v). During this RO phase, the interactions break the regular flagellar beat and result in the alignment of the heads. Finally, under the combined influence of the hydrodynamic and mechanical cell-to-cell interactions, the sperm bundles resume regular flagellar beats during the SS phase (Fig. 2A, v and vi and B, vi).

Fig. 2.

The transition from individual cells to a bundle of two cells is observed in low- and high-viscosity media. (A) In the relatively high-viscosity medium of 15 mPas, two sperm cells beat their flagellum from side to side and swim toward each other during the far field–locking (FFL) phase (i and ii) and then align during the rotational-oscillation (RO) phase (iii and iv). Finally, the heads adhere rigidly, and the flagellar beats are synchronized during the steady-swimming (SS) phase (v and vi). (B) In the relatively low-viscosity medium of 1.2 mPas, two sperm cells exhibit one-sided flagellar beats. During the FFL phase (i and ii), the cells are attached and form a configuration that their flagella beat toward each other. Thus, the spermatozoa are repelling each other during the RO phase first, leading cell 1 and cell 2 to rotate clockwise and counterclockwise, respectively (iii to iv). Then, the heads are aligned by the hydrodynamic forces on the flagella (iv to v). In the SS phase (vi), the head-to-head attachment is weak such that the heads can still rotate and the flagellar beats fail to synchronize.

Flow Fields during Far Field–Locking Phase.

From a kinematic perspective, the only way spermatozoa interact with neighbor cells is through the induced flow field. To elucidate the influence of the intrinsic and external factors on the locomotion of sperm cells, we construct a 3D fluid model to calculate the hydrodynamic forces on the cells and the flow field by solving the Stokes equations using regularized Stokeslets method (Materials and Methods). Previous studies show that a large proportion of the sperm cells near the bottom are approximately between 0.05 and 0.2 times their body length from the bottom surface (35–37). With a body length of 60 µm of bovine sperm, we can assume that they swim approximately between 3 and 12 µm from the bottom surface. In our 3D model, the two sperm cells swim in the same plane with distance d from the bottom surface. (Fig. 1A and Fig. 3 A, i). A series of calculations for hydrodynamic force ⟨ΔF_y⟩ on the sperm cells are performed at different distances of 3, 4, 10 µm as well as the far-field condition (Fig. 3 and SI Appendix, Fig. S1). The compliance of the flexible flagella is also considered in the calculation by reconstructing the flagellar wave patterns of the cells with the time-averaged wave variables over the far field–locking phase measured in the experiments (Table 1).

Fig. 3.

Hydrodynamic interactions between spermatozoa with distance 4 µm from the bottom surface. (A) Seven representative time-averaged flow fields in the swimming plane induced by the sperm cells over one beat cycle T in the medium with a viscosity µ of 15 mPas. (i) The cells are in the swimming plane 4 µm from the bottom surface. The surfaces of the top and bottom of the chamber and the sperm cells are discretized for the calculation of hydrodynamic forces using regularized Stokeslets. The flagellar wave shift Δϕ is zero, and the angle between the heads Δθ equals 0 (ii), /6 (iii), /3 (iv), /2 (v), 2/3 (vi), 5/6 (vii), and (viii), respectively. (B) The hydrodynamic forces for the spermatozoa with Δϕ = /3 and Δθ = /2 are time-varying during the same beat cycle T. Here, F${}_x$(t), ⁱF${}_y$(t), and ⁱF${}_z$(t) are the hydrodynamic force on the ith sperm cell along the x-, y-, and z-axis, respectively. The curves for ¹F${}_z$(t) and ²F${}_z$(t) are overlapped as their differences are very small. (C) The difference between the forces ⟨ΔF_y⟩ = ⟨²F_y⟩ − $⟨{}^1{\mathbf{F}}_y⟩$ characterizes the cell-to-cell attraction/repulsion and is computed for Δθ (the radial coordinate) in the range of 0 to and Δϕ (the angular coordinate) in the range of 0 to 2. Each combination of Δθ and Δϕ represents a configuration of the two cells. Each dot in the polar scatter charts denotes a value of ⟨ΔF_y⟩ regarding a configuration of the two cells. (i) The force ⟨ΔF_y⟩ for a pair of cells swimming in the high-viscosity medium of µ = 15 mPas is calculated. The maximum repulsive force emerges from the configuration of Δθ = and Δϕ = 3/2. The waveforms of the spermatozoa in the high-viscosity medium of 15 mPas are reconstructed with the wave variables (i.e., the mean flagellar curvature K${}_0$, bending amplitude A${}_0$, wavelength, and angular frequency ω), such that ¹K${}_0$ = 5.3 rad/mm, ¹A${}_0$ = 9.8 rad/mm, ${}_1$ = 45.6 µm, ω${}_1$ = 45.5 rad/s, ²K${}_0$ = 24.8 rad/mm, ²A${}_0$ = 11.2 rad/mm, ${}_2$ = 36.8 µm, and ω${}_2$ = 45.5 rad/s. The values of these wave variables are the averaged values over the far field–locking phase (Table 1). (ii) The force ⟨ΔF_y⟩ for a pair of cells swimming in the low-viscosity medium of µ = 1.2 mPas is calculated. The maximum attractive force is induced when the configuration of the cells is Δθ = 0 and Δϕ = /2. In the simulation, the radii and lengths of the flagella are 0.25 µm and 60 µm, respectively. For each cell, the head is modeled as an ellipsoid, whose dimensions are 9 µm (length), 5 µm (width), and 1 µm (height), respectively. The head-to-head distance is 50 µm. The waveforms of the spermatozoa in the low-viscosity medium of 1.2 mPas are reconstructed with the wave variables, such that ¹K${}_0$ = 24.6 rad/mm, ¹A${}_0$ = 11.4 rad/mm, ${}_1$ = 59.6 µm, ω${}_1$ = 98.2 rad/s, ²K${}_0$ = −23.0 rad/mm, ²A${}_0$ = 12.0 rad/mm, ${}_2$ = 57.5 µm, and ω${}_2$ = 98.2 rad/s. The values of these wave variables are the averaged values over the far field–locking phase (Table 1).

Table 1.

Experimental results of time-averaged wave variables

µ		〈1K0〉	〈2K0〉	〈1A0〉	〈2A0〉	〈λ1〉	〈λ2〉	〈ω1〉	〈ω2〉	N ${}_1$	N ${}_2$
[mPas]	Phase	[rad/mm]	[rad/mm]	[rad/mm]	[rad/mm]	[µm]	[µm]	[rad/s]	[rad/s]	[cycles]	[cycles]
15	FFL	5.3 ± 1.0	24.8 ± 2.1	9.8 ± 1.2	11.2 ± 1.6	45.6 ± 3.5	36.8 ± 2.9	37.3 ± 2.5	55.6 ± 7.4	5	7
	RO	6.6 ± 2.1	22.2 ± 1.7	9.7 ± 1.7	8.8 ± 1.4	46.7 ± 3.8	42.5 ± 4.0	42.6 ± 6.0	52.8 ± 8.8	24	29
	SS	7.1 ± 1.1	7.1 ± 1.0	7.6 ± 1.1	7.3 ± 1.3	49.2 ± 2.6	47.3 ± 2.7	51.1 ± 6.1	50.0 ± 7.2	11	11
1.2	FFL	24.6 ± 1.4	23.0 ± 1.7	11.4 ± 1.2	12.0 ± 1.2	59.6 ± 3.1	57.5 ± 3.3	115.3 ± 4.7	89.4 ± 7.4	9	9
	RO	24.8 ± 1.5	23.7 ± 2.0	10.3 ± 1.4	9.7 ± 1.3	60.5 ± 5.2	64.2 ± 4.2	109.5 ± 18.0	86.2 ± 11.6	27	22
	SS	25.1 ± 1.3	23.9 ± 1.5	10.1 ± 1.3	9.2 ± 1.4	60.1 ± 3.4	65.4 ± 3.2	106.6 ± 9.8	86.5 ± 10.7	7	6

The wave variables here are represented as mean ± SD and averaged over respective phases. In the low-viscosity medium of µ = 1.2 mPas, the averaged angular frequency 〈ω₂〉 excludes the 8th, 9th, and 10th beat cycles, which correspond to the period when cell 1 drastically decelerates its beat for unknown reasons. In the high-viscosity experiment of µ = 15 mPas, the flagellar waves of the cells are synchronized during the steady-swimming (SS) phase; hence, both the cells have 11 beat cycles. However, because the sperm cells regulate their beat during the formation of sperm bundles, the number of beat cycles analyzed for cell 1 (N₁) and cell 2 (N₂) is different even in the same phases. The values of N₁ and N₂ at each phase are the number of beat cycles for cell 1 and cell 2 during the same phase, respectively.

In biological fluids, the orientation of sperm cells and propagating waves along the flagella vary among cells. Our calculation shows that both the relative orientation of two sperm cells Δθ and the phase shift between the flagellar wave Δϕ affect the flow field as well as the associated hydrodynamic forces on the cells (Fig. 3 B and C). The time-averaged flow field in the swimming plane is shown in Fig. 3A, ii–viii. Here, the relative orientation Δθ is denoted by the difference between the angles Δθ = θ₁ − θ₂, as illustrated in Fig. 1B. The phase shift Δϕ is denoted by the difference between the first Fourier modes of the tangent angle ψ(s_i, t) of the centerline of the two flagella (Materials and Methods). Further, the hydrodynamic forces on the cells are time-varying over one beat cycle T. For example, for the case where Δθ = π/3 and Δϕ = π/2, the hydrodynamic force along the y-axis ${}^1{\mathbf{F}}_y(t)$ on cell 1 propels it to move along the positive y-axis (0 <  t/T <  0.4 s), then negative y-axis (0.4 s ≤ t/T <  0.8 s), and positive y-axis (0.8 s ≤ t/T <  1 s) again during one beat cycle, as shown in Fig. 3B. Over one beat cycle, the time-averaged hydrodynamic force on cell 1 along the y-axis 〈¹F_y〉 is positive (Materials and Methods), which indicates that the net displacement of cell 1 along the y-axis in the laboratory frame is positive. Similarly, cell 2 has a smaller positive displacement along the y-axis over the same beat cycle. Therefore, the distance between cells decreases by the attractive flow field.

The force difference between the cells 〈ΔF_y〉=〈²F_y〉−〈¹F_y〉 is used to denote the forces that attract (negative values in Fig. 3C) or repel (positive values in Fig. 3C) the cells. For the cells in the high-viscosity medium of μ = 15 mPas, the forces 〈ΔF_y〉 are attractive only when Δθ = π/3 or π/2. For the cells in the low-viscosity medium of μ = 1.2 mPas, the forces lead to the cell-to-cell repulsion only when Δθ = π. The difference results from the distinct flagellar wave patterns. In the high-viscosity medium, both the flagella have a positive mean flagellar curvature, while in the low-viscosity medium, cell 1 and cell 2 have a positive and negative mean flagellar curvature, respectively (SI Appendix, Movies S1 and S2).

Moreover, we find that the fluid flow and hydrodynamic forces are affected by the separation distance between the cells and the viscosity of fluids. Because the sperm cell is a swimmer close to combined time-reversal and parity invariant, the average flow around the cell has a l⁻³ dependence, where l is the distance away from the cell (22). Consequently, the cells in both viscosities generate increasingly greater attractive/repulsive force 〈ΔF_y〉 (dots with darker color in Fig. 3C) with the reduction of Δθ due to the closer distance between the flagella. Further, the fluid viscosity μ affects the time-averaged hydrodynamic force 〈ΔF_y〉 in two aspects. First, the hydrodynamic force 〈ΔF_y〉 scales linearly with the fluid viscosity μ (SI Appendix, Fig. S2). Second, the viscosity regulates the flagellar beat, thereby affecting the hydrodynamic forces (26). Further, a series of calculation results for hydrodynamic force 〈ΔF_y〉 on the sperm cells at different distances are qualitatively consistent (SI Appendix, Fig. S1). The hydrodynamic attractive/repulsive forces between the cells increase at almost every configuration when the cells are closer to the bottom surface. The sperm cells always induce maximum hydrodynamic attractive forces when the phase shift Δϕ = π/2, and maximum hydrodynamic repulsive forces at Δϕ = 3π/2, regardless of the distance of the sperm from the bottom surface.

Hydrodynamic Torque Balance During Rotational-Oscillation Phase.

Besides hydrodynamic forces, sperm cells also experience hydrodynamic torque when their heads are attached and pivot around the axis ^ije. Here, we focus only on the hydrodynamic force/torque in the swimming plane, as the hydrodynamic forces along the z-axis F_z are very small compared with the forces along the x- and y-axis, F_x and F_y (Fig. 3B). The total torque on the ith cell must be zero and we have

$$\begin{array}{c}\hfill {}^i{\mathbf{M}}_{\mathrm{h}}(t)+\underset{0}{\overset{L_i}{\int }}{}^i{\mathbf{f}}_{\mathrm{xy}}(s_i,t)\times {}^i\mathbf{r}(s_i,t)\mathrm{d}{s}_i+\kappa \sin \left(\mathrm{\Delta }\theta \right){}^{\mathit{ij}}\mathbf{e}=0,\end{array}$$ [1]

where ⁱf_xy(s_i, t) is the force along the ith flagellum in the swimming plane. The first and second terms of this equation are the hydrodynamic torque on the head and flagellum of the ith cell, respectively. The hydrodynamic torque in the swimming plane ⁱM_h is computed by ${}^i{\mathbf{M}}_{\mathrm{h}}=8\pi a{b}^2\mu C_1{\mathbf{\Omega }}_i(t)$, where ${\mathbf{\Omega }}_i(t)$ is the angular frequency of the rotating head, C₁ is the geometric coefficient for the rotation, and a and b are the semiminor axis and semimajor axis of the projection of the head in the swimming plane, respectively (38). The relative translational motion between the heads is negligible when they are attached; therefore, we consider only the relative rotational motion. There exist adhesive/repulsive forces between the heads (14, 39), which are modeled as a linear spring torque with elastic constant κ, as shown in the third term in Eq. 1. Therefore, the hydrodynamic torque balance on the sperm bundle is given by

$$\begin{array}{c}\hfill {{}^1\mathbf{M}}_{\mathrm{h}}-{{}^2\mathbf{M}}_{\mathrm{h}}+{{}^1\mathbf{M}}_{\mathrm{f}}-{{}^2\mathbf{M}}_{\mathrm{f}}+2\kappa \sin \left(\mathrm{\Delta }\theta \right){}^{12}\mathbf{e}=0,\end{array}$$ [2]

where ¹M_f and ²M_f are the hydrodynamic torque on the flagellum of cell 1 and cell 2, respectively. The flagellar beat is periodic/quasi-periodic; therefore, we model the hydrodynamic torque on the flagellum in the swimming plane M_f with a sinusoidal function M_f = M_asin(ωt + ϕ₀), where ϕ₀ is the initial phase. The flagellar beat frequency ω and initial phase ϕ₀ are results from our experimental measurements. M_a is an averaged hydrodynamic torque on the flagellum derived from the regularized Stokeslets. Eq. 2 is a first-order nonlinear ordinary differential equation with constant coefficients. The coefficients depend on the characteristics of the fluid, the morphology of the heads, and head-to-head adhesion.

The solution to Eq. 2 characterizes the rotational dynamics of the sperm cells, as shown in Fig. 4. When the angle between the heads Δθ decreases to zero, the heads are aligned. The angle Δθ oscillates owing to the energy transfer between the distributed contractile and elastic elements of the active flagellum. The decaying Δθ results from the energy loss in the viscous medium, the friction between the heads, and the friction between the dynein motors of the flagellum (40).

Fig. 4.

Time response of the angle between the heads Δθ. (A) The blue, red, and black dots denote the measurements of Δθ during the far field–locking phase, rotational-oscillation phase, and steady-swimming phase, respectively. For the viscosity µ of 15 mPas (i), the angle between the heads of the spermatozoa Δθ reduces asymptotically to zero. Compared with the low-viscosity case (ii), the high viscosity leads to a slower alignment of the heads. The calculation (green line) indicates that high viscosity exerts a stronger constraint on the oscillation amplitude of the Δθ, which is consistent with the measurements where the norm of the residuals of the fitting is 125 for the high-viscosity case (µ = 15 mPas) and 182 for the low-viscosity case (µ = 1.2 mPas). The fitting lines (dashed lines) are nine-degree polynomial curves. Notice that only the absolute value of the angle is measured. (B) The time response of Δθ is computed for four representative viscosities of 3, 7, 11, 15 mPas for the high-viscosity case (i) and 1.2, 2.4, 3.6, 4.8 mPas for the low-viscosity case (ii). Here, the phase shift is. The lower viscosity causes faster alignment of the heads for the two experiments. (C) The time response of Δθ is calculated for four representative phase shifts Δϕ of 0, /3, 2/3, and for the high-viscosity case (i) and the low-viscosity case (ii). For the high-viscosity case (i), the phase shift has no impact on the rate of the alignment. Due to very small differences between the values of Δθ at different Δϕ, the curves are overlapped. For the low-viscosity case (ii), the phase shift has no impact on the rate of the alignment. A larger phase shift Δϕ leads to a larger oscillation amplitude of Δθ.

It is common to observe sperm cells with different types of chirality in biological environments (36, 41). When a sperm bundle is formed by two cells with the same chirality, the hydrodynamic torques on the cells are in the same direction, leading the angle Δθ to decrease to zero, as predicted by the theory described by Eq. 2 (Fig. 4A, i). When the cells have opposite chirality, the hydrodynamic torques on the cells are in the opposite direction, leading to a possible scenario that the angle Δθ first increases to π and then declines to zero (Fig. 4A, ii). Compared with the high-viscosity medium, the low-viscosity medium leads to a faster alignment of sperm bundles. This is a direct result of the faster beat frequency of sperm cells in the low-viscosity fluid. In contrast to the low-viscosity medium, the high-viscosity medium exerts stronger suppression on the oscillation amplitude of the angle between the heads Δθ (Fig. 4B). The smaller amplitude of the oscillation of the angle Δθ results from the smaller oscillation of the heads of individual cells. Further, flagellar propagating waves vary among spermatozoa, therefore a nonzero phase shift is likely to be present between ${{}^1\mathbf{M}}_{\mathrm{f}}$ and ${{}^2\mathbf{M}}_{\mathrm{f}}$ during the RO phase. Our calculation shows that a larger phase shift Δϕ fails to affect the relaxation time of Δθ but may increase the oscillation amplitude of Δθ (Fig. 4C). Note that in the low-viscosity case, only the stage when Δθ decreases is shown in Fig. 4B, ii and C, ii. The stage when Δθ increases has similar results.

In summary, the agreement of the experimental results with the calculation infers that the rotational dynamics of sperm bundles depend on the coupled hydromechanical cell-to-cell interactions. Our numerical results demonstrate that the heads of two sperm cells eventually align regardless of the initial angle (Fig. 4A), chirality (Fig. 4A), fluid viscosity (Fig. 4B), and phase shift (Fig. 4C). This conclusion is confirmed by our experiments (Fig. 2) and can be drawn from the hydrodynamic torque balance on the sperm bundle, which predicts that Δθ = 0 is the stable equilibrium point.

Thrust and Net Swimming Velocity of Sperm Bundles During Steady-Swimming Phase.

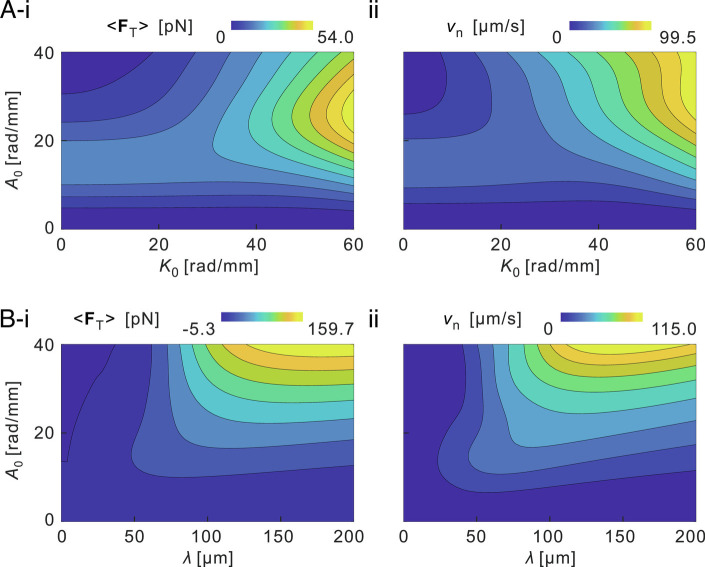
After spermatozoa form a bundle, their flagellar waveform is likely to be regulated, and thereby, the sperm bundle obtains propulsive thrust and swimming speed that may be enhanced, reduced, or averaged. Thus, we calculate the time-averaged thrust of sperm bundle over one beat cycle 〈F_T〉 and the net swimming velocity v_n for a range of K₀, A₀, and λ (Materials and Methods). The net swimming velocity characterizes the effective motion of spermatozoa and is defined by v_n = ΔS/T, where T is the period of one flagellar beat cycle, and ΔS is the displacement of the head during one beat cycle.

The calculation reveals that 〈F_T〉 and v_n are a complicated result of the wave variables (Fig. 5). A sole increase in the amplitude cannot guarantee enhanced net swimming velocity. Some abnormal flagellar wave patterns even generate a backward time-averaged propulsive force such that sperm bundles have a negative net displacement along the averaged swimming path (Fig. 5A, i and B, i). In common cases in biological environments (e.g., some K₀-A₀-λ combinations in the range K₀ < 30 rad/mm, A₀ < 20 rad/mm, and λ < 100 µm), sperm bundles can increase their net swimming velocity with a larger flagellar wave amplitude A₀ or wavelength λ but cannot with reducing mean flagellar curvature K₀ (Fig. 5A, ii and B, ii). For instance, for a sperm bundle with A₀ = 10 rad/mm, K₀ = 13.3 rad/mm, and λ = 44.8 µm, its net swimming velocity v_n increases 24% when A₀ increases to 15 rad/mm, 13% when λ increases to 60 µm, and only 3% when K₀ decreases to 5 rad/mm, provided A₀, λ, and K₀ are the only varying wave variables, respectively. However, on large time scales, smaller mean flagellar curvature leads to a straighter trajectory and thus a greater rectilinear velocity (14).

Fig. 5.

The influence of flagellar waveform on the time-averaged propulsive thrust 〈F_T〉 and net swimming velocity v_n of the sperm bundle. (A) Time-averaged thrust 〈F_T〉 (i) and net swimming velocity v_n (ii) are computed over the mean flagellar curvature K${}_0$ in the range of 0 to 60 rad/mm and amplitude rise A${}_0$ of 0 to 40 rad/mm. Here, the wavelength 〈λ〉 and angular frequency 〈ω〉 are the average values over the three phases in the high-viscosity experiment, such that 〈λ〉 = 44.8 ± 4.8 µm and 〈ω〉 = 47.2 ± 8.8 rad/s (mean ± SD). (B) Time-averaged propulsive thrust 〈F_T〉 (i) and net swimming velocity v_n (ii) are computed over the wavelength in the range of 0 to 200 µm and amplitude rise A${}_0$ of 0 to 40 rad/mm. Here, the mean flagellar curvature 〈K₀〉 and angular frequency 〈ω〉 are the average values over the three phases in the high-viscosity experiment, such that 〈λ〉 = 13.3 ± 8.1 rad/mm and 〈ω〉 = 47.2 ± 8.8 rad/s (mean ± SD). A correction factor C_f of 0.8 for the hydrodynamic friction on sperm heads is used to characterize the impact of the head-to-head attachment on the net swimming velocity. Note that only the module of the net swimming velocity is considered.

Further, the flagellar beat frequency ω accelerates when flagellar beats are synchronized (8). Our calculation shows that the net swimming velocity v_n or the time-averaged thrust 〈F_T〉 is linear proportional to the flagellar beat frequency (SI Appendix, Fig. S3). It is a direct result derived from the relation that the instantaneous swimming speed scales linearly as the beat frequency (42).

Furthermore, in biological environments, sperm bundles are formed with their heads attached (Fig. 2). The attachment is thought to enable the sperm bundle of two cells to achieve a double bending force and a double elastic force but experience a less-than-twofold viscous force, whereby its swimming speed is enhanced (8). The impact of the attachment on the net swimming velocity is yet unknown, so we evaluate the impact by simply modifying the friction coefficients with a correction factor C_f. The numerical results show that the relation between the net swimming velocity and the correction factor is approximately linear proportion (SI Appendix, Fig. S4).

Flagellar Beats During the Transition in High-Viscosity Medium.

Without varying external forces, freely swimming spermatozoa usually exhibit regular flagellar beats according to the balance of bending forces, elastic forces, and viscous forces (32, 34). The l⁻² dependence of the force dipole suggests that hydrodynamic cell-to-cell interactions between flagella are nonnegligible when the cells are close (38, 43). In the high-viscosity medium of μ = 15 mPas, the time-dependent wave variables seem erratic due to hydrodynamic interactions, but significant changes in the wave variables can be seen from their trends (illustrated by the fitting curves in Fig. 6), such that the frequency of cell 2 is declining significantly as the cells approach during the FFL phase (Fig. 6D).

Fig. 6.

Time-dependent wave variables are extracted from the observed flagellar waveform during swimming in the high-viscosity medium of 15 mPas across the three consecutive phases: far field–locking, rotational-oscillation, and steady-swimming. The mean flagellar curvature K${}_0$ (A), amplitude rises A${}_0$ (B), wavelengths (C), beat frequencies ω (D), and net swimming velocities v_n (E) of cell1 (blue triangle) and cell 2 (red circle) gradually converge due to the coupled hydro-mechanical interactions. (F) The flagellar waveforms in each phase are reconstructed using the averaged wave variables over their respective phases. These waveforms during one beat cycle (t/T, 0–1) demonstrate the significant influence of the cell-to-cell interactions on the flagellar beats. The fitting lines are nine-degree polynomial curves. Note that the mean flagellar curvature here is denoted by its absolute value.

After the cells come into contact and adhere to each other, the cell-to-cell interactions can affect every wave variable significantly. However, the effect of the interactions on the wave variables is not always “equal.” For instance, for cell 2 during the time 0.9 to 1.6 s, its mean flagellar curvature ²K₀ remains almost invariant, whereas its beat frequency ω₂ increases significantly. It means that only some aspects (e.g., the beat frequency) of the flagellar wave pattern are regulated significantly, rather than every aspect. Further, the effect of the interactions is not always “equal” for the sperm cells. For example, the ¹K₀ increases, whereas the ²K₀ decreases during the RO phase. The differences in the interactions between the cells may result from the configuration of the sperm bundle where the position of the cells is not identical and interchangeable. An alternative possible cause is that the flagella have a different intrinsic bending stiffness, given the different flagellar wave patterns shown in the FFL phase.

In addition, cell-to-cell interactions during the RO phase cause more erratic flagellar wave patterns than those during the FFL phase, which is reflected in the standard deviations (SDs) of the time-dependent wave variables. For instance, the SDs of beat frequencies of the flagella over the RO phase are 6.0 rad/mm and 8.8 rad/mm, which are larger than that over the FFL phase, 2.5 rad/mm and 7.4 rad/mm (Table 1).

During the RO phase, the flagellar waves of the cells are repeatedly in transitions between synchronization and desynchronization (SI Appendix, Movie S1). However, once the heads of the spermatozoa are firmly fixed together, flagellar beats are synchronized immediately by mechanical coupling. Owing to the coupled hydro-mechanical interactions, the sperm cells resume steady flagellar beats. During this SS phase, the wave variables and net swimming velocity of the cells converge, as shown in Fig. 6. Further, the SDs of the wave variables during the SS phase in the high-viscosity experiment are smaller than those in the other phases, implying that the mechanical coupling between the heads can promote the stability of flagellar wave patterns even in the presence of hydrodynamic interactions.

Comparing these averaged wave variables in Table 1 over the FFL phase and SS phase, we find that the synchronization of the flagella has an averaging effect on the mean flagellar curvature, while the amplitudes and wavelengths of both the cells decrease. Note that the net swimming velocity of the sperm bundle is enhanced rather than averaged between the cells (Fig. 6E). The average net swimming velocities of the cells over the FFL phase are ${\langle {}^1{v}_{\mathrm{n}}\rangle }_{\mathrm{FFL}}=32.7\pm 3.1$ µm/s, ${\langle {}^2{v}_{\mathrm{n}}\rangle }_{\mathrm{FFL}}=11.6\pm 3.3$ µm/s (mean ± SD), and the average net swimming velocity of the sperm bundle over the SS phase is 〈vn〉_SS = 40.4 ± 5.2 µm/s because the angular frequency ω₁ is enhanced greatly by cell 2, while there is only a slight variation in ω₂, ¹A₀, ²A₀, ¹λ₀, and ²λ₀.

Flagellar Beats During the Transition in Low-Viscosity Medium.

Different from the sperm cells that beat their flagella from side to side in the high-viscosity medium of μ= 15 mPas, the cells in the low-viscosity medium of μ= 1.2 mPas exhibit one-sided strokes due to weaker suppressing effect of low-viscosity media on the flagellar chirality (26, 27) and lateral head displacement (44) (SI Appendix, Movie S2). Cell 1 beats its flagellum in the negative direction of ${}^1{\mathbf{e}}_2$, and cell 2 beats its flagellum in the positive direction of ${}^2{\mathbf{e}}_2$, leading the cells to swim clockwise and counterclockwise during the FFL phase, respectively (SI Appendix, Movie S1 and S2). Facilitated by the cell-to-cell attraction, the spermatozoa approach. The hydrodynamic interaction leads cell 2 to achieve a longer wavelength and hence an enhanced net swimming velocity during the time 0 to 0.5 s (Fig. 7). However, cell 1 drastically decelerates its beating during a short time before and after the cells adhere (0.4 to 0.7 s) for unknown reasons, accounting for its declined net swimming speed.

Fig. 7.

Time-dependent wave variables of the cells are measured across the bundle formation in a low-viscosity medium of 1.2 mPas. Different from the high-viscosity experiment, the wave variables mean flagellar curvature K${}_0$ (A), amplitude rises A${}_0$ (B), wavelengths (C), beat frequencies ω (D) of cell 1 (blue triangle) and cell 2 (red circle) fail to converge because mechanical coupling between the heads is weak. As a result of the weak head-to-head attachment, the net swimming speeds (E) are not enhanced. (F) The flagellar waveforms are reconstructed using the averaged wave variables of their respective phases. The waveforms during one beat cycle (t/T, 0–1) illustrate the adaptation of the cells to the interactions. Here, the fitting lines are nine-degree polynomial curves, and only the module of the mean flagellar curvature is denoted.

After the cells assemble into a bundle, the swimming velocity of cell 2 is immediately decreased by cell 1. But the wave variables of the cells change gradually. For both the cells, the amplitudes first decrease (0.6 to 1.2 s) and then increase (1.2 to 1.9 s) (Fig. 7B), while the wavelengths increase first (0.2 to 1.2 s) and then decrease (1.2 to 1.9 s) (Fig. 7C). The suppressing effect on the amplitudes is attributed to the coupled hydro-mechanical interactions rather than only the hydrodynamic interactions. Because if the suppressing effect resulted only from the hydrodynamic interaction, the amplitudes would be most suppressed immediately after the heads come into contact, when the flagella are so close that they can induce significant hydrodynamic forces. Comparing the average wave variables over the SS phase and that over the FFL phase, we can find that the amplitudes of both cells decline (Table 1). This is likely to result from the physical constraint between the cells. A similar phenomenon has been reported when spermatozoa are confined in a microtube which resulted in a smaller bending amplitude of the cells (45).

However, unlike in the high-viscosity case, no significant changes in the mean flagellar curvature are found during the bundle formation. This is because the attachment of the heads is weak, allowing the heads to rotate relatively. The hydrodynamic interaction by itself is not sufficient to alter the mean flagellar curvature significantly, as reported previously (8). Besides, the weak mechanical coupling between the heads causes failure of flagellar synchronization. Consequently, the net swimming speed of the sperm bundle is not enhanced, and instead, it is averaged between the two cells. The average net swimming velocities of the cells over the FFL phase are ${\langle {}^1{v}_{\text{n}}\rangle }_{\text{FFL}}=34.2\pm 11.5$ µm/s, ${\langle {}^2{v}_{\text{n}}\rangle }_{\text{FFL}}=48.0\pm 21.7$ µm/s, and the average net swimming velocity of the sperm bundle over the SS phase is ${〈v_{\mathrm{n}}〉}_{\mathrm{SS}}=42.3\pm 26.2$ µm/s. We also find that the wavelength of cell 2 is elongated significantly from an average value of ${\langle {}^2\lambda \rangle }_{\text{FFL}}=57.5\pm 3.3$ µm to ${\langle {}^2\lambda \rangle }_{\text{SS}}=65.4\pm 3.2$ µm. The elongated wavelength has also been observed previously in sperm bundles with flagellar synchronization (8).

Discussion

Cell-to-cell interactions exist across the whole course of the bundle formation; therefore, the motion of sperm bundles cannot be simply described as the locomotion of two individual spermatozoa. Spermatozoa are usually regarded as “pusher” swimmers, which repel fluid lengthwise and draw fluid laterally (46, 47). The fluid repelled lengthwise provides thrust for the cells, while the fluid drawn laterally attracts the cells. The cell-surface attraction has been observed in spermatozoa (48) and Escherichia coli bacteria (49, 50). It seems that the cell-to-cell attraction occurs certainly. However, unlike the hydrodynamic cell-surface interaction, the hydrodynamic cell-to-cell interaction involves two or more motile entities. A change in the relative orientation Δθ, distance d between two cells, the phase shift between flagellar waves Δϕ, or flagellar waveform may turn a pusher into a puller (Fig. 3A), which is in agreement with previous numerical studies (12, 18, 19). Note that recent studies indicate that a microswimmer may oscillate between a pusher and a puller during its flagellar beat and behave as a puller on average (51, 52).

Further, both viscosity and elasticity of fluids can significantly influence the locomotion of sperm cells and hence the hydrodynamic interactions between cells when the storage modulus of the fluid is significant (26, 53). Beyond the linearity limit, the storage modulus of the medium in our high-viscosity experiment is very small compared with the loss modulus, rendering it a highly viscous–weakly elastic fluid. Thus, it can be assumed that the elastic properties of the fluid are small compared to the viscous properties. The high-viscosity fluid is shear-thinning. In our calculation, we consider the viscosity of the high-viscosity fluid as a constant during one beat cycle for simplicity. Hydrodynamic forces scale linearly with the fluid viscosity. A sole increase/decrease in the fluid viscosity will lead to greater/weaker hydrodynamic attraction/repulsion (SI Appendix, Fig. S2). However, a change in the fluid viscosity often leads sperm cells to exhibit different flagellar wave patterns, whereby sperm cells may behave as pullers at certain points during the beat cycle (52, 54).

Our results raise the question of whether sperm cells have evolved structures that are inclined to attract other cells to form sperm bundles. Further studies need to be conducted. However, assuming that they induce attractive flow fields, it is certain that not every sperm cell can form a bundle for at least two reasons. First, the attractive flow field is not always sufficient to overcome stochastic thermal fluctuations, especially when the cells are at a large distance (18, 50). Additionally, the head-to-head attachment is impacted by adhesion proteins on the sperm surface (55) as well as the presence of calcium cations (56), heparin (57), or other membrane charge–changing components in fluids. Therefore, the heads of sperm do not always succeed in adhering when the heads come into contact, which can be confirmed by some cells observed in SI Appendix, Movie S1.

Thus far, we know that the flagellar beat of sperm bundles is regulated by the coupled hydro-mechanical cell-to-cell interactions. Is the hydrodynamic interaction or the mechanical interaction dominant in inducing the flagellar synchronization? Our experiments support the latter. In the high-viscosity experiment, the flagella are in the transition between synchronization and desynchronization during the RO phase and synchronized immediately when the sperm heads are attached rigidly. Another supporting example is the sperm bundle in the low-viscosity experiment, whose head-to-head attachment is weak and flagellar beats are out of phase. Our observations are in agreement with the previous theory predictions (58) and experimental observations (8) that mechanical coupling is a dominant mechanism for flagellar synchronization in sperm bundles. Although previous investigation suggests that flagellar/ciliary synchronization can be achieved only through hydrodynamic interactions (18, 59), which is seemingly not observed experimentally.

Flagellar synchronization highlights the temporal component of flagellar waves, whereas the waveform represents the spatial component of flagellar waves. Is the hydrodynamic interaction or the mechanical interaction dominant in regulating the waveform? Our experiments support the latter. In the high-viscosity experiment, a significant change in the mean flagellar curvature of cell 2 occurs immediately when the relative rotational motion of the heads is stopped by the mechanical coupling between the heads, after which the wave variables become less erratic even in the presence of hydrodynamic interactions (Fig. 6A). Our observations infer the dominant role of mechanical interactions in the synchronization of sperm flagellar beats and the regulation of sperm flagellar waveform. However, because of the limited number of observations of sperm bundle formation, more observations are required to further investigate the correlation between the interactions and the flagellar waveform or synchronization.

Synchronized flagella not only enhance the swimming speed of sperm cells but also consume less energy than desynchronized flagella (15, 16, 18, 53). This locomotion strategy of sperm cells can be further implemented into the design and development of multiflagellated soft microrobots that can generate increased propulsive thrust to overcome greater flow rates of bodily fluids (60). Note also that our theoretical and experimental framework for the formation of the sperm bundle of two cells can be generalized to investigate the formation of bundles of more than two cells. In the system of multiple cells, the formation course can also be divided into phases according to the experiment. The equations for a single cell in this study remain valid for any cell in the system of multiple cells.

In conclusion, the time-dependent wave variables are measured to characterize the collective locomotion of sperm cells during the transition from individual cells to bundles of two cells, which further reveal the dynamic mechanisms for bundle formation. We find that the cell-to-cell interactions can lead to the time-varying flagellar wave pattern as well as three consecutive collective behaviors: hydrodynamic attraction/repulsion, alignment, and synchronization. Further, the distinct wave variables during the three phases (i.e., the FFL, RO, and SS phase) infer that the rigid head-to-head attachment is necessary for the flagellar synchronization and hence the increased swimming velocity.

Materials and Methods

Sperm Cell Preparation.

Cryopreserved bovine semen straws are obtained from Masterrind GmbH and stored in liquid nitrogen until use. Semen straws are thawed in 37  ° C water bath and suspended in 1 mL modified Tyrode’s albumin lactate medium (SP-TALP) (Caisson Labs), supplemented with 60 mg bovine serum albumin (Sigma Aldrich), 10 µL gentamicin sulfate (Caisson Labs), and 0.5 mL 100 mM sodium pyruvate (Thermofisher), resulting in 1.2 mPas viscosity. The sperm medium with increased viscosity of 15 mPas (shear rate 100 1/s) is prepared by adding 1% methyl cellulose to SP-TALP medium (61).

Image Acquisition.

Five microliters of sperm suspension are pipetted into Leija slides with a chamber height of 20 μm. Videomicroscopy is performed in an inverted microscope with a heated stage (37  ° C) and a Phantom Miro high-speed camera and a 40× objective in phase contrast mode, obtaining video sequences with 200 and 500 frames per second for the high-viscosity experiment and the low-viscosity experiment, respectively. When acquiring the flagellar waveform, we track the flagella based on the customized script in Matlab. The shapes of the sperm cells are extracted from the recorded images at a constant time interval (5 ms for the high-viscosity experiment and 2 ms for the low-viscosity experiment). Further, the end frame of one beat cycle is the frame wherein the flagellum first recovers to the position in the start frame. Because the period of the beat cycles always changes, the number of frames for the beat cycles is determined artificially.

Rheological Measurements.

Oscillatory shear experiments for the high-viscosity fluid (1% methyl cellulose) are performed at 37  ° C, using a rheometer (MCR 92, Anton Paar) with a cone-plate geometry (CP-25-1, diameter: 25 mm, angle: 1°) (SI Appendix, Fig. S5). The limit of the linear viscoelastic region is approximately 1%, beyond which the storage modulus G′ decreases faster than the loss modulus G″. Beyond the linearity limit, storage modulus G′ is very small compared with loss modulus G″. For the low-viscosity fluid (SP-TALP), the storage modulus G′ is also small compared to loss modulus G″ (62).

Characterization of the Locomotion of Sperm Cells.

The extracted shapes of the ith sperm cell at a time t can be represented in terms of the position vector of the centerline of the flagellum ⁱr(s_i, t) in the laboratory frame for each arc length s_i as follows (33) (Fig. 1B):

$$\begin{array}{c}\hfill {}^i\mathbf{r}(s_i,t)={}^i\mathbf{r}-a{}^i{\mathbf{e}}_1-\underset{0}{\overset{s_i}{\int }}\mathrm{d}s\cos {}^i\psi (s,t){}^i{\mathbf{e}}_1+\sin {}^i\psi (s,t){}^i{\mathbf{e}}_2,\end{array}$$ [3]

where a is the semimajor axis of the head, ⁱr is the position vector of the center of the sperm head, and ⁱψ(s_i, t) is the tangent angle enclosed between the local tangent vector at ⁱr(s_i, t) to the flagellar centerline and the unit vector ${{}^i\mathbf{e}}_1$. In the material frame, the tangent angle ⁱψ(s_i, t) of the ith flagellum can be decomposed and approximated by the zeroth and first Fourier modes (32)

$$\begin{array}{c}\hfill {}^i\psi (s_i,t)\approx {}^i{\psi }_0(s_i)+{}^i{\psi }_1(s_i){\mathrm{e}}^{j{\omega }_{i}t}+{}^i{\psi }_1^{\ast }(s_i){\mathrm{e}}^{-j{\omega }_{i}t}.\end{array}$$ [4]

The mean flagellar curvature ${}^i{K}_0$, bending amplitude ${}^i{A}_0$, and wavelength λ_i of the principal traveling wave along the flagellum at frequency ω_i can be derived from the zeroth and first Fourier mode:

$$\begin{array}{c}\hfill {{}^{i}K}_0=\frac{{{}^i\psi }_0(s_i)}{s_i},{{}^{i}A}_0=\frac{|{{}^i\psi }_1(s_i)|}{s_i},{\lambda }_i=-\frac{2\pi s_i}{\arg {{}^i\psi }_1(s_i)}.\end{array}$$ [5]

The wave variables (K₀, A₀, λ and ω) complete the kinematics of the beating flagellum in the material frame. After the time-varying wave variables are derived from the recorded images of the sperm cells, position and velocity of every discretized element on the cells can be reconstructed (33) and used in the calculation of hydrodynamic forces on the sperm cells and flow fields.

Calculation of the Flow Fields and Hydrodynamic Forces on Sperm Cells.

The flagellum is modeled as a tube with a radius of 0.25 µm and a length of 60 µm. The head of sperm is modeled as an ellipsoid, and the dimensions of the head are 9 µm (length), 5 µm (width), and 1 µm (height), respectively. The flagellum is discretized with cross-sections along its length, and six regularized Stokeslets are used on the perimeter of each circular cross-section. The adjacent cross-sections are equally separated by a distance equal to the radius of the flagellum. The head is discretized with cross-sections along its long axis, and the adjacent cross-sections of the head are also equally separated by a distance equal to the radius of the flagellum. On each of the cross-sections, the distance between two adjacent regularized Stokeslets is equal to the distance between two adjacent regularized Stokeslets on the cross-section of the flagellum. Assume that there are N regularized Stokeslets on the surface of each cell. The fluid response u(x) at x${}_0$ to the hydrodynamic forces induced by two flagella is described by the regularized Stokeslets (63):

$$\begin{array}{c}\hfill \mathbf{u}\left({\mathbf{x}}_0\right)=\frac{1}{8\pi \mu }\sum _{k=1}^{2N}\sum _{i=1}^3{S}_{\mathit{ij}}^{ϵ}({\mathbf{x}}_k,{\mathbf{x}}_0){}^i{\mathbf{f}}_k{A}_k,\end{array}$$ [6]

where ${}^i{\mathbf{f}}_k$ is the ith component of the force on the fluid applied at x${}_0$ and A_k is the quadrature weight of the kth regularized Stokeslets. The regularized Green’s function $S_{\mathit{ij}}^{ϵ}$ is given by

$$\begin{array}{c}\hfill S_{\mathit{ij}}^{ϵ}\left(\mathbf{x},{\mathbf{x}}_0\right)={\delta }_{\mathit{ij}}\frac{r^2+2{ϵ}^2}{{\left(r^2+{ϵ}^2\right)}^{3/2}}+\frac{\left(x_i-x_{0,i}\right)\left(x_j-x_{0,j}\right)}{{\left(r^2+{ϵ}^2\right)}^{3/2}},\end{array}$$ [7]

where ϵ is the regularization parameter and is set as a value to be half of the radius of the flagellum. Note that the index i in Eqs. 6 and 7 is used for Einstein summation convention and does not represent the values for ith cell. Distance r is given by

$$\begin{array}{c}\hfill r=|\mathbf{x}-{\mathbf{x}}_0|.\end{array}$$ [8]

Eq. 6 shows that the fluid response u(x) is entirely dependent on the instantaneous motion and the configuration of sperm cells. In turn, the hydrodynamic force ${}^i{\mathbf{f}}_k$ is obtained using Eq. 6, where the velocity u(x) is derived from the experimental measurements of the time-dependent locomotion of the sperm cells.

Over one beat cycle T (discretized into 32 time steps), the time-averaged hydrodynamic force on the ith cell 〈ⁱF〉 is given by

$$\begin{array}{c}\hfill {\langle }^i\mathbf{F}\rangle =\frac{1}{32}\sum _{t=1}^{32}\sum _{k=1}^N{}^i{\mathbf{f}}_k\left(t\right).\end{array}$$ [9]

The time-averaged hydrodynamic force is used to characterize the net displacement of sperm cells over one beat cycle.

Calculation of the Propulsive Thrust of Flagella.

The propulsive thrust generated by the ith flagellum with length of L_i is computed using the resistive-force theory (42),

$$\begin{array}{c}{}^i{\mathbf{F}}_{\text{T}}=\underset{0}{\overset{L_i}{\int }}\left[{\xi }_{\perp }{}^i{\mathbf{v}}_{\perp }(s,t)+{\xi }_{\Vert }{}^i{\mathbf{v}}_{\Vert }(s,t)\right]\text{d}s,\end{array}$$ [10]

where ξ_⊥ and ξ_∥ are the friction coefficients, and ${}^i{\mathbf{v}}_{\perp }$ and ${}^i{\mathbf{v}}_{\Vert }$ are the local normal and parallel velocity components along the ith flagellum, respectively. The velocity ${}^i{\mathbf{v}}_{\perp }$ and ${}^i{\mathbf{v}}_{\Vert }$ are obtained by the force balance on the head and the flagellum as well as the torque balance described in Eq. 1 (38, 42):

$$\begin{array}{c}\hfill 6\pi \mu a{C}_2{}^i{v}_x={}^i{\mathbf{F}}_{\mathrm{T}}·{}^i{\mathbf{e}}_1,6\pi \mu a{C}_3{}^i{v}_y={}^i{\mathbf{F}}_{\mathrm{T}}·{}^i{\mathbf{e}}_2,\end{array}$$ [11]

where C₂ and C₃ are the friction coefficients on the head, and ⁱv_x and ⁱv_y are the velocity of the head along the x-axis and y-axis, respectively.

Supplementary Material

Appendix 01 (PDF)

Movie S1.

Assembly of spermatozoa in the high-viscosity medium of 15mPas. Two individual spermatozoa first come into contact during the far field–locking phase, then rotate to form an aligned configuration during the rotational-oscillation phase. Finally, the rigid head-to-head attachment stops the relative rotation of the heads and leads to the synchronized flagellar beat, whereby the swimming velocity is enhanced significantly.

Movie S2.

Assembly of spermatozoa in the low-viscosity medium of 1.2mPas. A similar transition from two individual cells to a bundle is recorded. However, the head-to-head attachment is not rigid sufficiently for the cells to form a steady configuration, and thereby the enhancement in the swimming velocity of cells is not 19 achieved.

Data, Materials, and Software Availability

All study data are included in the article and/or SI Appendix.