Integrating pH into the metabolic theory of ecology to predict bacterial diversity in soil

Significance

Understanding the mechanisms structuring soil bacterial diversity is central to predicting how organisms and communities respond to biotic/abiotic disturbances. Metabolic theory has provided a framework to explain patterns of physiology and diversity in ecological communities. We established a quantitative model to incorporate pH into metabolic theory to capture some of the unexplained variation in bacterial diversity across scales. We combined laboratory experiments at the level of a single species with meta-analysis at the level of community at continental and global scales to build predictive models of species and community diversity. The conceptual framework firstly incorporated pH into metabolic theory to advance accuracy in model predictions of bacterial diversity. Our study allows for further incorporation of multiple factors into MTE-based models.

Abstract

Microorganisms play essential roles in soil ecosystem functioning and maintenance, but methods are currently lacking for quantitative assessments of the mechanisms underlying microbial diversity patterns observed across disparate systems and scales. Here we established a quantitative model to incorporate pH into metabolic theory to capture and explain some of the unexplained variation in the relationship between temperature and soil bacterial diversity. We then tested and validated our newly developed models across multiple scales of ecological organization. At the species level, we modeled the diversification rate of the model bacterium Pseudomonas fluorescens evolving under laboratory media gradients varying in temperature and pH. At the community level, we modeled patterns of bacterial communities in paddy soils across a continental scale, which included natural gradients of pH and temperature. Last, we further extended our model at a global scale by integrating a meta-analysis comprising 870 soils collected worldwide from a wide range of ecosystems. Our results were robust in consistently predicting the distributional patterns of bacterial diversity across soil temperature and pH gradients—with model variation explaining from 7 to 66% of the variation in bacterial diversity, depending on the scale and system complexity. Together, our study represents a nexus point for the integration of soil bacterial diversity and quantitative models with the potential to be used at distinct spatiotemporal scales. By mechanistically representing pH into metabolic theory, our study enhances our capacity to explain and predict the patterns of bacterial diversity and functioning under current or future climate change scenarios.

Microbial communities are diverse and play essential roles in carbon storage and nutrient cycling across divergent terrestrial ecosystems (1–3). Understanding the processes and mechanisms underlying biogeographical patterns of microbial diversity is a fundamental and long-standing goal in ecology. Ecologists have long noted the latitudinal gradient in aboveground biodiversity, with many more species being found in warm, tropical regions—a pattern generally related to the greater stability, multifunctionality, and productivity (4, 5). For aboveground organismal communities, this pattern appears to hold at all levels of evolutionary differentiation and community organization, such as phylogenetic branches in animals and plants (5). However, soil bacterial communities seem to display considerable deviations from this pattern (1, 2, 6), indicating that potentially different eco-evolutionary processes and mechanisms operate on structuring and maintaining belowground (soil) bacterial diversity. Disentangling the main mechanisms determining the biogeographical patterns of bacterial diversity has still remained a considerable challenge. Previous efforts have used either qualitative and graphical frameworks (7, 8), or simple analytical treatments that incorporate only a few coexisting species (8, 9) or whole-system models focused on emergent patterns rather than on underlying mechanisms (10).

The metabolic theory of ecology (MTE) provides a unique conceptual synthesis to develop quantitative models aiming at explaining and potentially predicting patterns of microbial diversity across temperature gradients (11–15). This is centered on the notion that temperature affects diversity via influences on species’ metabolic rates (i.e., growth and mutation rates) (5, 12). The metabolism provides a tangible link between the biology, ecology, and evolutionary trajectories of species, populations, and communities (12, 13). The MTE predicts that the metabolism of species, the growth of populations, and the number of species in a local community increase exponentially with the environmental temperature (12). However, empirical and theoretical evaluations of MTE have produced variable and seemingly contradictory results in explaining species diversity across divergent systems (14–17). In fact, previous studies have examined the theoretical foundation and empirical validity of MTE in predicting microbial diversity. For instance, by providing evidence that the fitted slope values (i.e., the inverse number of activation energy, −E_a) of negative diversity-temperature relationships in natural ecosystems are lower than expected by the model prediction (14–16). This has been suggested to occur because most models fail to account for soil properties and their importance in structuring microbial diversity (16). Therefore, the development of MTE models applicable to microbes should benefit from taking into account those variables that mostly contribute to species divergence across communities.

Soil pH has long been recognized as a major determinant of bacterial diversity across diverse soils worldwide (6, 17, 18). It has been shown that bacterial diversity reaches a maximum at neutral pH and gradually decreases below and above neutral conditions in soils (1, 2, 6, 17). This general hump-shaped pattern illustrates the importance of pH on the abundance, distribution, and diversity of soil bacterial communities (1, 6). It is plausible to assume that the combination of soil pH with temperature fundamentally (and significantly) drives soil bacterial diversity through their effects on bacterial metabolism. Survival and growth rates under acidic or alkaline conditions require distinct adaptations and changes in metabolic processes and rates, as well as require evolutionary adaptations (19). These include the structural changes in cell biology, transport of molecules, and energy transfer adaptations that collectively determine species growth and reproduction. Multiple lines of evidence suggest the activity and structure of various membrane proteins depend heavily on environmental pH, with direct implications on bacterial metabolic rates (19, 20). Given the importance of soil pH broadly affecting bacterial metabolism, it is likely to be a key factor explaining some of the unexplained variation in bacterial diversity across soils. Here, we developed a mathematical model to test whether the incorporation of pH could improve our capacity to explain the variation in bacterial diversity at different spatial scales in soil (Fig. 1).

Fig. 1.

Conceptual framework of taxa diversification. (A) At the single species level, the ancestor strain displays a mutation probability (α_t, nucleotide·mutations⁻¹ generations⁻¹) per unit of time, based on the cell proliferation rate. The progressive accumulation of nucleotide mutations U_n (U, mutant nucleotide) leads to the emergence of new phylotypes/species. (B) At the community level (disregarding species movement, that is, dispersal), different species accumulate mutation at variable paces due to divergences in cell metabolism, growth rate, etc., collectively leading to the emergence of distinct community types. (C) High temperatures (within a reasonable range) will accelerate the microbial cell metabolism and directly increase the mutation rate (upper left-hand red). The environmental pH will exert an influence on the activity of carrier proteins on the microbial cell membrane with implications for survival, reproduction, and growth, thus affecting the mutation rate (upper right-hand blue). The conceptual framework integrates three models aiming at fitting the relationships between diversity and temperature (Model I), diversity and environmental pH (Model II), and diversity, temperature, and pH (Model III).

Initial Model Development

As single-cell organisms, the metabolic rate of bacteria is often mostly determined by the rate of substrate exchange across cellular membranes, which is known to be mediated by diverse membrane-bound transporter proteins (21). We assumed that under nutrient-unlimited conditions, the metabolic rate (μ) of a bacterial species would depend on the effective amount of transporter proteins, E_e (μg cell⁻¹) (SI Appendix, Theoretical model). This was modeled as follows:

$$\mu =\sum _{i=1}^n{k}_i[E_{\mathit{ti}}]=\overline{k}·E_e,$$ [1]

where μ represents the metabolic rate and $\overline{k}$ represents the chemical reaction rate constant that is dimensionless, the value of which is related to the structure of the bacterial cell membrane transporter proteins, temperature, and nutrients, regardless of the number of cells and the concentration of nutrients.

Allen (2006) integrated the metabolic rate of species with genetic divergence through population genetics and neutral theory (22). We performed modifications to the Allen’s model to explore potential relationships between species metabolic rates and bacterial community diversity (Fig. 1 A and B). For a complete description of the model, see SI Appendix, Theoretical model. In brief, the metabolic rate affects the speciation rate (v, species individual⁻¹ s⁻¹) by changing the generation time (g, generations s⁻¹) and the mutation rate (α, mutations·nucleotide⁻¹ s⁻¹) of bacteria (23). MTE has an intrinsic assumption that the speciation rate should have a positive effect on species richness (12, 22). We assumed here the baseline expectation that species richness should increase proportionally with speciation rate. This expectation is supported when considering together the results of Allen et al. (13) and Allen et al. (22). As such, we can deduce that species richness (H) and the speciation rate (v) are driven by the metabolic rate (μ),

$$H\propto v\propto \mu .$$ [2]

We further devised three models that take into account environmental gradients in temperature and soil pH based on these conceptual frameworks.

Model I: Modeling Variation in Temperature

The chemical reaction rate constant ($\overline{k}$) is assumed to increase exponentially with temperature within the optimum temperature range of the population (22, 23). We, therefore, modeled $\overline{k}$ using the Boltzmann–Arrhenius equation (24),

$$\overline{k}=b_0·e^{\frac{{-E}_{\alpha }}{\mathit{KT}}},$$ [3]

where b₀ is the normalized parameter independent of temperature that is only related to species traits, E_α is the average activation energy of the respiratory complex (≈0.65 eV; 1 eV = 1.602 × 10⁻¹⁹ J), K is the Boltzmann constant (8.62 × 10⁻⁵ eV K⁻¹), and T is the absolute temperature (K). By integrating the Eqs. 2 and 3 into the Eq. 1, we can deduce

$$\begin{array}{c}\mathit{ln} H\propto \mathit{ln} \mu =\ln (\stackrel{-}{k}·E_e)=\ln (b_0·E_e)-\frac{E_{\alpha }}{\mathit{KT}}=B_0-\frac{E_{\alpha }}{\mathit{KT}}.\hfill \end{array}$$ [4]

Eq. 4 shows that the logarithm of microbial diversity has a negative linear relationship with the derivative of absolute temperature (1/KT), and its slope (−E_α) ranges between −0.6 and −0.7, and the intercept is B₀.

Model II: Modeling Variation in pH

Changes in environmental pH are assumed to affect the structure and function of bacterial proteins at the cell membrane (E_e) (25), thereby causing changes in the metabolic rate (μ) (19, 20). According to Henderson-Hasselbalch formula (26):

$$\begin{array}{c}\mu =\overline{k}\cdot E_e=\{\begin{array}{c}\overline{k}·C\left(E_{all}\right)\times \frac{1}{\left(1+{10}^{\left(p{K}_a-pH\right)}\right)}\hfill \\ \overline{k}·C\left(E_{all}\right)\times \frac{1}{\left(1+{10}^{\left(pH-p{K}_b\right)}\right)}\end{array}\hfill \\ =\{\begin{array}{c}{B}_1\times \frac{1}{\left(1+{10}^{\left(p{K}_a-pH\right)}\right)} \text{pH < optimal pH}\hfill \\ B_1\times \frac{1}{\left(1+{10}^{\left(pH-p{K}_b\right)}\right)} \text{pH > optimal pH,}\end{array}\hfill \end{array}$$ [5]

where B₁ is a normalized parameter related to the number of cell carriers, carrier characteristics, and temperature, E_all is the number of transporter proteins on the cell membrane at a maximum metabolic rate, and K_a and K_b indicate the acid hydrolysis constant and the alkali hydrolysis constant, respectively, when the metabolic rate is at half of its maximum (μ_max/2). The K_a and K_b vary depending on specific species traits. By integrating the Eqs. 2 and 5 into Eq. 1, we can model

$$\ln H\propto \text{ln }\mu =\{\begin{array}{c}{B}_1-\ln \left(1+{10}^{\left(p{K}_a-pH\right)}\right) \text{pH}<\text{optimal pH}\\ B_1-\ln \left(1+{10}^{\left(pH-p{K}_b\right)}\right) \text{pH}>\text{optimal pH}\end{array}$$ [6]

.

Eq. 6 shows that the logarithm of bacterial diversity and pH can be displayed as a hump-shaped function. The optimum pH (pH_opt) indicates the pH at which diversity is highest. The pK_a and pK_b indicate the acid and alkali pH, respectively, when the diversity (lnH) is at half of its maximum (lnH_max/2) (Fig. 1C). Note that the model does not account for proton motive force (PMF)-related energetic requirements. These are known to be associated with the maintenance of intracellular pH homeostasis and chemiosmotic gradients across the cell membrane (SI Appendix, Theoretical model).

Model III: Integrating Variation in Temperature and pH

Chemical reaction rate constants, including pK_a and pK_b, are dimensionless and are dynamically influenced by temperature. As such, there is a clear interaction between changes in temperature and pH. This interaction was modeled as follows:

$${\mathit{pk}}_a=-\ln K_a=\frac{E_{\beta }}{\mathit{KT}}-\ln b_1,$$ [7]

$${\mathit{pk}}_b=-\ln K_b=\frac{E_{\gamma }}{\mathit{KT}}-\ln b_2,$$ [8]

where b₁ and b₂ are the normalized parameters and E_β and E_γ are the average activation energy for the acid and alkali hydrolysis rate constants, respectively. And

$$B_2=\ln \left[b_0·C\left(E_{all}\right)\right],$$ [9]

where B₂ is a normalized parameter. By integrating Eqs. 3, 5, 7, 8, 9, and 2 into Eq. 1, the result is

$$\begin{array}{c}\ln H=\ln \mu \hfill \\ =\{\begin{array}{c}{B}_2-\frac{E_{\alpha }}{KT}-\ln \left(1+{10}^{\left(\left(\frac{E_{\beta }}{KT}-\ln b_1\right)-pH\right)}\right) \hfill \\ \text{pH < optimal pH}\hfill \\ B_2-\frac{E_{\alpha }}{KT}-\ln \left(1+{10}^{\left(pH-\left(\frac{E_{\gamma }}{KT}-\ln b_2\right)\right)}\right) \\ \text{pH > optimal pH}\mathrm{\text{.}}\hfill \end{array}\hfill \end{array}$$ [10]

Eq. 10 describes the relationship between the logarithm of bacterial diversity and the reciprocal of absolute temperature and pH. Temperature affects the relationship between pH and diversity by changing the pK_a/pK_b, thus establishing a modeling dependence between temperature and pH (Fig. 1C).

Based on the above derivation, our models further make the following key predictions:

(1) For Model I, the logarithm of ‘diversity’ (lnH) is inversely related to the reciprocal of temperature (1/KT) based on Eq. 4. The slope and the intercept are determined by −E_α and B, respectively, and B is related to the intrinsic characteristics of bacterial species.

(2) For Model II, the relationships between bacterial diversity and pH can be displayed as a hump-shaped function. The optimum pH determines the pH at which diversity is highest. The pK_a and pK_b indicate the acid and alkali pH, respectively, when the diversity (lnH) is at half of its maximum (lnH_max/2)).

(3) For Model III, temperature and pH interactively influence the patterns of bacterial diversity, as indicated in Eq. 10. Specifically, pH affects the slope of the relationship between lnH and 1/KT, and temperature affects the opening direction and scale of the hump-shaped function of lnH and pH (SI Appendix, Fig. S2). Importantly, in the model temperature affects the relationship between pH and diversity by changing the pK_a/pK_b (Eqs. 7 and 8), thus establishing a modeling dependence between temperature and pH.

We tested three predictions of models at three different levels to explore whether metabolic models incorporating pH could more accurately predict bacterial diversity patterns. We initially performed a laboratory experiment based on the rapid evolution of morphotypes of the model bacterium Pseudomonas fluorescens SBW25. This experiment was performed to generate data to test our model at the single species level. P. fluorescens SBW25 has been broadly used to study the bacterial diversification and evolution (27). This bacterium is capable of growing in a wide range of temperatures (5 °C to 35 °C) and pH (4.5 to 9.5). When subjected to growth under heterogeneous static conditions, SBW25 rapidly diversifies from the ancestral smooth (SM) morphotype. This process of short-term diversification results in the coexistence of the ancestral smooth (SM) morphotype, with two other morphotypes, i.e., the wrinkly spreader (WS) and the fuzzy spreader (FS) morphotypes. The underlying genetic mutations associated with these morphotypes have been previously well characterized (28, 29). We then extended our analyses to community-level diversity in soil at continental and global scales (SI Appendix, Fig. S3). Community-level analyses were performed using two large datasets of soil bacterial communities. First, we collected and analyzed patterns of bacterial diversity across 45 soil samples from a paddy soil system displaying a natural gradient of pH and temperature in East Asia (18). Then, to evaluate our model performance at a global scale, we conducted a meta-analysis using a well-curated dataset comprising 870 soil samples collected worldwide across divergent ecosystems (1).

Results

Model Performance at the Species Level.

P. fluorescens SBW25 had the maximum growth rate and metabolic rate at 28 °C and pH 7 (SI Appendix, Figs. S4−S6 and S8). Model I (Eq. 4) was used to assess the relationship of diversity (in this case, diversification) with variation in temperature (Fig. 2A and SI Appendix, Fig. S7 and Tables S2−S4). The results indicated that the logarithmic diversity index had a strong Boltzmann exponential relationship with the reciprocal of temperature (1/KT) ranging from 5 °C to 28 °C (P < 0.01). The fit (R²) of Model I for diversity was 82%, with a slope value (−E_a) of −0.62. When pH ranged from 4.5 to 9.5, Model II (Eq. 6) indicated that the logarithmic diversity followed a hump-shaped function with pH, where pH of 4.5 and pH of 9.5 were the corresponding pK_a and pK_b parameters, and pH of 7 was the optimum pH (R² = 85%, P < 0.01, Fig. 2B and SI Appendix, Fig. S9 and Tables S2−S3 and S5).

Fig. 2.

Model fit from the single species level to the community level at continental and global scales. Model I displays the relationship between diversity and temperature; Model II displays the relationship between diversity and pH; and Model III integrates variations in diversity, temperature, and pH. (A–C) The fit of the models at the individual level (using the strain P. fluorescens SBW25), S_obs represents the number of observed morphotypes. (D–F) The fit of the models at the community level is based on samples collected at a continental scale (paddy soils displaying a natural gradient in soil pH and temperature in East Asia). (G–I) The fit of the models at the community level at a global scale (based on a meta-analysis including a total of 870 soil samples collected from diverse ecosystems worldwide). Richness represents the number of observed OTUs. Pearson correlational analyses were performed, and statistics and R² values are provided. Linear regressions represent the least squares regression fits, and shaded areas represent the 95% CIs.

Next, the relationship between diversity and the combined variation of temperature (ranging from 5 °C to 28 °C) and pH (ranging from 5 to 9) was examined using a two-way ANOVA (SI Appendix, Figs. S10 and S11). The results showed that the interactive term of temperature and pH significantly explained the diversity of P. fluorescens (R²= 0.04, P = 0.001, SI Appendix, Table S1). Using Model III (Eq. 10) to integrate both temperature and pH, the R² of the variation in diversity was 79% (P < 0.001, Fig. 2C). The Boltzmann slope (−E_a) of the temperature-diversity relationship was −0.60, and the pH-diversity relationship consistently followed a hump-shaped function, in which pH of 7 was the optimum pH.

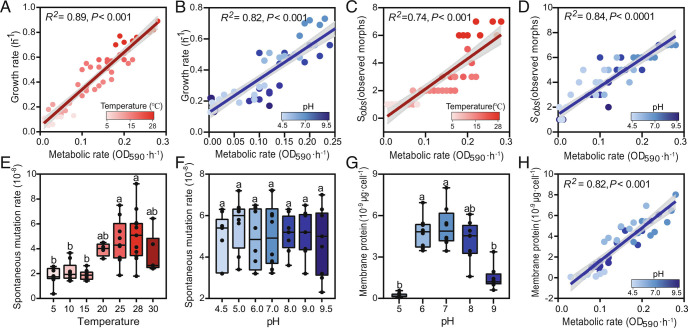
We found the metabolic rate to be significantly correlated with the growth rate (R²_5−28 °C = 0.89, P < 0.001; R²_5−35 °C = 0.84, P < 0.001, Fig. 3A and SI Appendix, Fig. S12A) within two ranges of temperature (5 °C to 28 °C and 5 °C to 35 °C). This was also significant for pH values ranging from 5 to 9 (R²_diversity= 0.82, P < 0.001, Fig. 3B). The metabolic rate was also significantly correlated with diversity (R²_5−28 °C = 0.74, P < 0.001; R²_5−35 °C = 0.76, P < 0.001, Fig. 3C and SI Appendix, Fig. S12B) within two temperature ranges (5 °C to 28 °C and 5 °C to 35 °C) and with pH values ranging from 5 to 9 (R²_diversity = 0.84, P < 0.001, Fig. 3D). We also found the spontaneous mutation rate to significantly increase at high temperatures within the optimum temperature range. Worth mentioning, no significant relationship was found for pH (Fig. 3 E and F). The membrane protein content reached the maximum at neutral pH and gradually decreased when deviating from pH 7 (Fig. 3G). Additionally, the membrane protein content of P. fluorescens SBW25 was significantly correlated with the metabolic rate when pH values ranged from 5 to 9 (R²= 0.82, P < 0.001, Fig. 3H).

Fig. 3.

Mechanisms of species diversification. Relationships between metabolic rate and growth rate at different temperatures (A) and pH values (B). Relationships between metabolic rate and diversity at different temperatures (C) and pH values (D), S_obs represents the number of observed morphotypes. Mutation rate (per cell per generation, for gentamycin resistance) at different temperatures (E) and pH values (F). The membrane protein content of a single cell at different pH values (G) and relationships between membrane protein content and growth rate at different pH values (H). Pearson correlation analyses were performed, and statistics and R² values are provided. Linear regressions represent the least squares regression fits, and shaded areas represent the 95% CIs.

Model Performance at the Community Level across Continental and Global Scales.

The analysis based on two-way ANOVA revealed both temperature and soil pH to exert both independent and interactive effects on bacterial diversity across continental and global scales (R² = 0.01 to 0.35, P < 0.05, SI Appendix, Table S1). The microbial community showed the maximum metabolic rate at 28 °C and pH 7 at three typical paddy soils (SI Appendix, Fig. S13). The fit (R²) of Model I for bacterial diversity in paddy soils and the global soil dataset were 57% and 39%, with slopes (−E_a) of 0.16 and −0.19, respectively (P < 0.05, Fig. 2 D–G). Likewise, the R² of Model II for bacterial diversity in paddy soils and the global soil dataset was 29% and 20%, respectively (P < 0.001, Fig. 2 E–H). At the continental scale (i.e., paddy soil data), pH of 3.6 was the corresponding pK_a parameter, and pH of 7.5 was the optimum pH. At the global scale (i.e., global soil dataset), pH of 2.2 and 10.0 were the corresponding pK_a and pK_b parameters, and pH of 7.2 was the optimum pH. The R² of Model III for bacterial diversity in paddy soils and the global soil dataset was 30% and 43%, respectively (P < 0.001, Fig. 2 F–I).

We further evaluated the applicability of these models at the level of different phyla/classes within communities and across various ecosystems (i.e., continental and global scales). Specifically, the results of Model I showed that the diversity-temperature relationship followed a non-universal trend, ranging from being negative to positive, or not displaying a significant relationship (Fig. 4A). The optimum average annual air temperature ranged from 16.1 °C to 28 °C, and the R² and slope (−E_a) of Model I ranged from 3 to 53% and −0.44 to 0.27, respectively (SI Appendix, Tables S2−S4). Model II predicted the soil pH-diversity relationship with R² ranging from 7 to 45%, the optimum soil pH from 6.10 to 9.35, the pK_a from 1.08 to 4.43, and the pK_b from 8.86 to 11.70 (Fig. 4B and SI Appendix, Tables S2, S3 and S5). When compared to Models I and II, Model III showed greater explanatory power and higher R² values for the relationships between bacterial diversity, temperature, and pH within and across ecosystems (P < 0.05, Fig. 5 A and B), as well as the occurrence of 13 dominant bacterial phyla (P < 0.05, Fig. 5  C and D). The R² of Model III ranged from 7 to 66%, the Boltzmann slope (−E_a) from −0.03 to −0.45, the optimum pH from 6.10 to 9.35, the pK_a from 1.08 to 4.43, and the pK_b from 8.86 to 11.70. Three different commonly used statistical models, that is, one linear model, one quadratic polynomial model, and one piecewise relationship model, were also used to estimate the relationships between temperature, pH, and bacterial diversity (SI Appendix, Tables S4 and S5). The results showed that Model I ($|\mathrm{A}\mathrm{I}\mathrm{C}|$ _avg = 211, R²_avg = 0.22) and Model II ($|\mathrm{A}\mathrm{I}\mathrm{C}|$ _avg = 212, R²_avg = 0.24) both had the lower Akaike information criterion (AIC) and higher R²(SI Appendix, Tables S4 and S5). These comparative analyses validate the best fit and higher accuracy of our models compared to previously developed ones.

Fig. 4.

Model parameters of soil bacterial communities across distinct ecosystems at a global scale. (A) The slope (−E_a) of the relationships between temperature and diversity of bacterial communities at distinct ecosystems or the phyla/classes levels. The dark red bars indicate significantly positive correlations (P < 0.05), and gray bars indicate non-significant correlations (P > 0.05). (B) The pK_a, pH_opt, and pK_b of the relationship between pH and diversity of soil bacterial communities across ecosystems or at the phylum/class levels. Richness represents the number of observed OTUs, and Chao1 represents the number of estimated OTUs.

Fig. 5.

Testing the performance of the models. Variation in the model fit R² of soil bacterial communities at a global scale (A) and per ecosystem type (B). Variation in the model fit R² of soil bacterial communities at the community level (C) and partitioned at the phylum/class levels (D). Red, blue, and purple lines correspond to Models I, II, and III, respectively. Model I displays the relationship between diversity and temperature; Model II displays the relationship between diversity and pH; and Model III integrates variations in diversity, temperature, and pH. Richness represents the number of observed OTUs, and Chao1 represents the number of estimated OTUs.

Discussion

Our study provides the advances in quantitative models aiming at exploring the influence of temperature and pH—and their interactive effects—structuring patterns of bacterial diversity in soils across distinct systems and scales (Fig. 1). The explicit consideration of temperature and pH ranges into the models was based on their known effects on bacterial cell metabolism (5, 6). These models were empirically tested across distinct scales of biological organization, ranging from single species at the level of individual bacterium strain to soil bacterial communities within an ecosystem gradient and across global ecosystems. Advancing research on the development of quantitative models able to explain bacterial diversity across spatial scales is still a challenge. For example, Okie et al. (2015) proposed a model primarily based on environmental filtering associated with metabolic theory (11). In line with this study, our models provide a new synthesis that further integrates diversification rate and pH across scales with principles of the MTE. Despite the fundamental importance of temperature and pH in structuring bacterial diversity in soils has long been recognized (1, 2), relatively less attention has been given to integrating these variables into predictive models of biodiversity. A mechanistic understanding of how these factors jointly structure patterns of soil diversity can enhance our ability to prospectively predict dynamic changes in bacterial communities and the impacts on their functioning across distinct spatial scales and systems. The outcome results of the models confirmed our hypothesis that the growth rate and diversity of P. fluorescens were highly correlated and displayed similarly a high dependence on temperature and pH (Fig. 3). Interestingly, corroborating our single species level experiment, these relationships were also ubiquitous across communities both at the continental and global scales. Together, our models provide a new framework that successfully and more accurately integrates the theoretical predictions of cell metabolism as the foundation of all life processes with patterns of biodiversity.

As predicted by Model I, we observed the logarithmic of the diversity index at the species level to have a strong Boltzmann exponential relationship with the reciprocal of temperature (1/KT) ranging from 5 °C to 28 °C (P < 0.01), with a slope value (−E_a) of −0.62 (Fig. 2A). Higher temperatures within this range tend to accelerate metabolic rates and biochemical processes and thereby should promote bacterial diversity. Particularly for microbes, this would increase ‘effective’ evolutionary time, given their general shorter generation times, faster mutation rates, and faster selection (12, 30). Considering higher temperature would impose a physiological constraint on organisms (12, 31), our model assumed that both growth and mutation rates increased exponentially with temperature over a biologically realistic range of temperature. However, the Boltzmann relationship between temperature and species life processes involved in growth rates and diversity disappeared once the temperature exceeded 28 °C (Fig. 2A). Furthermore, the enhanced spontaneous mutation rate of P. fluorescens SBW25 was observed at high temperature (Fig. 3E). Although the MTE holds that spontaneous mutation rate is independent of temperature, numerous studies have shown that high temperature can frequently facilitate spontaneous mutation rates of various bacterial species (22, 32, 33). This occurs possibly due to the trade-off between genetic conservatism and variability of bacteria once exposed to stringent habitat selection (34). Consequently, speciation rate would be expected to augment the temperature dependence of diversity (i.e., activation energy) compared to the temperature dependence of metabolic rate (and generation time) alone. As such, the speciation rate strengthens the relationship between the logarithm of species diversity and the inverse of absolute temperature, as indicated by the steeper slope. However, our results showed that the slope values (e.g., the inverse number of activation energy, −E_a) of negative diversity-temperature relationships in natural ecosystems are lower or even opposite when compared to the model’s expectation at the community level at both continental and global scales, which does not follow the Model I predictions. This result can be explained by distinct non-mutually exclusive points. That is, the variable diversity is not proportional to the speciation rate, and the effective activation energy for metabolic rate (or speciation rate) (here parametrized as 0.65 eV) may likely differ across distinct microbial taxa. This also may be due to other abiotic factors—in particular pH and salinity—known to explain the variation in microbial community in soils (35, 36), potentially weakening the temperature-diversity relationship at the community level (SI Appendix, Fig. S2). For instance, temperature and pH exhibited counteractive effects in the paddy soil samples (R² = 0.63, P < 0.001, SI Appendix, Fig. S14), with higher bacterial diversity detected in colder samples being found at closer-to-optimal pH values, which led to a positive diversity (lnH)-temperature (1/KT) relationship.

By using Model II, we found the diversity of P. fluorescens SBW25 to follow a hump-shaped function over a wide range of pH values (Fig. 2B). This is consistent with previous research (37, 38), and our results also suggested that the membrane protein activity, the bacterial growth rate, and the bacterial metabolic rate are all expected to display a hump-shaped function relationship with pH (Fig. 3 G and H and SI Appendix, Figs. S4 and S5). Thus, the consistent relationship across ontogeny to ecological processes likely implies a certain unified mechanism of metabolic processes. The metabolism of individual living cells is largely dependent on extracellular pH, and this occurs because distinct ranges of pH will impact the functional performance of a variety of proteins in the cell membrane (25). It is worth mentioning that the pH-metabolic model is supported by the significant correlation between metabolic rates and the number of cell membrane proteins. However, the observed correlation could possibly reflect the increased energy cell expended at non-neutral pH to maintain homeostasis. As such, caution is warranted in interpreting this model, as it is primarily based on correlation and does not aim at providing an integrative mechanistic metabolic understanding. Importantly, pH also affects the PMF, which is involved in the maintenance of cellular homeostasis and provides energy requirements for essential bacterial metabolism processes (39). The PMF and cell membrane carrier proteins synergistically affect the bacterial metabolic processes when pH changes. However, the diverse and non-uniform PMF responses to pH variation hinder the incorporation of this variable into our metabolic model. As for the community-level comparison, although the R² of Model II (both at the continental and global scales) was much lower than that at the single species level under controlled conditions, the model still strongly predicted the relationship between pH and soil bacterial diversity. There were no differences between Model I and Model II for all diversity indexes in terms of R² (Fig. 5 A and B), and our results do not support an absolute dominance of temperature (15) or pH⁶ in structuring bacterial diversity. In fact, our results suggest that their relative importance may vary across ecosystem types or at the detailed level of distinct bacterial phyla. The observed optimal pH range for ecosystem types and bacterial phyla ranged widely from 6.10 to 9.35 (Fig. 4B). In addition, soil pH also dynamically affects other soil parameters, e.g., nutrient cycling dynamics, organic carbon transformation, soil moisture regimes, and salinity (1, 3). And, worth mentioning, at a lower phylogenetic resolution, different microbial taxa are also expected to have distinct pH optimum values.

The combined influence of temperature and pH on the patterns of soil bacterial diversity was more accurately predicted by Model III, with R² ranging from 7 to 66%, for the patterns of community diversity at the continental and global scales. The two predictor variables improved the accuracy of the model prediction of bacterial diversity patterns (Fig. 5). High temperature (in this case, within the operational temperature range) and optimum pH were found to directly and indirectly result in high bacterial diversity in soils. First, as predicted by our modeling approach, higher temperatures and optimal pH promote higher metabolic rates, growth rates, and shorter population growth cycles (12). These biological rates set the pace of population dynamics and underlie nearly all biochemical activities at multiple levels of organismal organization (12, 40, 41). Second, it is important to acknowledge that other factors might also affect these observed biodiversity patterns. For example, the growth rate can—to some extent—enhance colonization by favoring dispersal, which would augment richness at optimal pH and warmer temperatures. Besides, optimal pH ranges can be associated with higher speciation rates due to there being a wide variety of environments or a greater number of niches or stable enzymes at this pH. Last, both pH and temperature modulate multiple parameters in soils (e.g., resource availability, organic carbon types, soil moisture regimes, and salinity), all of which exert an effect on bacterial diversity.

It is worth discussing that the R² values of all three models at the community level were lower than that obtained at the population level under laboratory conditions. The low R² value is likely a reflection of the complex interplay of ecological processes and mechanisms operating in structuring bacterial communities from populations to communities and from local to global scales. The different abiotic variables have distinct levels of stringency in imposing species selection. In line with that, pH has been suggested to be a more stringent filter in soil bacterial taxa (6, 17, 18), whereas selection imposed by variation in temperature tends to be weaker. This corroborates the fact that microbial thermal sensitivity is lower than that of macro-organisms and the fact that microbes can persist under harsh—albeit non-stringent—environmental conditions under low metabolic states, dormant, via spore formation (15, 35). It can also be reasoned non-deterministic factors—in this case, random dispersal—can partially counterbalance local selection and be a more important factor in structuring communities at broader scales. This nicely aligns with a recent consensus in ecology stating that most of the factors explaining variation in community dissimilarities tend to be scale-dependent (42). For example, while pH was a strong predictor of community assembly processes at a local scale in salt marsh soil bacterial communities, variation in the content and concentration of organic carbon better explained the assembly processes when the model was applied at a regional scale (43). Collectively, it is thus expected a steady decrease in the model fit as communities become progressively more diverse and models attempt to cover broader scales of biological organization (15, 16, 35).

In conclusion, the novel quantitative models devised here enable reliable quantitative prediction of bacterial diversity in soil, by adding another parameter (i.e., pH) to the current MTE, which solely focuses on the influences of temperature. While it is generally accepted that temperature and pH are two of the most important environmental factors that determine bacterial diversity in soil, their relative importance remains controversial and their potential interactions have rarely been addressed (15–18). We show that the new models fit well the experimental evolution data with a single bacterial and can also explain the microbial community data from previous field studies at regional and global scales. However, given the diversity of soil environments, other environmental factors such as soil moisture, salinity, and resource availability may play dominant roles under certain conditions, it is thus important to further develop the models, allowing the integration of multiple environmental factors. To the best of our knowledge, this study is the first to explicitly incorporate pH into existing metabolism theory, highlighting the capacity to improve our mechanistic understanding of microbial biodiversity biogeography. Improving this mechanistic understanding of the variation in microbial communities across broad environmental gradients will be essential in our efforts to model and forecast the variation in microbial biodiversity under current and future climate scenarios.

Materials and Methods

Bacterial Strain and Growth Conditions.

The bacterium P. fluorescens SBW25 was well-suited for our study, as population-level evolution was detected at the phenotypic level by visual differences in colony morphology after 3 d of culture in a spatially heterogeneous environment (27). Three dominant morphs named smooth (ancestral), WS, and FS were observed. The genetic bases of these diversification trajectories at the population level have been well-established. For instance, the WS and FS morphotypes arise through gene mutations that cause the constitutive over-production of cellulose and lipopolysaccharide polymers, respectively (28, 29). SBW25 was routinely cultivated in King’s medium B (KB) at 28 °C. Growth properties were determined in KB medium under either orbital shaking (180 rpm) or static conditions. Acidity and alkalinity were maintained with the addition of morpholineethanesulfonic acid (pH at 4.5, 5, and 6) (44) and the N-[Tris(hydroxymethyl) methyl]-3-aminopropanesulfonic acid (pH at 8, 9, and 9.5), respectively (45). Morpholinepropanesulfonic acid was used to maintain pH 7. The maximum growth rate of each culture in each temperature and pH was calculated as the average value of eight cultures.

Fluctuation Test.

Bacterial mutation rates were estimated using the standard method of fluctuation test with slight modification (46). Each temperature and pH treatment involved ten replicate microcosms each inoculated with ~500 bacterial cells. These treatments were cultured up to an absorbance (OD₆₀₀) of 1.0. Mutants were identified using serial dilution and plating of aliquots onto KB Petri dishes supplemented with 15 mg mL⁻¹ of gentamicin. The Ma-Sandri-Sarkar Maximum Likelihood Estimator method was used to calculate the mutation rate from the average and median frequency of the gentamycin-resistant colonies.

Static Culture Test.

To quantify bacterial diversification, the ancestral strain was inoculated into 6 mL KB microcosms and grown under static conditions as previously described (27, 32). Diversity was regularly measured by daily sampling over a period of 7 to 25 d, depending on the growth and diversification rate at different temperature (5 °C, 10 °C, 15 °C, 20 °C, 25 °C, 28 °C, 30 °C, 32 °C, and 35 °C) and pH (4.5, 5, 6, 7, 8, 9, and 9.5) environments. The three distinct morphotypes (SM, WS, and FS) were identified in KB plates, and more than 100 colonies were counted for each treatment. The effects of temperature were tested at the optimum pH 7, whereas the effects of pH were examined at the optimum growth temperature of 28 °C. To test the combined effects of temperature and pH, diversity data were also obtained from seven temperatures (5 °C, 10 °C, 15 °C, 20 °C, 25 °C, 28 °C, and 30 °C) across three pH (5, 7, and 9).

Membrane Protein Extraction.

SBW25 cells at logarithmic phase (OD₆₀₀ = 0.6) at five pH gradients (pH = 5, 6, 7, 8, and 9, eight repetitions) were centrifuged at 4 °C at 10,000 g for 5 min, and cell pellets were resuspended in 0.1 M phosphate buffer (pH 7) and washed twice. Subsequently, membrane proteins were extracted using a Bacteria Membrane Protein Extraction Kit (Bestbio, Shanghai, China) according to the manufacturer’s instruction. Finally, an approximately 50 μL suspension was obtained, and the protein content was determined using a BCA Protein Assay Reagent Kit (BestBio, Shanghai, China). Plate counting was used to determine the number of bacteria in each culture. The membrane protein content of a single cell was determined based on the ratio of the total amount of extracted cell membrane proteins and the number of cells counted on the plate.

Metabolism Rate.

SBW25 cells at logarithmic phase (OD₆₀₀ = 0.6) were diluted into fresh KB media (w/w 1:5) and amended with 100 μg mL⁻¹ of resazurin solution. We set up a gradient of temperature treatments (5 °C, 10 °C, 15 °C, 20 °C, 25 °C, 28 °C, 30 °C, 32 °C, and 35 °C) under optimal pH 7 and a gradient of pH treatments (4.5, 5, 6, 7, 8, 9, and 9.5) under optimal temperature of 28 °C. In parallel, cell-free experiments were set up as controls. The experiments were incubated in the dark on a shaker at 180 rpm. Measurements were made every 30 min and lasted 4 h. The cultured bacterial suspensions were centrifuged at 10,000 rpm for 4 min, and the supernatant was collected. In the existence of an active bacterial culture, the dehydrogenase enzyme activity changes resazurin to the reduced compound resorufin, and thus the color turns from blue to pink. Fluorescence was measured in a microplate reader at the excitation wavelength of 560 nm and emission wavelength of 590 nm. The metabolic rate (OD₅₉₀ h⁻¹) was determined by the slope of the reduced resazurin line, which was measured by recording the colorimetric shift at OD₅₉₀.

Three typical paddy soils (i.e., black soil, red soil, and fluvo-aquic soil) were selected to examine the metabolic rates of microbial communities. For each soil sample, the 10⁻¹ soil suspension was obtained by mixing 10 g of fresh soil in 100 mL of sterile distilled water using a blender (5 min). The obtained solution was diluted into fresh media (w/w 1:5) amended with 100 μg mL⁻¹ of resazurin solution. Sterile soil suspensions amended with 100 μg mL⁻¹ of resazurin solution were used as controls. The metabolic rates of soil bacterial communities at different temperatures and pH settings were determined by fluorescence as described above.

Soil sampling and data collection.

The paddy soil dataset is derived from previously published data (18, 35). Briefly, a total of 45 soil samples were collected in a paddy ecosystem along the north–south transect across East Asia. The latitude of the sampling area ranged from 15.90°N to 44.31°N, the average annual air temperature from 2 °C to 27.5 °C, and the average annual precipitation from 550 mm to 2345 mm. The soil sampling was performed as previously described (18). The Global Positioning System coordinates recorded at each sampling site were imported into the NOAA website to calculate the average annual air temperature. Soil bacterial community was analyzed using high-throughput sequencing as previously described (35). Alpha-diversity values (Richness and Chao1) of bacteria communities were calculated after rarifying all samples to the same sequencing depth.

Acquisition of global scale metadata and public datasets.

All meta-analysis data were obtained from The Earth Microbiome Project (EMP, http://www.earthmicrobiome.org). Sample processing, sequencing, and core amplicon data analysis were performed by the Earth Microbiome Project (www.earthmicrobiome.org), and all amplicon sequence data and metadata have been made public through the EMP data portal (qiita.microbio.me/emp) (1). Briefly, we got 870 soil samples in total, in average annual air temperature from −16.8 °C to 26.9 °C, soil pH from 3.3 to 10.4, and a rough gradient of latitude from −78.19°N to 71.30°N. Climate data including monthly temperature and precipitation were obtained from the WorldClim database (http://www.worldclim.org).

Diversification at the population level.

Here, we counted the number of observed colony morphotypes (S_obs) and applied a diversification index based on the number of estimated morphotypes (S_est). The calculation method of S_est refers to the calculation method of Chao1 richness in ecological communities (47). The calculation formula for the number of estimated morphotypes is as follows:

$$S_{est} = S_{obs}+\frac{n_1\left(n_1-1\right)}{2\left(n_2+1\right)},$$

where S_est is the number of estimated morphs, S_obs is the number of observed morphs, n₁ is the number of morphs with only one morphotype, and n₂ is the number of morphs with only two morphotypes.

Here, the diversification index is calculated based on morphological variation. Although P. fluorescens colonies evolved in a spatially heterogeneous environment and populations displayed substantial morphotype diversity [smooth type, WS, and FS] after 7 to 25 d (32), we cannot classify these morphs as new species. As such, we refer to these metrics as ‘number of morphs’ and ‘estimated number of morphs’. In addition, we further subdivided each morphotype into three types: large (diameter > 2 mm), medium (1 mm < diameter < 2 mm), and small (diameter < 1 mm) to increase morphological variation sensitivity.

Statistical analyses.

Pearson correlations were used to test the linear dependence between two variables. The significance of Pearson correlations was inferred using the Student’s t-distribution. The coefficient of determination (R²) and the AIC were used to assess the goodness of fit of the model, and the R² was calculated as follows:

$$R_2 = 1-\frac{{\mathrm{SS}}_{res}}{{\mathrm{SS}}_{tot}},$$

where SS_res is the sum of squares of residuals and SS_tot is the total sum of squares. Since the residuals can be considered as the variance of the model errors, the term SS_res/SS_tot represents the unexplained proportion, and thus R² is the proportion of the explained variance of the model.

The AIC was calculated as follows:

$$\mathrm{AIC} = -2 \times \ln (L) + 2n\mathit{,}$$

where L is the likelihood function which is the probability of the data given a model and n is the number of parameters. Model selection was based on AIC, followed by explained variance (R²), and parameter significance (P-values). If the differences in AIC values between two models are <2, the models are considered competitive (15). Lower AIC values indicate better model fits.

Fittings of models.

One of the major predictions of Model I is the relationship between the logarithm of bacterial diversity and the reciprocal of absolute temperature. We tested this prediction by using estimated and observed bacterial species diversity and annual average air temperatures. We employed the ordinary least squares estimation of linear regression to determine the parameters. The Model I is,

$$\ln \left(H\right)=B_0-\frac{E_{\alpha }}{KT},$$

where H is species’ diversity, K is Boltzmann’s constant, T is absolute temperature in Kelvin, B₀ is the intercept, and −E_α (activation energy) is the slope of this linear model. Two statistical models, a quadratic polynomial model (48) and a piecewise relationship model (49), were also used for estimating the relationships between temperature and bacterial diversity.

One of the major predictions of Model II is the logarithm of bacterial diversity and pH can be displayed as a hump-shaped function. The optimum pH indicates the pH at which diversity is highest. The pK_a and pK_b indicate the acid and alkali pH, respectively, when the diversity (lnH) is at half of its maximum (lnH_max/2)). pK_a and pK_b are free parameters, with values ranging from 0 to 14. We tested this hypothesis using estimated and observed bacterial species diversity and pH. We employed the ordinary least squares estimation of nonlinear regression to determine the parameters. The Model II is,

$$\ln H=\{\begin{array}{c}{B}_1-\ln \left(1+{10}^{\left(p{K}_a-pH\right)}\right) \text{pH}\text{<}\text{optimal pH},\\ B_1-\ln \left(1+{10}^{\left(pH-p{K}_b\right)}\right) \text{pH}\text{>}\text{optimal pH}.\end{array}$$

where B₁ is the normalized parameter. Three statistical models, a liner mode, a quadratic polynomial model (48), and a piecewise relationship model (49), were also used for estimating the relationships between pH and bacterial diversity.

One of the major predictions of Model III is the relationship between the logarithm of bacterial diversity and the reciprocal of absolute temperature and pH. The temperature affects the relationship between pH and diversity by changing pK_a/pK_b, thus establishing a modeling dependence between temperature and pH. We employed the ordinary least squares estimation of nonlinear multiple regression to determine the parameters. The Model III is,

$$\begin{array}{c}\ln H=\ln \mu \hfill \\ =\{\begin{array}{c}{B}_2-\frac{E_{\alpha }}{KT}-\ln \left(1+{10}^{\left(\left(\frac{E_{\beta }}{KT}-\ln b_1\right)-pH\right)}\right) \hfill \\ \text{pH < optimal pH}\hfill \\ B_2-\frac{E_{\alpha }}{KT}-\ln \left(1+{10}^{\left(pH-\left(\frac{E_{\gamma }}{KT}-\ln b_2\right)\right)}\right) \\ \text{pH > optimal pH}\mathrm{\text{.}}\hfill \end{array}\hfill \end{array}$$

where B₂, b₁, and b₂ are the normalized parameter independent of temperature and pH. b₁ and b₂ are free parameters, and the value results of equations (E_β/KT−ln b₁) and (E_γ/KT−ln b₂) range from 0 to 14.

Supplementary Material

Appendix 01 (PDF)

Data, Materials, and Software Availability

The sequence (genomic) data of the bacterial 16S rRNA gene generated in this study have been deposited in the Sequence Read Archive (SRA) at the National Center for Biotechnology Information (NCBI) with the accession number PRJNA607877 (50). All other data used in this study have been deposited in figshare (https://doi.org/10.6084/m9.figshare.20485986) (51).