Abstract
利用超声心动图进行心室分割能够获得心室容积参数，对评价心功能有重要意义。但超声图像有噪声大、难以分割等特点，仅仅靠人工对目标区域进行手动分割工作量巨大，且目前自动分割技术尚无法保证分割精度。针对这些问题，本文提出了一种全新的算法框架对心室结构进行了分割提取。首先，采用更快速的基于区域的卷积神经网络目标检测算法对目标区域进行定位，得到感兴趣区域；然后使用 K 均值（K-means）算法对目标区域进行初始聚类；接着使用一种自适应核函数带宽的均值漂移（mean shift）算法进行分割；最后采用种子填充算法提取目标区域。该算法结构实现了自动提取分割目标区域，免去了人工定位的过程。实验表明，在定量评价标准下，这种分割框架能够对目标区域进行精确的提取，同时提出的自适应均值漂移算法较传统固定带宽均值漂移算法更稳定，且分割效果更好。研究结果显示，本文所述方法有助于实现超声心动图左心室切面的自动分割。
Keywords: 左心室分割, 左心室定位, 像素聚类, 均值漂移分割, 自适应核函数带宽
Abstract
The use of echocardiography ventricle segmentation can obtain ventricular volume parameters, and it is helpful to evaluate cardiac function. However, the ultrasound images have the characteristics of high noise and difficulty in segmentation, bringing huge workload to segment the object region manually. Meanwhile, the automatic segmentation technology cannot guarantee the segmentation accuracy. In order to solve this problem, a novel algorithm framework is proposed to segment the ventricle. Firstly, faster region-based convolutional neural network is used to locate the object to get the region of interest. Secondly, K-means is used to pre-segment the image; then a mean shift with adaptive bandwidth of kernel function is proposed to segment the region of interest. Finally, the region growing algorithm is used to get the object region. By this framework, ventricle is obtained automatically without manual localization. Experiments prove that this framework can segment the object accurately, and the algorithm of adaptive mean shift is more stable and accurate than the mean shift with fixed bandwidth on quantitative evaluation. These results show that the method in this paper is helpful for automatic segmentation of left ventricle in echocardiography.
Keywords: left ventricle segmentation, left ventricle localization, pixel clustering, mean shift segmentation, adaptive bandwidth
引言
超声心动图是分析人体心脏结构和功能的重要技术手段。医学上对人体心脏超声检查主要有 6 个基本标准切面，特殊情况下还会对患者心脏采取更多的切面检查。如此大量的超声图像需要进行人工采集并且对每个切面予以分析，整个过程十分繁琐。因此如果在超声心动图中对一些关键部位实现自动定位分割能够有利于简化诊断流程。尽管超声成像因为其廉价、无创和实时性等特点在临床诊断中发挥着巨大的作用，但对于超声图像的自动分割一直存在几个问题：一是超声图像本身带有大量斑点噪声，为计算机的自动处理带来了很大困难；二是难以自动定位图像中的感兴趣区域（region of interest，ROI）。对于临床医生来说，获取了超声图像后，通常只需关心其中的某个结构，如：左心室等，所以如何确定超声图像中的感兴趣区域是目前图像自动分割中亟待解决的问题；三是每个患者采集的图像差异较大，所需分割区域形状的不规则为自动分割的实现带来了挑战。
目前对超声图像进行分割一般要经过图像预处理、感兴趣区域定位和图像分割 3 个阶段：① 图像预处理阶段是对超声图像的斑点噪声进行去除以及对人体组织结构边缘进行增强；② 感兴趣区域的定位是在整个超声图像中选取需要进行分割的位置；③ 最后对目标区域进行分割提取。在医学图像上进行分割的方法主要分为两类，一类是基于训练集学习的分割算法，包含监督学习和半监督学习，需要由人工标注图像进行训练。这类方法包含了基于活动形状模型的分割算法[1-2]和最近兴起的深度学习语义分割相关算法[3-5]，前者需要依赖初始轮廓的定位，后者不仅需要手动制作大量分割训练集，还需要加入一些传统分割方法辅助来提高分割精度。而分割训练集往往很难去标注，并且目标区域往往由于疾病影响差异巨大，导致某些特定病例无法获取大量数据。另一类是基于聚类的分割算法，即无监督分割算法，不需要人工制作训练集，先后有马尔科夫随机场的分割算法[6]、遗传算法优化的活动轮廓模型[7]、规范化切割方法结合 K 均值（K-means）算法[8]等，该类算法使用简单但是需对整幅图像进行分割，因此要加入一些先验知识才能够得到最后的分割区域。
均值漂移（mean shift）算法作为一种聚类算法，在医学图像分割中也已广泛应用。McClymont 等[9]采用固定带宽核函数的 mean shift 算法和图割算法对核磁共振图像胸腔病变区域进行分割；也有学者将 mean shift 算法和图割算法运用于乳腺超声图像分割上[10]，Kim 等[11]采用 K-means 结合 mean shift 算法对脑肿瘤部分进行分割。但是传统 mean shift 算法在进行聚类时的效果往往决定于其核带宽的选择，因此采用固定核带宽的 mean shift 算法进行聚类并不能对每一幅图像都能够达到良好的效果。所以 Mayer 等[12]提出了一种自适应核带宽的 mean shift 算法并将其应用于医学图像上，算法通过灰度排序构建了颜色带宽的选取，但是仅仅考虑了灰度空间上的核带宽选取，没有考虑到位置空间的核带宽问题，并且带宽选取方式过于简单，分割结果并不理想。此外，目前的算法自动化程度较低，大部分需要医生手动指定分割区域的位置，因此有必要提出一种由定位到分割的自动化算法。
基于以上研究，本文提出一种新的弱监督的分割框架，通过采用目前较为先进的目标定位算法寻找需要分割的感兴趣区域，然后使用自适应带宽的 mean shift 像素聚类算法对目标区域进行分割，最后采用区域增长算法获取最终目标。本文采用这种框架的优势是一方面不需要对整幅图像进行整体的分割也能够获取最终区域，另一方面免除了制作分割训练集的复杂步骤，仅仅需要标注区域的位置即可完成训练集的制作，并且不会因为目标区域的形状各异对分割结果造成影响。本文算法的提出，不仅有利于提高左心室自动定位的精度，而且大幅度减少了分割过程中的人工操作。
1. 基于 mean shift 算法的图像分割
mean shift 是一种聚类算法，算法主要思想是通过特征空间分析进行聚类[13]。该算法将特征空间中的类别中心定义为概率密度的极大值点，通过多重梯度下降找到核密度函数的极值，从而实现聚类。同时 mean shift 聚类看重的是局部特征，不易造成过分割。基本的 mean shift 密度估计方程，如式（1）所示：
 |
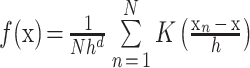1 |
其中 N 为样本空间大小，h 为核函数带宽，d 为特征空间维度，xn 为第 n 个样本所表示的 d 维特征，x 为当前需要分类的样本，K 为核函数的表达式，如式（2）所示：
 |
2 |
其中 c 为标准化参数，满足让 K（x）积分为 1。对式（1）求导，如式（3）所示：
 |
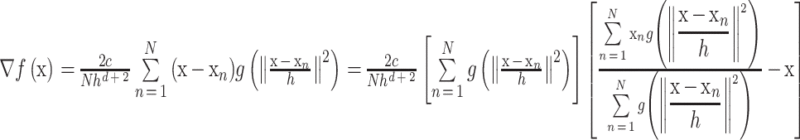3 |
其中 g（x）= – k’（x），式中第二项称为 mean shift 向量，表达式如式（4）所示：
 |
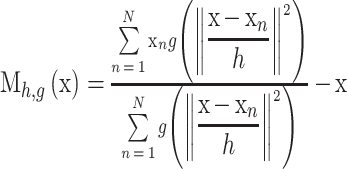4 |
迭代过程通过如式（5）所示实现：
 |
5 |
其中 x（i） 表示迭代第 i 步所处位置，所有被判断为同一类别的特征点会收敛到同一特征向量。
2. 左心室分割的实现
2.1. 左心室定位算法
更快速的基于区域的卷积神经网络（faster region-based convolutional neural network，Faster RCNN）目标检测算法是 Ren 等[14]在基于区域的卷积神经网络[15]和快速的基于区域的卷积神经网络[16]的基础上提出的一种快速的目标检测算法，是目前较为先进的检测框架。该算法首先使用卷积神经网络提取特征，再加入了候选区域生成网络（regional proposal network，RPN）并使用最后一层卷积特征图映射回原图构建候选区，然后送入感兴趣区域池化层统一特征尺寸，最后以全连接层对候选区分类，并且采用边界框回归算法调整最终区域。本文采用文献[17]提出的网络结构，使用自然图像分类数据集[18]的分类结果初始化网络参数，再使用本文超声图像数据进行迁移学习。如图 1 所示展示了Faster RCNN的算法流程。
图 1.
Architecture of Faster RCNN
Faster RCNN 流程
2.2. mean shift 核函数带宽的自适应
本文选取颜色空间和坐标空间作为聚类的特征空间。使用多元核函数进行核密度估计，核函数表达如式（6）所示：
 |
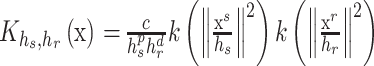6 |
其中 hs 和 hr 分别代表坐标空间和颜色空间的核带宽，xs 和 xr 分别代表坐标特征向量和颜色特征向量。本文选取高斯核函数作为核带宽函数，让聚类中心选取更为平滑，高斯核函数中 k（x）如式（7）所示。
 |
7 |
由于普通 mean shift 算法采用的是固定的核函数带宽参数，这样若带宽选取过小，聚类类别就会过多，导致分割过于精细，若带宽选取过大则分割就会过于粗糙，针对文献[11]所提出的自适应带宽较为简单，在超声图像上分割结果不够理想，本文提出一种新的自适应核函数带宽方法。将式（5）变形得到颜色空间的迭代公式如（8）所示：
 |
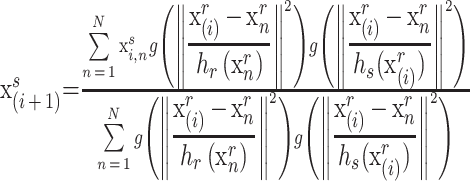8 |
即当前迭代的颜色空间核函数带宽对每个像素来说是不同的，而当前核函数的位置空间带宽是由该像素决定的。
对图像中像素 a 的颜色空间核函数带宽
和位置空间带宽
构建规则为：
（1）对超声图像目标区域 I 采用 k = 3 的 K-means 聚类得到图像 F，因为 3 种灰度基本能够体现超声图像的基本结构。
（2）在图像 F 上找到离像素 a 最近的和 a 不属于同一类别的像素 b，将 a 和 b 之间的欧式距离作为当前核函数位置空间带宽
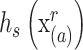，空间带宽选取示意图如图 2 所示，图中图像代表超声图像经过 K-means 聚类后的图像。
图 2.
Diagram of bandwidth on the image after K-means
在 K-means 聚类过后的图像上选取空间核带宽示意
（3）颜色空间核带宽
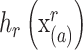选取为在
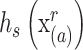范围内像素灰度均值和像素 a 灰度之差，如式（9）所示：
 |
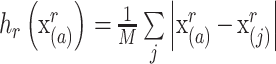9 |
其中 j 满足式（10）的条件：
 |
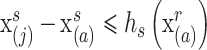10 |
则 M 为满足式（9）的所有像素个数。
2.3. 目标区域的提取
区域生长算法是一种能简单提取图像边界信息的算法，经过 mean shift 算法的聚类，超声图像左心室轮廓较为明显，并且图像噪声得到很大程度的抑制，使用区域生长算法能够较为准确地提取目标轮廓，为了提取最终区域辅助计算左心室容积，使用区域生长算法对左心室轮廓进行提取。区域生长算法流程为：
（1）将 2.1 小节所得检测结果中心点设置为种子点，加入集合 P，定义阈值 t 为该中心点和 8 邻域像素差的均值；
（2）依次从 P 中取出像素 w 并放入已填充像素集合 S，考虑 w 的 8 邻域像素 o，若 w 与 o 的灰度差小于阈值 t，并且 o 不在 S 中，则将 o 加入集合 P；
（3）重复步骤（2）直到集合 P 为空集。
3. 实验结果及分析
3.1. 实验数据集
本文所用实验数据包含 25 个左室短轴视频和 25 个四腔心视频，视频来源于四川大学华西医院麻醉科，视频采集不包含患者信息，每个视频代表一个超声心动图，包含数个心动周期，每个视频手动选取包含心室舒张末期和收缩末期的图像 6 张，共 300 张，图像尺寸为 800 × 600。实验标注其中 250 张作为 Faster RCNN 定位训练集，剩余 50 张作为实验测试集。
3.2. 实验评价方法
本文利用交并比系数（mean intersection over union，MIU）（符号记为：MIU）进行分割精度评价。其中，表示正确分类的像素个数为真阳性（true positive，TP）（符号记为：TP）；表示被错误分类的负样本像素个数为假阳性（false positive，FP）（符号记为：FP）；表示被错误分类的正样本像素个数为假阴性（false negative，FN）（符号记为：FN），MIU 值越接近 1 分类正确率越高，表达式如式（11）所示：
 |
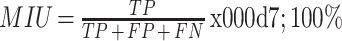11 |
实验还采用了峰值信噪比（peak signal to noise ratio，PSNR）（符号记为：PSNR）对聚类过程进行评价，I 表示原始图像，MAXI 表示图像 I 的像素最大值，F 表示经过算法处理后的图像，I（i，j）表示原始图像在（i，j）处的灰度值，F（i，j）表示经过算法处理后图像在（i，j）处的灰度值，采用平均平方差（mean square error，MSE）（符号记为：MSE）衡量两幅图之间的像素差异，峰值信噪比数学表达式如式（12）表示：
 |
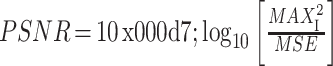12 |
其中平均平方差表达式如式（13）所示：
 |
13 |
3.3. 实验结果
如图 3 所示，经过 Faster RCNN 的定位能够准确获取左心室区域。如图 4 所示为输入一张模拟图像后对其加入噪声，经过不同自适应核带宽 mean shift 方法后的结果对比。对不同核函数带宽选取方式取得的结果如图 5 所示，图中 hr 表示颜色空间带宽，hs 表示位置空间带宽，采用文献[11]提出的自适应方法无法对有噪声的图像进行有效处理，而本文方法对噪声不敏感，处理结果具有较高的峰值信噪比。固定算法其余流程，针对 mean shift 核带宽选取，展示了真实超声图像中采用不同核带宽获取方法获得最终区域的对比。可以发现本文方法和手动选取带宽中最好的结果差不多，并且分割边界较为平滑，而文献[11]提出的自适应算法分割效果较差。如图 6 所示，展示了一幅左室短轴切面的图像使用本文算法处理得到的各阶段效果。如图 7 所示，展示的是四腔心切面左心室区域提取的各个流程处理结果。
图 3.
Localization of left ventricle
左心室目标定位
图 4.
Result of different methods with adaptive bandwidth
不同自适应核带宽算法对比
图 5.
Result of segmentation with different bandwidth
使用不同带宽得到的最终结果
图 6.
Process of segmentation in left ventricular mid short axis
左室短轴分割流程
图 7.
Process of segmentation in middle esophageal four hambers
四腔心切面分割流程
如表 1 所示，展示了使用本文提出的算法与文献[11]提出的自适应核带宽的 mean shift 算法，以及固定核带宽算法得到分割结果的对比。可以看出在评价标准下，本文自适应算法能够在左室短轴获取上效果更好，在四腔心的左心室分割上其效果也和手动选取带宽中最好的效果接近。
表 1. MIU of different bandwidth.
不同核带宽分割 MIU 对比
| 核带宽选取 | 切面类型 | |
| 四腔心 | 左室短轴 | |
| hr = 10，hs = 10 | 75.03% | 86.12% |
| hr = 20，hs = 10 | 70.19% | 83.37% |
| hr = 10，hs = 20 | 67.44% | 85.15% |
| 文献[11] | 72.54% | 85.59% |
| 本文算法 | 74.12% | 89.90% |
4. 结语
超声心动图能够反映患者左心室的健康情况，对其进行心室分割的目的是获取最终区域计算心室相关参数并分析患者病情，由于超声图像噪声多、边缘模糊，造成分割难度非常大。因此本文提出了一种新的分割框架，首先利用快速目标检测算法确定待分割区域位置，接下来采用一种新的自适应核带宽的 mean shift 算法进行聚类，最后采用区域生长算法提取目标轮廓，从而实现了由定位到分割的自动化提取左心室的过程。
此外，本文算法在使用过程中要注意待分割的区域需要是闭合区域，这样才能有效提取整个心室。实验过程中也发现自适应核函数带宽会带来部分额外计算量，未来研究方向是在保证分割精度的情况下加快分割速度。
针对超声图像手动分割需要大量时间的问题，本文提出了一种基于自适应核带宽的 mean shift 算法的分割方案，在几乎不需要人工对图像进行操作的情况下自动提取左心室，并且实验结果表明其在分割效果的定量评估上优于传统的 mean shift 算法。
Funding Statement
四川省科技支撑计划基金项目（2016JZ0035）
References
- 1.纪祥虎, 高思聪, 黄志标, 等 基于 Centripetal Catmull-Rom 曲线的经食道超声心动图左心室分割方法. 四川大学学报: 工程科学版. 2016;48(5):84–90. [Google Scholar]
- 2.孙申申, 范立南, 康雁, 等 基于改进主动形状模型的含胸壁粘连型肿块的肺区分割方法研究. 生物医学工程学杂志. 2016;(5):879–884. [Google Scholar]
- 3.Carneiro G, Nascimento J C, Freitas A The segmentation of the left ventricle of the heart from ultrasound data using deep learning architectures and derivative-based search methods. IEEE Transactions on Image Processing. 2012;21(3):968–982. doi: 10.1109/TIP.2011.2169273. [DOI] [PubMed] [Google Scholar]
- 4.Milletari F, Ahmadi S A, Kroll C A, et al Hough-CNN: deep learning for segmentation of deep brain regions in MRI and ultrasound. Computer Vision and Image Understanding. 2017;164(SI):92–102. [Google Scholar]
- 5.Gao Mingchen, Xu Ziyue, Lu Le, et al. Segmentation label propagation using deep convolutional neural networks and dense conditional random field//2016 IEEE 13th international symposium on biomedical imaging (ISBI), 2016: 1265-1268
- 6.Mignotte M, Meunier J, Tardif J C Endocardial boundary e timation and tracking in echocardiographic images using deformable template and markov random fields. Pattern Analysis Applications. 2001;4(4):256–271. [Google Scholar]
- 7.Mishra A, Dutta P K, Ghosh M K A GA based approach for boundary detection of left ventricle with echocardiographic image sequences. Image Vis Comput. 2003;21(11):967–976. [Google Scholar]
- 8.Sadek I, Elawady M, Stefanovski V. Automated breast lesion segmentation in ultrasound images. arXiv preprint. 2016. arXiv: 1609.08364
- 9.McClymont D, Mehnert A, Trakic A, et al Fully automatic lesion segmentation in breast MRI using mean-shift and graph-cuts on a region adjacency graph. Journal of Magnetic Resonance Imaging. 2014;39(4):795–804. doi: 10.1002/jmri.24229. [DOI] [PubMed] [Google Scholar]
- 10.Zhou Zhuhuang, Wu Weiwei, Wu Shuicai, et al Semi-automatic breast ultrasound image segmentation based on mean shift and graph cuts. Ultrason Imaging. 2014;36(4):256–276. doi: 10.1177/0161734614524735. [DOI] [PubMed] [Google Scholar]
- 11.Kim J H, Lee S, Lee G S, et al Using a method based on a modified K-means clustering and mean shift segmentation to reduce file sizes and detect brain tumors from magnetic resonance (MRI) images. Wireless Personal Communications. 2016;89(3, SI):993–1008. [Google Scholar]
- 12.Mayer A, Greenspan H An adaptive Mean-Shift framework for MRI brain segmentation. IEEE Trans Med Imaging. 2009;28(8):1238–1250. doi: 10.1109/TMI.2009.2013850. [DOI] [PubMed] [Google Scholar]
- 13.Comaniciu D, Meer P Mean shift: a robust approach toward feature space analysis. IEEE Trans Pattern Anal Mach Intell. 2002;24(5):603–619. [Google Scholar]
- 14.Ren Shaoqing, He Kaiming, Girshick R, et al. Faster R-CNN: towards real-time object detection with region proposal networks//Computer Vision and Pattern Recognition, 2015: 91-99
- 15.Girshick R, Donahue J, Darrell T, et al. Rich feature hierarchies for accurate object detection and semantic segmentation//Proceedings of the IEEE conference on computer vision and pattern recognition, 2014: 580-587
- 16.Girshick R. Fast R-CNN//Proceedings of the IEEE International Conference on Computer Vision, 2015: 1440-1448
- 17.Zeiler M D, Fergus R. Visualizing and understanding convolutional networks//Computer Vision–ECCV 2014, Zurich, 2014: 818-833
- 18.Deng Jia, Dong Wei, Socher R, et al. Imagenet: a large-scale hierarchical image database//Computer Vision and Pattern Recognition, Miami, 2009: 248-255