基于隐马尔可夫模型的枕下无扰式新型睡眠监测方案

Abstract

Sleep status is an important indicator to evaluate the health status of human beings. In this paper, we proposed a novel type of unperturbed sleep monitoring system under pillow to identify the pattern change of heart rate variability (HRV) through obtained RR interval signal, and to calculate the corresponding sleep stages combined with hidden Markov model (HMM) under the no-perception condition. In order to solve the existing problems of sleep staging based on HMM, ensemble empirical mode decomposition (EEMD) was proposed to eliminate the error caused by the individual differences in HRV and then to calculate the corresponding sleep stages. Ten normal subjects of different age and gender without sleep disorders were selected from Guangzhou Institute of Respirator Diseases for heart rate monitoring. Comparing sleep stage results based on HMM to that of polysomnography (PSG), the experimental results validate that the proposed noninvasive monitoring system can capture the sleep stages S1–S4 with an accuracy more than 60%, and performs superior to that of the existing sleep staging scheme based on HMM.

引言

睡眠分期结果可以对睡眠质量进行评估，是相关疾病诊断的重要指标^[1-4]。20 世纪 60 年代美国加州大学脑研究所通过对脑电（electroencephalogram，EEG）、2 路颌肌电（electromyogram，EMG）以及 2 路眼电（electrooculogram，EOG）信号的分析研究，将睡眠状态分为 6 期，即清醒期（wake，W）、快速眼动期（rapid eye movement，REM）、非快速眼动期（non-rapid eye movement，NREM），其中 NREM 期包括睡眠 Ⅰ 期（sleep stage 1，S1）、睡眠 Ⅱ 期（sleep stage 2，S2）、睡眠 Ⅲ 期（sleep stage 3，S3）、睡眠 Ⅳ 期（sleep stage 4，S4）。目前，EEG 已成为判断睡眠分期的金标准，但是在此类监测方式下，受试者需长时间接触多路电极，其自然睡眠会受到影响，不适于家居环境下的睡眠监护；而且研究所需的庞大数据量会耗费巨大的人力和时间成本。因此，探索其他生理信号在睡眠过程中的变化规律，并据此规律研究更加准确、高效的睡眠分期方法，是当前的研究热点^[5-8]。

心率的变化与自主神经系统的调控息息相关，自主神经系统的活动在不同睡眠期的表现也各不相同，现有研究^[9-11]表明心率变异性（heart rate variability，HRV）中隐含着潜在的睡眠信息，具体表现为在上述 6 个分期阶段心率变化呈现出不同的特点，通过合适的信号处理方法并结合先验知识就可以反过来推算睡眠结构。Kortelainen 等^[12]利用频谱分析的方法对 RR 间期（RR interval，RRI）信号进行小波变换，将 RRI 通过频谱变换分解成超低频（very low frequency，VLF）、低频（low frequency，LF）和高频（high frequency，HF）三个频谱区，经过对频谱区特征的对比发现，LF/HF、VLF、VLF/HF 的均值与睡眠期存在线性关系，而且如果降低低频信号的功率谱，能大大提高 S3 和 S4 期睡眠的识别率。庄志等^[13]利用隐马尔可夫模型（hidden Markov model，HMM）对 HRV 进行分析，在信号处理的过程中采用标准化的方式消除个体差异，对于睡眠分期的识别准确率可以接受。王金海等^[14]利用支持向量机（support vector machin，SVM）实现了基于 HRV 信息的睡眠自动分期方法，采用主成分分析方法（principal component analysis，PCA）来降低数据冗余度，用少数几个不相关的主成分替代原来相关互联的众多指标，获得了较高的预测准确度。针对 HRV 的获取方式，Wisse 等^[15]利用压力传感的铂电极传感器获得 HRV 信号，再结合体动信息通过 HMM 来预估睡眠分期。Ebrahimi 等^[16]以睡眠心脏健康研究数据库 HRV 信号为依据，提取特征值信息，再计算不同频带的能量和熵等指标对睡眠分期进行预估，能够区分觉醒期和深睡期。

然而，目前睡眠分期方案存在以下 3 方面的问题：① 针对 HRV 信号的获取，均需要用户与多路电极直接接触，用户体验度低^[17-20]；② 国际公认的睡眠分期将睡眠状态分为 6 期，现有睡眠分期方案仅分析对比睡眠/觉醒期，没有针对 S1～S4 不同间期的睡眠分期对比验证；③ 现有分期方案中，未考虑因用户个体化差异带来的分期误差，分期输出结果可信度相对较低。

针对上述问题，本文率先设计了一种枕下无扰式睡眠监控方案，主要贡献可归纳为两方面：

（1）针对 HRV 的获取，提出采用压电传感器置于枕下的方式，无扰地采集用户心率及 HRV 信息。所设计的采集平台相较传统院内、院外智能心率监测设备具有如下优势：① 采样率高达 1 000 Hz，达到医疗精准级别（目前院内心电采样频率 300～500 Hz），而市面可穿戴设备受功率制约采样率极低，无法用于 HRV 的测量；② 新型非接触无扰式检测，不需与检测对象直接接触，相较现有院内专业采集设备需用户与多路电极直接接触的约束，具有明显的用户体验度优势。

（2）利用无扰心率检测平台进行睡眠分期的检测，提出基于 HMM 的睡眠分期方案。与现有方案不同，为了消除因个体化差异导致的训练输出误差，提出利用集合经验模态分解（ensemble empirical mode decomposition，EEMD）去除基线漂移等归一化预处理方案，消除 HRV 的个体化差异，同时，对归一化后的信号进行限幅量化编码，减少数据冗余度。所提优化方案将会在用户体验度和睡眠分期结果的准确性方面有显著提升。

1. 枕下无扰式实验平台

HRV 信号的采集通过枕下无扰式实验平台来实现，系统整体设计由枕下压电传感、信号采集卡以及终端处理三部分组成，设计简图如图 1 所示。传感器置于一块平板中，放于枕头底下，集成了印制电路板（printed circuit board，PCB）的采集卡放置于床边，采集信号经过处理后在终端显示。各部分的具体实现及功能如下：

图 1.

The overall design of the system

系统总体设计简图

（1）枕下压电传感内置采集模块（系统的“感受装置”），主要通过压电传感器来实现，通过比较后我们选择的传感器是压电陶瓷蜂鸣片，它具有厚度薄、体积小、稳定性好、灵敏度高、耗能低、耐高低温、寿命长、耐高压、无需供电等优点，可以使信号采集模块在枕下发挥功效。当压电陶瓷蜂鸣片被施加直流电压时，产生交替重复的机械弯曲变形，从而在空气中产生声波；然而当有外力施加时，压电陶瓷片会受外力影响产生电波，将机械能转化为电信号。因此我们可以使用压电陶瓷蜂鸣片作为一个无源传感器。

（2）采集卡集成了信号调理模块和 A/D 转换模块，各模块的具体实现及功能为：① 信号调理模块，先利用高通滤波电路（截止频率 0.2 Hz）、低通滤波电路（截止频率 159 Hz）和两级放大电路（放大倍数分别为 11 倍和 1.21 倍）将采集信号滤波、放大和抬升，并经过钳位电路使输出电压被钳位在 — 0.7～4 V 之间，起到保护后级模数转换器（analog to digital converter，ADC）芯片的作用；②A/D 转换模块，采用 TI 公司 12 位 ADC 芯片 ADS1013，标准 I2C 接口，低功耗，转换速率为 1.6 ksps。将通过信号调理模块后的模拟信号进行 A/D 转换，将所得数字信号通过串口实时发送至上位机进行处理。

（3）终端处理利用 LabVIEW 应用软件通过串口接收 A/D 转换后的数字信号，经过处理分析，最终以波形图的形式实时显示所采集的原始生命体征信号。

上述枕下式睡眠监测系统采用单通道方式采集数据，采样频率为 1 000 Hz，波特率为 115 200，采集到的原始生命体征信号如图 2 所示。由图 2 可知，所得生命体征信号混杂着不同频率、不同振幅的生物电信号以及不可避免的工频干扰、设备仪器噪声、人为运动等噪声信号，我们首先通过时频联合分析法设计巴特沃斯带阻滤波器、陷波滤波器以及低通滤波器等滤除噪声并初步分离信号，再通过形态滤波去除基线漂移，最终从原始生命体征信号中分离出脉搏信号、呼吸信号与体动信号，如图 3 所示。

图 2.

The original vital signals collected by the sleep monitoring system under pillow

由枕下式睡眠监测系统采集的原始生命体征信号

图 3.

Signals separated from the original vital signals collected by the sleep monitoring system under pillow

经枕下式睡眠监测系统采集的原始生命体征信号中分离出的信号

a. pulse signals; b. breath signals; c. movement signals

a. 脉搏信号；b. 呼吸信号；c. 体动信号

2. 信号预处理

利用 HMM 对 HRV 进行分析，识别 HRV 在不同睡眠分期的模式变化，从而推算出相应的睡眠分期，需要注意的是，现有基于 HRV 的睡眠分期方案^[21-22]，忽略了个体化差异会对睡眠分期分析产生影响。因此，所提分期模型仅适用于共性个体，难以实现针对年龄、性别存在明显差异化个体的精准睡眠分期。本文首先对利用枕下式睡眠监测系统采集的生命体征信号以及获取的 RRI 进行预处理，在最大程度上消除由于用户性别、年龄等个体化差异带来的分期影响。

2.1. RRI 提取

由枕下式睡眠监测系统采集的原始生命体征信号中分离出如图 3 所示的脉搏信号、呼吸信号以及体动信号后，通过时频联合分析设计滤波器、峰值检测、协方差匹配、自回归模型算法等计算出准确的呼吸率、脉率，得到呼吸、脉搏的波形，并得到准确的的 RRI。整个 RRI 获取的算法步骤如下所示：

Algorithm

要求：从图 2 所示的原始生命体征信号中分离出的脉搏信号、呼吸信号，按照每 10 s 划分为一组

初始化：j = 1，k = 1，pulse ≠ φ

1：for i = 1 to N_n

2：　corr（i） = cov（p（i），pulse）

3：end for

4：while（corr（j） ≠ φ）

5：　P_max = max{window（corr（j））}

6：　∀P∈P_max

7：　if T_j^min < P < T _j^max

8：　　保留 P 并通过差分方程获得初步 RRI

9：　else

10：　　去除 P

11：　end if

12：end while

13：将得到的初步 RRI 信号按照每 6 s 划分一组

14：while（RRI（n） ≠ φ）

15：　∀R∈RRI（n）

16：　Y（n） = a * R（n – 1） + a² * R（n – 2） + a³ * R（n – 3）

17：其中 a 由以下公式获得 a + a² + a³ = 1

18：　if R（n）*（1 – 30%）<|Y（n） – R（n）|<R（n）*（1 + 30%）

19：　　Y（n） 保留

20：　else

21：　　Y（n） 去除

22：　end if

23：end while

pulse 是从原始脉搏信号中选取的一段脉搏波形脉冲，将脉搏信号每 10 s 划分成一组，p（i） 表示第 i 组的脉搏信号，Nn 是分成的组数。Corr（i）是 p（i）和 pulse 进行协方差匹配的结果。然后建立一个移动窗口，将窗口在相关函数中移动，选取每个窗口内的最大值为 P_max。

6～12 行是去除不在阈值 和 之间的无关信号点，计算出初步 RRI，它表示将 RRI 以 6 s 为间期进行分组。14～23 行建模一个间期内有效峰值信息的 AR 模型，根据第 16 行公式由前三个点的值估计第四个点的值 Y（n），最后将 Y（n）与 6 s 间期内的第四个点的实际值 R（n）进行比较，将约束范围设定为 30%，即当|Y（n）– X（n）|的值在 X（n）的 ± 30% 以内时，记录此 RRI；如不满足，视为失败检测。

2.2. 差异化均衡

为消除因个体化差异导致的睡眠分期误差，本文提出基于 EEMD^[23-24]的 RRI 差异化预处理方案，可有效消除现有 EMD 模态混淆问题，具体实现步骤如下：

（1）提取并删减异常 RRI，此类信息视为干扰，不做统计，包括过长（如 > 1 500 ms）、过短（如<300 ms），以及早搏前后的不规则 RRI。考虑到医院多导睡眠图（polysomnography，PSG 每 30 s 产生一个睡眠分期值，本文将排除异常干扰后的 RRI 设定为 30 s 一组，计算每一组的均值和方差。在排除异常 RRI 后，提出基于 EEDM 的个体差异均衡，具体步骤如下：

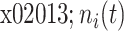步骤 1：在原始信号 S（t）中，分别添加均值为零的白噪声信号 和 ，即：

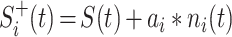1

2

其中 表示添加噪声信号的幅值，i = 1，2， ，Ne，Ne 表示添加白噪声的对数。

步骤 2：分别对 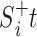和 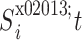进行 EMD 分解，得到 IMF 分量序列和 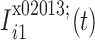，对上述得到的分量 进行集成：

3

步骤 3：重复以上步骤直至 IMF 分量不是异常信号。

步骤 4：将已分解的前 p — 1 个分量从原始信号中分离出来，即：

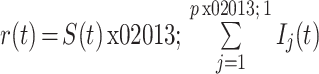4

步骤 5：对剩余信号 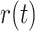进行 EEMD，将得到的所有 IMF 分量按高频到低频排列。

上述步骤中，EEMD 通过对原始信号多次加入不同的白噪声进行 EMD 分解，将多次分解的结果进行平均即得到最终的 IMF。我们把去除异常值的 RRI 以 30 s 为周期分组计算出均值和方差以后，再将所得的 RRI 均值进行 EEMD，从而得到从高频到低频依次顺序排列的 IMF 分量，最后 5 层低频的 IMF 分量最能代表 RRI 均值的整体趋势，于是将最后 5 层叠加来重构 RRI 均值的低频从而得到其趋势图，结果如图 4 所示（由于 PSG 每 30 s 产生一个睡眠分期值，因此图中横轴物理量采用与 PSG 相同的方式，标记为 u，即每 30 s 产生一个 RRI 均值）。

图 4.

The trend RRI signals of reconstructing the low frequency

重构低频所得 RRI 趋势信号

（2）在上述 EEMD 重构低频得到趋势信号后，将采用以下步骤进一步消除个体差异：

步骤 1：将 RRI 均值和 RRI 方差全部除以上述重构的趋势信号，对 RRI 均值和方差归一化。

步骤 2：为了减少观察量的取值数目，对归一化 RRI 均值和方差进行非均匀量化处理。预先设定好量化级数 S，将上述归一化的值进行限幅编码，从而得到与量化级数 S 相等的观察量的取值数目。

步骤 3：在保证 HMM 准确度的前提下，尽量减少 HMM 输入参数的个数，将由量化后的 RRI 均值和方差组成的二维训练集通过线性关系映射到一维数组上，从而得到一组标识着 RRI 特征值的经过量化和归一化的一维训练集 RIS（i）。

3. 基于 HMM 的睡眠分期

通过对枕下式睡眠监测系统 HRV 信息的差异化预处理，采用 HMM 对 HRV 进行分析，识别 HRV 在不同睡眠分期的模式变化，从而推算出相应的睡眠分期。HMM 是一种用参数表示的用于描述随机过程统计特性的概率模型，是一个双重随机过程，由两个部分组成：马尔可夫链和一般随机过程。其中，马尔可夫链用来描述状态的转移，用转移概率描述；一般随机过程用来描述状态与观察序列间的关系，用观察值概率描述。HMM 由初始状态概率向量 pi、状态转移概率矩阵 A 和观测概率矩阵 B 决定，pi 和 A 决定状态序列，B 决定观测序列。因此，HMM 的 lambda 可以用三元符号表示，即：lambda = （pi，A，B）。

总结起来，HMM 相关的算法主要分为三类，称为 HMM 的三个基本问题：评估问题、解码问题和学习问题，分别描述如下。

（1） 评估问题：已知观察序列 O 和模型 lambda = （pi，A，B），如何有效计算在给定模型 lambda 条件下产生观察序列 O 的条件概率即 P（O|lambda）；

（2） 解码问题：已知观察序列 O 和模型 lambda = （pi，A，B），如何选择相应的在某种意义上最佳（最好能解释观察序列）的状态序列；

（3） 学习问题：如何调整模型参数 lambda = （pi，A，B），以使条件概率 P（O|lambda）最大。

本文采用 Baum-Welch^[25]算法实现基于 HRV 分析的 HMM 睡眠分期问题。HMM 的输入如下：

（1） PSG 采集的训练集的睡眠分期结果：W、REM、NREM（S1，S2，S3，S4）；

（2） 前文预处理部分将 RRI 均值和方差经过归一化以及量化后的一组标识着 RRI 特征值的一维训练集 RIS（i）；

（3） 睡眠分期状态总数 M；

（4） 观察序列状态总数 N。

在建立由以上输入对应的 HMM 的 lambda = （pi，A，B） 时，睡眠分期状态总数 M 定为 4，观察序列状态总数 N 为 9（由上述量化级数 S 而定），建立离散 HMM 的过程，为三个基本问题中的学习问题，即对于一个训练样本 RIS（i），确定 HMM 的参数 lambda = （pi，A，B），使得概率 P（RIS（i）|lambda）最大。具体步骤如下：

步骤 1：首先定义两个辅助变量，第一个变量定义为 t 时状态 i 和 t + 1 时状态 j 的概率，即：

5

第二个变量定义为后验概率，即在给定观察状态序列和 HMM 的情况下，t 时状态 i 的概率，即：

6

步骤 2：根据公式（7）、（8）、（9）计算重估的 HMM 参数，即：

7

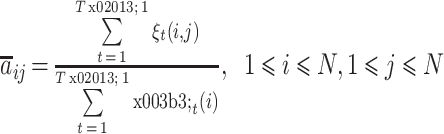8

9

步骤 3：重复步骤 1 和步骤 2，不断地重新估计 HMM 的参数，在多次迭代以后得到 HMM 的一个最大似然估计，即为学习问题的最优解。

得到 HMM 模型以后，就得到状态转移矩阵 A 以及观测概率矩阵 B，将测试集作为观察序列 O，选择在某种意义上最佳的状态序列来解释观察序列，这个最佳的状态序列即为最终测试集睡眠分期的估计结果，即对应 HMM 模型的第二个经典问题解码问题。本文采用维特比算法来实现，具体步骤如下：

步骤 1：定义一个部分概率 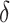和部分最优路径。 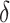为到达某个中间状态的概率，部分最优路径为到达每一个中间状态和终止状态的最可能的路径。用 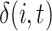来表示在 t 时刻到达状态 i 的所有可能的路径中概率最大的序列的概率，部分最优路径即为到达这个最大概率的路径。

步骤 2：计算 t=1 时刻的部分概率。当 t=1 时，到达某个状态最大可能的路径还不存在，但是我们可以直接使用在 t=1 时刻某个状态的概率和这个状态可观察序列 k₁ 的转移概率 ，即：

10

步骤 3：计算 t > 1 时刻的部分概率。根据公式（11）由 t — 1 时刻的部分概率求 t 时刻的部分概率，其中 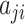表示从状态 j 到状态 i 的概率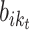， 表示状态 i 到状态 的概率。

11

步骤 4：根据公式（12）利用一个后向指针 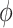来记录导致某个状态最大局部概率的前一个状态，即：

12

步骤 5：重复步骤 3、4，即可找到最可能生成这个可观察状态序列的隐藏状态序列，这个隐藏状态序列即为某种意义上最佳的解释观察序列的状态序列，即为最终测试集睡眠分期的估计结果。

通过以上 HMM 建模和识别的过程，最终得到测试集的睡眠分期的估计值。

4. 结果

4.1. 枕下采集准确性对比

本文将所提枕下式睡眠监测系统应用于广州医学院呼吸疾病研究所，同时与 PSG 测试数据进行同步比对，以验证所提方案的可行性。

首先，验证枕下非接触压电传感方案获取 RRI 的准确性，与 PSG 采集到的 HRV 信号的对比如图 5 所示。由图 5 所示，所设计的枕下心率检测方案与 PSG 的心电信息在时间上保持严格同步（枕下式监测系统与 PSG 设备开机时间存在 10 s 左右的时延）。特别地，可以看到在图 5a 中间部分心电信号发生了畸变，而与之相对应的图 5b 中也同步出现了严重的波形变化。此外，心率所定位的 R 峰与 PSG 心电保持了良好的拟合度。

图 5.

Synchronous acquisition of HRV signals

同步采集 HRV 信号

a. by PSG; b. by sensor

a. PSG 采集；b. 传感器采集

为了进一步验证获取 RRI 的准确性，按照前述 RRI 获取的方法，得到一段 10 min 的 RRI，如图 6 所示。对获取的 RRI 进行傅里叶变换后的频谱如图 7 所示。由图 6、7 可知，所设计的枕下式睡眠监测系统所获取的 RRI 与 PSG 心电信息高度一致，误差在 ± 50 ms 以内，经过傅里叶变换后得到的幅度谱和相位谱吻合率也非常之高，进一步表明本文所设计的枕下式睡眠监测系统可实现高准确度的心率 RRI 捕捉，可用于进一步基于 HRV 的深入分析。

图 6.

RRI signals of 10 minutes by PSG and sensor

PSG 与压电传感方案采集的 10 分钟 RRI 信号

图 7.

Fourier transform spectrum of RRI

对 RRI 进行傅里叶变换后的频谱

4.2. 睡眠分期

为了验证所提分期方案的准确性，将本试验结果与 PSG 分期金标准进行对比。为方便分析，试验预设中将 NREM-1、2、3 合并为一种状态，即共输出四种睡眠分期的状态，并采用 leave-one-out cross-validation 的交叉验证方式。试验数据由广州中科新知科技有限公司授权，选取广州医学院呼吸疾病研究所 10 例不同年龄及性别的无睡眠障碍的院内正常受试者，10 名测试对象中，男、女各 5 例，最大年龄差异为 53 岁，其中年龄在 18 岁以下的有 3 人（1 男 2 女），在 18～50 岁之间的有 4 人（2 男 2 女），50 岁以上的有 3 人（2 男 1 女）。试验过程为，采用前述枕下式睡眠监测系统分别采集 10 位测试对象夜间 HRV 信息，受试者同时采用 PSG 记录当晚的睡眠分期结果。选择第一位受试者作为测试集，剩余作为训练集，通过 HMM 后得到估计的睡眠分期结果，然后将其与 PSG 采集的睡眠分期结果进行对比，结果如图 8 所示，各分期时长及准确率如表 1 所示。经统计测算，分期准确率达 64.48%，证明本文非接触的枕下睡眠监测分期与 PSG 睡眠分期相比，具备较高的拟合度。

图 8.

Comparison of sleep staging results

睡眠分期结果对比

表 1. Comparison of the result of each sleep staging between PSG and sleep monitoring system under pillow.

PSG 与枕下式睡眠监测系统睡眠分期结果对比表

睡眠 分期	PSG 所得各 分期时长/s	Sensor 所得各 分期时长/s	各分期 准确率
1	1 650	1 800	91.67%
2	4 860	14 070	34.52%
3	5 100	5 640	90.42%
4	4 710	7 440	63.30%

依次改变测试集，分别将第 2，3， ，10 组作为测试集，剩余作为训练集，经大量的重复性测试，得到的睡眠分期的准确率如表 2 所示。可以看出，本文所提出的 RRI 预处理消除个体化差异后的 HMM 睡眠分期方案准确率远优于未归一化组的 HMM 睡眠分期，以 PSG 为金标准，睡眠分期准确性超过 60％。上述数据对比试验证明了本文所提方案的有效性。

表 2. Comparison of sleep staging results before and after data normalization based on sleep monitoring system under pillow.

枕下式睡眠监测系统数据归一化前后睡眠分期结果对 比表

测试集 序号	量化 级数	未归一化识 别准确率	归一化后识 别准确率
1	4	23.22% ± 3%	64.48% ± 2%
2	4	21.36% ± 4%	63.37% ± 3%
3	4	19.45% ± 3%	61.41% ± 2%
4	4	18.67% ± 3%	59.92% ± 4%
5	4	21.45% ± 4%	61.02% ± 3%
6	4	22.56% ± 2%	63.01% ± 2%
7	4	19.77% ± 3%	57.33% ± 4%
8	4	24.12% ± 4%	59.41% ± 2%
9	4	18.54% ± 2%	63.14% ± 4%
10	4	21.48% ± 3%	62.47% ± 3%
平均值		20.93% ± 3%	61.51% ± 3%

5. 总结与讨论

本文设计了一种置于枕下的睡眠监测方案，采用枕下无扰采集装置精确识别 HRV，在此基础上，提出 EEMD 消除 HRV 个体化差异后，结合 HMM 进行睡眠分期监测。经过验证，所提方案在对用户无扰非接触环境下获取的 RRI 与 PSG 心电信息具有较高的拟和度，时域误差范围在 ± 50 ms 以内。以差异化预处理后的 HRV 为依据，采用 HMM 估计所得睡眠分期结果与 PSG 结果相比，在四期睡眠的划分标准下，睡眠分期 S1～S4 正确匹配率达 61.51% ± 3%。为了验证本文算法的有效性，同时验证了文献[12]中未经差异化预处理的 HMM 睡眠分期算法。经对比分析，本文所提方案睡眠分期的平均准确率具有较大的优势，反映出不同个体差异化对睡眠分期建模具有较大的影响。

针对本文方案进一步的改进，包括：① 借助枕下传感挖掘不同分期内呼吸、体动等参数特征，挖掘与 RRI 的相关性；借助此类相关特性，预期可以提高分析正确率，同时消除数据冗余，提高分析速度。② 从实验和理论上寻找新的归一化方法，在不同尺度下消除个体差异的影响，预期将进一步提升 HMM 建模的普适度与准确率。

Funding Statement

国家自然科学基金（61471176，61471175）；华南师范大学研究生创新计划项目（20161kxm47）；广东省科技计划项目（2017A010101015，2017B030308009，2017KZ010101）；广东省特支计划（2016TQ03X100）；广东省优秀青年教师培养计划（YQ2015046）；广州市珠江科技新星专项（201610010199）；广东省大学生科技攀登计划（pdjh2017a0127）