初始压力与支撑刚度对圆窗激振听力补偿影响的数值研究

Abstract

为了研究初始压力与支撑刚度对圆窗激振式人工中耳听力补偿性能的影响，建立了包括作动器和支撑体在内的人耳力学有限元模型。该模型基于一位无任何听力损伤病史的成年人的右耳，采用微计算机断层扫描技术（Micro-CT）和逆向成型技术建立而成，并通过与相关实验数据进行对比，验证了模型的可靠性。基于该模型，通过在圆窗上施加不同幅值的初始压力和改变支撑体的支撑刚度，对比分析相应的基底膜动态响应变化，研究其对圆窗激振听力补偿性能的影响。结果表明：初始压力的施加将恶化低频段的听力补偿效果，但提高了圆窗激振中高频段的听力补偿性能；相对于现有临床上所用的筋膜支撑作动器的方法，采用刚度较大的钛合金作为支撑结构，将在全频段提升圆窗激振的听力补偿性能。

引言

听力损伤是国内最常见的疾病之一^[1]。根据损伤部位的不同，听力损伤主要分为感音神经性听力损伤和传导性听力损伤两类。其中，由于毛细胞和听神经故障造成的感音神经性听力损伤至今没有有效的药物治疗方法，患者主要还是通过佩戴助听器加以缓解^[2]，但传统助听器具有输出增益小、伴有声反馈、佩戴舒适性差等问题。针对该问题，国内外很多机构开始研究人工中耳，即一种直接采用机械激振听骨链来补偿听力损伤的植入式助听装置^[3-4]。而临床上，很多患者还伴有听骨链损伤，这使得人工中耳的作动器无法有效激振听小骨。为此，Colletti 等^[5]提出避开听骨链，直接激振圆窗来补偿听力损伤，并通过临床应用证明了其可行性，为混合性耳聋的治疗提供了一种新的方案。

然而，临床报道显示，圆窗激振的听力补偿效果具有较大的不确定性^[6]。为了确定其原因，国内外很多学者做了相关研究。Arnold 等^[7]实验研究表明，在作动器与圆窗间增加耦合层将更有助于听力损伤的补偿；而作动器的支撑与否对听力补偿效果影响不大。但其实验过程中所用的支撑材料为皮下软组织，刚度较小，且未做其他支撑材料的对比研究。Zhang 等^[8]通过有限单元法，研究了作动器端面尺寸、重量对圆窗激振的影响。但建模过程仅以质量单元简化模拟作动器，没有考虑其支撑结构。此外，Maier 等^[9]实验研究显示在作动器上施加初始压力有利于提高听力补偿效果。但该结果与 Lupo 等^[10]研究结果不符，Lupo 指出初始压力对听力补偿没有影响，听力补偿效果随着初始压力增大是否会存在变化还有待进一步研究。

针对上述问题，本文基于逆向成型技术及有限元法建立了整耳传声力学模型，并通过实验对比验证了模型的可靠性。在此基础上，系统研究了圆窗激振式人工中耳作动器支撑刚度及初始压力的变化对听力补偿效果的影响，为圆窗激振式人工中耳性能的提升提供优化准则。

1. 方法

1.1. 人耳有限元模型建立

本文所建的人耳有限元模型包括鼓膜，由锤骨、砧骨和镫骨组成的听小骨，以及肌腱和韧带、耳蜗等。该模型基于新鲜的人体颞骨标本（男性，45 岁，右耳，无任何听力损伤病史），采用微计算机断层扫描技术（Micro-computed tomography, Micro-CT）以及逆向成型技术。该模型基于我们前期文献报道的模型^[11]。为了提高计算速度，且由于耳道阻抗相对较小^[12]，将对本文分析影响不大的耳道部分删除。此外，由于本文研究耳蜗内部动态响应，为了使得耳蜗基底膜响应更逼近实验值，对部分组织的材料属性进行微调：将锤骨侧韧带和锤骨上韧带的弹性模量分别调整为 6.7 × 10⁴ Pa 和 4.9 × 10⁴ Pa；砧镫关节弹性模量调整为 4.4 × 10⁵ Pa；鼓膜环韧带和镫骨肌的弹性模量分别调整为 2.6 × 10⁷ Pa 和 1.5 × 10⁵ Pa。基底膜的阻尼系数为 α = 0 s^–1，β = 7.5 × 10^–6 s^[13]。并在此基础上建立圆窗激振式作动器-人耳耦合力学模型，如图 1 所示。

图 1.

The coupling finite element model of the human ear and the round window stimulation type actuator

圆窗激振式作动器-人耳耦合有限元模型

1.2. 初始压力及支撑刚度模拟

为了模拟作动器激振圆窗，在圆窗膜处施加 50 μN 幅值的简谐作用力，作用力方向垂直于圆窗膜^{[8, 14]}。选择该幅值是为了能在耳蜗内激振起近似 100 dB 声压级（sound pressure level，SPL）鼓膜声压激振下的基底膜位移量，使其能够补偿中重度听力损伤^[8]。在该力的基础上，施加不同大小的静力（10、50、100 μN），来模拟作动器上分别作用不同幅值的初始压力。最终，通过瞬态分析，对比各情况下基底膜运动情况，进而评估作动器上施加不同初始压力对其听力补偿效果的影响。

模拟支撑刚度影响时，我们需要结合具体作动器结构。本文中作动器为压电式作动器，其通过向两端做伸缩运动对外做功，两端的总伸缩量与输入的驱动电压成比例。为了研究支撑刚度对听力补偿效果的影响，我们必须构建支撑体刚度与作动器作用在圆窗膜端的输出量间的关系。但这种关系无法直接获得，故较难在有限元软件中通过施加已知函数来模拟。为了降低建模的难度，基于我们前期提出的压电式圆窗作动器^[15]，文中通过建立压电叠堆对内部作动器进行直接模拟。考虑到该作动器植入在中耳腔内，而人体中耳腔空间及圆窗的几何尺寸较小以及现实中制造作动器的困难程度，确定作动器为横截面积为 1 mm²、高度为 2 mm 的圆柱体。选择压电材料为锆钛酸铅 PZT-4，其密度为 7 500 kg/m³，弹性常数、压电常数、介电常数如表 1 所示^[16]。在作动器的基础上，建立相应的支撑体，如图 1 所示。该支撑体简化设计为帽状：顶端为面积为 1 mm²的圆，底部为面积为 2 mm²的圆，帽沿的宽度为 0.1 mm，模型整体厚度为 0.1 mm。顶部与作动器耦合并且正好将作动器包裹住，帽沿与骨板固定。通过改变支撑体刚度，对比分析作动器在相同电压驱动下的基底膜动态响应的不同，进而评估支撑体刚度对听力补偿的影响。

表 1. Material parameters of PZT-4.

PZT-4 材料特性参数

弹性常数/（GN·m–2）							压电常数/（C·m–2）				介电常数/（F·m–1）
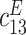
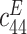
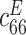
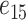
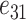
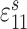
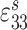
139.0	77.8	74.3	115.0	25.6	30.6		12.7	–5.2	15.1		370	635

1.3. 等效声压级

文中通过在圆窗膜上施加法向激振力来模拟作动器激振圆窗，以激振起近似 100 dB SPL 在鼓膜声压激振下的基底膜位移量。考虑到耳蜗内基底膜的动态响应与人耳感声直接相关^[17]，为了准确评估圆窗激振听力补偿效果，在此引入基底膜位移的等效声压级（equivalent sound pressure，ESP）来评估圆窗激振性能的标准，如式（1）：

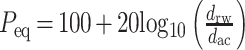1

式中，d_ac 为由鼓膜处 100 dB SPL 声压激励下的基底膜位移，d_rw 为圆窗激振对应的基底膜位移。

2. 结果

2.1. 模型的可靠性

为了保证修改后的人耳模型的可靠性，依次将基底膜选频特性、基底膜纵向特定部位的频率响应和耳蜗输入阻抗的计算结果与相关实验值进行对比验证。

耳蜗内基底膜选频特性对验证模型中耳蜗部分可信度有决定性的作用，也是判断模型可靠性的重要依据。通过对模型中鼓膜处施加 90 dB SPL 声压激励，测得计算后的基底膜最大响应位置到镫骨足底板的距离，并将得到的结果与 Békésy ^[18]和 Kringlebotn 等^[19]的实验结果进行比较。由图 2a 可见，模型计算结果略高于实验值，但是在中频段，模型计算结果逼近于实验值，且在总体趋势上与实验值一致，从而验证了模型的可靠性。此外，还增加了基底膜上离镫骨足板 12 mm 处的频响特性对比结果，如图 2b 所示。从中可见，模型计算该处基底膜速度与镫骨足底板速度之比与 Gundersen 等^[20]的实验测量结果较为一致。

图 2.

Comparison of the model-predicted basilar membrane’s vibration with the experimental data

基底膜响应对比验证

a. position of peak amplitude on the basilar membrane; b. frequency response curves of the basilar membrane at 12 mm from the stapes

a. 基底膜峰值响应的位置与频率的关系；b. 基底膜上距离镫骨 12 mm 处频率响应曲线

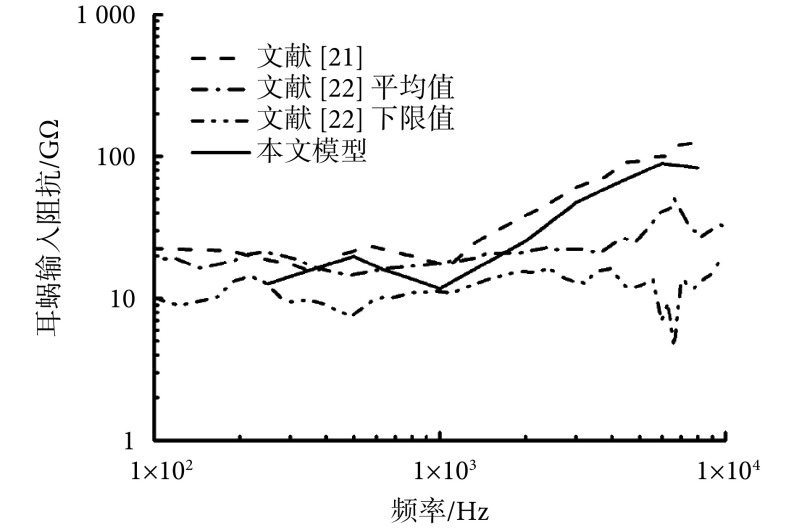
为了进一步验证模型的可靠性，本文还计算了耳蜗输入阻抗，并与 Puria 等^[21]和 Aibara 等^[22]的实验数据进行对比，如图 3 所示。从中可见，模型所得的耳蜗输入阻抗与实验数据较吻合，在趋势上更是与 Puria 等^[21]相同。通过上述三组数据对比，可以验证本文人耳有限元模型能够较准确地模拟人耳传声特性，可以用于圆窗激振分析。

图 3.

Comparision of model predicted cochlear input impe dance with the experimental data

耳蜗输入阻抗仿真与实验值对比

2.2. 初始压力对听力补偿的影响

图 4 右图中，纵坐标代表不同的初始压力与初始压力为 0 μN 的等效声压级差值。从图 4 可见，在圆窗上施加不同幅值的初始压力对于耳蜗激振补偿效果的影响不同。当对作动器施加 10 μN 初始压力时，降低了圆窗激振在低频段（< 750 Hz）的等效声压级，且频率越低降低幅度越大，在 250 Hz 处达到最大值（减小了 0.21 dB）。与此同时，该初始压力的施加增大了圆窗激振中高频段性能，且增幅基本随着频率的增大而增大，至 2 000 Hz 处达到 0.4 dB。此外，将作动器施加的初始压力增加到 50 μN 和 100 μN 时，发现依旧可以降低圆窗激振的低频段等效声压级，增大中高频段听力补偿效果，且这种低频恶化及中高频段提升的程度随着所施加初始压力的增大而增大。

图 4.

The effect of the preload on the performance of round window stimulation

初始压力对圆窗激振听力补偿的影响

2.3. 作动器层数的确定

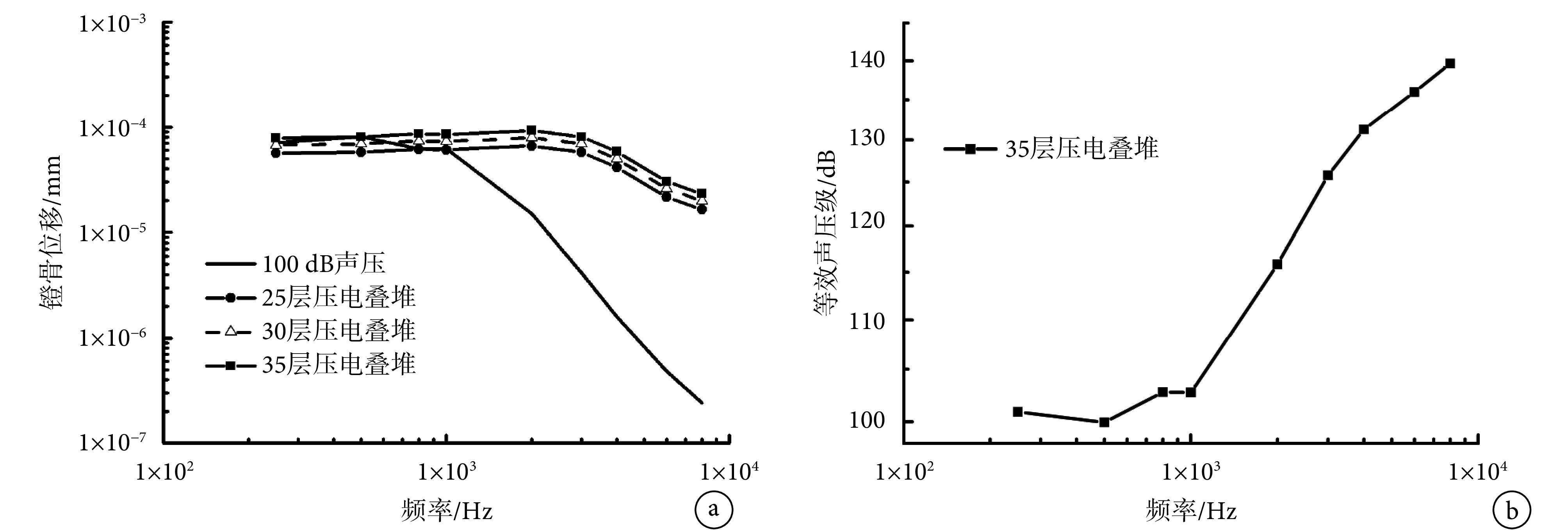
如前所述，为了研究支撑刚度对圆窗激振听力补偿性能的影响，需要对作动器内部具体结构进行建模。文中所建作动器为我们前期提出的高频增益好、不受电磁干扰的压电式作动器^[15]，该作动器主要由压电叠堆实现，通过逆压电效应进行驱动。为使建模简便，本文采用机械、电路皆串联的方法来近似模拟压电叠堆，即建模时不考虑压电叠堆间的电极层，只将电极设在叠堆的两端面，通过改变两端面的电压来分析压电叠堆层数对激振效果的影响^[23-24]。将作动器的最大电压取为 10.5 V_rms^[25]，进行谐响应分析。得到在该电压驱动下压电叠堆层数对作动器激振起的镫骨运动位移幅值的影响，并将该结果与正常 100 dB SPL 声压在鼓膜处的激励下镫骨的位移进行比较，如图 5a 所示。从图中可见，35 层压电叠堆就能在 10.5 V_rms 安全驱动电压下，激振起 100 dB SPL 鼓膜声压激励所对应的响应，满足人工中耳振子的听力补偿性能要求^[26]，故将压电叠堆中压电层数确定为 35。为了能够定量分析该作动器的听力补偿能力，将 35 层 PZT-4 作动器在 10.5 V_rms 的电压驱动下所激起的镫骨位移，按式（1）转化成鼓膜处的等效声压级，如图 5b 所示。由于过大的声音会让人听神经产生疼痛，故本文与多数人工中耳研究报道一致，将 100 dB SPL 作为设计标准^[26]。

图 5.

The effect of the piezo-stack vibrator’s layer number on stapes vibration

作动器层数对镫骨响应的影响

a. stapes footplate displacement from acoustic stimulation (100 dB SPL) and actuator stimulation at 10.5 V_rms; b. ESP at the tympanic membrane for 35 layer’s piezo-stack vibrator excitation at 10.5 V_rms

a. 100 dB SPL 声压激振和作动器激振的镫骨底板位移；b. 等效鼓膜处声压（35 层压电叠堆在 10.5 V_rms 驱动电压作用下）

2.4. 支撑刚度对圆窗激振听力补偿性能影响

在实际的圆窗激振式人工中耳中，作动器需要支撑装置的固定，但现有临床使用的圆窗激振式人工中耳都是直接采用传统人工中耳，没有专门设计支撑装置，直接采用筋膜包裹固定^[5]。为了研究作动器支撑装置支撑刚度对其听力补偿性能的影响，改变模型中支撑体的支撑刚度，分析相同作动器激振下不同支撑刚度的影响，并将其按照式（1）转化成鼓膜处的等效声压级，结果如图 6 所示（图 6 右图中纵坐标代表不同材料的支撑装置与无支撑装置的等效声压级差值）。其中，设定的支撑体的杨氏模量分别为 1.778 MPa^[14]和 110 GPa^[23]，分别对应筋膜和钛合金的材料属性。从图中可见，相对于不用支撑结构，采用筋膜支撑作动器将会提高低频段（< 850 Hz）听力补偿性能，等效声压级的最大增大量出现在 250 Hz 处（30.79 dB）；但对中、高频段影响不大。而当采用钛合金支撑，则能够提升整个频段的听力补偿效果。特别是相对于临床上用的筋膜支撑，使用钛合金支撑进一步提高了圆窗激振的中、高频段性能。

图 6.

The effect of the support’s stiffness on the performance of round window stimulation

支撑刚度对圆窗激振听力补偿性能的影响

3. 讨论

传统的人工中耳通过激振听小骨补偿听力，其听力补偿评估方法主要是通过分析镫骨足底板运动来实现。但圆窗激振不同于传统人工中耳，它避开听骨链直接激励耳蜗圆窗，属于逆向激振，即激励圆窗带动耳蜗内淋巴液，通过淋巴液的流动带动镫骨足底板运动。由此可见，逆向激振时镫骨足底板的运动与正常感声对应的镫骨足底板运动反应的实际感声存在不同。考虑到基底膜运动是将机械运动转换为神经信号的直接原因^[17]，故本文用基底膜运动的位移来评估圆窗激振听力的补偿效果，以提高评估的准确性。

为了确保模型更逼近真实人耳，文中中耳部分采用 Micro-CT 逆向成型技术建模。本文采用简化的双腔导管模拟耳蜗的实际螺旋形结构，并且这种耳蜗简化建模方法已被国内外学者采用并证实了其可靠性^{[13-14, 17]}。研究显示，采用简化耳蜗模型对低频段准确性影响较大^[27]，由于感音神经性听力损伤多发生在高频段，故低频段的偏差对本文研究影响不大。此外，从图 3 可以看出 Aibara 等^[22]实验所测均值与最小值曲线间的较大差异，能看出这种样本个体差异所造成的耳蜗输入阻抗差异较大。本文模型计算结果逼近于 Puria 等^[21]实验数据却远离 Aibara 等^[22]实验数据的现象，可能是样本个体差异所致^[28]。

关于初始压力对耳圆窗激振听力补偿效果的影响，Maier 等^[9]与 Lupo 等^[10]得到不同的结论。本文研究结果表明，初始压力将提高圆窗激振高频段听力补偿性能，且提高量随着初始压力的增大而增大；当初始压力从 50 μN 提升至 100 μN 时，在 4 000 Hz 处将提高圆窗激振的听力补偿性能为 1.25 dB SPL。考虑到感音神经性听力损伤多发生在高频段^[2]，故手术植入时对作动器施加初始压力将有助于其实际听力补偿。此外，我们发现初始压力的施加对听力补偿性能的提升量较小，这或许是 Lupo 等^[10]在实验中没有发现的原因。该结论对临床植入手术指导意义较大，可以让医生在手术中不用过于担心留下的初始压力。此外，文中研究的初始压力（10、50、100 μN）远小于 Maier 等^[9]实验研究中所施加的初始压力，主要是参考作动器工作中所需施加的激振力（50 μN）。从文中结果也能看出，当初始压力进一步提高至 Maier 等^[9]实验研究中所施加幅值时，将使该影响更加明显。但这种初始压力的提高，需要先分析圆窗膜能否长期承担这么大的作用力，这也是本文没有进一步研究的原因。

关于支撑刚度对圆窗激振听力补偿效果的影响，Arnold 等^[7]实验研究表明，作动器的支撑与否对听力补偿效果影响不大。但该结论是基于分析筋膜支撑作动器前后的镫骨运动得到，并且没有对比分析其他支撑材料的影响。本文研究结果表明，用筋膜固定作动器在低频段（0～850 Hz）较大程度地提高了听力补偿性能；但在中频段（850～2 000 Hz）反而降低了听力补偿效果；在高频段对圆窗激振性能无较大影响。但当把支撑装置材料改为医疗器械中常用的钛合金时，作动器补偿听力的性能在全频段得到提升，尤其在中、高频段的性能远优于筋膜支撑，这有利于感音神经性听力损伤的听力补偿^[2]。故针对圆窗激振式人工中耳，应对其作动器专门设计支撑装置，并且提高支撑刚度，进而提升其听力补偿性能。此外，本文主要分析支撑体刚度的影响，为了简化建模，将支撑体做成一密封盖状体。实际工作中若采用文中的支撑体结构设计作动器时，会对圆窗膜通透性的生理功能造成影响，所以在临床使用作动器时，应该根据需求设计满足刚度要求的支撑结构，如改用支撑杆来实现支撑。

4. 结论

本文通过 Micro-CT 扫描和逆向成型技术，建立了人耳传声力学模型，并通过三组实验数据对比，验证了模型的可靠性。基于该模型分析了初始压力和支撑刚度对圆窗激振听力补偿性能的影响，结果表明：作动器初始压力的施加会提高圆窗激振高频段的听力补偿效果，且提升量随着初始压力的增大而增大。考虑到感音神经性听力损伤多发生在高频段，这对该类耳聋的补偿特别有利。此外，相对于目前临床上采用筋膜支撑作动器，采用钛合金来支撑将继续在中、高频段提升圆窗激振性能。同样，考虑到感音神经性听力损伤多发生在高频段，应针对圆窗激振设计专门的支撑装置，进而提高其实际听力补偿性能。

Funding Statement

国家自然科学基金资助项目（51775547）；江苏高校优势学科建设工程资助项目