位姿对支架虚拟释放结果影响的数值模拟研究

Abstract

目前关于血管支架扩张的有限元分析并未将支架释放位姿这一因素对扩张结果的影响考虑在内。本研究利用 Pro/E 软件建立了支架和血管模型，通过 ABAQUS 软件构建了 5 种有限元装配模型，分别为 0 度无偏心模型、3 度无偏心模型、5 度无偏心模型、0 度轴向偏心模型和 0 度径向偏心模型，分为角度和偏心两组实验进行扩张模拟。计算了各模型的轴向缩短率、径向回弹率、狗骨头率等力学参数，通过比较分析，得出支架虚拟释放时的角度、偏心对数值模拟的影响。计算得到 5 种模型支架扩张后的残余狭窄率分别为 38.3%、38.4%、38.4%、35.7%、38.2%。研究表明位姿对数值模拟结果的影响较小，在对结果精度要求不高的情况下可以忽略这种影响，采用 0 角度无偏心的基本模型进行扩张模拟。

引言

冠状动脉粥样硬化是引起冠脉血管狭窄而导致冠心病的主要原因^[1-2]。冠状动脉支架植入术以创伤小、手术风险低等优势被普遍应用于冠心病的介入治疗。术后血管的残余狭窄率是医生和患者的关注重点，而支架的轴向缩短率、径向回弹率、狗骨头率等力学参数也是评价支架植入术后疗效的重要指标。采用有限元法模拟分析支架力学性能成为研究冠脉支架性能的一种有效方法^[3]。血管和支架之间的相对位姿和相互作用是有限元分析时需要考虑的主要问题之一。

关于模拟支架的单独扩张，Whitcher^[4]于 1997 年最先利用有限元法模拟了自膨胀式镍钛合金血管支架的扩张过程。Walke 等^[5]利用有限元分析方法研究了支架扩张的生物力学性能。但这些研究没有考虑血管的存在，支架的位姿问题也因此而被忽略。

在真实的支架植入术中，支架在植入血管进行释放时的位置、姿态并不是确定的，而且在扩张过程中也并非均匀扩张，因此就存在支架与血管相对位姿不同的问题，即有角度和有偏心的多种可能性。在数值模拟时，我们也经常忽略了这一问题。Migliavacca 等^[6-7]、Auricchio 等^[8]、Zahedmanesh 等^[9]建立了支架-血管模型，分析了支架扩张过程中支架-血管之间的接触问题。虽然增加血管模型后考虑了支架和血管之间的相互作用，但是这些研究并没有定量讨论支架与血管装配的角度和偏心问题。

Takashima 等^[10]模拟了支架在有斑块血管和无斑块血管中的不同状态。Wu 等^[11]分别对支架在直血管与弯曲血管中的扩张做了有限元模拟，关于支架对血管抻直效应的影响进行了相关讨论。徐江等^[12]对比分析了血管支架在基于计算机断层扫描（computed tomography，CT）的狭窄血管模型和理想化狭窄血管模型中的力学行为，其中基于 CT 的狭窄血管模型中支架处于偏心位置，而理想化模型中支架与血管轴线重合。这些研究定性考虑了支架在不同血管内的位姿问题，但是并没有定量研究位姿对模拟结果的影响。

目前针对支架在血管模型中扩张过程的有限元分析大多基于理想化狭窄血管模型，虽然已经不同程度地验证了数值模拟的合理性，但这些研究在模拟支架的虚拟释放时选择的大多是无角度无偏心的基本模型，并没有将支架可能存在的角度变化和偏心情况考虑在内。因此，角度和偏心等位姿问题对有限元模拟结果是否有影响尚不明确。

本文针对以上问题，应用有限元模拟分析方法，基于一种不锈钢支架与理想化狭窄血管模型，建立支架-斑块-血管的耦合模型，分别将它们装配成三种不同角度的无偏心模型和三种不同偏心的 0 角度模型来模拟支架的虚拟释放。计算出残余狭窄率、轴向缩短率、径向回弹率和狗骨头率等力学参数，得出力学性能的变化规律，揭示出不同释放位姿对支架扩张结果的影响，这对有限元方法的灵活应用具有重要的借鉴价值。

1. 模型和方法

1.1. 几何模型

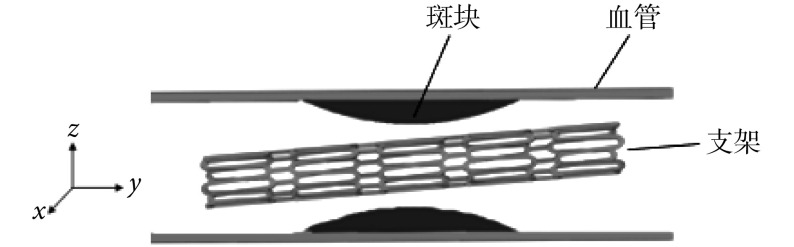
根据不同的释放位姿，分别建立角度（实验Ⅰ）和偏心（实验Ⅱ）两组实验，共计 5 个分析模型对支架进行扩张模拟。角度指的是支架与狭窄血管的中心轴线之间的夹角，偏心指的是支架和血管的中心轴线在横向及纵向的偏移。第Ⅰ组实验的 3 个模型分别为：模型 A，0 度模型；模型 B，3 度模型；模型 C，5 度模型，保证它们都无偏心。实验Ⅱ的 3 个模型分别为：模型 A，0 度模型（无偏心）；模型 D，轴向上有偏心模型；模型 E，径向上有偏心模型，保证它们的角度都为 0 度。以支架中心轴上一点为原点建立柱坐标系（见图 1），以此坐标系为基准，将支架、斑块、血管进行同轴装配，得到无角度、无偏心的基本模型 A，在实验Ⅰ和Ⅱ中公用。全局坐标系下（见图 1），在模型 A 的基础上令支架绕 Y 轴旋转 3° 得到模型 B，在模型 A 的基础上令支架绕 Y 轴旋转 5° 得到模型 C。在模型 A 的基础上令支架沿着 Y 方向平移 0.3 mm 得到模型 D，在模型 A 的基础上令支架沿着 Z 方向平移 0.3 mm 得到模型 E。模型示意图见图 1。

图 1.

Model diagram

模型示意图

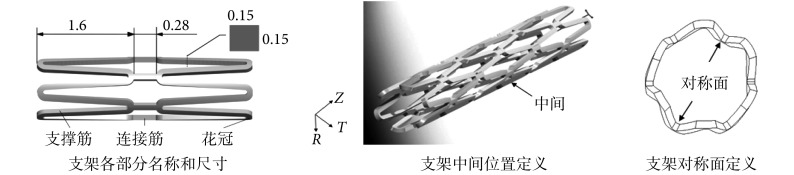
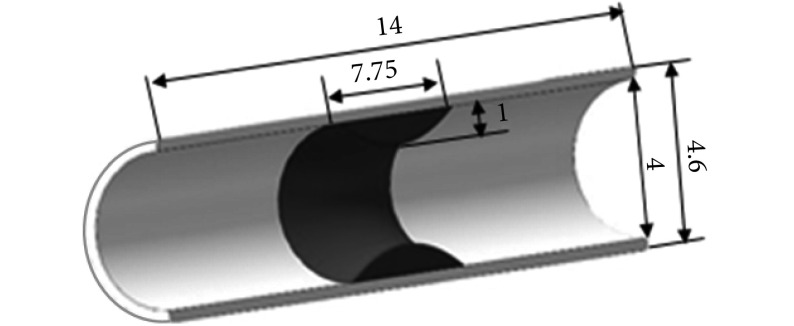
本文所采用的支架模型、理想化血管和斑块模型都是首先在 Pro/E 软件中建立几何模型，然后导入有限元分析软件 ABAQUS 中划分网格并计算。支架的整体模型如图 2 所示，周向均匀分布 6 个正弦波形单元，单个单元高为 1.6 mm，轴向由六组支撑筋和五组 I 型连接筋组成。支架内径 1.3 mm，外径 1.6 mm，长度 11 mm。支架支撑筋和连接筋采用相同的宽度与厚度，均为 0.15 mm。支架具备周向对称性、轴向周期性以及载荷均布性的特点。理想化血管与斑块模型如图 3 所示。以血管直径计算的狭窄率达到 50%。

图 2.

Stent model

支架模型

图 3.

Idealized vascular and plaque model

理想化血管与斑块模型

1.2. 材料模型参数

本文选取的支架材料为 304 不锈钢，赋予其双线性弹塑性材料属性；血管和斑块材料为钙化血管和钙化斑块，赋予其理想的线弹性、各项同性且不可压缩的材料属性。支架、血管、斑块的材料属性见表 1^[13]。

表 1. Material properties of the stent, vessel and plaque.

支架、血管、斑块的材料属性

	材料	弹性模量/MPa	泊松比	屈服强度/MPa
支架	304 不锈钢	193 000	0.270	207
血管	钙化血管	175	0.499	—
斑块	钙化斑块	219	0.499	—

1.3. 边界条件

为了尽可能地模拟支架扩张的真实情况并使有限元分析顺利进行，本文对支架系统采用以下约束方式：斑块外表面与血管内表面采用绑定的条件约束，保证斑块与血管之间力与位移的传递，同时不发生相对滑移。支架外表面与斑块、血管内表面均采用滑动摩擦的面面接触属性，摩擦因数为 0.2。约束支架中间对称面上的轴向位移和周向旋转如图 2 所示。最后在血管模型的一端施加固定约束，作为整个计算模型的基础约束。

1.4. 载荷与分析步

支架的扩张变形过程分为 3 个阶段：位移加载、保持、位移卸载。研究中支架扩张的载荷选用位移进行施加，依此来模拟支架在狭窄血管模型内的释放过程^[14]。在支架的内表面施加径向向外的位移载荷，加载到支架扩张后的外径尺寸达到血管内径正常尺寸的 1.1 倍时为止。当支架扩张完成后，对载荷进行保持与卸载。首先停止施加位移载荷，对这一位移量进行保持。之后将位移载荷卸载，支架在斑块与血管壁弹性收缩力以及自身径向回弹的作用下发生径向收缩。

1.5. 力学性能评价指标

为了定量描述各方案中支架虚拟释放结果的不同，引入血管的残余狭窄率 X₁、支架的轴向缩短率 X₂、径向回弹率 X₃、狗骨头率 X₄ 等指标，具体定义如下^[15]：

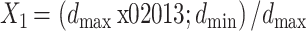1

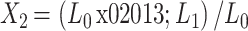2

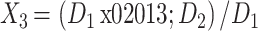3

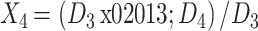4

式中，d_max 为卸载后血管最大直径，d_min 为卸载后血管最狭窄处的直径；L₀ 为支架初始长度，L₁ 为支架扩张后长度；D₁ 为支架扩张最大时的平均直径，D₂ 为支架卸载后的平均直径，平均直径即最大直径与最小直径的均值；D₃ 为支架卸载后的端部直径，D₄ 为支架卸载后的最小直径。

残余狭窄率是指支架卸载后恢复正常血运的血管的狭窄率；残余狭窄率越大，说明支架治疗效果越差。轴向缩短率是指支架在体内扩张后轴向总长度大小变化的性能参数；轴向缩短率越大，则支架扩张卸载后的轴向长度越短。径向回弹率是指支架在体内扩张后半径方向的回弹参数；径向回弹越大，说明支架扩张后径向支撑刚度越小。狗骨头率即扩张不均匀率，是指支架在扩张过程中前后两端出现翘起的现象；狗骨头率越严重，说明支架植入后对血管壁造成的损伤越大，从而越容易引起病变部位的炎症反应^[16]。

2. 结果

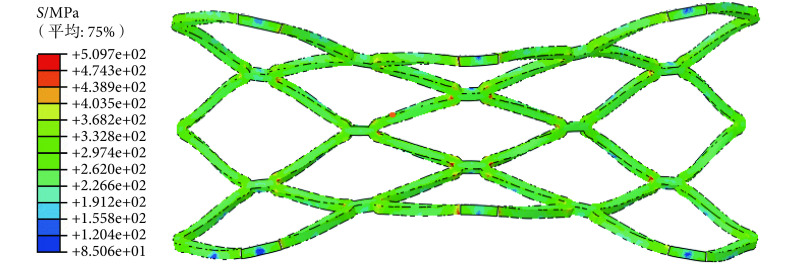
通过有限元分析软件 ABAQUS 进行扩张模拟，得到各扩张实验的模拟结果，它们的最大残余应力值分别为 509.7、510.8、510.1、515.0、510.9 MPa，差异较小，且应力集中区域都在支撑筋拐弯处。由于应力变化趋势基本相同，文中只列出方案 A 的 Mises 应力云图，如图 4 所示。计算得到各方案的力学性能参数结果在表 2 中列出。

图 4.

Contour of Mises stress in Model A

模型 A 的 Mises 应力云图

表 2. The mechanical performance parameters of each scheme.

各方案的力学性能参数结果

模型	残余狭窄率	轴向缩短率	径向回弹率	狗骨头率
A（0 度无偏心）	38.3%	12.3%	24.3%	44.3%
B（3 度无偏心）	38.4%	12.4%	22.0%	46.9%
C（5 度无偏心）	38.4%	12.3%	22.0%	46.9%
D（0 度轴向偏心）	35.7%	12.2%	23.3%	41.1%
E（0 度径向偏心）	38.2%	12.3%	23.2%	45.4%

由于临床医生最为关注的是残余狭窄率，因此本研究的关注重点也放在残余狭窄率的变化上。比较表 2 中实验Ⅰ和实验Ⅱ的残余狭窄率变化情况，发现不同角度模型计算得到的结果差异甚小，随着角度的增加残余狭窄率呈现增大的趋势，但变化幅度最大不超过 0.1%，因此可以认为角度因素对支架虚拟扩张结果中残余狭窄率的影响不大。相比于角度对残余狭窄率造成的影响，偏心对残余狭窄率造成的影响稍大。而轴向上偏心模型比径向上偏心模型造成残余狭窄率的变化更大，达到了 2.6%。这说明轴向上偏心比径向上偏心对于有限元模拟结果的影响更大。因此，在有限元模拟时应当准确放置支架的实际偏心状态以达到精确的模拟结果。

比较表 2 中实验Ⅰ、实验Ⅱ的轴向缩短率，实验Ⅰ和实验Ⅱ的波动范围均不超过 0.1%，即不同位姿下，各模型的轴向缩短率相差不大。

比较表 2 中实验Ⅰ、实验Ⅱ的径向回弹率，实验Ⅰ中径向回弹率波动范围小于 2.3%，实验Ⅱ中径向回弹率波动范围小于 1.1%。不同位姿下，各模型的径向回弹率较轴向缩短率的变化来说差异较大。

比较表 2 中实验Ⅰ、实验Ⅱ的狗骨头率可以发现波动范围分别小于 2.6%、3.2%。不同位姿下，各模型狗骨头率的数值较大，但是彼此间的差异较小，处于可接受的范围。

3. 讨论

不同的模型构建和计算方法往往会产生不同的生物力学评价结果^[17-19]。支架在植入血管的过程中有不同的位姿状态，在进行有限元模拟时通常选择的是无角度无偏心的模型，而考虑支架释放的角度和偏心等位姿问题的必要性分析还未见研究。本文正是充分考虑到这种必要性，从角度和偏心两个方面比较了数值模拟中支架植入狭窄血管的不同位姿对支架虚拟释放结果的影响。

本研究的主要目的在于探究数值模拟中由于研究者的主观因素造成装配角度和偏心的差异对于计算结果影响的大小。本文要验证的是，用无角度无偏心的模型能否较为准确地模拟有角度有偏心的不同手术情况。因此本研究无法预测多大的位姿变化在临床应用中才会产生明显的不良后果，但本文的研究结果可以从支架植入位姿的原理上给医生提供建议。

临床介入操作中，医生都是依靠经验来进行手术，通过人工操作将支架推送到病变部位，而对支架在病变部位的角度和偏心并不关注，也无法准确测量。目前在临床介入操作中关于放置的支架与血管之间的角度还没有具体的数据，位姿与支架预后也没有相关的临床数据或研究，但本文中提出的位姿问题对研究者和临床医生进行基础研究和临床应用时将有一定的启发。

本文采用的角度模型和偏心模型都是结合临床手术过程在理论上预测的。由于支架植入血管中的角度和偏心程度受到狭窄血管内径的约束，位姿变化并不会太大，可选择的变化幅度有限，因此本研究中考虑的角度和偏心模型参数是根据所建立的理想血管模型尺寸预设的，在角度方面只设置了三组，在偏心方面只设置了两组。数值模拟的结果证实了有限元分析中主观原因造成的位姿不同对计算结果的影响不大，可以不必太计较数值模拟中的位姿问题。同时本研究的结果对于临床实践也是有参考意义的，研究得到有偏心模型的残余狭窄率更小，那么在临床手术中可以参考这一结果对支架植入手术的位姿进行调整，通过术后随访来验证疗效，提高手术的效果。

有研究表明残余狭窄的发生与支架的结构特点、材料属性以及斑块的狭窄程度有直接的关系^{[3, 20-22]}。同时，残余狭窄的发生也与支架的扩张直径、放置位置有一定联系^[23-24]。本研究未采用真实的狭窄血管进行模拟，不同角度和不同偏心的计算模型也没有考虑更多情况。这需要在今后的研究中作进一步的模拟和实验来验证。

4. 结论

综上所述，角度或偏心会对有限元模拟结果造成一定的影响，但这种影响无论是对于支架的轴向缩短率、径向回弹率、狗骨头率等参数，还是对于临床医生最关心的血管残余狭窄率来说影响都较小，因此基本模型的数值模拟结果作为提供给临床医生进行参考的数据可以认为是合理的。

研究得出，在微小的角度变化范围内，随着角度的增加，残余狭窄率呈现增大的趋势，但角度因素对支架虚拟扩张结果中残余狭窄率的影响不大。支架轴向上的偏心和径向上的偏心均会对残余狭窄率造成一定的影响，其中轴向偏心比径向偏心对结果的影响更大。因此在模拟支架虚拟释放时，位姿对数值模拟的结果有影响，但是在对结果精确度要求不高的情况下可以忽略这种影响，采用 0 角度无偏心的基本模型进行计算。

本研究对于研究者们在今后进行有限元分析时模型装配位姿的考虑上具有一定的指导意义，为了令数值模拟结果更贴近真实情况就需要考虑支架在血管中的真实位姿，即支架在血管中是以怎样的角度和偏心放置并实现扩张的。这种考虑将有利于数值模拟为支架设计和临床手术提供更准确的参考意见。而对于临床手术的效果来说，位姿与支架的预后尚没有相关的临床数据或研究，本文中提出的位姿问题为研究者和临床医生提供了新的思考和启示。

Funding Statement

北京市教委科技计划重点项目暨北京市自然科学基金B类项目（KZ201710005007）；北京市教委科技计划面上项目（KM201711417011）