基于卷积神经网络的先心病心音信号分类算法

Abstract

心脏听诊是先天性心脏病（简称：先心病，CHD）初诊和筛查的主要手段。本文对先心病心音信号进行分析和分类识别研究，提出了一种基于卷积神经网络的先心病分类算法。本文算法基于临床采集的已确诊先心病心音信号，首先采用心音信号预处理算法提取并组织一维时间域上心音信号的梅尔系数转变成二维特征样本。其次，以 1 000 个特征样本用于训练和优化卷积神经网络，使用自适应矩估计（Adam）优化器，获得了准确率 0.896、损失值 0.25 的训练结果。最后，用卷积神经网络对 200 个心音信号样本进行测试，实验结果表明准确率达 0.895，灵敏度为 0.910，特异度为 0.880。同其它算法相比，本文算法在准确率和特异度上有明显提高，证实了本文方法有效地提高了心音信号分类的鲁棒性和准确性，有望应用于机器辅助听诊。

引言

心音（heart sounds，HS）信号是由于血流使心脏瓣膜打开或关闭时振动产生的声音信号，是人体重要的生物信号^[1]。心音信号包含了大量的心脏生理、病理性信息，临床医生可以通过听诊识别出心音信号是否异常，从而辅助诊断心血管疾病^[2]。目前，电子听诊器和心音信号数据采集设备日趋成熟，可以通过数字化分析手段，提取心音信号的病理特征，达到对心音信号分类识别的目的。这项工作对实现远程心脏疾病的诊断和监测具有重要意义。因此对心音信号的有效去噪、分析和识别是实现远程医疗和计算机辅助听诊的前提。

心音信号在国内外生物医学信号实验室一直备受关注，Abbas 等^[3]首先提出了心音信号预处理的基本步骤：去噪、包络提取、分段定位以及特征提取。近年来，研究人员重点关注的是心音信号的分类研究。心音信号的分类算法主要有：① 传统模式识别的方法，例如：文献[4]使用小波包分解对 59 个心音信号提取特征输入支持向量机（support vector machine，SVM）分类器准确率可达 0.95；文献[5]对心音信号使用梅尔频率倒谱系数（mel frequency cepstrum coefficient，MFCC）提取特征后使用隐马尔可夫模型（hidden markov model，HMM）进行分类，准确率超过了 0.8；文献[6]对 392 个心音信号样本使用 MFCC-SVM 的方法获得了 0.86 的准确率。② 深度学习的方法，例如：Maknickas 等^[7]直接将心音信号分成 4 ms 片段输入卷积神经网络（convolutional neural network，CNN）进行训练并验证，在 1 391 个心音信号样本上验证获得了 0.841 的准确率。③ 人工神经网络（artificial neural network，ANN）的方法，例如：文献[8]采用 ANN 法进行研究，实验样本最小的只有 5 个，最多的只有 215 个，准确率从 0.92～0.99 不等；④ 综合几种不同模式识别的方法，例如 Papadaniil 等^[9]采用经验模态分解算法和 ANN 方法对心音信号进行特征提取和分类识别，准确率达到了 0.845；文献[10]使用K最近邻（K-nearest neighbor，KNN）算法和 HMM 算法进行心音信号的分类识别，准确率可达 0.825。

上述研究中，部分文献报道的算法准确率较高，有的准确率高达 0.99，但离应用在远程医疗或机器智能辅助听诊领域还有一定差距，原因是：① 预处理步骤复杂，传统模式识别的方法需人工干预挑选有效的特征，例如文献[4]和文献[6]利用小波分解提取特征，但心音信号成分复杂，能否提取到有效的特征尚需探索；② 训练样本量过小，例如文献[8]的 ANN 心音信号分类算法样本数最大仅 215 个，传统模式识别分类的文献[6]也仅 392 个样本，尽管这些算法准确率较高，但是无法保证心音信号分类算法的普适性和鲁棒性；③ 准确率低，文献[7]训练样本数达 1 391 个，但其准确率仅为 0.841，还不足以达到实际应用的要求，尚需进一步的提升。这些不足之处都极大地制约了心音信号分类算法将来的推广实用和实时化辅助诊断决策。

基于已有算法的不足之处，本文提出了一种基于 CNN 心音信号分类算法，算法流程如图 1 所示。该算法主要有两个核心步骤组成：一是构建一种适于 CNN 的心音信号预处理模型，重点需阐述如何将一维（one dimension，1D）心音信号组织成二维（two dimension，2D）特征图；二是利用预处理得到的“特征图”，训练优化 CNN 网络结构，寻找最适合心音信号的 CNN 结构和参数。本文期望通过基于 CNN 的深度学习方法，有效提取心音信号的特征，从而解决以往分类算法过程复杂、分类准确率不高、普适性差的问题。

图 1.

Heart sound classification recognition algorithm flowchart in this study

本文心音分类识别算法流程图

对比以往研究，本文创新之处在于：① 训练样本数量较大，网络训练使用了 1 200 个样本，较以往算法数据量明显增大，增强了算法的普适性，保证了算法的有效性；② 准确率有较大提高，本文算法在大样本量的前提下，算法准确率可达 0.895，对比文献[7]使用的也是深度学习算法，样本量大，本文算法同其相比有较大提升。

综上所述，本文基于 CNN 心音信号分类算法，训练样本量大，保证了算法的鲁棒性，提高了心音信号分类准确率，为心音信号的研究做出了积极有意义的探索，旨在推动心音信号分类算法能应用于先心病临床诊断和筛查。

1. 预处理方法

1.1. 数据来源

本文研究的心音信号数据来源于云南省阜外心血管病医院和昆明医科大学第一附属医院临床采集的数据，以及在云南省各地州参加先心病筛查时采集所建立的心音信号样本库。该心音信号样本库中，志愿者年龄在 6 个月到 18 岁之间，所有志愿者均签署知情同意书，并经过云南大学医学院伦理委员会审查同意后，授权可以使用志愿者的心音信号数据。样本库所有心音信号数据所属分类疾病，均经过便携式超声心动仪（Acuson Cypress，西门子股份有限公司/德国）确诊。本实验室（云南大学信息学院生物信号处理实验室）自行研发了一套心音信号采集设备用于处理经心音信号传感器（THE ONE，ThinkLabs 公司/美国）采集的模拟信号，采样频率为 5 000 Hz，采集时长为 30 s，该电路能够将模拟信号转变为数字信号，便于存储和处理。

1.2. 去噪

心音信号在采集过程中不可避免地存在一些噪声干扰，干扰由多种原因造成，例如皮肤与传感器的摩擦音、采集环境的背景噪声、患者的呼吸扰动音等噪声干扰，故需对心音信号进行去噪处理，得到噪声较少的心音信号。去噪的方法有高通滤波、低通滤波、切比雪夫滤波、卡尔曼滤波等，而目前广泛应用在心音信号去噪处理的是小波去噪^[11]。文献[11]在小波基选择、小波分解层数、阈值确定方面做了大量的研究工作，指出如果选择 db6 小波，将分解层数设置为 5 层或 6 层，阈值选择为每一层细节分量最大值的 10%，可得到较好的去噪效果。采用小波去噪的方法是为了获得最好的包络效果，利于心音信号分段定位，但未关心去噪后心音信号的有效性信息。去噪过程中，分解层数直接影响去噪后心音信号的有效成分，最终影响分类的准确率，过多的分解层数会对原始心音信号产生变形，不利于保留心音信号的信息量，选择合适的小波分解层数是本文的一个研究内容。

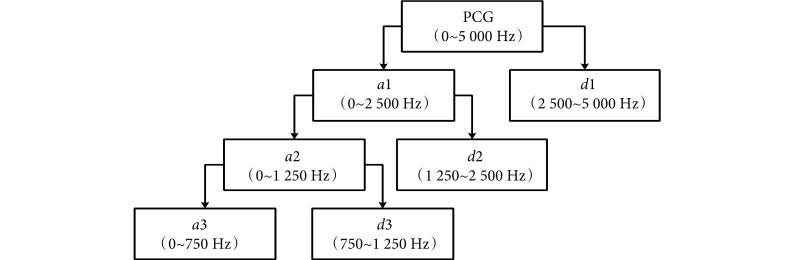
小波去噪算法基本思想是根据信号频率按层分解，每层分解是从原始信号的起始频率到信号的二分之一频率。心音信号小波去噪算法分解示意图如图 2 所示。

图 2.

Decomposition of heart sound wavelet denoising algorithm

心音信号小波去噪算法分解示意图

图 2 中心音图（phonocardiogram，PCG）（以符号PCG表示）表示原始心音信号，ai（i = 1，2， ，n）表示分解层数第i层的近似分量，di（i = 1，2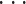， ，n）表示分解层数第i层的细节分量。正常心音信号的频率在 5～600 Hz 范围内，心音信号中的某些病理性杂音频率可以到 1 500 Hz。通常认为 2 000 Hz 以上基本不包含有效信息，信号重构中可以直接置零，结合图 2，n的求解满足如式（1）所示：

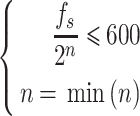1

其中，f_s表示心音信号的采样频率，由于本文实验数据采样频率为 5 000 Hz，由式（1）可知，分解层数n为 4，信号重构可以表示为如式（2）所示：

2

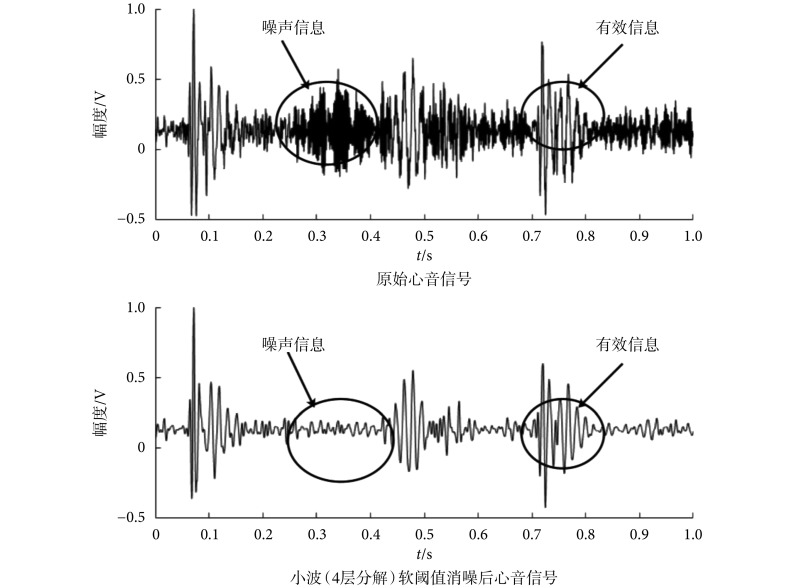
任意选取一例心音信号样本数据，按照 db6 小波基、分解层数 4 层、软阈值（阈值等于每一层细节分量最大值的 10%）进行去噪实验，其去噪效果如图 3 所示。

图 3.

4-layer wavelet decomposition results

4 层小波分解结果图

从图 3 可知，4 层小波已能够将大部分心音信号的噪声信息滤除，且去噪后的心音信号在外观形态上同原始心音信号基本相似，即最大程度地保留了有效信息，因此本文选择小波软阈值去噪，具体参数是：db6 小波基、4 层小波、软阈值 10%。

1.3. 数据截取

数据截取的目的是将长时间的心音信号截断成若干个片段，将质量比较好（采集时噪声较小）的数据片段标记为 CNN 方法的输入样本。数据截取应考虑两个问题：从何处开始截取和心音信号应截取的时间长度。

CNN 在识别过程中是将图片分割成若干个像素，通过卷积核依次对这些像素做卷积操作^[12]。图片中相邻像素具有相似性质，且同一类 CNN 样本图片中的起始位置也相同。当 CNN 在语音信号中做语义分析时，为了排除起始位置不同的干扰，其样本语音均需具有相同的句首。那么，由于心音信号的病理杂音通常发生在心脏的收缩期，即主要病理信息包含在第一心音（S₁）到第二心音（S₂）时间片段内，因此可以选择 S₁ 的起始位置作为数据截取的起始点。

S₁ 的起点可以通过心电信号来确定，心电信号中 R 波波峰的位置是 S₁ 的起始位置，T 波结束的位置为 S₂ 结束位置。S₁～S₂ 的时间间隔小于 S₂～S₁ 的时间间隔，根据心音信号这两个特性可以确定 S₁ 的起始位置，也就确定了数据截取的起始位置。数据截取时间的长短受 MFCC 变换过程影响，本文在 1.4 节中给出具体推导公式。

1.4. 维度变换

心音信号是 1D 数据，而卷积样本（图像）是 x 轴和 y 轴上一系列像素值的排列，尤其是彩色图像的红、绿、蓝色彩模式（red green blue，RGB）值可以被视为三幅的 2D 灰度图，即 CNN 进行模式识别时必须将输入样本组织为 2D 数据。CNN 在样本训练和识别时都是在输入的“图像”上运行一个“窗口”，在“窗口”内学习特征参数，进行全连接权重共享。因此可以通过提取心音信号特征参数，并将这些特征参数适当组织，实现从 1D 到 2D 的变换，从而满足 CNN 识别需求。

心音信号同语音信号具有共性特点：① 两者都是音频信号，这两个信号都是通过人耳对音高的变化传递信息；② 两者在短时间内都可以看作是平稳准周期信号。目前，MFCC 已广泛应用在语音和语义识别等信号处理中，心音信号也常使用 MFCC 来提取特征，进行分类识别^[13]。考虑到 CNN 带来的一些新特性，本文采用梅尔对数频率系数（log Mel-frequency spectral coefficients，MFSC）^[14]来替代 MFCC 提取心音信号特征，并组织 MFSC 成“特征图”，作为后期 CNN 的输入样本。

1.4.1. 梅尔频率系数

MFCC 中的梅尔刻度是一种基于人耳对等距的音高变化的感官判断而制定的非线性频率刻度，能较好地反映人耳对声音的特点。MFSC 是省略离散余弦变换步骤的 MFCC 的特殊形式，即直接对 MFCC 取对数能量。MFSC 相比较 MFCC 光谱能量能保持局部特性，MFSC 提取的特征与原始心音信号具有高度相关，在频谱上更为平滑，少量的 MFSC 特征即可代表绝大部分信号的信息。

MFSC 处理的基本步骤如下：

（1）预加重。将信号 x（n）通过一个高通滤波器，其目的是补偿高频部分，突显在高频的共振峰。

（2）分帧、加窗。心音信号是一种短时非平稳信号，研究起来困难，分帧可以使信号近似为平稳信号，加窗可以防止信号相邻两帧之间变化过大，使相邻两帧有重叠部分，克服频谱泄露现象。分帧时，信号交叠一般为 50%，以提高时间分辨率。心音信号分帧后的帧数M的计算如式（3）所示：

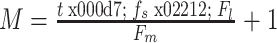3

式（3）中，t为截取的心音信号时间长度，F_l为帧长，F_m为帧移，f_s为采样频率。

（3）频域变换。信号在时域上的变化很难观察信号的能量特性，通常将它转换成频域上的能量分布来观察，不同的能量分布，代表不同心音信号的特性。本文使用傅里叶变换，其计算公式如式（4）所示：

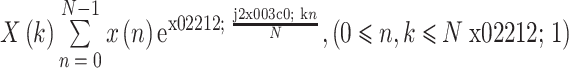4

其中 X（k）表示频域信号，N 是帧长所包含的点数。

（4）梅尔刻度转换。经傅里叶变换之后的信号尚需经过梅尔滤波器组和梅尔刻度转换，其原因是频域信号有很多冗余，梅尔滤波器组可以对频域的幅值进行精简，每一个频段用一个值来表示，一个滤波器产生一个频段值，而梅尔刻度则与人耳的听觉特性相符。CNN 识别的样本一般要求为方图，因此滤波器个数N和帧数M的关系应当满足如式（5）所示：

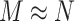5

式（5）中，M的取值一般在 24～80 之间，故由式（3）和（5）可以大致确定数据截取的长度。

（5）能量值取对数。人耳对声音的感知并非线性关系，以取对数的这种非线性关系可以更好地描述人耳对声音感知的特性。

（6）差分。由于心音信号是时域连续的，分帧提取的特征信息只反映了本帧心音信号的特性，为了使特征更能体现时域连续性，故在特征维度增加前后帧信息的维度，即常用一阶差分（∆）和二阶差分（∆−∆）实现。

1.4.2. 特征数据的组织

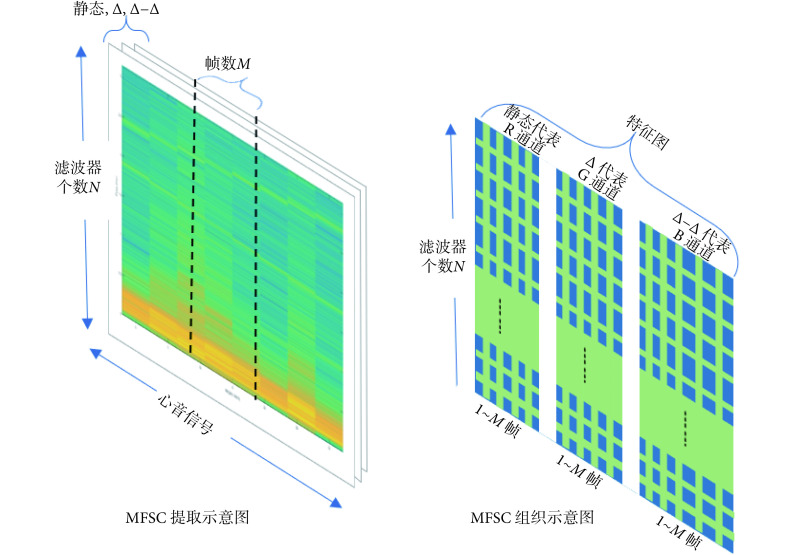
本节介绍的是如何将 MFSC 组织成 CNN 所需要的特征图。每一个 MFSC 是一段信号在分帧加窗之后的时间段（帧）内在某一频率段上的系数总和，即心音信号经过 MFSC 后，从 1D 变换到 2D。MFSC 取一阶和二阶差分，即可描述心音信号的时域连续性，因此一段心音信号将会得到 3 幅 M × N 的“特征图”，即时间段取 M 帧，频率系数取 N 个。CNN 提取特征时，将沿着时间和频率方向执行三维卷积。数据组织方式如图 4 所示，3 幅 2D 特征图分别对应图像中 RGB 的三个通道，构成一幅彩色“特征图”。CNN 根据 MFSC 组成的彩色“特征图”进行深层次学习，调整网络参数，完成心音信号分类任务。这种数据组织方式既最大限度地结合了心音信号时域特性和频域特性，又实现了数据的维度变化，满足了 CNN 输入样本要求。

图 4.

MFSC data organization of heart sound signals

心音信号的 MFSC 数据组织方式

2. CNN 分类识别模型

2.1. 数据准备

心音信号预处理方法，如图 5 所示。提取 MFSC 时，选择F_l为 2 048 点，F_m为 512 点，梅尔滤波器个数 N = 34，由式（3）和（5）可知，信号截取长度t = 4 s。因此心音信号“样本图”（下文简称样本）大小为 34 × 34 × 3。根据第 1 节中心音信号预处理方法，本文预处理了 1 200 个心音信号样本，1 000 个样本用于 CNN 训练，200 个用于单独测试，其中正样本 600 个，负样本 600 个。

图 5.

CNN heart sound preprocessing method

CNN 心音信号预处理方法

2.2. 训练环境

（1）软件环境。本文使用的 CNN 在深度学习开源软件 Keras 2.0.9（Google，美国）中实现。Keras 由纯 Python 语言编写而成，具有高度模块化、极简和可扩充特性，可以在中央处理器（central processing unit，CPU）和图形处理器（graphics processing unit，GPU）中无缝切换，用户界面友好，可以快速搭建网络模型。因此选择 Keras 作为心音信号分类识别开发工具。

（2）硬件环境。所有训练和测试都在桌面电脑中完成，其中，CPU（Core i5 @3.4 GHz，Intel，美国），内存（DDR4 16 GB，宇瞻，中国），显卡（NVIDIA 1060 6 GB，英伟达，美国）。

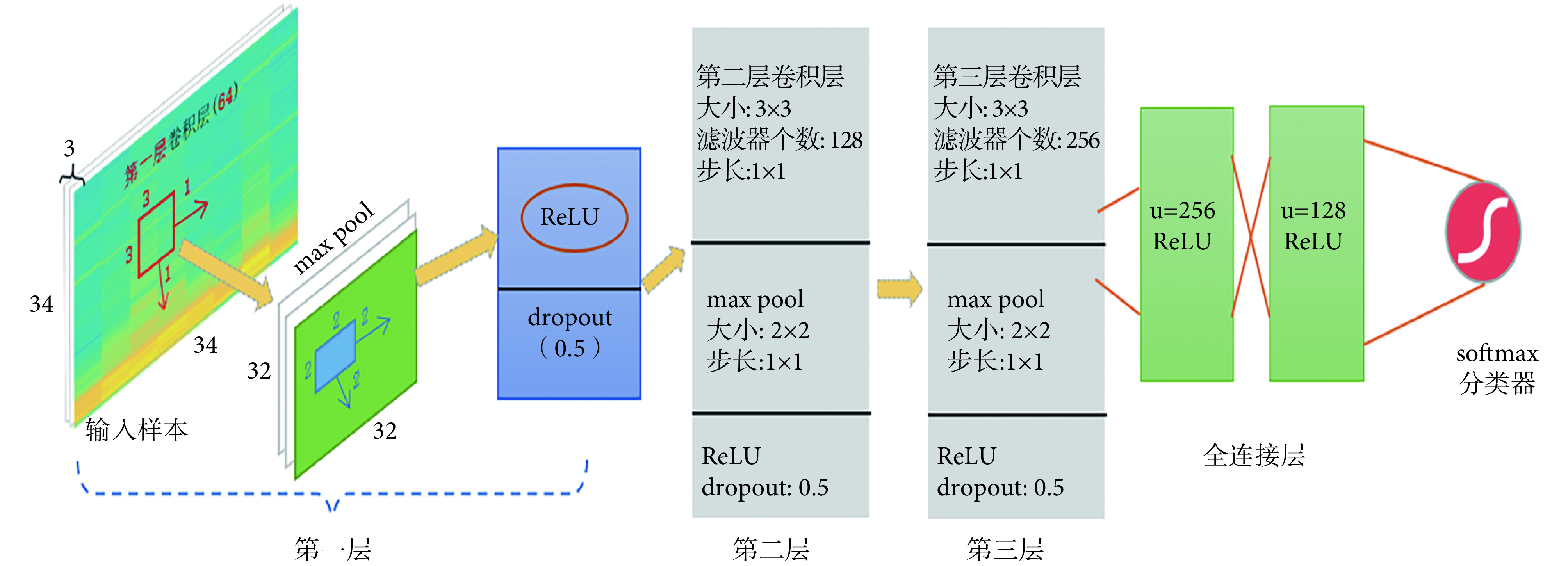
2.3. CNN 结构

网络架构如图 6 所示，采用递增型网络结构。该网络共 6 层，其中包含 3 层卷积层，2 层全连接层，1 层归一化指数函数柔性最大（softmax）分类层。网络架构的输入样本是预处理后的心音信号样本，大小是 34 × 34 × 3。图 6 所示网络架构是已经训练和优化之后的 CNN 架构图，每层网络参数如下：第 1 层卷积层使用了 128 个过滤器，卷积核大小为 3 × 3，步长为 1 × 1；池化为最大池化（max pool），大小为 2 × 2，步长为 1 × 1；采用修正线性单元（rectified linear unit，ReLU）激活函数，随机失活（dropout）率为 0.5。第 2 层和第 3 层卷积层分别使用了 128、256 个滤波器，卷积核大小均 3 × 3，步长 1 × 1；池化操作、激活函数和 dropout 概率均与上一层相同。2 个全连接层，输出维度分别为 512、256，采用 ReLU 激活函数，中间使用 dropout（概率 0.5）进行连接。最后分类器为 softmax 分类器。

图 6.

CNN architecture

CNN 架构图

值得特别注意的是，该网络架构包括网络的层数、核函数的选择、核函数大小以及数目均是该心音信号样本下的网络训练调整后的最优结果。需指出的是，只有使用 ReLU 激活函数时，网络才会收敛，这与大部分深度学习所提及的激活函数选择是一致的。文献[15]指出 ReLU 激活函数相比传统的双曲正切函数（tanh）、S 型（sigmoid）函数的输出更具备稀疏性，没有梯度消失的问题，使得收敛速度更快。选择 2D 卷积滤波器的理由是，心音信号正常和异常在时间和频率上都有所表现，2D 卷积滤波器能更好地在时间和频率两个维度上提取相关特征。dropout 是以随机的方式删除隐层节点数目，可以有效减轻过拟合，一定程度上达到正则化的目的，一般 dropout 概率设置为 0.5 或者 0.3^[16]。softmax 函数是 sigmoid 函数在多分类问题上的一个推广，常用在 CNN 网络分类器上。

3. CNN 训练及结果

网络训练是指，向网络输入一定量的样本，在一定算法的调节下，不断优化网络的权值，使网络的输出与预期值相符。训练神经网络主要包括：网络架构的调整、各层激活函数的选择、模型编译优化器的选择。准则是使训练样本损失值不断减少，以提高训练精度，并使验证集准确率随之提高，防止模型过拟合。本文训练时使用了 Keras 提供的早停法（EarlyStopping）函数以寻求迭代中的最佳模型，防止模型过拟合。前文给出了网络架构的层数、核函数的选择和大小的最终结果，此处给出模型编译优化器的选择，展示 CNN 的训练过程，显示网络训练的一些最终结果，期望最终能从优化器的选择中寻找到神经网络训练的一般步骤和规律。

训练前，首先将训练数据进行划分，对 1 000 个训练样本按照 0.7 概率随机划分，即每次迭代过程中 700 个样本用于训练，而 300 个样本用于监督学习，并采用交叉验证的方式进行验证。训练中，块的大小为 32，该 CNN 模型有 2 600 065 个参数需要学习，采用对数损失函数对模型进行监督，用 Keras 提供的 EarlyStopping 函数寻求迭代中的最佳模型，防止过拟合，考虑不同优化器函数对准确率的影响。不同优化器函数模型的损失函数和模型准确率如图 7 所示。

图 7.

Model loss values and accuracy

模型损失值和准确率

训练不同的优化器函数对模型的训练结果有很大的影响，本文只展示了训练中的 4 种优化器结果。从图 7 来看，递归神经网络中经典的均方根反向传播（root mean square prop，RMSprop）优化器对本文心音信号样本并不适用，反而在所有的优化器函数中表现最差，采用该优化器时，训练结果不收敛；其次效果较差的优化器是梯度下降法（stochastic gradient descent，SGD），损失值下降速度很快，但是准确率较低，模型迭代第 11 次时，已经没有改善趋势，损失值为 0.56，准确率为 0.773；采用自适应矩估计（adaptive moment estimation，Adam）优化器时，模型精度有明显提高，在训练迭代 31 次后，获得了最佳值，损失值为 0.25，准确率为 0.896；使用 Adam 的改进型优化器最大自适应矩估计（max adaptive moment estimation，Adamax）优化器，模型收敛速度更快（迭代 28 次），损失值为 0.28，准确率为 0.882。Adamax 相比较 Adam 梯度下降时，更平稳，可以较快获得一个最小值，但是容易陷入鞍部^[17]。本文选择的优化器函数是 Adam，模型训练 31 次，可获得损失值 0.25，准确率 0.896。

4. 实验结果及讨论

本节重点对比讨论本文的心音信号分类算法和其它分类算法，使用本文心音信号采集样本库中大小为 200 个的测试样本集进行对比测试，该测试集中有正样本 100 个，负样本 100 个。二分类算法常采用灵敏度（sensitivity）（符号记为：se）、特异度（specificity）（符号记为：sp）和准确率（accuracy）（符号记为：acc）作为算法评价指标。其中表示正确分类的异常心音信号为真阳性（true positive，TP）（符号记为：TP）；表示错误分类的异常心音信号为假阳性（false positive，FP）（符号记为：FP）；表示正确分类的正常心音信号为真阴性（true negative，TN）（符号记为：TN）；表示错误分类的正常心音信号为假阴性（false negative，FN）（符号记为：FN）。se、sp和acc的计算如式（6）～式（8）所示：

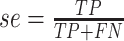6

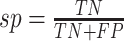7

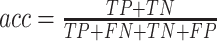8

根据模型预测结果和式（6）～式（8）计算结果显示，se = 0.910，sp = 0.880，acc = 0.895，同其它算法的对比结果如表 1 所示。

表 1. Comparison of different classification algorithms.

各分类算法的比较

各分类算法	心音信号
	acc	se	sp
SVM[4]	0.820	0.880	0.760
MFCC+SVM[6]	0.850	0.860	0.840
MFCC+KNN[18]	0.840	0.820	0.860
MFCC+CNN[7]	0.860	0.811	0.872
MFSC+CNN	0.895	0.910	0.880

表中所列出的几种对比算法，来源于最近两年发表的文章，其测试数据均来源于本文数据库中相同的 200 个心音信号样本。

从表中数据来看，本文提出的算法，在准确率、灵敏度、特异性方面都有竞争优势，准确率同训练时候的验证集准确率也基本相符。然而，文献[4]使用 SVM 作为心音信号分类器，算法准确率 0.820 比本文准确率低，同引言中使用的 SVM 算法实验数据相差较大，说明 SVM 算法对样本的适应性较差，算法的普适性和鲁棒性差，不具备推广应用的条件。文献[6]、[18]其准确率不如本文算法准确率理想，同时使用的这些传统模式识别的分类方法，需要人工干预挑选有效特征，数据预处理工作较为复杂，这在一定程度上制约了其样本集大小，样本集增大将增加样本特征有效性的不确定性。人工挑选特征难以验证其有效性，本文的 CNN 心音信号分类方法，网络自动提取相关特征，并优化网络结构，因此其准确率提升明显。

文献[7]用 CNN 作为分类器，本文方法与之相比准确率有所提升，分析原因有：① 本文预处理算法，采用 MFSC 代替 MFCC，MFSC 相比较 MFCC 光谱能量能保持局部特性，具有高度相关，在频谱上较为平滑，少量的 MFSC 特征即可代表绝大部分信号的信息，MFSC 系数得到的“样本图”更加精简，利于 CNN 识别；② 本文预处理中数据截取的起始位置使得“样本图”更符合网络的需求，且截取的心音信号长度，包含了 5 个心动周期（文献[7]中样本未包含一个完整的心动周期）；③ 本文心音信号采集更为规范，都是 6 个月到 18 岁的先心病患者，有利于 CNN 提取到统一的特征。

本文算法准确率，是在大样本测试下获得的，训练时验证集样本 300 个，单独测试集样本 200 个，准确率均在 0.895。表明实验的准确率并不是偶然的，同时相比较一些传统的小样本算法鲁棒性强，为将来应用于实际起到了助力作用。

5. 结论

本文提出基于 CNN 的心音信号分类算法，首先利用本文预处理算法将带有大量背景噪声的一维心音信号转换成干净的二维的“样本图”，以适合 CNN 分类器的需求。这些特征图作为 CNN 的输入用来优化和训练网络架构，实验发现 5 层 CNN 模型，Adam 优化器具有较高的准确率，训练结果显示，有模型训练准确率为 0.896，损失值为 0.25。该算法在测试集上达到了 se = 0.910，sp = 0.880，acc = 0.895。本文准确率同其他算法有一定竞争力，模型是在大样本条件下优化而得，普适性和鲁棒性有一定的保证。相比传统的算法，预处理方法相对简便，本文算法，可以为以后应用于机器辅助听诊和远程医疗提供一种较好的选择。今后，课题组将致力于算法准确率提升以及实际应用的开展。

利益冲突声明：本文全体作者均声明不存在利益冲突。

Funding Statement

国家自然科学基金资助项目（61261008）；2018云南省重大科技专项资助项目（2018ZF017）