Abstract
精神分裂症和抑郁症患者的临床表现不仅有一定的相似性，而且会随着患者情绪的变化而变化，因此容易导致临床诊断出现误诊。脑电图 (EEG) 分析为准确区分和诊断精神分裂症与抑郁症患者提供了重要的参考和客观依据。为了解决精神分裂症与抑郁症患者之间误诊的问题，提高区分和诊断这两类疾病的准确率，本研究提取了 100 名抑郁症患者和 100 名精神分裂症患者的静息态 EEG 信号特征，包括：① 信息熵、样本熵、近似熵；② 统计学属性；③ 各节律相对功率谱密度（rPSD）。然后，利用这些特征组成特征向量，结合支持向量机（SVM）和朴素贝叶斯（NB）分类器对精神分裂症和抑郁症患者进行分类研究。实验结果表明：① 以各节律的 rPSD 组成的特征向量 P 的分类效果最好，平均准确率可达 84.2 %，最高达 86.3%；② SVM 的分类效果明显优于 NB；③ β 节律的可分性最好，准确率最高，可达 76%；④ 特征权重较大的电极主要集中在额叶和顶叶。本研究结果表明，SVM 结合各节律 rPSD 组成的特征向量 P 组成的分类模型，对精神分裂症和抑郁症患者的区分具有较好的效果，或可对相关的临床诊断起到一定的辅助作用。
Keywords: 脑电图, 抑郁症, 精神分裂症, 特征提取, 支持向量机, 朴素贝叶斯
Abstract
The clinical manifestations of patients with schizophrenia and patients with depression not only have a certain similarity, but also change with the patient's mood, and thus lead to misdiagnosis in clinical diagnosis. Electroencephalogram (EEG) analysis provides an important reference and objective basis for accurate differentiation and diagnosis between patients with schizophrenia and patients with depression. In order to solve the problem of misdiagnosis between patients with schizophrenia and patients with depression, and to improve the accuracy of the classification and diagnosis of these two diseases, in this study we extracted the resting-state EEG features from 100 patients with depression and 100 patients with schizophrenia, including information entropy, sample entropy and approximate entropy, statistical properties feature and relative power spectral density (rPSD) of each EEG rhythm (δ, θ, α, β). Then feature vectors were formed to classify these two types of patients using the support vector machine (SVM) and the naive Bayes (NB) classifier. Experimental results indicate that: ① The rPSD feature vector P performs the best in classification, achieving an average accuracy of 84.2% and a highest accuracy of 86.3%; ② The accuracy of SVM is obviously better than that of NB; ③ For the rPSD of each rhythm, the β rhythm performs the best with the highest accuracy of 76%; ④ Electrodes with large feature weight are mainly concentrated in the frontal lobe and parietal lobe. The results of this study indicate that the rPSD feature vector P in conjunction with SVM can effectively distinguish depression and schizophrenia, and can also play an auxiliary role in the relevant clinical diagnosis.
Keywords: electroencephalogram, depression, schizophrenia, feature extraction, support vector machine, naive Bayes
引言
精神分裂症（schizophrenia，SCZ）和抑郁症（depression，DP）是现今高发且危害较大的精神疾病，及时准确的诊断将有助于此类疾病的治疗。脑电图（electroencephalogram，EEG）记录的是大脑神经细胞的电活动信号。研究表明，SCZ 和 DP 患者的 EEG 信号在节律、波幅和功率等方面均与正常人存在差异，因此对 EEG 信号进行深入研究，有助于精确区分和诊断这两种疾病。
EEG 信号的分析方法主要包括时域、频域、时频域分析和非线性动力学分析等。Begić等[1]通过量化 EEG 信号对 SCZ、DP 患者和正常人进行比较研究，发现 SCZ 患者和 DP 患者 EEG 信号的不同节律在各电极分布的情况存在明显差异。当前，EEG 信号的时频域分析方法已被广泛应用 [2-4]，如 Boashash 等[3]通过综合分析时频域的统计量特征、时频域图像特征和时频域信号特征，对新生儿 EEG 信号癫痫病例进行分类识别，最高准确率达到 86.61%。另一方面，非线性动力学分析方法主要包括信号的样本熵、近似熵、信息熵和 Lempel-Ziv 复杂度等度量分析[2-7]，在分类研究中常与时频域的特征相结合。例如，Sabeti 等[5]将样本熵、近似熵和 Lempel-Ziv 复杂度等组成的特征向量用于 SCZ 患者和正常人的 EEG 信号分类，准确率达到了 91.26%。Li 等[6]用 Lempel-Ziv 复杂度研究 SCZ、DP 患者和正常人的 EEG 数据，发现 SCZ 组患者和 DP 组患者 EEG 信号的 Lempel-Ziv 复杂度有明显的差异，且都高于正常人组。而在分类方法方面，Faust 等[7]利用非线性动力学分析方法提取 DP 患者和正常人的 EEG 信号特征向量进行多种分类器比较研究，发现概率神经网络要优于其他方法。通过以上研究分析发现，目前的研究主要集中在患者和正常人之间的分类与识别，直接针对 SCZ 和 DP 患者的相关分类研究非常少。在 EEG 信号的特征选择和特征提取方面，虽然有多种方法的结合应用，但是这些方法没有充分考虑到不同频段的 EEG 信号对特征选择和特征提取有不同影响。
针对以上问题，本研究在频域上结合非线性动力学分析方法和时域统计学分析的方法，提取不同的特征向量，利用不同的分类器对 SCZ 患者和 DP 患者的 EEG 信号进行分类研究。本研究整体流程如图 1 所示，首先将采集的静息态 EEG 信号进行预处理，并将其转换成频域信号，求得每段信号的功率谱密度（power spectral density，PSD）。然后，提取 PSD 的特征向量，即统计量特征、非线性动力学特征以及不同频段的相对功率谱密度（relative power spectral density，rPSD），并且利用单变量特征选择方法和基于惩罚项的特征选择方法对 PSD 数据进行特征选择和降维，再将得到的特征向量输入到支持向量机（support vector machine，SVM）和朴素贝叶斯（naive Bayes，NB）分类器中进行分类研究。最后，利用查准率、查全率和准确率进行模型评估，比较不同的特征向量结合不同分类器的分类效果，检验不同特征的识别度，为精确区分 SCZ 患者和 DP 患者提供参考。此外，本研究利用以上特征选择方法对特征属性进行打分评估，计算每个电极的特征权重，找到了权重较大的脑区，以期为患者的临床诊断和区分提供相关参考。
图 1.
The overall flow chart
整体流程图
1. 材料和方法
1.1. 数据来源和采集
本研究的数据来自于四川大学华西医院第二门诊部心理卫生中心，本课题组和该中心签署了合作协议和保密协议，得到了数据的使用授权许可，且所有参与数据采集的患者都签署了患者知情同意书。本课题组从符合国际疾病分类（international classification of diseases，ICD）确诊的 SCZ 患者和 DP 患者中，按照 1∶1 匹配筛选出 SCZ 患者和 DP 患者各 100 例，其中：SCZ 患者男女各 50 名，平均年龄为（41.5 ± 4.37）岁；DP 患者男女各 50 名，平均年龄为（41.5 ± 4.35）岁，所有患者的年龄均在 32～51 岁之间，且服从正态分布，两种患者的年龄、性别差异均无统计学意义（P > 0.05）。
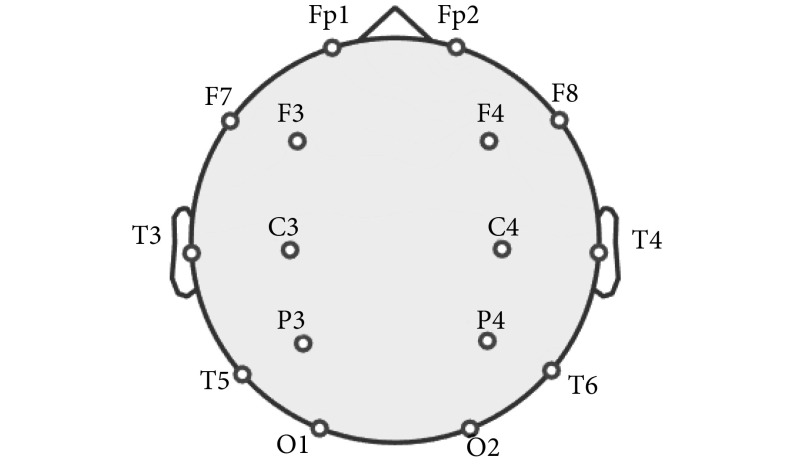
本研究 EEG 信号的采集使用的是动态 EEG 仪（NATION8128W，上海诺诚电气有限公司，中国），采样频率为 128 Hz，信号采集使用的是 16 通道的脑电帽，电极安置的方法遵循国际 10-20 导联标准，电极的分布如图 2 所示。信号采集全程在安静封闭的室内进行，患者需闭眼，并保持安静、清醒、放松的状态。提示患者开始后，记录 EEG 信号。首先，患者先闭眼做深呼吸 3 min，深呼吸结束后睁眼，给予 10 s 左右的缓和时间。然后，闭眼保持 7 s，紧接着睁眼保持 7 s，以此为一个闭、睁眼采集周期，连续采集三个这样的闭、睁眼周期之后结束采集。但在实际采集过程存在操作误差，所以闭、睁眼保持的时间实际是在 5～10 s 之间。
图 2.
Electrodes distribution map
电极分布图
1.2. 数据预处理
本研究的数据参照文献[8]进行预处理，具体的处理步骤包括：① 电极重定位；② 剔除无用电极；③ 滤波处理，带通滤波器的频段为 0.5～45 Hz，陷波为 50 Hz；④ 根据睁、闭眼的标记将数据分段；⑤ 用独立成分分析方法去除伪迹；⑥ 用所有电极的平均电位进行电位重参考。
通过以上预处理后，得到长度在 5～10 s 之间的数据段。再分别计算睁、闭眼状态下每段数据的 PSD。其中睁眼状态下的数据共有 580 段，包含 DP 患者的 292 段、SCZ 患者的 288 段；闭眼状态下的数据共有 585 段，包含 DP 患者的 295 段、SCZ 患者的 290 段。
1.3. 特征向量
1.3.1. PSD 的特征
信息熵（information entropy，InEn）（以符号InEn表示）由 Shannon 提出，是系统不确定性和信息量大小的度量，也是整个系统不确定性的期望。当一个系统越有序，信息熵就越低；越混乱，信息熵就越高。其定义公式如式（1）所示[9-10]：
 |
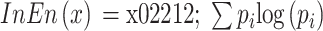1 |
其中，pi 表示事件发生的概率，i 表示样本数量。
本研究中 PSD 的频率为 1～55 Hz，故可以把每个电极的信号看成是一个频率的固定序列，每个频率点对应的 PSD 值为Pi，且
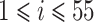，通过归一化后表示为PNi，且
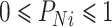。则求 PSD 数据的某一个电极的信息熵公式如式（2）所示：
 |
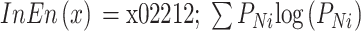2 |
其中，
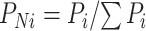，且
。
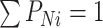近似熵（approximate entropy，ApEn）（以符号ApEn表示）是一种用于量化时间序列变化的非线性动力学非负参数，表示一个时间序列的复杂性，反映了时间序列中新信息发生的可能性，越复杂的时间序列其近似熵就越大[5, 10]，算法步骤表述如下：
（1）对于等时间间隔的N维时间序列
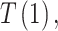
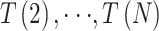，定义相关参数m，r；其中m表示重构向量的长度，r是相似系数，用于重构向量间相似度的度量。
（2）定义
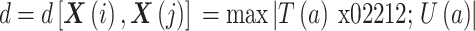表示重构向量之间的距离。其中，
、
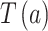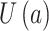表示重构向量
、
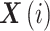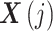对应位置的元素，
、
。
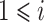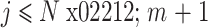（3）对于上述序列，重构 m 维向量
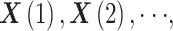
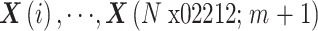，其中
。
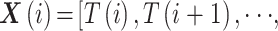
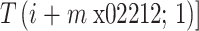（4）计算重构向量
、
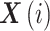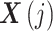间的距离。当
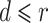时，两重构向量相似。
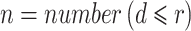表示相似重构向量个数。计算相似的重构向量所占比例为：
。
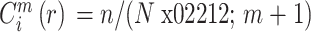（5）定义公式：
。
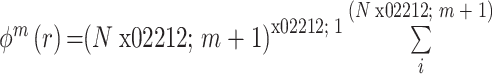
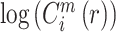（6）最后定义近似熵为：
。
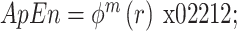
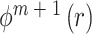样本熵（sample entropy，SaEn）（以符号SaEn表示）也是表征时间序列复杂度的指标[4]。与近似熵比较，样本熵优点在于其算法需要的数据量更小，所用时间少[5]，不同点在于相较于前述近似熵算法中的（2）、（4）步中，样本熵的步骤中多了
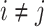的条件，且第（4）步中相似度量的条件是
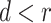。由于步骤（1）～（4）与近似熵一样，故不再赘述，步骤（5）、（6）的具体算法表述如下：
（5）定义公式：
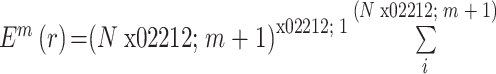
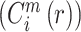，即计算
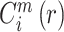的均值。
（6）定义样本熵为：
。
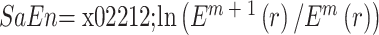本研究把频率序列等效成时间序列，分别计算每个电极的近似熵和样本熵，参数设置为 m = 2，r = 0.2·std。其中，符号std表示序列的标准差（standard deviation）。
统计学变量能反映数据本身的特性，本研究计算了每个电极 PSD 数据Pi的均值m、方差v、偏度s和峰度k来描述该数据。此外，将 PSD 分成 δ（1～3 Hz）、θ（4～7 Hz）、α（8～13 Hz）、β（14～30 Hz）四段节律，分别求每段节律的 rPSD。δ 的 rPSD 计算公式如式（3）所示：
 |
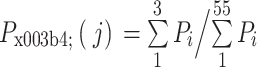3 |
其中，Pi表示 PSD 值，i表示频率点，j表示电极，
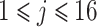，同理可得Pθ（j），Pα（j），Pβ（j）。
1.3.2. 多通道特征提取和融合
本研究先计算每个电极上的数据特征，再将其组成一个特征向量，以此来描述每一段 PSD 数据。具体的方法如下：
（1）将睁、闭眼状态下的每一段 PSD 数据看成一个样本，分别计算每个样本中每一个电极的信息熵、近似熵和样本熵，组成 3 个 16 维的熵向量，
，
，
。
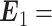
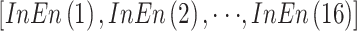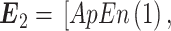
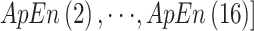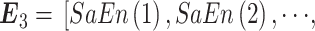
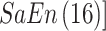（2）将步骤（1）中的 3 个 16 维的向量融合成一个 48 维的熵特征向量
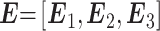。同理，可得到 64 维的统计量特征向量
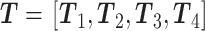，其中
，
，
，
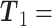
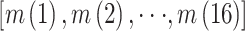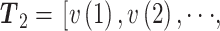
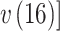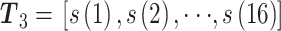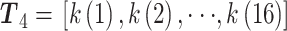。64 维的 rPSD 特征向量
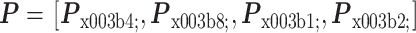，其中
，
，
，
。
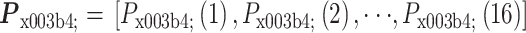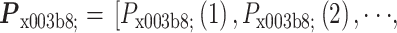
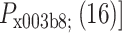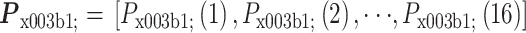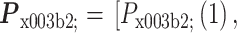
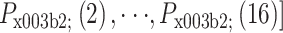通过以上的处理方法，特征向量的维数会成倍增加。因此，本研究除了对特征做标准化处理之外，还利用了单变量特征选择方法和基于惩罚项的特征选择方法进行特征选择[11]。
1.3.3. 特征选择
对于预处理好的数据，为了减少数据的特征数量，防止过拟合现象，使模型泛化能力更强，需要选择最有利于分类的特征进行模型训练和分类识别，通常从特征的发散程度和特征与目标变量的相关性两方面的统计指标去考虑。
单变量特征选择方法是通过计算每一个特征的某个统计指标，以此来评价该特征的重要性。本研究使用了卡方检验（chi-square test，CT）和互信息检验（mutual information test，MT）两个指标对应的算法来做特征选择。CT 用来度量特征与目标变量之间的独立性，MT 则是评价特征与目标变量间的相关性。最终，选择前K个最重要的特征用于分类识别[11]。该特征选择方法的优点是原理简单易懂，利于数据理解，缺点是没有考虑特征之间的独立性和相关性，会丢失特征之间相关的信息。
基于惩罚项的特征选择方法是利用算法本身的打分机制，通过训练得到各个特征的权值系数，再根据权值系数从大到小排列，选择权值系数较高的特征。本研究使用了基于 L1 范数作为惩罚项的线性支持分类机（linear support vector classify，LS）和逻辑回归（logistic regression，LR）两种算法作为对比来进行特征选择。此类方法的特点是特征选择过程和模型训练过程是同时进行的，可以减少训练时间，且引入 L1 范数可以有效地降低过拟合的风险。
本研究也利用以上的特征选择方法，对每个电极的特征权重进行评估，筛选出了特征权重最大的电极及相应的脑区。
1.3.4. 分类器
本研究使用了 NB 和 SVM 两种分类器。NB 算法的核心是贝叶斯公式，即利用贝叶斯公式计算待分样本属于每一个类别的概率，最终将待分样本归为概率最大的那一类别。NB 逻辑简单易于实现，但是其假设样本特征之间相互独立，会降低模型的泛化性能。
SVM 的主要思想是将特征通过核函数映射到一个高维空间，在这个高维空间中寻找一个最优决策超平面，使得该超平面不仅可以将两个样本分开，而且使该超平面距其两侧最近的样本之间的距离最大化，从而使其具有良好的泛化能力。其中距超平面最近的样本被定义为支持向量。实际中会根据数据的特性，选用相应的核函数。
本研究数据集的 80% 用于训练，20% 用于测试。在训练过程中，本研究使用K折交叉验证法（K = 10）无重复抽样地划分训练数据为训练集和验证集，训练集用来训练模型，验证集用来评估模型性能，这样能充分降低模型过拟合现象，提高模型的稳定性和泛化能力。本研究也使用了网格化搜索函数来优化模型[12]。
1.3.5. 分类结果评估
本研究用查准率（precision）（以符号Pr表示）、查全率（recall）（以符号Re表示）、准确率（accuracy）（以符号Acc表示）来评价模型的性能[12-13]。以 DP 患者的度量为例，查准率、查全率、准确率的定义公式如式（4）～（6）所示：
 |
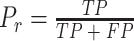4 |
 |
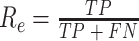5 |
 |
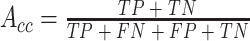6 |
其中，真阳性（true positive，TP）（符号记为：TP）表示本来是 DP 患者被预测为 DP 患者的个数；假阳性（false positive，FP）（符号记为：FP）表示本来是 SCZ 患者被预测为 DP 患者的个数；真阴性（true negative，TN）（符号记为：TN）表示本来是 SCZ 患者被预测为 SCZ 患者的个数；假阴性（false negative，FN）（符号记为：FN）表示本来 DP 患者被预测为 SCZ 患者的个数。为了便于表达，以符号 mPr 表示两种疾病的平均查准率，以符号 mRe 表示两种疾病的平均查全率。
2. 结果
本研究在实验初期将患者的睁、闭眼状态下的 EEG 信号各自组成数据集和联合组成数据集进行二分类。实验结果发现，睁眼状态下的最高准确率是 76%，两种状态联合情况下的最高准确率是 77%，都没有闭眼状态下的分类效果好，且睁眼状态数据集的加入反而降低了闭眼状态数据集的分类效果。所以本研究选择了闭眼状态下的数据进行深入的分类研究。
本研究分别利用闭眼状态 PSD 的三种特征向量
、
、
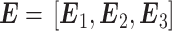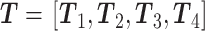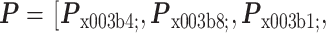
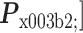作为 SVM 和 NB 分类器的输入，利用单变量特征选择方法和基于惩罚项的特征选择方法进行特征选择和降维。实验结果如表 1 所示，其中效果最好的是 P + LS + SVM 的组合模型，即以 P 作为特征向量，以 LS 算法进行特征选择，以 SVM 作为分类器，此时两种疾病的平均查准率和平均查全率最高，都达到 85%。根据表 1 中的结果主要得到以下结论：
表 1. Classification performance.
分类效果
| 输入特征 | 性能度量 | NB | SVM | |||||||
| CT | MT | LS | LR | CT | MT | LS | LR | |||
| E | mPr | 68% | 70% | 66% | 67% | 64% | 70% | 77% | 76% | |
| mRe | 66% | 70% | 66% | 67% | 64% | 70% | 74% | 76% | ||
| T | mPr | 55% | 35% | 75% | 62% | 65% | 61% | 72% | 73% | |
| mRe | 49% | 44% | 49% | 50% | 64% | 62% | 72% | 73% | ||
| P | mPr | 69% | 73% | 74% | 73% | 69% | 77% | 85% | 81% | |
| mRe | 66% | 72% | 73% | 73% | 68% | 77% | 85% | 80% | ||
（1）SVM 的分类效果优于 NB。
（2）三种特征向量中，rPSD 组成的特征向量P的分类效果最好。
（3）基于惩罚项的特征选择方法处理的特征向量分类效果比单变量特征选择方法的更好。
为了验证表 1中最优组合模型的泛化性能，本研究将 P + LS + SVM 的组合模型结合 K 折交叉验证法进行 10 次实验，记录最低、最高和平均准确率。同时，为了进一步验证 rPSD 的识别度，再以 P + LS + SVM 的组合模型结合留出法[13]进行 10 次实验，记录相应的结果。实验结果如表 2 所示，其中最优组合模型结合K折交叉验证法得到的准确率最高为 84.6%、最低为 81.2%、平均为 83.1%；结合留出法得到的准确率最高为 86.3%、最低为 82.0%、平均为 84.2%。
表 2. Classification results of model P + LS + SVM with K fold and holdout method .
P + LS + SVM 组合模型结合K折交叉验证法和留出法的 分类结果
| 模型评估方法 | 实验次数 | Acc最高值 | Acc最低值 | Acc平均值 |
| 留出法 | 10 | 86.3% | 82.0% | 84.2% |
| K折交叉验证法 | 10 | 84.6% | 81.2% | 83.1% |
如表 3 所示，比较了以各个节律的 rPSD 分别作为特征向量进行分类的结果。其中 β 节律 rPSD 组成的特征向量Pβ 的平均查准率和平均查全率最高，都可达 76%。
表 3. Classification results of EEG signals rPSD of each rhythm.
EEG 信号各个节律 rPSD 的分类效果
| 输入特征 | 性能度量 | NB | SVM | |||||||
| CT | MT | LS | LR | CT | MT | LS | LR | |||
| P δ | mPr | 52% | 52% | 52% | 52% | 61% | 55% | 55% | 57% | |
| mRe | 52% | 52% | 52% | 52% | 62% | 56% | 56% | 57% | ||
| P θ | mPr | 66% | 66% | 66% | 67% | 68% | 67% | 67% | 69% | |
| mRe | 66% | 66% | 66% | 67% | 68% | 68% | 68% | 69% | ||
| P α | mPr | 68% | 68% | 66% | 67% | 66% | 65% | 61% | 64% | |
| mRe | 68% | 68% | 66% | 67% | 66% | 64% | 61% | 64% | ||
| P β | mPr | 76% | 76% | 75% | 73% | 76% | 72% | 74% | 74% | |
| mRe | 76% | 76% | 75% | 73% | 76% | 72% | 74% | 74% | ||
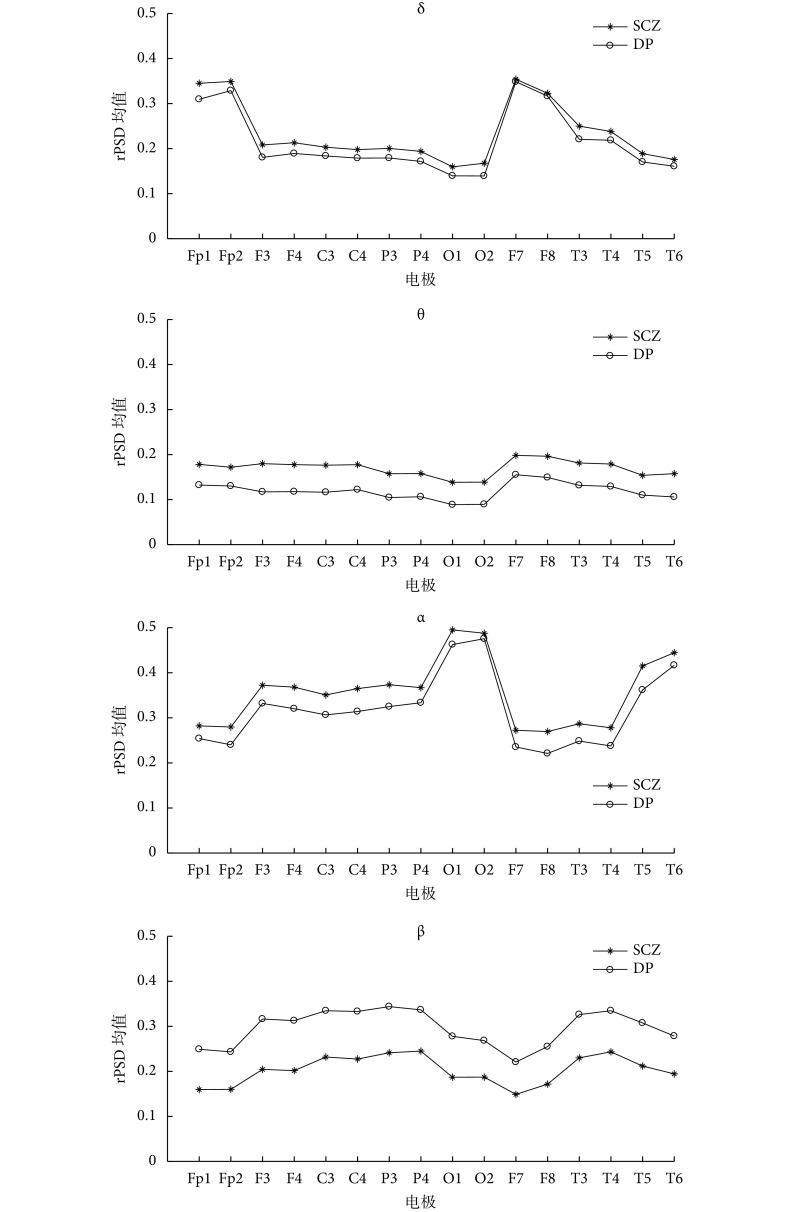
此外，各电极不同节律的 rPSD 的均值对比情况如图 3 所示，可以发现同一节律 rPSD 的均值在各电极上的变化趋势一致。
图 3.
Comparison of the distribution of rPSD mean of each rhythm in each electrode of two diseases
各个节律的 rPSD 均值在两种疾病中各个电极的分布情况对比图
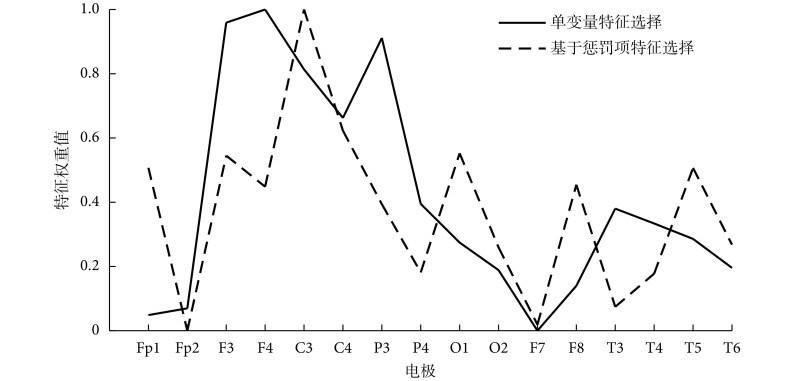
根据前文可知，特征向量P具有更高的识别度。所以，本研究在特征向量P的基础上，分别利用 CT 和 MT 算法给各个电极打分，将 CT 算法对各个电极所打分数归一化处理后以符号Sci表示，将 MT 算法对各个电极所打分数归一化处理后以符号Smi表示，其中i表示电极，再将各个电极Sci、Smi分别求和后归一化处理，得到各个电极的单变量特征选择特征权重；利用 LS 和 LR 算法经过相同的处理，得到各个电极基于惩罚项的特征选择特征权重。最终，各个电极的特征权重结果如图 4 所示。
图 4.
Characteristic weight value of each electrode
各个电极的特征权重值
3. 讨论与分析
本研究主要利用静息态 EEG 信号的不同特征向量，结合 SVM 和 NB 分类器，对 SCZ 患者和 DP 患者进行分类识别。如表 1所示，非线性动力学的相关特征即信息熵、近似熵和样本熵组成的特征向量的分类准确率最高为 76%，而文献[5]以近似熵、信息熵、谱熵和 Lempel-Ziv 复杂度等组成特征向量结合 Adaboost 算法对 SCZ 患者和正常人进行分类，最高准确率为 90%，出现这种差距的原因可能是 SCZ 患者和 DP 患者的 EEG 信号复杂度的差异程度没有 SCZ 患者和正常人之间的高[6]。此外，表 1中P + LS + SVM 的组合模型的分类效果最好，结合表 2 中的验证结果可知，此组合模型具有良好的泛化性能且各节律 rPSD 组成的特征向量P具有良好的识别度。各节律在 SCZ 患者和 DP 患者脑区中的分布情况存在明显的差别[1, 6]，结合表 3 和图 3 的结果可知，本研究中 β 节律的 rPSD 识别度最高，且其 rPSD 均值在 DP 患者中更高，在 SCZ 患者中更低，而其他节律的 rPSD 均值则在 SCZ 患者中更高，在 DP 患者中更低。另外，β 节律的 rPSD 均值在两种疾病间的差值最大，这与其分类准确率最高的结果保持一致。所以类似的研究中 β 节律更值得关注。相较于单独节律，各个节律组合在一起的分类效果明显提高，说明各节律之间存在较强的相关性。统计量特征属性是对数据宏观上的刻画和描述，但在分类研究中样本个性的描述更有利于分类，故表 1 中统计量的特征向量 T 的分类效果最差。
如图 4 所示，各电极的两种特征权重并非完全一致，权重都比较大的电极主要包括 F3、F4、C3、C4 和 P3，集中在额叶和顶叶，且呈现出半球间对称性分布的特点；权重都最小的电极是 Fp1 和 F7，分布在左前额叶；O1、F8、T5 则是其他基于惩罚项特征选择特征权重较大的电极，分布在右前额叶和左枕叶。额叶异常与 SCZ 患者的主要症状相关[14]；顶叶与人体的空间记忆认知能力密切相关；枕叶在听觉和视觉功能处理上起着重要作用，与精神障碍患者的幻觉和错觉等症状密切相关；以上区域的异常变化对诊断此类疾病有着重要的参考意义。
本研究表明 SVM 的分类效果优于 NB，与相关研究有 SVM 分类效果普遍优于其他分类器的结论一致[3, 7]。此外，以 Pβ 为特征向量进行分类时，NB 的分类效果有明显提升，原因可能是 Pβ 数据间的相关性更小，因为 NB 的前提条件是假设属性之间相互独立。
综上所述，本研究发现 rPSD 组成的特征向量具有很好的识别度，最高准确率可达 86.3%，并发现权重大的特征主要集中在额叶、顶叶和左枕叶，该研究结果可为 SCZ 和 DP 的准确区分和诊断提供有力的参考。目前本研究只在频域提取特征，下一步将尝试结合脑网络特征进一步研究精神障碍疾病的分类，为此类疾病的临床诊断提供更加可靠的参考。
利益冲突声明：本文全体作者均声明不存在利益冲突。
Funding Statement
国家重点研发项目（2016YFC0904300）；四川大学华西医院学科卓越发展1·3·5工程项目（ZY2016203，ZY2016103）
Contributor Information
涛 李 (Tao LI), Email: xuntao26@hotmail.com.
军鹏 张 (Junpeng ZHANG), Email: Junpeng.zhang@gmail.com.
References
- 1.Begić D, Popović-Knapić V, Grubišin J, et al Quantitative electroencephalography in schizophrenia and depression. Psychiatr Danub. 2011;23(4):355–362. [PubMed] [Google Scholar]
- 2.Bairy G M, Niranjan U C, Puthankattil S D Automated classification of depression EEG signals using wavelet entropies and energies. J Mech Med Biol. 2016;16(03):1650035. doi: 10.1142/S0219519416500354. [DOI] [Google Scholar]
- 3.Boashash B, Ouelha S Automatic signal abnormality detection using time-frequency features and machine learning: a newborn EEG seizure case study. Knowledge-Based Systems. 2016;106:38–50. doi: 10.1016/j.knosys.2016.05.027. [DOI] [Google Scholar]
- 4.Gajic D, Djurovic Z, Di Gennaro S, et al Classification of EEG signals for detection of epileptic seizures based on wavelets and statistical pattern recognition. Biomedical Engineering: Applications, Basis and Communications. 2014;26(02):1450021. doi: 10.4015/S1016237214500215. [DOI] [Google Scholar]
- 5.Sabeti M, Katebi S, Boostani R Entropy and complexity measures for EEG signal classification of schizophrenic and control participants. Artif Intell Med. 2009;47(3):263–274. doi: 10.1016/j.artmed.2009.03.003. [DOI] [PubMed] [Google Scholar]
- 6.Li Yingjie, Tong Shanbao, Liu Dan, et al Abnormal EEG complexity in patients with schizophrenia and depression. Clin Neurophysiol. 2008;119(6):1232–1241. doi: 10.1016/j.clinph.2008.01.104. [DOI] [PubMed] [Google Scholar]
- 7.Faust O, Alvin A P, Puthankattil S D Depression diagnosis support system based on EEG signal entropies. J Mech Med Biol. 2014;14(3):1450035. doi: 10.1142/S0219519414500353. [DOI] [Google Scholar]
- 8.Purcell S M, Manoach D S, Demanuele C, et al Characterizing sleep spindles in 11,630 individuals from the national sleep research resource. Nat Commun. 2017;8:15930. doi: 10.1038/ncomms15930. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Shannon C E A mathematical theory of communication. Bell System Technical Journal. 1948;27(3):379–423. doi: 10.1002/j.1538-7305.1948.tb01338.x. [DOI] [Google Scholar]
- 10.Inouye T, Shinosaki K, Sakamoto H, et al Quantification of EEG irregularity by use of the entropy of the power spectrum. Electroencephalogr Clin Neurophysiol. 1991;79(3):204–210. doi: 10.1016/0013-4694(91)90138-T. [DOI] [PubMed] [Google Scholar]
- 11.Pedregosa F, Varoquaux G, Gramfort A A, et al Scikit-learn: Machine Learning in Python. Journal of Machine Learning Research. 2011;12(10):2825–2830. [Google Scholar]
- 12.Raschka S Python machine learning. Michigan State: Packt Publishing. 2014:288–330. [Google Scholar]
- 13.周志华. 机器学习: Machine learning. 北京: 清华大学出版社, 2016: 21-35.
- 14.Shad M U, Muddasani S, Keshavan M S Prefrontal subregions and dimensions of insight in first-episode schizophrenia--a pilot study. Psychiatry Res. 2006;146(1):35–42. doi: 10.1016/j.pscychresns.2005.11.001. [DOI] [PubMed] [Google Scholar]