基于突触可塑性的无标度脉冲神经网络的动态特性研究

Abstract

生物神经网络具有小世界属性和无标度属性的双重特性，目前神经网络的研究大多基于小世界网络或聚类系数较低的无标度网络，而真实脑网络为具有小世界属性的无标度网络。为此本文构建了一个聚类系数较高的具有小世界属性的无标度脉冲神经网络，并从突触调节过程、放电特性和复杂网络特性三个方面分析了网络的动态演化过程。实验结果表明，随着时间的进行，突触强度逐渐减小并趋于稳定，导致网络的连接强度减弱并趋于稳定；神经元的放电率逐渐减小并趋于稳定，同步性逐渐变差；网络局部信息传输效率稳定，全局信息传输效率降低并趋于稳定，小世界属性比较稳定。无标度神经网络的动态特性随时间变化且相互影响，突触的调节是基于神经元放电时刻的，突触的调节会影响神经元放电情况和网络的复杂特性。本文构建了具有生物真实性的无标度脉冲神经网络，为人工神经网络的研究及其工程应用奠定了基础。

引言

人工神经网络从信息处理的角度模拟了人脑的结构及其功能，人脑自组织、自适应、自学习的特点在信息、经济、医学、控制等领域有重要应用，对推动人工智能的发展有重要意义。无标度网络的度分布服从幂律分布^[1]，即只有少数节点度较高，大多数节点的度相对较低。大量研究表明脑网络具有高聚类系数和低路径长度的小世界属性，而且度分布服从幂律分布，即脑网络是一种具有小世界属性的无标度网络^[2-3]，因此构建一个具有高聚类系数的无标度神经网络对神经网络的研究尤为重要。突触可塑性是大脑学习和记忆的基础^[4-6]。陈云芝等^[7]基于脉冲时间依赖可塑性（spike timing-dependent plasticity，STDP）机制构建了前馈神经网络，该模型具有较好的抗扰能力，且这种特性与 STDP 机制密切相关。王蕾等^[8]将脉冲神经网络的高效处理能力与自组织映射神经网络相结合，构造了一种基于 STDP 规则的自组织映射（self-organization map，SOM）脉冲神经网络模型。兴奋性突触可塑性根据 STDP 规则动态调控，这些研究大多是基于兴奋性突触可塑性，然而抑制性突触可塑性在神经网络的动态调控中同样具有重要作用^[9]。本研究采用的是兴奋性与抑制性突触共存的更为完备的突触可塑性调节机制。目前，人工神经网络的模型、算法越来越丰富，在工程领域的应用也越来越广泛。Kim 等^[10]通过改变噪声强度来研究小世界神经网络中 STDP 对随机脉冲同步的影响，发现在突触可塑性中存在“Matthew”效应是因为有正反馈，原来同步性较好的通过突触强度的长期增强可以变得更好，而原来同步性较差的则因长期的抑制而变得更差。杨刚等^[11]提出以小世界网络连接模式进行初始稀疏化的连接自组织发育稀疏跨越–侧抑制神经网络设计方法实现网络智力的自组织发育，证明了在同等连接复杂度的情况下，稀疏连接的跨越–侧抑制神经网络具有更好的泛化能力。Baysal 等^[12]基于无标度神经元网络，研究了神经元轴突或胞体与自身树突形成的一种突触对弱信号传递的影响。弭元元等^[13]提出了一个具有无标度拓扑结构的神经网络模型，很好地再现了实验中观察到的长时程周期性同步发放现象，证明神经系统能通过局部网络动力学分布式地处理时序信息。这些研究大多基于小世界网络或者聚类系数较低的无标度网络，而真实的脑网络为聚类系数较高的具有小世界属性的无标度网络。本文基于 Izhikevich 神经元模型与兴奋性突触和抑制性突触共存的突触可塑性模型，构建了聚类系数较高的具有小世界属性的无标度脉冲神经网络，在突触模型与拓扑结构方面能够较全面地呈现脑网络的属性，网络具有生物真实性。

1. 无标度脉冲神经网络的构建

神经网络的三个基本要素是拓扑结构、神经元模型和突触调节机制。网络的拓扑结构决定了神经元之间的连接，神经元模型是神经网络的基本单元，而突触调节机制则是神经元间信息传递的基础。

1.1. 无标度网络的生成及分析

1.1.1. 无标度网络的生成

本文采用高聚类系数的无标度网络模型生成 500 个节点的网络拓扑，模型演化机制如下^[14]：

（1）初始网络：网络初始状态含有 m₀ 个完全连接的节点，边初始权值设置为 w₀ = 1。

（2）加入新节点：按概率 p 在网络中加入一个新的节点 v，其中 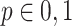。新增节点携带 m 条边，并与网络中已存在的节点按照权重优先选择相连，即一个旧节点 i 被选择的概率为：

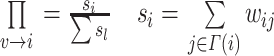1

（3）加入新边：按照概率 1 − p，网络不断增加新的边，仅增加 m_t 条边。新增边的两个端点按照三角机制选取。首先随机选取网络的一个边 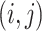，然后选取节点 j 的另外一个邻节点（排除节点 i），设其为 k，选取节点 k 时按照如下概率进行，即按照边的权值大小选取：

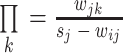2

如果节点 i 和节点 k 之间不存在连接，则建立新边，如果存在连接，则权值增加 σ。两种情况下，边 w_ij 和 w_jk 的权值均增加 σ。其中 σ = 1。

本文中，m₀ = 4，m = 3，m_t = 2。最后将生成的网络转化为无权网络，即有连边的边权值设置为 1，没有连边的边权值设置为 0，得到无标度网络的拓扑结构。

1.1.2. 复杂网络特性分析

网络是由节点和连线组成的，并具有一定的拓扑性质。复杂网络的拓扑性质主要包括节点度、聚类系数、最短路径长度、全局效率、小世界属性等，针对本文的研究，对所构建的无标度拓扑从如下六个方面进行复杂网络特性分析：

（1）节点度

度定义为与节点直接相连的边数，节点的度越大，节点在网络中的地位也就越重要，其数学表达式如下：

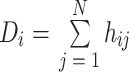3

两个节点之间有连接则 h_ij 为 1，无连接则为 0。平均度为网络中所有节点的度的平均值。

（2）聚类系数

聚类系数表示某一节点 i 的邻节点之间也是邻居的可能性，与节点实际连边数 e_i 和可能出现的最大连边数 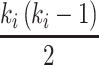有关，其数学表达式如下：

4

用平均聚类系数来表征网络的聚集特性，其数学表达式如下：

5

（3）最短路径长度

最短路径长度 d_ij 为两个节点 i、j 之间边数最少的一条通路经过的边数。平均最短路径长度为网络中任意两个节点之间距离的平均值，其数学表达式如下：

6

（4）全局效率

一般对连通图进行最短路径长度的计算，对于不连通的网络，最短路径长度就会无穷大，因此有人提出了全局效率，其数学表达式如下：

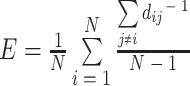7

（5）小世界属性

根据 Humphries 等提出的统一指标 σ 判定，σ > 1 的网络具有小世界属性，且 σ 越大网络的小世界属性越强^[15]，其数学表达式如下：

8

（6）无标度属性

无标度网络的度分布服从幂律分布，幂律指数的大小可以说明无标度中度大小的差异程度，且幂律指数越大，节点度的差异越明显。幂律指数在 1～2 之间的为亚标度，在 2～3 之间的为无标度。

本文设置的节点个数为 500，通过调节加点概率 p，可以得到不同的无标度拓扑。本文将加点概率 p 在[0.1 1]范围进行调节，步长为 0.1，不同拓扑下网络的复杂网络特性如表 1 所示。

表 1. Characteristic parameters of scale-free network.

无标度网络特性参数

概率 p	平均度	平均聚类系数	平均最短路径	全局效率	小世界属性	幂律指数
0.1	18.48	0.702 8	2.283 6	0.465 1	20.04	1.551
0.2	11.45	0.623 6	2.345 0	0.450 2	34.47	1.823
0.3	9.94	0.500 1	2.460 1	0.430 3	29.88	2.154
0.4	8.94	0.470 7	2.492 0	0.424 9	35.04	2.405
0.5	8.24	0.418 0	2.553 5	0.414 3	36.93	2.513
0.6	7.54	0.388 4	2.562 7	0.412 5	39.99	2.759
0.7	6.93	0.313 3	2.662 4	0.396 9	37.18	2.863
0.8	6.61	0.252 4	2.720 5	0.389 0	29.57	2.872
0.9	6.30	0.188 9	2.835 4	0.373 7	21.28	2.975
1.0	5.98	0.164 3	2.854 8	0.371 3	18.04	3.177

从表 1 可以看出，随着 p 的增大，网络的平均度越来越小，平均聚类系数越来越小，平均最短路径越来越大，全局效率越来越低，幂律指数越来越大，网络的小世界属性均远远大于 1，说明本文构建的网络是具有小世界属性的无标度网络。

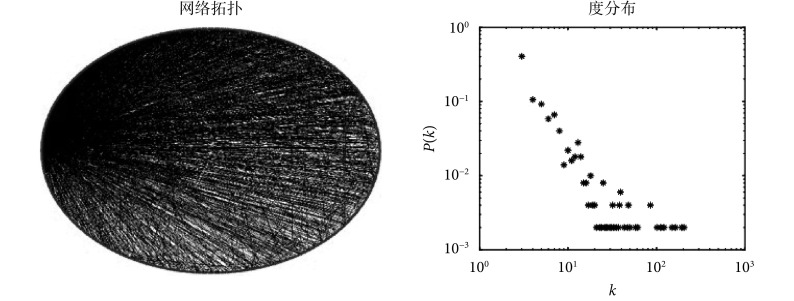
根据文献中对人脑功能特性的研究结果，脑网络无标度属性的幂律指数在 2 左右^[16]，因此本文选取 p = 0.3 的无标度拓扑进行下面的实验研究。p = 0.3 时无标度网络的拓扑和度分布图如图 1 所示，度分布图中横坐标为节点的度值，纵坐标为相应的度值出现的频率。

图 1.

Network topology and degree distribution

网络拓扑以及度分布图

1.2. Izhikevich 神经元模型

神经网络构建的基本单元就是神经元，本文采用比较接近实际神经元放电特性、计算简单且易于进行大规模仿真的 Izhikevich 神经元模型，其数学表达式如下：

9

其中，v 表示神经元膜电位；u 表示膜电压恢复变量，反映生物神经元中钾离子通道电流的激活和钠离子通道电流的失活，同时为膜电压提供一个负反馈；I 表示外部输入电流和经多个突触传导来的突触电流的总和。a、b、c、d 是无量纲参数，通过调节模型中 a、b、c、d 四个参数，可以将神经元调节为兴奋性神经元和抑制性神经元。本文采用典型的规则放电模式（regular spiking，RS）作为神经网络中兴奋性神经元的放电模式，采用低阈值放电模式（low-threshold spiking，LTS）作为抑制性神经元的放电模式，如图 2 所示。其中 RS 模式的参数设置为：a = 0.02，b = 0.2，c = − 65， d = 8；LTS 模式的参数设置为：a = 0.02，b = 0.25，c = − 65， d = 2。

图 2.

The firing patterns of Izhikevich neuron

Izhikevich 神经元放电模式

1.3. 突触可塑性调节机制

突触是神经元之间信息传递的基础，处理和储存信息的能力是中枢神经系统最显著的特性之一。本研究中采用兴奋性突触和抑制性突触共同作用的完备的突触可塑性调节机制。在突触模型中，其突触输出电流与输入电压近似呈线性关系，可表示为：

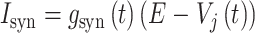10

其中，I_syn 为突触电流；g_syn 为突触电导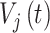； 为突触后神经元的膜电位；E 为反转电位，本文设定兴奋性反转电位 E_ex 为 0 mV，抑制性反转电位 E_in 为 − 70 mV。兴奋性突触和抑制性突触都通过突触电导的变化对神经元之间的信息传递效率进行调节，它们具有不同的调节规律，每种突触都存在以下两种不同的变化情况：

（1）当突触后神经元 j 没有接收到突触前神经元 i 的动作电位时，兴奋性突触和抑制性突触的权重会呈指数衰减，分别如下所示：

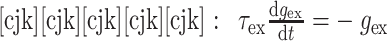11

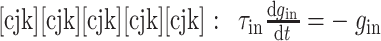12

其中，τ_ex 和 τ_in 分别为兴奋性电导和抑制性电导的衰减常数，本文中设定 τ_ex = τ_in = 5 ms。

（2）当突触后神经元 j 接收到突触前神经元 i 的动作电位时，兴奋性突触的权重 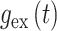和抑制性突触的权重 变化如下：

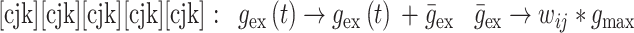13

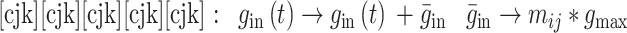14

其中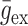， 和 分别为动作电位引起的兴奋性电导增量和抑制性电导增量。兴奋性突触权重增量 由 w_ij 进行调节，抑制性突触权重增量 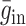由 m_ij 进行调节。本文中 g_max 设为 0.015，当突触权重小于 0 时，则设置为 0，当突触权重大于 g_max 时，规定突触权重为 g_max。w_ij 和 m_ij 与突触前神经元和突触后神经元的脉冲放电有关，其数学表达式如下：

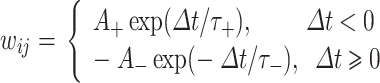15

16

其中，Δt 为突触前后神经元放电时刻间隔；τ₊和 τ₋为突触增强和减弱时突触前后神经元放电时刻间隔范围，本文设定 τ₊ = τ₋ = 20 ms；A₊和 A_-为兴奋时突触电导在增强和减弱时的最大修正值；B₊和 B₋为抑制时突触电导在增强和减弱时的最大修正值。经查阅相关文献，本文设定 A₊ = 0.1,A₋ = 0.105，B₊ = 0.02，B₋ = 0.03。

本文采用具有小世界属性的无标度拓扑结构，以 Izhikevich 神经元模型为节点，基于兴奋性突触和抑制性突触共存的更为完备的突触可塑性机制，构建了 500 个节点的神经网络，其中兴奋性神经元与抑制性神经元的比例遵从神经解剖的实验结果按 4∶1 分布^[17]。

2. 无标度神经网络的动态特性分析

对无标度网络的动态特性分析可以反映网络的动态演化过程。突触可塑性在神经网络中起调节作用，因此本文从突触动态调节入手，并对放电特性和网络复杂特性进行分析来研究网络动态特性。

2.1. 突触动态调节分析

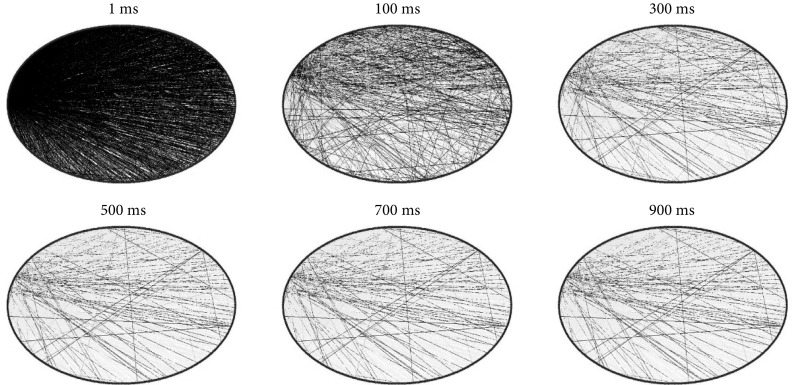
突触在神经网络中起着重要的调节作用，突触强度随着时间不断变化。为了观察网络演化过程中突触强度的变化，采用 pajek 软件对突触权值按权重进行可视化，结果如图 3 所示。灰度越高表示相应的突触权重越大，灰度越低表示相应的突触权重越小。

图 3.

Grayscale image of synaptic weight

突触权重灰度图

从图 3 可以看出，1～100 ms 期间颜色较深的较多，说明此时处于高权重的突触较多，300～500 ms 期间颜色变浅，说明此时突触强度减弱，700～900 ms 期间灰度差异不大，说明此时突触强度变化较小，网络突触调节趋于稳定。结果表明突触在不断地调节，突触耦合强度逐渐减小，700 ms 时突触调节趋于稳定。

为了更准确地说明不同时刻的突触强度变化，本文采用突触权重总和代表突触强度，对不同时刻的突触强度以及各个时刻突触强度相较于初始时刻的相对变化率进行了统计，结果如表 2 所示。

表 2. Synaptic strength at different times.

不同时刻突触强度

时间/ms	1	100	200	300	400	500	600	700	800	900	1 000
突触强度	74.55	30.12	16.47	9.89	6.88	5.06	4.56	4.28	4.08	3.98	3.87
相对变化率（%）	–	59.60	77.91	86.73	90.77	93.21	93.88	94.26	94.53	94.66	94.81

从表 2 中可以看出，随着时间的进行，突触强度逐渐减小。与初始时刻相比较，100～300 ms 期间相对变化率分别为 59.60%、77.91% 和 86.73%，波动非常大，说明此时突触调节剧烈。在 700～1 000 ms 期间，相对变化率分别分布在 94.26%、94.53%、94.66% 和 94.81%，波动非常小，说明网络在到达 700 ms 时基本稳定。

为了直观地展示突触强度的波动情况，本文计算了各个时刻的突触强度相对于前一时刻的相对变化量，即该时刻与前一时刻的突触强度差的绝对值，相对变化量越小，突触调节越稳定，结果如表 3所示。

表 3. Relative changes of synaptic strength.

突触强度相对变化量

时间/ ms	1	100	200	300	400	500	600	700	800	900	1 000
突触强度相对变化量	–	44.43	13.65	6.58	3.01	1.82	0.50	0.28	0.20	0.10	0.11

从表 3中可以看出，100～300 ms 期间相对变化量较大，说明此时突触调节剧烈。400～600 ms 期间相对变化量较小，说明此时突触调节逐渐趋于稳定。700～1 000 ms 期间相对变化量非常小，说明此时突触调节基本稳定。

为了进一步说明突触的调节过程，对突触权重的分布和突触均值随时间变化进行了统计。图 4a 为无标度神经网络突触权值的分布比重，定义权值 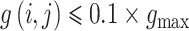的突触为弱耦合突触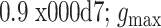， 为强耦合突触，其余为中等耦合突触。从图中可以看出，突触耦合强度处于不断调节的过程中，在 700 ms 左右趋于稳定。在调节过程中，中等耦合突触的比重在 100 ms 内急速下降，之后缓慢下降直至平稳；弱耦合突触的比重随时间慢慢增长直至稳定；强耦合突触在仿真开始剧增，之后缓慢下降直至稳定。稳定后，突触强度集中在弱耦合和强耦合，分布出现两极化。

图 4.

Distribution of synaptic weight

突触权值分布

a. distribution of synaptic weight ratio; b. changes of the mean value of synaptic weights

a.突触权重比重分布；b.突触均值变化

图 4b 为突触权值的均值随时间的变化。从图中可以看出，突触权值的均值随时间增长逐渐减小，在 700 ms 时趋于稳定，且均值比较小。图 4a 也可以解释这种现象，随着时间的进行，弱耦合比重增大，强耦合和中等耦合比重减小，导致权值均值慢慢减小。稳定后弱耦合强度的突触占 90% 左右，所以稳定后的突触权值的均值较小。

2.2. 放电特性分析

放电栅图可以反映神经元放电同步状况。无标度神经网络的放电栅图如图 5 所示，横坐标代表仿真时间，纵坐标代表神经元编号。从图中可以看出，200 ms 内神经元放电时刻比较集中，放电同步性较好。200 ms 以后放电时刻分布比较分散，放电同步性变差。

图 5.

The firing spatiotemporal map of scale-free neural network

无标度神经网络放电栅图

为了观察神经元的放电情况，本文选取高等度、中等度和低等度节点进行放电序列分析，如图 6 所示，实线表示神经元放电时刻的位置。从图 6 可以看出，100 ms 内高等度节点的放电密集程度高于中等度节点，中等度节点的放电密集程度高于低等度节点。随着时间的进行，在突触可塑性的调节下，三种程度神经元的放电间隔均逐渐趋于稳定。

图 6.

Firing sequence diagram of neurons

神经元放电序列图

神经元的放电率反映了神经元在一段时间的放电快慢情况。本文分别计算了高等度节点、低等度节点与中等度节点的平均放电率，来反映不同程度节点的放电情况，结果如图 7 所示。

图 7.

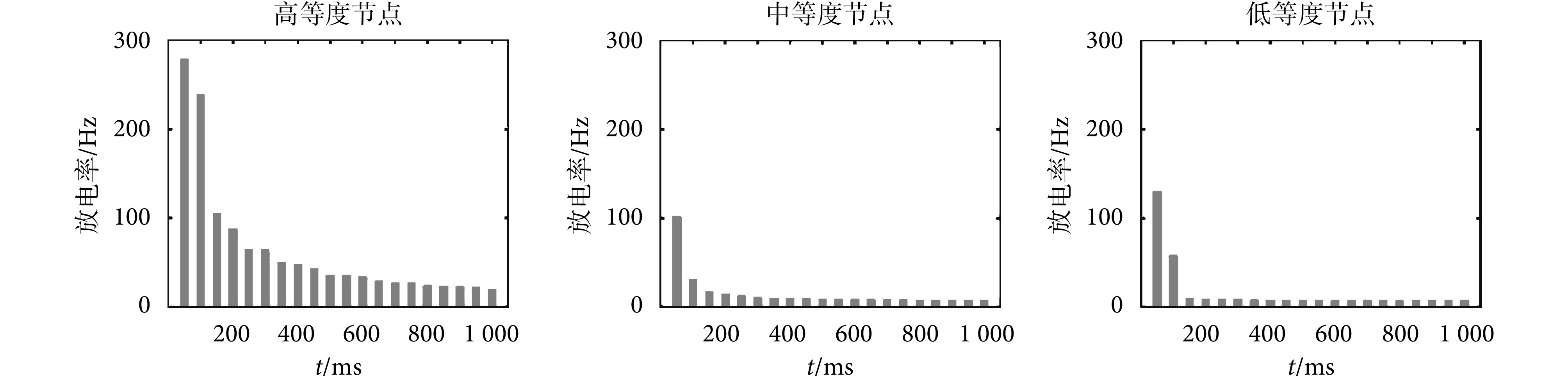
The change of firing rate with time

放电率随时间的变化

从图 7 可以看出，高等度节点的放电率大于中等度节点和低等度的节点，中等度节点与低等度节点的放电率相差不大。随着时间的进行，三种程度的神经元节点放电率均呈现逐渐减小并趋于稳定的趋势。中等度节点和低等度节点的放电率稳定时间较早，高等度节点的放电率稳定时间较晚，在 700 ms 后三种程度节点放电率全部趋于稳定。

2.3. 复杂网络特性分析

对无标度神经网络的复杂网络特性的分析可以反映网络的动态演化过程。本文通过计算网络的平均度、聚类系数、平均最短路径长度、全局效率、小世界属性等复杂网络特性随时间的动态变化来研究网络的动态演化过程。无标度脉冲神经网络的复杂网络特性随仿真时间的变化如图 8 所示。

图 8.

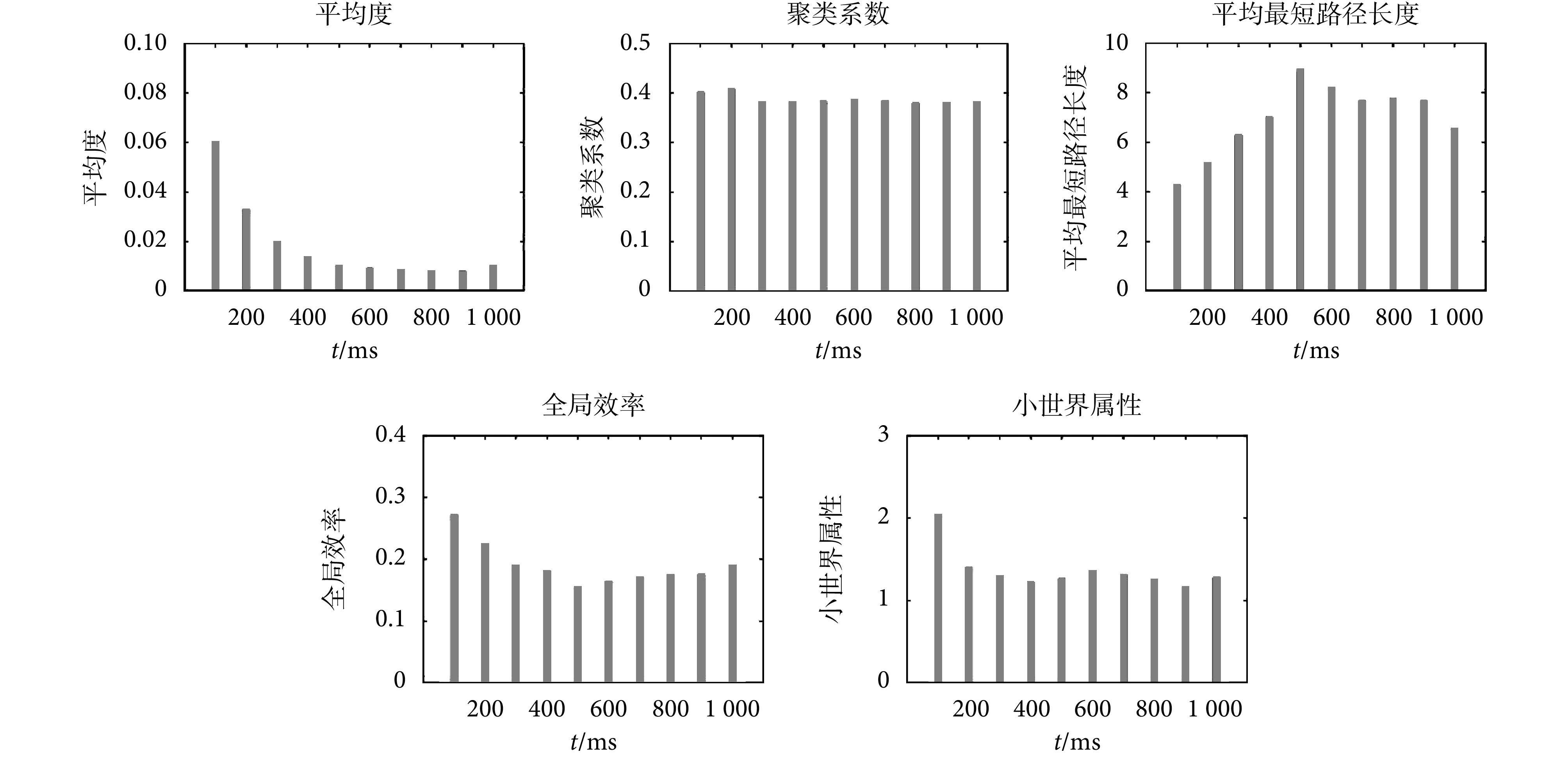
Characteristic analysis of complex network of the scale-free neural network

无标度神经网络的复杂网络特性分析

2.3.1. 平均度

平均度可以反映网络的连接强度，平均度越大，网络的连接强度越强。无标度神经网络的平均度是所有节点之间突触权值的平均值，变化如图 8 所示。随着时间的进行，无标度神经网络的平均度急剧下降，600 ms 后，平均度变化比较小。实验结果表明，在突触可塑性的调节下，无标度神经网络的连接强度逐渐减弱并趋于稳定。图 4 可以解释这种现象，突触权重减小，网络的平均度会减小，网络的连接强度也会减弱。

2.3.2. 聚类系数

聚类系数表征网络的集团化程度和局部信息传输效率，也在一定程度上反映了网络防御随机攻击的能力。聚类系数越大，网络的局部信息传输效率越高。无标度神经网络的聚类系数变化如图 8 所示。从图中可以看出，网络的聚类系数随时间变化较小，前 200 ms 聚类系数较高，随着时间的进行，聚类系数减小，但波动较小。说明随着时间的进行，网络的局部信息传输效率减小并趋于稳定。整体来看，聚类系数分布较稳定，网络局部信息传输效率较稳定。

2.3.3. 平均最短路径长度

最短路径长度表征神经网络的全局信息传输效率，最短路径长度越短，网络的信息传输效率越高，信息或能量在该网络上进行交换所需的代价越小。无标度神经网络的平均最短路径长度变化如图 8 所示。从图中可以看出平均最短路径长度在 100～500 ms 之内呈增长趋势，600～1 000 ms 波动较小，说明随着时间的进行，网络的全局信息传输效率减小并趋于稳定。

2.3.4. 全局效率

全局效率与最短路径长度均可表征网络的全局信息传输效率。全局效率越高，网络的信息传输效率就越高。无标度神经网络的全局效率变化如图 8 所示。从图中可以看出，无标度神经网络的全局效率在 100～500 ms 之间呈下降趋势，600～1 000 ms 之间波动较小，说明随着时间的进行信息传输效率减小并趋于稳定。全局效率与最短路径有关，最短路径越长，全局效率越低，图 8 全局效率与平均最短路径长度的结果均反映了随着时间的进行，全局信息传输效率减小并趋于稳定。

平均度可以反映网络的连接强度，平均度越大，网络的连接强度越强。无标度神经网络的平均度是所有节点之间突触权值的平均值，变化如图 8 所示。随着时间的进行，无标度神经网络的平均度急剧下降，600 ms 后，平均度变化比较小。实验结果表明，在突触可塑性的调节下，无标度神经网络的连接强度逐渐减弱并趋于稳定。图 4 可以解释这种现象，突触权重减小，网络的平均度会减小，网络的连接强度也会减弱。

2.3.5. 小世界属性

小世界神经网络的小世界属性分布如图 8 所示。从图中可以看出无标度神经网络的小世界属性在 100 ms 时较强，在 200～1 000 ms 之间小世界属性有波动但波动较小且小世界属性值均大于 1，说明本文构建的无标度神经网络具有小世界属性。

课题组前期工作已经进行了小世界脉冲神经网络的动态特性研究^[18]，经过比较，发现无标度脉冲神经网络的平均度低于小世界脉冲神经网络，说明无标度脉冲神经网络的连接强度低于小世界脉冲神经网络；无标度脉冲神经网络的聚类系数低于小世界脉冲神经网络，说明网络的局部信息传输效率低于小世界脉冲神经网络；无标度脉冲神经网络的平均最短路径长度低于小世界脉冲神经网络，即全局效率高于小世界脉冲神经网络，说明全局信息传输效率高于小世界脉冲神经网络。综上所述，在局部信息传输方面小世界脉冲神经网络更具优势，而在全局信息传输方面无标度脉冲神经网络更具优势，两者各有一定的适应性。

3. 总结

本文基于 Izhikevich 神经元模型与兴奋性突触和抑制性突触共存的突触可塑性模型，构建了具有高聚类系数的无标度脉冲神经网络，并从放电特性、突触调节过程和复杂网络特性三个方面对网络进行了分析。实验结果表明：① 突触可塑性在实验过程中不断进行调节，强耦合和中等耦合突触比重逐渐下降，弱耦合突触比重上升，导致突触均值逐渐减小，网络耦合强度降低。② 神经元的放电时刻逐渐分散，同步性变差。放电率在突触可塑性的调节下逐渐减小并趋于稳定。③ 在突触可塑性的调节下，网络的连接强度减弱并趋于稳定，网络局部信息传输效率比较稳定，网络的全局信息传输效率降低并趋于稳定，小世界属性较为稳定。无标度神经网络的动态特性随时间变化且相互影响，突触的调节基于神经元的放电时刻，且突触的调节会影响神经元放电和网络的复杂特性。④ 在局部信息传输方面小世界脉冲神经网络更具优势，在全局信息传输方面则无标度脉冲神经网络更具优势。基于已经构建的无标度脉冲神经网络，本研究将进一步开展不同刺激以及损伤下的网络抗扰特性的研究，为提高电子系统在复杂电磁环境下的防护能力奠定理论基础。

利益冲突声明：本文全体作者均声明不存在利益冲突。

Funding Statement

国家自然科学基金（61571180）；河北省自然科学基金（E2016202128）