基于改进锁相位算法的脑区功能同步性研究

Abstract

锁相位算法是分析脑区同步特性的有效方法。基于传统锁相位算法只针对脑电信号的相位分量进行分析，而不能有效地分析脑电信号的其他特征分量的问题，本文提出了一种改进锁相位算法。该算法首先基于经验模态分解获得固有模态函数，以此作为希尔伯特变换的输入求出所需瞬时幅值，计算锁幅值。基于此算法，不仅可以度量脑电信号采集位点之间的变化情况，而且可以度量各个位点自身的脑电信号瞬时振幅的变化情况，从而达到提取脑电信号同步特征的效果。本文采集了 14 名受试者在不同难度认知任务下的脑电信号，并基于改进锁相位算法，分析大脑在完成认知任务过程中各脑区之间的同步性。结果表明，大脑幅值同步程度与认知活动之间呈负相关，且大脑中央区和顶叶最为敏感。基于改进锁相位算法进行的同步性量化，能够真实地反映数据之间的生物信息，为大脑同步性研究提供了一种新的方法，为更好地探索脑区的相关性与同步性提供新思路。

引言

脑电信号具有同步现象^[1-2]，脑区功能同步性分析可以通过分析脑电信号同步特性实现^[3-5]。常用的脑电信号分析方法分为线性和非线性两类，线性方法包括：时域分析（如：自回归模型）、频域分析（如：功率谱法、同步性分析法）、时频分析（如：小波变换）等；非线性分析则涵盖了人工神经网络、熵值以及支持向量机等方法。

锁相位（phase locking value，PLV）算法是一种能够有效分离脑电信号相位成分的分析方法，它能体现信号强度对功能连通性的影响，并挖掘其中隐藏的重要信息^[6-7]。锁相位算法作为相位同步分析工具，不仅可用于分析大脑皮层随心理压力变化引起的同步变化^[8]，而且可以帮助早期筛查癫痫^[9]、帕金森和阿尔茨海默症^[10-11]。Yang 等^[8]利用锁相位方法分析时间相关压力任务对皮层信息处理的影响，结果表明，与无时间压力的任务相比，在限定时间内执行任务状态下，大脑半球的皮层同步性下降。Lachaux 等^[7]基于锁相位算法分析癫痫患者的脑电信号，发现 gamma 频带的相位同步性最高。Hassan 等^[9]采用锁相位算法对癫痫发作时的脑电信号进行特征分析，结果表明，提取的脑电特征参数可以较好地辅助预测癫痫发作。Park 等^[10]基于锁相位算法分析了帕金森症患者的脑电信号同步性，研究结果表明，抑制 beta 波同步的方法可能是一种潜在的治疗帕金森症运动机能障碍的方法。Stam 等^[11]分析了静息状态下阿尔茨海默症患者和正常人的脑电信号的锁相位特征，发现阿尔茨海默氏症患者脑电信号的 alpha 和 beta 波的平均锁相位值较正常人减少。

对于脑电信号而言，信号幅值是一个重要的参数指标。传统锁相位算法只专注于分析信号的相位成分，信号的振幅分量作用常常被忽略。针对这一问题，本文提出了一种改进锁相位算法（optimized phase locking value，OPLV），即锁幅值（amplitude locking value，ALV）同步特征提取算法，算法在分析脑电信号相位成分的同时，更关注于分析脑电信号的幅值分量，进而实现脑电信号的同步性分析。

有研究表明，大脑区域之间神经活动的同步性是大脑皮层和皮层下网络的基本属性，为大脑提供了各种功能的认知过程^[12-13]，因此，在本研究中，受试者是在执行不同难度的认知任务情况下，闭眼放松的状态下完成脑电信号的采集。

本文基于锁幅值同步特征提取算法，分析不同认知任务下的脑电信号特征，实现了不同认知任务下脑电信号同步性分析和脑区定位。这种锁幅值同步特征提取算法为大脑同步性研究提供了一种新方法，并为更好地探索脑区的相关性与同步性提供了新思路。

1. 数据采集

本文试验共招募了 14 名受试者，男女生各 7 名，平均年龄 24.3 岁，右利手，无任何脑损伤疾病史。本文试验中使用的脑电信号采集仪器是 Neuroscan（64 导，美国），按照国际标准 10-20 系统，采集位置为 F7、F8、F3、F4、Fz、T3、T4、C3、C4、Cz、T5、T6、P3、P4、Pz、O1、O2、Oz，信号采样率设为 1 000 Hz。试验设计及过程已通过燕山大学伦理委员会批准，所有受试者均自愿参加本次试验，并签署了知情同意书。

已有研究表明，大脑区域之间神经活动的同步性是大脑皮层和皮层下网络的基本属性，提供了各种功能的认知过程^[12-13]。本试验设计了两种不同复杂程度的认知任务，即两种难度不同的连续减法运算，受试者在闭眼放松的状态下完成这两种任务，采集受试者在此过程中的脑电信号。

试验 1：受试者进行连续减法运算，计算的数值范围从 100 开始默减 7，之后再减 7，直到减至最小正值为止，最后小声报出答案。

试验 2：受试者进行连续减法运算，计算的数值范围从 1 000 开始默减 13，之后再减 13，连续减到 800，得到最小正值为止，最后小声报出答案。

试验完成后，对采集到的原始脑电信号进行去除眼电伪迹等预处理。

2. 特征提取

脑电信号的相位同步性分析是在提取脑电数据相位的基础上再对同步性进行分析，主要有互相关函数、互信息熵、同步指数法、锁相位以及节律波峰值高度等。互相关函数方法是线性的，在表达非线性的脑电信号序列直接的相关关系时存在局限性；互信息熵法和同步指数法更适用于非线性的脑电信号，但与互相关函数方法相比，两种方法的计算量较大；锁相位方法虽然更适合测量脑电信号的同步现象，但它仅考虑了信号的相位信息；节律波峰值高度是以 0.1 Hz 带宽滤波得出某节律频率段的多个窄波信号，每个信号计算多个平均锁相位，最后计算多个平均锁相位中最大值与最小值的差^[14]。上述方法均是针对相位信息进行的同步性分析，而本文则引入了瞬时振幅特征并结合锁定值，基于振幅分量进一步分析脑电信号的同步性。

锁幅值同步特征提取算法流程如图 1 所示。

图 1.

The flow chart of amplitude locking value

锁幅值同步特征提取算法流程图

算法首先对时间序列x（t）进行经验模态分解（empirical mode decomposition，EMD）得到多个固有模态函数（intrinsic mode function，IMF），对固有模态函数进行希尔伯特变换（Hilbert transformation，HT）得到解析信号，解析信号的实部为原信号，虚部为原信号的希尔伯特变换，计算解析信号的瞬时幅值，确定锁幅值。

2.1. 经验模态分解

经验模态分解本质上是对信号的平稳化处理，其结果是将信号中真实存在的不同尺度的波动或趋势逐级分解开来，产生一系列固有模态函数。经验模态分解过程是自适应的，产生固有模态函数的个数与信号的复杂度相关。

对于时间序列x（t），用三次样条曲线分别对极小值点和极大值点进行拟合，得到上包络曲线和下包络曲线。它们的均值为平均包络l（t），计算原始信号与均值之间的差值，得到一个新的函数h（t），如式（1）所示：

1

这一过程称为筛选，在一次筛选得到的结果不是固有模态函数的情况下，需要进行多次筛选，直到筛选的结果符合筛选停止条件为止。停止条件用符号D表示，如式（2）所示：

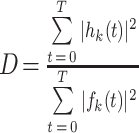2

其中，k为筛选的次数，T表示时间，f_k（t）表示第k次筛选得到的固有模态函数分量。

若f（t）不满足固有模态函数定义，则将f（t）取代x（t）重复上述步骤；否则，f（t）分离出一个固有模态函数，并计算剩余信号r（t），如式（3）所示：

3

重复上述筛选过程，直到r（t）满足筛选停止条件为止。原始信号最终被分解成n个固有模态函数分量和一个残差分量，如式（4）所示：

4

其中，r（t）为残余分量。

2.2. 瞬时幅值

基于希尔伯特变换计算瞬时幅值^[15]。对固有模态函数f（t）进行希尔伯特变换得到F（t），如式（5）所示：

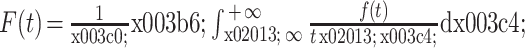5

其中，ζ为柯西主值。

由f（t）和F（t）构成复解析信号Y（t），如式（6）所示：

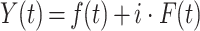6

则瞬时幅值可以如式（7）所示计算得到：

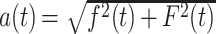7

2.3. 锁幅值

定义锁幅值（以符号ALV表示）的计算方法，如式（8）所示：

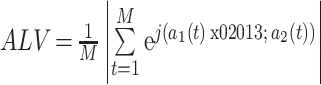8

如式（8）所示，锁幅值的取值范围为［0，1］，并且仅对幅值的瞬时值敏感。锁幅值反应了两个信号振幅的波动情况，若两个信号瞬时振幅差值小，即振幅变化小甚至没有区别，那么锁幅值接近于 1，若两个信号瞬时振幅差值大，即幅值波动大，那么锁幅值趋近于 0。

3. 结果及分析

3.1. 锁相位与锁幅值同步特征提取算法

首先，仿真比较锁相位与锁幅值同步特征提取算法效果。设原始信号分别为复合函数x（t）和正弦函数y（t），如式（9）～（10）所示：

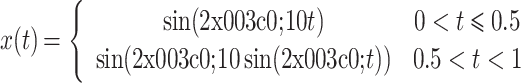9

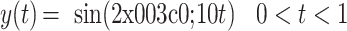10

设滑动窗长为 1，步长为 1。

如图 2 所示，与传统锁相位算法相比，锁幅值同步特征提取算法更能够充分反映两个信号的波动情况。

图 2.

Comparison of phase locking value and amplitude locking value

锁相位与锁幅值同步特征提取算法比较

3.2. 不同难度认知任务

已有研究表明，认知难易程度与认知反应响应时间呈正相关^[16]，难度水平越高、反应响应时间越长。本文以受试者的平均反应时间作为判断任务难易程度的依据，分析试验 1 和试验 2 的难度。试验 1 中，受试者完成一次递减计算的平均时间为 3 s，而在试验 2 中，完成一次任务需要的平均时间为 5 s。进一步，分析这两种不同难度任务情况的受试者脑电信号。

3.3. 锁幅值同步性分析

脑电信号主要组成为四种基本节律：alpha 波（8～12 Hz）、beta 波（12～30 Hz）、delta 波（0.1～3 Hz）、theta 波（4～7 Hz）。其中 alpha 波是正常成年人处于清醒放松状态呈现的脑电节律，特别是在安静闭目状态下，alpha 波更占优势，因此，本文针对 alpha 波分析。

基于锁幅值同步特征提取算法分析结果：

（1） 信号经经验模态分解得到多个固有模态函数分量，如图 3 所示。

图 3.

Intrinsic mode function component diagram

固有模态函数分量图

（2） 根据信号的频谱选取敏感固有模态函数分量，如图 4 所示，针对该敏感固有模态函数分量进行希尔伯特变换得到瞬时幅值。

图 4.

Intrinsic mode function component spectrum

固有模态函数分量频谱图

针对敏感固有模态函数分量的选取问题：通过计算 8～13 Hz 频段能量的分布情况，选出该频带能量所在的固有模态函数分量。

计算各阶固有模态函数中的 8～13 Hz 频带能量，如式（11）所示：

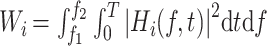11

其中，f₁、f₂ 为上下限频率，分别取值为 8 Hz 和 13 Hz，i = 1，2，3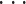， ，k，k为固有模态函数的个数。

分别计算每一个固有模态函数中的 8～13 Hz 频带能量占所有频带的比例，如式（12）所示：

12

经计算，本文依据 alpha 波所在的固有模态函数阶分量作为希尔伯特变换的输入信号。

（3） 计算锁幅值。

本文研究通道来自于均匀分布在 6 个头皮脑区的 14 个电极，如表 1 所示，包括额叶、左侧颞叶、右侧颞叶、中央区、顶叶和枕叶。

表 1. Relationship between channel number and brain area.

通道号与脑区对应关系

通道	F3	F4	F7	F8	T3	T4	T5	T6	C3	C4	P3	P4	O1	O2
脑区	左额	右额	左前颞	右前颞	左中颞	右中颞	左后颞	右后颞	左中央	右中央	左顶	右顶	左枕	右枕

随机选取某位受试者，在某次试验中的脑电同步性分析结果，锁幅值同步特征提取算法与锁相位算法结果对比，如图 5 所示。

图 5.

The synchronization of EEG information under different tasks

不同难度任务下的脑电信息同步性特征

如图 5 所示，基于改进锁相位的锁幅值同步特征提取算法分析中，试验 1 与试验 2 的锁幅值的特征点差异更明显。进一步，采用统计产品与服务解决方案软件 SPSS 17.0（SPSS Inc.，美国），对 14 名受试者，两种试验状况下的锁相位特征和锁幅值特征进行t检验，其中，不同难度下的锁幅值特征差异具有统计学意义（P < 0.05），而锁相位特征之间的差异不具有统计学意义。

为了减小个体差异的影响，随机选择 6 名受试者，进一步分析两种不同复杂程度任务时的左、右脑的锁幅值特征，如表 2、表 3 所示。

表 2. The amplitude locking value of left brain.

左脑锁幅值

		F7-Fz	F3-Fz	T3-Cz	C3-Cz	T5-Pz	P3-Pz	O1-Oz
受试者 1	试验 1	0.188	0.419	0.256	0.230	0.230	0.249	0.309
	试验 2	0.263	0.394	0.183	0.121	0.306	0.184	0.310
受试者 2	试验 1	0.163	0.388	0.248	0.281	0.246	0.252	0.389
	试验 2	0.183	0.325	0.201	0.202	0.367	0.162	0.398
受试者 3	试验 1	0.178	0.397	0.265	0.269	0.212	0.231	0.331
	试验 2	0.222	0.298	0.198	0.108	0.313	0.177	0.413
受试者 4	试验 1	0.152	0.430	0.280	0.301	0.206	0.284	0.319
	试验 2	0.194	0.387	0.175	0.199	0.330	0.192	0.397
受试者 5	试验 1	0.201	0.459	0.289	0.238	0.307	0.287	0.296
	试验 2	0.245	0.342	0.172	0.154	0.369	0.149	0.337
受试者 6	试验 1	0.159	0.398	0.285	0.250	0.278	0.226	0.327
	试验 2	0.201	0.365	0.203	0.187	0.337	0.161	0.376

表 3. The amplitude locking value of right brain.

右脑锁幅值

		F8-Fz	F4-Fz	T4-Cz	C4-Cz	T6-Pz	P4-Pz	O2-Oz
受试者 1	试验 1	0.065	0.191	0.210	0.468	0.280	0.360	0.432
	试验 2	0.248	0.391	0.199	0.257	0.249	0.226	0.382
受试者 2	试验 1	0.146	0.203	0.240	0.509	0.298	0.376	0.447
	试验 2	0.283	0.403	0.202	0.392	0.234	0.254	0.392
受试者 3	试验 1	0.092	0.189	0.260	0.493	0.305	0.339	0.459
	试验 2	0.198	0.372	0.207	0.372	0.262	0.217	0.362
受试者 4	试验 1	0.102	0.178	0.289	0.460	0.290	0.387	0.491
	试验 2	0.259	0.376	0.217	0.242	0.212	0.291	0.352
受试者 5	试验 1	0.081	0.210	0.310	0.496	0.265	0.402	0.433
	试验 2	0.222	0.389	0.287	0.308	0.213	0.298	0.379
受试者 6	试验 1	0.098	0.234	0.271	0.460	0.287	0.319	0.457
	试验 2	0.239	0.431	0.240	0.290	0.220	0.238	0.370

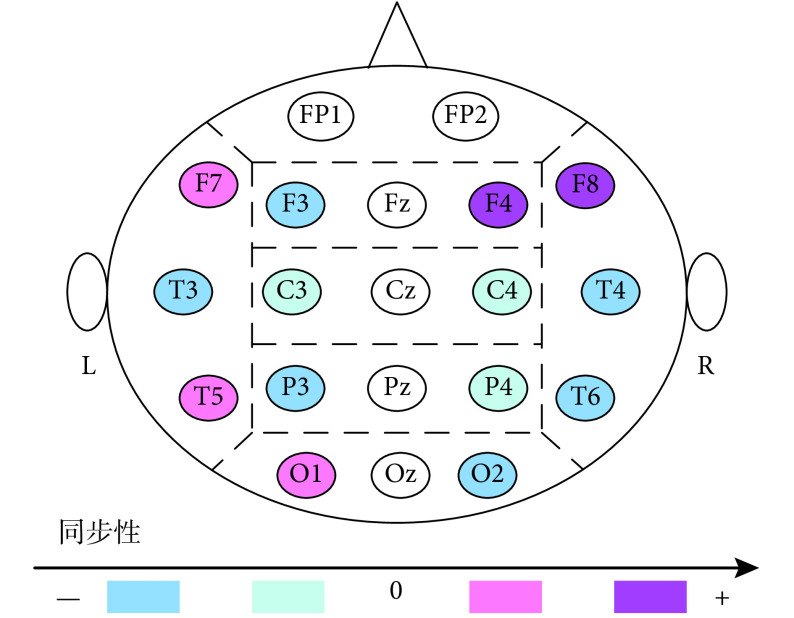
如表 2 所示，当心算难度增加时，位于大脑中央区的通道组 C3 与 Cz 之间的锁幅值特征，C4 与 Cz 之间的锁幅值特征均呈现下降趋势，即两个电极间的变化存在一致性；顶叶的通道组 P3 与 Pz 之间的锁幅值特征，P4 与 Pz 之间的锁幅值特征均呈现下降趋势，说明顶叶的两个电极具有一致的变化趋势。结果表明，中央区和顶叶的幅值同步程度，随着心算过程中难度的增大而减小，其幅值同步程度与心算任务难度具有反向变化的趋势。而额叶的 F3 与 Fz 之间的锁幅值特征降低，F4 与 Fz 之间的锁幅值特征增高，右侧电极的锁幅值升高，表明两对电极的变化趋势不一致。同样的，颞叶的通道组 F7 与 Fz、F8 与 Fz、T3 与 Cz、T4 与 Cz、T5 与 Pz、T6 与 Pz，枕叶的 O1 与 Oz、O2 与 Oz，同时存在上升和下降两种变化，表现杂乱并不一致。图 6 描述了随着认知任务难度的增加，锁幅值的差异变化情况。

图 6.

Brain synchronization under cognitive task with increa sing difficulty

认知任务难度增加下的同步性情况

3.4. 锁幅值敏感脑区分析

如图 6 所示，以零点为基准，负半轴表示同步性降低，正半轴表示同步性增加。以蓝色说明幅值同步性减少，以粉色说明幅值同步性增加。其中，颜色的深浅反映了锁幅值变化的差异程度，随着颜色深度的增加，同步性逐渐增大。深蓝色意味着锁幅值降低的变化率大，浅蓝色意味着变化的差值小；深粉色体现了锁幅值较大差异的变化，浅粉色体现了较小的差异变化。两种难度心算下的锁幅值差值，存在正负两种情况。位于大脑中央区和顶叶的通道组 C3 与 Cz、C4 与 Cz、P3 与 Pz、P4 与 Pz 之间的锁幅值差值始终处于负值，说明其幅值同步程度与心算任务难度呈反向变化的趋势。

已有研究表明，枕叶对应视觉皮层，颞叶对应听觉皮层，额叶对应情感皮层，中央区及顶叶对应认知皮层。在执行认知任务时，大脑的主要连通区域集中在中央区和顶叶。Dimitriadis 等^[16]设计累加心算任务，从低至高分为 5 个难度等级，可以观察到锁相位逐渐降低。魏金河等^[17]发现心算时相干幅值下降。宋利清等^[18]设计 3 种不同复杂度的心算任务，发现信息流增益均在中央—顶叶较活跃，认为该脑区为心算过程中的连接区域。李颖洁等^[19]研究发现，心算时脑电信号的互信息传输矩阵的复杂度数值呈现出高复杂区域转移至中央区和顶叶。

本文在传统锁相位的基础上，提出了一种改进锁相位的脑区同步性分析研究方法——锁幅值同步特征提取算法，结果表明，由中央区至顶叶，锁幅值同步特征提取算法的特征量——锁幅值特征与心算难度呈反向变化的趋势，额叶、颞叶和枕叶呈现出不确定性。两种心算任务下，通道组 C3 与 Cz、C4 与 Cz、P3 与 Pz、P4 与 Pz 之间的锁相位差值较大，说明中央区和顶叶最为敏感。

4. 结论

本文提出一种改进锁相位同步特性分析方法，对两组难度不同的心算任务下脑电信号进行了分析。试验结果表明，锁幅值同步特征提取算法能够充分挖掘脑电信号同步特性，为大脑同步性分析提供帮助。

（1）不同大脑区域对认知活动的敏感程度不同，中央区和顶叶最为敏感。

（2）中央区至顶叶，锁幅值同步特征提取算法的特征量——锁幅值特征与心算难度呈反向变化的趋势，额叶、颞叶和枕叶呈现不确定性。

锁幅值同步特征提取算法，不仅可以度量各个脑电信号采集位点之间的变化情况，而且可以度量各个位点自身的脑电信号瞬时振幅的变化情况，是一种分析脑区功能相关性的有效方法。

Funding Statement

中国博士后科学基金资助项目（2014M550582）；河北省自然科学基金资助项目（F2014203244）