Abstract
医学核磁共振图像重构技术是核磁共振成像领域的关键技术之一。压缩感知理论指出利用核磁共振图像的稀疏性能够从高度欠采样的观测值中精确重构图像。如何利用图像的稀疏性先验以及更多的先验知识来提高重构质量成为核磁共振成像的一个关键问题。本文根据综合稀疏模型和稀疏变换模型的相互补充作用，利用核磁共振图像在这两种模型下的稀疏性先验，将结合了综合稀疏模型与稀疏变换模型的双稀疏模型应用于压缩感知核磁共振图像的重构系统，提出了一种融合双字典学习的自适应图像重构模型。本文充分利用了图像在自适应综合字典学习和自适应变换字典学习下的两种稀疏先验知识，使用交替迭代最小化法对提出的模型进行分阶段求解，求解过程中引入了综合 K-奇异值分解（K-SVD）算法和变换 K-SVD 算法。通过实验验证，与目前较好的核磁共振图像重构模型对比，本文提出模型的图像重构效果更好、收敛速度更快，且具有更好的鲁棒性。
Keywords: 核磁共振图像, 压缩感知, 综合稀疏模型, 稀疏变换模型, 图像重构
Abstract
The medical magnetic resonance (MR) image reconstruction is one of the key technologies in the field of magnetic resonance imaging (MRI). The compressed sensing (CS) theory indicates that the image can be reconstructed accurately from highly undersampled measurements by using the sparsity of the MR image. However, how to improve the image reconstruction quality by employing more sparse priors of the image becomes a crucial issue for MRI. In this paper, an adaptive image reconstruction model fusing the double dictionary learning is proposed by exploiting sparse priors of the MR image in the image domain and transform domain. The double sparse model which combines synthesis sparse model with sparse transform model is applied to the CS MR image reconstruction according to the complementarity of synthesis sparse and sparse transform model. Making full use of the two sparse priors of the image under the synthesis dictionary and transform dictionary learning, the proposed model is tackled in stages by the iterative alternating minimization algorithm. The solution procedure needs to utilize the synthesis and transform K-singular value decomposition (K-SVD) algorithms. Compared with the existing MRI models, the experimental results show that the proposed model can more efficiently improve the quality of the image reconstruction, and has faster convergence speed and better robustness to noise.
Keywords: magnetic resonance image, compressed sensing, synthesis sparse model, sparse transform model, image reconstruction
引言
医学核磁共振（magnetic resonance，MR）图像是采用核磁共振成像（magnetic resonance imaging，MRI）技术利用人体中氢原子核的能态变化，产生不同电磁波信号，经处理而得到人体组织的立体图像[1]。医学 MR 图像重构技术是指利用某种方法更新 MR 图像傅里叶频域空间（K-空间）数据，再将数据表示的频域信号进行傅里叶逆变换，从而得到以空间位置表示的 MR 图像[1]。随着医学图像处理技术的迅速发展，MR 图像重构技术已经被广泛应用于医学临床检测，成为医疗诊断的重要手段。在实际医疗应用中，若要得到高质量 MR 图像，传统方法是按照香农-奈奎斯特采样方式进行数据采样。然而，传统方法获得 MR 图像需要大量的采样数据，导致对 MR 图像的数据采样设备和存储设备提出了很高的要求。如何在采样数据尽量少、采样时间尽量短的前提下，实现 MR 图像的精确重构是亟待解决的问题。MR 图像的精确重构不仅用于辅助医生诊断疾病，也是 MR 图像分析和可视化的基础。
2006 年，由 Donoho[2]和 Candes 等[3]提出的压缩感知（compressed sensing，CS）理论指出，若信号可压缩或在某个变换域稀疏，可用一个与变换基不相关的观测矩阵将高维信号影射到低维空间，再通过求解一个优化问题就可从少量的投影中以高概率重构出原信号。CS 理论已经被广泛应用于多种生物医学成像系统和物理成像系统[4-8]，如计算机断层成像、超声医学成像和单像素相机成像等。目前，CS 已经应用到核磁共振快速成像中[9-10]，基于 CS 的 MR 图像重构（compressed sensing magnetic resonance imaging，CS-MRI）可通过少量的采样数据重构出高质量的 MR 图像，明显缩短了对患者的磁共振扫描时间，加快了 MRI 处理过程，提高了工作效率。CS 对 MR 图像的压缩和采样是同时进行的，在一定程度上突破了 MRI 扫描速度慢的瓶颈。于是，如何利用稀疏正则约束，从 K-空间高度欠采样的数据中压缩感知重构 MR 图像引起了学者们的极大兴趣。2007 年，Lustig 等[11]首次将 CS 应用到 MRI 中，将欠采样 MR 图像重构问题表示为 l0 范数最小化问题，通过贪婪算法求解。然而，l0 范数最小化问题是一个 NP-hard 问题。因此，Lusting 将求解 l0 范数松弛为求解 l1 范数问题，采用共轭梯度法求解。为了提高图像重构速度和精度，文献[11]中提出将全变差应用于 CS-MRI 重构模型，采用两个正则条件作为约束，加强了 MR 图像的稀疏性以保证高质量的图像重构。然而，以上算法的稀疏先验是针对整幅图像，且字典或变换是事先设计好的，对 MR 图像的自适应能力较差，导致在图像采样率较低的情况下，图像重构效果较差。为了增强算法的自适应性，随着 CS 理论的发展和字典学习算法的提出，字典学习算法被应用于 CS-MRI 中，提出了多种基于自适应字典学习的 MR 图像重构算法。2011 年，Ravishankar 等[12]提出的基于综合 K-奇异值分解（K-singular value decomposition，K-SVD）算法的自适应综合字典学习 MRI（dictionary learning MRI，DLMRI）重构模型，是经典的 CS 与综合字典学习相结合的 MR 图像重构模型，实现了较好的图像重构效果。然而，DLMRI 的综合稀疏编码阶段消耗时间较长。2013 年，Ravishankar 等[13]将 MR 图像进行自适应稀疏变换，提出了自适应稀疏变换与 MR 图像重构同时进行的图像重构模型（transform learning MRI，TLMRI），实现了较好的图像重构效果，同时改进了图像重构耗时较长的问题。2015 年，在 TLMRI 重构模型的基础上，Ravishankar 等[14]将盲压缩感知应用到 MR 图像重构，实现了较好的 MR 图像重构效果。
本文主要围绕自适应 MR 图像重构模型展开研究。为了进一步改善 MR 图像重构质量，加强重构模型的收敛性和鲁棒性，本文利用基于变换 K-SVD（transform K-SVD，TK-SVD）算法的稀疏变换模型，将自适应综合字典学习的综合稀疏模型与基于 TK-SVD 算法的稀疏变换模型相融合应用于 MR 图像重构。利用 MR 图像在自适应综合字典学习和自适应变换字典学习下的稀疏表示，提出一种基于自适应字典学习的双稀疏 CS-MRI 重构模型（double sparse transform K-SVD CS-MRI model，DTKMRI）。为了体现 DTKMRI 模型的有效性与优越性，本文将 DLMRI 和 TLMRI 图像重构模型作为对比模型，将其 MR 图像重构实验结果与 DTKMRI 模型进行比较。本文提出的 DTKMRI 模型是利用交替迭代最小化法[12]有效地进行求解，求解过程中引入了 TK-SVD 算法。同时，为了减少计算量，本文将图像分块思想[15-16]应用到 DTKMRI 模型。
1. 基于双稀疏模型的压缩感知 MR 图像重构
1.1. 基于综合稀疏模型的 MR 图像重构
若已知
 |
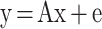1 |
式中，
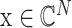为 MR 图像向量；
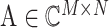为观测矩阵；
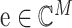为加性高斯白噪声；
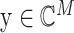为含噪声的测量值。多数情况下
，因此要从含噪声测量值
中重构出原图像 x 是一个病态问题。通常，从病态问题的多解中找到最近似 x 的解需要利用稀疏表示这一先验知识。稀疏表示是图像处理领域广泛应用的信号模型，而综合稀疏模型是较为成熟的稀疏表示模型。综合稀疏模型中，对于图像 x，可近似为综合字典
中少量原子的线性组合，即
 |
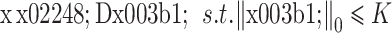2 |
式中，
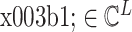为 x 在
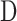下的综合稀疏系数，若
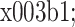仅有
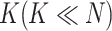个非零值，称
的稀疏度为 K。
基于综合稀疏模型的 MR 图像重构[12]可表示为
 |
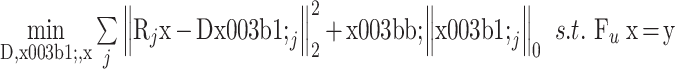3 |
式中，
表示从 x 中取第 j 个局部块 Rjx 的操作算子；αj 是图像块 Rjx 在 D 下的综合稀疏系数，α 由 αj 构成；
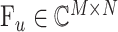为部分采样傅里叶变换矩阵；y 是在
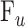矩阵下的 K-空间观测值；λ 为正则化参数；
和
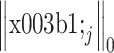项为第 j 个图像块利用综合字典进行稀疏表示，其中
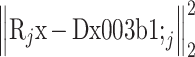项表示综合字典对 Rjx 的稀疏逼近程度。式（3）的求解过程中利用了综合 K-SVD 算法[12]，其中涉及到求解 l0 范数非凸优化问题。通常，l0 范数问题求解方法包括正交匹配追踪（orthogonal matching pursuit，OMP）和子空间追踪等。
1.2. 基于 TK-SVD 算法的稀疏变换模型
随着解析稀疏模型的发展，出现了一些对图像进行解析稀疏表示的解析字典学习算法[17-21]，其中典型的是解析 K-SVD 算法。最近，稀疏变换模型受到一些学者的青睐，该模型与解析稀疏模型结构相似，然而稀疏变换模型是在稀疏变换域中求解代价函数[22]。稀疏变换模型可表示为
 |
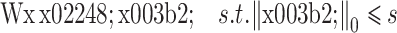4 |
式中，
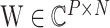为稀疏变换字典；
为 x 在 W 下的稀疏变换系数，若 β 中仅有
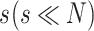个非零值，称 β 的稀疏度为 s。
Eksioglu 等[23]提出了将自适应变换字典学习与解析 K-SVD 算法结合的 TK-SVD 算法，该算法在噪声较大时图像处理效果较好，并能降低算法复杂度。TK-SVD 算法的优化问题为
 |
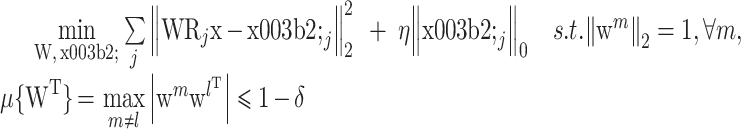5 |
式中，
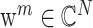（m = 1，2，
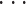，P）是 W 的第 m 行；βj 是第 j 个 Rjx 的稀疏变换系数，β 由 βj 构成；
表示 W 各行互相关，其中上标 T 表示矩阵转置操作；δ 为常数；η 为正则化参数；范数约束
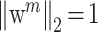和互相关约束
避免了 W 的平凡解；
项为第 j 个图像块的稀疏误差。式（5）的求解过程包括两个阶段：第一阶段为稀疏变换编码，固定 W，求解 β，其优化问题为
 |
6 |
式（6）可用迭代硬阈值法求解。第二阶段为更新 W，固定 β，求解 W 的最小化问题为
 |
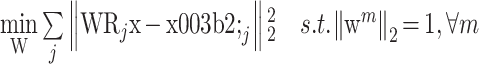7 |
式中，忽略了约束条件
[23]。W 的求解可通过更新 W 的第 m（m = 1，2，
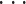，P）行 wm 来实现[23]，将求解式（7）近似等效为在 m = 1，2，
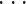，P 时依次求解下式：
 |
8 |
式中，Rjxm 是 Rjx 选择部分行的子向量，且 Rjx 中行的选择符合 βj 中 0 的位置。式（8）的优化解由 Rjxm 的奇异值分解获得。由于 TK-SVD 算法中求解 β 的过程得以简化，使 W 的更新速度更快，所以 TK-SVD 算法兼有稀疏变换学习与解析 K-SVD 算法的优势[23]。
1.3. 基于双稀疏模型的 MR 图像重构
利用更多的稀疏先验约束来提高图像的重构质量是本文对 CS-MRI 重构模型研究的重点。综合稀疏模型是 CS 领域典型的图像稀疏表示模型，而稀疏变换模型是在稀疏变换域表示图像的模型，对于图像重构而言这两种模型具有一定的相互补充作用。为进一步提高 MR 图像重构质量，本文根据综合稀疏模型和稀疏变换模型的相互补充作用，利用 MR 图像在自适应综合字典与自适应变换字典下的两种稀疏先验知识，将基于综合稀疏模型与稀疏变换模型的双稀疏模型应用于 CS-MRI 重构，提出一种新的融合自适应字典学习的双稀疏 MR 图像重构模型，即 DTKMRI 模型。在综合字典 D 和变换字典 W 都进行自适应学习的情况下，本文对 DTKMRI 模型利用交替迭代最小化法进行求解，该求解过程中引入了综合 K-SVD 算法进行综合字典的自适应学习和 TK-SVD 算法进行变换字典的自适应学习。CS 系统中，对整幅 MR 图像进行稀疏表示的计算复杂度很高[20]，因此将图像分成大小相同的重叠图像块，然后对图像块进行分块稀疏表示，可降低对系统硬件的要求。
DTKMRI 模型的优化问题为
 |
9 |
式中，x 为待重构的 MR 图像，图像分块大小为
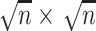；D 为自适应综合字典，
（q = 1，2，
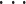，L）为 D 的第 q 个原子，范数约束
用于避免 D 存在平凡解；η1、η2、η3、η4、τ 为数据保真项与各正则项的权衡因子；
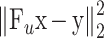为 K-空间的数据保真项，用以保证图像在欠采样下的重构精度；
和
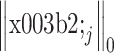项为第 j 个图像块利用变换字典进行稀疏表示，其中
项为第 j 个图像块的稀疏误差，它表示图像块在变换域的稀疏与图像块实际稀疏的偏离程度；互相关约束
，用于避免自适应变换字典 W 存在平凡解。式（9）是利用自适应综合字典 D 和自适应变换字典 W 下图像的稀疏表示来保证图像重构误差最小，实现对 MR 图像的精确重构。
本文利用交替迭代最小化法求解式（9），求解过程包括三个阶段：首先，固定 MR 图像 x，利用综合 K-SVD 算法更新综合稀疏系数 α 与自适应综合字典 D；其次，固定 x，利用 TK-SVD 算法更新稀疏变换系数 β 与自适应变换字典 W；最后，固定 α、β、D 与 W，利用最小二乘法更新 x。其具体求解过程为：
第一阶段固定图像 x，对于第 k 次迭代，更新 αk 与 Dk 的优化问题为
 |
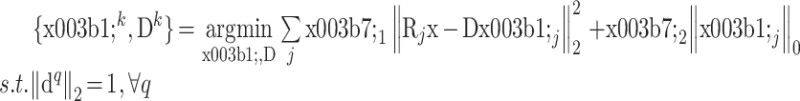10 |
式（10）的求解分为两步，即更新综合稀疏系数 αk 和更新自适应综合字典 Dk。第一步更新 αk 时，固定 Dk–1，此时表达式为
 |
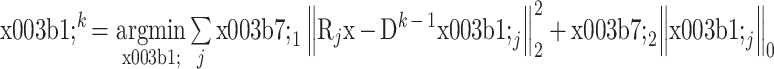11 |
式（11）为 l0 范数非凸优化问题，本文使用 OMP 算法进行求解。第二步是根据式（11）求得的 αk，更新 Dk，其表达式为
 |
12 |
本文利用综合 K-SVD 算法求解式（12）。
第二阶段为固定 x，更新 βk 与 Wk，该优化问题表示为
 |
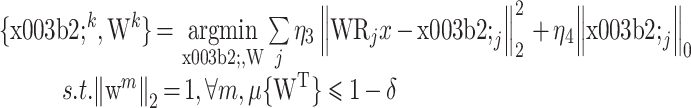13 |
式（13）与式（5）相同，可利用 TK-SVD 算法求解[23]，其求解过程分为两步：第一步为固定 Wk−1，更新稀疏变换系数 βk，其表达式为
 |
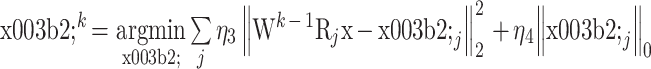14 |
式（14）与式（6）的形式相同，可采用迭代硬阈值法求解。第二步是根据式（14）求得的 βk，更新自适应变换字典 Wk，其表达式为
 |
15 |
式（15）可采用与式（7）相同的方法求解，即奇异值分解进行字典 Wk 更新。
第三阶段为固定 αk、Dk、βk 与 Wk，更新 MR 图像 x，该优化问题为
 |
16 |
求解式（16）可获得 MR 图像 x 的更新。式（16）是关于 l2 范数的最小二乘问题，可得其解析解为
 |
17 |
式中，F 与 F-1 分别为傅里叶正变换和逆变换矩阵；
是对角阵；
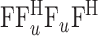为对角阵，其对角元素由 0 或 1 构成；
为零填充的傅里叶域采样值[12]。DTKMRI 的具体求解步骤如表 1 所示。
表 1. DTKMRI solution procedure.
DTKMRI 求解步骤
| 输入：采样值 y，稀疏度 s、K，参数 η1、η2、η3、η4、τ，字典更新次数 J |
| 输出：MR 图像 x |
（1） 初始化：x0 =
，W0，D0
|
| （2） While 终止条件不满足，do |
| （3） Fork = 1:J |
| （4） 根据式（11）更新 αk； |
| （5） 根据式（14）更新 βk； |
| （6） 根据式（12）更新 Dk； |
| （7） 根据式（15）更新 Wk； |
| （8） End for |
| （9） 根据式（17）更新 MR 图像 x； |
| （10） End while |
2. MR 图像重构及结果分析
为了验证 DTKMRI 模型对 MR 图像重构的有效性，采用 BMR2、Brain、t2axialbrain、foot-012、Pulmonaryangio 和 herniateddisclspine 六幅大小均为
的 MR 图像作为测试图像进行重构实验，如图 1 所示（实验图像在网址
http://www3.americanradiology.com/pls/web1/wwimggal.vmg 上获得）。实验中，重构模型的算法迭代 30 次；MR 图像分块大小为 8 × 8；观测噪声为随机复高斯白噪声，噪声标准偏差 σ 为 15、25 或 35；自适应综合字典 D 和自适应变换字典 W 大小均为
；s = 10，K = 10；图像分块的步长为一个像素，即 r = 1；算法每次迭代时，自适应字典均更新 2 次（J = 2），用于字典学习的图像块数量为 12 800。实验中采用峰值信噪比（peak signal to noise ratio，记作 PSNR）和高频误差范数（high-frequency error norm，记作 HFEN）作为衡量模型性能的指标[12]，其中 HFEN 是衡量重构图像边缘结构特性的指标，HFEN 值越小，图像重构的边缘结构特性越好。本文在相同噪声水平、同一采样模式的相同采样率下对每幅图像进行 10 次重构实验，然后计算重构图像 PSNR 和 HFEN 的均值和标准差（standard deviation，记作 Std）作为每个重构实验的最终结果。经过大量实验验证，DTKMRI 模型在参数为 η1 = 1、η2 = 0.01、η3 = 0.01、η4 = 0.01、δ = 0.05 时，MR 图像重构实验可得到较好的实验效果。实验中，针对不同的采样率对参数 τ 进行调节。
图 1.
MR test images
MR 测试图像
a. BMR2; b. Brain (the part in the white rectangle is the magnified region of Fig.3); c. t2axialbrain; d. foot-012; e. Pulmonaryangio; f. herniateddisclspine
a. BMR2；b. Brain（图中白框标注部分为图 3 放大区域）；c. t2axialbrain；d. foot-012；e. Pulmonaryangio；f. herniateddisclspine
为了验证 DTKMRI 模型在不同采样率下的图像重构效果，分别采用 2D 变密度随机采样（采样率 R 分别为 5% 和 10%）和伪射线采样（采样线条数 l 分别为 55 和 80）两种采样模式对六幅 MR 测试图像进行重构实验。实验中，噪声标准偏差选择σ = 35，将实验结果 PSNR 与 HFEN 的均值分别与 Zero-filling、DLMRI[12]和 TLMRI[14]三种对比模型的实验结果比较，如表 2 所示。为了对比的公平性，对比模型的参数进行了调节，使对比模型能达到最佳的 MR 图像重构性能。文献[12]提出的 DLMRI 是基于自适应综合字典学习的压缩感知 MR 图像重构，文献[14]提出的 TLMRI 是基于自适应变换字典学习的盲压缩感知 MR 图像重构，它们是近几年压缩感知 MR 图像重构领域较好的模型。从表 2 的数据可知，DTKMRI 模型重构图像 PSNR 和 HFEN 的均值在两种采样模式、不同采样率下均优于对比模型，提高了 MR 图像重构质量和改善了重构图像的边缘结构特性，图像总体重构效果较好。以 t2axialbrain 图像为例，表 2 中 2D 变密度随机采样在采样率为 10% 的情况下，DTKMRI 图像重构 PSNR 均值相比 TLMRI 和 DLMRI 分别提高了 1.62 dB 和 2.65 dB，DTKMRI 图像重构 HFEN 均值相比 TLMRI 和 DLMRI 分别降低了 0.51 和 0.81；伪射线采样在采样线条数为 80 的情况下，DTKMRI 图像重构 PSNR 均值相比 TLMRI 和 DLMRI 分别提高了 1.27 dB 和 2.59 dB，DTKMRI 图像重构 HFEN 均值相比 TLMRI 和 DLMRI 分别降低了 0.45 和 0.62。
表 2. Comparisons of image reconstruction PSNR (dB) and HFEN using different sampling modes in various sampling rates (σ = 35) .
不同采样方式在不同采样率下的图像重构 PSNR（dB）与 HFEN 比较（σ = 35）
| 图像 | 模型 | 2D 变密度随机采样 | 伪射线采样 | |||
| R = 5% | R = 10% | l = 55 | l = 80 | |||
| PSNR ± Std/HFEN ± Std | PSNR± Std/HFEN ± Std | PSNR ± Std/HFEN ± Std | PSNR ± Std/HFEN ± Std | |||
| BMR2 | Zero-filling | 19.38 ± 0.17/4.75 ± 0.02 | 22.79 ± 0.08/3.90 ± 0.01 | 23.24 ± 0.23/5.16 ± 0.01 | 26.57 ± 0.18/4.37 ± 0.01 | |
| DLMRI | 33.57 ± 0.04/2.16 ± 0.02 | 34.29 ± 0.02/1.88 ± 0.01 | 31.98 ± 0.03/2.62 ± 0.02 | 32.29 ± 0.03/2.23 ± 0.01 | ||
| TLMRI | 33.19 ± 0.03/2.19 ± 0.01 | 35.07 ± 0.04/1.65 ± 0.01 | 32.36 ± 0.03/2.75 ± 0.01 | 34.27 ± 0.05/2.11 ± 0.02 | ||
| DTKMRI | 35.74 ± 0.02/1.55 ± 0.01 | 37.14 ± 0.03/1.21 ± 0.01 | 34.27 ± 0.03/2.10 ± 0.01 | 35.95 ± 0.04/1.69 ± 0.02 | ||
| Brain | Zero-filling | 16.55 ± 0.03/6.52 ± 0.01 | 18.70 ± 0.08/5.35 ± 0.02 | 20.18 ± 0.09/7.24 ± 0.01 | 21.94 ± 0.19/6.14 ± 0.01 | |
| DLMRI | 31.35 ± 0.05/2.78 ± 0.02 | 33.02 ± 0.03/2.28 ± 0.02 | 29.59 ± 0.02/3.71 ± 0.01 | 30.96 ± 0.03/3.01 ± 0.02 | ||
| TLMRI | 31.17 ± 0.06/2.89 ± 0.02 | 33.63 ± 0.03/1.91 ± 0.01 | 29.08 ± 0.04/4.12 ± 0.02 | 32.01 ± 0.02/2.92 ± 0.01 | ||
| DTKMRI | 33.12 ± 0.04/2.01 ± 0.01 | 35.80 ± 0.03/1.19 ± 0.02 | 31.11 ± 0.04/2.85 ± 0.02 | 33.57 ± 0.02/2.28 ± 0.02 | ||
| t2axialbrain | Zero-filling | 20.10 ± 0.13/5.24 ± 0.01 | 22.30 ± 0.08/4.36 ± 0.01 | 24.64 ± 0.01/5.79 ± 0.01 | 26.22 ± 0.04/5.09 ± 0.01 | |
| DLMRI | 32.45 ± 0.03/2.82 ± 0.02 | 33.41 ± 0.03/2.21 ± 0.02 | 30.36 ± 0.03/3.50 ± 0.02 | 31.28 ± 0.03/2.95 ± 0.02 | ||
| TLMRI | 32.54 ± 0.04/2.63 ± 0.02 | 34.44 ± 0.02/1.91 ± 0.01 | 30.77 ± 0.03/3.64 ± 0.02 | 32.60 ± 0.04/2.78 ± 0.02 | ||
| DTKMRI | 34.41 ± 0.03/1.92 ± 0.02 | 36.06 ± 0.02/1.40 ± 0.01 | 32.05 ± 0.02/3.16 ± 0.01 | 33.87 ± 0.03/2.33 ± 0.02 | ||
| foot-012 | Zero-filling | 14.60 ± 0.03/7.31 ± 0.01 | 17.65 ± 0.03/5.95 ± 0.02 | 20.48 ± 0.13/8.08 ± 0.01 | 21.82 ± 0.21/7.04 ± 0.02 | |
| DLMRI | 29.68 ± 0.03/3.60 ± 0.02 | 30.83 ± 0.05/2.67 ± 0.02 | 26.91 ± 0.03/5.47 ± 0.03 | 28.31 ± 0.03/4.29 ± 0.03 | ||
| TLMRI | 30.11 ± 0.03/3.33 ± 0.02 | 31.90 ± 0.03/2.29 ± 0.01 | 27.02 ± 0.03/5.55 ± 0.03 | 29.65 ± 0.02/3.93 ± 0.01 | ||
| DTKMRI | 30.97 ± 0.03/2.60 ± 0.02 | 32.91 ± 0.02/1.92 ± 0.01 | 28.41 ± 0.03/4.22 ± 0.02 | 31.18 ± 0.02/2.76 ± 0.01 | ||
| Pulmonaryangio | Zero-filling | 19.84 ± 0.07/3.96 ± 0.01 | 23.83 ± 0.07/3.28 ± 0.01 | 25.97 ± 0.06/4.32 ± 0.01 | 27.63 ± 0.15/3.73 ± 0.01 | |
| DLMRI | 33.38 ± 0.04/2.46 ± 0.02 | 34.27 ± 0.03/2.18 ± 0.01 | 30.55 ± 0.03/3.14 ± 0.02 | 31.98 ± 0.03/2.60 ± 0.02 | ||
| TLMRI | 34.14 ± 0.04/2.05 ± 0.02 | 35.38 ± 0.03/1.81 ± 0.01 | 30.74 ± 0.04/3.26 ± 0.02 | 33.23 ± 0.04/2.46 ± 0.01 | ||
| DTKMRI | 35.27 ± 0.03/1.89 ± 0.03 | 36.83 ± 0.02/1.51 ± 0.02 | 32.07 ± 0.03/2.35 ± 0.02 | 34.65 ± 0.03/1.94 ± 0.02 | ||
| herniateddisclspine | Zero-filling | 17.02 ± 0.04/4.88 ± 0.01 | 20.00 ± 0.01/4.10 ± 0.01 | 23.13 ± 0.13/5.16 ± 0.01 | 25.48 ± 0.14/4.67 ± 0.01 | |
| DLMRI | 31.06 ± 0.04/2.76 ± 0.02 | 33.54 ± 0.06/2.31 ± 0.02 | 30.89 ± 0.04/3.33 ± 0.02 | 32.06 ± 0.04/2.77 ± 0.03 | ||
| TLMRI | 30.57 ± 0.04/2.83 ± 0.02 | 34.11 ± 0.05/1.99 ± 0.01 | 28.79 ± 0.02/3.83 ± 0.02 | 32.89 ± 0.05/2.56 ± 0.02 | ||
| DTKMRI | 31.70 ± 0.03/2.64 ± 0.01 | 35.76 ± 0.03/1.53 ± 0.02 | 31.28 ± 0.02/3.11 ± 0.03 | 33.79 ± 0.04/2.23 ± 0.02 | ||
为了验证 DTKMRI 模型在不同噪声标准偏差下图像重构的抗噪性能，分别采用 2D 变密度随机采样和伪射线采样对六幅 MR 测试图像进行重构实验。实验中采样率 R = 5%，伪射线条数 l = 55，噪声标准偏差 σ 分别取 15 和 25，将 DTKMRI 模型的实验结果分别与对比模型相比较，如表 3 所示。从表 3 的数据可知，DTKMRI 模型在不同噪声标准偏差下图像重构 PSNR 和 HFEN 的均值优于对比模型，实现了更好的图像重构效果，具有较好的抗噪性和鲁棒性。以 BMR2 图像为例，表 3 中 2D 变密度随机采样在噪声标准偏差为 25 的情况下，DTKMRI 模型的图像重构 PSNR 均值相比 TLMRI 和 DLMRI 模型分别提高了 1.56 dB 和 1.91 dB，DTKMRI 模型的图像重构 HFEN 均值相比 TLMRI 和 DLMRI 模型分别降低了 0.41 和 0.53；伪射线采样在噪声标准偏差为 25 的情况下，DTKMRI 模型的图像重构 PSNR 均值相比 TLMRI 和 DLMRI 模型分别提高了 1.62 dB 和 1.74 dB，DTKMRI 模型的图像重构 HFEN 均值相比 TLMRI 和 DLMRI 模型分别降低了 0.48 和 0.57。
表 3. Comparisons of image reconstruction PSNR (dB) and HFEN using different modes in various noise standard deviations .
不同采样方式在不同噪声标准偏差下的图像重构 PSNR（dB）与 HFEN 比较
| 图像 | 模型 | 2D 变密度随机采样（R = 5%） | 伪射线采样（l = 55） | |||
| σ = 15 | σ = 25 | σ = 15 | σ = 25 | |||
| PSNR ± Std/HFEN ± Std | PSNR ± Std/HFEN ± Std | PSNR ± Std/HFEN ± Std | PSNR ± Std/HFEN ± Std | |||
| BMR2 | Zero-filling | 19.51 ± 0.05/4.46 ± 0.01 | 19.45 ± 0.09/4.58 ± 0.02 | 23.55 ± 0.11/5.02 ± 0.01 | 23.38 ± 0.13/5.11 ± 0.01 | |
| DLMRI | 35.64 ± 0.02/1.77 ± 0.01 | 34.66 ± 0.03/1.94 ± 0.03 | 34.22 ± 0.02/2.31 ± 0.02 | 33.17 ± 0.03/2.48 ± 0.03 | ||
| TLMRI | 36.28 ± 0.04/1.48 ± 0.01 | 35.01 ± 0.05/1.82 ± 0.01 | 34.28 ± 0.03/2.26 ± 0.02 | 33.29 ± 0.02/2.39 ± 0.02 | ||
| DTKMRI | 37.51 ± 0.03/1.24 ± 0.02 | 36.57 ± 0.04/1.41 ± 0.02 | 36.07 ± 0.03/1.57 ± 0.01 | 34.91 ± 0.03/1.91 ± 0.02 | ||
| Brain | Zero-filling | 16.89 ± 0.01/6.33 ± 0.01 | 16.67 ± 0.01/6.42 ± 0.01 | 20.47 ± 0.06/7.01 ± 0.01 | 20.35 ± 0.07/7.13 ± 0.01 | |
| DLMRI | 33.00 ± 0.03/2.43 ± 0.01 | 32.22 ± 0.05/2.60 ± 0.02 | 31.27 ± 0.04/3.31 ± 0.02 | 30.52 ± 0.03/3.47 ± 0.01 | ||
| TLMRI | 32.68 ± 0.03/2.27 ± 0.01 | 31.91 ± 0.04/2.51 ± 0.01 | 30.39 ± 0.02/3.72 ± 0.02 | 29.98 ± 0.03/3.91 ± 0.02 | ||
| DTKMRI | 35.23 ± 0.03/1.64 ± 0.01 | 34.13 ± 0.03/1.82 ± 0.02 | 33.24 ± 0.03/2.29 ± 0.02 | 32.10 ± 0.01/2.57 ± 0.02 | ||
| t2axialbrain | Zero-filling | 20.42 ± 0.08/4.90 ± 0.01 | 20.23 ± 0.08/5.08 ± 0.01 | 25.09 ± 0.01/5.68 ± 0.01 | 24.86 ± 0.01/5.74 ± 0.01 | |
| DLMRI | 34.22 ± 0.03/2.42 ± 0.01 | 33.39 ± 0.04/2.59 ± 0.01 | 32.09 ± 0.02/3.18 ± 0.02 | 31.31 ± 0.03/3.31 ± 0.01 | ||
| TLMRI | 35.29 ± 0.03/1.90 ± 0.01 | 34.37 ± 0.06/2.31 ± 0.02 | 32.77 ± 0.02/2.94 ± 0.01 | 31.63 ± 0.03/3.31 ± 0.01 | ||
| DTKMRI | 36.76 ± 0.02/1.53 ± 0.01 | 35.95 ± 0.04/1.71 ± 0.01 | 34.49 ± 0.02/2.51 ± 0.01 | 33.13 ± 0.02/2.79 ± 0.02 | ||
| foot-012 | Zero-filling | 14.93 ± 0.02/7.05 ± 0.01 | 14.75 ± 0.02/7.20 ± 0.01 | 20.91 ± 0.09/8.01 ± 0.01 | 20.69 ± 0.12/8.05 ± 0.02 | |
| DLMRI | 31.09 ± 0.03/3.13 ± 0.02 | 30.34 ± 0.02/3.45 ± 0.02 | 28.16 ± 0.03/5.05 ± 0.03 | 27.53 ± 0.03/5.21 ± 0.03 | ||
| TLMRI | 32.11 ± 0.02/2.54 ± 0.01 | 31.23 ± 0.02/2.87 ± 0.02 | 28.43 ± 0.02/4.63 ± 0.01 | 27.87 ± 0.03/5.08 ± 0.03 | ||
| DTKMRI | 33.27 ± 0.02/1.87 ± 0.01 | 32.28 ± 0.03/2.24 ± 0.01 | 31.02 ± 0.02/3.18 ± 0.02 | 30.06 ± 0.02/3.65 ± 0.02 | ||
| Pulmonaryangio | Zero-filling | 20.06 ± 0.05/3.61 ± 0.01 | 19.94 ± 0.10/3.79 ± 0.02 | 26.49 ± 0.03/4.19 ± 0.01 | 26.24 ± 0.03/4.28 ± 0.02 | |
| DLMRI | 36.06 ± 0.03/1.82 ± 0.01 | 35.04 ± 0.05/2.01 ± 0.01 | 31.95 ± 0.03/2.89 ± 0.02 | 31.33 ± 0.03/3.12 ± 0.01 | ||
| TLMRI | 36.89 ± 0.05/1.58 ± 0.02 | 35.56 ± 0.05/1.92 ± 0.02 | 31.69 ± 0.01/2.97 ± 0.01 | 31.29 ± 0.02/3.17 ± 0.03 | ||
| DTKMRI | 38.27 ± 0.03/1.03 ± 0.02 | 36.69 ± 0.04/1.54 ± 0.02 | 33.55 ± 0.02/1.96 ± 0.02 | 32.91 ± 0.03/2.21 ± 0.02 | ||
| herniateddisclspine | Zero-filling | 17.38 ± 0.03/4.66 ± 0.01 | 17.15 ± 0.05/4.76 ± 0.01 | 23.62 ± 0.09/5.05 ± 0.01 | 23.34 ± 0.13/5.12 ± 0.01 | |
| DLMRI | 31.82 ± 0.02/2.37 ± 0.01 | 31.42 ± 0.02/2.53 ± 0.01 | 32.00 ± 0.03/3.07 ± 0.01 | 31.50 ± 0.03/3.19 ± 0.02 | ||
| TLMRI | 31.28 ± 0.02/2.60 ± 0.01 | 30.99 ± 0.03/2.71 ± 0.02 | 29.87 ± 0.02/3.30 ± 0.02 | 29.35 ± 0.03/3.62 ± 0.02 | ||
| DTKMRI | 32.97 ± 0.02/1.94 ± 0.01 | 32.56 ± 0.02/2.11 ± 0.01 | 33.31 ± 0.02/2.57 ± 0.02 | 32.56 ± 0.02/2.81 ± 0.01 | ||
为了验证 DTKMRI 模型的收敛性与优越性，图 2 给出了 Brain 图像在 2D 变密度随机采样 R = 10%、σ = 35 时，重构实验的 PSNR 和 HFEN 值随着迭代次数的变化曲线。从图 2 可知，DTKMRI 模型的收敛速度最快，大约经过 12 次迭代重构图像的 PSNR 达到最大值，且随着迭代次数的增加 PSNR 值基本保持不变，表示模型收敛；随后依次是 TLMRI 和 DLMRI 模型重构图像的 PSNR 值随着迭代次数基本保持不变，表明这两个模型亦达到收敛。可见，DTKMRI 模型相比 TLMRI 和 DLMRI 模型具有较快的收敛速度，且 PSNR 值较大。从图 2 还可知，DTKMRI 模型相比 TLMRI 和 DLMRI 模型的 HFEN 值更小，这表明 DTKMRI 模型的图像边缘结构重构效果更好。由图 2 可见，DTKMRI 模型具有较快的收敛速度，MR 图像重构质量优于 TLMRI 和 DLMRI 模型。
图 2.
PSNR and HFEN changing curves of Brain image along with iterations
Brain 图像的 PSNR 与 HFEN 随迭代次数的变化曲线
为了进一步体现本文提出模型的优越性，将从主观视觉效果方面评价 MR 图像的重构效果。图 3 给出了 2D 变密度随机采样 R = 10%、σ = 35 时，各重构模型对 Brain 图像局部（所取部分在图 1b 中已标出）重构结果的比较图；图 4 给出了伪射线采样 l = 80、σ = 35 时，各重构模型对 t2axialbrain 图像的重构结果和重构误差图。由图 4h、4i、4j 可见，相比 TLMRI 和 DLMRI 模型，DTKMRI 模型图像重构质量在红色矩形区域得到明显改善。图 3 和图 4 给出的重构结果中，Zero-filling 的 MR 图像重构质量最差，细节信息丢失最多，平滑和边缘部分模糊；DLMRI 的 MR 图像重构质量明显优于 Zero-filling，但仍丢失了大量细节信息，图像过于平滑，边缘轮廓结构不清晰；TLMRI 的 MR 图像重构质量优于 DLMRI，边缘轮廓结构较之更为清晰，但仍丢失了部分细节信息；DTKMRI 的 MR 图像重构结果中保留了更多的细节信息，边缘轮廓结构较清晰，重构结果中噪声不明显。可见，DTKMRI 能够更精确地重构 MR 图像的细节信息和边缘轮廓结构信息。
图 3.
Reconstruction results of the local Brain image (the original part is the region which is in the white rectangle of Fig.1b) by 2D variable density random sampling
2D 变密度随机采样下 Brain 图像的局部（图 1b 中白框标注区域为本图的原图）重构结果放大图
a. 2D variable density random sampling in the K-space; b. original part; c. Zero-filling; d. DLMRI; e. TLMRI; f. DTKMRI
a. K-空间的 2D 变密度随机采样；b. 原图像；c. Zero-filling；d. DLMRI；e. TLMRI；f. DTKMRI
图 4.
The t2axialbrain image reconstruction results and errors of different models under pseudo radial sampling
伪射线采样下 t2axialbrain 图像的不同模型重构结果及重构误差图
a. pseudo radial sampling in the K-space; b. original image; c & g. Zero-filling; d & h. DLMRI; e & i. TLMRI; f & j. DTKMRI. Compared to DLMRI and TLMRI, DTKMRI remarkably improves the reconstruction quality of the image in the red rectangle boxes of Fig.4 h, i, j
a. K-空间的伪射线采样；b. 原图像；c & g. Zero-filling；d & h. DLMRI；e & i. TLMRI；f & j. DTKMRI。图 h、i、j 的红色矩形区域表示：相比 DLMRI 和 TLMRI，DTKMRI 的图像重构质量得到明显改善
综合上述实验表明，DTKMRI 模型的 MR 图像重构效果相比 DLMRI 和 TLMRI 模型有较好的改善。究其原因，DLMRI 模型是利用自适应综合字典学习下的稀疏先验知识，使图像重构效果得以改善；TLMRI 模型是利用自适应变换字典学习下的稀疏先验知识，使图像重构效果得以进一步改善；与 DLMRI 和 TLMRI 模型相比，DTKMRI 模型将解析 K-SVD 算法结合自适应变换字典学习得到的 TK-SVD 算法应用于稀疏变换模型，然后根据稀疏变换模型和综合稀疏模型的稀疏性先验相互补充作用，结合自适应综合字典学习和自适应变换字典学习，使 MR 图像重构质量进一步提高，获得更多的 MR 图像细节特征信息和边缘轮廓结构特征信息，模型的有效性更好、适用性更强。
3. 结论
本文将自适应综合字典学习和自适应变换字典学习相结合，提出了基于双稀疏模型的 MR 图像重构 DTKMRI 模型。DTKMRI 模型将两种稀疏模型同时应用于 CS-MRI 重构系统，其优势是既利用了 MR 图像的图像域稀疏先验知识又利用了图像的稀疏变换域先验知识。DTKMRI 模型的优化问题利用交替迭代最小化法进行了有效的求解，在求解过程中引入了 TK-SVD 稀疏变换学习算法。本文对 DTKMRI 模型进行了 MR 图像重构实验，将实验结果与 Zero-filling、DLMRI 和 TLMRI 模型进行了比较。实验结果表明，无论是客观评价还是主观视觉评价，DTKMRI 模型对 MR 图像的细节信息和边缘结构信息都实现了较好的重构，对图像重构效果起到了很好的改善作用。本文提出的 MR 图像重构模型的鲁棒性优于 Zero-filling、DLMRI 和 TLMRI 图像重构模型，且收敛速度较快。如何将其他稀疏先验以及更多的稀疏先验应用到 MR 图像重构模型，进一步有效地提高图像重构质量，实现更低采样率下对 MR 图像迅速和精确的重构，是今后的研究方向。
Funding Statement
国家自然科学基金项目资助（61471313）；安徽科技学院基金项目资助（AKZDXK2015C02）
References
- 1.贺超 核磁共振成像系统原理及 MR 图像研究. 云南大学学报: 自然科学版. 2010;32(S1):245–248. [Google Scholar]
- 2.Donoho D L Compressed sensing. IEEE Transactions on Information Theory. 2006;52(4):1289–1306. [Google Scholar]
- 3.Candes E, Roberg J, Tao T Robust uncertainty principles: exact signal recognition from highly incomplete frequency information. IEEE Transactions on Information Theory. 2006;52(2):489–509. [Google Scholar]
- 4.李修寒, 朱松盛 基于压缩感知理论的医学图像重构算法研究现状. 生物医学工程学进展. 2014;35(4):216–242. [Google Scholar]
- 5.Takhar D, Laska J N, Wakin M B, et al A new compressive imaging camera architecture using optical domain compression//Proceedings of the 2006 IS&T/SPIE Symposium on Electronic Imaging: Computational Imaging. San Jose, California, United States: SPIE. 2006;6065:43–52. [Google Scholar]
- 6.李中源, 李光, 孙翌, 等 一种基于全局字典学习的小动物低剂量计算机断层扫描降噪方法. 生物医学工程学杂志. 2016;33(2):279–286. [PubMed] [Google Scholar]
- 7.李龙珍, 姚旭日, 刘雪峰, 等 基于压缩感知超分辨鬼成像. 物理学报. 2014;63(22):42011–42016. [Google Scholar]
- 8.吴建宁, 徐海东, 王佳境, 等 基于随机投影的快速稀疏表示人体动作识别方法. 中国生物医学工程学报. 2016;35(1):38–46. [Google Scholar]
- 9.Liu Y, Cai J F, Zhan Z, et al Balanced sparse model for tight frames in compressed sensing magnetic resonance imaging. PLoS One. 2015;10(4):1–19. doi: 10.1371/journal.pone.0119584. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Huang Jinhong, Guo Li, Feng Qianjin, et al Sparsity-promoting orthogonal dictionary updating for image reconstruction from highly undersampled magnetic resonance data. Phys Med Biol. 2015;60(14):5359–5380. doi: 10.1088/0031-9155/60/14/5359. [DOI] [PubMed] [Google Scholar]
- 11.Lustig M, Donoho D, Pauly J M Sparse MRI: the application of compressed sensing for rapid MR imaging. Magn Reson Med. 2007;58(6):1182–1195. doi: 10.1002/mrm.21391. [DOI] [PubMed] [Google Scholar]
- 12.Ravishankar S, Bresler Y MR image reconstruction from highly undersampled space data by dictionary learning. IEEE Trans Med Imaging. 2011;30(5):1028–1041. doi: 10.1109/TMI.2010.2090538. [DOI] [PubMed] [Google Scholar]
- 13.Ravishankar S, Bresler Y Sparsifing transform learning for compressed sensing MRI//IEEE International Symposium on Biomedical Imaging: From Nano to Macro. San Francisco, USA: IEEE. 2013:17–20. [Google Scholar]
- 14.Ravishankar S, Bresler Y Efficient blind compressed sensing using sparsifying transforms with convergence guarantees and application to magnetic resonance imaging. SIAM J Imaging Sci. 2015;8(4):2519–2557. [Google Scholar]
- 15.Wang X Y, Guo X, Zhang D D An effective fractal image compression algorithm based on plane fitting. Chin Phys B. 2012;21(9):090507. [Google Scholar]
- 16.宁方立, 何碧静, 韦娟 基于 lp 范数的压缩感知图像重建算法研究 . 物理学报. 2013;62(17):42121–42128. [Google Scholar]
- 17.Yaghoobi M, Nam S, Gribonval R, et al Constrained over-complete analysis operator learning for co-sparse signal modeling. IEEE Transactions on Signal Processing. 2013;61(9):2141–2355. [Google Scholar]
- 18.Hawe S, Kleinsteuber M, Diepold K Analysis operator learning and its application to image reconstruction. IEEE Transactions on Image Processing. 2013;22(6):2138–2150. doi: 10.1109/TIP.2013.2246175. [DOI] [PubMed] [Google Scholar]
- 19.Chen Yunjin, Ranftl R, Pock T Insights into analysis operator learning: from patch-based sparse models to higher order MRFs. IEEE Transactions on Image Processing. 2014;23(3):1060–1072. doi: 10.1109/TIP.2014.2299065. [DOI] [PubMed] [Google Scholar]
- 20.Giryes R, Nam S, Elad M, et al Greedy-like algorithms for the co-sparse analysis model. Linear Algebra Appl. 2014;441:22–60. [Google Scholar]
- 21.Rubinstein R, Peleg T, Elad M Analysis K-SVD: A dictionary-learning algorithm for the analysis sparse model. IEEE Transactions on Signal Processing. 2013;61(3):661–677. [Google Scholar]
- 22.Ravishankar S, Bresler Y Learning sparsifying transforms. IEEE Transactions on Signal Processing. 2013;61(5):1072–1086. [Google Scholar]
- 23.Eksioglu E M, Bayir O K-SVD meets transform learning: transform K-SVD. IEEE Signal Process Lett. 2014;21(3):347–351. [Google Scholar]