基于 t 分布邻域嵌入算法的流式数据自动分群方法

Abstract

流式细胞仪中多参数流式数据分群传统方法主要是利用专业软件采取人工设门方式，圈出目标细胞进行分析，分析过程较为复杂，专业性较强。基于此，本文提出了一种基于 t 分布邻域嵌入（t-SNE）算法对多参数流式数据进行分群处理。该算法将样本数据在高维空间中的欧几里德距离转化为条件概率来表征相似性，使数据降到低维空间。本文通过使用流式细胞仪处理染色后的人体外周血细胞，并将处理后的数据导出作为实验样本数据，对其利用 t-SNE 算法进行降维，并与核主成分分析（KPCA）降维算法对比，分别使用 K 均值（K-means）算法对降维得到的主成分数据进行分类。结果表明，t-SNE 算法对呈非对称且有拖尾分布的细胞类群具有很好的分群效果，分群准确率可达 92.55%，或可有助于多色多参数流式数据进行自动分析。

引言

随着科技的进步，传统的精密医疗仪器也在向全自动、智能方向发展。全自动流式细胞仪作为一种常规分析仪器，在各大医院及实验室需求巨大。目前，常规的流式细胞仪，包括：光学系统、流动室及液流驱动系统、光电检测系统和信号处理系统四大核心组分。其中，信号处理系统的一部分工作是要对大量多色多参数流式数据进行分析，分析难度较大，因此对此部分的研究也成为了研究热点。通常对流式数据进行分析是使用仪器专门配备的软件，将流式数据导入软件中，然后在多组荧光特征中选取两组作为二维图的横纵坐标，绘制散点图或密度图等，然后根据经验设门，圈出想要分析的目标数据；或是选取一组数据绘制直方图，观察被目标荧光参数所染色的细胞数量，做出定量分析^[1-4]，但随着各种医学技术和流式细胞术的快速发展，传统人工设门的方法已无法适应大量多维度流式数据的快速分析，主要原因如下：

（1）人工设门缺乏客观性。专家凭借自身经验从多种荧光特征中选取两组特征绘制散点图，且圈门和做出细胞类群的判断也因人而异，没有量化标准。

（2）分析结果可重复性差。针对不同的数据，人工设门方法并没有标准统一的画法。

（3）需要操作者有专业背景。流式数据分析软件是流式细胞仪专用软件，涉及到的医学知识是一般使用者不具备的，存在局限性。

（4）无法结合多维数据间的特征差异进行处理。数据分析只能显示二维特征，并寻找差异，而多色多参数高维流式数据的特征只能在多维空间才能显示出来。

（5）过程繁琐、效率低、资源浪费巨大。人工设门分析过程消耗人力、浪费时间，而且分析结果往往可靠性差^[5-8]。

为了克服传统细胞分群方法的不足，国内外的研究人员提出了流式数据自动分群方法，并针对这一内容进行了深入的研究。例如基于无监督聚类的 K-means 算法^[6]，通过计算样本点间的欧几里德距离划分样本数据，实现聚类；Sugár 等^[9]提出了基于渗透理论的非监督密度轮廓聚类算法（unsupervised density contour clustering algorithm），通过绘制实验样本直方图并寻找峰值点，实现了流式数据中多种形状细胞类群的快速聚类分析；Qian 等^[6]提出了基于网格划分和合并（grid-based partitioning and merging）类群识别算法；Morris 等^[10]利用支持向量机进行流式细胞分类识别，方法是选取一部分实验数据作为测试样本，设定类别标签，训练出支持向量机分类模型，再利用模型测试需要分类的样本，实现细胞自动识别；Aghaeepour 等^[7]提出基于层次聚类思想；搭建高斯混合模型等^[11-13]。以上研究分别利用了不同的类型算法来处理流式数据以得到细胞自动分群结果，包括基于监督聚类和非监督聚类的方法，但是大多重点研究针对细胞自动聚类的方法，很少有考虑到细胞类群的分布状态。

本文针对呈非对称且有拖尾分布的细胞类群，提出了一种基于流行学习的 t 分布邻域嵌入算法（t-distributed stochastic neighbor embedding，t-SNE）的多参数流式数据自动分群方法。利用 t-SNE 算法处理高维数据可以很好地表征数据的多维特性，其将样本数据投影到低维空间的可视化效果较好，由于其相比于传统常用的主成分分析（principal component analysis，PCA）降维方式有显著优势，目前已被作为大数据的降维预处理手段，广泛应用于诸多领域，例如图像处理、语义编码、声音识别、机械故障排查等方面^[14-18]。本文使用 t-SNE 算法对原始数据降维，并提取出对可视化结果贡献度最高的特征主成分，选取前两组或前三组主成分数据作为坐标轴，绘制可视化散点图。降维后得到的主成分矩阵利用 K 均值（K-means）算法进行自动聚类，从而得到细胞自动分群结果。最后，将基于 t-SNE 算法与核主成分分析（kernel principal component analysis，KPCA）算法处理数据得到的分群结果进行对比，并使用流式细胞仪专用软件对原始数据进行专业人工设门分析，得到理想人工分群结果，并与本文提出的 t-SNE 算法对呈非对称且有拖尾分布的细胞类群的分群效果为对照，以验证算法的准确性^[18]。通过本文研究，或可进一步促进对流式细胞仪数据自动化分析的研究。

1. 原理及方法

1.1. t-SNE 算法

假设待处理的流式数据样本位于一个统计流形上，利用概率分布描述样本数据点，可得到高维和低维空间里任意两点间的条件概率分布函数，记流式数据样本为有 N 个数据点的有限高维数据集 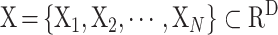，每一个数据点的维度为 D，高维数据点到低维数据点之间的映射记为 。

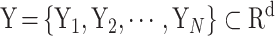整个算法步骤如下：

（1）在同一空间中，用对应数据点间条件概率表征相似性。p_j|i 表示高维数据点 x_i 与 x_j 之间条件概率分布，且分布函数服从高斯分布，p_j|i 越大，数据点之间的相似度越大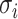， 是高斯分布标准差，条件概率计算式，如式（1）所示：

1

将高维数据点 x_i 和 x_j 在低维中的映射点记为 y_i 和 y_j，计算其相似的条件概率 q_j|i，如式（2）所示：

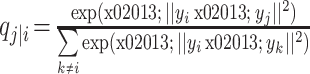2

（2）为了进一步研究高低维空间特征参数之间的分布关联，用对应的条件概率分布表征同一空间下的数据点间联合概率分布 p_ij 和 q_ij，并假设任意 p_ij = p_ji，q_ij = q_ji，且 p_ii = q_ii = 0，联合概率表示，如式（3）、式（4）所示：

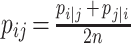3

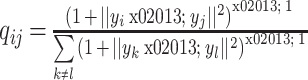4

（3）描述低维空间中的联合概率分布函数与高维空间中数据分布的相似程度用损失函数 C 表示，任意选择低维空间中的一个数据点，其联合概率分布为 p_ij，且与其相对应的高维空间联合概率分布为 q_ij，则计算公式如式（5）所示：

5

其中，KL 散度（Kullback-Leibler divergence，KL）（以符号KL表示）为相对熵，用来衡量相同事件空间里的两个概率分布的相似情况，P 和 Q 分别为高维空间和低维空间中度量点的概率分布。损失函数在于将 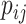与 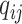的 KL 距离最小化，即使 P 与 Q 两个分布的匹配度最高。函数 C 对 y_i 求偏导，计算损失函数的偏导数即为梯度，利用梯度下降法进行迭代更新，直到函数值收敛，即得到两个概率分布相似最大化。

（4）在低维空间下，由于流式数据样本类群分布呈非对称且有拖尾，并且不完全服从标准的高斯分布，因此任意样本数据点之间的相似度使用 t 分布（studentt-distribution）来表达。t 分布曲线尾部随自由度的增加而变高，因而使得有拖尾的细胞类群分布尾部数据从高维映射到低维后有一个较大的距离，从而避免拥挤问题，t-SNE 梯度计算式可以表示如式（6）所示：

6

（5）输入参数困惑度（以符号 perp 表示）可以表示一个点附近的有效近邻点个数：N 个数据点的条件概率分布有 sigma = { }，困惑度用二分搜索的方式来寻找一个最佳的 ，其定义如式（7）所示：

7

其中 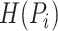为 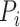的香农熵，用来表征样本数据的不确定性，是混乱程度的量化指标，熵越大，困惑度越大，样本数据的概率就越相近，即增加目标数据点的近邻数据数量。

1.2. 流式细胞类群分布拟合

为验证细胞类群分布状态，使用了商业数学软件 MATLAB（R2013b，MathWorks，美国）进行仿真并拟合数据。实验数据为健康志愿者的上肢前臂的静脉外周血细胞样本，由实验室合作单位北京宣武医院提供。实验仪器是流式细胞仪 Facscalibur（Becton，Dickinson and Company，美国）^[19]。选取人体外周血细胞中的淋巴细胞、嗜中性粒细胞、单核白细胞和破碎的细胞及杂质中的前向散射光脉冲面积（orward light scatter area，FSC-A）数据，共 11 324 组，基于统计学理论对数据进行采样处理，得到细胞类群分布图，如图 1 所示。

图 1.

Cell population distribution fitting

细胞类群分布拟合

由拟合图可以看出，单核白细胞和破碎的细胞及杂质类群是呈非对称分布且有拖尾的，因此使用 t 分布拟合相比于用高斯分布描述流式细胞样本数据更加准确，可以较好地表征数据的整体特征，这也恰好满足细胞分群需求。

1.3. 基于 t-SNE 的流式数据分群方法

t-SNE 算法处理流式数据主要步骤如下所示：

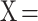
第一步：输入待降维多参数流式数据 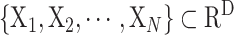，设定需要降到的维数 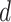以及损失函数参数困惑度为 30（默认值）；

第二步：对样本矩阵 X 进行初始化，计算相应矩阵之间的距离，使用固定的困惑度计算条件概率 p_j|i；

第三步：令 ，用 随机初始化低维数据 ；

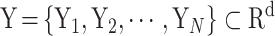第四步：开始优化，进入循环迭代：

• 计算低纬度下的 q_ij

• 由公式（6）计算梯度

• 迭代寻优，更新低维数据 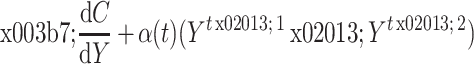，迭代结束后得到的 Y 矩阵即为降维后新的主成分参数。

1.4. K-means 聚类算法

K-means 算法利用函数求极值得到迭代优化结果，是一种硬聚类方法，通常采用欧几里德距离来衡量样本与各个簇的相似度，该算法时间复杂度低、简洁高效，在处理大数据方面有明显优势，具体算法描述如下：

（1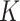） 是聚类数，随机选取 个对象作为聚类质心点 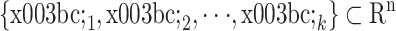，质心 表示程序初始时对样本数据各个类别中心点的估计值。

（2）重复下面过程直到收敛，得出分类标签：

① 对于每一个样例 i，计算其应该属于的类，计算其到 k 个质心中每一个的距离，然后选取距离最近的类别作为 ，如式（8）所示：

8

② 对于每一个类 j，重新计算该类的质心直到其不变或者变化很小，如式（9）所示^[18-20]：

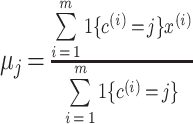9

2. 实验结果及分析

为验证本文提出的方法对流式数据自动分析的能力，利用 t-SNE 算法对多参数流式细胞数据进行处理，实验数据为本文 1.2 节使用的数据。人体外周血细胞包括淋巴细胞、嗜中性粒细胞、单核白细胞和破碎细胞及其杂质共 4 大类细胞，并分别用异硫氰酸荧光素（fluorescein isothiocyanate, FITC）、藻红蛋白（P-phycoerythrin，PE）、异藻蓝蛋白（allophy cocyanin，APC）、多甲藻黄素—叶绿素—蛋白复合物（peridinin-chlorophyll-protein complex，PerCP）4 种荧光染料标记^{[18, 21-22]}，细胞分群策略如图 2 所示，被染色的流式细胞数据包括 14 个属性参数，分别为激光照射细胞后产生的前向散射光（forward light scatter）、侧向散射光（sideward light scatter）和 4 色荧光信号的脉冲高度，脉冲面积和脉冲宽度^[18]。

图 2.

Cell cluster strategy

细胞分群策略

2.1. 基于 t-SNE 的流式细胞分群

选取 3 200 组被染色的 4 类细胞数据，绘制数据样本的“t-SNE 算法降低维数与聚类指标关系”曲线图，此时困惑度取经验值 30，每组试验取 10 次计算结果，去掉极值取平均值，以此确定最佳降低维度。为确保验证结果的普遍适用性，重新选取 4 类细胞数据样本，并重复上述实验，得到 3 组实验结果如图 3 所示。

图 3.

Relationship between reduced dimension of t-SNE and cluster index

t-SNE 降低维度与聚类指标的关系

根据维度与聚类指标的关系曲线，可以看出用 t-SNE 算法降到 4 维时，聚类指标值最大，即此时的主成分贡献率最大，因此确定最佳降低的维度为 4 维。

利用 t-SNE 和 KPCA 算法对原始流式细胞样本进行降维处理，并利用K-means 算法对降维后的数据分类，从而得出分类标签，实现细胞自动聚类。对比使用两种降维算法处理后实验结果的分群效果，以此验证处理多维度流式数据时，利用 t-SNE 算法是否可以更好地提取样本数据特征。利用 K-means 对两种降维算法得到的主成分进行分群处理，利用前 3 个主成分（principal component，PC）（记为 PC1～PC3）绘制可视化散点图，得到最终细胞自动聚类结果如图 4 所示。

图 4.

Streaming data clustering results

流式数据分群结果

由以上分群散点图可看出，t-SNE 算法与 KPCA 算法都可以对高维流式数据进行预处理，将高维数据映射到低维空间，并尽可能地保留原始数据的特征信息。但 t-SNE 算法处理后细胞类群之间的距离明显更远，类群之间的聚合程度也更加密集，能够更大程度地区分各类细胞，即该算法可以在低维空间中更好地表征高维数据，因此利用 t-SNE 算法降维处理后的主成分分群可视化效果更好。为了量化分析两种算法的准确率，实验请专业操作人员使用专业流式数据分析软件 cytospec（1.0.0.0，普度大学）对原始数据进行人工设门分析，并得到理想人工分群结果。计算两种算法的分群准确率，如表 1 所示，基于 t-SNE 的流式数据分群的平均准确率可达 92.55%，优于 KPCA 算法。其中，对于类群分布呈非对称且有拖尾的单核白细胞和破碎细胞及其杂质，t-SNE 算法分群准确率较高，对于正常的服从高斯分布的类群（淋巴细胞和嗜中性粒细胞）的识别能力也较 KPCA 算法有所提高。

表 1. KPCA and t-SNE clustering accuracy .

KPCA 和 t-SNE 分群准确率

算法	准确率
	淋巴细胞	嗜中性粒细胞	单核白细胞	破碎细胞及杂质	平均值
KPCA 算法	99.32%	93.03%	79.02%	54.52%	85.16%
t-SNE 算法	90.92%	99.76%	94.06%	79.88%	92.55%

2.2. 实验结果分析

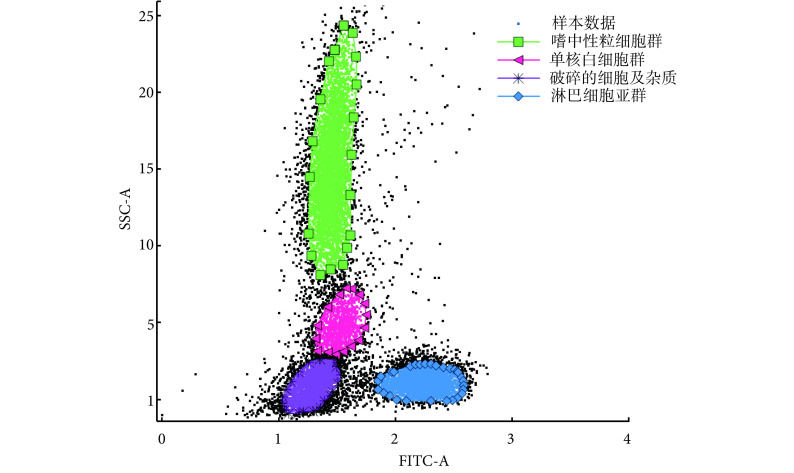
专业操作人员对流式数据进行传统分群方法是人工设门，通过将流式数据的荧光特征参数 FITC 的脉冲面积和侧向散射光脉冲面积分别作为横纵坐标，绘制散点图，然后圈门分析即可得到理想人工分群结果，如图 5 所示，图中分别为淋巴细胞群、嗜中性粒细胞群、单核白细胞群和破碎的细胞及杂质。

图 5.

Artificial clustering result

人工分群结果

为了直观地对比两种算法对细胞分群的结果与理想人工分群结果的差异，本文使用平均相对误差（mean relative error，MRE）（以符号 MRE 表示）和均方根误差（root mean square error，RMSE）（以符号 RMSE 表示）作为评价指标进行横向对比，如式（10）、式（11）所示：

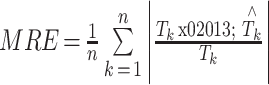10

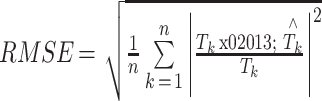11

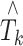式中 k 表示样本次序，k = 1，2，3， ，n；n 表示预测样本数量，T_k 代表实际值， 代表预测值。

MRE 反应了测量值与真实值之间的总体差异，RMSE 可以很好地反应出测量值与真实值之间差异的精密度。两种误差的值越小，说明算法与理想人工分群算法得到的结果越相近。如表 2 所示，分别计算了 KPCA 和 t-SNE 算法与传统理想人工分群结果的 MRE 和 RMSE，为验证算法的普遍适用性，重新选取 4 类细胞数据样本，并重复上述实验，分别计算评价指标，得到 4 组实验结果。

表 2. Calculation results of evaluation index for each clus tering algorithm.

各分群算法评价指标计算结果

组别	分群算法	MRE	RMSE
1	KPCA	17.19%	0.163
	t-SNE	7.68%	0.077
2	KPCA	20.25%	0.203
	t-SNE	12.37%	0.125
3	KPCA	17.30%	0.173
	t-SNE	8.58%	0.087
4	KPCA	21.17%	0.212
	t-SNE	9.40%	0.097

由表 2 可知，利用 t-SNE 算法计算与实际值较为接近，最大 MRE 为 12.37%，其他 3 组测试点 MRE 均控制在 10% 以内，RMSE 最大为 0.125。而利用 KPCA 算法降维得到的细胞分群结果 MRE 在 20% 左右。因此，在多参数流式数据分析中利用 t-SNE 算法降维准确率更高，泛化能力更强，可以得到较好的分群结果。

3. 结论

随着流式细胞术的快速发展，当前医学上对多色多参数流式数据进行自动分析已成为研究热点，传统的人工设门方法存在一定局限，已经难以满足市场需求，而将机器学习算法应用于流式数据自动分群上，是未来仪器自动化的研究方向。本文针对类群呈非对称且有拖尾分布的细胞，提出了基于 t-SNE 降维结合 K-means 算法的自动分群方法。首先利用 t-SNE 算法对原始高维流式数据降维，提取特征主成分，使得降维后的数据在特征空间中呈现的类群分离效果最好；然后利用 K-means 算法处理主成分数据，实现细胞的自动聚类。实验数据为人体外周血细胞，利用 t-SNE 算法与 KPCA 算法处理的分群结果，分别与传统人工分群结果进行对比，结果表明，利用 t-SNE 算法处理类群呈非对称且有拖尾分布的细胞，分群准确率有较大提高，对于普通的服从高斯分布的细胞类群分群识别能力也有所提高，分群准确率为 92.55%，在流式细胞仪数据的自动化分析领域有较好的应用前景。

Funding Statement

国家自然科学基金（61605010）；教育部“长江学者和创新团队”发展计划（IRT_16R07）