鸽子目标导向抉择任务中锋电位和局部场电位解码性能对比研究

Abstract

锋电位（spike）和局部场电位（LFP）是神经信息解码中最重要的两种候选信号。目前对于哺乳类动物的spike信号和LFP信号的解码性能已有诸多研究，但是鸟类大脑这两种信号的解码性能并不清楚。本文利用6只鸽子为模式动物，基于留一法和k近邻的神经解码算法（LOO-kNN）研究了目标导向抉择任务中弓状皮质尾外侧区spike信号和LFP信号的解码性能，探讨了通道个数、解码窗口的位置、长度以及最近邻k值等参数对解码性能的影响。本文研究结果表明，spike信号和LFP信号都能有效解码出目标导向抉择任务中鸽子的运动意图，但是相比之下，LFP信号解码性能更优异，而且受通道个数的影响较弱。对于解码窗口而言，最佳解码窗口位于目标导向抉择过程的后半段，而且LFP信号最佳解码窗口长度（0.3 s）明显短于spike信号最佳解码窗口长度（1 s）。对于LOO-kNN算法来说，解码正确率与k值的大小基本成反比，k值越小解码正确率越高。通过以上本文研究结果，期望本文方法有助于大脑神经信息处理机制的解析，对于脑—机接口等进一步深入研究提供一定的参考价值。

引言

神经信息解码是基于大脑神经信号并利用信号处理与模式识别算法，实现对外界刺激参数的预测或解读，比如图像、气味、运动轨迹、意图等^[1-4]，其对于神经信息处理机制解析及脑—机接口研发等都具有十分重要的意义。在神经信息解码的候选信号中，基于微电极阵列胞外方式采集的神经信号由于具有较高的时间和空间分辨率^[5]，得到了大多数研究人员的青睐。微电极阵列记录的神经活动主要由两种信号组成，即以耗能形式主动传播的高频锋电位（spike）（0.25～5 kHz）和在传播中会发生衰减和变形的低频局部场电位（local field potential, LFP）（0～0.25 kHz）。虽然这两种信号分布在不同的频带，而且具有不同的编码模式，但是它们都携带有外界刺激信息，在目前运动意图神经信息解码中得到了广泛应用。

对于 spike 和 LFP 信号解码性能的研究由来已久。早在 20 世纪 90 年代末，Chapin 等^[6]就利用大鼠运动皮层 spike 信号实现了对压杆行为中前肢运动意图的解码，并且针对不同动物的解码正确率基本都在 60% 以上。2003 年，Mehring 等^[7]对比分析了 spike 信号和 LFP 信号的解码性能，发现在猴子手部运动的解码中，LFP 信号和 spike 信号具有类似的解码性能。随后，经过大量的实验研究发现，在神经信息解码中 spike 信号和 LFP 信号各有千秋，在解码精度上 spike 信号的性能要优于 LFP 信号，但是在长期解码中，LFP 信号则具有更好的可靠性和稳定性^[8-9]。但是，目前对于 spike 信号和 LFP 信号解码性能的研究都是在大（小）鼠、猴子等哺乳动物上开展的，鸟类的研究较少。相对于哺乳动物，鸟类独自经历了近 3 亿年的进化历程，而且在运动方式、生活习性等上都存在差异，它们是否分享了类似的神经计算原理还有待检验。

针对鸟类大脑 spike 信号和 LFP 信号的解码性能，本文以鸽子为模式动物，利用基于留一法（leave-one-out, LOO）和 k 最近邻（k-nearest neighbor, kNN）的神经解码算法——LOO-kNN 算法，结合微电极阵列采集当鸽子执行以食物和指示灯为目标，选择最终目的地的“目标导向抉择任务”时弓状皮质尾外侧区（nidopallium caudolaterale, NCL）的神经信号，对比了 spike 信号和 LFP 信号的解码性能，讨论了通道个数、解码窗口的位置、长度等参数对于解码性能的影响，并分析了最近邻 k 值变化时解码正确率的动态变化特性。基于本文的研究结果，将有助于解析鸽子大脑的神经信息处理机制，今后对于脑—机接口等智能假肢的研究或可具有一定的参考价值。

1. 材料与方法

1.1. 神经解码算法

在神经信息解码中，本文利用 LOO-kNN 算法，分析了目标导向抉择任务中 NCL 区 spike 信号和 LFP 信号对鸽子运动意图的解码性能。本文将 kNN 算法与 LOO 算法相结合，不仅能够提高样本的利用率，而且在类别决策时，只与极少量的相邻样本有关，可在一定程度上减少噪声样本对分类的干扰。

1.1.1. kNN 算法

kNN 算法是一种经典的非参数分类方法，其工作原理是首先找到被分类对象在训练数据集中的 k 个最近的邻居，然后根据这些邻居的分类属性进行投票，将得出的预测值赋给被分类对象的分类属性^[10]。假设存在 n 个样本 x₁, x₂, , x_n，已知每个样本的分类属性 y₁, y₂, , y_n。样本 x_i（i = 1, 2, , n） 为多维变量，分类属性 y_i 为离散性变量，其值域定义为 C，C = {c₁, c₂, , c_m}，y_i ∈ C，m ≤ n。对于一个新样本 x，为了获得其分类属性 y，首先应计算新样本与每个已知样本的距离，然后根据距离的大小对已知样本重新进行排序，即如式（1）所示：

1

其中‖·‖表示距离范式，x_（i）（i = 1, 2, , n）表示重新排序的样本。与新样本 x 距离最小的 k 个已知样本即为新样本的 k 个最近邻，x 的分类属性就由其 k 个近邻的分类属性投票决定，即如式（2）所示：

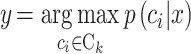2

其中 C_k 为样本 x 的 k 个最近邻分类属性的值域。

综上所述，kNN 算法的性能由两个参数决定，即最近邻的个数和距离范式。根据文献[10]的研究结果，如果没有特别说明，本文选用近邻个数 k = 1 和欧氏（Euclidean）距离进行 kNN 算法的计算。

1.1.2. LOO-kNN 解码算法

LOO 算法是一种通常用来训练和测试分类器的交叉验证方法^[11]，本文将其与 kNN 算法进行了结合。假设每只鸽子进行 N 次实验并分别记录，即 N 个样本，共包含有 M 个运动方向，即其分类属性的值域为 C = {c₁, c₂, , c_m}。

关于 LOO-kNN 算法的基本原理在文献[12-13]已进行过详细叙述，本文简述如下：每只鸽子，对于其 N 个样本，首先选取其中 1 个样本作为测试集，其余 N – 1 个样本则作为训练集，并对其进行类别标记；其次利用 kNN 算法和训练集获得测试样本的类别属性，作为该样本的解码结果。如此循环，直到解码出所有 N 个样本的类别属性，即运动方向。最后，将解码出的 N 个样本的类别与其真实类别进行对比，即可得到解码的正确率（accuracy，以符号 A 表示），即如式（3）所示：

3

其中 N_right 为正确解码的样本个数。

1.2. 信号采集与处理

本文实验动物选用 6 只经过预训练筛选后的成年家鸽，体重 450～550 g，雌雄各半。实验中，训练鸽子在十字迷宫中执行目标导向抉择任务，如图 1 所示。关于实验鸽子行为训练范式和神经信号的采集与处理详细信息参考文献[12-13]，本文简述如小节 1.2.1～1.2.3 所示。

图 1.

Behavioral apparatus and experiment design

实验装置与训练范式

1.2.1. 行为训练

如图 1 所示，训练中首先将鸽子放置在等待区，训练鸽子在提示音响起后由抉择臂进入“十字迷宫”，在十字路口根据放置在奖励臂末端的线索（食物和指示灯）进行“目标导向抉择任务”（左转、右转或直行），待鸽子获得食物奖励后，必须返回实验等待区，等待下一次实验的开始。如果鸽子正确执行了行为范式，将在等待区额外获得一次食物奖励。每次实验中，提示线索出现的方向是随机的。待鸽子在连续两天中行为正确率大于 90% 时，进行微电极阵列的植入。

1.2.2. 信号采集

微电极阵列植入手术前，将实验鸽子进行全身麻醉，俯卧固定于脑立体定位仪（ST-5ND-C，成都仪器厂，中国）上。参考鸽子脑立体定位图谱^[14]，确定 NCL 区位置，去除颅骨和硬脑膜，进行微电极阵列（4 × 4 排列，共 16 通道）植入。待电极到达目标位置后，用牙科水泥（II 型，香港德派实业有限公司生产）对电极进行固定，并进行伤口缝合和消毒处理，等待动物苏醒与恢复。经过 5～7 d 恢复之后，开始对鸽子进行神经信号采集，即在鸽子执行 1.2.1 小节介绍的相关行为任务的同时，用神经信号采集装置（Cerebus^TM, Blockrock Inc., 美国）检测鸽子 NCL 区的神经信号。实验中共采集了 6 只鸽子的神经信号，这 6 只鸽子分别编号为 P010、P600、P601、P605、P609 和 P619。

1.2.3. 信号处理

针对 1.2.2 小节采集后的 spike 信号，处理方式依序为：滤波（0.25～5 kHz）、spike 信号检测、去噪，获得不同通道的 spike 信号发放序列。其中滤波器采用神经信号采集装置默认的二阶巴特沃斯（Butterworth）滤波器；spike 信号检测采用经典的幅度阈值法，阈值为 4～5 倍信号均方根，用于将 spike 信号与背景噪声分离；去噪算法采用具有较高识别精度且易于实现的电极间相关法^[15]，用于去除 spike 信号中误检的大幅值干扰。而对于采集的 LFP 信号，同样需经过以下处理：滤波（0～0.25 kHz）、去除基线漂移、降采样、去噪，获得不同通道的 LFP 信号。其中去噪环节采用自适应共同空间参考算法^[16]，该算法将自适应干扰对消与共同空间参考相结合，能在提高信号去噪性能的同时降低信号的畸变。spike 信号的采样频率为 30 kHz，LFP 信号的采样频率为 2 kHz。

1.3. 统计分析

文中解码特征和解码正确率等一般以均值 ± 标准差的形式表示。在统计分析中，利用威尔科克森（Wilcoxon）秩和检验度量差异是否具有统计学意义^[17]，显著性水平设置为 5%，即 P < 0.05 被认为差异具有统计学意义。在统计分析中，威尔科克森秩和检验是一种非参数检验方法，其利用样本秩代替了样本值，不要求样本总体服从正态分布。

2. 结果

2.1. 单个通道解码性能的对比分析

如图 2 所示，给出了目标导向抉择任务中微电极阵列采集的典型 spike 信号和 LFP 信号，图中自动门、转向前红外检测器（turning begin sensor, TBS）和转向后红外检测器（turning end sensor, TES）的位置分别用红色竖直线标识。图中的红色矩形虚线标记了实验鸽子在执行目标导向抉择任务中的 spike 信号发放序列和 LFP 信号波形图。由图 2 可知，在实验鸽子执行目标导向抉择任务中 spike 信号发放率和 LFP 信号的高频振荡都明显增加，在 TES 附近达到峰值。因此，在分析 spike 信号和 LFP 信号解码性能时，选取 TES 附近 1 s 的窗口内，即从 TES 前 0.5 s 到 TES 后 0.5 s 之间的神经信号作为解码信号。

图 2.

Spike signal and LFP signal during goal-directed decision-making task

目标导向抉择任务中 spike 信号和 LFP 信号

此外，为了提取实验鸽子执行目标导向抉择任务过程中神经信号的解码特征，根据文献[12-13]的研究结果，对于 spike 信号，将解码时间窗中 spike 信号发放率作为 spike 信号的解码特征，而对于 LFP 信号，将 LFP 信号中 0～100 Hz 均分成 10 个不同的子带，即 0～10 Hz, 10～20 Hz, , 90～100 Hz，通过计算不同子带的发放率，选取 40～50 Hz 和 50～60 Hz 两个子带，即 40～60 Hz 中信号能量作为 LFP 信号的解码特征。

如图 3 所示，给出了单个通道 spike 信号和 LFP 信号的解码性能。图中的虚线为随机解码正确率（1/3≈33%），即三个方向随机进行选择的正确率。由图 3 可知，对于 spike 信号，单个通道的解码正确率并不高，6 只鸽子的解码正确率都低于 60%，而且只有两只鸽子，编号为 P600 和 P605的解码正确率高于随机解码正确率，差异具有统计学意义（P < 0.05）。但是对于 LFP 信号，大部分鸽子的解码正确率都高于 60%，而且 6 只鸽子单个通道的解码正确率都高于随机解码正确率，差异具有统计学意义（ P < 0.05），甚至有些通道的解码正确率高于 95%，比如编号为 P605 的第 13 通道和编号为 P609 的第 10 和第 16 通道。

图 3.

Comparison of single channel decoding performance between spike signal and LFP signal

spike 信号和 LFP 信号单个通道解码性能的对比

2.2. 通道个数对解码性能的影响分析

如图 4 所示，给出了 spike 信号和 LFP 信号解码正确率与通道个数之间的变化关系。图中解码正确率曲线为所有通道（共 16 个）根据通道个数随机选择的 10 次重复实验平均值，即每次计算时从所有通道中随机选择相应的通道数计算解码正确率，并重复 10 次，计算其平均值。由图可知，对于 spike 信号，随着通道个数的增加，除编号为 P605 和编号为 P609 的鸽子之外，其余 4 只鸽子的解码正确率都有明显提高，其中编号为 P600 的鸽子最大解码正确率甚至达到了 95% 以上。而对于 LFP 信号，随着通道个数的增加，LFP 信号解码正确率增加并不明显。但是对于不同的通道个数，LFP 信号都能获得较好的解码性能。

图 4.

Effect of the number of channels on decoding performance

通道个数对解码性能的影响

* P < 0.05

* P < 0.05

在此基础上，本文对比分析了单个通道和全部通道（即 16 个通道）作为解码特征时 spike 信号和 LFP 信号解码正确率，结果如图 4 所示。由图 4 可知，对于 spike 信号，全部通道作为解码特征时的解码正确率明显高于单个通道作为解码特征时的解码正确率，差异具有统计学意义（P < 0.05）。而对于 LFP 信号，尽管全部通道作为解码特征时解码正确率也高于单个通道作为解码特征时的解码正确率，但是差异并不具有统计学意义（ P > 0.05）。

此外，如图 4 所示，进一步分析了全部通道作为解码特征时解码正确率的混淆矩阵（confusion matrix）。混淆矩阵也被称作错误矩阵（error matrix），是一种评价分类性能的可视化矩阵，其中每一列表示预测的类别，每一行表示真实的类别，每个矩阵块中的数值表示预测的正确率。从混淆矩阵可知，对于 spike 信号，其对左转和直行的分类能力要优于对右转的分类能力，而对于 LFP 信号，其对不同方向的预测能力比较均衡，预测性能也优于 spike 信号的预测性能。

2.3. 解码窗口位置对解码性能的影响分析

在 2.1 节和 2.2 节对 spike 和 LFP 信号解码性能分析的基础上，进一步分析了解码窗口位置对解码性能的影响，结果如图 5 所示。图中的圆圈为 6 只鸽子的平均解码正确率，实线为二阶多项式的拟合结果。为了获得最佳的解码窗口位置，在分析解码窗口位置对解码正确率的影响时，将其分为以 TBS 位置为对齐点和以 TES 位置为对齐点两种情况进行讨论，两种情况中窗长都为 1 s，步长为 0.1 s，总时长为 3 s。

图 5.

Effect of the position of decoding window on decoding performance

解码窗口位置对解码性能的影响

由图 5 中的二阶多项式的拟合曲线可知，无论是以 TBS 为对齐点还是以 TES 为对齐点，结果都显示，在实验鸽子执行目标导向抉择任务过程中，越接近 TES 解码正确率越高，这一结果也与神经信号响应的位置基本吻合。但相比之下，以 TES 为对齐点的解码正确率峰值要高于以 TBS 为对齐点的解码正确率峰值。而且，就整体而言，LFP 信号的解码正确率高于 spike 信号的解码正确率。

2.4. 解码窗口长度对解码性能的影响分析

除了解码窗口的位置，解码窗口的长度也影响着神经信号的解码性能。由图 6 所示，分析了解码窗口的长度对解码正确率的影响。根据 2.3 节的分析结果，解码窗口的位置以 TES 为对齐点，初始解码窗口的长度和步长都设置为 0.1 s，总时长为 2 s。图中的圆圈为 6 只鸽子的平均解码正确率，实线为二阶多项式的拟合结果。由图 6 可知，随着解码窗口长度的增加，spike 信号和 LFP 信号的解码正确率都是先增加后下降，但是 spike 信号在解码窗口长度为 1 s 附近达到峰值，LFP 信号则在解码窗口长度为 0.3 s 附近达到峰值。基于二阶多项式的拟合结果来看，spike 信号解码正确率出现了明显的峰值，但是 LFP 信号解码正确率则近似为直线下降。这一结果表明在获得最优的解码性能时 spike 信号的耗时可能更长。

图 6.

Effect of the length of decoding window on decoding performance

解码窗口长度对解码性能的影响

2.5. 最近邻 k 值对解码性能的影响分析

由图 7 所示，分析了最近邻 k 值对解码正确率的影响。最近邻 k 值的初始值设置为 1，步长也设置为 1。图中的圆圈为 6 只鸽子的平均解码正确率，实线为一阶多项式的拟合结果。由图 7 可知，无论是 spike 信号还是 LFP 信号，随着 k 值的增加，解码正确率基本呈下降趋势。但相比之下，LFP 信号解码正确率的下降趋势更明显。而且最近邻 k 值的大小与解码正确率基本呈反比，即 k 值越大解码正确率越低。这一结果表明，最近邻 k 值也影响了神经信号的解码性能。

图 7.

Effect of nearest neighbor k value on decoding performance

最近邻 k 值对解码性能的影响

3. 讨论

在神经信息解码中，spike 信号和 LFP 信号是两种最主要的候选信号^[18]，对于脑—机接口、大脑信息处理机制解析等都具有重要意义。本文对比分析了鸽子 NCL 区 spike 信号和 LFP 信号在神经信息解码中的性能，并在此基础上进一步分析了通道个数、解码窗口的位置、长度及最近邻 k 值等参数对解码正确率的影响。研究结果表明：① 尽管 spike 信号和 LFP 信号都能解码目标导向抉择任务中鸽子的运动意图，但是相比之下，LFP 信号具有更优异的解码性能；②spike 信号解码性能受通道个数的影响较大，LFP 信号解码性能受其影响则较小，这表明不同通道之间 LFP 信号可能具有更大的信息冗余；③ 解码窗口的位置和长度都会影响解码正确率，研究发现响应越强烈的位置解码正确率一般越大；④ 对于 LOO-kNN 解码算法，解码性能与最近邻 k 值的大小成反比，较小的近邻个数得到的解码性能更优。

对于微电极阵列采集的两种不同频带范围的神经信号，spike 信号来自于电极尖端附近单个神经元的活动，LFP 信号则是电极尖端附近神经元兴奋性和抑制性突触后电位的总和^[19]。本文的研究发现，对于单个通道而言，LFP 信号解码正确率要优于 spike 信号解码正确率，但是随着通道个数的增加，6 只鸽子中 4 只鸽子的 spike 信号解码正确率都明显增加，但所有鸽子的 LFP 信号解码正确率变化都不明显。这一结果表明不同通道 LFP 信号之间的信息冗余要大于 spike 信号之间的信息冗余，这与这两种信号的特性基本是一致的。此外，研究还发现，大部分鸽子的 spike 信号和 LFP 信号之间的解码性能基本一致，即如果 spike 信号表现出较好的解码性能，则 LFP 信号的解码性能也不差。但是这种对应关系并不是绝对的，比如编号为 P605 鸽子，其 spike 信号的解码正确率并不高，而 LFP 信号却表现出较高的解码正确率。而且，就整体而言，LFP 信号的解码正确率整体上也要优于 spike 信号的解码正确率。这意味着对于长期植入的微电极阵列信号采集实验，LFP 信号可能更适合作为神经信息解码的候选信号。

此外，在解码参数上，本文的研究结果发现，无论是以 TBS 为对齐点还是以 TES 为对齐点，TES 附近的解码正确率都明显高于 TBS 附近的解码正确率，而且相比之下，以 TES 为对齐点的解码正确率整体上要高于以 TBS 为对齐点的解码正确率。这表明，神经信号的解码性能除了与解码窗口的位置有关外，与对齐点的位置可能也有关，这暗示着在微电极阵列信号采集实验中对齐点的位置也影响着实验结果。在目标导向抉择任务中，诱导鸽子进行抉择的线索，即目标位于奖励臂的末端，鸽子到达十字路口并发现目标位置之前，是不能进行抉择的，因此鸽子进行抉择的行为应该是看到食物后进行的，即靠近 TES 位置，这可能也是 TES 附近解码正确率高于 TBS 附近解码正确率的原因。此外在神经信息解码中，解码窗口的长度也影响着解码正确率。实验结果显示，LFP 信号的最优解码窗口集中在 0.3 s 附近，而 spike 信号的最优解码窗口则在 1 s 附近，这可能暗示着神经元集群信号解码性能要优于单个神经元信号的解码性能，但是深层次原因还需深入研究。

对于解码算法，LOO 方法是一种统计分析中对分类器进行交叉验证的方法，其有两个优点：① 每一次计算中几乎所有样本皆用于模型训练，使得训练样本最接近原始样本分布，解码结果比较可靠；② 实验过程中没有随机因素影响实验数据，确保实验过程可以被复制。但其主要缺点就是计算成本高、速度慢。而 kNN 算法的优势就是计算简单、易于实现，特别适合多分类问题。因此将 LOO 算法和 kNN 算法相结合，可以充分发挥各自优势。此外，LOO 算法和 kNN 算法都是非参数算法，影响 LOO-kNN 算法解码结果的最主要参数就是最近邻 k 值。研究结果显示，LOO-kNN 算法解码性能与 k 值基本成反比，即随着 k 值的增加，spike 信号和 LFP 信号的解码正确率都呈下降趋势，这与目前的研究结果基本一致^[10]。这一结果也为 LOO-kNN 算法的应用提供了有益的借鉴。

综上所述，本文利用 NCL 区 spike 信号和 LFP 信号针对鸽子运动意图的神经解码问题，对比分析了这两种信号的解码性能，并探讨了通道个数、解码窗口的位置、长度及最近邻 k 值等参数对解码正确率的影响。结果表明，尽管 spike 信号和 LFP 信号都能有效解码目标导向抉择任务中鸽子的运动意图，但是 LFP 信号具有更优的解码性能，受通道个数的影响也较弱。在解码窗口位置的选择上，最佳的解码窗口位于 TES 附近，而且 LFP 信号的最佳解码窗口长度（0.3 s）明显短于 spike 信号的最佳解码窗口长度（1 s）。对于 LOO-kNN 算法，spike 信号和 LFP 信号的解码正确率与最近邻 k 值基本成反比。本文的结果将有助于鸽子大脑神经信息处理机制的解析，而且对于脑—机接口等也有重要的参考价值。

Funding Statement

国家自然科学基金资助项目（61673353, 61603344）；河南省科技厅科技攻关项目（182102210099）；河南省脑科学与脑机接口技术重点实验室开放基金（HNBBL17005）