基于 Gabor 小波-传递熵的脑-肌电信号同步耦合分析

Abstract

Synchronization analysis of electroencephalogram (EEG) and electromyogram (EMG) could reveal the functional corticomuscular coupling (FCMC) during the motor task in human. A novel method combining Gabor wavelet and transfer entropy (Gabor-TE) is proposed to quantitatively analyze the nonlinearly synchronous corticomuscular function coupling and direction characteristics under different steady-state force. Firstly, the Gabor wavelet transform method was used to acquire the local frequency-band signals of the EEG and EMG signals recorded from nine healthy controls simultaneously during performing grip task with four different steady-state forces. Secondly, the TE of local frequency-band was calculated and the unit area index of the transfer (A_TE) was defined to quantitatively analyze the synchronous corticomuscular function coupling and direction characteristics under steady-state force. Lastly, the effect of EEG and EMG signal power spectrum on Gabor-TE analysis was explored. The results showed that the coupling strength in the beta band was stronger in EEG→EMG direction than in EMG→EEG direction, and the A_TE values in the beta band in EEG→EMG direction decreased with the force increasing. It is also shown that the difference in TE values of gamma band present a varying regularity as the increase of force in both directions. In addition, EMG power spectrum was significantly correlated with the result of Gabor-TE inspecific frequency band. The results of our study confirmed that Gabor-TE can quantitatively describe the nonlinearly synchronous corticomuscular function coupling in both local frequency band and information transmission. The analysis of FCMC provides basic information for exploring the motor control and the evaluation of clinical rehabilitation.

引言

大脑运动皮层的脑电（electroencephalogram，EEG）信号和相应的肢体对侧的肌电（electromyographic，EMG）信号能够分别反映大脑对肢体运动的控制信息及肌肉对大脑的反馈信息，揭示了肢体运动过程中大脑皮层与相应肌肉间的功能耦合（functional corticomuscular coupling，FCMC）连接^[1]。皮层肌肉功能耦合研究在一定程度上能够反映大脑皮层与肌肉间的相互作用关系^[2]，有助于理解运动控制与运动障碍病理机制。

皮层与肌肉之间的神经振荡是由皮层将控制指令传递到肌肉，同时肌肉将感觉信息传递回皮层^[3]。1995 年有学者发现在运动过程中 EEG-EMG 信号间存在相关性^[4]，随后有研究者基于相干分析方法（coherence）探究了健康受试者 EEG-EMG 信号间的耦合关系^[5]；但利用相干分析难以描述 EEG-EMG 信号间复杂的相频关系，因此有研究将格兰杰因果关系（granger causality，GC）应用于 EEG-EMG 信号同步分析^[6-8]，并发现了 EEG-EMG 信号间的双向耦合，上述方法能够描述 EEG-EMG 信号间的双向因果性传递规律；然而 EEG 信号和 EMG 信号间还存在非线性耦合关系，上述一致性和格兰杰因果分析方法不能有效刻画 EEG-EMG 信号间非线性耦合特征；基于此，Schreiber^[9]提出的传递熵（transfer entropy，TE）具有不依赖既定模型、非线性、定量分析等特点，可应用于探索 EEG-EMG 信号间的非线性耦合特征^[10]。

另一方面，由于 EEG、EMG 信号非平稳、频域特征突出，在不同的特征频段耦合特征存在明显差异。已有研究表明，在手部微弱或适中的静态力输出时 β 频段（15～35 Hz）相干性较强^[8]，而在较大肌力或动态力输出时 γ 频段（35～50 Hz）出现同步振荡^{[7, 11]}，可见有必要研究特定频段的 EEG-EMG 信号同步耦合特征。为此，有研究将经验模态分解（empirical mode decomposition，EMD）^[12]、变分模态分解（variational mode decomposition，VMD）^[13]、小波分解^[14]等方法应用于 EEG、EMG 信号的分解，从而进行动作特征提取或 EEG-EMG 信号特征分析，但 EEG-EMG 信号局部非线性耦合特征复杂，因此需将 EEG、EMG 信号分解至单个频带，进一步提取特征频段进行分析。其中，Gabor 小波变换具有高频率分辨率特性，可以将包含不同频率成分的 EEG、EMG 信号分解至局部频带^[15]。进而，有研究提出基于 Gabor 小波和格兰杰因果关系的 EEG-EMG 信号同步性分析方法^[16]，该方法有效地刻画了 EEG-EMG 信号间的线性耦合关系，但对于大脑皮层与肌肉组织之间的高度复杂非线性的特征，需更进一步地研究 EEG-EMG 信号间非线性同步耦合特征。

基于以上研究，本文提出基于 Gabor 小波变换和 TE 的 Gabor-TE 方法，用于定量描述特定频段 EEG-EMG 信号间局部非线性同步耦合特征，并用于分析在恒定握力下运动皮层和肌肉间功能耦合关系。通过分析在 4 种不同恒定握力水平下局部频段非线性同步耦合特征和方向特性，以验证该方法的可行性，为进一步探索运动功能障碍的产生机制及康复过程中的运动功能评价方法提供了依据。

1. 信号采集与预处理

1.1. 数据采集

本研究募集了 9 名无任何病史的健康受试者，性别为 2 男、7 女，年龄（24.2 ± 3.0）岁，所有受试者均自愿签订知情同意书。试验环境为安静的屏蔽室，受试者右手持握力传感器端坐在舒适的座椅上，如图 1 所示。在距离受试者 80 cm 的屏幕上可显示目标力（target force，TF）（以红线表示）和受试者实际输出力（exerted force，EF）（以绿线表示），如图 1 所示。本试验要求受试者实时维持绿线追踪红线从而维持恒定力输出，握力信号的采样频率为 50 Hz。首先测试每位受试者的最大自主收缩握力（maximum voluntary contraction，MVC），再分别记录受试者在自身 MVC 范围内 10%、20%、40% 和 60% 的数据。为防止受试者产生疲劳，分别进行 30 次试验，每次试验时间为 10 s，彼此时间间隔为 2～3 min。

图 1.

The synchronous acquisition of the EEG and EMG signals

不同握力下 EEG 和 EMG 信号同步采集试验

试验采用脑电采集系统 Neuroscan（Synamp2.，美国）同步采集 EEG 和 EMG 信号并做好相关数据记录。采集 64 通道 EEG 信号，电极位置按照国际标准导联 10–20 系统安放，同时采集水平和垂直两通道的眼电信号。另外，利用脑电信号采集系统预留的 2 通道采集受试者两块肌肉处的 EMG 信号，分别为前臂尺侧腕屈肌和桡侧腕长伸肌，其采样频率为 1 000 Hz。

1.2. EEG 信号与 EMG 信号预处理

基于 EEG 信号和 EMG 信号非常微弱、易受干扰，首先对采集的原始 EEG 信号进行 5～50 Hz 滤波处理，并进行去除基线漂移和去工频等干扰，再运用独立分量分析方法去除眼电、EMG 信号等伪迹；其次对采集到的 EMG 信号进行滤波处理（5～200 Hz），并进一步采用自适应滤波方法去除工频干扰；最后，对预处理后的 EEG、EMG 信号进行降采样，并对 EMG 信号进行全波整流处理。截取受试者握力水平处于较为平稳状态下的 EEG-EMG 数据，每位受试者每种试验任务（10%、20%、40% 和 60% MVC）各得到 240 段数据。

2. EEG-EMG 信号的 Gabor-TE 方法分析

2.1. Gabor 小波变换

Gabor 小波变换可以达到频域局部化的目的，能够按照数据分析要求实现局部频带 EEG 信号及 EMG 信号的获取。其中，x（t）和 y（t）分别表示预处理后的 EEG-EMG 信号，经过 Gabor 小波变换方法进行时频分解的公式如下^[16]：

$X(f,t)=h(f,t)*x(t)\equiv {\displaystyle \int h(u)x(t+u)\text{d}u}$ (1)

$Y(f,t)=h(f,t)*y(t)\equiv {\displaystyle \int h(u)y(t+u)du}$ (2)

X（f，t）、Y（f，t）分别表示频率 f 的 EEG- EMG 信号在时间点 t 处的幅值特征，本文将频率分辨率设置为 1 Hz，并分别提取中心频率 Hz 的 EEG、EMG 信号。h（f，t）为 Gabor 函数，如公式（3）所示：

3

式中，ω₀ 为无量纲常数，k₁ 为归一化系数，它决定了时频分辨率。中心频率 ω = ω₀/a，a 为尺度因子。

利用 Gabor 小波变换将 1.2 节预处理后的 EEG 信号和 EMG 信号的时间序列信号在 1～50 Hz 频段范围内分解为间隔为 1 Hz 的 49 个子频带信号。

2.2. EEG-EMG 信号的 Gabor-TE 方法分析

首先，基于 2.1 节分解后的 EEG、EMG 信号，构建 EEG 信号序列 和 EMG 信号序列 ，G₁ 和 G₂ 分别为 EEG 信号和 EMG 信号子频带个数。

然后，根据 TE 的定义^[17]，分别计算 到 的 TE 值（TE_G-EEG→EMG），如式（4）所示，

4

式中，t 为离散的时间指标；u 为预测时间；m、n 分别为延迟向量；p（·）为变量之间的联合概率。同理可计算出 到 的 TE 值（TE_G-EMG→EEG），如式（5）所示，

5

TE_G-EEG→EMG 和 TE_G-EMG→EEG 分别代表 EEG→EMG 和 EMG→EEG 方向上的 TE 值，TE 值越大，说明在该特征频段内大脑皮层与肌肉间的耦合关系越强，反之亦然。

2.3. EEG-EMG 信号间同步耦合定量指标

TE 值可描述 EEG、EMG 信号在各频段间的耦合强度及方向特性，为进一步定量刻画 β 和 γ 特征频段在不同方向上 EEG-EMG 信号间的同步耦合特征差异，本文借鉴一致性分析的相干面积指标^[18]，提出单位传递面积指标 A_TE，计算公式如下：

6

7

式中，∆f 表示频率分辨率，f₁～f_n 代表频率范围，β 频段范围为 15～35 Hz，γ 频段范围为 35～50 Hz。A_TE-EEG→EMG 和 A_TE-EMG→EEG 则分别表示在不同方向上 EEG-EMG 信号间的 TE 单位传递面积指标，A_TE 值越大表示在该特征频段 EEG-EMG 信号耦合强度越高，反之亦然。

3. 试验结果与讨论

人类运动神经系统由皮层与肌肉间的神经振荡来传递相应信息，从而引起相应的神经元与运动单元之间的同步振荡活动，进而揭示了运动过程中人类大脑皮层与肌肉间的耦合特征规律。本文基于 Gabor-TE 方法，对 EEG-EMG 信号在不同方向、局部频带的非线性同步耦合特征进行分析。

首先，按照 2.1 中试验过程介绍的将同步采集的 9 名健康受试者在 10%、20%、40% 和 60% 的 MVC 下 4 种恒定握力水平的 EEG、EMG 信号进行预处理，进一步运用 Gabor 小波变换方法分别提取 EEG-EMG 数据在 1～50 Hz 内各频带的信号。

为描述 EEG-EMG 信号间的耦合特征，本文计算了不同频段间的 TE 值，并定义了 A_TE，定量描述 EEG-EMG 信号在不同耦合方向上特征频段（β、γ）的非线性耦合特征。如图 2 所示为所有受试者在 10%、20%、40% 和 60% MVC 握力水平下的平均 TE_G-EEG→EMG 和 TE_G-EMG→EEG。分析结果显示，不同握力恒定输出时，所有受试者的皮层肌肉功能耦合具有双向性（EEG→EMG、EMG→EEG），同时，皮层与肌肉 β 频段（15～35 Hz）间的耦合强度最强，这与 Witham 等^[2]研究得到的“在肌肉稳定收缩过程中，振荡在感觉运动皮层和响应的肌肉间双向传导”的结论相一致，表明随着皮层的运动指令下行达到肌肉的同时也伴随着来自收缩肌肉的传入神经反馈过程^[19]。

图 2.

The average TE values analysis of all the subjects

所有受试者平均 TE 分析

为进一步定量描述不同握力水平下 β 和 γ 频段 EEG-EMG 信号间的同步耦合强度差异及方向特性，按照 2.3 节方法计算所有受试者 EEG→EMG 及 EMG→EEG 方向上的 β 和 γ 频段 A_TE 值。所有受试者 A_TE 平均值如图 3 所示，分析结果显示： ① 在维持较小恒定握力输出时，β 频段 A_TE 值在 EEG→EMG 方向上强于 EMG→EEG 方向，γ 频段 A_TE 值在 EEG→EMG 和 EMG→EEG 方向上均无明显差异性。② 随着握力水平增大，EEG→EMG 方向上 β 频段 A_TE 值明显降低，EMG→EEG 方向上 γ 频段 A_TE 值明显增大。这表明，较大的恒定握力下受试者运动皮层耗费更多能量以维持稳定运动，使得神经肌肉功能耦合系统处于一个非稳定的状态，导致 β 频段功能耦合强度降低，证实了 β 频段的皮层肌肉功能耦合体现运动皮层对稳定状态的控制功能^[20]；γ 频段 EMG→EEG 方向上 A_TE 的变化与受试者在维持较大握力水平时注意力更加集中有关，Bauer 等^[21]指出 γ 频段神经耦合振荡与受试者注意力相关，当受试者注意力处于集中状态时相应的 γ 频段的耦合振荡增强。因此，γ 频段的皮层肌肉功能耦合特性体现了与试验注意力相关的运动信息动态处理过程。

图 3.

The average unit area analysis of all the subjects

所有受试者平均单位传递面积分析

综上所述，由图 2、图 3 分析可得，γ 频段 TE、A_TE 值在 EMG→EEG 和 EEG→EMG 不同方向上随握力的增加而变化。在握力水平较低时，γ（35～50 Hz）频段 TE 值在 EEG→EMG 方向上高于 EMG→EEG 方向，但随着握力增大，γ 频段 TE 值在 60%MVC 下 EMG→EEG 方向上出现峰值，如图 2 所示。相关研究表明，γ 频段 EEG-EMG 信号同步性与较大或动态力输出相关^{[20, 22]}，这说明 γ 频段皮层肌肉功能耦合主要体现了运动信息动态处理与非线性信息传递过程，这与 Tsujimoto^[23]和 Ohara 等^[24]的研究结果一致。

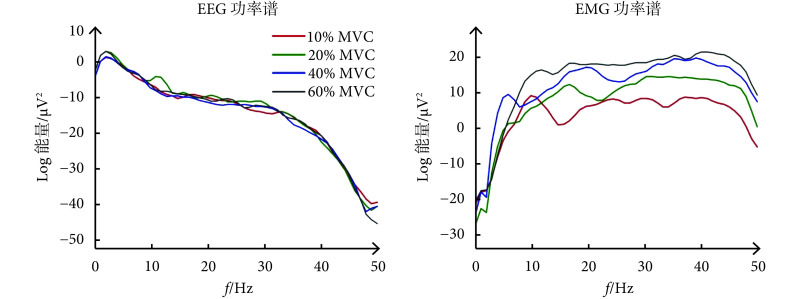
已有研究表明，神经肌肉功能耦合与信号能量、运动性能、性别及年龄等有关^[25-26]。也有研究表明，神经肌肉功能耦合与能量、运动性能等无关^[27]。本文从信号能量方面对 EEG-EMG 信号耦合的影响进行分析研究。如图 4 所示，随握力水平增加，EMG 功率谱随之增加，而 EEG 功率谱无明显变化。进一步进行皮尔逊相关分析结果如表 1 所示，β、γ 频段 EEG 功率谱与不同方向上 β、γ 频段 A_TE 无相关作用；β、γ 频段 EMG 功率谱与不同方向上 β、γ 频段 A_TE 存在极强相关作用（P<0.05，即有统计学意义）。结果表明，EEG 能量对神经肌肉功能耦合没有影响，EMG 能量在神经肌肉功能耦合方面起到一定作用。

图 4.

The average spectral power analysis of all the subjects power

所有受试者平均功率谱分析

表 1. The Pearson correlation-based statistical results between the A_TE values and the power spectrum area of EEG and EMG .

A_TE 和 EEG、EMG 信号功率谱 Pearson 相关统计结果

		EEG→EMG			EMG→EEG
		ATE (β)	ATE (γ)		ATE (β)	ATE (γ)
EEG 功率谱	相关系数	0.008	0.276		–0.086	0.102
	P 值（双边）	0.080	0.139		0.121	0.230
EMG 功率谱	相关系数	0.872	0.763		0.867	0.902
	P 值（双边）	0.015	0.019		0.021	0.009

4. 结论

本文将 Gabor 小波变换引入到 EEG-EMG 信号同步耦合分析之中，并与 TE 方法相结合，构建一种 Gabor-TE 方法以分析研究手部不同恒定握力输出下特征频段 EEG-EMG 信号非线性同步耦合特征的差异及方向特性。Gabor 小波变换便于提取 EEG、EMG 信号局部频域特征且利于不同耦合方向上、不同频段间皮层肌肉耦合分析，有利于全面揭示 EEG-EMG 信号同步耦合的方向性和非线性特征。试验结果表明，皮层肌肉耦合具有方向性，β 频段 TE 值在 EEG→EMG 方向上明显强于 EMG→EEG 方向；随着握力水平的增加，γ 频段 TE 值在 EMG→EEG 方向上出现峰值，并高于 EEG→EMG 方向且同步振荡幅值增加；EMG 功率谱对特征频段的 EEG-EMG 信号耦合强度有一定影响。因此，本文提出的 Gabor-TE 算法能够有效刻画不同频段、不同传递方向上的皮层肌肉间能量耦合特征，为研究运动控制及反馈信息解码及患者康复评价提供一定的理论依据。

Funding Statement

国家自然科学基金资助项目（61271142，61673336）；河北省自然科学基金资助项目（F2015203372）