基于体表心音的左心室血压预测方法研究

Abstract

本文以心音特征为基础，实现了连续的左心室收缩压预测。通过对 3 只比格犬进行实验，以肾上腺素诱发心脏血流动力学发生变化，然后同步采集实验犬的心音、心电、左心室血压等信号，共获取了 28 组有效数据。通过提取心音特征，借助人工神经网络实现了反推左心室收缩血压，获得了较好的预测效果。本研究在较大的血压动态变化范围内，得到了绝对误差均值仅为 7.3 mm Hg、预测血压与测量血压的平均相关系数为 0.92 的实验结果。研究结果显示，本文所述方法有助于实现无创的左心室血流动力的连续监测。

引言

心音图（phonocardiogram，PCG）是心脏及其周围血管组织在血流动力作用下产生的一系列机械振动信号。通过放置在胸腔体表面的传感器，可以将这些声音信号收集起来，俗称体表心音。正常人在一个心动周期内可闻及两组声音，分别是第一心音（sound1，S1）和第二心音（sound2，S2）。它们都能在一定程度上反映出心脏血流动力学的状态，有助于疾病的早期诊断^[1-5]。

早在 50 年前，研究者们就已经开始探索心音特征与血流动力学之间的相互联系。Sakamoto 等^[6]通过对 51 只成年犬进行实验研究，发现了 S1 的幅度与左心室血压上升速率存在着密切的线性关系。Blick 等^[7]在理论上提出了一维瓣膜振动模型来模拟生物瓣膜的振动。以瓣膜两侧血压梯度来代替振动模型所受外力，并根据瓣膜的振动方程求解出位移曲线。通过理论分析，发现瓣膜两侧血压梯度与瓣膜振动所产生的声压幅度存在着密切的联系。Sikarskie 等^[8]借助一维振动模型的理论分析，发现随着瓣膜两侧压力差和压力梯度的增加，瓣膜振动幅度随之增大。以此为基础，Zhang 等^[9]进一步发现主动脉压的增高可同时引发心音振动幅度与频率的增加。Ozcan 等^[10]通过对成人进行主动脉弓处收缩压的有创采集，得出 S2 的幅度与主动脉压有着正相关的线性关系。Hoon 等^[11]通过对健康成人进行数据采集，发现 S1、S2 的幅度比值与收缩压存在较强的相关性。

除了心音幅度特征，诸如时间特征和频率特征也逐渐被人们重视起来。Zhang 等^[12-13]提出了一种心音的时间域特征物理量——RS₂，定义为左心室血压的上升起点到 S2 的开始时刻这一时间间隔。通过理论建模，发现 RS₂ 与血压呈现密切的负相关关系。在此基础上，Wong 等^[14-15]对 RS₂ 这一变量进行了重新定义。在新的定义中，RS₂ 表示以心电信号的 R 波为起点，到 S2 的波峰位置处这一时间间隔。重新定义的 RS₂ 同样与血压呈现出密切的负相关关系，不仅在健康的个体中，甚至在高血压患者中均已证实了该理论的合理性。在 2015 年，Peng 等^[16]通过采集 32 个健康成人的心音信号，并利用 S2 的频率特征，实现了血压预测。

基于以上研究结果，本文选取了 3 只健康比格犬，以肾上腺素诱发动物心脏血流学发生改变，通过信号处理和网络模型训练等方法，实现基于心音信号的左心室血压连续预测的功能。本文工作与前人研究的区别在于：① 本文的左心室血压是通过导管有创采集的，血压值真实可靠，有利于评价血压反推方法的有效性。② 本文实验中血压的动态变化范围较大，收缩压从最小值 100 mm Hg 到最大值 280 mm Hg，有利于评估反推方法在较大血压动态范围内的有效性。③ 本文采用了多个心音特征，有利于研究多特征的联合预测效果。基于以上几点可见，本文提出了一个无创的连续监测左心室血压的方法，从而改进了传统有创监测的弊端。并且本文的血压值范围较传统预测模型有很大提高，这在一定程度上增加了模型的可信度。

1. 方法

1.1. 动物实验

本文动物实验已获得重庆医科大学伦理委员会的批准，并在附属的动物实验中心完成实验。实验过程中采取了相关保护动物的措施^[17-18]。

在数据采集之前，3 只实验犬已进行了为期两周的适应性饲养。实验开始时，先对实验犬进行称重，并以 0.2 mL/kg 的麻醉剂陆眠宁（盐酸塞拉嗪注射液，1 mg∶1 mL，兽药字（2011）070011077，吉林省华牧动物保健品有限公司）对其进行麻醉。将处于麻醉状态下的实验犬以仰卧的姿势固定在实验台上，并用留置针在实验犬的前肢静脉进行穿刺，慢速滴注入 0.9% 的生理盐水以维持后续肾上腺素的注射通道。剪去实验犬左、右肩部和心尖处（左侧胸骨外缘）的毛，将心电电极片贴在肩部剪毛处并将心音传感器（MLT201，ADInstrument，Austra-lia）放置在心尖位置。将心电电极片、心音传感器与生理信号记录仪（PL3508，Powerlab8/35 ADInstru-ment，Australia）连接好并同步采集信号，持续采集 2 min。剪去实验犬颈部表皮的绒毛并用碘酒对颈部裸露的表皮进行消毒，沿颈部正中位纵向切开表皮后分离出一小段右侧颈总动脉，在颈总动脉下端的空隙处穿线备用以固定后续的导管连接。将三通管、导管与生理信号记录仪连接好，该导管与标定好的压力传感器（MLT0699，ADInstrument，Australia）连接。借助三通管向导管内注射肝素（500 units/mL）以防止血液凝固并同时排除导管内的气泡。将连接好的导管沿颈总动脉逆向插入实验犬的左心室。在压力换能器的作用下，记录仪上可以观察到左心室的血压信号。当导管插入到一定的深度后，当出现突破感和落空感并且血压波形变为左心室内压波形时，停止插入。此时的导管前端已到达左心室，并用之前预留的线将导管固定。

准备工作完成后，观察并记录一段同步的心电、心音及左心室血压信号。在此过程中，实验犬处于正常的生理状态。随后，通过预留的静脉通道注入肾上腺素，实验中注射的剂量如表 1 所示。在肾上腺素的作用期间，同步记录信号，直至血压恢复到基线为止，为1组数据采集完毕。改变肾上腺素的注射剂量，重复以上操作。

表 1. Changes of cardiac cycles based on adrenaline function.

肾上腺素作用下的心动周期数变化情况

实验犬	数据记录	肾上腺素 0.5 μg/kg	肾上腺素 1 μg/kg	肾上腺素 2 μg/kg	选取组数
×表示操作不当或因实验犬自身原因等未采用的数据
1	记录编号	#1，#2，#3，#4	#5，#6，#7	#8，#9，#10，#11	5
	心动周期个数	×，326，318，432	447，414，×	×，×，×，×
2	记录编号	#12，#13，#14，#15	#16，#17，#18，#19，#20	#21，#22，#23，#24	10
	心动周期个数	×，611，593，596	719，588，×，537，×	471，449，458，489
3	记录编号	#25，#26，#27，#28	#29，#30，#31，#32，#33	#34，#35，#36，#37	13
	心动周期个数	534，575，536，380	573，582，605，605，584	614，594，508，474

实验结束后，取出实验犬的动脉插管，结扎其颈总动脉并对手术区域进行缝合。对实验犬进行精心饲养，直至其自然死亡。

本文共采集了 37 组数据记录，选取了 28 组有效数据，分布如表 1 所示。其中删去的 9 组无效数据，是因操作不当或实验犬自身原因而存在较大的误差，予以弃除不用，在表中以“×”标记。每组数据包含的心动周期数范围为 326～719。28 组有效数据共包含了 14 612 个心动周期。就目前的文献看，在研究心音特征与心脏血流动力学的关系中，本文所涉及的心动周期数最多。

1.2. 数据处理

1.2.1 心音分割　心音信号分割是将 S1 和 S2 从心音信号中分离出来，为后续的心音特征提取做准备。本文所采用的手段是基于香农能量包络的心音分割方法^[19-20]。

首先对心音信号进行零相位巴特沃斯低通滤波处理，截止频率设置为 160 Hz，以去除噪声干扰。其次，将心音信号进行归一化处理，使其幅度范围在[—1, 1]的区间内，并求出其香农能量E。

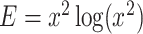1

其中，x 是归一化后的心音信号。随后，用一个宽为 20 ms 的窗对香农能量进行平均滤波，滑动窗有 10 ms 的重叠，如式（2）所示：

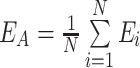2

其中，E_A 表示平均香农能量，E_i 表示位置 i 处的心音信号香农能量，N 表示截取窗宽。因本信号的采样频率为 1 000 Hz，这里的窗宽选取 20。再对平均香农能量进行标准化，如式（3）所示：

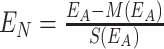3

其中，E_N 是标准化后的平均香农能量，M（E_A）和S（E_A）分别表示平均香农能量的均值和标准差。

设置两个能量阈值来筛选 S1 和 S2 的主峰。根据同步采集的心音信号 R 波位置来对齐 S1 位置，从而可将筛选出来的主峰划分为 S1 和 S2，如图 1 所示。为了较好地统一后续心音信号的整齐性，分别以 S1 和 S2 的最大幅值处为中心，对 S1 和 S2 进行宽度为 141 ms 和 101 ms 的截取。

图 1.

Heart sound segmentation

心音分割示例图

1.2.2 特征提取　根据前人的研究可知，心音信号与血流动力学之间存在着密切的相互联系，其幅度、频率等特征可在一定程度上反映血流动力学状态。为了提高血压预测的实时性，本文选取了部分心音特征，如最大幅值，心音能量，时间特征等，具体描述如下：

（1）幅度特征：分别选取每个心动周期 S1、S2 的最大绝对幅度值，并将其表示为 S1 最大幅度（amplitude of S1，Amp1）和 S2 最大幅度（amplitude of S2，Amp2）。

（2）能量特征：心音能量（Energy，Ener）可表达为式（4）^[21]：

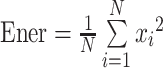4

其中，x_i 表示待求心音，N 表示所截取心音信号的宽度。分别将 S1 和 S2 的能量表示为 S1 的心音能量（Energy of S1，Ener1）和 S2 的心音能量（Energy of S2，Ener2）。

（3）时间特征：在同一个心动周期中，以心电信号的 R 波为起点，到 S2 波峰的时间间隔被定义为时间特征 RS₂^[14-15]。

从每个心动周期内提取以上心音特征和对应的左心室收缩压（systolic blood pressure，SBP）。这些心音特征与 SBP 之间的典型关系，如图 2 所示，为实验犬 3 的数据展示。由图中可以看出，在肾上腺素作用下，实验犬的左心室 SBP 迅速增加，随着肾上腺素代谢，经过约 300 个心跳，血压逐渐恢复到正常值。在此过程中，左心室 SBP 与心音幅度特征、能量特征表现出正相关关系，与时间特征 RS₂ 表现出负相关关系。

图 2.

Relationship between left ventricular systolic pressures and heart sound features

左心室 SBP 与心音特征的关系

1.3. 预测模型

本文引入反向传播（back propagation，BP）人工神经网络作为预测模型，来完成基于心音特征的左心室 SBP 反推。BP 神经网络是一种按误差逆传播算法训练的多层前馈型网络，是目前应用最为广泛的神经网络模型之一^[22-24]，通过其自身的训练及学习，实现了从输入到输出的非线性映射。BP 网络的每一个神经节点（Node）都可表示为输入的加权之和，如式（5）所示：

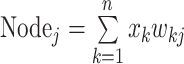5

其中，x_k 表示节点 j 的输入，n 代表输入的维数，w_kj 表示连结节点 k 和结点 j 之间的权系数。

本实验的预测模型选用 4 层神经网络结构，其隐层为 2 层。输入层为所选取的心音特征（5 维），输出层为左心室 SBP（1 维）。第一隐层和第二隐层的节点数分别被设置为 5 和 3。其中第一隐层的传递函数采用非线性 Sigmoid 函数，如式（6）所示。第二隐层的传递函数则采用线性函数，如式（7）所示。

6

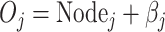7

其中，β_j 表示节点 j 的阈值，O_j 表示节点 j 的最终输出。输出层的传递函数同样采用式（7）的线性函数。

BP 网络的训练过程是一个权系数不断迭代更替的过程，其误差能量，如式（8）所示，随着迭代次数的增加逐渐减小直至稳定，从而可获得最小的训练误差。

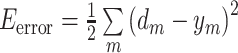8

其中，E_error 是误差能量，m 是训练数据输入输出对的个数，d 是理想输出，y 是实际输出。在整个的训练过程中，沿着能量梯度下降的方向进行系数迭代。

2. 实验结果

本文采用了十折交叉验证（10-fold cross-vali-dation）评估网络预测性能^[25]。实验获得了 28 组记录。将每组记录的心音特征向量作为输入、左心室 SBP 作为输出，平均分成 10 段，并编号为 1 至 10。用 1～9 段对神经网络进行训练，第 10 段用于测试。再以 2～10 段进行训练，第 1 段用于测试。以此重复，直到每一段都被测试过。这种交叉验证的思想保证了每一个心动周期的数据都被测试。将血压的估测结果与实际测量结果进行比较，通过皮尔森相关系数（correlation coefficient，CC）、误差均值（mean error，ME）、绝对误差均值（mean absolute error，MAE）和误差标准差（standard deviation，SD）等指标对预测性能进行定量评价。这些指标的计算，如式（9）～式（12）所示：

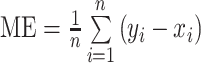9

10

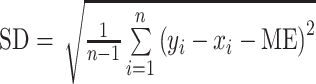11

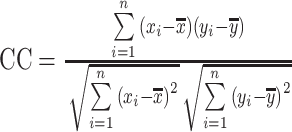12

其中，y 表示网络预测输出值，x 表示血压传感器测量值，n 表示某组数据中心动周期的个数。

对于参与训练的 28 组数据，其预测结果的评价指标如图 3、表 2 所示，MAE 整体水平稳定在 7 mm Hg 附近，ME 整体在 0 mm Hg 位置上下浮动，个别数据出现较大振动，但均不超过±3 mm Hg。SD 水平整体稳定在 10 mm Hg 左右，均未超过 18 mm Hg。从皮尔森 CC 可以看出，整体数值均高于 0.8，多达半数高于 0.9 的水平。这意味着，该方法估计的左心室 SBP 与实际测量得的 SBP 在数值上有很高的相关性，说明该方法的血压预测结果较为准确。

图 3.

Evaluations of SBP estimation

SBP 预测结果的评价指标

表 2. Statistical parameters among all data.

统计参数表

参数	最小值	最大值	均值
MAE/mm Hg	4.33	13.10	7.34
ME/mm Hg	–2.37	2.51	–0.04
SD/mm Hg	6.10	17.47	10.33
CC	0.82	0.98	0.92

如图 4 所示，为来自不同犬的 3 组血压预测结果，图中展示了实验犬 1 的#6 数据、实验犬 2 的#23 数据、实验犬 3 的#35 数据。BP 网络预测的左心室 SBP 与传感器所测量的实际左心室 SBP 之间的皮尔森 CC 值分别为 0.95、0.91 和 0.98，均同时保证了较高的置信水平。

图 4.

A typical example of the BP prediction

BP 预测的典型示例

3. 讨论与分析

本文通过挑选出有效的心音特征，借助 BP 神经网络，实现了对左心室 SBP 的预测。如表 2 所示，血压预测的 MAE 总体均小于 14 mm Hg，最小值为 4.33 mm Hg，最大值为 13.10 mm Hg，均值为 7.34 mm Hg。血压预测 ME 的误差范围维持在上下 3 mm Hg 以内，均值接近 0 mm Hg 的水平。预测水平的 SD 总体均小于 18 mm Hg，最小值为 6.10 mm Hg，最大值为 17.47 mm Hg，均值为 10.33 mm Hg。SBP 的最终预测结果与实际数值之间的相关系数在 0.82 与 0.98 之间，平均水平为 0.92。由上述的结果可以看出，基于 BP 网络的血压预测有着较高的准确性，误差范围低，预测输出与实际输出相关系数较高。尽管左心室 SBP 在 100 mm Hg 到 280 mm Hg 之间，有较大的动态变化范围，本文也获得了较好的估计结果。这一结论进一步证实了，通过心音特征实现血压预测是可行的。

本文主要选取了心音信号的幅度特征、能量特征和时间特征，还有其他有效的特征有待深入发掘。在更加广泛的代表性特征支持下，预测结果可能会进一步提高。另外，模型参数、模型种类也可能影响预测性能，本文采用了经典的 BP 模型来完成血压的预测，并取得了较好的结果，而其它模型的预测性能还有待进一步研究。本文的结论验证了心音特征与心脏血流动力学的密切关系。本文提出的血压预测方法是无创的、连续的，区别于传统的袖带血压检测，具有较好的舒适性、便利性，有利于长期监测心脏的血流动力。

Funding Statement

国家自然科学基金项目（61471081）；中央高校基本科研业务费项目（DUT15QY60，DUT16QY13）