Skip to main content
PMC home page
ACS Measurement Science Au logoLink to ACS Measurement Science Au
. 2022 Oct 5;3(1):1–9. doi: 10.1021/acsmeasuresciau.2c00044

Continuous Square Wave Voltammetry for High Information Content Interrogation of Conformation Switching Sensors

Sanduni W Abeykoon †, Ryan J White †,‡,*
PMCID: PMC9936610  PMID: 36817008

Abstract

graphic file with name tg2c00044_0008.jpg

Square wave voltammetry (SWV) is a voltammetric technique for measuring Faradaic current while minimizing contributions from non-Faradaic processes. In square wave voltammetry, the potential waveform applied to a working electrode and the current sampling protocols followed are designed to minimize contributions from non-Faradaic processes (i.e., double layer charging) to improve voltammetric sensitivity. To achieve this, the current is measured at the end of each forward and reverse potential pulse after allowing time for non-Faradaic currents to decay exponentially. A consequence of sampling current at the end of a potential pulse is that the current data from the preceding time of the potential pulse are discarded. These discarded data can provide information about the non-Faradaic contributions as well as information about the redox system including charge transfer rates. In this paper, we introduce continuous square wave voltammetry (cSWV), which utilizes the continuous collection of current to maximize the information content obtainable from a single voltammetry sweep eliminating the need for multiple scans. cSWV enables acquiring a multitude of voltammograms corresponding to various frequencies and, thus, different scan rates from a single sweep. An application that benefits significantly from cSWV is conformation switching, functional nucleic acid sensors. We demonstrate the utility of cSWV on two representative small molecules targeting electrochemical, aptamer-based sensors. Moreover, we show that cSWV provides comparable results to those obtained from traditional square wave voltammetry, but with cSWV, we are able to acquire dynamic information about the sensor surfaces enabling rapid calibration and optimization of sensing performance. We also demonstrate cSWV on soluble redox markers. cSWV can potentially become a mainstay technique in the field of conformation switching sensors.

Keywords: square wave voltammetry, continuous square wave voltammetry, soluble redox marker, aptamers, frequency, peak current

Introduction

Square wave voltammetry (SWV) possesses several unique characteristics that have enabled the technique to be a mainstay in measuring surface-bound redox systems. These characteristics result from the pulsed potential waveform and coordinated current measurement that precludes interferences from non-Faradaic processes.1 SWV utilizes a square wave potential pulse waveform superimposed on a staircase step to generate a voltammetric linear sweep. Typically, the current sampling technique of SWV considers the current response during the latter half of the potential pulse, which minimizes any non-Faradaic contributions (e.g., charging currents).2 The current–voltage curve is presented as the difference between the forward and reverse current samples (taken from the forward and reverse pulse), which further reduces any remaining charging current and amplifies the peak current providing square wave voltammetric data with high sensitivity.2−5

SWV is useful for measuring surface-bound processes. It facilitates the monitoring of current responses as a function of frequency and allows for characterization of the charge transfer rates in these systems.6,7 Komorsky-Lovrić and Lovrić demonstrated that SWV peak currents can be used to determine the standard rate constant by finding the critical frequency, which is the maximum of the relationship between normalized peak current and inverse frequency. The normalized peak current is defined as the ratio between peak current (ip) and frequency (f). The normalized current maximum occurs analogously to a resonance frequency in spectroscopy—current is maximized when the perturbation frequency, and thus the characteristic timescale of the voltammetric experiment, is similar to the charge transfer rate. The authors utilized SWV to determine the kinetic parameters, defined as the standard rate constant and the frequency ratio.6 This critical frequency analysis was similarly applied to folding-based sensors that utilize functional nucleic acids and the target-induced conformation change, to build sensors by White and Plaxco. They demonstrated that the critical frequency, and thus the charge transfer rate, changes upon target addition, which results in a conformation change of the surface-bound nucleic acids.7

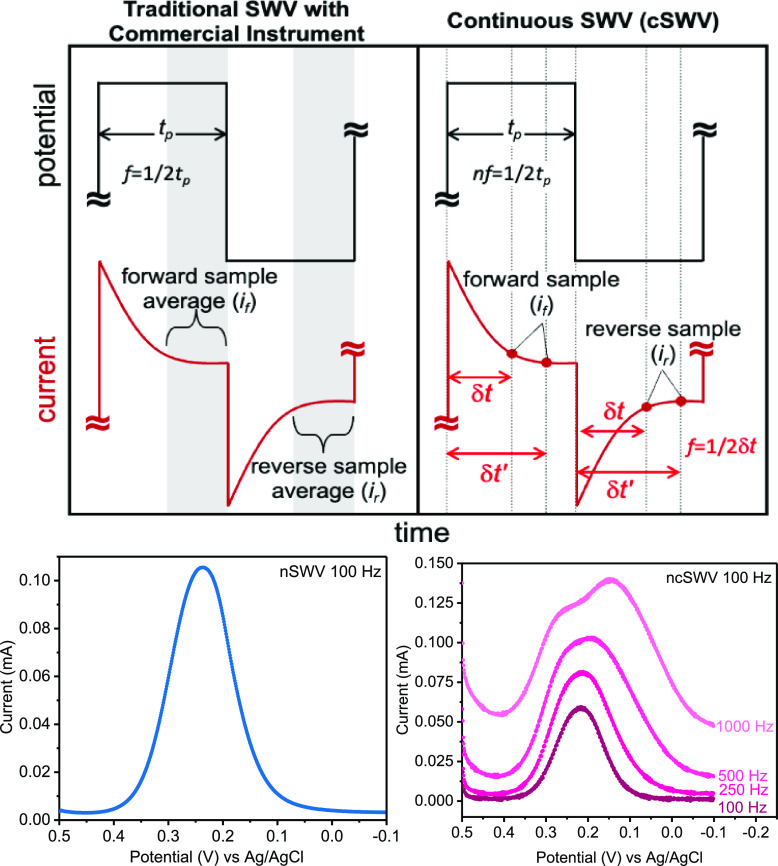
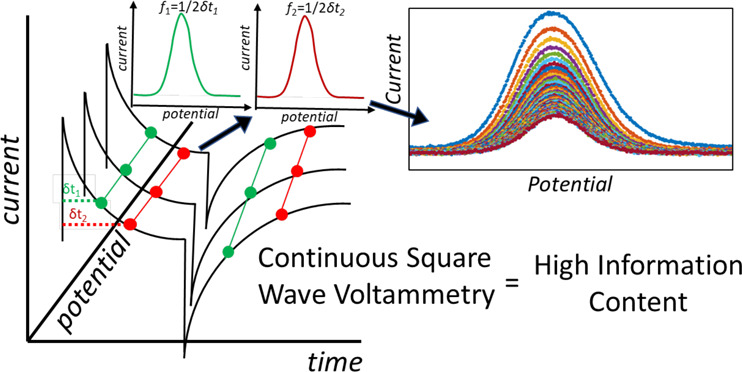
The power of SWV, as described above, relies on its ability to sample current at the end of each forward and reverse potential pulse (defined as forward current if and reverse current ir; Figure 1). The delay in current sampling allows non-Faradaic processes to decay before sampling current contributions from Faradaic processes occurring at the electrode surface. Schematically, the current is sampled at the end of the forward and reverse pulse, but commercial instruments sample several current points along the potential pulse and average these data for better signal-to-noise ratio voltammograms. While the exact region of the pulse that is collected and utilized for data analysis may vary between instrument manufacturers, the net result is averaged current for a better signal and current is discarded at the beginning of the pulse. While this works well for many applications, as demonstrated in the field of electrochemical aptamer-based sensors,8,9 this method leaves data behind.

Figure 1.

Figure 1

Open in a new tab

Continuous square wave voltammetry (cSWV) employs the same applied potential waveform as what is used in commercial instruments (here CH Instruments) employing square wave voltammetry. (Left) In traditional square wave voltammetry, the frequency (f) of the square wave potential pulse is defined as 1/(2tp) where tp is the pulse width. Typically, current is sampled at the end of the forward pulse and reverse pulse, and the difference (if – ir = idiff) is plotted against the potential. The commercial instrument used here averages the current from the latter half of each pulse to determine if and ir. (Right) cSWV continuously collects current data throughout the applied potential waveform at a native SWV frequency of nf = 100 Hz with a data collection rate of 100 kHz. Selecting current at a given time after the application of a pulse (δt) allows the extraction of a voltammogram at a frequency of 1/2δt. At nf = 50 Hz, a data collection frequency of 100 kHz allows for the extraction of 500 voltammograms from a single voltammetric sweep.

There is scientific value to capturing more current data generated during square wave voltammetry. For example, Macpherson and Cobb have recognized the importance of the neglected data in the traditional SWV and presented a measure where the first half of the potential pulse is considered. They demonstrated that it contains valuable information about the double layer charging and interfacial processes occurring at short timescales.10 More specifically, they showed that analyzing the current–time data from the non-Faradaic region of the potential pulse can provide crucial information related to the conductivity of solutions and prevent electrode fouling. Similarly, Mirceski and coworkers have developed a technique for obtaining multiple voltammograms from a single traditional SWV sweep by incorporating chronoamperometry.11,12 In this multisampling protocol, each potential pulse is divided into 50 segments, and the current values are obtained from the 40th segment onward to minimize any non-Faradaic influences on the series of voltammograms obtained.11,12

In this paper, we demonstrate that by continuously collecting current for the entire voltammetric sweep (100 kHz data sampling frequency), we can pull out information equivalent to running several voltammograms at various frequencies that range from 50 kHz to the nominal square wave frequency used in the potential waveform. We first demonstrate the technique of cSWV for soluble redox markers and then its applications in electrochemical, aptamer-based (E-AB) sensors. Because E-AB sensors display a well-known frequency-dependent response that is used to perform sensor optimization13 and can be utilized with innovative measurements using dual-frequency voltammograms for baseline correction and on-the-fly calibration, cSWV provides significant time advantages, mitigating the need for multiple sweeps to perform the same analysis. Here, with cSWV, we demonstrate that this technique can be utilized to perform the same experiments that require multiple voltammograms, with a single voltammetric sweep. Given the utility of the frequency dependence of E-AB sensors and the need to minimize surface interrogation for long-term sensing applications, we believe that cSWV will be widely adaptable to this field of sensors.

Materials and Methods

Chemicals and Solutions

Potassium ferricyanide (K3[Fe(CN)6]), ferrocene (Fe(C5H5)2), Tris-2-carboxyethyl-phosphine (TCEP), 6-mercapto-1-hexanol, Trizma (tris) base (2-amino-2-hydroxymethyl-1,3-propanethiol), adenosine triphosphate (ATP), magnesium chloride (MgCl2), tobramycin, 10× Tris-EDTA, and tetrabutylammonium hexafluorophosphate (TBAPF6) were purchased from Sigma-Aldrich (St. Louis, MO, USA) and were used as received. Potassium chloride (KCl), sodium hydroxide (NaOH), hydrochloric acid (HCl), sodium chloride (NaCl), sulfuric acid (H2SO4), and acetonitrile (C2H3N) were purchased from Thermo Fisher Scientific (Ward Hill, MA, USA) and were used as received. Solutions were prepared with ultrapure water (18.0 MΩ cm at 25 °C) using a Biopak Polisher Millipore ultrapurification system (Millipore, Billerica, MA). Parent tobramycin sequence: 5′-HS-C6-GGGACTTGGTTTAGGT-AATGAGTCCC-MB-3′;14 destabilized ATP sequence: 5′-HS-C6-CTGGGGGAGTATTGCGGAGGAAA-MB-3′.15 DNA aptamer sequences were dual HPLC-purified (Thermo Fisher) and were used as received.

Electrode Preparation for Soluble Redox Marker Experiments

Polycrystalline gold electrodes of 2 mm diameter (CH Instruments, Austin, TX, USA) were hand-polished with 1 μm diamond suspension solution on a microcloth (Buehler) for 2 min following a figure-eight motion. Similarly, the electrodes were then polished in ultrapure water (Milli-Q ultrapure water purification, Millipore, Billerica, MA, USA) in the same manner. Hand-polished electrodes were sonicated with ultrapure water for 5 min and were electrochemically cleaned in different concentrations of sodium hydroxide and sulfuric acid solutions as discussed. The electrodes were cycled in 0.5 M NaOH solution to reductively desorb any attached sulfur molecules to the gold surface. Then, oxidation and reduction reactions were performed in 0.5 M H2SO4, which aids the oxidation of any organic compounds or other available contaminants attached to the gold surface. The surface was then etched with 0.1 M H2SO4/0.01 M KCl for further cleaning. These electrochemically cleaned bare electrodes were then interrogated with SWV and cSWV. Soluble redox marker solutions were prepared as follows: 5 mM K3[Fe(CN)6] in 0.1 mM KCl in DI water and 5 mM ferrocene in 0.1 mM TBAPF6 in acetonitrile.

Fabrication of E-AB Sensors

E-AB sensors were fabricated as explained elsewhere.16 First, 1 μL of aptamer solution was incubated with 2 μL of 100 mM TCEP for 1 h to reduce the disulfide bonds of the aptamer sequences. Then, the electrodes were incubated in a probe solution of 200 nM prepared with 20 mM Trizma base, 100 mM NaCl, and 5 mM MgCl2 at a pH of 7.40 for 1 h in room temperature. Then, the electrodes were washed well with ultrapure water to remove any excess aptamer and then incubated in 30 mM 6-mercapto-1-hexanol prepared in ultrapure water for passivation. Finally, the well rinsed electrodes were incubated in tris buffer for 1 h of equilibration.

Electrochemical Measurements

All electrochemical measurements were performed with CH Instruments 660E and 1040C workstations (CH Instruments, Austin, TX, USA). All electrochemical measurements were collected using a three-electrode cell system consisting of a platinum counter electrode, a Ag/AgCl (3 M NaCl) reference electrode, and 2 mm polycrystalline gold electrodes as working electrodes. Voltammetry parameters were as follows: the amplitude and the increment were 25 and 1 mV, respectively, unless otherwise noted. The potential window between 0 and −0.5 V and frequencies ranging from 50 to 625 Hz were used for the interrogation of E-AB sensors. Soluble redox markers ferrocene and K3(Fe[CN]6) were interrogated at the potential windows between 0.8 and 0.1 V and 0.5 and −0.1 V, respectively. They were tested at frequencies ranging from 10 to 2500 Hz with SWV. The same parameters were used with continuous square wave measurements, and native frequencies of 10 and 50 Hz were selected for soluble redox marker measurements and E-AB sensor measurements, respectively, unless otherwise noted. All experiments were conducted with at least three or more electrodes, and their standard deviations are represented as error bars.

Continuous Square Wave Voltammetry

Continuous square wave voltammetry was achieved via utilization of the potentiostat capabilities of a CH Instruments (model 660E) and the potential driving and measurement capabilities of LabVIEW. Briefly, in-house written LabVIEW code (see cSWV.vi in the Supporting Information) was developed to generate the square wave voltammetric waveform and apply the voltage waveform through the serial voltage input port on the CH instrument. The serial port on the back of the CH Instruments potentiostat (model 660E) has the following assignments: 9-pin D connection; pin 1 - current 1 output; pin 2 - current 2 (bipotentiostat); pin 3 - inverted potential output; pin 4 - external potential input; pin 5 - external signal input; pins 6–9 - ground. Note that pin 4 was intentionally disabled as default to avoid instrument noise so it must be enabled to accept inputs via a jumper to connect the proper pins (communication with CH Instruments). Simultaneously, triggered via an external voltage trigger, the output voltage from the serial port on the CH instrument (corresponding to the measured current) was collected via LabVIEW all through an NI USB-6251 data acquisition board at 100 kHz and stored as a .TDMS file. In order to properly interface NI USB-6251 with the CH Instruments, the instrument was run in the chronoamperometric mode in order to turn the electrochemical cell on. Finally, all software filters were disabled prior to the measurements.

Data Analysis

The data analysis for the collected cSWV data was done by using MATLAB R2021b as explained. First, the collected data were categorized to the relevant time increments (δt, explained later in the text) that correspond to each voltammogram. The original obtained data were smoothed by performing the moving mean averaging technique to reduce the noise and facilitate integration of the voltammograms to obtain peak current values. Voltammograms obtained for ATP were noisier compared to the other voltammograms collected via cSWV. Therefore, an additional step of box car averaging was performed to get smoother data that facilitated peak integration.

Results and Discussion

In this paper, we utilize the complete current–time response gained during the application of the square wave voltammetry waveform to collect continuous square wave voltammograms (cSWV) of both soluble and surface-bound redox markers to maximize the information content obtainable from a single voltammetric sweep. In traditional square wave voltammetry (SWV), the frequency (f) of the square wave potential pulse is defined as 1/(2tp), where tp is the pulse width (Figure 1). Typically, the current is sampled at the end of the forward and reverse pulse, and the difference (if – ir = idiff) is plotted against the potential. In practice, many commercial instruments used here average the current from the latter half of each pulse to determine if and ir, which provides an average current over that time period. This will provide an increased signal-to-noise ratio in the resulting voltammograms. In either case, the majority of the current data obtained during the voltammetry are discarded.

We define square wave voltammetry that collects all current–time data as continuous square wave voltammetry (cSWV). To conduct cSWV, a native frequency is selected, which is equivalent to a traditional square wave frequency (f). This native square wave frequency dictates the length of each potential pulse (Figure 1). However, during a single native frequency voltammetric sweep, the current is collected at a sampling frequency of 100 kHz. Because of this collection frequency, we can extract individual voltammograms at effective frequencies as defined below. To better describe cSWV, we defined the following variables (Figure 1). First, we define δt (s) as the time after applying individual forward and reverse pulses. The cSWV frequency is then calculated as 1/2δt (Hz), where the native frequency is defined as 1/(2δtmax) or the length of the entire pulse tp as defined above. Since we collect data at 100 kHz, a voltammogram taken at a native frequency of 50 Hz can generate 1000 different voltammograms corresponding to 1000 frequencies (no. of voltammograms = tp × sampling frequency). The experiments are performed using an in-house written LabVIEW code and are run simultaneously with the CH instrument’s amperometric trace to collect the entirety of the current–time data. The current values corresponding to each voltammogram are plotted against the potential window used to monitor the reaction (Figure S1).

cSWV Response from Soluble Redox Markers

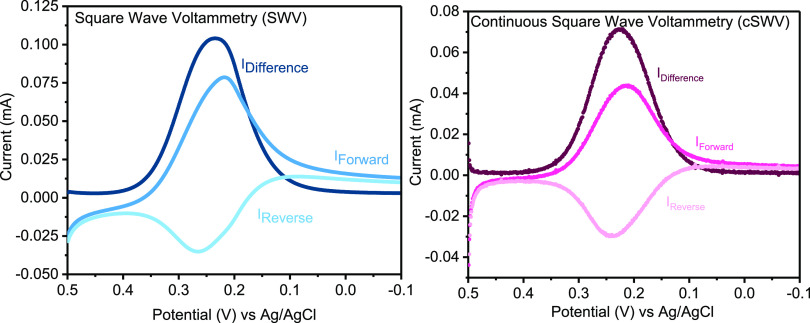
cSWV voltammograms of the soluble redox marker K3[Fe(CN)6] are similar to those collected via SWV when using a 100 Hz native frequency. For example, the voltammetric response for the forward, reverse, and difference voltammograms of 5 mM K3[Fe(CN)6] in 0.1 mM KCl followed the typical response for a soluble redox marker. Both the traditional SWV and cSWV voltammograms were performed at a native frequency of 100 Hz, and in the cSWV case, the voltammogram displayed is at δtmax = tp = 5 ms (Figure 2). Of note, the absolute value for current obtained from cSWV is less than that obtained using the traditional method. Lower currents are expected when extracting at higher frequencies because the applied waveform is done so at a lower frequency, which gives time for the diffuse layer to become more established. Therefore, comparing a normal SWV at 100 Hz should yield a higher current than a cSWV at 100 Hz with a native frequency of 10 Hz (Figure S2 left). However, comparing normal SWV at 100 Hz with cSWV at a native frequency of 100 Hz also exhibits lower currents, which is perplexing as the diffuse layer thickness should be the same. Averaging the latter half of the cSWV pulse also does not account for this dissimilarity (see Figure S2 right). We do not yet fully understand why cSWV yields lower absolute values for current at matched native frequencies, but we find that the trends with changing frequency match between the two modes of data collection (vide infra). To further understand the voltammetric responses and the trends followed with changing interrogation frequencies, low-, medium-, and high-frequency voltammograms are compared with the soluble redox marker K3[Fe(CN)6] for the two techniques (Figure S3). In addition, this observation is related to the system being measured. A sweep run with a 150 ± 5 kΩ resistor in place of the electrochemical cell for simplicity yields the correct current predicted by Ohm’s law (Figure S4).

Figure 2.

Figure 2

Open in a new tab

Continuous square wave voltammetry (cSWV) provides similar diffusion-limited current–voltage responses for soluble redox markers to what is observed with traditional square wave voltammetry. (Left) Traditional SWV for 5 mM K3[Fe(CN)6] in 0.1 mM KCl yields typically forward, reverse, and difference voltammograms taken at 100 Hz with an increment of 1 mV and a step size of 25 mV. (Right) cSWV voltammograms extracted from a voltammogram at a native frequency of 10 Hz using a δt of 5 ms (1/2δt = 100 Hz) yielding equivalent voltammograms at 100 Hz.

The frequency response, and thus the scan rate response, of soluble redox markers, is the same for both traditional SWV and cSWV (Figure 3). When studying K3[Fe(CN)6] with 0.1 mM KCl, with traditional square wave voltammetry, the peak current increases monotonically until ∼625 Hz followed by a decreasing trend in peak current as expected since the reaction behaves in a quasi-reversible way at these higher frequencies because of the finite electron transfer kinetics.1 The response of ferrocene with 0.1 mM TBAPF6, conversely, plateaus at a similar frequency indicating the reaction behaving reversibly even at the highest frequency tested (2500 Hz). Using the same set of electrodes, we find a similar peak current response with cSWV up to 2500 Hz; however, we can probe at much higher frequencies with cSWV. We still find that peak currents begin to roll over or plateau at ∼625 Hz, similar to SWV for K3[Fe(CN)6] with 0.1 mM KCl and ferrocene in 0.1 mM TBAPF6 (Figure 3 middle). To better visualize the comparison of peak current responses obtained from traditional SWV to the equivalent frequencies of cSWV performed at a native frequency of 10 Hz, they are shown in Figure S5. More specifically, we observe maximum current responses at 957 ± 32 and 1721 ± 162 Hz for K3[Fe(CN)6] with 0.1 mM KCl and ferrocene in 0.1 mM TBAPF6, respectively, when all the frequencies from cSWV are analyzed (Figure 3 right). We do not attempt to pull out rate constants from these data at present. We believe that we are limited by the background capacitive currents that occur after each application of a potential pulse. That is, accessible rate constant measurements will be limited to a time region at which the non-faradaic charging currents decay below the faradaic components. This will be a function of properties such as the electrode area/geometry as well as solution conditions like supporting electrolyte concentrations. We also observe peak splitting at these higher frequencies (see Figure S6) taken from a single cSWV run with frequencies ranging from 10 to 50,000 Hz. However, unlike typical peak splitting in SWV that is a result of shifting forward and reverse wave movement, we observe splitting in the reverse wave. While the origin of the observed peak splitting at these frequencies is not clear, given the known interactions of K3[Fe(CN)6],17 the emergence of a second peak may indicate an adsorbed species of the redox couple. This is under further investigation.

Figure 3.

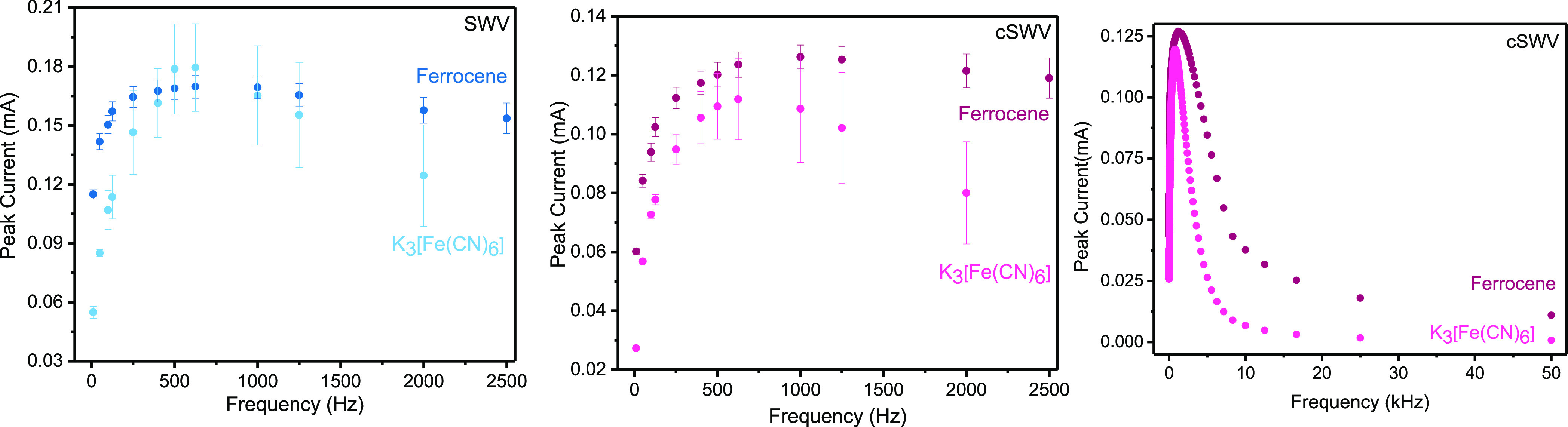
Figure 3

Open in a new tab

The peak current dependence on the frequency with the soluble redox markers K3[Fe(CN)6] and ferrocene was investigated with both techniques. (Left) Peak currents analogous to voltammograms acquired with traditional SWV at different frequencies for 5 mM K3[Fe(CN)6] in 0.1 mM KCl and 5 mM ferrocene in 0.1 mM tetrabutylammonium hexafluorophosphate are shown. SW voltammograms were obtained by scanning from the 0.5 to −0.1 V potential window for K3[Fe(CN)6] and at 0.8–0.1 V for ferrocene with frequencies ranging from 10 to 2500 Hz. (Middle) Peak current responses extracted from voltammograms obtained at frequencies equivalent to SWV from cSWV runs at a native frequency of 10 Hz. (Right) All the peak current values are plotted against the full range of frequencies given from cSWV. Solution conditions and parameters used are the same as those of traditional SWV.

cSWV to Interrogate Electrochemical, Aptamer-Based (E-AB) Sensors

Square wave voltammetry is a common electrochemical technique used to interrogate electrochemical, aptamer-based (or E-AB) sensors. E-AB sensors are utilized as an analytical detection tool for a wide variety of target molecules ranging from small molecules to proteins. They can even be employed in vivo for continuous therapeutic monitoring.18,19 Briefly, E-AB sensors employ nucleic acid aptamers (single-stranded DNA or RNA oligonucleotide strands that bind to targets of interest) thiol modified at the 5′ end and attached to the electrode surface (gold). In contrast, the 3′ end is modified with a redox marker like methylene blue.20 In the presence of the target, the aptamer undergoes a conformational change bringing the redox tag closer to the electrode surface, facilitating the electron transfer process.21 SWV is particularly well-suited to monitor this class of sensor because of the ability to reduce background currents (non-faradaic charging current) while maximizing signaling differences between the target-free and target-bound states. White and Plaxco reported the optimization of electrochemical signaling via the variation of interrogation frequency as well as a measure of the apparent charge transfer rates with these types of folding-based sensors.7 More recently, Plaxco and coworkers have expanded on using variable frequency interrogation to perform on-the-fly calibration of a sensor and eliminate sensor drift when employed in vivo.22 As such, measuring the frequency-dependent response of E-AB sensors is critical to the function and application of this powerful class of sensors.

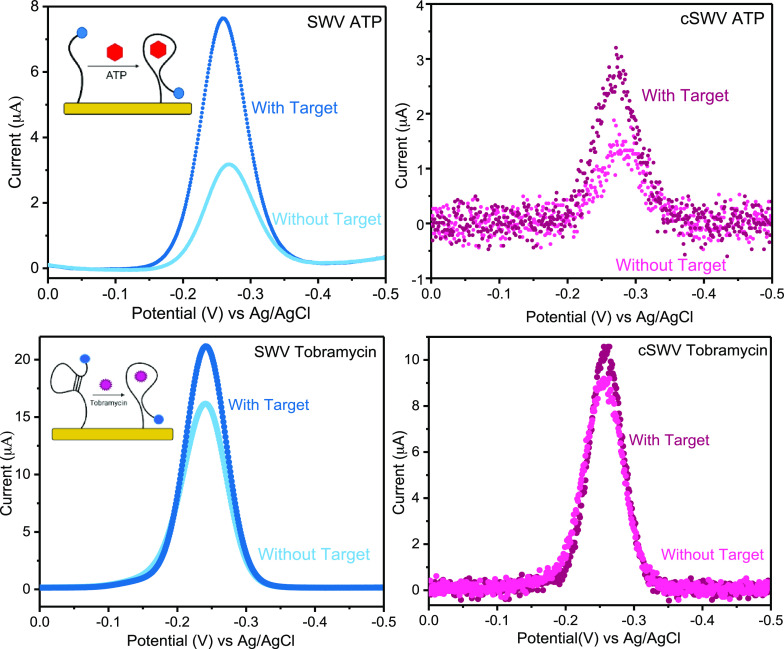
To demonstrate the applicability of cSWV to E-AB sensors, we tested the method with two representative sensors fabricated to detect adenosine triphosphate (ATP) and aminoglycoside antibiotics (tobramycin). Qualitatively and quantitatively, E-AB sensors interrogated via SWV and cSWV performed comparably. For example, sensors fabricated with the destabilized ATP aptamer15 exhibit a 154 ± 10% signal change when interrogated at an SWV frequency of 400 Hz. Similarly, a percent signal change of 90 ± 5% is shown with an equivalent 400 Hz SWV frequency (δt = 1.25 ms) extracted from a 50 Hz native cSWV frequency upon target addition of 1 mM ATP (Figure 4 top). Sensors fabricated with the aminoglycoside binding aptamer14 behaved similarly, exhibiting a signal change of 31 ± 1% with SWV at 500 Hz and 17 ± 1% with cSWV at δt = 1 ms upon addition of the 1 mM tobramycin target (Figure 4 bottom).

Figure 4.

Figure 4

Open in a new tab

Representation of voltammetric response from the two techniques for bound and unbound states. (Top) Voltammograms obtained for ATP sensors interrogated with SWV at 400 Hz for the bound and unbound stages and voltammograms equivalent to 400 Hz (δt = 1.25 ms) acquired with cSWV at a native frequency of 50 Hz under identical conditions to SWV. (Bottom) Aminoglycoside tobramycin sensor voltammetric response at 500 Hz upon 1 mM target addition with both techniques. The equivalent voltammogram for 500 Hz with cSWV is obtained at δt = 1 ms.

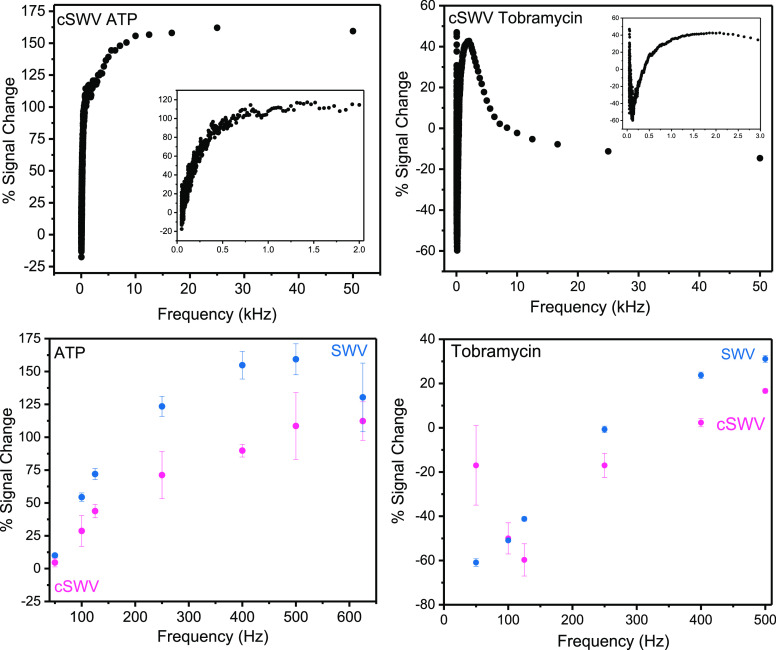
The advantage of using cSWV is that the entire frequency response of an E-AB sensor is obtained from simply two voltammetric sweeps—one without a target and one with saturated target conditions. Typically, a frequency sweep is obtained by running voltammograms over a range of frequencies in buffer and buffer saturated with the target.7 Accordingly, a typical frequency sweep for the ATP and tobramycin sensors taken with SWV exhibits an expected frequency-dependent signal change19 (Figure 5). To quantify the sensor responses gathered by the two techniques, the percent signal change was calculated using the equation (iWT – iNT/iNT) × 100, where iWT is the peak current response in the presence of the target and iNT is the peak current response with no target. Note that these data required taking 12 voltammograms for 6 frequencies (with and without a target). Conversely, two voltammetric sweeps of cSWV taken at a native frequency of 50 Hz with and without a target yield 1000 voltammograms between 50 Hz and 50 kHz (Figure 5 top). When the same 6 frequencies are isolated from the native 50 Hz sweep, we find that the signal change upon target addition matches with what is observed with SWV (Figure 5 bottom). Plotting signal changes at every collected δt, and thus frequency, gives a highly resolved view of the frequency response of the respective E-AB sensor.23 The most remarkable percent signal change for ATP sensors is observed at around 175% given at 25,000 Hz, and overall higher percent signal changes (>100%) are observed at higher frequencies (>500 Hz). Similarly, tobramycin sensors provided the highest percent signal changes, around 50%, and both signal on and off responses were observed as expected from tobramycin sensors. Moreover, they both exhibit frequencies of no response, as described by Plaxco and coworkers.24 The key difference here is that data (peak currents or the signal change) can be acquired at desired frequencies (maximum signal change and frequency of no response) with only a single voltammetric sweep. Alternatively, one can perform an entire frequency sweep to find the optimal signaling with only two voltammetric sweeps. There is a slight discrepancy seen in percent signal changes obtained for ATP and tobramycin E-AB sensors. However, the two techniques are comparable to each other and follow a matching trend. The dissimilarity in the values between the two techniques could be due to the difference in the sampling procedure followed by the two techniques. Averaging of the data in nSWV could result in more gain compared to cSWV and could lead to dissimilarities in the percent signal changes observed. For tobramycin E-AB sensors, much higher error bars are observed with the cSWV technique compared to nSWV, especially with 50 Hz, and causes a slight deviation from the nSWV response. This may be an artifact of the sensor-to-sensor variability, which can impact the overall signal gain by individual sensors.

Figure 5.

Figure 5

Open in a new tab

Calculated percent signal change responses for ATP and tobramycin E-AB sensors from SWV and cSWV. (Top) All the percent signal change values given by cSWV for the full range of frequencies from 50 Hz to 50 kHz were acquired with ATP and tobramycin sensors. The insets represent an expanded view of the percent signal change at lower frequencies up to 2000 Hz. (Bottom) The percent signal change responses for ATP and tobramycin sensors were calculated for the frequencies ranging from 50 to 500 Hz with SWV. Their comparison with equivalent frequencies acquired from cSWV of 50 Hz native frequency is shown.

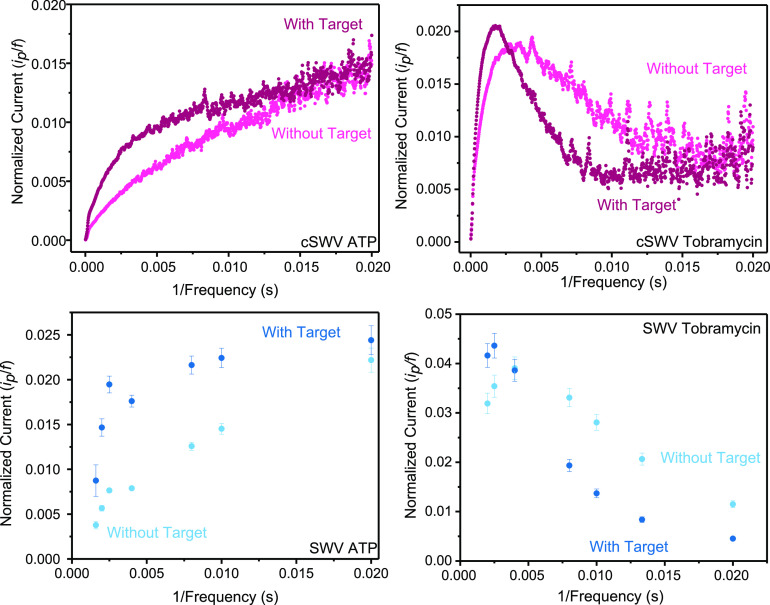
Finally, another advantage of using cSWV is assessing the charge transfer rates of tethered redox molecules quickly and accurately with a high resolution. cSWV allows the determination of the critical frequency, as shown in Figure 6. The critical frequency is given by the maximum of the ip/f vs 1/f, where ip is the peak current and f is the frequency. The charge transfer rates for the bound and the unbound probes for tobramycin-fabricated sensors are determined to be at 480 ± 14 and 251 ± 37 s–1, respectively, with the cSWV technique. Similar observations were noted with SWV where the charge transfer rates for the bound state and the unbound state are 400 ± 150 and 250 ± 150 s–1, respectively. However, when using cSWV, the frequency resolution is much higher (the 100 kHz sampling rate leads to voltammograms at every 1/20 μs frequency) compared to the resolution using nSWV, which is based on how many sweeps the experimenter performs. For example, in our nSWV determination for tobramycin, we find a charge transfer rate of 400 s–1. This determination is based on a max current value observed at 400 Hz flanked by a measurement at 500 and 250 Hz; thus, the charge transfer rate can only be known within a ±150 Hz range using this spacing on nSWV. Both techniques provide comparable charge transfer rates for the tobramycin sensor, assuring that the cSWV technique could be of many advantages to the E-AB sensor field. Similar to the observations with the tobramycin sensors, comparable trends in the plots for ATP sensors are observed further confirming the capabilities of the technique. According to the trend given in the plot for ATP, a maximum could not be determined since the plots depict an increasing trend with 1/f. Therefore, a critical frequency value for the states of the ATP sensor with and without a target is undetermined.

Figure 6.

Figure 6

Open in a new tab

Square wave voltammetry allows determination of electron transfer kinetics between the electrode and the redox probe, and this can be incorporated with the new technique cSWV. (Top) Plots of normalized current (ip/f) vs 1/frequency (1/f) could provide the apparent electron transfer rates from the plot maximum and are displayed for ATP and tobramycin sensors. (Bottom) To compare electrode kinetic information obtained from cSWV, traditional SWV was performed in a selected range of frequencies for the same E-AB sensors. Similar trends are observed with the two techniques for the states with and without a target.

Conclusions

This paper introduces the analytical technique continuous square wave voltammetry, which collects the entire set of current–time data related to a single voltammetric sweep. Unlike square wave voltammetry that provides a single averaged voltammetric response for a faradaic reaction, cSWV provides multiple voltammograms corresponding to frequencies ranging from 50 kHz to the native interrogation frequency. The main advantage of using cSWV is the ability to perform these same types of measurements in a series of 1 to 2 voltammetric sweeps as opposed to a large number of sweeps. For example, sensor optimization to determine the optimal interrogation frequency often requires approximately >20–30 voltammetric sweeps at a wide range of SW frequencies (10–5000 Hz). This can now be achieved with two sweeps, one with a target and one without it. Moreover, the dual frequency approach discussed by Plaxco and coworkers is a calibration-free technique where target concentrations are determined regardless of sensor-to-sensor surface variation and without the need to be recalibrated against the reference sample. They achieved this by voltammetrically interrogating two different SWV frequencies corresponding to a responsive and nonresponsive (current independent of the target concentration) signal.24 Another instance where the frequency dependence of E-AB sensors employed is explained by the same group where they have shown an improved calibration system for E-AB sensor interrogation by tuning the square wave frequency in order to get the maximum peak current responses given at signal on and signal off instances by the same sensor, hence determining the “kinetic differential measurement” (KDM) values. This application enables determination of the target concentration with clinical accuracy.9 Our cSWV technique can be effectively incorporated for many such applications. The key advantage in each of these two examples is the improved temporal resolution achievable by negating the need to perform multiple scans. A single sweep can provide information at two or more different frequencies for calibration purposes, thus improving the rate at which quantitative target concentration data can be collected. First, continuous square wave voltammetry was tested with soluble redox markers ferrocene and K3[Fe(CN)6] followed by interrogation with E-AB sensors fabricated with ATP and tobramycin aptamers. Similar trends in the variation of the peak current with frequency were observed with both soluble redox markers and E-AB sensors. Furthermore, this technique allows the determination of the critical frequency, which provides information related to kinetics and sensor behavior.

Acknowledgments

Funded research reported in this publication was supported by the National Institute of General Medical Sciences of the National Institutes of Health under award number R01GM117159. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.

Glossary

Abbreviations

cSWV

continuous square wave voltammetry

SWV

square wave voltammetry

ATP

adenosine triphosphate

E-AB sensor

electrochemical aptamer-based sensor

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsmeasuresciau.2c00044.

  • Additional voltammograms—both SWV and cSWV—and frequency characterization plots (PDF)

  • Code VI file used for potential drive and data collection via LabVIEW (ZIP)

Author Contributions

CRediT: Sanduni Wasuththara Abeykoon conceptualization (equal), formal analysis (equal), project administration (equal), visualization (equal), writing-review & editing (equal); Ryan J. White conceptualization (equal), data curation (lead), formal analysis (equal), methodology (equal), project administration (equal), resources (equal), software (equal), supervision (equal), writing-review & editing (equal).

The authors declare no competing financial interest.

Supplementary Material

tg2c00044_si_001.pdf (920.8KB, pdf)
tg2c00044_si_002.zip (116.1KB, zip)

References

  1. Lovrić M.Square-Wave Voltammetry. In Electroanalytical Methods: Guide to Experiments and Applications; Springer Berlin Heidelberg, 2010. [Google Scholar]
  2. Mirceski V.; Gulaboski R.; Lovric M.; Bogeski I.; Kappl R.; Hoth M. Square-Wave Voltammetry: A Review on the Recent Progress. Electroanalysis 2013, 25, 2411–2422. 10.1002/elan.201300369. [DOI] [Google Scholar]
  3. Osteryoung J. G.; Osteryoung R. A. Square Wave Voltammetry. Anal. Chem. 1985, 57, 101. 10.1021/ac00279a004. [DOI] [Google Scholar]
  4. Mendoza S.; Bustos E.; Manríquez J.; Godínez L. A. Voltammetric Techniques. Agric. Food Electroanal. 2015, 21–48. 10.1002/9781118684030.ch2. [DOI] [Google Scholar]
  5. Brookes B. A.; Ball J. C.; Compton R. G. Simulation of Square Wave Voltammetry: Reversible Electrode Processes. J. Phys. Chem. B 1999, 103, 5289–5295. 10.1021/jp9901390. [DOI] [Google Scholar]
  6. Komorsky-Lovrić Ś.; Lovrić M. Kinetic Measurements of a Surface Confined Redox Reaction. Anal. Chim. Acta 1995, 305, 248–255. 10.1016/0003-2670(94)00455-U. [DOI] [Google Scholar]
  7. White R. J.; Plaxco K. W. Exploiting Binding-Induced Changes in Probe Flexibility for the Optimization of Electrochemical Biosensors. Anal. Chem. 2010, 82, 73–76. 10.1021/ac902595f. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Pellitero M. A.; Curtis S. D.; Arroyo-Currás N. Interrogation of Electrochemical Aptamer-Based Sensors via Peak-to-Peak Separation in Cyclic Voltammetry Improves the Temporal Stability and Batch-to-Batch Variability in Biological Fluids. ACS Sens. 2021, 6, 1199–1207. 10.1021/acssensors.0c02455. [DOI] [PubMed] [Google Scholar]
  9. Downs A. M.; Gerson J.; Leung K. K.; Honeywell K. M.; Kippin T.; Plaxco K. W. Improved Calibration of Electrochemical Aptamer-Based Sensors. Sci. Rep. 2022, 12, 1–10. 10.1038/s41598-022-09070-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Cobb S. J.; Macpherson J. V. Enhancing Square Wave Voltammetry Measurements via Electrochemical Analysis of the Non-Faradaic Potential Window. Anal. Chem. 2019, 91, 7935–7942. 10.1021/acs.analchem.9b01857. [DOI] [PubMed] [Google Scholar]
  11. Mirceski V.; Guziejewski D.; Bozem M.; Bogeski I. Characterizing Electrode Reactions by Multisampling the Current in Square-Wave Voltammetry. Electrochim. Acta 2016, 213, 520–528. 10.1016/j.electacta.2016.07.128. [DOI] [Google Scholar]
  12. Mirceski V.; Guziejewski D.; Gulaboski R. Electrode Kinetics from a Single Square-Wave Voltammogram. Maced. J. Chem. Chem. Eng. 2015, 34, 181–188. [Google Scholar]
  13. Chamorro-Garcia A.; Ortega G.; Mariottini D.; Green J.; Ricci F.; Plaxco K. W. Switching the Aptamer Attachment Geometry Can Dramatically Alter the Signalling and Performance of Electrochemical Aptamer-Based Sensors. Chem. Commun. 2021, 57, 11693–11696. 10.1039/D1CC04557A. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Rowe A. A.; Miller E. A.; Plaxco K. W. Reagentless Measurement of Aminoglycoside Antibiotics in Blood Serum via an Electrochemical, Ribonucleic Acid Aptamer-Based Biosensor. Anal. Chem. 2010, 82, 7090–7095. 10.1021/ac101491d. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. White R. J.; Rowe A. A.; Plaxco K. W. Re-Engineering Aptamers to Support Reagentless. Self-Reporting Electrochemical Sensors. Analyst 2010, 135, 589–594. 10.1039/b921253a. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Sykes K. S.; Oliveira L. F. L.; Stan G.; White R. J. Electrochemical Studies of Cation Condensation-Induced Collapse of Surface-Bound DNA. Langmuir 2019, 35, 12962–12970. 10.1021/acs.langmuir.9b02299. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Hua X.; Xia H. L.; Long Y. T. Revisiting a Classical Redox Process on a Gold Electrode by Operando ToF-SIMS: Where Does the Gold Go?. Chem. Sci. 2019, 10, 6215–6219. 10.1039/C9SC00956F. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. McKeague M.; Derosa M. C. Challenges and Opportunities for Small Molecule Aptamer Development. J. Nucleic Acids 2012, 2012, 396. 10.1155/2012/748913. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Santos-Cancel M.; Lazenby R. A.; White R. J. Rapid Two-Millisecond Interrogation of Electrochemical, Aptamer-Based Sensor Response Using Intermittent Pulse Amperometry. ACS Sens. 2018, 3, 1203–1209. 10.1021/acssensors.8b00278. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Schoukroun-Barnes L. R.; Macazo F. C.; Gutierrez B.; Lottermoser J.; Liu J.; White R. J. Reagentless, Structure-Switching, Electrochemical Aptamer-Based Sensors. Annu. Rev. Anal. Chem. 2016, 9, 163–181. 10.1146/annurev-anchem-071015-041446. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Belmonte I.; White R. J. 3-D Printed Microfluidics for Rapid Prototyping and Testing of Electrochemical. Aptamer-Based Sensor Devices under Flow Conditions. Anal. Chim. Acta 2022, 1192, 339377. 10.1016/j.aca.2021.339377. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Arroyo-Currás N.; Dauphin-Ducharme P.; Ortega G.; Ploense K. L.; Kippin T. E.; Plaxco K. W. Subsecond-Resolved Molecular Measurements in the Living Body Using Chronoamperometrically Interrogated Aptamer-Based Sensors. ACS Sens. 2018, 3, 360–366. 10.1021/acssensors.7b00787. [DOI] [PubMed] [Google Scholar]
  23. Pellitero M. A.; Arroyo-Currás N. Study of Surface Modification Strategies to Create Glassy Carbon - Supported , Aptamer - Based Sensors for Continuous Molecular Monitoring. Anal. Bioanal. Chem. 2022, 5627. 10.1007/s00216-022-04015-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Li H.; Dauphin-Ducharme P.; Ortega G.; Plaxco K. W. Calibration-Free Electrochemical Biosensors Supporting Accurate Molecular Measurements Directly in Undiluted Whole Blood. J. Am. Chem. Soc. 2017, 139, 11207–11213. 10.1021/jacs.7b05412. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

tg2c00044_si_001.pdf (920.8KB, pdf)
tg2c00044_si_002.zip (116.1KB, zip)

Articles from ACS Measurement Science Au are provided here courtesy of American Chemical Society

RESOURCES