Observation of phononic skyrmions based on hybrid spin of elastic waves

Abstract

Skyrmions with topologically stable configuration have shown a promising route toward high-density magnetic and photonic information processing due to their defect-immune and low-driven energy. Here, we experimentally report and observe the existence of phononic skyrmions as new topological structures formed by the three-dimensional hybrid spin of elastic waves. We demonstrate that the frequency-independent spin configuration leads to ultra-broadband feature of phononic skyrmions, which can be produced in any solid structure, including chip-scale ones. We further experimentally show the excellent robustness of the flexibly movable phononic skyrmion lattices against local defects of disorder, sharp corners, and even rectangular holes. Our research opens a vibrant horizon toward an unprecedented way for elastic wave manipulation and structuration by spin configuration and offers a promising lever for alternative phononic technologies, including information processing, biomedical testing, and wave engineering.

Phononic skyrmions, which are topological structures formed by the three-dimensional hybrid spin of elastic waves, are observed.

INTRODUCTION

Skyrmion, a topologically stable three-component vector field, was initially developed in elementary particles and has since been demonstrated in condensed matter systems (1) and helimagnetic materials (2–4). The skyrmions, characterized by a real-space nontrivial topological number, were considered a promising route toward high-density magnetic materials for information storage and transfer (5–8) due to their defect-immune and low-driven energy (9, 10). These topological skyrmions have been recently extended to photonics (11–15) based on dynamic electromagnetic fields with surface plasmons polaritons (11, 12) and spin-orbit coupling in the evanescent fields (13, 14). This shows a promising horizon (11–14) for robust photonic information processing, sensing, and lasing. More recently, acoustic skyrmion lattices were also observed in the air by the dynamic acoustic velocity fields (16, 17). However, the nontrivial skyrmion configurations have so far remained untapped for elastic phonons, classically known as elastic waves in solids (18–21), due to their more sophisticated polarization states.

Elastic phonons are an excellent platform for carrying and processing information because of their unique advantages, including orders of magnitude lower phononic wavelength in comparison with photonic systems (19, 22), scalability toward integrated devices (23), anti-jamming capability (24) (negligible cross-talk between devices and with the environment), and extremely low losses (22). The development of phonon physics has advanced the technology in high signal-to-noise information processing (22, 25, 26), high-sensitive remote sensing (18), and intense wave-matter interaction for future quantum networks (27–32). Thus, in actual solid carriers with ubiquitous defects, realizing a new topological robust mode, i.e., phononic skyrmion, could lead to transformative phononic applications, especially in a generally concise configuration that can be scaled accordingly for future chip-scale technologies.

Elastic waves describe the basic dynamic principle of the deformation [i.e., the three-dimensional (3D) displacement field u] of solids in a periodic form (33, 34), reflecting the properties from classical solid motion to lattice oscillation in a quantum field. Helmholtz theorem unveiled that u can be decomposed into curl-free longitudinal waves u_L and divergence-free transverse waves u_T. A large variety of research has shown that transverse waves (i.e., optical waves) have spin characteristics (35–37), which support the nontrivial Berry phase and quantum spin Hall effect (38). Recently, the hybrid spin induced by mixed transverse-longitudinal waves, which is responsible for abnormal phenomena beyond pure transverse waves and longitudinal waves (i.e., acoustic waves), has been uncovered in the elastic phononic system (39). The hybrid spin can inspire strong spin-momentum locking of the elastic edge modes. However, the trivial topological invariant of the latter is not robust against defects (40). Here, we construct a new nontrivial topological structure of ultra-broadband phononic skyrmion based on the 3D hybrid spin of elastic waves. It should be pointed out that the formation of phononic and photonic skyrmions comes from different spin textures, with the latter being based on transverse wave spin.

RESULTS

Formation of phononic skyrmions by intrinsic hybrid spins

The elastic spin can arise from the hybridization between transverse and longitudinal waves in an elastic interface. The interface can be a free surface of a plate-like structure supporting the classical Lamb waves, or a free surface of a semi-infinite (for wavelength) bulk structure supporting the Rayleigh surface waves. The hybrid spin can also exist in an infinite isotropic bulk space without interfaces based on two-wave interference (39).

To make the structure compact, we have built the phononic skyrmion system in a thinplate model supporting the hybrid spin of the Lamb wave arising from the hybridization between the longitudinal wave and the transverse wave in the upper and lower plate interfaces. The 3D hybrid spin field of plane Lamb waves can be expressed by the axial (out-of-plane) and transverse (in-plane) field components

$$\begin{array}{c}{u}_z=a_z(z)e^{-\mathrm{i}(k\cdot \mathbf{t}\cdot \mathbf{r}-\mathrm{\omega }t)}\\ {\mathbf{u}}_{\parallel }=\frac{a_{\parallel }(z)\cdot \mathbf{k}}{\mid \mathbf{k}\mid }{e}^{-\mathrm{i}(k\cdot \mathbf{t}\cdot \mathbf{r}+\frac{\mathrm{\pi }}{2}-\mathrm{\omega }t)}\end{array},$$ (1)

where a_z and a_∥ are real amplitude components (detailed derivations can be found in text S1). k is the Lamb wave vector. The r and k are the position and direction vectors, respectively. The motion of any particle (r, z) in the 3D plate obeys an elliptical spin trajectory of $\frac{{\mathrm{Re}}^2(u_z)}{{a_z}^2}+\frac{{\mid \mathrm{Re}({\mathbf{u}}_{\parallel })\mid }^2}{{a_{\parallel }}^2}=1$ (Fig. 1E), whose geometry is determined by the polarization ϑ = a_∥/a_z (Fig. 1G). The larger the polarization, the closer the elliptical trajectory is to a circle one. In particular, the lowest-order antisymmetric Lamb wave (A0-mode wave) approximates the flexural wave (33). The corresponding spin angular momentum ${\mathbf{S}}_p=-\mathrm{\epsilon }\frac{\mathrm{\rho }\mathrm{\omega }}{2}\mid \mathrm{Im}({{\mathbf{u}}_{\parallel }}^{\ast }{u}_z-{u_z}^{\ast }{\mathbf{u}}_{\parallel })\mid \approx -zk\mathrm{\rho }\mathrm{\omega }{a_z}^2\mathrm{\epsilon }$ is linearly distributed along with the plate thickness (along the range of −d < z < d in Fig. 1F), and ε is a unit vector perpendicular to the plane formed by the z axis and the direction vector k. The sign of S_p is tightly correlated with the sign of k at z = d, demonstrating the spin-momentum locking of the Lamb wave, which is analogous to the optical case (38, 41). We find that nonresonant pillared resonators (shown in the illustration of Fig. 1F) can linearly amplify S_p of the hosting plate due to the continuous rotation geometry (see experimental vector field of 3D time-resolved spin in movie S1). This opens up a new degree of freedom in tuning spin texture (more details in text S4). As shown in Fig. 1F, S_p of the Lamb wave is linearly amplified along the range of d < z < d + l by the pillared resonator with the height of l.

Fig. 1. Formation of phononic skyrmions.

(A) Interference of three pairs of counterpropagating plane Lamb waves with hybrid spins construct the phononic skyrmion lattice in a hexagonal elastic metaplate. (B) Enlarged view of the local vector field. (C) The metaplate with periodically pillared resonators. (D) Theoretical axial (out-of-plane) u_z and transverse ∣u_∥∣ (in-plane) fields of the skyrmion lattices. (E) Axial u_z and transverse u_∥ fields have a phase difference of π/2, creating a spiral spin geometry with an elliptical trajectory. The inset is a spin vector field at the plane formed by the z axis and χ axis (same as the direction vectors k). (F) Inset shows a unit structure with sixfold rotational symmetry, including an oscillating nonresonant pillared resonator on the hosting plate with a thickness of h. The resonator with the height of l (here l = h/2 = d = 0.5 mm at the frequency of 8 kHz) can linearly amplify spin angular momentum S_p and the polarization ϑ = a_∥/a_z along the z axis (−d < z < 2d). The coordinate origin is on the neutral plane of the hosting plate. The S₀ and ϑ₀ are the spin angular momentum magnitude and the polarization on the plate surface (i.e., z = d). (G) Elliptical spin trajectories of different particles along the plate thickness.

To produce the phononic skyrmions, we have designed a hexagonal metaplate with pillared resonators (Fig. 1C) and excited three pairs of counterpropagating plane Lamb waves with hybrid spins along with the directions of θ = 0^o, 60^o, and −60^o, as shown in Fig. 1A. The corresponding wave number of these exciting plane waves can be presented by six points in the momentum space (the lower right corner of Fig. 1A). The interference of these wavefields constructs the 3D skyrmion lattice configuration of the real wavefield $\overline{\mathbf{u}}=({\overline{u}}_x{\overline{u}}_y{\overline{u}}_z)$, which is expressed by (detailed derivations can be found in text S5)

$$\overline{\mathbf{u}}=\sum _{\mathrm{\theta }=-\frac{\mathrm{\pi }}{3},0,\frac{\mathrm{\pi }}{3}}[\frac{a_{\parallel }(z)\cdot \mathbf{k}}{\mid \mathbf{k}\mid }\sin (k\mathbf{t}\mathbf{r}),a_z(z)\cdot \cos (k\mathbf{t}\mathbf{r})]\cos ({\mathrm{\varphi }}_0+\mathrm{\omega }t)$$ (2)

The corresponding axial and transverse field components in a 2D x-y plane (Fig. 1D), calculated by ${\overline{u}}_z$ and $\sqrt{{({\overline{u}}_x)}^2+{({\overline{u}}_y)}^2}$, respectively, show the skyrmion lattice with the hexagonal symmetry feature. The lattice constant a_s = λ/ sin (π/3) is determined by the Lamb wave wavelength λ = 2π/k. The axial field of the lattice varies progressively from the central “up (down)” state to the edge “down (up)” state. The zero-amplitude point of the transverse field at the center of each lattice corresponds to the polarization singularity, one typical feature of topological defects. The nontrivial real-space topology configuration can be characterized by the skyrmion number $S=\frac{1}{4\mathrm{\pi }}{\iint }_{A}sdxdy$, where s = n ⋅ (∂_xn × ∂_yn) is skyrmion number density and $\mathbf{n}=\overline{\mathbf{u}}/\mid \overline{\mathbf{u}}\mid$ is the 3D unit vector field. Area A covers one single lattice in the x-y plane. For such a lattice in Fig. 1D, the calculated skyrmion number S = 1 confirms the nontrivial topology, leading to the robustness of the skyrmion field.

Ultra-broadband and tunable characteristics of phononic skyrmions

For classical waves, constructed photonic (11) or acoustic (16) Néel-type skyrmions, with the former based on transverse waves and the latter based on longitudinal waves, require an evanescent wavefield to create the 3D wavefields. Once their carrier structure is designed, these skyrmions have a limited bandwidth because the evanescent waves in the near field can only be visualized in a narrow frequency band. Here, the phononic skyrmions have an ultra-broadband topological robustness feature due to the frequency-independent 3D hybrid spin texture of the elastic wave (A0-mode wave).

The horizontal solid blue line in Fig. 2A shows that the theoretical skyrmion number of the A0-mode wave in the plate structure (l = 0; see the unit cell model in the illustration of Fig. 2A) is always equal to one in the wide frequency band below the first-order cutoff frequency-thickness product fh < f_c1h = c_T²/c_L (see details in text S2), where c_T and c_L are the wave velocities of the bulk transverse and longitudinal waves, respectively. The solid blue line means that the perfect phononic skyrmion field can be constructed as long as the frequency fh is less than f_c1h = 0.52 MHz ⋅ mm (viz. the theoretical frequency band is 0 < f < 0.52 MHz, here h = 1 mm). A smaller thickness h leads to a wider frequency band. For example, reducing the plate thickness h of 1 mm to 10 μm will increase the frequency band to 0 < f < 52 MHz according to the scaling law. When the fh is greater than f_c1h, it will introduce the first-order antisymmetric Lamb wave (A1-mode wave) (see the band-like dispersions in Fig. 2B) to disturb the perfect skyrmion field. The imperfect skyrmion configuration, annihilated by a small-amplitude A1-mode wave, also has robustness due to the nontrivial topology. We point out that the skyrmion number of A0-mode waves on the hosting plate modulated by periodic pillared resonators is still equal to one in a wide frequency band below the resonance cutoff frequency f_rh (see details in fig. S5).

Fig. 2. Ultra-broadband and tunable characteristics of phononic skyrmions.

(A) Skyrmion number S (solid blue line) for an elastic plate as a function of the frequency-thickness product fh. The solid and dotted magenta lines indicate the skyrmion number density contrast δ of the wavefields in the top plane of elastic structures without and with pillared resonators, respectively. The two illustrations are unit cell models with sixfold rotational symmetry, a plate with thickness of h = 1 mm, and a pillar resonator with height of l = d on the plate top. (B and C) Top subfigures are the polarization ϑ of the wavefields in the top plane of elastic structures without and with pillared resonators. The bottom subfigures are band-like dispersions in the ΓM direction. The lattice constant of the unit cell model is a₀ = 4h. (D to F) Vector fields (color bar for the amplitude of its axial field). (G to I) Theoretical skyrmion number density profile obtained from the theoretical calculations. The unit cell models for profiles in (G) to (I) are consistent with those indicted by solid and dotted magenta lines in (A).

The skyrmion number density contrast δ = (s_max + s_min)/(s_max − s_min) is a parameter that provides a quantitative index of the spatial confinement of the skyrmion density (11). The solid magenta line of Fig. 2A shows that the frequency-thickness product fh can tune δ of the plate structure (l = 0; see the unit cell model in the illustration of Fig. 2A). The physical nature of the tunable characteristic is that as the fh increases, the polarization ϑ (shown in Fig. 2B) of the excited spin trajectory increases. The latter determines the skyrmion texture with a small δ due to the geometrical property. For point I with a small fh in Fig. 2A, the corresponding ϑ approaches 0, i.e., the spin trajectory approximates an up-and-down oscillation. This leads to bubble-type skyrmions with clear domain walls separated between two specific field states (the vector field in Fig. 2D). Note that despite the dominance of the axial field, the skyrmion number is still one because the nonzero transverse field always exists because of the geometry property. For point II with a large fh in Fig. 2A, the large ϑ degenerates the domain walls and converts the bubble-type skyrmions to the Néel-type–like skyrmions (the theoretical vector field in Fig. 2E). The corresponding skyrmion number density profiles are shown in Fig. 2 (G and H).

The pillared resonator acts as a new degree of freedom capable of linearly increasing the polarization of the spin trajectory while maintaining the spin configuration (movie S2 and see details in text S4). Therefore, by introducing pillared resonators, the wavefields at the top plane of pillared resonators can keep the skyrmion configurations while the δ decreases (the dotted magenta line of Fig. 2A). This can be realized if the excitation frequency is below the resonance cutoff frequency f_rh = 0.18 MHz ⋅ mm (marked in the band-like dispersions in Fig. 2C) (42) to hold the wavefield symmetry. Figure 2 (F and I) shows the theoretical vector field and skyrmion number density profile at the top plane of pillared resonators where the actual wavefield exists only at the region of the pillar position. This wavefield configuration is also robust because of the nontrivial topology of the coupled wavefield in the hosting plate. These topological pillared resonators can couple well with the fluid through their bending vibrations. The fluid-solid coupling leads to a nontrivial acoustic skyrmion field in fluids, which has the same ultra-broadband and tunable characteristics as the phononic skyrmion field (see details in fig. S7). This new mechanism of generating the acoustic skyrmion break through the narrow-band property of the acoustic skyrmion (16) constructed by evanescent waves.

Observation of elastic phononic skyrmions

We have used a 3D printer to fabricate a hexagonal-symmetry metaplate with pillared resonators, as shown in Fig. 3A. Single-side piezoelectric patch arrays excite three pairs of counterpropagating plane Lamb waves. We have used Polytec scanning laser vibrometer (PSV-500) to measure the dynamic displacement field. Without loss of generality, we have measured the wavefield in the frequency range from 6 to 9 kHz. Theoretically, perfect skyrmion wavefields can be measured at any frequency below the cutoff frequency of Lamb waves when the structure size is large enough. Before measuring the skyrmion wavefield, we first only turn on one piezoelectric patch array (i.e., 1^# array in Fig. 3A) to excite a plane A0-mode wave. The band-like experimental dispersions were obtained by Fourier transforming the scanned (z component) displacement field. The numerical ones were obtained by full-wave simulations. One can observe a good agreement between the experimental and simulated dispersions (colors and lines, respectively, in Fig. 3B). The dominance of the A0-mode wave indicates that the symmetry Lamb modes (S0) from slight mode conversion by the pillared resonators or imperfect exciting can be neglected, which ensures the wavefield symmetry.

Fig. 3. Observation of phononic skyrmions.

(A) Experimental metaplate. (B) Experimental and simulated band-like dispersions (colors and lines, respectively). (C) Experimental and theoretical skyrmion number in the whole measure frequency range. (D and E) Axial and transverse displacement fields in 8 kHz. (F) 2D fast Fourier transform of the measured axial displacement field. (G) Experimental and theoretical skyrmion number as a function of time delay for two cycles of the skyrmion lattice in 8 kHz. T = 0.125 ms is one cycle. (H) Snapshot of movie S3 for the experimental Néel-type skyrmion vector field in the 3D space. The image beneath the vectors shows the vertical component of the wavefield. (I) Vector fields at the 2D top plane of pillared resonators (Néel-type–like skyrmion). (J) Vector fields at the bottom plane of the hosting plate (bubble-type skyrmion).

For all the measured frequencies, we have calculated the skyrmion numbers by the measured wavefields of the central lattices based on eq. S41. These experimental results, shown in Fig. 3C, have good agreement with the theoretical ones, which confirms the broadband characteristic of the phononic skyrmions. Taking an example of skyrmion configuration in 8 kHz, we have shown the experimental axial (out-of-plane) and transverse (in-plane) displacement fields in Fig. 3 (D and E), respectively. One can see good agreement between the theoretical and experimental results, especially for the central skyrmion lattice. The slight distortion for the six other skyrmion lattices around the central one is mainly due to the fact that the excited nearfields are imperfect plane waves in our compact structure. Figure 3F illustrates the 2D fast Fourier transform (FFT) of the experimental displacement field in Fig. 3D, which shows a clear hexagonal symmetry map.

The measured 3D time-resolved Néel-type skyrmion vector field is shown in movie S3. We have extracted the skyrmion number as a function of the time delay in Fig. 3G for two cycles of the skyrmion wavefield. The skyrmion wavefield emanates from the interference of hybrid spin wavefields. The wavefield interference forms standing wavefields. Because the up-and-down oscillation of the standing wavefield reverses the vector direction of the 3D wavefield, measured S are 1 and −1 in the first and second half of the wave cycle, respectively, which is consistent with the theoretical ones (calculated from an analytical model shown in text S5). Note that the measured S is far from 1 and −1 in the middle of a cycle because, at these moments, the skyrmion wavefield displacement approaches 0 because of oscillation of the standing wavefield, which amplifies the error brought by the imperfect symmetry of the attached excitation source and measurement noise. For the moment (delay time τ = 22.064 ms) of maximum axial displacement of the skyrmion wavefield, the snapshot of movie S3 exhibits a distinct Néel-type skyrmion configuration in the 3D space, as shown in Fig. 3H. The vector fields at the 2D bottom plane of the hosting plate (bubble-type skyrmion) and the top plane of pillared resonators (Néel-type–like skyrmion) are shown in Fig. 3 (J and I), respectively. The transition of the different skyrmion types in the geometric space demonstrates that the pillared resonators can contribute to constructing 3D skyrmion configurations.

Robustness of phononic skyrmions

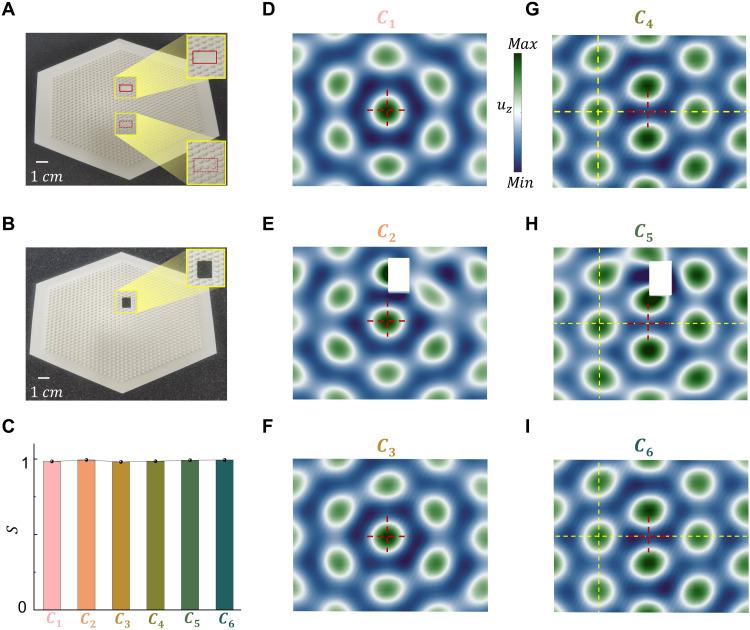
The nontrivial topological phononic skyrmion lattice leads to the robustness of wavefield texture against defects. As shown in Fig. 4A, we have introduced defects into the reference structure (illustrated in Fig. 3A) by removing and disorderly arranging the pillared resonators near the structure center, marked as structure I. The defect location can be in any region of the structure, including its center (see details in fig. S9). These defects lead to wave scattering and distorting the wavefield. However, the measured wavefield of structure I (Fig. 4D) demonstrates that the skyrmion lattice is hardly affected by these defects, compared with that of the reference structure (i.e., the one in Fig. 4F). To go further, we have introduced a strong defect into the structure by drilling a rectangular hole with sharp corners, as shown in Fig. 4B, marked as structure II. We have experimentally observed that the skyrmion lattices in structure II (Fig. 4E) are only slightly affected by the rectangular hole defect, except for the wavefield enhancement observed around the defect, which is due to the stress concentration (43, 44). In addition, we have experimentally calculated the skyrmion numbers for the central skyrmion lattices in structures I and II, marked as cases C₁ and C₂, respectively. These experimental results shown in Fig. 4C indicate very small changes in the skyrmion numbers compared with that of the reference structure (case C₃), which confirms that the phononic skyrmions are robust against the defects. The skyrmion number does not change with local perturbations because the latter do not affect the global C6 symmetry, which leads to the stability of the skyrmion field.

Fig. 4. Robustness of phononic skyrmions.

(A) Structure with the defects of removing (see the solid line box) and disorderly arranging (see the dashed line box) pillars, i.e., structure I. (B) Structure with a rectangular hole, i.e., structure II. (C) Experimental skyrmion numbers for cases from C₁ to C₆. (D to F) Experimental axial wavefields at the center of structure I, structure II, and reference structure without defects, respectively, marked as cases from C₁ to C₃. (G to I) Experimental wavefields for cases from C₁ to C₃ are shifted leftward by λ, respectively, marked as cases from C₄ to C₆. The dotted red line intersection is the midpoint of the central lattice before it shifts. The distance between the dotted yellow line intersection and the red one is λ.

The phononic skyrmion lattices are created from the spin field interference of excited plane Lamb waves in the hexagonal-symmetry metaplate. According to the coordinate transformation in the geometric space, the topological wavefield can be flexibly moved by tuning the phase of the three pairs of excitation sources, even in the presence of defects. To move the skyrmion lattice by Δr = (Δx, Δy), we can tune the phase of three pairs of excitation sources by $\text{Δ}{\mathrm{\varphi }}_{\mathrm{\theta }=-\frac{\mathrm{\pi }}{3},0,\frac{\mathrm{\pi }}{3}}=k\cdot \text{Δ}\mathbf{r}\cdot \mathbf{t}(\mathrm{\theta })$. For one simplest case of shifting leftward λ, i.e., Δr = (λ,0), the modulated phases are $(\text{Δ}{\mathrm{\varphi }}_{\mathrm{\theta }=-\mathrm{\pi }/3}\text{Δ}{\mathrm{\varphi }}_{\mathrm{\theta }=0}\text{Δ}{\mathrm{\varphi }}_{\mathrm{\theta }=\mathrm{\pi }/3})=(\mathrm{\pi }0\mathrm{\pi })$. Therefore, we only need to tune the phase of excitation sources in the directions of θ = − π/3 and θ = π/3 by π. Figure 4 (G to I) shows the measured shifting of wavefields in Fig. 4 (D to F), marked as cases from C₄ to C₆, respectively. Their experimentally calculated skyrmion numbers, as shown in Fig. 4C, all approach one. This confirms that the phase of excitation sources is an effective degree of freedom to manipulate the topological skyrmion configuration, even in the presence of defects.

DISCUSSION

We have theoretically and experimentally demonstrated and observed the formation of ultra-broadband phononic skyrmions based on the 3D hybrid spin of elastic waves. The phononic skyrmion provides an unprecedented topological phononic structure, which has robustness against local defects of disorder, sharp corners, and even rectangular holes due to the nontrivial topology. The phononic skyrmion, with high robustness and ultra-bandwidth, could pave a new path for high-speed and topological phononic information processing technologies. The 3D hybrid spin states also open new pathways for topological phonons manipulation and may facilitate the exploration of new topological orders.

Our research opens possibilities to realize novel topological phononic materials in different scales from macro to microstructures. Although our reported experimental results here concern frequencies around 8 kHz, the dimensionless dispersions shown in fig. S2 allow our established skyrmion configuration to be readily scaled to higher frequencies (see constructed phononic skyrmion field on a silicon chip at a frequency of 1.5 MHz in fig. S12). For example, reducing the plate thickness h of 1 mm in our model to 100 nm (chip-scale level) and maintaining the same magnitude order of material parameters will raise operating frequencies to near 80 MHz, which could be used for high-frequency signal-processing chip-scale (20) technology based on the topological phononic materials. The latter can overcome the difficulty of sensitivity of the conventional chip-scale technology to defects in high frequencies.

The phononic skyrmion can be created in any elastic wave system with a large impedance-mismatch solid-solid interface, solid-gas interface, or solid-liquid interface. The reason is that the longitudinal and transverse waves will hybrid at these interfaces to form the elastic spin field (33), allowing linearly tuning its S_p by pillared resonators. The tunable spin fields can be used to construct the tunable phononic skyrmion configuration. Especially for the solid-liquid interface, phononic skyrmions constructed on the solid structure can induce skyrmions in fluids through strong fluid-solid coupling, which promotes the excitation and interaction of wavefield information in multiple fields. This fluid-solid coupling also paves the way toward skyrmion lattices “on demand” for matter systems in fluids [e.g., cell manipulation in microfluidics (45), acoustofluidic pump (46), and biomedical testing (47)].

Last, efficient transduction between elastic and electromagnetic waves can be achieved using piezoelectric coupling with microwaves (48–50) and optomechanical coupling with light (51). These couplings between different physical fields may give rise to a high–degree-of-freedom topological skyrmion system and facilitate an advanced integrated information platform of interdisciplinary physics among electronics, photonics, and phononics.

MATERIALS AND METHODS

Structure fabrication and materials

Our established paradigm for generating and manipulating phononic skyrmions is universal and applicable to almost all solid materials. Here, we have chosen a 3D printer to fabricate our structures. 3D printing allows us to easily fabricate phonon structures with any geometry, providing an excellent platform for exploring and verifying the physics of phonons. The printed metaplate is shown in Fig. 3A. The thickness of the hosting plate below pillar resonators is h = 1 mm. The height and radius of pillar resonators are 3h and h, respectively. All unit cell models in Figs. 3 and 4 are the same and required to be sixfold rotational symmetry (similar to the one in the illustration of Fig. 1F) due to the symmetry of the phononic skyrmion lattices. The lattice constant of the unit cell model is a₀ = 4h. The 3D printed material is polylactic acid (PLA). Its material parameters were tested in our previous work (42). Young’s modulus, Poisson’s ratio, and the density are E_PLA = 3.44 GPa, υ_PLA = 0.35, and ρ_PLA = 1086.3 kg/m³, respectively. The material of all the studied models in this work is PLA, except as noted in particular.

Experiments

The lead-zirconate-titanate patch arrays (SMPL7W8T02412WL) are driven by a signal generator (Tektronix, AFG3022C) to excite plane lamb waves. The PSV-500 scanning head records the displacements of all measurement points in the far field. An ensemble average with 20 samples is used at every measurement point to ensure signal quality. For the measured 3D time-resolved vector field shown in movies S1 to S4, the excitation signal is a 50-cycle tone burst w_t = A₀[1 − cos (2πf_ct/50)] sin (2πf_ct), where f_c = 8 kHz is the central frequency. The sampling frequency in the time domain is set as 125 kHz, and the measure resolution is 8 μs. The images are processed to create vector representations of the wavefield, which, in turn, are combined in a time sequence to create a movie of the time development of the wavefield vectors.

Numerical simulations

The full-wave simulations were implemented by the commercial software COMSOL Multiphysics with the solid mechanics module and acoustic-solid interaction module based on the finite element method. An eigenfrequency study was used to simulate the band-like dispersion. The largest mesh element size was set lower than ¹/₁₂ of the lowest wavelength, and finer meshes were applied at the region with pillars. The parameters of the simulated structures are consistent with those of the experimental structures.

Supplementary Materials

This PDF file includes:

Supplementary Text

Figs. S1 to S13

References

Other Supplementary Material for this : manuscript includes the following:

Movies S1 to S4