Graph embedding and Gaussian mixture variational autoencoder network for end-to-end analysis of single-cell RNA sequencing data

Summary

Single-cell RNA sequencing (scRNA-seq) is a revolutionary technology to determine the precise gene expression of individual cells and identify cell heterogeneity and subpopulations. However, technical limitations of scRNA-seq lead to heterogeneous and sparse data. Here, we present autoCell, a deep-learning approach for scRNA-seq dropout imputation and feature extraction. autoCell is a variational autoencoding network that combines graph embedding and a probabilistic depth Gaussian mixture model to infer the distribution of high-dimensional, sparse scRNA-seq data. We validate autoCell on simulated datasets and biologically relevant scRNA-seq. We show that interpolation of autoCell improves the performance of existing tools in identifying cell developmental trajectories of human preimplantation embryos. We identify disease-associated astrocytes (DAAs) and reconstruct DAA-specific molecular networks and ligand-receptor interactions involved in cell-cell communications using Alzheimer’s disease as a prototypical example. autoCell provides a toolbox for end-to-end analysis of scRNA-seq data, including visualization, clustering, imputation, and disease-specific gene network identification.

Graphical abstract

Highlights

• •autoCell imputes heterogeneous and sparse sc/snRNA-seq data
• •autoCell improves the performance of capturing cell developmental trajectories
• •autoCell captures disease-relevant cellular pathobiology in latent space
• •autoCell identifies cell-type-specific gene networks in Alzheimer’s disease

Motivation

Single-cell RNA sequencing (scRNA-seq) enables researchers to study gene expression at cellular resolution. However, noise caused by amplification and dropout may hamper precise data analyses. It is urgent to develop scalable denoising methods to deal with the increasingly large, but sparse, scRNA-seq data. Here, we present autoCell, a graph-embedded Gaussian mixture variational autoencoder network algorithm for scRNA-seq dropout imputation and feature extraction. Our autoCell provides a deep-learning toolbox for end-to-end analysis of large-scale single-cell/nucleus RNA-seq data, including visualization, clustering, imputation, and disease-specific gene network identification.

Xu et al. develop a graph-embedded Gaussian mixture variational autoencoder network algorithm (termed autoCell) for end-to-end analyses of single-cell/nuclei RNA-seq data, including visualization, clustering, imputation, and cell-type-specific gene network identification. autoCell offers a useful tool for large-scale single-cell genomic data analyses to accelerate translational biology and disease discoveries.

Introduction

Single-cell technology is a revolutionary breakthrough, allowing us to study the genome, transcriptome, and multi-omics systems of each cell, in each state, in tissues.^1,2 Combined with technologies such as fluorescent labeling and microdissection, it can also determine spatial attributes and cell-cell communication. These technologies have been widely used, leading to a revolution in basic and translational medicine.

Single-cell or single-nucleus RNA sequencing (sc/snRNA-seq) is important for identifying biological and disease-relevant cell types and subpopulations from heterogeneous cells.^3,4,5,6 Low-dimensional analysis of expression in different cell states can also be highly effective in reconstructing the cell developmental trajectory.^{7,8,9,10,11,12} However, the amount of mRNA in a single cell is small, which necessitates a nearly million-fold amplification. Although the measurement technology has been greatly improved, technical factors still cause considerable noise in data generated in scRNA-seq experiments, including amplification deviation, library size difference, and extremely low capture rate. In particular, the extremely low RNA capture rate leads to undetectable, albeit expressed, genes, namely “dropout” events.¹³ An essential difference is found between the “false” zero count caused by the “dropout” event and the true zero count. Given the sparse expression metrics, traditional analytic tools cannot achieve scientific rigor, and they lack high data reproducibility.¹⁴

Deep-learning algorithms have shown compelling performance in high-dimensional data processing, including sparse genomic data. DeepImute, an interpolation algorithm based on a deep neural network, is one such example. It uses the dropout layer to learn the patterns in the data to achieve accurate imputation.¹⁵ Another denoising model is to denoise scRNA-seq datasets through a depth-counting autoencoder (DCA) network. A DCA takes the count distribution, overdispersion, and sparsity of the data into account using a negative binomial noise model with zero inflation.¹⁶ scScope, a scalable deep-learning-based method, can accurately and quickly identify cell-type composition from millions of heterogeneous single-cell transcriptomic profiles.⁹ Compared with DCA and scScope, scVI¹⁷ uses a variational autoencoder (VAE) to reduce the dimensionality of scRNA-seq data. However, the standard VAE implemented by scVI¹⁷ only uses a single isotropic multi-variate Gaussian distribution on the latent variable, which is not generally suitable for representing multi-category data such as scRNA-seq data containing multiple types of cells/nuclei. scVAE is another method based on VAEs, which uses Gaussian mixture models (GMMs) as prior distributions and introduces Poisson or negative binomial distributions to obtain latent representations of cells.¹⁸ However, the model considers the mean and variance of the GMM as random variables, and it is approximated by a neural network with a parameter $\beta$, which makes model optimization challenging. As the number of measurable cells/nuclei and additional emerging sc/snRNA-seq data analysis challenges increase, the demand for faster and scalable estimation methods becomes a pressing need.

With the rapid development of graph neural networks, graph autoencoders can learn low-dimensional representations of graph topology and train node relationships with a global, entire graph view. Increasingly, exploiting a graph neural network framework in sc/snRNA-seq data analysis can be considered. Single-cell graph neural network (scGNN)¹⁹ establishes cell-cell relationships through graphical neural networks and uses left-truncated mixed Gaussian models to model heterogeneous gene expression patterns. It also integrates three iterative multi-mode autoencoders. However, the iterative autoencoder framework requires more computing resources, which is more time consuming.

In this study, we present a deep-learning framework, namely autoCell, for dropout imputation and feature extraction from scRNA-seq data. The accuracy index indicates that autoCell outperformed six state-of-the-art published imputation methods in simulated datasets and biologically relevant sc/snRNA-seq datasets with varying degrees of human diseases. Therefore, autoCell is a scalable and accurate scRNA-seq data processing method that is superior to other scRNA-seq data analysis tools.

Results

Overview of the autoCell framework

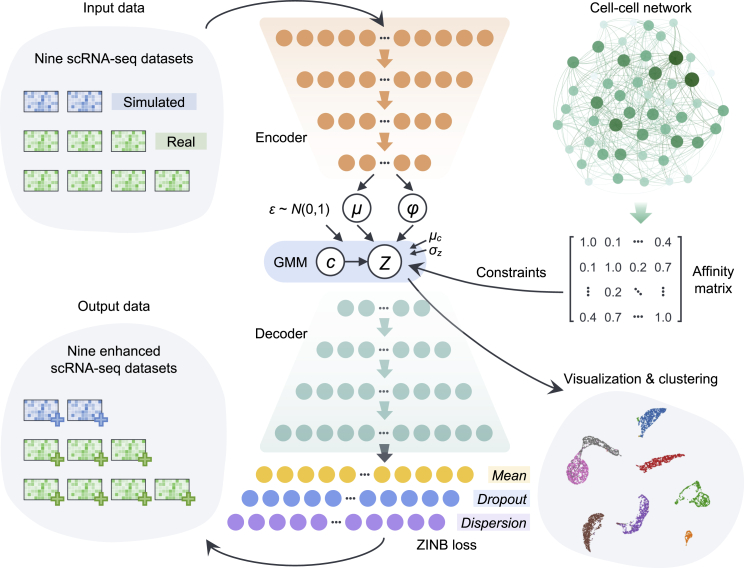
The overview of autoCell is shown in Figure 1. It is a VAE network that combines graph embedding and GMMs to model the distribution of high-dimensional, sparse scRNA-seq data. autoCell architecture can use biological representations of cells and genes to perform different scRNA-seq data analysis tasks. By integrating GMMs, autoCell can better estimate data distribution. We apply graph embedding to deal with sc/snRNA-seq data. Capturing the graphical information of the local data structure is a good complement to deep GMMs, making the network learn a global model with local structure constraints. Recent studies have showed that zero-inflated negative binomial (ZINB) distribution for modeling is an appropriate tool to solve the “dropout” event for scRNA-seq data. In reducing the impact of dropout events in highly sparse and over-dispersed count data, we introduce the ZINB distribution model, thereby denoising scRNA-seq data (see STAR Methods).

Figure 1.

Overview of the autoCell framework

autoCell uses a Gaussian mixture model (GMM) and a deep neural network (DNN) to model the process of data generation. It uses zero-inflated negative binomial (ZINB) loss to process “dropout” events in scRNA-seq. The encoder and decoder are a two-layer neural network (128–128) with 10-dimensional latent variables (features) directly connected to the output. The cell-cell network is used to constrain the latent feature $Z$; thus, similar cells have similar latent features and cluster assignments. The yellow nodes depict the mean of the negative binomial distribution, which is the main output of the method representing denoised data, whereas the purple and blue nodes represent the other two parameters of the ZINB distribution, namely, dispersion and dropout.

autoCell effectively imputes scRNA-seq data

We first applied autoCell to simulated scRNA-seq data to assess its imputation performance.²⁰ We simulated two datasets with three cell types, including 1,000 cells and 2,000 genes. For the simulation of the two datasets, 60% and 71% of the data values were set to the zero matrix to simulate dropout events in real data. We divided the entry of the simulated raw expression data into zero and non-zero space. Based on the density plot of the estimated and real values, the recovery values of DCA and autoCell are closer to the true expression values, and scGNN is at a medium level. MAGIC,²¹ SAVER,²² and SAUCIE²³ always tend to underestimate the original value. We also calculated the median L1 distance, root-mean-square error (RMSE) scores, and cosine similarity (see STAR Methods) score between the real expression value and restored expression value to measure the estimation accuracy. As shown in Figure 2, autoCell achieves overall better performance than the others. In particular, autoCell ranks second in the median L1 distance of gene expression restoration on the two simulated datasets and ranks second in the cosine similarity score on the simulated dataset with a synthetic dropout rate of 71%. In addition, the dropout event will increase the noise, muddling the identity of cell types, which can be restored through interpolation by value recovery algorithms. We also found that autoCell outperforms existing methods in the two simulation datasets (Figures S1A and S1B).

Figure 2.

Performance comparison between autoCell and other state-of-the-art methods under 10% synthetic dropout rate

(A) Density plots of imputed versus original data masked. The x axis corresponds to the imputed values, and the y axis represents the true values of the masked data points. Each row is a different dataset, and each column is a different imputation method. Pearson correlation coefficient (PPC; higher is better).

(B) Comparison of the cosine similarity (higher is better), median L1 distance (lower is better), and root-mean-square error (RMSE) scores (lower is better) between autoCell and the other six imputation tools.

In evaluating the performance of autoCell in imputing missing values, we also selected two biologically relevant sc/snRNA-seq datasets^24,25 with well-annotated cell types as benchmarks. We simulated the dropout effects by randomly flipping 10% non-zero entries to the zero matrix. Similarly, three indicators between the original dataset and imputed values of these synthetic items are calculated as a measure of estimation accuracy. Compared with several state-of-the-art algorithms (Figure 2), autoCell achieves the best performance evaluated by the median L1 distance, cosine similarity, and RMSE at the 10% synthetic dropout rate. Furthermore, autoCell imputation is closer to the true expression value based on the density plot of the estimated and true values (Figure 2). Collectively, autoCell outperforms state-of-the-art methods in sc/snRNA-seq data imputation analysis (Figure S2).

autoCell improves the performance of existing tools for capturing cell developmental trajectories

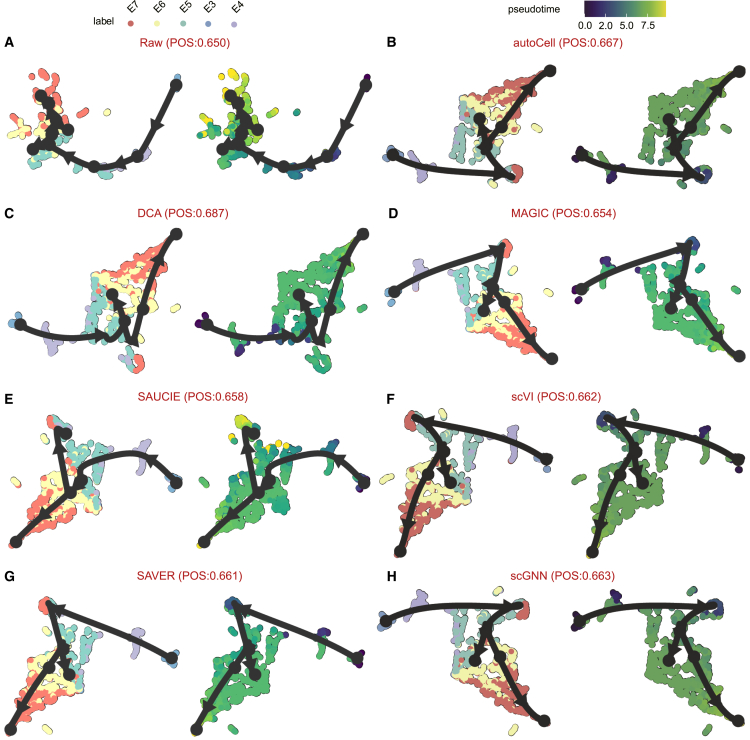
Apart from identifying cell types, scRNA-seq facilitates the organization of cells by time course or developmental stage (i.e., cell trajectory). The transition of cells from one functional state to another is a critical event in development. However, transitions are difficult to characterize since trapping and purifying cells in between stable endpoint states are challenging. Although some models currently exist to infer cell developmental trajectories based on scRNA-seq data, most inference methods do not address dropout events. We tested the accuracy of inferring the cell trajectory of scRNA-seq data after interpolation via autoCell. We used a benchmark dataset²⁶ with 1,529 single cells with five stages of well-annotated human preimplantation embryonic development from embryogenesis embryonic day 3 (E3) to E7. We reconstructed cell trajectories using monocle3²⁷ after various interpolation processes. The interpolation of autoCell produced the highest correspondence between the inferred pseudotime and the real-time cellular development (Figure S3). Pseudotime order score (POS; see STAR Methods) increased from 0.838 to 0.850. On the contrary, the POS obtained by other algorithms is lower than the original scRNA-seq dataset (Figure S3). Furthermore, we used another common trajectory analysis model, slingshot,^28,29 to test whether autoCell improves trajectory analysis. We found that cell development trajectory is well captured by interpolation from autoCell (Figure 3). Therefore, autoCell captures more accurate transcriptome dynamics and cell developmental trajectories across different developmental stages.

Figure 3.

autoCell improves pseudotime analysis in the human preimplantation embryonic development dataset

(A and B) Results of slingshot estimated pseudotime using (A) raw data as input and (B) processed data from autoCell as input.

(C) Processed data from DCA as input.

(D) Processed data from MAGIC as input.

(E) Processed data from SAUCIE as input.

(F) Processed data from scVI as input.

(G) Processed data from SAVER as input.

(H) Processed data from scGNN as input.

POS, pseudotime order score (the higher the value the better). Pseudotime is a measure of how much progress an individual cell has made through a process such as cell differentiation.

autoCell captures cellular pathobiology in latent space

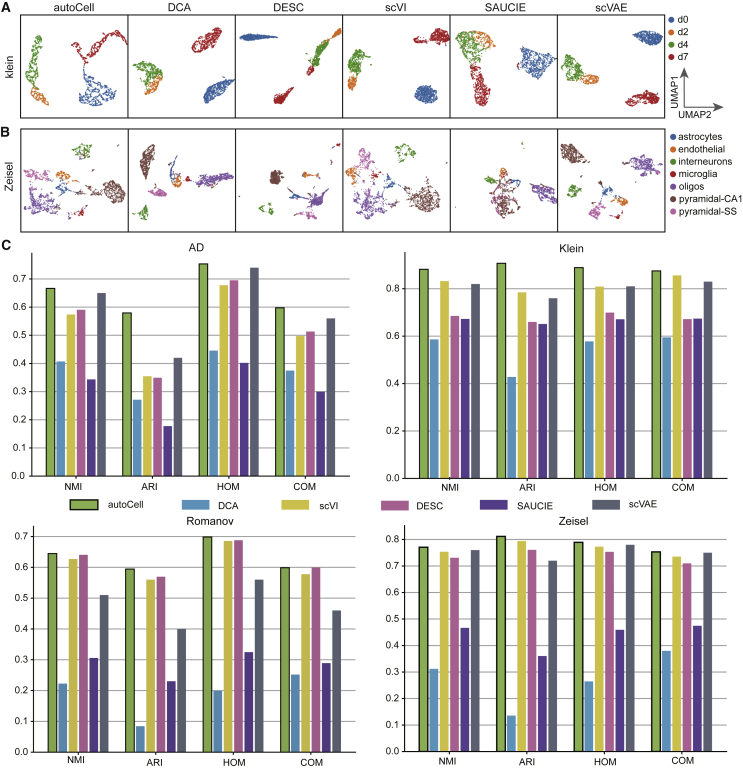
We also assessed the extent to which the latent space inferred by autoCell reflects the biological variability among cells based on the previous stratification of cells into biologically important subpopulations through unsupervised clustering followed by manual inspection and annotation. We applied autoCell to two simulated datasets and four biologically relevant scRNA-seq datasets. The zero ratio of these six datasets ranges from 60% to 90%. By default, autoCell extracted 10 features from the input data. For a fair comparison, we further applied common scRNA-seq data dimension reduction methods, including scVI, DESC,³⁰ scVAE, DCA, and SAUCIE, to reduce the input data to 10 dimensions. We used uniform manifold approximation and projection (UMAP) to visualize the features extracted from these tools and the original data. We found that the feature embeddings of autoCell were well separated among cell types with closer inner-group distances and larger between-group distances. However, the embedding and original data of DESC, scVAE, DCA, and SAUCIE overlapped among certain cell types. We found that autoCell is the best approach to identify all three cell types in the two simulated datasets (Figure S1C). For the Klein dataset,²⁵ scVI, scVAE, and autoCell showed better performance, and DCA caused the cell types d0 and d2 to be closely linked. However, SAUCIE and DESC only separated cells with cell type d0 and incorrectly divided cell type d7 into two cell types (Figure 4A). For the Zeisel dataset,²⁴ we found that autoCell, scVI, and scVAE still outperformed the other models, and autoCell and scVAE achieved a closer intra-group distance (Figure 4B).

Figure 4.

UMAP visualization of the extracted features using different approaches

(A and B) We evaluated autoCell with DCA, DESC, scVI, SAUCIE, and scVAE using two datasets: (A) Klein and (B) Zeisel datasets. For comparison, autoCell, DCA, DESC, scVI, SAUCIE, and scVAE all performed dimension reduction to 10 dimensions before applying UMAP.

(C) Comparison on the effect of clustering on four benchmark datasets. Clustering accuracy was evaluated by applying K-means clustering on the extracted features to obtain cluster assignments.

NMI, normalized mutual information (the higher the value the better); ARI, adjusted rand index; COM, completeness (the higher the value the better); HOM, homogeneity (the higher the value the better).

We applied K-means clustering on autoCell-extracted latent features and assessed the clustering accuracy by comparing it with scVI, DESC, scVAE, DCA, and SAUCIE. We found that autoCell displays the best performance across all tested scRNA-seq datasets (Figure 4). In the Klein dataset,²⁵ the clustering output using autoCell (Figure 4C) was more consistent with the predefined unit-type annotation (normalized mutual information [NMI] = 0.882 and adjusted Rand index [ARI] = 0.907) than the second ranked model, scVI (NMI = 0.832, ARI = 0.784). In the Zeisel dataset,²⁴ the clustering performance of autoCell was considerably better than other existing tools. Then, we changed K-means to another four clustering algorithms (including spectral clustering, affinity propagation, birch, and agglomerative clustering). autoCell shows the best performance across all tested scRNA-seq datasets (Table S1).

In addition, we compared the visualization performance using principal-component analysis (PCA). As shown in Figure S4, in the Klein dataset, the feature embedding of autoCell, scVI, and scVAE was well separated among cell types. For the Zeisel dataset, autoCell and DESC showed the best performance, although they mixed astrocytes and brain endothelial cells, both of which were glial cells located in the CNS, but they can effectively separate most cell types. For the Romanov dataset, all models identify two glial clusters (astrocytes and brain endothelial cells) close to each other in the latent space. However, autoCell was the only model that effectively separated the microglia (Figure S4).

Collectively, autoCell presented elevated accuracy in capturing cellular pathobiology than existing state-of-the-art approaches for simulated and real-world biologically relevant scRNA-seq datasets (Figures S4 and S5).

Discovery of cell-type-specific molecular networks by autoCell

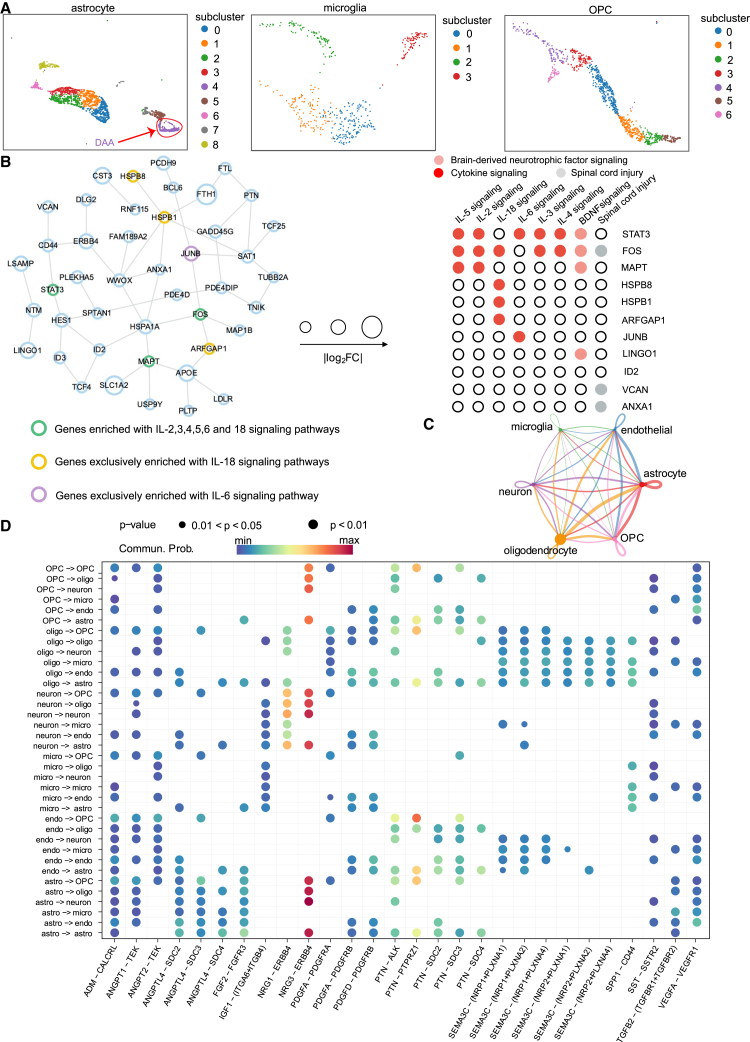
In testing whether the autoCell-inferred cell type can capture specific pathobiology of human diseases, we analyzed astrocytes, microglia, neurons, and oligodendrocyte progenitor cells (OPCs) using Alzheimer’s disease (AD) as a prototypical example. In total, we re-analyzed 13,214 high-quality nuclei generated from the entorhinal cortex of AD brains and healthy controls. Using autoCell, we identified four microglia clusters, nine astrocyte clusters, and five OPC clusters (Figure 5A). Recent studies using human postmortem brain tissues identified disease-associated astrocyte (DAA) involved in crucial roles of AD pathogenesis and disease progression of AD. Using 11 experimentally validated DAA marker genes (four upregulated marker genes [GFAP, CD44, HSPB1, and TNS] and seven downregulated marker genes [SLC1A2, SLC1A3, GLUL, NRXN1, CADM2, PTN, and GPC5]),³¹ we identified astrocyte subcluster 4 as a DAA by autoCell (Figure S6). Next, we built a DAA-specific molecular network using a state-of-the-art network-based algorithm, GPSnet,³² under the human protein-protein interaction (PPI) network model. The DAA-specific module network included 50 PPIs connected by 44 proteins, such as APOE, MAPT, CD44, FOS, and STAT3 (Figure 5B; Table S2). APOE and microtubule-associated protein Tau (MAPT) were two of the most well-known risk genes for AD.^33,34 CD44 was an inflammation-associated protein. The inhibition of CD44 could be a potential strategy for AD treatment.³⁵ In a mouse model study, Stat3-deficient and Stat3-deletion astrocytes presented dropped levels of β-amyloid and pro-inflammatory cytokine activities.³⁶ Proteins from the DAA-specific molecular network were enriched by multiple AD-related pathways, such as cytokine signaling, spinal cord injury, and brain-derived neurotrophic factor signaling pathways (Figure 5B; Table S3). For example, several proteins in the DAA-specific network (STAT3, MAPT, HSPB8, HSPB1, JUNB, and LINGO1) were enriched in multiple cytokine signaling pathways, including interleukin-5 (IL-5), IL-2, IL-18, IL-3, and IL-4, consistent with the important role of neuro-inflammation mediated by microglia in AD.^37,38 Therefore, using autoCell, we can identify disease-associated, cell-type-specific molecular network involved in key AD pathobiology.

Figure 5.

Discovery of cell-type-specific molecular networks and significant ligand-receptor interactions in Alzheimer’s disease (AD) using autoCell

(A) UMAP visualization of subclusters of astrocytes (including disease-associated astrocyte [DAA]), microglia, and OPCs, labeled with autoCell clusters.

(B) Reconstruction of the DAA-specific molecular subnetwork from the human protein-protein interactome. The DAA-specific module network included 50 protein-protein interactions (PPIs) connected by 44 proteins (e.g., APOE, MAPT, CD44, FOS, and STAT3). The proteins from the DAA-specific molecular network are enriched with multiple AD-related pathways, including cytokine signaling pathways. The proteins from the DAA-specific molecular network are enriched with multiple cytokine signaling pathways.

(C) Inferred cell-cell interactions using CellChat.

(D) Top selected significant ligand-receptor pairs among autoCell-identified cell types. Ligand-receptor interactions were predicted by CellChat (see STAR Methods).

We also identified significant ligand-receptor interactions involved in cell-cell communications in AD. We first inferred cell subpopulations using autoCell and the predicted ligand-receptor interaction using CellChat.³⁹ As shown in Figure 5C, we found strong ligand-receptor interactions among astrocytes, OPCs, and oligodendrocytes compared with the other three cell types (neuron, microglia, and endothelial). Two ligand-receptor pairs (NRG3-ERBB4 and NRG1-ERBB4) revealed strong interactions across multiple cell-cell pairs (Figure 5D; Table S4). Multiple single-nucleotide polymorphisms in the NRG3 gene were found to be associated with the onset of AD.⁴⁰ In addition, the overexpression of ERBB4 in neurons was found to be associated with AD neuropathology.⁴¹ A recent AD mouse model study found that immunoreactivity of NRG1 and ERBB4 was associated with plaques in the hippocampus region.⁴² Using AD as a prototypical example, we demonstrated that the disease-associated cell subtype identified by autoCell could identify molecular targets and networks (i.e., ligand-receptor interactions) involved in AD pathogenesis and provide potential drug targets for AD or other human diseases if broadly applied.

autoCell is scalable to large datasets

The increasing number of cells is the main challenge in scRNA-seq analysis. In large projects such as the Human Cell Atlas,⁴³ the number of cells may be hundreds of thousands. In large datasets, identifying cell populations is challenging because many existing scRNA-seq clustering methods cannot scale up to handle them. Thus, we used the Zheng-68k⁴⁴ dataset and the Zheng-73k⁴⁴ dataset to study whether autoCell is suitable for large datasets. These cell types were used as references when benchmarking autoCell. autoCell worked well on these two large datasets and obtained good clustering performance (Figures S2 and S4). In addition, we performed time and memory comparisons on three datasets with different sizes: (1) Zeisel (3,005 cells), (2) AD dataset (13,214 cells), and (3) Zheng-68k dataset (68,579 cells). As shown in Figure 6, autoCell ranks fourth among all algorithms with regard to time. With regard to memory, autoCell ranks second after MAGIC. Thus, autoCell is scalable to large datasets and is comparable to computing time and memory compared with existing methods.

Figure 6.

Comparison of running time and memory usage

autoCell scales linearly with the number of cells. The plot shows the running time and memory on three different size datasets: (1) Zeisel (3,005 cells); (2) AD dataset (13,214 cells/nuclei); and (3) Zheng-68k dataset (68,579 cells). Colors indicate different methods. The experimental environment is Intel Core i9-10900K CPU@3.70GHz, NVIDIA RTX 3080.

Discussion

Single-cell technology is a revolutionary breakthrough that leads to the study of genomic, transcriptomic, and multi-omics systems of each cell in each tissue for the first time. With the development and wide application of technology, computational methods have been developed to solve problems posed by its generated data. Among these methods, dimensionality reduction (or low-dimensional representation) is the basis of scRNA-seq data visualization and downstream analysis. However, the technical shortcoming of single-cell sequencing and the transcription burst effect in single cells cause the data to be noisier than bulk RNA-seq data. Among the problems, dropout events usually occur, in which the false value of genes in some cells is zero or close to zero, limiting the performance of dimensionality reduction.

Here, we proposed a deep model autoCell for feature extraction and dropout imputation of scRNA-seq data. The key innovation of autoCell is the use of GMMs to estimate the latent feature distribution of the data. Compared with the previous application of the VAE in scRNA-seq data analysis, autoCell captures the graphical information of the local data structure by introducing graph embedding. This is an excellent supplement to the deep GMM, which allows network learning to follow the global model with local structure constraints. In reducing the impact of dropout events, we introduced the ZINB distribution, which can model highly sparse and over-dispersed count data, thereby denoising scRNA data. Through systematic comparison between simulated and real datasets, autoCell achieves better interpolation performance and feature extraction. In addition, we have shown that autoCell can provide greater flexibility in dealing with large datasets different from other imputation algorithms.

Limitations of the study

We acknowledge several potential limitations in autoCell. For example, compared with scVI and SAUCIE, autoCell cannot handle batch effects in scRNA-seq data. However, batch effects are inevitable in studies involving human tissues because the data are usually generated at different times, and batches may affect biological variation. Failure to eliminate batch effects will tarnish downstream analysis and lead to incorrect interpretation of results. In the future, we can improve the model to explicitly allow for the discovery and elimination of batch effects. In addition, with the progress of sequencing technology, multi-omics sequencing technologies such as scMT-seq (single-cell methylome and transcriptome sequencing) and scTrio-seq (single-cell triple omics sequencing) can simultaneously detect DNA methylation and transcriptome data from the same cell. DNA methylation is an important epigenetic regulatory signal. However, its regulatory effect on gene expression in single cells remains a challenge. Therefore, in the future, we will continue to enhance autoCell by implementing a heterogeneous map mosaic to support the integration of single-cell multi-omics data. Finally, compared with methods based on statistical models, the pre-training processing of the autoCell model requires more computing resources, which is more time consuming. Thus, we will study the creation of a more efficient autoCell model through the architecture of block and parallel processing in the near future.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited data
Mouse cortex	Zeisel et al.,24	GEO: GSE60361
Embryonic Stem Cells	Klein, A. M. et al.,25	GEO: GSE65525
Mouse hypothalamus	Romanov, R.A. et al.,45	GEO: GSE74672
Alzheimer’s disease	Grubman A et al.,46	GEO: GSE138852
Healthy human and principally involves major cell	Zheng et al.,44	10X GENOMICS: SRP073767
Fluorescence-activated cell sorting cells in a healthy human	Zheng et al.,44	10X GENOMICS: http://support.10xgenomics.com/single-cell/datasets
Human preimplantation embryonic	Petropoulos et al.,26	ArrayExpress E-MTAB-3929
Software and algorithms
MAGIC	Van Dijk, et al.,21	https://github.com/KrishnaswamyLab/magic
SAVER	Huang, et al.,22	https://github.com/mohuangx/SAVER/releases
DCA	Eraslan et al.,16	https://github.com/theislab/dca
scVI	Lopez et al.,17	https://github.com/YosefLab/scVI
DESC	Li, et al.,30	https://eleozzr.github.io/desc/
scVAE	Grønbech et al.,18	https://github.com/scvae/scvae
SAUCIE	Amodio, et al.,23	https://github.com/KrishnaswamyLab/SAUCIE/
scGNN	Wang et al.,19	https://github.com/juexinwang/scGNN
autoCell	This paper	https://github.com/ChengF-Lab/autoCell, https://doi.org/10.5281/zenodo.7331392.

Resource availability

Lead contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Feixiong Cheng (chengf@ccf.org).

Materials availability

This study did not generate new unique reagents.

Method details

Deep Gaussian mixture model

Using a Gaussian distribution as the prior probability distribution of z only allows for one mode in the latent representation. In the presence of inherent clustering in data, such as scRNA-seq data where the cells represent different cell types, multiple modes are desirable, for example, one for every cluster or class. This strategy can be implemented by using a Gaussian-mixture model in place of Gaussian distribution.

We aim to cluster a given set of $D$-dimensional training samples $\left\{x_n\right\}{}_{n=1}^N$ into K categories. For each training sample $x$, we learn a latent feature $z\in R^{M\times 1}$. We assume that the underlying features follow a Gaussian mixture distribution. We introduce a binary vector $c\in \left\{\mathrm{0,1}\right\}{}^{K\times 1}$ to indicate which Gaussian component the latent feature z belongs to.

Zero-inflated negative binomial model

ZINB distribution is favored in single-cell RNA data analysis. Previous studies have shown that the ZINB distribution model can effectively denoise single-cell RNA data by modeling highly sparse and over-dispersed data. Therefore, in this study, we use ZINB to model scRNA-seq data:

$$B\left(x;\mu ,\phi \right)=\frac{\Gamma \left(x+\phi \right)}{\Gamma \left(\phi \right)}{\left(\frac{\phi }{\phi +\mu }\right)}^{\phi }{\left(\frac{\mu }{\phi +\mu }\right)}^x$$

$$ZINB\left(x;\lambda ,\mu ,\phi \right)=\lambda I_0\left(x\right)+\left(1-\lambda \right)NB\left(x;\mu ,\phi \right)$$ (Equation 1)

where $\lambda$ represents the proportion of zero value; $\mu$ and $\phi$ are the parameters of the negative binomial distribution, and $I_0$ is the indicator function. When the independent variable is 0, the value is 1, otherwise it is 0.

Generative model

In our model, we assume that the data are drawn from a Gaussian mixture distribution. In particular, for scRNA-Seq data x, we model the generation process as follows:

$$p\left(c,\pi \right)=\left(p_1,\dots p_k\right)=\prod _{k=1}^K{\pi }_k^{c_k}$$

$$p\left(c_k=1\right)={\pi }_{ik}$$

$$p\left(z|c_k=1\right)={\rm N}\left({\mu }_k,diag\left({\sigma }_k^2\right)\right)$$

$$P_{\theta }\left(x|z\right)=ZINB\left(x;\lambda ,\mu ,\phi \right)=\lambda I_0\left(x\right)+\left(1-\lambda \right)NB\left(x;\mu ,\phi \right)$$ (Equation 2)

where $c_k$ and ${\pi }_k$ represent the $k$ th entry of $c$ and $\pi$, respectively, and ${\pi }_k$ must satisfy ${\sum }_{k=1}^K{\pi }_k=1$. ${\mu }_k$ and ${\sigma }_k^2$ represent the mean and variance of the $k$ th Gaussian component, respectively. $\left(\lambda ,\mu ,\phi \right)=g\left(z_n;\theta \right)$, where $g$ is a neural network with a parameter $\theta$ that can be trained. Detailed parameter information is provided in Table S5.

Inference model

Finding the maximum a posteriori of potential variables and the maximum likelihood estimation of parameters by directly solving the generative model is difficult.⁴⁷ In addressing this problem, we use a new distribution $q_{\phi }\left(z,c|x\right)$ to approximate the posterior distribution $p_{\theta }\left(z,c|x\right)$. The distribution is extracted from a specific category and parameterized by the trainable parameter $\phi$. In particular, we assume that $q_{\phi }\left(z,x|c\right)$ can be decomposed into $q_{\phi }\left(z,c|x\right)=q_{\phi }\left(z|x\right)q_{\phi }\left(x|c\right)$. Then, we define the following equations:

$$q_{\phi }\left(z|x\right)={\rm N}\left(\tilde{\mu },diag\left({\tilde{\sigma }}^2\right)\right)$$

$$q_{\phi }\left(x|c\right)=Multinomial\left(\tilde{\pi }\right)$$ (Equation 3)

where

$$\left[\tilde{\mu },\mathit{log}\left({\tilde{\sigma }}^2\right)\right]=f\left(x;\phi \right)$$

$$\tilde{\pi }=f\left(z;\phi \right)$$ (Equation 4)

here $f$ represents neural networks with parameter $\phi$.

In the framework of the generative and inference models, the parameters can be estimated by maximizing the log likelihood function:

$$\underset{\phi ,\theta }{\max }\sum _{i=1}^N\ln p_{\theta }\left(x_i\right)$$ (Equation 5)

Equation 5 is usually solved by maximizing the lower limit of evidence of the log likelihood function using multiple parameterization. We observed that the model consists of two networks, namely, $g$, and $f$, which were referred to as decoder and encoder, respectively, because they form a variational autoencoder (VAE).

Graph embedding

Graph embedding aims to find low-dimensional features in a sample similarity graph, which keeps the similarity between vertex pairs. In general, under graph embedding, training sample $\left\{x_n\right\}$ is regarded as the vertex of similar graph, and the characteristic of similar graph is regarded as the affinity matrix $W$. The optimal feature $\left\{z_n^{\ast }\right\}$ can be obtained using Equation 6:

$$\left\{z_n^{\ast }\right\}=\arg \underset{Z{Z}^T=I}{\min }\sum _{i=1}^N\sum _{j=1}^N{w}_{ij}{\left||z_i-z_j|\right|}_2^2$$ (Equation 6)

where $Z=\left[z_1,\dots z_n\right]$ and $w_{ij}$ denotes the $\left(i,j\right)$ th element of the affinity matrix $W$. The constraint ${ZZ}^T=I$ is used to avoid trivial solutions. Based on Equation 6, if samples are connected on the graph, then their features will be close to one another. Thus, we hypothesize that if the two samples are connected on the graph, then they should have similar potential features and cluster assignments. Our model considers latent features and cluster assignments as random variables. Therefore, we add a constraint to Equation 6 by measuring the distance of the posterior distributions and obtain the following equation:

$$\underset{\phi ,\theta }{\max }\sum _{i=1}^N\left(\ln p_{\theta }\left(x_i\right)-\sum _{j=1}^N{w}_{ij}d\left(q_{\phi }\left(z,c|x_i\right),q_{\phi }\left(z,c|x_j\right)\right)\right)$$ (Equation 7)

where $d\left(:,\text{:}\right)$ is a measure of the distance between two distributions. Furthermore, we require ${\sum }_j{w}_{ij}=1$ to balance the weight of each training sample. Here, we select the Jenson–Shannon (JS) divergence:

$$\underset{\phi ,\theta }{\max }\sum _{i=1}^N\left(\ln p_{\theta }\left(x_i\right)-\sum _{j=1}^N{w}_{ij}JS\left(q_{\phi }\left(z,c|x_i\right),q_{\phi }\left(z,c|x_j\right)\right)\right)$$ (Equation 8)

Construction of affinity matrix

In other graph embedding methods, a properly constructed affinity matrix is important. A typical option of affinity matrix is a set of nearest neighbors for a given data point, with a predefined kernel function to calculate their similarity. For example, for a Gaussian kernel, the elements of the affinity matrix are defined as follows:

$$w_{ij}=\{\begin{array}{cc}\frac{1}{a_i}\exp \left(-\frac{{\left|\left|x_i-x_j\right|\right|}_2^2}{2s_i^2}\right)& if{x}_j\in N\left(x_i\right)\\ 0\text{,}& othrewise\end{array}$$ (Equation 9)

where $s_i$ is a predefined scalar; $N\left(x_i\right)$ represents the nearest $N_s$ neighbor of set $x_i$, and the default number is 10. $a_i$ is standardized, that is, ${\sum }_j{w}_{ij}=1$, and the default number is 1.

Imputation evaluation

We evaluated the median L1 distance, cosine similarity, and RMSE between the real expression values of the original dataset and the estimated values obtained by various imputation algorithms. For all flipped entries, $X$ is the row vector of the original expression, and $Y$ is the row vector of its corresponding imputed expression. The L1 distance is the absolute deviation between the values of the original expression and those of the imputed expression. Lower L1 distance indicates higher similarity.

$$L1=\left|x-y\right|,L1\in [0,+\infty )$$ (Equation 10)

The cosine similarity indicates the dot product between the original expression and estimated expression.

$$\cos \left(x,y\right)=\frac{x{y}^T}{\Vert x\Vert \Vert y\Vert },\mathit{cos}\in \left[\mathrm{0,1}\right]$$ (Equation 11)

The RMSE indicates the square root of the quadratic mean of the difference between the original expression and the estimated expression.

$$RMSE(x,y)=\sqrt{\frac{{\sum }_{i=1}^N{\left(x_i-y_i\right)}^2}{N}},RMSE\in [0,+\infty )$$ (Equation 12)

Evaluation metric for clustering

We selected four commonly used cluster evaluation indicators, including normalized mutual information (NMI),⁴⁸ adjusted Rand index (ARI),⁴⁹ completeness (COM),⁵⁰ and homogeneity (HOM).⁵⁰

Adjusted rand index

ARI is an improved version of the rand coefficient. In general, the rand coefficient is used to evaluate the clustering results by calculating the similarity between the two clusters. The adjustment of the rand coefficient is an improvement of the rand coefficient based on probability regularization. We define a confusion matrix. In the case of a given gold standard, $a$ is the number of cell pairs correctly classified into the same category by clustering; $b$ is the number of cell pairs that belong to different categories but are divided into the same cluster; $c$ is the number of cell pairs that belong to the same category but are divided into the number of different clusters, and $d$ is the number of cell pairs correctly divided into different clusters.

$$ARI=\frac{2\left(ad-bc\right)}{\left(a+b\right)\left(b+d\right)+\left(a+c\right)\left(c+d\right)}\text{.}$$ (Equation 13)

Normalized mutual information

Mutual information (MI) measures the degree of agreement between two dataset distributions. MI is also an important metric of information, which refers to the correlation between two sets of events. Moreover, NMI is improved on the basis of mutual information. $U=\left\{u_1,u_2,u_3\dots ,u_n\right\}$ and $V=\left\{v_1,v_2,v_3\dots ,v_n\right\}$ denote the gold standard and partition obtained by k-means clustering algorithm, respectively.

$$\mathrm{N}\mathrm{M}\mathrm{I}=\frac{2I\left(U,V\right)}{H\left(U\right)+H\left(V\right)}$$ (Equation 14)

$$I\left(U,V\right)=\sum _{i=1}^n\sum _{j=1}^n\frac{\left|u_i\cap v_j\right|}{N}\log \frac{N\left|u_i\cap v_j\right|}{\left|u_i\right|\times \left|v_j\right|}$$ (Equation 15)

$$H\left(U\right)=-\sum _{i=1}^n\frac{u_i}{N}\log \frac{u_i}{N}andH\left(V\right)=-\sum _{j=1}^n\frac{v_j}{N}\log \frac{v_j}{N}$$ (Equation 16)

Completeness

COM indicates that samples of the same category are classified into the same cluster. If all samples of the same type are grouped in the same cluster, then the integrity is 1. If the samples of the same type are grouped in different clusters, then the conditional empirical entropy $H\left(V|U\right)$ is calculated. The larger the value, the smaller the completeness.

$$COM=1-\frac{H\left(V|U\right)}{H\left(V\right)}$$ (Equation 17)

Homogeneity

HOM indicates that each cluster contains only a single category of samples. If only one category is found in a cluster, then HOM is 1. If multiple categories are found, then the conditional empirical entropy $H\left(U|V\right)$ of the cluster under the category is calculated. The larger the value, the smaller the homogeneity.

$$\mathit{HOM}=1-\frac{H\left(U|V\right)}{H\left(U\right)}$$ (Equation 18)

For all metrics, including ARI, NMI, COM, and HOM, a larger value (up to 1) indicated good performance.

Pseudotime order score (POS)

In measuring the accuracy of reconstruction pseudotime, we defined a POS as follows: $POS=C/\left(N_c+C\right)$, where $C$ and $N_c$ represent the number of cell pairs that are consistent and inconsistent between the inferred pseudotime and the gold standard (e.g., true data collection time), respectively.

Protein-protein interactome (PPI) network

To build the comprehensive human interactome from the most contemporary data available, we assembled 18 commonly used PPI databases with experimental evidence and the in-house systematic human PPI that we have previously utilized: (i) binary PPIs tested by high-throughput yeast-two-hybrid (Y2H) system;⁵¹ (ii) kinase-substrate interactions by literature-derived low-throughput and high-throughput experiments from KinomeNetworkX,⁵² Human Protein Resource Database (HPRD),⁵³ PhosphoNetworks,⁵⁴ PhosphositePlus,⁵⁵ DbPTM 3.0 and Phospho.ELM;⁵⁶ (iii) signaling networks by literature-derived low-throughput experiments from the SignaLink2.0;⁵⁷ (iv) binary PPIs from three-dimensional protein structures from Instruct;⁵⁸ (v) protein complexes data (∼56,000 candidate interactions) identified by a robust affinity purification-mass spectrometry collected from BioPlex V2.0;⁵⁹ and (vi) carefully literature-curated PPIs identified by affinity purification followed by mass spectrometry from BioGRID,⁶⁰ PINA,⁶¹ HPRD,⁶² MINT,⁶³ IntAct,⁶⁴ and InnateDB.⁶⁵ Herein, the human interactome constructed in this way includes 351,444 PPIs connecting 17,706 unique human proteins.

Description of GPSnet

GPSnet³² algorithms take two inputs: node score and one background PPI network. The node score was defined as |log2FC| for significant (FDR <0.05) differentially expressed genes (DEGs), and 0 for non-significant DEGs. GPSnet builds raw module in each iteration by starting with a random seed gene/protein (node). After that, one of the candidate neighboring genes that satisfy the subsequent two conditions is added: (1) connectivity significance P(i) (Equation 19) is less than 0.01; (2) the updated module score is greater than the current one (Equation 20). We repeated steps (1) and (2) until no more genes (nodes) can be added to each raw module. In this study, we built ∼100,000 raw modules ranked by module scores with the corresponding module score computed in (Equation 20). All generated raw modules are ranked in decreasing module score order. The final network module is generated by assembling truncated top-ranked raw modules.

$$P\left(i\right)=\sum _{d=d_n}^{d_i}\frac{\left(\begin{array}{c}n\\ d\end{array}\right)\left(\begin{array}{c}N-n\\ d_i-d\end{array}\right)}{\left(\begin{array}{c}N\\ d_i\end{array}\right)}$$ (Equation 19)

$$M{S}_{n+i}\left(i\right)=\frac{\left(s\left(i\right)-\mu \right)+{\sum }_{j\in M}\left(S\left(j\right)-\mu \right)}{\sqrt{n+1}}$$ (Equation 20)

Where, $N$ denotes all proteins/genes in the PPI, n represents numbers of nodes in the module, $d_n$ is the numbers of neighbors of node $i$ in the current raw module, $d_i$ is the degree of gene $i$, ${MS}_{n+1}\left(i\right)$ denotes the updated module score if adding node $i$ to current raw module, $s\left(i\right)$ denotes the score of node $i$, $M$ denotes the current module, and $\mu$ is the average node score of all genes in the complete PPI network.

Datasets and pre-processing

autoCell takes raw sc/snRNA-seq gene expression profile as input. Data filtering and quality control are the first step of data pre-processing. Given the high loss rate of sc/snRNA-seq expression data, only genes expressed as non-zero in more than 1% of cells and cells expressed as non-zero in more than 1% of genes are included. Then, the genes are sorted on the basis of the SD that is, the first $k$ genes (Table S6) in the variance are used. In addition, our model automatically log-transforms all data.

In order to test the performance of autoCell, we analyzed two simulated datasets and seven commonly used real-world datasets (Table S6) from both human and mouse to test performance of autoCell across cross-species single-cell/nuclei RNA-seq datasets. Real datasets were obtained from diverse sequencing platforms and experimental protocols (Table S6).

The simulation dataset was generated using the splatter R package. For the two sets of simulated datasets, the following parameters were used in the setParams() function: batchCells = 500, nGenes = 2000, group.prob = c(0.30, 0.3, 0.4), de.prob = c(0.05, 0.08, 0.01), de.facLoc = 0.5, de.facScale = 0.8. The following parameters were used in the splatSimulate() R function: dropout.shape = c(−0.20, −0.20, −0.20) or dropout.shape = c(−0.05, −0.05, −0.05), dropout.mid = c(0,0,0), dropout.type = "group".

The Zeisel²⁴ dataset consists of 3,005 cells from the somatosensory cortex and hippocampus of the mouse brain (Table S6). The Zeisel dataset has real labels for seven different cell types, including pyramidal cells, oligodendrocytes, parietal cells, interneurons, astrocytes, ependymal cells, and endothelial cells in the brain.

The Klein dataset²⁵ consists of 2717 cells derived from mouse embryonic stem cells (Table S6). This dataset reveals the heterogeneity of the population structure and differentiation after the withdrawal of leukemia inhibitory factor. The reproducibility of these high-throughput single-cell data allows people to deconstruct cell populations and infer gene expression relationships.

The Romanov dataset⁴⁵ consists of 2881 cells from the mouse hypothalamus (Table S6). The dataset includes 1001 oligodendrocytes, 267 astrocytes, 356 ependymal cells, 48 microglia, 240 endothelial cells, 71 vascular smooth muscle cells, and 888 neurons.

The AD dataset (GEO accession number GSE138852)⁴⁶ contains 13,214 single-core scRNA-Seq datasets collected from six AD and six control brains (Table S6). This dataset has true labels for eight different cell types: microglia, astrocyte neuron, oligodendrocyte, OPC, endothelial, unidentified, and hybrid.

The Zheng-68k⁴⁴ dataset contains fresh peripheral blood mononuclear cells from healthy people, primarily involving the main cell types of peripheral blood mononuclear cells, such as T-cells (T), Natural killer (NK) cells, B-cells (B), and myeloid cells (Table S6). In addition, the Zheng-73k⁴⁴ dataset is composed of fluorescently activated sorting cells from healthy people, including T, NK, and B cells.

The Petropoulos dataset²⁶ included the single cells from five stages of human preimplantation embryonic development from the developmental day (E) 3 to day 7(Table S6).

Quantification and statistical analysis

Enrichment analysis

The pathway enrichment analyses were conducted using WikiPathways⁶⁶ from Enrichr.⁶⁷

Differential expression analyses

With the cell types annotated by autoCell, we utilized one R package ‘MAST’⁶⁸ for the sequential differential expression analyses. The results of differential expression analyses were used as input for the GPSnet algorithm (Method details - Description of GPSnet).

Published: January 5, 2023

Data and code availability

• •This paper analyzes existing, publicly available data. The accession numbers for the datasets are listed in the key resources table.
• •Source codes are available: https://github.com/ChengF-Lab/autoCell. All original code has been deposited at Zenodo and is publicly available as of the date of publication. DOIs are listed in the key resources table.
• •Resource Availability: Any additional information required to reanalyze the data reported in this work paper is available from the lead contact upon request.