Research on sustainable development evaluation and improvement path of resource-based cities based on coupling of emergy and system dynamics

Abstract

The evaluation of the sustainable development of resource-based cities is still one of the hotspots in today’s social research. Taking Jining, Shandong Province, as the research object, this work combines a relevant emergy evaluation index system with system dynamics, establishes a resource-based city emergy flow system dynamics model, and studies sustainable development path in the next planning year. In the work, the key factors affecting the sustainable development of Jining are obtained through the coupling of regression and SD sensitivity analysis, and some scenarios are set up by combining them with the local 14th Five-year plan. Besides, the appropriate scenario (M–L–H–H) for Jining's future sustainable development is chosen in accordance with regional circumstances. That is, during the 14th Five-year Plan period, the appropriate development ranges for the growth rate of social fixed assets investment, the growth rate of raw coal emergy, the growth rate of grain emergy and the reduction rate of solid waste emergy are 17.5–18.3%, − 4.0 to − 3.2%, 1.8–2.6% and 4–4.8%. The methodology system constructed in this article can serve as a reference for similar studies, and the research findings can aid the government in formulating pertinent plans for resource-based cities.

Introduction

Ecological and environmental protection has emerged as a major worldwide concern, particularly in the ecological improvement and development of resource-based cities (Mcphearson et al., 2015). A resource-based city is established or developed on the basis of resource exploitation. It is a special type of city dominated by mining or primary processing industries. (Qu et al., 2017). In the process of the city’s development, the single development model frequently leads to its ecosystem more fragile than typical cities, with noticeable characteristics of complexity, vulnerability, ecological sensitivity, and heterogeneity (Cui et al., 2015). Predatory exploitation has brought many resource depletion and urban development problems, such as unreasonable economic structure, high resource dependence, large energy consumption, and serious deterioration of ecological environment, because of over-reliance on local resources (Wu et al., 2015; Zhang et al., 2003). Many countries have formulated remedies in response to these problems. The typical ones are mainly to realize industrial upgrading through industrial structure adjustment or vigorously develop circular economy to transform economic development mode (Huang et al., 2011; Ren, 2011). The common cities of the former mainly include Potosi, a gold mining city in Bolivia (Pretes, 2002), Lorraine of France (Huang et al., 2011) and Fuxin in Liaoning Province of China (Tan et al., 2016). The latter mainly include Ruhr in Germany (Yuan et al., 2012), Taiyuan in Shanxi Province (Zhang et al., 2012), and Zibo in Shandong Province of China (Ren, 2011). Although the above measurements have played a vital role in the sustainable development of resource-based cities in various countries, some problems still persist in the specific analysis of its implementation process, especially for China's resource-based cities, where the development mode of “pollution first and treatment later” is prominent, the path to sustainable development is unclear, and there is a lack of high-level design planning (Chiu et al., 2004). Therefore, the sustainable development evaluation and promotion path of resource-based cities must be further studied as the world is pursuing the development of a green and low-carbon recycling model.

According to the literature analysis, most scholars’ research on the sustainable development level of resource-based cities mainly focuses on two aspects: evaluation and prediction. The main research methods for evaluation are emergy analysis and index system evaluation. Cheng and Cheng (2017) contrasted the ecological economic systems of Hakka and non-Hakka villages in the Lui–Tui area in southern Taiwan through emergy analysis, and provided useful suggestions for local sustainable development. Wan et al. (2020) constructed the evaluation index system of rural environmental value added based on the emergy analysis theory, and put forward corresponding strategies for the sustainable development of the socioeconomic natural compound ecological environment in Queshan village, Shanxi Province of China. Zhang et al. (2014a) established the low-carbon economy evaluation index system for resource-based cities and proposed specific promotion strategies for the development of low-carbon economy in resource-based cities to provide a reference for the sustainable development of these cities. Yang et al. (2021) constructed ecological vulnerability indexes coupled with natural and human factors to form a corresponding index system, and evaluated the ecological vulnerability of Huaibei based on it. Compared with the traditional index system evaluation (Yang et al., 2021; Zhang et al., 2014a), the biggest advantage of emergy analysis is that it can realize the unification and comparison of material, energy, currency and information flow. Therefore, as an important method to evaluate the value of natural resources and social economy by taking into account ecology and economics, emergy has gradually evolved into an important means of evaluating regional sustainability and circular economy development (Wang et al., 2021a, 2021b). In order to reflect these characteristics of resource-based cities, it is necessary to objectively evaluate and compare various ecological flows of it, so it is feasible to use emergy theory to evaluate their sustainable development.

The main research methods for prediction are mathematical modeling, SD, and scenario analysis. Jiang et al. (2019) proposed a new urban ecological carrying capacity prediction model composed of a radial basis function (RBF) neural network to predict the future ecological pressure index of Yulin, Shaanxi Province, China. Zang et al. (2015) applied the multiple regression “land use” dynamic model (Z-H model) to predict the land use change trend in Daqing, Heilongjiang Province, China and determined the feasible land use operation mode of the urban ecosystem. Xing et al. (2021) established a SD model from the perspective of ecology, conducted a situation simulation, and proposed corresponding suggestions to improve the sustainability of resource-based cities. Zhang et al. (2014b) proposed the sustainable indexes of resource-based cities, including environmental, social, and economic dimensions, adopting three weighting scenarios to provide policymakers with a comprehensive perspective of future urban supervision. Among these, the mathematical modeling method considers few influencing factors, and there may be errors when dealing with problems (Jiang, 2019), which cannot reflect the complex ecosystem of resource-based cities. The scenario analysis method is highly subjective and requires high accuracy, logic and causality of scenario data (Zhang et al., 2014b). System dynamics is a system analysis method, which reflects not only the feedback between the stock, flow and auxiliary variables of each part of the system, but also the dynamics, feedback, delay and complexity of the system (Selvakkumaran et al., 2020). It has become an important method to predict dynamic complex systems (Liu et al., 2022). In view of the fact that the resource-based city is a dynamic complex system, which needs to consider the complex logical relationship between variables and subsystems as well as the feedback between various parts, the above characteristics are more consistent with the functional properties of system dynamics, so it is feasible to choose it as the main research method in this study.

Based on the above literature analysis, if only the emergy analysis (Cheng et al., 2017; Wan et al., 2020) is used, considering the vulnerability and ecological sensitivity of resource-based cities (Cui et al., 2015), any small change to one factor could have a significant impact on the entire system, and it is difficult to represent statically the city's dynamic interaction. Therefore, it is necessary to dynamically analyze the relationship between the internal structure of the system and different subsystems (Fang et al., 2016), and system dynamics can just reflect the dynamics of resource-based cities, making up for the lack of dynamic of emergy analysis. Therefore, it is feasible to choose the coupling of emergy and system dynamics to explore the sustainable development of resource-based cities. In addition, some scholars have made some research achievements (Fang et al., 2016; Zhao et al., 2022) in exploring urban sustainability by the coupling of emergy and system dynamics, but few of them use it as research on resource-based cities. We applied this method to resource-based cities, which is also a major contribution of this paper.

In the first part of the article, we summarize the literature related to resource-based cities and determine the research methods; In the second part, we establish the methodology systems about emergy, system dynamics, regression analysis and Monte Carlo; In the third part, we introduce the specific contents and results of the above methodology systems, discuss the results, and select the optimal scenario; In the fourth part, we put forward conclusions and relevant policy recommendations based on the results.

Method and methodology

Research framework

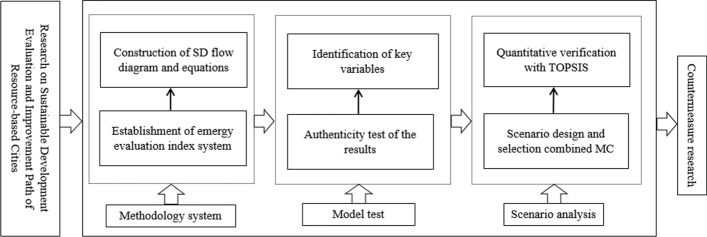
First, on the basis of constructing emergy flow diagram, we use emergy analysis method to construct evaluation index system of sustainable development in resource-based cities. Second, the system model is constructed by SD modeling, and the corresponding emergy evaluation indexes are embedded. Third, based on the authenticity test of the SD model, the four key variables that have the greatest impact on the sustainable development of Jining are selected by regression analysis and sensitivity analysis. Fourth, combined with MC simulation, the four key variables are designed according to the arrangement and combination of low, medium and high schemes. Later, the SD model is used to predict and compare the emergy indicators under different scenarios, and the most suitable development model is selected. Finally, the TOPSIS method is used to quantitatively validate the chosen conclusion. The most suitable path for the sustainable development of resource-based cities is obtained according to the verification conclusion. The research framework of this study is shown in Fig. 1.

Fig. 1.

Technical roadmap for research on the SDEIP

Case selection

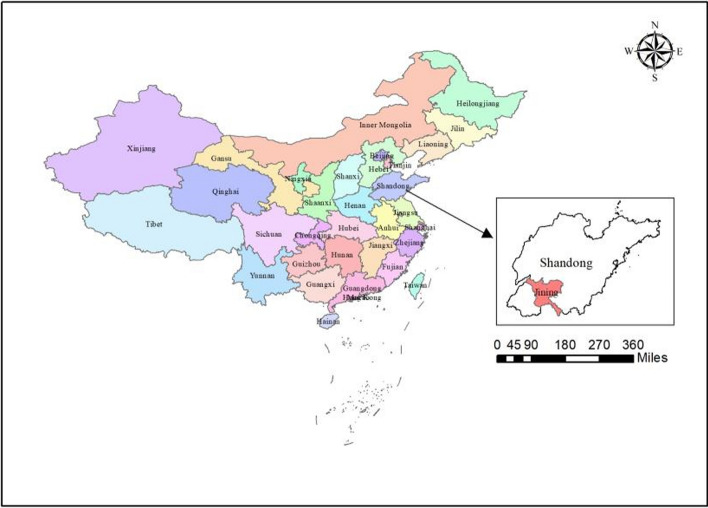
Jining is rich in mineral resources, mainly coal resources. According to exploration and prediction, the city’s coal reserves are 26 billion tons, accounting for 50% of Shandong Province. This city is one of the eight key coal bases in China (Jining, 2020). Jining has a developed coal power industry. In 2017, the raw coal output was 79.0749 million tons, accounting for 57.69% of the total output of Shandong Province. Meanwhile, the total coal consumption was 69.6631 million tons, accounting for 18.25% of the total coal consumption of Shandong Province. Jining’s power plant density ranks second in China, with a total installed capacity of 10.25 million kW, accounting for 17% of Shandong Province, and more than 70% of the power is transmitted to the outside (Zhao et al., 2007). The city’s economic development model is characterized by a single industrial structure and obvious characteristics of heavy coal power, resulting in certain continuous problems, such as high resource development intensity, insufficient reserve resources, environmental damage, and serious pollution, which has brought many negative effects on the local economic development and social stability. According to the findings, Jining urgently needs to improve its level of ecological sustainability through ecological transformation. A large number of cities in China rely on their natural resources. We chose Jining, a prototypical resource-based city, as our case study, because it is highly representative and could provide a useful reference for the ecological transformation of other prototypical resource-based cities. The geographical location of Jining is shown in Fig. 2.

Fig. 2.

Geographical location map of Jining

Emergy analysis

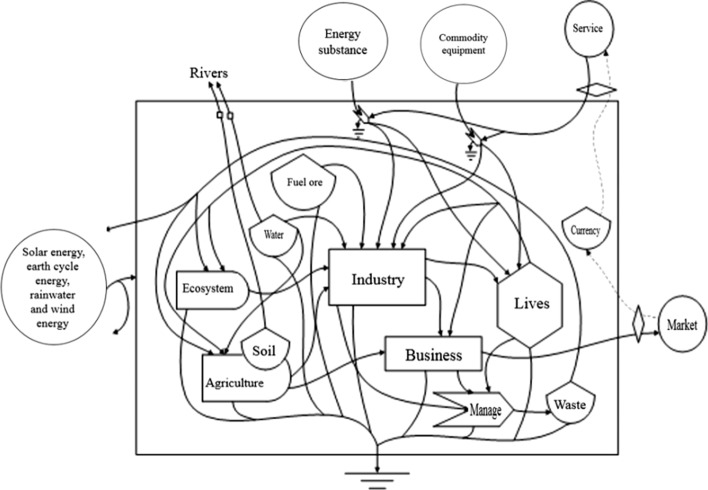
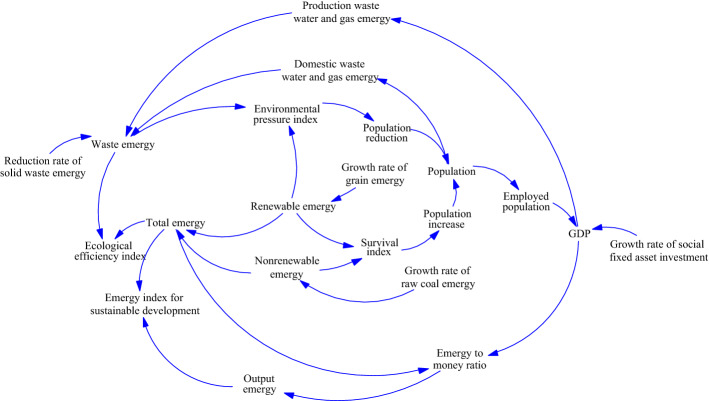
Emergy system diagram of Jining eco-economic system

According to the characteristics of resource-based cities, the emergy system diagram of resource-based cities is constructed, as shown in Fig. 3. The diagram is composed of two parts: inside and outside. Outside the system, the natural renewable resources dominated by solar energy are on the left; the market closely related to currency and commerce is on the right; the energy materials and the tertiary industry products dominated by goods, equipment and services are above the system. They partly flow into the system, and partly are supplemented by other subsystems in the main system. Within the system, renewable resources, nonrenewable resources and input resources are put into industry and lives. Taking industry and lives as the center, the secondary emergy generated by them is invested in agriculture and commerce, or transmitted to each other. The emergy generated by each part of the system is transmitted to each other, which together constitute the emergy flow chart of Jining.

Fig. 3.

Emergy system diagram of Jining urban eco-economic system

Construction of the emergy flow list

The original data of the above five categories of emergy in the recent 20 years are collected by exploring various statistical yearbooks, such as Shandong Statistical Yearbook (Shandong, 2020) and Jining Statistical Yearbook (Jining, 2020), and relevant documents issued by government departments (a small amount of missing data are obtained by linear fitting, and the fitting errors are within the acceptable range). The Jining emergy flow list is provided in Appendix 1.

Establishment of an emergy evaluation index system

According to the research results of Fang et al. (2016) and Wang et al. (2022), we construct evaluation indexes based on environment, economy, society, and sustainability to accurately reflect the systematicness of the sustainable development in resource-based cities. These indexes serve as a reference for scenario selection. The sustainable indexes are the main basis to characterize the corresponding situation of sustainable development of Jining. Table 1 provides the details.

Table 1.

Emergy evaluation index system of Jining

Emergy indexes	Calculation expression	Unit	Significance	References
Emergy flow
Renewable emergy	R	sej	Systematic environmental renewable resource wealth base	(Wang et al., 2022)
Nonrenewable emergy	N	sej	Systematic environmental nonrenewable resource wealth base	(Wang et al., 2022)
Input emergy	IMP	sej	Input resources and services from outside	(Ren et al., 2022)
Total emergy	U = R + N + IMP	sej	Total emergy of the system	(Wang et al., 2021a, 2021b)
Output emergy	EXP	sej	Exported resources and services	(Ren et al., 2022)
Waste emergy	W	sej	Emergy of waste discharged from the system to the environment	(Wang et al., 2021a, 2021b)
Environmental assessment index
Waste emergy to total emergy ratio	EWR = W/U	%	The pressure of waste on the surrounding environment	(Fang et al., 2016)
Economic evaluation index
Emergy to money ratio	EMR = U/GDP	sej/yuan	Degree of economic modernization	(Fang et al., 2016)
Social evaluation index
Emergy per head	EPC = U/P	sej/person	The mark of living standard and quality	(Wang et al., 2021a, 2021b)
Sustainable evaluation indexes
Emergy index for sustainable development	EISD = U*R/(EXP*(N + IMP))	–	The sustainable index taking into account emergy exchange ratio	(Wang et al., 2021a, 2021b)
Ecological efficiency index	UEI = (1-W/U)^2*(1-N/U)^2* (U/IMP)	–	Reflect sustainable development capability that takes into account resources, economy and ecology	(Li et al., 2015)

Emergy exchange ratio Evaluate the benefits and losses of foreign exchanges

EISD is a sustainable development index considering emergy exchange rate. This factor takes into account the environmental, economic, and social benefits. The higher this factor is, the higher the social and economic benefits under unit environmental pressure and the stronger the sustainable development ability of the system will be. UEI explores the sustainable development ability from the perspective of system metabolic efficiency, which is a sustainable development index reflecting urban resource, environmental, and economic efficiencies. Coordinated improvement of economic, resource, and environmental efficiencies is the fundamental way to enhance the ecological efficiency of urban material metabolism. The higher this factor is, the stronger the system sustainable development ability will be.

SD analysis

Subsystem division and variable determination

According to the different types of emergy indexes established in the previous article, the system dynamics model is divided into economic, environmental, social and energy subsystems, and five different types of emergy evaluation indexes are also part of the corresponding subsystems. See Appendix 2 for specific division contents and basis.

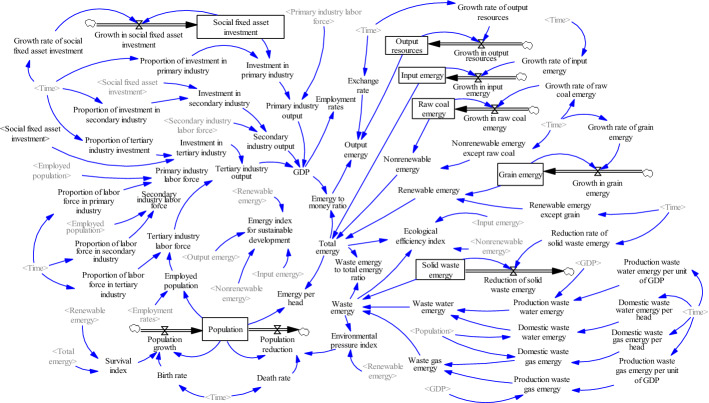
System flow diagram and equation construction

The corresponding system flow diagram is demonstrated according to the division basis of subsystems in the preceding article (see Fig. 4). The state variables are calculated by the cumulative values of the annual changes of the rate variables, the rate variables are calculated by establishing the logic equation of the auxiliary variables, and each auxiliary variable is obtained by the logic equation or querying the relevant statistical yearbook. Most of the logical equations are the real results obtained through literature or logical analysis. A few are obtained by SPSS fitting due to the lack of relevant literature. See Appendix 3 for details.

Fig. 4.

System dynamic flow diagram of the SDEIP of Jining

Regression analysis

Drawing on the results of existing studies (Xing et al., 2022; Jensen et al., 2001), this work conducts MLR analysis on the main factors affecting UEI and EISD, discusses the impact of different independent variables on the two evaluation indicators, and determines several key variables with greater impact. In this Study, the software SPSS is used for data analysis. For two dependent variables, five variables related to them are selected as independent variables, and the data from nearly 20 years are selected for each variable. See Table 2 for details.

Table 2.

Classification of specific variables

Dependent variable	Independent variable
EISD	Social fixed asset investment, Raw coal emergy, Grain emergy, Input emergy, Output emergy
UEI	Raw coal emergy, Grain emergy, Solid waste emergy, Input emergy, Social fixed asset investment

MC simulation

This method uses the mechanism of random generation of results to simulate the function and development law of the real system, so as to reveal the operation law of the system. Assume that function Y = f (X); X = (x₁, x₂ … x_n), where X is a random variable subject to a specific probability distribution, and f (X) is an unknown or very complex function. Each random variable X is obtained by direct or indirect sampling, and then it is substituted into the equation to obtain the function value: Y. In this way, a series of data Y₁, Y₂ … Y_n can be obtained. When the number of independent simulations is quite large, the probability characteristics of Y can be determined, and its accuracy can replace the analytical solution as the final result (Zhou et al., 2004). In scenario setting, we take four regulatory factors as independent variables and two sustainable evaluation indexes as dependent variables to change the results from numerical form to interval form. In scenario selection, four regulatory factors also serve as independent variables and GDP serves as dependent variable. After the dependent variable changed into interval form, select this scenario according to whether the area composed of the target value and the upper limit exceeds half of the area of the upper and lower limit (More than 50% meet the standard). The introduction of Monte Carlo simulation can reduce the errors between the simulation results and the actual values caused by the instability of regulatory factors, and increase the accuracy of the article.

Results

Authenticity test

The relative errors are calculated through the compare of fitted data and actual data, the annual relative errors should be limited to less than 5%. In this test, referring to the research method of Fang et al. (2016) and Zhao et al. (2022), the most representative variables from each subsystem are selected for verification (GDP, population, waste emergy and UEI), and their data in the recent ten years (2011–2020) are selected for comparison. Table 3 illustrates the specific comparison results.

Table 3.

Comparison of GDP, population, waste emergy and UEI simulation values with real values in Jining

Time	Analog GDP	Actual GDP	Relative errors (%)	Analog population	Actual population	Relative errors (%)
2011	2367.44	2475.0	− 4.35	836.48	813	2.89
2012	2787.40	2789.8	− 0.09	840.43	816	2.99
2013	3113.09	3040.5	2.39	843.89	821	2.79
2014	3409.30	3301.5	3.27	846.19	824	2.69
2015	3770.53	3658.1	3.07	851.79	830	2.63
2016	3890.67	3881.9	0.23	855.96	835	2.51
2017	3995.78	4142.4	− 3.54	859.76	838	2.60
2018	4197.50	4336.8	− 3.21	863.92	835	3.46
2019	4567.37	4370.2	4.51	868.99	836	3.95
2020	4561.28	4494.3	1.49	871.88	836	4.29

Time	Analog waste emergy	Actual waste emergy	Relative errors (%)	Analog UEI	Actual UEI	Relative errors (%)
2011	4.78E + 21	4.79E + 21	− 0.18	0.570	0.570	0.00
2012	6.14E + 21	6.09E + 21	0.86	0.533	0.533	− 0.03
2013	4.31E + 21	4.25E + 21	1.46	0.542	0.542	− 0.04
2014	3.24E + 21	3.18E + 21	1.88	0.479	0.480	− 0.03
2015	3.94E + 21	3.87E + 21	1.69	0.471	0.471	− 0.04
2016	3.25E + 21	3.22E + 21	1.06	0.463	0.463	− 0.02
2017	4.85E + 21	4.83E + 21	0.48	0.444	0.444	− 0.02
2018	5.37E + 21	5.35E + 21	0.29	0.472	0.473	− 0.02
2019	3.92E + 21	3.87E + 21	1.19	0.459	0.459	− 0.04
2020	3.33E + 21	3.31E + 21	0.52	0.564	0.564	− 0.02

As shown in Table 3, all relative errors of the four variables in the recent 10 years are less than 5%.

Regression analysis results

Tables 4 and 5 are the results of the regression analysis of two sustainable evaluation indicators. According to the analysis in Table 4, the R² of the model is 0.989, which means that the above five independent variables can explain the reason for the 98.9% change of EISD. The model passes the F-test (f = 227.625 p = 7.0863e-13 < 0.05), which also shows that at least one of the above five independent variables will have an impact on EISD. Durbin–Watson value is 1.678, close to 2, which can be considered that the model has no autocorrelation. Among the five independent variables, output emergy (t = − 7.927, p = 0.000002), social fixed asset investment (3.851, p = 0.002) and grain emergy (t= 3.310, p = 0.006) have a significant impact on EISD because of p < 0.05. EISD represents the social and economic benefits under unit environmental pressure while taking into account market factors, and the above three independent variables have a significant impact on EISD from market factors (output emergy), economic benefits (social fixed asset investment) and environmental pressure (grain emergy), respectively.

Table 4.

Regression results of main influencing factors on EISD (n = 20)

Emergy index for sustainable development
Independent variable	Standardization coefficient	t	P	R2	D-W value	F
Constant	–	1.021	0.283	0.989	1.678	F(5,14) = 227.625, p = 7.0863E-13
Social fixed asset investment	1.477	3.851	0.002**
Raw coal emergy	− 0.199	− 2.014	0.065
Grain emergy	0.315	3.310	0.006**
Input emergy	− 0.357	− 0.773	0.479
Output resources	− 1.875	− 7.927	0.000002**

*p < 0.05 **p < 0.01

Table 5.

Regression results of main influencing factors on UEI (n = 20)

Ecological efficiency index
Independent variable	Standardization coefficient	t	p	R2	D-W value	F
Constant	–	5.475	0.000082**	0.978	2.435	F(5,14) = 451.367 p = 5.7730E-15
Raw coal emergy	− 0.209	− 5.385	0.000127**
Grain emergy	0.055	0.899	0.384
Solid waste emergy	− 0.955	− 3.989	0.001**
Input emergy	− 0.023	− 1.132	0.286
Social fixed asset investment	0.091	0.325	0.773

*p < 0.05 **p < 0.01

According to the analysis in Table 5, the R2 of the model is 0.978, which means that the above five independent variables can explain the reason for the 97.8% change of UEI. The model passes the F-test (f = 451.367, p = 5.7730E-15 < 0.05), which also shows that at least one of the above five independent variables will have an impact on UEI. Durbin–Watson value is 2.435, close to 2, which can be considered that the model has no autocorrelation. Among the five independent variables, raw coal emergy (t = − 5.385, p = 0.000127) and solid waste emergy (t = − 3.989, p = 0.001) have a significant impact on UEI because of p < 0.05. UEI is a function including the ratio of nonrenewable emergy to total emergy, the ratio of waste emergy to total emergy and emergy yield ratio. It can integrate the discharge of system waste and consumption of nonrenewable resources. Therefore, the raw coal emergy (nonrenewable resources) and solid waste emergy (system waste) in Table 5 are the most influential factors to UEI.

EISD emphasizes economic benefits more than UEI. Its fundamental purpose is to maximize economic benefits under less environmental pressure. Its advantage is that it takes market factors into account, but its characterization of environmental pressure is not specific enough (waste emissions are not taken into account). UEI can overcome this defect and emphasize the balanced development of metabolic efficiency of economy, resources and environment.

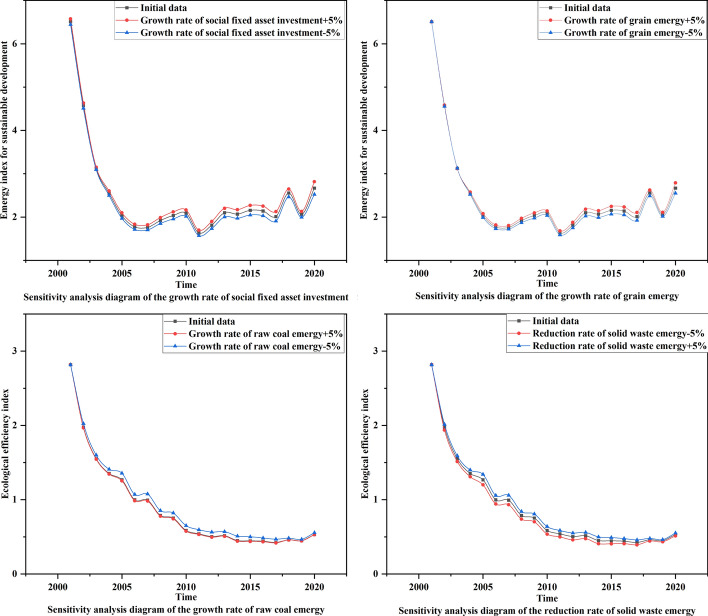
Sensitivity analysis

Sensitivity refers to the effect on the simulation results when an independent variable in the model changes. The higher the sensitivity of the variable is, the greater the effect on the simulation results will be. The sensitivity is calculated as Eq. (1):

$$\epsilon =\left(\frac{\left(Y2-Y1\right)/Y1}{\left(X2-X1\right)/X1}\right)$$ 1

where ε represents the sensitivity of each variable; ${\mathrm{X}}_1$ and ${\mathrm{X}}_2$ represent the value before and after the change of an independent variable; and ${\mathrm{Y}}_1$ and ${\mathrm{Y}}_2$ represent the value before and after the change of dependent variable, respectively. The sensitivity of each variable is obtained by changing the input value of each independent variable (floating up and down by 5%).

The independent variables with high sensitivity corresponding to the two sustainable evaluation indexes are obtained according to Eq. (1), as shown in Fig. 5.

Fig. 5.

Sensitivity analysis diagram of the key variables

According to the analysis of Fig. 5, the factors that have the greatest effect on UEI and EISD are the growth rate of grain emergy, the growth rate of raw coal emergy, the growth rate of social fixed asset investment, and the reduction rate of solid waste emergy, respectively.

According to the analysis of Table 6, each sustainable evaluation index is directly or indirectly affected by the other three key variables, indicating that each sustainable evaluation index is jointly determined by all key variables. Figure 6 shows the specific way in which each sustainable evaluation index is affected by all key variables.

Table 6.

Influence of the key variables on emergy indexes

Key Emergy Variables indexes	Reduction rate of solid waste emergy	Growth rate of social fixed asset investment	Growth rate of grain emergy	Growth rate of raw coal emergy
UEI	√	√	√	√
EISD	√	√	√	√

Fig. 6.

SD flow diagram of the influence of the key variables on the sustainable evaluation indexes

Scenario design based on MLR and SD coupling

By comparing the results of SD sensitivity analysis and regression analysis, it is found that the key variables affecting the sustainable indicators under the two methods overlap to a certain extent, indicating that these variables have a greater impact on the sustainable development of Jining no matter which method is used. Therefore, these overlapping variables are selected as the key variables of scenario design. These variables are the growth rate of social fixed assets investment, the growth rate of raw coal emergy, the growth rate of grain emergy, and the reduction rate of solid waste emergy. Referring to the research of Liu et al. (2022), the above regulatory factors are designed according to three different gradients: low, medium and high (L, M, H), and different gradients of each regulatory factor is arranged in pairs. A total of 3 ^ 4 = 81 scenarios are constructed. The order of the above key variables is same as the order of the actual independent variables of each scenario. For example, scenario H–L–H–M represents the growth rate of social fixed assets investment, the growth rate of raw coal emergy, the growth rate of grain emergy and the reduced rate of solid waste emergy is taken as high, low, high and medium gradient, respectively. See Appendix 4 for the design of scenario variables and the basis of scenario scheme design under each scheme.

Scenario design and selection

Scenario selection based on reference scenario

Select the most moderate scenario M–M–M–M from the above 81 scenario combinations, and serve it as the reference group. Compare each scenario with the reference group, and find out the scenarios where at least 4 emergy evaluation indexes (including two sustainable evaluation indexes) are superior to the reference group in 2025.

Scenario design based on MC

Before MC simulation, it is necessary to determine the probability distribution of key variables. The probability distribution of a given variable should be set to a triangular distribution when the most likely value, the minimum and maximum values are known (Ramírez et al., 2008). In this article, the minimum and maximum values of the key variables in each scenario are set as 5 and 95% of the confidence interval. According to the most likely value (actual value), minimum value and maximum value of each key variable, the most likely value, upper and lower limit values of the sustainable emergy indexes and GDP are simulated, respectively.

Scenario selection based on MC

Considering that during 14th Five-year Plan, Jining Municipal Government requires that the average annual GDP growth rate should not be lower than 6% (2021), we find out the scenarios in which the growth rate of social fixed assets investment is “low” from the remaining scenarios. Comparing the upper and lower interval values of GDP with the target value (6%), it is found that the area composed of the lower limit of the interval and the target line exceeds half of the area composed of upper and lower limit of the interval in some scenarios, as shown in Fig. 7, which shows that there is a great probability that the average annual growth rate of GDP in the next five years will not reach the expected target of 6%. These scenarios are removed, and then some contradictory and repeated scenarios are also removed. Finally, there are 18 remaining scenarios, which are divided into economic preference, environmental preference and energy preference according to the different preferences of key variables, see Table 7 for specific classification results.

Fig. 7.

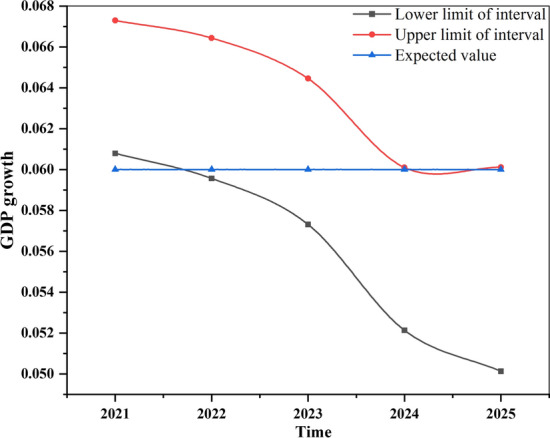
MC simulation interval of GDP growth rate

Table 7.

Classification results of each scenario after preliminary screening

Economic preferences	Environmental preferences	Energy preferences
H–H–L–M	M–H–L–H	H–M–H–H
H–M–M–L	M–M–L–H	M–H–H–L
H–H–M–M	M–H–M–H	M–H–H–M
H–M–L–H	H–M–M–H	H–H–M–H
H–M–H–M	M–H–H–H	M–M–M–L
H–L–H–L	M–L–H–H	M–M–H–M

Scenario simulation analysis

The EISD and UEI under the above 18 different preference scenarios are simulated, and their real data in the past few years and prediction results in the next few years are horizontally compared. The results are shown in Tables 8, 9, 10, 11, 12 and 13 and Figs. 8, 9 and 10, and the differences in the results are analyzed one by one according to different preference scenarios. (The table shows the upper and lower range value of each year, and the picture shows the most likely value of each year) The differences in the results are analyzed one by one according to different preference scenarios.

Table 8.

UEI simulation results under economic preference during the 14th Five-year Plan period

Scenarios	2021	2022	2023	2024	2025
H–H–L–M	0.490–0.491	0.492–0.493	0.496–0.497	0.501–0.503	0.508–0.510
H–M–M–L	0.495–0.496	0.501–0.502	0.509–0.511	0.518–0.521	0.529–0.532
H–H–M–M	0.492–0.493	0.496–0.497	0.502–0.503	0.509–0.511	0.518–0.520
H–M–L–H	0.493–0.494	0.497–0.498	0.503–0.505	0.511–0.513	0.520–0.522
H–M–H–M	0.497–0.498	0.505–0.507	0.515–0.517	0.527–0.529	0.540–0.543
H–L–H–L	0.499–0.500	0.510–0.512	0.522–0.525	0.536–0.539	0.552–0.556

Table 9.

EISD simulation results under economic preference during the 14th Five-year Plan period

Scenarios	2021	2022	2023	2024	2025
H–H–L–M	2.770–2.788	2.911–2.937	3.070–3.104	3.235–3.280	3.422–3.484
H–M–M–L	2.801–2.819	2.975–3.004	3.171–3.209	3.378–3.427	3.610–3.678
H–H–M–M	2.785–2.803	2.942–2.969	3.119–3.155	3.305–3.353	3.516–3.580
H–M–L–H	2.786–2.804	2.944–2.972	3.121–3.157	3.305–3.354	3.514–3.579
H–M–H–M	2.816–2.834	3.007–3.036	3.222–3.261	3.451–3.503	3.710–3.779
H–L–H–L	2.832–2.851	3.041–3.072	3.276–3.371	3.526–3.581	3.808–3.882

Table 10.

UEI simulation results under energy preference during the 14th Five-year Plan period

Scenarios	2021	2022	2023	2024	2025
H–M–H–H	0.497–0.498	0.505–0.507	0.515–0.517	0.527–0.529	0.540–0.543
M–H–H–L	0.494–0.495	0.500–0.502	0.508–0.509	0.517–0.519	0.528–0.530
M–H–H–M	0.490–0.491	0.492–0.493	0.496–0.497	0.501–0.503	0.508–0.510
H–H–M–H	0.492–0.493	0.496–0.497	0.502–0.503	0.509–0.511	0.518–0.520
M–M–M–L	0.495–0.496	0.501–0.502	0.509–0.511	0.418–0.521	0.529–0.532
M–M–H–M	0.497–0.498	0.505–0.507	0.515–0.517	0.527–0.529	0.540–0.543

Table 11.

EISD simulation results under energy preference during the 14th Five-year Plan period

Scenarios	2021	2022	2023	2024	2025
H–M–H–H	2.816–2.834	3.007–3.036	3.223–3.262	3.451–3.503	3.710–3.779
M–H–H–L	2.799–2.816	2.971–2.988	3.166–3.202	3.371–3.419	3.602–3.668
M-H–H–M	2.771–2.788	2.911–2.938	3.071–3.104	3.235–3.281	3.423–3.485
H–H–M–H	2.785–2.803	2.942–2.969	2.119–3.155	3.305–3.353	3.515–3.581
M–M–M–L	2.800–2.818	2.972–3.000	3.167–3.204	3.371–3.420	3.600–3.666
M–M–H–M	2.814–2.833	3.004–3.033	3.218–3.256	3.445–3.494	3.669–3.768

Table 12.

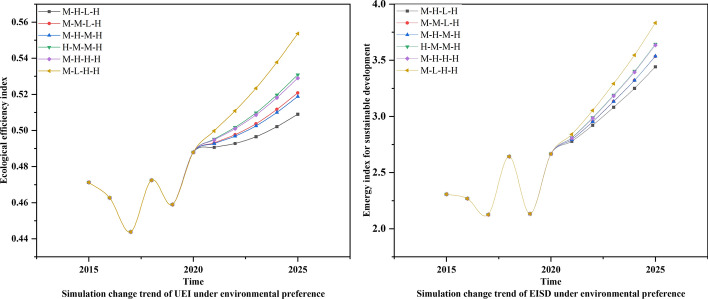
UEI simulation results under environmental preference during the 14th Five-year Plan period

Scenarios	2021	2022	2023	2024	2025
M–H–L–H	0.490–0.491	0.492–0.493	0.496–0.497	0.501–0.503	0.508–0.510
M–M–L–H	0.493–0.494	0.497–0.498	0.503–0.505	0.511–0.513	0.520–0.522
M–H–M–H	0.492–0.493	0.496–0.497	0.502–0.503	0.509–0.511	0.518–0.520
H–M–M–H	0.495–0.496	0.501–0.503	0.509–0.511	0.518–0.521	0.529–0.532
M–H–H–H	0.494–0.495	0.500–0.502	0.508–0.509	0.517–0.519	0.528–0.530
M–L–H–H	0.499–0.500	0.510–0.512	0.522–0.525	0.536–0.539	0.552–0.556

Table 13.

EISD simulation results under environmental preference during the 14th Five-year Plan period

Scenarios	2021	2022	2023	2024	2025
M–H–L–H	2.769–2.786	2.908–2.934	3.066–3.099	3.229–3.272	3.412–3.472
M–M-L–H	2.785–2.803	2.941–2.969	2.116–3.152	3.299–3.346	3.504–3.567
M–H–M–H	2.784–2.801	2.939–2.966	3.115–3.150	3.298–3.345	3.506–3.567
H–M–M–H	2.801–2.819	2.975–3.004	3.171–3.209	3.377–3.428	3.611–3.678
M–H–H–H	2.798–2.816	2.971–2.998	3.165–3.202	3.370–3.418	3.601–3.668
M–L–H–H	2.830–2.850	3.038–3.069	3.272–3.313	3.519–3.573	3.798–3.870

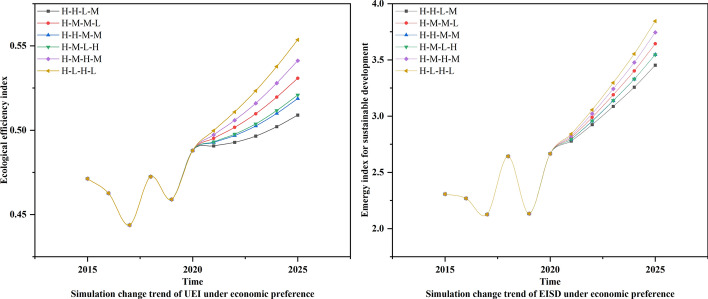
Fig. 8.

Simulation change trend of EISD and UEI under economic preference during the 14th Five-year Plan period

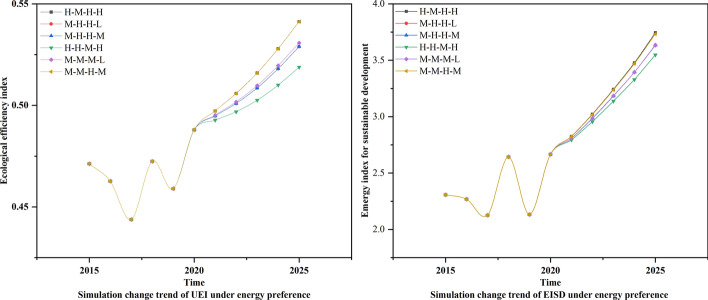
Fig. 9.

Simulation change trend of EISD and UEI under energy preference during the 14th Five-year Plan period

Fig. 10.

Simulation change trend of EISD and UEI under environmental preference during the 14th Five-year Plan period

Economic preferences

According to the analysis of Fig. 8 and Tables 8–9, the sustainable evaluation indexes under economic preference show different development trends under the macro-control of the above-mentioned six scenarios during the 14th Five-year Plan period. Scenario H–H–L–M strictly limits the development speed of renewable resources and increases the investment in nonrenewable resources, resulting in a decline growth rate of EISD and UEI, which is the worst development scenario. Scenarios H–H–M–M and H–M–L–H are slightly better than the former. This group has appropriately reduced the input of nonrenewable resources or increased the input of renewable resources, so that the growth rate of UEI and EISD increase appropriately, reaching 0.518–0.522 and 3.514–3.580 in 2025. However, the sustainable indexes are not prominent enough due to too small adjustments, so it is not the best choice. Scenarios H–M–M–L and H–M–H–M have increased energy input while vigorously developing the economy so that economic efficiency and resource efficiency are relatively balanced. UEI and EISD have also further increased, reaching 0.529–0.543 and 3.610–3.779 in 2025. However, due to the high investment in key variables, it is difficult to achieve, so this group of scenarios is not the best solution. Scenario H–L–H–L takes economic development as the core, reduces the input of nonrenewable resources to the minimum, and vigorously develops renewable resources, so that the proportion of renewable resources gradually increases, achieving the balanced development of economic efficiency and resource efficiency, and the ability of sustainable development gradually enhances. UEI and EISD reach 0.552–0.556 and 3.808–3.882 in 2025, which is the best scenario under economic preferences. Zhu et al. (2012) believe that over-reliance on nonrenewable resources is difficult to ensure long-term sustainable development, and we need to vigorously develop the economy to drive energy transformation, so that renewable resources take up a larger proportion, which is consistent with scenario H–L–H–L.

Energy preferences

According to the analysis of Fig. 9 and Tables 10–11, the sustainable evaluation indexes under energy preference show different development trends under the overall macro-control of the above-mentioned six scenarios during the 14th Five-year Plan period. Scenarios M–H–H–L and M–H–H–M pay too much attention to the input of energy, and invest both nonrenewable and renewable resources to the biggest extent, resulting in the uncoordinated development of environmental efficiency and resource efficiency. UEI and EISD are only 0.508–0.530 and 3.423–3.668 in 2025, so they are not the appropriate choices. Scenario M–M–M–L appropriately reduces energy input compared with the former, so that the environment, economy and resource development are relatively balanced. UEI and EISD rise to 0.529–0.532 and 3.600–3.666 in 2025, but the relatively mediocre design of various key variables leads to the inability to achieve the best sustainable indicators, so it is not the best choice. Scenarios M–M–H–M and H–M–H–H vigorously develop renewable resources, appropriately develop nonrenewable resources, and integrate environmental protection and economic development. The comprehensive and balanced design of key variables has achieved the best sustainable indicators. UEI and EISD are 0.540–0.543 and 3.669–3.779 in 2025, but scenario H–M–H–H is difficult to achieve because of the high investment in key variables. Therefore, scenario M-M-H-M is the best scenario under energy preference. Mehmood et al. (2022) believe that the best energy for sustainable development is renewable resources such as hydropower, solar energy and wind energy. Meanwhile, Feng et al. (2019) believe that the economic development model of resource-based cities in China driven by energy, especially coal, is difficult to change for a long time, so nonrenewable resources are still important driving force for their economic development. They agree with scenario M–M–H–M.

Environmental preferences

According to the analysis of Fig. 10 and Tables 12–13, the sustainable evaluation indexes under environmental preference show different development trends under the overall macro-control of the above-mentioned six scenarios during the 14th Five-year Plan period. Scenario M–H–L–H restricts the development speed of renewable resources on the basis of vigorously protecting the environment, and vigorously develops non- renewable resources. The uncoordinated development mode of environment and energy has made it the worst solution, UEI and EISD are only 0.508–0.510 and 3.412–3.472 in 2025. The proportion of nonrenewable resources input in scenarios M–M–L–H and M–H–M–H is higher than that of renewable resources. This traditional development model leads to poor sustainable indicators. UEI and EISD are only 0.518–0.522 and 3.504–3.567 in 2025, so they are not the best choices. Scenarios H–M–M–H and M–H–H–H integrate both energy and economic development on the premise of vigorously developing environmental protection, so that resource efficiency, environmental efficiency and economic efficiency have reached a relative balance. UEI and EISD reach 0.528–0.532 and 3.601–3.678 in 2025. However, the high input of various key variables makes it difficult to achieve, so they are not the optimal scenarios. Scenario M–L–H–H takes environmental protection as the core of development and strictly restricts the development of nonrenewable resources. In order to achieve the most coordinated development of resources, environment, and economy, it simultaneously vigorously develops renewable resources and appropriately develops the economy. UEI and EISD reach 0.552–0.556 and 3.798–3.870 in 2025, which is the optimal scenario under environmental preferences. Liu et al. (2022) believe that it is necessary to appropriately slow down economic development, reduce the proportion of nonrenewable resources, vigorously develop renewable energy, and further improve the green low-carbon cycle system to achieve more sustainable development, which is consistent with the research conclusion of scenario M–L–H–H.

Optimal scenario selection

By comparing and analyzing the appropriate scenarios under the above three preferences, the appropriate scenario M–M–H–M under the energy preference is basically consistent with the research conclusion of Yu et al. (2015), that is, the core driving force of economic growth of resource-based cities lies in the development and processing of local mineral resources. However, this model pays too much attention to the input of nonrenewable resources. The research shows that (Li, 2020) the COVID-19 has led to unsustainable industry and production is not high enough in Shandong Province. Considering that Jining is a resource-based city relying mainly on industry, this will further restrict the output of nonrenewable resources, so it is difficult to implement this scheme. The suitable scenario H–L–H–L under economic preferences does not integrate environmental protection while developing the economy. Sun et al. (2021) believes that ignoring the protection of the ecological environment in the development process of resource-based cities will have an adverse impact on the subsequent economic development, thus affecting the sustainable development of the city. Therefore, the uncoordinated development of the economy and environment leads to the unsatisfactory result of this scheme. The core idea of M–L–H–H under environmental preferences is to reduce the investment of nonrenewable resources while doing a good job in environmental protection, and pay attention to the coordinated development of resources, economy and environment. According to the research results of Sun et al. (2021), based on the assumption of not exceeding the ecological carrying capacity, we should reasonably formulate resource development planning, appropriately slow down economic development, and take environmental improvement as an important way for the development of resource-based cities. Only in this way can we achieve sustainable development. Therefore, the suitable scenario M–L–H–H is the best development model to improve the sustainable development ability of resource-based cities in the next planning year.

TOPSIS method verification

In order to verify the accuracy of the results and reduce the uncertainty caused by subjectivity, this study selects TOPSIS method for verification. Considering the differences in the degree of difficulty in the implementation of different scenarios, on the basis of the two sustainable evaluation indicators, the implementation difficulty is added as an important basis for the selection and assessment of the optimal scenario. See Appendix 5 for the specific calculation process. The sorting results are shown in Table 14.

Table 14.

Ranking of TOPSIS verification results

Scenarios	EISD	UEI	Difficulty	Close value	Ranking
M–L–H–H	3.584	0.525	0.709	0.9335	1
M–M–H–M	3.513	0.516	0.810	0.5968	2
H–L–H–L	3.596	0.525	0.793	0	3

According to the analysis in Table 14, through ranking the closeness values obtained by TOPSIS method, scenario M–L–H–H ranks first, which is the most suitable mode for the future development of Jining. The research conclusion is consistent with the conclusion analyzed in Chapter 3.7.

Conclusions

The innovative work and contributions of this article are mainly reflected in two aspects. First, in order to fully reflect the problems of resource-based cities such as “irrational economic structure, high resource dependence and serious environmental pollution,” the ecological efficiency index that can integrate economic efficiency, resource efficiency and environmental efficiency is selected as the emergy index reflecting the sustainable development of resource-based cities. Second, in order to reduce the uncertainty of the research results and overcome the disadvantage of using only sensitivity analysis to screen the key parameters in the past, we introduce the regression analysis model and couple it with sensitivity analysis to screen key variables, so that the selected key variables are more consistent with the development characteristics of resource-based cities, which increases the accuracy of the results of the scenario analysis.

Comparing the appropriate scenarios under three different preferences, the appropriate scenario M–L–H–H under environmental preference takes environmental protection as the core of development, strictly restricts the development of non- renewable resources, vigorously develops renewable resources, and moderately develops the economy. Among them, the large input of renewable resources has not only made up for the lack of energy caused by the reduction of nonrenewable resources, but also maintained a moderate economic growth; In addition, due to the more scientific and green energy conversion (renewable resources replacing nonrenewable resources), the environmental protection has been further enhanced and the environmental development is more sustainable. This scenario truly achieves the coordinated development of resource efficiency, environmental efficiency and economic efficiency, making UEI and EISD increase to 0.552–0.556 and 3.798–3.870, respectively, in 2025, indicating this scenario is the best scheme to improve the sustainable development level of Jining. Based on this, it is suggested that the appropriate development ranges of the growth rate of social fixed assets investment, the growth rate of raw coal emergy, the growth rate of grain emergy and the reduction rate of solid waste emergy in Jining during the 14th Five-year Plan period are 17.5–18.3%, − 4.0 to − 3.2%, 1.8–2.6% and 4–4.8%. According to the design of parameters in the appropriate scenario, it is suggested that the focus of work should be directed to improve the environmental quality and optimize the adjustment of energy structure during the 14th Five-year Plan of Jining. First, a complete environmental protection governance system should be established, especially increasing investment in green infrastructure. Second, we should further increase the proportion of renewable resources, slow down the development of nonrenewable resources, transform traditional industries into new energy industries, and form a closed loop of nonrenewable resources from raw material reuse to recycling.

In the scenario setting, the “medium” and “high” modes of the regulatory factors are screened only by experts’ consultation due to the lack of explicit requirements of the government during the development period of 14th Five-year Plan, which may lead to uncertainty of conclusions due to subjectivity. In addition, we hope the research method of “emergy + system” dynamics based on resource-based cities can attract the attention of relevant scholars, so that they can further expand and deepen in this field.

Appendix 1

With reference to the research results of Wang et al., (2021a, 2021b), the emergy indexes are selected according to the flow of material, energy, currency and labor in Jining. Generally, emergy indexes are classified into the following five categories: local nonrenewable emergy, renewable emergy, input emergy, output emergy and waste emergy. The local nonrenewable emergy is the wealth base of systematic environmental nonrenewable resources, which is mainly composed of the emergy of topsoil loss, fossil fuels, metal resources, cement and other resources; Renewable emergy is the wealth base of systematic environmental renewable resources, which is mainly composed of renewable natural resource emergy (solar, rain, wind, earth cycle, etc.) and renewable product emergy (crops, livestock, aquatic products, etc.), wherein, in order to avoid the duplication of the earth's cycle energy, solar energy, rain water and wind energy in emergy calculation, we select the largest one of them as the representative of renewable natural resource emergy based on the research results of (Brown & Ulgiati, 2016). Input emergy is the resources and services imported from outside, mainly composed of imported goods and services and tourism income; Output emergy is the output resources and services, mainly composed of the emergy of exported goods and services. Waste emergy is the waste discharged to the environment from system, which is mainly composed of solid waste, waste water and waste gas. The total emergy is the sum of local nonrenewable emergy, renewable emergy and input emergy, representing the total emergy of the system.

Abbreviations

Gemr	Global emergy to money ratio	Ece	Earth cycle energy	Cs	Caustic soda
Cemr	Chinese Emergy to money ratio	Pe	Poultry and eggs	Cf	Chemical fertilizer
Ecr	Emergy conversion rate	Ap	Aquatic product	Sa	Synthetic ammonia
Se	Solar energy	Sp	Steel products	Igs	Imported goods and services
Rce	Rainwater chemical energy	Ve	Vegetables	Ti	Tourism income
Rpe	Rainwater potential energy	Tl	Topsoil loss	Egs	Export goods and services
We	Wind energy	Rc	Raw coal	Sw	Solid waste

See Tables 15, 16, 17, and 18.

Table 15.

The original emergy analysis data of Jining urban eco-economic system

Project	Unit	Raw data
		2001	2002	2003	2004	2005	2006	2007	2008	2009	2010
Renewable resources
Se	J	6.32E+ 19	6.32E + 19	6.32E + 19	6.32E + 19	6.32E + 19	6.32E + 19	6.32E + 19	6.32E + 19	6.32E + 19	6.32E + 19
Rce	J	3.97E + 16	3.97E + 16	3.97E + 16	3.97E + 16	3.97E + 16	3.97E + 16	3.97E + 16	3.97E + 16	3.97E + 16	3.97E + 16
Rpe	J	3.56E + 15	3.56E + 15	3.56E + 15	3.56E + 15	3.56E + 15	3.56E + 15	3.56E + 15	3.56E + 15	3.56E + 15	3.56E + 15
We	J	3.93E + 15	3.93E + 15	3.93E + 15	3.93E + 15	3.93E + 15	3.93E + 15	3.93E + 15	3.93E + 15	3.93E + 15	3.93E + 15
Ece	J	1.12E + 16	1.12E + 16	1.12E + 16	1.12E + 16	1.12E + 16	1.12E + 16	1.12E + 16	1.12E + 16	1.12E + 16	1.12E + 16
Grain	g	3.80E + 12	3.65E + 12	3.23E + 12	3.46E + 12	3.50E + 12	3.95E + 12	3.96E + 12	4.17E + 12	4.46E + 12	4.65E + 12
Ve	J	1.40E + 16	1.63E + 16	1.79E + 16	2.08E + 16	2.64E + 16	2.33E + 16	2.39E + 16	2.26E + 16	2.26E + 16	1.98E + 16
Meat	J	5.72E + 15	5.17E + 15	5.82E + 15	6.24E + 15	7.93E + 15	6.95E + 15	7.32E + 15	6.01E + 15	6.63E + 15	7.06E + 15
Pe	J	1.89E + 15	1.93E + 15	2.22E + 15	2.35E + 15	2.53E + 15	2.20E + 15	2.35E + 15	2.17E + 15	2.41E + 15	2.59E + 15
Dairy	J	6.51E + 14	6.51E + 14	9.87E + 14	9.66E + 14	1.57E + 15	1.93E + 15	3.15E + 15	3.20E + 15	3.44E + 15	2.91E + 15
Ap	J	9.44E + 13	8.79E + 13	6.92E + 13	7.94E + 13	1.24E + 14	1.26E + 14	1.32E + 14	1.23E + 14	1.30E + 14	1.40E + 14
Local nonrenewable resources
Tl	J	2.42E+ 16	2.42E + 16	2.42E + 16	2.42E + 16	2.42E + 16	2.42E + 16	2.42E + 16	2.42E + 16	2.42E + 16	2.42E + 16
Rc	J	1.81E + 18	2.11E + 18	2.18E + 18	2.32E + 18	2.76E + 18	2.80E + 18	2.94E + 18	2.93E + 18	3.06E + 18	3.45E + 18
Sp	g	7.27E + 11	7.28E + 11	7.28E + 11	7.28E + 11	7.29E + 11	7.29E + 11	7.29E + 11	5.26E + 11	9.17E + 11	9.08E + 11
Cement	t	4.72E + 06	5.55E + 06	5.75E + 06	6.89E + 06	8.85E + 06	8.47E + 06	8.20E + 06	7.61E + 06	6.45E + 06	7.36E + 06
Cs	g	5.87E + 10	7.65E + 10	1.31E + 11	1.56E + 11	1.93E + 11	2.59E + 11	2.67E + 11	3.08E + 11	3.13E + 11	2.98E + 11
Cf	g	4.59E + 11	3.23E + 11	3.31E + 11	3.81E + 11	3.40E + 11	5.32E + 11	3.79E + 11	3.60E + 11	3.61E + 11	2.50E + 11
Sa	g	7.30E + 11	7.27E + 11	7.23E + 11	7.15E + 11	7.01E + 11	6.64E + 11	5.07E + 11	4.95E + 11	5.08E + 11	3.56E + 11
Import and transfer in resources
Igs	$	2.02E + 08	2.77E + 08	3.30E + 08	5.64E + 08	7.04E + 08	8.45E + 08	9.19E + 08	1.40E + 09	1.28E + 09	2.17E + 09
Ti	$	4.12E + 08	4.87E + 08	6.66E + 08	8.13E + 08	1.01E + 09	1.29E + 09	1.71E + 09	2.20E + 09	2.72E + 09	3.37E + 09
Export and transfer out resources
Egs	$	2.50E + 08	3.60E + 08	5.30E + 08	7.88E + 08	1.16E + 09	1.50E + 09	1.72E + 09	1.86E + 09	2.11E + 09	2.30E + 09
Waste resources
Sw	J	7.53E + 14	1.31E + 15	7.44E + 14	6.70E + 14	6.18E + 14	6.06E + 14	7.85E +14	1.23E + 15	1.22E + 15	7.77E + 14
Waste water	J	1.19E + 15	1.18E + 15	9.28E + 14	9.78E + 14	9.82E + 14	1.08E + 15	1.21E + 15	1.28E + 15	1.37E + 15	1.67E + 15
waste gas	J	2.40E + 11	4.32E + 11	4.74E + 11	6.12E + 11	5.60E + 11	5.01E + 11	4.21E + 11	4.08E + 11	4.00E + 11	3.69E + 11

Table 16.

The original emergy analysis data of Jining urban eco-economic system

Project	Unit	Raw data
		2011	2012	2013	2014	2015	2016	2017	2018	2019	2020
Renewable resources
Se	J	6.32E + 19	6.32E + 19	6.32E + 19	6.32E + 19	6.32E + 19	6.32E + 19	6.32E + 19	6.32E + 19	6.32E + 19	6.32E + 19
Rce	J	3.97E + 16	3.97E + 16	3.97E + 16	3.97E + 16	3.97E + 16	3.97E + 16	3.97E + 16	3.97E + 16	3.97E + 16	3.97E + 16
Rpe	J	3.56E + 15	3.56E + 15	3.56E + 15	3.56E + 15	3.56E + 15	3.56E + 15	3.56E + 15	3.56E + 15	3.56E + 15	3.56E + 15
We	J	3.93E + 15	3.93E + 15	3.93E + 15	3.93E + 15	3.93E + 15	3.93E + 15	3.93E + 15	3.93E + 15	3.93E + 15	3.93E + 15
Ece	J	1.12E + 16	1.12E + 16	1.12E + 16	1.12E + 16	1.12E + 16	1.12E + 16	1.12E + 16	1.12E + 16	1.12E + 16	1.12E + 16
Grain	g	4.88E + 12	5.69E + 12	5.78E + 12	5.78E + 12	5.87E + 12	5.87E + 12	5.75E + 12	4.71E + 12	4.75E + 12	5.99E + 12
Ve	J	1.89E + 16	1.61E + 16	1.62E + 16	1.59E + 16	1.59E + 16	1.55E+ 16	1.76E + 16	1.83E + 16	1.59E + 16	1.55E + 16
Meat	J	7.29E + 15	7.71E + 15	7.71E + 15	7.35E + 15	6.65E + 15	5.59E + 15	5.62E + 15	5.43E + 15	4.78E + 15	4.21E + 15
Pe	J	2.68E + 15	2.77E + 15	2.76E + 15	2.29E + 15	2.19E + 15	1.59E + 15	1.61E + 15	1.73E + 15	1.56E + 15	1.55E + 15
Dairy	J	2.91E + 15	2.95E + 15	2.85E + 15	2.74E + 15	2.57E + 15	2.22E + 15	2.22E + 15	2.08E + 15	2.44E + 15	2.03E + 15
Ap	J	1.51E + 14	1.58E + 14	1.64E + 14	1.27E + 14	1.28E + 14	1.34E + 14	1.34E + 14	1.34E + 14	1.26E + 14	1.13E + 14
Local nonrenewable resources
Tl	J	2.42E + 16	2.42E + 16	2.42E + 16	2.42E + 16	2.42E + 16	2.42E + 16	2.42E + 16	2.42E + 16	2.42E + 16	2.42E + 16
Rc	J	3.38E + 18	3.70E + 18	3.46E + 18	3.90E + 18	3.75E + 18	3.38E + 18	3.45E + 18	2.65E + 18	2.56E + 18	2.58E + 18
Sp	g	1.04E + 12	1.16E + 12	6.33E + 11	5.52E + 11	5.28E + 11	4.36E + 11	3.03E + 11	8.86E + 11	1.06E + 12	7.34E + 11
Cement	t	9.11E + 06	9.43E + 06	1.04E + 07	9.90E + 06	9.43E + 06	9.90E + 06	9.84E + 06	8.83E + 06	1.03E + 07	1.12E + 07
Cs	g	2.38E + 11	3.24E + 11	2.21E + 11	2.85E + 11	4.33E + 11	5.04E + 11	4.60E + 11	5.61E + 11	6.22E + 11	7.06E + 11
Cf	g	2.04E + 11	2.10E + 11	1.73E + 11	4.23E + 10	3.87E + 10	3.01E + 10	2.98E + 10	2.31E + 10	1.99E + 10	1.76E + 10
Sa	g	2.84E + 11	2.83E + 11	2.33E + 11	5.63E + 10	5.23E + 10	5.09E + 10	5.00E+ 10	4.73E + 10	4.53E + 10	4.32E + 10
Import and transfer in resources
Igs	$	2.68E + 09	1.92E + 09	1.90E + 09	1.96E + 09	2.00E + 09	2.04E + 09	2.57E + 09	2.71E + 09	2.88E + 09	3.04E + 09
Ti	$	4.33E + 09	5.48E + 09	6.47E + 09	7.33E + 09	8.14E + 09	8.69E + 09	1.04E + 10	1.13E + 10	1.27E + 10	6.83E + 09
Export and transfer out resources
Egs	$	3.07E + 09	3.20E + 09	3.33E + 09	3.27E + 09	3.44E + 09	3.38E + 09	3.57E + 09	3.08E + 09	4.14E + 09	3.08E + 09
Waste resources
Sw	J	1.82E + 15	2.37E + 15	1.35E + 15	7.04E + 14	1.07E + 15	7.74E + 14	1.59E + 15	1.90E + 15	1.10E + 15	8.00E + 14
Waste water	J	1.76E + 15	2.11E + 15	2.12E + 15	2.22E + 15	2.26E + 15	2.12E + 15	2.30E + 15	2.24E + 15	2.20E + 15	2.17E + 15
Waste gas	J	4.88E + 11	4.91E + 11	4.95E + 11	5.04E + 11	4.50E + 11	3.15E + 11	1.87E + 11	2.53E + 11	2.85E + 11	2.20E + 11

Table 17.

Emergy accounting of Jining urban eco-economic system

Project	Ecr(sej/unit)	References	Solar emergy (sej)
			2001	2002	2003	2004	2005	2006	2007	2008	2009	2010
Renewable resources
Se	1	(Wang et al., 2021a, 2021b)	6.32E + 19	6.32E + 19	6.32E + 19	6.32E + 19	6.32E + 19	6.32E + 19	6.32E + 19	6.32E + 19	6.32E + 19	6.32E + 19
Rce	2.31E + 04	(Wang et al., 2021a, 2021b)	9.17E + 20	9.17E + 20	9.17E + 20	9.17E + 20	9.17E+ 20	9.17E + 20	9.17E + 20	9.17E + 20	9.17E + 20	9.17E + 20
Rpe	3.54E + 04	(Wang et al., 2021a, 2021b)	1.26E + 20	1.26E + 20	1.26E + 20	1.26E + 20	1.26E + 20	1.26E + 20	1.26E + 20	1.26E + 20	1.26E + 20	1.26E + 20
We	1.90E + 03	(Wang et al., 2021a, 2021b)	7.47E + 18	7.47E + 18	7.47E + 18	7.47E + 18	7.47E + 18	7.47E + 18	7.47E + 18	7.47E + 18	7.47E + 18	7.47E + 18
Ece	4.37E + 04	(Wang et al., 2021a, 2021b)	4.89E + 20	4.89E + 20	4.89E + 20	4.89E + 20	4.89E + 20	4.89E + 20	4.89E + 20	4.89E + 20	4.89E + 20	4.89E + 20
Grain	3.34E + 09	(Wang et al., 2018)	1.27E + 22	1.22E + 22	1.08E + 22	1.16E + 22	1.17E + 22	1.32E + 22	1.32E + 22	1.39E + 22	1.49E + 22	1.55E + 22
Ve	4.42E + 05	(Wang et al., 2021a, 2021b)	6.19E + 21	7.20E + 21	7.91E + 21	9.19E + 21	1.17E + 22	1.03E + 22	1.06E + 22	9.99E + 21	9.99E + 21	8.75E + 21
Meat	1.70E + 06	(Peng et al., 2018)	9.73E + 21	8.79E + 21	9.89E + 21	1.06E + 22	1.35E + 22	1.18E + 22	1.24E + 22	1.02E + 22	1.13E + 22	1.20E + 22
Pe	1.08E + 06	(Wang et al., 2021a, 2021b)	2.04E + 21	2.08E + 21	2.40E + 21	2.54E + 21	2.73E + 21	2.37E + 21	2.53E + 21	2.34E + 21	2.60E + 21	2.80E + 21
Dairy	1.30E + 06	(Wang et al., 2021a, 2021b)	8.46E + 20	8.46E + 20	1.28E + 21	1.26E + 21	2.04E + 21	2.51E + 21	4.10E + 21	4.16E + 21	4.47E + 21	3.78E + 21
Ap	1.96E + 06	(Cheng et al., 2017)	1.85E + 20	1.72E + 20	1.36E + 20	1.56E + 20	2.43E + 20	2.47E + 20	2.59E + 20	2.41E + 20	2.55E + 20	2.74E + 20
Subtotal			3.26E+ 22	3.33E + 22	3.45E + 22	3.83E + 22	4.28E + 22	4.13E + 22	4.40E + 22	4.18E + 22	4.44E + 22	4.40E + 22
Local nonrenewable resources
Tl	9.40E + 04	(Wang et al., 2021a, 2021b)	2.27E + 21	2.27E + 21	2.27E + 21	2.27E + 21	2.27E + 21	2.27E + 21	2.27E + 21	2.27E + 21	2.27E + 21	2.27E + 21
Rc	8.17E + 04	(Wang et al., 2021a, 2021b)	1.48E + 23	1.72E + 23	1.78E + 23	1.90E + 23	2.26E + 23	2.29E + 23	2.40E + 23	2.39E + 23	2.50E + 23	2.82E + 23
Sp	5.80E + 09	(Jing et al., 2020)	4.22E + 21	4.22E + 21	4.22E + 21	4.22E + 21	4.23E + 21	4.23E + 21	4.23E + 21	3.05E + 21	5.32E + 21	5.27E + 21
Cement	1.92E + 15	(Chen et al., 2016)	9.06E + 21	1.07E + 22	1.10E + 22	1.32E + 22	1.70E + 22	1.63E + 22	1.57E + 22	1.46E + 22	1.24E + 22	1.41E + 22
Cs	7.66E + 09	(Corcelli et al., 2018)	4.50E + 20	5.86E + 20	1.00E + 21	1.19E + 21	1.48E + 21	1.98E + 21	2.05E + 21	2.36E + 21	2.40E + 21	2.28E + 21
Cf	3.62E + 09	(He et al., 2019)	1.66E + 21	1.17E + 21	1.20E + 21	1.38E + 21	1.23E + 21	1.93E + 21	1.37E + 21	1.30E + 21	1.31E + 21	9.05E + 20
Sa	2.22E + 09	(Saladini et al., 2018)	1.62E + 21	1.61E + 21	1.61E + 21	1.59E + 21	1.56E + 21	1.47E + 21	1.13E + 21	1.10E + 21	1.13E + 21	7.90E + 20
Subtotal			1.67E + 23	1.93E + 23	1.99E + 23	2.14E + 23	2.54E + 23	2.57E + 23	2.67E + 23	2.64E + 23	2.75E + 23	3.08E + 23
Import and transfer in resources
Igs	Gemr	(NEAD., 2015)	3.22E + 20	4.35E + 20	5.15E + 20	8.74E + 20	1.08E+ 21	1.27E + 21	1.34E + 21	2.05E + 21	1.87E + 21	3.14E + 21
Ti	Cemr	(NEAD., 2015)	1.69E + 21	2.11E + 21	3.07E + 21	3.84E + 21	4.98E + 21	6.39E + 21	7.04E + 21	8.54E + 21	1.07E + 22	1.34E + 22
Subtotal			2.01E + 21	2.55E + 21	3.58E + 21	4.71E + 21	6.06E + 21	7.66E + 21	8.39E + 21	1.06E + 22	1.26E + 22	1.66E + 22
Export and transfer out resource emergy flow
Egs	Emergy to money ratio	This paper	6.80E + 21	9.79E + 21	1.28E + 22	1.66E + 22	2.45E + 22	2.73E + 22	2.61E + 22	2.16E + 22	2.37E + 22	2.56E + 22
Emergy flow of waste resources
Sw	1.80E + 06	(Wang et al., 2021a, 2021b)	1.36E + 21	2.37E + 21	1.34E + 21	1.21E + 21	1.12E + 21	1.09E + 21	1.42E + 21	2.22E + 21	2.2E + 21	1.4E + 21
Waste water	8.60E + 05	(Wang et al., 2021a, 2021b)	1.02E + 21	1.01E + 21	7.98E + 20	8.41E + 20	8.45E + 20	9.29E + 20	1.04E + 21	1.10E + 21	1.18E + 21	1.44E + 21
Waste gas	4.8E + 04	(Wang et al., 2021a, 2021b)	1.15E + 16	2.07E + 16	2.28E + 16	2.94E + 16	2.69E + 16	2.41E + 16	2.02E + 16	1.96E + 16	1.92E + 16	1.77E + 16
Subtotal			2.38E + 21	3.37E + 21	2.14E + 21	2.05E + 21	1.96E + 21	2.02E + 21	2.45E + 21	3.31E + 21	3.37E + 21	2.83E + 21

Table 18.

Emergy accounting of Jining urban eco-economic system

Project	Ecr (sej/unit)	References	Solar emergy (sej)
			2011	2012	2013	2014	2015	2016	2017	2018	2019	2020
Renewable resources
Se	1	(Wang et al., 2021a, 2021b)	6.32E+ 19	6.32E + 19	6.32E + 19	6.32E + 19	6.32E + 19	6.32E + 19	6.32E + 19	6.32E + 19	6.32E + 19	6.32E + 19
Rce	2.31E + 04	(Wang et al., 2021a, 2021b)	9.17E + 20	9.17E + 20	9.17E + 20	9.17E + 20	9.17E + 20	9.17E + 20	9.17E + 20	9.17E + 20	9.17E + 20	9.17E + 20
Rpe	3.54E + 04	(Wang et al., 2021a, 2021b)	1.26E + 20	1.26E + 20	1.26E + 20	1.26E + 20	1.26E + 20	1.26E + 20	1.26E + 20	1.26E + 20	1.26E + 20	1.26E + 20
We	1.90E + 03	(Wang et al., 2021a, 2021b)	7.47E + 18	7.47E + 18	7.47E + 18	7.47E + 18	7.47E + 18	7.47E + 18	7.47E + 18	7.47E + 18	7.47E + 18	7.47E + 18
Ece	4.37E + 04	(Wang et al., 2021a, 2021b)	4.89E + 20	4.89E + 20	4.89E + 20	4.89E + 20	4.89E + 20	4.89E + 20	4.89E + 20	4.89E + 20	4.89E + 20	4.89E + 20
Grain	3.34E + 09	(Wang et al., 2018)	1.63E + 22	1.90E + 22	1.93E + 22	1.93E + 22	1.96E + 22	1.96E + 22	1.92E + 22	1.57E + 22	1.59E + 22	2.00E + 22
Ve	4.42E + 05	(Wang et al., 2021a, 2021b)	8.35E + 21	7.10E + 21	7.16E + 21	7.04E + 21	7.04E + 21	6.86E + 21	7.79E + 21	8.08E + 21	7.02E + 21	6.86E + 21
Meat	1.70E + 06	(Peng et al., 2018)	1.24E + 22	1.31E + 22	1.31E + 22	1.25E + 22	1.13E + 22	9.50E + 21	9.55E + 21	9.23E + 21	8.13E + 21	7.16E + 21
Pe	1.08E + 06	(Wang et al., 2021a, 2021b)	2.89E + 21	2.99E + 21	2.98E + 21	2.47E + 21	2.37E + 21	1.72E + 21	1.74E + 21	1.87E + 21	1.68E + 21	1.68E + 21
Dairy	1.30E + 06	(Wang et al., 2021a, 2021b)	3.78E+ 21	3.83E + 21	3.70E + 21	3.56E + 21	3.34E + 21	2.88E + 21	2.88E + 21	2.70E + 21	3.17E + 21	2.64E + 21
Ap	1.96E + 06	(Cheng et al., 2017)	2.95E + 20	3.10E + 20	3.22E + 20	2.48E + 20	2.50E + 20	2.62E + 20	2.63E + 20	2.62E + 20	2.46E + 20	2.21E + 20
Subtotal			4.50E + 22	4.72E + 22	4.74E + 22	4.61E + 22	4.47E + 22	4.17E + 22	4.21E + 22	3.87E + 22	3.70E + 22	4.05E + 22
Local nonrenewable resources
Tl	9.40E + 04	(Wang et al., 2021a, 2021b)	2.28E + 21	2.28E + 21	2.28E + 21	2.28E + 21	2.28E + 21	2.28E + 21	2.28E + 21	2.28E + 21	2.28E + 21	2.28E + 21
Rc	8.17E + 04	(Wang et al., 2021a, 2021b)	2.76E + 23	3.02E + 23	2.83E + 23	3.19E + 23	3.06E + 23	2.76E + 23	2.82E + 23	2.16E + 23	2.09E + 23	2.11E + 23
Sp	5.80E + 09	(Jing et al., 2020)	6.01E + 21	6.73E + 21	3.67E + 21	3.20E + 21	3.06E + 21	2.53E + 21	1.76E + 21	5.14E + 21	6.18E + 21	4.25E + 21
Cement	1.92E + 15	(Chen et al., 2016)	1.75E + 22	1.81E + 22	2.00E + 22	1.90E + 22	1.81E + 22	1.90E + 22	1.89E + 22	1.70E + 22	1.97E + 22	2.15E + 22
Cs	7.66E + 09	(Corcelli et al., 2018)	1.82E + 21	2.48E + 21	1.69E + 21	2.18E + 21	3.32E + 21	3.86E + 21	3.52E + 21	4.30E + 21	4.77E + 21	5.41E + 21
Cf	3.62E + 09	(He et al., 2019)	7.38E + 20	7.60E + 20	6.26E + 20	1.53E + 20	1.40E + 20	1.09E + 20	1.08E + 20	8.37E + 19	7.22E + 19	6.38E + 19
Sa	2.22E + 09	(Saladini et al., 2018)	6.30E + 20	6.29E + 20	5.17E + 20	1.25E + 20	1.16E + 20	1.13E + 20	1.11E + 20	1.05E + 20	1.01E+ 20	9.60E + 19
Subtotal			3.05E + 23	3.33E + 23	3.12E + 23	3.46E + 23	3.33E + 23	3.04E + 23	3.09E + 23	2.45E + 23	2.42E + 23	2.45E + 23
Import and transfer in resources
Igs	Gemr	(NEAD., 2015)	3.83E + 21	2.71E + 21	2.64E + 21	2.67E + 21	2.66E + 21	2.55E + 21	3.36E + 21	3.74E + 21	3.18E + 21	2.93E + 21
Ti	Cemr	(NEAD., 2015)	1.71E + 22	2.12E + 22	2.45E + 22	2.64E + 22	2.71E + 22	2.88E + 22	3.37E + 22	3.57E + 22	3.91E + 22	2.05E + 22
Subtotal			2.09E + 22	2.40E + 22	2.72E + 22	2.91E + 22	2.98E + 22	3.14E + 22	3.71E + 22	3.94E + 22	4.23E + 22	2.34E + 22
Export and transfer out resource emergy flow
Egs	Emergy to money ratio	This paper	2.89E + 22	2.92E + 22	2.62E + 22	2.56E + 22	2.38E + 22	2.18E + 22	2.25E + 22	1.65E + 22	2.10E + 22	1.45E + 22
Emergy flow of waste resources
Solid waste	1.80E + 06	(Wang et al., 2021a, 2021b)	3.29E + 21	4.29E + 21	2.43E + 21	1.27E + 21	1.93E + 21	1.40E + 21	2.87E + 21	3.43E + 21	1.99E + 21	1.45E + 21
Waste water	8.60E + 05	(Wang et al., 2021a, 2021b)	1.51E + 21	1.82E + 21	1.82E + 21	1.91E + 21	1.95E + 21	1.82E + 21	1.98E + 21	1.93E + 21	1.89E + 21	1.87E + 21
Waste gas	4.80E + 04	(Wang et al., 2021a, 2021b)	2.34E + 16	2.36E + 16	2.38E + 16	2.42E + 16	2.16E + 16	1.51E + 16	8.95E + 15	1.21E + 16	1.37E + 16	1.06E + 16
Subtotal			4.79E + 21	6.09E + 21	4.25E + 21	3.18E + 21	3.87E + 21	3.22E + 21	4.83E + 21	5.35E + 21	3.87E + 21	3.31E + 21

Appendix 2

According to the different types of emergy indexes established in the previous article, the system dynamics model is divided into economic, environmental, social and energy subsystems, and five different types of emergy evaluation indexes are also part of the corresponding subsystems. The specific division basis is as follows, and the division content is shown in Table 19.

Table 19.

Variable set of each subsystem

Variable types	Economic subsystem	Environment subsystem	Social subsystem	Energy subsystem
State variables	Social fixed assets investment	Solid waste emergy	Population	Grain emergy
				Output resources
				Raw coal emergy
				Input emergy
Rate variables	Growth in social fixed assets investment	Reduction of solid waste emergy	Population growth	Growth in input emergy
			Population reduction	Growth in output resources
				Growth in grain emergy
				Growth in raw coal emergy
Auxiliary variables	Primary industry labor force	Production waste water emergy per unit of GDP	Birth rate	Growth rate of input emergy
	Secondary industry labor force	Production waste gas emergy per unit of GDP	Death rate	Growth rate of output resources
	Tertiary industry labor force	Domestic waste water emergy per head	Survival index	Growth rate of grain emergy
	Proportion of investment in primary industry	Domestic waste gas emergy per head	Environmental pressure index	Growth rate of raw coal emergy
	Proportion of investment in secondary industry	Production waste water emergy	Employment rates	Renewable emergy except grain
	Proportion of investment in tertiary industry	Production waste gas emergy	Employed population	Nonrenewable emergy except raw coal
	Investment in primary industry	Domestic waste water emergy	Emergy per head	Renewable emergy
	Investment in secondary industry	Domestic waste gas emergy		Nonrenewable emergy
	Investment in tertiary industry	Waste water emergy		Output emergy
	Primary industry output	Waste gas emergy		Exchange rate
	Secondary industry output	Reduction rate of solid waste emergy		Total emergy
	Tertiary industry output	Waste emergy		Emergy index for sustainable development
	Proportion of labor force in primary industry	Waste emergy to total emergy ratio		Ecological efficiency index
	Proportion of labor force in secondary industry
	Proportion of labor force in tertiary industry
	GDP
	Growth rate of social fixed asset investment
	Emergy to money ratio

Economic subsystem

The sources of GDP are divided into the primary industry output, the secondary industry output and the tertiary industry output. The calculation of the three industries output refers to Cobb Douglas production function. After determining the labor force and industry investment as independent variables, the multiple linear regression analysis is conducted on them in combination with the dependent variables to determine the functional relationship between the dependent variables and independent variables. The labor force is determined by the population and employment rate.

Social subsystem

Take population as state variable, birth population and death population as rate variable, and birth rate and death rate as auxiliary variables. Different kinds of emergy resources are used as auxiliary variables (survival index and environmental pressure index) to influence the population.

Environment subsystem

Determine the classification of waste emergy by querying the statistical yearbook, and divide it into solid waste emergy, waste water emergy and waste gas emergy. The emergy of waste water and waste gas are both divided into production and living parts. The production part is linked with GDP, and the living part is linked with the population, which enhances the integrity of the system.

Energy subsystem

Determine different energy classifications by querying the statistical yearbook, and divide it into renewable resources, nonrenewable resources, input resources and output resources. In order to highlight the characteristics of resource-based cities, the largest part of renewable and nonrenewable resources (grain and raw coal) will be extracted separately to pave the way for the subsequent scenario setting. The end point is the two sustainable indexes of UEI and EISD.

See Table 19.

Appendix 3

The following are all the equations required in the social subsystem:

Population = Population' + Population growth -Population reduction.

Population growth = Population × Birth rate × Survival index.

Population reduction = Population × Death rate × Environmental pressure index.

Employment rates = DELAY1I(0.503829 + 3.4e-05 × GDP,1,0.545085).

Employed population = Population × Employment rates.

Survival index = DELAY1I (Renewable emergy/Total emergy × 5,1,0.813461).

Environmental pressure index = DELAY1I (Waste emergy/Renewable emergy × 5,1,0.361827).

Emergy per head = Total emergy/Population.

Birth rate table function = ([(2001,0)-(2025,0.02)], (2001,0.0104291), (2002,0.0106609), (2003,0.0107872), (2004,0.0109753), (2005,0.011176), (2006,0.0104239), (2007,0.0107417), (2008,0.0130623), (2009,0.0148106), (2010,0.0119573), (2011,0.0111083), (2012,0.0122868), (2013,0.0105548), (2014,0.0151708), (2015,0.013075), (2016,0.0132262), (2017,0.0133221), (2018,0.0174518), (2019,0.0132656), (2020,0.0103714), (2021,0.0136495), (2022,0.0137918), (2023,0.0138272), (2024,0.0138499), (2025,0)).

Death rate table function = ([(2001,0)-(2025,0.01)], (2001,0.00509869), (2002,0.00519738), (2003,0.00524471), (2004,0.00532233), (2005,0.00540613), (2006,0.00513716), (2007,0.007289), (2008,0.00587039), (2009,0.00563131), (2010,0.00572145), (2011,0.00555417), (2012,0.00609394), (2013,0.00517899), (2014,0.00575022), (2015,0.00619604), (2016,0.00625708), (2017,0.00629211), (2018,0.00617343), (2019,0.00649167), (2020,0.00710848), (2021,0.00640754), (2022,0.00646517), (2023,0.00647289), (2024,0.00647487), (2025,0)).

The following are all the equations required in the environment subsystem:

Solid waste emergy = Solid waste emergy'-Reduction of solid waste emergy.

Reduction of solid waste emergy = Solid waste emergy × Reduction rate of solid waste emergy.

Production waste water emergy = GDP × Production waste water emergy per unit of GDP.

Production waste gas emergy = GDP × Production waste gas emergy per unit of GDP.

Domestic waste water emergy = Population × Domestic waste water emergy per head.

Domestic waste gas emergy = Population × Domestic waste gas emergy per head.

Waste water emergy = Domestic waste water emergy + Production waste water emergy.

Waste gas emergy = Domestic waste gas emergy + Production waste gas emergy.

Waste emergy = Solid waste emergy + Waste gas emergy + Waste water emergy.

Waste emergy to total emergy ratio = Waste emergy/Total emergy.

Production waste water emergy per unit of GDP table function = ([(2001,0)-(2025,1.5e + 10)], (2001,1.11e + 10), (2002,9.21e + 09), (2003,4.73e + 09), (2004,4.2e + 09), (2005,3.39e + 09), (2006,3.43e + 09), (2007,3.28e + 09), (2008,2.89e + 09), (2009,2.94e + 09), (2010,3.12e + 09), (2011,2.83e + 09), (2012,2.6e + 09), (2013,2.22e + 09), (2014,2.14e + 09), (2015,1.96e + 09), (2016,1.48e + 09), (2017,1.4e + 09), (2018,1.17e + 09), (2019,1.03e + 09), (2020,9.06e + 08), (2021,7.96e + 08), (2022,6.98e + 08), (2023,6.98e + 08), (2024,5.36e + 08), (2025,4.69e + 08)).

Domestic waste water emergy per head table function = ([(2001,0)-(2025,2e + 14)], (2001,4.33e + 13), (2002,4.77e + 13), (2003,5.24e + 13), (2004,5.28e + 13), (2005,5.6e + 13), (2006,6.04e + 13), (2007,6.58e + 13), (2008,6.97e + 13), (2009,7.33e + 13), (2010,9.19e + 13), (2011,9.85e + 13), (2012,1.34e + 14), (2013,1.41e + 14), (2014,1.46e + 14), (2015,1.49e + 14), (2016,1.5e + 14), (2017,1.66e + 14), (2018,1.67e + 14), (2019,1.68e + 14), (2020,1.69e + 14), (2021,1.69e + 14), (2022,1.7e + 14), (2023,1.7e + 14), (2024,1.7e + 14), (2025,1.71e + 14)).

Domestic waste gas emergy per head table function = ([(2001,0)-(2025,2e + 09)], (2001,4.57e + 08), (2002,4.13e + 08), (2003,3.93e + 08), (2004,4.13e + 08), (2005,3.89e + 08), (2006,3.23e + 08), (2007,3.41e + 08), (2008,3.11e + 08), (2009,3.08e + 08), (2010,1.08e + 08), (2011,3.12e + 08), (2012,3.19e + 08), (2013,3.32e + 08), (2014,4.75e + 08), (2015,6.92e + 08), (2016,7.94e + 08), (2017,5.69e + 08), (2018,8.07e + 08), (2019,8.81e + 08), (2020,8.18e + 08), (2021,7.62e + 08), (2022,8.32e + 08), (2023,1.03e + 09), (2024,9.63e + 08), (2025,1.04e + 09)).

Production waste gas emergy per unit of GDP table function = ([(2001,0)-(2025,300,000)], (2001,130,000), (2002,253,000), (2003,243,000), (2004,261,000), (2005,204,000), (2006,161,000), (2007,110,000), (2008,90,500), (2009,83,100), (2010,75,400), (2011,82,400), (2012,75,200), (2013,69,200), (2014,61,500), (2015,43,400), (2016,21,900), (2017,10,000),(2018,12,200), (2019,14,000), (2020,7720), (2021,4870), (2022,8110), (2023,11,500), (2024,9670), (2025,11,600)).

Reduction rate of solid waste emergy table function(low solution) = ([(2001,− 2)-(2025,2)], (2001,− 0.743209), (2002,0.433181), (2003,0.0992579), (2004,0.0782698), (2005,0.0189944), (2006,− 0.295444), (2007,− 0.564885), (2008,0.0094371), (2009,0.360956), (2010,− 1.34046), (2011,− 0.304892), (2012,0.43252), (2013,0.477134), (2014,− 0.515181), (2015,0.274725), (2016,− 1.05016), (2017,− 0.197084), (2018,0.421053), (2019,0.272727), (2020,0.036), (2021,0.038), (2022,0.040), (2023,0.042), (2024,0.044), (2025,0)).

The following are all the equations required in the economic subsystem:

Social fixed asset investment = Social fixed asset investment' + Growth in Social fixed asset investment.

Growth in Social fixed asset investment = Growth rate of Social fixed asset investment × Social fixed asset investment.

Primary industry labor force = Employed population × Proportion of labor force in primary industry.

Secondary industry labor force = Employed population × Proportion of labor force in secondary industry.

Tertiary industry labor force = Employed population × Proportion of labor force in tertiary industry.

Investment in primary industry = Social fixed asset investment × Proportion of investment in primary industry.

Investment in secondary industry = Social fixed asset investment × Proportion of investment in secondary industry.

Investment in tertiary industry = Social fixed asset investment × Proportion of labor force in tertiary industry.

Primary industry output = 0.01192 × Primary industry labor force^2 + 0.0006776 × Investment in primary industry^2 + 0.01421 × Primary industry labor force × Investment in primary industry-8.556 × Primary industry labor force-1.858 × Investment in primary industry + 1434.

Secondary industry output = 0.3819 × Secondary industry labor force^2 + 0.0002907 × Investment in secondary industry^2–0.02774 × Secondary industry labor force × Investment in secondary industry-76.09 × Secondary industry labor force + 3.971 × Investment in secondary industry + 4035.

Tertiary industry output = 0.01154 × Tertiary industry labor force^2 + 4.611e-11 × Investment in tertiary industry^2–0.002976 × Tertiary industry labor force × Investment in tertiary industry + 0.6904 × Tertiary industry labor force + 1.305 × Investment in tertiary industry-4.781.

GDP = Primary industry output + Secondary industry output + Tertiary industry output.

Emergy to money ratio = Total emergy/GDP.

Proportion of labor force in primary industry table function = ([(2001,0)-(2025,1)],(2001,0.537564),(2002,0.507676),(2003,0.508558),(2004,0.466059),(2005,0.454358),(2006,0.424443),(2007,0.426224),(2008,0.408512),(2009,0.40946),(2010,0.395873),(2011,0.37891),(2012,0.363725),(2013,0.342253),(2014,0.319402),(2015,0.277523),(2016,0.269453),(2017,0.262996),(2018,0.259395),(2019,0.236932),(2020,0.220351),(2021,0.192004),(2022,0.180882),(2023,0.170078),(2024,0.1585),(2025,0.146412)).

Proportion of labor force in secondary industry table function = ([(2001,0)-(2025,1)],(2001,0.246384),(2002,0.277783),(2003,0.263414),(2004,0.25924),(2005,0.268049),(2006,0.282485),(2007,0.282857),(2008,0.288237),(2009,0.281677),(2010,0.234822),(2011,0.295422),(2012,0.314316),(2013,0.323796),(2014,0.336066),(2015,0.337191),(2016,0.325552),(2017,0.321119),(2018,0.318173),(2019,0.32795),(2020,0.32551),(2021,0.323776),(2022,0.326271),(2023,0.328),(2024,0.327966),(2025,0.324872)).

Proportion of labor force in tertiary industry table function = ([(2001,0)-(2025,1)],(2001,0.216052),(2002,0.214541),(2003,0.228028),(2004,0.274701),(2005,0.277593),(2006,0.293071),(2007,0.29092),(2008,0.303251),(2009,0.308863),(2010,0.369304),(2011,0.325668),(2012,0.321959),(2013,0.333951),(2014,0.344532),(2015,0.385286),(2016,0.404995),(2017,0.415884),(2018,0.422432),(2019,0.435118),(2020,0.454139),(2021,0.48422),(2022,0.492846),(2023,0.501485),(2024,0.513534),(2025,0.528716)).

Proportion of investment in primary industry table function = ([(2001,0)-(2025,0.1)],(2001,0.006),(2002,0.01),(2003,0.004),(2004,0.029),(2005,0.024),(2006,0.047),(2007,0.05),(2008,0.061),(2009,0.044),(2010,0.032),(2011,0.019),(2012,0.027),(2013,0.02),(2014,0.021),(2015,0.023),(2016,0.022),(2017,0.015),(2018,0.01),(2019,0.012),(2020,0.0394),(2021,0.036),(2022,0.0436),(2023,0.0515),(2024,0.0489),(2025,0.0351)).

Proportion of investment in secondary industry table function = ([(2001,0)-(2025,1)],(2001,0.568),(2002,0.666),(2003,0.698),(2004,0.682),(2005,0.657),(2006,0.637),(2007,0.622),(2008,0.572),(2009,0.575),(2010,0.539),(2011,0.497),(2012,0.488),(2013,0.528),(2014,0.556),(2015,0.527),(2016,0.528),(2017,0.521),(2018,0.478),(2019,0.424),(2020,0.4652),(2021,0.4465),(2022,0.415),(2023,0.3813),(2024,0.356),(2025,0.3395)).

Proportion of tertiary industry investment table function = ([(2001,0)-(2025,1)],(2001,0.426),(2002,0.324),(2003,0.298),(2004,0.289),(2005,0.319),(2006,0.316),(2007,0.328),(2008,0.367),(2009,0.38),(2010,0.429),(2011,0.484),(2012,0.485),(2013,0.452),(2014,0.423),(2015,0.45),(2016,0.45),(2017,0.464),(2018,0.512),(2019,0.564),(2020,0.49543),(2021,0.517519),(2022,0.541391),(2023,0.567199),(2024,0.595115),(2025,0.625326)).

Growth rate of Social fixed asset investment table function(low solution) = ([(0,-0.05)-(3000,10)],(2001,0.122647),(2002,0.157643),(2003,0.21606),(2004,0.4629),(2005,0.162401),(2006,0.183547),(2007,0.231693),(2008,0.489221),(2009,0.338927),(2010,− 0.0416609),(2011,0.300352),(2012,0.209206),(2013,0.159896),(2014,0.138996),(2015,0.13421),(2016,0.0593169),(2017,0.08597),(2018,0.07916),(2019,0.07336), (2020,0.173),(2021,0.175),(2022,0.177),(2023,0.179),(2024,0.181),(2025,0).

The following are all the equations required in the energy subsystem:

Output resources = Output resources' + Growth in output resources.

Growth in output resources = Growth rate of output resources × Output resources.

Output emergy = Emergy to money ratio × Output resources × Exchange rate.

Input emergy = Input emergy' + Growth in input emergy.

Growth in input emergy = Growth rate of input emergy × Input emergy.

Raw coal emergy = Raw coal emergy' + Growth in raw coal emergy.

Growth in raw coal emergy = Growth rate of raw coal emergy × Raw coal emergy.

Grain emergy = Grain emergy' + Growth in grain emergy.

Growth in grain emergy = Growth rate of grain emergy × Grain emergy.

Renewable emergy = Renewable emergy except grain + Grain emergy.

Nonrenewable emergy = Nonrenewable emergy except raw coal + Raw coal emergy.

Total emergy = Renewable emergy + Nonrenewable emergy + Input emergy.

Emergy index for sustainable development = (Input emergy/Output emergy)*((Input emergy + Nonrenewable emergy + Renewable emergy)/Input emergy)/((Nonrenewable emergy + Input emergy)/Renewable emergy).

Ecological efficiency index = ((1-Waste emergy/Total emergy) ^2) × ((1-Nonrenewable emergy/Total emergy) ^2) × (Total emergy/Input emergy).

Growth rate of output resources table function = ([(2001,− 0.5)-(2025,0.6)],(2001,0.44),(2002,0.472222),(2003,0.486792),(2004,0.472081),(2005,0.293103),(2006,0.146667),(2007,0.0813954),(2008,0.134409),(2009,0.0900474),(2010,0.334783),(2011,0.0423453),(2012,0.040625),(2013,− 0.018018),(2014,0.0519878),(2015,− 0.0174419),(2016,0.056213),(2017,− 0.137255),(2018,0.344156),(2019,− 0.15604),(2020,0.253085),(2021,0.0141596),(2022,0.0113695),(2023,0.00910884),(2024,0.00728446),(2025,0)).

Exchange rate table function = ([(2001,0)-(2025,10)],(2001,8.28),(2002,8.28),(2003,8.28),(2004,8.28),(2005,8.19),(2006,7.97),(2007,7.6),(2008,6.95),(2009,6.83),(2010,6.77),(2011,6.46),(2012,6.31),(2013,6.19),(2014,6.14),(2015,6.23),(2016,6.64),(2017,6.75),(2018,7.19),(2019,6.89),(2020,6.9),(2021,6.42),(2022,6.38),(2023,6.35),(2024,6.31),(2025,6.28)).

Growth rate of input emergy table function = ([(2001,0)-(2025,0.5)],(2001,0.268657),(2002,0.403922),(2003,0.315642),(2004,0.286624),(2005,0.264026),(2006,0.0953),(2007,0.263409),(2008,0.188679),(2009,0.31746),(2010,0.259036),(2011,0.148325),(2012,0.133333),(2013,0.069853),(2014,0.024055),(2015,0.053691),(2016,0.181529),(2017,0.061995),(2018,0.073604),(2019,0.144208),(2020,1.041248),(2021,0.0582),(2022,0.0548799),(2023,0.0519203),(2024,0.04266),(2025,0)).

Growth rate of raw coal emergy table function (low solution) = ([(2001,− 1)-(2025,0.3)],(2001,0.162903),(2002,0.033266),(2003,0.066012),(2004,0.187565),(2005,0.014327),(2006,0.50549),(2007,− 0.00051),(2008,0.041667),(2009,0.128),(2010,− 0.02128),(2011,0.094203),(2012,− 0.06291),(2013,0.127208),(2014,− 0.04075),(2015,− 0.098039),(2016,0.021739),(2017,− 0.23254),(2018,− 0.03256),(2019,0.008644),(2020,− 0.032),(2021,− 0.034),(2022,-0.036),(2023,− 0.038),(2024,− 0.040),(2025,0)).

Growth rate of grain emergy table function (low solution) = ([(2001,− 0.3)-(2025,0.3)],(2001,− 0.039370),(2002,− 0.114754),(2003,0.0740741),(2004,0.0086207),(2005,0.128205),(2006,0),(2007,0.0530303),(2008,0.0719424),(2009,0.0402685),(2010,0.0516129),(2011,0.1656442),(2012,0.0157895),(2013,0),(2014,0.0155440),(2015,0),(2016,− 0.0204082),(2017,− 0.182292),(2018,0.0127389),(2019,0.257862),(2020,0.002),(2021,0.004),(2022,0.006),(2023,0.008),(2024,0.010),(2025,0)).

Nonrenewable emergy except raw coal table function = ([(2001,0)-(2020,4e + 22)],(2001,1.92886e + 22),(2002,2.05209e + 22),(2003,2.13434e + 22),(2004,2.38977e + 22),(2005,2.77653e + 22),(2006,2.81616e + 22),(2007,2.67874e + 22),(2008,2.469e + 22),(2009,2.484e + 22),(2010,2.5625e + 22),(2011,2.8978e + 22),(2012,3.0979e + 22),(2013,2.8783e + 22),(2014,2.6938e + 22),(2015,2.7016e + 22),(2016,2.7892e + 22),(2017,2.6679e + 22),(2018,2.88576e + 22),(2019,3.30772e + 22),(2020,3.35838e + 22),(2021,3.42595e + 22),(2022,3.48564e + 22),(2023,3.54083e + 22),(2024,3.59357e + 22),(2025,3.645e + 22)).

Renewable emergy except grain table function = ([(2001,0)-(2025,4e + 22)],(2001,1.99e + 22),(2002,2.00e + 22),(2003,2.25e + 22),(2004,2.46e + 22),(2005,3.11e + 22),(2006,2.81e + 22),(2007,3.08e + 22),(2008,2.78e + 22),(2009,2.95e + 22),(2010,2.85e + 22),(2011,2.86e + 22),(2012,2.82e + 22),(2013,2.82e + 22),(2014,2.67e + 22),(2015,2.52e + 22),(2016,2.21e + 22),(2017,2.31e + 22),(2018,2.30e + 22),(2019,2.11e + 22),(2020,1.95e + 22),(2021,1.37E + 22),(2022,1.36E + 22),(2023,1.26E + 22),(2024,1.17E + 22),(2025,1.07E + 22)).

Appendix 4

See Table 20.

Table 20.

Scenario design of variables under different control efforts during the 14th Five-year Plan period

Key variables	Code	Annual planning value					Scenario setting basis
		2020 (%)	2021 (%)	2022 (%)	2023 (%)	2024 (%)
Growth rate of social fixed asset investment	L	17.3	17.5	17.7	17.9	18.1	The GDP growth rate with the strongest correlation(98.39% correlation) with this index is selected as the indirect regulation factor, because there is no specific requirement for the amount of social fixed assets investment. According to the 14th Five-year Plan for national economic and social development of Jining and the outline of long-term goals for 2035 (2021), the average growth rate of Jining's GDP in the next five years is required to be 6%. In order to achieve the goal, the growth rate of social fixed assets investment in the low scheme is set at 17.3%~ 18.1%, After expert’s consultations, the medium and high schemes are 17.5–18.3% and 17.7–18.5%, respectively
	M	17.5	17.7	17.9	18.1	18.3
	H	17.7	17.9	18.1	18.3	18.5
Reduction rate of solid waste emergy	L	3.6	3.8	4.0	4.2	4.4	According to the historical data from 2001 to 2020, especially with reference to the relevant plans and measures of Jining industrial policies from 2011 to 2020, Origin is used to predict the reduction rate of solid waste emergy during 14th Five-year Plan, and the minimum average deceleration in the next five years is determined to be 3.6–4.4%. After consulting relevant experts, the medium and high schemes are set at 3.8–4.6% and 4.0–4.8%, respectively
	M	3.8	4.0	4.2	4.4	4.6
	H	4.0	4.2	4.4	4.6	4.8
Growth rate of grain emergy	L	0.2	0.4	0.6	0.8	1.0	According to the 14th Five-year Plan for national economic and social development of Jining and the outline of long-term goals for 2035, the minimum comprehensive grain production capacity of Jining in 2025 is required to be 480,000 kg, which is consistent with that in 2020. Based on this data and expert’s consultations, the low, medium and high schemes in the next five years are set to be 0.2–1.0%, 1.0–1.8% and 1.8–2.6%, respectively
	M	1.0	1.2	1.4	1.6	1.8
	H	1.8	2.0	2.2	2.4	2.6
Growth rate of raw coal emergy	L	− 3.2	− 3.4	− 3.6	− 3.8	− 4.0%	According to the 14th Five-year Plan for Jining energy development (2022) and the 14th Five-year Plan for Shandong energy development (2021), coal consumption is required to be reduced by 10% in the next five years. Based on this data and expert’s consultations, the low, medium and high schemes in the next five years are set to − 4.0 to − 3.2%, − 3.2 to − 2.4%, − 2.4 to − 1.6%, respectively
	M	− 2.4	− 2.6	− 2.8	− 3.0	− 3.2
	H	− 1.6	− 1.8	− 2.0	− 2.2	− 2.4

Appendix 5 Difficulty quantification

1. The specific share of each key variable is determined by Eq. (2), where Ase_i represents the average solar emergy of each variable (2001–2020), Dar_i represents the difficulty adjustment rate of each variable, and Ds_i represents the specific share of each key variable.

   $$As{e}_i\times Da{r}_i=D{s}_i$$ 2
2. According to the specific share of each key variable, the proportion of each key variable in the sum of the four key variables is calculated by Eq. (3), where W_i represents the proportion of each key variable.

   $$W_i=D{s}_i/\sum _{i=1}^{4}D{s}_i$$ 3
3. ③Calculate the difficulty scores according to Eq. (4), and assign 1, 0.8 and 0.6 (He, 2021) to the corresponding key variables of each scenario, respectively, where P_ij is the difficulty gradient scores of the corresponding key variables of different scenarios, and D_j is the comprehensive quantitative scores of the difficulty of each scenario. The higher the score is, the bigger the difficulty of solution is.

   $$D_j=\sum _{i=1}^4{W}_i\ast P_{\mathit{ij}},j=1,2\dots 19$$ 4

TOPSIS sort

1. Weight determination: UEI, EISD and difficulty are weighted by 40, 30 and 30%, respectively.

2. Isotropy: the index whose effect is proportional to the value is determined by Eq. (5), and the index whose effect is inversely proportional is determined by Eq. (6).

$$y_{\text{ij}}=\frac{x_{\text{ij}}-x_{jmin}}{x_{jmax}-x_{jmin}}$$ 5

$$y_{\text{ij}}=\frac{x_{jmax}-x_{\text{ij}}}{x_{jmax}-x_{jmin}}$$ 6

• (3)
  Normalization:

  $$Z_{\text{ij}}=x_{\text{ij}}/\sqrt{\sum _{i=1}^n{x}_{\text{ij}}^2}$$ 7
• (4)
  Determination of positive and negative ideal solutions

  $$Z-=min(r1j,r2j,...,r\text{mj});Z+=max(r1j,r2j,...,r\text{mj})$$ 8
• (5)
  Determination of Euclidean distance:

  $${\text{D}}_{\text{j}+}=\sqrt{\sum _{i=1}^m{\left(z_{i+}-z_{\mathit{ij}}\right)}^2};D_{j-}=\sqrt{\sum _{i=1}^m{\left(z_{i-}-z_{\mathit{ij}}\right)}^2}$$ 9
• (6)
  Determination of optimal closeness value:

  $$Ci=D_i^{-}/\left(D_i^{-}+D_i^{+}\right)$$ 10

See Table 21.

Table 21.

TOPSIS verification results

Scenarios	EISD	UEI	Difficulty	Close value
M-L–H-H	3.584	0.525	0.709	0.9335
H–L-H–L	3.596	0.525	0.793	0
M-M-H-M	3.513	0.516	0.810	0.5968

Funding

This research is supported by National Key R&D Plan (2019YFC1908100), National Natural Science Foundation (71974116), Shandong Natural Science Foundation (ZR2019MG009), and Shandong Province Social Science Planning Research Project (20CGLJ13), Taishan Scholar Project (tsqn202103010).

Data availability

The datasets used and/or analyzed during the current study are available from the corresponding author on reasonable request.

Declarations

Conflict of interests

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.