Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2023 Feb 10;14(7):1762–1768. doi: 10.1021/acs.jpclett.3c00020

Accurate Determination of the Bandgap Energy of the Rare-Earth Niobate Series

Alka B Garg †,‡, David Vie §, Placida Rodriguez-Hernandez ∥, Alfonso Muñoz ∥, Alfredo Segura ⊥, Daniel Errandonea ⊥,*
PMCID: PMC9940290  PMID: 36762867

Abstract

graphic file with name jz3c00020_0005.jpg

We report diffuse reflectivity measurements in InNbO4, ScNbO4, YNbO4, and eight rare-earth niobates. A comparison with established values of the bandgap of InNbO4 and ScNbO4 shows that Tauc plot analysis gives erroneous estimates of the bandgap energy. Conversely, accurate results are obtained considering excitonic contributions using the Elliot–Toyozawa model. The bandgaps are 3.25 eV for CeNbO4, 4.35 eV for LaNbO4, 4.5 eV for YNbO4, and 4.73–4.93 eV for SmNbO4, EuNbO4, GdNbO4, DyNbO4, HoNbO4, and YbNbO4. The fact that the bandgap energy is affected little by the rare-earth substitution from SmNbO4 to YbNbO4 and the fact that they have the largest bandgap are a consequence of the fact that the band structure near the Fermi level originates mainly from Nb 4d and O 2p orbitals. YNbO4, CeVO4, and LaNbO4 have smaller bandgaps because of the contribution from rare-earth atom 4d, 5d, or 4f orbitals to the states near the Fermi level.

Rare-earth and trivalent metals niobates (MNbO4) have been used for half a century as luminescent materials.1 These compounds crystallize in the monoclinic fergusonite structure (space group I2/a also described as I2/b or C2/c depending on the choice of vectors used to define the unit cell) and have exceptional chemical stability, luminescent characteristics, dielectric properties, and ionic conductivities.2 Because of this, they have been proposed for many different applications. These include lasers, light emitters, capacitors, optical fibers, medical applications, temperature detectors, bioimaging, photocatalysis for both contaminant degeneration and H2 generation, chemically robust hosts for nuclear materials and wastes, ion conductors for lithium batteries, solid oxide fuel cells, etc.2−6 The fact that MNbO4 niobates can be obtained as single crystals7 and nanocrystals8 leads to a great versatility regarding applications. One of the applications of MNbO4 niobates that has been gaining momentum in the past several years is their use for environmentally friendly white-light-emitting diodes (LEDs).9,10 In the past several years, these LEDs have replaced conventional light sources, including Edison’s incandescent lamp and the Hg discharge-based fluorescent lamp. LEDs have many advantages over the other light sources, including lower power consumption, longer lifetime, improved physical robustness, smaller size, and faster switching.11 One of the crucial steps to further optimize white LEDs based on orthoniobates is the precise determination of the energy of their electronic bandgap (Egap), which is still lacking. Experimental and density functional theory efforts have been devoted to it, but the information in the literature2,4,5,12−16 is limited to only some of the rare-earth niobates and, in some cases, contradictory as one can see in Table 1. Notice that bandgap values from 2.9 to 5.04 eV have been reported for orthoniobates. Such a large variation in Egap contradicts the know-systematic of related orthovanadates, which have been extensively studied.17,18 In particular, in YNbO4 (Egap = 3.7–4.96 eV), LuNbO4 (Egap = 4.2–5.04 eV), and GdNbO4 (Egap = 3.48–4.89 eV), there are significant discrepancies in the literature. These facts indicate that a systematic study of the bandgap energy of MNbO4 niobates is timely. Here we report diffuse reflectance measurements in YNbO4, LaNbO4, CeNbO4, SmNbO4, EuNbO4, GdNbO4, DyNbO4, HoNbO4, and YbNbO4. A systematic analysis of the results using an Elliot–Toyozawa model19,20 has allowed us to accurately determine the bandgap energy of the studied compounds. This analysis reveals that the traditional method of determination based on the Tauc plot21 underestimates the bandgap energy. Our method for the determination of Egap has been validated by performing diffuse reflectance measurements in InNbO4 and ScNbO4, giving an excellent agreement with accurate bandgap values determined via luminescence measurements, 4.7 and 4.8 eV, respectively.22,23 From our study, we conclude that most rare-earth niobates have a bandgap energy of 4.73–4.93 eV, with only CeNbO4 (3.25 eV), LaNbO4 (4.35 eV), and YNbO4 (4.55 eV) having narrower bandgaps. The observed results will be explained using available band-structure calculations.

Table 1. Bandgap Energies of Orthoniobates in Electronvoltsa.

compound Elliot fit Tauc plot literature value(s) refs
InNbO4 4.7 4.35 4.7 (22)
ScNbO4 4.8 4.38 4.8 (23)
YNbO4 4.55 4.15 3.7–4.96 (2), (4), (5), (14)
LaNbO4 4.35 3.80 4.0 (13)
CeNbO4 3.25 2.65    
PrNbO4     4.8 (15)
NdNbO4        
SmNbO4 4.95 4.45 4.7–5.0 (33)
EuNbO4 4.73 4.30 3.45 (12)
GdNbO4 4.93 4.50 3.48–4.89 (4), (12)
TbNbO4     2.9 (5)
DyNbO4 4.93 4.55    
HoNbO4 4.93 4.55    
ErNbO4     3.5 (16)
TmNbO4        
YbNbO4 4.90 4.45 3.46 (16)
LuNbO4     4.2–5.04 (2), (4)
Open in a new tab
a

Results obtained using the Elliot model and the Tauc plot are compared with values from the literature.

We start by presenting the results for InNbO4 and ScNbO4, which have been used to establish the method used to determine Egap. Both materials have a monoclinic wolframite-type structure (related to fergusonite), and their bandgap energies have been accurately determined previously.22,23 In Figure 1, we present the absorption spectra F(R∞) obtained from the diffuse reflectance measurements via the Kubelka–Munk transformation,24 which can be considered approximately proportional to the absorption coefficient (α).25 In both InNbO4 and ScNbO4, the absorbance has a sharp absorption onset above 4 GPa, reaching a maximum at 4.7 and 4.75 eV, respectively (see Figure 1). In the literature,22,23 there is an agreement that InNbO4 and ScNbO4 have direct bandgaps with Egap values of 4.7 and 4.8 eV, respectively. However, if we analyze our results using the traditional Tauc plot analysis,21 determining Egap from a linear least-squares fit to zero in [hυF(R∞)]2 versus hυ (as shown in Figure 1), we find values for Egap that are 0.4 eV smaller than the consensus values for Egap in InNbO4 and ScNbO4.22,33 We are not surprised by this fact because this method has been recently challenged.26 The main drawback is that it tends to underestimate the bandgap energy in materials due to sub-bandgap absorption tails related to defects, surface effects, and other phenomena that are reflected in the absorption spectrum as an Urbach tail.26 The fact that the Tauc analysis neglects the presence of excitons could also lead to the underestimation of Egap.27 In materials related to MNbO4 niobates, like InVO4, the application of the traditional Tauc plot analysis leads to underestimations of ≤1.8 eV in the value of Egap.28 Then, it is thus not surprising that in InNbO4 and ScNbO4, it could lead to an underestimation of 0.4 eV. We will show now that this is because of the excitonic contribution to the fundamental absorption spectrum. In InNbO4 and ScNbO4, the steplike absorption present above 4 eV (see Figure 1) is typical of direct transitions in which excitonic effects are observed even at room temperature.29 This can be confirmed by fitting the absorbance obtained by means of the excitonic Elliott–Toyozawa model19,20 in which

graphic file with name jz3c00020_m001.jpg

In this expression, the first term within the brackets is the discrete excitonic contribution and the second term is the continuum contribution. In our fitting, we have assumed that only the fundamental exciton state (j = 1) contributes to the peak, being E1B = Egap – EB, where EB is the exciton binding energy. The only fitting parameters are Egap, EB, and Γ, which take the spectral line width into account. This simple model can reproduce the absorbance of the two compounds as shown in Figure 1. From our fit, we have determined Egap values of 4.7 for InNbO4 and 4.8 eV for ScNbO4. These values are in excellent agreement with the literature.22,23 The obtained EB values are 70 and 120 meV, respectively. These values are comparable to the exciton binding energy of wide bandgap oxides.29 The excellent agreement with the literature and the good quality of fits (using a simple model with only the fundamental exciton) confirm that excitonic contributions are important in the absorbance of MNbO4 niobates. These contributions are caused by interactions between electrons and holes that produce extended states that cause a narrowing of the bandgap.19,20 We consequently will use the same model to analyze all of the rare-earth niobates we have investigated.

Figure 1.

Figure 1

Open in a new tab

(a) F(R∞) spectra of InNbO4 together with the fit used to determine the bandgap energy. The black line is the experiment, the blue line the fit, the green dashed line the continuum contribution, and the red dashed line the excitonic contribution. The arrow shows the maximum of the abosrbance. The bottom plot shows the Tauc plot traditionally used to determine Egap. (b) Same arrangement but for ScNbO4.

Once the correct method for determining the bandgap energy has been established, we will present the results for rare-earth niobates. We will first present the results for SmNbO4, EuNbO4, and GdNbO4. The results of our experiments and the analysis are provided in Figure 2. The three compounds have a sharp absorption edge typical of a direct bandgap. Below that energy, there is a sub-bandgap Urbach tail, typical of MXO430 oxides and weak peaks that can be attributed to internal 4f–4f transitions associated with the lanthanide cation.31,32 Upon application of the Elliott–Toyozawa model, the fundamental absorption edge can be fitted quite well. The determined bandgap energies are 4.95, 4.73, and 4.93 eV for SmNbO4, EuNbO4, and GdNbO4, respectively. The obtained values for the exciton binding energy (see Figure 2) are comparable to the values determined for InNbO4 and ScNbO4. The bandgap energy is very close to the energy of the maximum of F(R∞) as shown in Figure 2. In the figure, we also include a fit using the Tauc plot. The values estimated for Egap with this method are always <0.4 eV compared to the correct value as one can see in Table 1. In this table, we also compare our results with those of previous studies. For SmNbO4, this is the first determination of Egap. The value obtained is consistent with photoluminescence measurements, which constrain the bandgap energy to 4.7–5.0 eV.33 For the case of GdNbO4, our result (4.93 eV) is in excellent agreement with the result of Feng et al. (4.89 eV).12 This indicates that the bandgap of 3.48 eV reported by Hirano et al. is an underestimation. The same can be stated for the bandgap of 3.45 eV determined by the same authors for EuNbO4,12 which is 1.3 eV smaller than the value of Egap determined in the work presented here.

Figure 2.

Figure 2

Open in a new tab

(a) F(R∞) spectra of SmNbO4 (top) together with the fit used to determine the bandgap energy. The black line is the experiment, the blue line the fit, the green dashed line the continuum contribution, and the red dashed line the excitonic contribution. The arrow shows the maximum of the abosrbance. The bottom plot shows the Tauc plot traditionally used to determine Egap. (b) Same arrangement but for EuNbO4. (c) Same arrangement but for GdNbO4.

Figure 3 shows the results obtained for DyNbO4, HoNbO4, and YbNbO4. Again, the three compounds have a very large bandgap (Egap) of ∼4.9 eV (see Figure 3 and Table 1) comparable to that of the widest bandgap semiconductors, for instance, Ga2O3.29,34Figure 3 shows that the bandgap energy is very close to the energy of the maximum of F(R∞). The figure also shows how Egap is underestimated by ∼0.4 eV when Tauc plot analysis is performed. Notice that Egap in the three compounds is very similar to Egap in SmNbO4, EuNbO4, and GdNbO4. As we will explain toward the end of this work, this is a consequence of the fact that the electronic states at the bottom of the conduction band and the top of the valence band are dominated by O 2p states and Nb 4d states. Thus, as a first approximation, the bandgap is determined by the configuration of the NbO4 tetrahedron, which does not change significantly from one compound to the other. The three of them also have the typical Urbach tail and a contribution from absorptions from the 4f levels of the rare-earth atoms. In addition, HoNbO4 and DyNbO4 have in the F(R∞) sub-bandgap sharp absorptions caused by internal 4f–4f transitions of Dy and Ho.32 For DyNbO4 and HoNbO4, this is the first time that the band energy has been reported. In YbNbO4, our result (Egap = 4.9 eV) shows that Egap has been largely underestimated in a previous report.16

Figure 3.

Figure 3

Open in a new tab

(a) F(R∞) spectra of DyNbO4 (top) together with the fit used to determine the bandgap energy. The black line is the experiment, the blue line the fit, the green dashed line the continuum contribution, and the red dashed line is the excitonic contribution. The arrow shows the maximum of the abosrbance. The bottom plot shows the Tauc plot traditionally used to determine Egap. (b) Same arrangement but for HoNbO4. (c) Same arrangement but for YbNbO4.

In Figure 4, we present the results obtained for YNbO4, LaNbO4, and CeNbO4. The figure shows that Tauc analysis always underestimates values of Egap. According to the Elliot–Toyozawa model, YNbO4 has a bandgap energy of 4.56 eV (see Figure 4 and Table 1). This value is 10% smaller than in the previously discussed niobates, and it is comparable to the maximum value of Egap reported in previous studies.2,4,5,14 For LaNbO4, we have determined an Egap of 4.35 eV. The previously determined value was 10% smaller.13 For CeNbO4, this is the first time that Egap has been determined. The obtained value, 3.25 eV, indicates that this compound is the orthoniobate with the smallest bandgap. As in the other studied compounds, in the three compounds presented in Figure 4, the bandgap energy is very close to the energy of the maximum of F(R∞).

Figure 4.

Figure 4

Open in a new tab

(a) F(R∞) spectra of YNbO4 (top) together with the fit used to determine the bandgap energy. The black line is the experiment, the blue line the fit, the green dashed line the continuum contribution, and the red dashed line the excitonic contribution. The arrow shows the maximum of the abosrbance. The bottom plot shows the Tauc plot traditionally used to determine Egap. (b) Same arrangement but for LaNbO4. (c) Same arrangement but for CeNbO4.

It is interesting to stress that the bandgap energy of rare-earth niobates follows a very similar trend as observed for rare-earth vanadates.17,35,36 In the vanadates, except for LaVO4 and CeVO4, all of the members of the family have a bandgap close to 3.8 eV. LaVO4 has a bandgap of 3.5 eV, and CeVO4 a bandgap of 3.2 eV. The 3.8 eV bandgap is a consequence of the fact that states near the Fermi level are dominated by O 2 p and V 3 d states. In the other compounds, the bandgap is reduced due to the contribution of 5d or 4f electrons from La and Ce. A similar picture provides a qualitative explanation for the results reported here. The band structure and electronic density of states (DOS) of most niobates have been reported in the literature.2,13,37−39 They are qualitatively similar to the band structure and DOS of vanadates.35 In particular, the band structures of niobates and vanadates have a similar topology. The states near the Fermi level in niobates have a composition qualitatively similar to that in vanadates, being dominated by O 2p and Nb 4d (instead of V 3d) states. According to band-structure calculations, the studied niobates have an indirect gap, but the difference with the direct bandgap is <0.1 eV.2,13,37−39 Then the absorption edge will be dominated by the direct bandgap and F(R∞) can be analyzed assuming a direct bandgap as it has been done in this work.

To provide a more quantitative discussion, we will focus on LaNbO4, CeNbO4, EuNbO4, and YbNbO4,38 which are representative of the family of fergusonite-type niobates. In the four compounds, the minimum of the conduction band (CB) and the maximum of the valence band (VB) are located at the V and Γ points, respectively, of the Brillouin zone. However, there is a Γ–Γ direct bandgap very close in energy. According to the electronic DOS, in EuNbO4 and YbNbO4 the valence-band maximum is dominated by O 2p states. This behavior is typical of most wide bandgap oxides. On the contrary, the conduction-band minimum is predominantly dominated by Nb 4d states with a small contribution of O 2p states. This molecular orbital composition is analogous to what happens in vanadates with V 3d and O 2p states35 and in other ternary oxides like tungstates (molybdates) with W (Mo) 5d (4d) and O 2p states.40 Consequently, the configuration of the NbO4 tetrahedron, the coordination polyhedron of Nb in fergusonite, will have a determining role in the evaluation of the bandgap energy. Interestingly, the NbO4 tetrahedron is not modified significantly in going from one compound to the other, changing the average Nb–O bond distance by <1% along the series of rare-earth niobates. Thus, it is not surprising that most members of this family have a very similar Egap. It is also not surprising that these compounds have a bandgap energy comparable to that of Nb2O5 (Egap = 5.1 eV) in which states at the bottom of the CB and top the VB are also dominated by the hybridization of O 2p and Nb 4d states, and O 2p states, respectively.41 The reason for the bandgap energy closure of LaNbO4 and CeNbO4 is the fact that these are the only two compounds in which the lanthanide orbitals contribute to the conduction band. This is why LaNbO4 and CeNbO4 are the niobates with the smallest bandgap within rare-earth niobates. Exactly the same phenomenon happens in LaVO4 and CeVO4, which are the vanadates with the smallest bandgap energy within the family of rare-earth vanadates.17

In summary, herein we report diffuse reflectance measurements for rare-earth niobates and propose a method for accurately determining their bandgap energy. We have shown that in most previous studies the bandgap energy has been underestimated. The bandgap energies of the studied compounds are 3.25 eV for CeNbO4, 4.35 eV for LaNbO4, 4.5 eV for YNbO4, and 4.73–4.93 eV for SmNbO4, EuNbO4, GdNbO4, DyNbO4, HoNbO4, and YbNbO4. We also provide an explanation of the experimental results based on density functional calculations. The reported information is crucial for technological applications of rare-earth niobates. To conclude, we add two comments. (1) If the excitonic peak is not observed, obviously the Elliot–Toyozawa model cannot be accurately used. In such a case, the Tauc method can be used, but keeping in mind that the obtained energy is an energy that is always smaller than real bandgap energy, being sensitive to the thickness of the sample.29 (2) If the bandgap is indirect, the contribution of an indirect transition to the absorption coefficient is much weaker than that of an allowed direct transition and can be measured only when the indirect gap is situated at least 0.2–0.3 eV below the direct one.42 In such cases, the bandgap energy could be determined assuming for the absorption coefficient a dependence on the square root of the energy: 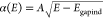Inline graphic, where A is a scaling parameter and Egapind is the bandgap energy of the indirect gap.43

Methods

Experimental Details. Polycrystalline rare-earth niobates were synthesized by the commonly used solid state reaction technique.44 Starting metal oxides, R2O3 and Nb2O5 (purity of >99.9%), were predried to remove any moisture or organic impurities. These dried binary oxides were weighed in a stoichiometric (1:1) ratio, hand mixed with a mortar and pestle, cold pressed into cylinders of 12.5 mm in diameter and 5 mm in height, and fired at 1200 °C for 24 h in a box-type programmable resistive furnace. These pellets were further sintered at 1300 °C for 48 h. Single phase formation of the compounds was confirmed by angle-dispersive powder X-ray diffraction. We confirmed that all synthesized rare-earth niobates crystallize in the fergusonite structure. For measurements of ScNbO4 and InNbO4, we used the same samples used in previous studies.22,23 For the diffuse reflectance measurements, powder samples were manually ground in an agate mortar, placed in the sample holder, and supported with a quartz window. Measurements were carried out on a Shimazdu UV–vis 2501PC spectrophotometer equipped with an integrating sphere for diffuse reflectance measurements. BaSO4 was used as a reference material and for background measurement. The spectral range covered by measurements was 220–900 nm, with a resolution of 1 nm and a spectral bandwidth of 5 nm. The spectra recorded in %R were transformed into absorbance spectra using the Kubelka–Munk function.24 The plotted F(R∞) spectra are proportional to the absorption coefficient and can be interpreted with the same physical model.25

Acknowledgments

This study was supported by the MALTA Consolider Team network (Project RED2018-102612-T) financed by MINECO/AEI/0.13039/501100003329, I+D+i Project PID2019-106383GB-41/43 financed by MCIN/AEI/10.13039/501100011033, and Project PROMETEO CIPROM/2021/075 (GREENMAT) financed by Generalitat Valenciana. This study forms part of the Advanced Materials Programme and was supported by MCIN with funding from European Union NextGenerationEU (PRTR-C17.I1) and by Generalitat Valenciana under Grant MFA/2022/007. The authors thank Prof. Ana Costero of Departamento de Quimica Orgánica at Universitat de València (València, Spain) for letting us use the Shimazdu UV–vis 2501PC spectrophotometer for diffuse reflectance measurements.

Author Contributions

A.B.G. synthesized the samples. D.V. performed the diffuse reflectance measurements. D.E. designed the study and carried out the data analysis. All authors contributed to the discussion, writing, and proofreading and have given approval to the final version of the manuscript.

The authors declare no competing financial interest.

References

  1. Blasse G.; Bril A. Luminescence Phenomena in Compounds with Fergusonite Structure. J. Lumin. 1970, 3, 109–131. 10.1016/0022-2313(70)90011-6. [DOI] [Google Scholar]
  2. Ding D.; Zhang H.; Liu W.; Sun D.; Zhang Q. Experimental and First Principle Investigation the Electronic and Optical Properties of YNbO4 and LuNbO4 Phosphors. J. Mater. Science: Materials in Electronics 2018, 29, 11878–11885. 10.1007/s10854-018-9288-5. [DOI] [Google Scholar]
  3. Graça M. P. F.; Peixoto M. V.; Ferreira N.; Rodrigues J.; Nico C.; Costa F. M.; Monteiro T. Optical and Dielectric Behaviour of EuNbO4 Crystals. J. Mater. Chem. C 2013, 1, 2913–2919. 10.1039/c3tc00793f. [DOI] [Google Scholar]
  4. Feng Z.; Lou B. B.; Chen Q.; Yin M.; Ma C. G.; Duan C. K. Self-Activated and Bismuth-Related Photoluminescence in Rare-Earth Vanadate, Niobate, and Tantalate Series: A First-Principles Study. Inorg. Chem. 2021, 60, 16614–16625. 10.1021/acs.inorgchem.1c02508. [DOI] [PubMed] [Google Scholar]
  5. Hirano M.; Dozono H. Hydrothermal Formation and Characteristics of Rare-Earth Niobate Phosphors and Solid Solutions between YNbO4 and TbNbO4. Mater. Chem. Phys. 2014, 143, 860–866. 10.1016/j.matchemphys.2013.10.025. [DOI] [Google Scholar]
  6. Nyman M.; Rodriguez M. A.; Rohwer L. E. S.; Martin J. E.; Waller M.; Osterloh F. E. Unique LaTaO4 Polymorph for Multiple Energy Applications. Chem. Mater. 2009, 21, 4731–4737. 10.1021/cm9020645. [DOI] [Google Scholar]
  7. Fulle K.; McMillen C. D.; Sanjeewa L. D.; Kolis J. W. Hydrothermal Chemistry and Growth of Fergusonite-type RENbO4 (RE = La–Lu, Y) Single Crystals and New Niobate Hydroxides. Cryst. Growth Des. 2016, 16, 4910–4917. 10.1021/acs.cgd.6b00466. [DOI] [Google Scholar]
  8. Hirano M.; Dozono H. Direct Formation and Luminescence Properties of Yttrium Niobate YNbO4 Nanocrystals via Hydrothermal Method. J. Am. Ceram. Soc. 2013, 96, 3389–3393. 10.1111/jace.12595. [DOI] [Google Scholar]
  9. Liu X.; Lü Y.; Chen C.; Luo S.; Zeng Y.; Zhang X.; Shang M.; Li C.; Lin J. Synthesis and Luminescence Properties of YNbO4:A (A = Eu3+ and/or Tb3+) Nanocrystalline Phosphors via a Sol–Gel Process. J. Phys. Chem. C 2014, 118, 27516–27524. 10.1021/jp508773t. [DOI] [Google Scholar]
  10. Lü Y.; Tang X.; Yan L.; Li K.; Liu X.; Shang M.; Li C.; Lin J. Synthesis and Luminescent Properties of GdNbO4:RE3+ (RE = Tm, Dy) Nanocrystalline Phosphors via the Sol–Gel Process. J. Phys. Chem. C 2013, 117, 21972–21980. 10.1021/jp4086415. [DOI] [Google Scholar]
  11. Lin C. C.; Liu R. S. Advances in Phosphors for Light-emitting Diodes. J. Phys. Chem. Lett. 2011, 2, 1268–1277. 10.1021/jz2002452. [DOI] [PubMed] [Google Scholar]
  12. Hirano M.; Ishikawa K. Direct Synthesis of Nanocrystalline GdNbO4 and GdNbO4-Based Phosphors Doped with Eu3+ through Hydrothermal Route. J. Cer. Soc. Japan 2016, 124, 42–48. 10.2109/jcersj2.15193. [DOI] [Google Scholar]
  13. Arai M.; Wang Y. X.; Kohiki S.; Matsuo M.; Shimooka H.; Shishido T.; Oku M. Dielectric Property and Electronic Structure of LaNbO4. Jpn. J. Appl. Phys. 2005, 44, 6596–6599. 10.1143/JJAP.44.6596. [DOI] [Google Scholar]
  14. Lee S. K.; Chang H.; Han C. H.; Kim H. J.; Jang H. G.; Park H. D. Electronic Structures and Luminescence Properties of YNbO4 and YNbO4:Bi. J. Solid State Chem. 2001, 156, 267–273. 10.1006/jssc.2000.8941. [DOI] [Google Scholar]
  15. Peixoto J. C.; Dias A.; Matinaga F. M.; Siqueira K. P. F. Luminescence Properties of PrNbO4 and EuNbO4 Orthoniobates and Investigation of Their Structural Phase Transition by High-Temperature Raman Spectroscopy. J. Lumin. 2021, 238, 118284. 10.1016/j.jlumin.2021.118284. [DOI] [Google Scholar]
  16. Zhang Z.; Guo L.; Sun H.; Peng D.; Zou H.; Sun N.; Zhang Q.; Hao X. Rare Earth Orthoniobate Photochromics with Self-Activated Upconversion Emissions for High-Performance Optical Storage Applications. J. Mater. Chem. C 2021, 9, 13841–13850. 10.1039/D1TC02987H. [DOI] [Google Scholar]
  17. Errandonea D. High Pressure Crystal Structures of Orthovanadates and Their Properties. J. Appl. Phys. 2020, 128, 040903. 10.1063/5.0016323. [DOI] [Google Scholar]
  18. Errandonea D.; Garg A. B. Recent Progress on the Characterization of the High-Pressure Behaviour of AVO4 Orthovanadates. Prog. Mater. Science 2018, 97, 123–169. 10.1016/j.pmatsci.2018.04.004. [DOI] [Google Scholar]
  19. Elliott R. J. Intensity of Optical Absorption by Excitons. Phys. Rev. 1957, 108, 1384–1389. 10.1103/PhysRev.108.1384. [DOI] [Google Scholar]
  20. Toyozawa Y. Theory of Line-Shapes of the Exciton Absorption Bands. Prog. Theor. Phys. 1958, 20, 53–81. 10.1143/PTP.20.53. [DOI] [Google Scholar]
  21. Tauc J. Optical Properties and Electronic Structure of Amorphous Ge and Si. Mater. Res. Bul. 1968, 3, 37–46. 10.1016/0025-5408(68)90023-8. [DOI] [Google Scholar]
  22. Botella P.; Enrichi F.; Vomiero A.; Muñoz-Santiuste J. E.; Garg A. B.; Arvind A.; Manjón F. J.; Segura A.; Errandonea D. Investigation on the Luminescence Properties of InMO4 (M = V5+, Nb5+, Ta5+) Crystals Doped with Tb3+ or Yb3+ Rare Earth Ions. ACS Omega 2020, 5, 2148–2158. 10.1021/acsomega.9b02862. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Ouahrani T.; Garg A. B.; Rao R.; Rodríguez-Hernández P.; Muñoz A.; Badawi M.; Errandonea D. On the High-Pressure Properties of Wolframite-type ScNbO4. J. Phys. Chem. C 2022, 126, 4664–4676. 10.1021/acs.jpcc.1c10483. [DOI] [Google Scholar]
  24. Kubelka P.; Munk F. An Article on Optics of Paint Layers. Z. Technol. Phys. 1931, 12, 593–603. [Google Scholar]
  25. Dolgonos A.; Mason T. O.; Poeppelmeier K. R. Direct Optical Bandgap Measurement in Polycrystalline Semiconductors: A Critical Look at the Tauc Method. J. Solid State Chem. 2016, 240, 43–48. 10.1016/j.jssc.2016.05.010. [DOI] [Google Scholar]
  26. Makuła P.; Pacia M.; Macyk W. How to Correctly Determine the Bandgap Energy of Modified Semiconductor Photocatalysts Based on UV–Vis Spectra. J. Phys. Chem. Lett. 2018, 9, 6814–6817. 10.1021/acs.jpclett.8b02892. [DOI] [PubMed] [Google Scholar]
  27. Ruf F.; Aygüler M. F.; Giesbrecht N.; Rendenbach B.; Magin A.; Docampo P.; Kalt H.; Hetterich M. Temperature-Dependent Studies of Exciton Binding Energy and Phase-Transition Suppression in (Cs,FA,MA)Pb(I,Br)3 Perovskites. APL Mater. 2019, 7, 031113. 10.1063/1.5083792. [DOI] [Google Scholar]
  28. Botella P.; Errandonea D.; Garg A. B.; Rodríguez-Hernández P.; Muñoz A.; Achary S. N.; Vomiero A. High-Pressure Characterization of the Optical and Electronic Properties of InVO4, InNbO4, and InTaO4. SN Appl. Sci. 2019, 1, 389. 10.1007/s42452-019-0406-7. [DOI] [Google Scholar]
  29. Segura A.; Artús L.; Cuscó R.; Goldhahn R.; Feneberg M. Bandgap of Corundum-like α–Ga2O3 Determined by Absorption and Ellipsometry. Phys. Rev. Mater. 2017, 1, 024604. 10.1103/PhysRevMaterials.1.024604. [DOI] [Google Scholar]
  30. Errandonea D.; Muñoz A.; Rodríguez-Hernández P.; Proctor J. E.; Sapiña F.; Bettinelli M. Theoretical and Experimental Study of the Crystal Structures, Lattice Vibrations, and Band Structures of Monazite-Type PbCrO4, PbSeO4, SrCrO4, and SrSeO4. Inorg. Chem. 2015, 54, 7524–7535. 10.1021/acs.inorgchem.5b01135. [DOI] [PubMed] [Google Scholar]
  31. Carnall W. T.; Crosswhite H.; Crosswhite H. M.. Energy Level Structure and Transition Probabilities in the Spectra of the Trivalent Lanthanides in LaF3. Argonne National Laboratory: Argonne, IL, 1978. [Google Scholar]
  32. Bandiello E.; Errandonea D.; Piccinelli F.; Bettinelli M.; Díaz-Anichtchenko D.; Popescu C. Characterization of Flux-Grown SmxNd1–xVO4 Compounds and High-Pressure Behavior for x = 0.5. J. Phys. Chem. C 2019, 123, 30732–30745. 10.1021/acs.jpcc.9b09473. [DOI] [Google Scholar]
  33. Nico C.; Soares M. R. N.; Costa F. M.; Monteiro T.; Graça M. P. F. Structural, Optical, and Electrical Properties of SmNbO4. J. Appl. Phys. 2016, 120, 051708. 10.1063/1.4958953. [DOI] [Google Scholar]
  34. Chi Z.; Asher J. J.; Jennings M. R.; Chikoidze E.; Pérez-Tomás A. Ga2O3 and Related Ultra-Wide Bandgap Power Semiconductor Oxides: New Energy Electronics Solutions for CO2 Emission Mitigation. Materials 2022, 15, 1164. 10.3390/ma15031164. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Panchal V.; Errandonea D.; Segura A.; Rodríguez-Hernández P.; Muñoz A.; Lopez-Moreno S.; Bettinelli M. The Electronic Structure of Zircon-Type Orthovanadates: Effects of High-Pressure and Cation Substitution. J. Appl. Phys. 2011, 110, 043723. 10.1063/1.3626060. [DOI] [Google Scholar]
  36. Muñoz-Santiuste J. E.; Lavín V.; Rodríguez-Mendoza U. R.; Ferrer-Roca Ch.; Errandonea D.; Martínez-García D.; Rodríguez-Hernández P.; Muñoz A.; Bettinelli M. Experimental and Theoretical Study on the Optical Properties of LaVO4 Crystals under Pressure. Phys. Chem. Chem. Phys. 2018, 20, 27314–27328. 10.1039/C8CP04701D. [DOI] [PubMed] [Google Scholar]
  37. Ding S.; Zhang H.; Zhang Q.; Chen Y.; Dou R.; Peng F.; Liu W.; Sun D. Experimental and First Principle Study of the Structure, Electronic, Optical, and Luminescence Properties of M-type GdNbO4 Phosphor. J. Sol. State Chem. 2018, 262, 87–93. 10.1016/j.jssc.2018.03.011. [DOI] [Google Scholar]
  38. Litimein F.; Khenata R.; Gupta S. K.; Murtaza G.; Reshak A. H.; Bouhemadou A.; Bin Omran S.; Yousaf M.; Jha P. K. Structural, Electronic, and Optical Properties of Orthorhombic and Triclinic BiNbO4 Determined via DFT Calculations. J. Mater. Sci. 2014, 49, 7809–7818. 10.1007/s10853-014-8491-x. [DOI] [Google Scholar]
  39. Materials Project web site. https://materialsproject.org/.
  40. Liang A.; Turnbull R.; Rodríguez-Hernandez P.; Muñoz A.; Jasmin M.; Shi L. T.; Errandonea D. General Relationship Between the Bandgap Energy and Iodine-Oxygen Bond Distance in Metal Iodates. Phys. Rev. Materials 2022, 6, 044603. 10.1103/PhysRevMaterials.6.044603. [DOI] [Google Scholar]
  41. Sathasivam S.; Williamson B. A. D.; Althabaiti S. A.; Obaid A. Y.; Basahel S. N.; Mokhtar M.; Scanlon D. O.; Carmalt C. J.; Parkin I. P. Chemical Vapor Deposition Synthesis and Optical Properties of Nb2O5 Thin Films with Hybrid Functional Theoretical Insight into the Band Structure and Bandgaps. ACS Appl. Mater. Interfaces 2017, 9, 18031–18038. 10.1021/acsami.7b00907. [DOI] [PubMed] [Google Scholar]
  42. Pellicer-Porres J.; Manjon F. J.; Segura A.; Muñoz V.; Power C.; Gonzalez J. Optical Absorption in GaTe under High Pressure. Phys. Rev. B 1999, 60, 8871–8877. 10.1103/PhysRevB.60.8871. [DOI] [Google Scholar]
  43. Manjón F.-J.; Errandonea D.; Segura A.; Muñoz V.; Tobías G.; Ordejón P.; Canadell E. Experimental and Theoretical Study of Band Structure of InSe and In. Phys. Rev. B 2001, 63, 125330. [Google Scholar]
  44. Garg A. B.; Rao R.; Errandonea D.; Pellicer-Porres J.; Martinez-Garcia D.; Popescu C. Pressure-Induced Instability of the Fergusonite Phase of EuNbO4 Studied by In Situ Raman Spectroscopy, X-ray Diffraction, and Photoluminescence Spectroscopy. J. Appl. Phys. 2020, 127, 175905. 10.1063/5.0004757. [DOI] [Google Scholar]

Articles from The Journal of Physical Chemistry Letters are provided here courtesy of American Chemical Society

RESOURCES