Abstract
Purpose
This study developed machine learning (ML) classifiers of postoperative corneal endothelial cell images to identify postkeratoplasty patients at risk for allograft rejection within 1 to 24 months of treatment.
Methods
Central corneal endothelium specular microscopic images were obtained from 44 patients after Descemet membrane endothelial keratoplasty (DMEK), half of whom had experienced graft rejection. After deep learning segmentation of images from all patients’ last and second-to-last imaging, time points prior to rejection were analyzed (175 and 168, respectively), and 432 quantitative features were extracted assessing cellular spatial arrangements and cell intensity values. Random forest (RF) and logistic regression (LR) models were trained on novel-to-this-application features from single time points, delta-radiomics, and traditional morphometrics (endothelial cell density, coefficient of variation, hexagonality) via 10 iterations of threefold cross-validation. Final assessments were evaluated on a held-out test set.
Results
ML classifiers trained on novel-to-this-application features outperformed those trained on traditional morphometrics for predicting future graft rejection. RF and LR models predicted post-DMEK patients' allograft rejection in the held-out test set with >0.80 accuracy. RF models trained on novel features from second-to-last time points and delta-radiomics predicted post-DMEK patients’ rejection with >0.70 accuracy. Cell-graph spatial arrangement, intensity, and shape features were most indicative of graft rejection.
Conclusions
ML classifiers successfully predicted future graft rejections 1 to 24 months prior to clinically apparent rejection. This technology could aid clinicians to identify patients at risk for graft rejection and guide treatment plans accordingly.
Translational Relevance
Our software applies ML techniques to clinical images and enhances patient care by detecting preclinical keratoplasty rejection.
Keywords: cornea, machine learning, feature extraction, image processing
Introduction
The determination and monitoring of endothelial cell density (ECD) changes following keratoplasty as a surrogate measure for graft success and risk for future graft failure has been one of the first uses of specular microscopy since invented by Maurice in 1968.1 With the ability to determine the central corneal ECD from both the donor and subsequently postoperatively with longitudinal studies in the recipient, numerous studies have been performed on the pattern and degree of endothelial cell loss (ECL) as well as the factors (donor, recipient, operative, postoperative) influencing ECL following penetrating keratoplasty (PKP),2–5 Descemet stripping automated endothelial keratoplasty (DSAEK),6–12 and Descemet membrane endothelial keratoplasty (DMEK).13–18 There, however, has been limited use of this imaging tool to study the impact of graft rejection on ECL following these procedures, much less its use to predict future clinical graft rejection episodes prior to rejection being clinically apparent (conjunctival injection, keratoprecipitates, endothelial rejection line, increased corneal thickness, and frank corneal edema).
One of the major limitations in studying the impact of graft rejection on ECL are that many endothelial rejection episodes are asymptomatic. In a study conducted by Price et al.,19 of the included 14 rejection cases, 11 (79%) remained asymptomatic and were diagnosed only in their second year of follow-up once keratoprecipitates were detectable. This, however, was only feasible due to frequent imaging follow-ups at 1, 3, 6, and 12 months post-DMEK. Similar results were reported by Hos et al.,20 in which 7 of the 12 (60%) rejection cases were asymptomatic, and Baydoun et al.,21 in which 4 of the 17 (25%) rejection cases were asymptomatic. Thus, it is difficult to assess the timing of a graft rejection due to asymptomatic grafts despite increased ECL, the absence or infrequent endothelial imaging postoperatively, and the inability to perform imaging once the graft has become edematous. Nevertheless, Stulting et al.22 reported a lower ECD in surviving DSAEK grafts at 3 years in the Cornea Preservation Time Study, while noting that graft rejection was not a leading cause of DSAEK failure. Li et al.23 found a similar result after annually imaging 615 eyes from patients with Fuch's dystrophy. The 45 cases of graft rejection saw greater decline in median percentage of ECD across all imaging time points compared to cases without rejection. Ohguro et al.24 expanded corneal endothelium imaging evaluation from the central region to include the periphery. It was found that among 20 corneas that had undergone penetrating keratoplasty, 10 experienced allograft rejection, demonstrating a significant decrease in ECD in both the central and the peripheral regions.
An intriguing use of specular microscopy to monitor the impact of graft rejection on subsequent graft failure was a study by Monnereau et al.25 These authors demonstrated a potential for identifying post-DMEK patients at risk for a graft rejection with a qualitative grading scale that evaluated cell morphology and arrangement. It proved effective as the scores between rejection and control patients were significantly different during the study's duration.25 Their observational findings by trained technicians raised the possibility that a machine learning approach to the analysis of prospectively acquired endothelial imaging could automate this observational approach. Thus, the prospect of the detection of early events in the rejection process prior to clinical rejection symptoms and signs is raised. These findings could then potentially change practices for postoperative management with more frequent endothelial imaging and lead to earlier intervention strategies to prevent further endothelial damage and ultimate graft failure.
Using the same cohort as that reported by Monnereau et al.,25 we will extract quantitative features from semiautomatically segmented post-DMEK endothelial cell images and use machine learning to predict at-risk patients prior to rejection. In addition to using single time point images, we propose utilizing techniques suggested by Chang et al.,26 Zhang et al.,27 and Rao et al.28 to incorporate delta-radiomics or the change in features between two time points as predictive measures for adverse outcomes.
Method
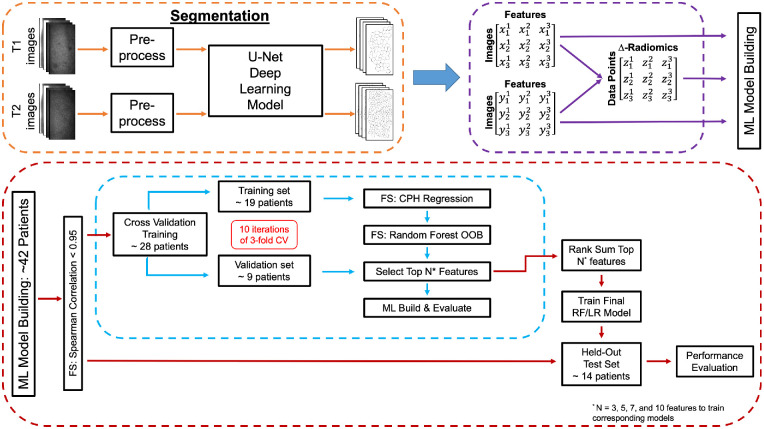
Figure 1 outlines the overall workflow of this study.
Figure 1.
Rejection keratoplasty prediction workflow. Images taken at the second-to-last imaging time point and last imaging time point prior to rejection (T1 and T2, respectively) are segmented by a U-Net deep learning model. Using cell segmentations, 432 features are extracted from each image. The delta-radiomics data set is calculated by taking the difference of the T2 and T1 features and dividing this difference by the time duration between the two sets of images. All three data sets are then split, with two-thirds of patient eyes used for training and one-third of patient eyes for held-out for testing. The training set underwent three feature selection (FS) techniques and 10 iterations of three-fold cross-validation to build RF and LR machine learning (ML) models. The top 3, 5, 7, and 10 features were collected from each of the three time point data sets to train final RF and LR models. Model prediction performance (e.g., accuracy) was evaluated on the patient eyes held-out test set. In total, 120 cross-validation models were trained and 8 final models were developed for postkeratoplasty rejection prediction.
Data Cohort
The Netherlands Institute for Innovative Ocular Surgery (NIIOS, Rotterdam, The Netherlands) provided 925 central endothelial cell images from 44 patient eyes that had undergone a DMEK. The criteria of eye and follow-up image selection were described in Baydoun et al.,21 in which 1077 DMEK eyes were analyzed, of which only 27 experienced allograft rejection. Five of the rejection eyes from the Baydoun et al.21 data set were excluded from their publication data as well as the data set included in the rejection data set of this study due to various reasons (poor image quality due to congenital glaucoma and rejection prior to imaging). These cases were more advanced rejection cases than the focus of this study, in which we were seeking to discover early rejection prediction prior to the onset of clinical symptoms. Our final set included 22 rejection eyes, which were age and gender matched to 22 control eyes (i.e., eyes undergoing DMEK but without rejection at any time postoperatively) for the study. The images were acquired using a Topcon SP3000 specular microscope (Topcon Europe Medical, Capelle a/d IJsse, The Netherlands) at multiple and various time points following keratoplasty ranging from 1 to 123 months. All images were deidentified and handled in a method approved by the University Hospitals Cleveland Medical Center (Cleveland, OH, USA) Institutional Review Board.
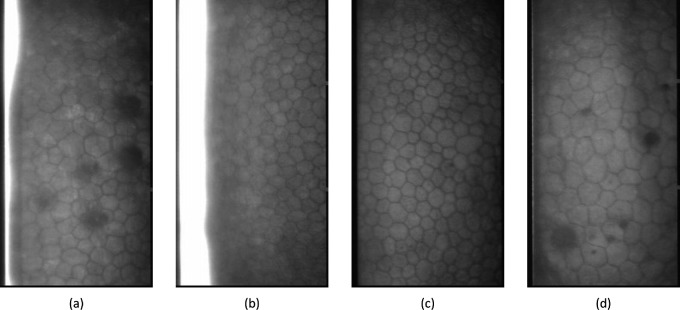
Images were normalized to a 0.8-µm2 pixel resolution resulting in dimensions of 675 × 359 pixels. Between two and six images were available for the rejection eyes and one per control eye at each imaging time point. We had 175 images from eyes with rejection at the last (time point 2 or T2) and second-to-last (time point 1 or T1) imaging time points prior to rejection. Approximately three to four images were available for each rejection eye at each time point. A similar number of images were selected from each control eye (DMEK without subsequent rejection) to create a balanced data set. For the 22 rejection eyes, their last imaging time point prior to rejection occurred between 3 and 78 months postkeratoplasty. To match this time range, four control images from each eye were randomly selected between 3 and 78 months postkeratoplasty. For the second-to-last time point, rejection eyes had images taken between 2 and 12 months prior to their corresponding last imaging time point. Four images taken 2 to 12 months prior to their corresponding first imaging time points were randomly selected from each control eye. In essence, all “last imaging time point” images were taken 3 to 78 months postkeratoplasty. All “second-to-last imaging time point” images were taken 1 to 72 months postkeratoplasty. This selection process collected 168 control eye endothelial cell (EC) images. Figure 2 shows four example images from this data set taken at multiple times postkeratoplasty. Each image varies in cell size and shape, physiologic findings, and image quality. Note that some images in the data set have columns of very bright or very dark pixels lacking available cellular data.
Figure 2.
Example endothelial cell images taken at (a) 1 month, (b) 3 months, (c) 86 months, and (d) 54 months post-Descemet membrane endothelial keratoplasty demonstrating varying cell size, shape, arrangement, and image quality.
Deep Learning Segmentation
Prior to cell-by-cell feature extraction, cell border segmentation was performed using a modified process described in Joseph et al.29 Image columns and rows were cropped if their pixel intensity sum was less than 22% of the image's column and row pixel intensity mean sum, respectively. They were also cropped if their pixel intensity sum was greater than 110,000. Next, the illumination gradient was removed from each image by subtracting the image's background and normalizing intensity between 0 and 255. This was followed by U-Net deep learning segmentation from a model trained as previously published.29 The final U-Net binary segmentations were manually edited using a guided software tool.30 Approximately 5 to 10 corrections were made per image to fine-tune the predictions.
Feature Extraction
A feature bank of 432 features that represent cellular and image intensity distribution, textures, and shape parameters was developed. See Supplementary 1 for the list of 432 features. Cell intensity average, maximum, minimum, standard deviation, and kurtosis were computed. Histogram features were computed where the range of pixel values was mapped to [0, 255] before being split into 25 bins and tallied as feature values. These values were multiplied by a weighting factor that took into consideration the size of each cell with respect to the segmented area. Prior to and after weighting the features, the feature averages were computed. The number of outlier pixels in each cell's intensity distribution was counted. The standard deviation of the above computations was also calculated. The same features were extracted for the entire segmented area. Finally, the percentage of image pixel intensities between each bin of the histogram features was recorded.
Texture features included cell entropy and cell skewness. Shape features included cell area, cell perimeter, and cell circularity. The average, standard deviation, and kurtosis were taken for each of these features. Like the intensity distributions, an image's distribution of cell area, cell perimeter, and cell circularity was analyzed. The number of cells was counted within each of the 25 bins created for cells areas between 0 and 2000 pixels, cell perimeters between 0 and 200 pixels, and cell circularity between 0.75 and 2.0. The number of cells was recorded with areas greater than 2000, perimeters greater than 200, and circularity less than 0.75 or greater than 2.0.
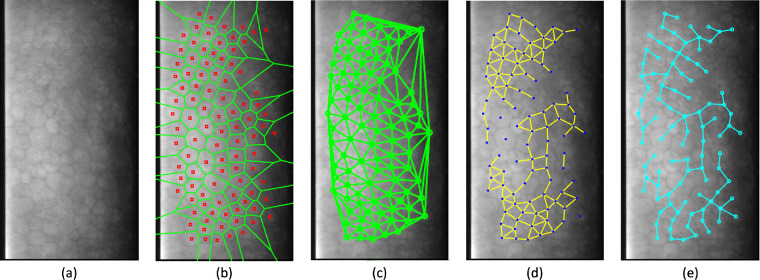
Our feature bank also included cell-graph features, which have shown promising results.31,32 Cell-graph features provide quantitative analysis of cellular spatial arrangement in images. Figure 3 represents the following cell graphs from which we extracted several features: Voronoi tessellations, Delaunay triangulations, cell-cluster graphs, and minimum spanning tree. The extracted features included statistical metrics of Voronoi tessellation area, perimeter, and chord lengths; Delaunay triangulation area and side lengths; and minimum spanning tree edge lengths. Also, from Voronoi tessellations, we acquired features about the number of polygons in each image, as well as the average, standard deviation, and disorder of distance between one cell centroid and its closest three, five, and seven nearest neighbors. Other features calculated from Voronoi tessellations included the average, standard deviation, and disorder of number of nearest neighbors within 10, 20, 30, 40, and 50 pixels of each cell centroid in each image. Features extracted from cell-cluster graphs included the number of nodes, edges, isolated nodes with no connections, center nodes with multiple connections, end nodes with one connection, and other clustering features. Finally, three traditional morphometrics—ECD, coefficient of variation (CV), and percentage of hexagonal cells (HEX)—were computed and compared to novel features for predictive ability.
Figure 3.
Graphs used to compute cell arrangement features. (a) Example post-Descemet membrane endothelial keratoplasty endothelial cell images with (b) Voronoi tessellation, (c) Delaunay tessellation, (d) cluster graph, and (e) minimum spanning tree feature graph overlays.
These features were extracted from single imaging time points. The predictive value of delta-radiomics or the change in features between two imaging time points was also investigated. Since pairs of images from a control eye was already formed via time-matching image selection mentioned in Data Cohort, the delta-radiomics were calculated using Equation (1).
| (1) |
Ftime point 2 is the feature from the last imaging time point image, Ftime point 1 is the feature from the second-to-last imaging time point image, ∆T is the time difference between the two images in months, and ∆-Radiomics is the resulting change in feature over time. For rejection eyes, every combination of images between the two time points was paired to compute the delta-radiomics. Thus, 330 delta-radiomic data points from 19 rejection eyes and 80 delta-radiomic data points from 22 control eyes were computed.
Machine Learning Model Prediction
Four machine learning models were developed from four feature data sets: time point 1 data, time point 2 data, delta-radiomics, and traditional morphometrics. Risk prediction models were trained via standard machine learning practices starting with cross-validation training, feature selection, model building, and held-out test set evaluation. Cross-validation training involved splitting the data into a training data set and a held-out test set. Two-thirds of the eyes and their corresponding images or data points were randomly selected for the training data set, and the remaining one-third made up the held-out test set. We ensured that the training and testing set maintained the same proportion of control and rejection eyes as the overall data set. Then, 10 iterations of three-fold cross-validation were performed by splitting the training data into two-thirds training and one-third validation. The cross-validation training set features were z-score normalized. The held-out test set was normalized to the means and standard deviations of each training set feature.
The feature selection process entailed three steps to select the top 3, 5, 7, and 10 features. The first step occurred prior to the first data-splitting step and removed highly correlated features. Among any group of highly correlated features (rs ≥ 0.95, Spearman correlation coefficient), all except one feature was removed. The training set features within each cross-validation's fold underwent a similar features selection process as described in Chang et al.26 A feature was removed if, after building a univariate Cox regression model, it was not significantly better than the null model (P < 0.1). The remaining features trained a random forest model from which the top 3, 5, 7, and 10 features were selected based on the out-of-bag loss.
The top 3, 5, 7, and 10 features were utilized to train two models: random forest (RF) and logistic regression (LR). These classifiers have shown promising results in other radiomic studies.27,33 Parameters of the RF model include 100 classification trees; hyperparameter optimization of minimum leaf size, number of predictors to sample, and maximum number of splits; and a 5:2 (false negative/false positive) cost matrix to penalize the network for false-negative predictions, or misclassifying a rejection image. The LR model was a multivariate logistic binomial regression with a logit link function. After training, the models were applied to the validation fold of images. After 120 models were generated (10 iterations of three folds trained on four feature sets of a different number of features) and performed well across the cross-validation folds, the final top 3, 5, 7, and 10 features were selected based on a rank sum (i.e., features selected most frequently across the 10 iterations). The four final models (RF and LR models trained on the top 3, 5, 7, and 10 features) were trained on their corresponding final feature selections extracted from all images in the training data set. Then, the performance of the trained models was evaluated on the held-out test sets. For the final prediction for an eye, predictions were averaged across the three to four images from the eye. If the probability of rejection is ≥0.5, the eye was deemed a future rejection eye. Accuracy was deemed an appropriate metric since the data were equally split between rejection and control cases. Confusion matrix metrics were also computed.
Results
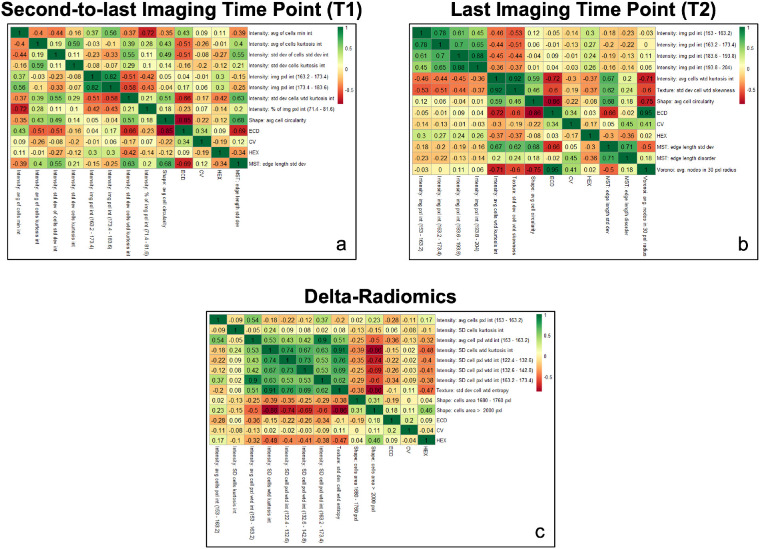
To train and meaningfully interpret the machine learning classifiers, the number of features was reduced to a maximum of 10. After removing highly correlated features, the initial 432 features were reduced by approximately 50%. The resulting Spearman correlation matrix is shown in Supplementary 2. Cox regression model and RF out-of-bag feature reduction methods identified the top 10 features within each fold of the 10 iterations of three-fold cross-validation. Across the 30 folds, the top 10 features were determined by rank sum (features selected the greatest number of times across all folds). The Spearman correlation matrix between the top 10 features selected from each data set, along with the traditional morphometrics, is shown in Figure 4. All novel features exhibited low correlation with ECD, CV, and HEX features, indicating they can enhance the predictability of a model trained to determine postkeratoplasty patient outcomes. Furthermore, shared intensity, shape, and cell-graph features (e.g., image pixel intensities between 163.2 and 173.4, average cell circularity, and minimum spanning tree [MST] edge length standard deviation) were selected in the final top 10 feature set for both the second-to-last and last imaging data sets.
Figure 4.
Correlation matrices of the traditional metrics (ECD, CV, and HEX) and the top 10 features determined by data sets collected from (a) the second-to-last imaging time point prior to rejection (T1), (b) the last imaging time point prior to rejection (T2), and (c) delta-radiomics.
Performance of RF and LR classifiers in the cross-validation study is shown in Table 1. It compares the mean and standard deviation accuracy values per patient-eye from the cross-validation training of both RF and LR models when applied to the validation sets across the 10 iterations. A paired t-test determined the significance of each optimal novel feature-trained machine learning classifier as compared to the traditional morphometrics-trained classifier for the three time-related data sets. For T1 (second-to-last imaging time point), the RF classifier trained on 10 features demonstrated the best prediction performance across the 10 iterations of threefold cross-validation. Its prediction accuracies were significantly different (P < 0.001) from those from the RF classifier trained on traditional morphometrics of the same data set. For T2 (last imaging time point), the prediction accuracies of the logistic regression classifier trained on 10 features were significantly different (P < 0.05) from those from the T2 traditional morphometrics classifier.
Table 1.
Prediction Accuracy of 10 Iterations of Threefold Cross-Validation Training on Post-DMEK Eyes
| Cross-Validation Training | ||||||
|---|---|---|---|---|---|---|
| Time Point 1 | Time Point 2 | Delta-Radiomics | ||||
| Features | RF | LR | RF | LR | RF | LR |
| 3 features | 0.64 ± 0.05 | 0.63 ± 0.07 | 0.58 ± 0.07 | 0.61 ± 0.1 | 0.61 ± 0.07 | 0.45 ± 0.02 |
| 5 features | 0.61 ± 0.08 | 0.63 ± 0.1 | 0.58 ± 0.09 | 0.61 ± 0.09 | 0.65 ± 0.05 | 0.43 ± 0.03 |
| 7 features | 0.63 ± 0.08 | 0.59 ± 0.09 | 0.59 ± 0.06 | 0.62 ± 0.07 | 0.66 ± 0.07 | 0.41 ± 0.03 |
| 10 features | 0.66 ± 0.06a | 0.61 ± 0.08 | 0.59 ± 0.05 | 0.63 ± 0.07a | 0.65 ± 0.09 | 0.41 ± 0.03 |
| Traditional | 0.45 ± 0.07 | 0.51 ± 0.07 | 0.53 ± 0.06 | 0.56 ± 0.06 | 0.64 ± 0.04 | 0.48 ± 0.02 |
Performance was significantly different (P < 0.05) from the corresponding traditional morphometrics model of the same classifier and time-related data set.
Table 2 shows the accuracy values from the final RF and LR models’ predictions on the held-out test set of each data set. Overall, the cross-validation training and held-out test set performances were similar. The held-out test set performances from the time point 2 (last imaging time point) classifiers slightly exceeded the cross-validation training performance. The RF models trained on the top 5, 7, and 10 features and the LR models trained on the top 3, 5, and 7 features performed well with a prediction accuracy greater than 0.80 for last imaging time point data. RF models trained on second-to-last imaging time point data performed better than LR models trained on the same data, with the best requiring three and five features to produce an accuracy of 0.71. The RF models trained on delta-radiomics data performed better than LR models on the same data. RF models trained on the top five novel features demonstrated a prediction accuracy above 0.77. Finally, all RF and LR models trained on 3 to 10 novel features from last and second-to-last imaging time points performed better than models trained on traditional features from the same images. Supplementary 3 and Supplementary 4 complement Table 2, displaying the confusion matrices of held-out test predictions from the RF models and LR models, respectively.
Table 2.
Prediction Accuracy of Held-Out Test Set Post-DMEK Eyes
| Held-Out Test Set | ||||||
|---|---|---|---|---|---|---|
| Time Point 1 | Time Point 2 | Delta-Radiomics | ||||
| Features | RF | LR | RF | LR | RF | LR |
| 3 features | 0.71 | 0.50 | 0.67 | 0.85 | 0.69 | 0.46 |
| 5 features | 0.71 | 0.64 | 0.83 | 0.85 | 0.77 | 0.46 |
| 7 features | 0.64 | 0.57 | 0.83 | 0.85 | 0.69 | 0.46 |
| 10 features | 0.64 | 0.64 | 0.83 | 0.79 | 0.62 | 0.46 |
| Traditional | 0.57 | 0.64 | 0.58 | 0.56 | 0.50 | 0.50 |
The bold values represent the best models with the highest accuracy metrics.
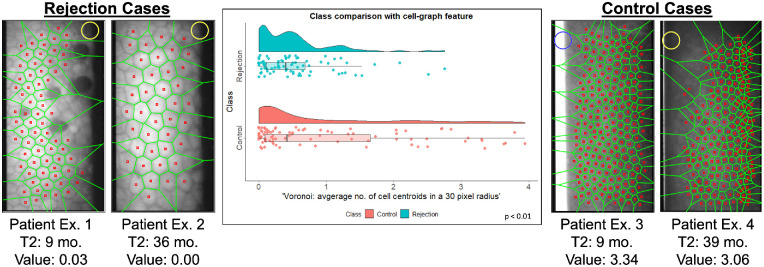
The performance of the models was attributed to their predictive features, some of which are illustrated in Figures 5 and 6. Violin and box plots show the difference in control and rejection distributions for “average number of cell centroids in a 30-pixel radius” and “mean cell circularity,” respectively. To enhance understanding, we now describe these features. The average number of cell centroids in a 30-pixel (24-µm) radius was calculated from a Voronoi tessellation. It is represented by centering a 30-pixel radius circle at a cell's centroid (marked by a red square) and counting the number of red squares within the circle. This step is repeated for each cell before averaging the count for a given image. The size of the 30-pixel radius circle is represented by the yellow and blue circles in Figure 5. In Figure 5, the two rejection eye images are associated with fewer average number of cell centroids in a 30-pixel radius (0.03 and 0 average nearest neighbors), as compared to the two control eye images at similar time points (3.34 and 3.06 average nearest neighbors). A two-sample t-test indicated a significant difference (P < 0.01) between the control and rejection distribution of the average number of cell centroids in a 30-pixel radius.
Figure 5.
Comparison of Delaunay triangulation feature between rejection (left) and control (right) patients. The two rejection images on the left were taken from a patient's eye 30 months and 36 months post-DMEK. The two control images on the right were taken from a patient's eye 25 and 32 months postkeratoplasty. The green graph arrangements overlaying each image is the corresponding Delaunay triangulation. The violin and box plots compare the distribution of Delaunay triangulation side length average calculated from control and rejection eye images.
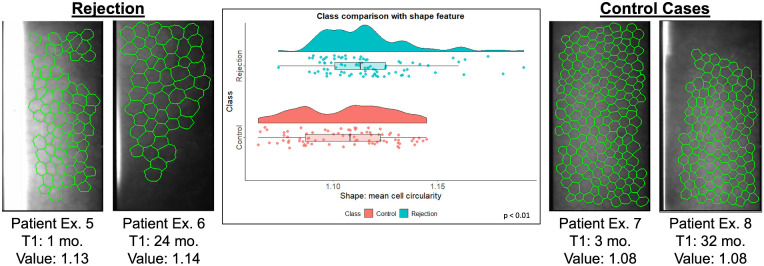
Figure 6.
Comparison of a cell-cluster graph feature between rejection (left) and control (right) patients. The two rejection images on the left were taken from the same patient's eye 16 months and 24 months post-DMEK. The two images on the right were taken from the same patient's eye 13 and 24 months post-DMEK. The images are overlaid with cell-cluster graphs. The violin and box plots compare the distribution of number of connected components in a cell-cluster graph calculated from control and rejection eye images.
Continuing with the description of important features in Figure 6, post-DMEK rejection and control EC images are overlaid with green automatic cell border segmentations to showcase more cells contributing to a uniform circularity in the control images than in the rejection images. Circularity is the ratio of a shape's squared perimeter to area. The circularity is 1 for a perfect circle, 1.10 for a hexagon, and >1 for irregular or noncircular shapes. The rejection eye images in Figure 6 are associated with a greater mean cell circularity (1.13 and 1.14) than control eye images from similar time points (1.08 and 1.08). A two-sample t-test indicated a significant difference (P < 0.01) between control and rejection distribution of mean cell circularity. Supplementary 5 displays another predictive feature distinguishing control and rejection eye images.
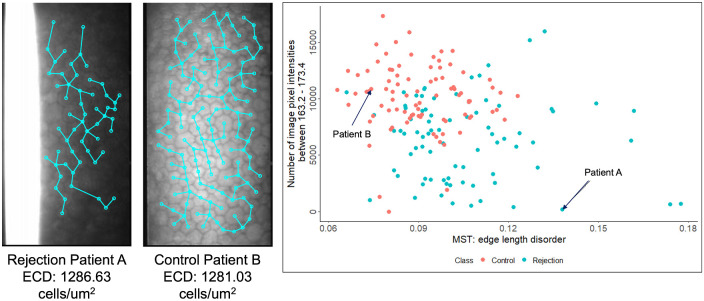
Figures 7 and 8 illustrate how four novel-to-this-application features are more predictive than traditional ECD and HEX features. Figure 7 shows control and rejection images from the last imaging time point data set that have a similar ECD value. The scatterplot demonstrates how two novel features (MST edge length disorder and the number of image pixel intensities between 163.2 and 173.4) cluster results in feature space. An MST is created by connected cell centroids (blue circles in Figure 7) with edges (blue lines) in such a way that the sum of the Euclidian edge lengths in an image is minimal. Equation (2) calculates the disorder of edge lengths.
| (2) |
Here, σedge is the standard deviation of all edge lengths in an image, and μedge is the mean of an image's edge lengths. A larger σedge for a given image will increase the MST edge length disorder. Rejection images tended to have higher MST edge length disorder than control images, as indicated by the scatterplot. The intensity feature, also referenced in Supplementary 5, counts how many pixels in the cellular region have a value between 163.2 and 173.4. From the scatterplot, it is evident that rejection images tend to have fewer pixels in this region than control images. The intensity range (163.2, 173.4) is slightly brighter than the middle of the 8-bit grayscale intensity range (0, 255), indicating that rejection eyes tend to have darker images than control eyes. Both features were in the top seven most predictive features for images taken at the last imaging time point prior to rejection.
Figure 7.
Limitations of HEX as a distinguishing feature between rejection and control patients. Both rejection and control eye images showcase the same percent hexagonality. A scatterplot compares two features, Voronoi tessellation area of polygons and cell-cluster graph number of components. The two data points corresponding to the two images are labeled in the scatterplot.
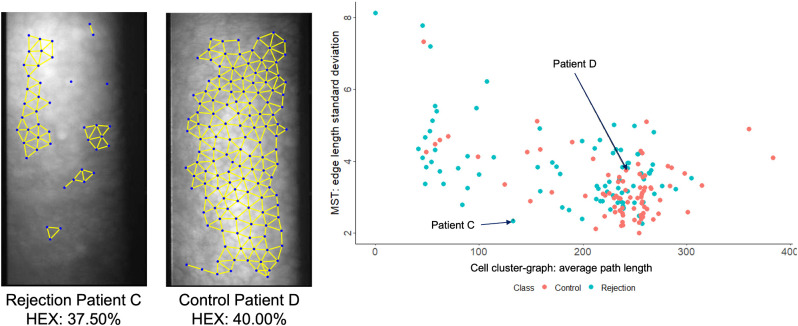
Figure 8.
Limitations of ECD as a distinguishing feature between rejection and control patients. Both rejection and control eye images showcase the same endothelial cell density. A scatterplot compares two features, Delaunay triangulation average triangle area and cell-cluster graph maximum eccentricity. The two data points corresponding to the two images are labeled in the scatterplot.
Figure 8 displays a rejection and control image from the second-to-last time point data set with similar HEX (i.e., the proportion of cells with six sides). The scatterplot clusters rejection and control images from the same data set in the feature space created by two novel-to-this-application features (average path length from cell-cluster graphs and MST edge length standard deviation). This feature space better predicts the correct class for the two images in Figure 8; see patients C and D). Cell-cluster graphs are overlaid on these two images and are composed of blue cell centroids connected with yellow edges. Following Ali et al.,32 the threshold for connectivity was determined by first introducing a kernel that relates the distance between two cell centroids and the probability they are connected. Specifically, the probability two cells are connected is set equal to the Euclidean distance between them, raised to a negative α term (0.43). An edge is introduced between cell centroids with connection probability greater than 0.2. Path length is defined as the sum of the Euclidean length of all edges in a path. The distance between two cells is the length of the shortest path between them, provided they are connected by some path. From here, the average path length of a given image is the average distance between all centroids connected by some path. From the scatterplot, rejection images tend to have shorter path lengths than rejection images. In summary, novel graph features capture the consequences of the gradual rejection mechanism by analyzing the distances between cells in local and global regions, the areas of polygons derived from centroid connections, and the change of these features over time.
Discussion
Using endothelial cell images, we investigated the ability of machine learning to predict future graft rejection following DMEK. We determined that novel-to-this-application features led to more accurate predictions than the traditional morphometrics (e.g., ECD, CV, and HEX), as shown by Table 2 and Figures 7 and 8. These features also showed predictive ability across three time point data sets: last imaging time point, second-to-last imaging time point, and the feature changes between these two points per Table 2 and Figures 5 and 6. Some of the novel features are based upon graphs, which provide more information about the spatial relationship of cells that is disrupted during the process of graft rejection as cells die and remaining healthy cells migrate to heal the defect. For example, due to diseased endothelial cells causing the distortion of surrounding cells’ shapes and forcing their enlargement to maintain the loose junctions within the endothelium, the distance between cell centroids will lengthen, thus decreasing the “average number of cell centroids in a 30-pixel radius” of a rejection image. A similar physiologic reasoning is followed by “cell-cluster graph average path length” and explains the increase in “MST edge length disorder,” “MST edge length standard deviation,” and “cell circularity.”
Cell-cluster graphs, Voronoi tessellations, and MST illustrate cell arrangement differently than traditional morphometrics such as ECD and HEX. In comparison to traditional morphometrics, which provide an average-like metric based on surrounding proximal cells, cell-graph features provide both a global assessment of cell arrangement and local compactness across the entire image. Figures 7 and 8 clearly show that these novel features are better than HEX and ECD, respectively, for prediction of graft rejection. Images of the corneal endothelium en route to a future graft rejection episode exemplify reduced local compactness of the endothelium, resulting in fewer cell-graph connections (yellow edges), fewer nearest neighbors (red cell centroid squares in each space), and longer MST edges (blue connections) due to increased cell death and cell arrangement distortion. Thus, the value of features such as “average path length” and “average number of cell centroids in a 30-pixel radius” is lower for images from a graft rejection eye than a control eye. Additionally, the value of “edge length disorder” feature will be higher for rejection endothelial images than for control endothelial images. Healthy and compact corneal endothelia saw more proximal cell centroids connected in cell-cluster graphs and shorter connecting edges in MSTs, enabling the most distant cell centroids to be connected by smaller edges throughout a given image. The reduction of cell-cluster graph connections and lengthening of MST edges in an unhealthy and less compact corneal endothelium limit the average path length and increase edge length disorder, respectively, between centroids.
Intensity and shape features also proved to be more predictive than ECD and HEX for identifying future graft rejection cases. It was noted that specular images from graft rejection eyes tended to have darker cells than specular images from control eyes. It is hypothesized that this darker intensity is the result of underlying physiologic changes in the graft, starting with subclinical inflammation. The subclinical inflammation could then lead to morphologic changes in corneal endothelial cells identifiable by certain shape features such as cell area and circularity. These morphologic changes could be indicative of endothelial dysfunction, leading to subclinical increased stromal thickness. It is this subclinical stromal thickening that could manifest itself as darker cellular intensities on specular microscopic imaging.
These features were used to build various machine learning models trained to predict future graft rejection across three data sets: second-to-last and last imaging time point images and delta-radiomics. The RF model trained on the top three and five features computed from second-to-last time point (T1) images best predicted future graft rejection within 4 to 24 months. The LR model trained on the top three, five, and seven features computed from last time point (T2) images best predicted future graft rejection within 1 to 12 months. Finally, the RF model trained on the top five delta-radiomic features best predicted future graft rejection within 1 to 12 months. The T1 and T2 novel feature-trained classifiers significantly (P < 0.05) outperformed corresponding traditional morphometric-trained classifiers. The improvement in prediction accuracy between the cross-validation training and held-out testing was due to the 50% increase in training samples when the final four models were trained using all training images for each data set. When working with smaller data sets, increases in data size can enhance model performance.
To understand the proposed model's (LR model trained on top three features from last imaging time point data) evaluation on patient care, we extrapolate its performance on a hypothetical cohort of 1000 patients. If we assume the graft rejection case prevalence reported in Baydoun et al.21 is 2.5%, we expect to correctly identify 21 of the 25 patients at risk for a future graft rejection. On the other hand, if the prevalence is 4%, as reported in Vasiliauskaitė et al.,34 then we expect to correctly identify 34 of the 40 patients at risk for a future graft rejection. A larger number of false positives are predicted (122 of 975 for 2.5% prevalence and 120 of 960 for 4% prevalence), but the actual penalty for this is minor as patients would just be followed more closely with postoperative visits to the ophthalmologist.
The importance of early graft rejection detection is highlighted by the consequences of delayed diagnosis, delayed treatment, and the future risks following a repeat keratoplasty.22,25,35 In PKP, DSAEK, and DMEK cases, studies have shown that despite survival of a rejection episode with intensive topical corticosteroid therapy, patients may still go on to experience marked damage to the corneal endothelium and graft failure. Musch et al.35 reported in a study that examined both control and rejection patients via specular microscopy before and after a rejection episode that patients with PKP who underwent an allograft rejection episode saw a significant decrease in ECD. Furthermore, severe allograft rejection episodes caused EC loss or damage that exceeded expectations compared to mild allograft rejection consequences.35 The Cornea Preservation Time Study found that patients with DSAEK grafts that survived at least one rejection episode, remaining clear for the following 3 years, showed significantly lower ECD and a greater percentage of ECL compared to patients with uncomplicated postkeratoplasty follow-ups.22 Finally, a similar experience was reported by Monnereau et al.25 for DMEK cases. Here, despite the intensified topical corticosteroid treatment following graft rejection, which resolved all rejection eyes in their study, the cell morphology did not return to normal levels; notably, postrejection diagnosis follow-up duration was 6 ± 6 months on average.
This study's results are promising, but there are limitations. One is the small data set and number of rejection eyes used to develop machine learning models. A larger number of rejection eyes, a more realistic ratio of control to rejection eyes that accurately reflects the population ratio, and post-DSAEK and post-PKP patient data would be necessary to validate the robustness and generalizability of this study. Additionally, this study did not include other conditions not related to rejection that may have an effect on endothelial morphology such as long-term contact lens wear36–40 or diabetes.24,41–45 Inclusion of other “abnormal” endothelium classes in future studies could strengthen the precision of the proposed machine learning classifiers and validate the sensitivity of the predictive features. Another limitation is the varying frequency of specular imaging. In general, specular microscopy imaging is seldom performed for keratoplasty-monitoring purposes unless it is part of a clinical study. While this study's patients were more frequently imaged compared to the standard practice of care, even more frequent imaging after keratoplasty could enhance the training and performance of machine learning classifiers. Additional corneal pachymetry measurements corresponding to imaging time points would validate the hypothesis that subclinical inflammation leads to endothelial dysfunction, causing an increase in subclinical corneal thickness and darker imaging intensities. Despite these limitations, this study's promising results provide a foundation for future larger studies investigating early morphometric changes by artificial intelligence (AI)–assisted endothelial image analyses prior to clinical signs of graft rejection and future development of clinical graft rejection and subsequent graft failure.
According to Evans et al.,46 transparency is one of the biggest ethical issues with implementing AI technologies at the clinical level. Transparency is one of this study's strengths due to the handcrafted novel features utilized to develop the machine learning models. Each feature in this study was manually derived and created based on imaging principles and/or cellular physiology. Furthermore, the classifiers built in this study were trained on at most 10 features, making the trends between these handcrafted features and class distinction more clinically and physiologically interpretable than the “black box” models described by Evans et al.46
Other fields of ophthalmology such as diabetic retinopathy,47,48 retinopathy of prematurity,49 glaucoma,50 and age-related macular degeneration51,52 produce larger quantities of imaging data for the training purposes of machine learning models, since imaging is part of routine management of these disorders. Multiple research studies have investigated implementing AI methods into these fields of ophthalmology, including use in outcomes research.53–55 However, in the cornea field, most AI studies have focused solely on developing methodology for endothelial image analysis.56–66 Few studies have trained AI models for diagnosis or addressing treatment management of corneal diseases (e.g., inflammatory and infectious conditions, dystrophies), since imaging is not routinely used to monitor them. One application, however, is with data analysis. For example, O'Brien et al.67 introduced machine learning application to the field of graft failure prediction by utilizing random survival forests. Their study found that intraoperative complications were the most predictive feature of DSAEK failure. Future applications could entail clinical research such as evaluation of corneal health after cataract or glaucoma surgery or intraocular inflammatory diseases, such as herpes uveitis, early diagnosis of patients with Fuch's endothelial corneal dystrophy, time to a postkeratoplasty rejection event, or monitoring treatment of a rejection episode according to the endothelial recovery. Our initial efforts in this study will hopefully stimulate greater interest in this diagnostic tool for outcomes research and guiding therapies at an earlier stage of disease.
In summary, this study introduces the potential benefits of two alterations to the standard practice of care for postkeratoplasty patients: consistent and frequent specular microscopy imaging and machine learning models trained on novel quantitative features extracted from specular microscopic imaging. Frequent imaging and AI approaches would enable identification of postkeratoplasty patients at risk of a future allograft rejection. As indicated by Monnereau et al.,25 the early asymptomatic rejection mechanism can be qualitatively analyzed via frequently specular microscopic imaging. The extraction of quantitative features from specular endothelial images allows machine learning models to formulate interpretable relationships between images, postkeratoplasty endothelial physiology, and allograft rejection. Early detection of subclinical rejection prior to a clinically recognized rejection episode could alert clinicians to administer the necessary treatment for reversing this clinically asymptomatic event before clinical symptoms and signs appear during an examination. Consequentially, the proposed techniques could further reduce graft failures, particularly in high-risk PKP, DSAEK, and DMEK cases.
Supplementary Material
Acknowledgments
The authors thank Satish Viswanath and Berkley Gryder for constructive advice regarding training machine learning classifiers on a smaller data set and feature selection techniques, respectively.
Supported by the National Eye Institute (R21EY02949801, PHS 5 T32 EB 7509-15, U10 EY12728, U10 EY012358, U10 EY020798). The content of this report was solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health (NIH). This work made use of the High-Performance Computing Resource in the Core Facility for Advanced Research Computing at Case Western Reserve University. This research was conducted in space renovated using funds from an NIH construction grant (C06 RR12463) awarded to Case Western Reserve University.
Disclosure: N. Joseph, None; B.A. Benetz, None; P. Chirra, None; H. Menegay, None; S. Oellerich, None; L. Baydoun, Consultant for DORC International (C); G.R.J. Melles, None; J.H. Lass, None; D.L. Wilson, None
References
- 1. Maurice D. A scanning slit optical microscope. Invest Ophthalmol Vis Sci. 1974; 13(12): 1033–1037. [PubMed] [Google Scholar]
- 2. Bourne WM. Cellular changes in transplanted human corneas. Cornea. 2001; 20(6): 560–569. [DOI] [PubMed] [Google Scholar]
- 3. Patel SV, Hodge DO, Bourne WM.. Corneal endothelium and postoperative outcomes 15 years after penetrating keratoplasty. Am J Ophthalmol. 2005; 139(2): 311–319. [DOI] [PubMed] [Google Scholar]
- 4. Zacks C, Abbott R, Fine M.. Long-term changes in corneal endothelium after keratoplasty: a follow-up study. Cornea. 1990; 9(2): 92–97. [PubMed] [Google Scholar]
- 5. Ing JJ, Ing HH, Nelson LR, Hodge DO, Bourne WM.. Ten-year postoperative results of penetrating keratoplasty. Ophthalmology. 1998; 105(10): 1855–1865. [DOI] [PubMed] [Google Scholar]
- 6. Lass JH, Benetz BA, Verdier DD, et al.. Corneal endothelial cell loss 3 years after successful Descemet stripping automated endothelial keratoplasty in the cornea preservation time study: a randomized clinical trial. JAMA Ophthalmol. 2017; 135(12): 1394–1400. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Price MO, Gorovoy M, Benetz BA, et al.. Descemet's stripping automated endothelial keratoplasty outcomes compared with penetrating keratoplasty from the cornea donor study. Ophthalmology. 2010; 117(3): 438–444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Price MO, Gorovoy M, Price FW, Benetz BA, Menegay HJ, Lass JH.. Descemet stripping automated endothelial keratoplasty 3-year graft and endothelial cell survival compared with penetrating keratoplasty. Ophthalmology. 2013; 120(2): 246–251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Price MO, Fairchild KM, Price DA, Price FW Jr. Descemet's stripping endothelial keratoplasty: five-year graft survival and endothelial cell loss. Ophthalmology. 2011; 118(4): 725–729. [DOI] [PubMed] [Google Scholar]
- 10. Price MO, Calhoun P, Kollman C, Price FW Jr, Lass JH.. Descemet stripping endothelial keratoplasty: ten-year endothelial cell loss compared with penetrating keratoplasty. Ophthalmology. 2016; 123(7): 1421–1427. [DOI] [PubMed] [Google Scholar]
- 11. Patel SV. Graft survival and endothelial outcomes in the new era of endothelial keratoplasty. Exp Eye Res. 2012; 95(1): 40–47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Price MO, Bidros M, Gorovoy M, et al.. Effect of incision width on graft survival and endothelial cell loss after DSAEK. Cornea. 2010; 29(5): 523–527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Rodríguez-Calvo-de-Mora M, Quilendrino R, Ham L, et al.. Clinical outcome of 500 consecutive cases undergoing Descemet's membrane endothelial keratoplasty. Ophthalmology. 2015; 122(3): 464–470. [DOI] [PubMed] [Google Scholar]
- 14. Feng MT, Price MO, Miller JM, FW Jr Price. Air reinjection and endothelial cell density in Descemet membrane endothelial keratoplasty: five-year follow-up. J Cataract Refract Surg. 2014; 40(7): 1116–1121. [DOI] [PubMed] [Google Scholar]
- 15. Baydoun L, Tong CM, Tse WW, et al.. Endothelial cell density after Descemet membrane endothelial keratoplasty: 1 to 5-year follow-up. Am J Ophthalmol. 2012; 154(4): 762–763. [DOI] [PubMed] [Google Scholar]
- 16. Quilendrino R, Höhn H, Tse WHW, et al.. Do we overestimate the endothelial cell “loss” after Descemet membrane endothelial keratoplasty? Curr Eye Res. 2013; 38(2): 260–265. [DOI] [PubMed] [Google Scholar]
- 17. Schaub F, Enders P, Snijders K, et al.. One-year outcome after Descemet membrane endothelial keratoplasty (DMEK) comparing sulfur hexafluoride (SF6) 20% versus 100% air for anterior chamber tamponade. Br J Ophthalmol. 2017; 101(7): 902. [DOI] [PubMed] [Google Scholar]
- 18. Schlögl A, Tourtas T, Kruse FE, Weller JM.. Long-term clinical outcome after Descemet membrane endothelial keratoplasty. Am J Ophthalmol. 2016; 169: 218–226. [DOI] [PubMed] [Google Scholar]
- 19. Price MO, Scanameo A, Feng MT, Price FW.. Descemet's membrane endothelial keratoplasty: risk of immunologic rejection episodes after discontinuing topical corticosteroids. Ophthalmology. 2016; 123(6): 1232–1236. [DOI] [PubMed] [Google Scholar]
- 20. Hos D, Tuac O, Schaub F, et al.. Incidence and clinical course of immune reactions after Descemet membrane endothelial keratoplasty: retrospective analysis of 1000 consecutive eyes. Ophthalmology. 2017; 124(4): 512–518. [DOI] [PubMed] [Google Scholar]
- 21. Baydoun L, Bruinsma M, Santander-García D, Ham L, Oellerich S, Melles GRJ.. Combined specular microscopy and Scheimpflug imaging to improve detection of an upcoming allograft rejection after DMEK. Acta Ophthalmol. 2020; 98(3): 261–266. [DOI] [PubMed] [Google Scholar]
- 22. Stulting RD, Lass JH, Terry MA, et al.. Factors associated with graft rejection in the Cornea Preservation Time Study. Am J Ophthalmol. 2018; 196: 197–207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Li JY, Terry MA, Goshe J, Shamie N, Davis-Boozer D.. Graft rejection after Descemet's stripping automated endothelial keratoplasty. Ophthalmology. 2012; 119(1): 90–94. [DOI] [PubMed] [Google Scholar]
- 24. Ohguro N, Matsuda M, Shimomura Y, Inoue Y, Tano Y.. Effects of penetrating keratoplasty rejection on the endothelium of the donor cornea and the recipient peripheral cornea. Am J Ophthalmol. 2000; 129(4): 468–471. [DOI] [PubMed] [Google Scholar]
- 25. Monnereau C, Bruinsma M, Ham L, Baydoun L, Oellerich S, Melles GRJ.. Endothelial cell changes as an indicator for upcoming allograft rejection following Descemet membrane endothelial keratoplasty. Am J Ophthalmol. 2014; 158(3): 485–495. [DOI] [PubMed] [Google Scholar]
- 26. Chang Y, Lafata K, Sun W, et al.. An investigation of machine learning methods in delta-radiomics feature analysis. PLoS ONE. 2019; 14(12): e0226348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Zhang B, He X, Ouyang F, et al.. Radiomic machine-learning classifiers for prognostic biomarkers of advanced nasopharyngeal carcinoma. Cancer Lett. 2017; 403: 21–27. [DOI] [PubMed] [Google Scholar]
- 28. Rao SX, Lambregts DM, Schnerr RS, et al.. CT texture analysis in colorectal liver metastases: a better way than size and volume measurements to assess response to chemotherapy? United Eur Gastroenterol J. 2016; 4(2): 257–263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Joseph N, Kolluru C, Benetz BAM, Menegay HJ, Lass JH, Wilson DL.. Quantitative and qualitative evaluation of deep learning automatic segmentations of corneal endothelial cell images of reduced image quality obtained following cornea transplant. J Med Imaging. 2020; 7(1): 1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Joseph NM, Benetz BA, Menegay H, et al.. Early detection of at-risk keratoplasties and prediction of future corneal graft rejection from pre-diagnosis endothelial cell images. In: Vol 11597; 2021, doi: 10.1117/12.2582171. [DOI] [Google Scholar]
- 31. Doyle S, Agner S, Madabhushi A, Feldman M, Tomaszewski J.. Automated grading of breast cancer histopathology using spectral clustering with textural and architectural image features. In: 2008 5th IEEE International Symposium on Biomedical Imaging: From Nano to Macro. 2008: 496–499, doi: 10.1109/ISBI.2008.4541041. [DOI]
- 32. Ali S, Veltri R, Epstein JA, Christudass C, Madabhushi A.. Cell cluster graph for prediction of biochemical recurrence in prostate cancer patients from tissue microarrays. In: Vol 8676; 2013, doi: 10.1117/12.2008695. [DOI] [Google Scholar]
- 33. Parmar C, Grossmann P, Bussink J, Lambin P, Aerts HJWL.. Machine learning methods for quantitative radiomic biomarkers. Sci Rep. 2015; 5(1): 13087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Vasiliauskaite I, Oellerich S, Ham L, et al. Descemet membrane endothelial keratoplasty: Ten-year graft survival and clinical outcomes. Am J Ophthalmol. 2020; 217: 114–120. [DOI] [PubMed] [Google Scholar]
- 35. Musch DC, Schwartz AE, Fitzgerald-Shelton K, Sugar A, Meyer RF.. The effect of allograft rejection after penetrating keratoplasty on central endothelial cell density. Am J Ophthalmol. 1991; 111(6): 739–742. [DOI] [PubMed] [Google Scholar]
- 36. Barr JT, Schoessler JP.. Corneal endothelial response to rigid contact lenses. Am J Optom Physiol Opt. 1980; 57(5): 267–274. [DOI] [PubMed] [Google Scholar]
- 37. Ohya S, Nishimaki K, Nakayasu K, Kanai A.. Non-contact specular microscopic observation for early response of corneal endothelium after contact lens wear. CLAO J. 1996; 22(2): 122–126. [PubMed] [Google Scholar]
- 38. Holden BA, Sweeney DF, Vannas A, Nilsson KT, Efron N.. Effects of long-term extended contact lens wear on the human cornea. Invest Ophthalmol Vis Sci. 1985; 26(11): 1489–1501. [PubMed] [Google Scholar]
- 39. Hirst LW, Auer C, Cohn J, Tseng SC, Khodadoust AA.. Specular microscopy of hard contact lens wearers. Ophthalmology. 1984; 91(10): 1147–1153. [DOI] [PubMed] [Google Scholar]
- 40. Mac Rae SM, Matsuda M, Shellans S, Rich LF.. The effects of hard and soft contact lenses on the corneal endothelium. Am J Ophthalmol. 1986; 102(1): 50–57. [DOI] [PubMed] [Google Scholar]
- 41. Lass JH, Spurney RV, Dutt RM, et al.. A morphologic and fluorophotometric analysis of the corneal endothelium in type I diabetes mellitus and cystic fibrosis. Am J Ophthalmol. 1985; 100(6): 783–788. [DOI] [PubMed] [Google Scholar]
- 42. Schultz RO, Matsuda M, Yee RW, Edelhauser HF, Schultz KJ.. Corneal endothelial changes in type I and type II diabetes mellitus. Am J Ophthalmol. 1984; 98(4): 401–410. [DOI] [PubMed] [Google Scholar]
- 43. Dong XG, Xie LX.. Specular microscopy of the corneal endothelial cells in diabetes. Zhonghua Yan Ke Za Zhi. 1994; 30(1): 14–15. [PubMed] [Google Scholar]
- 44. Terry MA, Aldave AJ, Szczotka-Flynn LB, et al.. Donor, recipient, and operative factors associated with graft success in the cornea preservation time study. Ophthalmology. 2018; 125(11): 1700–1709. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Aldave AJ, Terry MA, Szczotka-Flynn LB, et al.. Effect of graft attachment status and intraocular pressure on Descemet stripping automated endothelial keratoplasty outcomes in the cornea preservation time study. Am J Ophthalmol. 2019; 203: 78–88. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Evans NG, Wenner DM, Cohen IG, et al.. Emerging ethical considerations for the use of artificial intelligence in ophthalmology. Ophthalmol Sci. 2022; 2(2): 100141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. Abràmoff MD, Lou Y, Erginay A, et al.. Improved automated detection of diabetic retinopathy on a publicly available dataset through integration of deep learning. Invest Ophthalmol Vis Sci. 2016; 57(13): 5200–5206. [DOI] [PubMed] [Google Scholar]
- 48. Gargeya R, Leng T.. Automated identification of diabetic retinopathy using deep learning. Ophthalmology. 2017; 124(7): 962–969. [DOI] [PubMed] [Google Scholar]
- 49. Brown JM, Campbell JP, Beers A, et al.. Automated diagnosis of plus disease in retinopathy of prematurity using deep convolutional neural networks. JAMA Ophthalmol. 2018; 136(7): 803–810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50. Li Z, He Y, Keel S, Meng W, Chang RT, He M.. Efficacy of a deep learning system for detecting glaucomatous optic neuropathy based on color fundus photographs. Ophthalmology. 2018; 125(8): 1199–1206. [DOI] [PubMed] [Google Scholar]
- 51. Grassmann F, Mengelkamp J, Brandl C, et al.. A deep learning algorithm for prediction of age-related eye disease study severity scale for age-related macular degeneration from color fundus photography. Ophthalmology. 2018; 125(9): 1410–1420. [DOI] [PubMed] [Google Scholar]
- 52. Burlina PM, Joshi N, Pekala M, Pacheco KD, Freund DE, Bressler NM.. Automated grading of age-related macular degeneration from color fundus images using deep convolutional neural networks. JAMA Ophthalmol. 2017; 135(11): 1170–1176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. Abràmoff MD, Lavin PT, Birch M, Shah N, Folk JC.. Pivotal trial of an autonomous AI-based diagnostic system for detection of diabetic retinopathy in primary care offices. NPJ Digital Med. 2018; 1(1): 39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54. Ting DSW, Cheung CYL, Lim G, et al.. Development and validation of a deep learning system for diabetic retinopathy and related eye diseases using retinal images from multiethnic populations with diabetes. JAMA. 2017; 318(22): 2211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55. De Fauw J, Ledsam JR, Romera-Paredes B, et al.. Clinically applicable deep learning for diagnosis and referral in retinal disease. Nat Med. 2018; 24(9): 1342–1350. [DOI] [PubMed] [Google Scholar]
- 56. Al-Fahdawi S, Qahwaji R, Al-Waisy AS, et al.. A fully automated cell segmentation and morphometric parameter system for quantifying corneal endothelial cell morphology. Comput Methods Programs Biomed. 2018; 160: 11–23. [DOI] [PubMed] [Google Scholar]
- 57. Zhang Y, Higashita R, Fu H, et al.. A multi-branch hybrid transformer network for corneal endothelial cell segmentation [published online May 21, 2021]. arXiv:210607557 [cs], http://arxiv.org/abs/2106.07557. Accessed September 12, 2021.
- 58. Vigueras-Guillén JP, van Rooij J, van Dooren BTH, et al.. DenseUNets with feedback non-local attention for the segmentation of specular microscopy images of the corneal endothelium with Fuchs dystrophy [published online March 5, 2022]. arXiv:220301882 [cs, eess], http://arxiv.org/abs/2203.01882. Accessed March 8, 2022. [DOI] [PMC free article] [PubMed]
- 59. Scarpa F, Ruggeri A.. Segmentation of corneal endothelial cells contour by means of a genetic algorithm. In: Proceedings of the Ophthalmic Medical Image Analysis Second International Workshop. Munich, Germany: University of Iowa; 2015: 25–32. [Google Scholar]
- 60. Kucharski A, Fabijańska A.. CNN-watershed: a watershed transform with predicted markers for corneal endothelium image segmentation. Biomed Signal Process Control. 2021; 68: 102805. [Google Scholar]
- 61. Daniel MC, Atzrodt L, Bucher F, et al.. Automated segmentation of the corneal endothelium in a large set of ‘real-world’ specular microscopy images using the U-Net architecture. Sci Rep. 2019; 9(1): 4752. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62. Huang J, Maram J, Tepelus TC, et al.. Comparison of manual & automated analysis methods for corneal endothelial cell density measurements by specular microscopy. J Optom. 2018; 11(3): 182–191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63. Nurzynska K. Automatic segmentation of corneal endothelium images with convolutional neural network. In: Kozielski S, Mrozek D, Kasprowski P, Małysiak-Mrozek B, Kostrzewa D, eds. Beyond Databases, Architectures and Structures. Facing the Challenges of Data Proliferation and Growing Variety. Vol. 928. Communications in Computer and Information Science. Poznan, Poland: Springer International Publishing; 2018: 323–333. [Google Scholar]
- 64. Selig B, Vermeer KA, Rieger B, Hillenaar T, Luengo Hendriks CL. Fully automatic evaluation of the corneal endothelium from in vivo confocal microscopy. BMC Medical Imaging. 2015; 15(1): 13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65. Kang L, Ballouz D, Woodward MA.. Artificial intelligence and corneal diseases. Curr Opin Ophthalmol. 2022; 33(5): 407–417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66. Vigueras-Guillén JP, van Rooij J, Engel A, Lemij HG, van Vliet LJ, Vermeer KA.. Deep learning for assessing the corneal endothelium from specular microscopy images up to 1 year after ultrathin-DSAEK surgery. Transl Vis Sci Technol. 2020; 9(2): 49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67. O'Brien RC, Ishwaran H, Szczotka-Flynn LB, Lass JH; Cornea Preservation Time Study (CPTS) Group. Random survival forests analysis of intraoperative complications as predictors of Descemet stripping automated endothelial keratoplasty graft failure in the Cornea Preservation Time Study. JAMA Ophthalmol. 2021; 139(2): 191–197. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.