Abstract
Fugitive methane emissions from municipal solid waste landfills impact global climate change and reliable emissions quantification is of increasing importance. Ground-based cavity ring-down spectrometer (CRDS) measurements were used to determine methane concentrations and isotopic compositions of carbon in CH4. Then, CH4 oxidation through various cover materials was assessed using the Keeling plot method. A novel inverse modeling approach using Gaussian dispersion analysis, termed near-surface Gaussian plume estimation (NSGPE), was developed to predict whole-site landfill methane emissions. The concentration data obtained around the landfill perimeter with the mobile ground-based CRDS were used. Methane concentration data were integrated to parameterize discretized point source emissions from a Gaussian dispersion model. Post-processing algorithms were applied to refine modeling predictions to account for the influence of topographical and meteorological conditions on methane transport. Results indicate spatially resolved and consistent emissions estimates among multiple optimization simulations, with refinements increasing the resolution and spatial trends of emissions. Post-processing algorithms resolve consistent overestimation of emissions commonly observed using conventional Gaussian dispersion models.
-
•
Ground-based CRDS used to obtain methane concentration and oxidation data.
-
•
Novel inverse Gaussian dispersion modeling approach developed to predict methane emissions from landfills accounting for site-specific topography and meteorology.
-
•
Post-processing algorithms refine emissions estimates.
Keywords: Gaussian plume dispersion modeling, Inverse model, Numerical model, Cavity ring-down spectroscopy, Landfill, Methane, Keeling plot, Surface emissions
Method name: Determination of methane oxidation and landfill emissions by stable isotopic composition plot method and Gaussian plume dispersion modeling
Graphical abstract
Specifications Table
| Subject Area: | Engineering |
| More specific subject area: | Air emissions, landfill emissions, solid waste management, climate impacts |
| Method name: | Determination of methane oxidation and landfill emissions by stable isotopic composition plot method and Gaussian plume dispersion modeling |
| Name and reference of original method: | Liptay, K., Chanton, J., Czepiel, P., and Mosher, B., (1998), “Use of Stable Isotopes to Determine Methane Oxidation in Landfill Cover Soils,” Journal of Geophysical Research Atmospheres, Vol. 103, No. D7, p. 8243–8250. 10.1029/97JD02630. Kormi, T., Mhadhebi, S., Bel Hadj Ali, N., Abichou, T., and Green, R., (2018), “Estimation of Fugitive Landfill Methane Emissions Using Surface Emission Monitoring and Genetic Algorithms Optimization,” Waste Management, Vol. 72, p. 313–328. 10.1016/j.wasman.2016. |
| Resource availability: | NA |
Introduction
Municipal solid waste (MSW) landfills are the third most significant anthropogenic source of methane releases to the atmosphere across regional, state, and national scales [22,27]. Methane is a primary greenhouse gas that significantly contributes to the intensification of global climate change [22]. Therefore, reliable and consistent approaches to measure and monitor methane emissions from landfills are necessary to inform current engineering mitigation practices and future regulatory strategies to offset the global climate impacts of MSW landfills. In this study, field methane data were obtained using a cavity ring down spectrometer (CRDS). Isotopic compositions of carbon in CH4 measured with the CRDS were used to determine the level of methane oxidation through various cover materials by employing a novel application of the Keeling plot method. Oxidation in cover materials is significant as a potential mechanism to reduce methane releases to the atmosphere with limited methodologies available for direct assessment. In addition, a novel inverse Gaussian dispersion modeling approach to estimate landfill methane emissions was developed that uses the field methane concentration data obtained from the mobile CRDS platform. The modeling analysis provides a significant advancement to existing methane emissions estimation methods (e.g., [4,14,15]). The experimental and numerical methods underlying this integrated approach, termed Near Surface Gaussian Plume Estimation (NSGPE), are introduced. Following the technical description of the methodology, discussion is provided on the numerical validation, potential limitations, primary advantages, and future developments for the NSGPE approach.
Methods
Experimental method: ground-based cavity ring-down spectrometer analysis
Ground-based cavity ring-down spectrometer instrumentation was used to obtain methane concentrations from landfill perimeter and landfill interior locations (Fig. 1). Isotopic δ13CH4 were obtained concurrently with the methane concentration measurements (Fig. 2). Standards traceable to primary National Institute of Standards and Technology and National Oceanic and Atmospheric Agency standards were analyzed at the beginning and end of each day of measurement. The measurements were corrected for the calibration runs, interpolated for the time of the measurements.
Fig. 1.
Methane concentrations measured by the ground CRDS platform at Potrero Hills Landfill.
Fig. 2.
Isotopic δ13CH4 Measured by the Ground CRDS Platform at Potrero Hills Landfill.
In this analysis, the Keeling plot method was used, in which the isotopic composition of the pure CH4 component is given by the y-intercept of the best fit line provided for each location in Eq. (3),[13], derived from two mass balance formulations presented in Eqs. (1) and (2).
| (1) |
| (2) |
| (3) |
where, obs indicates the observed isotopic composition, bg indicates the background value, and src indicates the pure source component coming from the waste mass as determined downwind from the active face. The background values are not used in the final linear equation (Eq. (3)), except in the indeterminant slope (m). The background value was assumed to remain constant during the sampling period, as only an hour was required for sampling for each of the landfill regions studied. The data set was filtered to remove outliers, with minute averages greater than approximately 40–50 ppm CH4 or δ13C > −46‰, since these stand out from the general data set (Fig. 3). The resulting isotopic values, characteristic of the emissions from the various regions of the landfill, were then used to calculate the degree of oxidation, using the general method of Liptay et al. [17].
| (4) |
where, δ is isotopic composition of the carbon in the CH4, e is the emitted CH4, anox is the CH4 in the anoxic zone, αox is the fractionation factor for oxidation of carbon in CH4, and αtr is the fractionation expected for transport of the CH4. The αox used was 1.022 and the αtr was assumed to be 1.0 (e.g., [7,17]). The ground CRDS method was used to determine cover-specific methane oxidation in this investigation. Using the Keeling plot method can mitigate some of the previous concerns with this method (e.g., [7]), since the approach included herein extrapolates the mixing of the oxidized emissions and the ambient air to derive the composition of the pure oxidized endmember being emitted. As we are using this method for a small spatial area for a given cover material, a small number of measurements is sufficient [26]. The individual Keeling plots for the measurements obtained at the Potrero Hills landfill and maps showing the methane δ13C isotopic composition are in presented in Fig. 4.
Fig. 3.
Keeling plot for 1-minute averages of all measurements. The significant departure of δ13CH4 measurements at high CH4 mixing ratios, low 1/CH4, indicates that the instrument signal is disrupted and, therefore, the mixing relationship between ambient air CH4 and the CH4 emitted from the landfill is not valid for these high concentrations.
Fig. 4.
Keeling plots for the different sampling locations with intercepts summarized in Table 3 in Yeşiller et al. (2022) [28]. The uncertainty in the intercept is the standard error determined by linear regression.
Numerical method: Near Surface Gaussian Plume Estimation modeling
Inverse modeling incorporating Gaussian plume dispersion models, have been further developed to predict methane emissions from municipal solid waste landfills [4,10,14,15]. For landfill gas emissions analysis, methane concentration data is collected downwind from the site of interest and used to inversely estimate both the location and intensity of emission sources. If the gas concentration data can be reliably quantified and the model realistically constrained during calibration, an informed estimate of the site-wide emissions can be reached. In addition to these criteria, the dispersion model must contain the necessary mechanisms to replicate field behavior to reduce potential error between field observations and model predictions. Even though convenient from a computational/mathematical standpoint, Gaussian dispersion models often overly-simplify the gas emissions and transport behavior at MSW landfills, which leads to over- or under-estimation of site-wide emissions. Therefore, careful investigation into and application of inverse Gaussian dispersion models is warranted when applied to the topographical and meteorological complexities of the MSW landfill setting.
In this study, a novel approach to inverse Gaussian dispersion modeling of landfill methane emissions is developed and introduced that serves as a significant advancement from existing methods (e.g., [4,14,15]). This approach, termed Near Surface Gaussian Plume Estimation (NSGPE), integrates field observations of methane concentrations using ground-based cavity ring-down spectrometry from a mobile monitoring platform with Gaussian dispersion model predictions of methane emissions. Analysis is presented for Potrero Hills Landfill. The Gaussian dispersion model is structured to explicitly account for the unique topographical features of the landfill and includes multiple post-processing steps to obtain a more representative estimate of fugitive methane emissions.
In the NSGPE approach, ambient, near surface methane concentration data collected around the perimeter of the landfill were used to parameterize the methane emission rates from the landfill surface. A conventional, Gaussian plume dispersion model served as the basis for the estimation of the methane emission rates, Q (Eq. (5)). The Gaussian plume dispersion model makes several simplifying assumptions, including that methane, once-released, is non-reactive; effects of local surface topography on methane dispersion are not accounted for; there is a continuous release of methane from each point source location on the landfill surface; and, there exists constant meteorological conditions and steady state flow conditions (i.e., constant wind speed/direction, no vertical shear) during time of measurement [18]. Using this model, methane concentrations observed at any of the receptor locations downwind can be predicted given the known emission rates (Q), windspeed (u), locations (x, y), elevations (H), and dispersion characteristics () of all distinct methane emission sources. Given the windspeed (u) and direction (θ), x, y, and z represent the distances in the downwind, crosswind, and vertical directions, respectively, between each source and receptor pair (Fig. 5). Both and represent the dispersion coefficients in the vertical and crosswind directions, respectively. The total methane concentration predicted at each downwind receptor was calculated as the arithmetic sum of all n contributing emission sources across the landfill surface (Eq. (6)).
| (5) |
| (6) |
Fig. 5.
Source-receptor geometry used in the NSGPE Analysis.
The plume dispersion characteristics in the crosswind and vertical directions were estimated based on the distance downwind through previously developed, power law relationships describing atmospheric dispersion across multiple atmospheric stability classes (i.e., neutral, stable, unstable). Pasquill-Gifford stability classes [20] as well as the analytical expressions proposed by Briggs [11] were applied to approximate atmospheric conditions and dispersion characteristics, respectively, herein (Table 1, Table 2). Under the Pasquill-Gifford stability class framework, A, B, C, D, E, and F correspond to very unstable, moderately unstable, slightly unstable, neutral, slightly stable, and stable classifications, respectively. The average windspeed (u) and direction for the testing days were obtained from NOAA climate data online using the closest monitoring location. The methane concentrations obtained with the CRDS around the entire landfill perimeter, resulting in 71 unique receptor locations, were applied in the optimization tasks.
Table 1.
Definition of the Pasquill Stability Classes in NSGPE Model.
| Surface Windspeed (m/s) | Daytime Insolation |
Nighttime Cloud Cover |
|||
|---|---|---|---|---|---|
| Strong | Moderate | Slight | 4/8 | 3/8 | |
| <2 | A | A-B | B | – | – |
| 2–3 | A-B | B | C | E | F |
| 3–5 | B | B-C | C | D | E |
| 5–6 | C | C-D | D | D | D |
| >6 | C | D | D | D | D |
Table 2.
Briggs Model to Estimate Dispersion Coefficients in NSGPE Model.
| Pasquil Stability Class | ||
|---|---|---|
| A | ||
| B | ||
| C | ||
| D | ||
| E | ||
| F |
An existing framework to inverse Gaussian plume modeling based on genetic algorithms [4,14,15] served as the basis for initial development of the NSGPE approach. This existing framework was first modified to account for the surface elevations of the emission sources at the landfill. This modification was required to account for the high variation in surface elevations commonly observed at MSW landfills, where dispersion in the z-direction was expected to play a significant role across downwind and crosswind distances from source to receptor on small spatial scales (Fig. 6). This modification was accomplished in two steps. First, the ground surface elevations below mean sea level were transformed to positive values by raising the digital elevation map elevations by the lowest (negative) elevation observed across the site boundaries. This step avoided any inconsistencies with application of Eq. (5), given that this equation was derived using a no flux boundary condition set at a ground surface elevation of 0 [18]. Next, we made two main assumptions concerning the emissions from the point source locations. If the elevation of a given source was greater than that at a receptor location, we assumed that the emissions from each source location were analogous to the stack height (assuming plume rise was negligible from the surface), H, commonly used in the Gaussian plume dispersion model to account for point source emissions from elevated locations. If the elevation of a given source location was lower than that of a receptor, we applied Eq. (7), which is analogous to the release from a ground level source. Elevation data was retrieved from the most recent (2019), high resolution topographic surveys obtained from the operators of the landfill. The AutoCAD data were then georeferenced and transformed to an applicable raster dataset using a combination of Civil3D (2021) and ArcMap (v10.5.1) software. The raster dataset was finally integrated into MATLAB (r2018a) using the Mapping Toolbox to carry out the optimization tasks.
| (7) |
Fig. 6.
Raster elevation dataset of Potrero Hills Landfill (z-scale in feet). Warm and cool colors indicate low and high elevations, respectively. The historical waste placement boundary is purple and the downwind monitoring locations with blue diamonds.
In addition to elevation data, the existing framework was modified to apply a user defined number (n) of point source methane emissions from the landfill surface. As the spatial variability in gas emissions is significant at MSW landfills [28], this modification allowed for more flexibility during optimization and statistical representation of the heterogeneity in emissions. With this modification, a uniformly spaced grid of nodes, representing n different methane emission sources, was constructed (Fig. 7). The uniform rectangular areas encompassing each node (i.e., grid cells) were used with the raster dataset to estimate the average elevations of each point source location. The number of gridpoints (and corresponding size of each grid cell) was adjusted to obtain a reliable estimate of the spatial variability in methane emissions. It is important to note that these are relative locations of potential methane emissions, as the optimization assumed methane emissions were spatially homogenous within each grid cell.
Fig. 7.
Uniform structured grid used to define methane point source emissions at the landfill of interest. Magenta dots indicate the locations of point source emissions, green rectangles indicate individual grid cells, and the blue line and black crosses specify the waste placement boundaries and downwind monitoring observations, respectively.
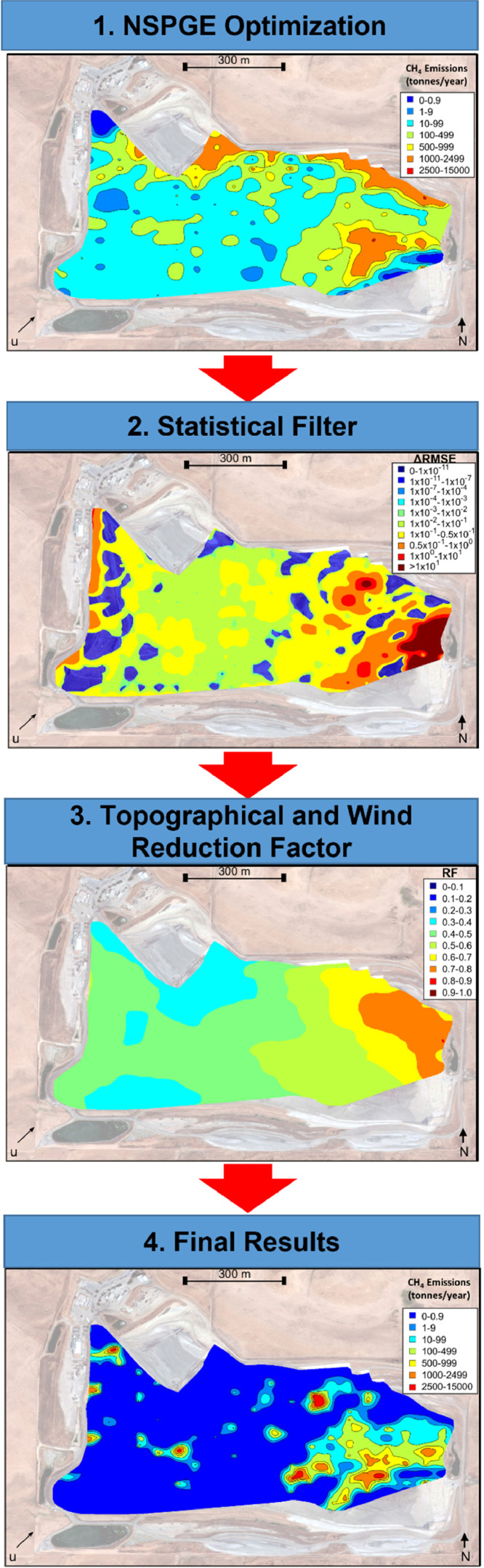
Fig. 8 summarizes the main workflow of the NSGPE approach. Field measurements of methane concentrations around the perimeter of the landfill are inverse modeled using the Gaussian plume dispersion model. A spatially unconstrained evolutionary optimization algorithm is applied to iteratively minimize the sum of squared error calculated between field observations and model predictions. The optimization algorithm is applied over 10 consecutive and independent runs to assess the magnitude and variation in methane emission estimates. Next, a statistical filter, based on a one at a time sensitivity analysis, is used to isolate the most probable emissions obtained from the inverse model results following Step 1. Final post-processing is applied to the statistical filtering results to capture the influence of topography and meteorology on methane transport across the site. This step ensures that the most significant limitations of the Gaussian dispersion model are addressed and avoids potential overestimation of site-wide emissions.
Fig. 8.
Summary workflow of the NSGPE approach.
NSGPE optimization approach
The NSGPE optimization of the methane emission rates from the n-different emission sources was performed using a similar approach to Kormi et al. [15]. A global optimization approach was applied to parameterize the unknown methane emission rates at the landfill. We relied on an evolutionary, stochastic search algorithm, LSHADE-EpSin-NLS, to converge to a stable, global solution [1,2]. The optimization settings applied in this algorithm are summarized in Table 3. The number of generations and population members were set to 500,000 and 500, respectively, to thoroughly explore the search space and repeatedly converge to an optimal, global solution. The optimization procedure was terminated when either the number of generations had been exceeded or if the range in objective function values among the population members was less than the specified tolerance (Table 3). The objective function (OF) to be minimized in this complex optimization task was the sum of square residuals calculated between the observed and measured methane concentrations across the i representative, downwind monitoring locations (Eq. (8)), assuming that the error residuals were independent, homoscedastic, and normally distributed with zero mean [8]. The methane emission rates were constrained within ranges reported from MSW landfills (0 to 10,000 mg/sec, [4],) to ensure convergence to a realistic global optimization solution (Eq. (9)). However, methane emission rates were not spatially constrained in this approach. Ultimately, avoiding spatial constraints on the objective function provided an impartial and unbiased approach to the modeling effort. Based on previous field research, methane emission rates are expected to decrease when progressing from daily, to intermediate, to final cover locations, reflecting variations in cover material design and integrity [5,12]. Cover materials transition from thin, loosely packed, heterogenous materials in daily cover areas to thick, well compacted, and homogenous engineered systems with low hydraulic conductivities in final cover areas. Omitting spatial constraints in the NSGPE approach is a factor that could potentially lead to overestimation of emissions, as discussed in the following sections.
| (8) |
| (9) |
Table 3.
Summary of parameters used in the LSHADE-EpSin-NLS optimization algorithm.
| Parameter | Notation | Nominal Value |
|---|---|---|
| Number of Generations | Ngen | 500,000 |
| Population Size | Psize | 500 |
| Tolerance | Ntol | 1E-6 |
| Adapted Scaling Parameter | Fde | 0.5 |
| Crossover Probability | CR | 0.5 |
| Frequency of Sinusoidal Search Function | – | 0.5 |
| Memory Size: Adaptive Storage | – | 5 |
| Memory Size: Learning Period | – | 20 |
| Mutation Strategy | – | Current2pbest/1 |
| Probability of performing crossover using CMA1 | – | 0.4 |
| Proportion of individuals used to generate the CM | – | 0.5 |
CMA = Covariance matrix adaptation.
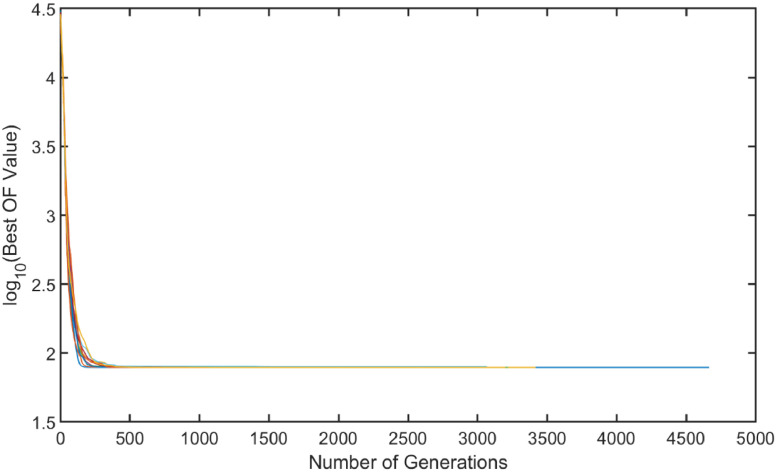
To develop the NSGPE approach, the number of uniform gridpoints (i.e., nodes) was first varied to investigate the optimal number of sources required to fit the observed methane concentrations. A total of nine different grid structures were investigated, each containing 14, 68, 152, 194, 273, 333, 416, 488, and 605 individual source locations. At least 10 different optimization runs were performed for each of the grids, where the starting point was randomly set to a different location prior to the start of each run. An example plot demonstrating the convergence of the LSHADE optimization algorithm to the global solution across ten independent runs is presented in Fig. 9. The logarithm (base 10) of the best (minimized) objective function value observed among all population members is presented. Each of the runs were observed to converge to an optimal, global solution after approximately 4300 generations were reached.
Fig. 8a.
Convergence of the LSHADE-EpSin-NLS algorithm to the global solution. Individual colors represent one of ten independent optimization runs.
Next, the effect of increasing the number of gridpoints on the mean objective function following completion of five independent runs is presented (Fig. 10). In general, as the number of gridpoints used to parameterize the methane emission sources at the landfill site increased, the mean objective function was observed to decrease (Fig. 10). However, as the number of gridpoints started to increase beyond 400 points, the mean objective function (and standard deviation across runs) increased, to some extent (Fig. 10). This result is associated with the complexity of the objective function surface as the number of gridpoints used to parameterize methane sources increased. The optimization algorithm had difficulty in locating the global solution with the associated increase in model parameters, which resulted in a wide range in objective function values. The number of gridpoints that was observed to balance the model complexity with prediction reliability was observed near a value of 300 (Fig. 10). This particular gridpoint number (333) was selected for further study to estimate the whole-site emissions from the landfill. Using this gridpoint number, each grid cell encompassed an area of 2182 m2 (36.4 m x 60 m). In addition, the spacing between gridpoints was calculated as 43 m.
Fig. 9.
Effect of increasing the gridpoint number on the reliability of model predictions.
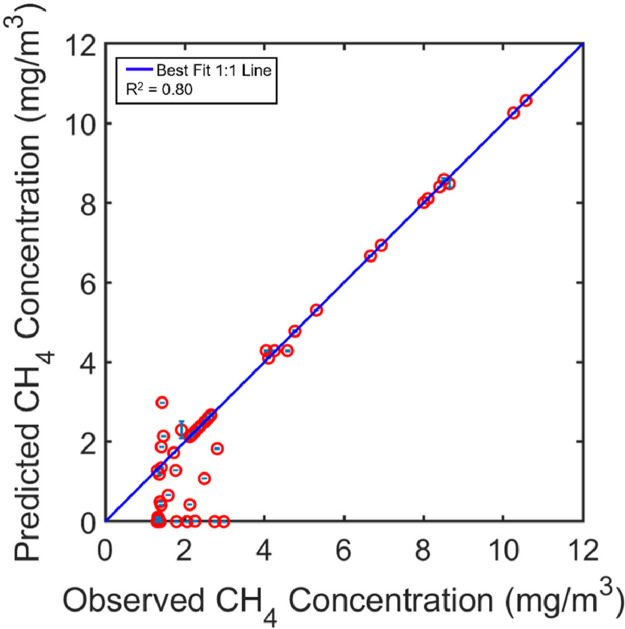
The optimization approach employing 333 gridpoints resulted in an acceptable fit to the observed methane concentration data downwind of the landfill (Fig. 11). Over ten independent runs, the overall, averaged R2, adjusted R2, and root mean square error (RMSE) were calculated as 0.80, 0.788, and 1.05, respectively. The magnitude of these summary indices demonstrated that the NSGPE approach could reliably reproduce the field data. The observed versus the predicted methane concentrations are plotted for comparison. In general, all receptor locations associated with higher observed methane concentrations (above 2 mg/m3) lie very close to the 1:1 line, indicating that the inverse modeling well approximated the methane emission rates across the site. The differences observed between predicted and observed data at lower concentrations was most likely due to the receptor locations located upwind of the emissions sources at the landfill (Fig. 11). As observed in Fig. 7, at least 6–7 monitoring locations were located upwind of a majority of sources within the landfill and may have potentially contributed to the mismatch observed between the field data and the model predictions. Furthermore, the NSGPE optimization approach could not account for methane sources located outside of the landfill domain, which likely contributed to detectable concentrations of ambient methane at receptors located both upwind and downwind of the landfill site. On-site landfill gas to energy operations along with nearby livestock/agricultural businesses as well as oil and gas operations cannot be ruled out as potential methane sources that remain unaccounted for using this approach.
Fig. 10.
Agreement between predicted and observed methane concentrations using the NSGPE approach. Error bars represent the standard deviation in the predicted methane concentrations across 10 independent trial runs.
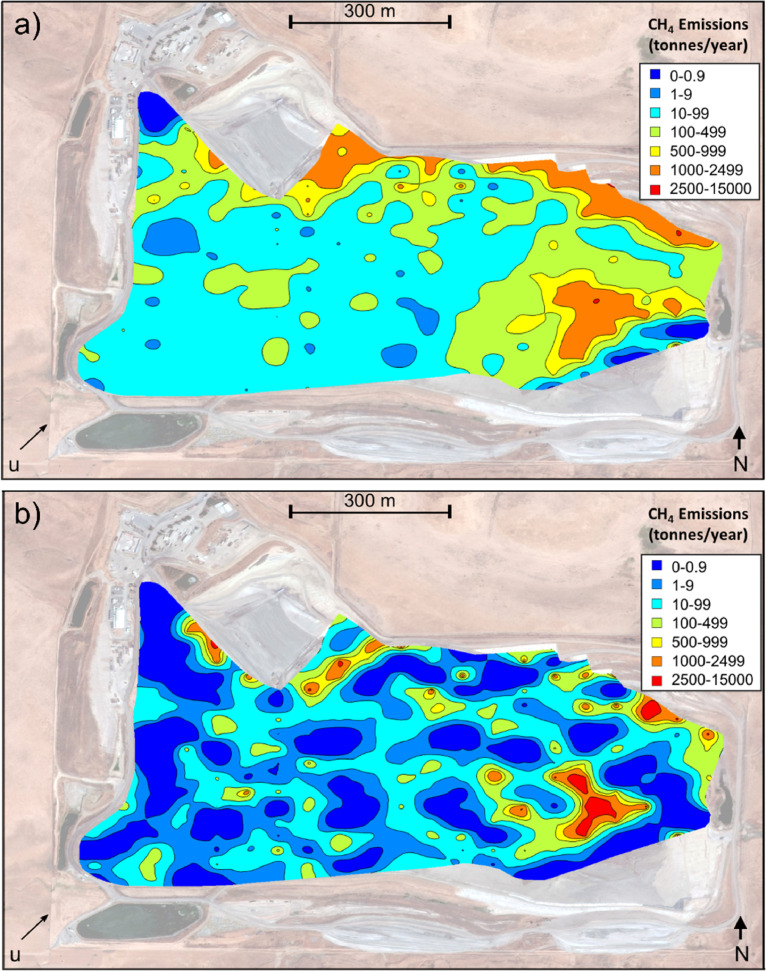
The spatial variability in methane emissions predicted at the study landfill using the NSGPE approach is presented in Fig. 12. Both the spatially averaged methane emission predictions from ten independent optimization runs (11a) and the single best performing optimization run (11b) are provided in the figure. A full kriging analysis (using MATLAB ordinary kriging toolbox with default parameters set for variogram construction, fitting, and kriging) was conducted to interpolate emissions from the gridpoints to all other areas of the landfill site [23]. Ultimately, predicted methane emissions tended to be significantly lower near the west and southwest corner of the site, which is associated with thicker final and interim cover materials overlying older waste materials (Fig. 12). In addition, predicted methane emissions were considerably higher near the active face and daily cover locations, where cover materials are thin (or absent), and waste age is younger (Fig. 12). Predicted methane emissions were also much higher around the northeastern and northern boundaries of the landfill site (Fig. 12). Collocation issues between source and receptor, which arise as an artifact of the unconstrained optimization process may have also contributed to higher emissions from these boundary locations [21,24]. These optimization issues were thoroughly handled with the statistical filtering approach described below. In addition, the methane emissions intensity plot for the best performing run demonstrated some significant differences compared to the spatially averaged methane emissions. For example, predicted methane emissions along the northeastern and central boundaries of PHL were considerably different when comparing Figs. 12a and 12b. This result is reflective of the spatial variability in emissions estimates when spatial constraints are omitted from the optimization procedure.
Fig. 11.
Methane emissions predicted using the NSGPE approach (raw results) for a) the average of 10 and b) best performing optimization runs.
Site-wide methane emissions from the landfill and uncertainty in methane emission predictions were further investigated in order to compare the reliability of the unconstrained NSGPE approach with other available methane emission measurement approaches. Whole-site methane emissions were calculated as the arithmetic sum of the emissions predicted at each gridpoint, deemed representative of the average emissions within each grid cell. The optimization run with the lowest objective function value was applied in this calculation. Results of the kriging interpolations were not included in these calculations as kriging introduces additional uncertainty in methane emissions estimates that further complicates whole-site emissions determination.
The variation in whole-site methane emissions was assessed through calculation of 95% confidence intervals (Eq. (10)). Here, we assume that the uncertainty in predicted emissions can be attributed to measurement error, parameter (source strength) identification, and model structure (epistemic) errors. A robust and simplified approach to estimate uncertainty in methane emissions using the NSGPE approach were investigated. In the robust approach, a residual error bootstrapping method was applied to estimate the parameter variance-covariance matrix required to compute 95% confidence intervals [6,9]. This bootstrapping method has previously been used as a statistical approach to validate the uncertainty of continuous point source emission intensities (i.e., source strengths) in a variety of near surface, atmospheric modeling applications [25]. This bootstrapping approach randomly samples the error residuals from the best fitting model prediction and synthesizes a new dataset for which the model is recalibrated against to obtain a new set of parameter values. This process is repeated a large number of times (M = 1000 in this study) until many realizations of the parameter values are reached. These parameter values are then combined to estimate the parameter variance-covariance matrix [6]. From this approach, the standard error of the methane emission rates from all 333 gridpoints was obtained. The overall standard error (SE) for site-wide emissions was then computed by combining the standard errors from each source contribution (. The 95% confidence intervals describing the uncertainty of the predicted site-wide methane emissions were then derived using Eq. (10), where is the inverse t-distribution estimate for the confidence interval of interest.
| (10) |
The resulting whole-site methane emission rate predicted from the unconstrained NSGPE approach was determined to be 3.72 × 105 kg/day (135,780 tonnes/year), with a 95% confidence interval ranging from 2.97 × 105 to 4.47 × 105 kg/day using the robust approximation method. The somewhat narrow bounds of the emissions estimate obtained from the bootstrapping approach indicate that the unconstrained approach still provides an acceptable prediction of the methane emission rates from the landfill.
A simplified method to estimate methane emissions uncertainty using the NSGPE framework was further explored. In the simplified method, the standard deviation of the site-wide methane emissions estimates was first obtained across the 10 independent optimization runs. The 95% confidence intervals were then constructed assuming a normal error distribution. The results of this analysis indicated that the 95% confidence interval ranged from 3.57 × 105 to 3.87 × 105 kg/day, which is similar in range to that reported for the robust approach. Therefore, the simplified method was applied to estimate the confidence intervals for the remaining steps of the NSGPE approach below.
Statistical filtering of NSGPE results
A statistical filtering approach was employed to isolate the most probable methane emissions obtained from the inverse model. This step was deemed necessary to remove any spurious, non-physical emissions estimates and to effectively smooth the methane emission results. Following model calibration, a sensitivity analysis was conducted by increasing each calibrated emission rate by 30%, one at a time (while holding all other rates constant), and then observing the response in RMSE values (. A filtered set of methane emission rates was obtained by isolating outlying (i.e., significant) values using a boxplot analysis. were considered outliers if they were more than 1.5 times greater than the interquartile range, resulting in a subset of methane emissions estimates of higher statistical confidence and reliability.
Site-wide variation in values obtained from the statistical filtering approach is presented in Fig. 13. The southeast region of the landfill was generally associated with the point source emission locations demonstrating the highest sensitivity to the overall objective function (yellow, orange, and red coloring). This region of the landfill is in close proximity to the active face and daily cover locations and contribute most to the receptor locations demonstrating the highest methane concentrations along the entire perimeter run. The central and western interior regions of the landfill were the least sensitive emission locations (dark blue, cyan, green). These regions of the landfill are generally representative of intermediate or final cover locations with low corresponding emissions. In addition, some peripheral regions were designated as non-sensitive from this analysis, which confirms that some colocation issues were resolved through development and application of the statistical filtering approach (as emissions from these locations were dropped completely from the analysis).
Fig. 12.
Spatial distribution in ΔRMSE values used in statistical filtering.
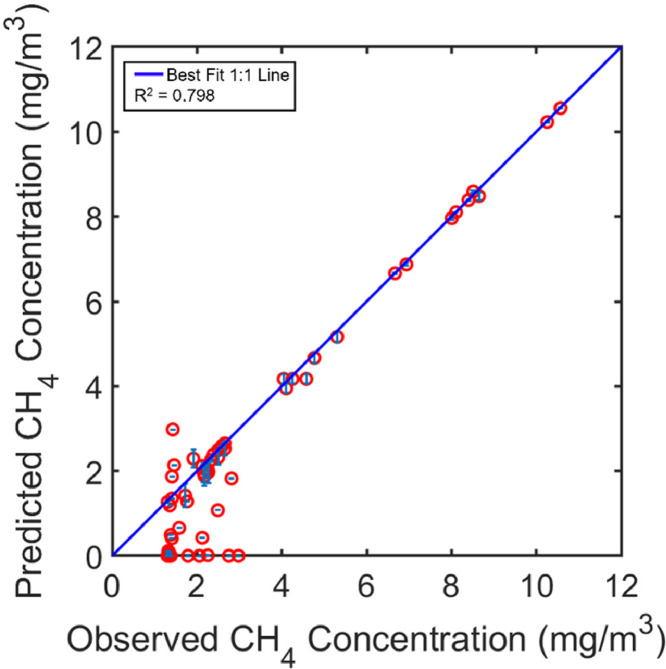
Whole-site methane emissions estimates following the statistical filtering approach were calculated as 2.25 × 105 kg/day (8.22 × 104 tonnes/year). This site-wide methane emissions value is significantly lower than that determined using the unfiltered NSGPE approach (40% reduction), demonstrating the utility in removing potential spurious and non-physical emission estimates obtained from the optimization algorithm. Over ten independent runs, the overall, averaged R2, adjusted R2, and root mean square error (RMSE) were calculated as 0.798, 0.786, and 1.06, respectively. In addition to these summary model-data fitting metrics, the reliability of the filtered NSGPE was preserved. As evidenced in Fig. 14, the filtered NSGPE approach was able to well replicate field measurements, after removing non-sensitive emission estimates obtained from the initial optimization runs. The uncertainty in methane emissions from the filtered NSGPE approach, as quantified using the simplified method, indicated that predicted whole-site methane emissions ranged from 2.15 × 105 to 2.35 × 105 kg/day.
Fig. 13.
Agreement between predicted and observed methane concentrations using the NSGPE approach with statistical filtering. Error bars represent the standard deviation in the predicted methane concentrations across 10 independent trial runs.
Spatial variation in predicted methane emissions for the filtered NSGPE approach are summarized in Fig. 15. Similar to Fig. 11, both the spatially averaged methane emission predictions from ten independent optimization runs (Fig. 15a) and the single best performing optimization run (Fig. 15b) are provided. When applying the statistical filter, the peripheral emissions, previously identified as a numerical artifact of the optimization algorithm, are significantly reduced, particularly at the north-northeastern region of the landfill (Fig. 11 vs. Fig. 15). Methane emissions also appear less broadly distributed across the site and more spatially refined in areas of high sensitivity (e.g., southeastern region). Lastly, the results obtained for the best performing optimization run are aligned somewhat well with the averaged results, where hot spot locations associated with high emissions are in general agreement with the averaged results. There are still some observed qualitative differences between these results, but the results are somewhat more aligned as compared to the unfiltered NSGPE results.
Fig. 14.
Methane emissions predicted using the NSGPE approach with statistical filtering for a) the average of 10 and b) best performing optimization runs.
Topographical reduction and wind modification factor approaches
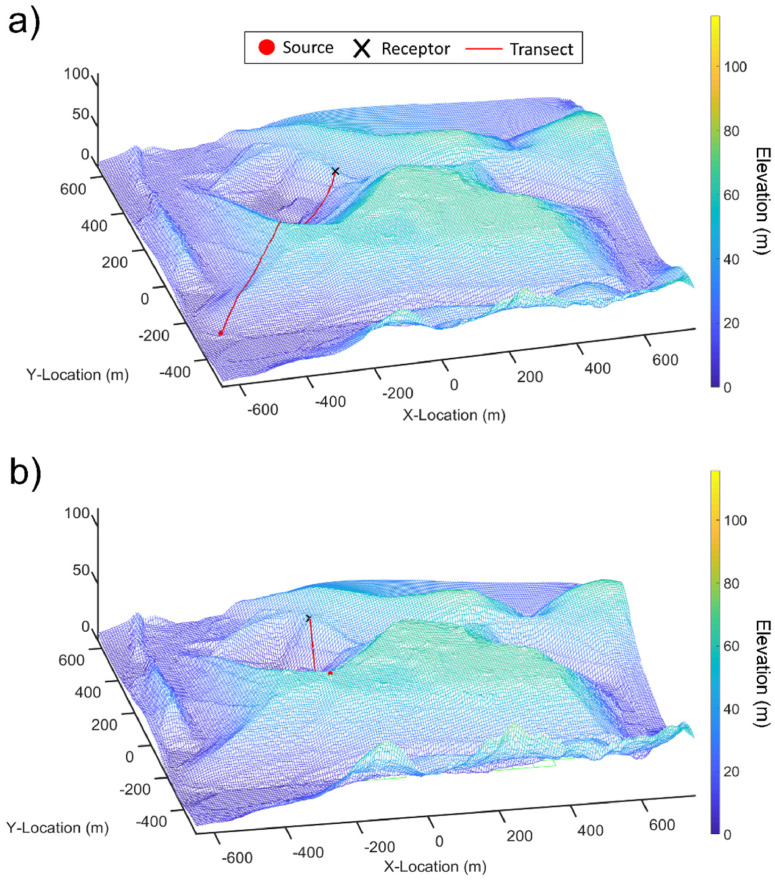
To further improve the application of the inverse modeling effort, a source specific set of reduction factors were developed and applied to offset non-physical methane emissions resulting from variations in topography across the landfill site. Two distinct cases were considered to develop the reduction factors. First, the presence of physical obstructions between source-receptor pairs was considered. Turbulent airflow conditions (i.e., eddies) near the ground surface are formed when the gas plume encounters physical obstructions along the flow path, thereby increasing the distance (and time taken) for gas molecules to reach receptor locations (Fig. 16a). In the second case, downwind receptor locations may be present at elevations that are well below the theoretical distance that gas molecules can disperse (i.e., the dispersion length), signifying that elevation differences between source and receptor locations must also be accounted for (Fig. 16b).
Fig. 15.
Development of an elevation transect in reduction factor estimation for a) the physical obstruction case and b) the large elevation difference between source and receptor case.
The methodology applied to develop and apply this set of source specific reduction factors is described herein. For each source-receptor pair, a 1D transect was obtained from the digital elevation model of the site along the direct pathway extending from the source to the receptor (Fig. 17a). The location associated with the highest elevation along the transect was then identified (Zmax), and the downwind distance (ΔX1) from the source to the highest elevation location was calculated. In addition, the height difference between the source and the highest elevation (ΔZ1) was determined. Lastly, the dispersion length in the Z-direction (σz,1) was estimated at the downwind distance (ΔX1) using the Briggs approximations and corresponding atmospheric stability class. A similar approach was applied for the second case; however, the source location was associated with the highest elevation on the transect and a new set of parameters were calculated (ΔZ2,ΔX2, and σz,2) based on spatial differences between the source and receptor locations (Fig. 17b).
Fig. 16.
Example of an elevation transect used in reduction factor estimation for a) the physical obstruction case and b) the large elevation difference between source and receptor case.
In both cases, the calculated height differences (ΔZ1 and ΔZ2) were compared to the estimated dispersion lengths (σz,1 and σz,2) to ascertain to what extent the emission source was affected by the two cases indicated above. A comparison algorithm was applied to conduct this classification. The algorithm was developed to first bin the source-receptor pair into one of the two cases described above, based on the equivalence between computed height difference values (ΔZ1 and ΔZ2). For both cases, if the height differences (ΔZ1 and ΔZ2) were greater than the dispersion lengths (σz,1 and σz,2), the source-receptor pair was classified as affected. If the first case classification results were determined to be unaffected, the source-receptor pair was then sequentially checked against criteria set forth for the second case to ensure that the elevation differences between the source and receptor were non-limiting. If the source was classified as affected, a follow up evaluation was conducted to determine the magnitude of the effect, as described below.
A statistical analysis was developed to return numerical scores characterizing the magnitude of the topographical effects. Since the Gaussian plume equation relies on a normal distribution approximation of the change in methane concentration as a function of elevation (due to dispersion), the probability of topographical influences on methane transport and detection () was computed using the distance between the height differences (ΔZ1 and ΔZ2) and dispersion lengths (σz,1 and σz,2) as the evaluation interval for the normal probability density function. The overall probability (P) was calculated by modifying the previous results so that lower values were indicative of a higher probability of being affected by topographical variations at the site (Eq. (11)). The magnitude of the overall probability was then used to assign a numerical score to the source-receptor pair. A scoring table using ten individual bins was established based on the range in computed probability values (Table 4). Evaluation scores assigned to each source-receptor pair using this approach ranged from 0 to 100, where low probability values were assigned a small evaluation score, signifying they were more likely to be affected by variations in topography.
| (11) |
Table 4.
Summary of the scoring scheme used in reduction factor calculation.
| Bin Number | Probability Range | Numerical Score |
|---|---|---|
| 1 | 0 | |
| 2 | 10 | |
| 3 | 20 | |
| 4 | 30 | |
| 5 | 40 | |
| 6 | 50 | |
| 7 | 60 | |
| 8 | 70 | |
| 9 | 80 | |
| 10 | 90 |
A modification factor to account for the wind direction at the site was also included in the estimation of the overall reduction factor for each methane emission point source. The wind modification factor was intended to weigh the receptor locations closer to the azimuth of the average wind direction higher in the overall reduction factor calculation. Ultimately, receptor locations that are located closer to the mean wind direction are associated with higher certainty in the inverse-modeling process and are more representative of the downwind methane concentrations than receptor locations located much farther away from the wind direction azimuth. This modification factor was calculated using the derivative of the hyperbolic tangent function (Eq. (12)), which was set to return values on a scale from 0.01 to 1, depending on the crosswind distance away from the wind direction azimuth. The x-value in Eq. (12) represents the crosswind distance of each receptor from the mean wind azimuth, scaled within a range from −3 to 3 to properly apply the hyperbolic tangent function. This function provides a non-linear estimate of the attenuation of the strength of the emissions as a function of crosswind distance from the mean wind direction azimuth. A value of 0.01 (1%) was used as the lower limit to ensure that the modification factor was not too severe in magnitude when discounting emissions across the site. A modification factor was calculated for each source-receptor pair and multiplied by the evaluation score obtained from the scoring table above to effectively account for the effects of wind direction on the overall reliability of methane emissions estimates.
| (12) |
This algorithm was repeated for all source-receptor combinations and the reduction factor for each point source emission was calculated according to Eq. (13) below as the ratio of the total combined evaluation scores to the total scoring potential. Therefore, lower reduction factors were indicative of point sources more likely to be affected by variation in topography across the landfill site, based on the two cases introduced above.
| (13) |
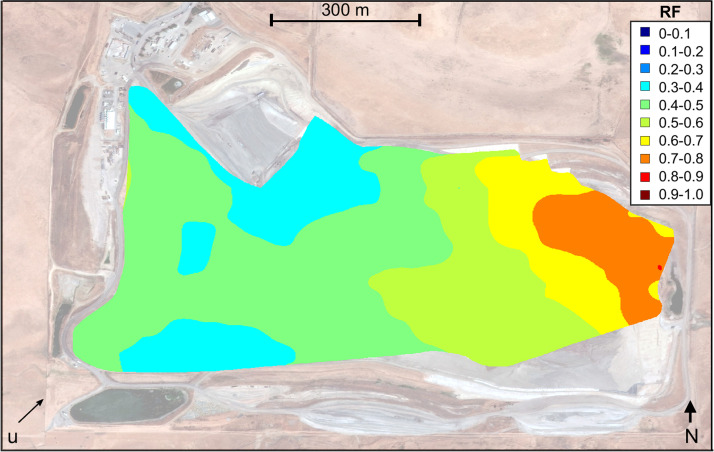
Once calculated, source location specific reduction factors were applied such that the overall agreement between model predictions and experimental observations of methane concentrations around the landfill perimeter were not significantly affected. An R2 and adjusted R2 threshold of 0.70 was integrated during the application of the source specific reduction factors. In a stepwise fashion, the reduction factors were applied one at a time, first targeting the least sensitive emission sources (as determined from the statistical filtering post-processing step) and ending with the most sensitive emission sources. After applying each reduction factor, both the R2 and adjusted R2 were calculated and compared against the threshold established above. This process continued, including additional reduction factors to the list, one at a time, until the R2 and adjusted R2 approached 0.70. This approach resulted in the application of 300 out of 333 reduction factors (∼90%) while still maintaining an acceptable model calibration performance (Fig. 18). Over ten independent runs, the overall, averaged R2, adjusted R2, and root mean square error (RMSE) were calculated as 0.734, 0.718, and 1.21, respectively. The spatial distribution in reduction factors resulting from this analysis were aligned with initial expectations, where higher values were obtained from locations with low elevation differences between source-receptor pairs as well as receptor locations in close proximity to the average wind azimuth (Fig. 19). These locations associated with high reduction factors (i.e., low influence of topography/meteorology on transport) were generally in the southeastern region of the landfill (yellow and orange). Progressing from the eastern to the western regions of the landfill, reduction factors generally decreased, indicating increasing effects of topography/meteorology on methane transport.
Fig. 17.
Spatial distribution in calculated reduction factor values.
Fig. 18.
Agreement between predicted and observed methane concentrations using the NSGPE approach with reduction factors. Error bars represent the standard deviation in the predicted methane concentrations across 10 independent trial runs.
Whole-site methane emissions estimates employing the NSGPE approach with statistical filter and reduction factors were determined to be 1.30 × 105 kg/day (47,414 tonnes/year). This site-wide emissions estimate is significantly lower than the original unfiltered NSGPE emissions estimate (65% reduction). Application of the simplified method for calculation of 95% confidence intervals resulted in the following range in methane emissions: 1.23 × 105 to 1.37 × 105 kg/day.
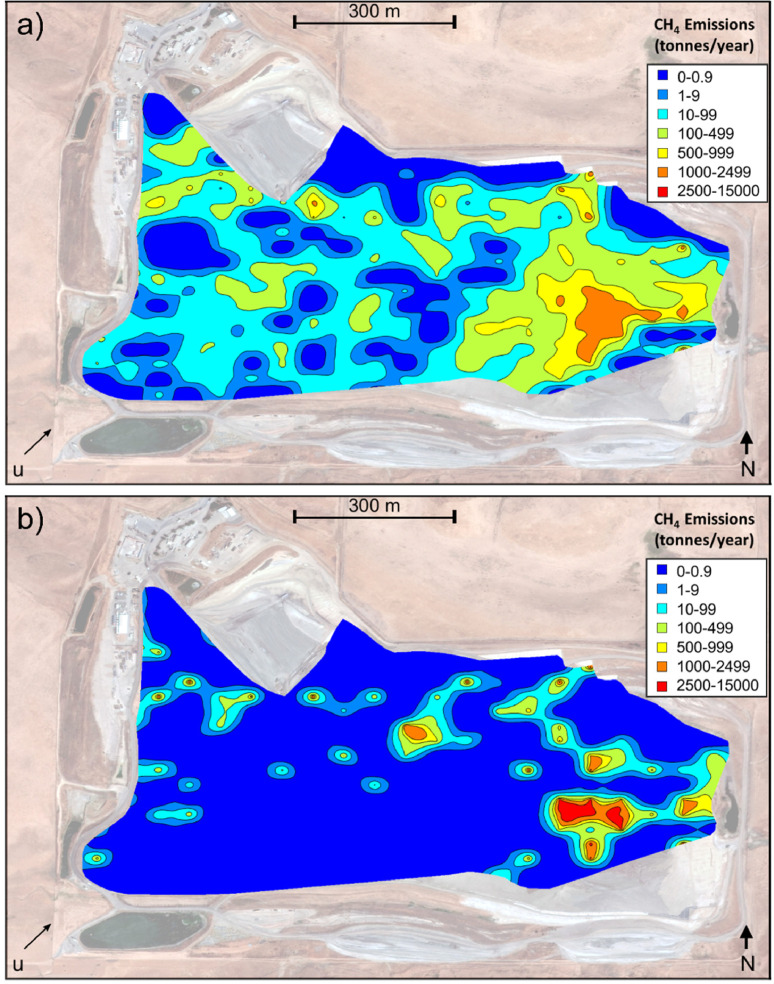
Spatial variation in methane emissions obtained from the filtered and reduction factor based NSGPE method are summarized in Fig. 20. Similar to Figs. 11 and 15, both the spatially averaged methane emission predictions from ten independent optimization runs (Fig. 20a) and the single best performing optimization run (Fig. 20b) are provided. As compared to results obtained from previous steps of the fully integrated NSGPE approach, the spatial estimates of methane emissions are significantly more resolved and co-located in regions with high sensitivity and low influence of topography/meteorology on methane transport. In general, emission hot spots from the best performing optimization run are well aligned with the averaged results, indicating that variability in results among optimization runs has been reduced with the inclusion of the reduction factors accounting for site-specific topographical and meteorological influence on methane transport.
Fig. 19.
Methane emissions predicted using the NSGPE approach with reduction factors for a) the average of 10 and b) best performing optimization runs.
NSGPE approach validation, current limitations, advantages, and future perspectives
Validation of the NSGPE inverse modeling predictions of whole-site methane emissions was included herein to evaluate the overall reliability of the approach. As part of the validation effort, results obtained from the NSGPE approach were compared to existing field measurements and predictions of methane emissions from municipal solid waste landfills in California (Table 5). Whole-site methane emissions data was inventoried and compiled from 50 active municipal solid waste landfills in California in a prior literature review [19]. Small, medium, and large size landfills were included in this review based on reported waste in place. The landfills inventoried varied in geographic region and corresponding climate zone. Emissions measurement methodology varied from ground-based (e.g., static flux chamber, vertical radial plume mapping) to aerial-based approaches (e.g., aircraft mass balance, remote sensing). In addition, whole-site methane emissions data were summarized from a recent field investigation comparing seven different measurement approaches applied concurrently at the same landfill from which the NSGPE approach was applied [29]. Measurement methodologies included in this companion study ranged from field approaches, including static flux chamber and aerial mass balance, to modeling predictions, including the California Methane Inventory Model (CALMIM) and inventory-based approaches. Reported California statewide methane emissions from active municipal solid waste landfills varied over eight orders of magnitude, where average emissions approached approximately 2000 tonnes/year. The range in whole-site methane emissions from the landfill studied herein was lower than that reported from the state (424 to 15,496 tonnes/year), but the variation among measurement methods (as indicated by the standard deviation) was significantly higher (Table 5). Whole-site methane emissions predictions from the NSGPE approach were generally higher than existing data, albeit on an equivalent order of magnitude as compared to the maximum values observed from California landfills in the literature. Even with post-processing refinements, the NSGPE approach still tended to indicate high methane emissions from the landfill site of interest compared to the other approaches (Table 5,[29]). However, the standard deviations and overall ranges were relatively low, indicating that the NSGPE approach was repeatable, consistently reproducing field observations of methane concentrations. In addition, the relative spatial distribution of the NSGPE emissions generally agreed with flux chamber data with high modeled emissions for the daily covers (and low modeled emissions for the final cover), as reported in the companion paper [29].
Table 5.
NSGPE summary comparison to existing whole-site methane emissions data (tonnes/year).
| Summary Statistic | NSGPE Unfiltered | NSGPE Filtered | NSGPE Filtered and Reduced | Potrero Hills Landfill Summary | CA Landfill Summary |
|---|---|---|---|---|---|
| Mean (Best Optimization Run) |
134,823 (135,780) |
73,589 (82,210) |
46,424 (47,414) |
6503 (N/A) |
2024 (N/A) |
| Standard Deviation | 9044 | 6128 | 3927 | 13,153 | 4166 |
| Maximum | 154,038 | 84,851 | 51,079 | 15,496 | 34,000 |
| Minimum | 122,792 | 66,153 | 41,243 | 424 | 0.00026 |
N/A Not Applicable.
High whole-site methane emissions from NSGPE can be attributed to various sources of uncertainty including measurement error, parameter (source strength) identification, and model structural (i.e., epistemic) errors. As measurement error is considerably reduced with the CRDS approach and given that parameter variation was generally within reasonable bounds, high whole-site methane emissions can be primarily attributed to the mechanistic structure of the Gaussian dispersion model. As introduced above, one of the inherent limitations of the Gaussian dispersion model is that it considers the model domain as a flat plane and does not consider the effects of topography or surface roughness on gas transport from source to receptor locations. The Gaussian model assumes stationarity, in that the atmospheric stability, wind speed, and direction, among other variables, are constant with space and time. The NSGPE approach does not spatially constrain methane emissions estimates during calibration. A main goal during the initial development of the NSGPE approach was to ensure objectivity in model design and analysis to increase the applicability and predictive utility of the modeling platform. Without designated spatial constraints applied during model calibration (i.e., applying emissions thresholds in daily, intermediate, and final cover regions), however, it is difficult to overcome all challenges observed herein with emissions overestimation. Despite these current limitations, the NSGPE approach developed and applied herein is promising in that it explicitly addresses issues with parameter overfitting using a statistical filter that isolates the most sensitive methane emission sources. Further, spatially resolved estimates of methane emissions were obtained by applying topographical and meteorological reduction factors that consider the unique topography of the site that is inverse modeled. In addition, the elevations of emission sources were integrated directly into the NSGPE inverse modeling effort, which addresses many current limitations with existing Gaussian dispersion model predictions [4,14,15].
The main advantages of applying the NSGPE approach include ease of use, spatial delineation of whole-site emissions, and flexibility to account for topographical and meteorological influence on methane transport through the use of novel post-processing algorithms. With further development, the NSGPE approach can be used in the field concurrently with ground CRDS to provide near-instantaneous estimates of methane emissions, which considerably reduces the time and cost-investment as compared to conventional methane emissions measurement and monitoring approaches (e.g., flux chamber, surface sweeps using FTIR). Future analysis is suggested to account for localized atmospheric boundary effects such as surface roughness/complexity on wind speed and turbulence intensity [16] and spatiotemporal variations in meteorological conditions (windspeed, direction, and atmospheric stability class) [10], to provide potentially improved mechanistic modeling of methane emissions processes. As part of this analysis, field measurements should be performed concurrently with perimeter measurements in the interior portion of the landfill to provide a basis for further validation of the NSGPE calibrated model. This research would provide indication of the predictive ability of the model, progressing beyond previous calibration efforts presented herein. Similarly, optimal experimental design can be integrated as a valuable tool to enhance the ground CRDS sampling effort to provide a dataset of higher information content for improved parameter identification [3]. Given site-specific topographical and meteorological conditions, optimal experimental design can be applied prior to the site visit to ascertain measurement locations and sampling intervals that return parameter sets of the highest certainty. The sampling design could be further extended to include sampling and concentration measurements conducted in the vertical direction from the mobile monitoring platform. Additional sampling ports mounted in a vertical orientation could provide improved knowledge and understanding of the vertical fluctuation in methane concentrations that would further constrain inverse modeling predictions. These future refinements would provide an integrated field-modeling approach that is highly efficient and adaptable to measure and monitor methane emissions from municipal solid waste landfills.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
This investigation was funded by the California Department of Resources Recycling and Recovery (Contract: DRR16109) and the California Air Resources Board (Contract: 16ISD006). Partial support was provided by the Global Waste Research Institute. The cooperation of Potrero Hills Landfill and Waste Connections, Inc. are appreciated. We appreciate the assistance in the field by Axum Teferra.
Footnotes
Co-Submission: Yeşiller, N., Hanson, J.L., Manheim, D.C., Newman, S., and Guha, A., (2022), “Assessment of Methane Emissions from a California Landfill Using Concurrent Experimental, Inventory, and Modeling Approaches,” Waste Management, Elsevier, Vol. 154, p. 146-159, doi.org/10.1016/j.wasman.2022.09.024.
Data availability
Data will be made available on request.
References
- 1.Awad N.H., Ali M.Z., Suganthan P.N., Reynolds R.G. Proceedings 2016 IEEE Congress on Evolutionary Computation, CEC 2016. Vol. 2016. Institute of Electrical and Electronics Engineers Inc.; 2016. An ensemble sinusoidal parameter adaptation incorporated with l-shade for solving CEC2014 Benchmark problems; pp. 2958–2965. [DOI] [Google Scholar]
- 2.Awad N.H., Ali M.Z., Suganthan P.N. 2017 IEEE Congress on Evolutionary Computation, CEC 2017 – Proceedings, IEEE. 2017. Ensemble sinusoidal differential covariance matrix adaptation with euclidean neighborhood for solving CEC2017 benchmark problems; pp. 372–379. [DOI] [Google Scholar]
- 3.Banga J.R., Balsa-Canto E. Parameter estimation and optimal experimental design. Essays Biochem. 2008;45:195–210. doi: 10.1042/bse0450195. [DOI] [PubMed] [Google Scholar]
- 4.Bel Hadj Ali N., Abichou T., Green R. Comparing estimates of fugitive landfill methane emissions using inverse plume modeling obtained with surface emission monitoring (SEM), drone emission monitoring (DEM), and downwind plume emission monitoring (DWPEM) J. Air Waste Manage. Assoc. 2020;70(4):410–424. doi: 10.1080/10962247.2020.1728423. [DOI] [PubMed] [Google Scholar]
- 5.Bogner J.E., Spokas K.A., Chanton J.P. Seasonal greenhouse gas emissions (methane, carbon dioxide, nitrous oxide) from engineered landfills: daily, intermediate, and final california cover soils. J. Environ. Qual. 2011;40(3):1010–1020. doi: 10.2134/jeq2010.0407. [DOI] [PubMed] [Google Scholar]
- 6.Cameron A.C., Trivedi P.K. Cambridge University Press; 2013. Regression Analysis of Count Data. [Google Scholar]
- 7.Chanton J.P., Powelson D.K., Abichou T., Hater G. Improved field methods to quantify methane oxidation in landfill cover materials using stable carbon isotopes. Environ. Sci. Technol. 2008;42(3):665–670. doi: 10.1021/es0710757. [DOI] [PubMed] [Google Scholar]
- 8.Draper N.R., Smith H. John Wiley & Sons; 1998. Applied Regression Analysis. [Google Scholar]
- 9.Efron B., Tibshirani R.J. CRC Press; 1994. An Introduction to the Bootstrap. [Google Scholar]
- 10.Figueroa V.K., Mackie K.R., Guarriello N., Cooper C.D. A Robust method for estimating landfill methane emissions. J. Air Waste Manage. Assoc. 2009;59(8):925–935. doi: 10.3155/1047-3289.59.8.925. [DOI] [PubMed] [Google Scholar]
- 11.Hanna S.R., Briggs G.A., Hosker R.P., Jr. National Oceanic and Atmospheric Administration; Oak Ridge, TN, United States: 1982. Handbook on Atmospheric Diffusion. [Google Scholar]
- 12.J.L.Hanson, N. Yesiller, D.C. Manheim, Estimation and Comparison of Methane, Nitrous Oxide, and Trace Volatile Organic Compound Emissions and Gas Collection System Efficiencies in California Landfills; Final Report Submitted to CalRecycle and CARB, 2020,https://ww2.arb.ca.gov/sites/default/files/202006/CalPoly%20LFG%20Flux%20and%20Collection%20Efficiencies%203-30-2020.pdf.
- 13.Keeling C.D. The concentration and isotopic abundances of atmospheric carbon dioxide in rural areas. Geochim. Cosmochim. Acta. 1958;13(4):322–334. doi: 10.1016/0016-7037(58)90033-4. [DOI] [Google Scholar]
- 14.Kormi T., Bel Hadj Ali N., Abichou T., Green R. Estimation of landfill methane emissions using stochastic search methods. Atmos. Pollut. Res. 2017;8(4):597–605. doi: 10.1016/j.apr.2016.12.020. [DOI] [Google Scholar]
- 15.Kormi T., Mhadhebi S., Bel Hadj Ali N., Abichou T., Green R. Estimation of fugitive landfill methane emissions using surface emission monitoring and genetic algorithms optimization. Waste Manage. (Oxford) 2018;72:313–328. doi: 10.1016/j.wasman.2016.11.024. [DOI] [PubMed] [Google Scholar]
- 16.Lehning M., Shonnard D.R., Chang D.P., Bell R.L. An inversion algorithm for determining area-source emissions from downwind concentration measurements. J. Air Waste Manage. Assoc. 1994;44(10):1204–1213. doi: 10.1080/10473289.1994.10467315. [DOI] [PubMed] [Google Scholar]
- 17.Liptay K., Chanton J., Czepiel P., Mosher B. Use of stable isotopes to determine methane oxidation in landfill cover soils. J. Geophys. Res. Atmos. 1998;103(D7):8243–8250. doi: 10.1029/97JD02630. [DOI] [Google Scholar]
- 18.T.J. Lyons, W.D. Scott, Principles of Air Pollution Meteorology,(1990) https://www.osti.gov/biblio/5719073 (accessed August 17, 2022).
- 19.Manheim D., Hanson J.L., Yeşiller N. Proceedings-Global Waste Management Symposium. 2022. A Systematic review of methane emissions from californian landfills; pp. 1–3. [DOI] [PubMed] [Google Scholar]
- 20.Pasquill F., Smith F.B. Ellis Horwood Limited; England: 1983. Atmospheric Diffusion. [Google Scholar]
- 21.Saide P., Bocquet M., Osses A., Gallardo L. Constraining surface emissions of air pollutants using inverse modelling: method intercomparison and a new two-step two-scale regularization approach. Tellus B: Chemical and Physical Meteorology. 2011;63(3):360–370. doi: 10.1111/j.1600-0889.2011.00529.x. [DOI] [Google Scholar]
- 22.Saunois M., et al. The global methane budget 2000-2017. Earth Syst. Sci. Data. 2020;12(3):1561–1623. doi: 10.5194/essd-12-1561-2020. [DOI] [Google Scholar]
- 23.W. Schwanghart, Ordinary Kriging, MATLAB Central File Exchange, (2020), https://www.mathworks.com/matlabcentral/fileexchange/29025-ordinary-kriging (retrieved August 5, 2020).
- 24.Singh S.K., Turbelin G., Issartel J.P., Kumar P., Feiz A.A. Reconstruction of an atmospheric tracer source in fusion field trials: analyzing resolution features. J. Geophys. Res. 2015;120:6192–6206. doi: 10.1002/2015JD023099. [DOI] [Google Scholar]
- 25.Singh S.K., Kumar P., Turbelin G., Rani R. Uncertainty characterization in the retrieval of an atmospheric point release. Atmos. Environ. 2017;152:34–50. doi: 10.1016/j.atmosenv.2016.12.016. [DOI] [Google Scholar]
- 26.Sparrow K.J., Chanton J.P., Green R.B., Scheutz C., Hater G.R., Wilson L.C., Abichou T. Stable isotopic determination of methane oxidation: when smaller scales are better. Waste Manage. 2019;97:82–87. doi: 10.1016/j.wasman.2019.07.032. [DOI] [PubMed] [Google Scholar]
- 27.USEPA, Inventory of US Greenhouse Gas Emissions and Sinks: 1990-2020. EPA 430-R-22-003, (2022),https://www.epa.gov/system/files/documents/2022-04/us-ghg-inventory-2022-main-text.pdf.
- 28.Yeşiller N., Hanson J.L., Sohn A.H., Bogner J.E., Blake D.R. Spatial and temporal variability in emissions of fluorinated gases from a California landfill. Environ. Sci. Technol. 2018;52(12):6789–6797. doi: 10.1021/acs.est.8b00845. [DOI] [PubMed] [Google Scholar]
- 29.Yeşiller N., Hanson J.L., Manheim D.C., Newman S., Guha A. Assessment of methane emissions from a California landfill using concurrent experimental, inventory, and modeling approaches. Waste Manage. 2022;154:146–159. doi: 10.1016/j.wasman.2022.09.024. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data will be made available on request.