Quantum mechanical analysis of excitation energy transfer couplings in photosystem II

Abstract

We evaluated excitation energy transfer (EET) coupling (J) between all pairs of chlorophylls (Chls) and pheophytins (Pheos) in the protein environment of photosystem II based on the time-dependent density functional theory with a quantum mechanical/molecular mechanics approach. In the reaction center, the EET coupling between Chls P_D1 and P_D2 is weaker (|J(P_D1/P_D2)| = 79 cm⁻¹), irrespective of a short edge-to-edge distance of 3.6 Å (Mg-to-Mg distance of 8.1 Å), than the couplings between P_D1 and the accessory Chl_D1 (|J(P_D1/Chl_D2)| = 104 cm⁻¹) and between P_D2 and Chl_D2 (|J(P_D2/Chl_D1)| = 101 cm⁻¹), suggesting that P_D1 and P_D2 are two monomeric Chls rather than a “special pair”. There exist strongly coupled Chl pairs (|J| > ∼100 cm⁻¹) in the CP47 and CP43 core antennas, which may be candidates for the red-shifted Chls observed in spectroscopic studies. In CP47 and CP43, Chls ligated to CP47-His26 and CP43-His56, which are located in the middle layer of the thylakoid membrane, play a role in the “hub” that mediates the EET from the lumenal to stromal layers. In the stromal layer, Chls ligated to CP47-His466, CP43-His441, and CP43-His444 mediate the EET from CP47 to Chl_D2/Pheo_D2 and from CP43 to Chl_D1/Pheo_D1 in the reaction center. Thus, the excitation energy from both CP47 and CP43 can always be utilized for the charge-separation reaction in the reaction center.

Significance

The excitation energy transfer (EET) coupling consists of Coulomb (Förster) and exchange (Dexter) couplings. The EET coupling was often approximated by Coulomb coupling, where the exchange coupling is neglected. However, when the edge-to-edge distance between chromophores is short (e.g., ∼4 Å in some chlorophyll pairs in photosystem II), exchange coupling cannot be neglected. In this study, we quantum-mechanically evaluated the EET coupling, taking into account exchange coupling, and identified the EET pathways from the core antennas to the reaction center in photosystem II.

Introduction

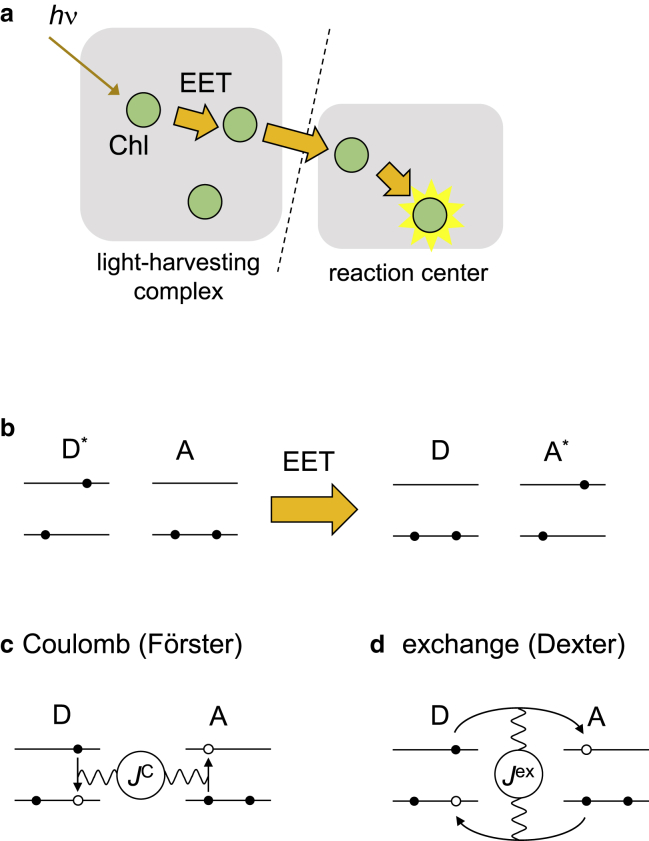
In photosynthesis, excitation energy transfer (EET) is a ubiquitous photophysical process (1,2). Photosynthetic organisms have peripheral light-harvesting (antenna) complexes to capture light energy efficiently. Light energy is absorbed by chromophores (e.g., chlorophylls (Chls)) in the light-harvesting complex and transferred to another chromophore via EET. Light energy is used in photochemical reactions in the reaction center (Fig. 1 a) (3). In EET, the electronic excitation energy is transferred from a donor molecule (D) to a nearby acceptor molecule (A) (1,2) (Fig. 1 b).

Figure 1.

Schematic illustration of EET. Schematic of (a) EET from the light-harvesting complex to the reaction center in photosynthesis, (b) EET reaction from a donor molecule (D) to an acceptor molecule (A), and its (c) Coulomb and (d) exchange mechanisms (4). A^∗ and D^∗ represent the excited states of A and D molecules, respectively. Black arrows indicate the motion of electrons during EET. The waves represent the Coulomb interactions between the electrons. To see this figure in color, go online.

The theory of EET was first formulated by Förster (5) in 1948 and was applied to various systems (1,2,6), including frontier biological single-molecule measurements (7). In a weak coupling scheme, the EET rate constant from a donor chromophore to an acceptor chromophore is given by the following formula based on Fermi’s golden rule (1,2,5,8,9):

$$k=\frac{{\hslash }^2}{2\pi }\left|J^2\right|S\text{,}$$ (1)

where S is the spectral overlap integral between the donor and acceptor and J denotes the coupling (interaction) of the EET, which was originally defined by the off-diagonal matrix element between the initial and final states of the Hamiltonian. In a normal case, it can be assumed that the initial and final electronic states involved in the EET are products of the ground state of donor $|{\mathrm{\Phi }}^{\text{Dg}}⟩$, the excited state of donor $|{\mathrm{\Phi }}^{\text{De}}⟩$, the ground state of acceptor $|{\mathrm{\Phi }}^{\text{Ag}}⟩$, and the excited state of acceptor $|{\mathrm{\Phi }}^{\text{Ae}}⟩$, namely, the initial state $|\mathrm{i}⟩=|{\mathrm{\Phi }}^{\text{De}}⟩\otimes |{\mathrm{\Phi }}^{\text{Ag}}⟩$ and the final state $|\mathrm{f}⟩=|{\mathrm{\Phi }}^{\text{Dg}}⟩\otimes |{\mathrm{\Phi }}^{\text{Ae}}⟩$. Subsequently, the EET coupling (J) can be expressed by the matrix element of the Coulomb interaction ($\hat{V}$) between two electrons as $J=⟨\mathrm{i}|\hat{V}|\mathrm{f}⟩$ and divided into two parts as follows (4):

$$J=J^{\mathrm{C}}+J^{\text{ex}}\text{,}$$ (2)

with (in atomic units)

$$J^{\mathrm{C}}=\sum _{i,j\in I_{\mathrm{D}}}\sum _{R,S\in I_{\mathrm{A}}}⟨{\mathrm{\Phi }}^{\text{De}}|c_{i\sigma }^{†}{c}_{j{\sigma }^{\prime }}|{\mathrm{\Phi }}^{\text{Dg}}⟩⟨{\mathrm{\Phi }}^{\text{Ag}}|c_{R\sigma }^{†}{c}_{S{\sigma }^{\prime }}|{\mathrm{\Phi }}^{\text{Ae}}⟩\times \iint d{\mathbf{r}}_{\mathbf{1}}d{\mathbf{r}}_2{\varphi }_i^{\ast }\left({\mathbf{r}}_{\mathbf{1}}\right){\varphi }_j^{\ast }\left({\mathbf{r}}_{\mathbf{1}}\right)\frac{1}{\left|{\mathbf{r}}_1-{\mathbf{r}}_2\right|}{\varphi }_R\left({\mathbf{r}}_2\right){\varphi }_S\left({\mathbf{r}}_2\right)\text{,}$$ (3)

$$J^{\text{ex}}=\sum _{i,j\in I_{\mathrm{D}}}\sum _{R,S\in I_{\mathrm{A}}}⟨{\mathrm{\Phi }}^{\text{De}}|c_{i\sigma }^{†}{c}_{j{\sigma }^{\text{'}}}|{\mathrm{\Phi }}^{\text{Dg}}⟩⟨{\mathrm{\Phi }}^{\text{Ag}}|c_{R\sigma }^{†}{c}_{S{\sigma }^{\text{'}}}|{\mathrm{\Phi }}^{\text{Ae}}⟩\times \iint d{\mathbf{r}}_{\mathbf{1}}d{\mathbf{r}}_2{\varphi }_i^{\ast }\left({\mathbf{r}}_{\mathbf{1}}\right){\varphi }_R^{\ast }\left({\mathbf{r}}_{\mathbf{1}}\right)\left\{{\hat{\mathrm{h}}}_{\mathrm{core}}+\frac{1}{|{\mathbf{r}}_1-{\mathbf{r}}_2|}\right\}{\varphi }_i\left({\mathbf{r}}_2\right){\varphi }_S\left({\mathbf{r}}_2\right)\text{,}$$ (4)

where $c_{m\sigma }^{†}$ and $c_{n{\sigma }^{\prime }}$ are the fermion creation and annihilation operators that create and annihilate electrons with spins σ and σ′ in the mutually orthogonal orbitals ϕ_m and ϕ_n, respectively. I_D and I_A denote the set of atomic orbital indices of the donor and acceptor molecules, respectively. $\hat{\mathrm{h}}$_core is the one-electron operator for electron-core interactions.

According to Eq. (2), EET mechanisms can be classified as either Coulomb or exchange (Dexter) mechanisms induced by J^C and J^ex, respectively (Fig. 1) (4). In the Coulomb mechanism, the multipole-multipole Coulomb interaction deexcites an initially excited electron on a donor molecule D and simultaneously excites an electron on an acceptor molecule A. In the exchange mechanism, excitation is transferred between D and A when an excited electron, initially belonging to D, is exchanged for a non-excited electron, initially belonging to A.

Eq. (4) indicates that the overlap of orbitals between D and A (e.g., (${\varphi }_i\left({\mathbf{r}}_2\right){\varphi }_S\left({\mathbf{r}}_2\right)$)) is required for J^ex to have a sufficient magnitude, whereas Eq. (3) indicates that overlap is not required for J^C. Therefore, when the center-to-center distance, R_DA, between D and A is sufficiently large, J^ex is negligibly smaller than J^C owing to a small overlap. Furthermore, in this case, J^C can be computed using the transition atomic charges (transition electrostatic potential (TrEsp) charges) as follows (10):

$$J\cong J^{\mathrm{C}}\cong J_{\text{TrESP}}=\sum _{i\in I_{\mathrm{D}},S\in I_{\mathrm{A}}}\frac{q_i{q}_S}{R_{iS}}$$ (5)

where q_i and q_S are the transition charges derived from the quantum mechanical (QM) calculations of excited states and R_iS is the distance between q_i and q_S. Eq. (5) can be expanded by multipole-multipole Coulomb interactions (2,11). In the simplest case, the multipole-multipole interaction in Eq. (5) can be approximated by the lowest-order multipole, i.e., the dipole-dipole interaction, as (11),

$$J\cong J^{\mathrm{C}}\cong J_{\text{dipol}}=\frac{{\mathbf{\mu }}_{\mathbf{D}}·{\mathbf{\mu }}_{\mathbf{{\rm A}}}}{R_{\text{DA}}^3}-\frac{3\left({\mathbf{\mu }}_{\mathbf{D}}·{\mathbf{R}}_{\mathbf{D}\mathbf{{\rm A}}}\right)\left({\mathbf{\mu }}_{\mathbf{{\rm A}}}·{\mathbf{R}}_{\mathbf{D}\mathbf{{\rm A}}}\right)}{R_{\text{DA}}^5}\text{,}$$ (6)

where μ_D and μ_A are the transition dipole moments of D and A, respectively, and ${\mathbf{R}}_{\mathbf{D}\mathbf{{\rm A}}}$ is the center-to-center vector from D to A. J_dipol can be recast as (1,11),

$$J_{\text{dipol}}=\kappa \frac{\left|{\mathbf{\mu }}_{\mathbf{D}}\right|\left|{\mathbf{\mu }}_{\mathbf{{\rm A}}}\right|}{{R_{\text{DA}}}^3}\text{,}$$ (7)

with an orientational factor of

$$\kappa =\cos {\alpha }_{\text{AD}}-3\cos {\beta }_{\mathrm{D}}\cos {\beta }_{\mathrm{A}}\left(-2\le \kappa \le 2\right)$$ (8)

where α_DA is the angle between μ_D and μ_A and β_A and β_D are the angles between μ_D and μ_A, respectively, and ${\mathbf{R}}_{\mathbf{D}\mathbf{{\rm A}}}$ (Fig. 2). Because the expression of J_dipol was first derived by Förster (5), the Coulomb mechanism in Eq. (3) is occasionally referred to as the Förster mechanism, whereas the exchange mechanism was first formulated by Dexter (9) (Fig. 1).

Figure 2.

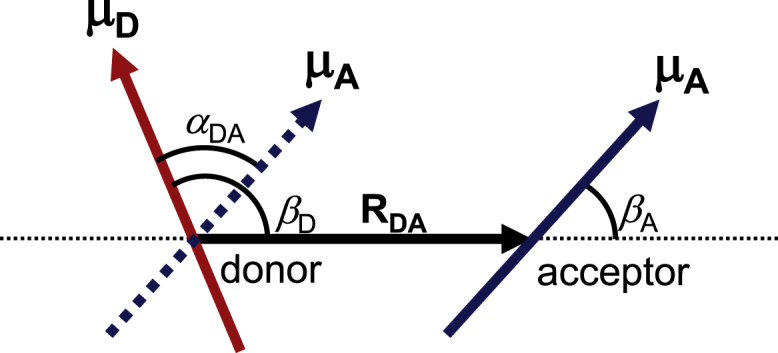
Geometric configurations of transition dipole moments of the donor (μ_D; red arrow) and acceptor (μ_A; blue solid and dotted arrows). R_DA is the inter-molecular center-to-center distance between the donor and acceptor chromophores. α_AD is the angle between the two transition dipole moments. β_D is the angle between μ_D and R_DA and β_A is the angle between μ_A and R_DA. To see this figure in color, go online.

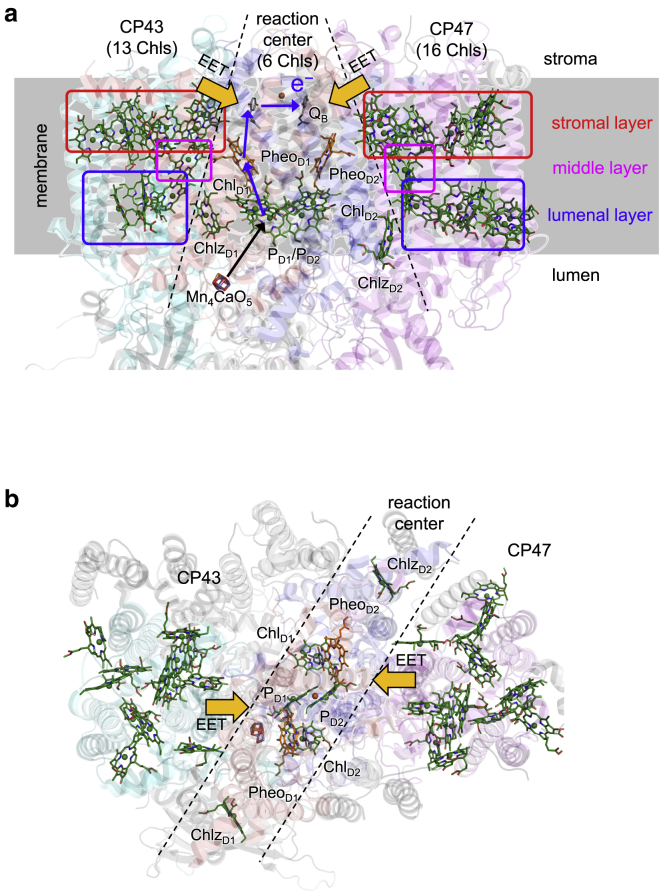
The photosynthetic water-splitting enzyme, photosystem II (PSII), is a multisubunit complex in the thylakoid membranes of higher plants, algae, and cyanobacteria (12,13). The PSII core complex is composed of Chl-binding proteins, a reaction center (D1/D2/cytochrome b₅₅₉ subunit), and core antennas, CP47 and CP43 (13). The reaction center has six Chl molecules, i.e., a central Chl pair of P_D1/P_D2, accessory Chls of Chl_D1/Chl_D2, peripheral Chls of Chlz_D1/Chlz_D2, and two pheophytins Pheo_D1/Pheo_D2. CP47 and CP43 have 16 and 13 Chls, respectively (Fig. 3) (13,14,15). Light energy is absorbed by these Chls and transferred to other Chls through EET. Finally, the energy reaches Chl_D1 in the reaction center and is used for initial energy fixation by forming a charge-separated state between the Chl pair of P_D1/P_D2 and Pheo_D1 (16,17,18,19,20). The EET dynamics from CP47 and CP43 to the reaction center were observed (21,22) and calculated (23,24) together with EET couplings.

Figure 3.

Arrangement of Chls and Pheos in the PSII core complex. Chls (green) and Pheos (orange) are shown (a) parallel and (b) perpendicular to the thylakoid membrane based on PDB code 3ARC (15). The stromal, middle, and lumenal layers in CP47 and CP43 are indicated by red, cyan, and blue boxes, respectively. The reaction center contains the accessory Chl_D1/Chl_D2, the central Chl dimer P_D1/P_D2, Pheo_D1/Pheo_D2, and Mn₄CaO₅ cluster. Light energy captured by CP47 and CP43 is transferred to the reaction center (orange arrows) via EET and induces a charge separation between P_D1/P_D2 and Pheo_D1; this is followed by subsequent electron transfers from Pheo_D1 to a quinone Q_B (blue arrows). The electron hole on the P_D1/P_D2 pair is reduced by the electron transferred from the Mn₄CaO₅ cluster (black arrow). To see this figure in color, go online.

To analyze the EET pathway, the magnitude of EET coupling |J| should be compared with the reorganization energy λ associated with the excitation because EET coupling is also a source for the formation of excitons among the chromophores. When λ ≫ |J|, EET can be described with the rate constant expressed by Fermi’s golden rule of Eq. (1) (the so-called Förster incoherent regime) (25). In contrast, when λ ≪ |J|, EET between the chromophore pairs cannot be described by the Förster incoherent regime of Eq. (1) because the chromophores form an exciton. Therefore, it is needed to classify the treatment of chromophores into the exciton-limit and Förster-limit domains before analyzing the EET pathway (26,27).

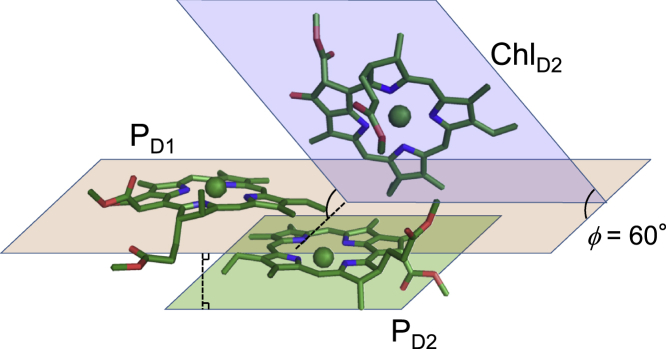
When an exciton is formed, the absorption band of the chromophore splits into low- and high-energy bands. In the reaction center of PSII, previous studies have reported that Chl_D1 has the lowest energy absorption band (19,28,29). In CP47 and CP43, spectroscopic studies (30,31,32,33,34,35,36,37,38) identified low-energy (i.e., red-shifted) trap states, which peaked in the spectra at ∼695 and ∼683 nm in CP47 (30,31,32,38) and CP43 (30,33,39), respectively. It was proposed that these peaks originated from an exciton among some Chls, and the exciton is a substance of the red-shifted trap state, i.e., “red Chl” (26,27,37,40,41). The roles of red Chls in efficient EET were proposed for PSII (42) and other photosynthetic proteins (e.g., PSI) (37,43,44,45). In the reaction center, four central Chls of P_D1, P_D2, Chl_D1, and Chl_D2 are located close to each other (Fig. 3). As the closest Chls pair among them is P_D1/P_D2, it was considered that P_D1 and P_D2 form an excitonic dimer (46,47,48). Notably, their edge-to-edge distance is short (∼4 Å) and the Mg-to-Mg distance is ∼8 Å. Alternatively, the excitonic multimer model comprising four central Chls was also proposed because the estimated EET coupling of P_D1/P_D2 was not sufficiently large in the same order as that of P_D1/Chl_D1 (∼100 cm⁻¹) (49,50). Thus, EET coupling is a crucial factor in the context of excitons, and the values of EET couplings should be accurately estimated to investigate the charge-separation mechanism in PSII.

The expression of J_dipol is beneficial because EET coupling can be estimated based on the orientation of chromophores with the measured transition dipole moment. Therefore, EET couplings were calculated in terms of the dipole approximation (or the transition-atomic-charge approach based on Eq. (5)) described in several studies (23,40,41,48,50,51), where the Dexter term was neglected. However, J is approximated by J_dipol (J^C) only when the donor and acceptor chromophores are sufficiently separated, as explained above. When they are closely located, the original expression of Eq. (2) is more approprite than J_dipol (J^C). Several methodologies were developed and applied to various systems (e.g., PSII (11), CP29 (52) and light-harvesting complex II (LHCII) antenna proteins (53), PSI (54,55), the Fenna-Matthews-Olson (FMO) complex (56), solid-state tetracenes (57), and nanocrystals (10)) to calculate EET coupling beyond the dipole approximation (e.g., multipole (11) and transition-charge (10) (including the Poisson-transition-charge-from-electrostatic-potential (52,54,55,56)) approaches, where only J^C is considered, and the energy-gap (53,57,58) and transition-density-fragment-interaction (59,60,61) approaches). The diabatization scheme developed by Tamura (62) is a QM method in the energy-gap approach to calculate J based on the original expression (Eq. (2)) using time-dependent density functional theory (TDDFT), which has been used in analyzing the EET and charge-separation processes in photosynthetic reaction centers, including PSII (19,20).

Although some Chl pairs in PSII are arranged with a short Mg-Mg distance (e.g., 8.1 Å for the P_D1/P_D2 pair) and a short edge-to-edge distance (e.g., 3.6 Å for the P_D1/P_D2 pair), thus far, EET couplings were calculated only in terms of Coulombic interactions, J^C, i.e., the dipole approximation (23,50,51) or the transition-charge approach (37,40,52). Here, we report EET couplings calculated quantum mechanically in the presence of a PSII protein environment, considering the Dexter term and using the diabatization scheme with quantum mechanical/molecular mechanical (QM/MM) calculations.

Methods

Geometry optimization

The optimized geometry of Chls in the PSII protein environment was obtained as follows: the atomic coordinates of PSII were taken from the X-ray structure of the PSII monomer unit “A” of the PSII complexes from Thermosynechococcus vulcanus at a resolution of 1.9 Å (PDB: 3ARC) (15). Atomic partial charges of amino acids were adopted from the all-atom CHARMM22 27 parameter set (63). D1-His337 was considered to be protonated (64). The electrostatic embedding QM/MM scheme was employed, wherein the electrostatic and steric effects created by a protein environment were explicitly considered. To perform the QM/MM calculation, we used the Qsite (65) program code, employing the restricted DFT method with the B3LYP functional and LACVP^∗ basis sets (LANL2DZ (double ζ quality basis set with Los Alamos effective core potential) for Mn and Ca atoms and 6-31G^∗ for other atoms) (66). The QM region was defined as Chl and Pheo without the phytyl tail and the axial ligand (Table 1). The coordinates of the heavy atoms in the surrounding MM region were fixed at their original X-ray coordinates, whereas those of the H atoms in the MM region were optimized using the OPLS2005 force field. All of the atomic coordinates in the QM region were fully relaxed (i.e., not fixed) in the QM/MM calculation.

Table 1.

Ligands of Chls in the reaction center (D1 and D2), CP47, and CP43

Layera	Chlb	Ligand	3ARCd	3WU2e	2AXTf	Chlb	Ligand	3ARCd	3WU2e	2AXTf
	D2					D1
	PD2	His197	605	402	354	PD1	His198	604	405	558
	ChlD2	Water	607	407	560	ChlD1	water (Thr179)c	606	406	559
	PheoD2	–	609	409	562	PheoD1	–	608	408	561
	ChlzD2	His117	611	403	355	ChlzD1	His118	610	410	563
	CP47					CP43
Lumen	[1]	water (Trp185-C=O, Gly186-C=O)c	612	602	11	–	–	–	–	–
	[2]	His201	613	603	12	–	–	–	–	–
	3	His202	614	604	13	3	His237	628	501	33
	4	His455	615	605	14	4	His430	629	502	34
	5	His100	616	606	15	5	His118	630	503	35
	[6]	His157	617	607	16		–	–	–	–
	7	water (Met37-C=O, Glu41)c	618	608	17	7	water (Met67, Glu71-C=O)c	631	504	37
Middle	13	His26	624	614	26	13	His56	637	510	46
stroma	8	His466	619	609	21	8	CP43-His441	632	505	41
	9	His216	620	610	22	9	CP43-His251	633	506	42
	10	water (Ser240, Ser241)c	621	611	23	10	water (Ser275, Tyr271-C=O)c	634	507	43
	11	His469	622	612	24	11	His444	635	508	44
	12	His23	623	613	25	12	His53	636	509	45
	14	His9	625	615	27	14	Asn39	638	511	47
	15	His142	626	616	28	15	His164	639	512	48
	16	His114	627	617	29	16	His132	640	513	49

^asee Fig. 3a.

^bBracketed Chls are not conserved between CP43 and CP47.

^cThese groups accept H-bond from the ligand or adjacent water molecules.

^dChl/Pheo number in PDB: 3ARC (15).

^eChl/Pheo number in PDB: 3WU2 (15).

^fChl/Pheo number in PDB: 2AXT (14). The Chl numbers in CP47 and CP43 were defined in the figure in (14).

EET coupling

The excited states were calculated in the optimized geometry using the TDDFT method with 6-31G(d) basis sets and the CAM-B3LYP functional (67), as used in previous computational studies for Chls (68,69). Here, the range separation parameters μ = 0.14 (70), α = 0.19, and β = 0.46 were used. Note that the calculated values of the transition dipole moments were essentially the same as those calculated using the LC-BLYP functional (Table S2). For calculations in the protein environment, we employed a TDDFT-QM/MM/polarizable continuum model (PCM) approach (19,20,71). Here, electrostatic interactions of the protein environments were explicitly considered in the presence of bulk water with a dielectric constant of 78.39, and the solvent radius was set to 3.0 Å. The CHARMM force field (63) was used for the MM atoms. We used the QuanPol method (72) implemented in the GAMESS code (73), in which the Lennard-Jones parameters describe the interactions between QM and MM atoms.

Using the obtained electronic structures of the excited states, the QM EET coupling, J_qm, was calculated using the diabatization scheme of adiabatic electronic states (62). The protocol of diabatization used in this study is summarized as follows: 1) for the dimer composed of donor (D) and acceptor (A) molecules, we prepared a set of reference wavefunctions {Φ_I} that possessed pure characteristics of the excited states, such as excitons on a single molecule (e.g., DA^∗ and D^∗A) and charge-transfer states (e.g., D⁺A⁻ and D⁻A⁺), where D^∗ and A^∗ represent excited states of the D and A molecules, respectively); 2) we calculated the adiabatic electronic states {Ψ_k} of the dimer (DA) in the pigment-protein complexes using TDDFT-QM/MM/PCM; and 3) the diabatic wavefunction Φ_I was expressed as a linear combination of the adiabatic wavefunctions {Ψ_k} by evaluating the overlap integrals between the reference and adiabatic wavefunctions as,

$${\mathrm{\Phi }}_I=\sum _k{C}_{Ik}{\mathrm{\Psi }}_k,C_{Ik}=⟨{\mathrm{\Psi }}_k|{\mathrm{\Phi }}_I⟩\text{.}$$ (9)

That is, the adiabatic states {Ψ_j} from the TDDFT-QM/MM/PCM calculations were considered to be basis functions for expanding the diabatic (reference) state Φ_I. The diabatic coupling J_qm between Φ_I and Φ_J was then evaluated as follows:

$$J_{\text{qm}}=H_{IJ}=⟨{\mathrm{\Phi }}_I|H|{\mathrm{\Phi }}_J⟩\text{,}$$ (10)

where H is the electronic Hamiltonian. Eq. 3 is considered for analyzing the pure Coulomb coupling, where the integrals are expanded by two-electron atomic orbital integrals (74).

The phase of wavefunctions was selected such that the sign of J_qm was the same as that of J_dipol. The EET coupling with the dipole approximation J_dipol was calculated using Eq. (6) with the transition dipole moment obtained from TDDFT calculations (Table S2), where R_DA is defined as the Mg-to-Mg distance (the center-to-center distance of the Pheo rings) of the geometry-optimized Chls (Pheos). The EET coupling with the transition-charge approximation J_TrEsp was calculated using Eq. (5) with the transition electrostatic charge obtained from TDDFT calculation, where R_i,s is defined based on the geometry-optimized Chls (Pheos).

Previous studies reported that the transition dipole moment calculated using TDDFT was overestimated (26,27,40). To reproduce the observed spectrum, Raszewski et al. proposed that the transition dipole moment was rescaled (26,27,40). It should be noted that the coupling calculated in this study can also be overestimated. For comparison with previous literature, the rescaled J_dipol values are provided in Table S6, although the raw values calculated quantum-mechanically without rescaling were used in this study because we primarily focused on a comparison between the couplings.

For a quantitative comparison with other studies, the J values, including the effect of the optical dielectric constant, were also calculated by applying an empirical screening factor s of (75) (Table S4).

$$s=A\exp \left(-{\beta R}_{DA}\right)+s_0\text{,}$$ (11)

where the pre-exponential factor is A = 2.68, the attenuation factor is β = 0.27, s₀ = 0.54 is the asymptotic value of s at large distances, and R_DA is the Mg-to-Mg distance (the center-to-center distance of the Pheo rings) in angstroms. The equation is valid when R_DA > 6.6 Å.

The J values of all pairs of 35 Chls and two Pheos (Table 1) in PSII were evaluated as follows: because J^ex is negligible when the overlap integrals between the donor and acceptor molecular orbitals are small, J was approximated by J_TrEsp when the edge-to-edge distance d of the Chl ring (Fig. 4) was larger than 10 Å. In contrast, when the overlap integrals can be expected to be large (d < 10 Å), the QM coupling J_qm was accurately calculated using the diabatization scheme. Note that the exact Coulombic interaction J^C could be sufficiently approximated by J_TrEsp even in Chl pairs with short edge-to-edge distances (Table S3).

Figure 4.

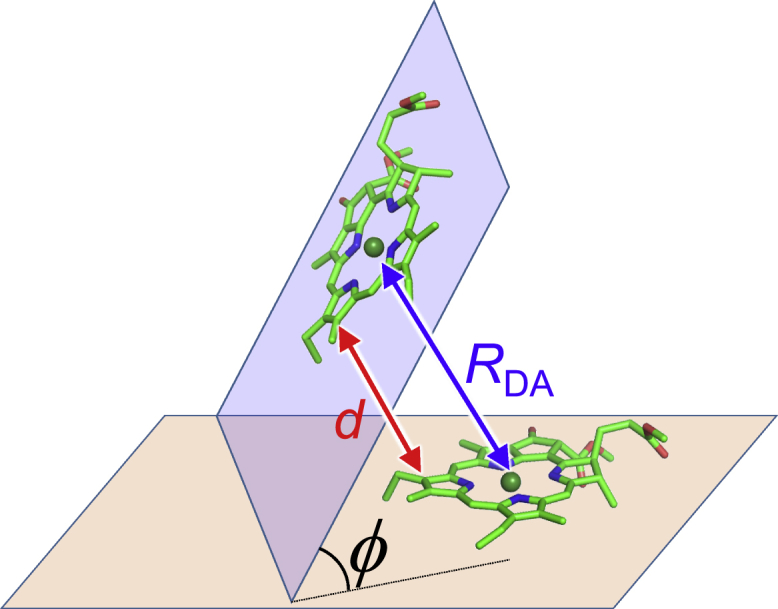
Geometric configurations of two Chls. R_DA, Mg-Mg distance; d, edge-to-edge distance between chlorine rings; and ϕ, angle between the chlorine planes. To see this figure in color, go online.

Results

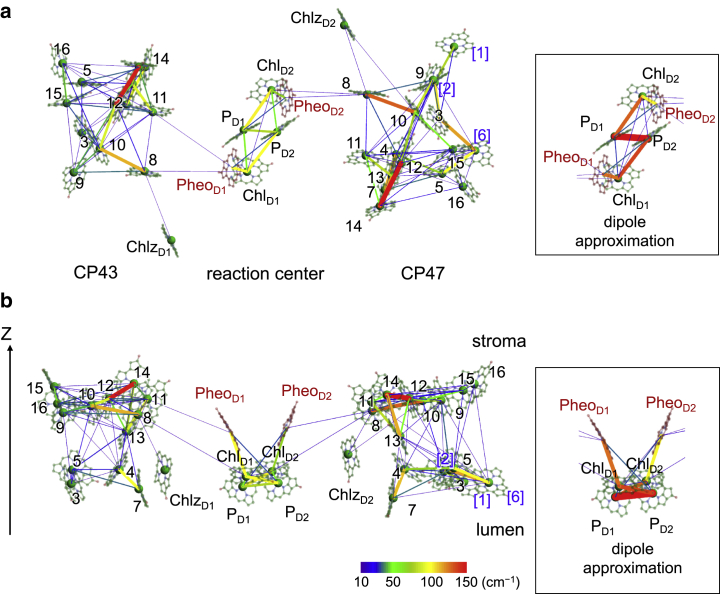
The J values of all pairs of 35 Chls and two Pheos in PSII were investigated (Tables 1, 2, and 3). The spatial positions and sequences of the axial ligands of all Chls are conserved between CP43 and CP47, although CP47 has three additional Chls (CP47-1, 2, and 6) (Table 1; Fig. 5; denoted with the bracket). In the reaction center, |J(P_D1/P_D2)| (= 79 cm⁻¹) is smaller than |J(Chl_D1/P_D2)| (= 104 cm⁻¹) and |J(Chl_D2/P_D1)| (= 101 cm⁻¹), in contrast to the large |J_dipol(P_D1/P_D2)| (= 236 cm⁻¹) in the dipole approximation (Fig. 6; Table 4). The large difference in J(P_D1/P_D2) from J_dipol indicates that the dipole approximation does not hold (J_dipol/J_qm = 3.2), especially in the P_D1/P_D2 pair, as reported in previous theoretical studies (56,76). In contrast, the Coulomb term J^C is well approximated by J_TrEsp within an error of ∼2% (Table 4). This result indicates that the TrEsp approximation (J_TrEsp) is appropriate provided that J^ex is sufficiently small (Table S3).

Table 2.

EET coupling J between Chls in the reaction center and CP47 (cm⁻¹)

Values for J_qm are shown in bold due to the short edge-to-edge distance (d < 10 Å). The bracketed Chls are not conserved between CP43 and CP47. Values are colored in red, orange, yellow, green, and blue for |J| > 150, 125, 100, 50, and 10 cm⁻¹, respectively. See Table S4 for the case in which the distance-dependent dielectric constant is considered.

Table 3.

EET coupling J between Chls in the reaction center and CP43 (cm⁻¹)

Values for J_qm are shown in bold due to the short edge-to-edge distance (d < 10 Å). Values are colored in red, orange, yellow, and blue for |J| > 150, 125, 100, 50, and 10 cm⁻¹, respectively.

Figure 5.

Sequence alignment of CP43 and CP47 from T. vulcanus with the axial ligands of Chls, His (yellow) and Asn (green), hydrogen-bond (H-bond) acceptor of the ligand water cluster of Chl (cyan), and transmembrane helix regions (gray), obtained using Clustal (77). The boxed numbers indicate Chls defined in Table 1. Bracketed Chls are not conserved between CP43 and CP47. To see this figure in color, go online.

Figure 6.

EET coupling network (|J| >10 cm⁻¹). View from the field (a) parallel and (b) perpendicular to the membrane. Color and width of the lines indicate the magnitude of J. The Chl number corresponds to that in Table 1 (the blue bracketed number indicates Chl existing only in CP47). The boxed picture shows EET coupling, J_dipol, calculated by the dipole approximation. To see this figure in color, go online.

Table 4.

Calculated couplings among the four central Chls and two Pheos in the reaction center

Chl pair		RDA (Å)	da (Å)	κb	ϕc (◦)	Jqm (cm−1)	Jexd (cm−1)	JC (cm−1)	JTrEsp (cm−1)	JTrEsp/JC	Jdipol (cm−1)	Jdipol/Jqm
PD1	PD2	8.1	3.6	0.92	1.2	79.1	−6.0	85.0	86.6	1.02	−235.7	3.20
PD1	ChlD1	10.4	4.5	−0.22	65.4	−58.0	4.9	−62.9	−63.1	1.00	−29.7	0.64
PD1	ChlD2	12.2	5.1	−1.59	72.3	−104.2	−11.3	−92.9	−92.5	1.00	132.4	1.19
PD1	PheoD1	15.4	7.8	−0.24	62.5	−7.4	1.9	−9.3	−9.4	1.01	−8.2	1.12
PD2	ChlD1	12.1	5.2	−1.54	64.5	−101.4	−10.4	−91.0	−91.7	1.01	131.5	1.26
PD2	ChlD2	10.5	5.0	−0.14	73.6	−48.4	5.4	−53.7	−54.2	1.01	−16.8	0.33
PD2	PheoD2	15.1	7.5	−0.24	66.0	−5.8	0.3	33.1	−7.5	1.00	−8.7	1.49
PheoD1	ChlD1	10.5	4.7	1.02	62.1	100.1	11.0	89.1	88.5	0.99	126.6	1.27
PheoD2	ChlD2	10.6	5.0	0.92	62.3	71.3	−0.8	72.0	71.4	0.99	103.3	1.45

Charactaristic values are shown in bold. For other chromophore pairs, see Table S3.

^aEdge-to-edge distance between chlorine rings (Fig. 4).

^bOrientational factor defined by Eq. (9).

^cAngle between chlorine planes (Fig. 4).

^dJ^ex = J_qm − J^C.

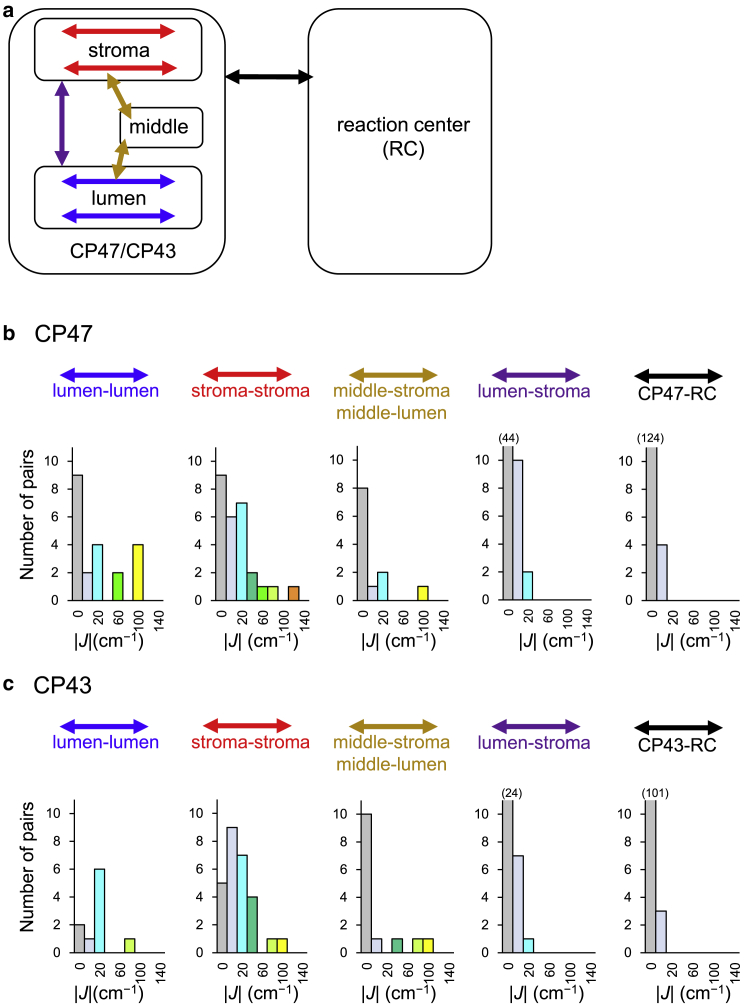
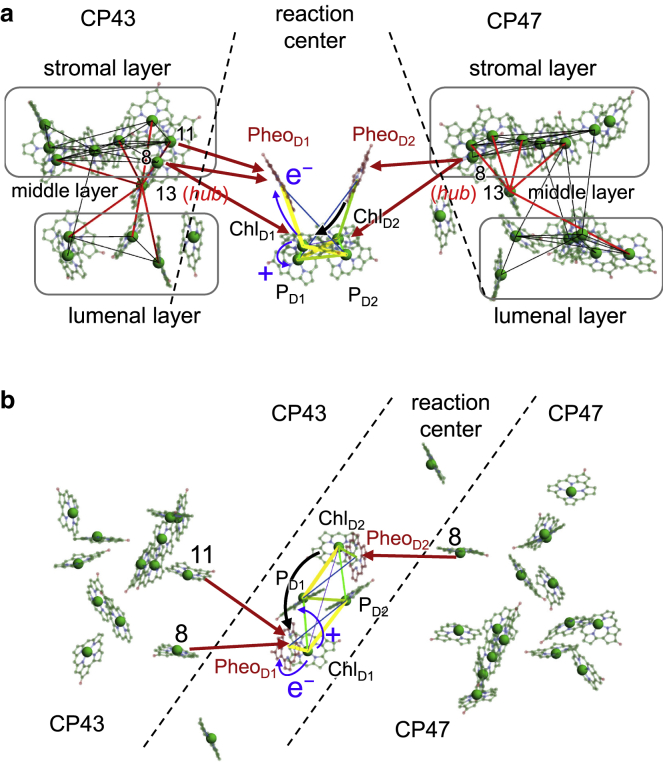
The calculated J values showed the same trend between the Chl pairs in CP43 (Table 2) and CP47 (Table 3) because of the similar sequential and spatial arrangement of Chls (Fig. 6). Chls in CP47 and CP43 can be classified into stromal-, middle-, and lumenal-layer Chls (Fig. 3 a; Table 1) (40). In both CP47 and CP43, intricate network of EET coupling are formed within the stromal and lumenal layers (Fig. 6; red and blue arrows in Fig. 7) and between the middle-layer Chls (CP47-13 and CP43-13) and both the stromal and lumenal Chls (light-brown arrow in Fig. 7) compared with the EET coupling of Chl pairs between the stromal and lumenal layers (purple arrow in Fig. 7). Furthermore, several Chl pairs have large EET couplings (|J| > 100 cm⁻¹) in CP47 and CP43 (Figs. 6 and 7). In contrast, between the reaction center and the core antennas (CP47 and CP43), only a few Chl/Chl and Chl/Pheo pairs are coupled with small J values (|J| ∼10–20 cm⁻¹), and other pairs have no couplings (Fig. 6; red and black arrows in Fig. 7). Note that the EET coupling of all Chl pairs between CP47 and CP43 could be approximated by J_dipol owing to their long distances and small magnitudes (<∼1 cm⁻¹) (Tables S5 and S7; Fig. S1).

Figure 7.

Distribution of the EET interaction J between Chls in the lumenal layer (blue arrow), Chls in the stromal layer (red arrow), middle-layer Chl (CP47-13/CP43-13) and lumenal or stromal Chls (light-brown arrow), lumenal Chls and stromal Chls (purple arrow), and core-antenna Chls and reaction-center Chls (black arrow). (a) Conceptual illustration of the classification of Chl pairs. (b) Distributions in CP47. (c) Distributions in CP43. Values greater than the vertical scale are shown in parentheses. To see this figure in color, go online.

Discussion

Nature of the P_D1/P_D2 pair

In the P_D1/P_D2 pair, the dipole approximation does not hold (J_dipol/J_qm = 3.2) (Table 4). This can be explained by the following reasons: the P_D1/P_D2 Chls are located at a short Mg-Mg distance of 8.1 Å with a short edge-to-edge distance of 3.6 Å (Table 4). In addition, they are arranged in a parallel manner (angle between the chlorine planes, ϕ = 1°) (Table 4; Fig. 8). In this case, the delocalization effect of the transition atomic charges of the Chls cannot be neglected. In contrast, both Chl_D1/P_D2 and Chl_D2/P_D1 Chls are arranged in a non-parallel manner (ϕ = ∼60°) (Table 4; Fig. 8), and the transition atomic charges of Chls can be approximated by the transition dipole. Thus, their couplings have similar values to those in the dipole approximation (J_dipol/J_qm, ∼1.2–1.3). The P_D1/P_D2 pair was considered to form excitons as a “special pair” (46,47,48) or an excitonic multimer (49,50) owing to their short distance and analogy with the special pair P_L/P_M in the bacterial reaction center (16), as the EET coupling of P_D1/P_D2 was estimated to be large (∼150–200 cm⁻¹) in theoretical studies (37,48,50). However, the calculations in the present study show that the P_D1/P_D2 pair has a weaker coupling (79.1 cm⁻¹) than the Chl_D1/P_D2 (−104.2 cm⁻¹) and Chl_D2/P_D1 pairs (−101.4 cm⁻¹). Furthermore, the site energy of P_D1 is 16 meV (130 cm⁻¹) smaller than that of P_D2; i.e., P_D1 and P_D2 are not degenerated (Table S1). This finding differs from results in previous theoretical studies, which reported that P_D1 and P_D2 were (almost) degenerated. This may originate from a difference in the treatment of the protein environment between our QM/MM calculations and methods used in the previous studies. In our QM/MM calculations, the protein structure was taken into account at the atomic level, whereas it was not in model Hamiltonian calculations (e.g., Novoderezhkin et al. (78)). In our QM/MM calculations, the steric effect of Chl geometries from the protein environment was taken into account, whereas it was not in Poisson-Boltzmann electrostatic calculations (e.g., Müh et al. (79)). Thus, P_D1 and P_D2 are two monomeric Chls rather than a special pair^, or a part of the excitonic multimer, as pointed out by Tamura et al. (20).

Figure 8.

Arrangement of P_D1, P_D2, and Chl_D2. Chlorine planes of P_D1 and P_D2 are arranged in a parallel manner (angle between the chlorine planes, ϕ = ∼0°), whereas those of P_D1 and Chl_D2 are arranged in a non-parallel manner (ϕ = ∼60°). To see this figure in color, go online.

Intriguingly, among all the Chl pairs in the reaction center, only the P_D1/P_D2 pair has a large contribution (21%) of the charge-transfer excited state to the adiabatic excitonic state of the Chl dimer (Table S8). The superexchange excitonic coupling of the P_D1/P_D2 pair involving the charge-transfer excited states (80) was calculated. The superexchange excitonic coupling from D to A states J_SX(D→A) is given by,

$$J_{\mathrm{S}\mathrm{X}}\left(\mathrm{D}\to \mathrm{A}\right)=\sum _{\mathrm{M}}\frac{J_{\mathrm{DM}}{J}_{\mathrm{MA}}}{E_{\mathrm{D}}-E_{\mathrm{M}}},$$ (12)

with elements of the Hamiltonian matrix given in Table S9: E_x is the diagonal element of state x and J_yz is the off-diagonal element between states y and z. The summation of M takes over the intermediate M states, which correspond to the charge-transfer excited states of P_D1⁻P_D2⁺ and P_D1⁺P_D2⁻ in this case. The calculated J_SX(P_D1^∗P_D2→P_D1P_D2^∗) and J_SX(P_D1P_D2^∗→P_D1^∗P_D2) are −6.4 cm⁻¹ and −7.4 cm⁻¹, respectively, whose magnitudes are smaller than the direct coupling of J_qm (79.1 cm⁻¹; Table 4). Therefore, our conclusion that the P_D1/P_D2 pair is monomeric does not change, even when the effect of J_SX is considered. The J values of the Chl_D1/P_D1 and Chl_D2/P_D2 pairs are smaller than those of the Chl_D1/P_D2 and Chl_D2/P_D1 pairs because of their small orientational factor (|κ| < ∼0.2) (Table 4).

Candidates of red chlorophyll

When the EET coupling is sufficiently stronger than the homogeneous energy broadening D (induced by the interaction between electrons in the Chl and the protein environment), the coupled Chls form an exciton (48). Here, D can be estimated by

$$D^2=2\lambda k_{\mathrm{B}}T\text{,}$$ (13)

when the thermal energy k_BT is sufficiently high compared with the typical quantum energy of the slow vibrational mode of the solvent molecules and λ represents the reorganization energy associated with the excitation (70). According to Eq. (13), D is estimated to be ∼60 cm⁻¹ at 77 K from the typical reorganization energy (λ = ∼30 cm⁻¹) estimated for Chla in PS II (48).

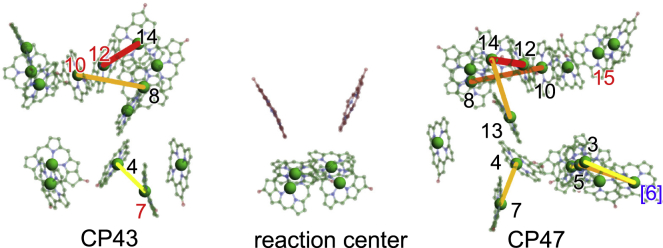
The calculated J values show that the Chl pairs of 12/14, 4/7, and 8/10 in both CP47 and CP43, and CP47-2/3, CP47-3/[6], CP47-5/[6], and CP47-13/14 have large EET couplings (>∼100 cm⁻¹) (Tables 2 and 3; Fig. 6). These Chl pairs can form excitons with a low absorption energy at ∼77 K because the magnitude of their couplings |J| is sufficiently larger than that of D and λ. Thus, they are the most likely candidates for red Chl, which absorbs a significantly longer wavelength than other Chls. In contrast to the P_D1/P_D2 pair in the reaction center, the contributions of the charge-transfer excited state to the adiabatic excitonic state of the dimer were negligibly small (<1%) in those Chl pairs (Table S8). A part of the strongly coupled Chls in CP43, i.e., CP43-7 (26,40,52), 10 (26,37,40), and 12 (26,37,40), is consistent with the proposed red Chls in previous studies. In contrast, no Chl was found in CP47, consistent with the proposed red Chl, where CP47-16 was proposed to emit a fluorescence of 695 nm (37) (Fig. 9). Because CP47-8 and -13 have small site energies (2.092–2.094 eV) (Table S1), the CP47-8/10 and -13/14 pairs are the most likely candidates for red Chls.

Figure 9.

Strongly coupled Chl pairs that are candidates of red Chls. The proposed red Chls (CP43-7 (26,40,52), 10 (26,37,40), and 12 (26,37,40), and CP47-16 (37)) are colored in red. To see this figure in color, go online.

Mechanism of charge separation

In EET couplings of the four central Chls (i.e., P_D1, P_D2, Chl_D1, and Chl_D2) and two Pheos in the reaction center with Chls in CP47 and CP43, only the Chl_D2/CP47-8, Pheo_D2/CP47-8, Chl_D1/CP43-8, Pheo_D1/CP43-8, and Pheo_D1/CP43-11 pairs have sufficiently large couplings (|J| = ∼10–15 cm⁻¹). Thus, the excitation energy is transferred through pathways from CP47-8 to Chl_D2 or Pheo_D1, from CP43-8 to Chl_D1 or Pheo_D1, and from CP43-11 to Pheo_D1. Because the Pheo_D1/Chl_D1 and Pheo_D2/Chl_D2 couplings are sufficiently large (|J| = ∼70–100 cm⁻¹), the excitation energies on Pheo_D1 and Pheo_D2 can be easily transferred to Chl_D1 and Chl_D2, respectively. The excited Chl_D1 can induce a charge-separation reaction between Pheo_D1 and the P_D1/P_D2 pair (20,29). In contrast, the excitation energy of Chl_D2 cannot cause a charge-separation reaction directly (20) but can be transferred through both a “direct” pathway from Chl_D2 to Chl_D1 (|J(Chl_D2/Chl_D1)| = 14 cm⁻¹) and an “indirect” pathway from Chl_D2 via P_D1 to Chl_D1 (|J(Chl_D2/P_D1)| = 104 cm⁻¹ and |J(P_D1/Chl_D1)| = 58 cm⁻¹). Although the excitation energy of P_D2 is higher than that of Chl_D2 (Table S1), the large |J(Chl_D2/P_D1)| (=104 cm⁻¹) allows the excitation energy to be transferred to Chl_D1 by overcoming the energy barrier of P_D2, as reported in a previous theoretical study (20). Thus, the excitation energy from both CP47 and CP43 can be used for the formation of a charge-separated state in the reaction center (Fig. 10).

Figure 10.

EET pathways and the charge-separation reaction in PSII. View from the field (a) parallel and (b) perpendicular to the membrane. The middle-layer Chls of CP47-13 and CP43-13 connect network between the lumenal and stromal layers. The excitation energy from CP47-8 and CP43-8/11 in the stromal layer reaches the reaction center (red arrows). Because Chl_D1/P_D2 and Chl_D2/P_D1 are strongly coupled (yellow line) compared with the P_D1/P_D2 pair (green line), the excitation energy on Chl_D2 can be transferred to Chl_D1 via P_D1 (black arrow); thus, it is used for the charge-separation reaction on Chl_D1(20) (blue arrows). To see this figure in color, go online.

EET between the lumenal and stromal layers

Light energy can be captured by Chls in both stromal and lumenal layers in CP47 and CP43. The excitation energy also reaches CP47 and CP43 from a peripheral antenna, LHCII. Based on the cryoelectron-microscopy structures of the PSII/LHCII supercomplex, the acceptor Chls in the EET from LHCII were identified (e.g., CP47-15, CP47-[6], CP43-15, and CP47-16 (51)) in both stromal and lumenal layers. As the excitation energy is transferred to the reaction center through stromal Chls of CP47-8, CP43-8, and CP43-11, as discussed above, the energy captured in the lumenal layer must be transferred to the stromal layer. However, the direct EET between the stromal and lumenal Chls appears to be inefficient because the Chl pairs between them are weakly coupled (Tables 2 and 3; purple arrow in Fig. 7). In contrast, the middle-layer Chls of CP47-13 and CP43-13 exhibit sufficient interactions (|J| > ∼40 cm⁻¹) with Chls in the lumenal and stromal layers and, thus, have several links with Chls in both the stromal and lumenal layers (Tables 2 and 3; light-brown arrow in Fig. 7). Therefore, middle-layer Chls are essential to transfer energy from the lumenal layer to the stromal layer. Here, middle-layer Chls play a role in the “hub” that connects the network between the stromal and lumenal layers (Fig. 10 a).

Comparison with other photosynthetic complexes

Other photosynthetic proteins (e.g., PSI, LHCI, and LHCII) also possess multiple Chls. Most of these Chls are localized in the lumenal and stromal layers, similar to CP47 and CP43. The localization is probably because polar substitution groups in Chls (e.g., carbonyl and methyl ester groups) make it difficult for them to locate in the hydrophobic middle layer of lipid bilayers. The PSII-LHCII (51) and PSI-LHCI (81) structures showed that these Chls in the lumenal and stromal layers are arranged at a short distance (Mg-Mg distance of ∼10 Å). Therefore, they may strongly couple to each other within the layer, forming an intricate EET network. As the excitation energy can be captured or received from the adjacent antenna systems by the Chls in both the lumenal and stromal layers, the excitation energy has to move between the layers. The protein structures shows that a few Chls are also located in the middle layer (e.g., Chls at His-A734 and His-B718 in PSI from Synechococcus elongatus (82) and His68 in LHCII from pea (83)). From the analogy of CP47 and CP43, these middle-layer Chls may play the role of a hub that connects the lumen side to the stroma side in other photosynthetic proteins.

When the edge-to-edge distance d is shorter than 10 Å, the quantum chemical calculation of the EET coupling was applied in the present study. In PSII, this situation holds true only for the intra-subunit Chl pairs. Therefore, the inter-subunit EET (i.e., between the reaction center and CP47, the reaction center and CP43, and CP47 and CP43) can be estimated based on the EET coupling via the Coulomb-term approximation, although the intra-subunit EET cannot. As the Chls are arranged at a short distance (Mg-Mg distance of ∼10 Å) in other photosystems (e.g., PSI, LHCI, and LHCII), the previous calculations of intra-subunit EET based on the approximated EET coupling (e.g., for the FMO complex(84)) may be revisited with EET couplings calculated quantum-mechanically.

Conclusions

In this study, we analyzed EET couplings quantum-mechanically in the presence of the PSII protein environment, considering the Dexter term and using the QM/MM diabatization scheme. In the reaction center, |J(P_D1/P_D2)| (= 75 cm⁻¹) is smaller than |J(Chl_D1/P_D2)| (= 110 cm⁻¹) and |J(Chl_D2/P_D1)| (= 104 cm⁻¹) (Table 4; Fig. 6). Because the P_D1/P_D2 pair has a weaker coupling than the Chl_D1/P_D2 and Chl_D2/P_D1 pairs, P_D1 and P_D2 are two monomeric Chls rather than a special pair^, or a part of the excitonic multimer.

Light energy captured by Chls in CP43 and CP47 can be transferred within stromal and lumenal layers through the intricate network of EET coupling (Fig. 10). The energy may be trapped by the red-shifted Chl state formed as an exciton delocalized over strongly coupled Chls (Chl pairs of 12/14, 4/7, and 8/10 in both CP47 and CP43, and 2/3, 3/[6], 5/[6], and 13/14 in CP47) (Fig. 9), especially at low temperature. The excitation energy can be transferred between the stromal and lumenal layers through the middle-layer Chls (CP47-13 and CP43-13), which play a role in the hub that connects the network between the layers (Fig. 10 a). Finally, the excitation energy in the core antennas is transferred from CP47-8 and -11 to Chl_D2/Pheo_D2 or CP43-8 to Chl_D1/Pheo_D1. After the energy reaches Pheo_D2 or Chl_D2 in the D2 subunit from CP43-8, it is transferred to Chl_D1 via P_D1 owing to the large |J(Pheo_D2/Chl_D2)|, |J(Chl_D2/P_D1)|, and |J(Pheo_D2/P_D1)| (>∼70 cm⁻¹) (20). Thus, the excitation energy from both CP47 and CP43 can always be utilized for the formation of a charge-separated state in the reaction center (Fig. 10).

Author contributions

H.I. and K.S. designed research. K.S. and K.M performed research. H.T. contributed analytic tools. All authors participated in analyzing data and writing the manuscript.

Editor: Judy Kim.