MNNMDA: Predicting human microbe-disease association via a method to minimize matrix nuclear norm

Abstract

Identifying the potential associations between microbes and diseases is the first step for revealing the pathological mechanisms of microbe-associated diseases. However, traditional culture-based microbial experiments are expensive and time-consuming. Thus, it is critical to prioritize disease-associated microbes by computational methods for further experimental validation. In this study, we proposed a novel method called MNNMDA, to predict microbe-disease associations (MDAs) by applying a Matrix Nuclear Norm method into known microbe and disease data. Specifically, we first calculated Gaussian interaction profile kernel similarity and functional similarity for diseases and microbes. Then we constructed a heterogeneous information network by combining the integrated disease similarity network, the integrated microbe similarity network and the known microbe-disease bipartite network. Finally, we formulated the microbe-disease association prediction problem as a low-rank matrix completion problem, which was solved by minimizing the nuclear norm of a matrix with a few regularization terms. We tested the performances of MNNMDA in three datasets including HMDAD, Disbiome, and Combined Data with small, medium and large sizes respectively. We also compared MNNMDA with 5 state-of-the-art methods including KATZHMDA, LRLSHMDA, NTSHMDA, GATMDA, and KGNMDA, respectively. MNNMDA achieved area under the ROC curves (AUROC) of 0.9536 and 0.9364 respectively on HDMAD and Disbiome, better than the AUCs of compared methods under the 5-fold cross-validation for all microbe-disease associations. It also obtained a relatively good performance with AUROC 0.8858 in the combined data. In addition, MNNMDA was also better than other methods in area under precision and recall curve (AUPR) under the 5-fold cross-validation for all associations, and in both AUROC and AUPR under the 5-fold cross-validation for diseases and the 5-fold cross-validation for microbes. Finally, the case studies on colon cancer and inflammatory bowel disease (IBD) also validated the effectiveness of MNNMDA. In conclusion, MNNMDA is an effective method in predicting microbe-disease associations.

Availability

The codes and data for this paper are freely available at Github https://github.com/Haiyan-Liu666/MNNMDA.

Graphical Abstract

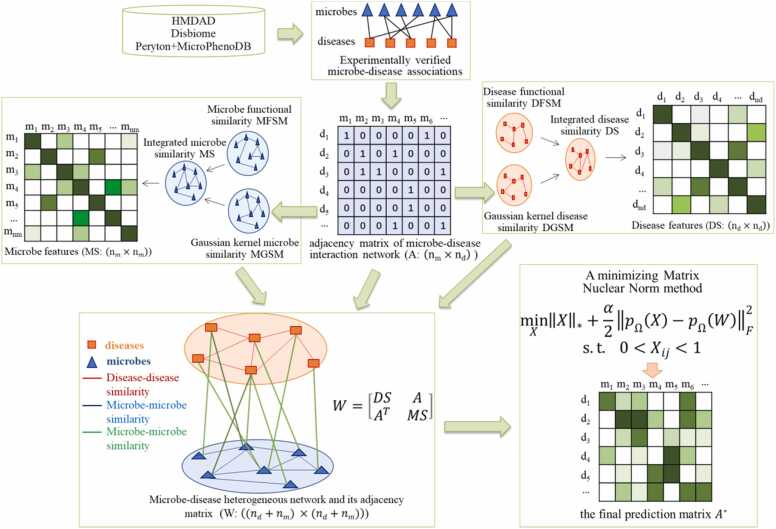
In this study, we proposed a novel method called MNNMDA, to predict microbe-disease associations (MDAs) by applying a minimizing Matrix Nuclear Norm method into known microbe and disease data. Specifically, we explored literatures and related databases to obtain high-quality known relationship between microbes and diseases. By incorporating multiple similarity networks between microbes and diseases, we formulated the microbe-disease association prediction problem as a low-rank matrix completion problem, which was solved by minimizing the nuclear norm of a matrix with a few regularization terms.

1. Introduction

Small in size and simple in structure, human microbe or microorganism is a category of tiny living organisms reproducing quickly and distributing widely [1], [2]. Human microbes are distributed in and on various organs of the human body, such as oral cavity, skin, gut, lung, gastrointestinal tract, and so on. Gut is called the largest microecosystem in the human body, since 80% human microbes are distributed in it [3], [4].

More and more studies have proved that microbes play important roles in the development, treatment and prognosis of many diseases, such as neuronal diseases and cancers [5], [6], [7]. Identifying disease-related microbes not only help reveal the pathological mechanism of human diseases, but also provide potential biomarkers for disease diagnosis and prognosis. Although biological experiment is the gold standard to confirm disease-microbe associations, it is a long process with a high cost. Computational models can prioritize confident disease-associated microbes for further experimental validation.

Recently, machine learning technologies have been widely used and achieved remarkable performances in association predictions, such as lncRNA-disease association prediction [8], [9], [10], [11], [12], [13], drug repositioning [14], [15], [16], [17], [18], [19], miRNA-disease association prediction [20], [21], [22], [23] and so on. Simultaneously, many computational methods have been developed to help identify the relationship between microbes and diseases. For instance, Chen et al. proposed the first KATZ-based computation method called KATZHMDA for predicting microbe-disease associations in 2016 [14]. Wang et al. proposed a LRLSHMDA method based on Laplacian regularized least squares framework in 2017, which used semi-supervised computational models to predict microbial-disease associations without negative samples, and achieved good results [24]. Shi et al. proposed a method called BMCMDA based on binary matrix completion to predict potential MDAs in 2018 [25]. Li et al. proposed a KATZBNRA method based on the KATZ model and bipartite network recommendation algorithm to discover potential associations between microbes and diseases in 2019 [26]. Yan et al. proposed a prediction method BRWMDA based on bi-random walk to predict potential MDAs in 2020 [27]. Liu et al. developed a multi-component Graph Attention Network based framework (MGATMDA) for predicting microbe-disease associations in 2021 [28]. Xu et al. developed a novel computational method (MDAKRLS) to discover potential MDAs based on the Kronecker regularized least squares in 2021 [29]. Hua et al. proposed a multi-view graph convolutional network (MVGCNMDA) to reveal disease-associated microbes using specific data augmentation and multi-view attention blocks in 2022 [30]. Chen et al. proposed a method based on heterogeneous network and metapath aggregated graph neural network (MATHNMDA) to predict MDAs in 2022 [31]. The above computational methods mainly utilized a basic assumption that microbes with similar functions will share similar non-interaction or interaction patterns with phenotypical diseases [32], [33].

Matrix factorization and matrix completion techniques are useful tools and have been widely applied to association prediction [34], [35], [36], [37], [38]. Yang et al. proposed to use a bounded nuclear norm regularization (BNNR) method to complete the drug-disease matrix under the low-rank assumption [39]. Liang et al. proposed a novel antiviral drug repositioning DRMNN method, which formulated the drug repositioning problem as a low-rank matrix completion problem solved by minimizing the nuclear norm of a matrix with a few regularization terms [40].

In this study, we proposed a novel matrix decomposition-based method to predict the association between microbes and diseases. Specifically, we first collected and downloaded data about microbes and diseases from the literature. Second, in order to mine more valuable similarity information, we employed different methods to explore the similarity of microbes and diseases. Third, we constructed a heterogeneous microbe-disease network, which integrates the microbe similarity network, disease similarity network and the microbe-disease association data. Fourth, we used the nuclear norm minimization method to obtain the microbes most likely to be involved in the pathogenesis of a disease. Finally, experimental results and case studies showed that MNNMDA is significantly better than the baseline methods on the HMDAD, Disbiome and Combined Dataset (Peryton and MicroPhenoDB).

2. Materials and methods

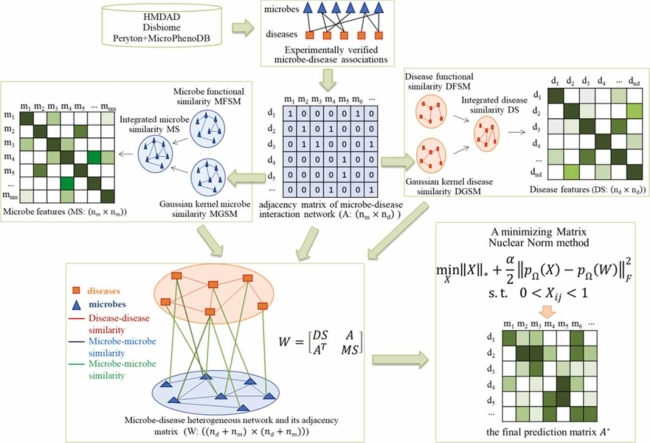
The workflow of MNNMDA for inferring novel MDAs was illustrated in Fig. 1. First, we explored literatures and related databases to obtain high-quality known relationship between microbes and diseases. Second, we calculated multiple similarity networks between microbes and diseases. Third, we built a heterogeneous network based on multi-view features of microbes and diseases. Finally, we applied the minimizing matrix nuclear norm method on the heterogeneous network to calculate the final possibility score of each microbe-disease pair.

Fig. 1.

The overall workflow of MNNMDA.

2.1. Materials

To establish the human microbe-disease interaction network, we retrieve known microbe-disease associations from the Human microbe-disease Association Database (HMDAD) (http://www.cuilab.cn/hmdad), which included 483 experimentally confirmed microbe-disease associations between 39 diseases and 292 microbes [41]. In HMDAD, a microbe-disease pair may include multiply entries from different evidence. Here we consider the same microbe-disease associations from different evidence as a pair. Subsequently, we obtain 450 various associations after removing the superfluous associations. In addition, Janssens et al. released a new microbe-disease association database named Disbiome (https://disbiome.ugent.be/home), where 5573 experimentally confirmed human microbe-disease associations were collected from previously published literature and different databases, including 240 diseases and 1098 microbes [42]. In Disbiome, a microbe-disease pair may be recorded more than one time according to different detection methods. Here we neglect the information of detection methods. After filtering out repetitive data, we finally download 4351 associations between 218 diseases and 1052 microbes. In addition, to evaluate the ability of MNNMDA in handling comprehensive data from multiple datasets, we referred as “Combined data” the dataset compiled by Liu et al. [28], using two different datasets Peryton [43] and MicroPhenoDB [44]. Peryton has 43 diseases and 1396 microbes with 7900 microbe-disease associations; MicroPhenoDB is a collection of microbe-disease association datasets such as HMDAD, Disbiome, VFDB [45], and CARD [46]. Among them, MicroPhenoDB contains 5511 associations between 1774 microbes and 500 diseases. After removing redundant data, 9600 associations were obtained, including 2456 microbes and 537 diseases. Overall, the specific statistics of the three microbe-disease association datasets were shown in Table 1.

Table 1.

The statistics for three microbe–disease association datasets used in this study.

Dataset	# Microbes	# Diseases	# Associations
HMDAD	292	39	450
Disbiome	1052	218	4351
Combined Data	2546	537	9660

We formatted an adjacency matrix of the known human microbe-disease interaction network as $A$, that is, if there exists the experimentally verified relationship between the $i^{\mathit{th}}$ disease $d_i$and the $j^{\mathit{th}}$ microbe $m_j$, $A_{\mathit{ij}}$ equals to 1, otherwise 0. The association between $n_d$ diseases and $n_m$ microbes are represented as a binary matrix $A_{\mathit{ij}}$ where:

$$A_{\mathit{ij}}=\left\{\begin{array}{c}1,\mathit{if}{d}_i\mathit{associats}\mathit{with}{m}_j\\ 0,\mathit{otherwise}\end{array}\right\}$$ (1)

The elements with the values of 1 in $A_{\mathit{ij}}$ are microbe-disease association data and taken as positive samples. The zero entities in $A_{\mathit{ij}}$ are unknown microbe-disease pairs and taken as unlabeled samples.

2.2. Functional similarity of microbes

In this study, we calculated microbe functional similarity based on the method proposed by Kamneva et al. [47]. In order to accurately calculate the functional similarity for a given pair of microbes, we first retrieved protein-protein functional association network from STRING v11 database (https://string-db.org.). More details about the calculation of microbe functional similarity could be found in [47]. We adopt the similarity scores to obtain a $n_m$ ×$n_m$ microbe functional similarity matrix MFSM, where MFSM ($m_i,m_j$) represents the similarity between microbe $m_i$ and microbe $m_j$.

2.3. Functional similarity of diseases

Based on the assumption that similar diseases tend to interact with similar genes [48], [49], we calculated disease functional similarity based on the functional associations between disease-related genes. The latest released HumanNet v2.0 database (https://www.inetbio.org/humannet/download.php) is available for effectively accessing gene interactions [50], [51], where each interaction has an associated log-likelihood score $(\mathrm{LLS})$ that evaluates the probability of a functional linkage between genes. For a disease pair $d_i$ and $d_j$, we first derived their related gene sets $G_i=\left\{g_{i1},g_{i2},\dots ,g_{\mathit{im}}\right\}$ and $G_j=\left\{g_{j1},g_{j2},\dots ,g_{\mathit{jn}}\right\}$ respectively, where $\mathrm{m}$ is the number of genes in $G_i$and $\mathrm{n}$ is the number of genes in $G_j$. We define the functional association between gene $\mathrm{g}$ and gene set $\mathrm{G}=\left\{g_1,g_2,\dots ,g_k\right\}$ as follows:

$$F_G\left(g\right)=\underset{g_i\in G}{\max }(\mathit{FSS}(g,g_i))$$ (2)

Where $\mathrm{FSS}$ represents the functional similarity score between genes, which is defined as follows:

$$\mathrm{FSS}\left(g_i,g_j\right)=\left\{\begin{array}{c}1\\ {\mathit{LLS}}^{\prime }(g_i,g_j)\end{array}\right\}\begin{array}{c}\mathit{if}i=j,\\ \mathit{if}i\ne j,\end{array}$$ (3)

Where ${\mathit{LLS}}^{\prime }$ is the normalized $\mathit{LLS}$ of genes, which is defined as follows:

$${\mathit{LLS}}^{\prime }\left(g_i,g_j\right)=\frac{\mathit{LLS}\left(g_i,g_j\right)-{\mathit{LLS}}_{\min }}{{\mathit{LLS}}_{\max }-{\mathit{LLS}}_{\min }}$$ (4)

Where ${\mathit{LLS}}_{\max }$and ${\mathit{LLS}}_{\min }$denote the maximum $\mathit{LLS}$ and minimum $\mathit{LLS}$ in HumanNet, respectively.

Finally, we formulated the disease functional similarity as:

$$\mathrm{DFSM}\left(d_i,d_j\right)=\frac{\sum _{g_t\in G(d_i)}{F}_{G\left(d_j\right)}\left(g_t\right)+\sum _{g_t\in G(d_j)}{F}_{G\left(d_i\right)}\left(g_t\right)}{m+n}$$ (5)

2.4. Gaussian interaction profile kernel similarity for microbes

We calculate the microbe Gaussian interaction profile kernel similarity via known experimentally confirmed human microbe-disease association network, which based on the assumption that functionally similar diseases generally tend to present interaction or non-interaction patterns with similar microbes. Specifically, the Gaussian interaction profile kernel similarity of microbe $m_i$ and $m_j$ can be defined as follows [52]:

$$\mathit{MGSM}\left(m_i,m_j\right)=\exp \left(-{\gamma }_m{‖\mathit{IP}\left(m_i\right)-\mathit{IP}\left(m_j\right)‖}^2\right)$$ (6)

Where $\mathit{IP}(m_i)$ represents the interaction between the microbe $m_i$ and each disease, ${\gamma }_m$ represents the normalized kernel bandwidth and is defined as follows:

$${\gamma }_m={\gamma }_m^{\prime }/\left(\frac{1}{n_m}\sum _{i=1}^{n_m}{‖\mathit{IP}\left(m_i\right)‖}^2\right)$$ (7)

Where ${\gamma }_m^{\prime }$ is the original bandwidth that affects ${\gamma }_m$. For the sake of simplicity, we set ${\gamma }_m^{\prime }=1$ according to previous relevant study [14]. $n_m$ represents the total number of microbes. $\mathit{MGSM}\left(m_i,m_j\right)$ at the $i^{\mathit{th}}$ row and $j^{\mathit{th}}$ column denotes the similarity between microbe $m_i$ and $m_j$.

2.5. Gaussian interaction profile kernel similarity for diseases

Similarly, the Gaussian interaction profile kernel similarity of diseases $d_i$ and $d_j$ can be computed by (8), (9):

$$\mathit{DGSM}\left(d_i,d_j\right)=\exp \left(-{\gamma }_d{‖\mathit{IP}\left(d_i\right)-\mathit{IP}\left(d_j\right)‖}^2\right)$$ (8)

$${\gamma }_d={\gamma }_d^{\prime }/\left(\frac{1}{n_d}\sum _{i=1}^{n_d}{‖\mathit{IP}\left(d_i\right)‖}^2\right)$$ (9)

Where $\mathit{IP}(d_i)$ represents the interaction between the disease $d_i$ and each microbe, ${\gamma }_d$ represents the normalized kernel bandwidths, and $n_d$ represents the total number of diseases. Again, we set the original bandwidth ${\gamma }_d^{\prime }$ to 1 based on previous research experience [14].$\mathit{DGSM}\left(d_i,d_j\right)$ at the $i^{\mathit{th}}$ row and $j^{\mathit{th}}$ column denotes the similarity between disease $d_i$ and $d_j$. It should be noted that in each cross-validation experiment, the similarities of diseases and microbes will be recalculated.

2.6. Integrated similarities for diseases and microbes

It is worth noticing that not all diseases have known associated genes. If a given disease have no related genes, we cannot calculate the functional similarity scores between the disease and other diseases. Therefore, we established a new similarity network for diseases by integrating multiple disease similarity networks calculated from different perspectives, namely the disease Gaussian interaction profile kernel similarity and the disease functional similarity. Specifically, the integrated disease similarity $\mathrm{DS}\in R^{n_d\times n_d}$ can be defined as follows:

$$\mathrm{DS}\left(d_i,d_j\right)=\left\{\begin{array}{c}\frac{\mathit{DFSM}\left(d_i,d_j\right)+\mathit{DGSM}\left(d_i,d_j\right)}{2}\\ \mathit{DGSM}\left(d_i,d_j\right)\end{array}\right\}\begin{array}{c}\mathit{if}\mathit{DFSM}\left(d_i,d_j\right)\ne 0\\ \mathit{otherwise}\end{array}$$ (10)

Similarly, the integrated microbe similarity $\mathrm{MS}\in R^{n_m\times n_m}$ was calculated as follows:

$$\mathrm{MS}\left(m_i,m_j\right)=\left\{\begin{array}{c}\frac{\mathit{MFSM}\left(m_i,m_j\right)+\mathit{MGSM}\left(m_i,m_j\right)}{2}\\ \mathit{MGSM}\left(m_i,m_j\right)\end{array}\right\}\begin{array}{c}\mathit{if}\mathit{MFSM}\left(m_i,m_j\right)\ne 0\\ \mathit{otherwise}\end{array}$$ (11)

2.7. Building a heterogeneous network

We constructed a human microbe-disease interaction network by using human microbes and diseases interaction associations, a microbe similarity network and a diseases similarity network. Then, the heterogeneous human microbe-disease network can be expressed as a bipartite graph $G=(\mathrm{M},\mathrm{D},\mathrm{E})$, where M represented all of microbes, D represents all of diseases, and E represents the interaction of microbes and microbes, diseases and diseases, and microbes and diseases. The heterogeneous network is represented by $(n_d+n_m)\times (n_d+n_m)$ adjacency matrix $W$. By the similarity between the microbes (MS) and the similarity between the diseases (DS), the coefficients of similarity can construct a heterogeneity network.

$$W=\left[\begin{array}{cc}\mathit{DS}& A^T\\ A& \mathit{MS}\end{array}\right]$$ (12)

The submatrix $A$ represents the relationship network between the microbe and the disease, $A^T$ is the transposition of $A$, the adjacency matrix of the $\mathrm{DS}$ and $\mathrm{MS}$ are the disease network and the microbe network, and their weights are set to the similarity of the paired microbe and disease, and the range is [0,1].

2.8. MNNMDA for predicting microbe-disease associations

The nuclear norm is the sum of the singular values of the matrix, which is used to constrain the low rank of the matrix. For sparse data, the matrix has a low rank and contains a lot of redundant information, which can be used to recover data and extract features. The nuclear norm has been widely used in various fields and has achieved good results [39]. Generally, when a matrix has a low rank, the kernel norm minimization problem can be expressed as:

$$\underset{X}{\min }{‖X‖}_{*}$$ (13)

Where${‖X‖}_{*}$ represents the kernel norm of $X$, which is defined as the sum of all singular values of $X$. The kernel norm minimization model is a convex optimization problem.

In order to predict the microbe-disease association, the elements in the microbe similarity matrix $\mathit{MS}$ and the disease similarity matrix $\mathit{DS}$ are in the interval [0,1]. The elements in the correlation matrix A are 0 or 1. The predicted value of the unknown entry is expected to be in the range of [0,1], where a predicted value close to 1 suggests that it may be indicative of an association and vice versa. However, in the above matrix completion model (12), the entries in the completed matrix can be any real values in ($-\mathrm{\infty }$, $+\mathrm{\infty }$). However, it has no practical significance for values greater than 1 and less than 0. Therefore, it is important to add a constraint to the matrix completion model to ensure that the missing elements that are not found are in the interval [0,1]. In addition, because there may be a lot of “noise” data in the microbe and disease data, the microbe-disease relocation model should tolerate the potential noise as much as possible. The noise-tolerant matrix completion model is:

$$\underset{X}{\min }{∥X∥}_{*}s.t.{∥p_{\mathrm{\Omega }}\left(X\right)-p_{\mathrm{\Omega }}\left(W\right)∥}_F\le \epsilon$$ (14)

Where $\epsilon$ is the measurement noise level, $\Omega$ is a set of index pairs ($i,j$) containing all known entries in $W$, and $p_{\mathrm{\Omega }}$ is the projection operator on $\Omega$.

$${{(p}_{\mathrm{\Omega }}\left(X\right))}_{\mathit{ij}}=\left\{\begin{array}{c}{X}_{\mathit{ij},}(i,j)\in \Omega \\ 0,\mathit{otherwise}\end{array}\right\}$$ (15)

However, for this model with inequality constraints, there are many difficulties in solving. For example: how to choose the appropriate model parameters and how to choose an effective solution algorithm. Therefore, we usually replace the inequality constraint model with a regularized model. The introduction of soft regularization can not only tolerate unknown noise, but also provide a lot of convenience for us to solve. Then the model can be rewritten as the following：

$$\underset{X}{\min }{∥X∥}_{*}+\frac{\alpha }{2}{∥p_{\mathrm{\Omega }}\left(X\right)-p_{\mathrm{\Omega }}\left(W\right)∥}_F^2\mathrm{s}.\mathrm{t}.0<X_{\mathit{ij}}<1$$ (16)

Where ${\mathrm{\Vert }\bullet \mathrm{\Vert }}_F$ denotes the Frobenius norm, $\alpha$ is the parameter that balances the nuclear specification and the error term. To solve the optimization problem in Eq. (16), we chose the more classic alternating direction multiplier method (ADMM) [53]. It is worth noting that our objective function is convex. With the introduction of the auxiliary matrix $H$, the ADMM framework can be optimized in the following equivalent form.

$$\underset{X}{\min }{∥X∥}_{*}+\frac{\alpha }{2}{∥p_{\mathrm{\Omega }}\left(H\right)-p_{\mathrm{\Omega }}\left(W\right)∥}_F^{2}s.t.X=H,0<H_{\mathit{ij}}<1$$ (17)

Therefore, the enhanced Lagrange function becomes the following:

$$\mathit{L}(H,X,Y,\alpha ,\beta )={‖X‖}_{*}+\frac{\alpha }{2}{‖p_{\mathrm{\Omega }}\left(H\right)-p_{\mathrm{\Omega }}\left(W\right)‖}_F^2+T_{\gamma }\left(Y^T\left(X-H\right)\right)+\frac{\beta }{2}{‖X-H‖}_F^2$$ (18)

where $Y$ is the Lagrange multiplier and $\beta >0$ is the penalty parameter. The solution process of MNNMDA belongs to iterative solution. Therefore, when we iterate $k$ times, we need to calculate the value of iterations $H_{k+1}$, $Y_{k+1}$ and $X_{k+1}$ according to the result of the $k^{\mathit{th}}$ iteration.

Update: Repeat the following steps until convergence or reaching a predetermined number of iterations. Fix $X_k$ and $Y_k$ and calculate a matrix $H_{k+1}$ to minimize Eq. (18).

$$H_{k+1}=\mathit{arg}\underset{0\le H\le 1}{\min }\mathit{L}\left(H,X_k,Y_k,\alpha ,\beta \right)=\mathit{arg}\underset{0\le H\le 1}{\min }\frac{\alpha }{2}{‖p_{\mathrm{\Omega }}\left(H\right)-p_{\mathrm{\Omega }}\left(W\right)‖}_F^2+T_{\gamma }(Y^T\left(X-H\right))+\frac{\beta }{2}{‖X-H‖}_F^2$$ (19)

Here, $H^{*}$ is the optimal solution of $\mathit{arg}\underset{0\le H\le 1}{\min }\mathit{L}\left(H,X_k,Y_k,\alpha ,\beta \right)$, if and only if holds,

$$\alpha p_{\mathrm{\Omega }}^{*}\left(p_{\mathrm{\Omega }}\left(H^{*}\right)-p_{\mathrm{\Omega }}\left(W\right)\right)-Y_k-\beta \left(X_k-H^{*}\right)=0$$ (20)

where $p_{\mathrm{\Omega }}^{*}$ represents the adjoint operator of $p_{\mathrm{\Omega }}$. Then, the closed solution becomes

$$H^{*}={\left(\mathrm{\Gamma }+\frac{\alpha }{\beta }{p}_{\mathrm{\Omega }}^{*}{p}_{\mathrm{\Omega }}\right)}^{-1}\left(\frac{Y_k}{\beta }+\frac{\alpha }{\beta }{p}_{\mathrm{\Omega }}^{*}{p}_{\mathrm{\Omega }}\left(W\right)+X_k\right)=\left(\mathrm{\Gamma }-\frac{\alpha }{\alpha +\beta }{p}_{\mathrm{\Omega }}^{*}{p}_{\mathrm{\Omega }}\right)\left(\frac{Y_k}{\beta }+\frac{\alpha }{\beta }{p}_{\mathrm{\Omega }}^{*}{p}_{\mathrm{\Omega }}\left(W\right)+X_k\right)=\left(\frac{Y_k}{\beta }+\frac{\alpha }{\beta }{p}_{\mathrm{\Omega }}\left(W\right)+X_k\right)-\frac{\alpha }{\alpha +\beta }{p}_{\mathrm{\Omega }}(\frac{Y_k}{\beta }+\frac{\alpha }{\beta }{p}_{\mathrm{\Omega }}\left(W\right)+X_k)$$ (21)

where $\mathrm{\Gamma }$ is the identity operator. ${\left(\mathrm{\Gamma }+\frac{\alpha }{\beta }{p}_{\mathrm{\Omega }}^{*}{p}_{\mathrm{\Omega }}\right)}^{-1}$ denotes the inverse operator of $\left(\mathrm{\Gamma }+\frac{\alpha }{\beta }{p}_{\mathrm{\Omega }}^{*}{p}_{\mathrm{\Omega }}\right)$ and is equal to $\left(\mathrm{\Gamma }-\frac{\alpha }{\alpha +\beta }{p}_{\mathrm{\Omega }}^{*}{p}_{\mathrm{\Omega }}\right)$. It’s worth noting that $p_{\mathrm{\Omega }}^{*}{p}_{\mathrm{\Omega }}=p_{\mathrm{\Omega }}$. Considering the interval [0,1] constraint, we limit the range of the elements of $H_{k+1}$ to [0,1] such that

$${{(H}_{k+1})}_{\mathit{ij}}=\left\{\begin{array}{c}1H_{\mathit{ij}}^{*}>1\\ H_{\mathit{ij}}^{*}0\le H_{\mathit{ij}}^{*}\le 1\\ 0H_{\mathit{ij}}^{*}<0\end{array}\right\}$$ (22)

Fix $H_{k+1}$ and $Y_k$ and calculate a matrix $X_{k+1}$ to minimize Eq. (18).

$$X_{k+1}=\mathit{arg}\underset{X}{\min }\mathit{L}\left(H_{k+1},X,Y_k,\alpha ,\beta \right)=\arg \underset{X}{\min }{‖X‖}_{*}+\frac{\beta }{2}{‖X-(H_{k+1}-\frac{Y_k}{\beta })‖}_F^2={\mathit{D}}_{\frac{1}{\beta }}(H_{k+1}-\frac{Y_k}{\beta })$$ (23)

where ${\mathit{D}}_{\tau }(X)$ is the singular value shrinkage operator defined as:

$${\mathit{D}}_{\tau }\left(X\right)={\sum }_{i=1}^{{\theta }_i\ge \tau }({\theta }_i-\tau ){\mu }_i{{\nu }_i}^T$$ (24)

Where${\theta }_i$ is the singular values of $X$ which is larger than $\tau$, while ${\mu }_i$ and ${\nu }_i$ are the left and right singular vectors corresponding to ${\theta }_i$, respectively.

Fix $H_{k+1}$ and $X_{k+1}$ and calculate a matrix $Y_{k+1}$.

$$Y_{k+1}=Y_k+\sigma \beta (X_{k+1}-H_{k+1})$$ (25)

where $\sigma$ is the learning rate, which is set to 1 in this study for simplicity. Iterate according to the above iteration rules until convergence, and finally, we obtain the matrix $H_k$ after convergence. Therefore, after supplying the adjacency matrix of the microbe-disease heterogeneous network to MNNMDA, we can obtain an updated microbe-disease association matrix $A^{*}$, where the unknown entries in $A$ are filled up, the final prediction matrix $A^{*}$ is:

$$A^{*}\leftarrow \left[\begin{array}{cc}{\mathit{DS}}^{*}& A^{*T}\\ A^{*}& {\mathit{MS}}^{*}\end{array}\right]\leftarrow H_k$$ (26)

The entries in $A^{*}$ with prediction scores close to 1 indicate the potential microbe-disease associations.

2.9. Evaluation methods

The performances of computational methods were evaluated by standard fivefold cross-validation (5-fold CV) under the following three different settings:

(i) 5-fold CVS1 (overall testing): CV on microbe-disease pairs-random known entries in A (i.e., microbe-disease pairs) are selected for testing.

(ii) 5-fold CVS2 (horizontal testing for diseases): CV on diseases-random rows in A (i.e., diseases) are blinded for testing.

(iii) 5-fold CVS3 (vertical testing for microbes): CV on microbes-random columns in A (i.e., microbes) are blinded for testing.

For 5-fold CVS1, we randomly divide all known microbe-disease associations into five equal and uncrossed groups. For each round, one group of microbe-disease associations (i.e., positive samples) with an equal-ratio set of unknown randomly sampled microbe-disease pairs (i.e., negative samples) are selected as test samples in turn. And the remaining four groups of microbe-disease associations together with the rest of unknown microbe-disease pairs are utilized to train the model. Specifically, all test samples would first obtain their prediction scores in each round and then be prioritized according to their scores. For a positive (or negative) test sample (microbe-disease pair), we consider that the model successfully predicts the microbe-disease pairs if its ranking is higher (or lower) than a specific threshold. As such, we could obtain the corresponding precision, true positive rates (TPR, sensitivity/recall) and false positive rates (FPR, 1-specificity) by setting different thresholds. Here, precision measures the percentage of the positive test samples among all samples that are predicted as positive with the given threshold. Sensitivity/recall is defined as the percentage of the positive test samples whose rankings are higher than the given threshold. Specificity means the percentage of the negative test samples that are ranked lower than the given threshold. Subsequently, the receiver operating characteristics (ROCs) curves and precision-recall (PR) curves could be drawn by plotting TPR versus FPR and precision versus recall at different thresholds, respectively. The performance is measured by area under ROC curve (AUC) and area under PR curve (AUPR). To reduce the influence of random division, each experiment is repeatedly conducted for 10 times. And the final AUC and AUPR scores are calculated over the average of 10 repetitions. Similarly, for 5-fold CVS2 and 5-fold CVS3, we randomly sample 20 % rows and columns in the adjacent matrix A as test samples, while the rest of the rows and columns are considered as training samples, respectively. It should be noted that 5-fold CVS2 and 5-fold CVS3 are set to predict novel microbe-disease associations for new diseases and new microbes, respectively.

3. Results

We demonstrated the performance of MNNMDA by comparing it with five methods from previous studies on the three data sets (i.e., HMDAD, Disbiome and Combined Data) under three different 5-fold CV settings (i.e., 5-fold CVS1, 5-fold CVS2, and 5-fold CVS3). In addition, we use AUPR and AUC values as indicators to assess the performance of MNNMDA. We also implemented case studies on two common diseases to further confirm the effectiveness of our method in predicting potential disease-related microbes.

3.1. Parameter tuning

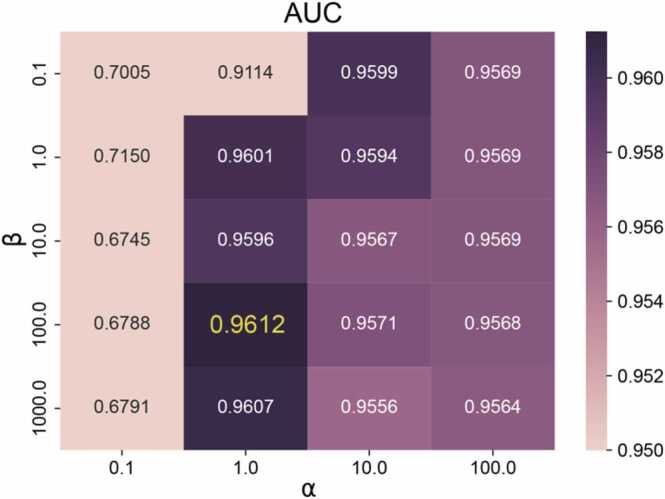
In this section, we investigated the influence of two important parameters in Formula (18), the balances the nuclear specification and the error term α and the penalty parameter β. We conducted two parameter combination experiments on the HMDAD dataset to select the optimal parameter combination of the MNNMDA method. First, we tuned $\alpha$ from the list $\{0.1,1.0,10.0,100.0\}$ and tuned $\beta$ from the list $\{0.1,1.0,10.0,100.0,1000.0\}$, then searched the best values on the 4 × 5 grid expanded by both $\alpha$ and $\beta$. We recorded the performance of MNNMDA for each pairwise value of ($\alpha$, $\beta$) under 5-fold CVS1 in terms of AUC (Fig. 2). Finally, we picked up the pair of ($\alpha$, $\beta$) = (1, 100), which achieves the highest one among 20 values of AUC, as the best value of ($\alpha$, $\beta$), and further applied them in all the following experiments.

Fig. 2.

The AUC values on different $\alpha$ and $\beta$ for the 5-fold CVS1 on HMDAD dataset.

3.2. MNNMDA is robust to fake associations

We assessed the robustness of our method on the HMDAD dataset by manually adding a few fake associations. Specifically, we randomly selected a predefined percentage of unknown associations and converted their labels to known associations. The percentage varies from 1 % to 5 %. The 5-fold CVS1 is then implemented on the new known microbe-disease associations to evaluate the performance of our method. The results were shown in Table 2, from which we can see that the AUCs and the AUPRs are stable with 5 % fake associations. It indicates that our method is robust to a small percentage of fake associations.

Table 2.

The robustness of MNNMDA.

Percentage	AUC	AUPR
0% 1% 2% 3% 4% 5%	0.958 0.939 0.940 0.926 0.918 0.916	0.662 0.630 0.674 0.685 0.686 0.681

3.3. Comparison with previous methods

To evaluate the performance of our proposed method, we compare MNNMDA with the following state-of-the-art methods on the same data set.

KATZHMDA [14] is a KATZ-based computational method, which calculated based on the number and length of paths between two nodes in microbe-disease heterogeneous network.

LRLSHMDA [24] is a semi-supervised learning calculation model based on Laplacian regularized least squares classification.

NTSHMDA [54] is a computational model based on random walk and network topology similarity to predict the associations between microbes and diseases.

GATMDA [51] is a computational framework, which combines inductive matrix completion and graph attention networks to complete the prediction task.

KGNMDA [55] is a knowledge graph neural network method for predicting microbe-disease associations.

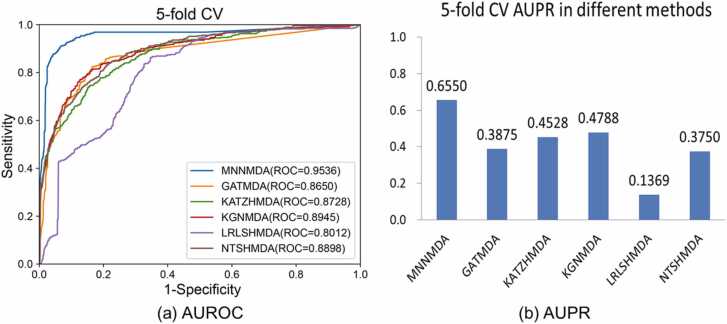
Our method was compared with five baselines under 5-fold CVS1 on the HMDAD dataset. We used the AUC value and AUPR value as indicators to evaluate each method. For better visual comparison, the corresponding ROC curves and AUPR values of MNNMDA, KATZHMDA, LRLSHMDA, NTSHMDA, GATMDA, and KGNMDA were shown in Fig. 3 Obviously, MNNMDA achieves the best performance compared to the other five methods, with an average AUC value of 0.9536 and an average AUPR is 0.6550. The results indicated that our method is effective in predicting novel microbe-disease associations.

Fig. 3.

Comparing the ROC curves and AUPR values of MNNMDA and other five methods based on 5-fold CVS1 on the HMDAD dataset.

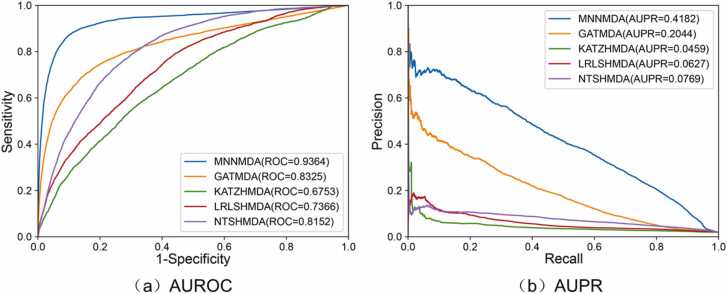
To further evaluate the effectiveness of our model, we conduct experiments under 5-fold CV on the Disbiome dataset and the Combined dataset (Peryton and MicroPhenoDB). We compare our method with four baseline methods on the data set Disbiome. The results under the 5-fold CVS1 were shown in Fig. 4, which demonstrated that our method consistently outperforms the four baseline methods with an average AUC of 0.9364 and an average AUPR of 0.4182.

Fig. 4.

Comparison of the ROC curves and PR curves of MNNMDA and four other methods under the 5-fold CVS1 on the Disbiome dataset.

The performances of MNNMDA under the 5-fold CVS1 on HMDAD, Disbiome, and Combined Data were summarized in Table 3. It can be seen that our method has the best AUC and AUPR on the HMDAD dataset. The main reason may be that the Disbiome and Combined Data are sparser than HMDAD. The density of HMDAD is 3.95 %, the density of the Disbiome is 1.90 %, and the density of combined data is 0.71 %. So the method MNNMDA can achieve relatively better training on HMDAD than Disbiome and Combined Data.

Table 3.

Performance of the MNNMDA method under 5-fold CVS1 on three datasets.

Dataset	AUC	AUPR
HMDAD Disbiome Combined Data	0.9536 0.9364 0.8858	0.6550 0.4182 0.3014

To further verify the performance of our method, we made 5-fold CVS2 and 5-fold CVS3 on the HMDAD dataset. In addition, comparing our method with five baseline methods, and the results were shown in Table 4, it could be significantly discovered from Table 4 that our method is slightly superior to other baseline methods in terms of AUC and AUPR under the settings 5-fold CVS3. Overall, our method is able to identify novel microbe-disease associations under different scenarios.

Table 4.

Performance comparison between five baseline methods and our method under the 5-fold CVS2 and 5-fold CVS3 on HMDAD data set.

Methods	5-fold CVS2		5-fold CVS3
	AUC	AUPR	AUC	AUPR
KATZHMDA LRLSHMDA NTSHMDA GATMDA KGNMDA MNNMDA	0.6573 0.6568 0.7231 0.6000 0.7541 0.7250	0.1579 0.1637 0.0861 0.1702 0.1534 0.4214	0.9079 0.9094 0.9111 0.8683 0.9093 0.9737	0.6579 0.6588 0.6568 0.6442 0.6582 0.9575

From all CV results, we observe that the AUC value of MNNMDA method under 5-fold CVS3 setting is significantly better than that under 5-fold CVS1and 5-fold CVS2 settings. For new diseases and new microbes, we have no known association pairs for them to train the model, which results in lower AUC value under 5-fold CVS1 and 5-fold CVS2. Furthermore, various methods achieve generally better performance under 5-fold CVS3 than under 5-fold CVS2 on HMDAD dataset. As the number of microbes (292) is much more than that of diseases (39), the microbe similarity matrix (292 × 292) is thus more informative than the disease similarity matrix (39 × 39). Therefore, new microbes can obtain more abundant and accurate information from neighbors than new diseases.

3.4. Case study

In this section, we select two common diseases of colon cancer and inflammatory bowel disease (IBD) for case studies on the HMDAD dataset to further verify the predictive ability of the MNNMDA method. For each disease, microbes that have known associations with the disease are first removed. Then the predicted scores of candidate microbes are sorted in descending order according to the MNNMDA method. Finally, we verify whether the top 10 microbes associated with the disease are confirmed by the previous publications.

Colon cancer, a common malignant digestive tract tumor, has a high incidence ranking second on the list of digestive tract tumor, greatly threatening human life and health [29], [56], [57], [58]. More and more evidences show that the occurrence and development of colon cancer is closely associated with the imbalance of microbial community [59]. We applied MNNMDA to the case study of colon cancer. Of the top 10 predicted microbes, 8 have been validated based on existing biological literature (see Table 5). For example, Oxalobacter formigenes might stand for a pathogenic factor in colon cancer, when antibiotics are prescribed generously [60]. Helicobacter pylori infection was found to be considered as a risk increase factor of left-sided colon cancer [61], [62]. Typically, it is reported that colon cancer patients aged 60 years or older who have inserted a metal stent preoperatively are identified as a risk factor for Clostridium difficile infection [63], [64] Staphylococcus aureus is a kind of tannase-producing bacteria, its activity may be related to the development of colon cancer [65]. The high prediction accuracy rates demonstrate that our model could be used in real-life applications.

Table 5.

The top 10 potential microbes related to colon cancer identified by MNNMDA.

Disease	Microbes	Rank	Evidence
Colon cancer	Helicobacter pylori	1	PMID: 22294430 PMID: 30636955
	Oxalobacter formigenes	2	PMID: 32880090
	Tropheryma whipplei	3	Unconfirmed
	Prevotella copri	4	PMID: 35682578
	Corynebacterium	5	PMID: 31609493
	Staphylococcus aureus	6	PMID: 26198124
	Clostridium difficile	7	PMID: 29245331 PMID: 21152135
	Desulfovibrio	8	PMID: 19496818
	Helicobacter pylori	9	PMID: 30636955 PMID: 22294430
	Dietzia maris	10	Unconfirmed

In addition, the main types of inflammatory bowel disease (IBD) include Crohn's disease and ulcerative colitis, which is caused in part by bacteria that may activate the patient's immune system to attack foreign substances. Once the patient's immune system is activated, it is difficult to regulate and destroy the gastrointestinal tract, resulting in IBD symptoms [66]. Recent researches have shown that a wide range of microbes are closely associated with IBD. MNNMDA method was used to calculate the top 10 microorganisms with the highest correlation row scores and analyze whether they were related to IBD. In Table 6, 8 of them have been verified to be related to IBD in the studies. Clostridium coccoides are less represented in A-IBD patients [67]. Lachnospiraceae and other taxa identified as translocating bacteria or targets of systemic immunity in IBD concomitantly exhibited heightened transcriptional activity and growth rates in IBD patient gut microbiomes [68]. The changes in the abundance of Proteobacteria of IBD patients are not only related to current activity but also to the course of the disease [69]. Research shows a significant relationship between Staphylococcus and IBD [70]. In a word, these two sets of case studies validate the powerful capability of MNNMDA in inferring new possible microbes for diseases again.

Table 6.

The top 10 potential microbes related to inflammatory bowel disease (IBD) identified by MNNMDA.

Disease	Microbes	Rank	Evidence
IBD	Actinobacteria	1	Unconfirmed
	Proteobacteria	2	PMID: 31530835
	Lachnospiraceae	3	PMID: 35976997
	Propionibacterium	4	PMID: 19847949
	Propionibacterium acnes	5	PMID: 28630242
	Pseudomonas	6	PMID: 31662859
	Staphylococcus	7	PMID: 27239107 PMID:23679203
	Clostridium coccoides	8	PMID: 27687331
	Verrucomicrobiaceae	9	PMID: 22572638
	Oxalobacteraceae	10	Unconfirmed

4. Discussion

Identifying microbe-disease associations is a hot topic, which can not only provide great insight into understanding the complex pathogenic mechanism of human diseases, but also reduces the cost and time of biological experiments. For example, systematic identification of potential pathological microorganisms can help doctors or biologists to identify biomarkers for diagnosis and treatment clinically or experimentally [7], [71], [72], [73], especially for complex human diseases. In addition, computational prediction of pathogenic microorganisms can help pharmacologists or biologists effectively narrow down the field of candidate compounds [74], [75]. This may further guide them in planning experiments and thus reducing costs. Therefore, a series of related information databases have been established. Based on the data in these information databases, more and more computational models have been proposed and applied to the field of microbe-disease association prediction, and these prediction models have achieved remarkable results. However, previous computational methods suffer from two major challenges. On the one hand, few methods did not suffer from decrease of accuracy owing to the high rate of false positive and false negative samples in the microbe-disease association database. On the other hand, most of them did not systematically integrate the biological knowledge information of microbes and diseases. That may be not made reasonable predictions about new diseases or microbes.

The reliable performance of MNNMDA results from several major factors as follows: to begin with, the observed experimentally confirmed human microbe-disease associations are reliable. In addition, the integration of multiple prior biological informations about microbes and diseases complements and improves the microbe similarity and disease similarity, respectively, which potentially enhances the prediction capability of our method.

Although the good prediction performance of MNNMDA method, there are some limitations that are expected to be further improved in the future. For example, our method cannot be applied to make predictions for all new microbes and new diseases. It is because for a new disease without any known associated genes, and new microbes that are lack of protein-protein interaction information, it fails to obtain its similarity between other diseases and it that is essential for new disease prediction. But this limitation could be overcome by collecting more prior information, such as microbe sequence similarity, disease gene-based similarity network and disease symptom similarity network or developing other effective similarity calculation method. In addition, there are too few known microbe-disease associations in the database. The data is imbalanced, leading to prediction deviation. Finally, though our model could predict potential disease-associated microbes, it still cannot determine how the microbial abundances influence disease status. We could further handle this problem by incorporating the microbial abundance information into the heterogeneous network.

5. Conclusion

An in-depth study of the microbe-disease relations will not only help doctors understand the complex pathogenic mechanism of human diseases, but also provide new insight for microbe-oriented medicine. In this work, we proposed a method based on the minimum nuclear specification, named MNNMDA, for human microbe-disease association prediction. We fully exploit multiply sources of biological data to construct similarity features for diseases and microbes. MNNMDA not only can restrict all predicted matrix entry values within a specific interval, but also exhibit robustness to tolerate potentially noise similarity calculations. We compared our method with five state-of-the-art methods based on the database HMDAD. MNNMDA achieved the average AUC value of 0.9536 based on the 5-fold CV. In addition, MNNMDA achieved good results in two common human diseases: colon cancer and IBD. Among the predicted top 10 microbe candidates, 8 microbes were confirmed by the previous research literature, respectively. Overall, MNNMDA is effective and promising in identifying potential microbe-disease associations.

Funding

This study was supported by Hunan Key Laboratory Cultivation Base of the Research and Development of Novel Pharmaceutical Preparations (No.2016TP1029), Hunan Provincial Innovation Platform and Talents Program (No. 2018RS3105), the Foundation of Hunan Educational Committee (Grant No. 19A060), the Provincial Key R & D Projects of Hunan Provincial Science and Technology Department (No. 2022SK2074), and the Training Plan for Young Backbone Teachers in Hunan Province.

CRediT authorship contribution statement

Haiyan Liu (First Author): Methodology, Formal analysis, and Writing – Original Draft; Pingping Bing: Methodology and Writing – Review & Editing; Meijun Zhang: Data Curation, Writing - Original Draft; Geng Tian: Writing – Review & Editing; Jun Ma: Visualization, Investigation; Haigang Li: Software, Validation; Meihua Bao: Visualization, Writing - Review & Editing Kunhui He: Writing – Review & Editing; Jianjun He (Corresponding Author): Conceptualization, Funding Acquisition, Resources, Writing - Review & Editing; Binsheng He (Corresponding Author): Supervision, Writing - Review & Editing; Jialiang Yang (Corresponding Author): Conceptualization, Resources, Writing – Review & Editing and Funding acquisition.

Declaration of Competing Interest

All authors disclosed no relevant relationships.