Abstract
We coexist with a vast number of microbes that live in and on our bodies. Those microbes and their genes are collectively known as the human microbiome, which plays important roles in human physiology and diseases. We have acquired extensive knowledge on the organismal compositions and metabolic functions of the human microbiome. Yet, the ultimate proof of our understanding of the human microbiome is reflected in our ability to manipulate it for health benefits. To facilitate the rational design of microbiome-based therapies, there are many fundamental questions to be addressed at the systems level. Indeed, we need a deep understanding of the ecological dynamics associated with such a complex ecosystem before we rationally design control strategies. In light of this, this Review discusses progress from various fields, e.g., community ecology, network science, and control theory, that are helping us make progress towards the ultimate goal of controlling the human microbiome.
Graphical Abstract
To facilitate the rational design of microbiome-based therapies, there are many fundamental questions to be addressed at the systems level. This Review discusses progress from various e.g., community ecology, network science, and control theory, that are helping us make progress towards the goal of controlling the human microbiome.
INTRODUCTION
We coexist with a vast number of microbes that live in and on our bodies. Those microbes and their genes are collectively known as the human microbiome, which plays very important roles in human physiology and diseases. Propelled by next-generation sequencing technologies, many scientific advances have been made through the work of large-scale, consortium-driven microbiome projects1–3, helping us acquire more accurate taxonomic and functional compositions of the human microbiome than before.
It is now well known that the largest portion of the microorganisms live in our gut, and most of them are bacterial4. The human gut microbiome can be altered by dietary changes5,6, medical interventions7, and many other factors8–10. The alterability of our gut microbiome offers a promising future for microbiome-based therapies for the prevention and treatment of diseases associated with disrupted gut microbiomes9,11. In particular, infections by human pathogens are likely preventable with microbiota-based approaches, offering an intriguing alternative to antibiotic treatment with the added benefit of helping to curb the rise of antibiotic resistant strains. Yet, due to its high complexity, untargeted interventions could shift our microbiome to an undesired state with unintended health consequences and hence raise safety concerns12–14. So far, FDA has not approved any microbiome-based therapeutics15. Only a handful of products have entered phase-3 trials. And those products are typically based on donor-derived treatments for recurrent Clostridioides difficile infection, for which the traditional treatment, i.e., fecal microbiota transplantation (FMT)16,17,18, has already been very successful.
Beyond some technical difficulties (e.g., the false negative and false positive issues in metagenomic profiling19, distinguish the living from the dead in microbial communities20, etc.), there are several conceptual challenges in developing microbiome-based therapies to control human microbiome. First, we don’t know the wiring diagram of the complex ecosystem associated with the human microbiome. Consequently, we don’t have a fully parameterized mathematical model to describe its systems-level dynamics in the absence or presence of different interventions. This represents the biggest hurdle to the development of any model-based control strategies. Second, our microbiome is highly personalized. We can never find two individuals who share the same microbial composition. This prompts us to ask how personalized the design of microbiome-based therapeutics should be. Third, our microbiome is stable, functionally redundant, and likely difficult to manipulate. Indeed, for the human gut microbiome, in the absence of large perturbations, such as repeated antibiotic treatment or drastic diet changes, it is very stable. This stability or resilience is closely related to its functional redundancy, which underscores the difficulty of manipulating its composition with mild or short-term perturbation.
In this Review, we will describe those three challenges in detail (Sec.2). Then, we will review recent progresses made from community ecology, network science, and control theory perspectives, which facilitate our understanding and control of complex microbial communities. In particular, we first introduce different modeling frameworks of microbial communities in Sec.3.1, serving as the foundation of designing model-based control strategies. In Sec.3.2, we focus on simple population-level models and discuss the universality of their microbial dynamics, which determines how personalized the design of microbiome-based therapeutics should be. In Sec.3.3, we introduce different computational methods to reconstruct the ecological network of complex microbial communities, using either temporal (“longitudinal”) data or steady-state (“cross-sectional”) data. In Sec.3.4, we introduce a theorical framework of controlling microbial communities and two practical control strategies. Finally, in Sec.4, we suggest a few promising directions that require insights and tools from other disciplines (e.g., bioinformatics, machine learning, and culturomics).
CONCEPTUAL CHALLENGES
Challenge 1: We don’t know the wiring diagram of this complex ecosystem.
We consider the human gut microbiome as a dynamic ecosystem associated with a complex ecological network. As such, tools from community ecology, network science, dynamical systems and control theory can be used to infer network structure and microbial interactions, predict temporal behavior, and design efficient control strategies. Unfortunately, the ecological network of the human gut microbiome is largely unknown. In fact, this is true for the microbiome of any site on or in the human body.
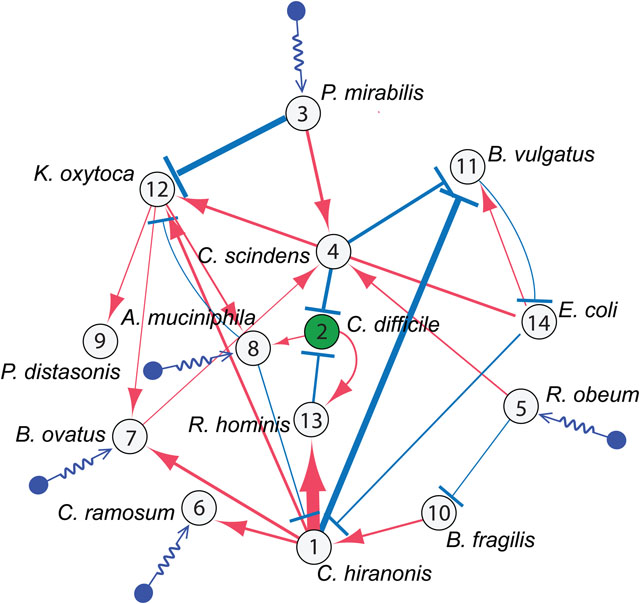
Depending on the model complexity, we can consider two different representations of the ecological network (see Fig.1). The first representation is a bipartite graph connecting two types of nodes: microbial species (denoted as ‘S’-nodes); and chemical compounds (denoted as ‘C’-nodes, representing nutrients, metabolites, toxins, etc.)21. The edges in this bipartite graph encode various mechanisms of microbial interactions, e.g., multiple species consume the same nutrients22, resulting in mutual competitions; one species produces some metabolites that are consumed by other species, leading to metabolic cross-feeding23; one species secrets antimicrobial peptides (e.g., bacteriocins24,25) that kill or inhibit other species; one species secrets signaling molecules that stimulate the growth of other species; etc. We emphasize that edges in this bipartite graph are determined by the functional repertoire encoded by the microbial genomes, and hence are mechanistic and relatively robust to changing environmental conditions or host factors over short ecological time scales. Some edges might be “silenced” sometimes, because species may choose to deactivate some functions, but activate other functions to consume certain resources to reduce the niche overlap with other species. However, we do not expect completely new edges will emerge over short ecological time scales. In other words, this bipartite graph represents a relatively constant wiring diagram or ecological network of microbial communities. However, mapping out this type of ecological network is very challenging, if not impossible. For complex habitats, e.g., the human gut, we don’t even have a comprehensive catalog of those chemical compounds that mediate various types of microbial interactions. (In Sec.3.1.2.2 and 3.1.2.3, we will describe population dynamics models based on this type of ecological network, and further explain the difficulty of parameterizing those models.)
Figure 1: The ecological network associated with a microbial community can have two different representations with different levels of complexity.
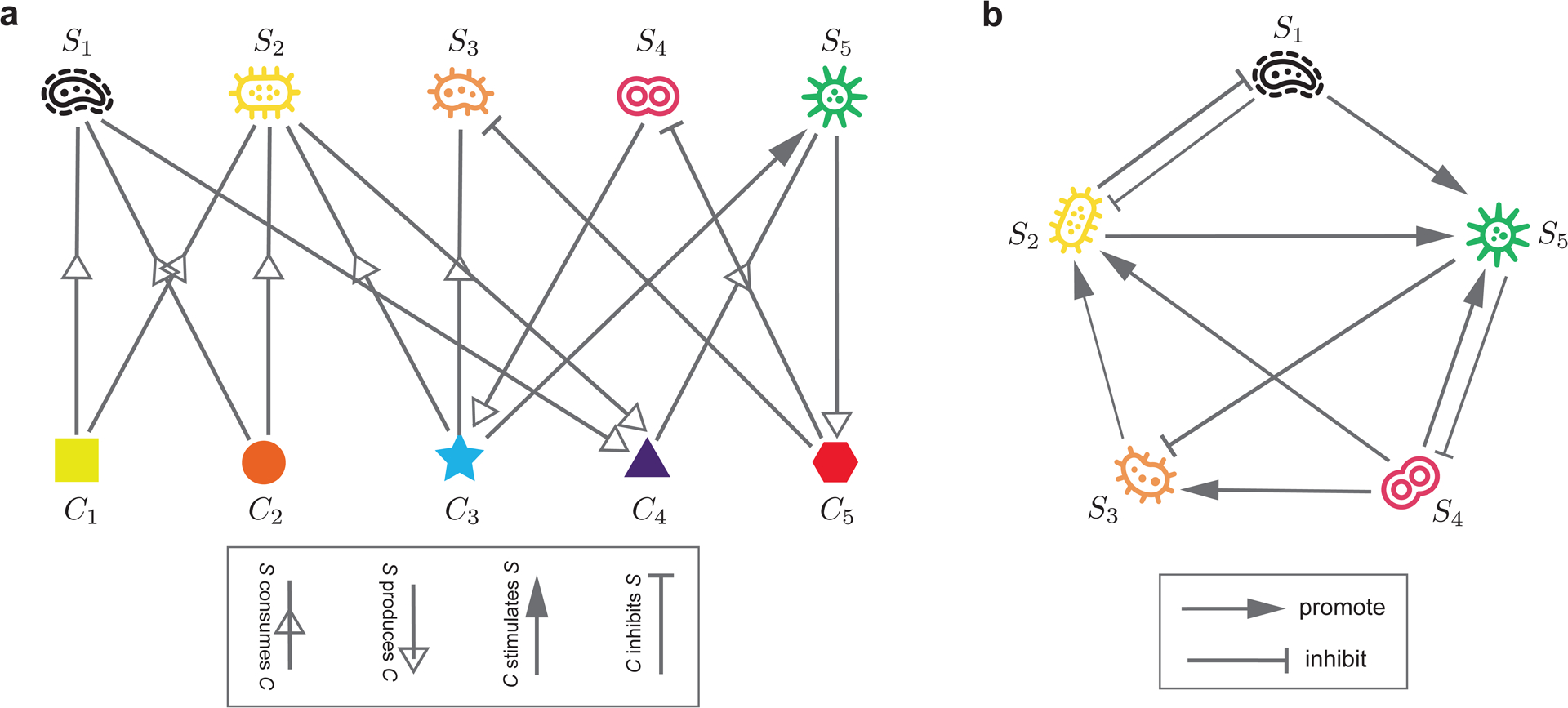
a, The first representation is a bipartite graph connecting two types of nodes: microbial species and chemical compounds (e.g., nutrients, metabolites, signaling molecules, toxins, etc.). Species can consume or produce consumable chemical compounds (e.g., metabolites); while reusable chemical compounds (e.g., signaling molecules and toxins) can stimulate or inhibit the growth of species21. b, The second representation is a unipartite graph where nodes represent microbial species and edges represent pairwise inter-species interactions. One species can promote or inhibit the growth of another species. The unipartite graph can be considered as a projection of the bipartite graph onto the species nodes. Although the projection is not perfect, it does simplify the network reconstruction problem. Figure courtesy of Dr. Xu-Wen Wang.
The second representation of the ecological network is a unipartite graph, where nodes represent microbial species and edges represent direct inter-species interactions (e.g., parasitism, commensalism, mutualism, amensalism, or competition) mediated by various mechanisms and chemical compounds as discussed above. The direction, sign and strength of a given edge in this unipartite graph might be jointly determined by several mechanisms together for a given set of environmental conditions or host factors. This unipartite graph (Fig.1b) can be conceptually considered as a projection of the bipartite graph (Fig.1a) onto the ‘S’-nodes. Even though this projection may not accurately capture all situations in which microbial interactions take place through different mechanisms (e.g., a change in the environment, or when the shared chemical compounds is produced or consumed by multiple species21,26, or higher-order interactions27,28), it does simplify the network reconstruction problem. In Sec.3.4, we will discuss two types of network reconstruction methods (based on longitudinal and cross-sectional data, respectively) and the caveats of their usage (especially the requirement on the data informativeness). Here we point out that edges in this unipartite graph are phenomenological or effective, which might be influenced by the change of environmental conditions or host factors (especially drastic change of diet or disease status) even over short ecological time scales. In a sense, the effective unipartite wiring diagram of a microbial community might change in response to large perturbations. Empirical data analysis indicates that for the human gut microbiome of healthy adults, despite they have different age, race, body mass index, long-term dietary pattern, and transit time through the gut, their effective wiring diagrams are relative universal or host-independent29. However, we don’t know if this is true for diseased microbiome or microbiome of infants or the elderly.
The two representations of the ecological network discussed here are fundamentally different from any correlation or co-occurrence network constructed from similarity-based techniques, e.g., Pearson or Spearman correlations for abundance data or the hypergeometric distribution for presence-absence data30. Those correlation or co-occurrence networks are undirected and cannot be used to predict the dynamic behavior of ecological systems, simply because correlation is not causation. In fact, mirage correlations can be observed even from a simple two-species system with deterministic dynamics31.
The fact that the ecological network of our gut microbiome (regardless of the unipartite or bipartite representation) is largely unknown raises fundamental challenges in designing microbiome-based therapies. Let’s consider the simplest scenario of an acute infection (e.g., Clostridioides difficile infection), where our control objective is simply to decolonize the pathogen (i.e., Clostridioides difficile). Bottom-up experimental approaches may offer mechanistic understanding on those microbial species that can directly inhibit the growth of the target pathogen (through either bacteriocin or niche competition). However, using species that directly inhibit the pathogen can backfire because these species may also indirectly enhance the growth of the pathogen through interactions with other “mediator” species. In other words, the effective or net impact of species-i on species-j is really context dependent. This is a typical network effect, which is ubiquitous in microbial communities32. Consequently, naive perturbations can ripple through an ecological network causing unexpected outcomes. This network effect underscores the importance of understanding the network structure in controlling the human microbiome effectively and safely. The reason is simple: our microbiome is highly personalized (See Sec.2.2). The mediator species might be present or absent for any given individual. So, the context matters.
Challenge 2: Our microbiome is highly personalized.
Thanks to big efforts of the Human Microbiome Project (HMP)1, we know that, for any given body site, we can never find two subjects who share exactly the same species collections and abundance profiles. In fact, community composition within the human microbiome varies a lot across individuals. This variation is sufficient to uniquely identify individuals within large populations and stable enough to identify them over time33. In other words, our microbiota is so personalized that it can serve as a “microbial fingerprint”.
The highly personalized microbial composition can be due to many host factors, such as birth mode (caesarean section delivery vs. vaginal delivery), breastfeeding vs. formula feeding, antibiotic exposure, environmental contaminants, medications, long-term dietary patterns, etc. Moreover, observational studies of ecological systems have shown that different species compositions can arise from distinct species arrival orders (or colonization history) during community assembly—also known as the priority effects34,35. Extensive numerical simulations have found that the strength of priority effects (calculated as the probability that community composition is dominated by colonization history) increases monotonically with community size, network connectance, and the variation of species intrinsic growth rates36.
Beyond all the influences from host factors and historical contingencies, the highly personalized microbial compositions raise a fundamental question: Do different hosts have different microbial ecosystems associated with different assembly rules and population dynamics? If this is the case, then designing generic microbiome-based therapeutics will be very challenging, because we need to consider not only the unique microbial compositions of different hosts, but also their unique microbial dynamics. (In Sec.3.2, we present a computational method to detect the universality of microbial dynamics and discuss its limitations.) However, if different hosts share similar microbial dynamics, then the highly personalized microbial compositions are simply due to their different species collections. In this case, we can design interventions based on universal dynamic rules to control the microbiome of different individuals, although caution is still warranted. It is hard to believe that a one-size-fits-all “probiotic cocktail” (a consortium of well-selected live microorganisms that presumably provide health benefits) will work for everyone, simply because our healthy baseline (and very likely the disrupted) microbiomes are highly personalized. We might have to design “personalized probiotic cocktails” to effectively control the microbiome of different individuals32. In Sec.3.4.2.2, we present a strategy of designing personalized probiotic cocktail to decolonize a single pathogen (e.g., Clostridioides difficile) and demonstrate its efficacy using simulations.
The highly personalized microbial compositions also make the test of true multi-stability in the human microbiome almost impossible. And whether true multi-stability exists in the human microbiome has implications for multiple computational analyses, e.g., the detection of universal microbial dynamics (see Sec.3.2), and the network reconstruction based on steady-state data (see Sec.3.3.2). Here, true multi-stability means that for a given set of species, there are multiple different stable states with all the species present in the same environment. Mathematically, those stable states are interior equilibrium points (rather than boundary equilibrium points where some species are absent) of the corresponding ecological system. True multi-stability has been well discussed in macro-ecological systems37. Yet, its detection in the human microbiome is rather difficult and has not been demonstrated experimentally.
Challenge 3: Our microbiome is stable, functionally redundant, and likely difficult to manipulate.
Many previous studies have reported the long-term stability of human gut, oral and skin microbiome40–42,43. For the human gut microbiome, compelling evidence has demonstrated that abundance fluctuations in the human gut microbiota are mainly due to temporal stochasticity44,45, and the human gut microbiota has two distinct dynamic regimes: auto-regressive and non-autoregressive38. In particular, most of the variance in gut microbial time series is non-autoregressive and driven by external day-to-day fluctuations in host and environmental factors (e.g., diet), with occasional internal autoregressive dynamics as the system recovered from larger shocks (e.g. facultative anaerobe blooms)38. Overall, the human gut microbiota (in the absence of drastic interventions, e.g., repeated antibiotic treatments or drastic diet changes) can be considered as a dynamically stable system, continually buffeted by internal and external forces and recovering back toward a conserved steady-state38. Note that for some healthy reproductive-age women, their vaginal microbial compositions changed markedly and rapidly over time, which has been associated with their menstrual cycle46. The notion of stability or equilibrium does not apply to this case (despite the metabolic functioning of the vaginal microbial community was probably maintained). The importance of long transients47, sustained oscillations48,49, or even chaos50 in microbial communities on host health is largely unknown and warrants further studies.
The stability or resilience of our gut microbiome against perturbations has been attributed to its high level of functional redundancy (FR)51–53. As a classical concept in community ecology, FR means that phylogenetically unrelated taxa perform similar functions in ecosystems so that they can be interchanged with little impact on overall ecosystem functioning54–57. The roots of FR extend back to the concept of ecological guilds58, whereby species are grouped together based on functional similarities in what they perform within communities. Naturally, high level of FR can be related to the reliability with which an ecosystem will continue to deliver services in the face of moderate species loss59,60. Moreover, an ecosystem with high FR will be resistant to the addition of new species, because newly added species will very likely be functionally similar to certain existing ones and hence fail in the competition with their functionally similar species, rendering poor engraftment. This could be an evidence of the competitive exclusion principle61 (only one species can occupy an ecological niche in one location at any one time), although this principle has often been challenged or reformulated (see Refs.62,63 and references therein).
For the human gut microbiome, compelling evidence of strong FR has been demonstrated1,52,64. For example, dietary carbohydrates can be processed by either Prevotella (from the phylum Bacteroidetes) or Ruminococcus (from the phylum Firmicutes)65. Short-chain fatty acids can be produced by multiple predominant genera: Phascolarctobacterium, Roseburia, Bacteroides, Blautia, Faecalibacterium, Clostridium, Subdoligranulum, Ruminococcus and Coprococcus66. An astonishing discovery from the HMP is that, despite the carriage of microbial taxa varies tremendously across individuals, the gene compositions or functional capacities remain highly conserved within a healthy population, regardless of the body site1. The finding implies for a healthy human microbiota changing its taxa composition will not drastically change its genetic potential or its overall metabolic capacity9. This is also a strong signal of FR.
Recently, a computational framework has been developed to quantify the FR for any microbiome samples using the whole-metagenome shotgun (WMS) sequencing data53. This framework is based on the genomic content network (GCN), a bipartite graph that links microbes to the genes in their genomes. It was reported that the GCN of the human microbiome exhibits several topological features (e.g., its strikingly nested structure) that favor high FR, because randomizing the GCN structure will significantly decrease FR53. The GCN-based framework enabled us to quantitatively test the intriguing relationship between the stability and FR of microbial communities. In particular, by analyzing WMS data from two published FMT studies67,68, it was found that high FR of the recipient’s pre-FMT microbiota raises barriers to donor microbiota engraftment53. In a sense, the FR level of the human microbiome may serve as a resilience indicator in response to perturbations such as FMT.
There are two sides to the high FR of the human microbiome. On one hand, high FR will help the human microbiome avoid drastic functional impairment from moderate taxa loss. On the other hand, it underscores the difficulty of manipulating its composition and functioning. For example, in the case of Clostridioides difficile infection, we want to decolonize the pathogen Clostridioides difficile (a notorious bacterium that is well known for producing toxins and causing serious diarrheal infections), and hence remove the functioning of toxin generation of the community. In this case, microbiome-based therapeutics, e.g., probiotic cocktails, have to be carefully designed, because the external/exogenous species cannot colonize a very stable ecosystem due to its high FR and preoccupied ecological niches. If those exogenous species cannot easily colonize our gut microbiota, we might have to keep consuming them.
THEORETICAL PROGRESSES
Modeling framework.
Mathematical models of microbial dynamics serve as the foundation of designing any model-based control strategy to manipulate the human microbiome. Different modeling frameworks with different levels of complexity have been adopted from macro-ecological systems or developed on purpose in the past to describe the dynamics of microbial communities. In this subsection, we will review those models and discuss the tradeoff between model complexity and parametric uncertainty. Not all the models discussed below are relevant to the central theme of controlling the human microbiome for this Review. Some of the complicated and more mechanistic models were actually developed for quite different purposes (e.g., explaining generic ecological patterns observed in microbial communities). Nevertheless, we introduce them here for the purpose of completeness so that readers can appreciate the whole spectrum of model complexities and better understand the motivation of working on simpler models for control strategy design (as discussed in Sec.3.4) or even completely model-free or data-driven approaches (as discussed in Sec.4.3).
Population-level models vs. Individual-based models
Various modeling frameworks of microbial dynamics have been developed69,70. Basically, they can be classified into either population-level models (PLMs) or individual-based models (IBMs). As the name suggests, PLMs directly describe the population changes of different microbial species present in the community. Some PLMs also explicitly model the abundance changes of abiotic resources (e.g., nutrients) consumed/produced by microbial species or chemical compounds that mediate the microbial interactions (see Sec.3.1.2.2 and 3.1.2.3). PLMs can be written as either differential or difference equations, depending on if time is treated as continuous or discrete. PLMs can be applied to spatially homogenous (or structured) environments using ordinary (or partial) differential equations (ODEs or PDEs), respectively. Thanks to their simplicity (especially for those PLMs that focus on the modeling of species population changes only), PLMs have proven to be of immense value in studying fundamental problems in microbial ecology and modeling the human microbiome to inform microbiome-based therapeutics design. Of course, PLMs have several intrinsic limitations: they do not incorporate phenotypic heterogeneities, adaptive processes, and interactions with local biotic or abiotic environment at the individual level.
IBMs are designed to resolve the limitations of PLMs69. In contrast to PLMs, IBMs do not describe changes on the population level at all. Instead, they only describe activities/properties of individuals, as well as their interactions with the environment or host. Thanks to remarkable technological advances in metagenomics, bioinformatics, and culturomics71, we have accumulated ever more properties and behaviors of individual microorganisms, facilitating the development of IBMs to provide insights into various emergent phenomena, e.g., self-organized spatial patterns of biofilms72, and the coevolution of the archaeal and bacterial adaptive immunity system, CRISPR-Cas, and lytic viruses73. Despite the success of IBMs in certain application scenarios, and the availability of generic open-source platforms for individual-based modeling (e.g., iDynoMiCS74), building IBMs for the human microbiome to inform microbiome-based therapeutics design can be a daunting task due to (i) a huge number of model parameters that are often difficult to infer from observed data; (ii) many environmental variables (such as the concentrations of bacteriocins and nutrients) are hard to measure in real time; (iii) spatial distribution of microbial species in certain body sites (e.g., gut) is hardly available.
In the following, we will review different PLMs that have been heavily used to study microbial communities (including the human microbiome). Regarding the application of IBMs in studying microbial sciences, we refer readers to Refs.69,75 for comprehensive reviews.
Population-level models: from simple to complex
Species-only models
When modeling a dynamical system, we first need to decide how complex the model needs to be so as to capture the phenomenon of interest. In the context of human microbiome, if we are just interested in exploring the impact that any given species has on the abundance of other species and predicting the abundance changes of microbial species present in the community, it is sufficient to use species-only PLMs written as a set of ODEs without assuming any spatial structure76,77:
i = 1, ⋯, N. Here, fi(x(t))’s are some unspecified functions characterizing the population dynamics of the community, is an N-dimensional vector with xi(t) denoting the abundance (or population density) of species-i at time t. Here we have implicitly assumed that chemical compounds or resources that mediate the microbial interactions rapidly reach steady state, hence can be mathematically eliminated from the model.
We can further decompose fi(x(t)) into the sum of intrinsic dynamics and microbial interactions. If we assume pair-wise microbial interactions, then the ODEs take the generic form of
i = 1, ⋯, N. The classical Generalized Lotka-Volterra (GLV) model is a representative species-only PLM with pairwise interactions:
i = 1, ⋯, N. Here, is the intrinsic growth rate vector, is the inter-species interaction matrix. Note that the model parameters (r, A) depend on both environment-independent factors (e.g., biochemical processes and metabolic pathways) and environment-specific ones (e.g., pH, temperature, nutrient intake, host immune system). Hence, environmental (or host) factors are not explicitly considered here but are absorbed in the model parameters. Therefore, this is a “phenomenological” or effective model.
The key advantage of the “phenomenological” PLMs, especially the GLV model, is its simplicity. In a sense, the GLV model is a minimal dynamical systems model of microbial communities. All the model parameters in the GLV model are relatively easy to infer from temporal or steady-state data of the community (given the data is informative enough, see Sec.3.3)77–79. Hence, this modeling framework is suitable for us to explore the impact that any given species has on the abundance of other species, and design microbiome-based therapeutics (e.g., personalized probiotic cocktails32) to achieve desired microbial compositions. Indeed, the GLV model has been heavily used to model host-associated microbial communities77,78,80,81.
It has been shown that for many commonly encountered microbial interactions traditional Lotka-Volterra pairwise interactions may not be adequate26. Furthermore, it was pointed out that the GLV model does not have the necessary complexity to explain a wide variety of independent growth outcomes82. These limitations might be due to multiple reasons. First, the steady-state assumption of the chemical compounds (e.g., consumable metabolites and reusable signaling molecules) that mediate the inter-species interactions may be violated, and hence should be modeled explicitly. Second, it is likely that microbial interactions occur in high-order combinations, whereby the interaction between two species is modulated by one or more other species27. Indeed, a recent experiment on a well-controlled microbial trophic chain has identified a higher-order interaction between its species28. In particular, it was observed that a single-celled algae (Chlamydomonas reinhardtii) modulates the interaction between a predatory ciliate (Tetrahymena thermophila) and the bacterium Escherichia coli. Directly incorporating higher-order interactions into the species-only PLMs with pairwise interactions, e.g., the GLV model, will lead to a very complicated model in the form of
i = 1, ⋯, N. The significant increase of the model parameters will render the parameterization extremely challenging, especially in the absence of any a priori knowledge on the sparsity of the model parameters.
Mediator-explicit models
To remedy the inadequate pairwise modeling approach and avoid directly modeling of higher-order interactions, mediator-explicit models have been proposed21,26. These models explicitly incorporate production/release of chemical compounds as well their consumption/degradation by microbes. Each chemical compound in turn can facilitate or inhibit the growth of microbes within the community. A general mediator-explicit model can be written as a set of coupled ODEs:
i = 1, ⋯, N; α = 1, ⋯, M. Here, xi still represents the abundance of species-i, Cα is the concentration of chemical compound-α, ri is the baseline growth rate of species-i in the absence of chemically-mediated interactions, (or ) represent the strength of facilitation (or inhibition) of compound-α on the growth rate of species-i, Kiα is the saturation concentration, pαi is the rate of production of compound-α per cell of species-i, and cαi is the maximum rate of consumption of compound-α per cell of species-i. In case of reusable mediators, microbes are affected by the mediator but without considerably consuming or degrading it (e.g., in response to a signaling molecule in quorum sensing), we set cαi = 0. Note that this model assumes the species growth rate linearly drops as the inhibitor concentration increases, but saturates as the facilitator concentration increases (in the Monod form Cα/Cα + Kiα). More complicated formulations of inhibitions (e.g., the inhibition threshold model, the growth inhibition model) and facilitations (in a general saturating form, i.e., the Moser form with n > 1) can be incorporated. This mediator-explicit model has been used to simulate a typical experimental process of enrichment (where a multi-species community is grown in excess shared resource and is periodically diluted to a pre-determined threshold cell density). In particular, it facilitates our understanding of how chemical-mediated microbial interactions lead to coexistence when external nutrients are replenished to be in excess21.
Parameterization of mediator-explicit models for large communities (e.g., the human gut microbiome) is a big challenge. Experimental characterization of the growth of microbial species in the presence of different concentrations of chemical compounds (including but not limited to metabolites) that stimulated or inhibited their growth could be a very demanding task. In fact, having a comprehensive catalog of those chemical mediators in the human gut microbiome requires extensive experimental efforts.
Consumer-resource models
The mediator-explicit model discussed in Sec. 3.1.2.2 can be considered as a special type of consumer-resource model (CRM) in which chemical mediators generated by species are modeled, but external resources are not modeled since they are assumed to be supplied in excess. To model all the resources explicitly, we need to build more complex and mechanistic CRMs. The starting point is MacArthur’s CRM83,84 where each of the N species (“consumers”) can consume some of M substitutable resources, whose dynamics are described by a set of coupled ODEs:
i = 1, ⋯, N; α = 1, ⋯, M. Here, xi is the abundance of species-i, Rα is the abundance of resource-α, wα is the value of one unit of resource-α to the consumer/species, ciα is the rate at which species-i captures and consumes resource-α per unit abundance of resource-α. Note that the matrix is often referred to as the consumer preference matrix, which naturally has a bipartite graph presentation. mi is the minimum maintenance energy required for the growth of species-i, bi is a factor converting the resource excess into the per capita growth rate of species-i. h(Rα) is the intrinsic resource dynamics (which usually takes the logistic form, i.e., rαRα(1 − Rα/Kα), representing logistic self-inhibition of resource-α by itself), and the term xiciαRα represents the mortality of resource-α imposed by the consumer species-i.
Note that in MacArthur’s CRM, different species may consume the same type of resource, which naturally leads to competition. In fact, one application of MacArthur’s CRM is to derive the competition coefficients in the Lotka-Volterra competition equations. Indeed, if we assume the population dynamics of resources are much faster than that of consumer species, and we can insert the consumer-dependent equilibrium value of Rα, i.e., , into the ODE of xi, rendering a competitive Lotka-Volterra equation: with and .
To better describe microbial interactions (which are certainly more diverse than competition), a more complicated CRM --- Microbial Consumer-Resource Model (MiCRM) has been proposed recently85–87,88,89. By introducing energetic fluxes and cross-feeding to the original MacArthur’s CRM, MiCRM takes the form of
i = 1, ⋯, N; α = 1, ⋯, M. Here, we assume a fraction lα of the energy imported by species-i from resource- α is returned (“leaked”) to the community as metabolic byproducts. specifies the fraction of leaked energy from resource-β that is released in the form of resource-α by species-i. By definition, . The matrix is referred to as the stoichiometric metabolic matrix of species-i.
MiCRM has been used to explain the emergent simplicity in the assembly of hundreds of soil- and plant-derived microbiomes in well-controlled minimal synthetic media87, as well as various ecological patterns found in environmental and human microbiomes, e.g., compositional gradients, dissimilarity/overlap correlations, richness/harshness correlations, and nestedness of community composition85,88. Note that in all the previous studies of MiCRM, model parameters were predetermined by modelers rather than inferred from real data. Moreover, for simplicity, it was often assumed that all species share a similar core metabolism encoded in a universal stoichiometric metabolic matrix . This assumption significantly reduces the number of model parameters. Another limitation of MiCRM (as well as MarArthur’s original CRM) is that it does not explicitly model the case of reusable resources (e.g., signaling molecules in quorum sensing, or antimicrobial metabolites such as bacteriocins) that drastically affect the growth of microbes but are not considerably consumed or degraded by microbes.
Despite the success of random CRMs in reproducing experimentally observed ecological patterns in various microbial communities, they will in general fail to capture species level details, unless all the model parameters are inferred from real data (which is a daunting task by itself). Consequently, directly using MiCRM to inform the design of microbiome-based therapeutics (e.g., probiotic cocktails) would be very challenging, if not impossible. After all, this type of models was not initially proposed for this purpose.
Metabolic Models
As discussed above, to capture the cross-feeding among microbial species, MiCRM explicitly models the metabolism of species (although a convenient assumption, i.e., all species share a similar core metabolism, is often made to reduce model parameters). Another big class of models, i.e., metabolic models, take this step even further and have emerged as a valuable framework for predicting, understanding and designing microbial communities. In particular, those models leverage metabolic networks of microbial species to perform flux balance analysis (FBA) and generate simulations of microbial species in molecularly complex and spatially structured environments. Here we briefly introduce the key component of existing metabolic models, i.e., FBA. As a constraint-based computational method in systems biology, FBA is used to predict the function or phenotype of an organism by simulating its metabolism90. The metabolic network of an organism is represented by the stoichiometric matrix , where siα represents the moles of metabolite-i consumed (siα < 0) or produced (siα > 0) by reaction-α, N and M are the number of metabolites and reactions, respectively. A key assumption of FBA is that intracellular metabolism is at steady state, i.e., S · v = 0, where is the flux (i.e., reaction rate) vector. This steady-state assumption can be motivated from two different perspectives91: (1) One can argue that metabolism is much faster than other cellular processes such as gene expression. Hence, the steady-state assumption can be considered as a quasi-steady-state approximation of the metabolism that adapts to the changing cellular conditions. (2) On the long run no metabolite can accumulate or deplete. FBA computes the flux vector v by optimizing an objective function represented in the form of a linear combination of the flux variables: c⊤v (e.g., maximization of biomass yield) with certain capacity constraints imposed by the lower and upper bounds on the M reactions, represented by two vectors l and u, respectively. Mathematically, this can be formalized as a linear programming problem:
and solved with established efficient optimizers (e.g., Gurobi and GLPK). Note that the search for a set of fluxes that optimizes a given objective implies the “optimal regulation” hypothesis, i.e., the organism has evolved to be able to regulate its metabolic fluxes to approach that optimum under a set of environmental conditions69.
To consider the spatial structure of microbial communities, we assume that the biomass of different species and the environmental metabolites can propagate from its current position to its neighborhood based on the physics laws of diffusion.
COMETS92,93 and BacArena94 are two representative metabolic modeling platforms. The former takes a population-level approach, while the latter takes an individual-based approach. Both platforms can be used to generate novel hypothesis concerning the metabolic interactions between microbes and investigate the importance of microbial geography in community assembly (e.g., biofilm formation).
Despite the success of those metabolic modeling platforms, we highlight a few limitations. First, parameterization of metabolic models is a big challenge. Indeed, to optimally employ any metabolic model for any specific applications, users should first determine whether genome-scale metabolic reconstructions of suitable quality for the microorganisms of interest are currently available. For the human gut microbiome, it is worthwhile mentioning that AGORA (assembly of gut organisms through reconstruction and analysis), a resource of genome-scale metabolic reconstructions semi-automatically generated for 773 human gut bacteria, was established in 201795. Recently, AGORA has been expanded in both scope and coverage to consist of microbial reconstructions for 7,206 strains, 1,644 species, and 24 phyla96. AGORA reconstructions could provide a starting point for the generation of high-quality, manually curated metabolic reconstructions. For the human oral microbiome, thanks to the expanded Human Oral Microbiome Database (eHOMD)97, the genome-scale metabolic reconstructions for 456 different microbial strains (from 371 different species, 124 genera, 64 families, 35 orders, 22 classes, and 12 phyla) have already been recently generated98.
Second, inputs of the metabolic models are sometimes hard to access. Users need to have a good understanding of the molecular composition of the environments or growth media of interest. For simple synthetic communities cultured in well-controlled laboratory conditions and relatively simple growth media, this is easy. But for complex multi-species communities with complex environment (e.g., the human gut microbiome with complicated dietary information), this is really a big challenge.
Finally, as a key component in metabolic models (regardless of its population-level or individual-based nature), FBA has its own intrinsic limitations. (1) The steady-state assumption of intracellular metabolism is not necessarily true all the times, even though a mathematical foundation for the steady-state assumption for long time periods has been proposed to justify its successful use in many applications91. (2) The ‘optimal regulation’ hypothesis is not necessarily true. A anecdotal example is the soil bacteria species Paenibacillus sp., which can modify its environmental pH to such a degree that leads to a rapid extinction of the whole population, a phenomenon coined as ecological suicide99. How such self-inflicted death of microbes can exist without evolution selecting against them is an outstanding question in microbial ecology.
Tradeoff: model complexity vs. parametric uncertainty
How complex should a microbial dynamics model be? Answer to this question certainly depends on the purpose of the modelling efforts. Simple models (e.g., the GLV model with only pairwise microbial interactions) are relatively easy to parameterize from existing microbiome data collected with existing techniques. But they are phenomenological or effective, may not capture all the details of the microbial interactions (such as higher-order interactions), and may completely ignore the host-microbiome interactions. Complex models (e.g., MiCRM or COMETS) are more mechanistic, may capture characteristics of various types of microbial interactions, may model the host-microbiome interactions, and even the microbiome biogeography. Yet, they are often difficult to parametrize. Of course, they can be used to study general principles of community assembly by sampling model parameters from certain distributions. But the same strategy will not allow us to inform microbiome-based therapeutics, e.g., a probiotic cocktail that decolonize a particular pathogen. Parameterizing complex PLMs can be equally difficult as parameterizing IBMs. For example, the state-of-the-art metabolic modeling platforms: COMETS (which takes a population-level approach) and BacArena (which takes an individual-based approach) require almost the same amount of efforts in parameterization. Both require high-quality genome-scale metabolic reconstructions of microbial species of interest. Recent advancements in experimental microbiology and culture-independent sequence-based metagenomics provide more data and lead to a better understanding of individual species. This additional data and knowledge could be used to build more complex and mechanistic models of microbial communities. However, it is questioned if this will always lead to better models for specific purpose, e.g., inform the design of microbiome-based therapeutics. After all, a model with higher complexity means more parameters, which lead to a more difficult parametrization and are often considered as the main source of uncertainty in modeling efforts.
A promising strategy is to “start complex and simplify later”. This strategy is based on the observation that some complex microbial communities appear to be at least partially “coarse-grainable”100. In other words, some properties of interest can be adequately described by effective models of dimension much smaller than the number of interacting species. For example, for industrial bioreactors consisting of hundreds of species, their properties (e.g., nitrate removal, biomethane production) can often be well described by models with fewer than ten functional groups101,102. Rigorously defining the coarse-grainability of complex microbial communities and understanding the conditions for its emergence is a very intriguing question. Recently, an inspiring theoretical framework was proposed to begin addressing this question100. In particular, a minimal model for investigating hierarchically structured ecosystems within the framework of resource competition was proposed and used to operationally define the coarse-graining quality based on reproducibility of the outcomes of a specified experiment. It was demonstrated that an ecosystem can be coarse-grainable under one criterion but not coarse-grainable at all under another criterion. Moreover, it was shown that a high diversity of strains may actually enhance the coarse-grainability. These results shed light on a theoretical understanding of which ecosystem properties, and in which environmental conditions, might be well described by coarse-grained models. Consider the example of the human gut microbiome. Perhaps the exact geometry of the gut epithelium, the effect of flow and peristaltic mixing, or the exact role of the vast diversity of uncharacterized chemical compounds (e.g., metabolites) might not be as important as we would expect, if we want to manipulate the community composition and functioning.
Harnessing the coarse-grainability of the human gut microbiome is of critical importance for understanding, predicting, or controlling the behavior of this complex ecosystem100. For example, inspired by the stable marriage problem in game theory and economics, a conceptual coarse-grained model of microbial communities was proposed103. With a key assumption that microbes utilize nutrients one at a time while competing with each other, this model can exhibit rich behaviors such as dynamic restructuring and multiple stable states connected by a hierarchical transition network. And all of this complexity is encoded in just two ranked tables (one with microbes’ nutrient preferences and the other with their competitive abilities for different nutrients), without assuming any other parameters. Leveraging this highly coarse-grained model to design control strategies would be a very interesting future direction.
Universality of microbial dynamics.
As mentioned in Sec.3.1.2, if we are just interested in exploring the impact that any given species has on the abundance of other species and predicting the abundance changes of microbial species present in the community, it is sufficient to use species-only PLMs written as a set of ODEs: without assuming any spatial structure. Here we have explicitly written down the set of model parameters, denoted as Θ, which depends on both environment/host-independent and environment/host-specific factors. In general, the parameters Θ estimated from a given habitat with certain characteristic environmental conditions do not necessarily map to other habitats with different environmental conditions. For microbiome samples collected from the same habitat (such as the human gut) but from different local communities (e.g., different hosts), are the ecological parameters Θ “host-independent” or “host-specific”?
Addressing this question is vital for developing microbiome-based therapies. There are three basic scenarios: (1) Θ’s are strongly host-specific, then we have to design truly personalized interventions: we need to consider not only the unique microbial state of an individual but also the unique dynamic rules (encoded by the host-specific Θ) of the underlying microbial ecosystems. (2) Θ’s can be classified into a few groups, for which we need to develop interventions based on group-specific dynamic rules. (3) Θ’s are host-independent or universal, the inter-personal variability stems solely from the different species collections. In this case, we can design interventions based on universal dynamic rules to control the microbial state of different individuals (although the intervention themselves, e.g., the recipes of the probiotic cocktails, might be quite different for different individuals due to the personalized baseline microbiomes).
A statistical method to detect universal dynamics
Directly addressing the dynamics universality question would require us to infer Θ from high-quality temporal data of each local community or host using system identification techniques (see Sec.3.3.1). Doing this for a large collection of local communities (hosts) is both logistically and ethically challenging. Recently, an indirect method called Dissimilarity-Overlap Curve (DOC) analysis was proposed29. The DOC analysis relies on two mathematically independent measures between any two microbiome samples (or local communities): (1) overlap (O), which is the average relative abundance of common species shared by the two communities; and (2) dissimilarity (D), which is the dissimilarity between the renormalized abundance profiles of the common species. Note that the renormalization of the common species’ abundance profiles is necessary to ensure the independency of the two measures: O and D. Hence, any dependency or relationship observed from real data deserves a dynamical or ecological explanation.
The basic steps of the DOC analysis are as follows. First, for a given set of microbiome samples, we calculate overlap and dissimilarity of all the sample pairs and represent each sample pair as a point in the dissimilarity–overlap plane. Second, since the exact relationship between those two measures is unknown, we use a standard nonparametric regression method, i.e., the robust LOWESS (Locally Weighted Scatterplot Smoothing) method to create a smooth line through the scatter plot to summarize a relationship and foresee the general trend, in a fashion that makes few assumptions initially about the form or strength of the D-O relationship. The gives us the DOC, representing the average trend of the dependency between D and O. Finally, to get the confidence interval of the DOC, we use the standard bootstrap technique.
Mathematical basis of the DOC analysis
The DOC analysis assumes the abundance profile of each microbiome sample represents (or at least approximates) the steady state x* of the corresponding ecosystem (or local community), i.e., it satisfies the steady-state equation f(x*, Θ(a)) = 0, where a represents the sample ID. The DOC analysis is inspired by the following observation: if two microbiome samples (local communities) that have the same species collection also have the same abundance profile (steady state), i.e., O = 1 and D = 0 simultaneously, then the two communities should share universal microbial dynamics f(x, Θ) characterized by the same set of model parameters Θ. This is because if x* satisfies both steady-state equations: f(x*, Θ(1)) = 0 and f(x*, Θ(2)) = 0, then given the large number of species and all the other levels of complexity in their interactions encoded in the highly nonlinear function f, we should have generically Θ(1) = Θ(2) except for some pathological cases with Lebesgue measure zero.
In reality, the case of two samples having the same species collection (O = 1) almost never happens for complex host-associated microbial communities, such as the human gut microbiome, due to highly personalized microbial compositions. But we can take a leap of faith through interpolation: if we observe a trend that steady-state sample pairs with higher O tend to have lower D, i.e., there is a negative slope in the high-overlap region of the DOC, we can argue that this trend is a strong signal of host-independent model parameters Θ, or equivalently, universal microbial dynamics in species-only PLMs.
Caveats in detecting universal dynamics
We emphasize that detecting the universality (or host-independency) of microbial dynamics makes sense only for simple phenomenological species-only PLMs, which only model the species dynamics and completely ignore the resource dynamics and any environment/host factor. In a sense, phenomenological species-only PLMs are coarse-grained models of complex mechanistic models. Generally speaking, more complex models are more likely to be universal. Indeed, for a mechanistic model that explicitly models all the relevant state variables (e.g., species abundances, resource concentrations, pH, temperature, etc.), its model parameters (e.g., the rate at which species-i captures and consumes resource-α per unit abundance of resource-α, the minimum maintenance energy required for the growth of species-i, etc.) should simply depend on biochemistry, and hence are host-independent by definition. As discussed in Sec.3.1.4, this modeling approach is challenging due to its parametrization difficulty. Coarse-grained models are simpler and easier to parameterize, but then we need to worry about their dynamics universality. The tradeoff between model complexity and dynamics universality has to be carefully considered in the modeling of the human microbiome.
Although the DOC analysis can be used to detect dynamics universality of species-only PLMs, caution is needed in the application of DOC analysis and interpretation of its results. First, the microbiome samples should (at least roughly) represent the steady states of the underlying ecosystem. For microbial communities subject to strong environmental stochasticity and demographic noise, the results of the DOC analysis will be meaningless. With cross-sectional data only, this steady-state assumption is unfortunately hard to validate. Fortunately, previous studies based on longitudinal data analyses have reported the long-term stability of human gut, oral and skin microbiome for healthy adults40,41. These findings justify the steady-state assumption to some extent. Second, the DOC analysis implicitly assumes that the true multi-stability does not exist. For complex host-associated microbial communities, the presence of true multi-stability is hard to validate (due to highly personalized microbial compositions). For simple experimental in vitro communities, the presence of true multi-stability is relatively easy to validate104. Third, interpretation of the DOC analysis should focus on the slope in the high-overlap region of the DOC. Ideally, the highest overlap should be close to 1. If all the sample pairs yield intermediate or very low overlap values, then the DOC analysis is not very meaningful. Finally, the negative slope in the high-overlap region of the DOC is also consistent with alternative hypotheses, such as communities assembling in environmental gradients, or situations when only a small fraction of samples have universal dynamics105. To rule out the hypothesis of environmental gradients, we need to systematically analyze microbiome samples while controlling for the effect of all the potential confounding factors. In the case of human gut microbiome, leading candidates of those factors include age, race, body mass index, long-term dietary pattern, and transit time through the gut (measured by stool consistency), which has been considered in the original work on the DOC analysis29. How to rule out the hypothesis of only a small fraction of samples have universal dynamics (and hence largely contribute to the negative slope in the high-overlap region of the DOC) is still an open question.
Reconstruction of the ecological network.
As discussed in Sec.3.1.2.1, if we assume pairwise microbial interactions in a species-only PLM, the ODEs of the system dynamics take the form of . Here, the inter-species interaction matrix can be represented by an ecological network 𝒢(A) = (𝒱, ℰ): there is a directed edge (j → i) ∈ ℰ if and only if aij ≠ 0. Here 𝒱 represents the set of all the species, while ℰ represents the set of all the edges. Hence, inferring the interaction matrix from observed abundance data can be considered as a network reconstruction problem106. In dynamical systems and control theory, the art and science of building mathematical models of dynamic systems from observed input-output data is termed as system identification107, which is a more general task than network reconstruction.
Conceptually, there are two ways to infer the inter-species interaction matrix: (1) bottom-up approach; (2) top-down approach. For small synthetic communities, one can systematically perform monoculture and co-culture experiments to directly quantify the impact of species-j on the growth of species-i and hence estimate aij. This bottom-up approach has been applied to infer inter-species interactions in a synthetic community composed of 8 soil bacterial species108, as well as a synthetic community encompassing 12 prevalent human-associated intestinal species109. This approach is not feasible for large complex communities for several reasons. First, many of the species in complex communities (e.g., the human gut microbiome) cannot be easily cultured in vitro. Second, if all the species can be cultured in vitro, the total number of monoculture and co-culture experiments N(N + 1)/2 increases rapidly as the number of species N increases. Finally, the inferred inter-species interactions in vitro might not capture the inter-species interactions in vivo.
For large complex communities, we have to rely on the top-down approach, i.e., inferring the inter-species interactions from (1) the informative longitudinal abundance data of the whole community; or (2) the steady-state abundance data of a large number of sub-communities with different species assemblages. Here, the sub-communities are far more complicated than mono-species and pairwise assemblages.
Methods based on longitudinal data
Many methods have been developed to infer inter-species interactions and reconstruct the ecological network based on longitudinal or time-resolved abundance data77,78,81. Those methods have demonstrated the capability to accurately forecast gut microbiota dynamics in mice77,78 and human studies80. In particular, the open-source software package Microbial Dynamical Systems Inference Engine (MDSINE) offers a suite of algorithms for inferring dynamical systems models from microbiome time-series data and predicting temporal behaviors78.
Key idea: gradient matching
Those methods are typically based on the extended GLV model that explicitly consider the impact of various external stimuli or perturbations on the system dynamics77:
i = 1, ⋯, N. Here, is the susceptibility matrix with biq representing the stimulus strength of a perturbation uq(t) on species-i. The perturbation uq(t) is binary-valued, indicating if the given perturbation is present at time t or not. This mimics realistic perturbations from antibiotics or prebiotics, which can inhibit or benefit the growth of certain microbes.
To estimate the model parameters from the longitudinal data {xi(tk), uq(tk)} at discrete time points (k = 0,1, ⋯, T), the “gradient matching” approach can be employed78. The key idea is that if estimates of the gradient are available, parameters can be estimated by solving a system of equations rather than a system of differential equations. For the extended GLV model, thanks to the linear functional response, the gradient matching approach can reduce the system of differential equations into a system of linear equations, which enables application of statistical models for linear regression77. Indeed, if we move xi(t) to the left-hand side of the ODE, integrate both sides over the time interval [tk, tk+1] and assume xi(t) and uq(t) are roughly constant over the time interval], then we have
Here, εi(tk) represents the error arising from the approximation of the integral by holding the integrand constant over the time interval. Now, we define the scaled log-difference matrix with yik = [logxi(tk+1) − logxi(tk)]/(tk+1 − tk), the time-series data matrix with , and the approximation error matrix with eik = (εi(tk)/(tk+1 − tk)), we have a system of linear equation in the following compact form:
Parameter inferences
Since the number of equations N × T is typically less than the number of unknowns N × (1 + N + M), the above system of linear equations is usually underdetermined. Different algorithms have been developed to compute Θ. They can be classified as (1) maximum likelihood-based methods, e.g., maximum likelihood ridge regression (MLRR)77 and maximum likelihood constrained ridge regression (MLCRR)78; and (2) Bayesian dynamical systems inference methods78, e.g., Bayesian Adaptive Lasso (BAL), and Bayesian Variable Selection (BVS). Note that Bayesian inference methods naturally offer two additional functionalities that the maximum likelihood-based methods do not, i.e., (1) estimation of confidence in model parameters Θ; and (2) statistical modeling of high-throughput sequencing count-based data over time. We emphasize that MLRR, MLCRR and BAL all rely on regularization techniques to reduce the overfitting issue, while BVS relies on variable selection techniques110: it directly models the 0/1 pattern of the inter-species interaction matrix A and the species-perturbation susceptibility matrix B.
A benchmark study78 using simulated ground-truth data demonstrated that MLCRR, BAL and BVS outperform MLRR on the following metrics: root mean square error (RMSE) for microbial growth rates (r); RMSE for microbial interaction parameters (A); RMSE for prediction of microbe trajectories on held-out subjects given only initial microbe concentrations for the held-out subject; and the area under the receiver operator curve (AUROC) for reconstructing the underlying ecological network of microbial interactions, i.e., 𝒢(A). Moreover, the two Bayesian algorithms (BAL and BVS) showed the greatest robustness to lower sequencing depths and lower resolutions of temporal sampling and demonstrated particularly strong performance on inferring A and the underlying network 𝒢(A).
Caveats
Despite the success of existing methods in various contexts, there are many caveats in inferring microbial dynamics from longitudinal metagenomics data111. Here, we list those caveats and point out possible solutions.
First, we need to choose a proper dynamics model for the microbial ecosystem. Although existing methods typically rely on the GLV model (to leverage its linear functional response that facilitates the gradient matching approach), it has been pointed out that the GLV model may not be adequate enough to model many commonly encountered microbial interactions26. Even if we just assume pairwise microbial interactions, the exact functional response encoded in the function g(xi, xj) is largely unknown. This challenge can be tackled through symbolic regression, a machine learning method that automatically infers both the model structure and parameters from temporal data112–116. A previous study using both synthetic and experimental data demonstrated that combining symbolic regression with a “dictionary” of possible ecological functional responses opens the door to correctly reverse-engineering ecosystem dynamics117. More efforts are needed to fully take advantage of the symbolic regression technique to analyze longitudinal metagenomics data of complex microbial communities, such as the human gut microbiome.
Second, we need to collect informative temporal data to infer model parameters. Note that The temporal data could be uninformative due to either low sampling rate or “unexcited” system dynamics. In system identification literature118, it is well known that the degree to which estimated parameters converge to their true values is highly correlated to the notion of persistent excitation, which means that the measured experimental signals need to be sufficiently “rich” (i.e., span the frequencies of dynamical interest) if one is to expect good parameter convergence. For the original GLV model, it has been shown that if the temporal data is not informative enough (such that the persistent excitation condition does not hold), indistinguishability will appear in the sense that different model parameters can produce exactly the same temporal data119. In the same spirit, it has been pointed out that, even for the extended GLV model with external stimuli or perturbations, accurate time-series prediction does not always imply accurate inference111. Mathematically, by persistent excitation of a signal vector v(t) we mean that there exist strictly positive constants α and T such that for any t ≥ 0, , where T is called the excitation period of v(t) and I is the identity matrix. In practice, we can define a measure to quantify the level of persistent excitation, where λmin is shorthand for the minimum eigenvalue of the matrix. So far, this data informativeness issue has not been seriously considered in inferring the dynamics of complex microbial communities.
Third, the compositionality nature of the relative abundance data will cause fundamental limitations in inference111. We know that the compositionality of relative abundance data will not significantly alter the original absolute abundance data if and only if the total microbial population is roughly time-invariant, which is of course not necessarily true. Even if the relative abundance data can approximate the original data, a time-invariant total population will be linearly correlated with the constant row in the time-series data matrix Φ, which will introduce linear correlations of rows of Φ and hence lead to the rank deficiency of ΦΦ⊤ and drastically worsen the inference results. In addition to rank deficiency, compositionality will cause another serious issue: distorting the original dynamics when the total population is time variant. Indeed, metagenomic sequencing data typically chart only the relative abundances of taxa, but not their absolute amounts. If a species’ relative abundance increases over time, we actually cannot determine whether that species is blooming, or other species are dying out. For certain small laboratory-based microbial communities, we can measure the absolute taxon abundances in a variety of ways, e.g., selective plating120, quantitative polymerase chain reaction (qPCR)121, flow cytometry122, and fluorescence in situ hybridization (FISH)123. For large bacterial communities, the total bacterial biomass can be measured by 16S rRNA qPCR using universal primers77,78. To quantify the absolute abundances of bacteria, fungi and archaea simultaneously within a microbiome sample, a scalable cell-based multi-kingdom spike-in method (MK-SpikeSeq) can be employed124.
Finally, grouping or ignoring low-abundance species lacks justification. Since the number of equations is typically much smaller than the number of unknowns, many previous studies group those low-abundance species together and treat them as a pseudo-species77,81,125. A numerical study demonstrated that this approach does not work as well as we expected, especially when the low-abundance species are also strongly interacting species (i.e., they interact strongly with their interacting partners)111. Even in the absence of strongly interacting species, the reconstructed network obtained by grouping some low-abundance species can be misleading, because grouping can create false interactions between the grouped species and highly abundant species. Hence, we emphasize that grouping low-abundance species is not a solution to the underdetermined problem. Generating informative temporal data with more time points is the solution. There is no short cut or free lunch.
Steady-state data-based Inference
Among all the caveats in inferring microbial dynamics from longitudinal metagenomics data, the data informativeness issue is the hardest one to resolve for the human microbiome. Indeed, any attempt to improve the informativeness of longitudinal human microbiome data is challenging and ethically questionable, as it requires applying drastic and frequent perturbations to the microbiome, with unknown effects on the host. Note that naively applying inference methods to longitudinal human microbiome data collected in observational studies (i.e., without any drastic interventions) is problematic. A previous attempt, using the GLV model, has demonstrated that the inter-species interaction matrix A inferred from the human gut microbiome time-series data collected in observational studies is almost the same as that inferred from the randomly shuffled time-series data where temporality is completely removed76. This finding simply implies that the observed time-series data of the human gut microbiome is not informative enough for dynamic inference purpose. This finding is also consistent with our general understanding on the stability of the human gut microbiome in the absence of drastic interventions, as discussed in Sec.2.3.
To circumvent the above fundamental limitation of inference microbial dynamics from temporal data, one can assume the observed microbiome samples (at least roughly) represent different steady states of the underlying ecosystem and infer the inter-species interactions from the difference between those “steady states”79. This approach does not require any external perturbations. In fact, for the human microbiome, this approach leverages the fact that our microbiome is highly personalized. Hence microbiome samples (with presumably very different species assemblages) collected from different hosts serves as natural perturbation experiments of the underlying ecosystem.
This inference approach based on steady state comparison actually has its root in inferring general dynamics on complex networks106. For microbial dynamics inference and network reconstruction, this approach was inspired by a theoretical study on the ecological explanation of the “community types” (i.e., densely populated areas in the compositional landscape)76. In particular, for the GLV model, it was found that if we introduce a new species to a system at equilibrium, and if the new species interacts with existing ones, then the new species will drive the system to a new equilibrium. The strengths of the interactions between the new species and the existing ones are encoded in the difference between the two equilibria76.
Mathematical basis
Consider a generic population dynamics model:
i = 1, …, N. Here, we explicitly factor out xi to emphasize that in the absence of species invasion or migration, those initially absent or later extinct species will never be present in the microbial community again. Mathematically, the inter-species interactions are encoded by the matrix with Jij(x(t)) ≡ ∂fi(x(t))/∂xj. The condition Jij(x(t)) > 0 (< 0 or = 0) means that species-j promotes (inhibits or doesn’t affect) the growth of species-i, respectively. The diagonal terms Jii(x(t)) represent intra-species interactions.
Denote the set of observed steady-state samples as 𝒳. Consider two steady-state samples xI and xK that share species-i. We have fi(xI) = fi(xK) = 0. Here, the species index sets I, K ∈ 2{1,⋯,N} determine which species are present in the samples. Denote Ji(x) = ∂fi(x(t))/∂x, representing the i-th row of the matrix J(x). Applying the mean value theorem for multi-variable functions, we obtain
This equation implies that the difference of any two steady-state samples xI and xK sharing species-i will constrain the integral of Ji over the line segment joining them in . This is the mathematical basis of inferring inter-species interactions from steady-state comparisons.
The structure of the ecological network is encoded in the zero-pattern of the matrix J(x(t)). Under a very mild assumption that holds if and only if Jij(x(t)) ≡ 0, the steady-state samples can be used to infer the zero-pattern of J(x), i.e., the structure of the ecological network, which is interesting by itself and can be very useful in control theoretical analysis of microbial communities126 (see Sec.3.4.1).
The ecological interaction types are encoded in the sign-pattern of J(x), denoted as sgn(J(x)). To infer sgn(J(x)), we need to make an explicit assumption that sgn(J(x)) = const across all the observed steady-state samples. This assumption might be violated if those steady-state samples were collected from the microbial community under drastically different environmental conditions (e.g., nutrient availability127). In that case, inferring sgn(J(x)) becomes an ill-defined problem. Interestingly, this assumption can be easily falsified by analyzing the observed steady-state samples, because it has been proved that if sgn(J(x)) = const, then the true multi-stability doesn’t exist. Here, a community of N species displays true multi-stability if there exists a subset of M (≤ N) species that has multiple different steady states, where all the M species have positive abundances and the other (N − M) species are absent. In practice, we can detect the presence of true multi-stability by examining the collected steady-state samples. If yes, then we know immediately that our assumption that sgn(J(x)) = const is invalid and we should only infer the zero-pattern of J(x). If no, then at least our assumption is consistent with the collected steady-state samples, and we can infer sgn(J(x)).
Inferring sign patterns
Here we introduce the methodology for inferring sgn(J(x)), which can be easily modified to infer the zero-pattern of J(x). The basic idea is as follows. Let ℐi be the set of all steady-state samples sharing species-i. For any two of those samples xI and xK, we can prove that the sign-pattern of the i-th row of J(x), denoted as a ternary vector si ∈ {−, 0, +}N, is orthogonal to (xI − xK). If we compute the sign-patterns of all vectors orthogonal to (xI − xK) for all I, K ∈ ℐi, then si must belong to the intersections of those sign-patterns, denoted as . As long as the number Ω of steady-state samples in 𝒳 is above certain threshold Ω*, then will contain only three sign-patterns {−a, 0, a}. To decide which of these three sign-patterns is the true one, we just need to know the sign of only one non-zero interaction. If such prior knowledge is unavailable, one can at least make a reasonable assumption that sii = ‘−’, i.e., the intra-species interaction Jii is negative (which is often required for community stability). If has more than three sign-patterns, then the steady-state data is not informative enough in the sense that all sign-patterns in are consistent with the data available in 𝒳. This situation is not a limitation of the inference algorithm but of the data itself. To uniquely determine the sign-pattern in such a situation, one has to either collect more samples (thus increasing the informativeness of 𝒳) or use a priori knowledge of non-zero interactions.
Extensive numerical simulations with species-only PLMs of different levels of complexity indicate that the minimal sample size Ω* required to obtain an accurate inference of sgn(J(x)) scales linearly with N. Note that for a microbial community of N species, in the absence of true multi-stability, there are at most Ωmax = (2N − 1) possible steady-state samples. Hence, we have Ω*/Ωmax ~ → 0 as N increases. This suggests that as the number of species increases, the proportion of samples needed for accurate inference actually decreases. This is a rather counter-intuitive result because, instead of a “curse of dimensionality”, it suggests that a “blessing of dimensionality” exists when we infer interaction types for microbial communities from steady-state samples.
Inferring interaction strengths
To infer the inter-species interaction strengths, we have to choose a priori a population dynamics model for the microbial community. If we choose to work with the GLV model, we have J(x) = A, which is a state-independent constant matrix. This considerably simplifies the inference because
for all I, K ∈ ℐi, where ai ≡ (ai1, …, aiN) represents the i-th row of A. This simple mathematical fact has an elegant geometric interpretation: all steady-state samples containing species-i align exactly onto a hyperplane, whose orthogonal vector is parallel to ai that we aim to infer. This geometric interpretation can actually serve as a consistency check of the GLV model and the observed steady-state samples.
Inferring interaction strengths for the GLV model from steady-state data reduces to finding a (N − 1)-dimensional hyperplane that best fits the steady-state sample points {xI|I ∈ ℐi} in the N-dimensional state space. In order to exactly infer ai, it is necessary to know the value of at least one non-zero element in ai, say, aii. Otherwise, we can only determine the relative interaction strengths by expressing aij in terms of aii. Once we obtain ai, the intrinsic growth rate ri of species-i can be calculated by averaging (−ai · xI) over all I ∈ ℐi, i.e., all the steady-state samples containing species-i. In case the samples are not collected exactly at steady states of the microbial community or there is noise in abundance measurements, those samples containing species-i will not exactly align onto a hyperplane. A naive solution is to find a hyperplane that minimizes its distance to those noisy samples. But this solution is prone to induce false positive errors and will yield non-sparse solutions (corresponding to very dense ecological networks). This issue can be partly alleviated by introducing a Lasso regularization, implicitly assuming that A is sparse. However, the classical Lasso regularization may induce a high false discovery rate (FDR), meaning that many zero interactions are inferred as non-zeros ones. This drawback can be overcome by applying the Knockoff filter procedure128, allowing us to control the FDR below a desired user-defined level.
Extensive numerical simulations with randomly selected subcommunities indicate that for the GLV model the minimal steady-state sample size Ω* required to obtain an accurate inference of A also scales linearly with N, indicating a blessing of dimensionality. A recent work pointed out that we can actually infer A using steady-state abundances from the N monocultures and the N leave-one-out subcommunities129. In other words, for such well-chosen subcommunities, Ω* = 2N. Note that in the classical experimental approach of studying inter-species interactions, i.e., comparing steady-state abundances from the N monocultures and the N(N − 1)/2 pairwise cocultures. In other words, we have to collect Ω = N(N + 1)/2 steady-state samples. For large N, this will be a daunting task.
Caveats
This blessing of dimensionality suggests that this steady-state based inference holds great promise for inferring the ecological networks of large and complex microbial communities. However, there are several caveats. Here, we list those caveats and point out possible solutions.
First, this approach requires the measurement of steady-state samples and absolute species abundances. For microbial communities that are under frequent and large perturbations, where steady-state samples are hard to collect, this approach is not applicable. For example, for certain reproductive-age women, their vaginal microbial compositions change markedly and rapidly over time46. The collected samples certainly do not represent steady states. For the human gut microbiome, it is well known that the gut microbial compositions of healthy adults remain stable for months and possibly even years until a major perturbation occurs through either antibiotic administration or drastic dietary changes. Hence, the gut microbiome samples collected from healthy adults very likely represent the steady states of the underlying ecosystem. However, the stability of gut microbial compositions associated with various diseases remains elusive. More studies are warranted.
Second, this approach implicitly assumes that different steady-state samples (or local communities) share universal microbial dynamics. In other words, those steady-state samples represent different boundary equilibria of a population dynamics model. This assumption is necessary because otherwise inferring microbial dynamics from steady-state samples is an ill-defined problem. This assumption will be satisfied when the samples were collected from similar environments. For in vitro communities, the universal dynamics assumption is satisfied if samples were collected from the same experiment or multiple experiments but with very similar environmental conditions. For in vivo communities, empirical evidence indicates that the human gut and oral microbiota of healthy adults display strong universal dynamics29. However, the universality of microbial dynamics in diseased microbiome has not been fully understood.
Finally, to infer the inter-species interaction strengths, we have to work with a particular population dynamics model, e.g., the GLV model. Although there is a simple consistency check of the GLV model and the observed steady-state samples, in case the consistency check falsifies the GLV model, this approach does not offer an alternative model to infer interaction strengths, but has to focus on the inference of interaction types, i.e., sgn(J(x)). Other techniques would have to be utilized to infer the dynamics model. For example, we can apply symbolic regression techniques to those steady-state samples to infer the dynamics model, leveraging the inferred interspecies interaction types. If we assume pairwise microbial interactions, then, mathematically, this is equivalent to inferring the functional form g(xi, xj) from a system of equations: , with a prior knowledge of sgn(aij).
Control Strategy Design
The ultimate proof of our understanding of the human microbiome is reflected in our ability to manipulate it for health benefits. Once we have reconstructed the ecological network or parameterized a reasonable dynamics model to mathematically describe the human microbiome as an ecological system, we can leverage concepts and tools developed in dynamical systems and control theory to design various control strategies.
A control theoretical framework
Recently, a theoretical framework for controlling complex microbial communities towards desired states was developed126 (see Fig.3). Here, a desired state can just be the baseline healthy gut microbiome of an individual before her/his gut microbiome was disrupted (e.g., by antibiotic administrations). This control theoretical framework is based on the new notion of structural accessibility, which allows us to use the ecological network of a microbial community to identify minimum sets of its driver species, whose abundance manipulation can control the whole community. Through numerical simulations, this framework has been demonstrated for controlling the gut microbiota of gnotobiotic mice infected with Clostridioides difficile and the core microbiota of the sea sponge Ircinia oros. This framework offers a systematic pipeline to drive complex microbial communities towards desired states.
Fig. 3: A control theoretical framework.
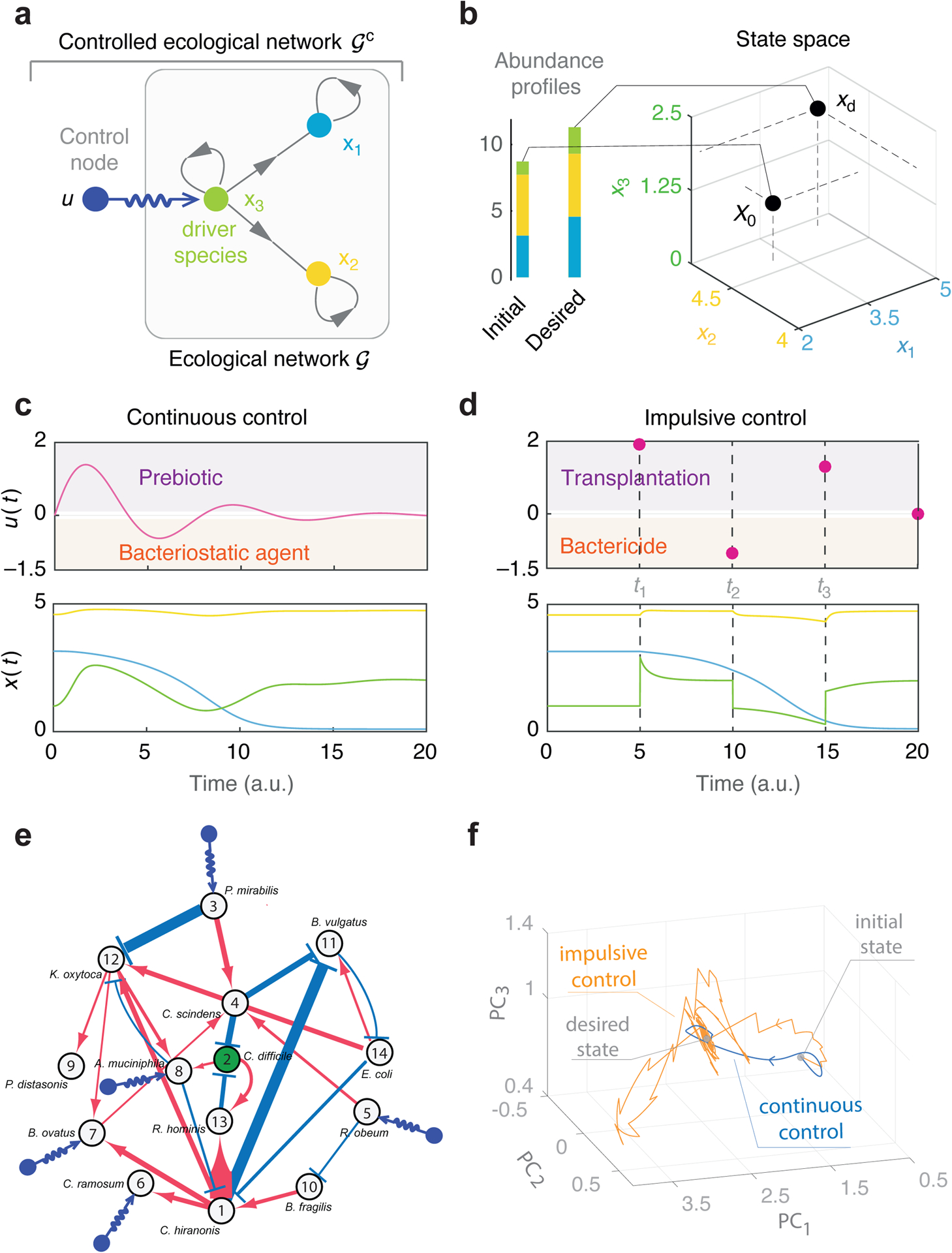
a, A toy community of N = 3 species (green, yellow, blue) with microbial interactions encoded in an ecological network 𝒢. The controlled ecological network 𝒢c contains one control input driving species-3. b, Initial and desired abundance profiles shown in stacked bars. The control objective is to steer the community from the (undesired) initial state x0 to the desired final state xd, represented by two points in the state space of the system. c, In the continuous control scheme, the control inputs u(t) are continuous signals modifying the growth of the actuated species. d, In the impulsive control scheme, the control inputs u(t) are impulses applied at the intervention instants , instantaneously changing the abundance of the actuated species. e, A minimum set of driver species can be identified from the ecological network 𝒢 by checking the graph-theoretical conditions of structural accessibility. Here, we show an ecological network involving the GnotoComplex microflora (a mixture of human commensal bacterial type strains) and C. difficile, inferred from mouse data (assuming the GLV model). Red (or blue) edges indicate the direct promotion (or inhibition), respectively. The five driver species are driven by five independent control inputs. f, Projection of the high-dimensional abundance profiles (states of the microbial communities) into their first three principal components (PCs). The calculated control strategies applied to the driver species succeed in driving the community to the desired state, using either continuous or impulsive control. Here, the controlled population dynamics is simulated using the controlled GLV equations. The intrinsic growth rates were adjusted such that the community has an initial “diseased” equilibrium state x0 in which C. difficile is overabundant compared to the rest of species. We chose the desired state x𝑑 as another equilibrium with a more balanced abundance profile. Figure adapted and modified from Ref.126.
Modeling controlled microbial communities.
Consider a generic species-only PLM with an unspecified function . Instead of knowing the exact functional form of f, we assume we know its underlying ecological network 𝒢 = (𝒱, ℰ), where 𝒱 = {x1, ⋯, xN} represents the set of N species nodes, and there is a directed edge (xj → xi) ∈ ℰ if and only if species-j has a direct ecological impact (i.e., direct promotion or inhibition of growth) on species-i.
Controlling the microbial community consists in driving it from an initial state (e.g., a “diseased” state) towards the desired final state value (e.g., the “healthy” state). Consider M control inputs directly applied to certain species. This results in a controlled ecological network 𝒢c = (𝒱 ∪ 𝒰, ℰ ∪ ℬ), where 𝒰 = {u1, ⋯, uM} represents the set of M control input nodes, and there is a directed edge (uj → xi) ∈ ℬ if any only if the j-th control input uj(t) directly control species-i. To model how the control inputs change the species abundance, we consider two different control schemes: continuous control and impulsive control. The continuous control scheme models a combination of prebiotics (if uj(t) > 0) and bacteriostatic agents (if uj(t) < 0) as continuous control inputs modifying the growth of the actuated species:
The impulsive control scheme models a combination of transplantations (if uj(t) > 0) and bactericides (if uj(t) < 0) applied at discrete intervention instants that instantaneously modify the abundance of the actuated species:
The function describes the direct susceptibility of the species to the control actions. The j-th control input control species-i if gij ≢ 0.
Identify the driver species
If we have an independent control input applied to each species (i.e., all species are directly controlled), of course the whole community can be driven to the desired state. This is far from being efficient or necessary. In fact, we can leverage the inter-species interactions encoded in the ecological network 𝒢 to identify minimum sets of species that we need to manipulate in order to drive the whole community. Those species are called “driver species”.
To identify the driver species, we need to introduce the notion of autonomous element, i.e., a constraint between some species abundances that the control input cannot break, confining the state of the community to a low-dimensional manifold. For example, considering a three-species community with GLV dynamics: , , , if we only control species-3, we will have an autonomous element ξ = x1x2, because , confining the whole community to a low-dimensional manifold: for any control input. If we control both species-3 and species-1 (or species-2), we can eliminate this autonomous element and hence control the whole system. So, species-3 and species-1 (or species-2) form a set of driver species.
In the general case of N species and M control inputs, we define a set of controlled species as a set of driver species if the corresponding controlled population dynamics {f, g} lacks autonomous elements. Note that for linear systems {f, g} = {Ax, B}, the absence of autonomous elements is equivalent to their controllability, i.e., the ability to drive the system between any two states in finite time, usually verified using Kalman’s condition: rank[B, AB, …, AN−1 B] = N. For nonlinear systems, the absence of autonomous elements defines the system’s accessibility130, which can be characterized using a mathematical formalism based on differential one-forms.
In reality, it is difficult to parameterize {f, g} that precisely models the controlled population dynamics of a microbial community. But we can still leverage the structure of the controlled ecological network of the community, i.e., 𝒢c, to check if the controlled system has autonomous elements or not, and use the ecological network 𝒢 to identify a minimum set of driver species. This is based on the notion of structural accessibility, which can be considered as a nonlinear generalization of structural controllability for linear systems131. Indeed, for linear systems , it is often hard to precisely measure the elements in A and B, but we can still use the structure of the controlled network 𝒢(A, B) to check if the controlled system is controllable or not131, and use the network 𝒢(A) to identify a minimum set of driver nodes132.
Consider the class 𝔇 of all possible controlled population dynamics models {f*, g*} that a controlled community can have given we know its 𝒢c. We call 𝔇 structurally accessible if almost all of its base models {f*, g*} and almost all of their deformations lack autonomous elements. Mathematically, this definition means that except for some pathological cases with Lebesgue measure zero, all the controlled population dynamics models that the community may take have no autonomous elements. It has been proven that, regardless of the control schemes (continuous or impulsive), 𝔇 is structurally accessible if and only if its corresponding controlled network 𝒢c satisfies the following two graph-theoretical conditions: (i) each species is the end-node of a path that starts at a control input node; and (ii) there is a disjoint union of cycles (excluding self-loops) and paths that cover all species nodes. Surprisingly, the two graph-theoretical conditions for structural accessibility are almost the same as those for structural controllability. The key difference is that for structural controllability self-loops (corresponding to intrinsic nodal dynamics) can be used to satisfy condition (ii). The graph-theoretical conditions of structural accessibility enable us to identify a minimum set of driver species efficiently from the ecological network 𝒢.
We emphasize that the graph-theoretical conditions for the structural accessibility in the continuous and the impulsive control schemes are identical. This implies that those two control schemes can be equally effective. This result is really assuring, because for the human microbiome, apparently impulsive control is much easier to implement than continuous control.
Calculate the control inputs
Once we have identified a minimum set of driver species, we need to calculate the control inputs to be applied to driver species to steer the whole community towards the desired state. It turns out it is more efficient to calculate impulsive control inputs , using the so-called model predictive control (MPC) approach133. Basically, from the current state of the community x(tk) at , we predict the sequence of states that the community will take in response to a sequence of L impulsive control inputs Uk,L = {u(tk), ⋯, u(tk+L−1)}, based on the controlled population dynamics {f, g}. The prediction horizon L > 0 determines how far into the future we predict, which can be chosen based on {f, g}. Then, we choose , which is the first element of the optimal control sequence calculated as:
Here, is the cost function penalizing deviations of the predicted trajectory from the desired final state xd. For example, we can define , representing the deviations of the predicted final state from the desired one. specifies constraints in the control inputs. The above equation represents a finite-dimensional optimization problem, which can be solved using algorithms like DIRECT134. By recalculating at each tk using the actual state of the community, the MPC approach creates a feedback loop enhancing its robustness against prediction errors.
The above MPC approach has two limitations. First, it requires detailed knowledge of the controlling population dynamics {f, g}, which is hard to parameterize for large complex communities. Second, it requires us to solve a non-convex optimization problem, which is quite challenging for large N or L. These two limitations can be circumvented by leveraging the controlled ecological network 𝒢c. In particular, we rewrite {f, g} = {Ax + wx, B + wu}, where is a weighted adjacency matrix of the ecological network 𝒢 (i.e., a proxy of the inter-species interaction matrix), B ∈ {0,1}N×M is a proxy of the susceptibility matrix, with bij = 1 if the j-the control input actuates the i-th driver species. In a sense, {Ax, B} provides a prediction of the community’s linear response to the control inputs, and wx and wu can be considered as perturbations. Using {Ax, B}, we can design a linear MPC by solving the finite-dimensional optimization problem with the following quadratic cost function:
Here, the positive definite matrices and are design parameters. In particular, Q penalizes the deviations of the predicted trajectory from the desired state, while R penalizes the control inputs magnitude. Then, the optimization problem can be solved in closed form yielding the linear MPC: u(tk) = K x(tk), where is the solution of a Riccati equation. Since the Riccati equation can be efficiently solved for large N, the linear MPC can be calculated for large communities.
Caveats
This theoretical framework allows us to systematically and efficiently control complex microbial communities towards desired states. Despite the theoretical soundness, this framework has several caveats. Here, we list those caveats and point out possible solutions.
First, identifying the driver species of a microbial community requires knowledge of its underlying ecological network 𝒢, which is highly nontrivial to infer for complex communities due to data informativeness issues (see Sec.3.3). Fortunately, it has been proven that once 𝒢c is structurally accessible, it cannot lose its structural accessibility with additional edges added to it. Hence, we can identify the driver species from an “incomplete” ecological network (e.g., containing only high-confidence edges). Note that there could be multiple different minimum sets of driver species for the same ecological network. If the cost of choosing any species as a driver species is known, a combinatorial optimization scheme can be employed to select the best minimum driver species set.
Second, this framework is based on species-only PLMs, which do not explicitly model the dynamics of resources provided to and/or chemicals produced by the microbial species. For general resource-explicit PLMs, to identify their driver species (which can drive the system to desired species abundance profile), we need to analyze the notion of “output accessibility”, which characterizes the absence of autonomous elements in the species dynamics and ignores autonomous elements in the resource dynamics. Then, we need to extend the notion of “output accessibility” to “structural output accessibility” (i.e., generic output accessibility given an adequate base model), which serves as a nonlinear counterpart of linear target controllability135. Similarly, structural output accessibility could also allow us to identify “driver resources” (which can drive the system to desired resource concentration profile) by characterizing the absence of autonomous elements in the resource dynamics and ignoring autonomous elements in the species dynamics.
Third, for large communities with uncertain dynamics, the linear MPC approach offers a robust and efficient way to calculate the control inputs. However, its performance strongly depends on the choice of (A, B) and the distance to the desired state. In general, the linear MPC is guaranteed to succeed only if the desired state is “close enough” to the initial state. But how “close” or “far” to a desired state depends on how well the linear dynamics {Ax, B} approximates the true controlled population dynamics {f, g} of the community.
Finally, this control theoretical framework requires very demanding control actions, e.g., increase or decrease the abundance of the driver species to a desired level at a given time. Those control actions are demanding because our control objective (i.e., precisely steering the whole community from an undesired/unhealthy state to a desired/healthy state) is very ambitious. Those control actions might not be feasible in reality, and implementing those actions requires detailed knowledge on the susceptibility of species to the various control actions. Moreover, for the human gut microbiome, implementing those control actions could be ethically questionable, because they might cause unintended consequence to the host. Numerical calculations have demonstrated that sometimes the control strategy succeeds in a very counter-intuitive way: although the driver species is more abundant in the final desired state than in the initial state, the initial control action is actually to decrease its abundance further126.
Practical control strategies
In most cases, controlling the human microbiome requires us to solve a less ambitious task than precisely steering the whole community to a desired state. For example, sometimes we just want to decolonize a particular pathogen (e.g., Clostridioides difficile), or steer the community to a particular community type (i.e., a densely populated area in the compositional landscape). In those cases, we can design more feasible control actions, e.g., a one-time transplantation of a well-defined consortium of species (“probiotic cocktail”).
Switch between different community types
Microbiome-based stratification of hosts into compositional categories, referred to as “community types” (or “enterotypes” in the case of gut microbiome), holds great promise for drastically improving personalized medicine. For example, the notion of enterotypes were originally proposed as distinct clusters in the compositional landscape of human gut microbiome that might respond differently to diet and drug intake136. Through standard cluster analysis, it was found that the gut microbial compositions of a human population display three distinct clusters (enterotypes), and each enterotype is a dominated by a particular genus (Bacteroides, Prevotella, or Ruminococcus) but not affected by gender, age, body mass index, or nationality of the host. However, a meta-analysis revealed smooth abundance gradients of key genera without discrete clustering of samples137. Hence, enterotype was a controversial concept as to whether human gut microbiome can be clustered into different types or just fall into a continuous gradient. Nowadays we usually do not consider enterotypes as distinct clusters (“islands”), but just as densely populated areas (“peaks”) in the compositional landscape138,139.
In principle the presence of community types could be explained by different mechanisms, e.g., the presence of true multi-stability140, or heterogeneous inter-species interactions76. Although the notion of true multi-stability has been well discussed in macro-ecological systems, its detection in host-associated microbial communities is rather difficult (see Sec.2.2) and has not been demonstrated experimentally30. Detection of heterogeneous inter-species interactions or the presence of strongly interesting species (SIS) in the human gut microbiome has not been successful either, due to the data informativeness issue76. Nevertheless, it has been numerically demonstrated that heterogeneity in the interspecific interactions or the presence of SISs is sufficient to explain community types, independent of the topology of the underlying ecological network. Moreover, by controlling the presence or absence of these SISs we can steer the microbial community to any desired community type. This open-loop control strategy still holds even when the community types are not distinct but appear as dense regions within a continuous gradient. The caveat is that target removal of those SISs could be a highly non-trivial task by itself. We may not have the specific narrow-spectrum antibiotics or phages that target each of those SISs effectively.
Decolonize pathogens
FMT has been successfully used in the treatment of recurrent Clostridioides difficile Infection (rCDI)16,141–148. Yet, the potential long-term safety concerns149 and the challenging donor recruitment and screening process150 have significantly limited the use of FMT. The development of live biotherapeutic products (LBP) containing only the effective components of FMT would alleviate these drawbacks largely due to the undefined nature of fecal preparations. However, such formulations are highly non-trivial. Many attempts have failed clinical trials151. Recent clinical trials provided some exciting results152,153. Yet, there is still much room for improvement. For example, the primary efficacy objective of one of the trials was to show superiority of the developed LBP as compared with placebo in reducing the risk of CDI recurrence153. It is unclear if the developed LBP outperforms FMT. In another trial, the LBP comprises 8 commensal Clostridia strains152. It is unclear if this one-size-fits-all approach works for all patients who presumably have very different baseline diseased microbiomes.
In order to decolonize a particular species (e.g., the pathogen Clostridioides difficile) from a community, targeting microbes that directly inhibit this species might have unintended consequences due to the network effect (see Sec.2.1). The complex network structure needs to be accounted for to design probiotic cocktails to decolonize a particular species from the microbial community.
To quantify the network effect in microbial communities32, let’s consider a metacommunity of N species labeled as Ω = {1, …, N}. We assume all samples or local communities obtained from this metacommunity share universal population dynamics, hence different local communities just differ by their initial species collections. Given a local community, labelled as ω, let’s assume that its population dynamics is described by the GLV model with and are the inter-species interaction matrix and intrinsic species growth rate vector of the local community ω, respectively. Here n = |ω| denotes the cardinality of the set ω. Consider two persisting species i and j (i.e., both species have non-zero steady-state abundances) in a local community ω. We can define the net impact of species-j on species-i in the local community ω as the independent contribution of species-j on the steady-state abundance of species-i. In other words, we can write the steady-state abundance of species-i as , where is the independent contribution (i.e., net impact) of species-j. For the GLV model, we have , where is the (j, i)-minor of matrix A(ω), and det(A(ω)) is the determinant of matrix A(ω). In particular, species j has a net inhibition (promotion or null) effect on species i in the local community ω if (> 0, or = 0, respectively). When the signs of and are different, this indicates a strong network effect. Applying this approach to two published microbial community datasets77,108 found evidence of strong network effects both in vitro and in vivo.
Once we know the ecological network of a microbial community, as well as the diseased state due to a particular pathogen X, we can formalize an optimization problem to design a personalized probiotic cocktail to decolonize X. The key idea is to calculate the net impact of a tentative probiotic cocktail on the growth of X and keep refining it by removing those species that could have a positive net impact on the growth of X in the altered community32. First, we form a tentative probiotic cocktail containing all the effective inhibitors of X calculated from the global ecological network 𝒢. Note that effective inhibitors include both direct and indirect inhibitors. But any species that already exists in the patient’s diseased microbiota will be removed from the initial cocktail. Second, for each species in the cocktail, we numerically test if it is still an effective inhibitor (i.e., has a negative net impact on the growth of X) in the altered local community (that contains all species in the patient’s diseased microbiota and all species in the current cocktail). If yes, we keep it in the cocktail; if no, we remove it. We repeat this process until all the species in the cocktail are indeed effective inhibitors in the altered local community. Finally, we are left with a minimal set of species, i.e., the optimal probiotic cocktail, which can effectively inhibit the growth of X for this particular disrupted microbiome (“patient”).
Applying the same algorithm to another “patient”, we will obtain another optimal probiotic cocktail. Note that the two optimal probiotic cocktails are naturally patient-specific or “personalized”, because they are designed based on the present species in each patient’s diseased microbiota.
Note that in case the global ecological network 𝒢 of the metacommunity is unknown (which is unfortunately the case for the human gut microbiome), we can leverage the ego network of X to design a near-optimal personalized probiotic cocktail to decolonize X. Here the ego network of X consists of the focal node/species (“ego”, i.e., the pathogen X), those nodes/species to which X directly interacts with (they are called “alters”), the links/interactions between X and its alters, as well as the links/interactions among the alters. The algorithm to design a probiotic cocktail based on the ego network of X is very similar to the algorithm based on the global ecological network. The only difference is that we need to construct the initial tentative probiotic cocktail based on the ego network, rather than the global ecological network.
The above probiotic cocktail design strategy has been applied to analyze the ecological network involving the so-called GnotoComplex microflora (a mixture of human commensal bacterial type strains) and Clostridioides difficile32 (Fig.4). This network was inferred from mouse experimental data78 with the assumption that the microbial community follows the GLV model. Based on the ecological network and the disrupted microbiota, we can design probiotic cocktails to effectively decolonize C. difficile. Numerical calculations demonstrated that the optimal probiotic cocktail Rglobal (designed based on the whole ecological network and the specific disrupted microbiota) can strongly suppress the abundance of C. difficile. Even the cocktail Rego designed based on the ego-network of C. difficile can suppress the abundance of C. difficile to a much lower level than that of the diseased state. Although the result is about an enteric pathogen, we believe that it demonstrates the advantages of the network-based design of probiotic cocktails in decolonizing generic pathogenic species for other body sites, e.g., Streptococcus mutans in the oral cavity.
Fig. 4. Personalized probiotic cocktails effectively decolonize C. difficile.
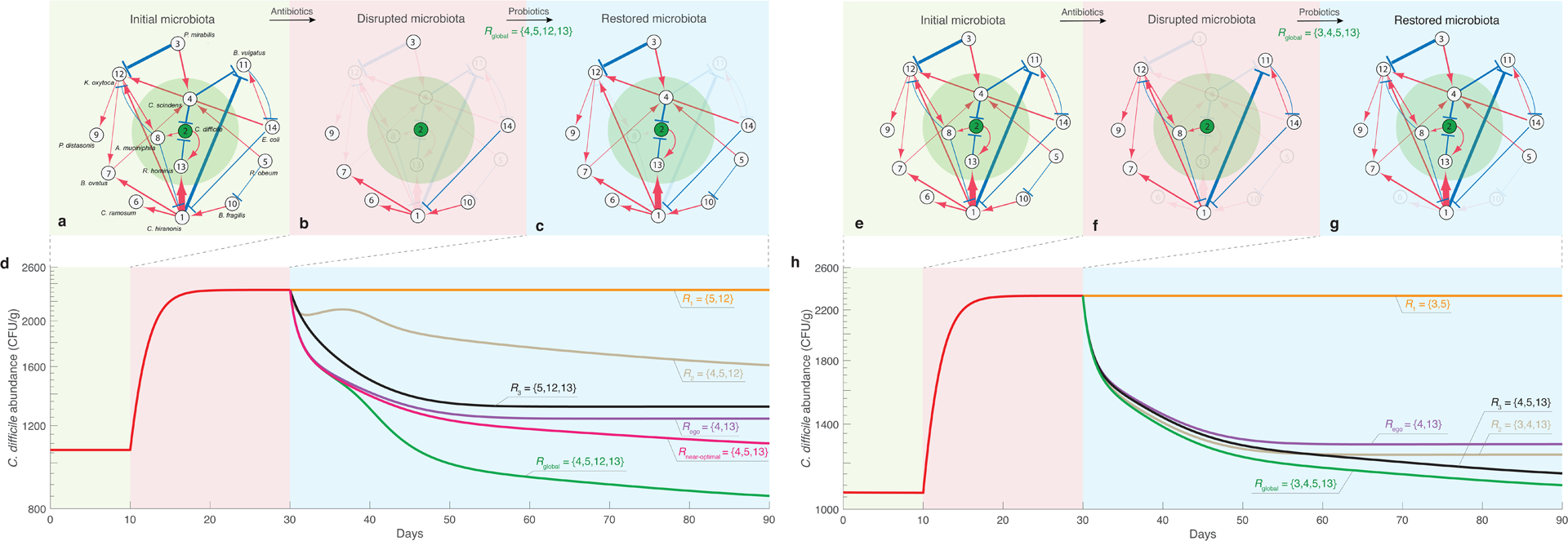
a, An ecological network involving the GnotoComplex microflora (a mixture of human commensal bacterial type strains) and C. difficile was inferred from mouse data. Red (or blue) edges indicate the direct promotion (or inhibition), respectively. b, A disrupted microbiota due to a hypothetic antibiotic administration. c, The restored microbiota due to the administration of a particular probiotic cocktail Rglobal. d, The trajectory of C. difficile abundance over three different time windows: (1) the initial healthy microbiota, (2) the disrupted microbiota, and (3) the microbiota post probiotic administration. In the third time window, we compare the performance of various probiotic cocktails in terms of their ability to decolonize C. difficile. Those cocktails were designed by considering the global ecological network (Rglobal), the ego-network of C. difficile (Rego), and randomly chosen subsets of Rglobal (R1, R2 and R3). Rnear–optimal is obtained by excluding species-12 (i.e., K. oxytoca, which is an opportunistic pathogen) from Rglobal. e-h, We start from the same initial microbiota as shown in (a), but another hypothetic antibiotic administration leads to a different disrupted microbiota (f), which can be restored through another probiotic cocktail (g). Performance of different probiotic cocktails in decolonizing C. difficile vary (h). Note that since the disrupted microbiota (f) is different from that shown in (b), the optimal cocktail Rglobal in (h) is also different from that shown in (d). Figure adapted and modified from Ref.32.
This probiotic cocktail design strategy has a clear limitation. The quantification of net impact of a species on the growth of the pathogen and the design of optimal personalized probiotic cocktails are largely based on the GLV model (which assumes linear functional response and pairwise microbial interactions). For more complicated population dynamics models with nonlinear functional response or higher-order interactions, it is still an open question how to analytically calculate the net impact.
OUTLOOK
The modeling and control framework discussed in this article has a strong flavor of community ecology, dynamical systems, network science, and control theory. However, to fully harvest the benefits of controlling the human microbiome, insights and tools from other disciplines will be very helpful. Here, we point out a few promising directions that require interdisciplinary synergy.
Towards more realistic control actions
In the control theoretical framework discussed in Sec.3.4.1, we considered four different control actions (prebiotics and bacteriostatic agents that modify the growth of the actuated species; probiotics and bactericides that directly modify the abundance of the actuated species) to steer microbial communities to desired compositions. In practice, the administration of prebiotics or probiotics or both (which is often called synbiotics, i.e., the combination of prebiotics and probiotics that work synergistically) is more realistic. How to design control strategies based on a particular choice of control action or a particular combination of them is an outstanding question that merits further investigation. Given the existing generic control theoretical framework, this presumably should be a low-hanging fruit.
Integrate taxonomic and functional data
To design control strategies for the manipulation of microbial compositions, current modeling frameworks of microbial communities typically start with a minimal dynamical model of species abundances to facilitate the parameterizing procedure, which thus does not explicitly model any functional changes of the communities. Further efforts should be dedicated to integrate both taxonomic and functional data to provide more comprehensive control strategies. For example, we can shift the control goal from the manipulation of microbial compositions to the manipulation of microbial functions (e.g., the secondary bile acid metabolism, the production of certain short-chain fatty acids, the digestion of lactose, and the generation of toxins). How to design safe microbiome-based therapeutics (e.g., personalized synbiotics) to effectively manipulate microbial functions in the long-run remains an open question. Metabolic control analysis154, a tool for designing strategies to manipulate metabolic pathways, might be useful. Development of bioreaction control systems could also be inspirational, at least from the conceptual perspective155.
Integrate microbiome and host data
All the modelling approaches discussed in Sec.3.1 focus on the dynamics of the microbiome itself, and do not explicitly model the impact of microbial dynamics on the host. Recently, a microbiome-immune system mathematical model was proposed to describe the activation of regulatory T-cells (Treg) in response to colonization profiles of Treg-stimulating Clostridia strains156. This model integrates a microbiome ecological model that describes the short and long-term temporal dynamics of Clostridia strains in germ-free mice78 and a microbiome-Treg model of CD4+FOXP3+Treg activation in response to long-term compositions in the microbiome. This pioneering work should inspire more research activities to integrate microbiome and host data, and to make the control goals more host-oriented (i.e., maximizing a desired host phenotype).
Data-driven control
Control strategies discussed in this review article are based on certain population dynamics models. Yet, parameterizing those dynamics models is a challenging task by itself. One way to circumvent this intrinsic challenge of any model-based control framework is to adopt a data-driven control framework157,158. Facilitated by recent advances in machine learning and artificial intelligence, data-driven control of dynamical systems has attracted a great deal of research interest over the last few years. In macro-ecosystem forecasting, the so-called empirical dynamic modeling (EDM) has been proposed as a data-driven (or equation-free) alternative to imposed model equations and offered more accurate and precise forecasts159. For microbial systems, the EDM approach has also been used to infer inter-species interactions from longitudinal microbiome data160. Recently, a deep-learning method (cNODE: compositional Neural Ordinary Differential Equations) was developed to predict microbial composition from steady-state species assemblage without assuming any microbial dynamics161. The long short-term memory (LSTM), a representative type of recurrent neural networks capable of learning order dependence in sequential or time-series data, has been applied to longitudinal species abundance data of synthetic microbial communities, and demonstrated better performance than the GLV model in predicting species abundances162. These deep-learning approaches hold great promise in data-driven control of the human microbiome. We anticipate that data-driven forecast and control of the human microbiome will be heavily studied soon. Indeed, the unprecedented availability of metagenomics sequencing data offers a great opportunity for us to better understand, predict, and, ultimately, control the behavior of the human microbiome.
Experimental validation.
Advances in culturomics71 will certainly facilitate the validation of control strategies for in vitro synthetic communities. Several in vitro continuous culture systems (e.g., SHIME163: Simulator of the Human Intestinal Microbial Ecosystem, HuMiX164: human-microbial crosstalk; and a human gut-on-a-chip microdevice165) have been developed. In particular, HuMiX and gut-on-a-chip can model microbiota-host interactions. Those culture systems would be extremely valuable to test control strategies, despite an important challenge still lies in further increasing their high-throughput analyses capacity166. In a very recent breakthrough, hCom1, a defined community of 104 gut bacterial species, was first constructed and characterized in vitro, and then augmented in vivo (by filling open niches) to form hCom2, a defined community of 119 species167. Up to our knowledge, this is the largest synthetic community designed so far that can serve as a model system of the human gut microbiome. We expect that this work will not only enable us to test many classical hypotheses in community ecology, but also trigger many mechanistic studies to reveal the critical roles of gut microbiome in human diseases. The ecology-based in vivo augmentation strategy developed by the authors is very insightful. It will inspire other researchers to design similar (and perhaps even larger) synthetic communities to model the human gut microbiome. Ultimately, we need carefully designed animal experiments and clinical trials to validate those proposed control strategies. Both pharmacokinetic and pharmacodynamics need to be carefully studied152. In the context of microbiome-based therapeutics (e.g., a defined probiotic cocktail or more precisely LBP), pharmacokinetics concerns the abundance of LBP strain colonization, proportion of LBP consortium strains colonizing a given host, and persistence of LBP strain colonization, while pharmacodynamics concerns the ecological impact of the LBP on the host resident microbial communities.
Finally, we hope this review article will catalyze more collaborative works between modelers, microbiologists, and clinicians. Given the advances in various disciplines, we anticipate that more interdisciplinary approaches will be developed to further enhance our ability to control the human microbiome.
Acknowledgements
The author would like to thank Dr. Xu-Wen Wang for the assistance in preparing Figures 1–2, and Dr. Shanlin Ke for valuable discussion. The author acknowledges grants from the National Institutes of Health (R01AI141529, R01HD093761, RF1AG067744, UH3OD023268, U19AI095219, and U01HL089856).
Figure 2: The human gut microbiome is highly personalized and very stable.
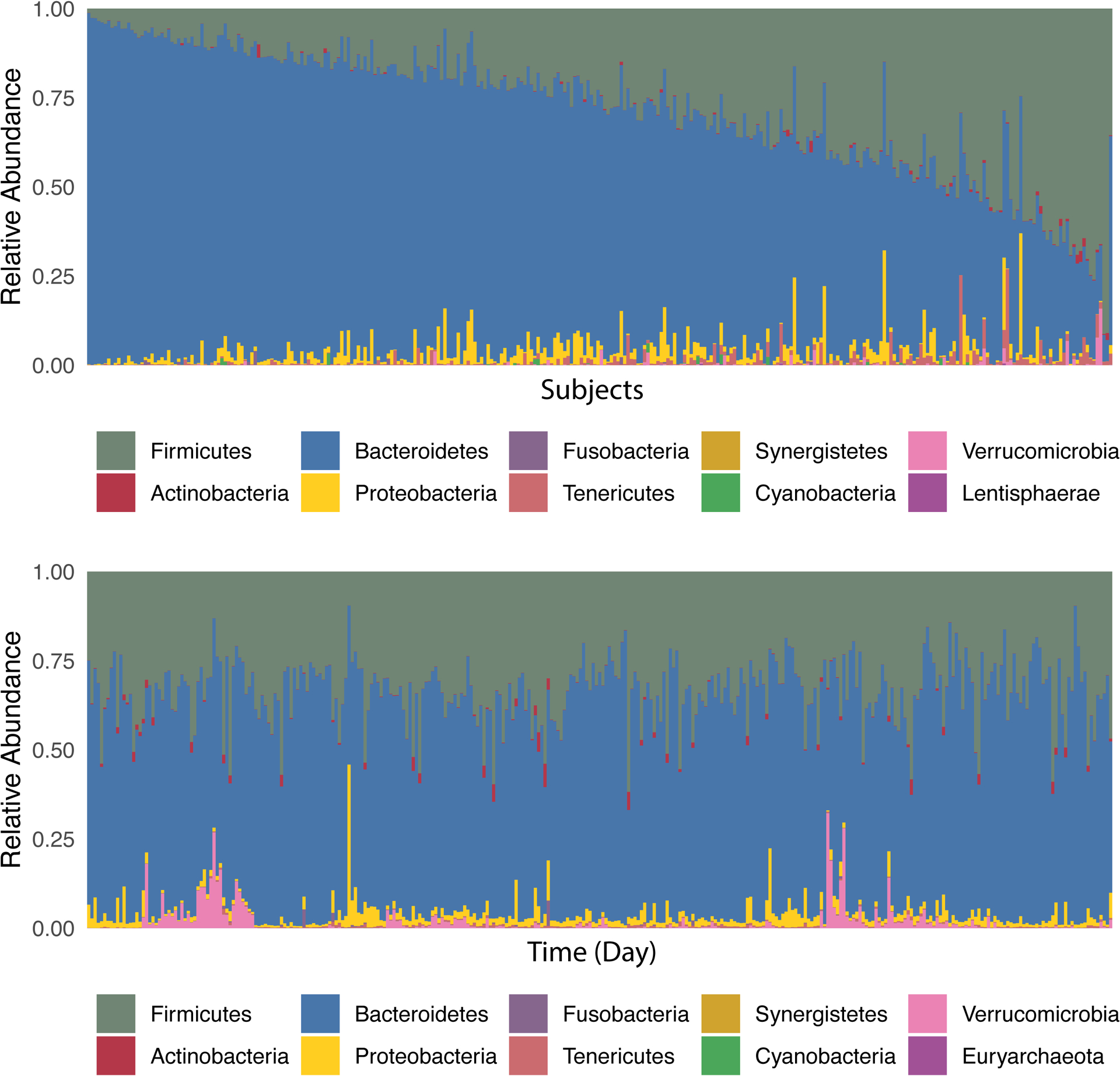
a, The taxonomic profile of the human gut microbiome varies a lot across different individuals. Here the stacked bar chart demonstrates the phylum-level gut microbial compositions of ~200 healthy adults in the HMP cohort1. b, The taxonomic profile of the human gut microbiome is highly dynamic but very stable. In the absence of drastic interventions, the human gut microbiome can be considered as a dynamically stable ecosystem, continually buffeted by internal and external forces and recovering back toward a conserved steady-state38. Here the stacked bar chart demonstrates the daily phylum-level gut microbial compositions of a healthy adult over ~200 days in the Moving Picture study39. Figure courtesy of Dr. Xu-Wen Wang.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
REFERENCES
- 1.HMP Consortium. Structure, function and diversity of the healthy human microbiome. Nature 486, 207–214 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Consortium HMP. A framework for human microbiome research. Nature 486, 215–221, doi: 10.1038/nature11209 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Qin J, Li R, Raes J, Arumugam M, Burgdorf KS, Manichanh C, Nielsen T, Pons N, Levenez F, Yamada T, Mende DR, Li J, Xu J, Li S, Li D, Cao J, Wang B, Liang H, Zheng H, Xie Y, Tap J, Lepage P, Bertalan M, Batto J-M, Hansen T, Le Paslier D, Linneberg A, Nielsen HB, Pelletier E, Renault P, Sicheritz-Ponten T, Turner K, Zhu H, Yu C, Li S, Jian M, Zhou Y, Li Y, Zhang X, Li S, Qin N, Yang H, Wang J, Brunak S, Doré J, Guarner F, Kristiansen K, Pedersen O, Parkhill J, Weissenbach J, Antolin M, Artiguenave F, Blottiere H, Borruel N, Bruls T, Casellas F, Chervaux C, Cultrone A, Delorme C, Denariaz G, Dervyn R, Forte M, Friss C, van de Guchte M, Guedon E, Haimet F, Jamet A, Juste C, Kaci G, Kleerebezem M, Knol J, Kristensen M, Layec S, Le Roux K, Leclerc M, Maguin E, Melo Minardi R, Oozeer R, Rescigno M, Sanchez N, Tims S, Torrejon T, Varela E, de Vos W, Winogradsky Y, Zoetendal E, Bork P, Ehrlich SD & Wang J A human gut microbial gene catalogue established by metagenomic sequencing. Nature 464, 59–65, doi: 10.1038/nature08821 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Clemente JC, Ursell LK, Parfrey LW & Knight R The impact of the gut microbiota on human health: an integrative view. Cell 148, 1258–1270, doi: 10.1016/j.cell.2012.01.035 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.David L. a., Maurice CF, Carmody RN, Gootenberg DB, Button JE, Wolfe BE, Ling AV, Devlin a. S., Varma Y, Fischbach M. a., Biddinger SB, Dutton RJ & Turnbaugh PJ Diet rapidly and reproducibly alters the human gut microbiome. Nature 505, 559–563, doi: 10.1038/nature12820 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Zmora N, Suez J & Elinav E You are what you eat: diet, health and the gut microbiota. Nature Reviews Gastroenterology and Hepatology, doi: 10.1038/s41575-018-0061-2 (2018). [DOI] [PubMed] [Google Scholar]
- 7.Dethlefsen L & Relman DA Incomplete recovery and individualized responses of the human distal gut microbiota to repeated antibiotic perturbation. Proc Natl Acad Sci U S A 108 Suppl 4554–4561, doi:1000087107 [pii]\r 10.1073/pnas.1000087107 [doi] (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Costello EK, Stagaman K, Dethlefsen L, Bohannan BJM & Relman DA The application of ecological theory toward an understanding of the human microbiome. Science 336, 1255–1262, doi: 10.1126/science.1224203 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Lozupone CA, Stombaugh JI, Gordon JI, Jansson JK & Knight R Diversity, stability and resilience of the human gut microbiota. Nature 489, 220–230, doi: 10.1038/nature11550 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Rothschild D, Weissbrod O, Barkan E, Kurilshikov A, Korem T, Zeevi D, Costea PI, Godneva A, Kalka IN, Bar N, Shilo S, Lador D, Vila AV, Zmora N, Pevsner-Fischer M, Israeli D, Kosower N, Malka G, Wolf BC, Avnit-Sagi T, Lotan-Pompan M, Weinberger A, Halpern Z, Carmi S, Fu J, Wijmenga C, Zhernakova A, Elinav E & Segal E Environment dominates over host genetics in shaping human gut microbiota. Nature 555, 210–215, doi: 10.1038/nature25973 (2018). [DOI] [PubMed] [Google Scholar]
- 11.Lemon KP, Armitage GC, Relman D. a. & Fischbach M. a. Microbiota-targeted therapies: an ecological perspective. Science Translational Medicine 4, 137rv135, doi: 10.1126/scitranslmed.3004183 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Alang N & Kelly CR Weight Gain After Fecal Microbiota Transplantation. Open Forum Infectious Diseases 2, ofv004–ofv004, doi: 10.1093/ofid/ofv004 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Wang S, Xu M, Wang W, Cao X, Piao M, Khan S, Yan F, Cao H & Wang B Systematic Review: Adverse Events of Fecal Microbiota Transplantation. Plos One 11, e0161174, doi: 10.1371/journal.pone.0161174 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.El-Matary W Fecal Microbiota Transplantation: Long-Term Safety Issues. The American Journal Of Gastroenterology 108, 1537, doi: 10.1038/ajg.2013.208 (2013). [DOI] [PubMed] [Google Scholar]
- 15.Taroncher-Oldenburg G, Jones S, Blaser M, Bonneau R, Christey P, Clemente JC, Elinav E, Ghedin E, Huttenhower C, Kelly D, Kyle D, Littman D, Maiti A, Maue A, Olle B, Segal L, van Hylckama Vlieg JET & Wang J Translating microbiome futures. Nature Biotechnology 36, 1037–1042, doi: 10.1038/nbt.4287 (2018). [DOI] [PubMed] [Google Scholar]
- 16.Borody TJ, Paramsothy S & Agrawal G Fecal microbiota transplantation: Indications, methods, evidence, and future directions. Current Gastroenterology Reports 15, 1–7, doi: 10.1007/s11894-013-0337-1 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Aroniadis OC & Brandt LJ Fecal microbiota transplantation: past, present and future. Curr Opin Gastroenterol 29, 79–84, doi: 10.1097/MOG.0b013e32835a4b3e (2013). [DOI] [PubMed] [Google Scholar]
- 18.Sadowsky MJ & Khoruts A Faecal microbiota transplantation is promising but not a panacea. Nature Microbiology 1, 16015, doi: 10.1038/nmicrobiol.2016.15 (2016). [DOI] [PubMed] [Google Scholar]
- 19.Sun Z, Huang S, Zhang M, Zhu Q, Haiminen N, Carrieri AP, Vazquez-Baeza Y, Parida L, Kim HC, Knight R & Liu YY Challenges in benchmarking metagenomic profilers. Nature Methods 18, 618–626, doi: 10.1038/s41592-021-01141-3 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Emerson JB, Adams RI, Román CMB, Brooks B, Coil DA, Dahlhausen K, Ganz HH, Hartmann EM, Hsu T, Justice NB, Paulino-Lima IG, Luongo JC, Lymperopoulou DS, Gomez-Silvan C, Rothschild-Mancinelli B, Balk M, Huttenhower C, Nocker A, Vaishampayan P & Rothschild LJ Schrödinger’s microbes: Tools for distinguishing the living from the dead in microbial ecosystems. Microbiome 5, 86, doi: 10.1186/s40168-017-0285-3 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Niehaus L, Boland I, Liu M, Chen K, Fu D, Henckel C, Chaung K, Miranda SE, Dyckman S, Crum M, Dedrick S, Shou W & Momeni B Microbial coexistence through chemical-mediated interactions. Nature Communications 10, doi: 10.1038/s41467-019-10062-x (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Bucci V, Bradde S, Biroli G & Xavier JB Social interaction, noise and antibiotic-mediated switches in the intestinal microbiota. PLoS computational biology 8, e1002497, doi: 10.1371/journal.pcbi.1002497 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Henriques SF, Dhakan DB, Serra L, Francisco AP, Carvalho-Santos Z, Baltazar C, Elias AP, Anjos M, Zhang T, Maddocks ODK & Ribeiro C Metabolic cross-feeding in imbalanced diets allows gut microbes to improve reproduction and alter host behaviour. Nat Commun 11, 4236, doi: 10.1038/s41467-020-18049-9 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Bucci V, Nadell CD & Xavier JB The evolution of bacteriocin production in bacterial biofilms. Am Nat 178, E162–173, doi: 10.1086/662668 (2011). [DOI] [PubMed] [Google Scholar]
- 25.Levy R & Borenstein E Metabolic modeling of species interaction in the human microbiome elucidates community-level assembly rules. Proceedings of the National Academy of Sciences of the United States of America 110, 12804–12809, doi: 10.1073/pnas.1300926110 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Momeni B, Xie L & Shou W Lotka-Volterra pairwise modeling fails to capture diverse pairwise microbial interactions. eLife 6, 1–34, doi: 10.7554/eLife.25051.001 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Bairey E, Kelsic ED & Kishony R High-order species interactions shape ecosystem diversity. Nature Communications 7, 1–7, doi: 10.1038/ncomms12285 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Mickalide H & Kuehn S Higher-Order Interaction between Species Inhibits Bacterial Invasion of a Phototroph-Predator Microbial Community. Cell Syst 9, 521–533 e510, doi: 10.1016/j.cels.2019.11.004 (2019). [DOI] [PubMed] [Google Scholar]
- 29.Bashan A, Gibson TE, Friedman J, Carey VJ, Weiss ST, Hohmann EL & Liu Y-Y Universality of Human Microbial Dynamics. Nature 534, 259–262, doi: 10.1038/nature18301 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Faust K & Raes J Microbial interactions: from networks to models. Nature reviews. Microbiology 10, 538–550, doi: 10.1038/nrmicro2832 (2012). [DOI] [PubMed] [Google Scholar]
- 31.Sugihara G, May R, Ye H, Hsieh C. h., Deyle E, Fogarty M & Munch S Detecting causality in complex ecosystems. Science (New York, N.Y.) 338, 496–500, doi: 10.1126/science.1227079 (2012). [DOI] [PubMed] [Google Scholar]
- 32.Xiao Y, Angulo MT, Lao S, Weiss ST & Liu Y-Y An ecological framework to understand the efficacy of fecal microbiota transplantation. Nature Communications 11, 3329, doi: 10.1038/s41467-020-17180-x (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Franzosa EA, Huang K, Meadow JF, Gevers D, Lemon KP, Bohannan BJM & Huttenhower C Identifying personal microbiomes using metagenomic codes. Proc Natl Acad Sci USA 112, E2930–E2938 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Fukami T Historical Contingency in Community Assembly: Integrating Niches, Species Pools, and Priority Effects. Annual Review of Ecology, Evolution, and Systematics 46, 1–23, doi: 10.1146/annurev-ecolsys-110411-160340 (2015). [DOI] [Google Scholar]
- 35.Sprockett D, Fukami T & Relman DA Role of priority effects in the early-life assembly of the gut microbiota. Nature Reviews Gastroenterology & Hepatology, doi: 10.1038/nrgastro.2017.173 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Zhao N, Saavedra S & Liu Y-Y The impact of colonization history on the composition of ecological systems. bioRXiv 2020.02.26.965715 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Connell JH & Sousa WP On the Evidence Needed to Judge Ecological Stability or Persistence. The American Naturalist 121, 789–824 (1983). [Google Scholar]
- 38.Gibbons SM, Kearney SM, Smillie CS & Alm EJ Two dynamic regimes in the human gut microbiome. PLOS Computational Biology 13, e1005364, doi: 10.1371/journal.pcbi.1005364 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Caporaso JG, Lauber CL, Costello EK, Berg-Lyons D, Gonzalez A, Stombaugh J, Knights D, Gajer P, Ravel J, Fierer N, Gordon JI & Knight R Moving pictures of the human microbiome. Genome biology 12, R50, doi: 10.1186/gb-2011-12-5-r50 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.David LA, Materna AC, Friedman J, Campos-Baptista MI, Blackburn MC, Perrotta A, Erdman SE & Alm EJ Host lifestyle affects human microbiota on daily timescales. Genome Biology 15, R89, doi: 10.1186/gb-2014-15-7-r89 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Oh J, Byrd Allyson L., Park M, Kong Heidi H. & Segre Julia A. Temporal Stability of the Human Skin Microbiome. Cell 165, 854–866, doi: 10.1016/j.cell.2016.04.008 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Faith JJ, Guruge JL, Charbonneau M, Subramanian S, Seedorf H, Goodman AL, Clemente JC, Knight R, Heath AC, Leibel RL, Rosenbaum M & Gordon JI The long-term stability of the human gut microbiota. Science (New York, N.Y.) 341, 1237439, doi: 10.1126/science.1237439 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Mehta RS, Abu-Ali GS, Drew DA, Lloyd-Price J, Subramanian A, Lochhead P, Joshi AD, Ivey KL, Khalili H, Brown GT, Dulong C, Song M, Nguyen LH, Mallick H, Rimm EB, Izard J, Huttenhower C & Chan AT Stability of the human faecal microbiome in a cohort of adult men. Nature Microbiology 3, 347–355, doi: 10.1038/s41564-017-0096-0 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Faust K, Bauchinger F, Laroche B, de Buyl S, Lahti L, Washburne AD, Gonze D & Widder S Signatures of ecological processes in microbial community time series. Microbiome 6, 1–13, doi: 10.1186/s40168-018-0496-2 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Grilli J in Nature Communications Vol. 11 1–11 (Springer US, 2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Gajer P, Brotman RM, Bai G, Sakamoto J, Schütte UME, Zhong X, Koenig SSK, Fu L, Ma ZS, Zhou X, Abdo Z, Forney LJ & Ravel J Temporal dynamics of the human vaginal microbiota. Science translational medicine 4, 132ra152, doi: 10.1126/scitranslmed.3003605 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Louca S & Doebeli M Transient dynamics of competitive exclusion in microbial communities. Environmental Microbiology 18, 1863–1874, doi: 10.1111/1462-2920.13058 (2016). [DOI] [PubMed] [Google Scholar]
- 48.Balagaddé FK, You L, Hansen CL, Arnold FH & Quake SR Long-Term Monitoring of Bacteria Undergoing Programmed Population Control in a Microchemostat. Science 309, 137–140, doi: 10.1126/science.1109173 (2005). [DOI] [PubMed] [Google Scholar]
- 49.Skupin P & Metzger M Oscillatory Behavior Control in Continuous Fermentation Processes. IFAC-PapersOnLine 48, 1114–1119, doi: 10.1016/j.ifacol.2015.09.117 (2015). [DOI] [Google Scholar]
- 50.Graham DW, Knapp CW, Van Vleck ES, Bloor K, Lane TB & Graham CE Experimental demonstration of chaotic instability in biological nitrification. The ISME Journal 1, 385–393, doi: 10.1038/ismej.2007.45 (2007). [DOI] [PubMed] [Google Scholar]
- 51.Sommer F, Anderson JM, Bharti R, Raes J & Rosenstiel P The resilience of the intestinal microbiota influences health and disease. Nat Rev Micro 15, 630–638, doi: 10.1038/nrmicro.2017.58 (2017). [DOI] [PubMed] [Google Scholar]
- 52.Moya A & Ferrer M Functional Redundancy-Induced Stability of Gut Microbiota Subjected to Disturbance. Trends in Microbiology 24, 402–413, doi: 10.1016/j.tim.2016.02.002 (2016). [DOI] [PubMed] [Google Scholar]
- 53.Tian L, Wang X-W, Wu A-K, Fan Y, Friedman J, Dahlin A, Waldor MK, Weinstock GM, Weiss ST & Liu Y-Y Deciphering functional redundancy in the human microbiome. Nature Communications 11, 6217, doi: 10.1038/s41467-020-19940-1 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Lawton JH & Brown VK in Biodiversity and Ecosystem Function (eds Schulze Ernst-Detlef & Mooney Harold A.) 255–270 (Springer; Berlin Heidelberg, 1994). [Google Scholar]
- 55.Loreau M Does functional redundancy exist? Oikos 104, 606–611, doi: 10.1111/j.0030-1299.2004.12685.x (2004). [DOI] [Google Scholar]
- 56.Hubbell SP Neutral theory in community ecology and the hypothesis of functional equivalence. Functional Ecology 19, 166–172, doi: 10.1111/j.0269-8463.2005.00965.x (2005). [DOI] [Google Scholar]
- 57.Allison SD & Martiny JBH Resistance, resilience, and redundancy in microbial communities. Proc Natl Acad Sci USA 105, 11512–11519, doi: 10.1073/pnas.0801925105 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Root RB The Niche Exploitation Pattern of the Blue-Gray Gnatcatcher. Ecological Monographs 37, 317–350, doi: 10.2307/1942327 (1967). [DOI] [Google Scholar]
- 59.Naeem S Species redundancy and ecosystem reliability. Conservation Biology 12, 39–45, doi: 10.1046/j.1523-1739.1998.96379.x (1998). [DOI] [Google Scholar]
- 60.Naeem S & Li S Biodiversity enhances ecosystem reliability. Nature 390, 507–509, doi: 10.1038/37348 (1997). [DOI] [Google Scholar]
- 61.Hardin G The Competitive Exclusion Principle. Science 131, 1292 (1960). [DOI] [PubMed] [Google Scholar]
- 62.Wang X & Liu Y-Y Overcome Competitive Exclusion in Ecosystems. iScience 23, 101009 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Dubinkina V, Fridman Y, Pandey PP & Maslov S Multistability and regime shifts in microbial communities explained by competition for essential nutrients. eLife 8, e49720, doi: 10.7554/eLife.49720 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Turnbaugh PJ, Hamady M, Yatsunenko T, Cantarel BL, Duncan A, Ley RE, Sogin ML, Jones WJ, Roe BA, Affourtit JP, Egholm M, Henrissat B, Heath AC, Knight R & Gordon JI A core gut microbiome in obese and lean twins. Nature 457, 480–484 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Ferrer M, Ruiz A, Lanza F, Haange S-B, Oberbach A, Till H, Bargiela R, Campoy C, Segura MT, Richter M, von Bergen M, Seifert J & Suarez A Microbiota from the distal guts of lean and obese adolescents exhibit partial functional redundancy besides clear differences in community structure. Environmental Microbiology 15, 211–226, doi: 10.1111/j.1462-2920.2012.02845.x (2013). [DOI] [PubMed] [Google Scholar]
- 66.Morrison DJ & Preston T Formation of short chain fatty acids by the gut microbiota and their impact on human metabolism. Gut Microbes 7, 189–200, doi: 10.1080/19490976.2015.1134082 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Li SS, Zhu A, Benes V, Costea PI, Hercog R, Hildebrand F, Huerta-Cepas J, Nieuwdorp M, Salojärvi J, Voigt AY, Zeller G, Sunagawa S, De Vos WM & Bork P Durable coexistence of donor and recipient strains after fecal microbiota transplantation. Science 352, 586–589, doi: 10.1126/science.aad8852 (2016). [DOI] [PubMed] [Google Scholar]
- 68.Smillie CS, Sauk J, Gevers D, Friedman J, Sung J, Youngster I, Hohmann EL, Staley C, Khoruts A, Sadowsky MJ, Allegretti JR, Smith MB, Xavier RJ & Alm EJ Strain Tracking Reveals the Determinants of Bacterial Engraftment in the Human Gut Following Fecal Microbiota Transplantation. Cell Host and Microbe 23, 229–240.e225, doi: 10.1016/j.chom.2018.01.003 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Hellweger FL, Clegg RJ, Clark JR, Plugge CM & Kreft J-U Advancing microbial sciences by individual-based modelling. Nature Reviews Microbiology 14, 461–471, doi: 10.1038/nrmicro.2016.62 (2016). [DOI] [PubMed] [Google Scholar]
- 70.Bucci V & Xavier JB Towards Predictive Models of the Human Gut Microbiome. Journal of molecular biology 426, 3907–3916, doi: 10.1016/j.jmb.2014.03.017 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Lagier JC, Khelaifia S, Alou MT, Ndongo S, Dione N, Hugon P, Caputo A, Cadoret F, Traore SI, Seck EH, Dubourg G, Durand G, Mourembou G, Guilhot E, Togo A, Bellali S, Bachar D, Cassir N, Bittar F, Delerce J, Mailhe M, Ricaboni D, Bilen M, Dangui Nieko NPM, Dia Badiane NM, Valles C, Mouelhi D, Diop K, Million M, Musso D, Abrahão J, Azhar EI, Bibi F, Yasir M, Diallo A, Sokhna C, Djossou F, Vitton V, Robert C, Rolain JM, La Scola B, Fournier PE, Levasseur A & Raoult D Culture of previously uncultured members of the human gut microbiota by culturomics. Nature Microbiology 1, doi: 10.1038/nmicrobiol.2016.203 (2016). [DOI] [PubMed] [Google Scholar]
- 72.Kreft JU, Picioreanu C, Wimpenny JW & van Loosdrecht MC Individual-based modelling of biofilms. Microbiology (Reading) 147, 2897–2912, doi: 10.1099/00221287-147-11-2897 (2001). [DOI] [PubMed] [Google Scholar]
- 73.Iranzo J, Lobkovsky AE, Wolf YI & Koonin EV Evolutionary dynamics of the prokaryotic adaptive immunity system CRISPR-Cas in an explicit ecological context. J Bacteriol 195, 3834–3844, doi: 10.1128/JB.00412-13 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Lardon L, Merkey B, Martins S, Kanchi C, Miles E, Clegg R, Alden K & Kreft J.-u. iDynoMiCS: individual-based Dynamics of Microbial Communities Simulator Software Setup and Tutorial. 2, 1–53 (2013). [Google Scholar]
- 75.Hellweger FL & Bucci V A bunch of tiny individuals-Individual-based modeling for microbes. Ecological Modelling 220, 8–22, doi: 10.1016/j.ecolmodel.2008.09.004 (2009). [DOI] [Google Scholar]
- 76.Gibson TE, Bashan A, Cao H-T, Weiss ST & Liu Y-Y On the Origins and Control of Community Types in the Human Microbiome. PLoS Comput Biol 12, e1004688, doi: 10.1371/journal.pcbi.1004688 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Stein RR, Bucci V, Toussaint NC, Buffie CG, Rätsch G, Pamer EG, Sander C & Xavier JB Ecological modeling from time-series inference: insight into dynamics and stability of intestinal microbiota. PLoS Comput Biol 9, e1003388, doi: 10.1371/journal.pcbi.1003388 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Bucci V, Tzen B, Li N, Simmons M, Tanoue T, Bogart E, Deng L, Yeliseyev V, Delaney ML, Liu Q, Olle B, Stein RR, Honda K, Bry L & Gerber GK MDSINE: Microbial Dynamical Systems INference Engine for microbiome time-series analyses. Genome Biology 17, 1–17, doi: 10.1186/s13059-016-0980-6 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Xiao Y, Angulo MT, Friedman J, Waldor MK, Weiss ST & Liu Y-Y Mapping the ecological networks of microbial communities. Nature Communications 8, 2042, doi: 10.1038/s41467-017-02090-2 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Buffie CG, Bucci V, Stein RR, McKenney PT, Ling L, Gobourne A, No D, Liu H, Kinnebrew M, Viale A, Littmann E, van den Brink MRM, Jenq RR, Taur Y, Sander C, Cross JR, Toussaint NC, Xavier JB & Pamer EG Precision microbiome reconstitution restores bile acid mediated resistance to Clostridium difficile. Nature 517, 205–208, doi: 10.1038/nature13828 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Fisher C & Mehta P Identifying keystone species in the human gut microbiome from metagenomic timeseries using sparse linear regression. Plos One 9, e102451, doi: 10.1371/journal.pone.0102451 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Brunner JD & Chia N Metabolite-mediated modelling of microbial community dynamics captures emergent behaviour more effectively than species–species modelling. Journal of The Royal Society Interface 16, 20190423, doi: 10.1098/rsif.2019.0423 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.MacArthur R Species packing and competitive equilibrium for many species. Theoretical Population Biology 1, 1–11, doi: 10.1016/0040-5809(70)90039-0 (1970). [DOI] [PubMed] [Google Scholar]
- 84.Chesson P MacArthur’s Consumer-Resource Model. Theoretical Population Biology 2638, 26–38, doi: 10.1016/0040-5809(90)90025-Q (1990). [DOI] [Google Scholar]
- 85.Marsland R, Cui W & Mehta P A minimal model for microbial biodiversity can reproduce experimentally observed ecological patterns. Scientific Reports 10, 3308, doi: 10.1038/s41598-020-60130-2 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Marsland R, Cui W, Goldford J & Mehta P The Community Simulator: A Python package for microbial ecology. Plos One 15, e0230430, doi: 10.1371/journal.pone.0230430 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Goldford JE, Lu N, Bajić D, Estrela S, Tikhonov M, Sanchez-Gorostiaga A, Segrè D, Mehta P & Sanchez A Emergent simplicity in microbial community assembly. Science 361, 469–474, doi: 10.1126/science.aat1168 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Marsland R, Cui W, Goldford J, Sanchez A, Korolev K & Mehta P Available energy fluxes drive a transition in the diversity, stability, and functional structure of microbial communities. PLoS Computational Biology 15, 1–18, doi: 10.1371/journal.pcbi.1006793 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Cui W, Marsland R & Mehta P Diverse communities behave like typical random ecosystems. Physical Review E 104, 034416, doi: 10.1103/PhysRevE.104.034416 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Orth JD, Thiele I & Palsson BØ What is flux balance analysis? Nature Biotechnology 28, 245–248, doi: 10.1038/nbt.1614 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Reimers A-M & Reimers AC The steady-state assumption in oscillating and growing systems. Journal of Theoretical Biology 406, 176–186, doi: 10.1016/j.jtbi.2016.06.031 (2016). [DOI] [PubMed] [Google Scholar]
- 92.Harcombe William R., Riehl William J., Dukovski I, Granger Brian R., Betts A, Lang Alex H., Bonilla G, Kar A, Leiby N, Mehta P, Marx Christopher J. & Segrè D Metabolic Resource Allocation in Individual Microbes Determines Ecosystem Interactions and Spatial Dynamics. Cell Reports 7, 1104–1115, doi: 10.1016/j.celrep.2014.03.070 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Dukovski I, Bajic D, Chacon JM, Quintin M, Vila JCC, Sulheim S, Pacheco AR, Bernstein DB, Riehl WJ, Korolev KS, Sanchez A, Harcombe WR & Segre D A metabolic modeling platform for the computation of microbial ecosystems in time and space (COMETS). Nat Protoc, doi: 10.1038/s41596-021-00593-3 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Bauer E, Zimmermann J, Baldini F, Thiele I & Kaleta C BacArena: Individual-based metabolic modeling of heterogeneous microbes in complex communities. PLoS Computational Biology 13, 1–22, doi: 10.1371/journal.pcbi.1005544 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Magnúsdóttir S, Heinken A, Kutt L, Ravcheev DA, Bauer E, Noronha A, Greenhalgh K, Jäger C, Baginska J, Wilmes P, Fleming RMT & Thiele I Generation of genome-scale metabolic reconstructions for 773 members of the human gut microbiota. Nature Biotechnology 35, 81–89, doi: 10.1038/nbt.3703 (2017). [DOI] [PubMed] [Google Scholar]
- 96.Heinken A, Acharya G, Ravcheev DA, Hertel J, Nyga M, Okpala OE, Hogan M, Magnúsdóttir S, Martinelli F, Preciat G, Edirisinghe JN, Henry CS, Fleming RMT & Thiele I AGORA2: Large scale reconstruction of the microbiome highlights wide-spread drug-metabolising capacities. bioRxiv, 2020.2011.2009.375451, doi: 10.1101/2020.11.09.375451 (2020). [DOI] [Google Scholar]
- 97.Escapa IF, Chen T, Huang Y, Gajare P, Dewhirst FE & Lemon KP New Insights into Human Nostril Microbiome from the Expanded Human Oral Microbiome Database (eHOMD): a Resource for the Microbiome of the Human Aerodigestive Tract. mSystems 3, doi: 10.1128/mSystems.00187-18 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Bernstein DB, Dewhirst FE & Segre D Metabolic network percolation quantifies biosynthetic capabilities across the human oral microbiome. Elife 8, doi: 10.7554/eLife.39733 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Ratzke C, Denk J & Gore J Ecological suicide in microbes. Nature Ecology and Evolution 2, 867–872, doi: 10.1038/s41559-018-0535-1 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100.Moran J & Tikhonov M Defining Coarse-Grainability in a Model of Structured Microbial Ecosystems. Physical Review X 12, 021038, doi: 10.1103/PhysRevX.12.021038 (2022). [DOI] [Google Scholar]
- 101.Jéglot A, Audet J, Sørensen SR, Schnorr K, Plauborg F & Elsgaard L Microbiome Structure and Function in Woodchip Bioreactors for Nitrate Removal in Agricultural Drainage Water. Frontiers in Microbiology 12 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102.Bertacchi S, Ruusunen M, Sorsa A, Sirviö A & Branduardi P Mathematical Analysis and Update of ADM1 Model for Biomethane Production by Anaerobic Digestion. Fermentation 7 (2021). [Google Scholar]
- 103.Goyal A, Dubinkina V & Maslov S Multiple stable states in microbial communities explained by the stable marriage problem. ISME Journal, doi: 10.1038/s41396-018-0222-x (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104.Vila JCC, Liu Y-Y & Sanchez A Dissimilarity–Overlap analysis of replicate enrichment communities. The ISME Journal 14, 2505–2513, doi: 10.1038/s41396-020-0702-7 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 105.Kalyuzhny M & Shnerb NM Dissimilarity-overlap analysis of community dynamics: Opportunities and pitfalls. Methods in Ecology and Evolution 8, 1764–1773, doi: 10.1111/2041-210X.12809 (2017). [DOI] [Google Scholar]
- 106.Timme M & Casadiego J Revealing networks from dynamics: an introduction. Journal of Physics A: Mathematical and Theoretical 47, 343001, doi: 10.1088/1751-8113/47/34/343001 (2014). [DOI] [Google Scholar]
- 107.Ljung L System identification: theory for user. (Prentice Hall, 1999). [Google Scholar]
- 108.Friedman J, Higgins LM & Gore J Community structure follows simple assembly rules in microbial microcosms. Nature Ecology and Evolution 1, 1–7, doi: 10.1038/s41559-017-0109 (2017). [DOI] [PubMed] [Google Scholar]
- 109.Venturelli OS, Carr AC, Fisher G, Hsu RH, Lau R, Bowen BP, Hromada S, Northen T & Arkin AP Deciphering microbial interactions in synthetic human gut microbiome communities. Molecular Systems Biology 14, e8157, doi: 10.15252/msb.20178157 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 110.Hara RBO & Sillanpää MJ A review of Bayesian variable selection methods: what, how and which. Bayesian Analysis 4, 85–117, doi: 10.1214/09-BA403 (2009). [DOI] [Google Scholar]
- 111.Cao H-T, Gibson T, Bashan A & Liu Y-Y Inferring Human Microbial Dynamics from Temporal Metagenomics Data: Pitfalls and Lessons. BioEssays 39, 1600188 (2017). [DOI] [PubMed] [Google Scholar]
- 112.Bongard J & Lipson H Automated reverse engineering of nonlinear dynamical systems. Proceedings of the National Academy of Sciences of the United States of America 104, 9943–9948, doi: 10.1073/pnas.0609476104 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 113.Schmidt M & Lipson H (Nutonian, Somerville, Mass, USA, 2013).
- 114.Bongard J & Lipson H Automated reverse engineering of nonlinear dynamical systems SCIENCES APPLIED BIOLOGICAL SCIENCES. The National Academy of Sciences of the USA 104, 9943–9948, doi: 10.1073/pnas.0609476104 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 115.Schmidt M & Lipson H Distilling free-form natural laws from experimental data. Science 324, 81–85 (2009). [DOI] [PubMed] [Google Scholar]
- 116.Udrescu S-M & Tegmark M AI Feynman: A physics-inspired method for symbolic regression. Science Advances 6, eaay2631, doi: 10.1126/sciadv.aay2631. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 117.Chen Y, Angulo MT & Liu Y-Y Revealing complex ecological dynamics via symbolic regression. BioEssays 41, 1900069, doi: 10.1002/bies.201900069 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 118.Narendra K & Annaswamy A Stable Adaptive Systems. (Dover Publications, 2005). [Google Scholar]
- 119.Angulo MT, Moreno JA, Lippner G, Barabasi AL & Liu Y-Y Fundamental limitations of network reconstruction from temporal data. J R Soc Interface 14, doi: 10.1098/rsif.2016.0966 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 120.Apajalahti JH, Kettunen A, Nurminen PH, Jatila H & Holben WE Selective plating underestimates abundance and shows differential recovery of bifidobacterial species from human feces. Appl Environ Microbiol 69, 5731–5735, doi: 10.1128/AEM.69.9.5731-5735.2003 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 121.Rinttilä T, Kassinen A, Malinen E, Krogius L & Palva A Development of an extensive set of 16S rDNA-targeted primers for quantification of pathogenic and indigenous bacteria in faecal samples by real-time PCR. Journal of Applied Microbiology 97, 1166–1177, doi: 10.1111/j.1365-2672.2004.02409.x (2004). [DOI] [PubMed] [Google Scholar]
- 122.Dubelaar GBJ & Jonker RR Flow cytometry as a tool for the study of phytoplankton. Scientia Marina 64, 135–156, doi: 10.3989/scimar.2000.64n2135 (2000). [DOI] [Google Scholar]
- 123.Amann R & Fuchs BM Single-cell identification in microbial communities by improved fluorescence in situ hybridization techniques. Nature Reviews Microbiology 6, 339–348, doi: 10.1038/nrmicro1888 (2008). [DOI] [PubMed] [Google Scholar]
- 124.Rao C, Coyte KZ, Bainter W, Geha RS, Martin CR & Rakoff-Nahoum S Multi-kingdom ecological drivers of microbiota assembly in preterm infants. Nature 591, 633–638, doi: 10.1038/s41586-021-03241-8 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 125.Marino S, Baxter NT, Huffnagle GB, Petrosino JF & Schloss PD Mathematical modeling of primary succession of murine intestinal microbiota. Proceedings of the National Academy of Sciences of the United States of America 111, 439–444, doi: 10.1073/pnas.1311322111 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 126.Angulo MT, Moog CH & Liu Y-Y A theoretical framework for controlling complex microbial communities. Nature Communications 10, 1045, doi: 10.1038/s41467-019-08890-y (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 127.Hoek TA, Axelrod K, Biancalani T, Yurtsev EA, Liu J & Gore J Resource Availability Modulates the Cooperative and Competitive Nature of a Microbial Cross-Feeding Mutualism. PLOS Biology 14, e1002540, doi: 10.1371/journal.pbio.1002540 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 128.Rina Foygel B & Emmanuel JC Controlling the false discovery rate via knockoffs. The Annals of Statistics 43, 2055–2085, doi: 10.1214/15-AOS1337 (2015). [DOI] [Google Scholar]
- 129.Ansari AF, Reddy YBS, Raut J & Dixit NM An efficient and scalable top-down method for predicting structures of microbial communities. Nature Computational Science 1, 619–628, doi: 10.1038/s43588-021-00131-x (2021). [DOI] [PubMed] [Google Scholar]
- 130.Conte Giuseppe, M. CH, Perdon Anna Maria. Algebraic Methods for Nonlinear Control Systems. (Springer; London, 2007). [Google Scholar]
- 131.Lin C-T Structural controllability. IEEE Trans. Auto. Contr 19, 201 (1974). [Google Scholar]
- 132.Liu Y-Y, Slotine J-J & Barabási A-L Controllability of complex networks. Nature 473, 167–173, doi:doi: 10.1038/nature10011 (2011). [DOI] [PubMed] [Google Scholar]
- 133.Camacho EF, B. C Model Predictive Control. (Springer; London, 2007). [Google Scholar]
- 134.Jones DR, Perttunen CD & Stuckman BE Lipschitzian optimization without the Lipschitz constant. Journal of Optimization Theory and Applications 79, 157–181, doi: 10.1007/BF00941892 (1993). [DOI] [Google Scholar]
- 135.Gao J, Liu Y-Y, D’Souza RM & Barabási A-L Target control of complex networks. Nat Commun 5, 5415, doi: 10.1038/ncomms6415 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 136.Arumugam M, Raes J, Pelletier E, Le Paslier D, Yamada T, Mende DR, Fernandes GR, Tap J, Bruls T, Batto J-M, Bertalan M, Borruel N, Casellas F, Fernandez L, Gautier L, Hansen T, Hattori M, Hayashi T, Kleerebezem M, Kurokawa K, Leclerc M, Levenez F, Manichanh C, Nielsen HB, Nielsen T, Pons N, Poulain J, Qin J, Sicheritz-Ponten T, Tims S, Torrents D, Ugarte E, Zoetendal EG, Wang J, Guarner F, Pedersen O, de Vos WM, Brunak S, Doré J, Antolín M, Artiguenave F, Blottiere HM, Almeida M, Brechot C, Cara C, Chervaux C, Cultrone A, Delorme C, Denariaz G, Dervyn R, Foerstner KU, Friss C, van de Guchte M, Guedon E, Haimet F, Huber W, van Hylckama-Vlieg J, Jamet A, Juste C, Kaci G, Knol J, Lakhdari O, Layec S, Le Roux K, Maguin E, Mérieux A, Melo Minardi R, M’rini C, Muller J, Oozeer R, Parkhill J, Renault P, Rescigno M, Sanchez N, Sunagawa S, Torrejon A, Turner K, Vandemeulebrouck G, Varela E, Winogradsky Y, Zeller G, Weissenbach J, Ehrlich SD & Bork P Enterotypes of the human gut microbiome. Nature 473, 174–180, doi: 10.1038/nature09944 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 137.Koren O, Knights D, Gonzalez A, Waldron L, Segata N, Knight R, Huttenhower C & Ley RE A guide to enterotypes across the human body: meta-analysis of microbial community structures in human microbiome datasets. PLoS computational biology 9, e1002863, doi: 10.1371/journal.pcbi.1002863 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 138.Falony G, Joossens M, Vieira-Silva S, Wang J, Darzi Y, Faust K, Kurilshikov A, Bonder MJ, Valles-Colomer M, Vandeputte D, Tito RY, Chaffron S, Rymenans L, Verspecht C, De Sutter L, Lima-Mendez G, Dhoe K, Jonckheere K, Homola D, Garcia R, Tigchelaar EF, Eeckhaudt L, Fu J, Henckaerts L, Zhernakova A, Wijmenga C & Raes J Population-level analysis of gut microbiome variation. Science 352, 560–564, doi: 10.1126/science.aad3503 (2016). [DOI] [PubMed] [Google Scholar]
- 139.Costea PI, Hildebrand F, Arumugam M, Bäckhed F, Blaser MJ, Bushman FD, Vos W. M. d., Ehrlich SD, Fraser CM, Hattori M, Huttenhower C, Jeffery IB, Knights D, Lewis JD, Ley RE, Ochman H, O’Toole PW, Quince C, Relman DA, Shanahan F, Sunagawa S, Wang J, Weinstock GM, Wu GD, Zeller G, Zhao L, Raes J, Knight R & Bork P Enterotypes in the landscape of gut microbial community composition. Nature Microbiology Accepted, doi: 10.1038/s41564-017-0072-8 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 140.Gonze D, Lahti L, Raes J & Faust K Multi-stability and the origin of microbial community types. ISME Journal 11, 2159–2166, doi: 10.1038/ismej.2017.60 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 141.Youngster I, Sauk J, Pindar C, Wilson RG, Kaplan JL, Smith MB, Alm EJ, Gevers D, Russell GH & Hohmann EL Fecal microbiota transplant for relapsing Clostridium difficile infection using a frozen inoculum from unrelated donors: a randomized, open-label, controlled pilot study. Clinical infectious diseases: an official publication of the Infectious Diseases Society of America 58, 1515–1522, doi: 10.1093/cid/ciu135 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 142.Colman RJ & Rubin DT Fecal microbiota transplantation as therapy for inflammatory bowel disease: A systematic review and meta-analysis. Journal of Crohn’s and Colitis 8, 1569–1581, doi: 10.1016/j.crohns.2014.08.006 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 143.Kassam Z, Lee CH, Yuan Y & Hunt RH Fecal microbiota transplantation for Clostridium difficile infection: systematic review and meta-analysis. The American journal of gastroenterology 108, 500–508, doi: 10.1038/ajg.2013.59 (2013). [DOI] [PubMed] [Google Scholar]
- 144.Brandt LJ & Aroniadis OC An overview of fecal microbiota transplantation: Techniques, indications, and outcomes. Gastrointestinal Endoscopy 78, 240–249, doi: 10.1016/j.gie.2013.03.1329 (2013). [DOI] [PubMed] [Google Scholar]
- 145.Rohlke F & Stollman N Fecal microbiota transplantation in relapsing Clostridium difficile infection. Therapeutic Advances in Gastroenterology 5, 403–420, doi: 10.1177/1756283X12453637 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 146.Aroniadis OC & Brandt LJ Fecal microbiota transplantation: past, present and future. Current Opinion in Gastroenterology, 1, doi: 10.1097/MOG.0b013e32835a4b3e (2012). [DOI] [PubMed] [Google Scholar]
- 147.Borody TJ & Khoruts A Fecal microbiota transplantation and emerging applications. Nature Reviews Gastroenterology & Hepatology 9, 88–96, doi: 10.1038/nrgastro.2011.244 (2011). [DOI] [PubMed] [Google Scholar]
- 148.van Nood E, Vrieze A, Nieuwdorp M, Fuentes S, Zoetendal EG, de Vos WM, Visser CE, Kuijper EJ, Bartelsman JFWM, Tijssen JGP, Speelman P, Dijkgraaf MGW & Keller JJ Duodenal infusion of donor feces for recurrent Clostridium difficile. The New England journal of medicine 368, 407–415, doi: 10.1056/NEJMoa1205037 (2013). [DOI] [PubMed] [Google Scholar]
- 149.Bunnik EM, Aarts N & Chen LA Physicians Must Discuss Potential Long-Term Risks of Fecal Microbiota Transplantation to Ensure Informed Consent. Am J Bioeth 17, 61–63, doi: 10.1080/15265161.2017.1299816 (2017). [DOI] [PubMed] [Google Scholar]
- 150.Kassam Z, Dubois N, Ramakrishna B, Ling K, Qazi T, Smith M, Kelly CR, Fischer M, Allegretti JR, Budree S, Panchal P, Kelly CP & Osman M in New England Journal of Medicine Vol. 381 2070–2072 (2019). [DOI] [PubMed] [Google Scholar]
- 151.Hudson LE, Anderson SE, Corbett AH & Lamb TJ Gleaning insights from fecal microbiota transplantation and probiotic studies for the rational design of combination microbial therapies. Clinical Microbiology Reviews 30, 191–231, doi: 10.1128/CMR.00049-16 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 152.Dsouza M, Menon R, Crossette E, Bhattarai SK, Schneider J, Kim Y-G, Reddy S, Caballero S, Felix C, Cornacchione L, Hendrickson J, Watson AR, Minot SS, Greenfield N, Schopf L, Szabady R, Patarroyo J, Smith W, Harrison P, Kuijper EJ, Kelly CP, Olle B, Bobilev D, Silber JL, Bucci V, Roberts B, Faith J & Norman JM Colonization of the live biotherapeutic product VE303 and modulation of the microbiota and metabolites in healthy volunteers. Cell Host & Microbe 30, 583–598.e588, doi: 10.1016/j.chom.2022.03.016 (2022). [DOI] [PubMed] [Google Scholar]
- 153.Feuerstadt P, Louie TJ, Lashner B, Wang EEL, Diao L, Bryant JA, Sims M, Kraft CS, Cohen SH, Berenson CS, Korman LY, Ford CB, Litcofsky KD, Lombardo M-J, Wortman JR, Wu H, Auniņš JG, McChalicher CWJ, Winkler JA, McGovern BH, Trucksis M, Henn MR & von Moltke L SER-109, an Oral Microbiome Therapy for Recurrent Clostridioides difficile Infection. New England Journal of Medicine 386, 220–229, doi: 10.1056/NEJMoa2106516 (2022). [DOI] [PubMed] [Google Scholar]
- 154.Moreno-Sánchez R, Saavedra E, Rodríguez-Enríquez S & Olín-Sandoval V Metabolic Control Analysis: A Tool for Designing Strategies to Manipulate Metabolic Pathways. Journal of Biomedicine and Biotechnology 2008, 597913, doi: 10.1155/2008/597913 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 155.Mitra S & Murthy GS Bioreactor control systems in the biopharmaceutical industry: a critical perspective. Systems Microbiology and Biomanufacturing 2, 91–112, doi: 10.1007/s43393-021-00048-6 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 156.Stein RR, Tanoue T, Szabady RL, Bhattarai SK, Olle B, Norman JM, Suda W, Oshima K, Hattori M, Gerber GK, Sander C, Honda K & Bucci V Computer-guided design of optimal microbial consortia for immune system modulation. eLife 7, 1–17, doi: 10.7554/eLife.30916 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 157.Kutz S. L. B. a. J. N. Data Driven Science & Engineering: Machine Learning, Dynamical Systems, and Control. (Cambridge University Press, 2019). [Google Scholar]
- 158.Baggio G, Bassett DS & Pasqualetti F Data-driven control of complex networks. Nature Communications 12, 1429, doi: 10.1038/s41467-021-21554-0 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 159.Ye H, Beamish RJ, Glaser SM, Grant SCH, Hsieh C. h., Richards LJ, Schnute JT & Sugihara G Equation-free mechanistic ecosystem forecasting using empirical dynamic modeling. Proceedings of the National Academy of Sciences 112, E1569–E1576, doi: 10.1073/pnas.1503154112 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 160.Suzuki K, Yoshida K, Nakanishi Y & Fukuda S An equation-free method reveals the ecological interaction networks within complex microbial ecosystems. Methods in Ecology and Evolution 2017, 1774–1785, doi: 10.1111/2041-210X.12814 (2017). [DOI] [Google Scholar]
- 161.Michel-Mata S, Wang X-W, Liu Y-Y & Angulo MT Predicting microbiome compositions through deep learning. iMeta 1, e3, doi: 10.1101/2021.06.17.448886 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 162.Baranwal M, Clark RL, Thompson J, Sun Z, Hero AO & Venturelli OS Recurrent neural networks enable design of multifunctional synthetic human gut microbiome dynamics. eLife 11, e73870, doi: 10.7554/eLife.73870 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 163.Van de Wiele T, Van den Abbeele P, Ossieur W, Possemiers S & Marzorati M in The Impact of Food Bioactives on Health: in vitro and ex vivo models (eds Verhoeckx K et al. ) 305–317 (2015). [Google Scholar]
- 164.Shah P, Fritz JV, Glaab E, Desai MS, Greenhalgh K, Frachet A, Niegowska M, Estes M, Jäger C, Seguin-Devaux C, Zenhausern F & Wilmes P A microfluidics-based in vitro model of the gastrointestinal human-microbe interface. Nature Communications 7, doi: 10.1038/ncomms11535 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 165.Kim HJ, Li H, Collins JJ & Ingber DE Contributions of microbiome and mechanical deformation to intestinal bacterial overgrowth and inflammation in a human gut-on-a-chip. Proceedings of the National Academy of Sciences 113, E7–E15, doi: 10.1073/pnas.1522193112 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 166.Vrancken G, Gregory AC, Huys GRB, Faust K & Raes J Synthetic ecology of the human gut microbiota. Nature Reviews Microbiology 17, 754–763, doi: 10.1038/s41579-019-0264-8 (2019). [DOI] [PubMed] [Google Scholar]
- 167.Cheng AG, Ho P-Y, Aranda-Díaz A, Jain S, Yu FB, Meng X, Wang M, Iakiviak M, Nagashima K, Zhao A, Murugkar P, Patil A, Atabakhsh K, Weakley A, Yan J, Brumbaugh AR, Higginbottom S, Dimas A, Shiver AL, Deutschbauer A, Neff N, Sonnenburg JL, Huang KC & Fischbach MA Design, construction, and in vivo augmentation of a complex gut microbiome. Cell 185, 3617–3636.e3619, doi: 10.1016/j.cell.2022.08.003 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]


