Context-Aware Technology Mapping in Genetic Design Automation

Abstract

Genetic design automation (GDA) tools hold promise to speed-up circuit design in synthetic biology. Their widespread adoption is hampered by their limited predictive power, resulting in frequent deviations between the in silico and in vivo performance of a genetic circuit. Context effects, i.e., the change in overall circuit functioning, due to the intracellular environment of the host and due to cross-talk among circuits components are believed to be a major source for the aforementioned deviations. Incorporating these effects in computational models of GDA tools is challenging but is expected to boost their predictive power and hence their deployment. Using fine-grained thermodynamic models of promoter activity, we show in this work how to account for two major components of cellular context effects: (i) crosstalk due to limited specificity of used regulators and (ii) titration of circuit regulators to off-target binding sites on the host genome. We show how we can compensate the incurred increase in computational complexity through dedicated branch-and-bound techniques during the technology mapping process. Using the synthesis of several combinational logic circuits based on Cello’s device library as a case study, we analyze the effect of different intensities and distributions of crosstalk on circuit performance and on the usability of a given device library.

1. Introduction

Although genetic design automation (GDA) has made significant progress in recent years,¹⁻³ its widespread adoption among synthetic biology researchers is still hampered by the limited number and modest size of well-characterized part libraries but also by the limited predictive power of those tools. That is, the circuit designs found by employed computer models often do not operate as predicted when realized within a cell. There are several reasons for this, but to some extent they can be traced back to the fact that our mechanistic understanding of the complex molecular biology operating within a cell is still incomplete. First, this leads to part libraries possibly omitting key physical and biochemical parameters that are required to fully specify the behavior of a part. As a consequence, the derived part models are under-specified.⁴ Second, the interactions among parts of a genetic circuit and moreover between those parts and the host cellular machinery are even less characterized or understood and not accounted for in current GDA tools. All those potential interactions are traditionally subsumed under the term context effects.^5,6 These effects include but are not limited to (i) the dependence of a genetic part on the adjacent up- and downstream sequences,⁷ (ii) the cross-talk among synthetic regulators due to their limited binding specificity,⁸ similarly (iii) the titration of regulators to noncognate binding sites on the host genome,⁹ (iv) the retroactive or loading effect exerted on upstream circuits elements by subsequent downstream loads,^10,11 and (v) the cross-talk between the host and genetic circuits on the energetic level through, e.g., the competing use of the energy-intensive translation machinery.¹²

Molecular means to counteract detrimental context effects are devised on a case-by-case basis,¹³⁻¹⁵ but their systematic inception requires models deployed in GDA tools to account for those effects. Moreover, certain titration effects turned out to be beneficial and could be leveraged with GDA to shape gene response characteristics if used in a controlled manner.¹⁶

Incorporating context effects into circuit models involves extending them through first-principles biophysical considerations, through acquisition of appropriate characterization data (circuit behavior under different environments) and—most effectively—through a combination of both. Context effects stemming from the dynamic molecular environment of a host cell will give rise to measurable cell-to-cell variability of circuit behavior.¹⁷ Those context variations were shown to be dominant contributors to noise, surpassing intrinsic contributions due to small-copy-number fluctuations.¹⁸ Hence, single-cell data for parts or circuits can be used to learn or calibrate context models. In turn, GDA tools incorporating context effects can then evaluate and score a circuit candidate based on its generated single-cell data across an in silico cell population.^19,20 This provides means to identify circuit candidates or additional regulatory motifs leading to robust circuit behavior in the presence of context effects.

Among the many context effects, two of them can be tackled by relying on available, more detailed biophysical models of gene regulation. That is, (i) cross-talk among gene expression units stemming from limited TF binding specificity of deployed transcription factors and (ii) titration of those TFs to a noncognate binding site among the host genome can be dealt with through thermodynamic models developed over the past four decades.²¹⁻²⁴ They work out the statistical mechanics of promoter occupancy states in order to derive rates of gene expression in a nearly parameter-free manner. They have been particularly successful in predicting promoter strengths within prokaryotic cells, where these occupancy dynamics are believed to happen at thermodynamic equilibrium. Moreover, they have allowed us to quantitatively reproduce the effect of titrating DNA binding sites on the dose–response characteristics of repressors in Escherichia coli (E. coli).⁹ Estimation of necessary thermodynamic parameters accounting for context effects is available through measurements. While in the case of cross-talk, measuring expression levels of TF-regulated parts in the presence and absence of noncognate TFs is sufficient, titration effects can be quantified by introducing titration plasmids with TF binding sites at different concentrations.⁹

Both Cello^2,25 and iBioSim²⁶ are well-known GDA tools with features particularly relevant to this work. Cello does not take context effects into account during circuit synthesis. It merely estimates the metabolic burden of every design in a postprocessing step and applies a hard threshold to discard toxic circuits. The tool uses a scoring function to heuristically optimize the assignment of library gates to the gates of a circuit. In a similar way iBioSim employs branch and bound to optimize the gate assignment. The optimization goal in this tool is the length of base pairs. Thus, it does not ensure the proper realization of the desired circuit function. Also, this tool does not take into account context effects. To the best of our knowledge, no current GDA tool is capable of optimizing circuit performance while taking context effects under consideration.

In this paper we present an approach for incorporating the effect of the two aforementioned context effects in the GDA technology mapping process. In particular, we make use of and extend thermodynamic models for gene regulation. As a consequence, the gates within the device library have a more fine-grained computational representation and ad-hoc phenomenological Hill-type characteristics can be avoided. As the incorporation of cross-talk renders the considered class of combinational circuits to be dynamic circuits encompassing feedback loops, we discuss the computational consequences of this and lay out efficient algorithms. In order to overcome the increased computational complexity incurred by such feedback structures, by the fine grained thermodynamic models, and by the single-cell circuit scoring we devise an efficient branch-and-bound algorithm for the mapping process. In particular, we derive score intervals for partial circuit topologies and, based on them, allow the pruning of entire branches of candidate assignments of library gates without evaluation even in the presence of cross-talk. We demonstrate the methodology using the gate library of Cello presented in ref (25), where we artificially introduced noncognate binding affinities of TFs for parts within the circuit and for the genomic DNA of the host.

2. Results and Discussion

2.1. Logic Circuit Architecture

The circuit and gate architecture in this work is similar to the one used in the Cello suite.²⁵ Accordingly, we consider combinational logic circuits that are built from NOR logic gates. Each of these NOR gates consists mainly of a fixed combination of a gene and an output promoter. The gene encodes a repressing transcription factor (TF) which binds to its cognate binding site at the output promoter. The output promoter activity then acts as the output level of the gate. Promoter activities of (noncognate) input promoters placed upstream and pointing toward the gene correspond to input levels of the gate. Thus, the TF encoded by the gene connects a gate’s inputs with its output in the form of a gate-internal connection. Binding characteristics of the TF with its cognate binding site at the output promoter and expression characteristics of the gene then implement the gate’s transfer function.

2.2. Modeling Context Effects in Genetic Circuits

2.2.1. Nuisance-Free Thermodynamic Circuit Description

Modeling the NOR gate’s transfer functions using equilibrium thermodynamics allows convenient integration of the considered context effects. We will elaborate on this in the following.

We start with a given concentration f of a translated product, i.e., its copy number w.r.t. constant volume. This product can be, e.g., a TF or a reporter. Since we work with averages of statistical ensembles, we also introduce an associated random variable F for the product concentration. Another random variable X ∈ {0, 1} accounts for the occupation of a single promoter upstream of the product’s encoding gene by RNA-Polymerase (RNAP). Finally, a collection of random variables C is used to quantify any considered molecular context moderating RNAP occupation of the promoter, i.e., changing X’s distribution. Now, let F = f be the realization of the product concentration given a fixed molecular context C = c. A fundamental model assumption w.r.t. gene expression is then that f and the expectation 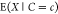are proportional, i.e., 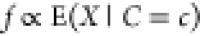. This expectation 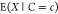is termed occupancy. A second fundamental model assumption directly related to equilibrium thermodynamics is that single binding states, i.e., the permutations of assignments of available molecules to available binding sites, follow a Boltzmann distribution. This itself implies that energetically indistinguishable binding states are equally probable. Thus, the model reduces the underlying complicated mechanics of gene expression to combinatorics on the ensemble of RNAP binding states.^21,23,24 Naturally, quantities considered to moderate RNAP promoter occupation (e.g., TF’s) and thus included in C either inflate the ensemble or increase statistical dependence among the binding states and thus complicate the combinatorics.²⁷ Approximate expressions then need to be found that are reduced to the dominating terms to maintain a certain scalability. As a final assumption, we set the promoter activity α to be proportional to the promoter occupancy, i.e., 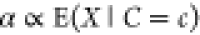, and thus α ∝ f. An illustration summing up the interactions that we can tackle using the equilibrium thermodynamic model is shown in Figure 1A.

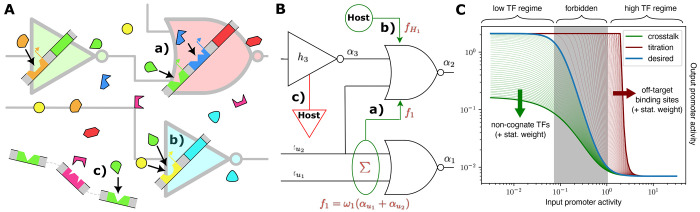
Figure 1.

(A) Illustration of the thermodynamic perspective of the logic circuit. (a) Desired binding of cognate TFs to cognate promoters implementing the gate’s transfer function. (b) Crosstalk with noncognate TF binding amplifying repression at the noncognate promoter. (c) Titration of available TFs to the host genome or other nonspecific binding sites. (B) Circuit topological view of the effects available to the model. (a) Crosstalk from another gate’s internal TF. (b) Crosstalk from out-of-circuit TFs available through the host context. (c) Titration to nonspecific binding sites available through the host context. (C) Effect of crosstalk and titration on a NOT/NOR gate’s transfer function. Crosstalk at the gate’s output promoter reduces the gate’s high output, while titration of the gate-internal TF to off-target binding sites skews the gate’s transition region to the right. The binding energies further moderate these effects

To initiate construction of a genetic logic circuit using thermodynamic gene expression, we first consider the construction of a simple NOT gate. We can understand this NOT gate as a NOR gate with a single input. As described in Section 2.1, the gate is comprised of an output promoter, its cognate (gate-internal) TF, and the gene that encodes the TF. To obtain the full transfer function h, we need to give it an input promoter activity α_in. The transfer function h determines the output promoter activity α as a function of its input promoter activity α_in. Let us say, the cognate TF concentration f is known and there is no cooperativity. Then, the promoter activity α can be given in terms of f by

where β ≡ (kT)⁻¹ is a thermodynamic constant with k the Boltzmann constant and T the temperature. E is a relative energy term encoding the energy expense of having an RNAP and a TF bound at the promoter. 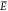on the other hand denotes the expense of having only a TF and no RNAP bound. The number c is the concentration of nonspecific “background” binding sites that are assigned average binding energy and q is a proportionality constant. With the exception of q, a similar expression can also be found in ref (28). In this work, we consider cooperativity by recruitment. This means any bound TF reduces the energy expense of an additional TF to be bound as well. We assume this effect to saturate at around N bound TFs and thus introduce N as a “cutoff” order of cooperativity. As a consequence, we allow the relative energies E(n) and 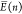to obtain an integer argument encoding how many TF are bound. For promoter activity α, we then obtain the expression

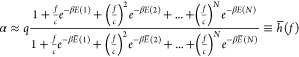The last step is to formulate the f as a function of α_in to obtain the gate’s full transfer function h. Since f and α_in are proportional, we can express f ≈ ωα_in using the proportionality constant ω and finally obtain

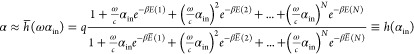1

We show in Methods 4.1.2 that 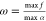. In the following, we introduce the circuit and in this context the expression for the transfer function of a NOR gate with an arbitrary number of inputs. Because of the complexity of the resulting expressions, we will resort to a more abstract notation in comparison to eq 1.

Let in the following the set of all gates in the circuit be 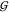and we have a set of integers 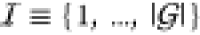enumerating the gates. 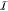assigns an index to each gate, so that for any gate from 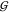with index 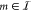, the quantity f_m is the concentration of the gate’s affiliated (internal) TF expressed by the gate’s gene. Again, we assign a random variable F_m to this concentration. The random variable of RNAP occupation of its output promoter will be written X_m and the collection of random variables considered to comprise its relevant molecular context will be C_m. The promoter activity of the output promoter of gate m is then denoted by α_m. In this section, only the ideal case of no titration nor crosstalk is considered. Thus, besides gate independent host constants, we consider only the affiliated TF concentration f_m to be relevant in moderating RNAP occupation of the output promoter, i.e., C_m ≡{F_m}.

Following the steps for the simple NOT gate, to obtain the NOR gate model, we first consider the function mapping the input promoter activity to the internal TF concentration f_m. The input promoter activity is roughly given by the sum of activities of all promoters upstream. Let 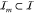denote the set of indices of gates wired to the input of the gate with index m. Then,

2

where α_i is the promoter activity of the output promoter of the i-th gate posing as one of the m-th gate’s input promoters and ω_m is a gate-specific proportionality constant. Second, we consider the promoter activity of the output promoter of the m-th gate as a function of the TF concentration f_m. We again assume that there exists a “cutoff” integer N_m which bounds the significant order of cooperativity for gate m’s TF. As a result, we obtain for the transfer function h_m of the m-th gate, i.e., for its output promoter activity α_m

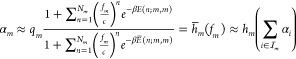3

where q_m is a proportionality constant. We again expanded the relative energy functions E and 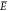by two integer arguments i and j, so that E(n; i, j) is the relative energy of the binding state where n TFs from the i-th gate bind to the j-th gate’s binding site. Since we consider no crosstalk here, only the E(n; i, i) are occurring (because they are finite). Note that also .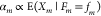

As a template model for the repression mechanics, we used a version of the “simple repression” from ref (21), a model suitable to describe most repression mechanisms in bacterial cells. This choice is reflected in the simple rational appearance of eq 3. To implement basal expression, we adopted the concept of imperfect competition between RNAPs and repressors from ref (28). This allows RNAPs to bind to promoters and initiate transcription under large energy expense even if a TF is bound to the repressor binding site. The original model prohibits this combination completely and is thus not able to model leaky gene expression in high copy number regimes of repressors. The choice to add this mechanism results in the appearance of the numerator polynomial featuring the larger energies E (in comparison to 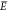) in eq 3.

As suggested by the two fundamental model assumptions and reflected in eq 3, the circuit can be fully parametrized using binding energies and proportionality constants—besides constants associated with the host environment that are independent of the circuit. Indeed, for the calculation of the whole circuit response, only these quantities are needed. In the following, we describe how to calculate this response.

Assume now, we are given a set of promoter activities 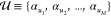as circuit inputs for a whole circuit. We further choose a set 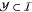of gate indices referring to those gates whose output promoter activities pose as the circuit’s output. Since any α_m for 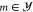cannot be measured directly, we introduce a postprocessing circuit that maps the output activities to a measurable reporter concentration, e.g., that of YFP. This postprocessing circuit then implements the transfer function 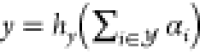with the reporter concentration y. As an example, we refer to Cello²⁵ where h_y is the identity function so that 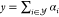(termed “implicit OR”). Then, the circuit response has a unique solution y for an input 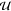if and only if the equation system

4

has a unique solution. In the case of a valid combinational circuit where each gate can be described by an equation of the type of eq 3, the system has a solution and there exists an order of successive calculation of eq 4 following which each equation can be solved explicitly.

Using the thermodynamic model, we can also introduce titration effects with the host genome. In this work, only first-order titration effects are considered. Furthermore, intracircuit titration can safely be ignored with reference to circuit function, since we restrict ourselves to NOR-only logic circuits and assume a small copy-number of the circuit plasmids in the host. To understand this, we can picture both possible scenarios of a gate-internal TF with index m titrated away from its target promoter. In the low copy-number regime, i.e., f_m is small, where we expect a high promoter activity at the output promoter, i.e., α_m ≈ max α_m, an effective reduction of f_m as the result of the titration would even increase the output promoter activity α_m, further strengthening the desired gate output. In the high copy-number regime, i.e., where f_m is large and α_m ≈ 0 is desired, a titration effect away from the target promoter can in principle alter the gate’s output by increasing α_m. However, under the assumption of a small concentration s_m of noncognate intracircuit binding sites due to a small copy-number of circuit plasmids, the effect can be ignored, even if the statistical weight of binding to the noncognate sites is extremely large (and thus, strong crosstalk is modeled). While dependent on the exact location of the gate’s transition region, we show in the Supporting Information that the worst-case is covered by an effective reduction f′_m ≈ f_m – s_m of the TF concentration f_m. Thus, if we require s_m to be small we can safely assume f′_m ≈ f_m . This idea is illustrated in Figure 1C. Thus, given a set of off-target binding sites provided by the host environment that attract a specific TF, we consider titration of these TFs away from the circuit. We call these host-provided off-target binding sites competitor sites. Introduction of a concentration s_m of competitor sites attracting the m-th TF can be effectively modeled using the transformation 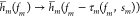where 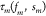is a monotonically increasing nonlinear function of f_m and s_m that can be precomputed for every fixed host-configuration. Then, we obtain for the modified transfer functions

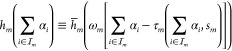where the function mapping the TF concentrations to the output promoter activity 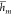stays unchanged as in eq 3. Note that this modification can be immediately applied to any gate for a fixed host, and the circuit equation (eq 4) stays formally unchanged using the modified h_m and h_y.

2.2.2. Calibration to Cello’s Gate Library

To obtain meaningful parameters for a whole set of NOR gates, we adopted the gate library from the Cello suite²⁵ and calibrated our gate’s transfer functions to match the corresponding transfer functions from the Cello gate library as closely as possible. For this, we used Simulated Annealing to minimize the logarithmic quadratic error over 1000 collocation points equally spaced in the logarithmic domain within the interval [10^–4, 10²] w.r.t. the thermodynamic parameters. The obtained curves had a peak | average | least cumulative (summed) error of 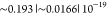in the logarithmic domain. To visually grasp this result, we supply the plots comparing both transfer functions in the Supporting Information.

2.2.3. Adding Crosstalk

The main advantage of the thermodynamic approach w.r.t. modeling crosstalk is the explicit formulation of TF binding. Therefore, to implement crosstalk for the target gate with index 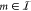we need to consider the occupancy 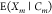to be dependent on more than only the cognate TF {F_m} ⊂ C_m. In this general case, where we assume the binding specificity of any TF to be potentially imperfect, we need to consider the concentrations of all available TFs, so 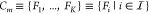. 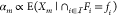We then find for the output promoter activity that

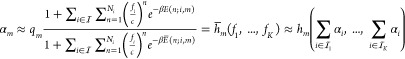5

Note, that eq 5 only holds under the assumption that cooperativity between different types of TF is negligible. Again, similar to the above, the circuit response has a unique solution y for the input 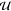if and only if the equation system

6

has a unique solution. In contrast to eq 4, eq 6 usually cannot be solved explicitly since the required order of successive calculations does not exist. Since crosstalk in general introduces feedback connections to the circuit, the computational resources needed are significantly increased because root finding or—in this case preferably—fixed-point algorithms need to be used to find a solution.

We explain how we solved eq 6 in Methods 4.2. In contrast to the combinational case (eq 4), where each 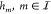, and h_y need to be evaluated only once, we need to iterate over h_m and h_y a few times until convergence. While the amount of iterations greatly varies with the circuit topology, around 10–20 iterations have been observed in an average scenario. Thus, using our approach, an increase in simulation runtime, i.e., the evaluation of one specific circuit implementation, by one order of magnitude has to be expected under consideration of crosstalk. Note that this increase depends on the algorithm used, and we cannot rule out the possibility to reduce the amount of iterations significantly by choosing a specific solution algorithm.

This increased demand of computational resources to determine the circuit response under crosstalk aggravates the runtime bottleneck in technology mapping of genetic logic circuits. While technology mapping in EDA typically finds near-optimal assignments for huge circuit structures in amenable time, in GDA the pronounced quantitative differences of functionally similar parts—and thus, their limited mutual compatibility—make already finding better-than-average assignments in small circuit structures computationally expensive. With increased computational complexity caused by the thermodynamic modeling and decreased number of good assignments caused by the now-considered context effects, scalability becomes a more important feature in the technology mapping process. We thus present a novel technology mapping procedure specifically tailored to the optimization requirements in current GDA problems in the following section.

2.3. Efficient Context-Aware Design of Genetic Circuits

A main objective of the design of genetic logic circuits is finding a topology and an assignment of gates from a library to this topology that maximize a given performance metric. In contrast to EDA, where metrics typically are based on circuit speed and size, metrics in GDA take into a account whether a circuit fulfills its functional specification. For example, the GDA tool Cello uses a circuit score based on the separation of the complementary Boolean outputs.²⁵ It has been shown that the circuit topology plays an important role in genetic circuit design.¹⁹ Yet, the computationally challenging part of circuit design is finding an assignment of genetic gates from a library to the topology. Each single assignment needs to be evaluated by simulating the circuit and determining its score, making the gate assignment a combinatorial optimization problem. To this end, we propose a method based on the Branch and Bound (B&B) optimization approach that takes into account context effects. It leverages fundamental features of the dose–response curve of gates based on transcriptional regulation and finds the optimal solution with respect to Cello’s circuit score. First, we introduce a notion of signal-compatibility of genetic gates that integrates into the B&B scheme and ensures robustness with respect to variability.

2.3.1. Compatibility of Genetic Gates

Genetic gates feature different transfer characteristics even if they represent the same logic function. In contrast to electronic circuits, there are no global levels for high and low signal values. This can lead to mismatches in the signal levels in a cascade of gates. In extreme cases, the complementary Boolean outputs of a logic gate can fall into the same region of a subsequent gate. This leads to a loss of logic information and thus to a nonfunctioning genetic circuit. In less severe cases, the subsequent gate is operating near the transition region of its transfer function. This results in a reduced tolerance with respect to signal perturbations and should be avoided when designing robust genetic circuits. In Cello, this is taken into account by ensuring that the minimum and maximum output values of a gate lead to an output of the subsequent gate that is higher than half the maximum or lower than twice the minimum output value.²⁵ Circuits that violate this criterion are filtered out during the technology mapping process. We propose to generalize this concept by defining 3 dB-thresholds of the output signal of each gate and determining the corresponding input signal levels (see Figure 2). Furthermore, the notion of compatibility is extended to include not only pairs of gates, but also (n + 1)-tuples of gates with n being the maximum number of inputs of gates in the library (see Methods 4.3). This renders possible the determination of the exact compatibility of all combinations of gates present in the circuit. Furthermore, it can be asserted that signal levels in a circuit of cascaded compatible gates do not cross the defined thresholds and thus exhibit a defined perturbation margin. By precomputing the compatibility of gates of a library into an (n + 1)-dimensional matrix, it can be integrated naturally into constructive technology mapping methods like the B&B approach presented in the following.

Figure 2.

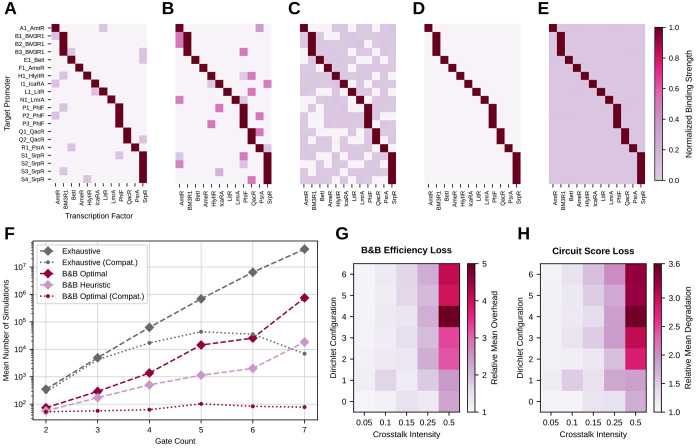
(A) Visualization of the 3 dB-thresholds on which the signal compatibility analysis is based. i₀, i₁ represent the output values at the upper and lower threshold respectively, and j₁, j₀ the corresponding input values. (B) Compatibility of gates in Cello’s library. For each pair of source gates, the number of compatible target gates is presented. Interestingly, there is a significant number of pairs not compatible with any subsequent NOR gate. This limits the number of gates available for assignment at a distinct position within the circuit.

We have evaluated the compatibility of the NOT and NOR gates from Cello’s library (see Figure 2). As the library features gates with at most two inputs, the resulting compatibility matrix is 3-dimensional, with Boolean elements representing the compatibility of a triple of two source gates and one target gate. Altogether, 21% of all triples that can be formed from the library have compatible signal characteristics.

2.3.2. Branch-and-Bound Gate Assignment

The Branch and Bound (B&B)²⁹ method is an optimization strategy for traversing search spaces in an efficient way and obtaining the optimum solution. Generally, in the branching step, partial or complete solutions are generated from other partial solutions according to a branching rule. By this, a search tree is generated iteratively. Then in the bounding phase, the quality of partial solutions is estimated optimistically and compared to the current best known solution. This enables pruning parts of the search tree that spring from inferior partial solutions and thus reaching the optimum more efficiently.

In the context of gate assignment for genetic circuits, the branching rule arises from the fact that the last gate in the cascade defines the maximum output interval of the circuit. Let x be the input promoter activity, h(x) the inhibitory Hill function modeling the dose–response curve of the transcriptional regulation, K the repression coefficient, n the Hill coefficient, and [α_min, α_max] the output interval. Then

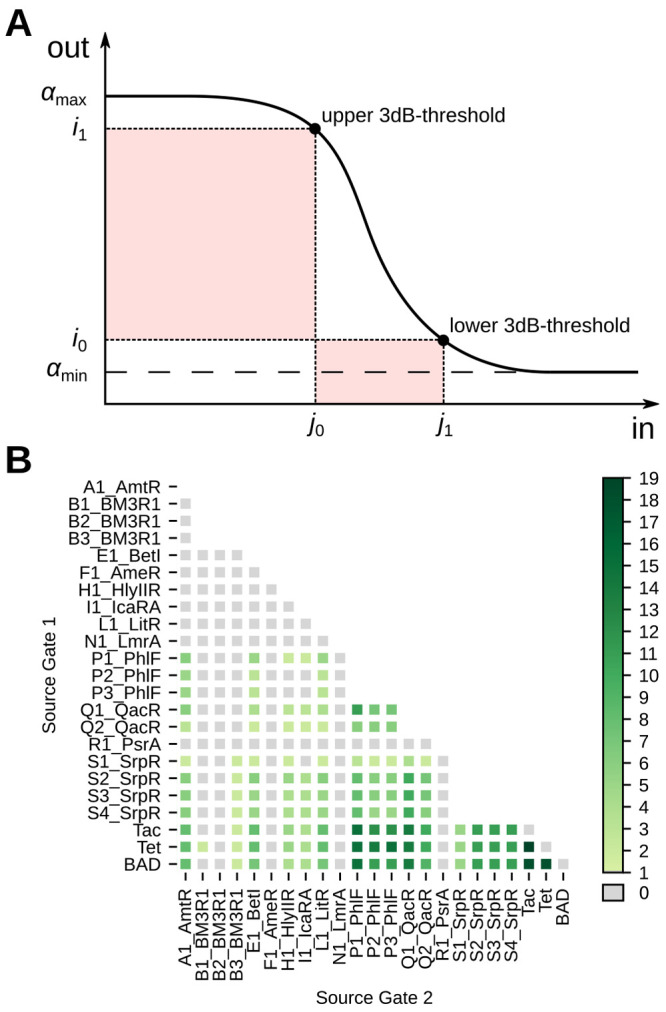
So the circuit’s output interval and thus its maximum score are limited by [α_min, α_max] of the last gate. Upstream gates only determine which portion of the interval is driven by the circuit. Thus, we propose to build partial solutions starting from the output gate and iteratively assign further gates in reversed topological order (see Figure 3A). This enables pruning considerable parts of the search tree early in the search process. Furthermore, it ensures that every partial solution to the problem represents a valid subcircuit of the original circuit with new inputs. To estimate the quality of these subcircuits optimistically, we make use of another feature of the Hill dose–response curve, its monotonicity. If ideal, i.e., maximal input values into the subcircuit are assumed, it can be stated that these translate to ideal output values and thus score (see Methods 4.4). Thus, by composing the maximally possible input values from the output intervals of the gates left in the library, each partial solution is embedded into an optimistic complete solution (see Figure 3B). By simulating the subcircuit configured in this way, the score maximally reachable with a complete solution that contains the partial solution is obtained. Thus, it represents an optimistic estimation of the partial solution’s quality.

Figure 3.

(A) Excerpt of B&B’s search tree. A branch is performed by mapping gate implementations in the library to the gate marked in red. The formed partial solutions are then scored by the optimistic estimator and pruned, if their estimated quality is below the current best known solution. (B) Estimation of input intervals exemplary shown for the signal m₃. The optimistic input interval is composed of the parameters [α_min, α_max] of gates left in the library. (C) Extension of the input interval estimation to crosstalk environments. The given assignment of Boolean input values leads to an expected “0”-output of the marked gate. Thus, during the estimation of the subcircuit the gate is embedded into its 0-environment that contains the maximum repressing crosstalk.

The estimation requires valid bounds to the possible signal values to be present at every site of the circuit. That is, every signal representing a Boolean 1 has to be estimated to the highest possible value at this site and vice versa. This requires a further step to be taken at gates with multiple inputs to guarantee optimality. For example, a NOR-gate with two inputs can be decomposed into the superposition of both input values x = x₁ + x₂ and the application of the inhibitory Hill function y = h(x). If input signals of mixed Boolean polarity are assumed, the gate is expected to output a value representing a Boolean 0 by its functional specification. The value of this output signal has to represent a valid lower bound to the signal values possible at this site. Due to the monotonicity of h(x), this translates to an upper bound at the gate’s input. However, if both input signals are assumed to be valid bounds, the superposition of these signals does not represent a valid upper bound due to their mixed polarity. Therefore, the output signal of the NOR gate does not represent a valid lower bound. Thus, the input signal representing a Boolean 0 has to be substituted by the highest value possible at this site to guarantee optimality. Generally, this is α_max of the gate driving the input. This reduces the tightness of the estimation as the substituted value typically deviates strongly from the value present at the site. When mapping a circuit under the constraint of signal-compatibility of gates, i₀ can be used as a substitute instead, as it represents a valid upper bound for the input signal representing a Boolean 0. This restores the tightness of the estimation and thus benefits the efficiency of B&B. Note that the substitution with i₀ only guarantees an optimistic estimation when mapping with compatibility and without crosstalk, as the feedback loops introduced violate the compatibility constraint. Thus, when mapping without compatibility or with crosstalk, we call the substitution with i₀ the “heuristic” mode of B&B, while substituting with α_max is called “optimal” mode.

So far, the estimation is only applicable to the evaluation of circuits without crosstalk. To find the optimal gate assignment under the influence of crosstalk effects, it is necessary to include them into the optimistic estimation. To achieve this, we propose the concept of crosstalk-environments in the following. Additionally to the desired inputs of a gate depicted by the wiring diagram, crosstalk introduces further inputs that model the crosstalk effect that other TFs have on the target gate. For each gate, depending on its desired Boolean output according to the functional specification, we compile an optimistic “0-” or “1-environment”. The gate is then embedded into it during the circuit simulation (see Figure 3C). Besides the optimistic values of the wired inputs, the environments contain the maximum crosstalk effects that benefit its specified output (see Methods 4.5). In a circuit consisting of gates based on transcriptional repression, e.g., maximum crosstalk from other gates would be assumed in the gate’s 0-environment. In its 1-environment, however, the minimal possible crosstalk is assumed. It is possible to estimate the extremal effect of crosstalk as it is limited by the maximum input values of the gate causing the crosstalk.

The signal compatibility of genetic gates presented in Section 2.3.1 can be used to further refine the proposed B&B method as it integrates naturally in the branching step. Naively, the compatibility of all gates in a circuit can be checked as soon as a complete assignment, that is a complete solution, exists. We propose a satisfiability (SAT) based look-ahead approach that is performed after every branching step on the search tree. It checks whether any combination of compatible gates left in the library exists that completes the assignment (see Methods 4.6). By this, the evaluation of subtrees that lead to invalid full solutions is suppressed as early as possible.

2.4. Experimental Results

To evaluate the performance of the proposed gate assignment methods and the behavior of genetic circuits considering crosstalk modeled thermodynamically, we perform the technology mapping for a set of circuits with different parameters. First, we examine the performance of the B&B method in the classic GDA scenario without the consideration of crosstalk. Then, technology mapping is performed with different distributions of crosstalk across the library of genetic gates. This allows conclusions about the performance of B&B and the performance degradation of genetic circuits with crosstalk.

For first evaluating the performance of the proposed B&B method without the consideration of crosstalk, we carried out the gate assignment for the 33 circuit topologies presented in ref (25) using Cello’s library of genetic gates. We then measured the number of circuit simulations needed as well as the deviation from the maximum circuit score, i.e., solution quality, observed in any circuit and compare it to an exhaustive search. Furthermore, all methods have been evaluated both with the application of the compatibility constraint and without.

Table 1 summarizes the results of all gate assignment runs. Without the consideration of compatibility of gates, B&B reduces the number of simulations needed 15-fold compared to exhaustive search, while also guaranteeing to find the optimum solution. In heuristic mode, B&B even exhibits a 664-fold efficiency gain, while the worst solution quality observed deviates only −2.7 × 10^–3 % from the maximum. The application of the compatibility constraint reduces the search space to 1.25% of the original one. In this reduced space, the optimal B&B exhibits a 108-fold gain in the number of needed simulations compared to exhaustive search. Finally, the gate assignment has also been carried out with Cello’s stochastic simulated annealing (SA) optimization method. Note the limitation that Cello applies a similar but not identical notion of compatibility (see Section 2.3.1). Furthermore, due to the stochastic nature of SA, all runs have been carried out 10 times and the worst case deviation has been determined by comparing the best and the worst solution quality observed for each circuit. Cello’s SA features a fixed number of 30 000 simulations per circuit, leading to a total number of 990 000 simulations needed, while a worst case deviation of −65% has been observed. B&B in comparison finds the optimum solution deterministically and exhibits a 83-fold efficiency gain.

Table 1. Number of Circuit Simulations Needed and Worst Case Deviation of the Reached Circuit Score for Mapping the Set off 33 Circuits Presented in Ref (25) without Consideration of Crosstalk.

method	compatibility	simulations	deviation (%)
exhaustive	×	103 687 206	–
B&B optimal	×	6 905 142	0
B&B heuristic	×	156 075	–2.7 × 10–3
exhaustive	✓	1 299 193	–
B&B optimal	✓	12 044	0
Cello (SA)a	✓	990 000	–65

^aCello uses a similar, but not identical notion of compatibility in which approx. 30% instead of 21% of gate triples are considered compatible.

Figure 4F relates the mean number of simulations needed per circuit and mapping method to the circuit size. The exponential problem complexity when not considering gate compatibility can clearly be seen. However, compared to exhaustive search, optimal B&B reduces the number of simulations by up to 2.4 orders of magnitude and heuristic B&B again by up to 1.6 orders of magnitude. When considering compatibility, the problem complexity is diminished due to the number of allowed gate assignments decreasing with increasing circuit size. In this case, the refined estimation of partial solutions enables optimal B&B to reduce the number of simulations up to 2.6 orders of magnitude,

Figure 4.

(A–E) Different distributions and total intensities of the considered crosstalk. (A) very peaked distribution, low total intensity. (B) Very peaked distribution, large total intensity. (C) Distribution with moderate entropy, moderate total intensity. (D) Distribution almost uniform, high entropy, low total intensity. (E) Distribution almost uniform, high entropy, large total intensity. (F) Mean number of simulations needed for mapping circuits with the proposed B&B methods compared to exhaustive search with respect to the number of gates. All results in this plot depict technology mapping runs without crosstalk. Dashed lines show results without the compatibility constraint, while dotted lines depict results with compatibility. (G) Number of simulations needed for mapping the set of 66 circuits with different crosstalk configurations in relation to the result without crosstalk. As a mapping method, optimal B&B with consideration of compatibility has been used. (H) Mean score of the 66 circuits mapped with optimal B&B with different crosstalk configurations in relation to the scores reached without crosstalk. The color encodes the multiplier needed to map the score with crosstalk to the one without crosstalk.

In the following, we evaluate the influence of crosstalk on the performance of the B&B gate assignment and genetic circuits by performing technology mapping with multiple gate libraries containing different crosstalk configurations. The crosstalk configurations were generated in the following way. First, for each available promoter with index m, a random vector of values 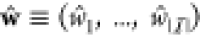, one for each noncognate TF k ≠ m, was generated by sampling a Dirichlet distribution with a single concentration hyperparameter γ > 0. This allowed us to control how sparse the random crosstalk will be distributed across the noncognate TFs. 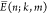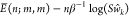These values were then used to obtain normalized relative energy terms of the binding state of the cognate TF at the promoter  ≡ for 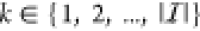and a number S > 0. The number S poses as a total intensity hyperparameter. This ensured that at 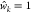and S = 1, a noncognate TF would repress transcription at the promoter equivalently to the cognate TF. Since the entries of any sample from a Dirichlet distribution are guaranteed to sum to one, i.e., 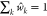, introduction of S allowed us to control the total crosstalk coming from all noncognate TFs. We generated 35 libraries for each combination of one of 7 different concentrations γ and one of 5 total intensities S. The γ and S used are given in the Supporting Information, but five libraries are visualized in Figure 4A–E. Additionally, the set of 33 circuits is extended with structural variants synthesized in ref (19) to form a set of 66 circuits. We could observe that for low to moderate total intensity in crosstalk only a small deterioration in either score of the found assignment or number of simulations w.r.t. the crosstalk-free case occurred. From around 15% total intensity on, the excess number of simulations and the reduction in score depended strongly on the concentration hyperparameter as shown in Figure 4G,H. For very peaked crosstalk distributions, the assignments were found in comparable time to the case of low intensity, but their scores were at around 50% to 60% of the crosstalk-free case. In this case, the acceptable results can be achieved by either distributing crosstalk across the gates to match their desired logic outputs or by mitigating assignments with gate combinations exhibiting crosstalk at all. For crosstalk distributions with high entropy on the other hand, the strongest observed decrease in score and the largest excess in number of simulations has been observed. In the most extreme case, we observed a reduction to 20% in average score and a 5-fold increase in number of simulations. In this scenario, with rising total intensity it seems to be increasingly hard to find assignments that correctly implement the logic function. Also the B&B algorithm’s bounding function becomes increasingly nondescriptive w.r.t. prediction of the final score, which leads to the search strategy starting to approach that of an exhaustive search across the assignments. In the observed worst-case crosstalk configuration, the heuristic B&B method exhibits a 10.5-fold efficiency gain compared to the optimal method, while obtaining near optimal results that feature a mean −0.7% deviation from the optimum score. Thus, heuristic B&B represents a viable alternative for efficient technology mapping of circuits that are subject to crosstalk. The nonsmoothness of the color plots in Figure 4G,H can be explained by the fact that each library represents a single sample of a random library with fixed total intensity and concentration.

3. Conclusion

In this contribution, we presented a novel technology mapping approach for GDA which can process device libraries that exhibit crosstalk between different transcription factors. This crosstalk leads to binding of TFs at noncognate binding sites and thus leads to unintended repression or activation. The approach is also capable of dealing with titration effects which reduce the number of TFs available for binding at the cognate binding sites due to off-target sites on the host genome. Both effects have to be taken into account during circuit scoring in order to find robust designs for genetic circuits, in particular, for combinational logic circuits. The underlying principle of our developed circuit models uses thermodynamic calculations of TF-DNA binding energies. We have shown that using this modeling approach we can find good gate assignments even in the presence of both context effects.

We investigated different types of crosstalk scenarios. They vary in the intensity and in the entropy of the crosstalk distribution, i.e., whether crosstalk is spread equally among the library parts or whether crosstalk is confined to a few pairs of parts of the library. It turns out that a certain amount of crosstalk can be tolerated in the library with a moderate degradation in circuit performance, quantified in terms of circuit score. For higher crosstalk levels, the circuit performance degrades significantly and the computational complexity of the proposed B&B assignment method increases concurrently. In case of severe crosstalk but with low entropy, the B&B run-time showed almost no degradation, but the circuit performance was strongly affected. In worst-case crosstalk scenarios, the heuristic B&B assignment still found near optimal results, yet still 13 times faster than the optimal, exhaustive method.

We believe that these findings will help other researchers to evaluate their device libraries at an early stage during research and circuit development. They can judge the crosstalk situation in their libraries and in their circuit designs without the need to build many different test circuits in the lab.

4. Methods

4.1. Thermodynamic Description of the Genetic Logic Circuit

In the following sections, we derive an equation which allows us to express the TF concentration f_m of a gate with index 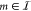as a function of all TF concentrations f_k, 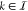of the other gates, and any additional nuisance TF’s in the circuit if present. Since the circuit is comprised of NOR gates that map promoter activities to promoter activities, we then reformulate the expression to obtain the transfer functions of the gates (eq 5) and as a simplification (eq 3).

4.1.1. Gate-Internal TF Expression

We first present the general expression for the partition function of bound RNAP for the NOT (1-input NOR) gate’s output promoter under potential crosstalk from all K available TF in the circuit. The quantity p is the number of available RNAP.

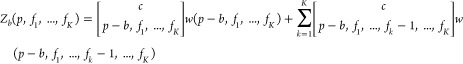with b ∈ {0, 1}, the completed multinomial coefficient

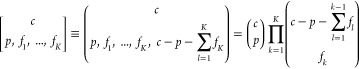and the general statistical weight function w

which covers the partition across the background and specific binding sites. For the background energy we assume independent binding. Thus, the function 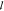_c takes on the simple form

with the absolute binding energies ε_c,p for RNAP and 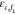for TF binding to a nonspecific background site. Whether or not the specific binding energy function 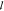can be written as a linear combination of only a few energy terms for most arguments depends on the degree of simplification in the model. A fully independent specific binding would lead to a similar appearance to 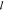_c. The particular choice for 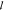implements, e.g., cooperativity and basal expression. Generally, we obtain the expression for the expectation 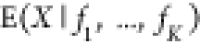via

The derivation of the final simplified expression takes a lot of space, so we refer to the Supporting Information for it. Under the assumption of no relevant RNAP titration, i.e., a sufficiently large copy number of RNAP’s available for binding, and no cooperativity, we then obtain as the result for the NOT gate with imperfect competition and arbitrary crosstalk from other TF’s

7

where the regulation factor d is given by

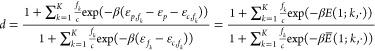where we introduced the relative energy functions 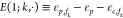and 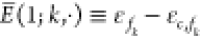 which encode the energy expense of the k-th TF binding to the promoter which has no index and thus obtains a · here. Note that d in the NOT case is approximately equal to the fold-change 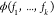. To extend the result to the cooperative case, we can simply follow the construction for dependent multiple bindings from ref (21).

In the following, we will add the superscript (n) to any “anonymous” input promoter for enumeration. In this way, there is no confusion with the gate index placed as a subscript and simultaneously allows us to specify an arbitrary n-th input promoter.

The output expression in the N-input NOR gate is given by a simple sum of the expressions for NOT gates with the same output gene. This means that the decomposition in the single expectations 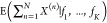= 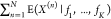yields a sum of expressions that match those of the NOT case. For this to happen, the random variables X⁽ⁿ⁾ need to be independent. We can argue analogous to ref (27) that they are independent under the assumption of no relevant intracircuit interpromoter TF and RNAP titration. This means that, conditioned on the binding of a TF or RNAP to binding sites of another gate, the probability of binding to the sites of the considered gate does not significantly change. This can be seen as a “large” copy-number approximation, while “large” will be relative to the potential binding sites present in the circuit.

It is now a straightforward task to construct the expression for the n-input NOR gate. Thus, in this case we directly obtain

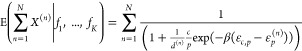with the promoter-specific regulation factors d⁽ⁿ⁾ given by

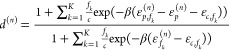which is the final expression for the output expression of the (N-input) NOR gate with imperfect competitivity (between RNAP and TF’s) and crosstalk from an arbitrary number of additional TF’s.

This is the first case where we are now interested in an expression for the overall fold-change. The fold-change is given by the expression

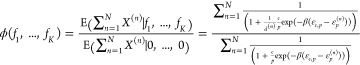which we can approximate closely by assuming that the factors 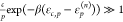for all n. This is based on the assumption that the expectation of encountering an RNAP bound at the specific promoter is in absolute numbers rather small, i.e., 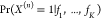is small for all n and the number of binding sites is reasonably small as well (it is even only 1 here at this moment). Also d⁽ⁿ⁾ ≤ 1 holds true anyway and even amplifies this aspect for the scaled terms 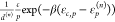. Then, we get for the fold-change

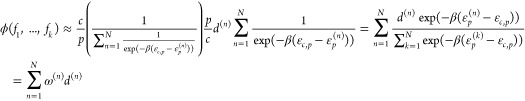which lets us state the final form for the fold-change by

where the weights ω⁽ⁿ⁾ are given by the equation

which relates the relative statistical weights of the promoters to each other. Finally, we repeat the expression for the regulation factors d⁽ⁿ⁾, which is given by

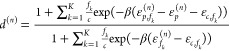We again refer to ref (21) on how to extend the d⁽ⁿ⁾ to the case with cooperativity. Actively repressing stronger promoters has a stronger influence on the overall fold-change of the NOR gate. The fold-change together with a proportionality constant then gives the absolute expression level f_m, i.e.,

for some 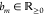. In accordance to previous works on thermodynamic gene expression,²¹ since ϕ_m ∈ (0, 1) and 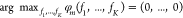, the proportionality constant b_m = max f_m equals the unrepressed, maximal TF concentration.

4.1.2. From TF Concentrations to Promoter Activity

While being intuitive, working with mappings of TF concentrations raises consistency issues with the gate and circuit models. This stems from the fact that TF concentrations are gate-internal quantities and thus any change in wiring would change the “transfer” functions to compute, This is also incompatible with common methods to improve performance, e.g., lookup tables of function values. Thus, to keep logic circuit and thermodynamic models consistent, we need to formulate the output promoter activities α_m as functions of the other promoter activities α₁, ..., α_K. First, we assume the output promoter activities 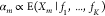to be proportional to their occupancies by RNAP. Thus, we obtain for the output activity that 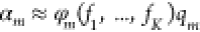with a new proportionality constant 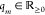. Clearly, by the same argument as used for b_m, we can see that q_m = max α_m, i.e., q_m must be the maximum unrepressed promoter activity. Thus, we obtain for the relationship between input promoter activity and TF concentration at the m-th gate

8

The final step is to relate the internal TF concentration f_m and the output promoter activity α_m. Since we decomposed the NOR gate’s input to a sum of inputs of NOT gates which is already reflected by eq 8, it is sufficient to consider this relation w.r.t. the fold-change of a NOT gate. Then, we obtain from eq 7 that

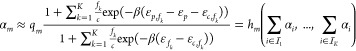4.2. Iterative Calculation of the Circuit Response

Before we calculate the circuit response under crosstalk (eq 6), we start by considering the crosstalk-free version (eq 4). Calculation of eq 4 is very fast because there exists at least one sorting of the equations in the system, such that each equation can be solved explicitly upon solution of the previous one. As a consequence, a single iteration, i.e., a single calculation of each equation in the system, is sufficient to obtain the final solution y given 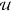. Thus, under the assumption that in most assignments traversed by the technology mapping process the incorporation of crosstalk through eq 6 does not fundamentally change the gate’s outputs in comparison to eq 4, we use the solution of eq 4 as an initial guess. As a nonlinear equation system, we can write eq 6 in matrix form with the vector of unknowns 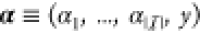including the response y. Then, with the fixed vector-valued function 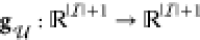which maps gate-outputs to gate-outputs, we can solve the fixedpoint problem 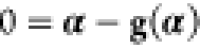with the vector of zeros 0. This can then, together with the initial guess α₀ obtained from eq 4, be fed into a state-of-the-art fixedpoint or root solver. For our evaluation, we simply used Python’s scipy.optimize package with the function root and chose the Levenberg–Marquardt algorithm as a solution method.

4.3. Defining Signal Compatibility of Genetic Logic Gates

Let [α_min, α_max] be the output interval of a genetic gate. Then 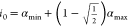represents its output at the lower 3 dB-threshold and j₁ = g^–1(i₀) the corresponding input value. Similarly, 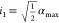is the output at the upper 3 dB-threshold and j₀ = g^–1(i₁) its corresponding input value.

Assume a library of gates based on repression with a maximum of two inputs per gate. A triple of two source gates r, s, and a target gate t is compatible if

i.e., the superposition of the maximum input values representing a Boolean 0 does not exceed the lower input threshold of the target gate. Further,

ensures that the lowest input superposition representing a Boolean 0 and a Boolean 1 does not fall below the target’s upper input threshold.

4.4. Optimality of the Branch and Bound Method

Let γ be the topology of the genetic circuit and a the assignment of gates from the library to the abstract nodes of the circuit. Let further be 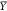the set of output signal values representing a Boolean 1 and 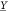the signal values representing a Boolean 0. Then the circuit score (eq 9a) introduced by Cello rates the minimum separation of the complementary Boolean output states of the final gate in the circuit.^25,30

9a

9b

9c

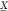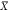Let j name that final circuit gate and let h_j(x) be its transfer function, the inhibitory Hill curve. Let be the maximum gate input value of all input values representing a Boolean 0, be the minimum gate input value of all input values representing a Boolean 1. Then eq 9b results from the monotonicity and inverting characteristic of h_j(x). Let [α_min,i, α_max,i] be the bounded output interval of the preceding gate i, then eq 9c represents a valid upper bound of the score, because , .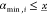

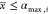4.5. Compilation of the Crosstalk Environments

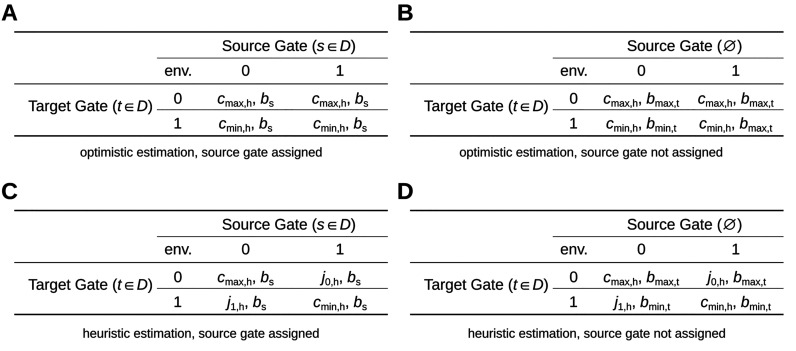
Let g ∈ G be the gate in the set of gates G comprising the abstract circuit topology for which the crosstalk-environment shall be built. Assume that it is assigned with a genetic gate implementation t ∈ D from the set D of implementations in the library. The crosstalk environment of g is built by superimposing the contributions of all other gates h ≠ g ∈ G in the circuit. Let furthermore [c_min,h, c_max,h] be the minimum and maximum input values into source gate h determining its output and thus crosstalk induced by it. If the input gates of h are assigned an implementation from the library, this interval comprises the superposition of the input gates’ minimum and maximum output values, respectively. If the input gates of h are unassigned, the interval is composed of the minimum and maximum output values of gates left in the library, representing an extremal estimation.

First, assume that the source gate h is assigned an implementation s ∈ D and its cognate TF is b_s. Its contribution to the crosstalk-environment of gate g is then calculated according to the input values and expressed TFs shown in Table 2A. To guarantee an optimistic estimation of the partially assigned circuit, its produced crosstalk is assumed to be maximal in the target gate’s 0-environment and minimal in the 1-environment. As the source gate’s TF is fixed, this is done by minimizing or maximizing its possible input values.

Table 2. Source Gate Activity and TF Assumed in Crosstalk Environments for Optimistic and Heuristic Estimation.

Let b_min,t and b_max,t be the noncognate TFs of gate implementation t assigned to target gate g that are not contained in the partial assignment and have the minimum and maximum binding affinity to t’s promoter, respectively. The contribution to the crosstalk of a source gate that is not assigned is then determined according to Table 2B. That is, additionally to assuming extremal input values for the crosstalk-inducing gate, it is assumed to express the TFs that have the minimum or maximum effect on the target gate.

The choice of the composition of the crosstalk environments depends only on the specified Boolean output value of the target gate. Furthermore, feedback loops introduced by crosstalk are cut by basing c_min,h and c_max,h solely on minimum and maximum activity values given in the library which represent physical bounds. Both aspects ensure that the estimation of the crosstalk is fully optimistic w.r.t. to the functional specification.

Analog to the heuristic mode introduced in Section 2.3.2 for the estimation of wired inputs, the crosstalk can be estimated heuristically. Let j_0,h and j_1,h be the input values of source gate h corresponding to the thresholds introduced in the signal-compatibility analysis Section 2.3.1. For circuits built from compatible gates, we can state that j_0,h represents a valid upper bound for the possible inputs of gate h when its specified output is a Boolean 1. Analog, j_1,h represents a valid lower bound for the possible inputs when the specified output of gate h is a Boolean 0. Note that these bounds are only valid for a circuit free of crosstalk, i.e., without feedback loops. Nonetheless, they can be used as a heuristic estimation for the output of h when considering circuits with crosstalk. We implemented this estimation into the heuristic mode of B&B according to Table 2C,D. In contrast to the optimal mode, the optimistic but not fully realistic estimation of the input activity c_max,h in the case of a specified Boolean 1 output of gate h is replaced by j_0,h. Analog, c_min,h is replaced by j_1,h in the case of a Boolean 0 output.

4.6. Branching with Compatibility Look-Ahead

After every branching step during the B&B, a look-ahead check is performed whether the formed partial assignment of genetic gates can be completed to form a valid solution that meets the constraints given by the compatibility matrix. To this end, a satifiability (SAT) problem is formulated that is solved by a SAT solver online during technology mapping. The problem consists of four clauses, one of which is optional. Let g ∈ G be a gate g from the set of all abstract gates in the circuit G and d ∈ R ⊂ D the genetic gate implementation d from repressor group R that forms a part of all implementations D present in the library. Then 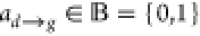is the Boolean variable representing an assignment of implementation d to gate g. Let further be y ∈ Y the logic type y of all logic types present in the library and t(g): G → T, t(d): D → T the functions mapping gates and implementations to their logic type. Then the first clause of the SAT problem

ensures that every gate is assigned at least one implementation of the same type. Further, the clause

states that every repressor must be assigned maximally once. Let furthermore be n the maximum number of inputs of gates in the library and (s₁, s₂, ..., s_n, t) ∈ T the (n + 1)-tuple of n source implementations s_n and target implementation t of all (n + 1)-tuples T present in the circuit. Let 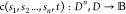be the function that queries the compatibility matrix for a given (n + 1)-tuple of implementations. Then the clause

ensures that every tuple present in the circuit consists of compatible implementations. The final clause

25

states that every gate is assigned maximally one implementation. It is optional for evaluating the compatibility, but can be useful as it enables the retrieval of valid assignments from the SAT model. To speed up the evaluation of the SAT problem, it is set up prior to the technology mapping process based on the circuit structure and the library of gate implementations. When a (partial) assignment shall be evaluated, the variables a are substituted with constants according to the existing assignment.

The source code of the proposed methods is available at https://www.rs.tu-darmstadt.de/ARCTIC.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acssynbio.2c00361.

• Comparison of the transfer functions of the thermodynamic library to those of the original Cello library; Proof of transfer function under crosstalk; Compatibility analysis of the gate library (PDF)

Special Issue

Invited contribution from the 13th International Workshop on Bio-Design Automation.

Author Contributions

^§ N.E., T.S., and E.K. contributed equally to this research. H.K. and C.H. provided the research idea and contributed methodology. N.E., T.S., and E.K. conceived novel modeling and technology mapping schemes and carried out mathematical analysis and software development. All authors contributed to the writing of the paper.

The authors declare no competing financial interest.