Abstract
Advances in continuous manufacturing in the pharmaceutical industry necessitate reliable process monitoring systems that are capable of handling measurement errors inherent in all sensor technologies and detecting measurement outliers to ensure operational reliability. The purpose of this work was to demonstrate data reconciliation (DR) and gross error detection methods as real-time process management tools to accomplish robust process monitoring. DR mitigates the effects of random measurement errors, while gross error detection identifies nonrandom sensor malfunctions. DR is an established methodology in other industries (i.e., oil and gas) and was recently investigated for use in drug product continuous manufacturing. This work demonstrates the development and implementation of model-based steady-state data reconciliation on 2 different end-to-end continuous tableting lines: direct compression and dry granulation. These tableting lines involve different equipment and sensor configurations, with sensor network redundancy achieved using equipment-embedded sensors and in-line process analytical technology tools for the critical process parameters and critical quality attributes. The nonlinearity of the process poses additional challenges to solve the steady-state data reconciliation optimization problem in real time. At-line and off-line measurements were used to validate the framework results.
Keywords: tableting, continuous processing, process analytical technology (PAT), quality by design (QbD), mechanistic modeling
Introduction
In 2002, the concepts of quality by design (QbD) and process analytical technology (PAT) were introduced by the United States Food and Drug Administration as important milestones in the path toward improved pharmaceutical manufacturing. The goal of the QbD initiative was to establish the importance of identifying the process variables, the critical process parameters (CPPs), and their impact on product critical quality attributes (CQAs) and to define the domain of values of these variables within which the product was acceptable for release. The PAT initiative envisioned the progress toward using instrumentation and automation systems for real-time monitoring of these CQAs and CPPs. By doing so, it was possible to both improve process understanding and enable the automatic control of the manufacturing process.1,2 With QbD and PAT now a well-accepted mindset, real-time process management is the next important concept on the path toward realizing process automation and smart manufacturing practices in the pharmaceutical industry.
Real-time process management is a systematic framework for supporting operational decision-making which includes process monitoring and advanced process control systems.3 Process systems engineering methods such as data reconciliation (DR) and state estimation leverage mechanistic understanding of the process for real-time qualification of measurements from field sensors and process analyzers to improve accuracy and sustainability of automation and quality assurance systems in continuous process operations.4 DR and gross error detection (GED) methodologies have evolved from applications in industries practicing continuous manufacturing such as petrochemical, bulk chemicals, and power plants5 for operational and business decisions. This work focuses on the design and implementation of robust process monitoring systems with the application of DR and GED in continuous drug product manufacturing.
DR provides estimates of the most likely state of the manufacturing system, given known random errors in the process measurements, and can be implemented in data-driven or model-based frameworks.6 The basic design and implementation details of the DR framework for continuous pharmaceutical manufacturing were recently presented by our research group.7 The application of state estimation in feeding blending systems was likewise recently presented.8 Moving forward, the objective of this work was to investigate the application of model-based steady-state data reconciliation (SSDR) to the continuous tableting via granulation and direct compaction processes at steady-state and to demonstrate the impact of effective management of process errors in reconciling measurements from a sensor network with varying levels of redundancy. The model-based form of SSDR is used in this work because it can accommodate process nonlinearities.7
Theory
DR combines domain knowledge in the form of a process model with the real-time data generated by online instrumentation systems to obtain maximum likelihood estimates of process variables. In general, the equations of the process model are functions of the measured variables, unmeasured variables, and model parameters.9
The sensor network is composed of measurements from sensors embedded in the unit operations equipment, from field devices that measure temperature, flow rate, pressure, and so forth and from process analyzers that measure CQAs. In SSDR-M, the process variables are classified as measured and unmeasured.10 The unmeasured variables can be observable or nonobservable.11 If they are observable, they can be estimated through the SSDR-M process model. Nonobservable variables are neither measured nor computable from the process model. Furthermore, the network is considered redundant if the number of measurements exceeds the process degrees of freedom. Redundancy in the sensor network is required for DR.10,11 If this condition is not met, in general, there may be no consistent solution of the process model, and then, the measurements must be used directly as they are the only information available to estimate the process state. Furthermore, a sensor network with insufficient measurements could result in an unobservable network.
SSDR-M is formulated as a form of the maximum likelihood optimization problem. The objective is to determine the reconciled values so as to minimize the sum of the squares of the differences between the raw measurements (x+) and their reconciled values (x), weighted by the covariance matrix (Q) of the measurements.12 Equation 1 represents the objective function.
| (1) |
The Q matrix is estimated from a priori information on the measurement errors inherent in the measurement technologies used. The problem variables are constrained to satisfy the process model, which consists of fundamental relationships such as material balance equations and mechanistic relationships (Eq. 2), as well as possibly inequality constraints (Eq. 3), such as bounds on the variables.13
| (2) |
| (3) |
where is a vector of measurements, is a vector of reconciled values of the n measurements, is a vector of the unmeasured process variables, Q is the covariance matrix, , is a vector of p process model parameters, is a set of equality equations which describe the steady-state behavior of the process, and is a set of inequality constraints, n is the number of reconciled variables, m is the number of unmeasured variables, and k is the number of relations or equations.
Before reconciling process measurements, GED is critical to identify and manage nonrandom measurement errors. Reconciliation using measurements that include with gross errors will result in a distorted set of reconciled variable values, in which the deviations due to the gross errors will distribute across all variables, a phenomenon called smearing. In this work, the established GED methods10,14 comprising the global test (GT) and the measurement test are used. The GT is used to identify whether an instrumentation fault has occurred in the network, while the measurement test is used to locate the sensor at which the gross error is likely to be found. A description of the impact of gross errors in an application involving a continuous drug product manufacturing subsystem was recently presented.7
The GT simply involves applying a statistical test to the solution of DR problem (Eqs. 1–3). The statistical criteria consist of the χ2 distribution, which is a function of the number of linear-independent equations of the process model and the selected confidence interval (e.g., 90% or 95%).15,16 If the value of Equation 1 at the reconciled solution is greater than the selected critical value χ2 value, corresponding to the degrees of freedom, then there is likely a gross error in the system. To locate the gross error, the measurement test is used, which is based on the critical test value (zc).7 The measurement test requires linearization of the process model at the current operating conditions. Equation 4 represents the model constraints in linearized form.
| (4) |
Where: is the linear constraint matrix, is a vector of reconciled values, is a vector of known coefficients.
If the measurement test for a given instrumentation system fails, the corresponding measurement has a gross error. The raw measurement is recorded in the process historian but is treated as an unmeasured variable in the DR problem. The measurement test is represented by Equations 5 and 6.
| (5) |
| (6) |
where: x+ and x are referred in Equation 2, is a vector of errors, and is a vector of the measurement test values;
The level of significance is defined as α, while β is the modified level of significance and it is dependent on the number of active measurements, as shown in Equation 7.
| (7) |
where n is the number of measurements, α is the level of significance (e.g., 5%), and β is the modified level of significance since it is a function of α and the number of measurements.
Experimental Systems
Tableting Line via Direct Compression
The direct compression (DC) tableting line is composed of 2 loss-in-weight (LIW) Schenck AccuRate AP-300 feeders. One feeder delivers a model active pharmaceutical ingredient (API) at a mass flow rate (FAPI) of 1 kg/h, while the second feeder conveys a model excipient at a mass flow rate (Fexc) of 9 kg/h to achieve a normal operating condition of 10% acetaminophen (APAP) at 10 kg/h. The load cells and auger speed measurements are used by the equipment-embedded control system to evaluate and report the flow rates from the LIW feeders. The API and excipient are blended in a Gericke GCM 250 mixer, operated at 200 rpm. The content uniformity of this stream is measured in real time using near infrared (NIR) spectroscopy method. Subsequently, a Schenck PureFeed DP-4-disc feeder feeds a model glidant at a mass flow rate (Fgli) of 20 g/h into the system to achieve a glidant concentration of 0.2% in the blend. The final mixture is blended in a second Gericke GCM 250 mixer, which is also operated at 200 rpm. A NIR sensor is used at the exit of the second blender to measure the content uniformity in real time.17 The total flow rate of this stream was measured in real time by means of an X-ray mass flow sensor.18 More details on the PAT tool development are provided in section Material and Methods. The blended powder is then transported by means of a “Z” incline conveyor and fed continuously into a Natoli BLP-16 tablet press. Round and flat tablets with 8 mm in diameter are produced in the 16-station tablet press using B-type tooling. The in-die tablet thickness was limited to 4.2 mm and was set manually at the beginning of the experimental campaign. The dosing position was set at 15 mm, while the feed frame rotation speed (FS) was set at 50 rpm, and the turret speed (TS) was set at 36 rpm. The feed FS and TS were set to match the overall flow rate of the integrated system. Other measurements provided by the tablet press are the main compression force (MCF), precompression force (PCF), the ejection force, temperature, and humidity. It is important to note that the press is a research unit, and thus, the thickness at MCF and PCF could not be adjusted during operation.
Tableting Line via Dry Granulation
In the dry granulation (DG) line, the API and excipient feeders and blender used in the DC tableting line are operated at the same conditions as in the DC instance. The mixture content uniformity is measured by a NIR probe, and the blend is fed into an Alexanderwerk WP120×40 roller compactor. In the compactor, the powder blend is conveyed by the feed screw to 2 counter-rotating rolls. The feed screw speed (NS) was set at 32 rpm. The rolls of this equipment have a diameter (DR) of 12 cm, and their width (W) is of 4 cm and were operated at roll speed (NR) of 6.5 rpm. The feed screw speed and roll speed were set to achieve the target throughput of the integrated system. The powder is gripped by the rolls and pulled into the nip area of the compacting rolls using the vacuum deaeration system before being compacted into a ribbon. The hydraulic pressure (Ph) was set at 45 bar, and the roll gap (S) control was disabled. A NIR probe was positioned to measure ribbon density in real time following the compaction step. The physical arrangement of the roller compactor was modified to accommodate the NIR sensor. To ensure robust sampling from the NIR sensor, a 3D printed part was designed as a sensor holder to maintain the position and angle of the NIR sensor. A horizontal conveyor was then used to feed the ribbon into the granulator of the DG machine. The granulator on the Alexanderwerk system was setup with an upper screen size of 1.25 mm, a lower screen size of 1.0 mm, and operated at 50 rpm.
No glidants or lubricants were added to the granules. The granule flow rate was measured by the X-ray sensor. Depending on the case scenario (section Experimental Systems), the granules flow was transported, by the “Z” incline conveyor, into the Natoli BLP-16 Tablet Press. For the DG runs, flat tablets were produced, which were of 8 mm diameter and 4.5 mm thickness. For the DG tableting line, the dosing position, FS, and TS were not varied; instead they were set at 10.7 mm, 29.7 rpm, and 41.5 rpm, respectively. The MCF, PCF, and ejection force were measured, but proportional-integral-derivative controller was not active between the thickness and main compression. Figure 1 shows the continuous tableting line configurations.
Figure 1.
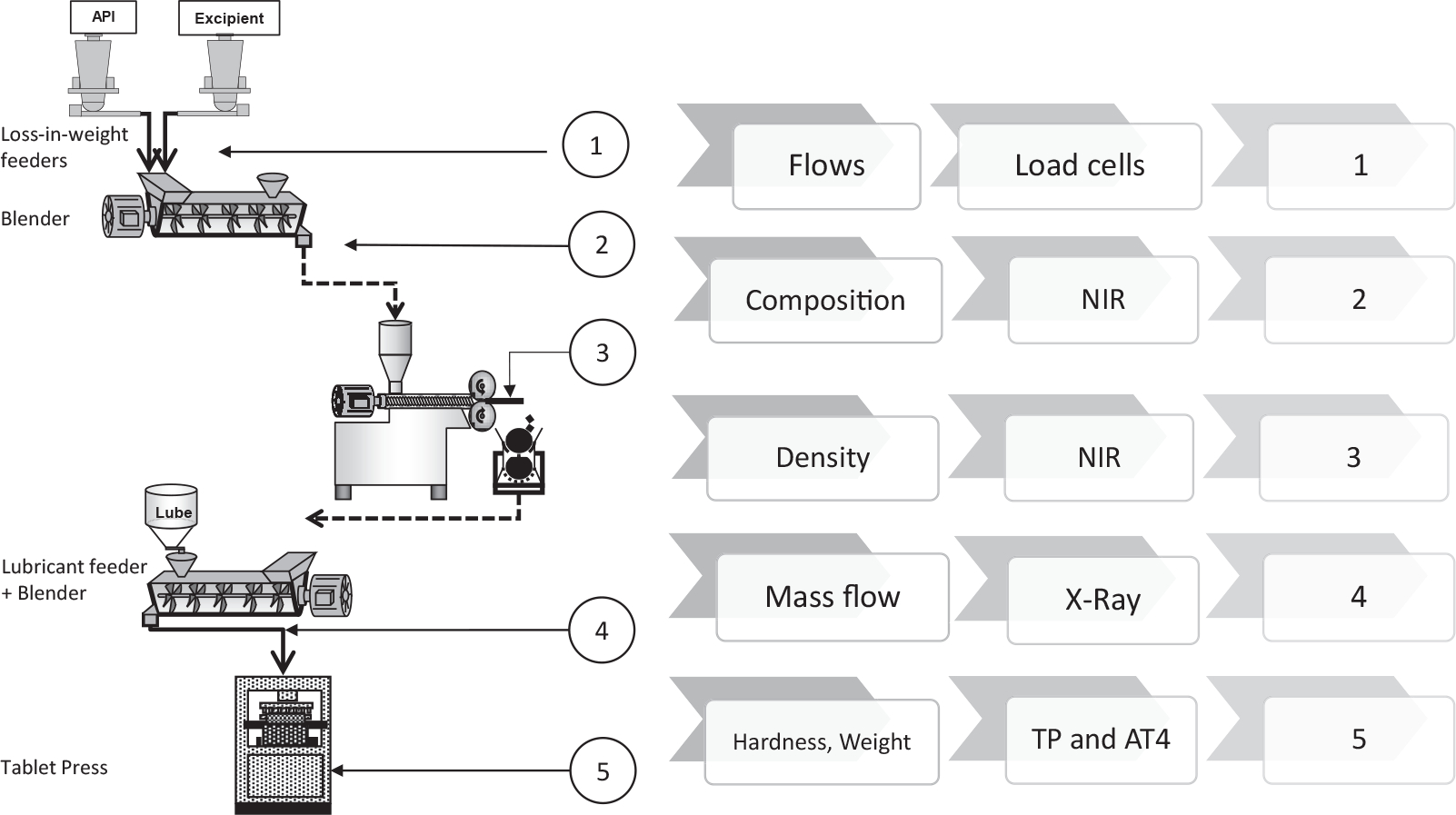
DC and DG continuous tableting line.
Material and Methods
Materials
APAP grade 0048 (Mallinckrodt Inc., Raleigh, NC) was used as the model API for both tableting lines. Microcrystalline Cellulose (FMC BioPolymer Corporation, Philadelphia, PA) grades Avicel PH 102 and PH 200 (MCC 102 and MCC 200, respectively), were used as the excipient. MCC200 was used for DC, while MCC102 was used in DG experiments. Silicon dioxide (SiO2), also known as Cab-O-Sil Untreated Fumed Silica (Cabot, Tuscola, IL), was employed as a model glidant only in the DC line.
Content Uniformity and Ribbon Density by NIR Method
In the DC tableting line, the APAP composition was measured at the exit of the first blender (xAPI,B1) and the exit of the second blender (xAPI,B2) using Control Development, Inc. (CDI) -256-1.7T1 NIR spectrometers, one located at each position, using wavelengths from 904 nm to 1687 nm.19 Both spectrometers used Solvias Turbido NIR probes and were positioned perpendicular to the powder flow. Partial least squares (PLS) models, with 2 principal components describing each model, were employed to relate the spectra and the APAP composition. Pretreatments for the raw spectra include a Savitzky-Golay filter, first derivative, and standard normal variate.17 For xAPI,B1, the calibration was done from 5% to 17% wt. APAP composition, established at an average flow of 10 kg/h with the rest of the mixture being MCC 200 and no lubricant or glidant added. For xAPI,B2, the calibration ranged from 5% to 15% wt. APAP composition, with 0.2% SiO2 and the rest being MCC 200, established at an average flow of 10 kg/h. The PLS models were developed using “Phi,” a latent variable toolbox in MATLAB.
In the DG tableting line, one of the CDI -256-1.7T1 NIR spectrometers was used to measure xAPI,B1. A PLS model with 2 principal components relates the spectra to the APAP composition. The calibration was done spanning a range of 5% to 15% wt. APAP composition, at an average flow of 10 kg/h with the rest of the mixture being MCC 102 and no lubricant or glidant. The second CDI-256-1.7T1 NIR spectrometer was used to measure the roller compacted ribbon density (ρRC). A PLS model with 2 principal components was developed to relate the raw NIR spectra to the ribbon density in the range of 0.9 to 1.15 g/cc with a root mean squared error of 0.026 g/cc.
X-Ray and Balance Flow Rate Measurements
In the DC tableting line studies, the X-ray was used to measure the flow at the exit of the second blender (Fout,B2), while the Mettler Toledo balance was used for measuring the tablet mass flow rate (Fout,TP). The tablet weight measurement generated by the scale was connected to the distributed control system using OPC data access, with a raw measurement frequency of 200 ms and a moving time window averaging corresponding to roughly 100 tablets to estimate the first-order derivative for the tablet production rate and tablet weight. With the DG tableting line studies, 2 alternative configurations were investigated (see section SSDR-M for the Continuous Tableting Processes). In the first configuration of the DG line, the tablet press was not used, and thus, the balance was placed below the X-ray sensor (Fout,B2,bal) to measure the granule flow. In the second configuration of the DG line, the balance was located at the exit of the tablet press to measure the tablet flow (Fout,TP).
Sotax AT4 Tablet Tester
The Sotax AT4 tablet tester provides at-line measurements of the weight (±0.1 mg), thickness (±0.01 mm), diameter (±0.01 mm), and hardness (±1 N) of the tablets produced.20 Of these measurements, the hardness test is a destructive test. The at-line measurements provide a method for validating the reconciled values. The tablets are transported pneumatically from the tablet press exit to the Sotax AT4 bowl and from there to the measurement stations. Ten tablets sampled in intervals of approximately 3 min are measured for the tablet properties. Furthermore, the tester has a self-cleaning step between samples that adds delay time. Therefore, the sampling time was set to every 6 min for automated sampling and testing during the run.
System Integration and Data Extraction
The systematic integration and data handling from multiple sources such as equipment control systems and PAT tools are important aspects in the implementation of DR and GED. An Emerson DeltaV 13.3 distributed control system is used to integrate process equipment and develop the automation platform in our pilot plant facility. A modular network architecture is adopted following ISA 95 and DeltaV Security Manual recommendations. The PLCs built into the LIW feeders and the variable frequency drive for the blender communicate using a Profibus network, while the Allen Bradley controller on the Alexanderwerk WP120 roller compactor equipment and a Yaskawa controller on the Natoli BLP-16 tablet press communicate with DeltaV via a VIM card, configured using VIMNet explorer. Control modules for the process equipment are implemented in the DeltaV system using Control Studio.
During an experimental campaign, the spectra from the NIR sensors are acquired using Spec32 and analyzed using MATLAB 2017b in a Dell Latitude E7470 laptop with an i7 processor and 8 GB RAM. The X-ray sensor measurements are obtained in a proprietary En’Urga Inc. system and communicated via ethernet IP to MAT-LAB2015b installed in the DeltaV Application Station. The real-time inline sensor data from MATLAB are transferred to the DeltaV OPC server using KEPServerEX and Kepware LinkMaster. The connections to the analyzers and OPC communication setup in MATLAB required access to the Communication Systems Toolbox and OPC Toolbox, respectively. The MATLAB licenses are accessed in the PAT computer and DeltaV Application Station from the Purdue network using appropriate configurations for firewalls and IT network in the pilot plant. The Sotax AT4 data is extracted directly from the proprietary TabStatPro software. Relevant process variables are recorded and extracted from the DeltaV historian, with a one second interpolation in reporting of raw data. The DR analysis in this study is executed later.
SSDR-M for the Continuous Tableting Processes
SSDR-M for the DC Line End-to-End Operation
The DC continuous tableting line was studied from the feeders to the tablet press running at steady state. It is assumed there is no material loss or accumulation in the hopper level as in the study by Moreno et al.7 Figure 2 shows the block diagram for the DC tableting line in end-to-end operation. This system is the first example (E1) employed to show the SSDR-M framework in this work.
Figure 2.
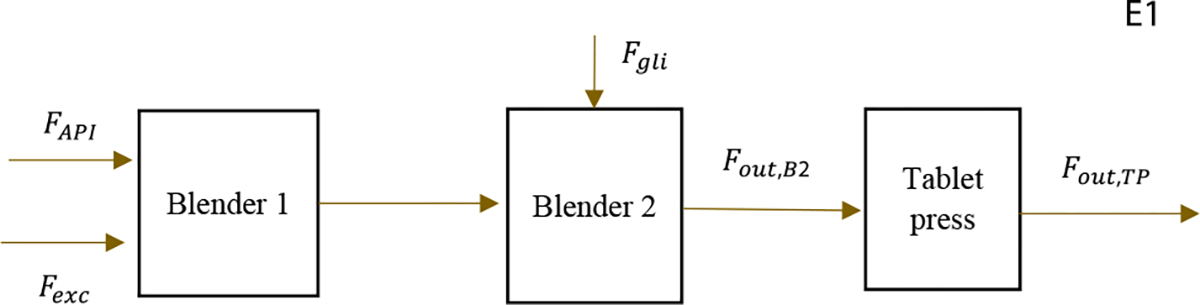
DC tableting line.
In a typical DR application, as many of the flow rates as possible are measured. In this case, only some of the flows’ measurements are available, namely, the API flow, the excipient flow, the glidant flow, the powder flow at the exit of the second blender, and the tablet flow at the exit of the tablet press. For the other streams, other physical properties relating powder flow through mechanistic equations were used. The API composition was measured at the exits of the first and second blender. Measurements for MCF and TS are obtained from the tablet press system. In total, this system involves 9 real-time measurements, with a sampling time of one second each in the DeltaV continuous historian. For the APAP and excipient flow rates, a moving average window of 7s was used for the raw measurements, while the remaining flow rate and the composition measurements had a moving average window of 10s.
At steady state, the API and excipient flows have to be equal to the flow at the exit of the first blender. Equation 8 represents the mass balance in the first blender, where the exit flow is unmeasured, but the API composition is measured.
| (8) |
Equation 9 represents the mass balance in the second blender, where the summation of the components flows is equal to the flow at the exit of the second blender.
| (9) |
Equation 10 consists of the material balance for the API component in the second blender. Equation 11 is used to estimate the glidant composition in the system.
| (10) |
| (11) |
The feeder and blender system was previously investigated in the study by Moreno et al.7 In this work, the study was expanded to include the tablet press. Equation 12 relates the MCF to the in-die relative density of the tablet.
| (12) |
This equation, which is derived from the Kawakita model, represents the behavior of powder under compaction pressure.21 Here, parameter a represents the relative volume decrease, 1/b represents the pressure that is needed to get a volume decrease of a/2, ρc is the critical relative density, and t is the tablet thickness. These parameters were estimated from prior design experiments, reported in the study by Su et al.,20 and are given by a = 0.7911, 1/b = 14.15 MPa, and ρc = 0.2499. The model has a coefficient of determination (R2) of 99.2%.
The flow at the exit of the second blender is equal to the tablet press inlet flow, assuming no loss of material in the conveying lines. The mass balance on the tablet press is represented in Equation 13.
| (13) |
Equation 14 indicates that the tablet flow material balance as a function of tablet production rate. Here, the tablet weight is an unmeasured variable; however, it is observable through the SSDR-M model. The tablet hardness is also an observable variable in the system, through the use of Equation 15.22,23
| (14) |
| (15) |
The parameter estimates for this model were generated in previous studies in our laboratory using the same tablet press,20 as described in Appendix A2. The tensile strength at zero porosity (σmax) is 9.976 MPa, the powder true density (ρt) was 1.52 g/cc, and the critical relative density at which the compact begins to exhibit strength (ρcσ) is 0.5875. The model R2 is 98.9%. These parameters were estimated at the given composition of 10% APAP, 89.8% MCC 200%, and 0.2% SiO2. For , randomly sampled tablets were measured in the AT4, and the averaged value is used as the parameter, following little or no observed variation in the measurement (less than 0.6% relative standard deviation [RSD]).
For this system, the initial number of independent equations is equal to 5, and the initial number of measurements is 9. Table 1 shows the measurement set-point (SP) or normal operating conditions (NOCs) employed in the DC tableting line. This table also shows the covariance used for each reconciled measurement and a summary of the variables classification from the SSDR-M perspective. The values were determined from a priori information of the DC tableting line NOC. Once the RSD of each variable is evaluated at the selected NOC, the values were used in establishing the covariance matrix. A 95% confidence interval was used.
Table 1.
NOC and Covariance of the DG Tableting Line
| Variable | Equipment | Set Point | Q(%) | Type of Variable |
|---|---|---|---|---|
|
| ||||
| FAPI (kg/h) | Load cells | 1 | 1.6 | Measured |
| Fexc (kg/h) | Load cells | 9 | 0.3 | Measured |
| XAPI,B1 (% wt) | CDI-NIR | 10 | 7.1 | Measureda |
| Fgli (g/h) | Load cells | 20 | 15.0 | Measured |
| XAPI,B2 (% wt.) | CDI-NIR | 9.9 | 7.1 | Measureda |
| Xgli (% wt.) | – | 0.2 | – | Unmeasureda |
| Fout,B2 (kg/h) | Load cells | 10.02 | 7.0 | Measureda |
| TS (rpm) | Tablet Press | 36 | 1.4 | Measured |
| MCF (kN) | Tablet Press | 7.8 | 5.0 | Measureda |
| Fout,TP (kg/h) | Balance | 10.02 | 7.0 | Measureda |
| W (mg) | Sotax AT4 | 293 | – | Unmeasureda.b |
| H(N) | Sotax AT4 | 370 | – | Unmeasureda,b |
These variables do not have a set point; therefore, the table shows NOC.
There are at-line measurements available for these variables.
SSDR-M for the DG Line
SSDR-M From the Feeders to the Roller Compactor
For the DG tableting line (Fig. 3), the powder flow from the exit of the first blender feeds into the roller compactor, where the blend is compressed by the rolls into a compacted ribbon. Equation 8 is the mass balance for the first blender. Equation 16 assumes that all the powder, entering the roller compactor, is compacted to a given density (ρRC). Therefore, at the point of compaction, the ribbon thickness is assumed to be equal to the roll gap, and the ribbon width is the width of the rolls. The ribbon flow can be estimated from its volume, density, and roll speed.
Figure 3.
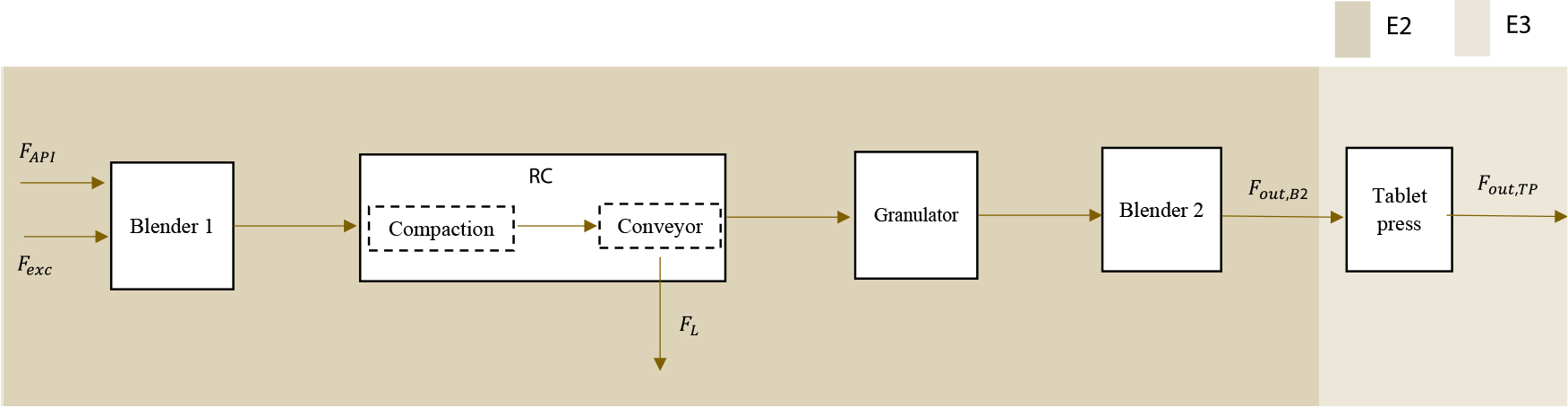
DG tableting line.
| (16) |
A mechanistic model, based on the modified Johanson’s rolling theory,24,25 is used to represent the roller compaction process.17 Equations 17 through 19 relates the ribbon density to the hydraulic pressure (PH), material properties, and equipment geometry.
| (17) |
and
| (18) |
where
| (19) |
where A is the compact surface area parameter, and K is an experimental constant related to the material compressibility.
After compaction, the NIR sensor is used to measure the density of the compacted ribbon. Owing to a modified setup in the roller compactor to accommodate the NIR sensor, loss of ribbon flakes is observed, and this loss (FL) is treated as an unmeasured but observable variable. In the granulator itself, the material loss is negligible, and granules are fed directly to the second blender. Equation 20 represents the mass balance in roller compactor to blender 2, considering the material loss.
| (20) |
In the second example (E2), the material flow proceeds from the feeders to blender 2 of the DG tableting line. The flow rate at the exit of the second blender is measured using the X-ray sensor, and thus, a mass balance equation which makes the (Fout,N2,Bal) measurement redundant is added to the process model. Equation 21 states that the flow measurement from the X-ray should be equal to the flow measured by the electronic weighing balance. Not implementing the electronic weighing balance would have resulted in the flow at the exit of the second blender as a nonredundant measurement, which impacts the reconciliation solution. Initially, E2 has 7 measurements and 4 degrees of freedom.
| (21) |
Table 2 shows the SP at NOC and the covariance used for the reconciled variables. The covariance used for the measurements was determined from a priori information reported in the Appendix. In the case of the roll gap, it was based on the variance of the ribbon thickness. The roll diameter, the roll width, and the roll pressure are considered to be fixed parameters in this process, due to their low variability.
Table 2.
NOC and Covariance of the DG Tableting Line
| Variable | Equipment | Q(%) |
Type of Variable |
|||
|---|---|---|---|---|---|---|
| SP | E2 | E3 | E2 | E3 | ||
|
| ||||||
| FAPI (kg/h) | Load cells | 1 | 2.0 | 1.60 | Measured | Measured |
| Fexc (kg/h) | Load cells | 9 | 0.3 | 0.30 | Measured | Measured |
| XAPI,B1 (% wt) | CDI-NIR | 10 | 7.0 | 7.10 | Measureda | Measureda |
| S (mm) | RC | 1.8 | 10.5 | 10.41 | Measureda | Measureda |
| ρR (g/CC) | CDI-NIR | 1.06 | 2.0 | 1.73 | Measureda | Measureda |
| Fout,B2 (kg/h) | Load cells | 9 | 8.0 | 7.50 | Measureda | Measureda |
| Fout,B2,bal (kg/h) | Load cells | 9 | 8.0 | – | Measureda | NA |
| TS (rpm) | Tablet Press | 29.7 | – | 1.40 | NA | Measured |
| MCF (kN) | Tablet Press | 11 | – | 5.00 | NA | Measureda |
| Fout,TP (kg/h) | Balance | 9 | – | 5.00 | NA | Measureda |
| W (mg) | Sotax AT4 | 318 | – | 3 | NA | Unmeasureda.b |
| H(N) | Sotax AT4 | 230 | – | 8 | NA | Unmeasureda,b |
These variables do not have a set point; therefore, the table shows NOC.
There are at-line measurements available for these variables.
SSDR-M for the DG Tableting Line, End-to-End
The third example (E3) involves the end-to-end DG tableting line. Equations 13–15 were used to represent the tablet press process. However, the parameters had to be reestimated because the physical properties of the granule stream are not the same as the physical properties of the powder flow used in DC. Common empirical models relevant for the tablet press include the Shapiro equation, the Heckel equation, and the Kawakita equation.26,27 These models are used according to the relative density of the material. The Shapiro equation can describe the compaction curve at small relative densities. The Heckel equation is suitable for describing the compaction curve at small to moderate relative densities. The Kawakita equation describes the compaction curve at large relative densities. Nordström et al.28 studied the Kawakita parameter estimation for granules created via wet granulation. A power law model can also be used to relate the force employed with the tablet density.26,27
The Kawakita equation was chosen for this study as it is a reduced first-order model that focuses on low porosity, high relative density tablets. This model is suitable for the SSDR framework because it is not necessary to predict the pressure for a wide range of relative densities; rather it suffices in this application to predict the pressure at certain relative density for the manufacturing processes described in section Experimental Systems. Monte Carlo sampling and MATLAB are used to estimate the Kawakita parameters for the granular material as a = 1.0, b = 0.00205 MPa−1, and ρc = 0.6452. The model has a coefficient of determination (R2) of 88.24%. The σmax is 5.44 MPa, and the ρcσ is 0.6743. The model R2 is 81.01%. These parameters were estimated at the given composition of 10% APAP and 90% MCC 102.
For E3, 4 scenarios were studied using SSDR-M, and the results were compared with the measurement performance. The first scenario is the current SSDR-M solution. The second scenario considers the bias correction of the API composition measurement at the exit of the first blender. For this scenario, the raw spectra of the CDI-NIR were reanalyzed with a new calibrated PLS model offline to correct the measurement bias observed in the real-time measurement. The third scenario involves an improvement in the calibration of the X-ray to measure the flow accurately. A correction for this measurement, after the runs are executed, is not possible. However, the NOC of E2 was used to obtain an estimate on the flow correction to see its effects in the SSDR-M performance. The last scenario covers all measurements corrected for the SDDR-M solution. The initial number of measurements for this system is 9, and the system involves 6 independent equations.
Table 2 shows the SP or NOC and the covariances used for the reconciled variables in E3. The confidence interval used was of 95%.
Results and Discussion
SSDR-M for the DC Line End-to-End Operation
The SSDR-M results for E1 are presented in Figure 4. In Figure 4a, the left-hand side plots show the measurements and reconciled values for the APAP flow, excipient flow, and APAP composition at the exit of the first blender. The initial SSDR-M result is the reconciled solution obtained when all measurements are used. The final SSDR-M solution is the result obtained when the measurements that exhibited a gross error are treated as unmeasured and estimated using mechanistic model and the reconciled values. In this case, the reconciled values are the remaining gross error-free measurements in the process. The measurements in gross error are reestimated using the process model evaluated using the reconciled values of the remaining variables. The right-hand side plots are the result of the measurement test, which indicate the utility and health of the sensor for process monitoring at the instant. The value of one indicated that the measurement had no gross error and is thus considered to be good and is included in the reconciliation; while, if the value was zero, then that measurement had a gross error, was excluded from reconciliation, and computed as an unmeasured variable using the model. The sensors could be investigated to determine the root cause of the error, which might be probe fouling, bias, or communication error. However, that fault diagnosis step is beyond the scope of this manuscript. In the trajectories shown in Figure 4a, no gross error was detected.
Figure 4.
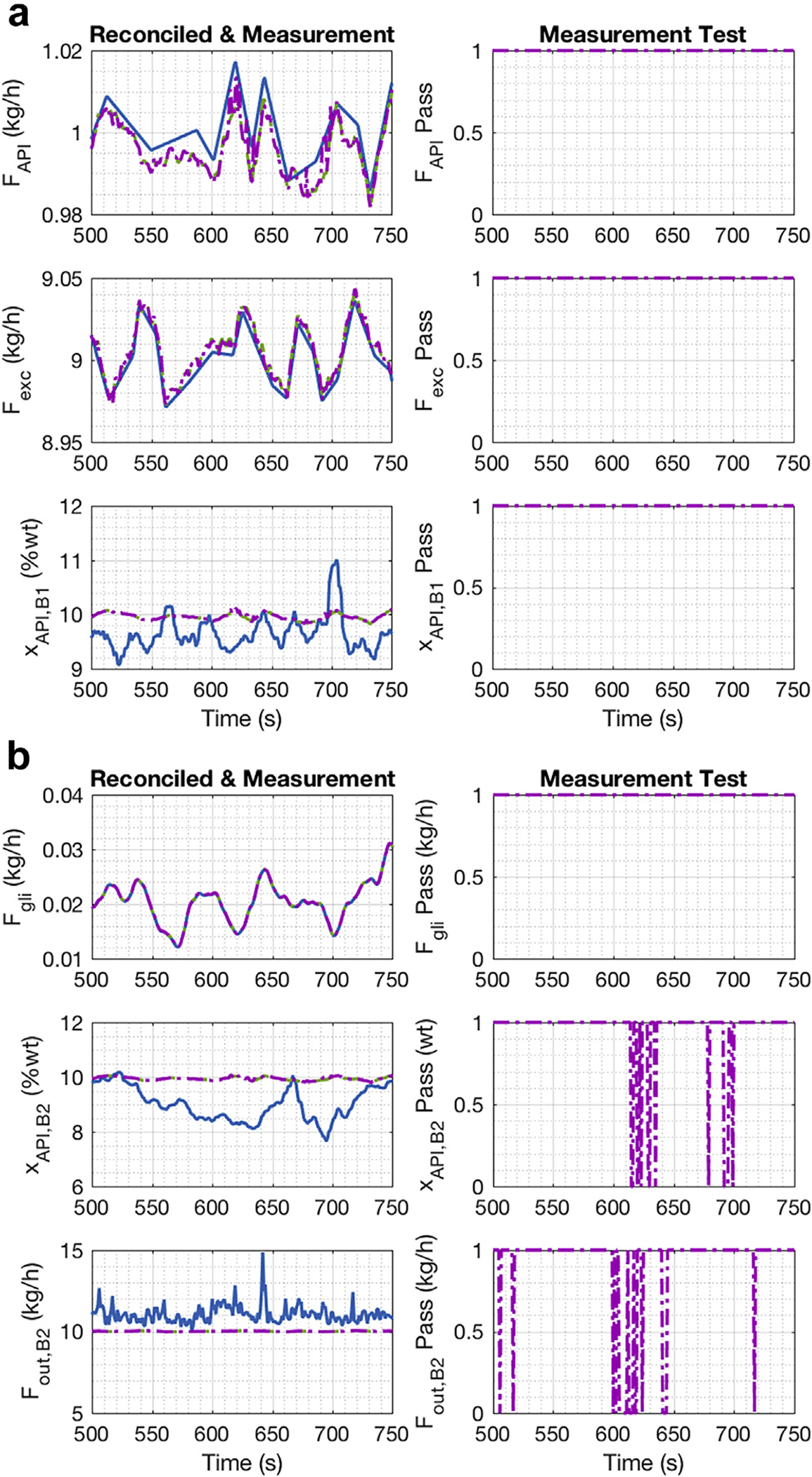
E1 DC reconciled and measurement values, no accumulation in the hopper: (a) Feeder 1, Feeder 2 to Blender 1; (b) Glidant Feeder to Blender 2.
In Figure 4b, the left-hand side plots show the measurements and reconciled values of the glidant flow, the APAP composition, and flow at the exit of the second blender. In the Figure 4b right-hand side plots, the measurement tests results are shown. The APAP composition at the exit of the second blender had an intermittent gross error detected around 600s to 700s. The flow measurement at the exit of the second blender had a small bias, so a gross error was identified in that measurement across the run.
Figure 5 shows the measured and unmeasured variable associated with the tablet press. The left-hand plots in Figure 5a show the measurements and reconciled values for the turret speed, the main compression force, and the tablet flow. The right-hand portion of Figure 5a displays the measurement test status as a binary variable, where a value of one indicates that the measurement did not have a gross error and value of zero meant that it did. The gross error was detected in the tablet flow because of the disturbance caused by the manual replacement of the container used to collect tablets on Mettler Toledo balance.
Figure 5.
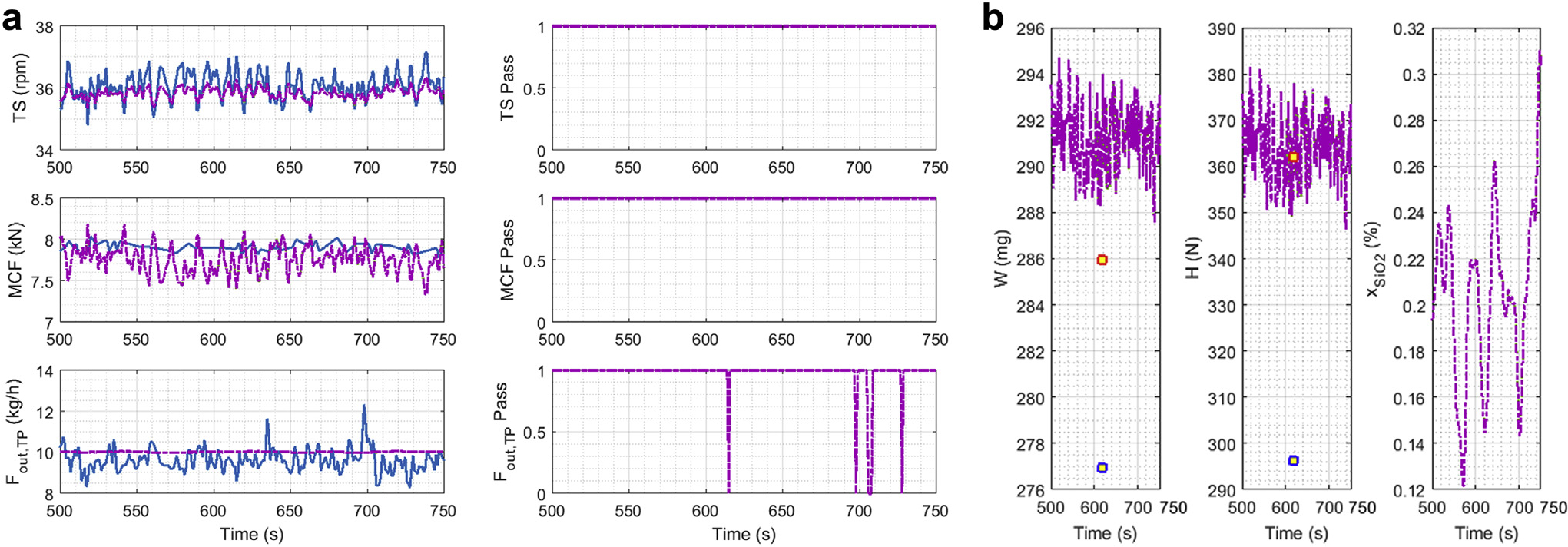
E1 DC data reconciliation results, no accumulation in the hopper: (a) Tablet Press; (b) unmeasured variables.
Figure 5b shows the time series of the unmeasured variables over the run. For the tablet weight and hardness, there are at-line measurements available, and the sample average was used as the real value. To demonstrate the value of the SSDR-M model, the tablet flow computed from the model was used to estimate the weight and hardness at the same point in time at which the at-line measurements were recorded on the Sotax. The at-line measurements are indicated with a red dot, filled with yellow. The weight and hardness equations were used to evaluate these variables using the balance flow and marked with the blue dot. The average error of estimation (AEE) was used as the performance indicator, which is a dimensional quantity.12 The AEE between the measurement and the actual value is 0.0315 for the tablet weight and 0.182 for the tablet hardness. On the other hand, the AEE between the reconciled value and the actual value is 0.0242 for tablet weight and 0.0282 for tablet hardness, thus indicating that the AEE is reduced by using the SSDR-M methodology.
The GT results for the DC tableting line over the time interval of the run are shown in Figure 6. It is important to note that the selected limit for the GT, χ2, is a function of the number of linear-independent equations (I). The number of linearly independent equations depends on the number of measured and unmeasured variables. If gross errors are detected, then depending on the measurement test results, variables that initially were considered measured variables and failed the measurement test would be classified as unmeasured. As a consequence, redundancy would be reduced and the test statistic χ2 changed, making the limit for the GT stricter. The left-hand side shows the GT value with its limit (red line). The initial solution for SSDR-M, shown in green, is the result of the Equation 1 value when the reconciliation is based in all measurements, regardless of if there are gross errors present. The purple line is the objective function value, once the gross errors are detected and treated as unmeasured variables. The right-hand side shows the binary variable result based on the final GT value (purple line) where one means pass and zero loss of redundancy. During this interval, the initial GT was violated at a different moment between 600s to 650s and 670s to 700s (see Fig. 6 left-hand side). Nevertheless, there was still enough measurements to allow reconciliation, and the final GT always passes since the GT binary variable was equal to one in this period (see the purple line in the left-hand side and its binary variable in the right-hand side).
Figure 6.
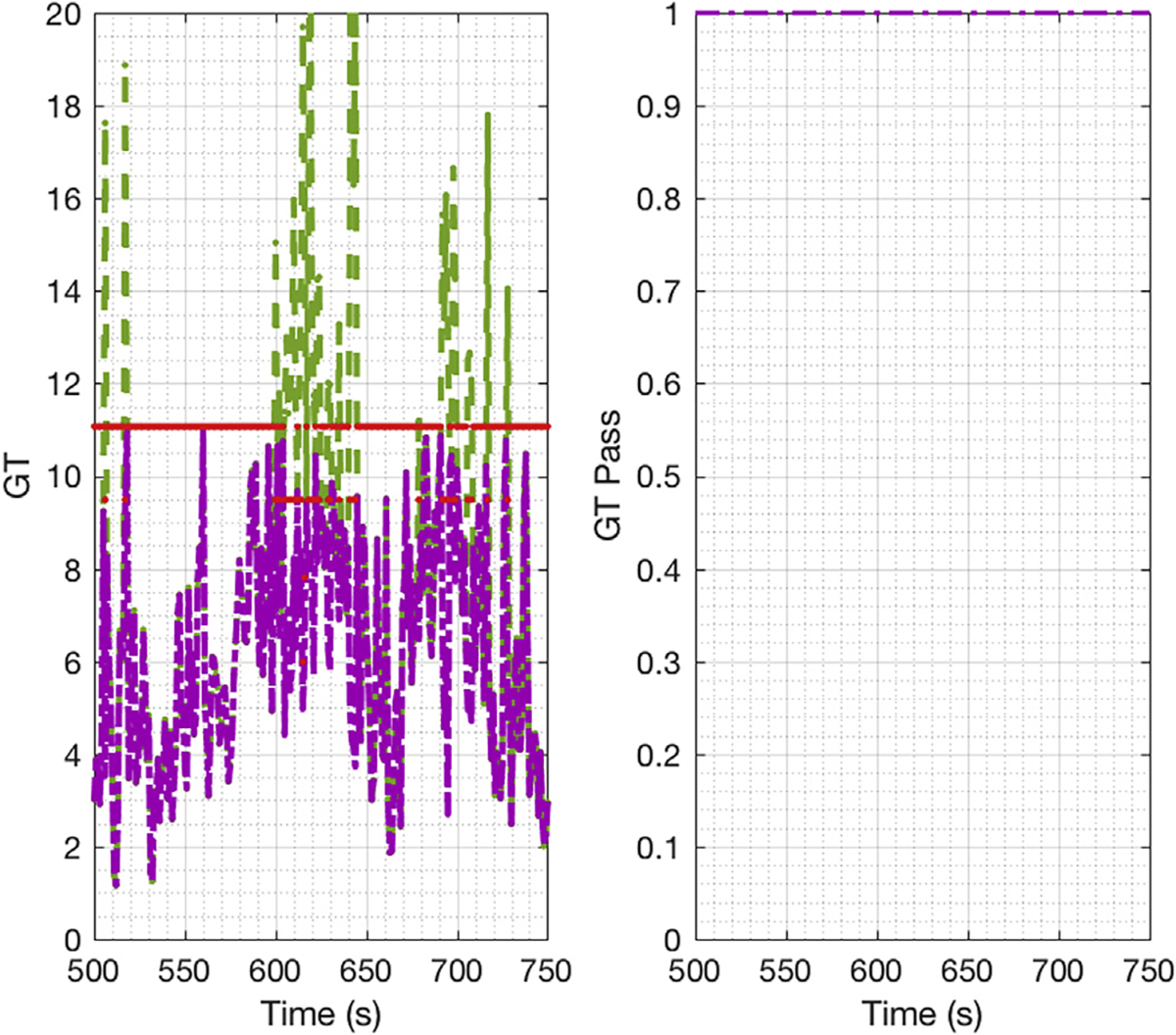
E1 DC tableting line global test.
SSDR-M for the DG Line
E2, Feeders to the Exit of the Second Blender Subsystem
Figure 7 shows the reconciliation results from the feeders to the roller compactor. The APAP flow, the excipient flow, and composition at the exit of the first blender are included in Figure 7a. The flows do not involve measurement errors. However, the APAP composition at the exit of the first blender has a bias, and thus, a measurement error is indicated across the run. However, the reconciled composition obtained when that variable is treated as unmeasured corrects that bias. Figure 7b shows the ribbon density and measured roll gap: these measurements have no measurement errors, but they have a measurement bias.
Figure 7.
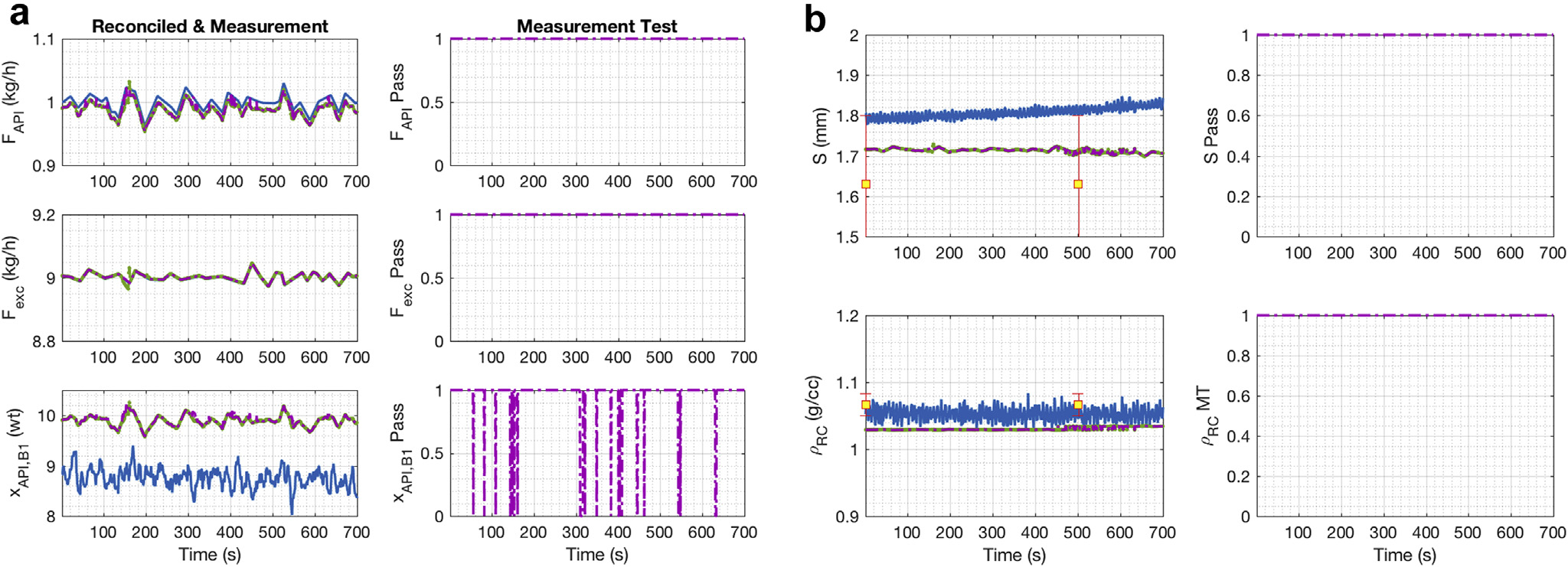
E2 DG reconciled and measurement values: (a) Feeder 1 and Feeder 2 to Blender 1; (b) RC.
During the run, several ribbon samples were taken to compare the ribbon density and ribbon thickness to the reconciled results. It is important to note that these sample measurements were not executed at-line. Rather, the ribbon density was measured the next day using GeoPyc (Micromeritics), while the ribbon thickness was measured during the run with a caliper. The interval of time, in which the sample was taken, is known but not the exact time. Both offline measurements were plotted at random points (see red dot filled with yellow) throughout the experiment to provide a comparison of the actual value of the variables. It should be noted that the ribbon thickness has significant variability because it is not uniform across the width. One side of the ribbon is thicker than the other side; the ribbon has a trapezoidal shape instead of a rectangular one. Therefore, the assumption that the roll gap is equal to the ribbon thickness is only valid for the largest side of the roller compacted ribbon. As shown in this figure, the roll gap reconciled value is closer to the average ribbon density of the run. The measurement test did not trigger for the roll gap because the drift in the measurement was within the standard deviation of the ribbon thickness used in the SSDR-M algorithm. The offline ribbon density measurements indicate that the real-time measurement and the SSDR-M results are without the presence of gross errors, thereby indicating satisfactory sensor health. However, independent at-line measurements would be desirable to make a proper comparison of AEE values.
The SSDR-M reconciled value for the roll gap is underestimated, but it is closer to the ribbon thickness average obtained with offline measurements. Since the ribbon in actuality has a trapezoidal shape, the assumption that the roll gap and ribbon thickness are equal at compaction is an approximation that needs improvement. At-line measurement of the ribbon thickness and offline measurement of the ribbon density confirm that the roll gap and ribbon density real-time measurements are within acceptable statistical limits, although a bias is observed in the raw measurements and it is not flagged by the GT.
Figure 8a shows the measurements and reconciled values of the flow at the exit of the second blender. Note that the flow is measured both via the X-ray as well the Metter Toledo balance. After passage through the X-ray, the powder flow was collected in a container on the Mettler Toledo balance. Every time the container was changed, a disturbance was created, and a measurement error was detected. It is interesting to note that during the change of container, the X-ray sensor was also disturbed, and thus for a few seconds, both sensors registered measurement errors and redundancy was lost. Figure 8b shows the GT results. A gross error was detected sporadically between 100s to 200s and 300s to 550s. The measurement test was used to identify the measurement with the gross error. Once the gross error was detected, that measurement was considered unmeasured. In this case, the gross error was caused by the bias in the composition measurement at the exit of the first blender (see Fig. 7a.) and the container change for the mass flow at the exit of the second blender (see Fig. 8a). Figure 8b also shows that the GT binary variable was always one. Therefore, during this period of time, redundancy was not lost in the system.
Figure 8.
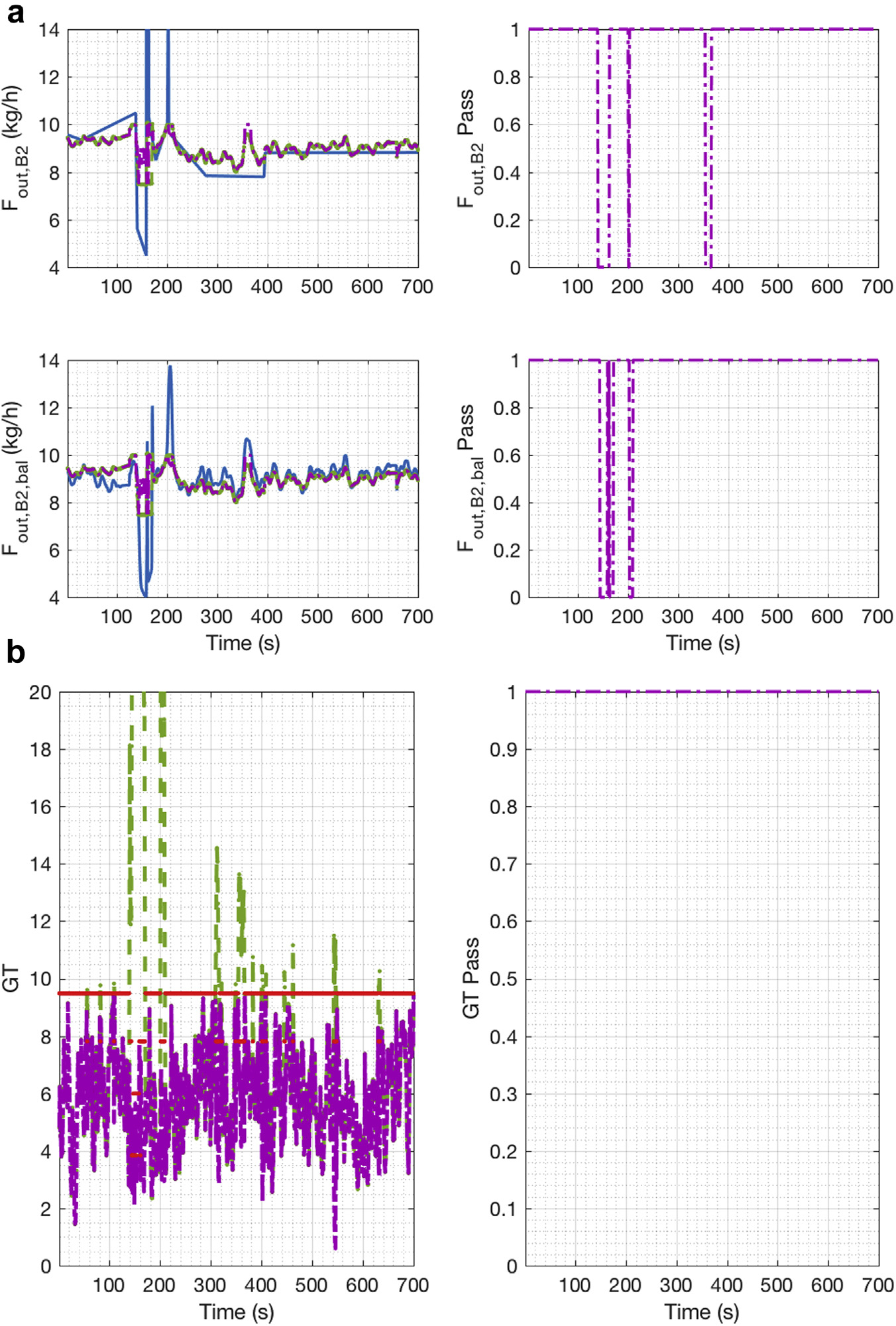
E2 DG reconciled and measurement values: (a) flow at the exit of blender 2; (b) global test.
E3: End-to-End Operation
This section reports on the DG tableting line run conducted end-to-end, including the tablet press. The results shown are for a period where the GT passed uninterrupted, but measurement errors were detected. In contrast to the previous run, the ribbon was not constrained from fluctuating distance from the CDI-NIR probe when the ribbon hit the breaker; as a result, there were some disturbances recorded in the ribbon density measurement. Figure 9 shows the plots for the 6 measurements and the reconciliation results from the feeders to the second blender in the DG tableting line. As shown in Figure 9a, a bias was detected for the APAP composition at the exit of the first blender, and thus, a measurement error was detected across the run. Figure 9b indicates intermittent deviations in the ribbon density measurement caused by ribbon position fluctuations, and thus, a measurement error was detected at those points. The roll gap also shows a small drift over time. One disadvantage of the measurement test is that it can misidentify the location of the gross error because it is based on a linearized estimate. In this run, the flow rate at the exit of the second blender showed a measurement drift over time.
Figure 9.
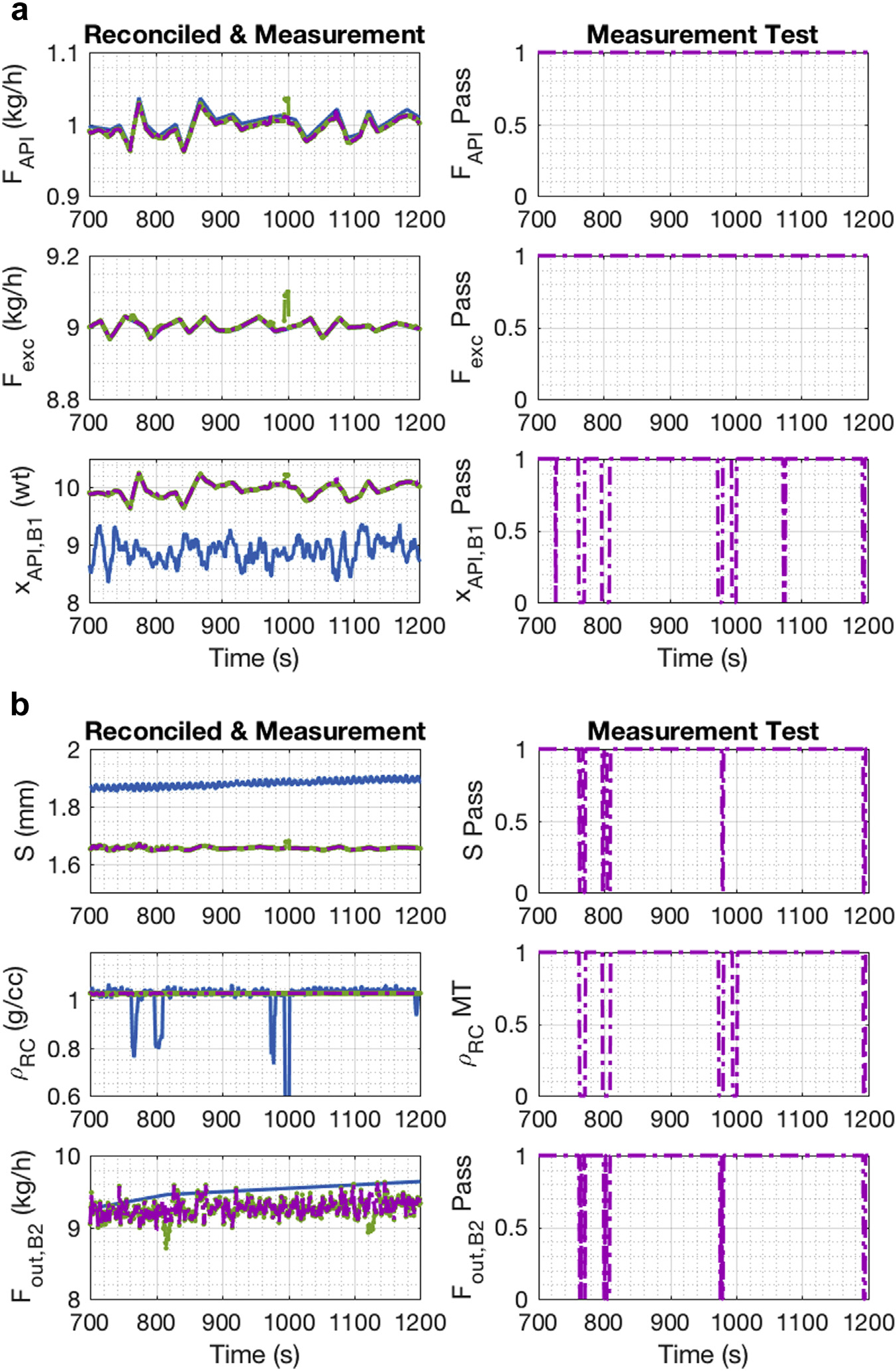
E3 DG reconciled and measurement values: (a) Feeder 1 and Feeder 2 to Blender 1; (b) RC.
Figure 10a shows the measurements and reconciled values for the 3 tablet press variables, turret speed, main compression force, and tablet mass flow rate. A measurement error was only detected in the tablet press flow, again caused by the disturbance to the balance from the changing of the container or by the removal of tablets separated for use by the Sotax AT4. Figure 10b includes the unmeasured variables (i.e., material loss in the RC, the tablet weight, and tablet hardness) of the system. The estimated material loss in the system ranges from 0.5 kg/h to 1 kg/h. For the tablet weight and hardness, at-line measurements were acquired. The red dot filled with yellow represents the at-line measurement from the Sotax equipment; these measurements were considered to be the real value for those variables. The blue dot is based on the balance flow measurement (based on M), and Equations 14 and 15 were used to estimate them.
Figure 10.
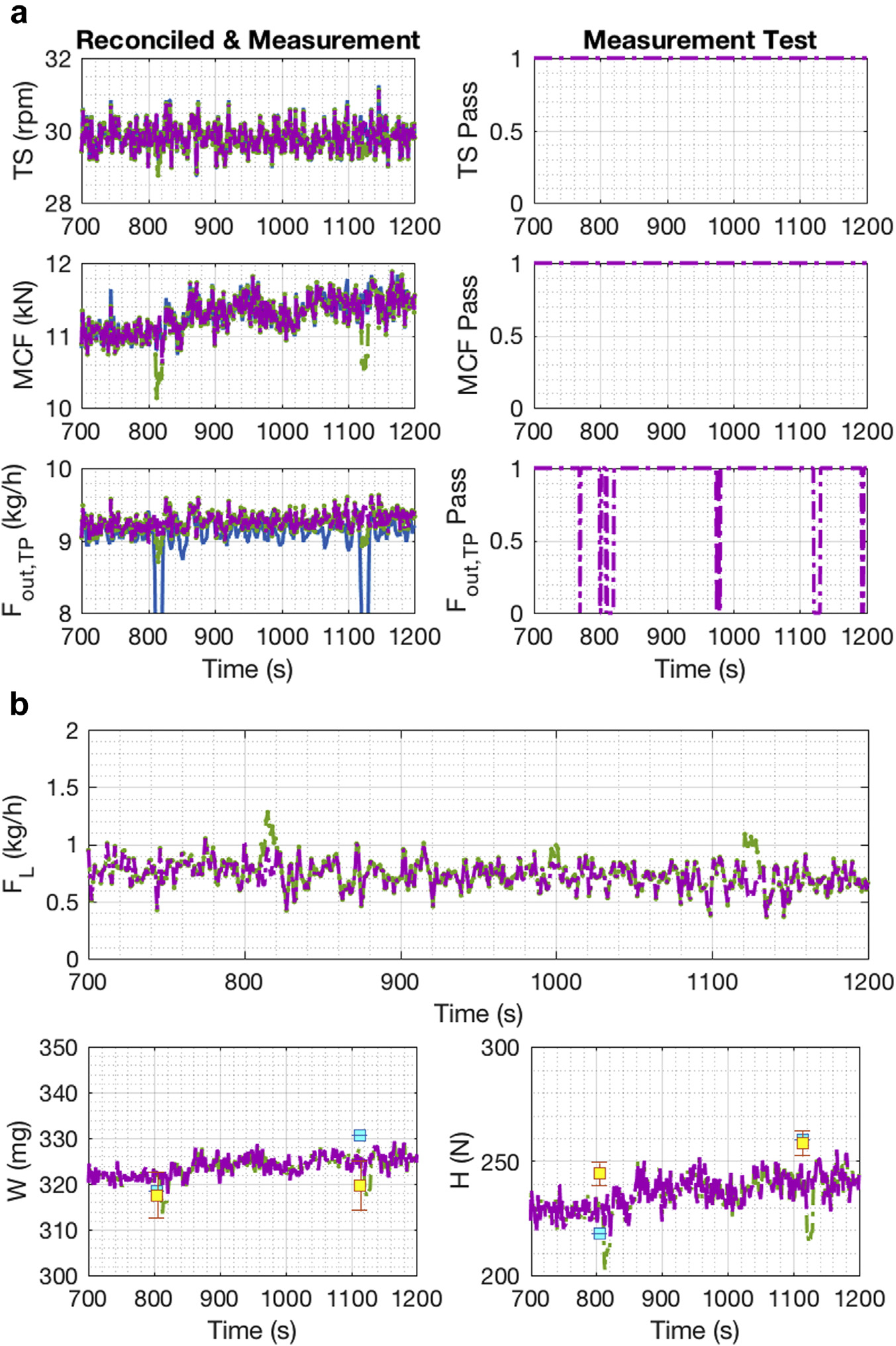
E3 DG reconciled and measurement values: (a) Tablet Press; (b) unmeasured variables.
Figure 11 is the GTs results for the end-to-end results. If a gross error was detected, that measurement was treated as unmeasured. Thus, the number of linear-independent equations changed and the limit for the GT as well. This figure proves that during the selected period, the GT passed and the system was redundant, except at 979s-980s and 1193s-1195s. If redundancy is lost, the SSDR-M estimation is distorted, and the measurement will have to be taken as the process state instead of the reconciled values.
Figure 11.
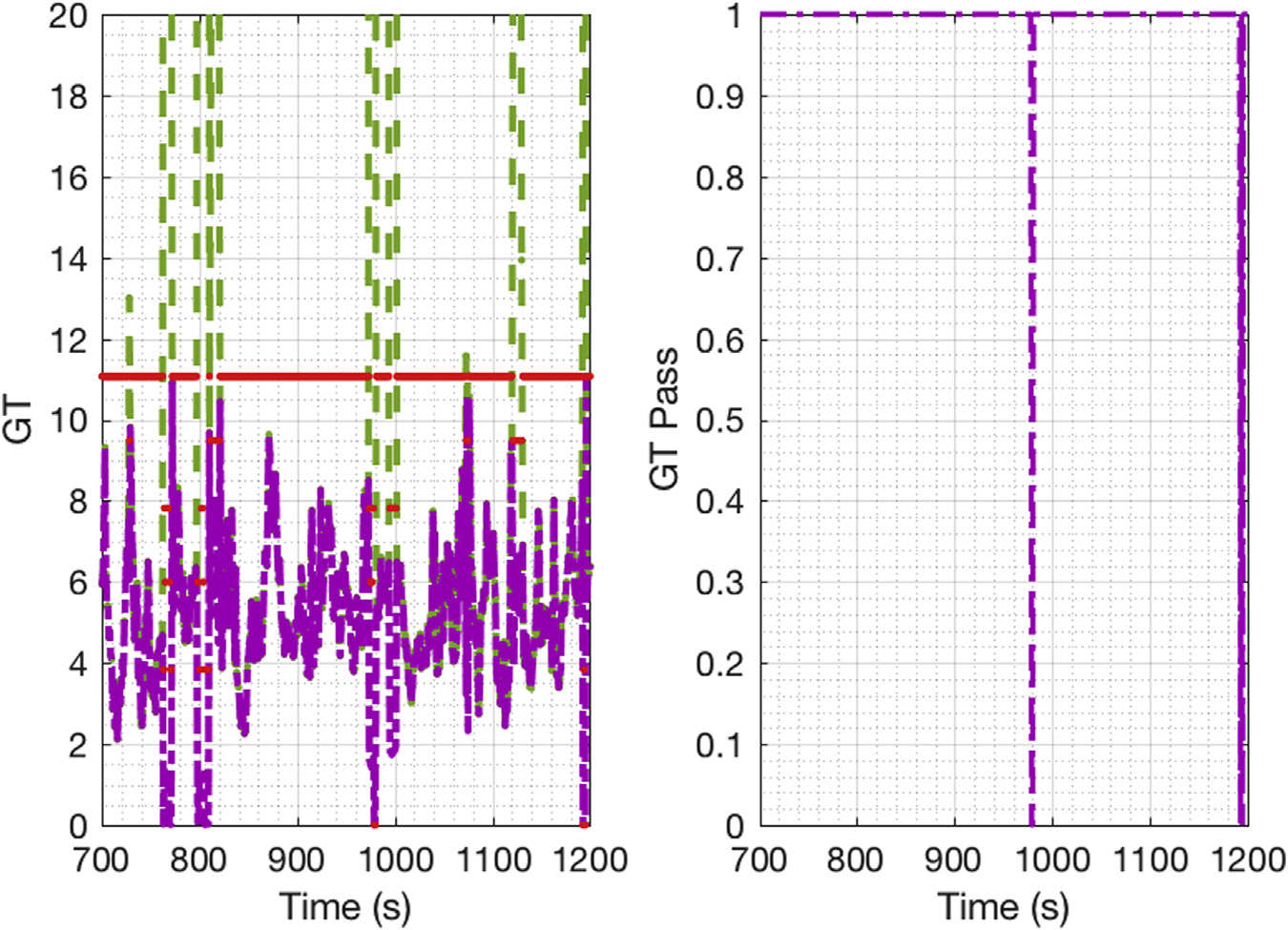
The global test for the end-to-end DG tableting line.
Table 3 shows the mean and RSD of the measurements, the current SSDR-M solution, the SSDR-M solution with the corrected APAP composition at the exit of the first blender, the SSDR-M solution with the corrected flow measurement at the exit of the second blender, and the ideal SSDR-M, with all measurements corrected (see section SSDR-M for the DG Line for cases details). If RSD for the current measurement is compared with the RSD of the original SSDR-M results, it can be seen that the variability for most variables was reduced. If the measurements are improved, such as correcting the PLS model for the APAP composition or reducing the bias of the flow rate, the RSD can be reduced even further. In the resulting ideal SSDR-M scenario, improvements are achieved in 7 of the 9 variables. However, the difference between SSDR-M and ideal SSDR-M is marginal. The importance of maintaining the sensors and correcting bias is to retain redundancy. Reconciliation of measured variables requires redundancy in the corresponding measurements.
Table 3.
Measured Variable Estimates After SSDR-M and GED
| Variable | NOC |
SSDR-M |
Corrected XAPI,B1 |
Corrected Fout, B2 |
Ideal SSDR-M |
|||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | RSD | Mean | RSD | Mean | RSD | Mean | RSD | Mean | RSD | |
|
| ||||||||||
| FAPI (kg/h) | 1.0 | 1.3 | 1.0 | 1.25 | 1.0 | 1.25 | 1.0 | 1.25 | 1.0 | 1.25 |
| Fexc (kg/h) | 9.0 | 0.1 | 9.0 | 0.14 | 9.0 | 0.14 | 9.0 | 0.14 | 9.0 | 0.14 |
| XAPI,B1 (% wt.) | 8.9 | 2.3 | 10.0 | 1.13 | 10.0 | 1.13 | 10.0 | 1.13 | 10.0 | 1.13 |
| S (mm) | 1.9 | 0.7 | 1.65 | 0.23 | 1.65 | 0.23 | 1.65 | 0.23 | 1.65 | 0.23 |
| ρR (g/cc) | 1.0 | 8.2 | 1.03 | 0.14 | 1.03 | 0.14 | 1.03 | 0.14 | 1.03 | 0.14 |
| Fout,B2 (kg/h) | 9.5 | 1.0 | 9.3 | 1.25 | 9.3 | 1.26 | 9.3 | 1.22 | 9.3 | 1.23 |
| TS (rpm) | 29.8 | 1.3 | 29.8 | 1.19 | 29.8 | 1.20 | 29.8 | 1.19 | 29.8 | 1.19 |
| MCF (kN) | 11.3 | 2.1 | 11.3 | 2.11 | 11.3 | 2.12 | 11.2 | 2.03 | 11.2 | 2.04 |
| Fout,TP (kg/h) | 9.0 | 6.0 | 9.3 | 1.25 | 9.3 | 1.26 | 9.3 | 1.22 | 9.3 | 1.23 |
The sampling of tablet hardness and weight was done across the run, and AEE was used as the performance indicator. Table 4 shows the AEE for the tablet weight and tablet hardness, according to the case. For tablet weight and hardness, the SSDR-M results in all cases give the best results because the error is minimized. If the sensors are improved, then it is possible to reduce the error of the tablet weight, while the tablet hardness error is the same or slightly higher.
Table 4.
AEE for SSDR-M Results and Measurements
| Variable | M | SSDR-M | Corrected XAPI,B1 | Corrected Fout,B2 | Ideal SSDR-M |
|---|---|---|---|---|---|
|
| |||||
| W | 2.41E-02 | 1.65E-02 | 1.65E-02 | 1.50E-02 | 1.50E-02 |
| H | 9.49E-02 | 6.16E-02 | 6.16E-02 | 6.81E-02 | 6.80E-02 |
Conclusion
Process monitoring is the foundation for automation and implementing continuous manufacturing for any process. The sensor network analysis using DR and GED plays a key role in real-time decision support by contextualizing the measurements of CPPs and CQAs using conservation laws, mechanistic models, and domain knowledge of the process and instrumentation systems to realize real-time release.
Multiple cases of SSDR-M were studied in end-to-end continuous tableting via direct compaction and DG, and their reconciled values were compared with the raw measurements. The results of case studies discussed in this work show the accurate detection of gross errors, by using the redundancy in the sensor network. The RSD was significantly reduced with the application of SSDR-M for the critical variables such as powder stream composition, the roll gap, ribbon density, and flow rates. Bias correction (SSDR-M ideal) of in-line process analyzers improves the reconciled measurements and makes process monitoring more robust. At-line measurements such as those obtained from the Sotax AT4 provide the true values of these variables to validate their estimated values. Further improvements in the sensor network can be made incorporating additional PAT tools such as level sensor in the roller compactor hopper, level sensor in the tablet press hopper, composition measurement in the feed frame and so on.
Through this work, the model-based steady-state DR framework is shown to accomplish its 2 objectives for robust monitoring in continuous drug product manufacturing processes: (1) improved the accuracy of measured variables in the presence of random errors and importantly (2) detecting gross errors in the measurement network and flagging them for further investigation. Additionally, SSDR-M estimates unmeasured variables through validated mechanistic equations that are used in process design, such as those for ribbon density or tablet weight and hardness. Efforts to further advance implementation of robust process control systems for assurance of real-time product quality and continuous improvement through the application of sensor network health monitoring and control system performance monitoring are being pursued in our research group.
Supplementary Material
Acknowledgments
Funding for this project was made possible, in part, by the United States Food and Drug Administration through grant U01FD005535. The views expressed by authors do not necessarily reflect the official policies of the Department of Health and Human Services; nor does any mention of trade names, commercial practices, or organization imply endorsement by the United States Government. This work was also supported in part by the National Science Foundation under grant EEC-0540855 through the Engineering Research Center for Structure Organic Particulate Systems. The authors thank Yasasvi Bommireddy for his modeling suggestions, Benjamin Rentz for his experimental support, and Dr. Salvador Garcia-Munoz for providing the phi MATLAB toolbox for multivariate models.
Abbreviations used:
- AEE
average error of estimation
- CPPs
critical process parameters
- CQAs
critical quality attributes
- DC
direct compression
- DG
dry granulation
- DR
data reconciliation
- FS
frame rotation speed
- GED
gross error detection
- LIW
loss-in-weight
- MCF
main compression force
- PAT
process analytical technology
- PCF
precompression force
- PLS
partial least squares
- SP
set-point
- SSDR
steady-state data reconciliation
- TS
turret speed
- QbD
quality by design
Footnotes
This article contains supplementary material available from the authors by request or via the Internet at https://doi.org/10.1016/j.xphs.2019.03.011.
References
- 1.of H USD and FDA HS Guidance for Industry PAT—a Framework for Innovative Pharmaceutical Development, Manufacturing, and Quality Assurance. Rockville, MD: FDA; 2004:16. [Google Scholar]
- 2.Lee SL, O’Connor TF, Yang X, et al. Modernizing pharmaceutical manufacturing: from batch to continuous production. J Pharm Innov. 2015;10(3):191–199. [Google Scholar]
- 3.Hamdan IM V, Reklaitis G, Venkatasubramanian V. Real-time exceptional events management for a partial continuous dry granulation line. J Pharm Innov. 2012;7(3):95–118. [Google Scholar]
- 4.Pantelides CC, Renfro JG. The online use of first-principles models in process operations: review, current status and future needs. Comput Chem Eng. 2013;51:136–148. [Google Scholar]
- 5.Benqlilou C Data reconciliation as a framework for chemical processes optimization and control. Catalonia, Spain: Ph.D. Thesis, Universitat Politécnica de Catalunya; 2004:1–211. [Google Scholar]
- 6.Rehrl J, Karttunen AP, Nicolaï N, et al. Control of three different continuous pharmaceutical manufacturing processes: use of soft sensors. Int J Pharm. 2018;543(1–2):60–72. [DOI] [PubMed] [Google Scholar]
- 7.Moreno M, Liu J, Su Q, et al. Steady-state data reconciliation framework for a direct continuous tableting line. J Pharm Innov. 2018;13:1–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Liu J, Su Q, Moreno M, Laird C, Nagy Z, Reklaitis G. Robust state estimation of feeding—blending systems in continuous pharmaceutical manufacturing. Chem Eng Res Des. 2018;134:140–153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Özyurt DB, Pike RW. Theory and practice of simultaneous data reconciliation and gross error detection for chemical processes. Comput Chem Eng. 2004;28(3):381–402. [Google Scholar]
- 10.Romagnoli JA, M.C. S. Data Processing and Reconciliation for Chemical Process Operations. San Diego, CA: Academic Press; 2000. [Google Scholar]
- 11.Crowe CM. Observability and redundancy of process data for steady state reconciliation. Chem Eng Sci. 1989;44(12):2909–2917. [Google Scholar]
- 12.Narasimhan S, Jordache C. Data Reconciliation and Gross Error Detection. Houston, TX: Gulf Publishing Company; 2000. [Google Scholar]
- 13.Cencic O, Fruhwirth R. A general framework for data reconciliation-Part I: linear constraints. Comput Chem Eng. 2015;75:196–208. [Google Scholar]
- 14.Kim I-W, Kang MS, Park S, Edgar TF. Robust data reconciliation and gross error detection: the modified MIMT using NLP. Comput Chem Eng. 1997;21(7):775–782. [Google Scholar]
- 15.Bagajewicz MJ. Smart Process Plants: Software and Hardware Solutions for Accurate Data and Profitable Operations: Data Reconciliation, Gross Error Detection, and Instrumentation Upgrade. 1st ed. New York, NY: McGraw-Hill Education; 2010. [Google Scholar]
- 16.Knopf C Introduction to Data Reconciliation and Gross Error Detection, in Modeling, Analysis and Optimization of Process and Energy Systems. Hoboken, NJ: John Wiley & Sons; 2011. [Google Scholar]
- 17.Vanarase AU, Alcalá M, Jerez Rozo JI, Muzzio FJ, Romañach RJ. Real-time monitoring of drug concentration in a continuous powder mixing process using NIR spectroscopy. Chem Eng Sci. 2010;65(21):5728–5733. [Google Scholar]
- 18.Ganesh S, Troscinski R, Schmall N, Lim J, Nagy Z, Reklaitis G. Application of X-ray sensors for in-line and noninvasive monitoring of mass flow rate in continuous tablet manufacturing. J Pharm Sci. 2017;106(12):3591–3603. [DOI] [PubMed] [Google Scholar]
- 19.Austin J, Gupta A, McDonnell R, Reklaitis GV, Harris MT. A novel microwave sensor to determine particulate blend composition on-line. Anal Chim Acta. 2014;819:82–93. [DOI] [PubMed] [Google Scholar]
- 20.Su Q, Bommireddy Y, Gonzalez M, Reklaitis GV, Nagy ZK. Variation and risk analysis in tablet press control for continuous manufacturing of solid dosage via direct compaction. In: Eden M, Towler G, Ierapetritou M, eds. Proceedings of the 13th International Symposium on Process Systems Engineering PSE 2018. San Diego, CA: Elsevier; 2018:2912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Mazel V, Busignies V, Duca S, Leclerc B, Tchoreloff P. Original predictive approach to the compressibility of pharmaceutical powder mixtures based on the Kawakita equation. Int J Pharm. 2011;410(1):92–98. [DOI] [PubMed] [Google Scholar]
- 22.Kuentz M, Leuenberger H. A new model for the hardness of a compacted particle system, applied to tablets of pharmaceutical polymers. Powder Technol. 2000;111(1–2):145–153. [Google Scholar]
- 23.Razavi SM, Callegari G, Drazer G, Cuitinño AM. Toward predicting tensile strength of pharmaceutical tablets by ultrasound measurement in continuous manufacturing. Int J Pharm. 2016;507(1–2):83–89. [DOI] [PubMed] [Google Scholar]
- 24.Gago AP, Reynolds G, Kleinebudde P. Impact of roll compactor scale on ribbon density. Powder Technol. 2018;337:92–103. [Google Scholar]
- 25.Hsu S-H, Reklaitis GV, Venkatasubramanian V. Modeling and control of roller compaction for pharmaceutical manufacturing. Part I: process dynamics and control framework. J Pharm Innov. 2010;5(1–2):14–23. [Google Scholar]
- 26.Gavi E, Reynolds GK. System model of a tablet manufacturing process. Comput Chem Eng. 2014;71:130–140. [Google Scholar]
- 27.Nordström J, Klevan I, Alderborn G. A protocol for the classification of powder compression characteristics. Eur J Pharm Biopharm. 2012;80(1):209–216. [DOI] [PubMed] [Google Scholar]
- 28.Nordström J, Welch K, Frenning G, Alderborn G. On the physical interpretation of the Kawakita and Adams parameters derived from confined compression of granular solids. Powder Technol. 2008;182(3):424–435. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


