An integrated chance constraints approach for optimal vaccination strategies under uncertainty for COVID-19

Abstract

Despite concerted efforts by health authorities worldwide to contain COVID-19, the SARS-CoV-2 virus has continued to spread and mutate into new variants with uncertain transmission characteristics. Therefore, there is a need for new data-driven models for determining optimal vaccination strategies that adapt to the new variants with their uncertain transmission characteristics. Motivated by this challenge, we derive an integrated chance constraints stochastic programming (ICC-SP) approach for finding vaccination strategies for epidemics that incorporates population demographics for any region of the world, uncertain disease transmission and vaccine efficacy. An optimal vaccination strategy specifies the proportion of individuals in a given household-type to vaccinate to bring the reproduction number to below one. The ICC-SP approach provides a quantitative method that allows to bound the expected excess of the reproduction number above one by an acceptable amount according to the decision-maker’s level of risk. This new methodology involves a multi-community household based epidemiology model that uses census demographics data, vaccination status, age-related heterogeneity in disease susceptibility and infectivity, virus variants, and vaccine efficacy. The new methodology was tested on real data for seven neighboring counties in the United States state of Texas. The results are promising and show, among other findings, that vaccination strategies for controlling an outbreak should prioritize vaccinating certain household sizes as well as age groups with relatively high combined susceptibility and infectivity.

1. Introduction

The COronaVIrus Disease of 2019 (COVID-19) caused by Severe Acute Respiratory Syndrome SARS-CoV-2 virus was reported in December 2019 and was declared a pandemic by the World Health Organization (WHO) in early 2020. It is arguably the most devastating pandemic in the last 100 years after the Spanish flu. The virus has spread globally and keeps mutating leading to new variants with uncertain disease transmission characteristics [1]. A number of vaccines have been developed and are being administered together with a variety of non-pharmaceutical interventions including lockdowns, border closures, gathering restrictions, social distancing, quarantining, mask mandates, business and school closures, travel restrictions and contact tracing. These interventions are intended to slow down community transmission of the disease, but have a great impact on global and regional economies [2], [3]. However, despite concerted efforts by health authorities to contain the disease, COVID-19 continues to spread and mutate. There is, therefore, a dire need for new models for determining optimal vaccination strategies that adapt to the uncertain emergence of new variants and vaccine effectiveness. This work makes an effort towards meeting that need.

An important measure of community transmission of an infectious disease is the basic reproduction number $R_0$, which is an epidemiology scale to measure the contagiousness of the disease. It is the number of secondary infections caused by a primary case within a completely susceptible population in the absence of any deliberate intervention in disease transmission [4], [5]. Essentially, the value of $R_0$ quantifies the transmissibility of an infectious disease at the initial stages of an epidemic and aids in understanding the course of a disease transmission and in the design of intervention strategies. In practice, it is necessary to evaluate the time-dependent variation in transmissibility under mitigation interventions and decline in susceptibility of the population [6]. This time-dependent variation is captured through the effective reproduction number $R_t$, which is the average number of secondary infections caused by a primary case at time $t$ [6], [7]. This means that a disease outbreak is under control if $R_t\le 1$, otherwise if $R_t>1$ it means that there is an epidemic. Therefore, the goal of vaccination and other mitigation interventions is to keep $R_t\le 1$.

At the time of this study, three vaccines were authorized and recommended in the United States: Pfizer-BioNTech, Moderna, and Johnson & Johnson’s Janssen [8]. Recent studies suggest that the authorized mRNA vaccines (Pfizer-BioNTech and Moderna) and the Johnson & Johnson’s Janssen are effective against the ancestral strain and Alpha variant [9], [10]. However, just like the influenza virus, the SARS-CoV-2 virus keeps mutating. Evidence shows that some of the new variants, such as the currently dominant Delta variant, can be more severe in terms of illness and transmissibility and the vaccines may be less efficacious [11], [12]. With new variants expected to continue emerging, there is an urgent need for effective vaccination strategies to compete with the variant mutation and decline in vaccine efficacy.

Vaccination strategies depend on various factors and have been widely studied in epidemiology. The studies include deterministic and stochastic models, computer simulation, and statistical prediction [13], [14], [15], [16]. Deterministic approaches to evaluate the impact of vaccine efficacy, susceptibility, infectivity, and population variation on mortality, cumulative incidence, and years of life lost have been attempted [17]. The consequences in hospitalization occupancy when varying the inter-dose interval have been investigated [18]. This work explores the impact of vaccination strategies under different scenarios regarding efficacy, coverage, vaccine-induced, and natural immunity. Another study involves a comparison of vaccination strategies under different hypothetical vaccine efficacy [19]. The above-listed works perform experiments under a wide range of scenarios in which a single parameter is varied. Other work investigate the vulnerability of variation among population subgroups and aim to find a decent balance between diversity and fairness measures [20]. However, the essential and conclusive epidemiological characteristics of the SARS-CoV-2 virus, vaccine efficacy, vaccine-induced, and natural immunity remains under study, and their variations coexist [21]. Therefore, stochastic optimization models that account for multiple parameters simultaneously under a set of realizations of the random parameters are needed.

Stochastic optimization models typically seek feasible vaccination strategies for all scenarios for a given objective and can thus be infeasible, i.e., may not find a vaccination strategy that prevents an epidemic under all scenarios. Thus, models that allow for accepting a certain level of infeasibility (risk) are what is needed in this case. An example of such a model is a chance-constrained stochastic programming (CC-SP) [22], [23], [24] model proposed by Tanner et al. [14]. This model determines optimal vaccination strategies to control the influenza outbreaks by allowing for infeasibility of the constraint $R_t\le 1$ at a specified level of risk. The model extends the deterministic epidemiology model of disease spread by Becker and Starczak [25] to the stochastic setting, is based on a single community, and assumes that no one is vaccinated at the beginning of the study. With COVID-19, however, this assumption is not valid because a certain percentage of the population has been vaccinated [26] and the model has to take this into account.

In this work, we consider a heterogeneous population comprising different age groups each with its own susceptibility and infectivity, household vaccination status (vaccinated or not), and virus variant related transmissibility. Building on the work of Tanner et al. [14], we derive an integrated chance constraints stochastic programming (ICC-SP) [27], [28] approach for finding optimal vaccination strategies for epidemics that incorporates uncertain disease transmission characteristic and population demographics. An optimal vaccination strategy specifies the proportion of individuals in a given household-type to vaccinate in order to bring the post-vaccination reproduction number to below one. Unlike CC-SP which involves qualitative constraints and is very challenging to solve, ICC-SP provides a quantitative alternative approach. It allows to bound the expected excess (or shortfall) of a chance constraint by the largest acceptable amount based on the decision-maker’s level of risk averseness. Specifically, we derive a multi-community ICC-SP model to determine household-based vaccination strategies to control the outbreaks of COVID-19 under data uncertainty and different risk levels.

The new approach was implemented and tested on real data for seven neighboring counties in the United States state of Texas, one of which has the largest population and was at the center of the outbreak in 2020. In general, a contagious disease has a higher likelihood to spread faster in a densely populated area due to the high number of social contacts [29]. The results are promising and show that the proposed approach can potentially aid in accurately determining vaccination strategies under different risk levels to quickly prioritize and stop outbreaks. In particular, the proportion to vaccinate in each county for different household sizes, vaccination status, and population demographics varies based on the risk level. The proposed stochastic model suggests to vaccinate more individuals than a benchmark deterministic model under all risk levels. The deterministic model is optimistic because it involves averaging scenario data which in turn suppresses extreme scenarios that require vaccinating more people.

The key contributions of this work include the following: (a) a new adaptable data-driven ICC-SP methodology for determining optimal vaccination strategies to control disease outbreaks in a set of communities under data uncertainty and risk; and (b) a computational study based on real demographic data and COVID-19 disease transmission characteristics that were prevailing at the time of the study. The key features of this approach include capturing uncertainty disease transmission outside and within households, age-related susceptibility and infectivity, virus variant characteristics, and vaccine efficacy. The rest of this paper is organized as follows: In Section 2 we present preliminaries on stochastic programming and the theoretical contributions of this work regarding the mathematical derivation of the proposed methodology. In Section 3 we derive the multi-community ICC-SP model of disease spread and describe model parameters and population datasets used in our computational study in Section 4. We report the results of our study and discuss findings in Section 5. We end the paper with concluding remarks and directions for further work in Section 6.

2. Preliminaries and theoretical contributions

The data-driven methodology proposed in this work is based on integrated chance constraints stochastic programming (ICC-SP), which is derived from chance-constrained stochastic programming (CC-SP). In this section, we provide preliminaries on CC-SP and ICC-SP essential to the understanding of the theoretical contributions of this work and give a detailed mathematical derivation of our generic ICC-SP model in the context of SP. We then show how to transform this generic ICC-SP model into a data-driven vaccine allocation model for disease spread by integrating into the model the fundamental equation in epidemiology that links vaccination to the reproduction number $R_0$ to prevent epidemics. The vaccine allocation model incorporates disease spread and vaccine data uncertainties as well as different risk levels for public health decision-making. We end this section with an overview of closely related work to show how the proposed model fits into the historical context and how it provides an advance towards data-driven models for vaccine allocation.

CC-SP was initiated by Charnes and Cooper [22], [23] and later pioneered by Prékopa [24]. This field of SP deals with optimization problems involving chance constraints that can only hold in a probabilistic sense. Such constraints are common in operations research and engineering problems involving reliability or quality of service constraints that do not hold all the time. More formally, let $\tilde{\omega }$ be a discretely distributed random variable with finitely many outcomes (scenarios) $\omega \in \Omega$, each with corresponding probability of occurrence $p\left(\omega \right)$. In general, the probability distribution can be continuous but for the purposes of this work we focus on discrete distributions. Now let $\alpha \in (0,1)$ be a given level of acceptable risk (or reliability) set by the decision-maker. Then, a CC-SP model can be written as follows:

$$\text{Min}{c}^{\top }x$$ (1a)

$$\text{s.t. }Ax\ge b$$ (1b)

$$\mathbb{P}\{T\left(\tilde{\omega }\right)x\le h\left(\tilde{\omega }\right)\}\ge \alpha$$ (1c)

$$x\ge 0,$$

where $x\in {\mathbb{R}}_{+}^{n_1}$ is the decision variable vector, $c\in {\mathbb{R}}^{n_1}$ is the cost vector, $A\in {\mathbb{R}}^{m_1\times n_1}$ is a known matrix, and $b\in {\mathbb{R}}^{m_1}$ is known right hand side (RHS) vector. The matrix $T\left(\tilde{\omega }\right)\in {\mathbb{R}}^{m_2\times n_1}$ is the random technology matrix and $h\left(\omega \right)\in {\mathbb{R}}^{m_2}$ is the random RHS vector. The objective function (1a) is linear while the set of constraints (1b) are deterministic. Constraint (1c) is the (joint) chance or probabilistic constraint which must hold $\left(\alpha \right).100\text{\%}$ of the time. In practice, typical values for $\alpha$ are between 0.9 and 1 to provide relatively high levels of risk averseness or reliability.

In terms of model properties, CC-SP problem (1) is generally nonconvex due to the (joint) chance constraints and it is, therefore, challenging to solve. To create an equivalent version of the problem that is amenable to solution methods, we can write the deterministic equivalent problem (DEP) formulation. Let $M_{\omega }$ be an appropriately sized scalar for scenario $\omega \in \Omega$ and let $e$ be an appropriately dimensioned vector of ones. Define a binary decision variable $z\left(\omega \right)$ as follows: $z\left(\omega \right)=1$ if under scenario $\omega$ at least one of the inequalities in the probabilistic constraint is violated, and $z\left(\omega \right)=0$ otherwise. Then, a DEP formulation for problem (1) can be written as follows:

$$\text{Min}{c}^{\top }x$$

$$\text{s.t. }Ax\ge bT\left(\omega \right)x-M_{\omega }e{z}_{\omega }\le h\left(\omega \right),\forall \omega \in \Omega$$ (2a)

$$\sum _{\omega \in \Omega }p\left(\omega \right)z_{\omega }\le 1-\alpha$$ (2b)

$$x\ge 0,z_{\omega }\in \{0,1\},\forall \omega \in \Omega .$$

Constraints (2a) ensures that for a given $\omega \in \Omega$, $T\left(\omega \right)x\le h\left(\omega \right)$ when $z\left(\omega \right)=0$, otherwise $z\left(\omega \right)=1$. Constraint (2b) bounds the total probability of violating the (joint) chance constraint. This is given by $\mathbb{P}\{T\left(\tilde{\omega }\right)x\nleqq h\left(\tilde{\omega }\right)\}\le {\sum }_{\omega \in \Omega }p\left(\omega \right)z\left(\omega \right)\le 1-\alpha$. When $z\left(\omega \right)=1$ it means that scenario $\omega$ is excluded from the CC-SP formulation. The parameter $1-\alpha$ is the amount of risk the decision-maker is willing to take. Thus, we assume that $p\left(\omega \right)\le \alpha ,\forall \omega \in \Omega$ so that the knapsack constraint (2b) has a well-defined subset of scenarios that can be excluded from the formulation without exceeding the risk/reliability level of $1-\alpha$. Notice that problem (2) is a mixed-integer program (MIP) and is thus, generally difficult to solve.

The CC-SP model is a qualitative risk model in the sense that a scenario $\omega$ is excluded from the model as long as $z_{\omega }=1$ and constraint (2b) is satisfied. In other words, the amount of constraint violation is not considered. In certain applications, however, the CC-SP approach may not be sufficient as the amount of constraint violation may significantly impact the optimal decisions. This motivated the development of ICC-SP [27], [28], which is a quantitative risk approach and allows to compute the amount of constraint violation. We should note that ICC-SP has been applied to optimizing pension funds in finance [30]. In the seminal paper by Klein Haneveld [27], ICC-SP was derived to quantify the amount of constraint violation formulated as a shortage to meet uncertain demand in the context of production planning. In this work, however, we adopt the ICC-SP framework for disease spread and quantify the amount of violation as an excess above a threshold in order to prevent epidemics. We shall make this clear a little later, but first, let us derive our generic ICC-SP model.

Let feasible set $X≔\{x\in {\mathbb{R}}_{+}^{n_1}:Ax\ge b\}$ and define the following stochastic problem:

$$\underset{x\in X}{\text{Min}}{c}^{\top }x$$

$$\text{s.t. }T\left(\tilde{\omega }\right)x\le h\left(\tilde{\omega }\right)$$ (3a)

$$x\ge 0.$$

Problem (3) can be thought of as a scenario subproblem of CC-SP problem (1) without the probabilistic constraint. Observe that constraint (3a) comprises $m_2$ random constraints, $T_i\left(\tilde{\omega }\right)x\le h_i\left(\tilde{\omega }\right),i\in I≔\{1,\dots ,m_2\}$, where $T_i\left(\tilde{\omega }\right)$ is the $i$th row of matrix $T\left(\tilde{\omega }\right)$, and $h_i\left(\tilde{\omega }\right)$ is the $i$th component of vector $h\left(\tilde{\omega }\right)$. Let us now define ${\eta }_i(x,\tilde{\omega })≔T_i\left(\tilde{\omega }\right)x-h_i\left(\tilde{\omega }\right),\forall i\in I$, and ${\eta }_i{(x,\tilde{\omega })}^{+}≔max\{0,{\eta }_i(x,\tilde{\omega })\}$. We refer to ${\eta }_i{(x,\tilde{\omega })}^{+}$ as the random excess of the constraint violation. Observe that constraint (3a) avoids any excess, but we know that for some scenarios this may not be possible due to the randomness of $T\left(\tilde{\omega }\right)$ and $h\left(\tilde{\omega }\right)$. Therefore, we define a statistic we refer to as the mean excess, $\mathbb{E}\left[{\eta }_i{(x,\tilde{\omega })}^{+}\right]$, which will enable constraint violation up to an acceptable level of risk set by the decision-maker. This is important because in certain applications such as vaccine allocation for preventing epidemics the amount of excess is critical. So the idea is to allow for constraint violation up to a certain amount by bounding the mean excess using a fixed risk aversion parameter ${\alpha }_i$. This is accomplished by imposing the following ICC constraints:

$$\mathbb{E}\left[{\eta }_i{(x,\tilde{\omega })}^{+}\right]\le {\alpha }_i,\forall i\in I,{\alpha }_i\in [0,\infty ],$$ (4)

where $\mathbb{E}$ is the expectation over the sample space $\Omega$. We are now in a position to define a DEP for our generic ICC-SP model. Let $z_{\omega }^i$ represent the excess of the $i$th constraint for $\omega \in \Omega$. Then, we can write the DEP for ICC-SP with finite discrete distribution as follows:

$$\underset{x\in X}{\text{Min}}{c}^{\top }x$$

$$\text{s.t. }{T}_i\left(\omega \right)x-z_i\left(\omega \right)\le h_i\left(\omega \right),\forall i\in I;\omega \in \Omega$$ (5a)

$$\sum _{\omega =1}^{\Omega }p\left(\omega \right)z_i\left(\omega \right)\le {\alpha }_i,\forall i\in I$$ (5b)

$$x\ge 0,z_i\left(\omega \right)\ge 0,\forall i\in I;\omega \in \Omega .$$

Constraints (5a) ensure that $T_i\left(\omega \right)x\le h_i\left(\omega \right)$ for a given $i\in I$ and $\omega \in \Omega$, otherwise the model calculates the mount of constraint violation $z_i\left(\omega \right)$. In turn, the expected amount of constraint violation, i.e., the mean excess, is computed and bounded using constraints (5b). Notice that unlike CC-SP DEP formulation (2) which is an MIP, ICC-SP DEP problem (5) is a large-scale LP. This is desirable for computational purposes, however, solving instances of the ICC-SP DEP with a large number of scenarios $\left|\Omega \right|$ is still computationally demanding.

Now that we have done the derivation of our generic ICC-SP model, let us turn transform this generic model into a vaccine allocation model for preventing epidemics. To this end, we draw from the literature on epidemiology regarding the relation between vaccination and the reproduction number $R_0$. In particular, we consider the last author’s early work on vaccination allocation for influenza using CC-SP [14]. During an epidemic or pandemic, $R_0$ is usually estimated based the effective reproduction number $R_t$, which is $R_t>1$. Vaccines are designed so that an effective vaccination strategy to contain the epidemic by achieving herd immunity can achieve $R_t\le 1$. Because in reality $R_t$ is a random variable at best, we shall denote it by $R_t\left(\tilde{\omega }\right)$. An effective vaccination strategy would specify the proportion of individuals based on demographics and disease that must be vaccinated to attain $R_t\left(\tilde{\omega }\right)\le 1$. The effective reproduction number after vaccination is called the post-vaccination reproduction number, denoted $R_{Vc}\left(\tilde{\omega }\right)$ for community $c$. What we want is a vaccination coverage that achieves $R_{Vc}\left(\tilde{\omega }\right)\le 1$ so that the herd immunity induced by vaccination in community $c$ is a able to prevent epidemics. To link $R_{Vc}$ to our generic ICC-SP model (5), observe that for certain outcomes $\omega$ of $\tilde{\omega }$ we may not achieve $R_V\left(\tilde{\omega }\right)\le 1$. This means that we can impose an ICC on $R_V\left({\tilde{\omega }}_c\right)\le 1$ over the set of all possible scenarios. Thus, we can replace the ICC constraint set (4) in the generic ICC-SP model with

$$\mathbb{E}[R_V\left({\tilde{\omega }}_c\right)-1]\le {\alpha }_c,{\alpha }_c\in [0,\infty ],$$ (6)

where the random excess ${\eta }_i{(x,\tilde{\omega })}^{+}≔R_V\left({\tilde{\omega }}_c\right)-1$ and ${\alpha }_i≔{\alpha }_c$ is the risk level for community $c$. Thus, ICC (6) computes the mean excess of the post vaccination reproduction number above one. This mean excess is bounded by the amount or risk level the public health decision-maker is willing to take. To the best of our knowledge, this is the first time ICC has been integrated with an epidemiology model to provide a data-driven vaccination allocation model that incorporates data uncertainties associated the post vaccination reproduction number as well as considering the public health decision-maker’s level of risk. In the next section, we derive $R_{Vc}\left({\tilde{\omega }}_c\right)$ based on the epidemiology model by Becker and Starczak [25] that considers the distribution of households (size and age groups) in each community. We expand our ICC-SP model to include vaccination status of households, disease transmission characteristics for each virus variant, and vaccine efficacy for each variant.

To end this section, we provide a summary of how our methodology fits into the theoretical and historical context of closely related works in Table 1. We list the publication, approach used, and the type of setting regarding the model or methodology. In the context of COVID-19, the closely related works include Acuña-Zegarra et al. [18], Bubar et al. [17], Miura et al. [31], and Rachaniotis et al. [32]. These works are listed in Table 2 in terms of the publication, approach used, and whether or not the proposed model incorporates different households, heterogeneity in terms of age-specific differences in disease susceptibility and infectivity, and household vaccination status.

Table 1.

Historical context of this proposed methodology.

Paper	Year	Approach	Setting
Charnes et al.	1958	CC-SP	Stochastic, qualitative risk
Prékopa	1970	CC-SP	Stochastic, qualitative risk
Haneveld & van der Vlerk	1986	ICC-SP	Stochastic, quantitative risk
Becker & Starczak (B&S)	1997	Epidemiology model	Deterministic
Ruszczyn’ski and Shapiro	2003	CC-SP	Stochastic, qualitative risk
Haneveld & van der Vlerk	2006	ICC-SP reduced form	Stochastic, quantitative risk
Tanner et al.	2008	Epidemiology model	Stochastic, qualitative risk
This work	2022	ICC-SP, epidemiology model	Stochastic, quantitative risk

CC: Chance-constrained; ICC: Integrated Chance Constraints; SP: Stochastic Programming.

Table 2.

Closely related models and how they differ from the proposed ICC-SP model.

Paper	Year	Approach	Household	Age-specific	Vacc. Status
Becker & Starczak (B&S)	1997	Deterministic	✓	X	X
Tanner et al.	2008	Stochastic	✓	X	X
Acuña-Zegarra et al.	2021	Deterministic	X	X	X
Bubar et al.	2021	Deterministic	X	✓	X
Miura et al.	2021	Simulation	X	✓	X
Rachaniotis et al.	2021	Stochastic	X	X	X
This work	2022	Stochastic, risk	✓	✓	✓

3. Multi-community stochastic model of disease spread

We consider an epidemiology model of disease spread for a heterogeneous population in terms of age under uncertainty in several model parameters, including disease transmission outside and within the household as well as vaccine efficacy. During an epidemic understanding the course of the transmission path and the likely number of infections is critical. A common approach to forecast the number of infections is to use epidemic compartmental models such as the susceptible–exposed–infected–recovered (SEIR) model. SEIR models can predict the number of individuals who are susceptible to infection, are exposed, are actively infected, or have recovered from infection at any given time. We consider a model of disease transmission in a community based on the work of Becker and Starczak [25] and Tanner et al. [14]. The later work extended the deterministic model in [25] to the stochastic setting using CC-SP by incorporating uncertainty in disease transmission parameters. Both models consider a single community of households and assume that no one in the community is vaccinated. In this work, we build on the two works and derive a multiple-community model of disease spread that considers uncertainty not only in disease transmission, but also in vaccine efficacy. The model takes into account the vaccination status of each household in a given community. We list the mathematical notation we use in defining our multi-community ICC-SP model in Table 3.

Table 3.

Nomenclature used to define the multi-community stochastic model.

Sets and indices
$ℂ$	Set of communities, element $c\in ℂ$.
$\mathbb{N}$	Set of household types, element $n\in \mathbb{N}$.
$\mathbb{K}$	Set of vaccination status, element $k\in \mathbb{K}$.
$\mathbb{I}$	Set of person age groups, element $i\in \mathbb{I}$.
$\mathbb{V}$	Set of vaccination strategies, element $v\in \mathbb{V}$.
${\mathrm{\Omega }}_c$	Set of outcomes (scenarios) for community $c\in ℂ$, element ${\omega }_c\in {\mathrm{\Omega }}_c$.
Model parameters
${\tilde{\omega }}_c$	Multivariate random variable whose outcome (scenario) is ${\omega }_c\in {\mathrm{\Omega }}_c$; describes the uncertain parameters
	for the post-vaccination reproduction number $R_{Vc}\left({\tilde{\omega }}_c\right)$.
$R_{Vc}\left({\omega }_c\right)$	Post-vaccination reproduction number for community $c\in ℂ$ under scenario ${\omega }_c$.
$a_{nkvc}\left({\tilde{\omega }}_c\right)$	Uncertain $R_{Vc}\left({\tilde{\omega }}_c\right)$ parameter that captures the impact of vaccination strategy $v\in \mathbb{V}$ in a type $n$ household
	with vaccination status $k$ in community $c\in ℂ$.
$m_c\left({\tilde{\omega }}_c\right)$	Uncertain number of close contacts that an infective makes on average with persons from other
	households in the course of his/her infectious period in a community $c\in ℂ$.
$H_{kc}$	Number of households with vaccination status $k$ in community $c\in ℂ$.
$p\left(n\right)$	Number of persons in a household of type $n$.
$f(n,v)$	Number of persons to vaccinate in a household type $n$ when vaccination strategy $v\in \mathbb{V}$ is implemented.
$h_{nkc}$	Proportion of type $n$ households with vaccination status $k$ in community $c\in ℂ$.
${\mu }_c$	Average household size in a community, ${\mu }_c={\sum }_{n\in \mathbb{N}}{\sum }_{k\in \mathbb{K}}p\left(n\right)h_{nkc}$.
$b\left({\tilde{\omega }}_c\right)$	Uncertain transmission rate within a household.
${\beta }_{kic}\left({\tilde{\omega }}_c\right)$	Uncertain susceptibility for $i\in \mathbb{I}$ age group person with vaccination status $k\in \mathbb{K}$ in community $c\in ℂ$.
${\lambda }_{kic}\left({\tilde{\omega }}_c\right)$	Uncertain infectivity for $i\in \mathbb{I}$ age group person with vaccination status $k\in \mathbb{K}$ in community $c\in ℂ$.
${ϵ}_k\left({\tilde{\omega }}_c\right)$	Uncertain vaccine efficacy towards population with vaccination status $k\in \mathbb{K}$.
${\alpha }_c$	Decision-maker specified risk level for community $c\in ℂ$.
$e\left({\omega }_c\right)$	Excess of effective reproduction number in each county under scenario $\omega$ when there is no vaccination.
Decision variables
$x_{nkvc}$	Proportion of type $n$ households with vaccination status $k$ under vaccination strategy $v\in \mathbb{V}$
	implemented in community $c\in ℂ$.

As explained in the previous section, during an epidemic $R_t\left(\tilde{\omega }\right)>1$ and an optimal vaccination strategy specifies the proportion of individuals under demographic variation that must be vaccinated to achieve $R_t\left(\tilde{\omega }\right)\le 1$. Therefore, a vaccination strategy depends on the distribution of households (size and age groups) in each community, vaccine status of households, disease transmission characteristics for each virus variant, and vaccine efficacy for each variant. In epidemiology, vaccination coverage refers to the proportion of individuals who are vaccinated. In this work, we define an optimal vaccination strategy as one that provides the minimum vaccination coverage to ensure that $R_t\left(\tilde{\omega }\right)\le 1$. In particular, we use the post-vaccination reproduction number $R_{Vc}\left(\tilde{\omega }\right)$ which represents the effective reproduction number after vaccination in community $c$. Thus, the vaccination coverage we want is one that achieves $R_{Vc}\left(\tilde{\omega }\right)\le 1$ so that the herd immunity induced by vaccination is at a sufficiently high level to prevent epidemics. However, computing $R_{Vc}\left(\tilde{\omega }\right)$ is not trivial and requires several parameters, which are all uncertain at best. For a scenario ${\omega }_c$ of ${\tilde{\omega }}_c$ we have $R_{Vc}\left({\omega }_c\right)$. Consequently, instead of using a deterministic model that uses point estimates of the random parameters of the model, we devise an ICC-SP model that discrete probability distributions for the random parameters. The downside to doing this is that it might not be possible to achieve $R_{Vc}\left({\omega }_c\right)\le 1$ for certain scenarios ${\omega }_c$ of the random parameters. This motivates us to impose an ICC on $R_{Vc}\left({\tilde{\omega }}_c\right)\le 1$ over the set of all possible scenarios and bounding the expected amount by the value or risk level the decision-maker is willing to take as given in relation (6).

We derive $R_{Vc}\left({\tilde{\omega }}_c\right)$ based on Becker and Starczak [25] model of disease spread and consider all the model parameters as random variables. In addition, to better capture the spread within a household, we consider two levels for vaccination status for each household: $k=0$ means that no one in type $n$ household is vaccinated, while $k=1$ means that at least one member of the household is vaccinated. Given $x_{nkvc}$, the proportion of type $n$ household with vaccination status $k$ in which vaccination strategy $v$ has been implemented, $R_{Vc}\left({\tilde{\omega }}_c\right)$ can be given as follows:

$$R_{Vc}\left({\tilde{\omega }}_c\right)=\sum _{n\in \mathbb{N}}\sum _{k\in \mathbb{K}}\sum _{v\in \mathbb{V}}{a}_{nkvc}\left({\tilde{\omega }}_c\right)x_{nkvc},$$ (7)

where $a_{nkvc}\left({\tilde{\omega }}_c\right)$ is an uncertain parameter that captures the impact of vaccination strategy $v\in \mathbb{V}$ in a type $n$ household with vaccination status $k$ in community $c\in ℂ$. In deriving the ICC-SP model, we assume that significant age and vaccination status related differences in the susceptibility and infectivity of individuals exist. To model these differences, we define a set of age groups $\mathbb{I}$ that differentiate susceptibility and infectivity by age. We denote the relative susceptibility and relative infectivity of group $i\in \mathbb{I}$ with vaccination status $k\in \mathbb{K}$ in community $c\in ℂ$ by ${\beta }_{kic}\left({\tilde{\omega }}_c\right)$ and ${\lambda }_{kic}\left({\tilde{\omega }}_c\right)$, respectively. We consider age groups, denoted $A,B$, $C$, and so on, based on the disease. For our COVID-19 computational study, we use the following three age groups: $A=(age\le 19)$, $B=(20\le age\le 64)$, and $C=(age\ge 65)$. These age groups were based on the available information at the time of this study but can be expanded (refined) as more information about age related COVID-19 infectivity, susceptibility and vaccine efficacy becomes known. For each household of type $n$, let $p\left(n\right)$ represent the total number of members in the household. Also, let $p_i\left(n\right)$ denote the number of members in group $i$ for type $n$ household, where $i\in \{A,B,C\}$. The possible vaccination strategies for a type $n$ household are represented by $(f_A(n,v),f_B(n,v),f_C(n,v))$, the number of household members vaccinated in group $A,B$, and $C$, respectively. Table 4 gives an example illustration of household types for households sizes $p\left(n\right)=1$ and $p\left(n\right)=2$.

Table 4.

Example household types and vaccination strategies under heterogeneous population for $p\left(n\right)=1$ and $p\left(n\right)=2$.

Household type	Household size	Household composition	Total vaccination strategies	Possible vaccination strategies for a type $n$ household
$n$	$p\left(n\right)$	$(p_A\left(n\right),$	$(p_A\left(n\right)+1)+$	$(f_A(n,v),f_B(n,v),f_C(n,v))$
		$p_B\left(n\right),$	$(p_B\left(n\right)+1)+$
		$p_C\left(n\right))$	$(p_C\left(n\right)+1)$
1	1	(1, 0, 0)	2	(0, 0, 0), (1, 0, 0)
2	1	(0, 1, 0)	2	(0, 0, 0), (0, 1, 0)
3	1	(0, 0, 1)	2	(0, 0, 0), (0, 0, 1)
4	2	(2, 0, 0)	3	(0, 0, 0), (1, 0, 0), (2, 0, 0)
5	2	(0, 2, 0)	3	(0, 0, 0), (0, 1, 0), (0, 2, 0)
6	2	(0, 0, 2)	3	(0, 0, 0), (0, 0, 1), (0, 0, 2)
7	2	(1, 1, 0)	4	(0, 0, 0), (0, 1, 0), (1, 0, 0), (1, 1, 0)
8	2	(0, 1, 1)	4	(0, 0, 0), (0, 0, 1), (0, 1, 0), (0, 1, 1)
9	2	(1, 0, 1)	4	(0, 0, 0), (0, 0, 1), (1, 0, 0), (1, 0, 1)

Given the proportion of type $n$ households with $v$ vaccinated members and $x_{nkvc}$, $R_{Vc}\left({\tilde{\omega }}_c\right)$ for community $c$ is given by Eq. (7). Under the assumption of heterogeneity, the explicit expression for $R_{Vc}\left({\tilde{\omega }}_c\right)$ considers the age-stratified groups. In Becker and Starczak’s model, $a_{nkvc}\left({\tilde{\omega }}_c\right)$ is deterministic and all the parameters are assumed to be known. On the contrary, we model $a_{nkvc}\left({\tilde{\omega }}_c\right)$ as a random variable with outcome (scenario) ${\omega }_c$ of ${\tilde{\omega }}_c$ defined as the following quintuple: ${\omega }_c≔\{m_c\left({\omega }_c\right),b\left({\omega }_c\right),ϵ\left({\omega }_c\right),{\beta }_{kc}\left({\omega }_c\right),{\lambda }_{kc}\left({\omega }_c\right)\}$. Thus ${\omega }_c$ specifies the uncertain average contact rate outside the household, within household contact rate, vaccine efficacy, relative susceptibility, and relative infectivity. Consequently, $a_{nkvc}\left({\tilde{\omega }}_c\right)$ can be defined as follows:

$$a_{nkvc}\left({\tilde{\omega }}_c\right)=\frac{m_c\left({\tilde{\omega }}_c\right)h_{nkc}}{{\mu }_c}\{\sum _{i\in I}^{}{\beta }_{kic}\left({\tilde{\omega }}_c\right){\lambda }_{kic}\left({\tilde{\omega }}_c\right)\times [(1-b\left({\tilde{\omega }}_c\right))(p_i\left(n\right)-f_i(n,v){ϵ}_k\left({\tilde{\omega }}_c\right))+b\left({\tilde{\omega }}_c\right)f_i(n,v){ϵ}_k\left({\tilde{\omega }}_c\right)(1-{ϵ}_k\left({\tilde{\omega }}_c\right))]+b\left({\tilde{\omega }}_c\right)\sum _{i\in I}\sum _{r\in I}{\beta }_{kic}\left({\tilde{\omega }}_c\right){\lambda }_{krc}\left({\tilde{\omega }}_c\right)(p_i\left(n\right)-f_i(n,v){ϵ}_k\left({\tilde{\omega }}_c\right))(p_i\left(r\right)-f_i(n,r){ϵ}_k\left({\tilde{\omega }}_c\right))\}.$$ (8)

In the absence of effective and successful treatment for optimal COVID-19, vaccination seems to be the most viable way to fight this epidemic. Then the goal is to have $R_{Vc}\left({\tilde{\omega }}_c\right)={\sum }_{n=1}^N{\sum }_{v\in \mathbb{V}}{a}_{nvc}\left({\tilde{\omega }}_c\right)x_{nkvc}\le 1$. In practice, however, there are often some extreme scenarios where the vaccines cannot prevent the epidemic. For instance, if vaccine efficacy is not sufficiently large, $R_{Vc}\left({\tilde{\omega }}_c\right)>1$. This means that constraint $R_{Vc}\left({\tilde{\omega }}_c\right)\le 1$ is violated. To capture and bound the amount of violation, essentially taking risk, we use the ICC approach which allows to have some amount of violation. We denote the amount of violation by $z\left({\omega }_c\right)$ and restrict the expected violation by ${\alpha }_c$, i.e., $\mathbb{E}\left[z\left({\tilde{\omega }}_c\right)\right]\le {\alpha }_c$. We assume that the value of ${\alpha }_c$ is set by the decision-maker (public health authorities) for each community.

We are now ready to state the multi-community ICC-SP formulation for optimal vaccination strategies under uncertainty as follows:

$$\text{Min}\sum _{n\in \mathbb{N}}\sum _{k\in \mathbb{K}}\sum _{v=0}^{p\left(n\right)}\sum _{c\in ℂ}{f}_i(n,v)h_{nkc}{x}_{nkvc}$$ (9a)

$$\text{s.t }\sum _{n\in \mathbb{N}}\sum _{k\in \mathbb{K}}\sum _{v=0}^{p\left(n\right)}{a}_{nkvc}\left(\omega \right)x_{nkvc}-z_{\omega c}\le 1,\forall c\in ℂ;\forall \omega \in \Omega$$ (9b)

$$\sum _{\omega \in \Omega }{p}_{\omega }{z}_{\omega c}\le {\alpha }_c,\forall c\in ℂ$$ (9c)

$$\sum _{v=0}^n{x}_{nkvc}=1,\forall n\in N;k\in \mathbb{K};\forall c\in ℂ$$ (9d)

$$x_{nkvc},z_{\omega c}\ge 0,\forall v\in \{0,\dots ,p\left(n\right)\};n\in \mathbb{N};k\in \mathbb{K};\forall c\in ℂ;\forall \omega \in \Omega .$$ (9e)

The objective function (9a) determines the minimum vaccination coverage across communities. Constraints (9b), (9c) comprises the integrated chance constraints, allowing $R_{Vc}\left({\tilde{\omega }}_c\right)={\sum }_{n=1}^N{\sum }_{v\in \mathbb{V}}{a}_{nkvc}\left({\tilde{\omega }}_c\right)x_{nkvc}\le 1$ to be violated by $z\left(\tilde{\omega }c\right)$, with the expected violation $\mathbb{E}\left[z\left({\tilde{\omega }}_c\right)\right]$ not to exceed ${\alpha }_c$. Constraints (9d) determine the proportion of persons to vaccinate for each household type in each community. Finally, constraints (9e) are nonnegativity restrictions on the decision variables.

4. Model data and case study

To gain insights into the ICC-SP model optimal vaccination strategies under uncertainty, we considered a case study based on a large population center in Texas, United States, involving several counties. We implemented the ICC-SP model using the C++ programming language and the CPLEX Callable Library and used data from several sources. In general, in a highly populated community, individuals have more frequent social interactions that can lead to a greater likelihood of an outbreak of a contagious disease. The outbreak eventually can spread to the surrounding communities if the more populated community is not under control. In the case study, we consider seven Texas counties: Travis, Williamson, Bastrop, Caldwell, Hays, Burnet, and Blanco. Travis county is the center of the outbreak with the largest population. We conducted several experiments to generate vaccination strategies for all seven counties under model uncertain parameters and different risk levels to drive the post-vaccination reproduction number $R_{H{V}_c}$ to be below one. The optimal vaccination strategy prescribes the minimum proportion of a population with different vaccination status required to be vaccinated to control the outbreak in each county. The vaccination strategies suggested by the model are not only driven by uncertain parameters, but also by the population demographics in each county. The population demographics include the distribution of the household types, age compositions in a household, and vaccination status of the household members. Next, we describe the uncertain parameters and data used in the ICC-SP model.

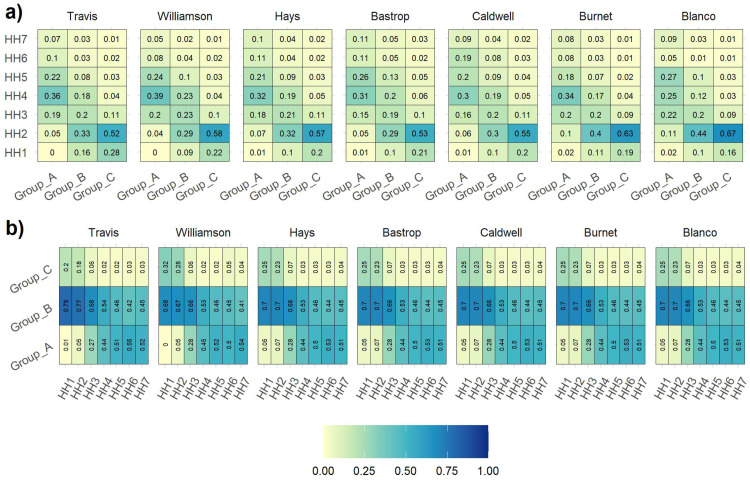
We used United States census data to capture the demographics of the communities and characterized each community in terms of the distribution of household types (see Table 4) with different age groups. For the uncertain model parameters, we constructed discrete distributions based on the information available on COVID-19 transmission, historical values for the effective reproduction number, and the advertised efficacy values for the approved vaccines at the time of this study. Below, we describe each type of data and provide the source for the data.

• •Demographic data: We implemented the ICC-SP model using actual population datasets for seven neighboring counties in Texas: Travis, Williamson, Bastrop, Caldwell, Hays, Burnet, and Blanco. These are listed in decreasing order of population size. The household type is a multivariate discrete distribution defined by: (1) the size of the household; (2) the vaccination status of the household; and (3) the number of household members in different age groups. We considered household types to range from one to seven (according to the United States census data) with different vaccination status and age group compositions. In the census data, there is a category for large dwelling but not specifically nursing homes, which are generally well vaccinated. Therefore, this data does not include nursing homes. The distribution of household types and age group composition were downloaded from 5-year American Survey data (https://data.census.gov/cedsci/) for years 2014–2018 [33] and from IPUMS (https://usa.ipums.org/usa/) [34]. The heat maps that depict the data are shown in Fig. 1. From sampled data, IPUMS (https://www.ipums.org/) provides the weights of each household type with age group composition, and using the weights, the household types with age group composition are scaled up to represent the household type distribution. Out of the seven counties, age group composition distribution was only available for Travis, Williamson, and Hays from IPUMS. Therefore, we assumed similar age group composition for the remaining counties. As for the distribution of household vaccination status, there was no explicit database available and we estimated the distribution using the overall proportion of the population vaccinated in Texas under different age groups [35]. Detailed demographic distribution data utilized in the experiments is provided in Supplementary File 1.
• •Household transmission rate$b\left(\tilde{\omega }\right)$: Household transmission rate is a quantitative parameter that measures how contagious the disease is within a household in a community $c$. In some studies, this parameter is referred to as household secondary attack rate or SAR. The value of SAR, i.e., $b\left(\tilde{\omega }\right)$, is between 0 and 1. It represents the probability that an infection occurs among susceptible people within a household. In the extreme case, $b\left(\tilde{\omega }\right)=0$ corresponds to no disease being transmitted within the household, while $b\left(\tilde{\omega }\right)=1$ means all members within the household are infected [25]. In our model, we assume that members in the same household are highly likely to be infected by the same virus variant. Therefore, the distribution of household transmission rate depends on the variant. At the time of this case study, three notable COVID-19 variants were actively circulating in the United States: Alpha, Gamma, and Delta [36], while the Omicron variant had just been discovered. A cross-sectional study on SAR in households after the Alpha variant became dominant in Japan was performed and the value of Alpha SAR was estimated to be 38.7% [37]. Several studies have shown the potential increase in household transmission rate with Delta and Gamma variants compared to Alpha [38]. Regarding the current dominating Delta variant, it is estimated to be 1.66 times more transmissible than the Alpha variant. Based on the values in the literature, we generated a discrete distribution for the within household transmission rate $b\left({\tilde{\omega }}_c\right)$.
• •Vaccine efficacy${ϵ}_k\left({\tilde{\omega }}_c\right)$: Mass vaccination efforts in the United States started at the beginning of 2021. A total of 370 million doses were administered, in which 54% were administered by August with Pfizer-BioNTech, 38% with Moderna, and the rest 8% with Johnson & Johnson [39]. According to several studies, vaccine efficacy $ϵ\left({\tilde{\omega }}_c\right)$ varies based on the COVID-19 variant. Pfizer-BioTech shows high effectiveness, 88%–94% against Alpha variant [40], [41], with a reduction of 5 % towards Gamma and 10% towards Delta variants. For the Moderna vaccine, the efficacy is estimated to be around 90% against Alpha variant, and 89% against Delta variant [9]. The studies regarding the efficacy of the Johnson & Johnson vaccine towards different variants are very few. We used the overall vaccine efficacy presented by Lopez Bernal et al. [41] to substitute for Johnson & Johnson. Based on these estimates from the literature, we generated vaccine efficacy distribution for households with vaccination status $k=0$, which is provided in Supplementary File 1 (see Table 5).
• •Relative susceptibility$\beta \left({\tilde{\omega }}_c\right)$: We consider age and vaccination status related differences in susceptibility to COVID-19. Relative susceptibility captures the variation in susceptibility due to the differences in social mixing and biological susceptibility among individuals. Several studies suggest that there is an increase in susceptibility with age for those who are not vaccinated [42], [43], [44]. One study estimates that the susceptibility of children (under 20 years old) is 43% (95% CI: [31%, 55%]) of the susceptibility of adults [45]. Due to the vaccine-induced immunity, the fully vaccinated individuals are less likely to be infected, in return, their susceptibility is relatively lower than those who are not vaccinated. Table 6 shows the relatively susceptibility of the three age groups for each level of vaccination status.
• •Relative infectivity$\lambda \left({\tilde{\omega }}_c\right)$:Relative infectivity captures the variation in infectiousness between infected individuals due to the differences in social mixing and biological infectivity between individuals. At the time of writing this paper, studies showed that younger age ($\le$20 years) was associated with increased infectivity for populations that were not vaccinated. The infectivity of children was estimated to be 63% (95% CI: [37%, 88%]) relative to that of adults [45]. One study statistically synthesized multiple data streams and showed that individuals under the age of 60 are 2.78 (95% CI: [2.10, 4.22]) times more infectious than the elderly [46]. This nuance is essential to the transmission of COVID-19 because the younger population generally has more human interactions [47] and does not develop severe symptoms as compared to older populations. A member of the younger population, then, is more likely to infect a susceptible person. The relative infectivity for different age groups of a vaccinated population was not explicitly available. Several studies suggest that vaccines can reduce the symptoms but do not block the infection. Therefore, in this study we assumed that there was no significant difference in relative infectivity for the non-vaccinated group ($k=0$) versus the vaccinated group ($k=1$). The relative infectivity of the three age groups for each level of vaccination status is shown in Table 6.
• •
  Outside household close contact$m\left({\tilde{\omega }}_c\right)$: In the ICC-SP model, we treat the transmission in communities as a proliferation of infected households. Under this consideration, we need to know the average number of close contacts that an infective makes with persons of other households. Close contact means being sufficient for transmitting the disease when the contact is with a susceptible person. Here, $m\left({\tilde{\omega }}_c\right)$ is a close contact rate. Vaccination does not affect the number of contacts. The effect of vaccination is absorbed in susceptibility and infectivity. Even though $m\left({\tilde{\omega }}_c\right)$ is independent of vaccination, it varies due to differences in human interactions under the impact of various mitigation measures and demographics of a community. To estimate the distribution of $m\left({\tilde{\omega }}_c\right)$ we used the following method:

  Recall that in Eq. (7), $R_{Vc}\left({\tilde{\omega }}_c\right)$ is the effective reproduction number after vaccination. When factors related to vaccination that affect the reproduction number can be excluded from the right hand side in Eq. (8), what is left is analogous to $R_t\left({\tilde{\omega }}_c\right)$. This can be achieved by setting $ϵ\left({\tilde{\omega }}_c\right)=0$, and all $x_{nkvc}=0$, for all $n\in \mathbb{N},k\in \mathbb{K},v\in 1,\dots ,p(n,v),c\in ℂ$. Basically, Eq. (7) is reduced to $R_t\left({\tilde{\omega }}_c\right)={\sum }_{n\in \mathbb{N}}{a}_{nk0c}\left({\tilde{\omega }}_c\right)x_{nk0c}$. Therefore, we used $R_t\left({\tilde{\omega }}_c\right)$ values and transmission rates for each variant to calculate $m\left({\tilde{\omega }}_c\right)$ [48], [49]. The probability associated with $m\left({\tilde{\omega }}_c\right)$ was calculated based on the proportion of circulating variants when the value of $R_t\left({\tilde{\omega }}_c\right)$ was observed. In other words, the probability of close contact rate $m\left({\tilde{\omega }}_c\right)$ is represented by the distribution of the circulating variants at the time of this study in 2020. For example, in Travis county, the close contact rates were calculated as 2.0973, 1.8296, 1.2092, and 1.6203 based on the Delta, Alpha, Gamma, and “Other” variants, respectively, with corresponding proportions (probabilities) of 0.5, 0.2, 0.1, and 0.2. The “Other” variant corresponds to the mix of the other variants that were in circulation or unknown. Therefore, we assigned the close contact rate for the “Other” variant to be the average of the Delta, Alpha and Gamma variants. The distribution of the close contact rates we used for our experiments is provided in Supplementary File 1.

• •Risk level$\alpha$: The acceptable risk levels are typically prescribed by public health officials based on the historical severity of the epidemic. With the parameters described in this section, we calculated the excess of effective reproduction number in each county under scenario $\omega$ when there are no vaccines in the future, denoted $e\left({\omega }_c\right)$. Table 7 shows the excess of the effective reproduction number, which ranges from 0.611 to 4.721. This means that the effective reproduction number is between 1.611 and 5.721 across all scenarios. For the case study, we experimented with different risk levels to assess the sensitivity of the model to the values of the reproduction number within the given range. We report on three risk levels, termed Low, Medium and High (see Table 8). For the risk level Low, we set the acceptable expected excess to 0.50% of the expected excess $\mathbb{E}\left[e\left({\tilde{\omega }}_c\right)\right]$ when there are no vaccinations, while for the Medium and High levels, we set the acceptable excess to 0.75% of $\mathbb{E}\left[e\left({\tilde{\omega }}_c\right)\right]$ and 1.00% of $\mathbb{E}\left[e\left({\tilde{\omega }}_c\right)\right]$, respectively.

Fig. 1.

This figure shows the demographic distribution for each county. Figure (a) shows the distribution of household types in each age group across all seven counties. Notice that the younger age group mostly resides in middle-size households, and Figure (b) shows the distribution of age groups in each household size across seven counties.

Table 5.

Vaccine efficacy $ϵ\left({\tilde{\omega }}_c\right)$ towards Alpha, Delta, Gamma and other variants.

Probability	0.1			0.7			0.2
Vaccine efficacy $ϵ\left({\tilde{\omega }}_c\right)$	Pfizer	Moderna	Johnson	Pfizer	Moderna	Johnson	Pfizer	Moderna	Johnson
Alpha	0.97	0.95	0.67	0.94	0.92	0.64	0.88	0.86	0.58
Delta	0.90	0.88	0.63	0.87	0.85	0.60	0.81	0.80	0.53
Gamma	0.93	0.91	0.65	0.90	0.88	0.62	0.84	0.82	0.56
Other	0.94	0.92	0.65	0.91	0.89	0.62	0.85	0.83	0.56

Table 6.

Relative susceptibility and infectivity for Group A, Group B and Group C population with different vaccination status.

Vaccination status	$k=0$			$k=1$
Age group	Group A	Group B	Group C	Group A	Group B	Group C
Proportion of population	0.11	0.33	0.06	0.16	0.29	0.04
Relative susceptibility	0.56	1.30	1.71	0.26	1.00	1.41
Relative infectivity	1.25	1.00	0.36	1.25	1.00	0.36

Table 7.

Expected, minimum and maximum excess for each county when no vaccines are allocated in the future.

Excess $e\left({\tilde{\omega }}_c\right)$	Travis	Williamson	Hays	Bastrop	Caldwell	Burnet	Blanco
Expected	2.590	2.532	2.416	2.361	2.257	1.961	1.715
Minimum	0.994	0.926	0.876	0.829	0.788	0.712	0.611
Maximum	4.721	4.706	4.511	4.468	4.280	3.649	3.217

Table 8.

Example risk levels for each community used in the case study.

Risk Level	Amount	Travis	Williamson	Hays	Bastrop	Caldwell	Burnet	Blanco
Low	0.50% * $\mathbb{E}\left[e\left({\tilde{\omega }}_c\right)\right]$	0.013	0.013	0.012	0.012	0.011	0.010	0.009
Medium	0.75% * $\mathbb{E}\left[e\left({\tilde{\omega }}_c\right)\right]$	0.019	0.019	0.018	0.018	0.017	0.015	0.013
High	1.00% * $\mathbb{E}\left[e\left({\tilde{\omega }}_c\right)\right]$	0.026	0.025	0.024	0.024	0.023	0.020	0.017

To create a benchmark for comparison purposes to the stochastic risk-averse model, we implemented a deterministic risk-neutral model of the ICC-SP model that uses the expected values of the uncertain parameters of the ICC-SP model to determine the vaccination strategies under the three risk levels. This alternative model is thus, risk-neutral, and mimics how decisions could be made in practice without considering uncertainty. The model was coded in the C++ programming language using the CPLEX Callable Library for optimization. We created and solved several instances of the deterministic and stochastic models set at the three risk levels, Low, Medium, and High. All computational experiments were conducted on an HP computer with about GHz Processor. The results are reported and discussed in the next section.

5. Results and discussion

We begin with the comparative results of using the deterministic risk-neutral and stochastic risk-averse models to determine the proportion of the population that has to be vaccinated in each county to prevent epidemics. The results are shown in Table 9. Several observations can be made from the table. First, we see that both models suggest vaccinating a relatively higher proportion of those that were previously unvaccinated in more populated counties. However, this is not necessarily true for those that were previously vaccinated. In this case, the proportion varies depending on how many were previously vaccinated in each county. Second, we see that within each county, both models recommend vaccinating more of the previously unvaccinated population compared to the previously vaccinated. However, we notice clear differences between the models in that the stochastic model recommends vaccinating relatively larger proportions for each of the three risk levels than the deterministic model. Under all the three risk levels, the deterministic model underestimates the proportion to vaccinate for both the previously unvaccinated and those that were vaccinated as follows: 23.33% and 8.37%, respectively, for Low risk; 15.98% and 5.52%, respectively, for Medium risk; and 12.44% and 4.4%, respectively, for High risk.

The third observation we make is with regard to the stochastic model. We see a relative decrease in the proportion of the population vaccinated that was not previously vaccinated with increase in the risk level for each county. However, the proportions to vaccinate of those that were previously vaccinated remain almost at the same level in each county across all risk levels. We believe this is because as the risk level increases the model has more flexibility to vaccinate less of the population and in this case, the model maintains the proportion of those that need booster shots across the risk levels to prevent epidemics. Furthermore, when the risk level is Low, i.e., when the decision-maker is unwilling to take much risk, the model calls for vaccinating more people in each county to control the epidemic compared to when the risk level is either Medium or High. Finally, both the deterministic and stochastic models can answer other key questions of interest regarding the vaccination strategies for each county. For example, public health policy decision-makers may be interested in answers to the three following questions:

• 1. What is the total proportion of the population to vaccinate in each county?
• 2. What is the proportion of the population to vaccinate in each county for each age group and vaccination status?
• 3. What is the proportion to vaccinate in each county per household size and vaccination status?

Both our deterministic and stochastic models are designed to provide answers to these questions, which we discuss in the next three subsections.

Table 9.

Proportion to vaccinate using the risk-neutral deterministic and risk-averse stochastic models.

County	Risk-Neutral		Risk-Averse
	(Benchmark)		Low risk		Medium risk		High risk
	Vaccination status		Vaccination status		Vaccination status		Vaccination status
	$k=0$	$k=1$	$k=0$	$k=1$	$k=0$	$k=1$	$k=0$	$k=1$
Travis	61.17%	39.71%	86.44%	46.44%	80.25%	41.07%	75.65%	40.55%
Williamson	57.62%	40.09%	83.68%	45.80%	75.10%	43.76%	70.16%	43.67%
Hays	54.78%	40.69%	82.03%	45.02%	71.54%	45.05%	67.72%	43.96%
Bastrop	54.34%	38.91%	78.11%	46.67%	70.04%	44.62%	67.55%	42.53%
Caldwell	53.90%	37.75%	74.20%	48.74%	68.56%	44.57%	66.12%	42.56%
Burnet	50.64%	37.58%	72.64%	46.62%	65.59%	43.68%	62.08%	42.68%
Blanco	44.36%	38.88%	66.02%	46.92%	60.57%	43.45%	57.60%	42.49%
Average	54.26%	38.23%	77.59%	46.60%	70.24%	43.75%	66.70%	42.63%

$k=0$: previously unvaccinated; $k=1:$ previously vaccinated.

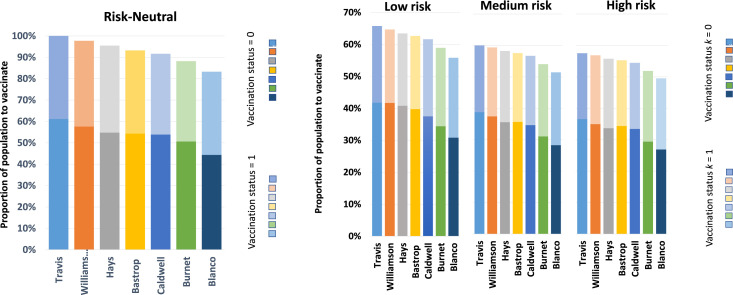
1. Proportion of total population to vaccinate

The proportion of the total population to vaccinate in each county is plotted in Fig. 2. The bar graphs show the total percentage to vaccinate as well as the proportion of the vaccination status using different shades; the lighter shade for $k=0$ and the darker shade for $k=1$. The plots clearly show a preference for vaccinating more individuals who were previously unvaccinated for both models and all risk levels. For example, for Travis county which is the most populated, under Low risk level the model suggests vaccinating about 66% of the total population. This is about 86% of the population that was not previously vaccinated and 46% of the population that was previously vaccinated and needed booster shots. The reason for this trend is due to the fact that, based on our model data, the previously unvaccinated individuals have higher relative susceptibility compared to those that were previously vaccinated.

Fig. 2.

Proportion of total population to vaccinate in each county.

We also observe that there is a reduction in the proportion to vaccinate with decrease in population for those that have not been previously vaccinated. In contrast, however, for those that were previously vaccinated the proportion to vaccinate remains at almost the same regardless of population size. This is probably an indication that the previously vaccinated population has some level of immunity.

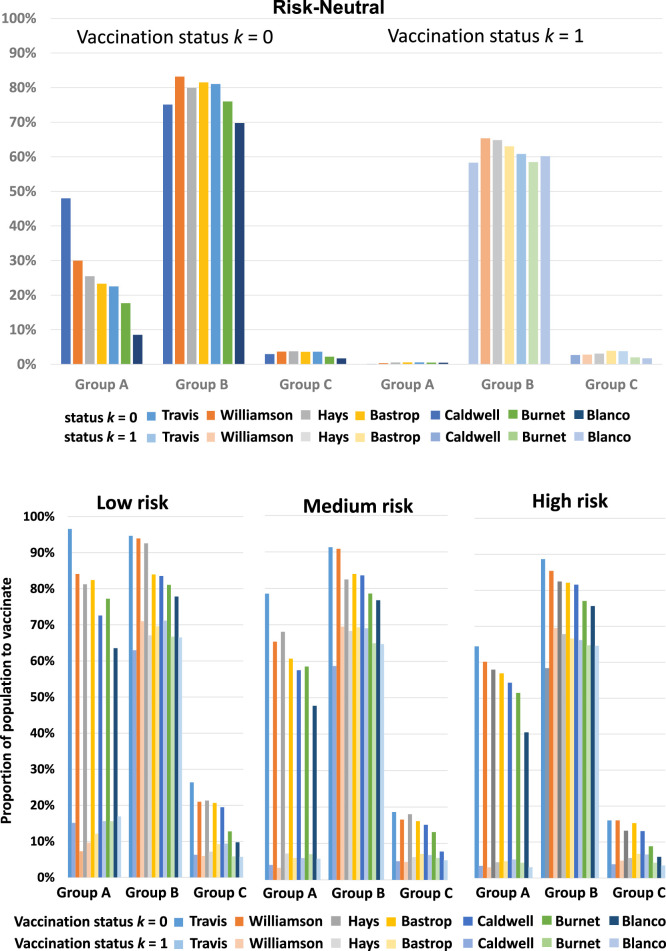
2. Proportion to vaccinate for each age group and vaccination status

The results for the proportion to vaccinate for each age group and vaccination status are plotted in Fig. 3. Recall that understanding the role of age in disease transmission and susceptibility is critical in determining the vaccination strategy. For the previously unvaccinated population, the deterministic model recommends vaccinating more of Group B, followed by Group A, which is followed by Group C. The age group vaccination preference order, in this case, is Group B-A-C. For the previously vaccinated, the model recommends Group B-C-A. Unlike the deterministic model, the age group vaccination preference order for the stochastic model depends on the risk level. For the previously unvaccinated population, the stochastic model recommends Group B-A-C in general for all three risk levels. However, for the previously vaccinated population, the model recommends Group B-A-C for Low risk and Medium risk levels, and Group B-C-A for High risk level. Note that from Table 9, the average proportion of the previously vaccinated population that needs booster shots under the risk-neutral case (38.23%) is closest to that under High risk level (42.63%). Thus, we see that the age group vaccination preference order Group B-C-A is the same for the deterministic model and stochastic model under High risk level.

Fig. 3.

Proportion to vaccinate in each age group for each vaccination status.

Gleaning further into the results, we observed that counties with relatively larger populations prioritize vaccinating a relatively high proportion of age Group A. This trend held true across all risk levels in general. From the census demographics data (Fig. 1), we see that age Group A and Group B tend to live in relatively larger household sizes compared to age Group C. Therefore, if an individual in Group A or Group B is infected, there are more members to transmit the disease to within the household. In addition, age Groups A and Group B tend to live in the same household of size three and larger. Based on the model data we used for this study, the Group B population has a relatively higher susceptibility to the disease compared to age Group A. Thus, a member of age Group B has a relatively higher chance to be infected, compared to one in age Group A in the same household. We also see that age Group C has the lowest proportion to vaccinate in general. We believe there are two reasons for this. First, at the time of this case study, 80% of the older population (age $\ge 65$) were already vaccinated and were not as susceptible as the unvaccinated group. Second, members of Group C primarily reside in smaller households of size one or two. Thus, if a member of Group C is infected, there are relatively fewer members to spread the disease to within the same household.

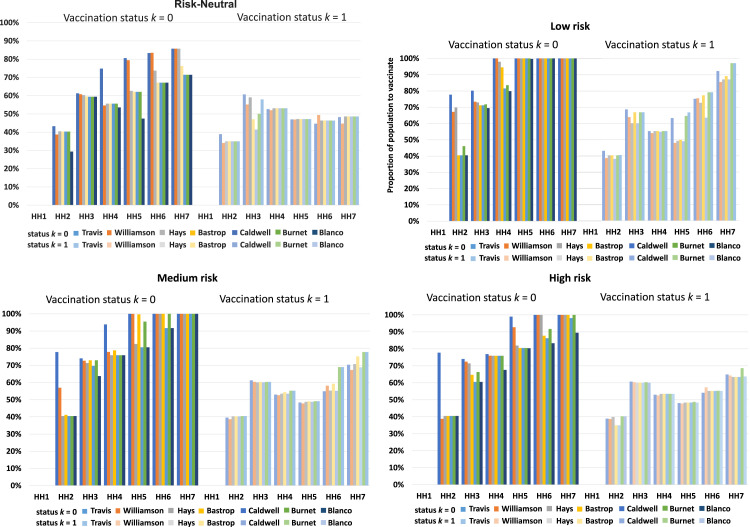
3. Proportion to vaccinate for each household size and vaccination status

Regarding the proportion to vaccinate in each household for each vaccination status, we provide plots in Fig. 4. For the previously unvaccinated, the graphs clearly show that both the deterministic and stochastic models recommend to vaccinate a relatively higher proportion for larger household sizes. However, for the previously vaccinated group, the two models offer different results. The deterministic model suggests vaccinating a relatively smaller proportion for household size two and a relatively larger proportion (around 50%) for household size three to seven. On the other, the stochastic model’s recommendations depend on the level of risk with no obvious trend. For example, for Low risk level there is an increase in the proportion to vaccinate from HH2 to HH3, then a general decrease from HH3 to HH5, and then a general increase from HH5 to HH7. The proportion to vaccinate in each county for different household sizes varies based on the risk level depending on the vaccination status and population demographics. Nonetheless, it is clear that the stochastic model suggests to vaccinate more individuals than the deterministic model under all risk levels. In this sense, the deterministic model is optimistic and this is because averaging suppresses the extreme scenarios which require vaccinating more people. Specifically, the stochastic model vaccinates around 20% more people than the deterministic model for the previously unvaccinated population, and around 5% more for the previously vaccinated population.

Fig. 4.

Proportion to vaccinate in each household for each vaccination status.

Lastly, our observations made from the computational results are in line with the conclusion that household size is an important contributor towards COVID-19 transmission [50] and is a critical factor in wider community spread [51]. Also, recent variants of the SARS-CoV-2 virus are showing a relatively high transmission rate within a household. If a member in a household is infected, the other members who live in the same household are more likely to be infected. This means that for those who reside in larger household sizes, if one of them is infected, then there are more members likely to spread the disease to than those who reside in smaller households.

6. Conclusion

Despite concerted efforts by health authorities to contain COVID-19, the SARS-CoV-2 virus has continued to spread and mutate leading to new variants with uncertain transmission characteristics. Therefore, there remains a need for new data-driven models for determining optimal vaccination strategies and other mitigation measures that adapt to the new variants and uncertain vaccine efficacy. Motivated by this challenge, we derived an integrated chance constraints stochastic programming (ICC-SP) approach for finding optimal vaccination strategies for epidemics that incorporates uncertain disease transmission characteristic and population demographics. An optimal vaccination strategy specifies the proportion of individuals in a given household-type to vaccinate to bring the post-vaccination reproduction number to below one. The ICC-SP approach provides a data-driven quantitative method that allows to bound the expected excess of the reproduction number above one by an acceptable amount based on the decision-maker’s level of risk. This new methodology involves a multi-community household based epidemiology model that uses census demographics data, vaccination status, age-related heterogeneity in disease susceptibility and infectivity, virus variants, and vaccine efficacy. The methodology was implemented and tested on real data for seven neighboring counties in the United States state of Texas, one of which was a large population center of the outbreak. A deterministic version of the model using the expected stochastic parameters was implemented to provide benchmark results for comparison. The results show that vaccination strategies for controlling an outbreak should prioritize vaccinating larger households as well as age groups with relatively high combined susceptibility and infectivity. The proportion to vaccinate in each county for different household sizes varies based on the risk level depending on the vaccination status and population demographics. The stochastic model suggests to vaccinate more individuals than the deterministic model under all risk levels. The deterministic model tends to be optimistic because averaging suppresses the extreme scenarios which require vaccinating more people. Considering a low-risk level, the model results recommend vaccinating about 78% of the population that were not previously vaccinated and administering booster shots to about 47% of the population that was previously vaccinated. In particular, the model suggests providing more vaccines to Group B, Group A, and Group C, in that order.

The ICC-SP model is a data-driven prescriptive model, i.e, it uses data to prescribe the courses of action to be taken and is thus, generalizable to a given multi-community setting and infectious disease. The model requires data regarding the population demographics and disease spread parameters for the given multi-community setting in the form of probability distributions to determine optimal vaccination strategies. Future work includes performing computational studies to incorporate new variants as they arise and their disease transmission data becomes available and incorporating vaccine supply chain and distribution aspects into the ICC-SP model.

CRediT authorship contribution statement

Jiangyue Gong: Conceptualization, Software, Validation, Visualization, Investigation. Krishna Reddy Gujjula: Conceptualization, Validation, Data curation, Visualization, Writing – original draft. Lewis Ntaimo: Conceptualization, Methodology, Software, Validation, Formal analysis Writing – review & editing, Supervision, Project administration.

Biographies

Jiangyue Gong obtained a B.S. in Industrial Engineering in 2016 and Ph.D. in Industrial Engineering in 2022, both from Texas A&M University, USA.

Krishna Reddy Gujjula obtained a B.S. in Mechanical Engineering in 2010 from the National Institute of Technology, Kurukshetra, India, and Ph.D. in Industrial Engineering in 2018 from Texas A&M University, USA.

Lewis Ntaimo obtained a B.S. in Mining Engineering in 1998, M.S. in Mining & Geological Engineering in 2000, and Ph.D. in Systems & Industrial Engineering in 2004, all from the University of Arizona, USA. He is Professor and Head of the Wm Michael Barnes ’64 Department of Industrial & Systems Engineering, Texas A&M University, USA.

Appendix A. Supplementary data

The following is the Supplementary material related to this article.

MMC S1

Model parameters, including household contact rate, vaccine efficacy, and demographic data.

Data availability

Data will be made available on request.