Resolving the enthalpy of protein stabilization by macromolecular crowding

Abstract

Proteins in the cellular milieu reside in environments crowded by macromolecules and other solutes. Although crowding can significantly impact the protein folded state stability, most experiments are conducted in dilute buffered solutions. To resolve the effect of crowding on protein stability, we use ¹⁹F nuclear magnetic resonance spectroscopy to follow the reversible, two‐state unfolding thermodynamics of the N‐terminal Src homology 3 domain of the Drosophila signal transduction protein drk in the presence of polyethylene glycols (PEGs) of various molecular weights and concentrations. Contrary to most current theories of crowding that emphasize steric protein–crowder interactions as the main driving force for entropically favored stabilization, our experiments show that PEG stabilization is accompanied by significant heat release, and entropy disfavors folding. Using our newly developed model, we find that stabilization by ethylene glycol and small PEGs is driven by favorable binding to the folded state. In contrast, for larger PEGs, chemical or soft PEG–protein interactions do not play a significant role. Instead, folding is favored by excluded volume PEG–protein interactions and an exothermic nonideal mixing contribution from release of confined PEG and water upon folding. Our results indicate that crowding acts through molecular interactions subtler than previously assumed and that interactions between solution components with both the folded and unfolded states must be carefully considered.

1. INTRODUCTION

The cell is the fundamental unit of life. It sequesters not only the genetic code but also all the macromolecular machinery and small molecules required for homeostasis and phenotypic outcomes (Ginzberg et al., 2015; Klumpp et al., ²⁰¹³; Spitzer et al., ²⁰¹⁵; Theillet et al., ²⁰¹⁴). To perform these essential functions, cells can concentrate macromolecules to concentrations up to 300 g/L, thus accounting for 40% of the cellular volume (Theillet et al., 2014). And yet, almost all protein biophysical studies are conducted in dilute solutions with macromolecular concentrations rarely exceeding 10 g/L. These discrepancies between the highly crowded cellular environment and dilute protein solutions that are used in most experiments can result in different protein behavior (Speer et al., 2022). Specifically, species observed in buffer are not necessarily observed in cells (Chu et al., 2022; Cohen & Pielak, ²⁰¹⁷) and disordered proteins can exhibit different ensembles in cells than they do in buffer (Dedmon et al., 2002). Surprisingly, how crowding impacts protein folding and folded state stability in concentrated environments is yet to be fully resolved.

Generally, crowders such as small cosolutes and large polymers mediate process like protein folding through forces intrinsically linked to their preferential interactions: greater exclusion of cosolutes from the unfolded protein results in protein folding, while inclusion results in unfolding (Parsegian, 2002). This relation between the excess or deficit of crowders near a macromolecular interface and the change in free energy can be described in terms of the Gibbs adsorption isotherm (Gibbs, 1878) or Wyman linkage (Wyman & Gill, 1990). However, the use of these relations alone does not elucidate the underlying stabilization mechanism and its enthalpic and entropic contributions.

The original model of Asakura and Oosawa (Asakura & Oosawa, 1954, 1958) explains the effects of crowders in terms of an apparent attraction between two surfaces in solution. This attraction arises because of an increase in translational entropy of the intervening cosolute crowders upon surface association and the necessary decrease in the cosolute excluding volume. Crowding through excluded volume interactions has often been used to interpret experimentally and computationally determined protein folding (Mittal & Best, 2010; Zosel et al., ²⁰²⁰) and protein–protein interactions (Guseman et al., 2018; Kim et al., ²⁰¹⁰). The original idea for this depletion force and later extensions that use scaled particle theory (Minton, 1981), however, assume only hard‐core repulsions between the surfaces and crowders and are thus entirely entropic. These theories, therefore, cannot account for the significant additional heat release during protein folding observed in the presence of crowders for many proteins and crowders (Gorensek‐Benitez et al., 2017; Senske et al., ²⁰¹⁴; Sukenik et al., ²⁰¹¹; Zhou, ²⁰¹³). The origin of this enthalpic contribution has remained elusive, although it is often assumed that it reflects chemical (soft or quinary) protein–cosolute interactions, which have been suggested to augment the depletion forces (Rivas & Minton, 2022). Several efforts have further incorporated cosolute–protein interactions together with excluded volume effects to fit proteins binding free energies (Kim & Mittal, 2013; Minton, ²⁰¹³) and the compaction of disordered proteins (Soranno et al., 2014) in the presence of crowders. Nevertheless, the contribution of water–cosolute interactions to crowding has not been explicitly considered, and the molecular origins of the enthalpic and entropic components have not been addressed. Therefore, to explain how crowding impacts protein stability, a new model is needed that consistently considers additional nonsteric effects over a range of cosolute sizes and concentrations.

Using a simple thermodynamic model, we resolve the stabilization mechanism of crowders of different sizes on protein folding. Our mean‐field model for crowding (Sapir & Harries, ^2015a) invokes three distinct types of interactions: hard‐core repulsions, nonideal mixing of cosolute and solvent, and soft chemical interactions between the crowder and protein. Each interaction is represented by a single parameter that can be measured in either bulk binary solution or determined by fitting experiment‐based protein unfolding free energies as a function of crowder size and concentration. By considering the temperature dependence of the nonideal mixing and the soft protein–crowder interactions, we can further dissect the enthalpic and entropic contributions to the unfolding process, resulting in a molecular level resolution of crowding‐induced stabilization. Beyond crowding, proteins can be stabilized by favorable binding to the folded state (Xie & Timasheff, 1997). We account for this interaction of cosolute and protein in the folded state (with its enthalpic and entropic contribution) as an additional empirical parameter that can be resolved by fitting data from unfolding experiments.

For the choice of protein, we require an experiment‐based system that can yield quantitative information. Two‐state folding (Anfinsen, 1973) of a single‐domain protein (Porter & Rose, 2012) is such a system. Requirements for the protein are reversibility and a method for direct detection of the folded and unfolded states. Given these features, we can obtain the free energy of unfolding and, via the temperature dependence, its enthalpic and entropic components. The combination of the metastable, 6.8 kDa N‐terminal Src homology 3 (SH3) domain of the Drosophila signal transduction protein drk (Zhang & Forman‐Kay, 1995) and ¹⁹F NMR detection (Arntson & Pomerantz, 2016; Smith et al., ²⁰¹⁶) fits these requirements. Another requirement is a set of highly soluble macromolecular crowders available in a range of molecule weights, all with similar surfaces. Ideally, these cosolutes would be globular proteins of variable molecular mass but similar surface groups, but such systems are unavailable. For this reason, we turned in polyethylene glycols (PEGs, to which, for larger PEGs, we append the molecular weight in grams per mole, e.g., PEG1000) and its monomer, ethylene glycol (EG). PEGs merit attention not only because they offer an outstanding test of any model but also because they are used in the chemical and pharmaceutical industries (Piszkiewicz & Pielak, 2019) and for better or worse, remain the go‐to macromolecules for crowding studies.

The measured unfolding free energies of the SH3 domain show increased folded state stability with PEG concentration and decreasing stabilization with PEG size for the same gram per liter concentrations. Additionally, measurements of the temperature dependence reveal a large, yet mostly compensating favorable enthalpy and unfavorable entropy, which does not fit a simple excluded volume model. Using our model, for large PEGs, although most of the enthalpic contribution originates with protein‐PEG soft interactions, these soft interactions are mostly compensated by corresponding entropy and alone cannot account for the net stabilizing effect of PEGs. In fact, attractive protein‐PEG interactions typically lead to weak protein destabilization. Instead, the net stabilization of the folded state by large PEGs stems from the increased exothermic nonideal water‐PEG mixing upon folding. This increase in mixing interactions is a direct result of changes in local concentration in the protein vicinity compared with the bulk. This unexpected result contrasts with current theories that consider soft protein–cosolute interactions as responsible for enthalpically dominated stabilization.

For small EG‐based cosolutes, from EG to tetraEG, the change in ¹⁹F chemical shift with cosolute concentration indicates binding to the folded state. Our model shows that these small PEGs are attracted to both the folded and unfolded states. However, stronger attraction to the folded state dominates, resulting in the net observed stabilization.

2. RESULTS

We used ¹⁹F NMR to measure the temperature dependence of SH3 stability as a function of PEG molecular weight and concentration. Such data allow quantification of the free energy, enthalpy (Figure 1), and entropy (Figure S1) of SH3 unfolding. The protein undergoes simple two‐state thermal unfolding (Zhang & Forman‐Kay, 1995), even under crowded conditions (Gorensek‐Benitez et al., 2017; Smith et al., ²⁰¹⁶), and the ¹⁹F spectra show only two resonances (Figure 1a): one for the folded state and the other for the unfolded state (Smith et al., 2016). The area under each resonance is proportional to species concentration because the states are in slow exchange on the NMR timescale. Therefore, the ratio of the area of the unfolded state resonance to that of the folded state gives the equilibrium constant for unfolding, $K_U$. The stability is expressed as the free energy of unfolding $\mathrm{\Delta }{G}_U^{{°}^{\prime }}$, which equals $-\mathit{RT}\ln K_U$, where $R$ is the gas constant and $T$ is the absolute temperature. Plots of $\mathrm{\Delta }{G}_U^{{°}^{\prime }}$ as a function of temperature (Figure 1b) are used to assess the enthalpy and heat capacity of denaturation, $\mathrm{\Delta }{H}_U^{{°}^{\prime }}$ and $\mathrm{\Delta }{C}_P^{{°}^{\prime }}$ respectively, by fitting the data to the integrated Gibbs–Helmholtz equation: $\mathrm{\Delta }{G}_U^{{°}^{\prime }}=\mathrm{\Delta }{H}_{U,m}^{{°}^{\prime }}\left[1-\left(T/T_m\right)\right]+\mathrm{\Delta }{C}_P^{{°}^{\prime }}\left[T-T_m-T\ln \left(T/T_m\right)\right]$(Becktel & Schellman, 1987). Here, $\mathrm{\Delta }{H}_{U,m}^{{°}^{\prime }}$ is the enthalpy of unfolding at the melting temperature, $T_m$ (values for all conditions are provided in Table S1). $\mathrm{\Delta }{H}_U^{{°}^{\prime }}$ and $\mathrm{\Delta }{S}_U^{{°}^{\prime }}$ at a temperature $T_{\mathrm{ref}}$ are assessed using the relationships $\mathrm{\Delta }{H}_{U,T_{\mathrm{ref}}}^{{°}^{\prime }}=\mathrm{\Delta }{H}_{U,\mathit{Tm}}^{{°}^{\prime }}+\mathrm{\Delta }{C}_P^{{°}^{\prime }}\left(T_{\mathrm{ref}}-T_m\right)$ and $\mathrm{\Delta }{S}_{U,T_{\mathrm{ref}}}^{{°}^{\prime }}=\left(\mathrm{\Delta }{H}_{U,T_m}^{{°}^{\prime }}/T_m\right)+\mathrm{\Delta }{C}_P^{{°}^{\prime }}\ln \left(T_{\mathrm{ref}}/T_m\right)$. We evaluate the cosolutes effects by subtracting the value in buffer to give $\mathrm{\Delta \Delta }{G}_{U,\mathrm{ref}}^{{°}^{\prime }}$, $\mathrm{\Delta \Delta }{H}_{U,\mathrm{ref}}^{{°}^{\prime }}$, and $-T\mathrm{\Delta \Delta }{S}_{U,\mathrm{ref}}^{{°}^{\prime }}$ such that positive values indicate stabilization.

FIGURE 1.

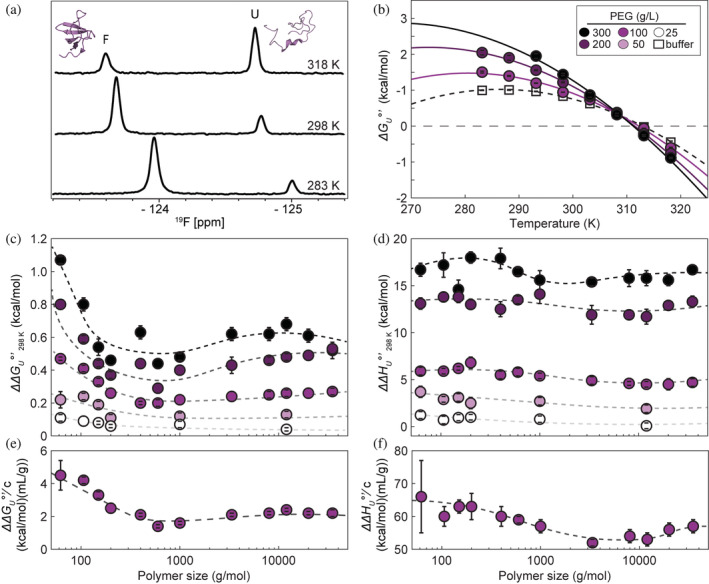
Structure and ¹⁹F spectra of SH3 (a), stability curves (fit to integrated Gibbs–Helmholtz equation) of SH3 in PEG400 and buffer (b), crowding effect on stability (c) and enthalpy (d) as a function of polyethylene glycol (PEG) size at 298 K. Efficacy of PEGs (i.e., the m‐values in g/mL) in terms of (e) free energy and (f) the enthalpy compared to buffer alone. $\mathrm{\Delta \Delta }{X}_U^{{°}^{\prime }}=\mathrm{\Delta }{X}_{U,\text{crowder}}^{{°}^{\prime }}-\mathrm{\Delta }{X}_{U,\text{buffer}}^{{°}^{\prime }}$, where $\mathrm{\Delta }{X}_U^{{°}^{\prime }}$ represents free energy or enthalpy of unfolding. Color intensity increases with PEG concentration. Error bars denote the standard deviation of the mean from triplicate experiments. Smooth curves are an aid to the eye and are of no theoretical significance.

EG and all PEGs increase the free energy of unfolding of SH3 compared to buffer at 298 K (Figure 1c). Stabilization increases with PEG concentration, $c$ in g/L, but tends to decrease with increasing PEG size, as has been observed for polyvinylpyrrolidones (Miklos et al., 2010). We divided the results into three groups: small PEGs (EG through tetraEG), medium PEGs (molecular weights 400–1000 g/mol), and large PEGs (>PEG1000). At a fixed $c$, small PEGs provide the greatest stability, medium PEGs provide the least stability, and larger PEGs provide slightly more stability than medium PEGs. Like $\mathrm{\Delta \Delta }{G}_U^{{°}^{\prime }}$, $\mathrm{\Delta \Delta }{H}_U^{{°}^{\prime }}$ increases with concentration but unlike $\mathrm{\Delta \Delta }{G}_U^{{°}^{\prime }}$, there is no size dependence. We did not detect a trend in $\mathrm{\Delta }{C}_P^{{°}^{\prime }}$ (Figure S2).

The slopes from linear fits of $\mathrm{\Delta \Delta }{G}_U^{{°}^{\prime }}$ and $\mathrm{\Delta \Delta }{H}_U^{{°}^{\prime }}$ against PEG concentration, $\mathrm{\delta \Delta \Delta }{X}_U^{o\prime }/\mathit{\delta c}$ (Figure 1e,f and Figure S3) often called m‐values, report on crowder efficacy. For cosolutes smaller than 400 g/mol, the plots of free energy against concentration deviate from linearity (Figure 2a). For this reason, we excluded points above 1 M in our calculation of m‐values. Specifically, data for EG  > 100 g/L and >200 g/L for diEG and triEG were excluded. Thus, the values for EG and smaller PEGs are considered “infinite‐dilution” m‐values. Both the free energy‐ and enthalpic‐efficacies (Figure 1e,f) decrease with increasing molecular weight and then flatten.

FIGURE 2.

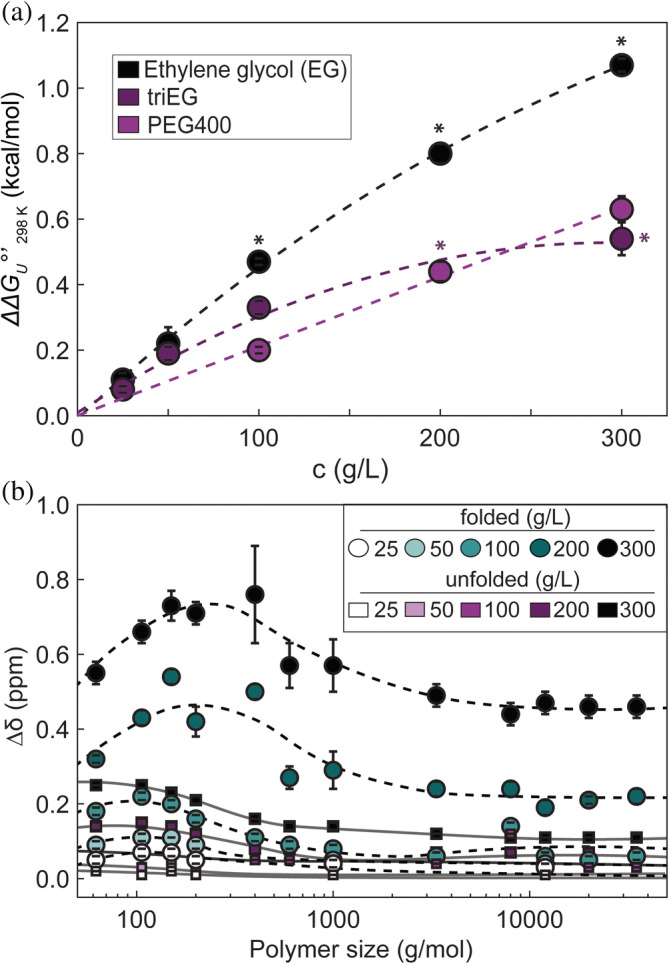
Stabilizing effects of small PEGs as a function of concentration at 298 K (a), PEG‐induced ¹⁹F chemical‐shift perturbation (b). Values excluded from calculation of m‐values are labeled with asterisks. ¹⁹F $\mathrm{\Delta }\delta$; folded, teal; unfolded, purple. Error bars denote standard deviation of the mean from triplicate experiments. The curves are of no theoretical significance.

To gain information about the nonlinearity of $\mathrm{\Delta \Delta }{G}_U^{{°}^{\prime }}$ with concentration for EG and small PEGs (Figure 2a), we assessed the change in ¹⁹F chemical shift ($\mathrm{\Delta }\delta ={\delta }_{\mathrm{PEG}}-{\delta }_{\text{buffer}}$) of folded and unfolded SH3 with respect to PEG size and concentration (Figure 2b, Figure S4 and Table S2). $\mathrm{\Delta }\delta$ values are independently interpretable because the folded and unfolded states are in slow exchange. The data for the unfolded state are flat and increases only weakly with concentration, suggesting there is only a small effect on the unfolded protein. The trend for the folded state is more interesting; values of $\mathrm{\Delta }\delta$ tend to be larger than those for the unfolded state, and, most importantly, at concentrations greater than 50 g/L, $\mathrm{\Delta }\delta$ increases from EG up to PEG1000 and then levels off.

3. DISCUSSION

3.1. Measured unfolding thermodynamics are inconsistent with existing crowding theories

All theories about macromolecular crowding effects on proteins predict increased stability. The data in Figure 1c are consistent with this expectation for temperatures below 308 K. The fact that $\mathrm{\Delta }{C}_P^{{°}^{\prime }}$ is greater than zero means that the stabilization turns to destabilization above this temperature. In addition, most hard‐core‐based theories predict that this stabilizing effect decreases with crowder molecular weight (Sharp, 2015), but we observe a sharp decrease followed by a slight increase. Simple theories also predict that stabilization is entirely entropic. This prediction is inconsistent with our observations (Figure 1d) and those of others (Speer et al., 2022). Since all the cosolutes are stabilizing ($\mathrm{\Delta \Delta }{G}_U^{{°}^{\prime }}>0$) and $\mathrm{\Delta \Delta }{H}_U^{{°}^{\prime }}$ is greater than $\mathrm{\Delta \Delta }{G}_U^{{°}^{\prime }}$, it necessarily follows that $‐T\mathrm{\Delta \Delta }{S}_U^{{°}^{\prime }}<0$ for all PEGs. Hence, the stabilization is entirely enthalpic, and the entropic effect is destabilizing (Figure S1).

The stronger stabilization at a given gram per liter concentration for low cosolute molecular weights (Figure 1c), in combination with the observation that plots of $\mathrm{\Delta \Delta }{G}_U^{{°}^{\prime }}$ and $\mathrm{\Delta \Delta }{H}_U^{{°}^{\prime }}$ against cosolute concentration for EG and small PEGs deviate from linearity (Figure 2a) led us to consider the existence of an attractive interaction of cosolute with the folded state of SH3. This idea is supported by analysis of chemical shifts (Figure 2b) and conclusions of a combined experimental and molecular dynamics study of EG and protein stability (Naidu et al., 2020). In agreement with (Knowles et al., 2015), the attractive interaction is likely associated with the hydroxyl groups on the cosolutes because the effect dies off at a fixed gram per liter PEG concentration with increasing PEG molecular weight.

3.2. PEG stabilization ascribed to crowding and adsorption

A model is required to gain molecular‐level information about the interactions that increase stability in PEG solutions. Here, we describe the model and the source of its parameters.

Consider a protein with two states, folded and unfolded, at equilibrium. The increase in stability can arise from two mechanisms. The first involves only crowding. Specifically, the folded state is stabilized relative to the unfolded state by excluding cosolute molecules from the larger solvent‐exposed surface of the unfolded state (Sapir & Harries, ^2015b). Stabilization by larger PEGs is explained by this mechanism. Stabilization by EG and smaller PEGs cannot be ascribed to crowder exclusion alone and follows the second mechanism, involving adsorption. Specifically, the folded state is stabilized by physical adsorption of cosolutes, as shown by the change in ¹⁹F chemical shift of the folded state for EG and small PEGs (Figure 2b).

The effects of cosolute exclusion are described by our recently developed model (Sapir & Harries, ^2015a, 2016, ²⁰¹⁷) that extends the Flory–Huggins (FH) mean‐field theory for binary solutions to ternary mixtures comprising solvent, cosolute, and protein. Specifically, the FH expressions are useful because they accurately depict the experiment‐derived water and cosolute chemical potentials over a wide range of concentrations and PEG sizes as well as their temperature dependence using few parameters.

In this model, the mixture is divided into a bulk domain and a protein surface domain (Figure 3a) of thickness, $a$ (Sapir & Harries, ^2015a, 2016). The transfer of protein into the binary solution induces a local change of composition in the protein domain, which directly translates to a change in solution free energy, even if there are only steric protein–crowder interactions. In particular, the two protein states induce different affected protein domain volumes resulting in a free energy difference between folded and unfolded states. The difference in protein domain volume originates in the different solute accessible surface areas ($\text{ΔSASA}$) in the folded and unfolded states. Since the unfolded protein is more disordered, the value $\text{ΔSASA}$ represents an average over many unfolded structures (see SI for more details). In our crowding model, the unfolding free energy is analogous to the free energy gained (or lost) upon insertion of a protein interface of size $\text{ΔSASA}$. The unfolding free energy is then given by, $\Delta \Delta G^{{°}^{\prime }}=\mathrm{\Delta \Delta }{G}_{\text{binary}}^{{°}^{\prime }}-\mathrm{\Delta \Delta }{G}_{\text{ternary}}^{{°}^{\prime }}$, where $\mathrm{\Delta \Delta }{G}_{\text{binary}}^{{°}^{\prime }}$ and $\mathrm{\Delta \Delta }{G}_{\text{ternary}}^{{°}^{\prime }}$ correspond to the system mixing free energies in absence and presence of the protein interface, respectively.

FIGURE 3.

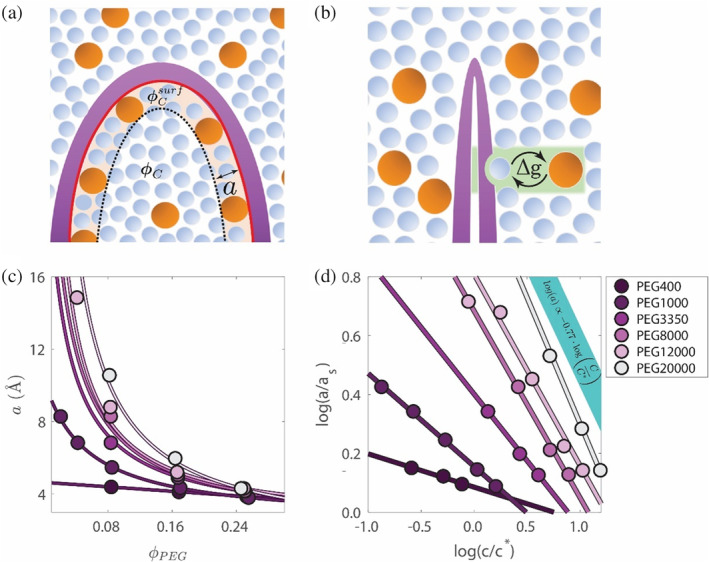
Protein unfolding models. Schematics of exclusion (a) and adsorption (b). The protein, cosolute, and solvent are shown in purple, orange, and blue, respectively. The surface domain (shaded yellow) thickness is indicated by $a$, and the relavent surface area of size $\mathrm{\Delta }\mathrm{SASA}$ is depicted in red. Since the protein domain in the exclusion model corresponds only to the interface that is buried in the folding process, only that part of the surface is marked. In panel b, the adsorption site and processes are shaded green. Values of $a$ that reproduce the experiment‐based unfolding free energies (c). Log–log plot of $a/a_s$ scaled to normalized mass concentration (d). $a$ scaling shown by linear fits; the blue bar represents the theoretical scaling law for polymer mesh size, $\xi$, in the semi‐dilute regime (de Gennes ¹⁹⁷⁹).

The mean‐field model allows us to solve the ternary mixture equilibrium condition (Equation S5 in the SI) using a small set of parameters: PEG excluded volume ($\nu$), nonideal solvent‐cosolute mixing ($\chi$), and soft protein–cosolute interactions that occur upon unfolding ($\epsilon$), all as a function of cosolute volume fraction (${\varphi }_C$). The parameter $\epsilon$ represents soft interactions in contrast to the hard‐core excluded volume interactions, embodied in the parameter $\nu$. Thus, $\epsilon$ corresponds to the free energy gain or loss associated with exposing the unfolded protein interface to the cosolute, measured relative to exposure to the pure solvent. Values of $\epsilon$ are protein specific but $\nu$ and $\chi$ are independent of protein identity and are measured in bulk binary solutions.

Values of $\nu$, quantified as the ratio of cosolute and solvent partial molar volumes $\left({\overline{V}}_C/{\overline{V}}_S\right)$, are derived for all PEGs from density measurements as a function of concentration (Figure S5). Values of $\chi$ are derived separately for nonvolatile (PEGs) and volatile (EG and diEG) cosolutes. For nonvolatile cosolutes, we extract $\chi$ by fitting PEG osmotic pressure at different concentrations and temperatures (Figure S6, Tables S3–S5). For EG and diEG, $\chi$ is derived by fitting vapor pressure data (Figures S7 and S8) because their high vapor pressure obviates use of our dew point osmometer. The enthalpic and entropic contributions to the nonideal interactions, ${\chi }_H$ and ${\chi }_{\mathit{TS}}$, are derived through a van ‘t Hoff analysis (Figure S9). Finally, the values of $\epsilon$ for SH3 with different cosolutes are derived by fitting the experiment‐derived $\mathrm{\Delta \Delta }{G}_U^{{°}^{\prime }}$ values.

To include effects of EG and small PEG stabilization through binding to the folded state, we use a discrete site model that describes the thermodynamics of cosolute adsorption and concomitant water release from specific binding sites (Figure 3b). We set the number of adsorption sites per protein to 1, resulting in a Langmuir‐like isotherm. Increasing the number of sites to 2 or 3 did not improve the quality of the fits to $\mathrm{\Delta \Delta }{G}_U^{{°}^{\prime }}$. Therefore, adsorption is described through a single equilibrium constant with an associated adsorption free energy ($\mathrm{\Delta }g$), enthalpy ($\mathrm{\Delta }h$), and entropy ($\mathrm{\Delta }s$) parameters. Finally, the bulk binary solution operates as a chemical reservoir for which the chemical potentials are derived from the appropriate FH expressions. Details about model derivation and parameter extraction from experiments are given in the SI.

3.3. Increased stability at higher PEG concentrations is limited because mesh size, $\xi$, decreases

The chemical shift perturbation data (Figure 2) indicate adsorption of EG and small PEGs to the folded state. The effects of these cosolutes are considered at the end of the Discussion.

Given the values for $\nu$ and $\chi$, $\mathrm{\Delta \Delta }{G}_U^{{°}^{\prime }}$ datasets for medium and large‐PEGs are fitted as a function of concentration to obtain $\epsilon$, the soft protein–cosolute interaction. Adsorption interaction parameters for the folded state, $\mathrm{\Delta }g$, $\mathrm{\Delta }h$, and $\mathrm{\Delta }s$, are set to $0$ for larger PEGs because experiments indicate no strong interactions between larger PEGs and the folded state (Figure 2).

We consider three direct, chemical, protein–PEG interactions: none, repulsive and attractive. We begin with no protein–cosolute interactions, $\epsilon =0$, so that any contribution that does not originate from excluded volume contributions stems from the cosolute–solvent interactions, $\chi \ne 0$. This is a reasonable starting point, since the excluded volume contribution of the larger PEGs is expected to dominate the net unfolding free energy, and $\mathrm{\Delta \Delta }{G}_U^{0\prime }$ increases with $\nu$ (Sapir & Harries, ^2015a). The possibility that $\epsilon \ne 0$ is discussed later. Unlike EG and smaller PEGs, the effective molecular volume of larger PEGs depends on concentration. In dilute aqueous solution, PEGs can be treated as a single chains in a good solvent (Zosel et al., 2020; de Gennes, ¹⁹⁷⁹; Devanand & Selser, ¹⁹⁹¹), and their size described by a concentration‐independent radius of gyration, $R_g$ (Lekkerkerker & Tuinier, 2011). The semi‐dilute region is reached at higher PEG concentrations where chain overlap begins. The overlap threshold concentration, in gram per liter, is given by $c^{*}=\left(M_{\mathrm{PEG}}/N_{\mathit{av}}{\overline{V}}_{\mathrm{PEG}}\right)\propto {R_g}^{-3}$ (Lekkerkerker & Tuinier, 2011; Zosel et al., ²⁰²⁰). In this regime, the polymer solution behaves like a network with an average mesh size, $\xi$, that is expected to follow the de Gennes scaling law, $\xi =R_g{\left(c/c^{*}\right)}^{-0.77}$ (de Gennes, ¹⁹⁷⁹). The semi‐dilute regime is reached in our experiments at high concentrations for PEGs larger than PEG1000. For PEGs larger than PEG3350, even the lowest concentrations are semi‐dilute (Table S6).

In our model, changes in PEG size between concentration regimes affect the unfolding free energy via the protein domain size, $a$, which should scale with cosolute size (Sapir & Harries, ^2015a). The size of $a$ impacts the unfolding free energy through the volume of the surface domain (Equation S3 in the SI). Specifically, a larger $a$ increases the contributions of excluded volume ($\nu$) and cosolute–solvent interactions ($\chi$). For small cosolutes, EG and small PEGs, the size is calculated as $a={\nu }^{\frac{1}{3}}$. For larger PEGs, $a$ increases with $R_g$ in the dilute regime (Lekkerkerker & Tuinier, 2011). In the semi‐dilute regime, $a$ is proportional to mesh size, $\xi$, which decreases with increasing concentration (de Gennes, ¹⁹⁷⁹). This decrease mitigates the stabilizing effect of PEG, whose expected impact on $\mathrm{\Delta \Delta }{G}_U^{{°}^{\prime }}$ would otherwise be too large compared to the values found by experiment if only simple excluded volume interactions are included.

We use $a$ as a single fitting parameter for experimental $\mathrm{\Delta \Delta }{G}_U^{{°}^{\prime }}$ values for cosolutes larger than PEG400 for all values of $\epsilon$; attractive, repulsive and noninteracting. Figure 3c shows the fitted values of $a$ versus PEG volume fractions that best match the experimental $\mathrm{\Delta \Delta }{G}_U^{{°}^{\prime }}$ for $\epsilon =0$ (details of fitting procedure in the SI). The model reproduces the data for medium and large PEGs (Figure 4a,b).

FIGURE 4.

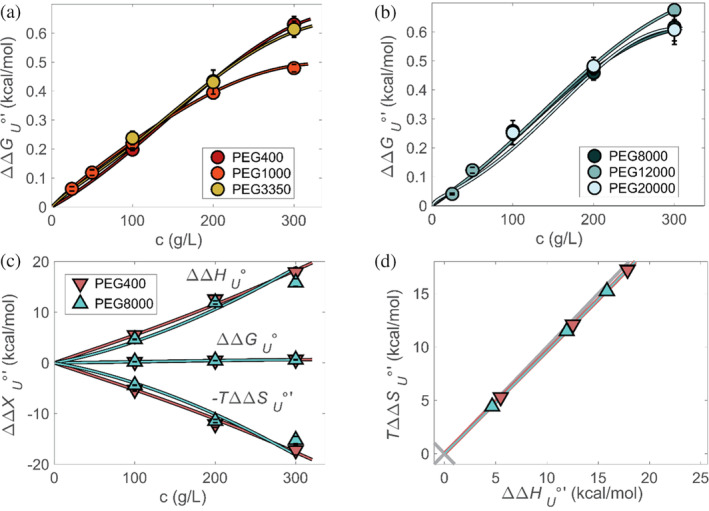
Fits to changes in unfolding free energy for medium and large PEGs (a, b). PEG400 and PEG8000 enthalpy–entropy concentration plots (c) and the corresponding enthalpy–entropy plot (d). Experiment‐based data, at 298 K, are shown as triangles.

The values of $a$ relative to water's molecular dimension, $a_s\approx 3 \mathrm{\AA }$, are shown on a log–log plot (Figure 3d). The slopes gradually decrease with PEG size from $-0.12$ for PEG400 to $-0.84$ for PEG20000. For large PEGs $a\approx \xi$, which agrees with the scaling law prediction (blue bar, Figure 3d). For the medium‐sized PEGs a different, weaker change of $a$ with concentration is observed. This weaker dependence is expected because most measurements are performed below $c^{*}$, where changes in typical polymer size are smaller. In summary, the stabilization of large PEGs at higher concentration is limited by the decreased mesh size and concomitant decrease in the protein domain volume.

3.4. Stabilization arises from polymer excluded volume and polymer–solvent nonideal mixing, but exothermicity is dominated by polymer–protein chemical interactions

Next, we turn to the enthalpic and entropic components. To account for the strong enthalpic effects (Figure 1d) we resolve the cosolute–protein surface interaction parameter into its entropic and enthalpic contributions, $\epsilon ={\epsilon }_H-{\epsilon }_{\mathit{TS}}$ (Sapir & Harries, ^2015a). We begin by assuming $\epsilon =0$, and therefore its enthalpic and entropic contributions are equal in size and opposite in sign. The entropic component, ${\epsilon }_{\mathit{TS}}$, is used as a fitting parameter for experimental results of entropy and enthalpy versus concentration (Figure 4c,d). For all PEGs, we find that ${\epsilon }_{\mathit{TS}}=0.6\pm 0.1$.

The positive value of ${\epsilon }_{\mathit{TS}}$ is consistent with protein‐adjacent PEG molecules facilitating release of water constrained to the surface of the unfolded protein when PEG interacts with the surface. This increase in the translational entropy of water molecules as they join the bulk has also been observed, for example, for the polymer xyloglucan near the surface of cellulose (Benselfelt et al., 2016; Kishani et al., ²⁰²¹). However, the exposure of SH3 surface to PEG comes with a compensating enthalpic penalty, that is, ${\epsilon }_H>0$. It is this interaction that leads to most of the observed enthalpic effect, which is not predicted by classic theories.

The contributions of $\nu$, $\chi$, and $\epsilon$ to $\mathrm{\Delta \Delta }{G}_U^{{°}^{\prime }}$, $\mathrm{\Delta \Delta }{H}_U^{{°}^{\prime }}$, and $T\mathrm{\Delta \Delta }{S}_U^{{°}^{\prime }}$ are presented in Figure 5a,b for PEG8000, but the effect is general to all PEGs (Figure 5c). Again, the changes in enthalpy and entropy are large, but there is no net effect of protein–cosolute interactions on $\mathrm{\Delta \Delta }{G}_U^{{°}^{\prime }}$, because we set $\epsilon =0$ (Figure 5a, green curve). Therefore, $\mathrm{\Delta \Delta }{G}_U^{{°}^{\prime }}$ arises solely from noncompensating contributions from the sum of excluded volume ($\nu$) and nonideal cosolute–solvent interactions ($\chi$). Excluded volume interactions result in a strong entropic stabilization $T\mathrm{\Delta \Delta }{S}_{U,\nu }^{{°}^{\prime }}$ (blue curve), while nonideal cosolute–solvent interactions, $\chi$, result in enthalpic stabilization ($\mathrm{\Delta \Delta }{H}_{U,{\chi }_H}^{{°}^{\prime }}$, yellow) but entropic destabilization ($T\mathrm{\Delta \Delta }{S}_{U,{\chi }_{\mathit{TS}}}^{\circ \prime }$, orange). The entropic contributions of $\nu$ and ${\chi }_{\mathit{TS}}$ oppose each other, while the enthalpic contribution of ${\chi }_H$ is entirely stabilizing. The stabilization from is due to release of solvent molecules to the bulk upon folding (Sapir & Harries, 2017), which in turn increases enthalpic PEG‐solvent mixing (${\chi }_H<0$).

FIGURE 5.

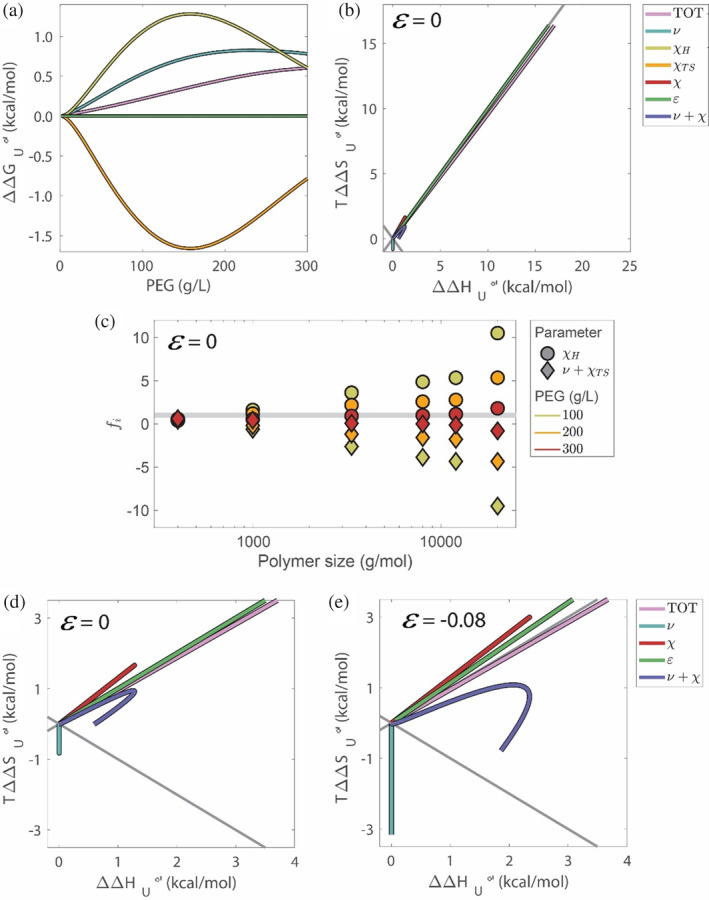
Contributions of $\nu$, ${\chi }_H$, ${\chi }_{\mathit{TS}}$, and $\epsilon$ with and without chemical interactions at 298 K. Contributions for PEG8000 to $\mathrm{\Delta \Delta }{G}_U^{\circ \prime }$ (a) and $T\mathrm{\Delta \Delta }{S}_U^{\circ \prime }$ versus $\mathrm{\Delta \Delta }{H}_U^{\circ \prime }$(b), for $\epsilon =0$. Relative contributions, $f$, of ${\chi }_H$ and $\nu +{\chi }_{\mathit{TS}}$ to the total free energy compared to buffer for different PEG sizes and concentrations (c). The gray line represents $f_{{\chi }_H}+f_{\nu +{\chi }_{\mathit{TS}}}=1$. Low $\mathrm{\Delta \Delta }{H}_U^{\circ \prime }$ and $T\mathrm{\Delta \Delta }{S}_U^{\circ \prime }$ regime of the entropy–enthalpy plot from panel b for $\epsilon =0$ (d), and $\epsilon =-0.08$ (e).

The partitioning into entropic and enthalpic contribution due to $\nu$, $\chi$, and $\epsilon$ can be followed using the enthalpy–entropy plot (Figure 5b). The largest contribution to $\mathrm{\Delta \Delta }{H}_U^{\circ \prime }$ and $T\mathrm{\Delta \Delta }{\mathrm{S}}_U^{\circ \prime }$ comes from ${\epsilon }_H$ and ${\epsilon }_{\mathit{TS}}$, respectively, but these contributions overlap the diagonal because they are completely compensatory, ${\epsilon }_H={\epsilon }_{\mathit{TS}}$. If protein stabilization does not arise from protein–cosolute interactions, where does it come from?

Deviation toward stabilization (i.e., below the diagonal in Figure 5b) is fully accounted for by the combination of $T\mathrm{\Delta \Delta }{\mathrm{S}}_{U.\nu }^{\circ \prime }$ and $\mathrm{\Delta \Delta }{G}_{U,\chi }^{\circ \prime }$ (purple curve), which are related to a combination of PEG's excluded volume and the increased solvent–cosolute nonideal mixing upon folding. The stabilizing contribution of $\mathrm{\Delta \Delta }{H}_{U,{\chi }_H}^{\circ \prime }$ is consistently larger than the sum $T\mathrm{\Delta \Delta }{S}_{U,\nu }^{\circ \prime }+T\mathrm{\Delta \Delta }{S}_{U,{\chi }_{\mathit{TS}}}^{\circ \prime }$, which is destabilizing under almost every condition. Stabilization is then entirely due to the heat released when both PEG and water are liberated from the protein domain into the bulk solution upon folding. This contribution persists even in the absence of a contribution from direct protein–PEG chemical interactions (panel b purple curve).

It is illuminating to consider the relative contributions of terms related to ${\chi }_H$ and the summed contribution of $\nu$ and ${\chi }_{\mathit{TS}}$ to the total free energy difference as a function of PEG size and concentration (Figure 5C, Table S6). This is calculated using $f_i=\mathit{\Delta \Delta }{G}_{U,i}^{°\prime }/\mathit{\Delta \Delta }{G}_U^{°\prime }$, where $f_i$ is the relative contribution of the $i$‐th parameter, that is, ${\chi }_H$ or $\nu$ plus ${\chi }_{\mathit{TS}}$; $\mathrm{\Delta \Delta }{G}_{U,i}^{°\prime }$ is the unfolding free energy relative to buffer originating from the $i$‐th term; and $\mathrm{\Delta \Delta }{G}_U^{°\prime }$ is the total free energy relative to buffer. The gray line in Figure 5c indicates the sum of $f_{{\chi }_H}$ and $f_{\nu +{\chi }_{\mathit{TS}}}$ that equals $1$ (because $\epsilon$ is set to $0$). Notably, the relative contribution to stabilization from the enthalpic term increases with PEG size, with a corresponding increase of entropic destabilization. Moreover, the degree of enthalpy–entropy compensation of these interactions, that finally determines $\mathrm{\Delta \Delta }{G}_U^{°\prime }$, decreases with PEG concentration. Only for PEG400 are both contributions, ${\chi }_H$ and the joint term from $\nu$ and ${\chi }_{\mathit{TS}}$, stabilizing at all concentrations, which is a result of the lower entropic penalty of $T\mathrm{\Delta \Delta }{S}_{U,{\chi }_{\mathit{TS}}}^{\circ \prime }$ for smaller PEGs.

3.5. For larger PEGs, direct PEG–Protein chemical interactions are absent or slightly destabilizing

For completeness, we considered the possibility that $\epsilon \ne 0$. For repulsive interactions, $\epsilon >0$, the fitted protein domain size falls sharply below the size of a water molecules, $a<a_s$, even at $\epsilon =0.06$, which is the smallest PEG–protein interaction reported (Sapir & Harries, ^2015a). This result is nonphysical, indicating that a repulsive chemical protein–PEG interaction is unlikely. For attractive interactions, $\epsilon <0$, specifically $\epsilon =-0.08$, which agrees with favorable EG–surface interactions (Table S7), the fitted protein domain size shows similar scaling behavior to that of $\epsilon =0$, with $a\propto \xi$ for large PEGs (Figure S10). This agreement suggests that we cannot rule out weak protein‐PEG attractive soft interactions, as has been observed for other proteins (Speer et al., 2022; Bhat & Timasheff, ¹⁹⁹²), yet this choice of $\epsilon$ does not affect the fit value for ${\epsilon }_{\mathit{TS}}$, which remains $0.6\pm 0.1$. Thus, although weak direct attractive (destabilizing) chemical interactions between larger PEGs and protein cannot be excluded, they do not change the conclusions from the fits derived by setting $\epsilon =0$.

We next compare the thermodynamics with and without attractive chemical interactions (Figure 5d,e). For $\epsilon =-0.08$ the contribution of $\epsilon$ to the free energy is destabilizing (i.e., above the diagonal), with ${\epsilon }_H$ and ${\epsilon }_{\mathit{TS}}$ still dominating the enthalpy–entropy plot. This destabilization is followed by enhancement of all other contributions, both stabilizing ($T\mathrm{\Delta \Delta }{S}_{U,\nu }^{\circ \prime }$ and $\mathrm{\Delta \Delta }{H}_{U,{\chi }_H}^{\circ \prime }$) and destabilizing ($T\mathrm{\Delta \Delta }{S}_{U,{\chi }_{\mathit{TS}}}^{\circ \prime }$). The enhanced effect of $T\mathrm{\Delta \Delta }{S}_{U,\nu +{\chi }_{\mathit{TS}}}^{\circ \prime }$ and $\mathrm{\Delta \Delta }{H}_{U,{\chi }_H}^{\circ \prime }$ is directly linked to the increase in protein domain size that we find for $\epsilon <0$. Taken together, the contributions that originate with $\nu$ and $\chi$ are more stabilizing for $\epsilon =-0.08$ compared to $\epsilon =0$, which compensates for the destabilizing contribution that stems from setting $\epsilon <0$. Overall, the mechanism of stabilization remains enthalpic even when we account for soft interactions and is due to increased solvent‐PEG mixing.

3.6. Stabilization by small PEGs is due to their adsorption to the folded state

The effects of EG and smaller PEGs are more complicated. For these cosolutes, which show a strong attractive interaction to the folded state (Figure 2), the parameters for interactions with the unfolded ($\epsilon$) and folded ($\mathrm{\Delta }g$) state are determined by fitting $\mathrm{\Delta \Delta }{G}_U^{\circ \prime }$ as follows. First, the contribution of cosolute exclusion from the unfolded protein is solved for a range of $\epsilon$ values, resulting in a matrix of free energies where each column is associated with a different $\epsilon$ as function of concentration. For these cosolutes, the protein domain size does not depend on the concentration and is equal to the linear dimension of the cosolute, $a={\nu }^{1/3}$. Then the $\epsilon$‐dependent free energies are subtracted from the experiment‐derived free energy, resulting in the free energies associated with adsorption to the folded state alone. For each of these adsorption free energies, the value of $\mathrm{\Delta }g$ is determined by fits to our discrete site model. Finally, we choose the $\epsilon$ and $\mathit{\Delta g}$ pair that results in the minimal root mean square deviation in the fit. The fits overlap the experiment‐based free energies (Figure 6a). We conclude that adsorption to the folded state dominates stabilization.

FIGURE 6.

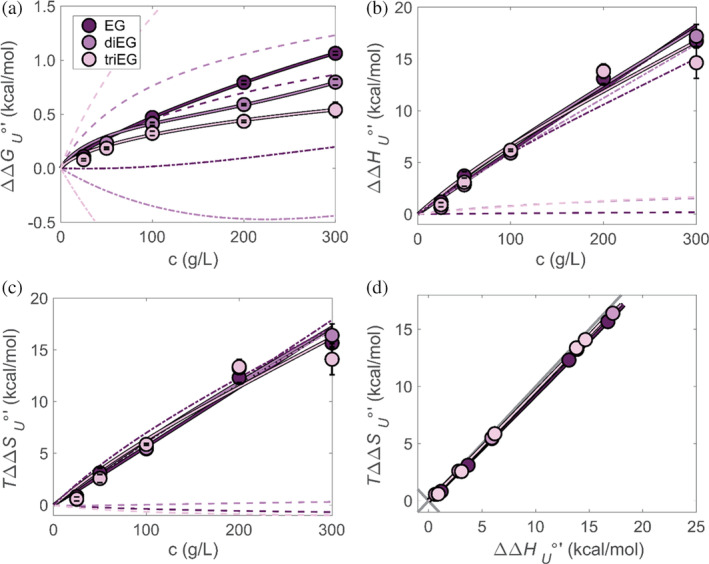
Change of SH3 unfolding free energy (a), enthalpy (b) and entropy (c) all relative to buffer as a function of EG, diEG, and triEG concentration at 298 K. Fits are to the effect of crowding on unfolding free energy (dashed‐dotted curves) and adsorption to the folded state (dashed curves). Plot of the enthalpic against the entropic components (d).

The negative values of $\epsilon$ and $\mathrm{\Delta }g$ (Table S7) correspond to an attractive soft interaction between the cosolute in both the folded and unfolded states. These interactions are reflected in the chemical shift data for the folded state $\mathrm{\Delta }\delta$ (Figure 2b). Although adsorption to the folded state is stabilizing, chemical attraction to the unfolded state reduces the stability. This destabilization is expected for strongly accumulated cosolutes that are overall preferentially included at the protein domain (Timasheff, 2002; Street et al., ²⁰⁰⁶). Moreover, the larger binding interaction, $\mathrm{\Delta }g$, for triEG compared to diEG, and diEG compared to EG, explains why we observe only small EG‐induced shift changes from the folded state, while triEG shows the largest shifts (Figure 2b). We suggest that EG's destabilizing effect arising from its soft interactions with the unfolded state is offset by its steric induced preferential hydration of the unfolded state as discussed by Naidu et al. (2020). For diEG and triEG, accumulation around the folded state exceeds the effect of preferential interaction with the unfolded state (Figure 6a).

The components of $\mathrm{\Delta }g=\mathrm{\Delta }h-T\mathrm{\Delta }s$ are extracted by fitting the measured $\mathrm{\Delta \Delta }{H}_U^{\circ \prime }$ and the derived $T\mathrm{\Delta \Delta }{S}_U^{\circ \prime }$, using ${\epsilon }_{\mathit{TS}}=0.6$ as determined from the medium‐large PEG data. Analogous to the fitting procedure for the free energy, the exclusion contribution to the enthalpy and entropy are calculated from ${\epsilon }_{\mathit{TS}}$ (${\epsilon }_H$ is then determined from $\epsilon$ and ${\epsilon }_{\mathrm{TS}}$), and a corresponding $\mathit{\Delta s}$ from the remainder of the unfolding enthalpy. The final value of $\mathrm{\Delta }s$ (i) minimizes the root mean squared deviation of the calculated enthalpy and (ii) reproduces the concentration dependence of both the enthalpy and entropy (Figure 6b,c).

The fits resulting in $\mathrm{\Delta }s$ are presented in an enthalpy–entropy plot (Figure 6d). The experiment‐based thermodynamic fingerprint for the effect of EG and small PEGs agrees with the fit. The contributions of crowding and adsorption (Figure 6b,c) show that the enthalpic and entropic parts stem mainly from the preferential interaction of the cosolutes with the unfolded state. The adsorption to the folded state, by contrast, involves weak interactions that result in low entropy–enthalpy compensation, but overall stabilize the folded state.

4. CONCLUSIONS

The stability of folded proteins is strongly influenced by the concentration and chemical identity of surrounding cosolutes. The main goal of this work is to understand the molecular‐level mechanisms of protein stabilization. We followed the changes in stability of the reversible and two‐state SH3 domain protein in the presence of PEGs of different molecular weights and concentrations and at a range of temperatures. These measurements provide a dataset useful for testing any theory of macromolecular crowding.

The prevailing models used to study the effects of crowding on protein stability are usually limited to entropic effects because of their exclusive consideration of excluded volume interactions. Although these steric effects play a significant role in protein stabilization, they do not act alone. Specifically, the net stabilizing $\mathrm{\Delta \Delta }{H}_U^{\circ \prime }$ observed for all PEGs is inconsistent with simple theories based exclusively on hard interactions. Inconsistencies have also been reported in other systems; for instance, attractive chemical interactions between PEGs and proteins, protein destabilization by PEG, increased protein stability only at low temperatures or with certain PEG sizes (Ahmad Parray et al., 2021; de Lencastre Novaes et al., ²⁰¹⁰; Hancock & Hsu, ¹⁹⁹⁶; Kumar, ²⁰⁰⁹; Lee & Lee, ¹⁹⁸⁷; Naidu et al., ²⁰²⁰; Parray et al., ²⁰²¹; Raina et al., ²⁰²¹; Wang et al., ²⁰²¹), and even crowding effects on RNA folding (Sung & Nesbitt, 2021). Our model, therefore, considers the effect of PEGs and other cosolutes through their preferential interaction with the protein surface that is exposed in the unfolded state and is buried during folding. We also consider the possibility of favorable interaction of small PEGs with the folded state. Importantly, all interaction parameters in the model have entropic and enthalpic components except for the excluded volume term, which is completely entropic.

Application of the new model suggests that the stabilizing effect of small PEGs arises from binding to the folded state, while attraction to the unfolded state is destabilizing. Specific binding of smaller PEGs, up to tetraEG, is supported by a strong change in folded state NMR chemical shift (Figure 2b). This cosolute binding is characterized by weak enthalpy–entropy compensation, and most of the measured heat release originates from the enthalpic penalty of PEG's soft interaction with the unfolded state.

As PEG size increases, the effect on stability become associated with their polymeric nature. For PEG400 and larger PEGs, binding to the folded state is insignificant as assessed by NMR and is not required to explain the data. Our model suggests that although most of the enthalpic signature for large PEGs originates from protein–PEG soft interactions, these interactions are largely compensated by a corresponding entropy and do not significantly impact stabilization. Specifically, the enthalpic and entropic components of the protein–PEG soft interactions fully compensate or are slightly destabilizing. The stabilization mechanism remains overall enthalpic, even if soft‐interactions are not considered, because of the increase in nonideal solvent‐PEG mixing upon protein folding with concomitant PEG and water release. Taken together, the contributions that favor stabilization of SH3 by large PEGs come from excluded volume interactions and nonideal mixing. Therefore, it is incorrect to interpret the positive $\mathrm{\Delta \Delta }{H}_U^{\circ \prime }$ as evidence of strongly attractive crowder‐protein interactions. This is an oversimplification that neglects another important contribution, and in this case, the dominant one: the change in nonideal cosolute‐water mixing contributions.

Our work sheds light on the effect of crowding and molecular‐level interactions in solution that lead to protein stability. This is a first step toward the goal of understanding how crowding and additional protein–protein interactions affect proteins in living systems. Unfortunately, the systematic study of proteins directly in their biologically relevant environment, such as the living cell, is experimentally and theoretically challenging. Yet data acquired from dedicated experiments that include temperature‐dependent information will be useful in building an understanding of macromolecular crowding, which can then be interpreted through improved models. This comprehensive foundation is necessary for devising predictive theories of crowding that can be applied not only to protein stabilization but also to the formation of biologically relevant protein complexes, protein aggregation and fibrillation, and phase separation of biomacromolecules in the crowded environments of cells.

AUTHOR CONTRIBUTIONS

Claire J. Stewart: Conceptualization (lead); data curation (lead); formal analysis (lead); investigation (lead); methodology (lead); validation (lead); visualization (lead); writing – original draft (lead); writing – review and editing (lead). Gil I. Olgenblum: Conceptualization (lead); data curation (lead); formal analysis (lead); investigation (lead); methodology (lead); validation (lead); visualization (lead); writing – original draft (lead); writing – review and editing (lead). Ashlee Propst: Investigation (supporting); methodology (supporting); validation (supporting). Daniel Harries: Conceptualization (lead); funding acquisition (lead); project administration (lead); writing – original draft (equal); writing – review and editing (equal). Gary J. Pielak: Conceptualization (lead); funding acquisition (lead); project administration (lead); writing – original draft (equal); writing – review and editing (equal).

CONFLICT OF INTEREST STATEMENT

The authors declare no competing financial interest.

Supporting information

Data S1: Supporting Information

Stewart CJ, Olgenblum GI, Propst A, Harries D, Pielak GJ. Resolving the enthalpy of protein stabilization by macromolecular crowding. Protein Science. 2023;32(3):e4573. 10.1002/pro.4573

DATA AVAILABILITY STATEMENT

All data are included in the manuscript and/or supporting information.