Non-invasive monitoring of blood oxygenation in human placentas via concurrent diffuse optical spectroscopy and ultrasound imaging

Abstract

Direct assessment of blood oxygenation in the human placenta can provide information about placental function. However, the monitoring of placental oxygenation involves invasive sampling or imaging techniques that are poorly suited for bedside use. Here we show that placental oxygen haemodynamics can be non-invasively probed, in real time, up to 4.2 cm below the body surface via concurrent frequency-domain diffuse optical spectroscopy and ultrasound imaging. We developed the multimodal instrument to facilitate assessment of anterior placental properties by leveraging image-reconstruction algorithms that integrate ultrasound information about the morphology of tissue layers with optical information on haemodynamics. In a pilot investigation involving pregnancies in the third trimester, we studied women with normal (15) or some type of abnormal (9) placental function. We found no significant differences in baseline haemoglobin properties, but we found statistically significant differences in the placental haemodynamic responses to maternal hyperoxia. The results suggest that non-invasive monitoring of placental oxygenation may aid the early detection of placenta-related adverse pregnancy outcomes and maternal vascular malperfusion.

Editorial summary

Concurrent frequency-domain diffuse optical spectroscopy and ultrasound imaging can be used to non-invasively monitor placental oxygen haemodynamics in pregnant women in real time.

Abnormal placental development is widely accepted as the cause of common adverse pregnancy outcomes (APOs) such as hypertensive disorders, foetal growth restriction and stillbirth. Moreover, placental dysfunction has been associated with morbidities in offspring, including perinatal mortality and long-term neurodevelopmental and cardiovascular consequences^1–3. To better understand human placental dysfunction associated with these APOs, non-invasive methods that measure placental oxygen dynamics are needed. Ultrasound imaging is the primary clinical modality used for assessing pregnancy. Although ultrasound imaging can provide indirect information about flow resistance in large blood vessels, it is used primarily to derive morphological information. In fact, clinical ultrasound guidelines do not include direct functional assessment of the placenta⁴.

Current knowledge about placental biology has been gleaned largely from ex vivo tissue and from animal research^5,6. Yet these models have limitations for the understanding of dynamical changes in placental pathophysiology during pregnancy^7,8. Similarly, the literature on placental oxygenation is derived largely from decades-old sheep studies and from scant human data using invasive sampling techniques that have yielded varying results^7,9. And magnetic resonance imaging (MRI) approaches for assessing placental oxygenation^10,11 are poorly suited for bedside monitoring, and generally rely on indirect signals¹².

Here we report the development of an instrument and methodology based on diffuse optical spectroscopy (DOS) and ultrasound that facilitates the measurement of oxygen haemodynamics in complex organs such as the placenta, which is buried far below the tissue surface amidst intervening layered tissues. DOS measures oxy-haemoglobin and deoxy-haemoglobin concentrations, and it has been successfully employed for the assessment of tissue haemodynamics^13–21 in clinical problems such as breast cancer diagnosis and therapy monitoring^19,22, brain function²³ and injury monitoring¹⁷. In most of these applications, however, reflected light penetration was limited to less than 2 cm below the surface^24,25. The new instrumentation and algorithms that we here report provide improvements in methodology needed to measure the oxygen haemodynamics of the anterior placenta amidst intervening heterogeneous tissue layers. Our human clinical measurements probed placental tissue located as deep as 4.2 cm below the surface, albeit more typically in the 2.3–3.3-cm range. These improvements enable continuous data collection for functional studies of the placenta at the bedside, and may create opportunities for the investigation of haemodynamics in other deep organs.

Continuous-wave diffuse optical spectroscopy (CW-DOS) has been explored for the non-invasive measurement of placental blood oxygenation^26–28, and some of this early research suggested that higher placental tissue oxygen at baseline can arise in patients with intrauterine growth restriction^26,28. Although encouraging, these early measurements had limitations. The instruments used comparatively short source-detector separations (~4 cm) on the tissue surface, which limited the penetration of light to ~2 cm. Furthermore, the analysis of CW data requires major assumptions about tissue homogeneity and tissue scattering that prevent the quantification of absolute oxy-haemoglobin and deoxy-haemoglobin concentrations²⁹ and that do not account for the layered morphology of the abdomen. This early work also pointed to clear avenues for improvement. Our work benefits from a more accurate implementation of light-transport models^13–15,30, and from sophisticated frequency-domain and time-domain (FD-DOS, TD-DOS) optical instrumentation that permits the relaxation of assumptions about tissue scattering and homogeneity^13,14,31. Tissue-phantom experiments indicate signal-to-noise ratios (SNRs) sufficient to permit source-detector separations (SDSs) as large as 10 cm, which could enable light penetration of ~5 cm, thus improving on previous SDS records^32–34. Importantly, the optical instrument is integrated with ultrasound imaging in the same probe head²². This multimodal FD-DOS/US combination facilitates the integration of anatomic ultrasound information about tissue-layer morphology with functional haemodynamic information about deep tissues from FD-DOS. The anatomic information enables tissue-specific and layered image reconstruction that separates the haemodynamic properties and responses of deep tissues, such as the placenta, from those of overlying layers.

We validated the methodology in layered tissue phantoms, and show its feasibility and utility by direct in vivo assessment of human placental oxygenation in 24 participants. Specifically, we measured placental oxy-haemoglobin $\left[Hb{O}_2\right]$ and deoxy-haemoglobin $\left[Hb\right]$ concentrations or, equivalently, total haemoglobin $\left[H{b}_T\right]$ concentration and oxygen saturation $(St{O}_2)$. We performed reproducibility and stability tests to characterize the technology. We also collected average tissue properties from each woman. We also show the detection of changes in dynamic placental oxygenation in maternal hyperoxia experiments by varying the maternal position. Notably, our pilot study shows that placental oxygen haemodynamics during maternal hyperoxia are significantly associated with placenta-related APOs and with placental maternal vascular malperfusion (MVM), a primary histopathologic pattern characteristic of placental dysfunction strongly associated with APO and with the risk of long-term disease^35,36. Our findings suggest the possibility of the non-invasive detection of placental dysfunction for the generation of improved clinical understanding of placental pathophysiology in vivo.

Results

FD-DOS instrumentation

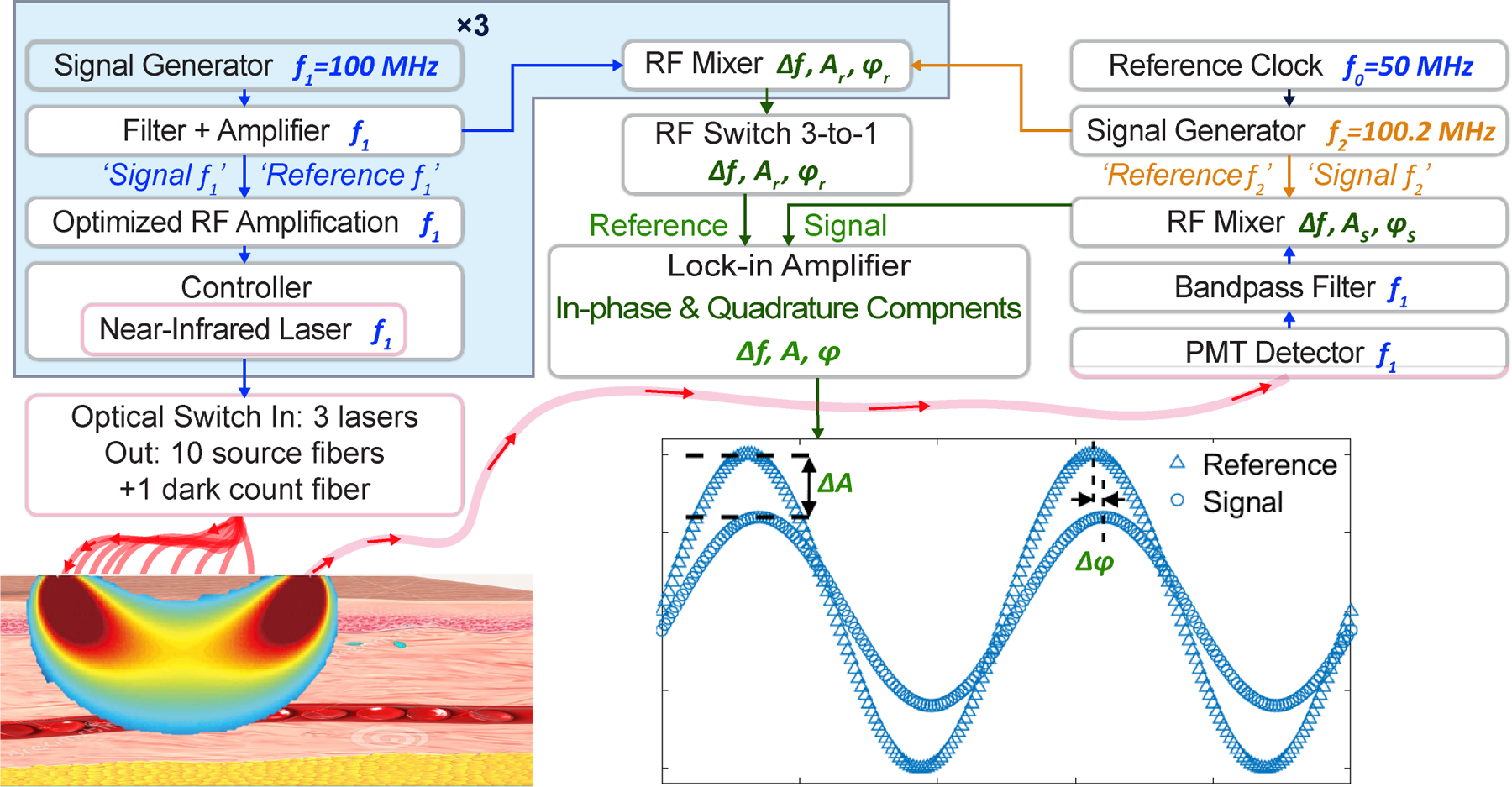
To measure placental oxygen haemodynamics in vivo, we built a low-noise heterodyne instrument for frequency-domain diffuse optical spectroscopy (FD-DOS). Tissue-phantom experiments showed that the instrument has a sufficient dynamic range and SNR to perform accurate FD-DOS measurements at SDSs of 10 cm. In the clinic, these capabilities facilitated quantitative determination of $\left[Hb{O}_2\right]$, $\left[Hb\right]$ and $\left[H{b}_T\right]$ concentrations as well as $\left(St{O}_2\right)$ of anterior placental tissue located as deep as 4.2 cm below the skin surface. Fig. 1a shows key features of the custom heterodyne FD-DOS instrument (details in Methods). It employs three lasers with wavelengths of 785, 808 and 830 nm. The output of each laser is radiofrequency (RF) amplitude-modulated at $f_1=100 MHz$. A new technical feature of the instrument is its nearly 100% laser-modulation depth. To achieve this improvement, we divided the source driver signal into four sub-signals, amplified each sub-signal in multiple stages with low-noise linear amplifiers, and then recombined and impedance-matched the amplified sub-signals for input to the laser drivers. Each laser’s RF driver power was individually optimized to achieve >90% light-modulation depth, thereby increasing the modulated diffusive-wave amplitude and decreasing the (unmodulated) background diffuse light. As a result, measurement SNRs were significantly better than in previous work^32,33 (specifically, by more than 20dB for an SDS of 8 cm), enabling longer distance SDS measurements with low laser powers (~40 mW).

Fig. 1 |. Integrated FD-DOS / US placenta instrumentation and three-layer modelling.

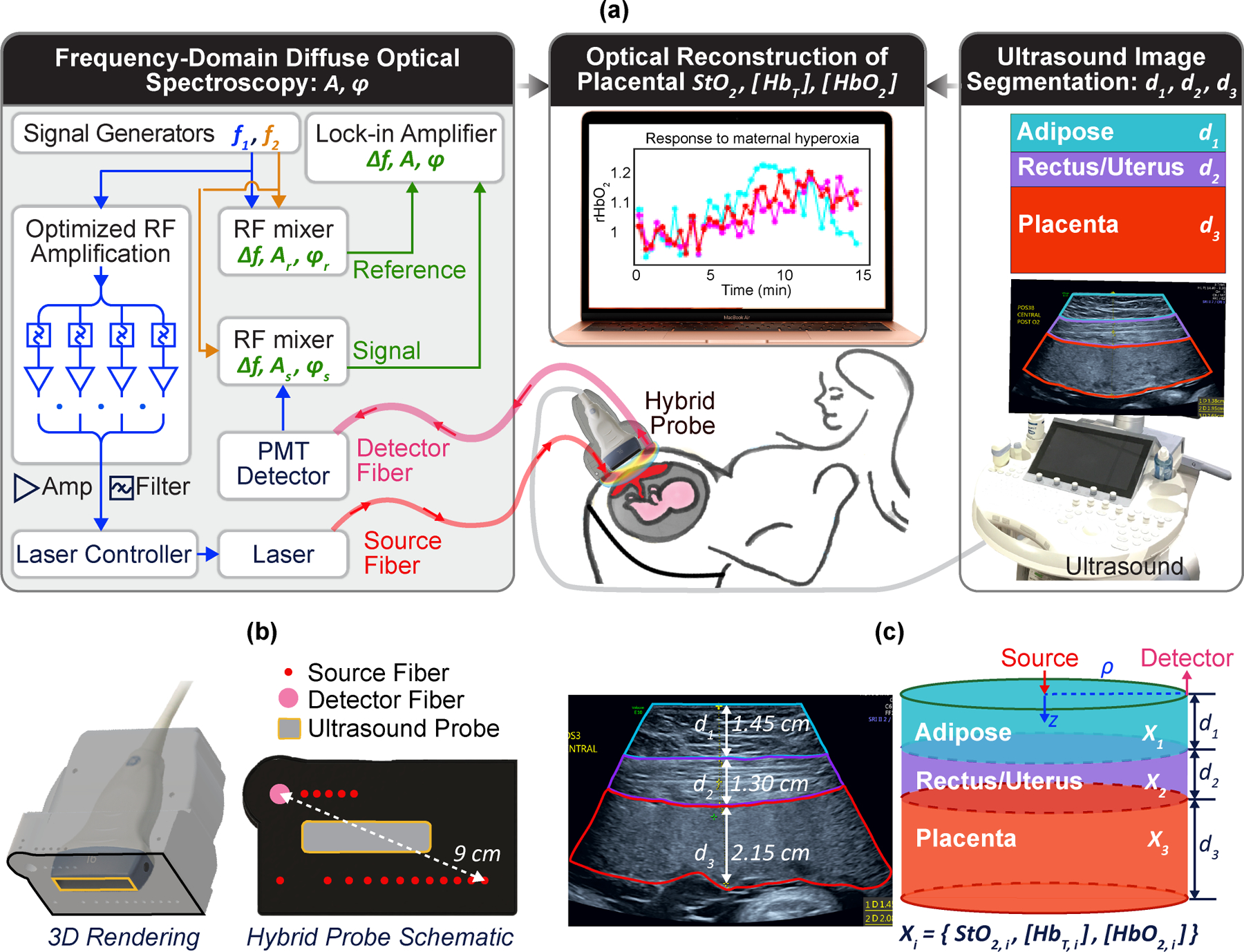
a, Schematic of the hybrid FD-DOS/US instrumentation showing laser-amplitude-modulation electronics, tissue light transmission, PMT detection, heterodyne mixing for frequency down-conversion, lock-in detection of light wave amplitude/phase, simultaneous ultrasound-image segmentation, and optical-image reconstruction of placental haemoglobin properties. b, 3D rendering and bottom-view of the probe showing FD-DOS/US integration into a single-probe head. c, Ultrasound image showing anatomical ‘segmented’ regions and the corresponding three-layer model for optical-image reconstruction.

The optoelectronic components were fibre-coupled into a custom optical probe head, within which a commercial ultrasound probe was mounted. Optical source fibres in this probe offer 17 SDSs for measurements ranging between 1 and 9 cm in humans (Fig. 1b). During measurements in the participants, 10 source-fibre locations are chosen to optimize coverage over the anatomic regions of interest for each woman, and we scanned sequentially through them. At the end of each cycle, a dark count measurement is made to correct for systemic noise. A high-transmission liquid light guide (detector fibre) with 5 mm in core diameter collects and directs light to a photomultiplier tube (PMT) detector. The PMT electrical signal is mixed with another RF wave at $f_2=100.2 MHz$ to generate heterodyne down-converted signals $\left(\Delta f=f_1-f_2=0.2 MHz\right)$. A high-sampling-rate lock-in amplifier captures amplitude and phase of the diffuse light waves.

Concurrent optical and ultrasound imaging

Custom integration of optics with a commercial ultrasound system (9L-D probe, Voluson E10, GE Healthcare) provides another substantial technical improvement over prior work³⁷. The custom probe facilitates concurrent measurement of tissue layer morphology and tissue physiological properties. This concept has been employed in breast cancer research²², but much deeper light penetration is required for the placenta. The ultrasound transducer at the probe’s centre generates images (Fig. 1c) that we used to segment target tissue into distinct layers that constrain optical reconstruction algorithms.

Differently from prior placenta research^26–28, we used tissue layer morphology from ultrasound imaging to constrain the photon-diffusion tomographic inverse problem. In practice, we model the abdomen as three-layers: adipose, rectus/uterus, and placental tissue. We approximate each layer as homogeneous and laterally infinite, but with thickness and depth determined by ultrasound (Fig. 1c).

The measurement geometry and modelling are shown in Fig. 1c. $\rho$ is the SDS on the tissue surface. With measured layer thicknesses and optical and physiological properties for each layer as inputs, standard methods^38,39 can be readily employed to generate predictions for the detected light-fluence rate on the tissue surface. Fig. 2a outlines our three-step reconstruction procedure (details in Methods). Briefly, each step of the three-step reconstruction finds ‘best’ tissue properties by minimizing the differences between the measured data and the predictions of diffuse optical tissue models of increasing complexity.

Fig. 2 |. Three-layer-model reconstruction algorithm and phantom-validation experiments.

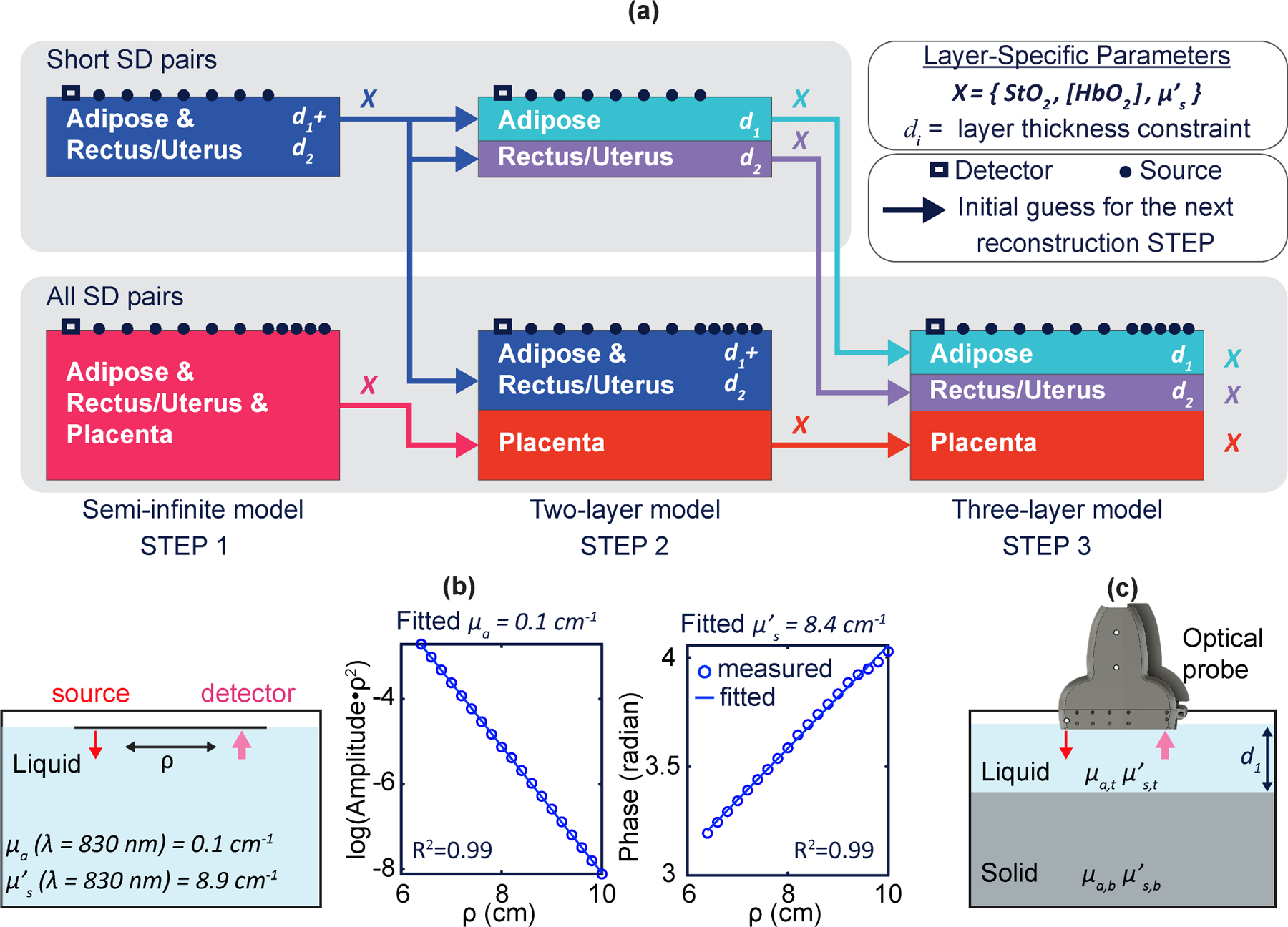
a, Three-layer-model initialization and reconstruction procedures. b, Tissue-simulating-phantom experiment for validating the accuracy and depth sensitivity of the optical properties. A translation stage moves the source fibre across the phantom for measurements at SDSs ranging from 6.2 cm to 10 cm. Nonlinear semi-infinite fitting is performed to reconstruct phantom absorption and scattering coefficients $\left(\lambda =830nm\right)$. c, Schematic of a two-layer phantom experiment.

Step 1 assumes that the underlying tissue is semi-infinite and homogeneous, and employs the simplest analytical model for optical-property reconstruction. Step 2 used solutions from Step 1 as initial guesses in a two-layer diffuse optical tissue reconstruction. Step 3 uses solutions from Step 2 as initial guesses in a three-layer diffuse optical tissue reconstruction. In all steps, layer thicknesses are fixed based on ultrasound imaging, but other tissue properties are permitted to vary to determine the best physiological and optical property solutions for each layer. The 3-step reconstruction approach provides accurate determination of the optical haemoglobin properties for each layer while maintaining reasonable processing time. Moreover, the three-step algorithm helps to prevent the fit-search from becoming trapped in local solution minima.

Importantly, the image reconstructions rely on the simultaneous fitting of data from all SDSs and all wavelengths. This multispectral multi-SDS approach builds global constraints directly into the inverse problem and is critical for robust fitting⁴⁰. To avoid reconstruction overfitting, Tikhonov regularization is employed to reduce ill-posedness (fitting and regularization procedures are detailed in Methods).

Validation and characterization with tissue-simulating phantoms

We first characterized the performance of the FD-DOS instrument and its SNR by using homogeneous liquid phantoms comprised of ink and 20% Intralipid (Baxter) (Fig. 2b); the phantom’s optical properties are known based on ink concentration (for absorption) and Intralipid concentration (for scattering)⁴¹. In the first study, fittings based on semi-infinite homogeneous solutions of the diffusion equation were employed to reconstruct the phantom’s optical properties (that is, the absorption coefficient, ${\mu }_a \left(c{m}^{-1}\right)$) and the reduced scattering coefficient ${\mu }_s^{\prime } \left(c{m}^{-1}\right)$)¹³. The data show good SNR at SDSs up to 10 cm (Fig. 2b), wherein the mean signal intensity was 28 times greater than the standard deviation of the measured intensity. The reconstructed optical properties at each wavelength had accuracies of 3%–9%.

In two-layer phantom experiments, a solid phantom with fixed optical properties was positioned inside a liquid phantom, and the optical probe (Fig. 1b) was placed on the liquid surface (Fig. 2c). The optical properties of the liquid phantom are known based on ink and Intralipid concentrations. The optical properties of the solid phantom were provided by the phantom manufacturer (INO). An absorption-titration experiment evaluated the instrument’s sensitivity to the absorption coefficient, holding the overlayer liquid phantom thickness (3 cm) constant while incrementally increasing the absorption coefficient of the top layer. A depth-changing experiment tested the sensitivity to superficial-layer thickness; here, the liquid phantom had fixed optical properties, and the superficial-layer thickness was increased from 1.5 cm to 3.0 cm. A deep two-layer phantom experiment verified the instrument’s ability to extract deep-layer optical properties for a superficial layer thickness of 4.3 cm. Each measurement was repeated three times; the resultant means and standard deviations are reported in Supplementary Table 1. These experimental results from tissue-simulating phantoms show that the instrument and algorithms extract deep-layer optical properties accurately with errors <10% in absorption and <15% in scattering. Semi-infinite fitting also produces an estimate of the optical properties, but as a weighted average of both layers and with a stronger weighting of superficial layers.

Validation with finite-element simulations

We generated simulated experimental data using a finite-element simulation tool (TOAST)⁴² that facilitated the creation of a three-layer model with segmented optical properties based on the layer morphology extracted from a participant’s ultrasound image (Fig. 1c). Since the participant’s layer interfaces are curved, we generated test data from curved layer interfaces (Fig. 1c, left). For the inverse problem, however, we assumed each layer interface to be flat (Fig. 1c, right). We carried out computer-simulation studies with simulated experimental data (Supplementary Table 2) based on the range of participant-derived haemoglobin optical properties observed in the clinical studies (that is, we employed median and upper (lower) 75th (25th) percentile properties from Supplementary Table 3). The three-layer reconstructions (Supplementary Table 2) produced good estimates for mean $St{O}_2$, $\left[H{b}_T\right]$, and $\left[Hb{O}_2\right]$ in each layer, with errors of $\lesssim 18\%$ and more typically $\lesssim 10\%$. By contrast, the semi-infinite fitting generates a weighted average of the optical properties of all three layers and is more sensitive to superficial layers; its placental layer errors are comparatively large; 30–42%. The data presented in Supplementary Table 2 compares semi-infinite fitting to three-layer reconstruction for a moderate range of variation of placental $\left[Hb{O}_2\right]$, and a moderate range of variation of $\left[H{b}_T\right]$ and $St{O}_2$ in the overlayers. The four datasets in the Supplementary Table 2 may be interpreted as four different participants with different haemoglobin properties. The three-layer reconstruction predicts placental properties with significantly increased accuracy compared to semi-infinite fitting for all participants. Specifically, by comparing the three-layer reconstructions, estimates of $\left[H{b}_T\right]$ and $\left[Hb{O}_2\right]$ based on the semi-infinite fitting are systematically worse, with ~3-fold greater percent-error. Percent-errors in semi-infinite fitting estimates of $St{O}_2$ across these participants are similar or greater than the three-layer reconstruction estimates. Additionally, it is important to appreciate that semi-infinite fittings are not typically used; they benefit from data at very large SDSs, which is made possible by our instrumentation. The simulated datasets can also be paired to compare two different dynamic conditions within the same participant, such as would arise in response to hyperoxia versus baseline. For this comparison, the three-layer reconstruction produces good estimates of $\left[H{b}_T\right]$ and $\left[Hb{O}_2\right]$ and their changes, but the semi-infinite fittings of placental $\left[H{b}_T\right]$ and $\left[Hb{O}_2\right]$ dynamics are significantly underestimated.

Placental oxygen dynamics in vivo

We performed a pilot clinical study of human placental oxygen-related haemodynamic properties (the study design is detailed in Methods). The study enrolled women with singleton pregnancies in their third trimester and with anterior placentas. The central region of the placenta was targeted for monitoring. Adipose, rectus/uterus, and placenta layers were characterized by ultrasound and FD-DOS.

Four experiments were conducted: (1) a reproducibility experiment (n = 18); (2) a stability experiment (n=24); (3) a maternal left tilt experiment (n = 3); (4) a maternal hyperoxia experiment (n = 24). The women in the hyperoxia study had a median (interquartile range (IQR)) gestational age of 34.5 (32.9, 35.4) weeks and pre-gravid BMI (body mass index) of 27.7 (24.6, 30.2). The median (IQR) depth of the anterior placentas was 2.7 (2.3, 3.3) cm beneath the skin surface, and the nulliparity of the participants was 29.2%. Women in the maternal tilt study had gestational age of 37.0 (35.1, 37.3) weeks and pre-gravid BMI of 30.4 (29.2, 31.7); the median (IQR) depth of these anterior placentas was 2.3 (1.9, 2.4) cm beneath the skin surface.

Reproducibility was assessed by calculating the intra-class correlation coefficient (ICC) for 3 repeated measurements at the same placental location in 18 participants. Placental ${\text{StO}}_2$, $\left[{\text{Hb}}_{\text{T}}\right]$, and $\left[{\text{HbO}}_2\right]$ were highly repeatable within participants (ICC ≥ 0.9).

Stability was assessed from the standard deviation (S.D.) of data derived during a continuous 10-frame (3.5 minutes) baseline measurement at the same location on each participant. This single-participant S.D. was then averaged over all 24 participants to derive a mean measurement S.D., which served as our stability criteria. The resulting mean values of S.D. for placental $St{O}_2$, $\left[H{b}_T\right]$ and $\left[Hb{O}_2\right]$ were small (2.2%, 0.9 μM, and 0.8 μM, respectively). Optically derived haemodynamic properties were stable at baseline (Fig. 6a), and ≥ 88% of the 24 stability measurements had S.D. for placental $St{O}_2$, $\left[H{b}_T\right]$ and $\left[Hb{O}_2\right]$ of less than 3%, 2.0 μM, and 1.5 μM, respectively (Fig. 6b).

Fig. 6 |. Static (baseline) and dynamic (during maternal hyperoxia) placental haemoglobin properties for participants with NPP or MVM.

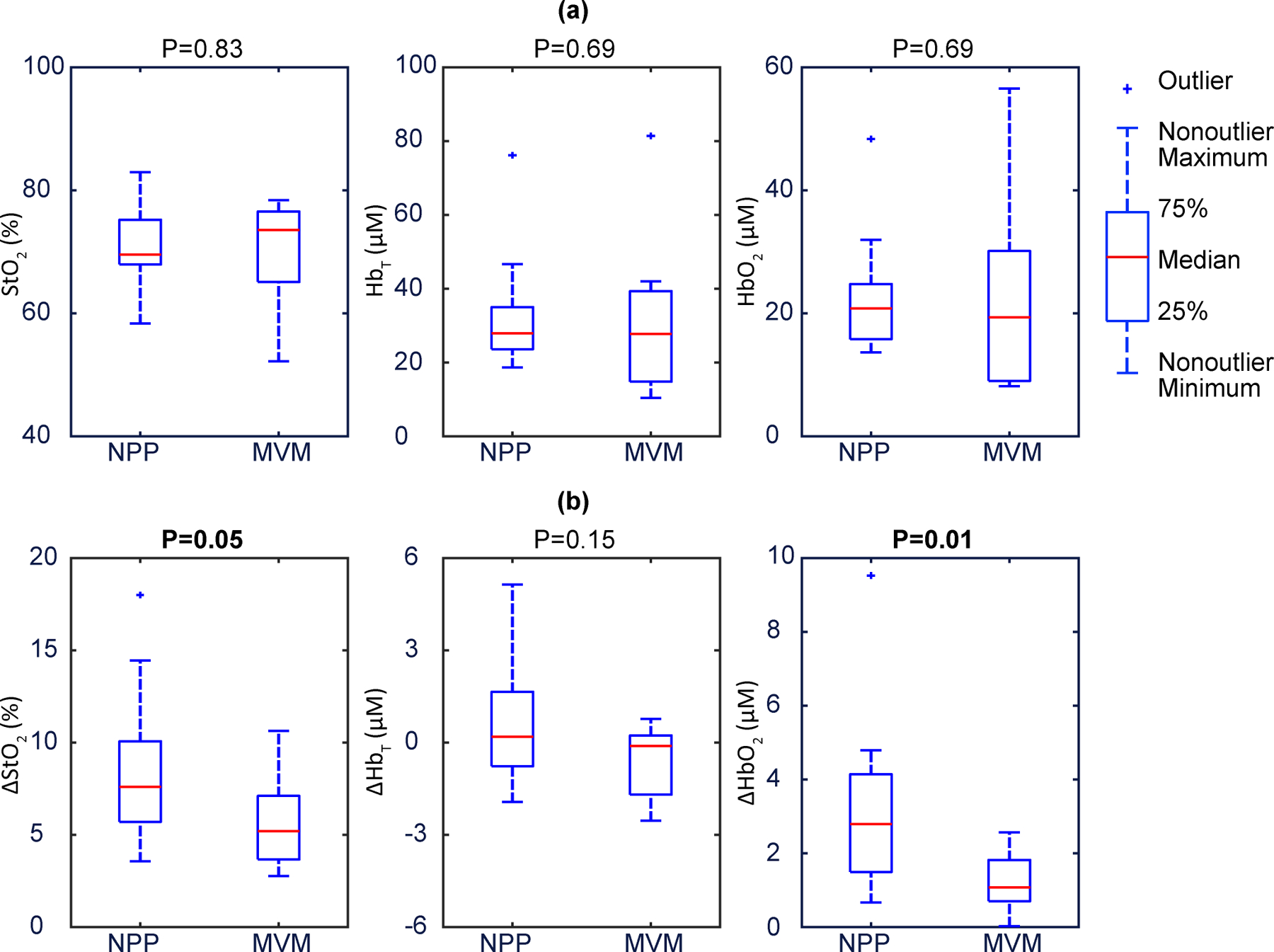
a, Baseline placental StO₂, $\left[H{b}_T\right]$, $\left[Hb{O}_2\right]$ illustrate that they are not associated with placental pathology. The data show no significant differences between NPP and MVM. The p-values are 0.83, 0.69, and 0.69 respectively. b, Placental $\text{Δ}St{O}_2$, $\text{Δ}H{b}_T$ and $\text{Δ}Hb{O}_2$ during maternal hyperoxia.$\text{Δ}St{O}_2$, $\text{Δ}H{b}_T$ and $\text{Δ}Hb{O}_2$ exhibit clear separation, no difference, and clear separation, respectively, amongst participants with NPP versus MVM. The p-values are 0.05, 0.15, and 0.01, respectively. In these boxplots, the red centre line denotes the median value, and the blue box shows the IQR (25% to 75% of dataset). The blue whiskers mark the non-outlier minimum and non-outlier maximum; outliers are marked with symbol ‘+’. Values of the median and IQR are presented in Table 1. p-values were calculated via a two-sided Wilcoxon rank sum test.

The maternal left tilt experiment is sensitive to positional changes in cardiac output and utero-placental perfusion, which can lead to an increase in maternal cardiac output of up to 20% (ref. ⁴³). We measured placental haemoglobin properties of 3 participants in the supine position, and then had them tilt to the left lateral position without removing the probe. The averaged relative increases in $St{O}_2$, $\left[H{b}_T\right]$ and $\left[Hb{O}_2\right]$ were 2.4%, 8.4% and 10.9%, respectively. Mean values of $St{O}_2$, $\left[H{b}_T\right]$, and $\left[Hb{O}_2\right]$ for each participant before and after the maternal tilt are shown in Fig. 3c. Although the number of participants is small, we observed a trend; $\left[H{b}_T\right]$ and $\left[Hb{O}_2\right]$ increased in the lateral position (p = 0.05 and p = 0.02, respectively, two-sided paired sample t-test), suggestive of an accompanying increase in placental perfusion with oxygenated maternal blood.

Fig. 3 |. Placental haemoglobin properties during stability-test measurements and the maternal left-tilt experiment.

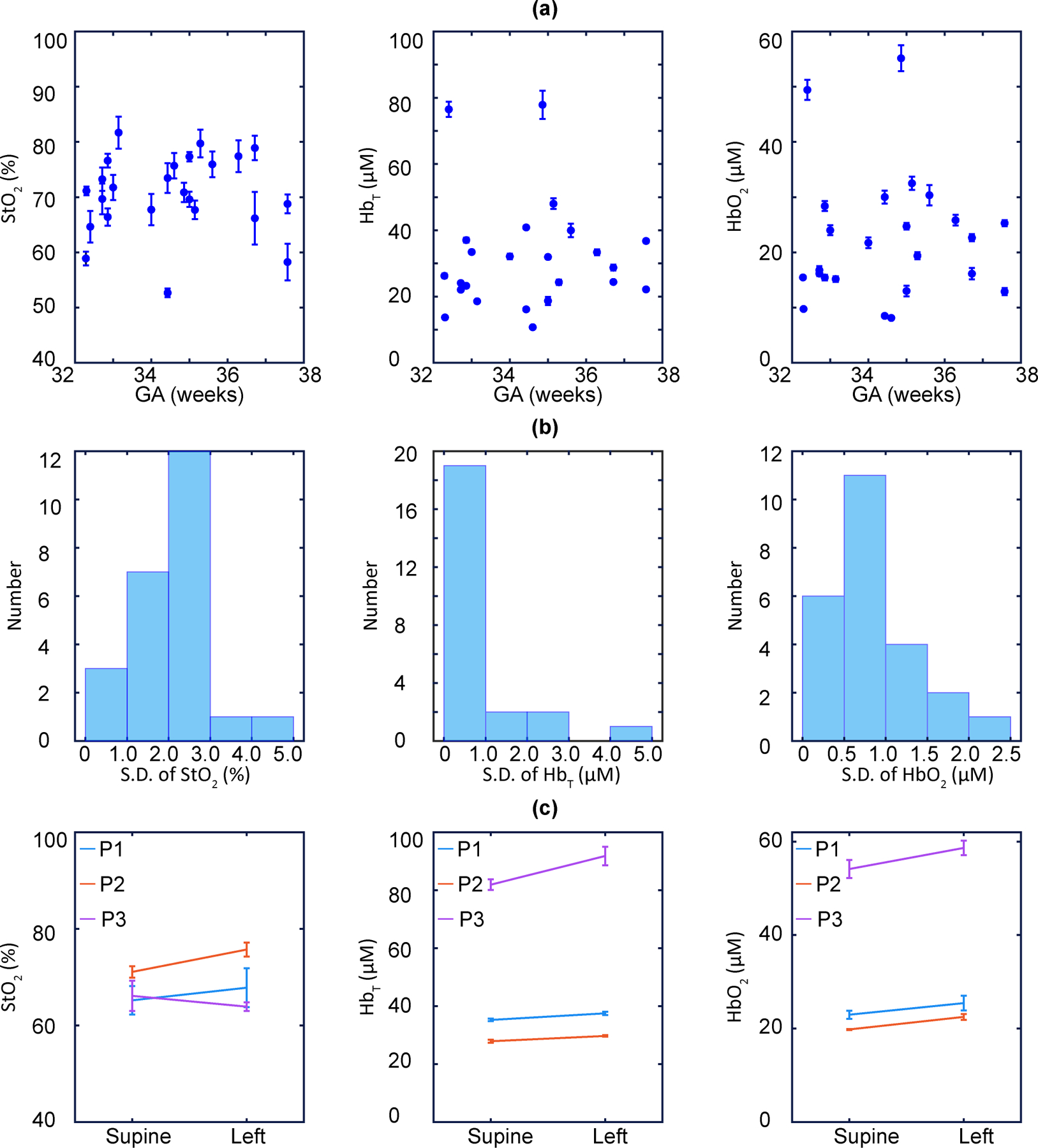
a, Mean of placental $St{O}_2$, $\left[H{b}_T\right]$ and $\left[Hb{O}_2\right]$ versus gestational stage (GA) derived from the stability test measurements (n = 24; error bars indicate the S.D.). b, Histograms showing the standard deviation of placental $St{O}_2$, $\left[H{b}_T\right]$ and $\left[Hb{O}_2\right]$ obtained from the stability test (n = 24). c, Mean of placental $St{O}_2$, $\left[H{b}_T\right]$ and $\left[Hb{O}_2\right]$ before and after maternal left tilt (n = 3; error bars indicate the S.D.).

Finally, we measured placental haemodynamic responses to maternal hyperoxia. The participants were given 100% $Fi{O}_2$ via a facemask for 20 frames (~7 min). We monitored haemoglobin concentrations continuously before, during and after maternal hyperoxia. Fig. 3a,b present a case example of variations in $St{O}_2$ and $\left[Hb{O}_2\right]$. Overall (n = 24), the method easily resolved changes in placental blood oxygenation owing to maternal hyperoxia. $St{O}_2$ and $\left[Hb{O}_2\right]$ were found to increase, by a median (IQR) of 7.1 (4.9, 9.3)% and 1.9 (1.1, 3.3) μM, respectively.

Optical biomarkers of placental dysfunction

Another goal of the maternal-hyperoxia study was to examine associations between placental oxygen dynamics and both APO and MVM. To this end, APO was defined as a composite of gestational hypertension (GHTN), preeclampsia, or intrauterine growth restriction (IUGR), and MVM was determined from the examination of delivered placentas by a single placental pathologist (R.L.L.). None of the participants had clinical evidence of GHTN, preeclampsia or IUGR at the time of their ultrasound/FD-DOS measurement, and the mean time interval from optical measurement to delivery was 3.1 (2.1, 5.4) weeks. APO was found in 9 of the 24 participants; MVM was found in 8 of the 24 participants. 2 of the 15 participants with normal pregnancy outcomes (NPOs) had MVM, and 3 of the 9 participants with APO had a normal placental pathology assessment (NPP).

We determined the absolute values of $St{O}_2$, $\left[H{b}_T\right]$ and $\left[Hb{O}_2\right]$, as well as their variation relative to baseline during maternal hyperoxia; that is, $rSt{O}_2$, $rH{b}_T$ and $rHb{O}_2$. Relative data were obtained by normalizing their time-series values to the mean of the last four frames of the baseline period.

The 24 participants were categorized into two groups, according to their pregnancy outcomes: NPO or APO. Both $rSt{O}_2$ and $rHb{O}_2$ increased substantially in response to maternal hyperoxia for the NPO group (Fig. 3c). However, the same parameters in participants with APO showed a more blunted response (Fig. 4d).

Fig. 4 |. Continuous monitoring of placental haemoglobin properties during maternal hyperoxia.

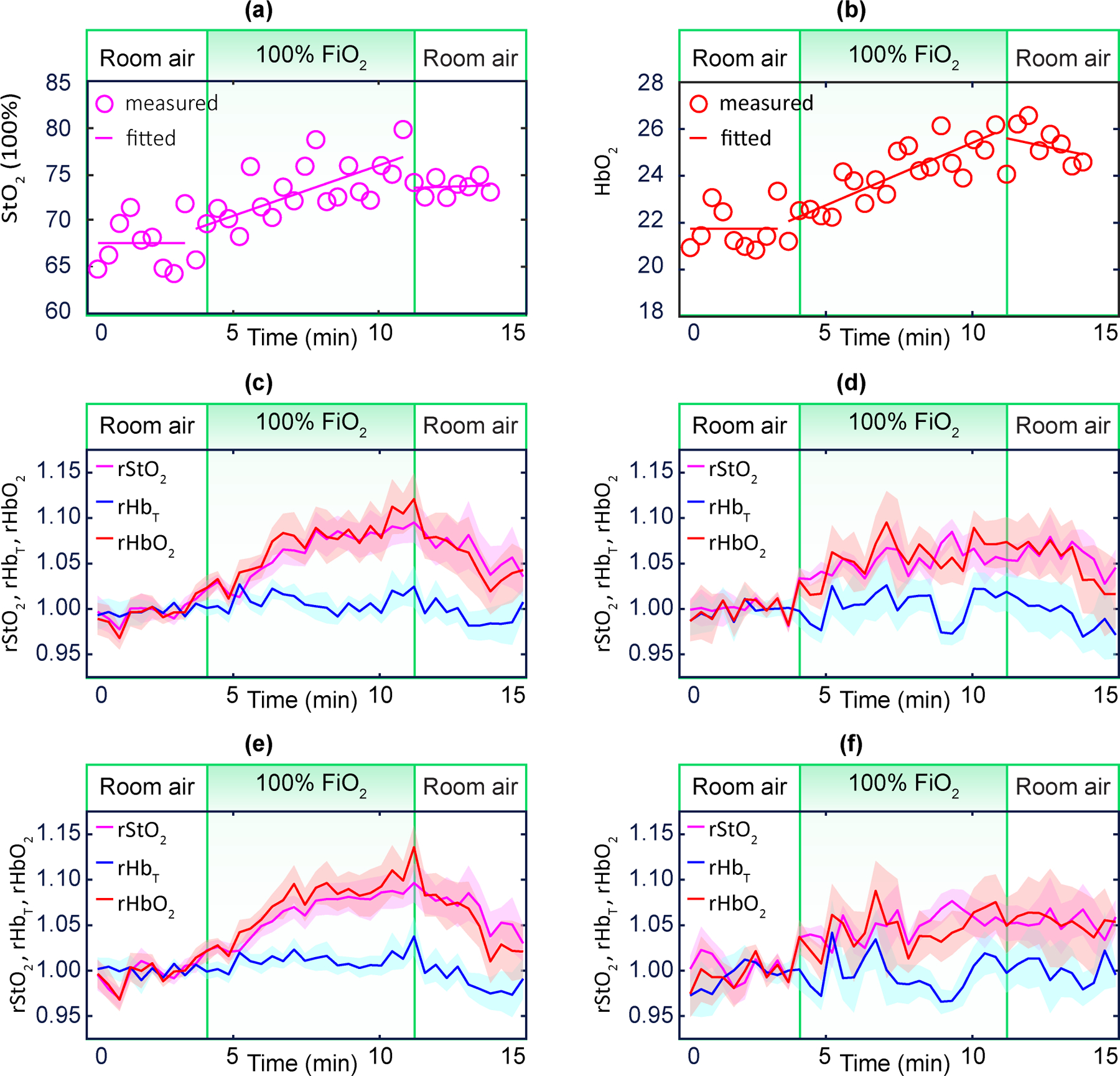
a,b, Exemple case of $St{O}_2$ and $\left[Hb{O}_2\right]$ during maternal hyperoxia. c,d, Averaged placental $rSt{O}_2$ (purple), $rH{b}_T$(blue), and $rHb{O}_2$ (red) for NPO participants (n = 15) and for participants with APO (n = 9). e,f, Averaged placental $rSt{O}_2$ (purple), $rH{b}_T$(blue) and $rHb{O}_2$ (red) for NPP participants (n = 16) and for participants with MVM (n = 8). Shaded regions represent the standard error. The cohort-averaged $rSt{O}_2$ and $rHb{O}_2$ exhibit a significant increase during maternal hyperoxia for the NPO and NPP groups, but a blunted response for the APO and MVM groups.

As for the participant’s placental histopathology, the same 24 participants were categorized into two groups: NPP or MVM. We observed significant, large and positive $\text{r}St{O}_2$ and $\text{r}Hb{O}_2$ in the NPP group (Fig. 4e). These same parameters, however, showed a blunted response in the MVM group (Fig. 4f). $rH{b}_T$ was comparatively constant for all groups.

We next sought to quantitatively determine whether placental haemoglobin properties were significantly associated with APO. For this analysis, mean baseline $St{O}_2$, $\left[H{b}_T\right]$ and $\left[Hb{O}_2\right]$ were calculated using the final 4 frames of the baseline period. Hyperoxia-induced changes from baseline (that is, $\text{Δ}St{O}_2$, $\text{Δ}H{b}_T$, and $\text{Δ}Hb{O}_2$) were defined using mean values in the 4-frame window wherein maximum $St{O}_2$ occurred. Baseline $St{O}_2$, $\left[H{b}_T\right]$ and $\left[Hb{O}_2\right]$ were not associated with APO (Fig. 4a, Table 1). On the other hand, $\text{Δ}Hb{O}_2$ and $\text{Δ}St{O}_2$ were significantly reduced in cases with APO compared to NPO (Fig. 4b, Table 1).

Table 1 |. Correlations of haemodynamic variables with placental dysfunction.

For all correlations, the total number of participants is 24. The parameters are summarized as median (IQR) within each group. The p-values were obtained using a two-sided Wilcoxon rank.

	$St{O}_2 \left(\%\right)$	$\left[H{b}_T\right] \left(\mu M\right)$	$\left[Hb{O}_2\right] \left(\mu M\right)$	$\mathbf{\Delta }St{O}_2 \left(\%\right)$	$\mathbf{\Delta }H{b}_T \left(\mu M\right)$	$\mathbf{\Delta }Hb{O}_2 \left(\mu M\right)$
Between placental static and dynamic haemoglobin properties and APO
NPO (n = 15)	69.5 (67.6, 73.4)	26.6 (22.5, 39.1)	19.9 (15.6, 28.6)	7.6 (5.6, 10.2)	0.0 (-0.8, 1.1)	2.6 (1.8, 4.4)
APO (n = 9)	75.9 (68.5, 77.3)	29.2 (15.4, 36.6)	23.2 (9.3 26.0)	4.9 (3.9, 7.1)	-0.1 (-0.9, 0.5)	1.3 (0.8, 1.8)
p-value	0.37	0.51	0.63	0.03	0.63	0.02
Between placental static and dynamic haemoglobin properties and MVM
NPP (n = 16)	69.5 (67.9, 75.2)	27.9 (23.6, 35.0)	20.8 (15.8, 24.7)	7.6 (5.7, 10.1)	0.2 (-0.8, 1.7)	2.8 (1.5, 4.1)
MVM (n = 8)	73.5 (65.1, 76.5)	27.7 (14.8, 39.3)	19.3 (9.0, 30.1)	5.2 (3.7, 7.1)	-0.1 (-1.7, 0.2)	1.1 (0.7, 1.8)
p-value	0.83	0.69	0.69	0.05	0.15	0.01

Similarly, we determined whether placental haemoglobin properties were significantly associated with MVM.

Baseline $St{O}_2$, $\left[H{b}_T\right]$ and $\left[Hb{O}_2\right]$ were not associated with MVM (Fig. 5a, Table 1). $\text{Δ}Hb{O}_2$ and $\text{Δ}St{O}_2$ were significantly reduced in cases with MVM, and $\text{Δ}St{O}_2$ (Fig. 5b, Table 1).

Fig. 5 |. Static (baseline) and dynamic (during maternal hyperoxia) placental haemoglobin properties for participants with NPO or APO.

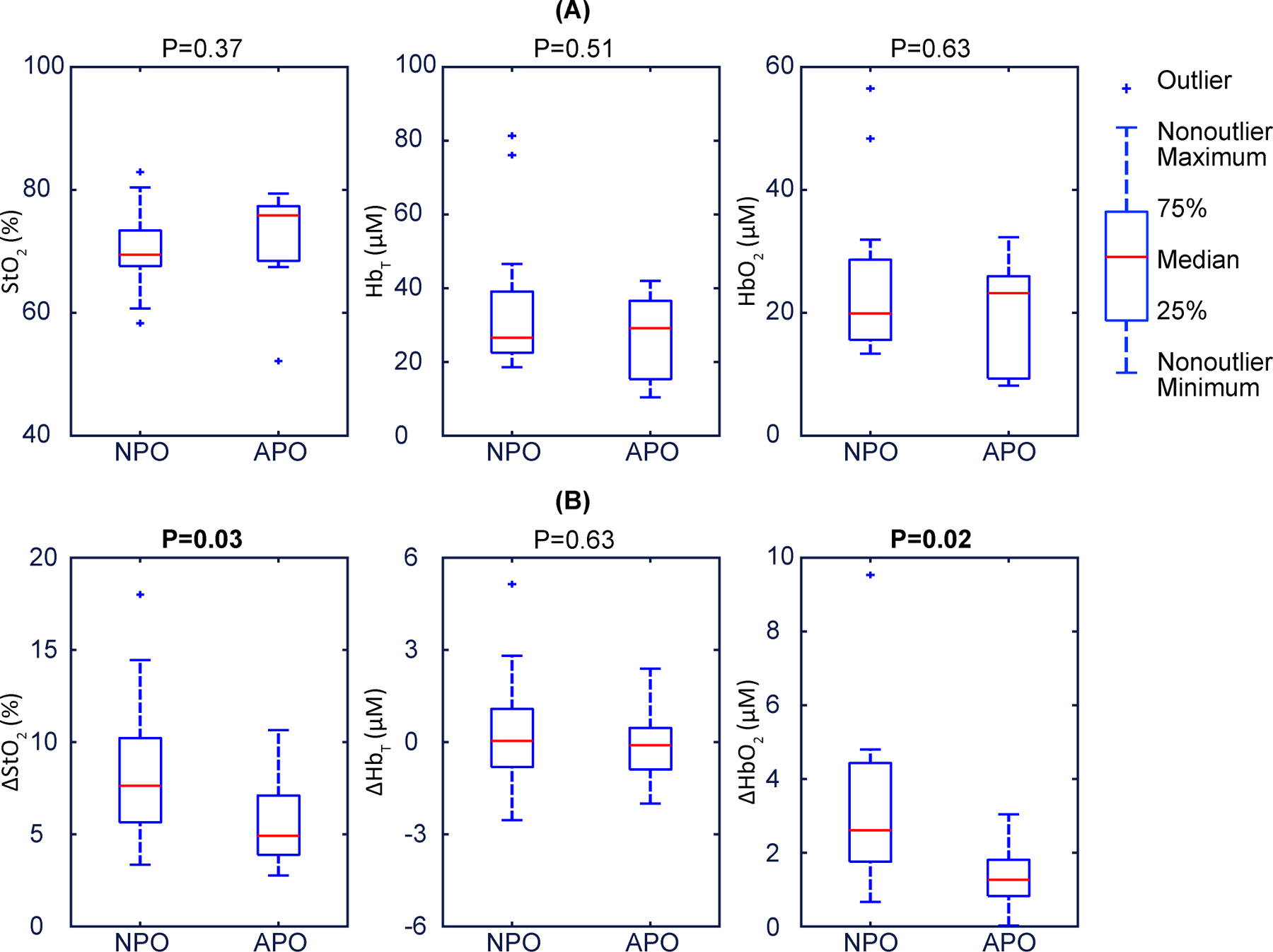
a, Baseline placental $St{O}_2$, $\left[H{b}_T\right]$ and $\left[Hb{O}_2\right]$ illustrate that they are not associated with pregnancy outcome. The data show no significant differences between NPO and APO. p-values are 0.37, 0.51, and 0.63 respectively. b, Placental $\text{Δ}St{O}_2$, $\text{Δ}H{b}_T$ and $\text{Δ}Hb{O}_2$ during maternal hyperoxia.$\text{Δ}St{O}_2$, $\text{Δ}H{b}_T$ and $\text{Δ}Hb{O}_2$ exhibit trending separation, no difference, and clear separation, respectively, amongst participants with NPO versus APO. The p-values are 0.03, 0.63 and 0.02 respectively. In these boxplots, the red centre line denotes the median value, and the blue box shows the IQR (25% to 75% of dataset). The blue whiskers mark the non-outlier minimum and non-outlier maximum; outliers are marked with symbol ‘+’. Values of the median and IQR are presented in Table 1. p-values are calculated via a two-sided Wilcoxon rank sum test.

As an additional check, we carried out the same univariate analysis with standard parameters such as maternal age, nulliparity, gestational age (GA) at study visit, maternal BMI, placental depth $\left(d\right)$, and uterine artery Doppler pulsatility index (UtA PI), which has been proposed as a surrogate indicator of trophoblastic invasion⁴⁴. We did not find any significant association between APO and/or MVM and either maternal age, nulliparity, GA at study visit or UtA PI (Table 2). However, we did observe a slight trend (not significant) towards larger d and BMI in participants with APO (p = 0.1, p = 0.1, respectively, two-sided Wilcoxon rank-sum test). Although our sample size is small and although these variables are not necessarily uncorrelated, for completeness we ran binary logistic regressions with pairs of variables: d,$\text{Δ}St{O}_2$; d, $\text{Δ}Hb{O}_2$; BMI, $\text{Δ}St{O}_2$; BMI, $\text{Δ}Hb{O}_2$. The results confirmed that a trend towards significant association between optically derived haemodynamic properties and outcomes of interest remained (Supplementary Table 4).

Table 2 |. Correlations of demographic variables with placental dysfunction.

For all correlations, the total number of participants is 24. The parameters are summarized as median (IQR) within each group except for nulliparity, which is presented as a percentage. The p-values were obtained using a two-sided Wilcoxon rank sum test except for nulliparity, for which they were obtained using a two-sided Fisher’s exact test.

	Age (years)	Nulliparity (%)	GA (weeks)	BMI	$d \left(cm\right)$	UtA PI
Between other variables and APO
NPO (n = 15)	27.0 (25.3, 32.3)	20.0	34.4 (32.8, 35.1)	25.7 (24.2, 28.9)	2.5 (2.3, 2.9)	0.7 (0.6, 0.8)
APO (n = 9)	27.0 (22.8, 33.3)	44.4	34.6 (32.9, 36.4)	30.1 (24.9, 33.4)	3.2 (2.5, 3.6)	0.8 (0.6, 1.1)
p-value	0.93	0.36	0.53	0.10	0.10	0.21
Between other variables and MVM
NPP (n = 16)	26.5 (24.0, 31.5)	18.8	34.2 (32.8, 35.2)	26.5 (24.6, 29.2)	2.5 (2.3, 3.0)	0.7 (0.6, 0.8)
MVM (n = 8)	29.5 (24.0, 34.0)	50.0	34.7 (33.6, 35.9)	30.2 (23.4, 34.3)	3.2 (1.9, 3.5)	0.7 (0.6, 1.1)
p-value	0.52	0.17	0.58	0.34	0.56	0.65

Lastly, our methodology permitted the study of adipose and rectus/uterus layers at baseline and during maternal hyperoxia (Supplementary Tables 3 and 5). The resultant adipose and rectus/uterus layer haemodynamic properties typically differed from those of the placenta. We did not find any statistically significant association of any overlayer haemodynamic property with APO or MVM (Supplementary Table 5). Collectively, these data suggest that without multilayer modelling, the computed placenta responses would have been attenuated; that is, the deep-tissue signal would have then been a weighted average of the placenta, rectus/uterus and adipose layers.

Discussion

Direct and non-invasive clinical methods to assess placental function in vivo and at the bedside would be desirable. The depth of the placenta below the skin surface, and the variability in the properties of the overlying layers, presents significant challenges for optical diagnostics. In this study, we report the development and performance of an instrument and methodology that substantially expands the capabilities of DOS to enable bedside dynamic monitoring of the placenta and potentially of other organs buried far below the tissue surface.

Tissue-simulating phantom experiments showed that the instrument has sufficient dynamic range and SNR to perform measurements at long-distance SDSs (up to 10 cm), thereby suggesting that deep placental layers can be optically interrogated in the clinic. Moreover, by coupling FD-DOS instrumentation with ultrasound imaging, we directly mapped the morphology of overlying layers of the abdominal wall and uterus. This mapping permits multilayer modelling of tissue properties that effectively isolates the placenta’s optical and physiological properties. We validated the methodology using tissue phantoms and finite-element simulations, and carried out a pilot study of third-trimester pregnancies.

Placental $St{O}_2$, $\left[H{b}_T\right]$ and $\left[Hb{O}_2\right]$ were noninvasively measured at the bedside, differentiating placenta from tissue overlayers. We also showed the repeatability and stability of the optical metrics. The baseline placenta properties between the normal and abnormal pregnancies were statistically similar. This finding is in agreement with a prior CW study²⁷ but is different from observations of higher placental oxygenation level in IUGR participants from two early CW studies^26,28 and from observations of lower placental oxygen level in women with pregnancy complications from a recent CW study⁴⁵. Regarding study comparisons, it should be noted that, besides important differences in technical approach (such as layer averaging, light penetration, participant BMI and other assumptions), the adverse outcomes in our study were generally not as severe as in some of the others^26,28. Moreover, we made assessments weeks prior to clinical disease and delivery. Hence, although studies with larger sample size are clearly warranted, the similar baseline placenta-tissue oxygen levels that we observed are not at odds with physiological expectations, even in the presence of underlying pathology.

Since gold-standard references for placental tissue haemoglobin values do not exist, we used functional perturbations to show sensitivity to expected physiologic changes. Maternal left lateral tilt positioning relieves caval compression and augments venous return to the heart, improving cardiac output. In pregnancy, ~20% of maternal cardiac output is directed to uteroplacental perfusion. Thus, this manoeuvre generally increases blood flow to the placenta. In fact, this position is used clinically as a foetal resuscitation manoeuvre during labour to maximize placental perfusion⁴⁶. Despite the limited sample size (n = 3), the FD-DOS/US device detected an increase for both $\left[H{b}_T\right]$ and $\left[Hb{O}_2\right]$, consistent with the expected increased maternal blood flow into the intervillous vascular spaces of the placenta.

More importantly, the maternal-hyperoxia experiments showed that the method can detect real time changes in placental $\left[Hb{O}_2\right]$ and $St{O}_2$ owing to inflow of the oxygen-enriched maternal blood into the placenta, whereas $\left[H{b}_T\right]$ remained comparably stable. These perturbation experiments validated our clinical expectations, and confirmed the sensitivity of the optical measures to underlying utero-placental haemodynamics. They are also consistent with MRI findings; for example, this effect was demonstrated in normal foetuses and in those with congenital heart disease¹¹, and a similar delayed response in abnormal versus normal placentas in twin pregnancies was observed with hyperoxic BOLD MRI⁴⁷, again consistent with our observations.

We also studied how optical metrics obtained during maternal-hyperoxia correlates with pregnancy outcome and placental pathology. APOs are significantly associated with both short-term and long-term morbidity and mortality^1–3. Similarly, MVM are associated with both APOs and long-term adverse outcomes35, with prevalence estimates as high as 32% in term births and over 50% in preterm births⁴⁸. Our pilot study indicates that the non-invasive optical monitoring of placental responses to maternal hyperoxia is feasible and that it holds potential as a methodology to detect signs of poor placental perfusion weeks before delivery.

The adipose and rectus/uterus layer haemoglobin properties of healthy participants during baseline and during maternal hyperoxia were not significantly different from participants with APO or MVM (Supplementary Table 5). These null results for the overlayers are not necessarily surprising from a physiological perspective. For example, since MVM presents a recognizable pattern of placental injury related to altered uterine and intervillous blood flow, we would not expect a significant association between adipose haemoglobin properties and MVM. However, we noticed that a few overlayer parameters exhibit trending associations (p-values as small as 0.06 for the rectus/uterus layer $\text{Δ}St{O}_2$ and APO, two-sided Wilcoxon rank-sum test); this observation should encourage further study in a larger sample size; that is, one might hypothesize that subclinical vascular dysfunction may predispose to poor placentation or be an indicator of placental dysfunction.

The need for new tools to assess placental function is well known to clinicians. Critical knowledge gaps exist in obstetrical care as a result. For this reason, some investigators have turned to MRI to derive functional parameters related to placental oxygenation. MRI does not have the same issues of depth penetration that limit optics, and specialized MRI techniques such as T2*, BOLD, and magnetic-resonance susceptibility are correlated with oxygen content^10–12. However, these correlations with oxygen have limitations, and MRI is not suitable for bedside measurements. DOS, by contrast, can directly measure deoxy-haemoglobin and oxy-haemoglobin concentrations at the bedside and non-invasively during clinical care. Here we have described a unique instrument that permits quantitative dynamic monitoring of the human placenta at the bedside, and the associations that we have found with APO and MVM support its continued development. However, our work thus far has some limitations: to date we have probed only anterior placentas within ~4 cm of the surface, and the placenta optical signals are due to a combination of maternal and foetal blood. Although the methodology holds clinical promise, a clinical study with larger sample sizes is desirable to corroborate the findings, and to enable more sophisticated statistical analyses that explore possible confounding variables and that generate composite metrics with improved specificity and sensitivity.

The technology will need to be refined. With improved spatial information from ultrasound, such as 3D imaging, we may be able to improve on the uniform slab-layer tissue model and derive optical properties with greater fidelity. With improved time resolution, the temporal responses to functional activation could be explored as a test variable. Additionally, an improved time resolution would increase the sensitivity to changing conditions and would facilitate the efficient evaluation of multiple placental sites; the latter is especially important given the potential spatial heterogeneity of pathology within the placenta. Exploration of placental oxygenation at earlier gestational ages, although challenging, could lead to the identification of early signs of placental insufficiency, and comparisons of uterine and placental responses during hyperoxia could improve our understanding of maternal and foetal oxygen consumption. Real-time optical monitoring feedback could alert clinicians to suspicious data owing to contraction or movement and thus improve data-acquisition quality. Currently, it takes ~90 minutes to determine the regularization hyperparameters; three-layer reconstruction of each frame data takes ~90 seconds on our 3.2GHz quad-core computer. These times can be reduced to ~12 minutes and ~12 seconds, respectively, with a 3.5GHz 32-core workstation. Looking forward, with machine learning and information from large datasets, we believe that the regularization hyperparameter could be determined in ~1 minute at the beginning of the measurement and thereby facilitate real-time layer-model reconstructions. Broadly, we anticipate that optical metrics of placental haemodynamics will enable scientists to better understand placental pathophysiology. Moreover, the instrumentation and methodology that we have reported here is potentially suited for in vivo studies of oxygen function in other internal organs buried deep below the tissue surface, such as the uterus and the kidney.

Methods

FD-DOS instrumentation

The details of the construction and operation of the custom heterodyne FD-DOS instrument are schematically shown in Extended Data Fig. 1. Briefly, three sinusoidal electromagnetic waves at radio frequency (RF) $\left(f_1=100 MHz\right)$, i.e., one for each laser diode, and one sinusoidal wave at frequency $\left(f_2=100.2 MHz\right)$, were generated from four low-noise, fractional-N phase-locked-loop signal generators (HMC833, Hittite Microwave Corporation). The waves were synchronized by an ultra-low-jitter programmable reference clock ($f_0=50 MHz$, LMK61E2, Texas Instruments). Each $f_1$ wave from the signal generator was amplified (ZX60-P103LN+ by Mini-Circuits), filtered (DC to $98 MHz$, SLP-100+, Mini-Circuits), and divided (2-way splitter, Z99SC-62-S+, Mini-Circuits) into two $f_1$ waves; one was prepared for the reference signal (‘reference $f_1$’) and the other was prepared for driving amplitude modulation for one laser (‘signal $f_1$’). Simultaneously, the $f_1$ wave from the signal generator was also amplified, filtered, and divided (4-way splitter, ZB4PD-52–20W-S+, Mini-Circuits) into four $f_2$ waves; three of these were prepared for frequency-mixing with the three detected signals (‘signal $f_2$’), and the other was prepared for frequency-mixing with the reference signal (‘reference $f_2$’).

The three of ‘signal $f_1$’ were further amplified and input into laser controllers (CLD1011LP, Thorlabs), which drive the light amplitude modulation of the three near-infrared lasers with wavelengths of 785 nm (LP785-SF1000, Thorlabs), 808 nm (LDPC-T3–808-62.5/125-M-35–3S-3–0.5–70-150LD, OZ Optics), and 830 nm (LDPC-T3–830-62.5/125-M-35–3S-3–0.5–70-150LD, OZ Optics). The laser controllers also maintain thermal stability using digital proportional-integral-derivative control. To enhance signal-to-noise ratio (SNR), the achievement of a modulation depth or amplitude modulation index, i.e., the ratio of the modulation excursions of the RF signal to the level of unmodulated carrier, of greater than 90% for each laser is critically important. Achievement of these large modulation depths required individually optimized RF amplification according to each laser’s characteristics. Each laser has a specific threshold current, maximum current, and optical power efficiency (mW/mA). To minimize unmodulated background light and maximize SNR, each laser has a unique RF driver that drives its amplitude with modulation depth >90% (93%, 95% and 98% respectively). Specifically, each ‘signal $f_1$’ wave was divided into four sub-signals via a 4-way power splitter. Each sub-signal was then amplified in one or two amplification stages (in each stage, the signal was amplified by ~8.6dB); the 830nm channel had 2 amplification stages and the 785nm and 805nm channels had 1 amplification stage. The sub-signals were then combined via a 4-way power splitter. A custom-built circuit containing a low noise amplifier (ZX60-P103LN+, Mini-Circuits) and low pass filter (DC to 98 MHz, SLP-100+, Mini-Circuits) was used in each amplification stage.

The three amplitude modulated laser diodes were fibre-coupled to an optical switch (MEMS 91545C4, Dicon), which was in turn connected to the 10 source fibres (400 µm core, 0.5 NA, FP400URT-Custom, Thorlabs) on the probe head (see main text Fig. 1 (b)). The optical switch sequentially cycled each laser diode through each source position and also a “dark count position” (i.e., a cycle of $3\times 11=33$ sequential measurements; 21 seconds per cycle). Of note, for the dark count measurement, no fibre was connected to the 11^th position on the switch (i.e., no light was delivered to the tissue).

Multiply scattered light emerging from the tissue at the detector position was collected by a high-transmission liquid light guide (5 mm core, 0.59 NA, LLG5–8H, Thorlabs) that was coupled to a high-sensitivity photomultiplier (PMT) detector (R12829, Hamamatsu). The PMT converts the diffuse light wave to a proportional electric voltage signal, which is then amplified and filtered by a high-speed current amplifier (DHPCA-100, FEMTO), and finally frequency-mixed (ZP-3-S+, Mini-Circuits) with one ‘signal $f_2$’. Mixing produces a heterodyne down-converted signal, related to the diffusive light wave (i.e., its amplitude and phase are proportional to those of the diffusive light wave), at frequency $\Delta f=f_1-f_2=0.2 MHz$. This lower-frequency signal, which can be very accurately quantified, is the heterodyne detected signal³¹. Simultaneously, a reference signal with the fixed frequency $\Delta f$, amplitude $\left(A_r\right)$, and phase $\left({\phi }_r\right)$ is generated by mixing the ‘reference $f_1$’ and ‘reference $f_2$’.

A high-sampling-rate lock-in amplifier (MFLI 500 kHz, Zurich Instruments) compares reference and detected signals to derive the amplitude $\left(A\right)$ and phase $\left(\phi \right)$ of the diffuse light wave (i.e., the lock-in output in-phase $\left(I=Acos\phi \right)$ and quadrature $\left(Q=Asin\phi \right)$ signals, from which $A$ and $\phi$ are calculated). Note, a 3-to-1 RF switch (G4J-520120, Charter Engineering Inc.) was employed to pair the correct reference signal with the corresponding detected wavelength. Note also, prior to computing $A$ and $\phi$, the $Q$ and $I$ for each wavelength at every source position were subtracted by the corresponding $Q_{noise}$ and $I_{noise}$ obtained from the dark count position in the same cycle. In summary, we collect diffuse light waves from 10 source-detector pairs with source-detector separations (SDSs) ranging from ~1 to ~9 cm in the human probe (and up to 10 cm in the tissue-phantom experiment); these data enable the depth-dependent optical determination of tissue properties.

Three-layer photon diffusion model and Green’s function

The human abdomen is multi-layered. We model it as a three-layer medium, wherein each layer is assumed homogeneous and laterally infinite in extension. The experimental geometry is described using cylindrical coordinates in the main text Fig. 1(c); the depth is denoted by $z \left(cm\right)$, and the source-detector separation (SDS) is denoted by $\rho \left(cm\right)$. Both source and detector are positioned on the surface $\left(z=0\right)$. In the diffusive medium, sources on the tissue boundary are well-modelled as an isotropic point source in the medium at depth of $z_0=l_{tr,1} \left(cm\right)$, which depends on tissue optical properties and is defined below. The diffusion equations (in the frequency-domain) for the spatially-dependent amplitude of the diffusive waves in each of the layers of the three-layer medium are^38,39,49:

$${\nabla }^2{U}_1\left(\rho ,z\right)-\left(\frac{{\mu }_{a,1}}{D_1}+i\frac{2\pi f_1}{v_1{D}_1}\right)U_1\left(\rho ,z\right)=-\frac{M{S}_0}{D_1}\delta \left(\rho -{\rho }_0,z-z_0\right);\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}0\le z<d_1;$$ (1–1)

$$\left.{\nabla }^2{U}_2(\rho ,z\right)-\left(\frac{{\mu }_{a,2}}{D_2}+i\frac{2\pi f_1}{v_2{D}_2}\right)U_2\left(\rho ,z\right)=0;\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{d}_1\le z<d_1+d_2;$$ (1–2)

$$\left.{\nabla }^2{U}_3(\rho ,z\right)-\left(\frac{{\mu }_{a,3}}{D_3}+i\frac{2\pi f_1}{v_3{D}_3}\right)U_3\left(\rho ,z\right)=0;\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{d}_1+d_2\le z.$$ (1–3)

Here, the diffusive wave, ${\Phi }_{AC,k}\left(\rho ,z,t\right)=U_k\left(\rho ,z\right)e^{i2\pi f_{1}t} \left(Wc{m}^{-2}\right)$; it is a complex representation of photon fluence rate within layer $k \left(k=1,2,3\right)$. $S_0 \left(W\right)$ is the time averaged power emitted by the light source, $f_1 \left(Hz\right)$ and $M \left(dimensionless\right)$ are the frequency $\left(f_1=100 MHz\right)$ and modulation depth of the source, respectively. The source is point-like and located at $\left({\rho }_0,z_0\right)$.$d_k\left(cm\right)$, ${\mu }_{a,k} \left(c{m}^{-1}\right)$, and ${\mu }_{s,k}^{\prime } \left(c{m}^{-1}\right)$ are the layer $k$ thickness, layer $k$ light absorption coefficient, and layer $k$ reduced scattering coefficient, respectively. $l_{tr,k}\equiv 1/\left({\mu }_{a,k}+{\mu }_{s,k}^{\prime }\right)\left(cm\right)$ and $D_k=\left(1/3\right)l_{tr,k}\left(cm\right)$ are the photon transport mean-free path and the diffusion coefficient of layer $k$, respectively. $v_k=c/n_k\left(cm/s\right)$ is the light velocity in layer $k$, where $c \left(cm/s\right)$ is the speed of light in vacuum and $n_k$ is the refractive index of layer $k$. The boundary conditions for the photon fluence rate and its normal derivative across the interfaces are well-known and are used to derive solutions⁵⁰.

Assuming large SDS, the equations can be solved using a Fourier transform approach and extrapolated-zero boundary conditions. The analytical Green’s function for the three-layer diffusion equation in the $z=0$ plane is^38,49:

$$G_{3L}\left(\left[\rho ,z=0\right],\left[{\rho }_s={\rho }_0, z_s=z_0\right]\right)=\frac{1}{2\pi }{\int }_0^{\infty }{\tilde{G}}_{3L}\left(s\right)s{J}_0\left(s\rho \right)ds;$$ (2–1)

$${\tilde{G}}_{3L}\left(s\right)=\frac{Z_{3L}\left(s\right)}{Y_{3L}\left(s\right)}/{\alpha }_1{D}_1;$$ (2–2)

$$\begin{array}{l}{Z}_{3L}\left(s\right)=N_{12}{M}_{23}exp\left({\alpha }_1{z}_0-{\alpha }_1{d}_1+{\alpha }_2{d}_2+{\alpha }_1{z}_{b,1}\right)-N_{12}{M}_{23}exp\left({\alpha }_1{z}_0-{\alpha }_1{d}_1+{\alpha }_2{d}_2-{\alpha }_1{z}_{b,1}\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}+N_{12}{N}_{23}exp\left(-{\alpha }_1{z}_0+{\alpha }_1{d}_1-{\alpha }_2{d}_2+{\alpha }_1{z}_{b,1}\right)-N_{12}{N}_{23}exp\left(-{\alpha }_1{z}_0+{\alpha }_1{d}_1-{\alpha }_2{d}_2-{\alpha }_1{z}_{b,1}\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}+M_{12}{N}_{23}exp\left({\alpha }_1{z}_0-{\alpha }_1{d}_1-{\alpha }_2{d}_2+{\alpha }_1{z}_{b,1}\right)-M_{12}{N}_{23}exp\left({\alpha }_1{z}_0-{\alpha }_1{d}_1-{\alpha }_2{d}_2-{\alpha }_1{z}_{b,1}\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}+M_{12}{M}_{23}exp\left(-{\alpha }_1{z}_0+{\alpha }_1{d}_1+{\alpha }_2{d}_2+{\alpha }_1{z}_{b,1}\right)-M_{12}{M}_{23}exp\left(-{\alpha }_1{z}_0+{\alpha }_1{d}_1+{\alpha }_2{d}_2-{\alpha }_1{z}_{b,1}\right);\end{array}$$ (2–3)

$$\begin{array}{l}{Y}_{3L}\left(s\right)=M_{12}{M}_{23}exp\left({\alpha }_1{d}_1+{\alpha }_2{d}_2+{\alpha }_1{z}_{b,1}\right)+N_{12}{M}_{23}exp\left(-{\alpha }_1{d}_1+{\alpha }_2{d}_2-{\alpha }_1{z}_{b,1}\right);\\ \hspace{1em}\hspace{1em}\hspace{0.33em}+ N_{12}{N}_{23}exp\left({\alpha }_1{d}_1-{\alpha }_2{d}_2+{\alpha }_1{z}_{b,1}\right)+M_{12}{N}_{23}exp\left(-{\alpha }_1{d}_1-{\alpha }_2{d}_2-{\alpha }_1{z}_{b,1}\right);\end{array}$$ (2–4)

$$M_{12}={\alpha }_1{D}_1+\frac{n_2^2}{n_1^2}{\alpha }_2{D}_2;M_{23}={\alpha }_2{D}_2+\frac{n_3^2}{n_2^2}{\alpha }_3{D}_3;N_{12}={\alpha }_1{D}_1-\frac{n_2^2}{n_1^2}{\alpha }_2{D}_2;N_{23}={\alpha }_2{D}_2-\frac{n_3^2}{n_2^2}{\alpha }_3{D}_3;$$ (2–5)

$${\alpha }_k=\frac{\left(D_{\text{k}}{s}^2+v_k{\mu }_{a,k}+i2\pi f_1\right)}{D_{\text{k}}} ;\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}k=1,2,3.$$ (2–6)

Here, $J_0$ is the Bessel function of the first kind and zero-order. $z_{b,1}\equiv \left(2/3\right)l_{tr,1}\left(1+R_{eff}/1-R_{eff}\right)\left(cm\right)$ is the extrapolation length, where $R_{eff}$ is related to the indices of refraction of the media⁵⁰. In practice, we solve the integral in equation (2-1) numerically by applying Gauss-Laguerre quadrature of 5000 points. Note, in order to minimize numerical errors, the hyperbolic functions are expanded and simplified.

Note, the analytical Green’s function for the two-layer diffusion equation in the z=0 plane can be derived from a special case of the three-layer model, where ${\mu }_{a,1}={\mu }_{a,2}$, ${\mu }_{s,1}^{\prime }={\mu }_{s,2}^{\prime }$, $n_1=n_2$, $d_1+d_2=d$, and $D_1=D_2$, ${\alpha }_1={\alpha }_2$.

$$G_{2L}\left(\left[\rho ,z=0\right],\left[{\rho }_s={\rho }_0, z_s=z_0\right]\right)=\frac{1}{2\pi }{\int }_0^{\infty }{\tilde{G}}_{2L}\left(s\right)s{J}_0\left(s\rho \right)ds;$$ (3–1)

$${\tilde{G}}_{2L}\left(s\right)=\frac{Z_{2L}\left(s\right)}{Y_{2L}\left(s\right)}/{\alpha }_1{D}_1;$$ (3–2)

$$Z_{2L}\left(s\right)=exp\left(-{\alpha }_1{z}_0\right)-exp\left(-{\alpha }_1{z}_0-2{\alpha }_1{z}_{b,1}\right) +\beta \cdot exp\left({\alpha }_1{z}_0-2{\alpha }_{1}d\right)-\beta \cdot exp\left({\alpha }_1{z}_0-2{\alpha }_{1}d-2{\alpha }_1{z}_{b,1}\right);$$ (3–3)

$$Y_{2L}\left(s\right)=1+\beta \cdot exp\left(-2{\alpha }_{1}d-2{\alpha }_1{z}_{b,1}\right);$$ (3–4)

$$\beta =\frac{{\alpha }_1{D}_1-\left(n_3^2/n_1^2\right){\alpha }_3{D}_3}{{\alpha }_1{D}_1+\left(n_3^2/n_1^2\right){\alpha }_3{D}_3} .$$ (3–5)

The photon fluence rate measured on the tissue surface is essentially the Green’s function multiplied by the constant amplitude of the source $M{S}_0$. The detected signal intensity is directly proportional this photon fluence rate:

$$U_1\left(\left[\rho ,z=0\right],\left[{\rho }_s={\rho }_0, z_s=z_0\right]\right)=M{S}_0\hspace{0.17em}G\left(\left[\rho ,z=0\right],\left[{\rho }_s={\rho }_0, z_s=z_0\right]\right);$$ (4–1)

$$I_m\left(\rho \right)=K{U}_1\left(\left[\rho ,z=0\right],\left[{\rho }_s={\rho }_0, z_s=z_0\right]\right)=CG\left(\left[\rho ,z=0\right],\left[{\rho }_s={\rho }_0, z_s=z_0\right]\right);$$ (4–2)

$$A_m\left(\rho \right)=\left|I_m\left(\rho \right)\right|; \hspace{1em}\hspace{1em}\hspace{1em}{\theta }_m\left(\rho \right)=arg\left[I_m\left(\rho \right)\right] .$$ (4–3)

Here, $C=C_{a}exp\left(-i{C}_p\right)$ is the complex light coupling coefficient (a proportionality constant); $C_a$ and $C_p$, are determined using calibration phantoms with known optical properties before/after the measurement. With equations (2) and (4), the signal at the tissue surface boundary can be calculated, given input optical properties for each layer and layer thicknesses. Such a calculation is called a solution of the forward problem. The reconstruction algorithms underlying the FD-DOS analysis solves the inverse problem by finding the tissue properties that minimize the difference between measured signal and the forward problem (theoretical) solution (with specific input properties).

Global optimization with multiple spectral/SDS channels

In practice, the two-layer or three-layer optical properties based on the photon diffusion model were reconstructed by solving a global optimization problem. Specifically, we carried out the data inversion using all source-detector pairs and wavelengths simultaneously. This approach builds-in global constraints about chromophore absorption and layer geometry into the inverse problem and is critical for robust fitting. Note, the accuracy of our determination of $\left[Hb\right]$ and $\left[Hb{O}_2\right]$ concentration (and thus $St{O}_2$, $\left[H{b}_T\right]$) is superior to that based on independent determination of absorption and scattering coefficients as a function of wavelength. This is because the use of the known chromophore extinction coefficients, the Mie power-law model for scattering, and the full collection of multi-spectral and multi-SDS data to fit to all wavelengths and SDSs simultaneously, effectively constrains the reconstruction problem⁴⁰.

The multispectral fitting assumed that ${\mu }_{a,k}\left({\lambda }_j\right)$, the absorption coefficient at layer k at wavelength ${\lambda }_j \left(j=1,2,3, {\lambda }_j=785, 808, 830 nm\right)$, is due to the absorption of ${\left[Hb{O}_2\right]}_k$, ${\left[Hb\right]}_k$, ${\left[H_{2}O\right]}_k$, and ${\left[lipid\right]}_k$.

$${\mu }_{a,k}\left({\lambda }_j\right)={\epsilon }_{Hb{O}_2}\left({\lambda }_j\right){\left[Hb{O}_2\right]}_k+{\epsilon }_{Hb}\left({\lambda }_j\right){\left[Hb\right]}_k+{\epsilon }_{H_{2}O}\left({\lambda }_j\right){\left[H_{2}O\right]}_k+{\epsilon }_{lipid}\left({\lambda }_j\right){\left[lipid\right]}_k.$$ (5)

In equation (5), ${\epsilon }_{Hb{O}_2}\left({\lambda }_j\right)$, ${\epsilon }_{Hb}\left({\lambda }_j\right)$, ${\epsilon }_{H_{2}O}$, and ${\epsilon }_{lipid}\left({\lambda }_j\right)$ are wavelength-dependent extinction coefficients for each chromophore, which are known⁵¹. ${\left[H_{2}O\right]}_k$ and ${\left[lipid\right]}_k$ are the concentration of water and lipid in layer $k$, which are assumed⁵¹. ${\left[Hb{O}_2\right]}_k$ and ${\left[Hb\right]}_k$ are the concentration of oxy- and deoxy-haemoglobin in layer $k$; they are determined by solving the inverse problem.

Notice, the total haemoglobin concentration ${\left[H{b}_T\right]}_k$ and the tissue blood oxygen saturation $St{O}_{2,k}$ in layer $k$ can also be readily obtained from:

$${\left[H{b}_T\right]}_k={\left[Hb{O}_2\right]}_k+{\left[Hb\right]}_k;\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}St{O}_{2,k}={\left[Hb{O}_2\right]}_k/{\left[H{b}_T\right]}_k;\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}k=1,2,3.$$ (6)

For multi-spectral fitting, we also assumed a Mie scattering model (equation just below) for the tissue scatterers¹⁵, wherein the scattering coefficient in layer $k$ is a power law function with scattering amplitude ${\gamma }_k$ and scattering power $b_k$. Here, ${\lambda }_0=700 nm$ is a reference wavelength chosen based on the range of the three wavelengths.

$${\mu }^{\prime }{}_{s,k}\left({\lambda }_j\right)={\gamma }_k{\left({\lambda }_j/{\lambda }_0\right)}^{-b_k}.$$ (7)

With equations (5), (6), and (7), $St{O}_{2,k}$ and ${\left[H{b}_T\right]}_k$ can be directly determined by global optimization using all data:

$$argmin\sum _{j=1}^3\sum _{l=1}^L{\left|{\epsilon }_{l,j}\left(\overline{X}\right)\right|}^2;$$ (8–1)

$$\Psi \left(\overline{X}\right)={\left|{\epsilon }_{l,j}\left(\overline{X}\right)\right|}^2=\sum _{j=1}^3\sum _{l=1}^L{‖ln\left[A_{c,l,j}/A_{c,l_0,j}\right]-ln\left[A_{m,l,j}/A_{m,l_0,j}\right]‖}^2+{‖\left[{\theta }_{c,l,j}-{\theta }_{c,l_0,j}\right]-\left[{\theta }_{m,l,j}-{\theta }_{m,l_0,j}\right]‖}^2;$$ (8–2)

$$\overline{X}=\left[St{O}_{2,1} {\left[H{b}_T\right]}_1{{\rm Y}}_1 b_1 St{O}_{2,2} {\left[H{b}_T\right]}_2 {{\rm Y}}_2 b_2 St{O}_{2,3} {\left[H{b}_T\right]}_3 {{\rm Y}}_3 b_3\right] .$$ (8–3)

In this global optimization, $\overline{X}$ is an array of all fitting variables, including haemoglobin concentrations and variants thereof, and Mie scattering model parameters for scattering. The objective function $\Psi \left(\overline{X}\right)$ is a “residual” function of $\overline{X}$; it is essentially a Chi-squared function that compares calculated to measured data. Represents the $L^2$ norm of the vector. $A_{c,l,j}$ and ${\theta }_{c,l,j}$ are the calculated (predicted) amplitude and phase using the forward solver with estimated optical properties. $A_{m,l,j}$ and ${\theta }_{m,l,j}$ are the measured amplitude and phase. Subscripts $l$ and $j$ represent the $l-th$ SDS and $j-th$ wavelength, respectively. Notice, the normalization amplitude and phase factors are also incorporated into the objective function; these terms are denoted with the subscript, $l_0$.

Regularization and initialization of the optimization problem

To avoid overfitting in the reconstruction, regularization is employed to reduce the ill-posedness of the inverse problem. A Tikhonov regularization term is added to the original objective function to provide additional constraints. Thus, the new objective function ${\Psi }^{\prime }\left(\overline{X}\right)$ is the sum of the residual function in (8-2) and a weighted regularization term⁵²:

$${\Psi }^{\prime }\left(\overline{X}\right)=\sum _{j=1}^3\sum _{l=1}^L{\left|{\epsilon }_{l,j}(\overline{X})\right|}^2+{\zeta }_{R}R(\overline{X});\hspace{1em}\hspace{1em}\hspace{1em}R(\overline{X})={‖\overline{X}-{\overline{X}}^{\left(0\right)}‖}^2.$$ (9)

$R\left(\overline{X}\right)$ is the Tikhonov regularization term, and ${\zeta }_R$ is the regularization hyperparameter, which calibrates the relative weight of the residual function and regularization term. Tikhonov regularization, as used here, seeks to minimize the difference between the initial estimated value ${\overline{X}}^{\left(0\right)}$ and the reconstructed value $\overline{X}$. The value for the regularization hyperparameter is determined using an L-curve method, which is a convenient graphical tool to find the optimized regularization parameter which balances the trade-off between fluctuation size and fluctuation smoothing. Once the ${\zeta }_R$ is determined, the optimization problem to minimize ${\Psi }^{\prime }\left(\overline{X}\right)$ can be solved iteratively. In practice, the iterative algorithm is performed by MATLAB fmincon function with a parallel search function- multi-start for global minimum⁵³.

The first and very important step in the iterative search is initialization, wherein a reasonable estimated value ${\overline{X}}^{\left(0\right)}$ is set. It is important that the initial guess is chosen to be reasonably close to the true value; otherwise, the iterative search may not converge to a meaningful solution. Main text Fig. 2 (a) schematically outlines our three-step reconstruction procedure for initialization and determination of placental haemodynamic properties.

In essence, each step of the three-step reconstruction finds “best” tissue properties by minimizing the difference between measured data and the predictions of diffuse optical tissue models of increasing complexity. STEP 1 assumes the underlying tissue is semi-infinite and homogeneous; it utilizes short SDSs (based on the superficial layer thickness, longest SDS ≥ 2*Depth+2) to derive an initial estimate for properties of the near-surface region and the full set of SDSs to derive an initial property estimate for the whole region. For predictions, a standard semi-infinite homogeneous medium analytic solution is used.

STEP 2 utilizes estimates from step one as initial guesses in an analytic two-layer diffuse optical tissue model. The two-layer (and three-layer) models fix layer thicknesses based on ultrasound data, but other tissue properties within each layer such as scattering, $St{O}_2$, and $\left[H{b}_T\right]$, are permitted to vary to minimize the difference between measurement and tissue model predictions. Short SDSs and a two-layer analytical light transport model are utilized to derive best estimates for properties of adipose and rectus/uterus layers; all SDSs, and this same two-layer analytic light transport model, are utilized to derive best estimates for the over-layer (adipose plus rectus/uterus) and placental regions.

STEP 3 utilizes estimates for each layer from step two as initial guesses in the final three-layer diffuse optical tissue model. Again, all layer thicknesses are fixed by ultrasound-image segmentation, but the other tissue properties within each layer are permitted to vary to minimize the difference between the measurement and the predictions of the three-layer analytic light transport model.

Validation and characterization with tissue-simulating phantoms

We characterized FD-DOS instrument performance using tissue-simulating phantoms with known optical properties (${\mu }_a=0.10 c{m}^{-1}$, ${\mu }_s^{\prime }=8.9 c{m}^{-1}$ for ${\lambda }_1=830 nm$). The simplest tissue phantoms were comprised of water, ink for absorption, and 20% Intralipid (Baxter) for scattering. During this experiment, we used a translational stage and a motion control motor to accurately change the source-detector distance with minimum change of coupling coefficient. Briefly, the detector fibre was fixed at the liquid surface and a source fibre was physically translated in the same surface plane with SDSs ranging from 6.2 cm to 10 cm using a translation stage (see main text Fig. 2 (b)). To good approximation, the coupling coefficients in equation (4) were the same at every SDS, and a nonlinear fitting based on semi-infinite homogeneous solutions of the diffusion equation was employed to reconstruct tissue phantom optical properties¹³. The measurement SNR is defined as the mean intensity of 10 distinct continuous measurement trains divided by the standard deviation of the same 10 measurements for a specified SDS; accuracies are defined as the difference of measured and expected values, divided by the expected value.

In the two-layer phantom experiments, a solid phantom (${\mu }_{a,b}=0.10 c{m}^{-1}$, ${\mu }_{s,b}^{\prime }=5.0 c{m}^{-1}$ for ${\lambda }_1=785 nm$) was positioned under the liquid phantom, and the full Ultrasound/FD-DOS optical probe was set on the liquid surface (see main text Fig. 2 (c)). An absorption-titration experiment tested sensitivity to absorption coefficient (chromophore concentration). The over-layer liquid phantom thickness was held constant at 3 cm, the over-layer scattering coefficient was held constant (${\mu }_{s,t}^{\prime }=9.10 c{m}^{-1}$ for ${\lambda }_1=785 nm$), and the absorption coefficient was incrementally increased in the top layer from ${\mu }_{a,t}=0.08$ to $0.13 c{m}^{-1}$. Results are given in Supplementary Table 1a. A depth-changing experiment tested sensitivity to superficial layer thickness (see main text Fig. 2 (c)). Here, the liquid had fixed optical properties (${\mu }_{a,t}=0.13 c{m}^{-1}$, ${\mu }_{s,t}^{\prime }=9.10 c{m}^{-1}$ for ${\lambda }_1=785 nm$), and the superficial layer thickness was increased from 1.5 to 3.0 cm; note this range encompasses the majority of our clinical placenta depths. Results are given in Supplementary Table 1b. The results are summarized as mean (S.D.) of 3 continuous measurements. The experiment accuracy is defined as the difference of measured and expected values, divided by the expected value. In Supplementary Table 1c, we show results from a two-layer phantom experiment with superficial layer thickness of 4.3 cm. Finally, we successfully carried out a deep layer absorption-titration phantom experiments to test our sensitivity to deep layer absorption coefficient. In these studies, the over-layer liquid phantom thickness was held constant at 3.25 cm, the top-layer optical properties were fixed, and the bottom-layer absorption was titrated. We reconstructed bottom-layer absorption variation of ${\mu }_a=0.10c{m}^{-1}$, ${\mu }_a=0.18c{m}^{-1}$, and ${\mu }_a=0.26c{m}^{-1}$ (all at $\lambda =785nm$) with error of 8.4%, -3.6%, and -14.8%, respectively. These experiments (and results) are consistent with other work in the literature³⁷. While our phantom work used larger source-detector separations to probe deep-layer optical properties, but the signal-to-noise and depth-to-SDS-ratio in our measurements and those of reference³⁷ was comparable; importantly, our inverse problem was more robust than in reference³⁷ because the overlayer thickness was known.

Ultrasound-image segmentation

The ultrasound transducer at the centre of optical probe was critical because it enabled us to derive tissue layer morphology and geometry information needed for the optical reconstruction algorithms. At the beginning of each ‘optical frame’, we captured an ultrasound image. Based on this ultrasound image, the clinician determined the depth below the tissue surface of the adipose, rectus, uterus, and placenta tissue layers in the left, middle and right sections of the ultrasound image. The difference between the left, middle and right depths was thus determined to ensure effective reconstruction of tissue optical properties. Note, if this difference was less than 0.5 cm, then we took data; on the rare occasion when the difference was larger than 0.5 cm, we repositioned the probe position/angle to decrease the difference and then took data.

Pregnancy outcome

After delivery, medical records were reviewed and relevant data on outcomes were extracted by a reviewer blinded to the optical data. Gestational hypertension (GHTN) and preeclampsia (PE) were defined per American College of Obstetricians and Gynecologists criteria⁵⁴; intrauterine growth restriction (IUGR) was defined as a birth weight below the 5^th percentile for gestational age⁵⁵.

Placental histopathology

The delivered placentas were evaluated using a standard procedure^36,56 by a single placental pathologist (R.L.L.) who was blinded to the optical properties. Maternal vascular malperfusion (MVM) was defined as a pattern of injury including placental hypoplasia (small for gestational age), villous infarcts, retroplacental haemorrhage (abruptio placentae), distal villous hypoplasia, villous agglutination, accelerated villous maturation and decidual arteriopathy. The minimum findings required for MVM diagnosis included decidual arteriopathy or at least 2 other features including accelerated villous maturation.

In vivo monitoring of placental oxygen dynamics

We designed a pilot clinical study of human placental oxygen-related haemodynamic properties. The study enrolled women with singleton pregnancies in the third trimester, anterior placentas, and pre-gravid BMI<40. For each experiment, participants were placed in supine, semi-recumbent position, and the central region of placenta was monitored. Prior to proceeding with the study, approval by the Institutional Review Board (IRB) at the University of Pennsylvania was obtained. Each participant signed the resultant informed consent forms prior to participating in the study.

Four experiments were completed: (1) a reproducibility experiment, wherein a 2-frame measurement was made both before and after lifting and placing the probe at approximately the same location for three times (n=18); (2) a stability experiment, wherein continuous data was collected for 10 frames (~3.5 minutes) with participant breathing room air (n=24); (3) a maternal left tilt experiment wherein 4 frames of data were collected, first in supine and then in left-lateral decubitus position, to characterize haemodynamic changes related to increased maternal cardiac output and uterine perfusion (n=3); (4) a maternal hyperoxia experiment (n=24), wherein the placenta was monitored continuously for 10 frames (~3.5min) of baseline at room air, 20 frames (~7 min) of maternal hyperoxia (100%$Fi{O}_2$), and 10 frames (~3.5min) of recovery at room air again. Note, a single “optical frame” corresponds to a measurement cycle through 11 light source-detector pairs and 3 wavelengths in ~21 seconds.

In total, n=24 participants participated in this study. Detailed information about the participants is provided in Supplementary Table 6. Note, data from two other participants were excluded because their signals were either too small (tissue optical absorption coefficient was very large, ${\mu }_a>0.2 c{m}^{-1}$) or too unstable (due to large fluctuations during baseline period).

Measurement reproducibility was evaluated using the Intra-class Correlation Coefficient (ICC). We measured the haemoglobin properties multiple times at the same placental location in 18 participants.

The stability test (n=24) results were represented by the standard deviation (S.D.) during the continuous 10 frames measurements (Fig. 6a). Note, occasionally during data acquisition, substantial movement artifacts can occur causing a single frame to exhibit >10% fluctuations in $St{O}_2$, $\left[H{b}_T\right]$, or $\left[Hb{O}_2\right]$ compared to the values of nearby frames. We identified these motion artifacts and filtered them out from the data.

To further validate the US/FD-DOS instrumentation and methodology in a physiologic context, we performed a left tilt experiment (n=3). In this experiment, the impact of increased maternal cardiac output on placental oxygen haemoglobin properties were determined. Briefly, in each participant, we measured $St{O}_2$, $\left[H{b}_T\right]$, and $\left[Hb{O}_2\right]$ for 4 frames both before and after the maternal tilt. Fig. 3c presents the mean values of $St{O}_2$, $\left[H{b}_T\right]$, and $\left[Hb{O}_2\right]$ for each participant, before and after the maternal tilt. To calculate the mean (S.D.) of relative increases, we first determined the “before/after” difference in mean value of each parameter for each participant. Then we normalized this difference by the mean of the “before” value. Finally, we averaged these fractional changes across all 3 participants (Fig. 3c). To calculate the P-values, the relative haemoglobin properties were obtained by normalizing the “after” mean values to the “before” mean values, and paired t test analysis was applied to the relative “before/after” values.

The placental haemodynamic response to maternal hyperoxia was examined by monitoring the placental haemoglobin properties ($\left[Hb\right]$, $\left[Hb{O}_2\right]$, $\left[H{b}_T\right]$, $St{O}_2$) before, during, and after maternal hyperoxia. After an initial baseline period, participants were given 100% FiO₂ via facemask for ~ 7 minutes (20 frames). Concurrent ultrasound and FD-DOS data were acquired throughout the process. Overall (n=24), the experimental methodology easily resolved changes in placental blood oxygenation due to maternal hyperoxia, making use of all source-detector pairs. Nevertheless, in processing we identified and excluded specific SDSs from our reconstructions. For example, occasionally an SDS would saturate or very unstable (owing to human movement), or, occasionally, the longest SDS was very noisy (owing to large absorption); such SDSs would be excluded from further processing. Similarly, during the hyperoxia measurements, movement artifacts occasionally occurred causing a single frame to exhibit unphysiologically large (negative) fluctuations compared to the nearby frames (and baseline); such a frame would be excluded.

We investigated potential associations between placental oxygen dynamics during maternal hyperoxia, (i.e., $\text{Δ}St{O}_2$, $\text{Δ}H{b}_T$, and $\text{Δ}Hb{O}_2$) and the APO / MVM outcomes. For these analyses, the mean baseline $St{O}_2$, $\left[H{b}_T\right]$, and $\left[Hb{O}_2\right]$ were calculated using the final 4 frames of the baseline period.$\text{Δ}St{O}_2$, $\text{Δ}H{b}_T$, and $\text{Δ}Hb{O}_2$ were defined as the difference between these mean baseline values and the “peak” values of the 4-frame window during maternal hyperoxia wherein maximum $St{O}_2$ occurred. Each participant (N=24) was then categorized into two groups based on pregnancy outcome: NPO or APO. We observed significantly larger $\text{Δ}St{O}_2$ and $\text{Δ}Hb{O}_2$ in response to maternal hyperoxia in the NPO group, compared to (the more blunted response in) the APO group (see main text Fig. 4 (b)). Similarly, when analysing placental histopathology as the outcome of interest, we observed significant (large) $\text{Δ}St{O}_2$ and $\text{Δ}Hb{O}_2$ in the NPP group compared to a blunted response in the MVM group (see main text Fig. 5 (b)). Wilcoxon rank sum tests were performed to calculate the p-values for comparison of different variables between NPO vs APO groups and NPP vs MVM groups.

Haemodynamic properties of adipose and rectus/uterus layers

Using the three-layer model, the optical and haemodynamic properties of adipose and rectus/uterus layers can also be reconstructed. Generally, we expect the accuracy of these overlayer results to be less than that of the placenta, because the probe SDSs were optimized for the deeper placental tissue. Note also, due to very thin adipose or rectus/uterus layer thickness, 4 of the 24 participants were processed with two-layer rather than three-layer model reconstruction; therefore, we excluded these 4 participants in the statistical analysis of adipose or rectus/uterus layer. The $St{O}_2$ and $\left[H{b}_T\right]$ of adipose and rectus/uterus layers are reported in Supplementary Table 3; these properties are within ~10% of values reported for somewhat similar tissues, e.g., breast⁵⁷ (for comparison to adipose) and muscle⁵⁸ (for comparison to rectus/uterus). For the placenta layer, we found good agreement between our reduced scattering coefficient and an ex-vivo placenta study⁵⁹; the placenta layer absolute haemoglobin properties have not been previously reported (to our knowledge), and the placenta layer $St{O}_2$ are roughly consistent with those observed by CW-NIRS⁴⁴.

The adipose and rectus/uterus baseline haemoglobin properties of healthy participants were not significantly different from participants with APO or MVM (Supplementary Table 5). This finding parallels our baseline placenta results. We also analysed the adipose and rectus/uterus layer haemodynamic response to maternal hyperoxia, and we compared their differences across participant groups (Supplementary Table 5). We did not find significant association of the overlayer haemodynamic properties in normal participants versus participants with APO or MVM. This finding is different from the placenta results during maternal hyperoxia. In total, these data provide in vivo evidence underscoring the importance of the multi-layer modelling to separate layer responses. Without the multi-layer model and associated instrumentation, quantitative estimates of placenta response are contaminated by signals from the other layers.

The null overlayer results are not necessarily surprising from physiological perspective. For example, since MVM presents a recognizable pattern of placental injury related to altered uterine and intervillous blood flow, we would not expect significant association between adipose haemoglobin properties and MVM. However, we noticed that the rectus/uterine layer blunted response to maternal hyperoxia exhibited a trending but statistically insignificant association to APO (P=0.06). Although it is possible that impaired uterine perfusion may be involved in the pathophysiology of placental dysfunction, in our view, further study in a larger sample size will be important to confirm and further elucidate these relationships.

Uterine-artery Doppler-pulsatility index

Each uterine artery was identified using a transabdominal C1–5 ultrasound probe (GE Healthcare) via power Doppler mapping. Pulsed wave Doppler was then used to obtain three similar consecutive waveforms. PI was defined as the difference between peak systolic and end diastolic velocities divided by the mean velocity. The mean PI of the two uterine arteries was used for analysis. No association was found between UtA PI and APO or MVM (Table 2). Furthermore, when including UtA PI as a covariate, the associations between $\text{Δ}St{O}_2$ and $\text{Δ}Hb{O}_2$ and our outcomes (i.e. APO and MVM) remained apparent (Supplementary Table 4).

Statistical analysis

Statistical analyses were performed using MATLAB 2019a. Accuracy in phantom experiments and simulations is defined as the difference between measured and expected values, divided by the expected value. Depending on the data-type, results from the clinical study are presented as mean (S.D.) or median (IQR). ICC in the reproducibility experiment was calculated by dividing the random effect variance by the total variance. Our study employed a relatively small sample-size (<30 participants), and the data in the two groups were not normally distributed. In this case, a non-parametric test is appropriate (i.e., a rank sum test with continuous data). Thus, P-values for studying correlations between different variables and placental dysfunction were obtained using the two-sided Wilcoxon rank sum test, a nonparametric test for two populations when samples are independent. P values for studying correlations between nulliparity and placental dysfunction were obtained by two-sided Fisher’s exact test. P-values for studying the before/after difference in the maternal left tilt experiment were calculated by two-sided paired sample t test analysis. Binary logistic regressions were also performed to study the correlation between APO/MVM and $\text{Δ}St{O}_2$ or $\Delta Hb{O}_2$ but with control of other variables: UtA PI, placental depth $\left(d\right)$, and pre-gravid BMI. We carried out this analysis for completeness with caveats that the sample size is small and that different pairs of variables might be partially correlated (and if so, that future inclusion of interactions in the statistical models is desirable). Supplementary Table 4 shows the resultant p-values of $\Delta Hb{O}_2$ and $\text{Δ}St{O}_2$ for prediction of APO or MVM from the binary logistic regression models. The results confirm that there remained a trend towards significant association between optically-derived haemodynamic properties and our outcomes of interest. For the future, a larger sample size will permit more sophisticated statistical analyses that explore the effects of possible confounding variables and that generate composite metrics with improved specificity and sensitivity.

Extended Data

Extended Data Figure 1.

Detailed schematic of custom heterodyne FD-DOS instrument.

Supplementary Material

Supplementary Table 3

Baseline hemoglobin-related properties of adipose, rectus/uterus, and placenta layers (n=20*).

Supplementary Table 4

Binary logistic regression of placental properties with two independent variables (n=24).

Supplementary Table 5

Correlation of overlayer hemodynamic with placental dysfunction (n=20).

Supplementary Table 1

Two-layer phantom experiment results (λ =785 nm)

Supplementary Table 2

Reconstructed optical and hemoglobin-related properties of three-layer finite element numerical simulations with realistic layer morphology.

Data availability

The main data supporting the results in this study are available within the paper and its supplementary information. All optical data generated in this study, including source data and the data used to make the figures, are available from figshare with identifiers https://doi.org/10.6084/m9.figshare.19451882, https://doi.org/10.6084/m9.figshare.19451879 and https://doi.org/10.6084/m9.figshare.19451876. The raw clinical and ultrasound data are available from the corresponding author, subject to approval from the Institutional Review Board of the University of Pennsylvania.