A microfluidic method to investigate platelet mechanotransduction under extensional strain

Abstract

Background

Blood platelets have evolved a complex mechanotransduction machinery to rapidly respond to hemodynamic conditions. A variety of microfluidic flow-based approaches have been developed to explore platelet mechanotransduction; however, these experimental models primarily focus on the effects of increased wall shear stress on platelet adhesion events and do not consider the critical effects of extensional strain on platelet activation in free flow.

Objectives

We report the development and application of a hyperbolic microfluidic assay that allows for investigation of platelet mechanotransduction under quasi-homogenous extensional strain rates in the absence of surface adhesions.

Methods

Using a combined computational fluid dynamic and experimental microfluidic approach, we explore 5 extensional strain regimes (geometries) and their effect on platelet calcium signal transduction.

Results

We demonstrate that in the absence of canonical adhesion, receptor engagement platelets are highly sensitive to both initial increase and subsequent decrease in extensional strain rates within the range of 747 to 3319/s. Furthermore, we demonstrate that platelets rapidly respond to the rate of change in extensional strain and define a threshold of ≥7.33 × 10⁶/s/m, with an optimal range of 9.21 × 10⁷ to 1.32 × 10⁸/s/m. In addition, we demonstrate a key role of both the actin-based cytoskeleton and annular microtubules in the modulation of extensional strain–mediated platelet mechanotransduction.

Conclusion

This method opens a window onto a novel platelet signal transduction mechanism and may have potential diagnostic utility in the identification of patients who are prone to thromboembolic complications associated with high-grade arterial stenosis or are on mechanical circulatory support systems, for which the extensional strain rate is a predominant hemodynamic driver.

Graphical abstract

Essentials

• •We described an extensional strain ($\stackrel{.}{\epsilon }$) microfluidic assay applied to platelet mechanotransduction.
• •We demonstrated that $\stackrel{.}{\epsilon }$ is a key driver of platelet activation.
• •Platelets mechanosense $\stackrel{.}{\epsilon }$ in the absence of adhesion receptor engagement.
• •This method accesses a novel mechanotransduction process and may have future diagnostic utility.

1. Introduction

Blood platelets are central players in physiologic hemostasis and pathologic thrombosis. Mechanical blood flow parameters (hemodynamics) are important drivers of platelet signal transduction and function [1]. Platelets experience a wide range of hemodynamic variables related to cardiovascular disease and/or blood-contacting medical devices that impact their function. These include increased wall shear stress/strain at sites of stenosis [2,3]; tensile and compressive forces on adhesion to vessel walls, thrombi, or the surface of medical devices [4,5]; and mass transport phenomena within regions of flow recirculation and because of red blood cell margination [[6], [7], [8]]. Platelets transduce these external mechanical cues into intracellular biochemical signals (mechanotransduction) [9]. A key nexus for these varying mechanotransduction mechanisms is cytosolic calcium [Ca²⁺]_c flux, which integrates disparate signal transduction pathways and drives associated platelet activation events such as changes in shape and activation of the integrin α_IIb β₃ [[10], [11], [12]].

The complex flow environments that can occur in the human vasculature (eg, at vessel bifurcations, stenosis, aortic aneurysms, heart valves, and capillary networks) are an integrated result of both shear and extensional (elongational flow) phenomena over relatively short timescales. A large body of literature has described the investigation of platelet activation and function in which constant shear stress/shear rate levels were maintained over exposure times much longer than physiologic timescales, primarily in the context of surface adhesion events. However, platelet responses to other hemodynamic forces over short timescales, prevalent in the vasculature and blood-contacting medical devices, have been poorly investigated. Very little previous work has been reported on the effects of extensional stresses on platelet activation; yet, when a platelet flows through a stenosis or enters a mechanical circulatory support (MCS) system, convective acceleration of blood flow produces such stresses (Figure 1) [[13], [14], [15]]. Typical cases of extensional stresses are found in areas of sudden contractions or expansions of the flow field, such as the entrance and exits of ventricular assist devices, reverse gap flow in artificial heart valves, microcirculation, and entrance to severe arterial stenoses [13,16]. In the specific case of platelet function, early studies, using experimental and numerical models to map hemodynamics and platelet thrombus formation in response to arterial stenosis, pointed toward a role of extensional strain (separate from shear stress) and associated platelet elongational deformation (Figure 1) in driving thrombosis [13,17].

Figure 1.

Shear flow versus extensional flow. (A) Shear flow characterised by a laminar flow profile with a velocity gradient perpendicular to the vessel wall. Frictional shear stresses act at the wall to oppose the driving force due to pressure. Shear stresses also exist between adjacent fluid layers (laminae) resulting in the tumbling behaviour of blood cells and platelets in free flow. Wall shear stress (WSS) at the vessel wall promotes platelet roll-ing/translocation through platelet GPIb/V/IX – VWF binding and triggers receptor mediated platelet Ca²⁺ activation. (B) Uniaxial extensional (elongational) flow characterized by a region of flow acceler-ation parallel to the vessel wall. Under extensional strain plasma components such as VWF and blood cells are stretched at a constant rate ($\stackrel{.}{\epsilon }$) leading to an overall change in aspect ratio (elongation). Blood cell exposures to extensional strain tend to be brief and intermittent due to acceleration of the cells in the flow field and typically occur at regions of vessel narrowing or changes in device geometry.

We recently demonstrated that isolated platelets are capable of directly transducing the extensional strain rate ($\stackrel{.}{\epsilon }$) component of flow acceleration in the absence of canonical adhesion receptor engagement and/or soluble agonist–mediated platelet amplification loops [18]. We demonstrated that platelets “mechanosense” their $\stackrel{.}{\epsilon }$ environment through membrane delimited extensional strain sensing ($\stackrel{.}{\epsilon }$-S) mechanosomes, which comprise Piezo1 as the strain sensor and P2X1 as a Ca²⁺ signal amplifier. We further demonstrated that the class II phosphoinositide 3 kinase C2α isoform acts as a critical regulator of this mechanotransduction mechanism through the modulation of the coupling of extensional force to the mechanosome [18]. Collectively, these findings raise significant questions regarding the specific nature of fluid-induced forces affecting initial platelet activation and downstream function.

Investigations of platelet mechanotransduction have been conducted using a variety of techniques, including cone-and-plate and parallel-plate rheometry [19], microfluidic flow assays [20], static adhesion assays on rigid and deformable elastic substrates [[21], [22], [23]], and micropipette aspiration/bead pulling methods [4,24]. These techniques, although useful in probing platelet adhesion receptor–mediated events, do not allow for the investigation of platelet mechanotransduction in the absence of adhesion receptor engagement or surface adhesions in free flow. In addition, common flow-based techniques, such as microcapillary, straight microfluidic, and parallel-plate methods, typically involve mixed kinematics (both shear and extensional components), with most studies only focused on wall shear effects [25]. To more accurately define the hemodynamic parameters driving the behavior of blood cells and platelets, approaches are shifting from simple, straight channels that provide steady-state laminar shear flow to the use of more complex geometries, such as stepped microcontraction geometries [26], complex bifurcating microfluidics [27,28], cross-slot devices [29,30], and hyperbolic contractions [18,31,32].

Cross-slot (stagnation-point) and hyperbolic microfluidic systems allow for specific impact of extensional strain on platelet function to be investigated. In cross-slot devices, cells are trapped at the intersection of converging microchannels by means of opposite flows from 2 inlets, reaching a stagnation point with maximum strain at convergence [29,30]. The advantage of these stagnation-point devices is that they provide a purely extensional strain field. In contrast, hyperbolic contraction geometries feature only 1 inlet and 1 outlet and impose strong extensional flow at the center line [33]. The chief advantage of hyperbolic microfluidics is that the reduced length scales of these geometries (typically ≤ 300 μm) allow for significantly higher linear extensional strain rates to be achieved as a function of their geometry and input flow rate. As a result, high deformation rates are attainable [34,35]. Although hyperbolic microfluidics have been applied to the investigation of deformation and function of red blood cells [32,36], we are the first (to our knowledge) to describe a method of applying hyperbolic microfluidics to the investigation of platelet mechanotransduction.

Here, we described and characterized the application of a hyperbolic microfluidic assay method to investigate platelet activation under varying extensional strain regimes. Using a combined computational and experimental approach, we explored the way in which instantaneous and time-dependent extensional strain dynamics impact platelet Ca²⁺ signaling and mechanotransduction. Using 5 cases of hyperbolic geometry, we defined the upper threshold of extensional strain that triggers maximal platelet [Ca²⁺]_c flux. In addition, we showed proof-of-concept pharmacologic experiments investigating the role of both the platelet actin cytoskeleton and annular microtubules in platelets’ $\stackrel{.}{\epsilon }$-S.

2. Methods

2.1. Hyperbolic microfluidic design and fabrication

The methodology described herein harnesses the hydrodynamic properties of defined hyperbolic microfluidic geometries that, under steady-state flow rates (Qs), induce linear flow acceleration of isolated platelet suspensions along the channel center line, resulting in controllable quasihomogenous extensional strain rates ($\stackrel{.}{\epsilon }$). Hyperbolic contraction channel microfluidics were designed to generate $\stackrel{.}{\epsilon }$ spanning both physiologic (300-5000/s) [13,17] and nonphysiologic/pathologic cases, approaching 50,000/s, depending on the hyperbolic geometry, flow rate, and viscosity. The hyperbolic geometry dimensions are described in Figure 2 and the Table, with contraction length (L_h) + (L_g), contracting from a straight (nonhyperbolic) channel with a width of 400 μm to maximal contraction (W_c) (Figure 2A). At the end of the hyperbolic contraction, a sudden expansion of 400 μm was used to investigate platelet [Ca²⁺]_c flux recovery after the release of the fluidic force (Figure 2A). Five hyperbolic cases (Figure 2B, Table) were investigated, with the L_h ranging from 150 to 300 μm (L_g = 20 μm) and W_c ranging from 40 to 72 μm, with these dimensions determining the rate of change in $\stackrel{.}{\epsilon }$ (Figure 2B, Table). All hyperbolic channel replicas had a constant height of 80 μm.

Figure 2.

Hyperbolic microfluidic design. (A) Schematic of hyperbolic design. Dotted line defines confocal line-scan with width = 0.1 x W_c. (B) Topleft: Macro-view of the microfluidic chip layout consisting of 14 channels each equipped with individual external pump connectors and sample outlet: [a] pump tubing pins for sample delivery and perfusion; [b] hyperbolic cases (Zoom); [c] vacuum chuck input and conduits allowing for rapid and reversible chip adhesion to underlying borosilicate glass No. 1 coverslip. Panels: Micrographs of hyperbolic cases 1 – 5. Note: Striations in the micrographs are an artefact of the maskless photolithography process and do not represent wall features impinging on sample flow.

Table.

Hyperbolic microfluidic cases.

Case	Wc (μm)	Lh (μm)	Wu/Wd (μm)	Lg (μm)	hz (μm)
1	40	300	400	20	80
2	50	225	400	20	80
3	40	225	400	20	80
4	72	150	400	20	80
5	40	150	400	20	80

h_z, constant height; L_g,; L_h, hyperbolic length; W_c, maximal contraction; W_d, width of expansion; W_u, width of straight channel.

All microfluidic devices were fabricated using established soft photolithography methods [18]. Briefly, using maskless lithography (MLA 150; Heidelberg instruments), a master template was patterned onto a 4-inch silicon wafer using the SU-8 3050 photoresist (MicroChem Corp) to produce defined channel features with a height of 80 μm. Polydimethyl siloxane (PDMS) (Sylgard 184) was mixed with a curing agent in a ratio of 1:10 by weight, degassed in a vacuum desiccator, cast on the master template, and cured at 130 °C in a convection oven for 20 minutes. The cured PDMS was peeled off the mold and cut to size, and a 0.75-mm hole was punched at the inlets, outlets, and vacuum chuck before it was reversibly sealed with vacuum onto a number-1 borosilicate microscope coverslip (Figure 2B—macroview). Microfluidic chips were recycled between use via sonication in 20% Extran MA05 (Merck Millipore), followed by sonication in deionized water, and baked in a convection oven at 110 °C following a final rinse with deionized water.

2.2. Computational fluid dynamics

The underlying computational fluid dynamic modeling of the hyperbolic cases was initially validated by reproducing the results (velocity calculated along the center line of the hyperbolic channel) obtained by Oliveira et al. [35] (Supplementary Fig. 1A, B). The geometry, assumptions employed in the simulation, and boundary conditions can be found in the studies by Zainal Abidin et al. [18] and Oliveira et al. [35]. Solid Edge (Siemens PLM Software) was used to extract 3-dimensional simulation domains (Cases 1-5) from Computer Aided Design (CAD) models (Figure 1B, Table). Hexahedral unstructured meshes for all the cases were generated using Pointwise, Inc (Fort Worth). Finer mesh elements were used around the domain’s center line in the hyperbolic stenosis and downstream of it. A mesh convergence study was conducted to ensure adequate mesh resolution (Supplementary Fig. 1C). The root mean squared percent error was calculated. For all considered mesh cases, the root mean squared percent error was <1%. Mesh 3 was chosen to ensure high-fidelity numerical simulations (Supplementary Fig. 1C). The flow was assumed to be laminar, incompressible, and Newtonian, with a Tyrode buffer dynamic viscosity (μ) of 4 × 10⁻³ Pa seconds.

Numerical simulation of the flow in the hyperbolic cases was performed using OpenFOAM, version 8 (The OpenFOAM Foundation Ltd). The steady-state solver for incompressible flow simpleFoam, which is based on the Semi-Implicit Method for Pressure Linked Equations algorithm, was chosen for the simulations. Constant uniform inflow was applied at the “Inlet” path of the model, with the model length upstream of the stenosis sufficient to allow for fully developed flow in the hyperbolic section. Constant pressure was applied at the “Outlet” path of the model. A no-slip condition was imposed at solid walls. Simulations were performed for inflow rates (Q) of 12.5, 50, 200, and 600 μL/min. An open-source, multiplatform data analysis and visualization application, ParaView 5.6.0 (Sandia National Laboratories, Kitware Inc), was used for visualization of the flow and extraction of velocity along the center line of the model (Supplementary Figs. 2, 3). The Python code was used to calculate $\stackrel{.}{\epsilon }$ along the center line numerically and analytically. The analytical solution was obtained using the following expression:

$$\dot{\epsilon }=\frac{Q}{\left(L_h+L_g\right)h_z}\left(\frac{k_c}{W_c}-\frac{k_d}{W_d}\right)$$ (1)

where k is the ratio between the center line velocity and average velocity in the cross-section of the model.

2.3. Blood collection and platelet isolation

Ethics approval was obtained from Monash University Human Research Ethics Committee. Blood from healthy consenting volunteers was withdrawn using a 19-gauge butterfly needle into syringes containing acid citrate dextrose (ACD) [the ratio of blood to ACD was 6:1]. The samples were gently inverted to mix the anticoagulant, transferred to 50-mL Falcon tubes, and allowed to rest for 10 minutes at 37 °C prior to use.

Platelet isolation from the ACD-anticoagulated whole blood was performed as per the methods detailed in the studies by Zainal Abidin et al. [18] and Nesbitt et al. [37]. Briefly, the ACD-anticoagulated whole blood was supplemented with 0.005-U/mL apyrase before incubation at 37 °C for 10 minutes. Platelet-rich plasma was isolated by centrifugation at 200 × g for 15 minutes, followed by repeat centrifugation at 1700 × g for 7 minutes, after which platelet-poor plasma was removed and the platelet pellet resuspended in an equal volume of platelet washing buffer (PWB) [4.3mM dipotassium phosphate, 4.3mM disodium phosphate, 24.3mM monosodium phosphate, 113mM sodium chloride, 5.5mM D-glucose, and 10mM theophylline [pH 6.5] containing 0.5% wt/vol bovine serum albumin, 0.01-U/mL apyrase, and 800-U/mL hirudin). Final centrifugation was performed on the platelet suspension at 1500 × g for 7 minutes, and the platelet pellet was resuspended in PWB (supplemented with 0.02-U/mL apyrase) to achieve a platelet concentration of 300 × 10⁹/L. Platelet counts were performed using full blood analysis using the Cell-Dyn Emerald hematology analyzer (Abbott Diagnostics).

2.4. Platelet [Ca²⁺]_c (2-aminophenoxy)ethane-N,N,N′,N′-tetra-acetic acid tetra(acetoxymethyl)ester (CAL520) assay

The assessment of platelet cytosolic [Ca²⁺]_c was performed as per the method used by Zainal Abidin et al. [18]. In brief, the isolated platelets (300 × 10⁹/L) in PWB were loaded with 1.25μM CAL520 (AAT Bioquest) for 45 minutes at 37 °C, followed by washing in PWB and resuspension in modified Tyrode buffer (pH 7.2) containing 1mM calcium chloride (CaCl₂), 1mM magnesium chloride, and ±0.5% wt/vol methyl cellulose (Sigma Aldrich).

Prior to experimentation, hyperbolic microchannels were incubated for 10 minutes with 2% wt/vol bovine serum albumin (10% wt/vol) to block platelet adhesion to the microfluidic. Sample perfusion and platelet [Ca²⁺]_c dynamics were monitored for a duration of 30 seconds, with a “no delay” interval for the highest speed using resonant scanning confocal imaging (Nikon A1R—Plan Fluor 40× WI/0.50 objective) using the Andor Zyla sCMOS camera at 0.586 frames/s for 30 seconds, with a focal point at 40 μm (midplane of the hyperbolic microfluidics). Fluorescence image analysis was restricted to a line scan running along the central axis of the microfluidic, with a width of 0.1 × W_c (Figure 1A). All image analyses were performed off-line in ImageJ. Corrected fluorescence values (F) for the line scan profiles were converted into pseudo-ratio values according to the methods in the studies by Zainal Abidin et al. [18] and Heemskerk et al. [38]:

$${\left[{\mathrm{C}\mathrm{a}}^{2+}\right]}_{\mathrm{c}}={\mathrm{K}}_{\mathrm{d}}\left[\left(\mathrm{F}-{\mathrm{F}}_{\min }\right)/\left({\mathrm{F}}_{\max }-\mathrm{F}\right)\right]\left[{\mathrm{K}}_{\mathrm{d}}\mathrm{C}\mathrm{A}\mathrm{L}520=320\mathrm{n}\mathrm{M}\right]$$ (2)

where F_min was derived for independent platelet flow experiments in which CAL520-loaded platelets were treated with 50μM ]imethyl,1,2-Bis(2-aminophenoxy)ethane-N,N,N′,N′-tetraacetic acid tetrakis(acetoxymethyl ester) (DM-BAPTA-AM) and resuspended in Tyrode buffer supplemented with 5mM ethylene-bis(oxyethylenenitrilo)tetraacetic acid (EGTA) and F_max was determined for each defined line scan by perfusing through the microfluidic platelets treated with 2.5μM A23187 in Tyrode buffer supplemented with 5mM CaCl₂.

3. Results

3.1. Initial assay characterization

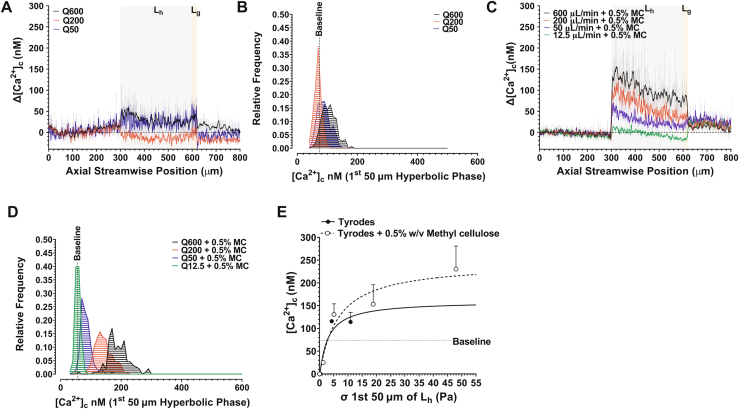
To initially validate the [Ca²⁺]_c imaging and microfluidic method, we investigated platelet [Ca²⁺]_c flux as a function of media viscosity μ and Q using case 1 (Figure 1B) as our proof of concept. This case was previously published in the study by Zainal Abidin et al. [18]. In initial experiments, isolated platelets (300 × 10⁹/L) were resuspended in modified Tyrode buffer (pH 7.2); μ = 9.11 × 10⁻⁴ ± 2.11 × 10⁻⁵ Pa seconds (final density = 997 kg/m³). Platelet samples were perfused through case 1 at Qs of 12.5, 50, 200, and 600 μL/min (the upper limit of the microfluidic system). Figure 3A, B demonstrates that under these conditions, minimal to no change in platelet [Ca²⁺]_c was observed. To investigate whether increasing buffer viscosity and, therefore, increased extensional stress (σ) modified the platelet response, the isolated platelets were suspended in modified Tyrode buffer supplemented with 0.5% wt/vol methyl cellulose (to increase buffer viscosity, limit platelet sedimentation, and allow for higher σ at lower Qs as per the method in the study by Piergiovanni et al. [39]); μ = 4 × 10⁻³ ± 1.5 × 10⁻⁴ Pa seconds (final density = 1016 kg/m³). The addition of methyl cellulose had no observable effect on platelet morphology (data not shown) and no observable effect on baseline [Ca²⁺]_c (Figure 3). In the presence of methyl cellulose, however, the platelets displayed a stepwise increase in [Ca²⁺]_c flux as a function of Q, with a significant right shift in the overall frequency distribution of platelet [Ca²⁺]_c (Figure 3C, D). Significantly, peak platelet [Ca²⁺]_c was directly dependent on media viscosity such that platelets resuspended in Tyrode buffer containing 0.5% wt/vol methyl cellulose displayed a peak platelet [Ca²⁺]_c at hyperbolic start that was ∼3-fold higher than those in Tyrode buffer alone at a Q of 600 μL/min (Figure 3). The maximal [Ca²⁺]_c flux ranged between 113 and 166 nM at a μ of 9.11 × 10⁻⁴ Pa seconds and 314 to 560 nM at a μ of 4 × 10⁻³ Pa seconds (Figure 3). These data are comparable with our previously published findings [18]. These data suggest that an initial σ of approximately ≥3 Pa is required to initiate platelet [Ca²⁺]_c flux (Figure 3E). As a result of this initial characterization, all subsequent experiments were performed in the presence of methyl cellulose (0.5% wt/vol).

Figure 3.

Platelet [Ca²⁺]_c flux as a function of v and Q (Case 1). (A) Platelet ▵[Ca²⁺]_c as a function of Q at μ = 9.11x10^-4 ± 2.11x10^-5 Pa.s. Solid lines are a rolling average (2nd order smoothing - 10 neighbours). All data has been normalised against baseline [Ca²⁺]_c derived as the average over pos. 0 – 200 μm non-hyperbolic segment. Grey region defines the hyperbolic phase L_h. Orange region defines L_g. (B) Frequency histogram showing the distribution of platelet [Ca²⁺]_c (10 nM bins) within the first 50 μm of Hyperbolic flow as a function of Q = 50 μL/min (N = 3 experiments); Q = 200 μL/min (N = 3 experiments); Q = 600 μL/min (N = 3 experiments). Dotted line represents baseline [Ca²⁺]_c cut-off = 69 nM. (C) Human platelet [Ca²⁺]_c as a function of Q at μ = 4x10^-3 Pa.s (+ 0.5%w/v methyl cellulose). (D) Frequency histogram showing the distribution of platelet [Ca²⁺]_c (10 nM bins) within the first 50 μm of Hyperbolic flow as a function of Q = 50 μL/min (N = 3 experiments); Q = 200 μL/min (N = 3 experiments); Q = 600 μL/min (N = 3 experiments). Dotted line represents baseline [Ca²⁺]_c cut-off = 63 nM. (E) Maximum platelet ▵[Ca²⁺]_c as a function of applied extensional stress (σ) at hyperbolic start (pos. = 300 – 350 μm) for Q = 12.5 – 600 μL/min. Dotted line represents baseline [Ca²⁺]_c cutoff = 74 nM. [Agonist] vs. response variable slope (three parameters) least squares fit (N = 3 independent experiments)

3.2. Extensional strain rate modulates platelet Ca²⁺ signaling dynamics

Initial characterization of platelet Δ[Ca²⁺]_c flux as a function of Q in the case 1 hyperbolic (L_h = 300; W_c = 40 μm) demonstrated overall dependency of peak [Ca²⁺]_c on flow rate and overall $\stackrel{.}{\epsilon }$ magnitude (Figures 3C, 4A, B). At all Qs, Δ[Ca²⁺]_c initiated immediately at hyperbolic start (streamwise position = 300-350 mm), characterized by a sharp jump in Δ[Ca²⁺]_c (Figure 4A). Notably, platelet [Ca²⁺]_c within the hyperbolic zone exhibited a decline in magnitude over a time of ∼75%, which related to a plateau (steady state) in $\stackrel{.}{\epsilon }$ (Figure 4A), suggesting that this mechanotransduction process is rapidly downregulated once steady-state $\stackrel{.}{\epsilon }$ is achieved. Notably, $\stackrel{.}{\epsilon }$-driven Δ[Ca²⁺]_c flux exhibited a rapid on/off behavior such that ejection of the platelet sample into downstream nonhyperbolic expansion resulted in immediate cessation of Δ[Ca²⁺]_c flux and return to baseline levels, which was related to a sharp negative transition in $\stackrel{.}{\epsilon }$ across L_g from 13,808/s to −22,107/s, suggesting that platelets under these experimental conditions are acutely responsive to both extensional and compressive strain components (Figure 4A).

Figure 4.

$\stackrel{.}{\epsilon }$ profile modulates platelet ▵[Ca²⁺]_c signalling dynamics (A, C, E, G, I) Platelet ▵[Ca²⁺]_c for cases 1 - 5 respectively as a function of Q = 12.5, 50, 200, 600 mL/min and $\stackrel{.}{\epsilon }$. Solid lines are a rolling average (2nd order smoothing - 10 neighbours). All data has been normalised against baseline [Ca²⁺]_c derived as the average over pos. 0 – 200 mm non-hyperbolic segment. Grey region defines the hyperbolic phase L_h. Orange region defines L_g. (B, D, F, H, J) Frequency histograms showing the distribution of platelet [Ca²⁺]_c (10 nM bins) within the first 50 μm of Hyperbolic flow for cases 1 - 5 respectively as a function of Q = 12.5, 50, 200, 600 mL/min. Dotted line represents baseline [Ca²⁺]_c cut-offs. (N = 3 experiments/donors per case per Q).

Cases 1, 3, and 5 were characterized by progressively shorter L_h of 300, 225, and 150 mm, respectively, and an equivalent ε_H of 2.30 (Table) but substantially different $\stackrel{.}{\epsilon }$ profiles (Figure 4A, E, I). Reduction in L_h markedly changed the peak $\stackrel{.}{\epsilon }$ to 18,098/s (L_h = 300 μm), 23,914/s (L_h = 225 μm), and 43,099/s (L_h = 150 μm) (Figure 4A, E, I), with peak $\stackrel{.}{\epsilon }$ achieved over a progressively shorter timeframe. This overall modification in the $\stackrel{.}{\epsilon }$ profile under constant ε_H modified the overall platelet Δ[Ca²⁺]_c response. The peak [Ca²⁺]_c at the start of L_h was significantly higher for case 3 (peak [Ca²⁺]_c = 366.6 ± 86.6 nM; Q = 600 μL/min) than for case 1 (P = .0117; Δ[Ca²⁺]_c = 114.6 ± 86.6 nM) and case 5 (P = .0288; Δ[Ca²⁺]_c = 161.3 ± 68.6 nM) (Figure 4A, E, I). In addition, the relationship between Q and Δ[Ca²⁺]_c was substantially different, with a Q of 50 μL/min resulting in a low Δ[Ca²⁺]_c in case 3 but leading to a measurable peak Δ[Ca²⁺]_c in cases 1 and 5 (Figure 4B, F, J). In all cases, Δ[Ca²⁺]_c was rapidly downregulated at the hyperbolic exit, regardless of the magnitude of $\stackrel{.}{\epsilon }$ reduction (Figure 4). Taken together, these data suggest that peak $\stackrel{.}{\epsilon }$ and the rate of change in $\stackrel{.}{\epsilon }$ at hyperbolic start may be critical parameters driving the platelets’ $\stackrel{.}{\epsilon }$-S response.

3.3. Rate of change in $\stackrel{.}{\mathbf{\epsilon }}$ at hyperbolic start critically modulates platelet Ca²⁺ flux

Based on our initial findings that [Ca²⁺]_c flux was initiated during the initial acceleration phase at the hyperbolic throat and the observation that Δ[Ca²⁺]_c was downregulated at steady-state $\stackrel{.}{\epsilon }$, we hypothesized that platelets are acutely sensitive to the initial rate of change in $\stackrel{.}{\epsilon }$. To examine this, we analyzed the relative fold change in platelet [Ca²⁺]_c as a function of d$\stackrel{.}{\epsilon }$/dx along center-line flow in all the cases. In all the cases, the greatest change in [Ca²⁺]_c occurred within 50 μm of the start of L_h. For cases 1 to 4, this coincided with peak d$\stackrel{.}{\epsilon }$/dx (Figure 5). Case 3 exhibited the greatest fold change in [Ca²⁺]_c flux, approaching 5× (Figure 5C). For case 5, however, peak d$\stackrel{.}{\epsilon }$/dx was apparently decoupled from the peak [Ca²⁺]_c change (Figure 5E). Examination of the relationship between input Q and d$\stackrel{.}{\epsilon }$/dx demonstrated that cases 3 and 5 generated markedly increased d$\stackrel{.}{\epsilon }$/dx at a Q of >50 mL/min compared with the other cases (Figure 5F). Taken together, these observations suggest that platelet $\stackrel{.}{\epsilon }$-S signaling is acutely attuned to the relative change in $\stackrel{.}{\epsilon }$ and that maximal $\stackrel{.}{\epsilon }$-S occurs within an “optimal range” that lies between 9.21 × 10⁷/s¹/m¹ and 1.16 × 10⁸/s/m (Figure 5G). At a d$\stackrel{.}{\epsilon }$/dx of <7.33 × 10⁶/s/m, platelets show minimal $\stackrel{.}{\epsilon }$-S signaling (Figure 5G). In all the cases tested, platelet [Ca²⁺]_c flux underwent rapid downregulation, which, in part, was associated with d$\stackrel{.}{\epsilon }$/dx approaching 0/s/m (Figure 5). This was most notable for case 1, which exhibited a prolonged steady state, attributable to its length scale (Figure 5A). Notably, in all the cases, platelets experienced significant deceleration through L_g, which was correlated with significant reduction in ε, which was associated with rapid return of platelet [Ca²⁺]_c to baseline levels (Figures 4, 5; Supplementary Fig. 2). Qualitatively, the rate of decay of Δ[Ca²⁺]_c was similar across all the cases, suggesting that the downregulatory process in play are not contingent on maximal Δ[Ca²⁺]_c (Figures 4, 5).

Figure 5.

$\stackrel{.}{\epsilon }$-S is critically dependent on the rate of change in $\stackrel{.}{\epsilon }$ (A-E) relative (fold) change in platelet [Ca²⁺]_c for cases 1 - 5 respectively as a function of Q = 12.5, 50, 200, 600 mL/min and change in ε (d$\stackrel{.}{\epsilon }$/dx). Solid lines are a rolling average (2nd order smoothing - 10 neighbours). All data has been normalised against baseline [Ca²⁺]_c derived as the average over pos. 0 – 200 mm non-hyperbolic segment. Orange region defines the first 50 μm of L_h. Dotted lines demarcate L_h + L_g for each case. (N = 3 experiments/donors per case per Q). (F) Relationship between input flow rate (Q) and peak dε/dx within the first 50 μm of L_h. Lines represent linear regression. (G) Maximal Δ[Ca²⁺]_c as a function of change in ε (d$\stackrel{.}{\epsilon }$/dx). Data is compiled from all hyperbolic cases and all Q tested. Note that there is an optimal range for maximal Δ[Ca²⁺]_c between 9.21 x10⁷.s^-1.m^-1 – 1.16 x 10⁸.s^-1.m^-1 (grey region) and a threshold for initial Δ[Ca²⁺]_c activation of ∼7.33 x10⁶.s^-1.m^-1.

Taken together, these data demonstrate and support our previously published observations [18], demonstrating that isolated platelets can mechanotransduce $\stackrel{.}{\epsilon }$ in free flow. In addition, these studies further define a role of the initial rate of change in $\stackrel{.}{\epsilon }$ in triggering $\stackrel{.}{\epsilon }$-S. By modifying the hyperbolic geometry and, therefore, the applied $\stackrel{.}{\epsilon }$ profile, we defined a threshold range for d$\stackrel{.}{\epsilon }$/dx that activates $\stackrel{.}{\epsilon }$-S [Ca²⁺]_c flux and defined a maximum d$\stackrel{.}{\epsilon }$/dx of ∼1.16 × 10⁸/s/m, above which no further increase in [Ca²⁺]_c flux is apparent.

3.4. $\stackrel{.}{\mathbf{\epsilon }}$-S is dependent on actin cytoskeletal dynamics

Using a series of stepped microfluidic geometries that imposed mixed kinematic flow on blood samples, we have previously demonstrated that the platelet actin cytoskeleton is an important modulator of free-flow platelet mechanosensing [18]; however, a direct role of the actin cytoskeleton in the modulation of platelet response to $\stackrel{.}{\epsilon }$ was not defined. To specifically examine the way in which cytoskeletal dynamics modulate platelet mechanotransduction of $\stackrel{.}{\epsilon }$ and as a proof of concept of our hyperbolic microfluidic method, we examined the way in which a series of cytoskeletal inhibitors impacted platelet [Ca²⁺]_c flux in the case 3 hyperbolic. Figure 6A, B demonstrates that platelet [Ca²⁺]_c flux in response to $\stackrel{.}{\epsilon }$ is critically dependent on active cytoskeletal dynamics such that inhibition of cytoskeletal polymerization (cytochalasin D; 5 μM; Sigma Aldrich), disordering of polymeric actin (jasplakinolide; 5 μM; Sigma Aldrich), or inhibition of myosin II activity (blebbistatin; 10 μM; Sigma Aldrich) significantly inhibited [Ca²⁺]_c flux, with a 68.1%, 79.3%, and 75.9% reduction, respectively, in peak [Ca²⁺]_c (Figure 6A, B).

Figure 6.

$\stackrel{.}{\epsilon }$-S [Ca²⁺]_c flux is modulated by actin cytoskeletal dynamics (A) Platelet ▵[Ca²⁺]_c for cases 3 as a function of Q = 600 mL/min following treatment of isolated platelets (10 min) with, DMSO (0.1%v/v) [N= 3 experiments]; cytochalasin D (5 μM) [N= 3 experiments]; jasplakinolide (5 μM) [N= 3 experiments]; blebbistatin (10 μM) [N= 3 experiments]. Solid lines are a rolling average (2nd order smoothing - 10 neighbours). All data have been normalised against baseline [Ca²⁺]_c derived as the average over pos. 0 – 200 μm non-hyperbolic segment. (B) Frequency histograms showing the distribution of platelet [Ca²⁺]_c (10 nM bins) within the first 50 μm of hyperbolic flow for case 3 following treatment of isolated platelets (10 min) with, DMSO (0.1%v/v) [N= 3 experiments]; cytochalasin D (5 μM) [N= 3 experiments]; jasplakinolide (5 μM) [N= 3 experiments]; blebbistatin (10 μM) [N= 3 experiments].

3.5. $\stackrel{.}{\mathbf{\epsilon }}$-S is dependent on microtubule dynamics

Although a role of the microtubule cytoskeleton has been recognized in platelet generation by megakaryocytes, platelet granule secretion [40], and platelet shape change, a critical role of the microtubule cytoskeleton in platelet mechanotransduction has not been forthcoming [41]. Given our findings that actin-based cytoskeletal dynamics are a major modulator of $\stackrel{.}{\epsilon }$-S [Ca²⁺]_c flux and the critical role of the annular microtubule ring in the maintenance of resting platelet structure and membrane morphology, we hypothesized that microtubule dynamics play an equally important role in the modulation of $\stackrel{.}{\epsilon }$-S [Ca²⁺]_c flux. As preliminary exploration of the role of microtubule dynamics in $\stackrel{.}{\epsilon }$-S, we examined the way in which stabilization of microtubules (paclitaxel [taxol]; 100 μM [3-minute incubation]; Sigma Aldrich) and inhibition of microtubule assembly (vinblastine; 100 μM [5-minute incubation]; Sigma Aldrich) impacted platelet [Ca²⁺]_c flux in the case 3 hyperbolic. Figure 7A, B demonstrates that $\stackrel{.}{\epsilon }$-S [Ca²⁺]_c flux is critically modulated by microtubule dynamics such that both stabilization and inhibition of microtubule assembly significantly inhibited $\stackrel{.}{\epsilon }$-S [Ca²⁺]_c flux, with a 55.4% and 66.6% reduction, respectively, in peak [Ca²⁺]. The resting discoid platelet morphology was unaffected by paclitaxel treatment, whereas resting platelets treated with vinblastine displayed spherical morphology prior to the assay (data not shown). Taken together, these data suggest that actin-based membrane/cytoskeletal dynamics, in conjunction with microtubule dynamics, play a significant modulatory role in $\stackrel{.}{\epsilon }$-S.

Figure 7.

$\stackrel{.}{\epsilon }$-S [Ca²⁺]_c flux is modulated by microtubule dynamics (A) Platelet ▵[Ca²⁺]_c for cases 3 as a function of Q = 600 μL/min following treatment of isolated platelets with, DMSO (0.2%v/v) for 5 mins [N = 3 experiments]; paclitaxel (100 μM) for 3 mins [N = 3 experiments]; and vinblastine (100 μM) for 5 mins [N = 3 experiments]. (B) Frequency histograms showing the distribution of platelet [Ca²⁺]_c (10 nM bins) within the first 50 μm of hyperbolic flow for case 3 following treatment of isolated platelets with, DMSO (0.2%v/v) [N = 3 experiments]; paclitaxel (100 μM) [N = 3 experiments]; and vinblastine (100 μM) [N = 3 experiments].

4. Discussion

The present study describes a novel method applying hyperbolic microfluidic geometries to the investigation of the effect of $\stackrel{.}{\epsilon }$ and, more specifically, the rate of change in $\stackrel{.}{\epsilon }$ on platelet activation and mechanotransduction. The use of experimental measurements in different hyperbolic geometries, together with computational simulations and time-averaged confocal imaging of platelet [Ca²⁺]_c dynamics, enable detailed evaluation of free-flow platelet activation mechanisms not achievable using conventional, straight or stepped microfluidics, in which flow exhibits mixed kinematics. A key advantage of the hyperbolic designs and associated [Ca²⁺]_c imaging assay described is the ability to focus on the impact of linear accelerations and, therefore, quasihomogenous extensional strain rates on platelet activation in free flow in the absence of platelet adhesion receptor engagement. This approach, wherein plasma and surface-adhered ligands, such as von Willebrand factor and fibrinogen, are absent, has enabled us to further characterize a novel platelet mechanotransduction mechanism that is attuned to applied $\stackrel{.}{\epsilon }$ that we refer to as the extensional strain sensing ($\stackrel{.}{\epsilon }$-S) mechanosome [18].

Extensional flow is prevalent in a number of contexts with regard to blood flow, including constrictions in the microcirculation [42], severe arterial stenosis due to cardiovascular disease [13], jetting through artificial heart valves [16], entrance and exit of ventricular assist devices [16], and under conditions of turbulent flow [15,43]. Extensional flow is most commonly seen when vessels transition in diameter. This is schematically shown in Figure 1, in which conservation laws dictate that under a pressure driver, the velocity in smaller diameters must be faster than that in larger diameters. During transition through such a contraction (such as a stenosis), blood is required to accelerate such that locally suspended proteins (such as von Willebrand factor) and cells (erythrocytes and platelets) feel an elongational pulling force (extensional strain, $\stackrel{.}{\epsilon }$) because the forward portion of blood elements experience a greater flow velocity than the trailing portions.

Early computational modeling studies proposed a role of $\stackrel{.}{\epsilon }$ in platelet function and thrombosis. Strony et al. [17], using experimental Folt and computational fluid dynamic models to correlate hemodynamics and platelet thrombosis, raised the possibility that $\stackrel{.}{\epsilon }$ and elongational platelet deformation at stenosis entry are important drivers of thrombus formation. These findings were supported by Bluestein et al. [13], who proposed that elongational stresses produced by convective acceleration at severe (85%) arterial stenosis play a role in platelet activation. They reported that $\stackrel{.}{\epsilon }$ reached values of up to 600/s (at Reynolds Number = 3600) and that platelets experience a considerable amount of stretching at stenosis entry, followed by a strong compression stress at stenosis expansion [13]. The present study experimentally supports these early computational findings and suggests that an $\stackrel{.}{\epsilon }$ of ≥747/s (case 1; Q = 50 μL/min; Figure 4A) is sufficient to initiate platelet [Ca²⁺]_c flux, with maximal [Ca²⁺]_c flux achieved at an $\stackrel{.}{\epsilon }$ of 3319/s (case 4; Q = 200 μL/min; Figure 4E). In addition, the upper $\stackrel{.}{\epsilon }$ threshold of 3319/s determined in the present study is comparable with the findings in the microcirculation, where changes in the vessel radius of ∼20% at a typical preconstriction blood velocity of ∼0.1 m/s have been shown to generate an $\stackrel{.}{\epsilon }$ of ∼5600/s [42]. Our data demonstrate that there is a clear “optimal range” of dε/dx that falls between 9.21 × 10⁷/s/m and 1.16 × 10⁸/s/m (Figure 5G). We can speculate that below this range, adaptive changes in the platelet cytoskeleton desensitize the Piezo1 and P2X1 mechanosome to the applied extensional strain. In the case of dε/dx, above this optimal range, we can speculate that exposure times are so brief that the mechanosome and associated platelet cytoskeleton are too slow to respond. The details of this regulatory mechanism, however, are outside the scope of the current study and will be addressed in future publications.

Notably, our data demonstrate that on hyperbolic exit, where platelets experience a strong negative dε/dx and, presumably, compression stress, the platelet [Ca²⁺]_c flux is immediately downregulated to baseline levels. These findings suggest that platelets are not only responsive to rapid increases in extensional strain but also respond reciprocally to rapid compressive strain. The current data also qualitatively track with our previously published observations that platelet [Ca²⁺]_c flux within the hyperbolic phase progressively downregulates and continues to downregulate after stenosis, returning to baseline levels [18]. This short-range effect further reinforces the concept that the $\stackrel{.}{\epsilon }$-S mechanosome is triggered by acute changes in membrane and cytoskeletal elastic deformations and/or rapid changes in membrane tension under $\stackrel{.}{\epsilon }$ loading that become quiescent once steady-state ε is achieved. Although structural accommodations of the plasma membrane and underlying spectrin-based-membrane skeleton to the applied steady-state $\stackrel{.}{\epsilon }$ may, in part, explain this refractory behavior, voltage-dependent inactivation and desensitization of Piezo1 [44] and rapid desensitization of P2X1 [45] may also contribute to the observed decay of $\stackrel{.}{\epsilon }$-S [Ca²⁺]_c flux.

Our working model of $\stackrel{.}{\epsilon }$-S posits that the platelet plasma membrane and underlying cortical actin cytoskeleton play a modulatory role in coupling applied $\stackrel{.}{\epsilon }$ to mechanosomes that comprise Piezo1 as the sensor and P2X1 as the signal amplifier [18]. The present study reinforces this concept by directly tying $\stackrel{.}{\epsilon }$ exposure to actin cytoskeletal dynamics and platelet [Ca²⁺]_c flux. The specifics by which the underlying actin cytoskeleton structurally modulates $\stackrel{.}{\epsilon }$-S is a subject of future studies; however, we can speculate that the cytoskeleton controls the overall dynamic rigidity of platelets within a set point range necessary for efficient force coupling. This concept is underpinned and supported by studies demonstrating that the inactivation of platelet phosphoinositide 3 kinase C2α results in a change in the composition of the spectrin-based membrane skeleton, with measurable reductions in the levels of spectrin, myosin, filamin, and moesin as well as associated rigidification of the platelet membrane, leading to reduced shear-mediated platelet functional response [[46], [47], [48]].

Similar to the cortical actin cytoskeleton, circumferential microtubules underlying the marginal band of platelets play a critical role in the maintenance of discoid platelet shape [3,41]. Under resting conditions, microtubules in the annular ring undergo continuous assembly and disassembly [41]. Following platelet activation by soluble agonists, such as adenosine diphosphate (ADP) and thrombin, or through adhesion receptor–mediated signaling, the microtubule coil becomes compressed and undergoes fragmentation and depolymerization. The preliminary studies described here suggest (for the first time) that active microtubule remodeling is a critical modulator of $\stackrel{.}{\epsilon }$-S, with both pharmacologic stabilization and depolymerization of microtubules significantly inhibiting $\stackrel{.}{\epsilon }$-S [Ca²⁺]_c flux. The specifics by which microtubules modulate $\stackrel{.}{\epsilon }$-S is a subject of future studies; however, given the emerging evidence that significant crosstalk occurs between both microtubules and actin-based cytoskeletal elements [49], we can speculate that the 2 work in concert to regulate the overall deformation of platelets under $\stackrel{.}{\epsilon }$ loading and, therefore, affect coupling to $\stackrel{.}{\epsilon }$-S mechanosomes.

The novel methodology described herein may have significant utility in the understanding of how $\stackrel{.}{\epsilon }$ dynamics affect platelet activation and thrombosis in blood-contacting medical devices. Despite the hemodynamic efficacy of MCS systems, such as left ventricular assist devices (LVAD) and extracorporeal membrane oxygenation (ECMO), for restoration of failing circulation, thromboembolic events continue to severely impact morbidity and overall mortality associated with these therapies [50,51]. Extensive research has been conducted to improve device thromboresistance, focusing on the optimization of pump design as a means of reducing shear stress exposure. However, despite significant technologic advancements, thrombosis continues to occur even with the latest generation of devices. Notably, current pharmacologic management, combining both anticoagulant and antiplatelet therapies, has proven to be relatively ineffective in the management of associated thrombotic complications [52]. Given the nonphysiologic flow accelerations associated with these systems and the lack of a modulatory endothelium, it is highly likely that $\stackrel{.}{\epsilon }$ is a critical driver of thrombotic complications in this setting. Therefore, a better understanding of the role of $\stackrel{.}{\epsilon }$ in this context may be critical to improve patient management and limit thrombotic complications.

In conclusion, we developed a hyperbolic microfluidic assay that allows for the assessment of platelet mechanotransduction under defined quasihomogenous extensional strain rates. By varying the hyperbolic geometry and input flow rate, the assay method allows for the exploration of different extensional strain regimes appropriate to both physiologic and pathologic blood flow environments. This method opens a window onto a novel platelet signal transduction mechanism and may have potential diagnostic utility in the identification of patients who are prone to thromboembolic complications associated with high-grade arterial stenosis or on MCS systems in which extensional strain rate is a predominant hemodynamic driver. In future studies, we aim to harness the described methodology to further explore the signal transduction processes underpinning $\stackrel{.}{\epsilon }$-S [18]. A better understanding of this novel adhesion-independent mechanism may lead to new developments in antiplatelet therapies that specifically target supraphysiologic hemodynamics, minimize the risk of systemic bleeding, and outperform current therapies in the management of device-related thrombosis.