Highlights
-
•
Soft boundary deformation has a major effect on cavitation inception.
-
•
The softer the boundary, the less effective the cavitation.
-
•
Geometrically guided photoacoustic energy enables generation of secondary cavitation.
-
•
Secondary cavitation can be induced in distant difficult to reach spaces.
Keywords: Cavitation, Soft-solid interface, Periodontal and peri-implant pockets, Secondary cavitation
Abstract
In periodontology and implantology, laser-induced cavitation has not yet been used to treat biofilm-related problems. In this study we have checked how soft tissue affects the evolution of cavitation in a wedge model representing periodontal and peri-implant pocket geometry. One side of the wedge model was composed of PDMS mimicking soft periodontal or peri-implant biological tissue, the other side was composed of glass mimicking hard tooth root or implant surface, which allowed observations of the cavitation dynamics with an ultrafast camera. Different laser pulse modalities, PDMS stiffness, and irrigants were tested for their effect on the evolution of cavitation in the narrow wedge geometry. The PDMS stiffness varied in a range that corresponds to severely inflamed, moderately inflamed, or healthy gingival tissue as determined by a panel of dentists. The results imply that deformation of the soft boundary has a major effect on the Er:YAG laser-induced cavitation. The softer the boundary, the less effective the cavitation. We show that in a stiffer gingival tissues model, photoacoustic energy can be guided and focused at the tip of the wedge model, where it enables generation of secondary cavitation and more effective microstreaming. The secondary cavitation was absent in severely inflamed gingival model tissue, but could be induced with a dual-pulse AutoSWEEPS laser modality. This should in principle increase cleaning efficiency in the narrow geometries such as those found in the periodontal and peri-implant pockets and may lead to more predictable treatment outcomes.
1. Introduction
Laser-induced cavitation is a widely used tool for in vivo microsurgery [1], medical diagnostics [2], cell lysis [3], as well as for cleaning of cell debris and biofilm during endodontic treatments [4], [5], [6]. However, in periodontology and implantology laser-induced cavitation has not yet been used to treat biofilm-related problems. In contrast to endodontic cavities which are bound by the solid dentine surface, periodontal and peri-implant pockets are formed by a solid tooth root or implant surface on one side, and by the soft gingival tissue on the other side [7]. How the soft-tissue boundary affects the evolution of cavitation in the periodontal and peri-implant pockets is poorly understood, but crucial for the success of laser-induced cavitation treatments.
It is expected that shock waves emitted after collapse of laser-induced primary bubble will trigger pressure oscillations which may induce secondary cavitation, a phenomenon that is currently understudied. Acoustic cavitation can be broadly defined as a process by which small nano- or micro-scale gas bubbles already present in a fluid pulsate, grow, divide, or interact as a result of pressure wave oscillations [8]. Lasers with wavelengths in the range of 1 to 3 μm are often used to generate cavitation, with the erbium:yttrium–aluminum-garnet (Er:YAG) laser holding a special position since it emits pulsed light with a wavelength of 2.94 μm – where absorption in water is the highest [9]. The high-intensity Er:YAG radiation, delivered into the water via a small-diameter fiber tip (FT), forms a rapidly dissipating primary bubble near the FT due to the efficient optodynamic conversion of the laser pulse energy into the mechanical energy of the bubble [10], [11], [12]. This triggers pressure perturbations throughout the fluid-filled volume, which can lead to secondary cavitation when the negative pressure threshold is exceeded [13].
In an infinite liquid medium with no boundaries, laser-induced cavitation emits shock waves radially from the optical breakdown point where transient localized plasma develops [14], [15], [16]. The emitted shock waves are followed by slower cavitation relaxation processes, where the liquid–primary bubble boundary is first inflated and then deflated until the bubble collapses and emits another shock wave, thereupon draining some of the mechanical energy from the bubble [14]. The primary bubble is followed by a rebound bubble that grows to a smaller maximum radius, implodes, and releases a new shock wave. It should be noted that in the final stage of the bubble collapse, the cavitation bubble retains spherical symmetry and emits radial shock waves only under idealized conditions, when no boundaries and pressure gradients are present in the vicinity of the cavitation bubble [17], [18], [19], [20]. An elongated plasma source or any pressure gradient in the liquid, even if caused by gravity, makes the collapse asymmetric [21]. An asymmetrical collapse is accompanied by the emission of multiple collapse shock waves, originating from different points in space and time [14], [19]. In comparison with the symmetric collapse, the asymmetric collapse is accompanied by additional phenomena, such as high-velocity liquid jets, annular cavitation bubbles, and interaction between multiple shock waves and multiple collapsing bubbles [19].
Cavitation in the vicinity of solid boundaries has been a subject of extensive research due to the wide range of practical applications [22]. The shape of the bubble expansion and collapse varies from a spherical shape to micro-jets towards or away from the boundary [23], [24], fast thin needle-like jets [25], or non-axial jets [26]. Additionally, bubbles can exhibit mushroom-shaped [17] and pear-shaped [27] collapse modes, or even develop multiple opposing jets that lead to bubble splitting and a break up into smaller fragments [28]. In general, the bubble shape and dynamics are primarily determined by the geometric configuration, structural properties of the boundary material, and the distance from the boundary [29].
When solid boundaries are present the effects of geometry can be significant [58], [59], [60], and even small changes in the system’s geometry can change the entire flow pattern and the resulting cleaning effectiveness of the cavitation [30]. The shock waves emitted during the bubble collapse get reflected or scattered from the solid boundaries and will, depending on the geometry, either diverge or refocus and cause formation of secondary cavitation bubbles. For example, for plane or convex solid boundaries the reflection of the shock waves does not modify the initially divergent nature of the emitted shock waves. In contrast, a presence of a concave solid boundary can result in the refocusing of divergent shock waves, causing secondary cavitation [31].
In narrow geometries, the cavitation dynamics is altered due to the friction with the walls and the limited space available for the rapid fluid movement during the expansion and contraction of the bubbles. How cavitation behaves in narrow confined spaces with multiple reflections from the boundaries is not well understood. This applies especially to reflections from soft material boundaries and biological tissues. Numerical results indicate that the cavitation density in the hole increases with the decreasing hole volume and the increasing taper ratio [61]. When it comes to solid boundary cavities, a Super Short Pulse (SSP) Er:YAG modality was developed originally for the creation of acoustic waves in narrow volume geometries of the dental root canal [32], [33], [34]. Since SSP usually does not create shock waves in narrow geometries, it was further upgraded by the SWEEPS modality (Shock Wave Enhanced Emission Photoacoustic Streaming [32], [33]. Unlike with SSP, the SWEEPS modality delivers pulses in pairs. The second laser pulse puts pressure on the initial bubble and accelerates its collapse. This generates shock waves also in confined narrow spaces. The optimal time lag between pulses in the pair depends on the volume and geometry of the liquid tank. The correlation is exact, but it is only known for defined geometries. For situations where the correlation between the geometry, the volume of the liquid tank, and the optimal time lag between the laser pulses is not known, the AutoSWEEPS modality was introduced, where the time delay between laser pulses in the pair varies continuously back and forth in increments of 20 microseconds in the range from 200 to 650 microseconds. This ensures that during each sweeping cycle, there is always a period of an optimal time delay between the pulses in pairs, required for the efficient emission of shock waves, and thus for the optimal irrigant flow [32], [33], [35].
There is scarce data for cavitation dynamics in narrow geometries composed of combined soft – solid boundaries such as those frequently found in medicine (e.g., dental peri-implant and periodontal pockets). Soft boundaries influence the ratio between the reflected and transmitted cavitation energy, due to their high compliance, slow wave speeds, and non-linear viscoelasticity. By analyzing the temporal evolution of the bubble radius in the viscoelastic medium, the mechanical properties of the soft medium can be determined [36], [37], [38]. It has been shown that significant inelastic effects can occur during and after the initial bubble collapse in a model composed of soft and stiff polyacrylamide hydrogels [39]. Hydrogels and elastomers such as Polydimethylsiloxane (PDMS) have been used extensively in biology as tissue-engineering scaffolds [40], [41]. They show remarkable similarities to load-bearing biological tissues [42], and can be fabricated to mimic the complex shapes and high fatigue resistance of biological tissues [43].
In this work, we studied experimentally the influence of a soft-tissue material in contact with a solid boundary on the evolution of cavitation, which is expected to correlate with the irrigation and cleaning effectiveness of the treated surfaces [44]. A narrow-wedge geometry was constructed mimicking the periodontal and peri-implant space that is in general difficult to reach with mechanical debridement instruments. One side of the wedge model was composed of PDMS mimicking soft periodontal or peri-implant biological tissue, and the other side was composed of glass mimicking a hard tooth root or implant surface, which allowed observations of the cavitation dynamics with the ultrafast camera. Different laser pulse modalities, stiffnesses of the PDMS boundary, and irrigants were used to test their effect on the evolution of cavitation in the narrow wedge geometry. The PDMS stiffness varied in a range that corresponded to severely inflamed, moderately inflamed, or healthy gingival tissue as determined by a panel of dentists. Depending on the stiffness of the PDMS, either only a laser-induced primary bubble or a combined primary bubble and secondary cavitation cloud were observed in the wedge pocket model, which suggests that mechanical properties and geometry of the soft tissue can have a dramatic impact on the inception and effectiveness of the cavitation.
2. Methods and materials
2.1. Model of periodontal/peri-implant pocket
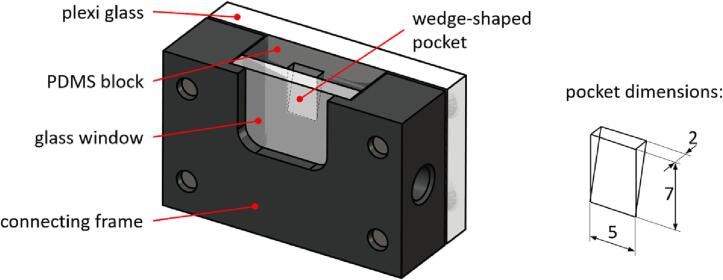
The model of the periodontal/peri-implant pocket (PI model) is shown in Fig. 1. It consists of four parts, a PDMS block, a glass window, a Plexiglas plate, and a connecting frame. A PDMS block (20 × 20 × 7 mm) has a wedge-shaped pocket with a height of 7 mm, width of 5 mm, and thickness of 2 mm at the top of the wedge, which simulates the geometry of the periodontal/peri-implant pocket. On the pocket side, the PDMS block is covered with a 3-mm-thick glass window in order to enable observation of the evolution of the cavitation with a high-speed camera. The glass window and PDMS block are inserted into the seat of the connecting frame and clamped with a 5 mm thick plexiglas plate to prevent fluid from leaking from the sides of the pocket during laser-induced cavitation experiments.
Fig. 1.
The model of a periodontal/peri-implant pocket consists of a soft PDMS block that has a wedge-shaped pocket and is covered with a glass window that allows visual observation of the evolution of cavitation with a high-speed camera. The dimensions of the pocket are shown on the right.
The PDMS (Dow Europe GmbH, Germany) was prepared according to the manufacturer’s instructions. Briefly, 10 g of PDMS was mixed with 0.3–1.4 g of curing agent, degassed at room temperature for 30 min, after which 4 g of the PDMS mixture was carefully poured into the fabrication mold. The molds were placed in the oven at 70 °C for 1 h. After baking, we waited for approximately 10 min before carefully removing the PDMS blocks from the mold. The PDMS blocks were freshly prepared. This is especially important for soft PDMS blocks, where material properties change over time.
2.2. Experimental setup
The experimental setup for studying the laser-induced phenomena in the periodontal/peri-implant pocket model is shown in Fig. 2. The PI model was immersed 5 mm deep into the irrigant bath (dimensions 100 × 120 × 60 mm), ensuring that the pocket was constantly filled with the irrigant. The excitation laser light was guided from the Er:YAG source (Fotona, LightWalker) through an articulated arm to a laser handpiece ending with a cylindrical fiber tip (FT) with diameter 400 mm and length 14 mm (FlatSweeps 400/14; Fotona d.o.o.) which was inserted 2.5 mm into a wedge-shaped pocket. The accurate and repeatable positioning of the FT was performed by a collaborative robotic arm (Universal Robots, UR5) coupled to the handpiece.
Fig. 2.
Experimental setup for studying laser-induced phenomena in the simulated periodontal/peri-implant pocket from the operator's point of view (a). Details of the bath filled with an irrigant, the immersed PI model, the fiber tip (FT), and the high-brightness illumination (HB LED) are shown (b). Laser pulses are delivered to the PI model via the laser arm, handpiece, and FT. A robot (Universal Robots UR5) provides accurate positioning of the FT within the PI model. A high-speed camera (HS) (Photron, SA -Z) records phenomena in the PI model through the glass window (see also Fig. 1). The typical sequence of recorded images shows the evolution of the primary bubble, which starts to grow immediately after the laser pulse (c). After its collapse (at time 300 μs), the secondary cavitation in the lower part of the PI model starts to develop.
The laser-induced phenomena in the pocket were monitored with a high-speed camera (HS) (Photron, Fastcam SA -Z) equipped with a 1:1 macro lens (Sigma APO Macro, f = 180 mm, F2.8) providing an optical resolution of 20 μm. We used a high frame rate of 100,000 fps at a reduced resolution of 360x384 pixels and a shutter speed of 248 ns. The observation area (approximately 7.5 × 7.7 mm) was backlit (through the transparent components of the PI model) with a high brightness white LED light (HB LED) (Thorlabs, MWWHLP2 − 3000 K, 1713 mW). The HS camera was synchronized with laser pulses using a trigger photodiode in the laser system. The transparent plexiglas, PDMS, and glass windows provided uniform propagation of light, resulting in a bright image background, while the FT and cavitation bubbles appeared dark, as shown in Fig. 2c, where a typical sequence of the primary bubble’s growth and collapse, and the subsequent appearance of the secondary cavitation (at the bottom of the pocket) are shown.
2.3. Analysis of high-speed video data
Three interdependent phenomena were detected and analyzed in each high-speed video image: (i) the area of the primary bubble (AP) that expands and contracts near the fiber tip; (ii) the area of the secondary bubbles (AS) that appeared in the lower part of the pocket when pressure fluctuations were large enough; and (iii) in-plane deformations of the PDMS material (D) that also resulted from pressure fluctuations.
Deformation of the PDMS material was measured by using the Lucas-Kanade optical flow algorithm [45], where the image acquired before the laser pulse was used as a reference and an averaging window of 15 × 15 pixels was used to reduce the optical noise. The result of this step was the measured two-dimensional deformation field shown in Fig. 3a. For further analysis, we have extracted a representative vertical deformation of PDMS chosen on the symmetry axis of the pocket 3 mm below the FT. It is worth noting that for the detection of these deformations, it is essential that the surface of the pocket is textured, for which we have used PDMS blocks casted in a 3D-printed mold. And that the deformation measurements only work correctly in areas where bubbles do not overlap with the textured pocket surface.
Fig. 3.
A) the processing steps of high-speed video data consist of measuring the deformation of the pdms block on the textured surface, background subtraction using the image taken before the laser pulse, and segmenting the bubbles using the image threshold. the primary bubble is detected and measured within the roi1, and the secondary bubbles within the roi2. b) an example of measured bubble areas is shown for an AutoSWEEPS pair of Er:YAG laser pulses. Two primary bubbles (blue curve) resulting from two AutoSWEEPS laser pulses are detected and their areas measured within the ROI1, and the two areas of the accompanying secondary bubbles (red curve) are detected within the ROI2. The two AutoSWEEPS laser pulses are schematically presented in green. c) Deformation dynamics of PDMS is measured 3 mm below the FT during the above AutoSWEEPS laser pulse pair.
To detect primary and secondary cavitation bubbles, the i-th image was then subtracted from the initial image, correcting the background variability. A typical result of this process is shown in Fig. 3a. The image was then segmented using an image threshold, where the threshold was chosen to reliably separate the bubbles from the background. Finally, the area of each bubble type was measured by summing all segmented pixels within the selected region of interest (ROI1 for the primary bubble and ROI2 for the secondary cavitation bubbles). Therefore, ROI1 is located around the FT, and ROI2 is located in the lower half of the pocket where the secondary cavitations can occur.
By processing the entire image sequence, we have measured the evolution of the area of the primary bubble AP(t) and of the secondary bubbles AS(t), and the deformation of the surrounding surface D(t). Typical examples of the measurements are shown in Fig. 3b and 3c, where the AutoSWEEPS double-pulse modality was used (the delay between micro-pulses was 460 µs). It can be seen that the primary bubble starts to grow immediately after the pulse and reaches the maximum size APmax around the middle of the bubble’s life time, Tbubble. The bubble rebound and regrowth occur immediately after its collapse due to inertial forces and fluid elasticity. In this process, a significant fraction of the energy of the primary bubble is converted into an emitted pressure wave [46], which triggers the formation of the secondary cavitation when the negative pressure exceeds the cavitation threshold [47]. This can be seen in Fig. 3b, where the secondary cavitation (red curve) begins immediately after the primary bubble collapses (blue curve).
An example of the deformation of the surrounding material can be seen in Fig. 3c, where we see that the material initially (the first 50 µs) follows the expansion of the primary bubble. However, due to elasticity, it reverses the direction, reaching an extreme negative value at about 120 µs. The initial deformation dynamics was estimated with the maximal-positive to maximal-negative amplitude of deflection (Dp.n), as well as by the oscilation period of PDMS deformation (TPDMS) and the duration of deformation (1.5·TPDMS), defined as the time in which the deformation passes through the zero value for the second time from positive to negative. As you will see in the results, the selected times importantly correlate with the appearance of secondary cavitation.
2.4. Soft-tissue mechanical properties
To mimic the mechanical properties of the gingival tissues, PDMS materials were prepared with different amounts of curing agents and their mechanical properties were determined with rotational rheometry. PDMS was prepared as described above and poured into a cylindrical mold with a 25 mm diameter and height of 9 mm to fit the plate–plate system (PP25). Viscoelastic properties of the PDMS were determined on a rotational rheometer, Anton Paar Physica MCR 302. The temperature was kept at (20.00 ± 0.01) °C. All samples were loaded with the same normal force (0.09 N) prior to the measurement. The amplitude sweep test was performed from 0.01 to 100 % in 31 logarithmically spaced steps, at a constant frequency of 10 Hz. From the viscoelastic curves of the selected samples shown in Fig. 4, it follows that the stiffness of PDMS, i.e., the resistance of PDMS to deformation, increases with the concentration of the curing agent. For simplicity, in what follows, the stiffness of the PDMS is represented as the concentration of the curing agent (PDMS stiffness (in curing agent %)). With increasing concentration of PDMS curing agent, the storage modulus increased linearly up to 6 % and then gradually leveled off (Fig. 4B). The loss factor tan δ, which measures the ratio of energy lost to energy stored during the cyclic deformation, was higher for softer PDMS blocks and exponentially decayed. This indicates a transition to a more solid like viscoelastic material at the curing agent concentration > 6 % (Fig. 4C). The yield strain was determined at the end of the linear viscoelastic region when the material begins to yield. Significantly higher yield strain were observed for PDMS curing agents below 6 % (Fig. 4D).
Fig. 4.
(A) raw viscoelastic data, SM and LM are storage G′ and loss modulus G″, respectively (B) storage modulus, G’, dependence on PDMS curing agent concentration, (C) loss factor tg δ = G″/G′ dependence on PDMS curing agent concentration, (D) yield strain γy dependence on PDMS curing agent concentration.
The consistency and stiffness of different PDMS models and their relevance to the periodontal and peri-implant gingival tissue model systems were tested by a panel of 7 dentists who independently determined the correspondence between PDMS stiffness and periodontal and peri-implant tissue response upon a manual periodontal probing. They marked the response of PDMS materials as severely inflamed, moderately inflamed, or healthy gingival tissue (see Supplementary Table 1). Based on this evaluation, we constructed gingival tissue models with PDMS stiffness of ≤ 5 % (representing “soft” or severely inflamed tissue); > 5 % to ≤ 8 % (representing “intermediate”or moderately inflamed tissue); and ≥ 9 % (“stiff” or healthy tissue). The clinical relevance of our model is also consistent with the classification of periodontitis published in [62], where our model refers to stage III and IV with an interdental probing depth of 5 mm or more.
2.5. Irrigant solutions
The following irrigant solutions were used: distilled water (H2O), 17 % EDTA (Sigma, USA), 2 % H2O2 (Fluka, Germany), 0.2 % chlorhexidine digluconate (CHX) (Alfa Aesar, Germany), and 5 % sodium hypochlorite (Kemika, Croatia). H2O water was autoclaved at 121 °C, 1.2 bar, for 30 min. EDTA was resuspended in degasified water with a pH adjustment to 8 and autoclaved at 121 °C, 1.2 bar, for 30 min. Distilled water was used in all experiments for which the irrigant is not specifically defined.
3. Laser modalities
The Er:YAG laser system LightWalker® (Fotona d.o.o) was used to deliver either single ultrashort pulses with a pulse duration of 25 µs (USP modality), or double pulses (2 × 25 µs) with periodically varying delays (AutoSWEEPS modality). In the AutoSWEEPS modality, the delay between the two laser pulses was continuously cycled between 260 µs and 540 µs in steps of 20 µs, in order to ensure that there was always at least one approximately optimal delay during each sweeping cycle where the second pulse could enhance the development of the secondary cavitation. Unless specified differently, the frequency of 15 Hz, and the laser pulse energy (Ep) of 20 mJ were used.
4. Results
4.1. Single-pulse (USP) laser modality
The cavitation dynamics in soft (5 %) and stiff (10 or 12 %) pockets, mimicking corresponding severely inflamed and healthy gingival tissues, are shown in Fig. 5 and Movie 1. After the triggering of a single USP (20 mJ) pulse, a large millimeter-sized asymmetric primary bubble formed with a life time of Tbubble = 250 ± 10 µs. Under appropriate conditions, the collapse of the primary bubble was accompanied by a secondary cavitation cloud generated at the apex of the wedge pocket. The bubbles within this cloud were much smaller (micrometer size), but due to their density, they coalesce and have a similar lifetime (250 ± 20 µs) as the primary bubble. The number of secondary microbubbles was higher for the stiffer (12 %) in comparison to the less stiff (10 %) pocket. No secondary bubble cloud was observed in the case of the soft pocket.
Fig. 5.
Cavitation dynamics in soft and stiff wedge pocket geometries. The cavitation was triggered by the Er:YAG laser using the single-pulse USP modality (pulse energy 20 mJ). The top images show the formation of the primary bubble at the FT’s exit, following a laser pulse (at time 100 μs after onset of the laser pulse). The middle images show the primary bubble at the end of its life cycle (at time 270 μs) when the primary bubble has collapsed and rebounded, leading to the formation of the secondary cavitation cloud in the distal part of the stiff pockets. The bottom images show fully developed secondary cavitations (at time 400 μs) in the stiff (i.e., “healthy”) pockets, while no secondary bubbles can be seen in the soft (i.e., “severely inflamed”) pocket. See also Video 1 in the supporting material.
The effect of the PDMS stiffness on the primary and secondary cavitation for the USP modality is shown in Fig. 6. For PDMS stiffness below 5 %, the size of the primary bubble was comparable to the size of the primary bubble in an infinite liquid reservoir (see APinf and the green dashed line). There was a step decrease in the size of the primary bubble at a stiffness of about 5–6 %. The size of the primary bubble at the highest stiffness was approximately 2-times smaller compared to that in the infinite cavity. The development of secondary cavitation was qualitatively and quantitatively different from primary cavitation. The secondary cavitation formed only for PDMS stiffness above 8 %, indicating that no secondary cavitations would be formed in severely inflamed pockets.
Fig. 6.
The size of the a) primary (AP) and b) secondary (AS) cavitation for different values of the PDMS stiffness of the water-filled wedge pocket. The dashed green line represents the primary bubble's size in an infinite water reservoir, while the blue line is a guide for the eye. The laser energy of the USP modality was kept constant at 20 mJ, and the fiber tip was 400 µm in diameter.
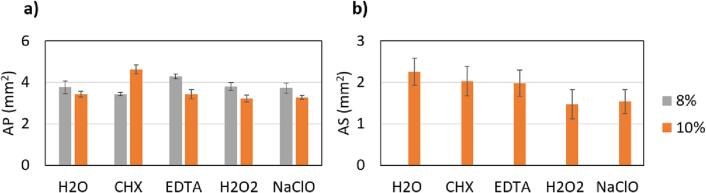
The dependence of the USP cavitation effectiveness on the irrigant type used is shown in Fig. 7. Please note that secondary cavitation is negligible in cases of 8 % PDMS stiffness, therefore the gray columns are missing in Fig. 7b.
Fig. 7.
Influence of different irrigants on a) primary (AP) and b) secondary (AS) cavitation effectiveness in pockets with 8 or 10 % PDMS stiffness. The laser energy of the USP modality was kept constant at 20 mJ, and the fiber tip was 400 µm in diameter.
Throughout the study, the secondary cavitation’s effectiveness was strongly correlated with the PDMS’ stiffness. As can be seen in Fig. 6b, the softer the PDMS, the less effective was the secondary cavitation, indicating that the soft PDMS material absorbed significantly more of the primary cavitation’s energy. A visual clue is provided by the time evolution of the PDMS deformation (Fig. 8a). PDMS deformation was five times bigger in soft PDMS compared to the stiffest (see Fig. 8b), which suggests that the deformation of the PDMS elastomer was strongly coupled to the expansion and contraction of the primary cavitation bubble. Similarly, the oscillation time of the deformation (TPDMS) was two times longer for the softest PDMS (see Fig. 8c). That implies that most of the cavitation energy in the soft pocket went into boundary deformation, resulting in less violent collapse. With increasing PDMS stiffness, the amplitude and oscillation time of the deformation decreased, suggesting that less cavitation energy was expended for elastic deformation and more was available for induction of the secondary cavitation. We can see that the appearance of secondary cavitation starts when TPDMS < Tbubble (see the green region in Fig. 8c).
Fig. 8.
Deformation of the PDMS during the primary bubble formation. a) Temporal evolution of the vertical displacements of PDMS at a location 3 mm below the FT in the PI model after a laser pulse was triggered. For clearer presentation, the time evolutions of different PDMS curing agent concentrations are scaled and offset in the y-axis. Red dots indicate collapses of the primary bubbles. b) Influence of PDMS stiffness on the deflection amplitude (Dp.n). c) Influence of PDMS stiffness on the oscillation period of PDMS deformation (TPDMS) and primary bubble life times (Tbubble). The green region indicates at which PDMS stiffness the secondary cavitation was detected. The laser energy of the USP modality was kept constant at 20 mJ, and the fiber tip was 400 µm in diameter.
4.2. Dual pulse (AutoSWEEPS) laser modality
An example of the cavitation dynamics in the narrow wedge geometry when the pocket is irradiated by the dual-pulse AutoSWEEPS modality is presented in Fig. 9 and Movie 2. Similarly to the irradiation with a single USP pulse (top images in Fig. 9a), an asymmetric initial primary bubble gets generated by the initial (1st) AutoSWEEPS laser pulse (bottom images in Fig. 9a). Also, the collapse of the initial primary bubble is similar to the primary bubbles collapse for the USP modality. Since the dynamics in a pocket with an intermediate (8 %) stiffness is shown, no secondary cavitation cloud can be seen for either of the modalities following the initial primary bubble’s collapse. However, as opposed to the USP modality, a secondary cavitation cloud can be observed at the pocket’s distal part after the subsequent primary bubble gets generated as a result of the subsequent (2nd) AutoSWEEPS pulse being delivered at an appropriate delay.
Fig. 9.
Cavitation dynamics in the narrow wedge geometry for the dual-pulse AutoSWEEPS modality. a) Comparison of images of bubble formation for single-pulse USP (top images) and AutoSWEEPS (bottom images) modality. First column: primary cavitation developed after triggering laser. Middle column: collapse of the primary bubbles. Third column: generation of secondary bubbles for the AutoSWEEPS modality. b) Temporal development of the two primary bubbles generated by the two laser pulses of the AutoSWEEPS pulse pair, for different pulse delays. Green dots show the periodic “zig-zag” changes of the time when the second laser pulse is delivered. c) Development of the secondary cavitation during the dual-pulse AutoSWEEPS irradiation, shown for different pulse delays during the AutoSWEEPS cycling. d) Temporal evolution of the PDMS deformation during the AutoSWEEPS sweeping. Red circles indicate when the subsequent laser pulses occur at the moment when the PDMS deformation is decreasing to zero at a high rate. All presented results are for the PDMS stiffness of 8 %, 20 mJ laser energy, 15 Hz pulse frequency and 400 µm laser tip diameter at the depth of 2 mm. See also Video 2 in the supporting material.
The temporal development of the two primary bubbles generated by the two laser pulses of the AutoSWEEPS pulse pair is presented in Fig. 9b. Green dots show the periodic “zig-zag” changes of the time when the subsequent (2nd) laser pulse is delivered. Since the time delay between the two laser pulses is being swept within the pulse delay sweeping range, the corresponding sweeping behaviour can be observed also for the initial and subsequent primary bubbles. The influence of the pulse delay on the generation of the secondary cavitation can be seen in Fig. 9c, which shows the temporal development of secondary cavitations for different AutoSWEEPS delays. As can be seen, secondary cavitation occurs at “resonant” time delays of 420 ± 40 μs. Fig. 9d, which shows the temporal evolution of the PDMS deformation during the AutoSWEEPS sweeping, provides insight into the observed resonance phenomena. At the time of 420 μs following the initial laser pulse, the deformation of the PDMS material is decreasing to zero at a high rate. Therefore, when the subsequent laser pulse occurs the deformation rate reverses with a large acceleration, leading to an enhanced negative pressure and subsequent formation of the secondary cavitation. The red circles in Fig. 9d indicates the appearance of the just-mentioned condition.
The influence of the AutoSWEEPS pulse delay on the size of the primary and secondary bubbles, for the “moderately inflamed” pocket (8 % PDMS stiffness) and “healthy” pocket (10 % PDMS stiffness), is shown in Fig. 10.
Fig. 10.
Top: dependence on the AutoSWEEPS delay of the size of the initial (after 1st pulse) and subsequent (after 2nd pulse) primary bubbles for “Moderately infected” (intermediate, 8 %) and “Healthy” (stiff, 10 %) pocket models. Bottom: dependence of the AutoSWEEPS delay on the size of the initial and subsequent secondary bubbles for “moderately infected” and “healthy” pocket. Lines are guides for the eye and are calculated as an approximation of Gaussian (red lines) and linear (black lines) function.
As can be seen from Fig. 10, the sizes of the initial primary and initial secondary cavitations (after 1st pulse) are independent of the AutoSWEEPS delay. However, the subsequent cavitation (after 2nd pulse) is significantly influenced by the delay. Subsequent primary cavitation grows steadily up to approximately 450 us of delay in both pockets, i.e. intermediate (left graphs) and stiff (right graphs), and reaches a similar size as the initial primary cavitation. Similarly, subsequent secondary cavitation grows steadily with increasing delay in the case of a stiff pocket (bottom right graph). Here, the initial secondary cavitation is bigger throughout the entire interval of AutoSWEEPS delays. On the other hand, for the intermediate (“moderately inflamed”) pockets there are no initial secondary cavitations, while the subsequent secondary cavitations reach a peak approximately at the “resonant” deformation time TD ≈ 420 ms.
Fig. 11a compares the dependence of secondary cavitation on the PDMS stiffness for single- and double-pulse modalities, showing the AS values in the resonance region for AutoSWEEPS. It can be seen that with the AutoSWEEPS modality we achieve secondary cavitation even for much softer samples, up to a stiffness of 4 % (equal to severely inflamed), while for single pulses (USP modality) secondary cavitation stops completely at stiffness of < 8 %. From the comparison of the optimal AutoSWEEPS delays and the duration of the PDMS deformation (see Fig. 11b), it can be seen that the maximum secondary cavitation occurs when the SWEEPS delay is equal to the resonant deformation time 1.5TPDMS. At this time the PDMS deformation is rapidly decreasing (see also Fig. 3c and 9d) and when the subsequent primary bubble starts growing, the pressure transients of both phenomena superimpose each other, leading to the subsequent formation of the secondary cavitation. The marked blue points are for the lowest PDMS stiffness, where almost negligible secondary cavitation was detected.
Fig. 11.
A) comparison of secondary cavitation induced by a single pulse (USP modality) and a double pulse (AutoSWEEPS modality) at different PDMS stiffness. b) Influence of PDMS stiffness on the resonant deformation times (1.5TPDMS) and the optimal SWEEPS delay of the second pulse, where maximum secondary cavitation occurs. Lines are guides for the eye. The marked blue points are for the lowest PDMS stiffness, where almost negligible secondary cavitation was detected.
5. Discussion
The interaction of cavitation bubbles with soft materials and biological tissues in narrow geometries is important in a number of medical applications. In this study, we show how cavitation is modified or even quenched in the narrow wedge geometry composed of soft and solid boundaries resembling the soft periodontal tissue / hard tooth, or soft peri-implant / hard implant boundaries in periodontal and peri-implant pockets, respectively. We have measured the evolution of primary and secondary cavitations triggered by single-pulse or dual-pulse Er:YAG laser irradiations of irrigant-filled narrow wedge models for different stiffness values of the model’s soft boundary, with the soft boundary mimicking a severely inflamed periodontal gingival tissue, and the stiff boundary representing a healthy tissue.
As opposed to hard tissues, soft tissues are capable of undergoing large deformations and still returning to the initial configuration when unloaded. Soft tissues are hyperelastic materials with nonlinear stress–strain curves, as well as incompressible, viscoelastic, and usually anisotropic [48]. To mimic soft-tissue mechanical properties, polydimethylsiloxane (PDMS) is widely used in biomedical research and technology as a soft-tissue substitute [38], [40], [41], [42], [43]. PDMS is transparent, has good thermal and oxidative stability, high oxygen permeability, hydrophobicity, is biocompatible, interacts with salivary proteins, has good resistance to blood corrosion, is odorless, and has low biodegradation [43], [49], [50]. By varying the mixing ratio of the PDMS polymer and the curing agent or additives, it is possible to fine-tune the PDMS’ elastomer properties to mimic the mechanical properties of biological tissues [51]. In this work, we have tuned the PDMS’ mixing ratio to the consistency and stiffness of severely inflamed, moderately inflamed, and healthy periodontal and peri-implant tissues as determined by a panel of dentists. The results indicate that the state of the infection of the soft tissue may have a dramatic effect on the effectiveness of laser-induced cavitations, and especially on the evolution of secondary cavitations. Secondary cavitations may have an important treatment potential since they develop at the hard-to-treat bottom of the wedge-shaped pocket. The development of secondary cavitations also indicates an effective pressure dynamics within the pocket.
Two principal mechanisms, namely, photoacoustic streaming and cavitation, are known to predominantly occur in solutions irradiated with lasers [52], [53]. It is generally believed that both streaming and cavitation are instrumental in particle removal, whereas cavitation is the main cause of damage to fragile and compliant structures such as biofilms [54]. Therefore, an absence of acoustic cavitations in a treated body cavity can dramatically reduce the cleaning ability of the laser-induced procedure.
In this study, cavitation was found to be most effective in the stiff models (>9 % curing agent) representing healthy gingival tissues. The deformation of PDMS representing the gingival tissue and the life time of the primary bubble were smaller compared to models with a lower stiffness. Due to the large stiffness of the healthy tissue model, the growth of the primary bubble was restricted. More reflected energy at the stiffer boundary resulted in a more violent collapse of the primary bubble, and in the generation of a large secondary cavitation cloud at the single laser pulse energy of 20 mJ, with a small secondary cloud observed also already at 10 mJ. The collapse of the acoustic bubbles produced a highly erratic deformation pattern in the soft-tissue model, likely due to multiple rounds of shock wave reflections that fed and sustained the secondary cavitation.
The size of the primary bubble was larger for the moderately inflamed tissue model (between 6 and 8 % curing agent). The deformation of the soft tissue was more pronounced and the period of the deformation oscillation increased, suggesting that more energy was absorbed in the soft boundary. A single laser pulse did not generate secondary cavitation at laser energies ≤ 20 mJ. Consistent secondary cavitations were observed only when the laser energy was increased to 30 mJ, while only a few secondary bubbles were occasionally observed at 20 mJ (see Supplementary information, Fig. S1).
No secondary cavitations, and the largest primary bubbles were observed for the severely inflamed gingival tissue model (<5 % of the curing agent), with the bubble’s size comparable to that generated in an infinite volume. This suggests that the severely inflamed tissue is not a major obstacle to the primary bubble’s development. This is due to the fact that the severely inflamed model material is compliant, has a low storage modulus, and strongly deforms upon the formation of the primary bubble. It is also rather sticky and has high cohesive energy, which prevents material failure during the primary bubble expansion. However, the bubble’s energy is expended in deforming the tissue, leaving less energy for driving the collapse of the primary bubble. Consequently, the implosion of the primary bubble in the severely inflamed model tissue is less violent and cannot generate shock waves and secondary cavitations in the distal region of the pocket. This observation is significant since it indicates that the cavitation effectiveness in narrow geometries with soft boundaries which resemble periodontal or peri-implant pockets can be dramatically changed upon bacterial infection. This can alter the ability of laser-induced irrigation to clean biofilms in severely infected pockets.
From the results we can see (Fig. 8c) that the appearance of secondary cavitation after the initial laser pulse starts when the oscilation time of PDMS is shorter than the life time of the primary bubble (TPDMS < Tbubble). This can be explained by the fact that, in the case of soft material, it is bubble-driven dynamics, where the bubble drags the material behind it throughout its life cycle and transfers its energy to the material. However, in the case of stiffer material, the deformation overtakes the bubble oscillation, so in the phase of the bubble collapse, the energy from the PDMS is returned to the accelerated contraction of the bubble, which results in a more violent collapse and, consequently, in the formation of secondary cavitation.
In this study, the dual-pulse AutoSWEEPS modality was introduced with the goal to develop an effective periodontal treatment protocol at the lowest possible laser pulse energies. Namely, high laser energies may lead to the ablation of the surrounding tissue and potentially an extrusion of the irrigant into the tissue, as well as an undesirable splashing of the irrigant out of the treated pocket. The AutoSWEEPS modality has been originally introduced in endodontics to improve the efficacy of the Er:YAG laser-induced irrigation of dental root canals. The SWEEPS dual-pulse technique consists of delivering a subsequent laser pulse into the irrigant at an optimal time when the initial bubble generated by an initial pulse is in the final phase of its collapse. The growth of the subsequent bubble exerts pressure on the collapsing initial bubble, accelerating its collapse and the collapse of secondary bubbles, resulting in the emission of primary and also secondary shock waves.
Our study demonstrates that the SWEEPS technique can be of benefit also in periodontics, since when the AutoSWEEPS laser modality was used, secondary cavitations were generated also in infected tissue models already at the laser pulse energy of 20 mJ. However, the mechanism of the enhancement of cavitation in periodontal pocket models appears to be different from that observed in endodontic canals [35]. Namely, in the hard endodontic tissue, the pressure in the irrigant generated by the growth of the subsequent (i.e., 2nd) primary bubble accelerates the collapse of the initial (i.e., 1st) primary bubble, resulting in the generation and collapse of the accompanying “initial” secondary bubbles. This is why the resonant SWEEPS delay time is correlated with the primary bubble’s life time.
On the other hand, our measurements in the periodontal pocket models show that it is the pressure generated by the oscillating deformation of the soft boundary which has the major role. The oscillating deformation which gets activated by the growth and collapse of the initial primary bubble, accelerates the collapse of the primary bubble, leading to the generation of the “subsequent” secondary bubble cloud. This is why in this study the resonant SWEEPS delay where the secondary cavitations are strongest, corresponds to the deformation time of the soft boundary, and not to the initial primary bubble’s life time. It should be noted, however, that as the material becomes progressively softer, energy dissipation also increases, so that the amplitude of secondary cavitation decreases exponentially with decreasing pocket hardness (see Fig. 11a). However, it is evident that secondary cavitation can be achieved with the double-pulse regime in much softer materials up to highly infected tissue. In future studies, it will be necessary to investigate the extent of cavitation required for sufficient cleaning of the pocket surface.
The observed difference in the cavitation dynamics in endodontic and periodontal cavities can be explained by the fact that in hard endodontic cavities, the boundary deformations are small and do not play an important role in the irrigant pressure dynamics. A question remains as to why the same mechanism that is observed in endodontic cavities is not additionally present also in periodontal cavities. Tentatively, we attribute this observation to the difference in geometries (cylindrical or wedge) of the two types of cavities. It is to be noted that in the endodontic cavity models the initial primary bubble was observed to move away from the fiber tip ending, thus giving room to the unconstrained growth of the subsequent primary bubble. In the wedge model, the initial primary bubble does not move substantially away from the fiber ending (See Fig. 5), thus not providing sufficient space for the individual growth of the subsequent primary bubble, as required for the effective exertion of pressure on the initial primary bubble.
It is important to note that the secondary cavitation was induced only at the tip of the narrow wedge model system. Changing the vertical position of the laser tip did not change the position of the secondary cavitation (see Supplementary information, Fig. S2). As it is expected that both primary and secondary bubbles will be important for cleaning efficiency in the periodontal pocket it will be important to test this on biofilm loaded surfaces. The tip of the periodontal or peri-implant pocket is the most difficult area to reach with mechanical instruments, such as sickle scalers, curettes, files, hoes, and chisels or even specialized dental implant maintenance tools, such as universal, lingual, posterior, or buccal scalers [55], [56]. To reach the tip of the periodontal and peri-implant pocket, dentists use ultrasound and ultrasonic scalers to increase the streaming efficiency in the irrigation volume [57], [63]. In ultrasonically activated irrigation the file needs to be preshaped and inserted deep inside the confined anatomy to achieve better performance of irrigation [64]. In contrast, the fiber tip in laser assisted irrigation only needs to be placed at the entrance of the confined irrigation anatomy [65]. To our knowledge, laser induced cavitation has not been studied for cleaning periodontal or peri-implant pocket. The results of this study suggest that cleaning efficiency of laser induced cavitation in narrow geometries with soft boundaries could be increased as both primary and secondary bubbles will contribute to cleaning. To demonstrate this, however, it will be important to show that generation of secondary bubbles correlates with increased cleaning efficiency.
6. Conclusions
In conclusion, the results imply that deformation of the soft boundary has a major effect on Er:YAG laser-induced cavitation effectiveness in the narrow soft–solid wedge geometry mimicking peri-implant and periodontal pockets. The softer the boundary, the less effective the cavitation. In stiffer wedge geometries, photoacoustic energy can be guided and focused at the tip of the wedge, enabling generation of secondary cavitation and more effective microstreaming. The absence of secondary cavitation in soft-solid wedge geometries, mimicking inflamed gingival pockets, can be overcome by the use of the dual-pulse AutoSWEEPS modality, which was successful in generating secondary cavitation at the tip of the inflamed wedge model, which is notoriously difficult to clean. This should in principle increase cleaning efficiency in narrow geometries such as those found in the periodontal and peri-implant pockets, which may lead to more predictable treatment outcomes.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgement
The work was supported by the Slovenian Research Agency (ARRS), research project L7-3186, as well as national program grant P4-0116, and P2-0392.
Footnotes
Supplementary data to this article can be found online at https://doi.org/10.1016/j.ultsonch.2023.106329.
Appendix A. Supplementary data
The following are the Supplementary data to this article:
References
- 1.Hutson M.S. Ma X, Plasma and cavitation dynamics during pulsed laser microsurgery in vivo. Phys. Rev. Lett. 2007;99(15) doi: 10.1103/PhysRevLett.99.158104. [DOI] [PubMed] [Google Scholar]
- 2.Wei C.W., Xia J., Lombardo M., Perez C., Arnal B., Larson-Smith K., Pelivanov I., Matula T., Pozzo L., O'Donnell M. Laser-induced cavitation in nanoemulsion with gold nanospheres for blood clot disruption: in vitro results. Opt. Lett. 2014;39(9):2599–2602. doi: 10.1364/OL.39.002599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Rau K.R., Quinto-Su P.A., Hellman A.N., Venugopalan V. Pulsed laser microbeam-induced cell lysis: time-resolved imaging and analysis of hydrodynamic effects. Biophys. J. 2006;91(1):317–329. doi: 10.1529/biophysj.105.079921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Do Q.L., Gaudin A. The Efficiency of the Er: YAG Laser and PhotonInduced Photoacoustic Streaming (PIPS) as an Activation Method in Endodontic Irrigation: A Literature Review. J. Lasers Med. Sci. 2020;11(3):316–334. doi: 10.34172/jlms.2020.53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Eldeeb I.M., Nawar N.N., Saber S.M., Hassanein E.E., Schäfer E. Smear layer removal and sealer penetration with different tapers after using photon-initiated photoacoustic streaming technique. Clin. Oral Investig. 2021;25(8):5025–5032. doi: 10.1007/s00784-021-03813-y. [DOI] [PubMed] [Google Scholar]
- 6.Cheng X., Xiang D., He W., Qiu J., Han B., Yu Q., Tian Y. Bactericidal Effect of Er:YAG Laser-Activated Sodium Hypochlorite Irrigation Against Biofilms of Enterococcus faecalis Isolate from Canal of Root-Filled Teeth with Periapical Lesions. Photomed. Laser Surg. 2017;35(7):386–392. doi: 10.1089/pho.2017.4293. [DOI] [PubMed] [Google Scholar]
- 7.Jakubovics N.S., Goodman S.D., Mashburn‐Warren L., Stafford G.P., Cieplik F., Darveau R.P., Curtis M.A. The dental plaque biofilm matrix. Periodontol. 2021;86(1):32–56. doi: 10.1111/prd.12361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Elhelf I.A.S., Albahar H., Shah U., Oto A., Cressman E., Almekkawy M. High intensity focused ultrasound: The fundamentals, clinical applications and research trends. Diagn. Interv. Imaging. 2018;99(6):349–359. doi: 10.1016/j.diii.2018.03.001. [DOI] [PubMed] [Google Scholar]
- 9.Diaci J., Gašpirc B. Comparison of Er: YAG and Er, Cr:YSGG lasers used in dentistry. J .La&Ha (Online ed.) 2012;1:1–13. [Google Scholar]
- 10.Gregorcic P., Jezersek M., Mozina J. Optodynamic energy-conversion efficiency during an Er:YAG-laser-pulse delivery into a liquid through different fiber-tip geometries. J. Biomed. Opt. 2012;17(7) doi: 10.1117/1.JBO.17.7.075006. [DOI] [PubMed] [Google Scholar]
- 11.Lukač N., Gregorčič P., Jezeršek M. Optodynamic Phenomena During Laser-Activated Irrigation Within Root Canals. Int J Thermophys. 2016;37 doi: 10.1007/s10765-016-2071-z. [DOI] [Google Scholar]
- 12.Gregorcic P., Lukac N., Možina J., Jezeršek M. In vitro study of the erbium:yttrium aluminum garnet laser cleaning of root canal by the use of shadow photography. J. Biomed. Opt. 2016;21(1):15008. doi: 10.1117/1.JBO.21.1.015008. [DOI] [PubMed] [Google Scholar]
- 13.E. Herbert, S. Balibar S, F. Caupin, Cavitation pressure in water, Phys Rev E Stat Nonlin Soft Matter Phys, 74 (4) (Pt 1) (2006), 041603, doi:10.1103/PhysRevE.74.041603. [DOI] [PubMed]
- 14.Lauterborn W., Vogel A. In: Delale C., editor. vol 8. Springer; Berlin, Heidelberg: 2013. Shock Wave Emission by Laser Generated Bubbles. (Bubble Dynamics and Shock Waves. Shock Wave Science and Technology Reference Library). [DOI] [Google Scholar]
- 15.Tagawa Y., Yamamoto S., Hayasaka K., Kameda M. On pressure impulse of a laser-induced underwater shock wave. J Fluid Mech. 2016;808:5–18. doi: 10.1017/jfm.2016.644. [DOI] [Google Scholar]
- 16.Sinibaldi G., Occhicone A., Alves Pereira F., Caprini D., Marino L., Michelotti F., Casciola C.M. Laser induced cavitation: Plasma generation and breakdown shockwave. Phys. Fluids. 2019;31(10) doi: 10.1063/1.5119794. [DOI] [Google Scholar]
- 17.Brujan E.A., Nahen K., Schmidt P., Vogel A. Dynamics of laser-induced cavitation bubbles near an elastic boundary. J Fluid Mech. 2001;433:251–281. doi: 10.1017/S0022112000003347. [DOI] [Google Scholar]
- 18.Lindau O., Lauterborn W. Cinematographic observation of the collapse and rebound of a laser-produced cavitation bubble near a wall. J Fluid Mech. 2003;479:327–348. doi: 10.1017/S0022112002003695. [DOI] [Google Scholar]
- 19.Supponen O., Obreschkow D., Kobel P., Tinguely M., Dorsaz N., Farhat M. Shock waves from nonspherical cavitation bubbles. Phys. Rev. Fluids. 2017;2 doi: 10.1103/PhysRevFluids.2.093601. [DOI] [Google Scholar]
- 20.Dular M., Požar T., Zevnik J., Petkovšek R. High speed observation of damage created by a collapse of a single cavitation bubble. Wear. 2019;418–419:13–23. doi: 10.1016/j.wear.2018.11.004. [DOI] [Google Scholar]
- 21.Obreschkow D., Tinguely M., Dorsaz N., Kobel P., de Bosset A., Farhat M. The quest for the most spherical bubble: experimental setup and data overview. Exp. Fluids. 2013;54:1503. doi: 10.1016/10.1007/s00348-013-1503-9. [DOI] [Google Scholar]
- 22.Reuter F., Ohl C.D. Supersonic needle-jet generation with single cavitation bubbles. Appl. Phy. Lett. 2021;118 doi: 10.1063/5.0045705. [DOI] [Google Scholar]
- 23.M.S. Plesset, R.B. Chapman, Collapse of an initially spherical vapour cavity in the neighbourhood of a solid boundary, J Fluid Mech, 47 (2) (1971), pp. 283-290, ISSN 0022-1120, doi:10.1017/S0022112071001058.
- 24.Blake J.R., Gibson D.C. Cavitation Bubbles Near Boundaries. Ann. Rev. Fluid Mech. 1987;19(1):99–123. doi: 10.1146/annurev.fl.19.010187.000531. [DOI] [Google Scholar]
- 25.C. Lechner, W. Lauterborn, M. Koch, and R. Mettin, Fast, thin jets from bubbles expanding and collapsing in extreme vicinity to a solid boundary: A numerical study, Phys Rev Fluids, 4 (2) (2019), 021601, doi/10.1103/PhysRevFluids.4.021601.
- 26.J.R. Blake, D.M. Leppinen, Q. Wang, Cavitation and bubble dynamics: the Kelvin impulse and its applications, Interface Focus, 2015 Oct 6;5(5) (2015), p.20150017, doi: 10.1098/rsfs.2015.0017. PMID: 26442141; PMCID: PMC4549843. [DOI] [PMC free article] [PubMed]
- 27.Zhang Y., Chen F., Zhang Y., Zhang Y., Du X. Experimental investigations of interactions between a laser-induced cavitation bubble and a spherical particle. Exp. Therm. Fluid Sci. 2018;98:645–661. doi: 10.1016/j.expthermflusci.2018.06.014. [DOI] [Google Scholar]
- 28.Li S., Han R., Zhang A.M. Nonlinear interaction between a gas bubble and a suspended sphere. J. Fluids Struct. 2016;65:333–354. doi: 10.1016/j.jfluidstructs.2016.06.005. [DOI] [Google Scholar]
- 29.Reuter F., Ohl C.D. Nonspherical Collapse of Single Bubbles Near Boundaries and in Confined Spaces. Cavitation and Bubble Dynamics, Academic Press. 2021:37–72. doi: 10.1016/b978-0-12-823388-7.00003-5. [DOI] [Google Scholar]
- 30.Lukač M., Lukač N., Jezeršek M. Characteristics of Bubble Oscillations During Laser-Activated Irrigation of Root Canals and Method of Improvement. Lasers Surg. Med. 2020;52(9):907–915. doi: 10.1002/lsm.23226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Požar T., Agrež V., Petkovšek R. Laser-induced cavitation bubbles and shock waves in water near a concave surface. Ultrason Sonochem. 2021;73 doi: 10.1016/j.ultsonch.2020.105456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Lukac N., Tasic M.B., Jezersek M., Lukac M. Photoacoustic Endodontics Using the Novel SWEEPS Er: YAG Laser Modality. J. La&Ha. 2017;1 [Google Scholar]
- 33.N. Lukač, M. Jezeršek, Amplification of pressure waves in laser-assisted endodontics with synchronized delivery of Er: YAG laser pulses, Lasers Med Sci, May; 33 (4) (2018), pp.823-833, doi: 10.1007/s10103-017-2435-z. Epub 2018 Jan 11. PMID: 29327088; PMCID: PMC5911281. [DOI] [PMC free article] [PubMed]
- 34.Yang Q., Liu M.W., Zhu L.X., Peng B. Micro-CT study on the removal of accumulated hard-tissue debris from the root canal system of mandibular molars when using a novel laser-activated irrigation approach. Int. Endod. J. 2020;53(4):529–538. doi: 10.1111/iej.13250. [DOI] [PubMed] [Google Scholar]
- 35.Lukač M., Olivi G., Constantin M., Lukač N., Jezeršek M. Determination of Optimal Separation Times for Dual-Pulse SWEEPS Laser-Assisted Irrigation in Different Endodontic Access Cavities. Lasers Surg. Med. 2021;53(7):998–1004. doi: 10.1002/lsm.23357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Estrada J.B., Barajas C., Henann D.L., Johnsen E., Franck C. High strain-rate soft material characterization via inertial cavitation. J. Mech. Phys. Solids. 2018;112:291–317. doi: 10.1016/j.jmps.2017.12.006. ISSN 0022–5096, [DOI] [Google Scholar]
- 37.Gaudron R., Warnez M., Johnsen E. Bubble dynamics in a viscoelastic medium with nonlinear elasticity. J. Fluid Mech. 2015;766:54–75. doi: 10.1017/jfm.2015.7. [DOI] [Google Scholar]
- 38.J. Yang, C. Franck, Strain Stiffening Effects of Soft Viscoelastic Materials in Inertial Microcavitation. In: Lamberson, L. (eds) Dynamic Behavior of Materials, 1 (2020). Conference Proceedings of the Society for Experimental Mechanics Series. Springer, Cham. https://doi.org/10.1007/978-3-030-30021-0_30.
- 39.J. Yang, H.C. Cramer, C. Franck, Extracting non-linear viscoelastic material properties from violently-collapsing cavitation bubbles, Extreme Mech Lett, 39 (2020), p.100839, ISSN 2352-4316. doi.org/10.1016/j.eml.2020.100839.
- 40.Zhu J., Marchant R.E. Design properties of hydrogel tissue-engineering scaffolds. Expert Rev. Med. Devices. 2011;8(5):607–626. doi: 10.1586/erd.11.27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Yuanfang C., Weihua P., Rongyu T., Sanyuan C., Hongda C. Conformal coating of parylene for surface anti-adhesion in polydimethylsiloxane (PDMS) double casting technique. Sens. Actuators, A. 2013;189:143–150. doi: 10.1016/j.sna.2012.09.024. ISSN 0924–4247. [DOI] [Google Scholar]
- 42.F. Horkay, P.J. Basser, Hydrogel composite mimics biological tissues, Soft Matter, 18 (23) (2022), pp.4414-4426, Published 2022 Jun 15. Doi:10.1039/d2sm00505k. [DOI] [PMC free article] [PubMed]
- 43.Souza A., Ribeiro J., Araújo F. Study of PDMS characterization and its applications in biomedicine: A review. J. Mech. Eng. Biomech. 2019;4:1–9. doi: 10.24243/JMEB/4.1.163. [DOI] [Google Scholar]
- 44.Verhaagen B., Fernández R.D. Measuring cavitation and its cleaning effect. Ultrason Sonochem. 2016;29:619–628. doi: 10.1016/j.ultsonch.2015.03.009. [DOI] [PubMed] [Google Scholar]
- 45.Lucas B.D., Kanade T. An iterative image registration technique with an application to stereo vision. Proc. Imaging Understanding Workshop. 1981:121–130. [Google Scholar]
- 46.X.X. Liang, N. Linz, S. Freidank, G. Paltauf, A, Vogel, Comprehensive analysis of spherical bubble oscillations and shock wave emission in laser-induced cavitation, J Fluid Mech, 940 (2022) A5. Doi.org/10.1017/JFM.2022.202.
- 47.Herbert E., Balibar S., Caupin F. Cavitation pressure in water. Phys. Rev. E. 2006;74(4) doi: 10.1103/PhysRevE.74.041603. [DOI] [PubMed] [Google Scholar]
- 48.Goktas S., Dmytryk J.J., McFetridge P.S. Biomechanical behavior of oral soft tissues. J. Periodontol. 2011;82(8):1178–1186. doi: 10.1902/jop.2011.100573. [DOI] [PubMed] [Google Scholar]
- 49.Lee S., Müller M., Rezwan K., Spencer N.D. Porcine gastric mucin (PGM) at the water/poly(dimethylsiloxane) (PDMS) interface: influence of pH and ionic strength on its conformation, adsorption, and aqueous lubrication properties. Langmuir. 2005;21(18):8344–8353. doi: 10.1021/la050779w. [DOI] [PubMed] [Google Scholar]
- 50.Macakova L., Yakubov G.E., Plunkett M.A., Stokes J.R. Influence of ionic strength changes on the structure of pre-adsorbed salivary films. A response of a natural multi-component layer. Colloids Surf B Biointerfaces. 2010;77(1):31–39. doi: 10.1016/j.colsurfb.2009.12.022. [DOI] [PubMed] [Google Scholar]
- 51.Kilikevičius A., Balčiūnas E., Kilikevičienė K., Maknickas A., Bukelskienė V., Baltriukienė D., Kačianauskas R. Modelling of silk-reinforced PDMS properties for soft tissue engineering applications. Technol. Health Care. 2018;26(S2):679–688. doi: 10.3233/THC-182515. [DOI] [PubMed] [Google Scholar]
- 52.C. Wen, L. Yan, Y. Kong, J. Zhao, Y. Li, Q. Jiang, The antibacterial efficacy of photon-initiated photoacoustic streaming in root canals with different diameters or tapers, BMC Oral Health, 21 (1), p.542, doi:10.1186/s12903-021-01903-7. [DOI] [PMC free article] [PubMed]
- 53.De Moor R., Blanken J., Meire M., Verdaasdonk R. Laser Induced Explosive Vapor and Cavitation Resulting in Effective Irrigation of the Root Canal. Part 2: Evaluation of the Efficacy. Lasers Surg. Med. 2009;41:520–523. doi: 10.1002/lsm.20797. [DOI] [PubMed] [Google Scholar]
- 54.Yamashita T., Ando K. Low-intensity ultrasound-induced cavitation and streaming in oxygen-supersaturated water: Role of cavitation bubbles as physical cleaning agents. Ultrason. Sonochem. 2018;52 doi: 10.1016/j.ultsonch.2018.11.025. [DOI] [PubMed] [Google Scholar]
- 55.Suvan J., Leira Y., Moreno Sancho F.M., Graziani F., Derks J., Tomasi C. Subgingival instrumentation for treatment of periodontitis. A systematic review. J. Clin. Periodontol. 2020;47(Suppl 22):155–175. doi: 10.1111/jcpe.13245. [DOI] [PubMed] [Google Scholar]
- 56.F. Graziani, D. Karapetsa, B. Alonso, D. Herrera, Nonsurgical and surgical treatment of periodontitis: how many options for one disease?, Periodontol 2000, 75 (1) (2017), pp.152-188, doi:10.1111/prd.12201. [DOI] [PubMed]
- 57.Vyas N., Wang Q., Walmsley A. Improved biofilm removal using cavitation from a dental ultrasonic scaler vibrating in carbonated water. Ultrasonics Sonochemistry. 2020;70 doi: 10.1016/j.ultsonch.2020.105338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Kiyama A., Shimazaki T., Gordillo J.M., Tagawa Y. Direction of the microjet produced by the collapse of a cavitation bubble located in a corner of a wall and a free surface. Phys. Rev. Fluids. Aug. 2021;6(8) doi: 10.1103/PhysRevFluids.6.083601. [DOI] [Google Scholar]
- 59.Brujan E.-A., Noda T., Ishigami A., Ogasawara T., Takahira H. Dynamics of laser-induced cavitation bubbles near two perpendicular rigid walls. J. Fluid Mech. 2018;841:28–49. doi: 10.1017/jfm.2018.82. [DOI] [Google Scholar]
- 60.Tagawa Y., Peters I.R. Bubble collapse and jet formation in corner geometries. Phys. Rev. Fluids. 2018;3(8) doi: 10.1103/PhysRevFluids.3.081601. [DOI] [Google Scholar]
- 61.Yu Y., Mahmud M., Vyas N., Smith W.R., Wang Q., Damien Walmsley A. Cavitation in a periodontal pocket by an ultrasonic dental scaler: A numerical investigation. Ultrasonics Sonochemistry. 2022;90:106178. doi: 10.1016/j.ultsonch.2022.106178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.M. S. Tonetti, H. Greenwell, and K. S. Kornman, ‘Staging and grading of periodontitis: Framework and proposal of a new classification and case definition’, Journal of Periodontology, vol. 89, no. S1, pp. S159–S172, 2018, doi: 10.1002/JPER.18-0006. [DOI] [PubMed]
- 63.Vyas, N., Sammons, R., Kuehne, S., Johansson, C. B., Stenport, V., Wang, Q., & Walmsley, D. (2020). The effect of standoff distance and surface roughness on biofilm disruption using cavitation. PLoSONE, 15(7), [e0236428]. https://doi.org/10.1371/journal.pone.0236428. [DOI] [PMC free article] [PubMed]
- 64.Van der Sluis L., Versluis M., Wu M., Wesselink P. Passive ultrasonic irrigation of the root canal: A review of the literature. Int. Endod. J. 2007;40(6):415–426. doi: 10.1111/j.1365-2591.2007.01243.x. [DOI] [PubMed] [Google Scholar]
- 65.Su Z., et al. Characteristics of the Irrigant Flow in a Simulated Lateral Canal Under Two Typical Laser-Activated Irrigation Regimens. Lasers Surg. Med. 2021;53(4):587–594. doi: 10.1002/lsm.23317. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.