Rubble pile asteroids are forever

Significance

Monolithic-type asteroids that are more than a kilometer in diameter have been predicted to have a lifespan of few 100 million years. However, the durability of rubble pile asteroids is currently not known. This study shows that the formation age of the rubble pile Itokawa asteroid is older than 4.2 billion years. Such a long survival time for an asteroid is attributed to the shock-absorbent nature of rubble pile material and suggests that rubble piles are hard to destroy once they are created. Our results suggest that rubble piles are probably more abundant in the asteroid belt than previously thought and provide constrain to help develop mitigation strategies to prevent asteroid collisions with Earth.

Abstract

Rubble piles asteroids consist of reassembled fragments from shattered monolithic asteroids and are much more abundant than previously thought in the solar system. Although monolithic asteroids that are a kilometer in diameter have been predicted to have a lifespan of few 100 million years, it is currently not known how durable rubble pile asteroids are. Here, we show that rubble pile asteroids can survive ambient solar system bombardment processes for extremely long periods and potentially 10 times longer than their monolith counterparts. We studied three regolith dust particles recovered by the Hayabusa space probe from the rubble pile asteroid 25143 Itokawa using electron backscatter diffraction, time-of-flight secondary ion mass spectrometry, atom probe tomography, and ⁴⁰Ar/³⁹Ar dating techniques. Our results show that the particles have only been affected by shock pressure of ca. 5 to 15 GPa. Two particles have ⁴⁰Ar/³⁹Ar ages of 4,219 ± 35 and 4,149 ± 41 My and when combined with thermal and diffusion models; these results constrain the formation age of the rubble pile structure to ≥4.2 billion years ago. Such a long survival time for an asteroid is attributed to the shock-absorbent nature of rubble pile material and suggests that rubble piles are hard to destroy once they are created. Our results suggest that rubble piles are probably more abundant in the asteroid belt than previously thought and provide constrain to help develop mitigation strategies to prevent asteroid collisions with Earth.

Rubble pile asteroids consist of reassembled fragments of once larger monolithic asteroid parent bodies which have been shattered during catastrophic collisions between asteroids (1). Although their existence was only a hypothesis (2), recent and ongoing spacecraft missions to asteroids Itokawa, Ryugu, Bennu, and Dimorphos along with progress in numerical models indicate that rubble pile asteroids are much more common than previously thought, particularly in the 200 m to 10 km size range (3). Itokawa is a chondritic 535 × 295 × 209 m rubble pile asteroid and was the first asteroid clearly identified as a rubble pile (1) along with being the first asteroid from which ~ 1,500 particles were recovered and brought back to Earth during the first Hayabusa mission of Japanese Aerospace Exploration Agency (JAXA) (4, 5). Even though most particles recovered from Itokawa’s surface regolith have a diameter significantly smaller than 100 μm (5), they provide an invaluable means to study early solar system processes such as the formation of Earth’s oceans (6) and the formation, evolution, and longevity of rubble pile asteroids.

The particles retrieved from Itokawa are LL (low iron, low metal) chondritic in composition and consist mostly of equilibrated olivine, albitic plagioclase, and low- and high-Ca pyroxene crystals (5). Petrographic observations combined with phosphate U-Pb dating indicate that most of the particles experienced peak thermal metamorphism at 4.64 ± 0.36 Ga (Giga Annum; 7) at a temperature of ~ 800 °C followed by slow cooling, during the accretion and evolution of their monolithic parent body (5, 8). Such metamorphic conditions require that the primary parent body was a monolithic asteroid of at least a few 10’s of kilometers in diameter and, therefore, that it must have been shattered during a catastrophic impact breakup event (5). Some of the fragments were then reassembled to form the rubble pile asteroid Itokawa (9), which could have originally been a somewhat larger rubble pile and has lost material due to subsequent collisions (10, 11).

Constraining the age of the initial breakup event of the monolithic parent body is critical to elucidate the longevity of rubble pile asteroids in the inner solar system and therefore their resistance to the ambient level of bombardment throughout the solar system history. Previous work suggests that asteroid Itokawa had already formed at 1.3 ± 0.3 Ga (12) with more recent data suggesting a minimum age of 2.3 ± 0.1 Ga for the catastrophic asteroid breakup (13). Here, we studied three particles: RA‐QD02‐0010 (#0010, ~149 μm in diameter), RA‐QD02‐0288 (#0288, ~169 μm in diameter), and RB‐QD04‐0059 (#0059, ~191 μm in diameter) (Fig. 1 and SI Appendix, Fig. S1). We combined scanning electron microscopy (SEM), electron microprobe analysis (EMPA) SI Appendix, Figs. S2–S18 and Supplementary data), electron backscatter diffraction (EBSD), time-of-flight secondary ion mass spectrometry (ToF-SIMS), and, atom probe tomography (APT) to characterize the particles. We then use radioisotopic ⁴⁰Ar/³⁹Ar geochronology data and numerical models of ⁴⁰Ar* diffusion loss (SI Appendix) to constrain the time–temperature–shock histories of these three particles and derive a minimum formation age for asteroid Itokawa.

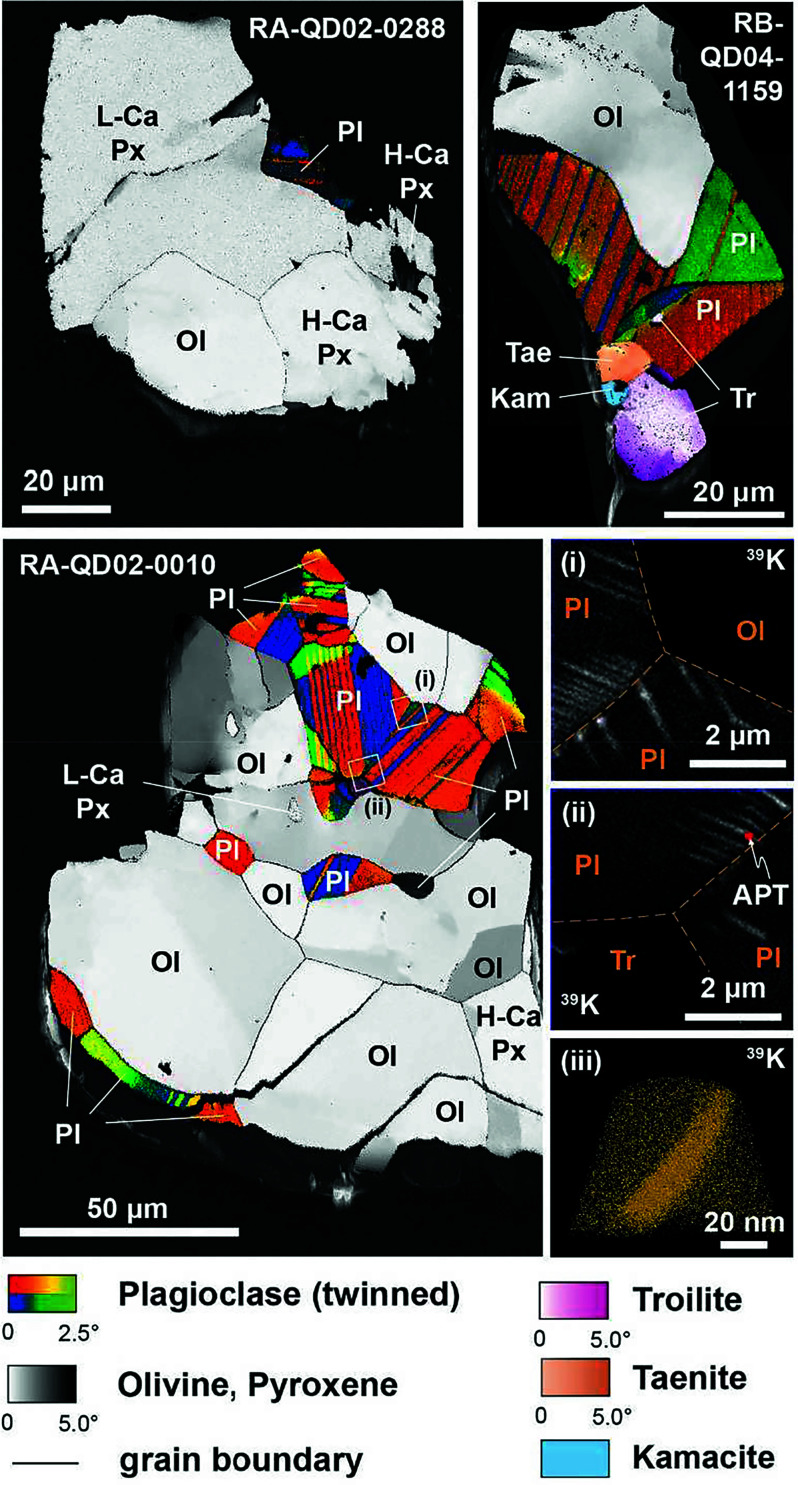
Fig. 1.

Crystallographic orientation maps of Itokawa particles measured by EBSD. Grains of each phase are colored for crystallographic misorientation angle (up to 5°) from the average orientation, showing very low total lattice strain in each grain. Insets (i) and (ii): distribution of ³⁹K revealed by ToF-SIMS from particle #0010. Orange dashed lines represents the boundary between grains. Inset (iii): nanoscale ³⁹K distribution by APT of the feature located on (ii). Each yellow sphere represents one atom of ³⁹K. The distribution of K in plagioclase of particle #0010 is heterogeneous with radiating K-rich lamellae around grain boundaries. Pl = plagioclase; Ol = olivine; H-Ca Px = high-Ca pyroxene; L-Ca Px = low-Ca pyroxene; Tr = troilite; Tae = taenite; Kam = kamacite.

Results

None of the three particles show any sign of amorphization, mosaicism, high-pressure polymorphs, or planar deformation features (Fig. 1 and SI Appendix, Figs. S19–S24). EBSD analyses show that the particles are polymineralic polycrystals with no crystallographic preferred orientation and have numerous 120° triple junctions indicative of high-temperature textural equilibration (~783 °C; 5). In all three particles, plagioclase contains polysynthetic twins. Particle #0059 has low-angle misorientations in a plagioclase and a troilite crystal and none in olivine (Fig. 1 and SI Appendix, Fig. S21 and S22), suggesting that this particle along with particle #0288, which shows a similar level of misorientations, experienced maximum shock pressure levels of ca. 5 to 10 GPa. This value was estimated by comparing our EBSD results with petrographic classifications (14, 15). Particle #0010 contains a few (n < 5) irregular fractures. Olivine and plagioclase crystals show very minor intragrain crystal-plastic strain (from <1° up to 10° misorientation) localized at the particle surface, at some grain–grain interfaces, and at low-angle boundaries in olivine (Fig. 1 and SI Appendix, Figs. S23 and S24). We attribute these features to shock by impact and the level of lattice deformation might be associated with a pressure level to an upper limit of 10 to 15 GPa (14). Such values are approximate because it is hard in practice to accurately convert these observations in absolute pressure levels (13), but particle #0010 must have had a strict upper pressure limit of 25 GPa given by the absence of diaplectic glass and pyroxene mosaicism (14, 15). By comparison with #0010, and due to their significantly lower level of deformation, particles #0288 and #0059 must have stayed largely below 15 GPa.

EMPA and ToF-SIMS results (Fig. 1 and SI Appendix, Figs. S25–S33) show that crystal compositions are fairly homogeneous for particles #0059 and #0288. However, ToF-SIMS ³⁹K maps and nanoscale APT analyses (Fig. 1 and SI Appendix, Figs. S30–S34 and SI Appendix) of plagioclase crystals from particle #0010 show “feather-like” orthoclase lamellae crosscutting twins a few micrometers long and 10 to 15 nm wide that are localized at the grain and twin boundaries (16) (SI Appendix, Figs. S31–S33). These lamellae likely result from exsolution processes, either due to cooling from high-temperature equilibration at ~ 800 °C or impact-related reheating.

⁴⁰Ar/³⁹Ar data on the two least shocked particles (#0059 and #0288) returned two well-defined plateau ages (Fig. 2 A and B and SI Appendix, Figs. S36–S41) of 4,219 ± 35 Ma (P = 0.58) and 4,149 ± 41 Ma (P = 0.27) indicating that the K/Ar clock has been fully reset during one or several thermal event(s) around 4.2 Ga, several hundred million years after their initial cooling (5). Particle #0010 failed to return a plateau age and yielded a pronounced hump-shaped age spectrum (Fig. 2C and  SI Appendix, Figs. S42–S44). Diffusion modeling suggests that the orthoclase exsolution lamellae in feldspar from particle #0010 are likely responsible for its complex age spectrum (SI Appendix, Figs. S54 and S55) and suggests that the particle has been affected by a relatively young impact <0.5 Ga.

Fig. 2.

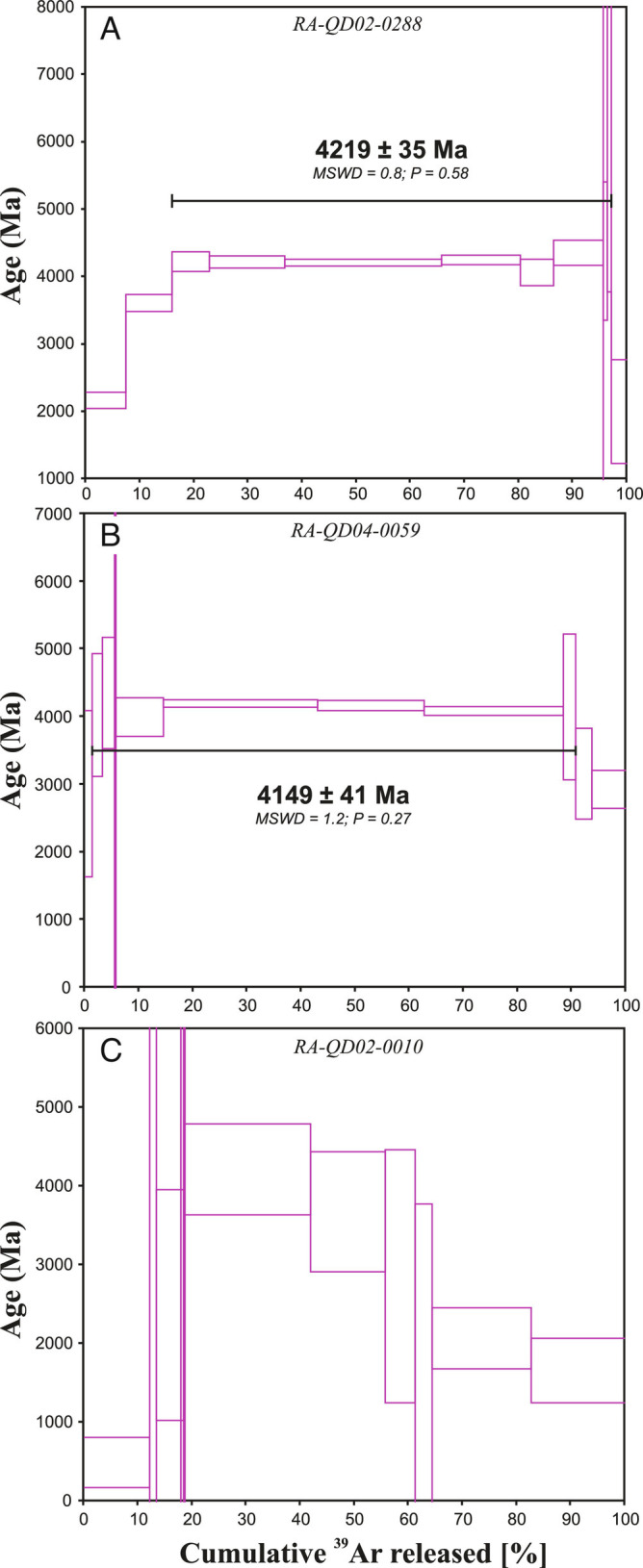
Single-grain laser step-heating ⁴⁰Ar/³⁹Ar age spectra of particles #0288 and #0059 and #0010 providing plateau ages of 4,219 ± 35 Ma and 4,149 ± 41 Ma. The solid line indicates the width of the plateau age (i.e., the steps included in the calculation). Detailed procedure and results are provided in the Supplementary Information.

Discussion

The texturally and compositionally equilibrated nature of the particles show that they were initially located deep in the monolithic parent asteroid, hence protected from ambient bombardment and shock heating processes. In order to be affected or subsequently affectable by impact-related thermal events at ~4.2 Ga, the particles would need to be brought near the surface, either by total disruption of the parent body or by deep crater excavations. Importantly, impact shock pressures less than 25 GPa will not raise the temperature by more than 50 °C in compacted material (14), clearly insufficient to raise the rock above its Ar closure temperature of 250 to 300 °C for plagioclase of this grain size (17). Also, it is unlikely that the particle recorded simple cooling inside its parent asteroid given the fast cooling rates of 10⁻² to 100 °C per year estimated for unshattered asteroids (18). For comparison, recent data-driven modeling of the L parent body by Gail and Trieloff (19) shows that a rock exposed to a peak temperature of 800 °C takes about 100 My to cool down below the closure temperature of plagioclase. This is similar to U-Pb and ⁴⁰Ar/³⁹Ar results obtained for a larger asteroid such as Vesta, where eucrites from 15 to 20 km depth have been shown to cool down below the closure temperature of ⁴⁰Ar in plagioclase ca. 50 to 70 My after accretion (20, 21). Therefore, considering the low shock–pressure (5 to 10 GPa) recorded by the ~4.2 Ga particles, the only other two conceivable scenarios that would cause a complete reset of the K/Ar systematics of the two particles involve either 1) a low-impact shock of 5 to 10 GPa in porous rubble pile material where the pressure wave can produce enough work through pore collapse to raise the temperature by few hundred degrees Celsius (13, 22, 23) or 2) unshocked (cold) particles brought in contact with shock-heated material and insulated from space long enough to allow relatively slow cooling over hundred thousand to several millions of years (18).

In order to test these three hypotheses, we have modeled the effect of ⁴⁰Ar* loss on plagioclase crystals for a range of pressure–porosity–temperature and cooling duration solutions (13). First, we have modeled the expected response of the ⁴⁰Ar/³⁹Ar chronometer of a 4.56 Ga sample to a simple monotonic cooling at ca. 30 kms deep inside of the monolithic parent body using the ArArDIFF algorithm (13) using the cooling rates of estimated by Gail and Trieloff (19). To test the porosity and blanketing models, we used a Monte Carlo simulation approach applied to a diffusion equation for spherical geometry (24). For completeness, we have also modeled the expected level of ⁴⁰Ar* loss due to surface heating of Itokawa at perihelion but since the Ar* loss was negligible, we will not discuss this point further in the text. The modelings and Monte Carlo simulations are provided in SI Appendix, and the results are summarized below.

The monotonic cooling model approximates the simple cooling of a particle formed at 4,565 Ma and which underwent peak metamorphism temperature of 800 °C at 4,560 Ma inside the parent asteroid (SI Appendix, Fig. S45 and SI Appendix). The model shows that a plagioclase particle would slowly cool down in 121 My and produce a plateau age of ca. 4,439 Ma. This scenario implies that the particle would have closed its ⁴⁰Ar* clock about 200 My too early to account for the two ⁴⁰Ar/³⁹Ar ages of 4.2 Ga obtained in this study. Therefore, we conclude that a slow cooling postaccretion process is an unlikely scenario to explain our results.

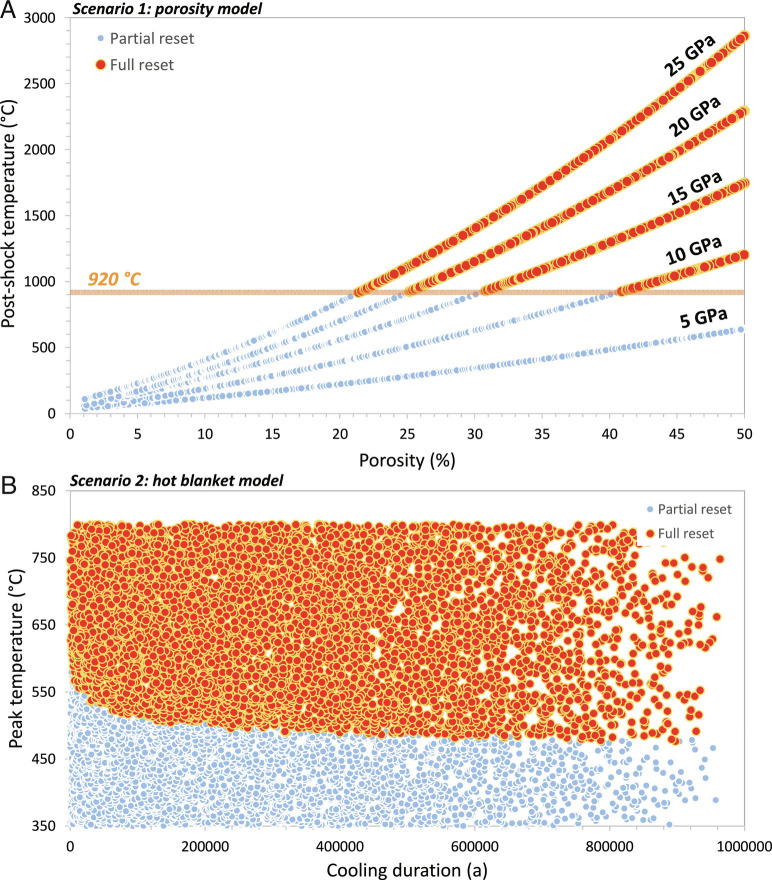
The impact in a porous material model (Fig. 3A and SI Appendix, Figs. S46–S50 and SI Appendix) simulates the effect of ⁴⁰Ar* loss following a heating event on a small plagioclase crystal for a range of pressure–porosity–temperature solutions initially presented by ref. 13 and using a Monte Carlo simulation approach (25). The model shows that in order to achieve full ⁴⁰Ar* reset in a relatively brief period of time, a particle must be heated to a minimum temperature of ~920 °C (Fig. 3) followed by a cooling period ranging from ca. 177 s up to 13.4 d (the latter value being the maximum duration allowed by our cooling calculations; SI Appendix, Fig. S46 and SI Appendix). Such a temperature can be generated by a minimum shock pressure of ~8 to 10 GPa as estimated for particles #0288 and #0059. However, to be able to generate ≥920 °C, a low energy impact must occur on a target rock with at least ~41 to 50 % porosity for 10 GPa (Fig. 3) or at very least 30% for a strict maximum estimate of 15 GPa. The reason is that the energy used to compact pores during impact is immediately converted into waste heat which causes a peak in temperature much higher than what would be observed from a nonporous material (13, 22, 23). Such a high level of porosity is unlikely to be found on a postcompaction monolithic asteroid with bulk properties consistent with LL chondrite meteorites as the latter have porosity ranging from 0 to 18 % (26). However, this level of porosity is consistent with the high-porosity rubble pile structure inferred for Itokawa [~40%; (27)]. This model requires that the very porous rubble pile structure of Itokawa already existed at ~ 4.2 Ga (Fig. 4), whereas the initial parent breakup of the monolith was older and perhaps as old as ~4.5 Ga, near peak metamorphism conditions (7) of its LL-chondrite parent body (18).

Fig. 3.

Monte Carlo simulations of the conditions required to fully reset the K/Ar systematic (>99% ⁴⁰Ar* diffusion loss) of plagioclase crystals. Partial and full ⁴⁰Ar* losses are indicated by small blue and large red circles, respectively. Scenario 1: Pressure–Temperature vs. porosity model. Discreet lines of pressure evolution derived from the model presented by ref. 13 and based on ANEOS equation of state for forsterite. Full isotopic reset can only be achieved if a minimum temperature of ~920 °C is reached. Scenario 2: Temperature vs. cooling duration showing that for the time scale involved, minimum temperatures of ca ~517° to 465 °C are required.

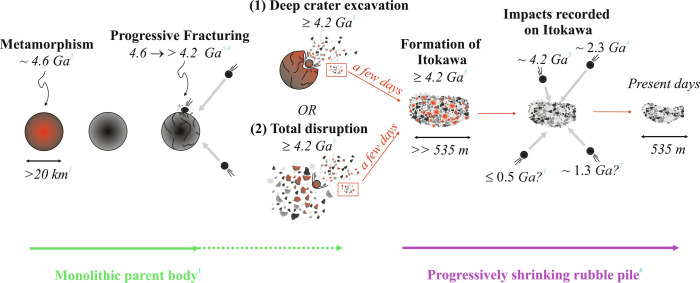
Fig. 4.

Schema showing the evolution of a 20-km LL-chondrite monolithic parent body, followed by partial or total disruption and reassembly of a small fraction of the material in the rubble pile asteroid Itokawa. Red–orange color filling indicate higher temperatures (metamorphism or impact heat). References: ¹Nakamura et al. (5)²Terada et al. (7)³Michel et al. (28)⁴Jourdan et al. (13)⁵this study, ⁶Nagao et al. (10)⁷Park et al. (12).

In the hot-blanket model (Fig. 3B), we have simulated the effect of the time–temperature history on the ⁴⁰Ar* budget of an unshocked particle which has been embedded in a hot insulating blanket. In this scenario, an initially unshocked cold rock or boulder has been excavated during a catastrophic breakup from few kilometers deep within the asteroid where it was initially equilibrated. This rock has then been reamalgamated into a large rubble pile asteroid where the cold fragments were then put in contact with strongly shocked and heated fragments. This process allows significantly longer cooling durations that the porosity model and shows that for cooling durations varying between 100,000 to 1 My, peak temperatures varying from ~517° to 465 °C, respectively (SI Appendix, Figs. S51 and S52 and Table S3) are sufficient to reset the K/Ar system. This scenario necessitates cold and unshocked equilibrated particles/rocks coming from >20 km deep in the monolithic parent asteroid, to be put in contact with strongly shocked and heated fragments during a catastrophic impact and, as a result, be heated to few hundred degrees and slowly cooled down. A slow cooling rate is enabled by the reduction of thermal conductivity of the porous insulating layer made of superimposed rubble pile material (18). Numerical models based on low closure temperature methods estimated cooling rates of 1 to 10 °C/Ma for reassembled fragments of an initially hot parent chondritic parent body at ~4.5 Ga (18). In our scenario, although the initial primordial heat of the asteroid is long gone, the additional heat comes from the collisional energy of the giant impact which caused the catastrophic breakup of the monolithic parent body at ~4.2 Ga (Fig. 4). A possible derivative of this scenario would be to have the monolithic parent body shattered around 4.5 Ga, reassembled as a rubble pile and slowly cooled until the plagioclase reached its Ar closure temperature at ~4.2 Ga. Current models rather predict that this would happen between 4.4 and 4.35 Ga (18). Regardless, both of these scenarios necessitate that the Itokawa rubble pile structure exists at the latest by 4.2 Ga.

All available isotopic ages for Itokawa particles are described in SI Appendix and range from ~0.5 Ga to ~4.6 Ga (this study; 7, 12, 13). Furthermore, we compared these ages with available ⁴⁰Ar/³⁹Ar ages on LL chondrites (SI Appendix). Although unequal in robustness and precision (SI Appendix, Figs. S55–S57), all the ages obtained on Itokawa are compatible with a formation age of ≥4.22 ± 0.04 Ga as given by the age of the oldest particle which can be demonstrated to have undergone complete isotopic reset during an impact event. Neither of the two scenarios proposed above can assess whether Itokawa-forming debris was ejected from a >20-km deep crater excavation within their monolithic parent body or if the total disruption of the monolithic parent body occurred at the time of the impact (Fig. 4). Nevertheless, these data show that once formed, a rubble pile asteroid can survive for billions of years without being completely destroyed by the ambient bombardment. Although Itokawa is presently a Near Earth Asteroid, observations and numerical models suggest that it left the main asteroid belt less than a million years ago through the υ6 secular resonance (7). Therefore, extended longevity for rubble pile asteroids is in contrast with the relatively short lifespan of 100’s of meters to kilometers size monolithic asteroids where numerical models predict that these asteroids have a lifecycle of few 10’s to 100 millions of years in the main asteroid belt (29). Of course, the dimensions of the initial rubble pile asteroid immediately after reassembly ≥4.2 billion years ago are not known. However, we hypothesize that it was probably slightly bigger than the present-day Itokawa asteroid. As proposed by Nagao et al. (10), Itokawa most likely gradually lost material into space over its ~4 billion years life span due to numerous collisions. Even if the initial diameter of the rubble pile was ~1 km and would have somehow shed >90% of its original volume, the average life span of a kilometer-sized monolithic body is predicted to be on the order of 440 My (29). Here, our results show that for a given size, rubble piles asteroids can survive almost an order of magnitude longer than their monolith counterparts. We attribute such a long duration to the shock-absorbent nature of rubble pile material during shock. Since rubble pile asteroids are extremely porous (27), pore collapses will absorb most of the increase of energy caused by the shock process rather than the energy being used to fracture solid rocks or to eject fragments away from Itokawa (30, 31). Numerical simulations are in agreement with our results in that the energy threshold necessary to totally disrupt rubble pile asteroids is >4 times higher than for monolithic asteroids (30). Furthermore, the contrast of resistance to fragmentation between the two types of asteroids drastically increases if monolithic asteroids are fractured and weakened by large impacts prior to disruption (28, 32).

Since rubble piles are hard to destroy once they are created compared to monolithic asteroids, this might suggest that they are much more abundant in the asteroid belt than previously thought. Furthermore, this information is critical to develop mitigation strategies to avoid asteroid collisions with Earth when the case will present itself (33). Porous asteroids are harder to deflect by kinetic impact since porosity decrease the efficiency of the transfer of momentum (34) and much remains to be learned from the successful impact of the Double Asteroid Redirection Test (DART) spacecraft on the rubble pile asteroid Dimorphos (35). Here, we showed that small rubble pile asteroids can survive billions of years against the ambient bombardment in the inner solar system due to their resistance to collisions and fragmentations. Therefore, more aggressive approaches (e.g., nuclear blast deflection) might have a higher chance of success against rubble pile asteroids (33, 36).

Materials and Methods

Sample Provision and Preparation.

Three dust particles were provided by JAXA. Particles RA-QD02-0288, RA-QD04-0059, and RA-QD02-0010, hereafter named #0288, #0059, and #0010, respectively (SI Appendix, Fig. S1). Upon delivery of particles to Tohoku University, Japan, particles #0059 and #0010 were each embedded in an epoxy disc (SI Appendix, Fig. S2) and were carbon- and gold-coated, respectively. Particle #0288 was embedded in a cylinder and in epoxy and carbon-coated. SEM and EMPA analyses were carried out at Tohoku University. Subsequently, the particles were shipped to Curtin University for further analyses.

Prior to SEM, EBSD, and Energy-Dispersive X-ray (EDX) mapping and ToF-SIMS analyses at Curtin University, all particles were repolished to remove surface damage from earlier sample preparation using a Buehler Vibromet II polisher and 0.06-μm colloidal silica in sodium hydroxide for 4 to 5.5 h (SI Appendix, Fig. S3). Inspection of the surface using reflected light microscopy revealed a high-quality polish with partially visible pits from previous ion probe analyses (37, 38), indicating the removal of <1 μm of material. A thin (~20 nm) carbon coat was applied to mitigate charging in the SEM.

EMPA.

The chemical composition of minerals was determined using FE-EPMA/WDS (wavelength-dispersive spectroscopy) using a JEOL JXA-8530F FE-EPMA/WDS instrument at Kyushu University equipped with four crystal spectrometers. Each element characteristic X-ray was measured for 20 s counting time and quantified by ZAF-oxide or ZAF correction procedures. Analysis was performed at accelerating voltage, electron current, and electron beam diameter to be 15 KeV, 10 nA, and 1 μm for olivine, pyroxene, and chromite, 15 KeV, 2 nA, and 2 to 3 μm for plagioclase and K-feldspar, 20 KeV, 10 nA, and 1μm for metal and sulfide. Analytical results are provided in Dataset S1.

Secondary Electron (SE) and Backscattered Electron (BSE) Imaging.

SE and BSE images were collected on a Tescan MIRA3 field emission (FE) SEM in the John de Laeter Centre (JdLC) at Curtin University. Images were collected with an acceleration voltage of 5 kV and working distances from ~13 to ~15 mm.

EBSD and EDX Mapping.

EBSD data were collected on a Tescan MIRA3 FE SEM fitted with Oxford Instruments AZtec combined EDX–EBSD acquisition system and Nordlys Nano EBSD camera in the JdLC at Curtin University. SEM operating conditions were routine for EBSD analysis (20 kV acceleration voltage, 70° sample tilt, ~18.5 mm working distance, ~1.5 nA beam current) (39). Match units for forsterite, chromite, troilite, diopside, enstatite, labradorite (An66), taenite, and kamacite were used to index the EBSD patterns. Maps were collected with 80 nm step size, with exception of one map of #0059, which was collected with a 100-nm step size. EBSD data were processed using Oxford Instruments Channel 5.12 software and included the removal of isolated erroneous points (wildspike correction) and systematically misindexed points, followed by zero solution extrapolation to five nearest neighbors. Comparison of the final data with band contrast map by visual inspection shows that no significant artifacts were generated.

Thematic EBSD maps were produced using the Tango module in Channel 5 using available functions and routines in service pack 5.12. Maps were collected in the sample x–y–z reference frame, where x–y represents the plane of the polished surface. Pattern quality (band contrast) maps show that the surfaces of both particles are free of scratches and damage from previous polishing stages, as well as qualitative variations in intrinsic crystallinity (SI Appendix, Figs. S7 and S8). Crystallographic orientation maps were generated by assigning three Euler angles that describe orientation relative to a reference to red, blue, and green channels, respectively (All Euler color scheme). Cumulative misorientation maps were generated using the “texture component” feature, in which grains were assigned color gradient corresponding to cumulative misorientation relative to a user-defined location in the grain.

Elements maps were collected via EDX simultaneously with EBSD maps at the same conditions using an XMax SDD 20 mm EDX detector and the AZtec acquisition system. EDX mapping utilized “TruMap” feature in AZtec, in which X-ray spectra for each element K-α map were processed to deconvolve signal from overlapping elemental peaks and removal of X-ray background. The tilted sample relative to the incident electron beam during EDX mapping resulted in an asymmetric activation volume and consequently some “shadowing” artifacts, visible on the lower edges of phase boundaries in the EDX element maps.

ToF-SIMS.

ToF-SIMS was used for high spatial resolution elemental mapping of major and trace components. A Tescan Lyra3 Focused Ion Beam (FIB)-SEM fitted with a ToF-SIMS detector located in the JdLC at Curtin University, Australia, was used for the analyses. The primary ion source was a monoisotopic ⁶⁹Ga⁺ ion beam, and the secondary ions are detected using a compact ToF-SIMS detector made by Tofwerk AG. The detection limit for alkalis using this system is expected to be in the ppm range. The Tescan Lyra3 was also fitted with an Oxford Instruments X-Max 20 mm² detector, which was used for complementary EDS analysis. EDS analysis was performed at 20 kV, and the data were analyzed using the Oxford Instruments AZtec version 3.4 software.

ToF-SIMS Explorer version 1.3 was used to acquire, process, and analyze the ToF-SIMS data. Further details on FIB-ToF-SIMS can be found in ref. 16. In this study, the acquisition was carried out with an ion beam energy and current of 30 kV and 75 pA, respectively. Elemental maps with 1,024 × 1,024 pixels (4 × 4 binning) were collected over square areas between 5 × 5 and 20 × 20 μm, resulting in a pixel resolution between 20 and 80 nm in both x- and y-directions. Collecting the data for 50 frames resulted in an analysis depth of approximately 100 nm. Because a mass spectrum is generated at every pixel in each frame, data were extracted from all or a subset of the full data cube and displayed as an intensity map for a particular ion.

APT.

A needle-shaped specimen was prepared from grain #0010 with the Ga⁺ Tescan Lyra3 FIB-SEM housed in the JdLC. The location of the specimen was precisely determined using an electron-beam deposited Pt marker (16). The final diameter of the specimen apex was approximately 50 nm. The specimen was analyzed with the Geoscience Atom Probe, a Cameca LEAP 4000X HR, at Curtin University. More details about the technique can be found elsewhere (40). The analysis was conducted in laser-assisted mode with a laser energy of 300 pJ, a 200 kHz repetition rate, an automated detection rate of 0.005 ion/pulse, and a base temperature of 70 K. In the mass spectrum, peaks at least twice above the background were identified and reconstructed in 3-dimensions using Cameca’s AP Suite 6 software. Following the recommendations of Fougerouse et al. (41), an average atomic volume of 0.01290 nm³/atom and an electric field value of 34.20 V/nm were used for the spatial reconstruction.

⁴⁰Ar/³⁹Ar Geochronology.

The ⁴⁰Ar/³⁹Ar technique is an improved derivative of the K/Ar method, which is based on the decay of ⁴⁰K to ⁴⁰Ar* with a half-life of ca 1.25 Ga. This technique can be used to date essentially all minerals and rocks that contain potassium. This technique requires that the samples are sent for irradiation in a nuclear reactor. ⁴⁰Ar/³⁹Ar dating allows the derivation of age information from a single analysis of similarly behaving isotopes. This feature enables the degassing of samples in multiple steps by incremental heating (using a laser or furnace). The step-heating degassing procedure allows the construction of age spectra (Fig. 2) and isochron diagrams, both of which present powerful statistical tests of the reproducibility of a sample age. Furthermore, owing to the next generation of noble gas machines such as the ARGUS VI (cf. below), regolith particles can now be analyzed on a single particle basis.

Particle extraction and packaging.

The preparation procedure followed here is similar to the approach used to analyze a set particle #0013 and #0030 and described by Jourdan et al. (13). It is briefly summarized here. The three grains were shipped by JAXA and arrived individually mounted in resin stubs, polished to expose the grain and coated in carbon for the purpose of previous analyses. After the removal of carbon coating (a possible contaminant for ⁴⁰Ar/³⁹Ar analyses) by gently polishing the surface with 0.06 µm colloidal silica-NaOH paste for 4 h, the grains were ready for extraction from the mount material.

We softened the contact bond between the grains and the resin with a drop of acetone and for each particle, we outward-draw a star of scored lines around the mounted grain which would dislodge the particle, enabling the removal of the whole grain without any adhering mount material. The particles were removed from their stubs and transferred on the tip of a probe to the individually prepared copper pits. Grain movement and possible loss were constrained by keeping the grain under a drop of liquid at all times; both on the stub and in the copper pit.

Tiny individual pits with a raised edge were prepared by embossing a small square of pure copper sheeting from behind. These were laid over the center pit of a standard aluminium sample irradiation disc. Three separate hand-cut “washers” of cleaned aluminium foil were placed over the pit after the grain was placed inside, and a cover of flat copper closed the set. The disc was tightly lidded with a flat disc, which created downward pressure on the raised edge of the copper pit, further sealed by the malleable aluminium foil layers. The whole group was wrapped tightly in an aluminium foil.

Irradiation and analytical procedures.

Each disc included a series of Hb3gr hornblende used as a neutron fluence monitor for which an age of 1,081.0 ± 1.0 Ma (1σ) was adopted (42) and a good intergrains reproducibility has been demonstrated (43, 44). The discs were Cd-shielded (to minimize undesirable nuclear interference reactions) and irradiated for 80 h in the TRIGA reactor (Oregon State University, USA), in a central position. The mean J-values computed from standard grains within small pits bracketing the particles yielded a value of 0.02135 (±0.15%). Mass discrimination was monitored regularly through the analysis using an automated air pipette and provided values of 0.99128 (±0.03%) and 0.991272 (±0.02) per dalton (atomic mass unit) relative to an air ratio of 298.56 ± 0.31 (45). The correction factors for interfering isotopes were (³⁹Ar/³⁷Ar)_Ca = 6.95 × 10⁻⁴ (±1.3%), (³⁶Ar/³⁷Ar)_Ca = 2.65 × 10⁻⁴ (±0.83%) measured on CaF₂ and (⁴⁰Ar/³⁹Ar)_K = 7.02 × 10⁻⁴ (±12%) determined on K–Fe glass (46). The most important correction value needed for Ca-rich samples was remeasured internally in 2017 and yielded a value of (³⁶Ar/³⁷Ar)_Ca = 2.65 × 10 ⁻⁴ (±1.6%), in agreement with the value measured by Renne et al. (46).

The ⁴⁰Ar/³⁹Ar analyses were performed at the Western Australian Argon Isotope Facility at Curtin University. Test plagioclase crystals, standards, and the two Itokawa particles were loaded in to a single laser disc. The three particles were step-heated using a continuous 100 W PhotonMachine© CO₂ infrared (10.6 µm) laser fired on the crystals during 60 s, and the gas was purified on a single AP10 for a total of 180 s. Each standard crystal was fused in a single step. The gas was purified in an extra low-volume stainless steel extraction line of 170cc and using one SAES AP10 getter. Ar isotopes were measured in static mode using a low volume (600 cc) ARGUS VI mass spectrometer from Thermofisher© set with a permanent resolution of ~200. Measurements were carried out in peak jumping mode using a very low background compact discrete dynode ion counter supplied with the ARGUS VI and using 10 cycles of peak-hopping and 33 s of integration time for each mass.

The raw data were processed using the ArArCALC software (47), and the ages have been calculated using the decay constants recommended by Renne et al. (42). Blanks were monitored every three to four steps and typical ⁴⁰Ar, ³⁹Ar, and ³⁶Ar blank values of ca. 3.4, 0.015, and 0.011 fA (particle #0288). Relative abundance of Ar isotopic data of the two particles are provided in Dataset S2 and have been corrected for blank, mass discrimination, and radioactive decay. Individual errors in Dataset S2 are given at the 1σ level.

No cosmogenic exposure age calculation could be attempted as the ³⁸Ar_total values remained at, or slightly above, the blank level (i.e., <1.3 fA). Trapped intercept ⁴⁰Ar/³⁶Ar values were tentatively measured using the inverse isochron. For particle #0288, the data defines a very slight spread with an intercept ratio of 1.3 ± 0.5 indistinguishable from the ratio of 1 ± 1 (48) adopted in this study but mostly cluster on the radiogenic x-axis thus preventing (and alleviating the need for) any trap Ar correction for particle #0288. For particle #0059, all data point clustered on the radiogenic axis. Particle #0010 did not yield either a concordant age nor defined a concordant isochron; hence, we applied a correction of 1 ± 1, similarly to the other particles. Note that the data for #0010 are much more scattered than for the two other particles suggesting a heterogeneous trapped component, possibly implanted during the impact event that disturbed the K/Ar system of the particle (49).

Our criteria for the determination of plateau are as follows: plateaus must include at least 70% of ³⁹Ar. The plateau should be distributed over a minimum of three consecutive steps agreeing at 95% confidence level and satisfying a probability of fit (P) of at least 0.05. Plateau ages are given at the 2σ level and are calculated using the mean of all the plateau steps, each weighted by the inverse variance of their individual analytical error. Inverse isochrons include the maximum number of steps with a probability of fit ≥0.05. Uncertainty on the decay constant and age of the monitor are not included in the age calculation but only add ±2 Ma on top of the relatively large uncertainties of ±35 and ±41 Ma obtained for particles #0288 and #0059 [hence full uncertainties are [±37] Ma and [±43] Ma, respectively, as calculated using the Monte Carlo optimization method of Renne et al. (50)].

Supplementary Material

Appendix 01 (PDF)

Dataset S01 (XLSX)

Dataset S02 (XLSX)

Dataset S03 (XLSX)

Data, Materials, and Software Availability

All study data are included in the article and/or SI Appendix.