Computational Optimization of Notch Spacing for a Transnasal Ear Endoscopy Continuum Robot

Abstract

This paper presents a computational framework to optimize the visual coverage attainable by a notched-tube continuum robotic endoscope inside the middle ear cavity. Our framework combines anatomically-accurate geometric (mesh) models of the middle ear with a sampling-based motion planning algorithm (RRT) and a ray-casting procedure to quantify what regions of the middle ear can be accessed and visualized by the endoscope. To demonstrate the use of this framework, we run computer simulations to investigate the effect of varying the distance between each pair of consecutive flexure elements (i.e., notches) in our robotic endoscope.

I. Introduction

Middle ear surgery is one of the most commonly performed surgical procedures in the United States, with the annual case volume in excess of 130,000 surgeries [1]. The challenges faced by physicians during middle ear surgery are manifold: difficult access and inadequate visualization [2], proximity to vital structures [3], and significant anatomical variability [4], [5] are some of the issues commonly reported in the medical literature. In the last decade, these challenges have motivated several research groups to investigate the benefits of robotic technology in the surgical care of the ear [6]. Miroir et al. [7], [8] created a teleoperated system called RobOtol which deploys surgical tools into the middle ear using a minimally-invasive approach, i.e., via the external ear canal (path marked as EAC in Fig. 1). Yasin et al. [9] further expanded on this concept, and built a robot equipped with a distal steerable cannula that offers a larger reachable workspace, enabling access to regions of the middle ear cavity that would normally be challenging to reach. A different way to access the middle ear is through a mastoidectomy where the bone behind the ear is drilled away. Dillon et al. [10] created an image-guided robot for mastoidectomy and showed that this robot can perform mastoidectomy more rapidly than a human surgeon (potentially saving precious operating room time) while at the same time ensuring the preservation of nearby vital anatomy (e.g., the carotid artery and the facial nerve) [11], [12]. Recently, a team led by Weber and Caversaccio published the first-ever clinical case report on the use of an image-guided robotic system for minimally-invasive cochlear implantation [13], [14], where access is provided by a thin channel drilled through the mastoid bone, rather than a traditional mastoidectomy.

Fig. 1.

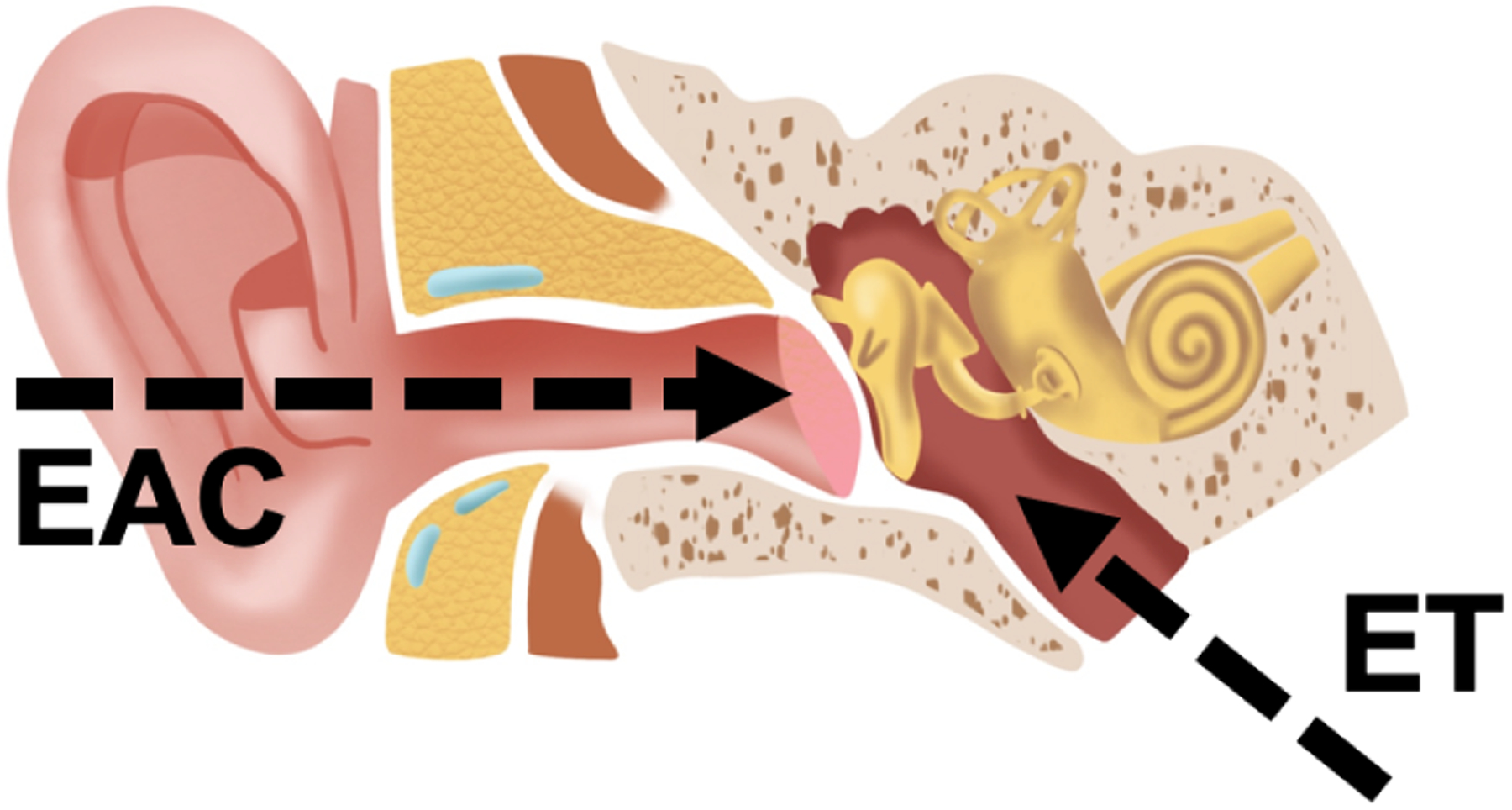
Anatomy of the human ear. Two natural orifices provide access to the middle ear cavity: the external ear canal (EAC) and the Eustachian tube (ET). To access the middle ear from the EAC, surgeons have to cut or lift the tympanic membrane. By contrast, accessing the middle ear by way of the ET does not require the disruption of any tissue.

The above results illustrate the potential of surgical robotics in middle ear surgery. The combination of robotic instrumentation and image guidance has enabled progressively less invasive access to the middle ear and the structures located therein. However, a perhaps even less invasive access path exists to the middle ear. The Eustachian tube presents a natural orifice that, in principle, could be used to pass instrumentation into the middle ear without having to disrupt any tissue at all. The Eustachian tube (marked as ET in Fig. 1) connects the ear to the nasal cavity. In recent work [15], our research group demonstrated proof-of-principle of a miniature continuum robotic endoscope capable of visualizing the middle ear from the Eustachian tube. The concept of our device is shown in Fig. 2: it consists of a digital chip-tip camera installed inside a notched steerable sheath made of superelastic Nickel-titanium (Nitinol). One of the applications that motivated the creation of this device is the surveillance of cholesteatoma, a type of benign cyst which affects approximately 10 in 100,000 adults every year [16], and which is responsible for hearing loss [17] and a variety of infections [18]. We experimentally validated our robotic endoscope by deploying it into a 3D-printed ear model. Using computer graphics techniques (ray casting), we found the endoscope to enable a 74% visual coverage of the sinus tympani, a sub-region of the middle ear where cholesteatoma is often found [19].

Fig. 2.

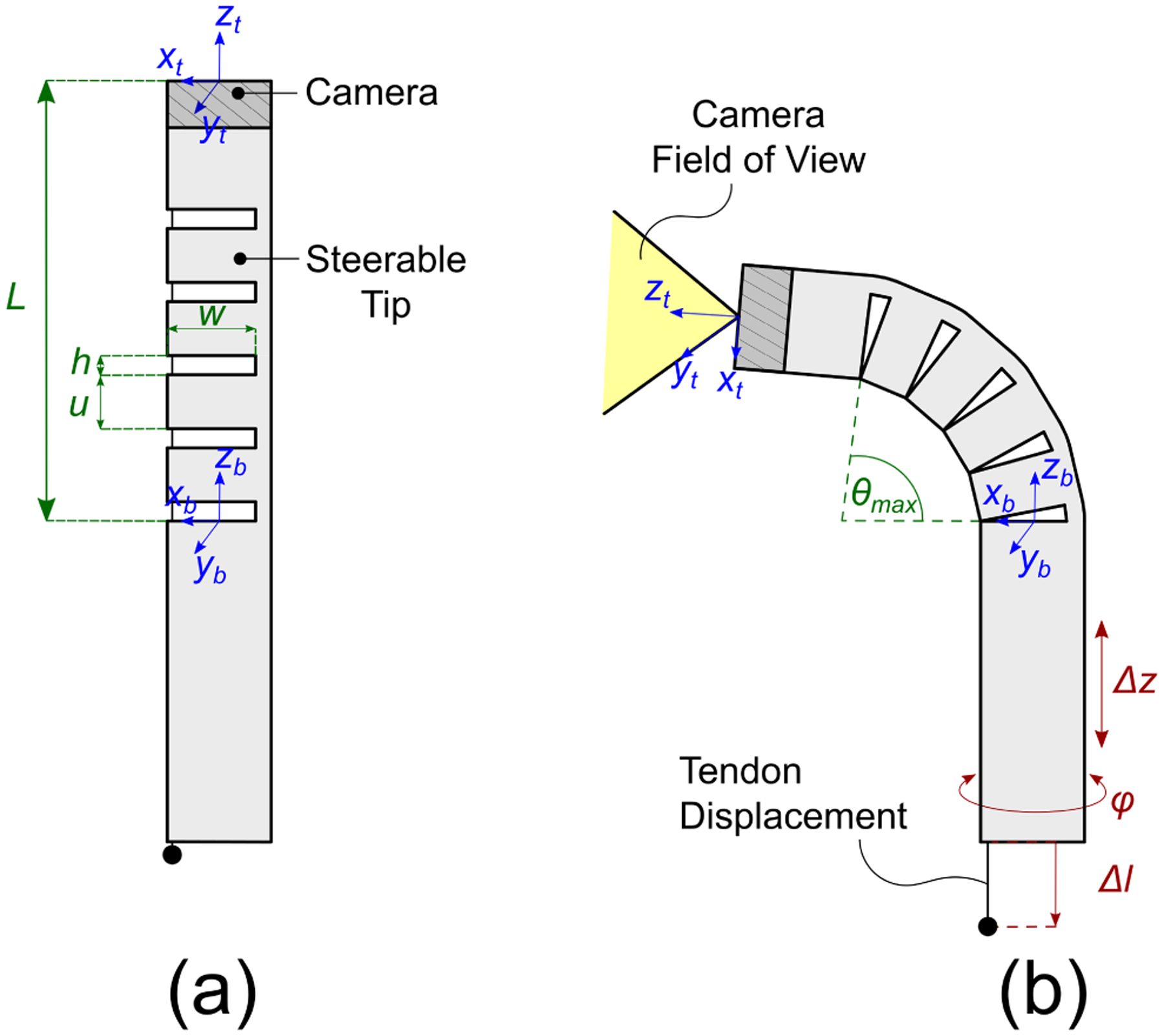
Robotic endoscope concept: a digital chip-tip camera is installed at the tip of a Nickel-Titanium (Nitinol) tube. Asymmetric notches are cut in the body of the tube, creating a compliant section that can be articulated by pulling a single tendon attached at the tip of the robot. (a) Robot in its base ”straight” configuration; the design parameters of the notched section include the number of notches n, the notch height h, the notch width w, and the spacing u between each pair of notches; (b) The robot is equipped with a total of three degrees of freedom, namely axial translation (Δz), axial rotation (φ) and tendon displacement (Δl).

In this paper, we extend our prior research by investigating the optimization of the endoscope’s geometric design. We focus our attention on the design parameters of the endoscope steerable section (these parameters include, among others, the number, height, and width of the notches that provide articulation) and investigate the following questions: (1) Does varying the design parameters (and thus the way in which the endoscope articulates) have an effect on the endoscope’s ability to visualize the middle ear cavity? (2) Is there a combination of design parameters that affords a higher visual coverage in specific parts of the ear (e.g., the sinus tympani)? We investigate these questions in simulation, and establish a general method that can be used to optimize the design of notched-tube continuum robotic endoscopes. The results of this optimization work will enable the design of noninvasive trans-Eustachian endoscopic systems that provide comprehensive, high-quality visual coverage of the middle ear.

II. Problem Formulation

Our continuum robotic endoscope consists of a 1.4 mm digital chip-tip camera (minnieScope-XS, Enable Inc., Redwood City, CA) installed inside a steerable Nickel-Titanium (Nitinol) sheath. This device was custom-made in collaboration with Enable; the slotted Nitinol was used to replace the standard outer sheath on the minnieScope. The camera has a resolution of 400×400 pixels (boosted to 1 Megapixel in software via linear interpolation) and a field of view of 90°. Tip deflection in our robot is enabled by means of a tendon-actuated bending mechanism [20], [21]: a number of asymmetric notches are cut in the body of the endoscope’s Nitinol sheath as shown in Fig. 2 and 3. Removing material from the tube in this manner offsets the neutral bending axis of the tube and enables bending of the entire structure with a single pull-wire. The kinematics of this mechanism will be briefly reviewed later in this section.

Fig. 3.

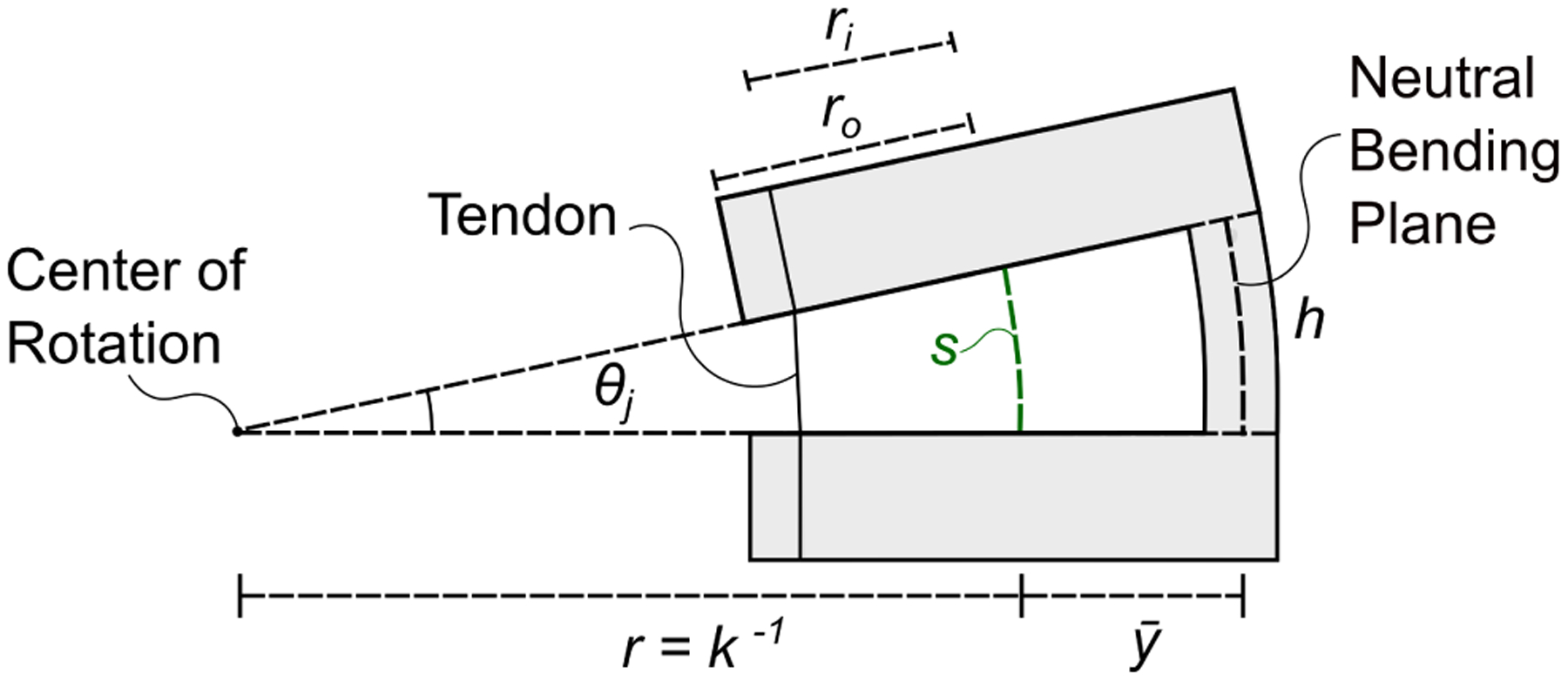
Close-up view of a single notch. Cutting asymmetric notches offsets the neutral bending plane of the tube, i.e. the plane which experiences no strain during bending, which is now located at a distance $\overline{y}$ from the center line of the tube. The value of $\overline{y}$ can be calculated using the equations in [20], [21]. Applying a tensile force on the tendon makes the notch bend in the shape of a constant-curvature arc characterized by an arc length s and a curvature κ. Another important geometric characteristic of a notch is the height h (which in this figure is measured by the neutral bending axis). Finally, r_o and r_i are the outer and inner radius of the Nitinol tube.

A. Design Space

We can represent the design of our robotic endoscope with a 6-dimensional vector d = [r_i r_o w h u n], where n is the total number of notches, u represents the spacing between consecutive notches, h and w are the height and width of the notches, and r_i and r_o are the inner and outer radius of the Nitinol sheath (refer to Figs. 2 and 3). We define the set of all kinematic designs vectors d as $𝒟\subset {ℝ}^6$. Our goal is to explore 𝒟 in search of a combination of design parameters that maximizes the endoscope’s visual coverage of the middle ear. To this aim, we generate multiple design vectors d_i and quantitatively estimate the visual coverage that each design is able to afford in simulation, using the methods described below.

B. Configuration Space and Kinematic Modeling

Our robotic endoscope is equipped with three degrees of freedom, which are illustrated in Fig. 2: these include the axial rotation φ, the linear translation Δz, and the tendon displacement Δl. Let us define the robot configuration as a vector $q\in 𝒬\subset {ℝ}^3$ containing φ, Δz, and Δl. The forward kinematics of the robot is then a function f that takes a design vector d and a configuration vector q and returns the resulting robot pose, i.e. f: (𝒟×𝒬) → SE(3), where SE(3) denotes the Special Euclidean group in 3 dimensions. In the following, we provide an overview of the robot’s forward kinematics. The articulation mechanism used in our robot was first proposed by York and Swaney [20], [21], and for a full derivation of the kinematics the reader is referred to these publications.

To formulate the forward kinematics, it is convenient to model the steerable section of the endoscope as a chain of interleaving notches and uncut tube sections, having length h and u respectively (refer to Fig. 2). For the i^th uncut section, we assume rigidity, so the transformation matrix consists of a simple translation of length u along the z axis:

$$T_{\text{transl }}(u)=e^{\widehat{\zeta }u}\text{, where }\zeta ={\left[\begin{array}{c}001000\end{array}\right]}^{\text{T}}$$ (1)

The operator ^ in Eq.(1) maps twists from ${ℝ}^6$ to elements of se(3) (i.e. the Lie Algebra of the special Euclidean group SE(3)). For the notched sections, we follow the same approach used in [20], [21] and assume bending in the shape of a constant curvature arc. The corresponding transformation for the i^th notched section can be expressed in terms of the arc curvature κ and length s:

$$T_{\text{curv }}(\kappa ,s)=e^{{\widehat{\xi }}_s}\text{, where }\xi ={\left[\begin{array}{c}0010\kappa 0\end{array}\right]}^{\text{T}}\text{. }$$ (2)

The arc parameters κ and s depend on the tendon displacement Δl, as it was shown by York et al. [21]:

$$\kappa \approx \frac{l}{h\left(r_i+\overline{y}\right)-l\overline{y}},s=\frac{h}{1+\overline{y}\kappa }$$ (3)

where r_i is the inner diameter of the tube, and $\overline{y}$ is the location of the neutral bending plane of the notch with respect to the centerline of the tube. The value of $\overline{y}$ can be calculated using the equations in [20], [21]. The transformation between the base of the steering section and the tip of the robot is then given by:

$$T_{\mathrm{b}}^{\text{t}}(\kappa ,s,u)=\prod _{i=1}^n{T}_{\text{curv}}(\kappa ,s)T_{\text{transl}}(u).$$ (4)

Finally, we account for the rotation φ and the translation Δz and calculate the forward kinematics for the entire robot as follows:

$$T_{\text{robot}}(d,q)=T_{\text{transl}}(\Delta z)T_{\text{rotz}}(\phi )T_{\mathrm{b}}^{\text{t}}(\kappa ,s,u)$$ (5)

where T_transl(Δz) and T_rotz(φ) represent a translation of length Δz, and a rotation φ, respectively along and about the z_b axis (as defined in Fig. 2).

Two important characteristics that capture the endoscope ability to reach distant locations and articulate around corners are the maximum bending angle θ_max (Fig. 2(b)) and the steerable section length L (Fig. 2(a)). From simple geometry, θ_max and L can be calculated as

$${\theta }_{\mathit{\text{max}}}=n\frac{h}{r_o+\overline{y}},L=n(h+u).$$ (6)

Later in this section, we will use these two quantities to guide the exploration of the endoscope design space 𝒟.

C. Visible Surface Estimation

To quantify the visual coverage afforded by an endoscope design d, we implemented the simulation illustrated in Fig. 4. A virtual model of the endoscope is passed into geometric (mesh) models of the middle ear generated from the Computed Tomography (CT) scan of real patients. These anatomical models were created in prior studies [22].

Fig. 4.

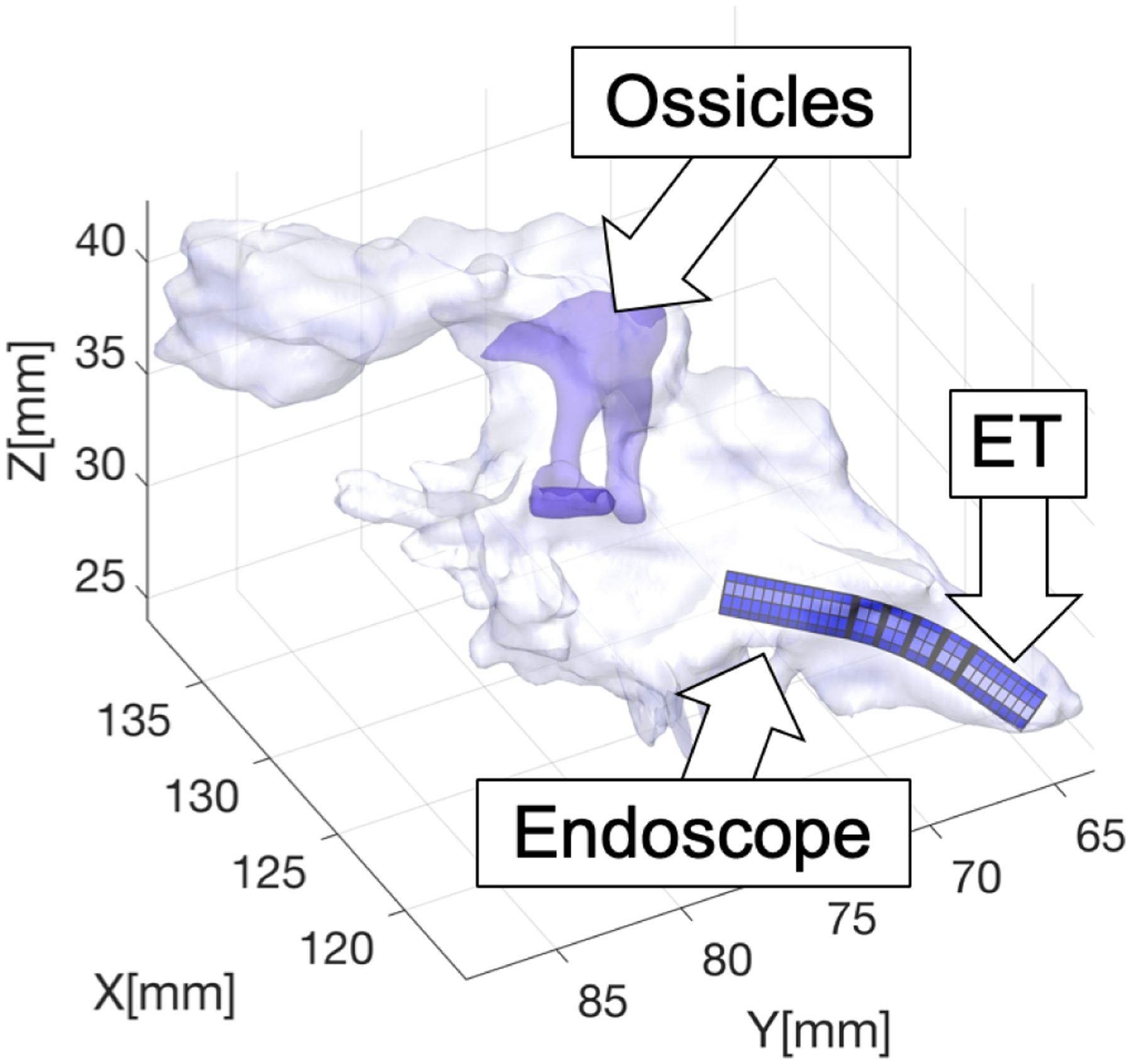
Simulation of trans-Eustachian middle ear endoscopy.

The estimation of the visual coverage is carried out in two steps. In the first step we estimate the reachable volume of the robot: inspired by the approach in [23], we run a sampling-based motion planning algorithm, i.e. Rapidly-Exploring Random Trees (RRT) [24], to let the robot explore the middle ear cavity. Starting from an initial configuration q₀, where the scope is aligned with the Eustachian tube and positioned at the entrance of the ET isthmus, RRT incrementally builds a tree of configurations that the endoscope can reach within the middle ear in a collision-free path. The RRT algorithm is known to have probabilistic completeness, which is a useful property for our study: it implies that the longer the algorithm runs for, the higher the likelihood of discovering the entire reachable workspace of the endoscope is. A ray-triangle intersection algorithm is used to detect collisions between the endoscope and either the walls of the middle ear cavity or the ossicles (the chain of bones responsible for transmission of the sound from the tympanic membrane to the cochlea - see Fig. 4), and any configuration found to collide is discarded from the tree. A video showing this RRT-based exploration of the middle ear is available at https://www.youtube.com/watch?v=n4jSRGHOdwY.

Once the set of reachable configurations has been generated, we use the forward kinematics model described earlier in section II-B, to map every configuration q into the corresponding homogeneous transformation matrix

$$T_{\text{robot}}(d,q)=\left[\begin{array}{cccc}{x}_t& y_t& z_t& p\\ 0& 0& 0& 1\end{array}\right]$$

where p is the location of the tip of the robot, and x_t, y_t, z_t represent the orientation of the robot (refer to Fig. 2). We then run a ray-casting procedure from point p to detect which parts of the middle ear mesh are visible. Rays are cast towards all of the vertices in ear mesh, and mesh triangles whose vertices are all visible (i.e. whose view is not occluded by any obstacle) are marked as visible. To simulate the 90° field of view of the minnieScope, we impose the condition that the angle between any ray and the endoscope approach vector z_t must not exceed 45 degrees. Sample visibility maps calculated with this approach are shown later in this paper (Fig. 7).

Fig. 7.

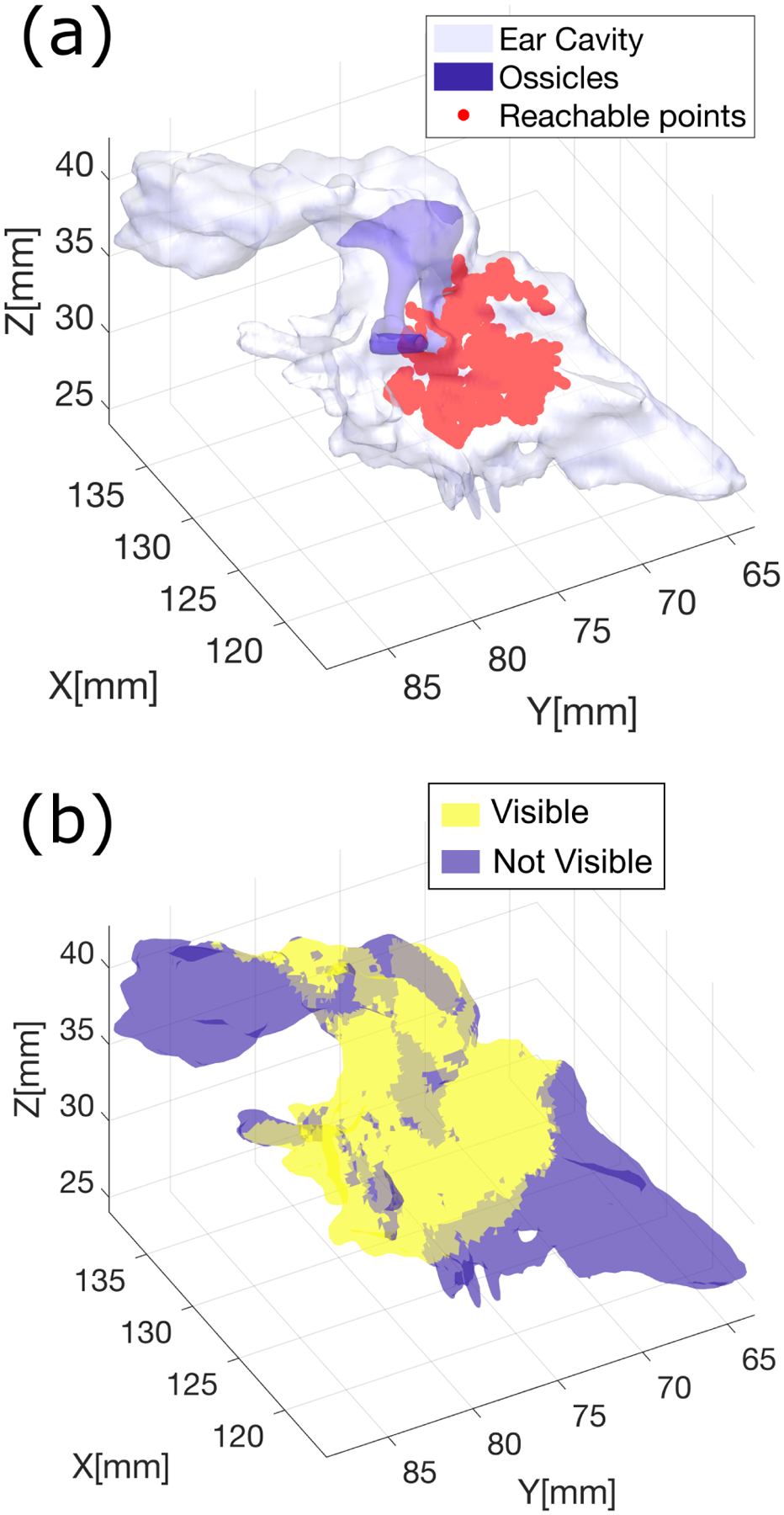
Visual coverage estimation: (a) Reachable points calculated via RRT; (b) Map showing visible regions within the ear.

D. Constraining the Design Space

Having introduced the methodology to estimate the visual coverage, we now focus on the design optimization problem. To reiterate, our goal is to explore the space of kinematic designs 𝒟 in search of a combination of design parameters d that maximizes the endoscope’s visual coverage inside the middle ear. A challenge is that the design space 𝒟 contains redundant solutions: with reference to Eq. 6, the same robot length L and maximum bending angle θ_max could in principle be achieved with different combinations of the design parameters. It is therefore convenient to constrain our search by making practical considerations on the choice of the design parameters.

1). Inner and outer radius (r_i and r_o):

Because our robot passes through the Eustachian tube, the outer diameter can only be as large as the maximum permissible diameter to transit the Eustachian tube, which prior studies have shown to be approximately 2 mm [25]. On the other hand, the inner diameter of the Nitinol sheath must be large enough to permit the installation of the digital chip-tip camera. Without loss of generality, in this paper we set the outer and inner diameter to be 1.60 mm and 1.40 mm, respectively, which implies r_i = 0.7 mm and r_o = 0.8 mm.

2). Notch width (w):

The choice of the notch width w determines the amount of tendon pulling force necessary to bend the instrument: intuitively, the wider the notches are, the more compliant the steering section will be, and the less actuation force will be required to bend the endoscope. A full statics analysis for the bending mechanism is available in [20], [21], [26]. Another aspect to consider for the selection of w is the amount of strain that the remaining material in the notches will be subject to during bending: such a value should not exceed the maximum recoverable strain of Nitinol (which is typically quoted around 8%), otherwise plastic deformation will occur. Typical values for w range between 80 – 90% of the tube’s outer diameter 2r_o [20], [21], [26]. Here we select w = 1.40 mm.

3). Number of notches (n), Notch Height (h), and Spacing (u):

From Eq. 6, n, h, and u all influence the maximum attainable bending angle θ_max and the robot length L. If we impose a desired maximum bending angle θ_max, we can derive a formulation for the notch height h:

$$h={\theta }_{\mathit{\text{max}}}\frac{\left(r_o+\overline{y}\right)}{n}$$ (8)

Similarly, if we impose a given endoscope length L we can solve Eq. 6 for u:

$$u=\frac{L}{n}-h$$ (9)

The two equations above still present a free parameter, i.e. the number of notches n. With θ_max and L now constrained, this parameter becomes a measure of how closely the endoscope bends in the shape of a constant curvature arc. This is visually explained in Fig. 5, where we solve the kinematics of the robot steering section (Eq. 4) for increasing values of n. In principle, a large number of notches would be desirable: as n increases, the notch height h decreases, thus reducing the risk of notch buckling during bending, and potentially increasing the longevity of the endoscope. In practice, there is a limit to how small the notches can be cut, as this depends on limitations of the fabrication technology. Femto-second laser cutters exist that can cut Nitinol with spot sizes as small as 0.021 mm [27].

Fig. 5.

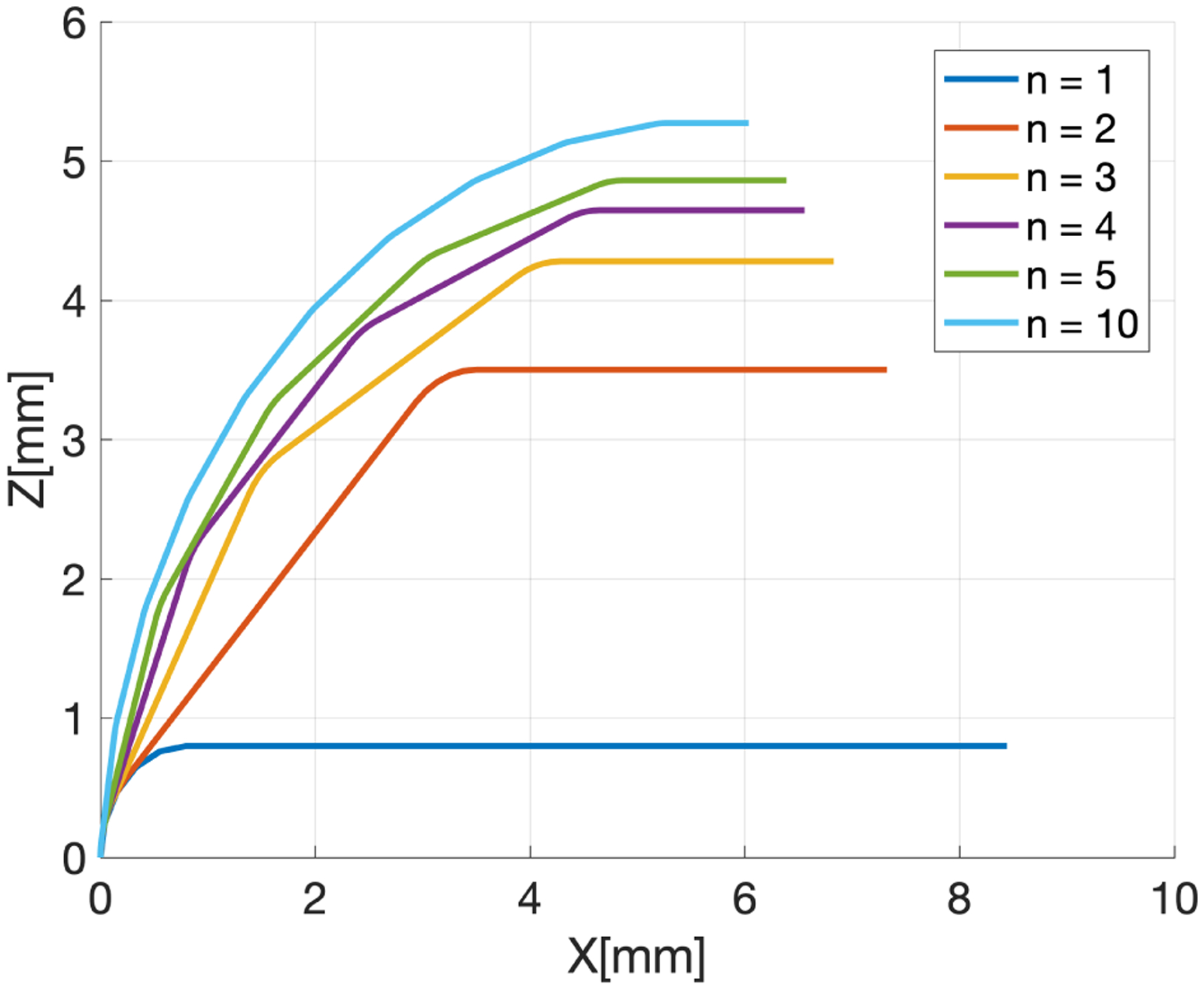
Effect of the number of notches n on the endoscope bending. The different lines represent the backbone of the endoscope at full bending. No rotation is applied, therefore bending occurs entirely in the XZ plane. The straight sections have length u, while the flexure elements have length s (Eq. 3). To generate these lines, we imposed θ_max = 90° and L = 10 mm.

III. Understanding the Effects of Notch Spacing

We performed simulations to investigate the effects of varying the notch spacing u on the endoscope visual coverage of the middle ear. Increasing the spacing between the notches creates longer steerable sections L, which is expected to enhance the endoscope ability to reach deeper into the middle ear. At the same time, having the notches too far apart from each other could make the endoscope unable to bend in tight radii, potentially impairing visualization in certain regions of the middle ear.

In our simulations, we tested seven different endoscope designs, which were synthesized as follows: we first arbitrarily set the desired maximum bending angle θ_max to 90°, and the number of notches n equal to 5. This resulted in a notch height h = 0.47 mm. We then used the Eq. 9 to generate designs with increasing lengths L, varying between 3 mm and 15 mm. Corresponding values of the notch spacing u are summarized in Table I.

TABLE I.

Endoscope Lengths tested In simulation and corresponding Notch Spacing

	Robot Steering Section Length (mm)
	3	5	7	9	11	13	15
Notch Spacing u (mm)	0.13	0.53	0.93	1.30	1.70	2.10	2.50

To estimate the visual coverage afforded by each design in our simulations, we use the same set of geometric ear models described in [22]. This is a collection of six models generated from Computed Tomography (CT) scans of real patients treated at Vanderbilt University Medical Center. These ear models were segmented using a semi-automatic procedure to highlight different sub-regions (Fig. 6). The use of these models enables us to understand the visibility of specific sub-regions. In each simulation, we generated a total of 5,000 reachable configurations and then calculated the reachable surface.

Fig. 6.

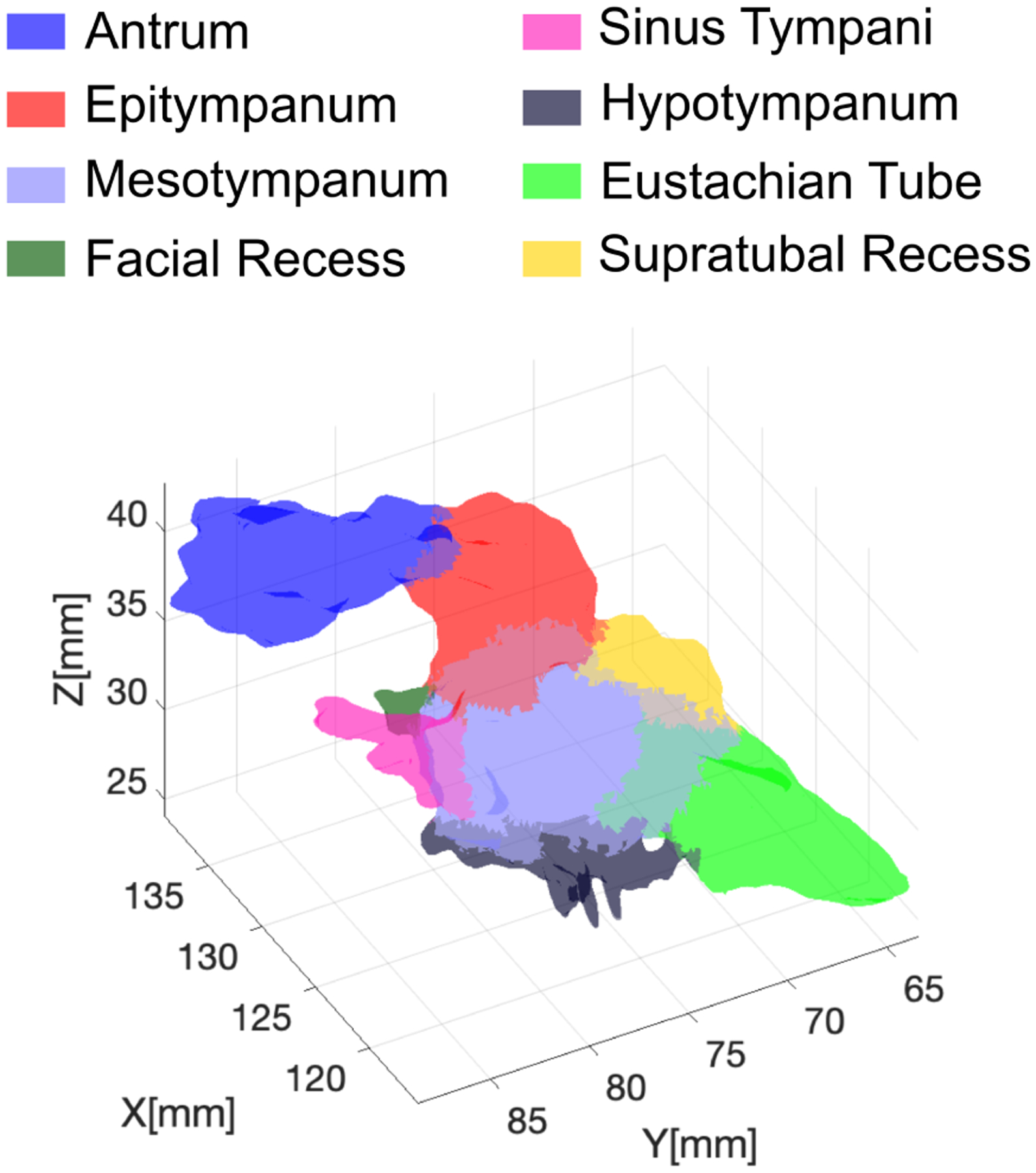
Geometric model of the ear highlighting different anatomical sub-regions.

Simulations were run in MATLAB, on a machine equipped with an Intel Xeon E5–2683 CPU (2.10 GHz) and 256 GB of RAM. To speed up the simulation runtime, multiple simulations were run in parallel using the MATLAB Parallel Computing Toolbox.

IV. Results

Sample reachable points and visual coverage estimation maps are shown in Fig. 7. Simulation results for each ear model are summarized in Fig. 8. With the exception of Patient 2, increasing the notch spacing (and, thus, the endoscope steerable section length) was found to produce an increase in the visual coverage of the sinus tympani in all considered ear models. The average visual coverage of the sinus tympani increased from 62.4% (with a 3 mm steering section length) to 72.3% (with a 15 mm steering section length). Placing notches closer to each other enhances the scope ability to visualize the supratubal recess and the hypotympanum. The visual coverage of the hypotympanum, in particular, degrades markedly as the spacing between the notches increases, moving from an average of 77.7% to 28.8%.

Fig. 8.

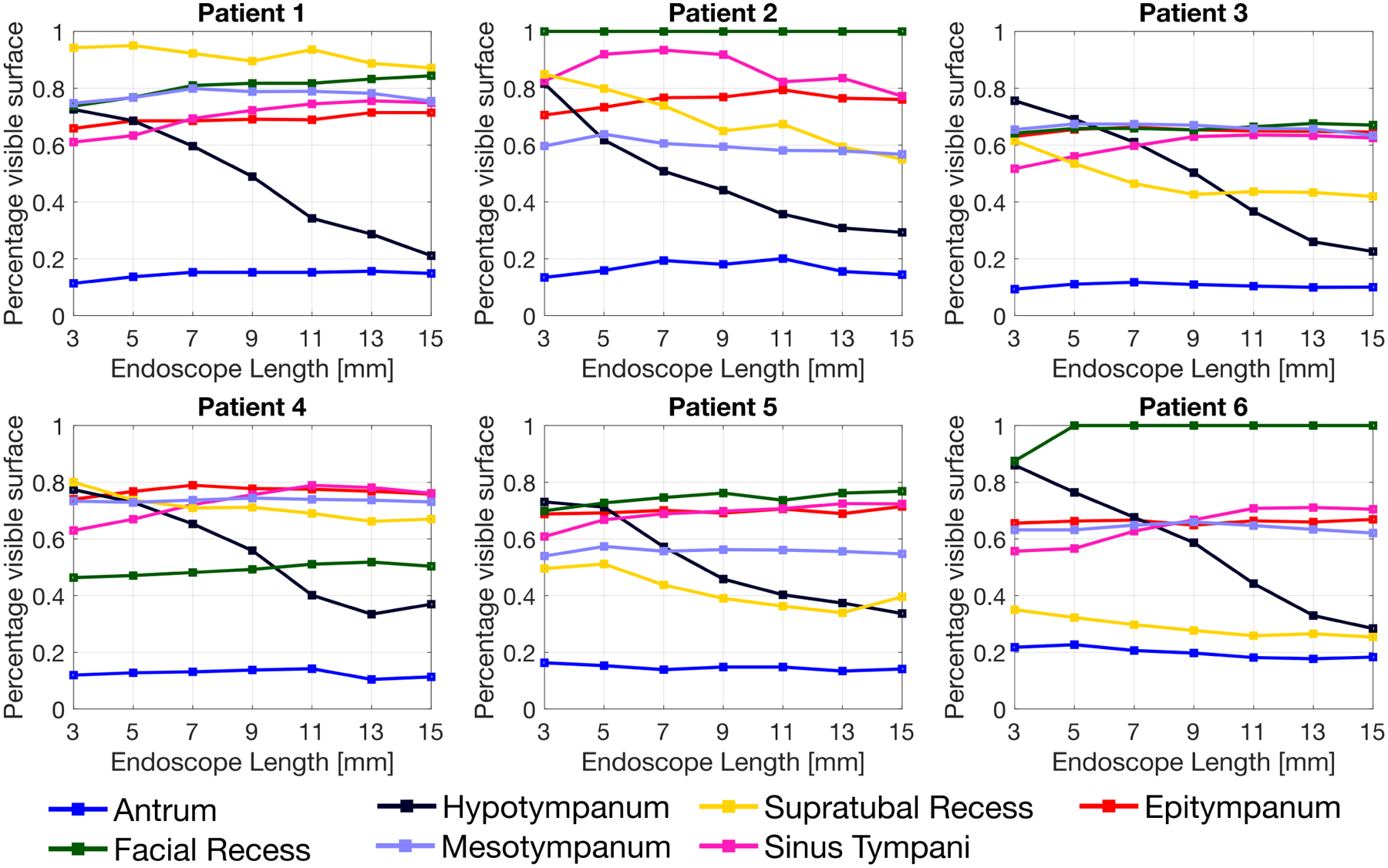
Simulation results. The visual coverage achieved by the endoscope in any given anatomical region is expressed as a percentage of the total surface in that region.

V. Discussion and Conclusion

Accessing the middle ear by way of the nose and the natural orifice of the Eustachian tube has the potential to transform the management of many middle ear diseases by eliminating the need for invasive surgical access. In prior research, we have demonstrated the technical feasibility of building a steerable endoscope small enough to pass through the Eustachian tube [15]. The results presented in this study quantify, for the first time, how much of each sub-region of the middle ear could be visualized by a steerable endoscope passed through the Eustachian tube.

In this paper, we formalized the problem of optimizing the endoscope kinematic design with the overarching goal of maximizing visual coverage inside the middle ear. As an initial step in our investigation, we studied how altering the notch spacing affects the ability of the endoscope to visualize different sub-regions of the middle ear. Other design parameters, including the notch heigth h and the total number of notches n (refer to section II-D.3 and Fig. 2) were selected arbitrarily and kept constant. A sensitivity analysis on these parameters will be the subject of future studies.

Simulation results suggest that varying the notch spacing may have a significant effect on what areas of the middle ear can be visualized, and that different endoscope designs should be considered based on the target anatomy. One area of particular interest is the sinus tympani, because of its tendency to host diseases hard to detect, including cholesteatoma [19]. The sinus tympani is among the most distant locations to reach from the Eustachian tube orifice, and it seems to benefit from the use of endoscope designs with longer steerable sections. This was observed to be true in all considered ear models with the exception of Patient 2. Visual inspection of the ear model for this patient revealed a peculiar morphology of the sinus tympani, to which the discrepancy in the results could be attributed. Prior research by Marchioni et al. [4] has analyzed the anatomical variations of the sinus tympani in a large patient cohort, and identified three main classes of sinus tympani morphology. This anatomical knowledge, combined with the framework presented in this study, opens up the possibility of generating endoscope designs that are optimal for specific classes of patients. In the future, we plan to apply the framework developed in this paper to a larger set of ear geometric ear models [28], with the goal of synthesizing morphology-specific endoscope designs.