Exploring the Limits of Second- and Third-Order Møller-Plesset Perturbation Theory for Non-Covalent Interactions: Revisiting MP2.5 and Assessing the Importance of Regularization and Reference Orbitals

Abstract

This work systematically assesses the influence of reference orbitals, regularization and scaling on the performance of second- and third-order Møller-Plesset perturbation theory wavefunction methods for non-covalent interactions (NCI). Testing on 19 data sets (A24, DS14, HB15, HSG, S22, X40, HW30, NC15, S66, AlkBind12, CO2Nitrogen16, HB49, Ionic43, TA13, XB18, Bauza30, CT20, XB51 and Orel26rad) covers a wide range of different NCI including hydrogen bonding, dispersion, and halogen bonding. Inclusion of potential energy surfaces from different hydrogen bonds and dispersion-bound complexes gauges accuracy for non-equilibrium geometries. 15 methods are tested. In notation where nonstandard choices of orbitals are denoted as method:orbitals, these are MP2, κ-MP2, SCS-MP2, OOMP2, κ-OOMP2, MP3, MP2.5, MP3:OOMP2, MP2.5:OOMP2, MP3:κ-OOMP2, MP2.5:κ-OOMP2, and κ-MP3:κ-OOMP2, κ-MP2.5:κ-OOMP2, MP3:ωB97X-V, and MP2.5:ωB97X-V. Furthermore, we compare these methods to the ωB97M-V and B3LYP-D3 density functionals as well as CCSD. We find that the κ-regularization (κ = 1.45 a.u. was used throughout) improves the energetics in almost all data sets for both MP2 (in 17 out of 19 data sets) and OOMP2 (16 out of 19). The improvement is significant (e.g. the RMSD for the S66 data set is 0.29 kcal/mol for κ-OOMP2, versus 0.67 kcal/mol for MP2), and for interactions between stable closed shell molecules, not strongly dependent on the reference orbitals. Scaled MP3 (with a factor of 0.5) using κ-OOMP2 reference orbitals (MP2.5:κ-OOMP2) provides significantly more accurate results for NCIs across all data sets with non-iterative 𝒪(N⁶) scaling (S66 data set RMSD: 0.10 kcal/mol). Across the entire data set of 356 points, the improvement over standard MP2.5 is approximately a factor of two: RMSD for MP3:κ-OOMP2 is 0.25 kcal/mol vs 0.50 kcal/mol for MP2.5. The use of high-quality density functional reference orbitals (ωB97X-V) also significantly improves the results of MP2.5 for NCI over a Hartree-Fock orbital reference. All our assessments and conclusions are based on the use of the medium-sized aug-cc-pVTZ basis to yield results that are directly compared against complete basis set limit reference values.

Graphical Abstract:

1. Introduction

Non-covalent intermolecular interactions (NCI) are important in many areas of chemistry ranging from catalysis to the structure of biological macromolecules.^1–9 For example, the network of hydrogen bonds and hydrophobic effects play a crucial role in the transmission rate of the highly contagious SARS-CoV-2 virus.¹⁰ Electron correlation is essential for an accurate description of NCI.^11,12 Dispersion is a type of NCI which is purely driven by electron-electron correlation as it is a long-range dynamic correlation effect with a well-known asymptotic behavior of 1/R⁶ where R is the distance between two fragments. Consequently, mean field methods like Hartree-Fock or approximate exchange correlation functionals within the Kohn-Sham density functional theory (KS-DFT) framework do not incorporate this effect unless an (empirical) correction term is applied.^13–16 or a Van der Waals functional such as VV10¹⁷ is included. Due to its highly accurate correlation treatment, coupled cluster theory with single, double, and perturbative triple excitations [CCSD(T)] is considered the “gold standard” for describing NCI.^12,18 Unfortunately, this method exhibits a steep computational scaling ($𝒪\left(N^7\right)$, where N is the system size) and thus its canonical implementation is limited to small systems. Reduced scaling CCSD(T) methods are very promising but require care to ensure adequate numerical precision.^19–21

Therefore, alternative methods are desirable to treat larger systems with a lower scaling and ideally similar accuracy. Perturbation theory (PT) based methods such as second-order Møller-Plesset perturbation theory (MP2) can be employed with a $𝒪\left(N^5\right)$ scaling. However, conventional MP2 is known to overbind dispersion-dominated interactions^18,22–24 and modifications to MP2 have been explored.^24–28

The first approach is to improve the reference orbitals used in MP2; instead of using Hartree-Fock (HF) orbitals, the MP2 energy can be determined via a self-consistent-field (SCF) procedure which includes the MP2 correlation energy yielding orbital-optimized MP2 (OOMP2) methods.^29–31 For systems where the unrestricted HF (UHF) reference exhibits spin-contamination (artificial spin-symmetry breaking), its use as a reference determinant can lead to poor performance of MP2.^32–35 Orbital optimization at the MP2 level often reduces the degree of spin-contamination and improves energetics.^29,30,36 Despite the benefits of OOMP2 described above, it is not without its own pitfalls. Orbital optimization of the MP2 correlation functional can produce divergent energy contributions as the orbital energy difference denominator approaches zero. Overstabilization of bond-stretched configurations by OOMP2 leads to significant underestimation of harmonic vibrational frequencies.³⁷ OOMP2 also has difficulty transitioning smoothly from a spin-restricted (ROOMP2) to a spin-unrestricted (UOOMP2) solution via a Coulson-Fischer point, further limiting its applicability for bond-breaking.^38,39

Recently our group has explored regularization of the MP2 correlation energy to prevent its divergence at zero gap via a κ-regularizer.⁴⁰ The resulting methods, κ-MP2 and κ-OOMP2, use the following modified form of the MP2 correlation energy:

$$E_{\kappa -\text{MP}2}(\kappa )=-\frac{1}{4}\sum _{ijab}\frac{|\langle ij\Vert ab;{|}^2}{{\mathrm{\Delta }}_{ij}^{ab}}{\left(1-e^{-\kappa ({\mathrm{\Delta }}_{ij}^{ab})}\right)}^2.$$ (1)

where i and j are occupied orbital indices, a and b are unoccupied orbital indices, ⟨ij||ab⟩ is an element of the two-electron repulsion integral, and ${\mathrm{\Delta }}_{ij}^{ab}$ is the orbital energy gap associated with orbitals i, j, a, b. The unregularized energy expression is recovered for large energy denominators while terms in the sum with small energy denominators are attenuated. The empirical κ parameter was trained for κ-OOMP2 on the TAE140 subset of the W4-11 set.⁴¹ An optimized value of $\kappa =1.45E_h^{-1}$ was shown to provide excellent results upon further testing on overall W4-11, RSE43,⁴² and TA13⁴³ sets. With this, κ-OOMP2 is fit to replace OOMP2 for general application. Complex restricted (cR) and complex general (cG) orbital extensions of κ-OOMP2 have also been developed.^44,45

The second approach is scaling or attenuated parts of the correlation energy: spin-component-scaled MP2 (SCS-MP2)^25,46–50 and orbital optimized SCS-MP2 (SCS-OOMP2)^29,30 methods, which weight correlation contributions coming from same-spin and opposite-spin pairs of electrons differently. These techniques have also been applied to the second-order correlation contribution in several double-hybrid density functionals.^51–55 However, different scaling parameters are necessary depending on the type of interaction (e.g. NCI) vs thermochemistry (TC).⁴⁹ Ochsenfeld and coworkers recently showed that MP2-F12 can yield good results for NCI when omitting expensive terms and re-scaling the remaining components allowing an efficient calculation of large systems.⁵⁶ Another set of approaches are the attenuated MP2 methods that partially cancel basis set superposition errors with errors in MP2 itself to yield improved intermolecular interaction energies in finite basis sets.^26–28,57

Lastly, for further improvements, one may include the third-order terms in the MP perturbative expansion (MP3) which have the following correlation energy expression:

$$E_{\text{MP}3}=\frac{1}{8}\sum _{ijabcd}{(t_{ij}^{ab})}^{*}\langle ab\Vert cd\rangle t_{ij}^{cd}+\frac{1}{8}\sum _{ijklab}{(t_{ij}^{ab})}^{*}\langle kl\Vert ij\rangle t_{kl}^{ab}-\sum _{ijkabc}{(t_{ij}^{ab})}^{*}\langle kb\Vert ic\rangle t_{kj}^{ac}.$$ (2)

Despite its higher computational cost $\left(𝒪\left(N^6\right)\right)$ compared to MP2, MP3 offers only a modest if any improvement over MP2 results. Specifically for weak NCI, MP3 does not improve the MP2 results.^{46,49,58–62} However, Hobza and coworkers^60–62 suggested scaling the third-order correlation energy to interpolate between MP2 and MP3, e.g. MP2.5. These methods substantially improve binding energies for NCI and can even be used for radical systems.⁶³ Bozkaya and coworkers^36,64–67 developed OOMP3 and OOMP2.5 and evaluated the performance of these methods on thermochemistry, kinetics, and NCI. OOMP2.5 was shown to outperform coupled cluster theory with single and double excitations (CCSD)^68,69 on reaction energies and barrier heights³⁶ and perform comparably to CCSD(T)⁷⁰ for NCI.⁶⁶ These results motivated recent work in our group, where we developed an MP3 method using reference orbitals generated by κ-OOMP2, denoted as MP3:κ-OOMP2. Furthermore, scaling the third-order contribution was explored and 0.8 (MP2.8:κ-OOMP2) was determined to be an optimal scaling parameter to further improve the energetics.⁷¹

This previous work⁷¹ showed promising results for both NCI and TC; however, the NCI analysis was limited to two small benchmark sets: A24,⁷² comprising 24 small dimer complexes and TA13, comprised of 13 radical-solvent complexes. This present work aims to provides a comprehensive analysis of NCI for novel MP2 and MP3 approaches by assessing 19 popular NCI benchmark sets (see Table 1). These data sets formed the basis for assessing the performance of DFT functionals for NCI in a previous study from our group.⁷³ We include various second- and third-order MP methods as well as the top performing DFT functional for NCI,⁷³ωB97M-V.⁷⁴

Table 1:

Non-covalent interaction data-sets used to evaluate the performance of various methods in this work. These data sets were all taken from ref. 73. # indicates the number of data points in each set. Max(E) and Min(E) denote the weakest and strongest interaction energy of the data set in kcal/mol, respectively.

Name	Data-type	#	Description	Max(E)	Min(E)	Ref
A24	NCED	24	small non-covalent complexes	1.10	−6.53	72
DS14	NCED	14	sulfur based small non-covalent complexes	−0.85	−6.33	88
HB15	NCED	15	ionic hydrogen complexes	−11.46	−28.56	89
HSG	NCED	21	protein-ligand docking relevant non-covalent complexes	0.38	−19.08	90
S22	NCED	22	hydrogen-bonded and dispersion-bound complexes	−0.53	−20.64	22
X40	NCED	31	halogenated hydrocarbons non-covalent complexes	−0.49	−14.32	78
HW30	NCED	30	hydrocarbon water dimers	−0.66	−3.81	91
NC15	NCED	15	small non-covalent interactions	−0.02	−3.31	92
S66	NCED	66	hydrogen-bonded and dispersion-bound complexes	−1.39	−19.68	77
AlkBind12	NCED	12	unsaturated hydrocarbon dimers	−1.99	−4.65	93
CO2Nitrogen	NCED	16	polyheterocyclic CO2 dimers	−1.18	−5.54	94
HB49	NCED	49	hydrogen bonding complexes	−1.75	−33.85	95
Ionic43	NCED	43	charged non-covalent complexes	−7.96	−120.80	96
TA13	NCD	13	binary radical-solvent complexes	−1.69	−64.20	43
XB18	NCD	8	halogen bonded dimers	−1.41	−8.60	102
Bauza30	NCD	30	halogen, chalcogen and pnicogen bonded complexes	−1.42	−46.42	103
CT20	NCD	20	ground state charge-transfer complexes	−0.32	−1.83	104
XB51	NCD	20	halogen bonded dimers	−0.74	−23.11	102
Orel26rad	NCD	26	aromatic radical dimer complexes	−1.89	−20.30	105

We do not want to overlook promising results with non-perturbative approaches. First, lower-order coupled cluster methods showed promising performance in atomization and reaction energies without any additional empirical parameters.⁷⁵ However, more benchmark data is necessary to test whether this high accuracy is transferable to NCI. Hobza and coworkers developed a same- and opposite-spin scaled CCSD method, specifically parameterized for NCI (SCS(MI)-CCSD),⁷⁶ parameterized on the S22 benchmark set²²). The method performs remarkably well for the S66 (RMSD: 0.08 kcal/mol) and X40 (RMSD: 0.06 kcal/mol) NCI benchmark sets.^77,78 In both cases the scaling is $𝒪\left(N^6\right)$ but iterative and thus more expensive than the perturbative approaches detailed above.

Modern density functionals (e.g ωB97M-V) perform excellent for all types of NCI when empirical dispersion corrections^16,46 or nonlocal correlation functionals¹⁷ are used. We refer the interested reader to ref. 73 which includes an extensive comparison of many DFT functionals and various NCI data sets. However, approximate exchange correlation functionals incorporate many empirical parameters, which are often trained and/or tested on these benchmark sets.^54,73,79 Alternatively, there are promising NCI results obtained by employing the random phase approximation (RPA) as a correction to DFT,^80–82 as well as active development and testing of further corrections to RPA.^83–85 However, we note that radical systems or charged systems can still pose a problem for density functionals due to the self-interaction error.^73,86,87

This paper is organized as follows: First, we give a short overview of the data sets used in this study which are separated in two categories NCED (non-covalent ‘easy’ dimers; easy refers to low sensitivity to the self-interaction error in these data sets) and NCD (non-covalent ‘difficult’ dimers). Second, we describe the electronic structure methods used in this study and the computational details. Third, we discuss the optimal scaling parameter for the third order methods for S66 and the whole NCED data category. Fourth, we discuss in detail the performance of each method in each data set and draw conclusion after both NCED and NCD data categories. Lastly, we conclude and summarize important findings in our work.

2. Overview of Benchmark Sets

The benchmark sets used in this study are inspired by the data categories for non-covalent interactions from ref. 73, which includes two data categories: “non-covalent easy dimers” (NCED) and “non-covalent difficult dimers” (NCD) (the classification “easy dimers” means that these systems are not sensitive to the self interaction error (SIE) of approximate exchange correlation functionals^73,86,87).

The NCED data category includes thirteen equilibrium geometry data sets: A24,⁷² DS14,⁸⁸ HB15,⁸⁹ HSG,⁹⁰ S22,²² X40,⁷⁸ HW30,⁹¹ NC15,⁹² S66,⁷⁷ AlkBind12,⁹³ CO2Nitrogen16,⁹⁴ HB49⁹⁵ and Ionic43.⁹⁶ These data sets cover a wide range of different NCI interaction motifs like classical hydrogen bonds, dispersion bound systems, ionic interactions and halogen bonding with various sub-classes such as π-stacking, aliphatic dispersion, halogen-π interactions, cyclic hydrogen bonds, charged-neutral and charged-charged ionic interactions; see Table 1 for a short description of each data set. We omitted the five non-equilibrium geometries data sets (NBC10,⁹⁷ BzDC215,⁹⁸ A21×12,⁹⁹ S66×8,¹⁰⁰ 3B-69-DIM¹⁰¹) in the overall statistical analysis. However, some data points in these data sets were included in the section about potential energy curve calculations.

The NCD is a collection of four non-covalent interactions: TA13,⁴³ XB18,¹⁰² Bauza30,¹⁰³ CT20,¹⁰⁴ XB51¹⁰² and we extended the category by adding the Orel26rad¹⁰⁵ set. These are classified as difficult for DFT functionals because these systems are prone to the SIE.⁷³ We excluded all complexes with iodide in both halogen bonding sets following ref. 73. In XB18 10 data points and XB51 30 data points were excluded analogous to ref. 73. This data category covers neutral and charged radical complexes, hydrogen bonding, halogen, chalcogen and pnicogen bonding; see Table 1 for a short description of each data set.

3. Overview of Methodology

The majority of interaction energies reported in this work are computed without a geometric distortion term, meaning that the geometry of monomers are identical for the complex and in isolation. In this case, all energies are computed using the standard BSSE approach:¹⁰⁶

$$\mathrm{\Delta }{E}_{int}=E_{AB}^{AB}(AB)-E_A^A(AB)-E_B^B(AB)-E_{BSSE}.$$ (3)

Where $E_M^N(X)$ denotes the energy of N ∈ {A, B, AB} in the basis of M ∈ {A, B, AB} and in the geometry of X; AB denotes the supersystem of A and B. The basis set superposition error correction¹⁰⁶ is defined as:

$$E_{BSSE}=E_{AB}^A(AB)+E_{AB}^B(AB)-E_A^A(AB)-E_B^B(AB).$$ (4)

The benchmark sets HB49, XB18, XB51 and TA13 include geometric distortion, meaning the reference states are optimized structures for both isolated and supersystem geometries. We use the following equation to compute interaction energies in accordance with reference 95:

$$\mathrm{\Delta }{E}_{int}=E_{AB}^{AB}(AB)-E_A^A(AB)-E_B^B(AB)-E_{BSSE}+E_{GD},$$ (5)

with the geometry distortion term¹⁰⁷ defined as:

$$E_{GD}=E_A^A(AB)+E_B^B(AB)-E_A^A(A)-E_B^B(B),$$ (6)

where (AB) correspond to the monomer geometry in the complex, (A) to the optimized isolated geometry of monomer A, and respectively for (B). This approach yields almost identical RMSDs to non-BSSE corrected values for ωB97M-V in ref. 73.

All perturbation methods used in this study are summarized in Table 2. All PT methods utilize an all-electron approach (no frozen core approximation) and the RI approximation. The non-iterative second-order methods include: standard MP2:

$$E_{MP2}=E_{HF}+E_D^{(2)},$$ (7)

κ-MP2 using the recently developed κ-regularizer⁴⁰ (using the recommended $\kappa =1.45E_h^{-1}$ for the parameter) for the MP2 correlation energy:

$$E_{\kappa -MP2}=E_{HF}+E_D^{(2)}(\kappa ),$$ (8)

this method is used to systematically assess the effect of regularization and orbital optimization in κ-OOMP2. We note, that the κ parameter is optimized for the orbital optimized variant, not the κ-MP2. In addition, spin-scaled (SCS) MP2 using 0.333 for same spin (ss) and 1.200 for opposite spin (os) scaling factors for the same spin and opposite spin correlation energy contribution of MP2 ($E_{ss}^{(2)}$ and $E_{os}^{(2)}$), as implemented in Q-Chem.:⁴⁶

$$E_{SCS-MP2}=E_{HF}+c_{ss}{E}_{ss}^{(2)}+c_{os}{E}_{os}^{(2)},$$ (9)

Table 2:

Summary and short description of all perturbation theory methods used in this study; X indicates that the contribution is not included, ✓ means included, 0 indicates the contribution is identically to 0, and κ indicates regularized second order contribution ($\kappa =1.45E_h^{-1}$), S indicates scaled second or third order contribution

Method	Orbitals	$E_S^{(2)}$	$E_D^{(2)}$	$E_S^{(3)}$	$E_D^{(3)}$
MP2	HF	0	✓	X	X
κ-MP2	HF	0	κ	X	X
SCS-MP2	HF	0	S	X	X
OOMP2	OOMP2	0	✓	X	X
κ-OOMP2	κ-OOMP2	0	κ	X	X
MP3	HF	0	✓	0	✓
MP2.5	HF	0	✓	0	S
MP3:OOMP2	OOMP2	✓	✓	X	✓
MP2.5:OOMP2	OOMP2	✓	✓	X	S
MP3:κ-OOMP2	κ-OOMP2	✓	✓	X	✓
MP2.5:κ-OOMP2	κ-OOMP2	✓	✓	X	S
MP3:ωB97X-V	ωB97X-V	✓	✓	X	✓
MP2.5:ωB97X-V	ωB97X-V	✓	✓	X	S
κ-MP3:κ-OOMP2	κ-OOMP2	X	κ	X	✓
κ-MP2.5:κ-OOMP2	κ-OOMP2	X	κ	X	S

The iterative second-order methods include orbital-optimized MP2 (OOMP2) and κ-regularized OOMP2 (κ-OOMP2) which minimize the E_MP2 and E_κ−MP2 energy expressions stated above.

The third-order methods include: standard MP3 and MP2.5^60–62 which scales the third-order contribution (c₃) to the correlation energy by 0.5:

$$E_{MP2.5}=E_{HF}+E_D^{(2)}+c_3{E}_D^{(3)}.$$ (10)

Additionally, we tested MP3 using OOMP2 reference orbitals (MP3:OOMP2); MP2.5 using OOMP2 reference orbitals (MP2.5:OOMP2); MP3 using κ-OOMP2 reference orbitals where the regularizer is only applied for the generation of the the reference orbitals (MP3:κ-OOMP2); and MP2.5 using κ-OOMP2 reference orbitals (MP2.5:κ-OOMP2). For these non-HF reference orbitals, the MP2 energy includes the singles contributions, $E_S^{(2)}$:

$$E_S^{(2)}=-\sum _{ia}\frac{{\left|F_{ia}\right|}^2}{{ϵ}_a-{ϵ}_i},$$ (11)

where F_ia denotes an element of the occupied-virtual block of the Fock matrix. We also combined (scaled) MP3 and regularized MP2 where the regularizer is applied for the MP2 energy with κ-OOMP2 reference orbitals (κ-MP3:κ-OOMP2):

$$E_{\kappa -MP2.5}=E_{HF}+E^{(2)}{(\kappa )}_D+c_3{E}_D^{(3)}$$ (12)

and the scaled version κ-MP2.5:κ-OOMP2. For these cases, $E_S^{(2)}$ is omitted.

Lastly, inspired by recent work in our group,¹⁰⁸ we also investigate the effect of KS-DFT reference orbitals using ωB97X-V⁷⁹ for both MP2.5 and MP3, where we use the converged KS-DFT orbitals to evaluate the HF, MP2 and MP3 energy (in contrast to double hybrid functionals). This functional is among the most accurate for dipole moments,¹⁰⁹ polarizabilities,¹¹⁰ electron density variances¹¹¹ and yielded among the most accurate reference orbitals for MP3 calculations.¹⁰⁸ Table 2 summarizes the range of perturbative methods assessed in this work.

4. Computational Details

All electronic structure calculations were performed with a local development version of Q-Chem (version 5.2.2).¹¹² The MP2 and MP3 correlation energy calculations were performed with the RI approximation and correlate all electrons. We refer to RI-MP2 and RI-MP3 as simply MP2 and MP3, respectively. The MP3 calculations are performed with an amplitude direct approach which only requires the cubic storage overall.^113,114 The aug-cc-pVTZ basis and the corresponding RI auxiliary basis were employed for all calculations,^115,116 except for parts of Orel26rad, TA13 and XB51. For Orel26rad, we used the more compact def2-tzvpd^117,118 and corresponding auxiliary basis^119–121 for the larger systems due to computational efficiency; for TA13, we used the cc-pVQZ auxiliary basis for Li because there is no auxiliary basis for aug-cc-pVTZ; for XB51, we used the aug-cc-pVTZ-PP basis and the corresponding ECP and auxiliary basis for Br¹²² and the frozen core approximation was employed to harmonize with the reference values which were also generated with aug-cc-pVTZ-PP and ECP for Br.¹⁰²

All geometries and reference interaction energies were taken from ref. 73 (see references therein) with the exception of the Orel26rad data set, which was taken from ref. 105. Note carefully that we compare our TZ-level calculations against reference values at the complete basis set limit. We do this to make the MP2 and MP3 calculations far more feasible than if larger basis sets were used. We note that this affects the optimal scaling parameter (see figure S2).

In addition, we performed density functional calculation using ωB97M-V with a fine integration grid (99 radial grid points and 590 Lebedev angular grid points) for quadrature, the resulting RMSD are almost identical to those reported in ref. 73. Some small discrepancies (maximum deviation: 0.02 kcal/mol in DS14) can be explained with the different computational set-up (aug-cc-pVTZ with BSSE correction used here versus def2-QZVPPD^118,123 without BSSE correction used in ref. 73). The data for B3LYP-D3 is directly taken from ref. 73 and CCSD numbers are taken from the references for each data set. We performed the whole NCED data category with restricted HF (RHF) and ROOMP2. The same is true for the NCED data category with the exception of TA13 and Orel26rad. In TA13, we used UHF (and restricted open-shell HF (ROHF) just for MP2) and UOOMP2. In Orel26rad, we used ROHF for all HF methods and UOOMP2 for all OOMP2 methods including the composite MP3 methods.

5. Results and Discussion

The systems included in this study cover a wide range of NCI such as σ dispersion, π-stacking, hydrogen, halogen and ionic bonding; the complete list of 19 data sets was already shown in Table 1. The root-mean-square deviations (RMSD) are given in kcal/mol. We discuss equilibrium geometry data sets of the two data categories NCED (non-covalent: easy dimers) and NCD (non-covalent: difficult; with Orel26rad added) taken from an extensive benchmark work for DFT functionals.⁷³ In addition, we include potential energy surface (PES) scans for benzene, pyridine, water and methylamine dimers. We assess the performance of 15 methods (see Table 2) to systematically gauge the effect of scaling, reference orbitals and regularization. We compare these results to the top performing functional for NCI, ωB97M-V (based on Ref 73). We also compare our results against those from a widely used exchange correlation functional B3LYP-D3, CCSD and SCS(MI)-CCSD wherever available. The results are summarized in tables 3 and 4. The SCS-MP2 results are consistently worse than regular MP2 as illustrated in tables 3 and 4. Consequently, we omit SCS-MP2 from most of the discussion below. In addition, we explore the option of using KS-DFT reference orbitals for MP3 and MP2.5 due to recent promising results employing this approach.¹⁰⁸

Table 3:

Results of the NCED data category; RMSD in kcal/mol. For each data set, all method cells are colored in a heatmap from green to yellow to red. Low RMSDs are represented in green and high RMSDs in red.

NCED	A24	DS14	HB15	HSG	S22	X40	HW30	NC15	S66	AlkBind12	CO2Nitrogen16	HB49	Ionic43
MP2	0.17	0.33	0.36	0.30	1.25	0.58	0.45	0.09	0.67	0.69	0.64	0.40	0.90
κ-MP2	0.16	0.18	0.34	0.29	0.50	0.30	0.12	0.07	0.28	0.43	0.31	0.29	0.74
SCS-MP2	0.50	0.73	1.22	1.05	1.45	0.75	0.37	0.20	1.18	1.20	0.80	1.31	2.21
OOMP2	0.13	0.39	0.40	0.28	1.52	0.66	0.16	0.07	0.81	0.84	0.78	0.27	0.93
κ-00MP2	0.16	0.10	0.45	0.12	0.65	0.28	0.13	0.06	0.29	0.24	0.39	0.18	0.53
MP3	0.23	0.46	0.44	0.52	1.41	0.71	0.18	0.09	0.81	0.82	1.03	0.74	1.48
MP2.5	0.17	0.22	0.29	0.35	0.50	0.28	0.09	0.08	0.36	0.30	0.36	0.53	1.08
MP3:OOMP2	0.19	0.37	0.23	0.28	1.37	0.66	0.13	0.07	0.71	0.74	1.03	0.45	1.04
MP2.5:OOMP2	0.09	0.06	0.15	0.10	0.28	0.12	0.06	0.05	0.17	0.20	0.09	0.20	0.69
MP3:κ-OOMP2	0.20	0.40	0.25	0.32	1.38	0.68	0.15	0.08	0.74	0.78	1.02	0.49	1.09
MP2.5:κ-OOMP2	0.09	0.05	0.13	0.05	0.18	0.09	0.04	0.06	0.10	0.09	0.11	0.21	0.63
ωB97M-V	0.09	0.13	0.20	0.11	0.28	0.22	0.17	0.04	0.15	0.12	0.09	0.24	0.70
B3LYP-D3 *	0.15	0.22	0.75	0.21	0.43	0.34	0.23	0.10	0.34	0.17	0.07	0.59	0.80
CCSD**	0.38	-	-	0.82	0.61	0.48	-	-	0.70	0.85	-	0.32	-
Best	MP2.5:OOMP2	MP2.5:κ-OOMP2	MP2.5:κ-OOMP2	MP2.5:κ-OOMP2	MP2.5:κ-OOMP2	MP2.5:κ-OOMP2	MP2.5:κ-OOMP2	MP2.5:OOMP2	MP2.5:κ-OOMP2	MP2.5:κ-OOMP2	MP2.500MP2	κ-OOMP2	H-OOMP2

^*B3LYP-D3(BJ) interaction energies were taken from ref. 73

^**CCSD interaction energies for A24 and HSG were taken from ref. 124 (CCSD/aTZ), for S22 from ref. 76 (CCSD/CBS), for XB40 and S66 from ref. 78 (CCSD/CBS), for AlkBind12 from ref. 93 (CCSD/CBS), and for HB49 from ref. 125 (CCSD/aTZ).

Table 4:

Results of the NCD data category; RMSD in kcal/mol; RO-HF is used as a reference for the three MP2 methods in Orel26rad. For each data set, all method cells are colored in a heatmap from green to yellow to red. Low RMSDs are represented in green and high RMSDs in red.

NCD	TA13	XB18	Bauza30	CT20	XB51	Orel26rad
MP2	2.14	0.31	0.72	0.12	0.36	3.03
κ-MP2	2.46	0.26	0.98	0.10	0.36	1.53
SCS-MP2	2.65	0.75	2.33	0.34	0.82	2.12
OOMP2	0.96	1.01	1.76	0.22	1.27	7.70
κ-OOMP2	0.88	0.50	1.31	0.13	0.36	0.59
MP3	1.85	1.09	2.40	0.23	1.32	6.50
MP2.5	1.95	0.45	1.21	0.14	0.54	2.23
MP3:OOMP2	0.63	0.62	1.62	0.09	0.76	7.01
MP2.5:OOMP2	1.16	0.59	1.11	0.16	0.70	1.10
MP3:κ-OOMP2	0.62	0.71	1.81	0.10	0.88	5.92
MP2.5:κ-OOMP2	0.93	0.35	0.88	0.12	0.34	0.78
ωB97M-V	2.85	0.32	0.59	0.08	0.26	1.59
B3LYP-D3 *	3.85	0.37	1.87	0.28	1.04	5.67
CCSD**	0.89	0.66	-	-	0.67	-
Best	MP3:κ-OOMP2	κ-MP2	MP2	MP3:OOMP2	MP2.5:κ-OOMP2	κ-OOMP2

^*B3LYP-D3(BJ) interaction energies were taken from ref. 73

^**CCSD interaction energies for TA13 are taken from ref. 43 (CCSD/CBS); XB18 (CCSD/aQZ) and XB51 (CCSD/aTZ) were taken from ref. 102 and adjusted to the subset.

5.1. Optimal Scaling of the Third-Order Energy

Both standard MP2 (c₃ = 0.0) and MP3 (c₃ = 1.0) (see equation 10) perform poorly for NCI as MP2 usually overbinds (too negative interaction energies) and MP3 underbinds (not sufficiently negative interaction energies). Therefore, Hobza and coworkers^60–62 suggested scaling the third-order correlation energy to interpolate between MP2 and MP3. Thus, we expect an optimum scaling parameter between 0 and 1. In two previous studies,^71,108 0.8 was determined as the optimal scaling parameter (c₃) for the third-order energy contribution (see equation 10) using the W4-11 thermochemistry data set as a training set and CCSD(T) with aug-cc-pVTZ as a reference. However, other studies specifically for non-covalent interaction found a scaling factor of 0.5 yields good results for both MP3 and orbital optimized MP3.^36,62 Therefore, we probed the scaling factor dependence for all four MP2.X methods (MP2.X, MP2.X:OOMP2, MP2.X:κ-OOMP2 and κ-MP2.X:κ-OOMP2) employed in this study. The results are depicted in Fig. 1 using the S66 benchmark set as a training set. A scale factor of around 0.5 is optimal for MP2.X, MP2.X:OOMP2 and MP2.X:κ-OOMP2 (optimal c₃ values were 0.45, 0.55, and 0.60 for MP2.X, MP2.X:κ-OOMP2, and MP2.X:OOMP2, respectively).

Figure 1:

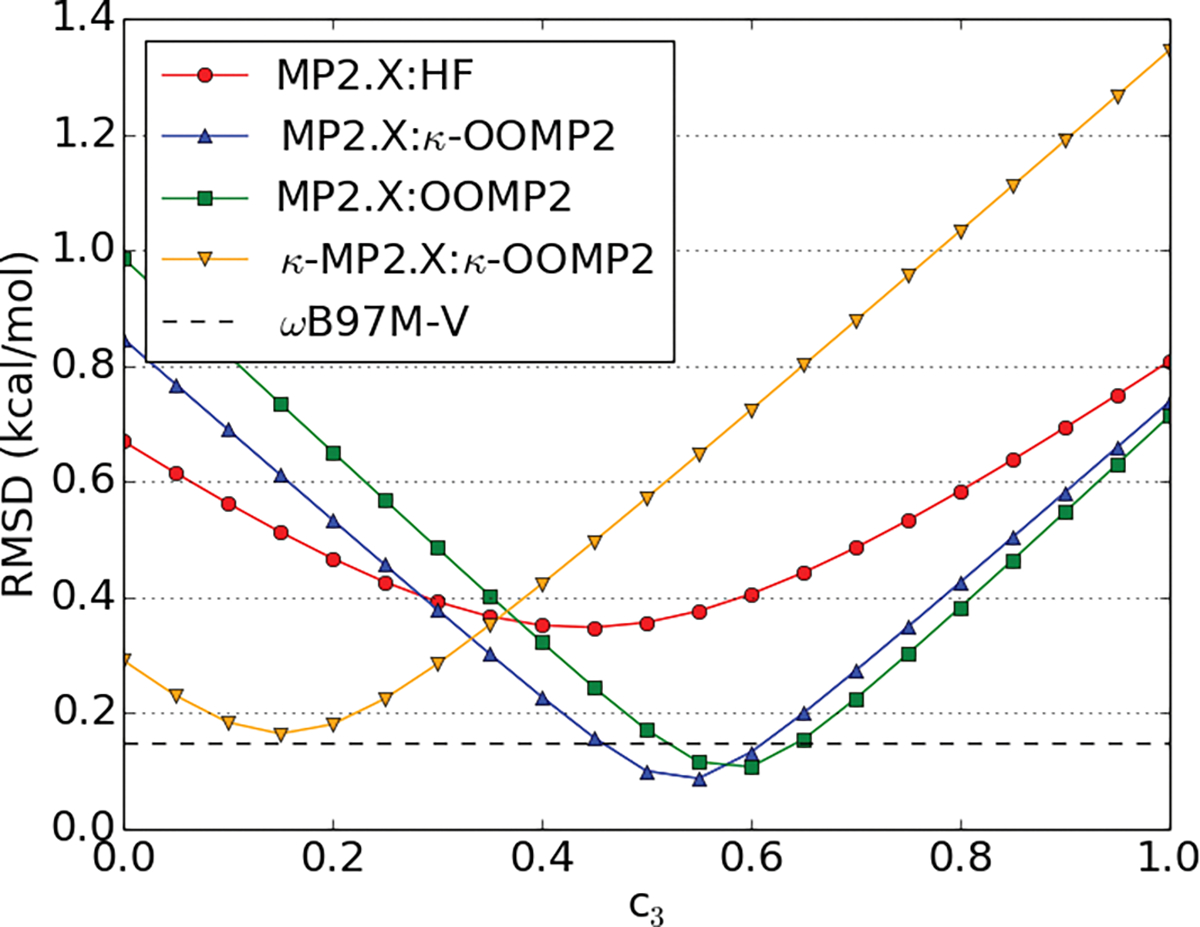
Dependence of the the root-mean square deviation on the scaling of the third-order energy (c₃) in the S66 training set; in kcal/mol; for four scaled MP2.X methods (MP2.X, MP2.X:OOMP2, MP2.X:κ-OOMP2, κMP2.X:κ-OOMP2); for reference, the RMSD of ωB97M-V is depicted as a flat line.

We stress again, however, that the c₃ coefficient is optimized in the medium sized aug-cc-pVTZ basis by training against CCSD(T)/CBS reference values. The c₃ parameter tends to shift to larger values for larger basis sets or when a CCSD(T)/aug-cc-pvtz reference is used (as in ref. 71 and 108). MP2 tends to overestimate correlation energy with larger basis sets and consequently a higher amount of third order contribution becomes optimal. We illustrate this for the A24 benchmark set in figures S1 and S2.

Returning to Fig. 1, it is very interesting that both MP2.X:OOMP2 and MP2.X:κ-OOMP2 exhibit a sharper and deeper minimum than MP2.X. A more detailed look at the individual plots reveals that in some data sets the minimum for MP2.X is at c₃ = 0 or very small. These sets mainly contain hydrogen bonding motifs such as the S66 hydrogen bonding subsection, HSG, HB49, Ionic43 and CT20. The optimal c₃ parameter for MP2.X:OOMP2 is always larger than MP2.X:κ-OOMP2 and notable deviations from c₃ = 0.5 are observed for A24 (c₃ ~ 0.3) and CT20 (c₃ ~ 0.8). The supporting information (SI) contains a plot for each of these data sets.

Furthermore, we combined both κ-regularization of the MP2 energy and scaling of the MP3 energy. We found, however, that the c₃ scaling factor was small and often did not yield a sizable improvement versus κ-OOMP2 (see Fig. 1). This is in accordance with the findings of our previous study.⁷¹ Therefore this method is omitted from further discussion.

5.2. NCED

We discuss the S22 and S66 data sets in detail since they are the most popular benchmark sets for NCI and many findings are transferable to the other sets. The results for all data sets of that category are summarized in table 3.

5.2.1. S22

The S22²² benchmark set comprises 22 non-covalent interactions of model systems relevant to biological molecules. Typical systems are π-stacked aromatic systems like the benzene dimer or hydrogen bonded systems like the formic acid dimer. The two largest systems are adenine-thymine complexes (30 atoms). The set is divided into three subgroups: (i) hydrogen bonded complexes; (ii) dispersion-bound complexes; and (iii) mixed electrostatic and dispersion complexes.

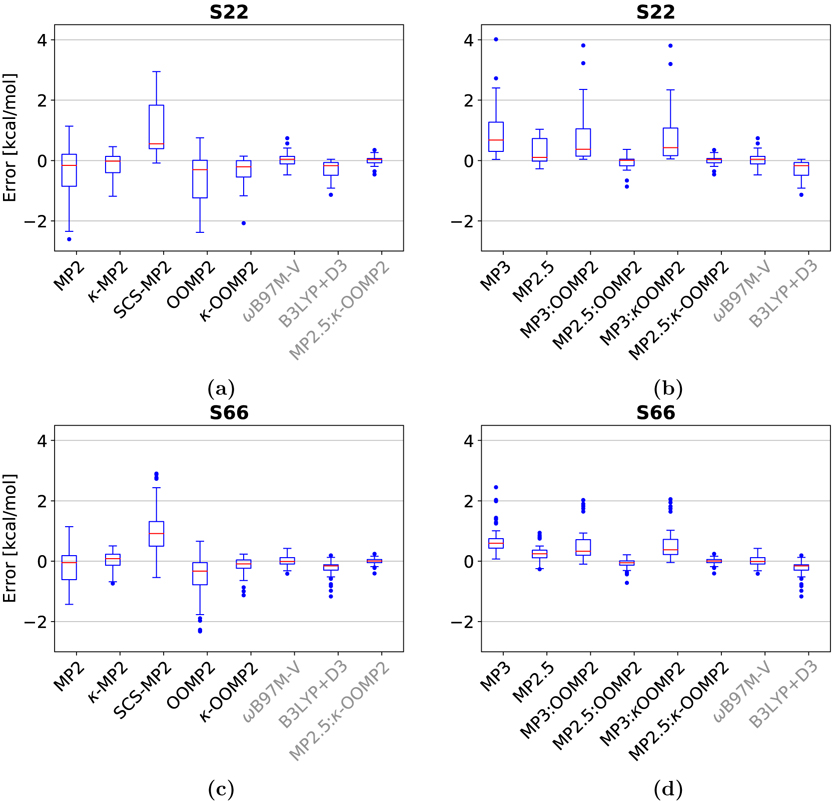
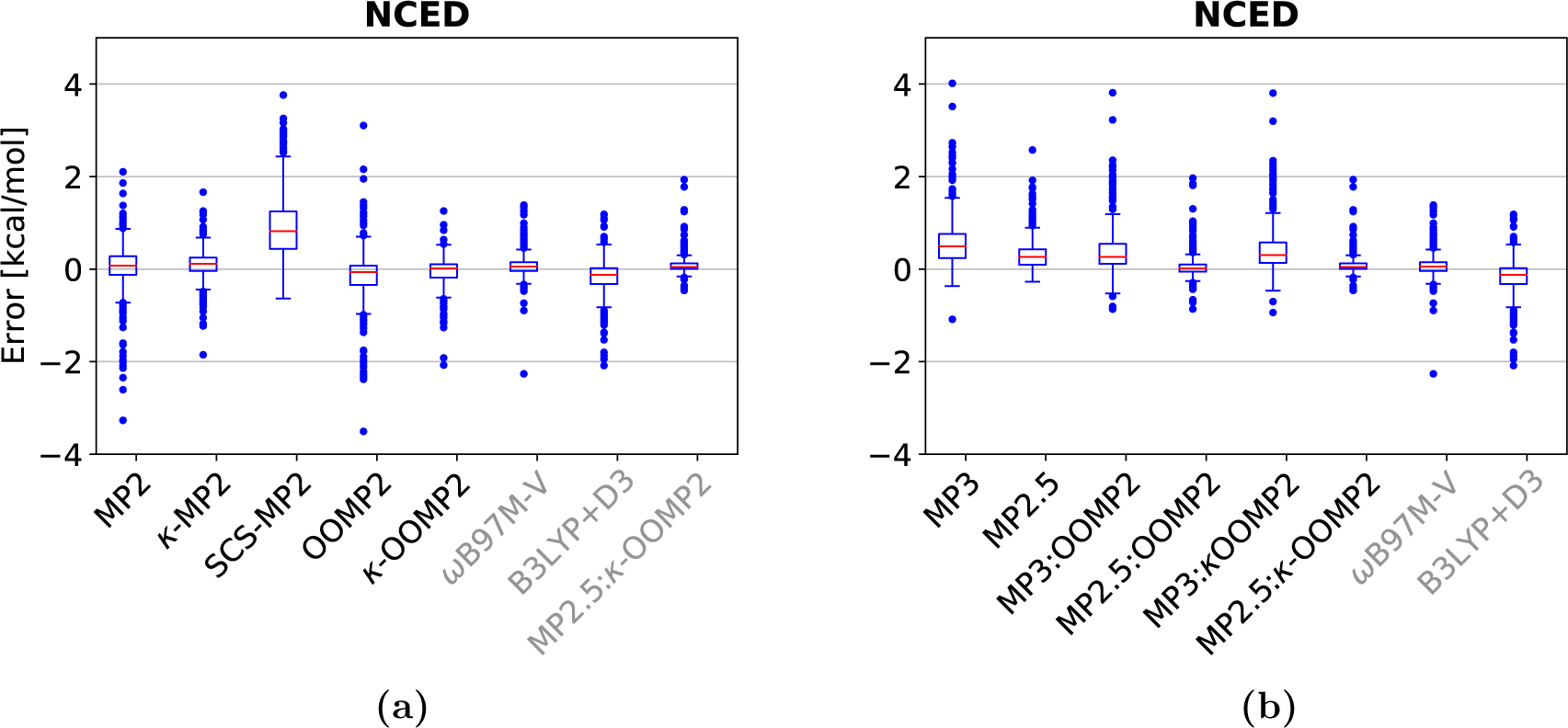
Among the second order methods, MP2 is well-known to overbind dispersion-driven complexes,^18,22–24 yielding a large RMSD of 1.25 kcal/mol and a mean signed deviation (MSD) of −0.45 kcal/mol. The largest deviations for MP2 are the π-stacked indole-benzene complex (−3.27 kcal/mol) and the adenine-thymine complex (−2.61 kcal/mol). Regularization damps the small gap correlation energy contributions which significantly decreases the RMSD to 0.50 kcal/mol for κ-MP2 (almost by a factor of 3). This is a remarkable improvement especially given that the κ value used in κ-MP2 was never trained on non-covalent interactions. The lower RMSD stems mainly from the improved binding energies of the π-stacked outliers described above: deviation of 1.18 kcal/mol for the indole-benzene complex and −1.18 kcal/mol for adenine-thymine complex. This is also seen in the boxplot of in Fig. 2 (a) where the spread of the error significantly decreases from MP2 to κ-MP2 and κ-OOMP2 to MP2.5:κ-OOMP2. By contrast, a currently more widely used MP2 variant, SCS-MP2 performs even worse than canonical MP2 for this data set. SCS-MP2 improves the performance of the π-stacked species e.g. deviation in the indole-benzene complex is −0.08 kcal/mol; however, this improvement in the dispersion category is accompanied by significant underbinding of hydrogen bonding, e.g. adenine thymine complex with 2.8 kcal/mol. This is further illustrated by both the mean signed deviation (MSD): 1.05 kcal/mol and the boxplots in figure 2. In total, the RMSD of SCS-MP2 is 1.45 kcal/mol performing worse than standard MP2.

Figure 2:

Boxplots of the S22 & S66 data-sets: (a) MP2 methods for S22, (b) MP3 methods for S22; (c) MP2 methods for S66, (d) MP3 methods for S66. Red lines mark the median deviation, boxes bound the central 50% of the data, whiskers enclose all data points within 1.5 times the inter-quartile range of the box edges, and points denote outlying data.

For the MP3 methods, scaling MP3 correlation energy contribution improves the RMSD for all three sets of reference orbitals by ~1 kcal/mol e.g., MP3:κ-OOMP2: 1.38 kcal/mol versus MP2.5:κ-OOMP2: 0.18 kcal/mol. Comparing the three scaled methods, the HF reference orbitals yield significantly worse binding energies (RMSD: 0.50 kcal/mol) than OOMP2 (RMSD: 0.28 kcal/mol), while κ-OOMP2 (RMSD: 0.18 kcal/mol) provides the best reference orbitals for scaled MP3. The box plots in Fig. 2 (a) and (b) show how all three MP2.5 methods significantly decrease the spread of the error in comparison to standard MP2.

Interestingly, for this dataset, the performance of the regularizer does not strongly depend on the reference orbitals, since both κ-MP2 (RMSD: 0.50 kcal/mol) and κ-OOMP2 (RMSD: 0.65 kcal/mol) yield similar accuracy. In addition, the comparison of κ-OOMP2 and OOMP2 show that improvements in the energetics mainly stem from the κ-regularizer (RMSD: OOMP2: 1.45 kcal/mol versus κ-OOMP2: 0.65 kcal/mol).

The two DFT functionals ωB97M-V (RMSD: 0.28 kcal/mol) and B3LYP (RMSD: 0.43 kcal/mol) perform less well than MP2.5:κ-OOMP2. In addition CCSD (CCSD/CBS) performs poorly with an RMSD of 0.61 kcal/mol⁷⁶ in comparison to MP2.5:κ-OOMP2; however, a scaled CCSD version, SCS(MI)-CCSD (RMSD: 0.06 kcal/mol)⁷⁶ outperforms MP2.5:κ-OOMP2 slightly; but the spin scaling parameters were trained on this data set.⁷⁶

In summary, the best performing method is MP2.5:κ-OOMP2 with an RMSD of 0.18 kcal/mol. The largest deviation is seen in the π-stacked adenine-thymine complex with −0.46 kcal/mol.

5.2.2. S66

The S66⁷⁷ benchmark set consists of 66 NCI. Similarly to S22, the data set covers a large variety of NCI relevant to biology with a more balanced representation of dispersion and electrostatic contributions. The interactions are also classified in three categories: (i) hydrogen bonds, (ii) dispersion and (iii) others/mixed. The largest data point is a pentane dimer (34 atoms).

Among the second-order methods both κ-OOMP2 and κ-MP2 are significant improvements on standard MP2. Similarly to S22, the improvements stem mainly from regularization and not orbital optimization which is illustrated by the RMSD of 0.28 kcal/mol for κ-MP2 and 0.29 kcal/mol for κ-OOMP2 versus standard MP2 0.67 kcal/mol. The boxplot in figure 2 illustrates this behaviour as MP2 shows a downwards bias and κ-MP2 (and κ-OOMP2) a significantly decreased spread in the data.

For the third-order methods, both scaling and κ-OOMP2 reference orbitals improve the energies; thus, the top performer is MP2.5:κ-OOMP2 with an RMSD of 0.10 kcal/mol. The largest MP2.5:κ-OOMP2 deviation is −0.41 kcal/mol for a π-stacked uracil complex. Both MP2.5 (RMSD: 0.36 kcal/mol) and MP3:κ-OOMP2 (RMSD: 0.74 kcal/mol) perform significantly less well than MP2.5:κ-OOMP2. As already mentioned, S66 was used as a training set to determine an optimal scaling parameter for the third-order correlation energy in the three MP3 methods surveyed and yielded optimal parameters of around 0.5 for each case, see Table 5. This is consistent with results reported previously using HF reference orbitals.^60–62 Interestingly, this holds for each of the three subclasses in this set (see Table 5 and S3).

Table 5:

Optimal scaling parameter for the MP3 energy contribution (c₃) for the whole S66 data set and the three subsets hydrogen bonds, dispersion and mixed.

Method	c3 tot	c3 h-bonds	c3 disp	c3 mixed
MP2.X	0.45	0.45	0.45	0.40
MP2.X:κ-OOMP2	0.55	0.50	0.55	0.50
MP2.X:OOMP2	0.60	0.60	0.60	0.55
κ-MP2.X:κ-OOMP2	0.15	0.10	0.15	0.15

The dispersion-bound subsection of S66 (23 data points) are of particular interest as standard MP2 is known to overbind these complexes.^18,22–24 This is illustrated by the high RMSD of 0.94 kcal/mol. The κ-regularized MP methods significantly improve binding: κ-MP2 with an RMSD of 0.39 kcal/mol, κ-OOMP2 with an RMSD of 0.44 kcal/mol and MP2.5:κ-OOMP2 with an RMSD of 0.13 kcal/mol. For MP2, the largest deviation is seen in the π-stacked pyridine dimer −1.97 kcal/mol; this is reduced to −0.74 kcal/mol for κ-MP2, to −0.64 kcal/mol for κ-OOMP2 and to 0.01 kcal/mol for MP2.5:κ-OOMP2. Consequently, κ-MP methods are suitable for describing dispersion-bound complexes because the regularizer damps the correlation energy appropriately.

The DFT functional ωB97M-V performs well with an RMSD of 0.15 kcal/mol and is only outperformed by MP2.5:κ-OOMP2. B3LYP-D3 performs worse with an RMSD of 0.34 kcal/mol and is also outperformed by κ-MP2. The coupled cluster method CCSD performs poorly in comparison to MP2.5:κ-OOMP2 with an RMSD of 0.70 kcal/mol (CCSD/CBS) but the scaled version SCS(MI)-CCSD performs similarly to MP2.5:κ-OOMP2 (RMSD: 0.08 kcal/mol SCS(MI)-CCSD/CBS).⁷⁸

In summary, the top performer is MP2.5:κ-OOMP2 with an RMSD of 0.10 kcal/mol. In addition, MP2.5:κ-OOMP2 results in a smaller spread in the data and fewer outliers than the other methods (see boxplots in Fig. 2 (c) & (d)).

5.2.3. A24

The A24⁷² benchmark set consists of 24 very small non-covalent complexes including the water-ammonia dimer and methane-ethane dimer. Among the second-order methods, only OOMP2 (RMSD: 0.13 kcal/mol) shows a considerable improvement over MP2 (RMSD: 0.17 kcal/mol). Among the third-order methods, the top performers are MP2.5:κ-OOMP2 with an RMSD of 0.09 kcal/mol, MP2.5:OOMP2 with an RMSD of 0.09 kcal/mol. ωB97M-V performs similarly with an RMSD of 0.09 kcal/mol. In contrast, CCSD performs significantly worse with an RMSD of 0.38 kcal/mol (CCSD interaction energies for A24 and HSG were taken from ref. 124 (CCSD/aTZ)). The spread in the error is smallest for MP2.5:κ-OOMP2 (see boxplots in figure S8). Overall, MP2.5:κ-OOMP2 is the top performer.

5.2.4. DS14

The DS14⁸⁸ benchmark set comprises of 14 non-covalent dimers with sulfur-containing species, e.g. the water-hydrogen sulfide dimer and methane-hydrogen sulfide dimer. The largest data point is the benzene-dimethyl sulfide dimer (21 atoms). The top performer on this data set is MP2.5:κ-OOMP2 with an RMSD of 0.05 kcal/mol, significantly outperforming ωB97M-V with an RMSD of 0.13 kcal/mol. Among second-order methods κ-OOMP2 performs best with an RMSD of 0.10 kcal/mol. Standard MP2 has an RMSD of 0.33 kcal/mol; the poor performance mainly stems from overbinding of the two benzene systems (benzene-dimethyl sulfide and benzene-methanethiol). Regularization almost halves (κ-MP2 RMSD of 0.18 kcal/mol) the MP2 RMSD by improving on the two outliers (see boxplots in figure S9), whereas orbital optimizing without regularization leads to slightly worse results (OOMP2 RMSD of 0.39 kcal/mol).

5.2.5. HB15

The HB15⁸⁹ benchmark set consists of 15 medium-sized ionic hydrogen bonded systems relevant to biology like the guanidinium-methanol dimer (16 atoms). The top performer is MP2.5:κ-OOMP2 with an RMSD 0.13 kcal/mol. Scaling the MP3 correlation energy and using κ-OOMP2 reference orbitals significantly improves the results from MP3 (RMSD of 0.44 kcal/mol). All second-order methods perform very similarly as neither regularization nor orbital optimization significantly improves the binding energies [e.g. MP2: 0.36 kcal/mol, κ-MP2: 0.34 kcal/mol]. It is noteworthy that all MP methods outperform the popular B3LYP functional, which has an RMSD of 0.75 kcal/mol. Charge delocalization error¹²⁶ makes these systems more challenging for DFT.

5.2.6. HSG

The HSG⁹⁰ data set comprises 21 NCIs relevant to protein-ligand docking. The largest data point is the butane-N-tert-butylformamide dimer (32 atoms). The top performer is MP2.5:κ-OOMP2 with an RMSD of 0.05 kcal/mol; runners-up are κ-OOMP2 with an RMSD of 0.12 kcal/mol performing similarly to ωB97M-V (0.11 kcal/mol). Interestingly, in this data set neither regularization (κ-MP2: 0.29 kcal/mol) nor OOMP2 (0.28 kcal/mol) significantly improve upon standard MP2 (0.30 kcal/mol), only the combination of both is effective via κ-OOMP2.

5.2.7. X40

The X40⁷⁸ data set comprises 31 π-stacking, halogen bonding and hydrogen bonding interactions containing halogenated molecules (we excluded the 9 dimers containing iodide in accordance with ref. 73). The largest system is bromobenzene-trimethylamine dimer (25 atoms). Among the second-order methods, κ-OOMP2 performs best with an RMSD of 0.28 kcal/mol; κ-MP2 performs similarly with 0.30 kcal/mol. Both improve upon standard MP2 with RMSD of 0.58 kcal/mol. Similar to other data sets, the poor performance of MP2 can be attributed to two π-stacked benzene data points, which MP2 overbinds by ~2 kcal/mol (see boxplots in figure S10). Regularization alone significantly improves the binding of those outliers (κ-MP2 has an RMSD of 0.30 kcal/mol).

Among the third-order methods, the top performer is MP3:κ-OOMP2 with an RMSD of 0.09 kcal/mol as both spin scaling and κ-OOMP2 (and OOMP2) reference orbitals improve the energetics significantly. This is illustrated by the comparison to MP2.5 (0.28 kcal/mol) and MP3:κ-OOMP2 (0.68 kcal/mol). The ωB97M-V functional performs quite well (0.22 kcal/mol), surpassing B3LYP-D3(BJ) (0.34 kcal/mol). CCSD performs worse than the top MP3 methods with an RMSD of 0.48 kcal/mol (CCSD/CBS⁷⁸) but SCS(MI)-CCSD performs similarly (SCS(MI)-CCSD/CBS RMSD: 0.08 kcal/mol⁷⁸). Overall, MP2.5:κ-OOMP2 is the top performer with an RMSD of 0.09 kcal/mol, which is three times lower than the best second order method (κ-OOMP2).

5.2.8. HW30

The HW30⁹¹ data set contains 30 hydrocarbon-water dimer interactions including the benzenewater and butane-water dimers. Among the second-order methods, κ-MP2 performs best with an RMSD of 0.12 kcal/mol improving significantly on standard MP2 with an RMSD of 0.45 kcal/mol. Orbital optimization does improve upon MP2 with an RMSD of 0.16 kcal/mol for OOMP2. However, κ-OOMP2with a RMSD of 0.13 kcal/mol performs slightly worse than k-MP2. Among the third-order methods, the top performer is MP2.5:κ-OOMP2 with an RMSD of 0.04 kcal/mol improving upon MP2.5 (0.09 kcal/mol). The popular B3LYP-D3 (0.17 kcal/mol) and ωB97M-V (0.23 kcal/mol) perform worse than both top performing MP2 and MP3 methods. The overall top performer is MP2.5:κ-OOMP2.

5.2.9. NC15

The NC15⁹² data set comprises 15 very small non-covalent interactions like the argon dimer. Among the second-order methods, κ-OOMP2 is the top performer (0.059 kcal/mol), even though standard also MP2 performs well (0.088 kcal/mol). Among the third-order methods, the top performers set are MP2.5:OOMP2 (0.052 kcal/mol), MP2.5:κ-OOMP2 (0.056 kcal/mol). However, none of the perturbative methods outperform ωB97M-V (0.040 kcal/mol).

5.2.10. AlkBind12

The AlkBind12⁹³ benchmark set comprises 12 medium-sized dispersion-bound saturated and unsaturated hydrocarbon dimers including the benzene dimer. Standard MP2 systematically overbinds these dispersion-bound complexes (MSD: −0.37 kcal/mol) and consequently performs poorly with an RMSD of 0.69 kcal/mol. Both κ-OOMP2 and κ-MP2 improve upon MP2 with RMSDs of 0.24 kcal/mol and 0.43 kcal/mol, respectively. The poor performance of MP2 results mainly from one outlier, the benzene dimer, with a deviation of −2.00 kcal/mol. Notably κ-OOMP2 reduces this error to −0.48 kcal/mol. In contrast, all of the unscaled MP3 methods systematically underbind these dispersion complexes (e.g. MP3 MSD: 0.754 kcal/mol). The scaling (MP2.5) improves the RMSD to 0.30 kcal/mol and κ-OOMP2 reference orbitals in MP2.5:κ-OOMP2 further improve the results (RMSD of 0.09 kcal/mol). ωB97M-V (0.12 kcal/mol), CCSD (RMSD 0.85 kcal/mol; CCSD/CBS⁹³) and SCS(MI)-CCSD (RMSD: 0.18 kcal/mol; SCS(MI)-CCSD/CBS⁹³) are outperformed by MP2.5:κ-OOMP2 making it the overall top performer for this set.

5.2.11. CO2Nitrogen16

The CO2Nitrogen16⁹⁴ benchmark set includes 16 model complexes for the absorption of CO₂ onto eight polyheterocyclic aromatic compounds ranging from pyridine and pyrazine to 1,6-diazacoronene. However, we excluded the two largest diazacoronene data points due to difficulty obtaining MP3 energies for these systems. Among the second-order methods κ-MP2 performs best with an RMSD of 0.31 kcal/mol followed by κ-OOMP2 (0.39 kcal/mol). Standard MP2 significantly overbinds (MSD: −0.30 kcal/mol) resulting in an RMSD of 0.64 kcal/mol. Among the third-order methods, the top performer for this set is MP2.5:κ-OOMP2 with an RMSD of 0.11 kcal/mol improving upon MP2.5 (0.36 kcal/mol). Both B3LYP-D3 (0.07 kcal/mol) and ωB97M-V (0.09 kcal/mol) functionals perform significantly better than all MP methods.

5.2.12. HB49

The HB49^95,125,127 data set consists of 49 small- and medium-sized hydrogen bonding complexes. The sets includes both neutral-neutral and ion-neutral complexes and thus governs a wide range of interaction energies (3–25 kcal/mol). A typical example is the guanidinium–methanol dimer (16 atoms). Among the second-order methods, the top performer on this set is κ-OOMP2 with an RMSD of 0.18 kcal/mol, halving the RMSD in comparison to standard MP2 (0.40 kcal/mol). This is the best-performing method on this set. For comparison, with regularization alone, κ-MP2 already improves significantly upon standard MP2 with an RMSD of 0.29 kcal/mol. Among the third-order methods MP2.5:OOMP2 performs best with an RMSD of 0.20 kcal/mol and MP2.5:κ-OOMP2 performs similarly (RMSD: 0.21 kcal/mol). Both κ-OOMP2 and MP2.5:κ-OOMP2 outperform ωB97M-V (0.24 kcal/mol) and B3LYP (0.59 kcal/mol).

5.2.13. Ionic43

The Ionic43⁹⁶ data set comprises 43 small- to medium-sized charged non-covalent interactions (cationic-neutral, anionic-neutral and anion-cation dimer), e.g. the formate-water dimer. Among the second-order methods (and indeed all methods), the top performer is κ-OOMP2 with an RMSD of 0.53 kcal/mol improving upon both standard MP2 (0.90 kcal/mol) and κ-MP2 (0.74 kcal/mol). Among the third-order methods, MP2.5:κ-OOMP2 performs best with an RMSD of 0.63 kcal/mol. Both ωB97M-V (0.70 kcal/mol) and B3LYP (0.80 kcal/mol) perform worse than most MP methods as these systems are prone to charge delocalization error making them more challenging for DFT calculations.¹²⁸ The boxplots indicate that the error is distributed similarly in all of the top performing methods (see figure S12).

5.2.14. Discussion

The accumulated NCED data category has 356 data points and the top performer is MP2.5:κ-OOMP2 with an RMSD of 0.25 kcal/mol. Notable among the second-order methods are κ-OOMP2 with an RMSD 0.33 kcal/mol and κ-MP2 with an RMSD of 0.37 kcal/mol; both improve upon standard MP2 by almost a factor of two (MP2 RMSD: 0.63 kcal/mol). This is further illustrated by Fig. 3 which shows a histogram of the absolute deviation from the reference energies for MP2, κ-MP2, κ-OOMP2 and MP2.5:κ-OOMP2. It shows how the error distribution is concentrated towards the smaller deviations, and larger deviations are significantly reduced moving from MP2 to MP2.5:κ-OOMP2. A similar picture emerges from boxplots of the NCED data category in Fig. 4. κ-MP2 reduces the spread of the data in both directions (over and underbinding) compared to MP2 but is more effective for overbinding. The quite systematic success of regularized κ-MP2 over standard MP2 is very encouraging: it appears to be a preferable choice for a wide range of NCI. The value of regularization is also clear from the fact that OOMP2 is significantly less effective than κ-OOMP2. While κ-OOMP2 outperforms κ-MP2 (overall and in 8 of 13 datasets), the energetic improvements for these mostly closed shell systems from regular MP2 to κ-OOMP2 stem mainly from the κ-regularization rather than the orbital optimization.

Figure 3:

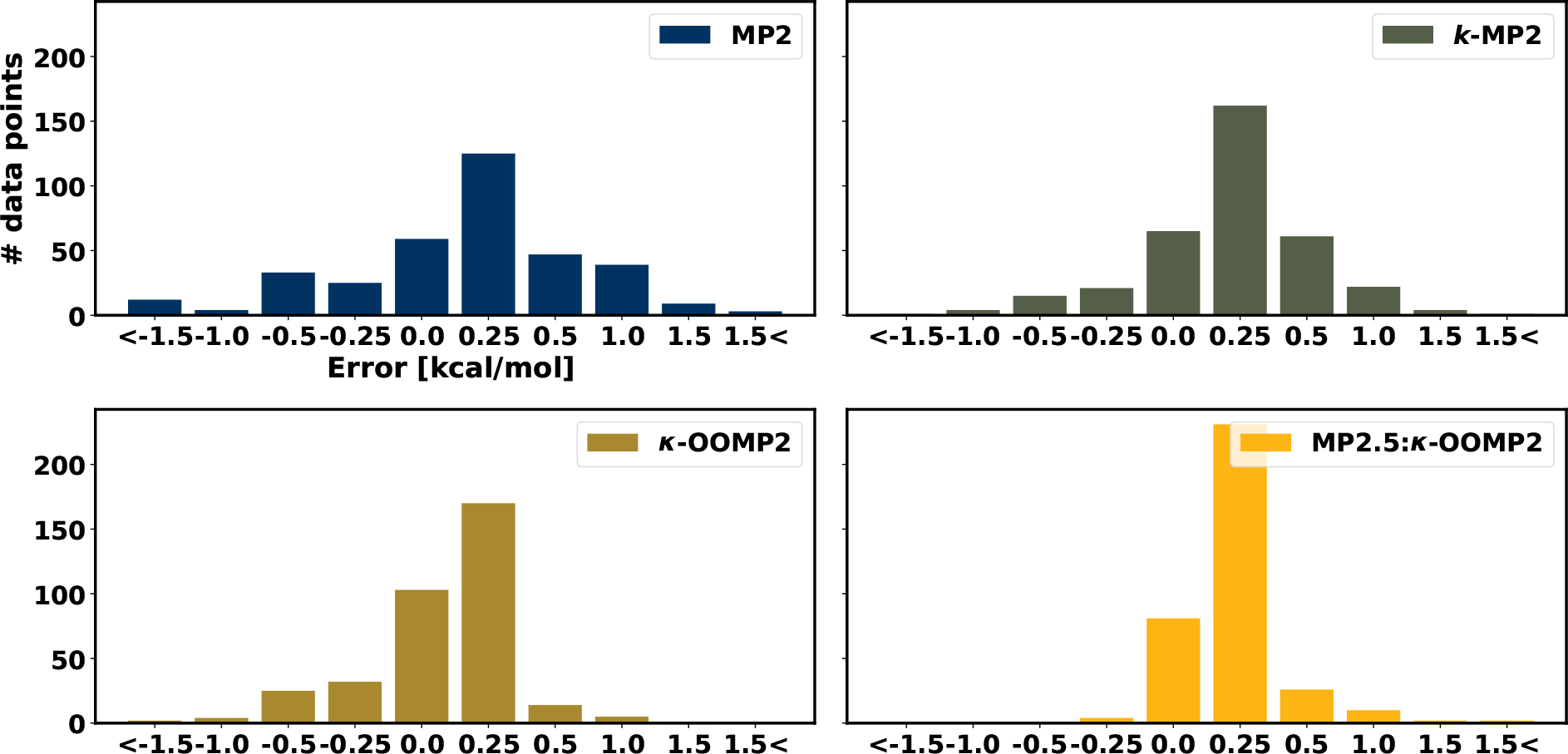
Histogram of the absolute deviation of MP2 (top left panel), κ-MP2 (top right panel), κ-OOMP2 (bottom left panel) and MP2.5:κ-OOMP2 (bottom right panel).

Figure 4:

Boxplots of the NCED data category for (a) MP2 methods, (b) MP3 and DFT methods. Red lines mark the median deviation, boxes bound the central 50% of the data, whiskers enclose all data points within 1.5 times the inter-quartile range of the box edges, and points denote outlying data. DFT and MP2.5:κ-OOMP2 are included in all plots for comparison.

In contrast, scaled MP3 (i.e. with HF orbitals) removes many of the overbinding outliers at the cost of a significant underbinding bias. Interestingly, the scaled MP3 methods not only remove underbinding outliers but also decrease the spread of the error more than just the κ-regularization. These findings are consistent with the fact that adding a scaled MP3 correlation energy on top of κ-MP2 led to a very small c₃ coefficient with only marginal improvement. Both the addition of the third-order term and the κ-regularization damp the correlation energy so as to remove the overbinding.

For the third order methods, using all of NCED to train the c₃ scaling parameter leads to the conclusion that the S66 training set results are transferable to the total NCED data category: the optimal c₃ values are close to 0.5 with 0.35, 0.50, and 0.55 for MP2.X, MP2.X:κ-OOMP2, and MP2.X:OOMP2, respectively. The dependence of the RMSD with respect to c₃ for MP2.X:κ-OOMP2, and MP2.X:OOMP2 is depicted in figure 5. This data supports keeping the established factor of 0.5 yielding MP2.5, MP2.5:OOMP2 and MP2.5:κ-OOMP2.

Figure 5:

Dependence of the the root-mean square deviation on the scaling of the third-order energy (c₃) for the whole NCED data data category; in kcal/mol; for four scaled MP2.X methods (MP2.X, MP2.X:OOMP2, MP2.X:κ-OOMP2, κMP2.X:κ-OOMP2); for reference, the RMSD of ωB97M-V is depicted as a flat line.

The standard MP3 RMSDs are in general worse than standard MP2; there is an improvement in only 1 (HW30) out of 13 data sets. Consistent with conventional wisdom, it cannot be recommended for NCI. Both scaling the third-order energy by a factor of 0.5 (MP2.5) or changing the reference orbitals (e.g. MP3:κ-OOMP2) improves the results. The combination of both in MP2.5:κ-OOMP2 yields very high accuracy in all benchmark sets. It is the top performer in 8 out of 13 benchmark sets and among the top performing methods in the others. It outperforms CCSD in all cases and even performs similarly to SCS(MI)-CCSD, which is more expensive (iterative $𝒪\left(N^6\right)$) and the spin scaling parameters were trained to perform well on NCI. We note that MP2.5:OOMP2 has a very similar RMSD in all benchmark sets; thus it is, perhaps surprisingly, a good alternative if the κ-regularizer is not available (we shall see later that ωB97X-V orbitals are another excellent alternative).

5.3. NCD

The NCD data category includes TA13, XB18, Bauza30, XB51 augmented with the Orel26rad data set. By contrast with NCED, this class is more difficult due to self-interaction errors, and also includes open-shell cases for which HF orbitals may exhibit significant spin contamination. The results for all data sets of that category are summarized in table 4.

5.3.1. TA13

The TA13 benchmark set includes thirteen small binary radical-solvent complexes like lithium water dimer.⁴³ For the MP2 methods, orbital optimization is necessary in this benchmark set to remove spin-contamination of the reference orbitals as illustrated by the improvement of κ-OOMP2 (0.88 kcal/mol) over standard MP2 (using canonical UHF reference orbitals, 2.14 kcal/mol). The maximum deviation in MP2 is seen in the HF···CO⁺ dimer with −5.07 kcal/mol. However, the RMSD for MP2 can be further decreased to 1.65 kcal/mol by using a restricted-open shell HF (RO-HF) reference.¹²⁹ Among the third-order methods, the top performer is unscaled MP3:κ-OOMP2 with an RMSD of 0.63 kcal/mol and the largest deviation is seen in H₂O···Al dimer with 1.04 kcal/mol. Scaling of the third-order energy significantly increases the error to 0.93 kcal/mol. This stems mainly from overbinding of both the H₂O· · ·F and H₂O· · ·Cl with the scaled MP3 energy contribution. All complexes are sensitive to the charge delocalization error and consequently both B3LYP (3.85 kcal/mol) and ωB97M-V (2.85 kcal/mol) perform poorly. CCSD performs similarly to κ-OOMP2 with an RMSD of 0.89 kcal/mol. Overall the top performer is MP3:κ-OOMP2 with an RMSD of 0.63 kcal/mol.

5.3.2. XB18

The XB18¹⁰² contains 8 halogen bonded complexes such as Br₂··· NCH (we omitted the 10 iodide containing complexes originally included). Furthermore, we used a slightly different computational set-up: the aug-cc-PVTZ-PP basis and the corresponding ECP were used for Br¹²² and the frozen core approximation was employed to harmonize with the reference values which were also generated with aug-cc-PVTZ-PP and ECP for Br.¹⁰²

Among the second-order methods κ-MP2 (0.26 kcal/mol) performed best followed by standard MP2 (0.31 kcal/mol). Notably, orbital optimization worsens the results for both κ-OOMP2 (0.50 kcal/mol) and OOMP2 (1.01 kcal/mol). Among the third-order methods, MP2.5:κ-OOMP2 performs best (0.35 kcal/mol) performing slightly worse than the MP2 methods. The top MP methods outperform B3LYP (0.37 kcal/mol) and are similar to ωB97M-V: (0.27 kcal/mol). CCSD performs worse than most MP methods with an RMSD of 0.66 kcal/mol suggesting that the inclusion of CC triples is important for halogen bonding motifs. In contrast, SCS(MI)-CCSD performs remarkably well with an RMSD of 0.11 kcal/mol (SCS(MI)-CCSD/aQZ); RMSD adjusted to the subset investigated here. Overall, the top performing method is κ-MP2 with an RMSD of 0.26 kcal/mol.

5.3.3. Bauza30

The Bauza30^103,130 data set includes 30 small halogen, chalcogen, and pnicogen bonded complexes, e.g. the Cl⁻· · ·BrF complex. The top performer is standard MP2 with an RMSD of 0.72 kcal/mol. Both regularization and orbital optimization increase the RMSD (κ-MP2: 0.98 kcal/mol, OOMP2: 1.76 kcal/mol). The runner-up is MP2.5:κ-OOMP2 with an RMSD of 0.88 kcal/mol which is still a significant improvement over B3LYP (RMSD: 1.87 kcal/mol). However, all MP methods perform worse than ωB97M-V with an RMSD of 0.59 kcal/mol.

5.3.4. CT20

The CT20¹⁰⁴ data set is comprised of 20 small ground state charge-transfer complexes of NF₃ with HCN, HNC, HF, or ClF. All MP2 methods perform very similarly but the top performer is κ-MP2 (0.10 kcal/mol). Among the third-order methods, MP3:OOMP2 (RMSD of 0.09 kcal/mol) and MP3:κ-OOMP2 (RMSD of 0.10 kcal/mol) also achieve virtually the same accuracy. All MP methods outperform B3LYP, which has an RMSD of 0.28 kcal/mol, but not ωB97M-V, which has an RMSD of 0.08 kcal/mol.

5.3.5. XB51

The XB51¹⁰² contains 20 halogen bonded complexes such as Br₂· · ·FCCH dimer; we omitted the 31 iodide containing complexes and the HLi complex following ref. 73. Furthermore, we used a slightly different computational set-up: the aug-cc-PVTZ-PP basis and the corresponding ECP were used for Br¹²² and the frozen core approximation was employed to harmonize with the reference values which were also generated with aug-cc-PVTZ-PP and ECP for Br.¹⁰²

Among the second-order methods, MP2 (RMSD: 0.36 kcal/mol) and κ-MP2 (0.36 kcal/mol) and κ-OOMP2 (0.36 kcal/mol) perform similarly. Interestingly both MP2 and κ-OOMP2 also slightly overbind with MSDs of −0.24 kcal/mol and −0.16 kcal/mol, respectively; but κ-MP2 underbinds with an MSD of 0.21 kcal/mol. Among the third-order methods, the top performer is MP2.5:κ-OOMP2 with an RMSD of 0.34 kcal/mol and a MSD of −0.25 kcal/mol suggesting that MP2.5:κ-OOMP2 slightly overbinds. MP2.5:κ-OOMP2 improves upon MP2.5 (0.54 kcal/mol) but is only slightly better than MP2. For comparison, B3LYP-D3 performs significantly worse with an RMSD of 1.05 kcal/mol, while but ωB97M-V performs well with an RMSD of 0.26 kcal/mol. Interestingly, both MP2.5:κ-OOMP2 and κ-OOMP2 outperform the more expensive CCSD (CCSD/aTZ) with an RMSD of 0.67 kcal/mol (adjusted to the subset investigated here).

5.3.6. Orel26rad

The Orel26¹⁰⁵ data set comprises 26 cationic radical dimer complexes of aromatic (hetero)cycles, such as py^•+ · · · py (where py is pyridine). The largest system is the tetrathia-fulvalene dimer complex (28 atoms). We use ROHF as a reference for the MP2 results as suggested in ref. 105 due to severe spin contamination in the UHF wave function for these systems. UKS and UOOMP2 are employed as those theories are less prone to spin contamination due to inclusion of electron correlation in the SCF procedure. We note that properly converging ROHF (and RO-SCF in general) can be significantly more challenging than UHF and thus is less desirable.

Among second-order methods, the top performer is κ-OOMP2 with an RMSD of 0.59 kcal/mol. κ-MP2 (RO reference) with an RMSD of 1.53 kcal/mol significantly improves on standard MP2 with an RMSD of 3.03 kcal/mol. MP2 strongly overbinds these dispersion-dominated interactions with an MSD of −2.36 kcal/mol (maximum deviation of −6.08 kcal/mol for the bithiophene dimer (π-stacked)). Interestingly, κ-regularization seems to slightly over-regularize which results in underbinding with an MSD of 1.29 kcal/mol. The maximum deviation is 2.91 kcal/mol for the thiophene dimer (π-stacked). In contrast, κ-OOMP2 only slightly overbinds with an MSD of −0.26 kcal/mol and a small and balanced spread of errors. The largest deviation is the bithiophene dimer (−1.32 kcal/mol); see boxplots in Fig. 6.

Figure 6:

Boxplots of the Orel26rad data set for (a) MP2 methods, (b) MP3 methods. Red lines mark the median deviation, boxes bound the central 50% of the data, whiskers enclose all data points within 1.5 times the inter-quartile range of the box edges, and points denote outlying data. DFT and MP2.5:κ-OOMP2 are included in all plots for comparison.

We used a more compact basis (def2-tzvpd^117,118 and corresponding auxiliary basis^119–121) for the MP3 calculations of the eight larger systems to reduce the computational cost (tetrathiafulvalene, thienothiophene, bifuran and bithiophene complexes; two isomers each). We checked the difference between aug-cc-pVTZ and def2-tzvpd for a few cases and the differences in the interaction energies were between 0.2–0.5 kcal/mol (pyridine dimer, thiophene and thienothiophene; see SI). Thus, the reported RMSDs for the MP3 methods have a mixed basis. However, the same trends hold if the larger systems are excluded. The top performer among the MP3 methods is MP2.5:κ-OOMP2 with an RMSD of 0.78 kcal/mol and an MSD of −0.58 kcal/mol. The maximum deviation is the thiophene dimer (−1.29 kcal/mol).

For context, these systems are quite challenging even for good hybrid DFT methods due to delocalization error, as illustrated by the high RMSDs of B3LYP-D3 (5.67 kcal/mol) and ωB97M-V (1.59 kcal/mol).

In summary, both MP3 and the κ-regularizer damp the correlation energy to avoid strong overbinding. κ-OOMP2 is recommended for these systems as the top performer. It restores spin-symmetry and yields accurate binding energies at moderate cost.

5.3.7. Discussion

The TA13 and Orel26rad results show the importance of good reference orbitals for radical and aromatic systems as a poor mean-field reference yields artificial symmetry breaking. This is illustrated by the good performance of κ-OOMP2 in both data sets. The κ-regularizer improves the energetics in both cases for OOMP2 (but for MP2 only in Orel26rad).

In the NCD data category the optimal c₃ deviates from 0.5 in several data sets: TA13 is the only data set where the unscaled MP3:κ-OOMP2 is the top performer as there is no minimum for the scaling parameter c₃ between 0.0 and 1.0. The optimal scaling for halogen bonding seems to be around 0.7 for both M2.X:OOMP2 and MP2.X:κ-OOMP2 but 0.2 for MP2.X. Similary for CT20, the optimal c₃ parameters are 0.80 for MP2.X:κ-OOMP2, 0.85 for MP2.X:OOMP2 and 0.15 for MP2.X.

For halogen bonding, standard MP2 performs remarkably well. It is the top performer in Bauza30 and performs only slightly worse than the top performing MP3 methods in XB18 and XB51. The top performer for halogen bonding is MP2.5:κ-OOMP2 but it provides less than 0.1 kcal/mol improvement for the XB sets and performs worse than MP2 in Bauza30 and thus is not worth the higher compute cost.

5.4. Potential energy surfaces

In order to gauge any distance dependence of our conclusions on accuracy of MP2 and MP3-based methods, we investigated potential energy surface (PES) scans for a few important NCI binding motifs. For dispersion-dominated interactions we chose the benzene dimer; the reference geometries and values are taken from the NBC10 data set.^97,131 We also use two hydrogen bonding motifs from S66×8:¹⁰⁰ the water dimer and methylamine (CH₃NH₂) dimer (classified as a mixed interaction).

The benzene dimer PES consists of 17 points from 3.2 to 10 Å. MP2 over-binds significantly, yielding an RMSD of 1.62 kcal/mol. The top performer is SCS-MP2 with an RMSD of 0.05 kcal/mol. Both κ-regularization (κ-MP2 0.36, κ-OOMP2 0.27) and all three MP2.5 methods also yield high accuracy (MP2.5 0.14, MP2.5:κ-OOMP2 0.13, MP2.5:OOMP2 0.08). The PESs for MP2, κ-MP2, κ-OOMP2, MP2.5, MP2.5:κ-OOMP2 (including the CCSD(T) reference values taken from ref. 97) are depicted in the left panel of Fig. 7. The plot shows that all methods besides standard MP2 produces accurate PESs. However, κ-MP2, κ-OOMP2, and MP2.5 underbind around the minimum, whereas MP2.5:κ-OOMP2 slightly overbinds (~0.15 kcal/mol).

Figure 7:

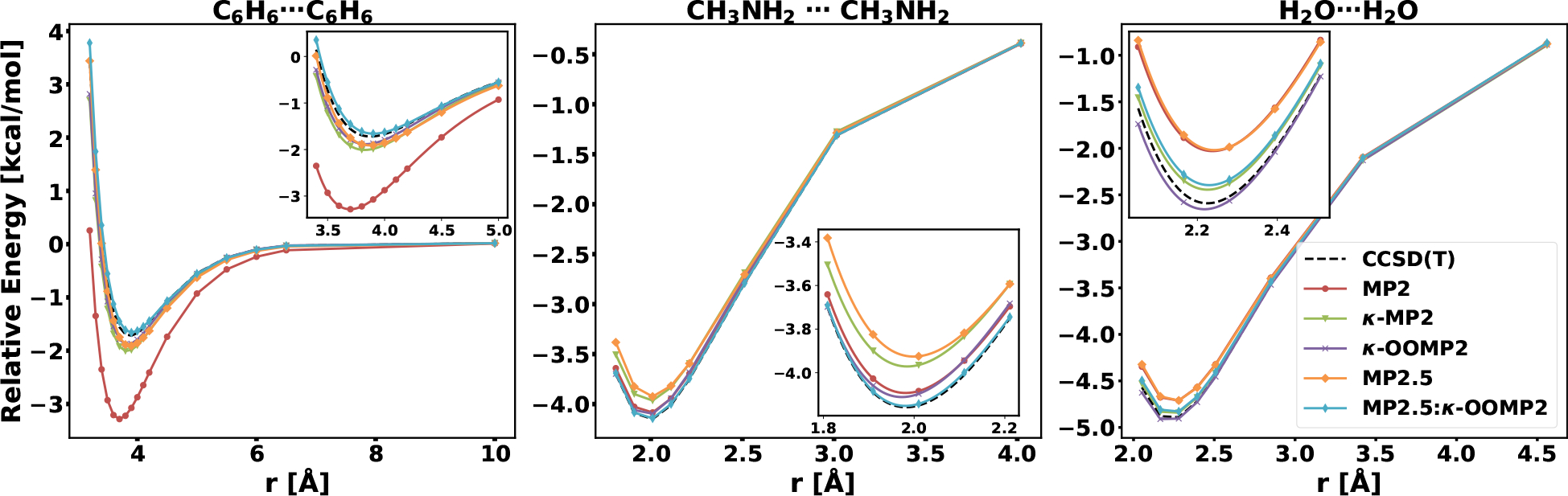
PES scan of the π-stacked benzene dimer with insets for the minimum region (geometries and reference values taken from the NBC10^97,131 data set and PES scan of CH₃NH₂ dimer and water dimer (geometries and reference values taken from the S66×8¹⁰⁰ data set).

Next, we investigate two hydrogen binding motifs from S66×8;¹⁰⁰ in both cases 8 points are taken along the PES based on the scaled equilibrium bond distance (r₀): 0.90, 0.95, 1.0, 1.05, 1.10, 1.25, 1.50, 2.0, where r₀ is 2.01 Å for the H₂O dimer and 2.28 Å for the CH₃NH₂ dimer. The top performer for the combined surfaces are κ-OOMP2, MP2.5:κ-OOMP2 and MP2.5:OOMP2 all with an RMSD of 0.04 kcal/mol. Both OOMP2 (0.10 kcal/mol) and κ-MP2 (0.11 kcal/mol) perform similarly to MP2 (0.11 kcal/mol), but SCS-MP2 performs significantly worse (0.63 kcal/mol). The PESs are depicted in Fig. 7, MP2.5 significantly underbinds around the minimum for both hydrogen bonds, MP2 underbinds for the water dimer and κ-MP2 for CH₃NH₂ dimer. κ-OOMP2 and MP2.5:κ-OOMP2 produce very accurate PES for both hydrogen bonding motifs.

5.5. Use of KS-DFT Orbitals for MP2.X

Another possible choice for reference orbitals, which already incorporate electron correlation, are KS-DFT orbitals. Our group recently demonstrated similar performance of (κ-)OOMP2 orbitals and KS-DFT orbitals for MP3 and MP2.X methods.¹⁰⁸ In addition, these results were robust with respect to the functional choice; even local functionals provided a good set of reference orbitals.¹⁰⁸ Consequently, the MP2.X:DFT is a potential alternative, especially if (κ-)OOMP2 capabilities are not available in the software package of choice.

To this end, we tested MP3:ωB97X-V and MP2.5:ωB97X-V for a subset of data sets. We not only use classic NCI data sets as A24 and S22 but also include those where charge delocalization is more prominent like Ionic43, TA13 and Orel26rad; the results are summarized in Table 6. In most cases the performance of significantly better MP2.5:ωB97X-V is better than MP3:ωB97X-V (except in TA13) and thus the following discussion focuses on the former. The performance of MP2.5:ωB97X-V is comparable to MP2.5:κ-OOMP2, even slightly better in some cases. For instance, in S22, the RMSD of MP2.5:ωB97X-V is 0.08 kcal/mol, a factor of two lower than MP2.5:κ-OOMP2, which is the top performing MP method. A similar trend is observed for the A24 data set: MP2.5:ωB97X-V outperforms MP2.5:κ-OOMP2 slightly with an RMSD of 0.07 kcal/mol. We note, however, that such an error reduction occurs at an energy scale comparable to the basis set error.

Table 6:

Results of MP3:ωB97X-V and MP2.5:ωB97X-V for A24, S22, Ionic43, TA13 and Orel26rad (8 data points omitted, see main text); for reference we included the results of κ-MP2, κ-OOMP2, MP3:κ-OOMP2 and MP2.5:κ-OOMP2; RMSD in kcal/mol. For each data set, all method cells are colored in a heatmap from green to yellow to red. Low RMSDs are represented in green and high RMSDs in red.

	A24	S22	Ionic43	TA13	Orel26rad
κ-MP2	0.16	0.50	0.74	2.46	1.72
κ-OOMP2	0.16	0.65	0.53	0.88	0.45
MP3:κ-OOMP2	0.20	1.38	1.09	0.62	3.94
MP2.5:κ-OOMP2	0.09	0.18	0.63	0.93	0.92
MP3:wB97X-V	0.19	1.24	1.10	0.70	3.96
MP2.5:ωB97X-V	0.07	0.08	0.62	1.27	0.71
ωB97M-V	0.09	0.28	0.70	2.85	1.00
ωB97X-V	0.08	0.30	0.81	3.08	2.02

Interestingly, as seen for Ionic43, TA13 and Orel26rad in Table 6, MP2.5:ωB97X-V works reasonably well even when the KS orbitals themselves behave poorly due to self-interaction error (SIE). For Ionic43, MP2.5:ωB97X-V performs well with an RMSD of 0.62 kcal/mol, similar to MP2.5:κ-OOMP2 (RMSD: 0.63 kcal/mol) and ωB97M-V (RMSD: 0.70 kcal/mol) but is not able to outperform the top performer κ-OOMP2 (RMSD: 0.53 kcal/mol). The TA13 data set comprises systems which are strongly affected by SIE and consequently most functionals perform poorly (e.g. ωB97M-V with an RMSD of 2.85 kcal/mol). Nonetheless, MP3:ωB97X-V performs surprisingly well with an RMSD of 0.70 kcal/mol, which is close to MP3:κ-OOMP2 (RMSD: 0.62 kcal/mol). This is surprising especially when considering the good performance of κ-OOMP2 itself (RMSD: 0.88 kcal/mol) versus the poor performance of density functionals on this set. For the Orel26rad data set we omitted the eight larger systems involving tetrathiafulvalene, thienothiophene, bifuran and bithiophene complexes due to computational cost. Consequently, we adjusted the RMSD for the other methods to that subset accordingly to assure comparability. MP2.5:ωB97X-V performs similarly to both MP2.5:κ-OOMP2 and ωB97M-V.

In summary, MP2.5:ωB97X-V is a comparable method to MP2.5:κ-OOMP2 and is also surprisingly reliable even for systems where spin-contamination is present, see table 7 for a detailed comparison using various metrics.

Table 7:

Comparison (via RMSD, MSD and largest outlier (MaxDev)) of MP2.5:κ-OOMP2 and MP2.5:ωB98X-V for for A24, S22, Ionic43, TA13 and Orel26rad (8 data points omitted, see main text); in kcal/mol.

Method	MP2.5:κ-OOMP2			MP2.5:ωB97X-V
Set	RMSD	MSD	MaxDev	RMSD	MSD	MaxDev
A24	0.09	0.08	0.24	0.07	0.05	0.16
S22	0.18	0.00	−0.46	0.08	0.02	−0.23
Ionic43	0.63	0.47	1.94	0.62	0.42	2.01
TA13	0.93	0.07	−2.28	1.26	−0.37	−3.64
Orel26rad	0.93	−0.82	−1.29	0.71	−0.60	−1.12

6. Conclusions

In summary, this work systematically assesses the influence of reference orbitals, regularization and scaling on the performance of second- and third-order Møller-Plesset perturbation theory wavefunction methods for non-covalent interactions (NCI). We employ 19 data sets (A24,⁷² DS14,⁸⁸ HB15,⁸⁹ HSG,⁹⁰ S22,²² X40,⁷⁸ HW30,⁹¹ NC15,⁹² S66,⁷⁷ AlkBind12,⁹³ CO2Nitrogen16,⁹⁴ HB49,⁹⁵ Ionic43,⁹⁶ TA13,⁴³ XB18,¹⁰² Bauza30¹⁰³, CT20,¹⁰⁴ XB51,¹⁰² Orel26rad¹⁰⁵) covering a wide range of NCI. The data is sub-divided into “easy dimers” (NCED; 356 data points), and “difficult” systems (NCD) that are subject to delocalization errors in DFT and spin-contamination in UHF. Furthermore, we include PESs from different hydrogen bonds and dispersion-bound complexes to gauge the accuracy for non-equilibrium geometries.

We test 15 perturbation theory based methods: MP2, κ-MP2, SCS-MP2, OOMP2, κ-OOMP2, MP3, MP2.5, MP3:OOMP2, MP2.5:OOMP2, MP3:κ-OOMP2, MP2.5:κ-OOMP2, and κ-MP3:κ-OOMP2, κ-MP2.5:κ-OOMP2, MP3:ωB97X-V, and MP2.5:ωB97X-V. Furthermore, we compare these methods to the density functionals ωB97M-V and B3LYP-D3 and CCSD. The main findings from this study are:

1. MP2.5:κ-OOMP2 is a very accurate method for NCI providing accurate results in nearly all data sets invested in this study (RMSD on the NCED data category: 0.25 kcal/mol). The improvement over standard MP2.5 is quite statistically significant (RMSD on the NCED data category: 0.50 kcal/mol) Furthermore, MP2.5:κ-OOMP2 performs also well for radical systems, halogen bonding and provides accurate PESs. It performs at least comparably to CCSD and even the spin-scaled CCSD method with parameters specifically optimized for NCI (SCS(MI)-CCSD⁷⁶). Furthermore, we investigated the effect of Kohn-Sham density functional reference orbitals (using ωB97X-V⁷⁹) for NCI as a previous study found promising results.¹⁰⁸ We find that ωB97X-V reference orbitals perform very similarly to using κ-OOMP2 orbitals even in NCD benchmark sets where the self-interaction error is prominent, such as Ionic43, Orel26rad and TA13.

2. We investigated the optimal scaling parameter for all scaled MP3 methods and find that a scaling factor near 0.5 is optimal for the Hartree-Fock reference and also for both OOMP2 and κ-OOMP2 reference orbitals based on the S66⁷⁷ benchmark set (optimal c₃ values were 0.45, 0.55, and 0.60 for MP2.X, MP2.X:κ-OOMP2, and MP2.X:OOMP2, respectively). These optimized parameters were similar for the entire NCED super set (optimal c₃ values were 0.35, 0.50, and 0.55 for MP2.X, MP2.X:κ-OOMP2, and MP2.X:OOMP2, respectively)

3. Limiting ourselves to second order perturbation theory, we find the substantial improvements over MP2 are attained using a κ-MP2 with $\kappa =1.45E_h^{-1}$, with κ-OOMP2 performing slightly better. It is noteworthy that this value was determined based on the W4-11 thermochemistry benchmark set, and was not optimized for NCI.⁴⁰ The RMSD for the NCED data category (356 data points) is 0.33 kcal/mol for κ-OOMP2 and 0.37 kcal/mol for κ-MP2; both improve upon standard MP2 by almost a factor of two (RMSD MP2: 0.63 kcal/mol). In radical systems κ-OOMP2 provides clearly better results as it removes spin-contamination of the reference and damps unphysical contributions to the correlation energy. This is illustrated by the excellent performance of κ-OOMP2 in Orel26rad (RMSD: 0.59 kcal/mol vs 1.53 kcal/mol for κ-MP2 and 3.03 kcal/mol for MP2) and TA13 (RMSD: 0.88 kcal/mol vs 2.46 kcal/mol for κ-MP2 and 2.14 kcal/mol for MP2).

4. We obtain high accuracy in a medium sized basis (aug-cc-pVTZ) with non-HF orbitals (either κ-OOMP2 or DFT) and scaling of the third-order contribution. The success of these MP2/MP3 methods versus CCSD(T) at the complete basis set (CBS) limit is encouraging, and indicates that modified double excitations can compensate for the lack of triples and basis set incompleteness. Accordingly, the scaling of the third-order methods is basis set dependent. We showed that 0.5 is optimal with a triple-zeta basis to approximate CCSD(T)/CBS results. However, a larger fraction of the third-order correlation energy is optimal when a larger basis is used or when CCSD(T) with a finite basis is used as a reference. This means that our results are broadly compatible with the recent success of MP2.8:κ-OOMP2 and MP2.8:DFT against CCSD(T) in a triple zeta basis,^71,108 on a far more limited set of NCI tests, and some thermochemistry test sets.