Volumetric ²³Na Single and Triple-Quantum Imaging at 7T: 3D-CRISTINA

Abstract

Purpose

To measure multi-quantum coherence (MQC) ²³Na signals for noninvasive cell physiological information in the whole-brain, the 2D-CRISTINA method was extended to 3D. This experimental study investigated the use and results of a new sequence, 3D-CRISTINA, on a phantom and healthy volunteers.

Methods

The 3D Cartesian single and triple-quantum imaging of ²³Na (3D-CRISTINA) was developed and implemented at 7T, favoring a non-selective volume excitation for increased signal-to-noise ratio (SNR) and lower energy deployment than its 2D counterpart. Two independent phase cycles were used in analogy to the 2D method. A comparison of 6-steps cycles and 12-steps cycles was performed.

We used a phantom composed of different sodium and agarose concentrations, 50 mM to 150 mM Na+, and 0–5% agarose for sequence validation. Four healthy volunteers were scanned at 7T for whole brain MQC imaging. The sequence 3D-CRISTINA was developed and tested at 7T.

Results

At 7T, the 3D-CRISTINA acquisition allowed to reduce the TR to 230 ms from the previous 390 ms for 2D, resulting in a total acquisition time of 53 min for a 3D volume of 4 × 4 × 8 mm resolution. The phase cycle evaluation showed that the 7T acquisition time could be reduced by 4-fold with moderate single and triple-quantum signals SNR loss. The healthy volunteers demonstrated clinical feasibility at 7T and showed a difference in the MQC signals ratio of White Matter (WM) and Grey Matter (GM).

Conclusion

Volumetric CRISTINA multi-quantum imaging allowed whole-brain coverage. The non-selective excitation enabled a faster scan due to a decrease in energy deposition which enabled a lower repetition time. Thus, it should be the preferred choice for future in vivo multi-quantum applications compared to the 2D method. A more extensive study is warranted to explore WM and GM MQC differences.

1. Introduction

Recently we proposed a 2D multi-quantum coherence (MQC) imaging method for ²³Na at 7T, CRISTINA [1], to fully exploit the potential of the spin 3/2 nuclei.

Sodium MRI is of interest for its noninvasive cell physiological information which are connected to multiple pathologies [2], [3], [4], [5], [6], [7], [8], [9], [10] and therefore could provide improved tissue characterization. MQC imaging focus lays on the joint measurements of single quantum (SQ) signal, for sodium concentration quantification, and triple quantum (TQ) signal, for information about the direct environment of the sodium nuclei, which differs from microscopic environment density and arises from the mechanism of biexponential relaxation.

The typical MQC three-pulses sequence leverages repetitions with a phase-cycling scheme for each quantum signal to follow different coherence pathways. CRISTINA provided an analytical understanding of phase cycling options, leading to an optimal phase-cycling design for simultaneous measurement of SQ and TQ coherence signals robust to B0 inhomogeneity, compared to the state-of-the-art SISTINA sequence that kept a bias due off-resonance phase accrual [11], [12]. The method consists of 2 × 6 steps phase cycles with a phase-increment of π/6. In the first cycle, the start phase for the first pulse is π/2, and the phase difference between the first and second pulse is also π/2. The second cycle has a start phase of 0 (first pulse) and a phase difference of 0 between the first and second pulse.

The experimental results were limited so far to elongated acquisitions for a single 2D plane [1]. The purpose of this study is to communicate practical benefits from the development of volumetric 3D-CRISTINA for 7T.

So far, the three pulses [13], multi-echo 2D-CRISTINA sequence was lacking a volumetric acquisition, needed for improved resolution, an extended field of view, and partial volume effects reduction to reach towards larger scale in vivo explorations. Further, the long acquisition times at 7T of up to an hour mainly due to an elongated repetition time (TR) of 390 ms from specific absorption rate (SAR) restrictions, with conservative 12-step sampling and 10-fold averaging for a single slice was too long for multi-slice acquisition. The long TR was needed to reduce the SAR of the sinc-shaped, slice selective excitation.

A barrier of ²³Na MRI is the low SNR and resulting long acquisition times which is why the higher field strength of 7T was favoured due to the supralinear rise of SNR with the static magnetic field B0 [14]. The purpose of this paper is to present 3D-CRISTINA feasibility at 7T. A phase cycle optimization led to the decrease of the total measurement time from 66 min to 32 min (phantom) and from 53 min to 13 min (in vivo). With 3D-CRISTINA, 3D single and triple quantum Images can be obtained simultaneously, within a reasonable acquisition time at 7T. The time efficiency of 3D-CRISTINA is validated on phantom measurements and MQC images are shown in vivo on four healthy volunteers.

2. Material and methods

2.1. Sequence development

The 2D-CRISTINA sequence [1] (Figure 1a) was modified for the 3D-CRISTINA sequence (Figure 1b) to feature a volumetric, multi-echo acquisition for joint multi-quantum signals and tissue sodium concentration (TSC) characterization. 3D-CRISTINA allows for a non-selective excitation to be employed with 3D Cartesian k-space sampling. CRISTINA used an optimal phase-cycle scheme of 2 × 6 = 12 steps with 1) first pulse start phase of π/2, a phase difference between the first and second pulse of π/2 and 2) first pulse start phase of 0 and phase difference between first and second pulse also 0 with a phase increment of π/6 was acquired. A detailed description about the underlying theory and choice can be found here: [1].

Figure 1.

The previous 2D-CRISTINA sequence (a) featuring three pulses for multi-quantum excitation, was extended to 3D-CRISTINA (b) by adding an additional phase encoding direction and substituting the slice selection by a non-selective excitation.

2.2. Experimental validation

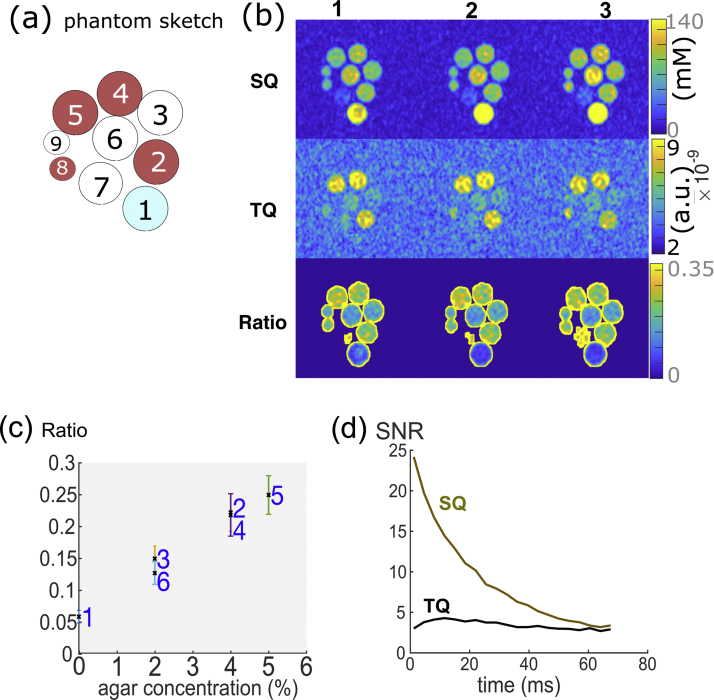
The sequence was tested on an agarose phantom on a 7T scanner (Siemens Healthcare, Magnetom 2^nd generation whole body research system, Erlangen, Germany) with a 1Tx/1Rx dual-tuned ¹H/²³Na birdcage head coil (Rapid, Biomedical). The phantom consisted of 9 tubes (14 and 40 mL) with varying concentrations of agarose (0–5%) and sodium (50–154 mM) (see Figure 2A).

Figure 2.

(a) Phantom design for subsequent sequence evaluation composed of nine tubes with different agar (in %) and sodium concentration (in mM): 1) 0%, 154 mM, 2) 4%, 100 mM, 3) 2% agar, 100 mM, 4) 4%, 154 mM, 5) 5%, 154 mM, 6) 2% 130 mM, 7) 4%, 50 mM, 8) 4%, 100 mM, 9) 2%, 100 mM. Phantom vial 8 and 9 have a much smaller volume with 14 mL compared to the 2–5 with 40 mL. The phantom vials indicated in red correspond to the high agar vials containing >4% agar. (b) Phantom result of 3D-CRISTINA, SQ and TQ signal and their ratio for 3 central slices each. (c) For the ratio versus agar concentration evaluation without phantom 7–9 the result was: R2 = 0.987, p = 6e−5. (d) The SNR of TQ and SQ over echo time shows the characteristic signal evolution respectively.

Signal-to-noise ratio (SNR) was evaluated as the mean signal in a region of interest (ROI) covering the brain over the standard deviation of the signal in a background ROI outside of the brain. A correction factor of 0.655 was applied to account for the Rayleigh distribution of background noise. SNR of the two 40 mL tubes with 100 mM of sodium and 4 and 5% agarose was compared between the 3D-CRISTINA and the 2D-CRISTINA images as previously described [1] for each echo time. The SNR was further corrected for the voxel size to evaluate SNR variation associated with 3D excitation.

The dataset was further downsampled along the phase cycle dimension to investigate optimal choice for phase cycling options to further reduce acquisition time. Detailed sequence parameters are listed in Table 1. The vendor internal shimming procedure was repeated at least three times, carefully checking the frequency offset to be zero before each ²³Na scan. An incremental free-induction decay-based B1+ calibration was carried out before each scan to calculate the exact reference voltage for the 90° pulses.

Table 1.

3D Sequence Parameters at 7T. In vivo, the TR varied from the first to the second volunteer due to a higher reference voltage and SAR restriction. The TR was fixed to a higher parameter for the latter two volunteers. Further parameters which did not change between phantom and in vivo scans were: ($\Delta \varphi =30°$) resulting in a phase cycle of 12 points, mixing time = 100 μs, evolution time = 10 ms, number of echoes = 20, asymmetry of echo = 0.8. Slice thickness 3D = 15 mm (in vivo), 8 mm (phantom).

3D_CRISTINA PARAMETERS	Phantom	In vivo volunteers (1–4)
matrix size	48 × 48 × 14 × 20 × 24	32 × 32 × 12 × 20 × 24
size after zero filling	256 × 256 × 14 × 20	128 × 128 × 12 × 20
base resolution	48	32
FOV resolution	200 mm 4 × 4 × 8 mm3	250 mm 7.8 × 7.8 × 15 mm3
1st pulse duration	1800 μs	1800
2nd/3rd pulse duration	1000 μs	1000
TE1, ΔTE	1.6 ms	1.6 ms
TR	160 ms	230 ms
Bandwidth	400 Hz/px	400 Hz/px
Phasecycles	2	2
total scan time	2 × 32.8 min = 66 min	2 × 26.7 min = 53 min
xRef Voltage	406 V	438 V, 452 V, 415 V, 437 V

2.3. In vivo validation

Four healthy volunteers (1 woman, 3 men, 21 ± 0.5 years old) were recruited after providing informed consent according to the Declaration of Helsinki. The study was approved by the local ethical committee. Four additional 60 mL phantom vials were placed next to the head for sodium quantification, containing 5% and 2% agarose each with 100 mM and 50 mM Na+ concentration. The phantoms were fixed to the subjects’ head with an elastic band. Additionally, to achieve TSC quantification the cerebrospinal fluid (CSF) Na⁺ literature value of 145 mM was used [15]. For one healthy volunteer we retrospectively undersampled the data to virtually reduce the measurement time according to the phantom 7T data.

2.4. Data reconstruction and fit

In analogy to the data reconstruction for the 2D-CRISTINA sequence, the reconstruction was extended to 3D including the additional slice dimension. A 3D B0 map was calculated from the first two echoes of the CRISTINA phase data to map the signal off-resonances for combination of the two phase cycles (${\xi }_1=\pi /2\text{and}{\xi }_2=0$) according to the method of Fleysher et al. [16] The voxel-wise multiparametric fit was updated to perform a joint fit of SQ and TQ signal, using GlobalSearch and fmincon solver in Matlab (R2019a, Mathworks, Natick, MA, USA), providing T2*slow and T2*fast maps. In the occurrence of one aberrant T2* value, the signal fit was reverted to a mono-exponential decay (as in the case of pure saline). The cost function of the fit was implemented to weight the TQ signal first echoes higher than the later echoes and the SQ signal. The first echoes were chosen empirically to range from one to eleven to follow the characteristic curve of the TQ signal (see Figure 1) and to weight down the later echoes which have lower SNR (see Eq. (1), (2), (3)).

$$\begin{array}{cc}\hfill f_{fitTQ\_\left(i\right)\left(x\right)}=A_{TQ}\left(\exp \left(-\frac{TE}{T2s^{*}}\right)-\exp \left(-\frac{TE}{T2f^{*}}\right)\right)\text{exp}\left(-\frac{\tau 1}{T2s^{*}}\right)+D{C}_{TQ};\hfill & \hfill i=\mathrm{1,2}\left(*\right)\hfill \end{array}$$ (1)

$$f_{fitSQ}\left(x\right)=\left(A_{SQ1}\text{exp}\left(-\frac{TE+\tau 1+\tau 2}{T2s^{*}}\right)+A_{SQ2}\text{exp}\left(-\frac{TE+\tau 1+\tau 2}{T2f^{*}}\right)\right)\text{exp}\left(-\frac{TE+\tau 1+\tau 2}{T2s^{*}}\right)+D{C}_{SQ}$$ (2)

$$L{2}_{\left(x\right)}=\text{w}1*\Sigma {\left({\text{TQ}}_{\text{data}\left(\text{TE}\_1:\text{TE}\_11\right)}-f_{\text{fitTQ}\_1}\left(\text{x}\right)\right)}^2+\text{w}2*\Sigma {\left({\text{TQ}}_{\text{data}\left(\text{TE}\_12:\text{TE}\_21\right)}-f_{\text{fitTQ}\_2}\left(\text{x}\right)\right)}^2+\text{w}2*\Sigma {\left({\text{SQ}}_{\text{data}}-f_{\text{fitSQ}}\left(\text{x}\right)\right)}^2\left(**\right)$$ (3)

The variables in Eq. (1), (2), (3) are:

A_TQ = triple quantum signal amplitude, A_SQ1 = single quantum amplitude slow term, A_SQ2 = single quantum amplitude fast term, DC_TQ,SQ = DC offset to account for noise, TE = echo time, T2s* = T2*slow, T2f* = T2*fast, τ1 = evolution time, τ2 = mixing time. ^(*) The TQ fit was split into two parts f_{fitTQ_1} and f_{fitTQ_2}: 1) data for echoes 1 to 11 that includes the expected TQmax signal and 2) data from echo 12 to the latest echo, after the expected TQmax signal, to allow for different weighting in the cost function L2.

^(**) w1, w2 = weightings. The weightings were empirically optimized to w1 = 0.8 and w2 = 0.2. The fit routine included both T2*fast and T2*slow with boundary settings T2*fast: [2 ms; 10 ms] and T2*slow [8 ms; 55 ms].

2.5. Phase cycle optimization

The phase increment of the chosen phase cycle was initially chosen with 30° to conform to Nyquist criterion of sampling the signal along the phase axis with twice the frequency of interest (i.e. 12 steps cycles). The minimum number of steps is 6 [1], with corresponding phase increment of 60°, for the TQ acquisition and a decrease to 30° increment results in a 2-fold measurement time increase. As an optimization of efficacy, 12-step ($\Delta \varphi =30°$) datasets were subsampled into the 6-step subset of $\Delta \varphi =60°$ with the initial start phase of ${\varphi }_1\left(t=0\right)=90°$. Additionally, two averages were used to obtain higher SNR within allotted time. The initial 12-steps 2-averages results were compared to the minimal 6-steps 1-average subset results in terms of SQ and TQ SNR, both in vitro and in vivo.

2.6. Data evaluation

We calculated the SNR of SQ and TQ along echo time within the whole image within the 6-pixel eroded body mask and the standard deviation of the noise in the background. Additionally, SNR was computed in the four 4% and 5% agar phantom vials using centered circular regions of interest, 2 pixels smaller than the outline, to avoid partial volume effects. The fit result contained T2*slow and T2*fast maps and the fitted amplitudes for A_SQslow, A_SQfast, A_TQ. The fit was performed for a single slice chosen at the center of the 3D datasets, respectively.

3. Results

3.1. Phantom results

The experimental results from 3D-CRISTINA with the phantom are given in Figure 2 for the five central slices of each dataset. Compared to previous 2D results from [1], SNR dropped by 2.27 ± 0.46-fold with chosen acquisition parameters (Supplementary Material Figure 1). When correcting for the voxel size (5.21 × 5.21 × 20 mm³ in 2D to 4 × 4 × 8 mm³ in 3D), which led to a global SNR loss of 4.24-fold, the actual SNR gain for moving from 2D to 3D was 4.24/2.27 = 1.87-fold improvement. With 3D-CRISTINA, the three phantom vials: 2, 4, and 5, with an agar concentration of 4%, 4% and 5% can be clearly distinguished from the remaining vials on the TQ image. The relationship of TQ signal to agar concentration of the different >40 mL vials, (vials 8,9 were not included due to their sizes) was linear with R² = 0.987 (Figure 2d, e). The phantom vial 7 was disregarded due to the low sodium concentration leading to a limited SNR in SQ and TQ images.

3.2. Fit results

For the center slice, a multiparameter fit was performed (Figure 3) along echo time (Equation 1–3). The average T2* values were evaluated within each phantom vial and resulted in a mean T2*_fast and T2*_slow value of the phantom vials 2, 4, 5 and 8 which contained 4% and 5% of agarose, of (T2*_fast: 5 ± 2 ms; T2*_slow: 34 ± 9 ms). For vials 3, 6, and 9, which contained 2% agarose, we obtained: T2*_fast: 8 ± 3 ms; T2*_slow: 50 ± 5 ms. Vial 7 with 4% agar and 50 mM resulted in T2*_fast of 6 ± 3 ms and T2*_slow of 44 ± 15 ms. The liquid saline solution resulted in T2*: 34 ± 11 ms.

Figure 3.

Fit result for the phantom dataset for a single slice at the center of the dataset. (a) results with the measurement and fit data side by side. The fit was performed only within the body mask therefore the Fit results and Ratios are zero in the background. (b) Resulting fit parameter maps corresponding to Eq. (1), (2), (3). The liquid vial follows a mono-exponential decay by comparing the signal amplitudes ASQslow and ASQfast maps. In the T2* maps it can be appreciated that the higher agarose phantoms show shorter relaxation times.

3.3. Phasecycle optimization results

To virtually cut down measurement time by 4× (from 53 min to 13 min in vivo, and 64 min to 16 min in the phantom), we compared the initial 12-step phase cycle ($\Delta \varphi =30°$) with two averages to a single cycle with $\Delta \varphi =60°$. The comparison of SQ and TQ signals can be seen in Figure 4 on phantom. By taking only a quarter of the data, the SQ SNR decreased by 39 ± 5% and the TQ SNR decreased by 31 ± 2%. The limited SNR drop (compared to expected 50%) reflected the influence of samples position within the phase cycle. The extra 6 steps with initial phases 120°, 180°, 240°, 300° and 360° are not participating in the TQ signal build-up as they correspond to zero-crossing of the TQ signal. Additionally, these points contributed sub-optimally to SQ signal considering their relative amplitude in the SQ coherence profile, shaped by a sinus wave. Figure 5 shows the results on in vivo data.

Figure 4.

(a) Phantom measurement comparison of TQ and SQ signal when doubling the phase cycle increment. (A) 64 min was acquired with a phase cycle increment of $\Delta \varphi =30°$ and two cycles of each 6 steps. For (B) 16 min, the increment was doubled to $\Delta \varphi =60°$, without averaging, acquiring only a fourth of the data. The SQ and TQ SNR for the whole image was evaluated in (b). Due to cutting the amount of data the SNR is higher for A than for B, however visibly the image quality is not compromised, confirming the possibility of a shorter measurement time. (c) The SNR in vial 4 shows the signal comparison for A versus B measurement time in the 4% 154 mM vial.

Figure 5.

Visual comparison of TQ and SQ signal when doubling the phase cycle increment, without averaging, in vivo for the 4 different healthy volunteers in analogy to the phantom measurement shown in Figure 4.

3.4. Invivo healthy volunteer results

Figure 6 showed the capacity of 3D-CRISTINAto visualize sodium SQ and TQ signals across the whole brain, even in regions of B0 inhomogeneity. TQ signal did not exhibit structured variations across slices, while SQ signal reflects the different concentrations of sodium between WM, GM and CSF. SQ results from the four healthy volunteers (Figure 7) showed consistent signal intensity distribution with conventional single pulse Na-MRI sequences [17]. From ROI measurements, mean TSC values showed an increase sodium concentration from WM to GM to CSF (52.9 ± 4.1, 96.6 ± 22.0 and 170.0 ± 23.9 mM respectively). Fitted signals TQ/SQ ratio exhibited a corresponding decrease from 0.28 ± 0.07 (WM) to 0.14 ± 0.04 (GM) and 0.10 ± 0.03 (CSF), reflecting a relatively homogeneous measured TQ signal in the whole brain. Figure 7 showed TQ signal variations were much lower than SQ signal variations in all volunteers. Consequently, the TQ/SQ ratio showed strong differences between gray and white matter. White matter exhibited low SQ signal, levelled TQ signal and thus higher TQ/SQ ratio, suggesting that despite a lower sodium concentration, a stronger bi-exponential signal separation derived from WM molecular environment. On the contrary, GM exhibited increased SQ signal from higher sodium concentrations, but TQ signal on the levels of WM. This relationship confirms a different balance of exponential components, with a larger component for the longer T2* decay [18]. Expectedly, CSF exhibited a negligible TQ/SQ ratio.

Figure 6.

7T in vivo results, different slices of volunteer 1. (A) T2w transversal ¹H image showing the corresponding slices. (B,C) ¹H-T2w overlay with SQ and TQ signal to relate the high intensity regions to the morphology better described by ¹H images. (D) B0 maps reconstructed from the multi-echo CRISTINA data, (E) SQ images quantified to Tissue Sodium Concentration, (F) TQ images as well as the ratio of SQ and TQ signal in (G).

Figure 7.

7T in vivo results of the four volunteers demonstrated homogeneous TQ signal within the brain, with occasional darker regions in the periphery. These signal losses might be associated with the extra B1 sensitivity of TQ signal (to the power of 5). Interestingly, the TQ/SQ ratio highlighted regions of white matter in all volunteers, and low ratio values in cerebro-spinal fluid area.

4. Discussion

In this study, 3D-CRISTINA demonstrated consistent MQ images at 7T in a dedicated agar phantom. The non-selective excitation allowed to improve the spatial resolution and decrease the acquisition time, also combined with an increase in SNR. Furthermore, the choices for phase cycling were investigated and optimized retrospectively. The conservative phase cycling of 12 ($\Delta \varphi =30°$) steps was evaluated against 6 steps ($\Delta \varphi =60°$) options in the well-controlled phantom experiments. An acquisition time reduction from 66 min to 16.4 min in the phantom was possible without moderate SNR loss in the TQ signal. The phantom results motivated in vivo exploration in healthy volunteers in the brain where we found consistent results across slices and subjects. In vivo, total scan time reached 53 min for a whole brain coverage. The same 4-fold time reduction in vivo led to limited SNR loss, motivating the use of the 6-steps cycles only, with more averages if examination time permits it. Nevertheless, further developments could improve resulting SNR within limited time, utilizing multi-channels coil hardware and/or advanced image reconstruction techniques (compressed sensing or deep learning techniques [19], [20], [21]).

For tissue sodium concentration quantification in vivo, the SQ signal at the first echo time (TE₁ = 1 ms) was employed instead of the more accurate the fitted SQ signal at TE = 0 ms to avoid potential bias introduced by the bi-exponential fitting. Additionally, TSC references were defined by the CSF and the 100 mM vial instead of the 50 mM phantom vial for accuracy. Indeed, external vials placed at the edges of the coil might experience inhomogeneous B1+ that penalizes lower signal estimation.

The in vivo data exhibited a difference of TQ/SQ ratio between GM, WM and CSF in the four volunteers. Considering WM contains myelinated structured axons while GM is made up of cell bodies, the molecular environment of sodium atoms in these compartments is expected to strongly differ. However, CSF is expected to present a very low TQ/SQ ratio from relatively free molecular environment. Our results suggest current noise levels could bias proper estimation of very low TQ signal in CSF. Nevertheless, a larger study is warranted to confirm these initial results based on only four volunteers. Further study microstructure similar to Kolbe et al. [22] could be envisioned combining 3D-CRISTINA with DTI to map these differences in regard to the brain architecture.

One limitation of this study was the loss of SNR from too ambitious spatial resolution. The reduction of the voxel size was too drastic compared to the 1.87-fold SNR improvement provided by 3D-CRISTINA. A relatively lower resolution would have better shown 3D-CRISTINA benefits. Another limitation is the limited number of in vivo data for justified GM and WM quantification. An additional T1-weighted sequence (e.g. the MP2RAGE sequence [23]) acquisition would have helped to provide a GM and WM segmentation. But the MP2RAGE sequence was designed to be employed with a multi-channel receiver coil array, requiring a change of coil which was incompatible with this study [24]. Another clear limitation is the low SQ and TQ signal of phantom vial 7 (4% agar and 50 mM ²³Na), further work is needed with standardized fabricated phantoms to explore limitations and rule out phantom ageing problems.

Further, signal variations in TQ images need to be explored to rule out variations due to B1+ field inhomogeneities. With our current coil, we measured flip angles deviation up to 10% within in the brain, which remains an acceptable precision. In addition, a comparison of healthy volunteers to pathological indications is necessary to evaluate the sensitivity of the TQ signal obtained by this sequence.

We reported an updated processing routine that is jointly fitting the SQ and TQ data to obtain T2* fast and slow parameters. We chose to weigh down the later TQ signal after TE > 15 ms in the loss function. The earlier part (TE < 15 ms) contains the characteristic curve and should be more accurate in the determination of T2* values. Nevertheless, it must be emphasized that the cost function weights were chosen empirically. The reported T2* values align with the literature [15]. We limited our conclusions for in vivo exploration based on TQ, SQ signals and their ratio, which are more consistent measures for tissue characterization than the higher complexity CRISTINA model.

While 2D-CRISTINA focused on phase cycling schemes and probing multi-quantum pathways with accuracy and efficacy, 3D-CRISTINA considers practical MRI acquisition towards in vivo sodium multi-quantum imaging. In this study, we explored the feasibility of CRISTINA in the whole brain at 7T. Next, further work towards the more readily available clinical field strength of 3T is also warranted for more accessible multi-quantum imaging. This could extend the current state of the art in sodium imaging that relies up to date on the single quantum imaging for tissue sodium characterization with ultrashort echo time sequences [25], [26].

In conclusion, the presented technological advances enabled consistent sodium MQC imaging in acceptable time for research investigations, which offers the possibility to study ionic distribution and environment in neuropathologies such as multiple sclerosis, stroke or tissue degradation after radiation therapy in dedicated protocols [27]. This step is important for the active research field of ²³Na imaging which is especially interested in the biochemical characterization of tissue.

Appendix A. Supplementary data

The following are the supplementary data to this article: