Dose-efficient assessment of trabecular microstructure using ultra-high-resolution photon-counting CT

Abstract

Photon-counting (PC) detectors for clinical computed tomography (CT) may offer improved imaging capabilities compared to conventional energy-integrating (EI) detectors, e.g. superior spatial resolution and detective efficiency. We here investigate if PCCT can reduce the administered dose in examinations aimed at quantifying trabecular bone microstructure. Five human vertebral bodies were scanned three times in an abdomen phantom (QRM, Germany) using an experimental dual-source CT (Somatom CounT, Siemens Healthineers, Germany) housing an EI detector (0.60 mm pixel size at the iso-center) and a PC detector (0.25 mm pixel size). A tube voltage of 120 kV was used. Tube current-time product for EICT was 355 mAs (23.8 mGy CTDI_{32 cm}). Dose-matched UHR-PCCT (UHRdm, 23.8 mGy) and noise-matched acquisitions (UHRnm, 10.5 mGy) were performed and reconstructed to a voxel size of 0.156 mm using a sharp kernel. Measurements of bone mineral density (BMD) and trabecular separation (Tb.Sp) and Tb.Sp percentiles reflecting the different scales of the trabecular interspacing were performed and compared to a gold-standard measurement using a peripheral CT device (XtremeCT, SCANCO Medical, Switzerland) with an isotropic voxel size of 0.082 mm and 6.6 mGy CTDI_{10 cm}. The image noise was quantified and the relative error with respect to the gold-standard along with the agreement between CT protocols using Lin’s concordance correlation coefficient (r_CCC) were calculated.

The Mean ± StdDev of the measured image noise levels in EICT was 109.6 ± 3.9 HU. UHRdm acquisitions (same dose as EICT) showed a significantly lower noise level of 78.6 ± 4.6 HU (p = 0.0122). UHRnm (44% dose of EICT) showed a noise level of 115.8 ± 3.7 HU, very similar to EICT at the same spatial resolution. For BMD the overall Mean ± StdDev for EI, UHRdm and UHRnm were 114.8 ± 28.6 mgHA/cm³, 121.6 ± 28.8 mgHA/cm³ and 121.5 ± 28.6 mgHA/cm³, respectively, compared to 123.1 ± 25.5 mgHA/cm³ for XtremeCT. For Tb.Sp these values were 1.86 ± 0.54 mm, 1.80 ± 0.56 mm and 1.84 ± 0.52 mm, respectively, compared to 1.66 ± 0.48 mm for XtremeCT. The ranking of the vertebrae with regard to Tb.Sp data was maintained throughout all Tb.Sp percentiles and among the CT protocols and the gold-standard. The agreement between protocols was very good for all comparisons: UHRnm vs. EICT (BMD r_CCC = 0.97; Tb.Sp r_CCC = 0.998), UHRnm vs. UHRdm (BMD r_CCC = 0.998; Tb.Sp r_CCC = 0.993) and UHRdm vs. EICT (BMD r_CCC = 0.97; Tb.Sp r_CCC = 0.991). Consequently, the relative RMS-errors from linear regressions against the gold-standard for EICT, UHRdm and UHRnm were very similar for BMD (7.1%, 5.2% and 5.4%) and for Tb.Sp (3.3%, 3.3% and 2.9%), with a much lower radiation dose for UHRnm. Short-term reproducibility for BMD measurements was similar and below 0.2% for all protocols, but for Tb.Sp showed better results for UHR (about 1/3 of the level for EICT). In conclusion, CT with UHR-PC detectors demonstrated lower image noise and better reproducibility for assessments of bone microstructure at similar dose levels. For UHRnm, radiation exposure levels could be reduced by 56% without deterioration of performance levels in the assessment of bone mineral density and bone microstructure.

1. Introduction

In addition to bone mineral density, trabecular bone microarchitecture is a determinant factor of bone strength [1]. Nevertheless owing to the small dimensions of trabecular struts, the assessment of trabecular bone microarchitecture in its native 3D milieu is challenging. Typical trabecular thickness and separations at the spine are about 0.14–0.20 mm and 0.5–1.3 mm, respectively [2], [3], [4], [5]. Techniques using dedicated high resolution peripheral CT equipment or dedicated imaging protocols devised for clinical CT scanners combined with sophisticated analysis software have been developed that permit evaluation of trabecular bone microstructure and to monitor physiological changes. Preferred skelettal sites have been the extremities which are less radiation sensitive, for example the calcaneus (ankle) [6], the forearm (wrist) [7] and the distal tibia [8], [9]. However, skeletal sites like the proximal femur (in particular the femoral neck) and the lumbar or thoracic spine should be preferred for fracture risk assessments. In fact, fragility or osteoporotic fractures at those skeletal sites are characterized by chronic pain, high morbidity and mortality and substantial economic costs [10]. Magnetic resonance imaging (MRI), on the other hand, is an ionizing radiation-free imaging technique. High resolution MRI can target trabecular bone structure in vivo at the central skeleton [11] but does not yield mineral density information and the relatively long scan times often result in image artifacts that complicate (but not impede) quantitative analysis. On the other hand, dual X-ray absorptiometry (DXA), a 2D projectional imaging technique, is the current radiological standard to estimate fracture risk and determine treatment pathways to follow on osteoporotic patients [10], [12]. DXA is slow in reflecting improvements in bone strength after (bisphosphonate) treatment and is only a poor predictor of fracture status in osteoporotic male patients with secondary osteoporosis [13]. Other studies performed ex vivo did not observe predictive power of vertebral bone strength by using 2D textural parameters of structure [14], [15]. High-resolution peripheral quantitative computed tomography (XtremeCT), a 3D imaging technique, currently provides the highest spatial resolution for in vivo patient studies. Spatial resolutions of 130 µm (90 µm in newer device generations) have been reported for XtremeCT systems [16], [17]. However, XtremeCT is only available for peripheral acquisitions at the forearm (radius, ulna, wrist) or distal tibia and ankle. Clinical multislice CT (MSCT) using high resolution CT protocols (HRCT), also termed high-resolution MSCT (HR-MSCT), has been used for the assessment of trabecular bone structure ex vivo and in vivo by exploiting state-of-the art clinical CT devices and protocols that deliver a high resolution image. A number of studies using human bone biopsies have shown the ability of HR-MSCT to assess trabecular bone structure at the forearm, the ankle and vertebral bodies and have successfully correlated those measurements with XtremeCT or micro-CT (µCT) [6], [7], [18], [19]. More recently, HR-MSCT derived measurements were compared with µCT using advanced microstructural algorithms for both ex vivo (ankles) and in vivo (tibiae of healthy volunteers) [9]. With respect to longitudinal in vivo studies, it has been shown that HR-MSCT derived apparent trabecular measurements like separation, number and bone volume fraction are capable of depicting treatment-induced changes in the trabecular bone compartment of osteoporotic patients [20]. Though these results showed that HR-MSCT can provide relevant information of the microstructural status at the spine, the administered radiation dose limits the scan length coverage in actual in vivo studies. At the spine, a HR-MSCT scan length between 8 and 10 cm, typically covering one or two thoracic or lumbar vertebrae, results in a radiation dose (CT dose index, CTDI_{32 cm}) of approximately 24–27 mGy, corresponding to an effective dose of 2.9–4.0 mSv for similar measurements in the abdomen. Such radiation dose represents a major hurdle for a wider application of HR-MSCT as a clinical screening tool for microstructural evaluations at the spine or hip, if there is not a particular indication for the scan.

Advances in clinical CT in recent years have been software- and hardware-based and include, but are by far not limited to, the introduction of fully iterative reconstruction methods, improved prefilters and higher scan speeds [21]. The recent FDA approval of photon-counting detectors marks the next major milestone in clinical computed tomography [22]. In the case of current energy-integrating detectors, an incoming x-ray photon is absorbed by the scintillator, typically gadolinium oxysulfide (Gd₂O₂S), which results in the emission of multiple light photons. Using reflecting lamellae, these optical photons are guided towards photodiodes or pixels, where the signal is formed. In the case of photon-counting detectors, the scintillator is replaced by a semiconductor, typically cadmium telluride (CdTe). The absorption of an incoming x-ray photon results in the formation of a charge cloud that is transported to electrodes or pixels using an applied bias voltage in the order of 1 kV [23]. To account for the high x-ray flux rates in clinical CT, the electrodes used are rather small compared to conventional detector pixels allowing for an increase in spatial resolution. Besides many favorable properties of photon-counting detectors, the high spatial resolution is of particular interest for the work presented herein. Recent studies have shown that acquisitions using the small detector pixels of PC detectors can be used to significantly reduce image noise, or conversely, lower the administered radiation dose if the high spatial resolution is not required and data are reconstructed to the lower spatial resolution of energy-integrating detectors [24], [25].

We investigate whether this effect can be used to reduce the radiation dose in acquisitions aiming at the quantification of trabecular microstructures at the spine, an interesting skelettal site for fracture risk assessment. In particular, using an energy-integrating detector and a previously described reference protocol, several scan protocols using the photon-counting detector were designed such that either dose or noise of the clinical reference HR-MSCT measurements are matched. Quantitative parameters of trabecular microstructure were obtained from the reconstructions and compared to the clinical reference protocol as well as to measurements conducted using an XtremeCT device. We hypothesized that the same microstructural information from current CT devices with energy integrating detectors could be obtained using new CT devices equipped with photon-counting detectors at a markedly reduced radiation dose. Consequently, acquisitions using a photon-counting detector conducted with the same dose as a corresponding acquisition in an energy-integrating CT can yield improved structural information.

2. Materials and methods

2.1. System

All CT measurements presented in this study were performed using an experimental whole-body photon-counting CT system (Somatom CounT, Siemens Healthineers, Forchheim Germany) [26]. This system is based on a dual-source CT (Somatom Definition Flash, Siemens Healthineers) and houses a conventional energy-integrating detector and a novel photon-counting detector allowing for a direct comparison of both technologies. The photon-counting detector offers a variety of scan modes highlighting distinct features of its technology. A scan mode referred to as ultra-high resolution (UHR) mode is of particular interest in the following. The UHR mode provides a detector pixel size of 0.25 mm (as measured in the center of rotation) and offers a spatial resolution of up to 22.4 lp/cm (MTF_10%) when appropriate ultra-high resolution kernels are used for image reconstruction. In contrast, the conventional energy-integrating detector provides a detector pixel size of only 0.60 mm in the center of rotation and higher resolutions can only be achieved using dedicated high-resolution combs or grids, introducing a siginificant dose penalty and usually prohibiting scans of body regions other than the extremities. Theoretical considerations and recent studies have illustrated that acquisitions using the UHR mode can be used to reduce radiation dose if the ultra-high spatial resolution is not required and image reconstruction is performed to the lower spatial resolution of the energy-integrating detector [27], [28]. In particular, image variance can be expressed as

$${\sigma }^2\propto \int du\frac{{\mathit{MTF}}^2(u)}{S^2(u)},$$ (1)

where σ is the image noise measured as the standard deviation over an appropriate region-of-interest and given in Hounsfield units (HU) and σ² is the corresponding variance. The modulation transfer function is denoted as MTF and S represents the presampling function in frequency domain. In case of larger detector pixels, like for the EI detector, the presampling function S_EI is smaller compared to the presampling function of smaller detector pixels S_UHR. Furthermore, if acquisitions using both systems are reconstructed to the same modulation transfer function, the image noise in UHR acquisitions is consequently lower compared to acquisitions using the EI detector at the same dose level. It should be noted that these considerations only hold for systems that are dominated by photon noise rather than electronic noise [28]. Details of the derivation of formula (1) can be found in Appendix A.

2.2. Image Acquisitions and Specimens

Acquisitions of five human defatted vertebral body specimens embedded in poly-methyl metaacrilate (PMMA) were performed with the energy-integrating detector and the photon-counting detector using the protocols summarized in Table 1 and detailed in the following. The specimens were collected by the anatomy institute of Kiel University (CAU, Kiel, Germany) and the institute for forensic medicine of the University Medical Center Hamburg-Eppendorf (UKE, Hamburg, Germany) and underwent previous approval for their scientific usage from an ethical comittee. The vertebral embeddings were performed such as to fit inside a custom-made anthropomorphic abdomen phantom (QRM, Moehrendorf, Germany) in order to simulate in vivo-like intersection lengths. For EI and PC technologies, all acquisitions were performed using a tube voltage of 120 kV and were reconstructed to the same spatial resolution using weighted filtered backprojection (wFBP) and a sharp B70 kernel. Reconstructions with two different field-of-views (FOVs) were obtained. A FOV of 150 mm that included the vertebral specimen and a calibration phantom and a second 80 mm FOV including the vertebral specimen enclosed by the abdomen phantom only. The reconstructed in-plane pixel size was 0.292 mm for the 150 mm FOV and 0.156 mm for the 80 mm FOV. All reconstructions were performed to a slice thickness of 0.6 mm and a slice increment of 0.3 mm.

Table 1.

CT protocols used in this study. Dose values marked with (*) were measured using a CTDI_{32 cm} phantom and values marked with (‡) were acquired using a CTDI_{10 cm} phantom. (EI: energy-integrating, PC: photon-counting, nm: noise-matched, dm: dose-matched)

Protocol	Technology	Energy (kV)	Exposure (mAs)	Slice Thickness (mm)	Slice Increment (mm)	Dose (mGy)
EI	EI	120	355	0.600	0.300	23.8*
UHRdm	PC	120	355	0.600	0.300	23.8*
UHRnm	PC	120	130	0.600	0.300	10.5*
XtremeCT	EI	60	0.39	0.082	0.082	6.6‡

The clinical reference protocol using the energy-integrating detector will be referred to as EI in the following and used a tube current-time product of 355 mAs resulting in a dose of 23.8 mGy (CTDI_{32 cm}). Furthermore, acquisitions were performed using the UHR mode of the photon-counting detector. A protocol referred to as UHRdm (dm – dose-matched) used the same tube current as the EI protocol and resulted in the same radiation dose of 23.8 mGy. Since all acquisitions were reconstructed to the same spatial resolution, this protocol was expected to result in a significant noise reduction given the effect described in Section 2.1. A protocol denoted as UHRnm (nm – noise-matched) used a tube current-time product of 130 mAs and was chosen to match the noise level of the EI protocol while resulting in a radiation dose of only 10.5 mGy. Furthermore, measurements of the embedded vertebral specimens without the enclosing semi-anthropomorphic abdomen phantom were conducted using a high resolution peripheral quantitative CT (HR-pQCT: XtremeCT, SCANCO Medical AG, Bruettisellen, Switzerland) in a prior study and were considered as gold-standard for work presented herein.

2.3. Data evaluation

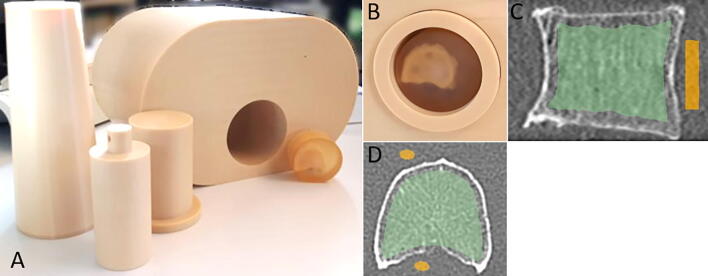
In a first step, calibration of the CT images from CT values to density units was conducted using a density calibration phantom (QRM-BDC/3, QRM, Moehrendorf, Germany) composed of three rods of known densities (water equivalent, 100 mgHA/cm³ and 200 mgHA/cm³) placed beneath the abdomen phantom in each CT scan. Further image pre-processing steps were carried out on the density-calibrated CT volumes to facilitate the image registration to their XtremeCT counterparts. The volumes were manually cropped to isolate the vertebral bodies from air gaps and other segments, e.g. parts of the abdomen phantom, and then rotated to obtain a coarse alignment with the XtremeCT. Prior to registration, the CT volumes were resampled to an isotropic voxel size of 0.156³ mm³ using tri-linear interpolation. Using the in-house developed software StructuralInsight (Section Biomedical Imaging, UKSH, Kiel, Germany), image segmentation of the spongiosa was conducted for one of the CT scans using a shape model algorithm with subsequent manual correction at the pedicles and endplate regions. The actual volume of interest (VOI) encompassed a 2 mm peeled spongiosa from the endocortical region. The pre-processed volumes were then registered with the rest of the CT and XtremeCT counterparts following a rigid 3D transformation implemented in ITK (Insight Segmentation and Registration Toolkit, Kitware Inc., NY, USA). The inverse of the spatial transformation obtained thereof was used to map the VOIs across all CT and XtremeCT volumes. The image registration step thus enabled quantitative evaluations on a given vertebral sample at the same spongiosa region across all CT and XtremeCT scans. Densitometric and structural analyses were performed also in StructuralInsight. Image noise was measured as the standard deviation over an elliptical region-of-interest in the PMMA enclosing the vertebra and included several slices along the z-axis, typically anterior to the vertebral body and between the endplates (see Fig. 1). Noise level was expressed in HU. Using the transformation parameters during the registration step ensured that the same PMMA region was evaluated for each sample across all CT and XtremeCT scans.

Fig. 1.

(A) Abdomen phantom used to simulate in vivo conditions of a CT scan using (B) PMMA-embedded human vertebral bodies. (C) Sagittal and (D) axial reformats illustrating a region defined outside the vertebral body to measure the average PMMA density and image noise (yellow) and the peeled spongiosa region (green) used for the trabecular microstrucure evaluations.

2.4. Structural parameters

Evaluations were conducted for bone mineral density (BMD) on the peeled spongiosa before and after correction for the influence of the embedding material PMMA. Rationale for and details on the correction procedure can be found in Appendix B. From the binarized volumes, trabecular separation (Tb.Sp) was estimated using the run-length algorithm (RLM). Details of this implementation have been published in the literature [29]. Briefly, a parallel grid of search rays is used to probe the complete VOI at a set of n angles α. In our case, α represents the smallest voxel dimension (0.156 mm for CT, 0.082 mm for XtremeCT). Each phase change of the search rays was recorded and their length was measured. From the distribution of lengths and phase changes, the 10%, 20%, 80% and 90% percentiles and the median of the distribution (i.e. Tb.Sp_median, denoted hereafter simply as Tb.Sp) were obtained for each sample and scan. The variability in the trabecular separation was quantified as the interquartile range (Tb.Sp-IQR) of the length distribution in the marrow (in our case the PMMA embedding) phase. Tb.Sp-IQR was calculated here as the 80% minus the 20% percentile of the Tb.Sp distribution and is a measure of the trabecular spacing inhomogeneity.

2.5. Threshold dependency of the structural parameters

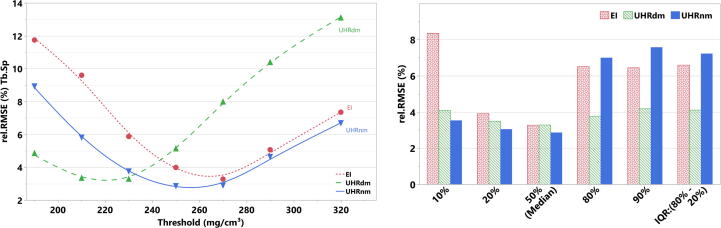
Structural parameters used to characterize trabecular bone almost always depend on the strategy used to define the bone tissue phase from the rest. In processing pipelines that include an image binarization step, this means that thresholds need to be selected. The gold-standard XtremeCT volumes were binarized with a threshold setting of 320 mgHA/cm³ (as recommended for XtremeCT in clinical measurements following Whittier [17]) but without any image filter prior to binarization. On the other hand, for algorithms intended to quantify structure at the spine or at the proximal femur the limited image quality and high image noise level pose an added challenge for segmentation. A clear-cut threshold selection is not straightforward because the intensity distributions are predominantly monomodal and skewed towards high density values. To account for the inherent difficulty of the threshold selection and to test the sensitivity of the structural parameters on this processing step, we conducted a linear regression analysis between the gold-standard XtremeCT and the corresponding CT measurements evaluated for different threshold settings. The following approach was used: for a given structural parameter, linear fittings were conducted between XtremeCT and every CT group for each of the three repeated scans. The relative root mean square error (rel. RMSE) was calculated in each linear fit as the RMSE divided by the range of the corresponding XtremeCT measurement and expressed on a percentual basis. The distribution rel. RMSE vs. threshold yielded an indicator of how robust the CT protocols are when predicting the gold-standard XtremeCT measurements. To account for a fair comparison between EICT- and PCCT-technology, we report results obtained for an optimum threshold setting for each CT protocol. These thresholds were 230 mgHA/cm³ for UHRdm, 250 mgHA/cm³ for UHRnm and 270 mgHA/cm³ for EI. One should bear in mind that such optimization process for a specific CT technology or protocol could potentially yield better results for a different threshold.

2.6. Statistical Analysis

The reproducibility for BMD and the structural parameters was determined using the short-term reproducibility (CV_SD) [30] for each CT protocol and was expressed on a percentual basis according to the following formula:

$${\mathrm{C}\mathrm{V}}_{\mathrm{S}\mathrm{D}}=\left(\mathrm{S}\mathrm{D}/\left(\sum _j{\overline{x}}_j\right)/M\right)\bullet 100\%$$ (2)

with SD as the root-mean square average of the standard deviations of the measurements for sample j and ${\overline{x}}_j$ as the average measurement of variable x, i.e.

$$\mathrm{S}\mathrm{D}=\sqrt{{\sum _j^M\sum _i^N\left(x_{\mathit{ij}}-{\overline{x}}_j\right)}^2/M\bullet (N-1)}$$ (3)

In our case, we used M = 5 samples and had N = 3 repeated measurements; x_ij represents a measurement from CT scan i of sample j for variable x. The agreement between the CT protocols was evaluated using the Pearson correlation coefficient (r) and a modified Lin’s concordance correlation coefficient (r_CCC) [31]. Simple linear regressions against the gold-standard XtremeCT were conducted to evaluate the prediction errors. Figures of merit were the root mean square error (RMSE) and as mentioned in Section 2.5, the relative RMSE (%). Furthermore, Bland-Altman analyses were conducted to examine biases and offsets between XtremeCT and the CT protocols. Non-parametric (Wilcoxon) paired statistical tests were conducted to compare the noise levels measured with the CT protocols and also to compare BMD between the CT protocols and XtremeCT before and after correction for the influence of the PMMA embedding material. All statistical analyses were performed in JMP (Pro v16.0, SAS Institute, Cary NC, USA).

3. Results

3.1. Dose and Noise

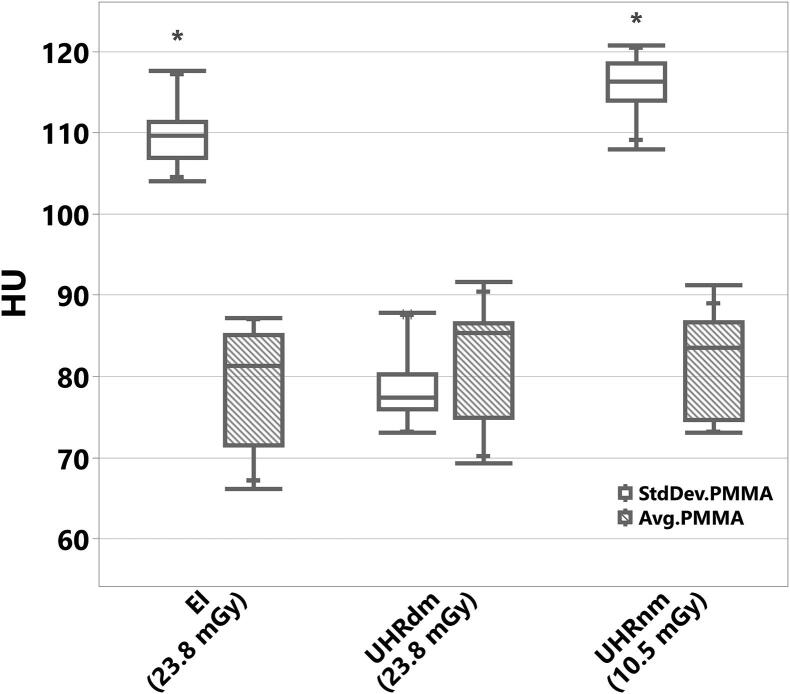
For the EICT protocol, the Mean ± StdDev of the image noise level was 109.6 ± 3.9 HU (range: [104, 118] HU) using a dose of 23.8 mGy (CTDI_{32 cm}, see Fig. 2, Fig. 3). A dose-matched PCCT protocol, UHRdm, using the same dose and employing the UHR-mode of the photon-counting detector resulted in a noise level of only 78.6 ± 4.6 HU (range: [73, 88] HU), which was significantly lower (p = 0.0122) than the noise level of the EICT and the noise-matched UHRnm protocol. Similarly, the UHRnm protocol at the same spatial resolution resulted in a noise level of 115.83.7 HU (range: [108, 121] HU), while using a radiation dose of only 10.5 mGy.

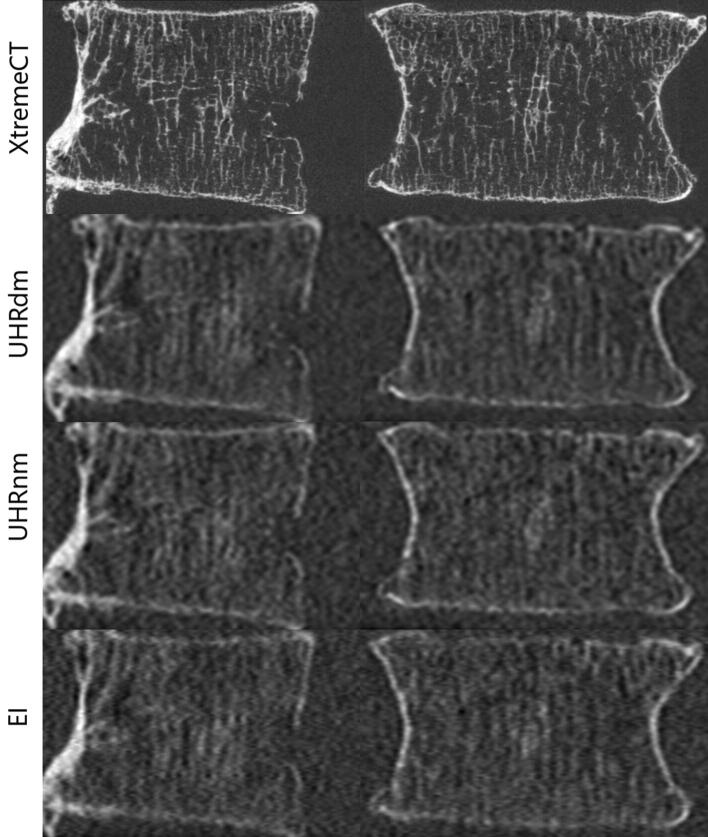
Fig. 2.

Sagittal (left) and Coronal (right) aligned reformats from CT scans of a vertebral body specimen. (Top) XtremeCT: high image quality but available only for extremities. Photon-counting UHRdm: second-best image quality (lower noise) at the same dose of the clinical EICT. UHRnm: same noise but lower dose than the clinical EICT protocol (bottom row). Notice that the XtremeCT scans were conducted without the abdomen phantom in contrast to the UHR and EICT scans. Window C/W in HU for XtremeCT: 463/3207; for UHRdm: 675/2523; for UHRnm: 679/2515 and for EI: 615/2296.

Fig. 3.

Average and standard deviation (StdDev) in HU of embedding material PMMA measured over the ellipse-like region (see Fig. 1 (C,D)). StdDev.PMMA (HU) was considered in this study as the image noise level. * Statistically significant lower noise levels were observed for the UHRdm protocol compared to EICT and UHRnm (p-value < 0.05 for both). For EICT and UHRnm practically the same noise level was observed but with a marked reduction of the radiation dose level (shown within parentheses on the x-axis) delivered with UHRnm.

3.2. Bone Mineral Density and Trabecular Microstructure

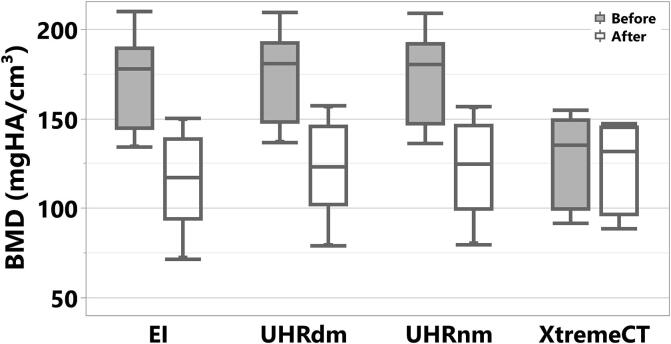
The total spongiosa volume of the samples evaluated showed a Mean ± StdDev of 16.25 ± 2.11 cm³ and a range of [13.07, 18.47] cm³. Fig. 4 shows results for BMD at the spongiosa before and after the correction for PMMA. The PMMA embedding material, showing a positive mineral equivalent density (see Avg. PMMA in Fig. 3) increased the measured BMD values, opposite to the true physiological condition where fatty bone-marrow would decrease the true BMD. Correcting for the PMMA influence effectively removed differences in BMD results with respect to XtremeCT as assessed with a Wilcoxon paired test.

Fig. 4.

Bone mineral density measured at the spongiosa for three CT protocols (UHR: photon-counting, EI: energy integrating) and XtremeCT, before (top row) and after (bottom row) correction for the influence of the embedding material PMMA.

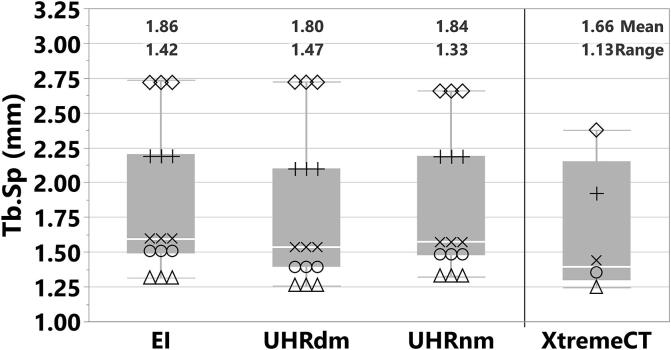
Table 2 summarizes the statistics of all measurements including the short-term reproducibility for each protocol. For BMD, all protocols showed a reproducibility of less than 0.2%. For Tb.Sp the best reproducibility was for UHRdm (CV_SD = 0.21%); the worst reproducibility was for the EI protocol (CV_SD = 0.82%). Figs. 5 and 6 illustrate the Tb.Sp and Tb.Sp-percentiles for the CT protocols and XtremeCT. In Fig. 6 the different percentiles represent the different scales of trabecular separations measured within a vertebral specimen. The Tb.Sp percentiles covered Tb.Sp scales from around 0.25 mm (10% percentile), as given by the average measurement of XtremeCT, up to 5.90 mm (90% percentile). For the lower percentiles there was some overestimation by the CT protocols. However, the ranking (order) of the data was maintained for all CT protocols throughout all Tb.Sp percentiles (scales). Fig. 7 shows results of the sensitivity analysis depicting the rel. RMSE (%) from linear regressions for Tb.Sp as a function of the threshold setting. Using the optimum threshold for each protocol, UHRdm showed more stable and consistent results across the different percentiles of the Tb.Sp (Range of rel. RMSE: [3.3%, 4.2%]) compared to UHRnm (Range: [2.9%, 7.6%]) and EICT (Range: [3.3%, 8.4%]).

Table 2.

Mean ± StdDev of the trabecular bone structure measured variables for each CT protocol. Results are pooled for N = 3 repeated scans and 5 samples. BMD results are for post-hoc correction for PMMA-influence. Short-term reproducibility, CV_SD(%), of the measured variables for each CT protocol. For XtremeCT only one scan per sample was available.

Protocol	BMD (mgHA/cm3)	Tb.Sp (mm)	Tb.Sp-IQR (mm)	CV BMD (%)	CV Tb.Sp (%)	CV Tb.Sp-IQR (%)
EI	114.8 ± 28.6	1.86 ± 0.54	3.39 ± 1.24	0.10	0.82	0.76
UHRdm	121.6 ± 28.8	1.80 ± 0.56	3.10 ± 1.34	0.11	0.21	0.40
UHRnm	121.5 ± 28.6	1.84 ± 0.52	3.11 ± 1.09	0.15	0.25	0.25
XtremeCT	123.1 ± 25.5	1.66 ± 0.48	3.44 ± 1.48	-	-	-

Fig. 5.

Trabecular Separation (Tb.Sp) measured for three CT protocols (UHR: photon-counting, EI: energy integrating) and XtremeCT.

Fig. 6.

Trabecular Separation (Tb.Sp) percentiles measured for three CT protocols (UHR: photon-counting, EI: energy integrating) and XtremeCT. The percentiles represent the different interspacing dimensions within a vertebral specimen. The rankings of the samples (data markers) were maintained in all CT protocols and XtremeCT.

Fig. 7.

(Left) Relative root-mean-square error (rel. RMSE (%)) obtained from linear fittings between Tb.Sp from XtremeCT and CT (photon-counting: UHRnm and UHRdm, EI: energy integrating) as a function of the threshold setting used to binarize the CT volumes. (Right) rel.RMSE(%) obtained for different percentiles of the Tb.Sp distributions for the three CT protocols.

Table 3 summarizes all results of the statistical analyses, including correlations between groups, linear regression against the gold-standard and slope and intercepts from a Bland-Altman analysis. With respect to EI and UHRnm, they showed very similar results across all variables but UHRnm generally showed lower relative errors, especially for BMD (5.4% vs. 7.1%) and Tb.Sp (2.9% vs. 3.3%) while for Tb.Sp-IQR the rel. Error was slightly lower for EI (7.2% vs. 6.6%). These error levels represent an absolute error (RMSE) in Tb.Sp that ranged from 0.03 to 0.04 mm. As shown in Table 2, the Mean ± StdDev in Tb.Sp (mm) was very similar between EI, UHRdm and UHRnm with values of 1.86 ± 0.53 mm, 1.80 ± 0.56 mm and 1.84 ± 0.52 mm, respectively, compared to 1.66 ± 0.48 mm for XtremeCT. This observation was reflected in the very good agreement between protocols for Tb.Sp (r_CCC > 0.99) and also in Tb.Sp-IQR (r_CCC > 0.96). The agreement in BMD before PMMA correction was excellent with all r_CCC > 0.995 and after correction was still very good: UHRnm vs. EICT (r_CCC = 0.97), UHRnm vs. UHRdm (r_CCC = 0.998) and UHRdm vs. EICT (r_CCC = 0.97).

Table 3.

Results of statistics analysis of trabecular bone structure variables measured with the gold-standard XtremeCT against photon-counting CT protocols (photon-counting: UHRnm and UHRdm, EI: energy integrating). Between-group correlations (Pearson r and Lin’s r_CCC) are the mean over N = 3 repeated scans. *RMSE: root mean square error given in corresponding units of each variable. **Relative error is the RMSE divided by the range of the XtremeCT corresponding measurements. RMSE and Relative Error are given as the Mean ± StdDev across N=3 measurements. ***BMD after post-hoc correction for the PMMA-influence.

	CT Protocol	Pearson r		Lin’s rCCC		Linear Regression		Bland-Altman
		UHRnm	UHRdm	UHRnm	UHRdm	RMSE*	Relative Error (%)**	Mean offset ± SEM	slope	intercept	p-value slope	p-value intercept
BMD	EI	0.999	0.999	0.997	0.996	4.4 ± 0.04	7.1 ± 0.1	−44.6 ± 3.0	−17.54	−0.18	0.12	0.27
	UHRnm	1	0.999	1	0.999	3.4 ± 0.05	5.4 ± 0.1	−46.2 ± 2.3	−24.05	−0.15	0.16	0.09
	UHRdm	0.999	1	0.999	1	3.3 ± 0.07	5.2 ± 0.1	−46.9 ± 2.3	−25.16	−0.14	0.11	0.08
Tb.Sp	EI	0.999	0.998	0.998	0.991	0.04 ± 0.002	3.3 ± 0.1	−0.21 ± 0.05	0.125	−0.19	0.01	0.16
	UHRnm	1	0.997	1	0.993	0.03 ± 0.001	2.9 ± 0.1	−0.19 ± 0.04	0.084	−0.15	0.02	0.27
	UHRdm	0.997	1	0.993	1	0.04 ± 0.001	3.3 ± 0.1	−0.14 ± 0.06	0.259	−0.23	0.01	0.03
Tb.Sp−IQR	EI	0.999	0.997	0.966	0.970	0.23 ± 0.010	6.6 ± 0.3	0.06 ± 0.10	−0.275	0.10	0.31	0.41
	UHRnm	1	0.993	1	0.983	0.26 ± 0.006	7.2 ± 0.2	0.33 ± 0.16	−0.396	0.22	0.08	0.28
	UHRdm	0.993	1	0.983	1	0.15 ± 0.008	4.1 ± 0.2	0.35 ± 0.06	0.295	0.02	0.77	0.19
BMD***	EI	0.999	0.999	0.970	0.970	4.9 ± 0.4	8.2 ± 0.7	8.30 ± 3.14	31.11	−0.19	0.13	0.07
	UHRnm	1	0.998	1	0.998	4.3 ± 1.0	7.3 ± 1.7	1.65 ± 3.05	25.40	−0.19	0.10	0.09
	UHRdm	0.998	1	0.998	1	5.1 ± 0.7	8.7 ± 1.2	1.52 ± 3.34	26.11	−0.20	0.14	0.13

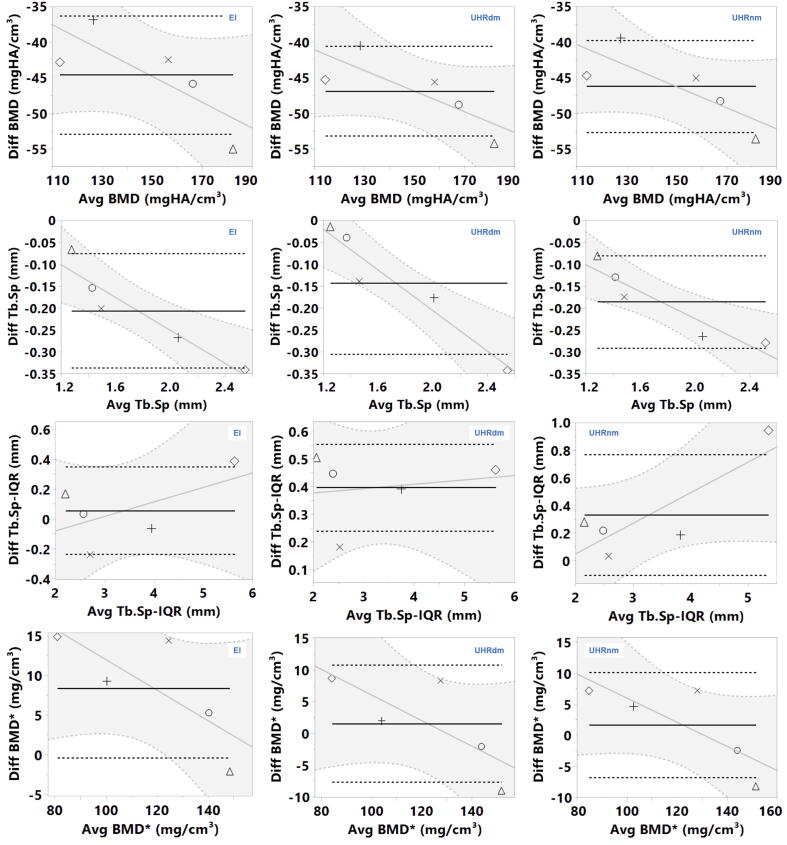
As shown in Table 3, the Bland-Altman analysis showed significant slopes (p < 0.05) for Tb.Sp for all three protocols against the gold standard. No signs of heteroscedasticity were observed, as the points were distributed homogenously along the fitted line, see Appendix C. This means that for calibration purposes, the bias can be corrected by means of a fitted line. In cases where no significant slope was observed, a calibration against the gold-standard can be carried out using a fitted mean offset, as listed in the Table 3 with its corresponding standard error of the mean (SEM).

4. Discussion

Using a novel PCCT-UHR detector, we evaluated its performance for the evaluation of bone mineral density and bone microstructure (represented by Tb.Sp and its percentiles) and demonstrated that Tb.Sp can be assessed in a reproducible way in addition to BMD. In an approach similar to ours, i.e. using a set of embedded vertebral specimens and an anthropomorphic phantom but implementing a different algorithm for the determination of trabecular spacing using fuzzy distance, Krebs [18] et al. showed that Tb.Sp could be estimated with HR-MSCT with residual errors (RMSE) as low as 0.031 mm compared to XtremeCT from Scanco Medical as the gold-standard. In that work, the RMSE was 0.078 mm when subdividing the volumes of interest into cuboids of about 230 mm³, thus expanding the range of separations observed to [0.400, 1.400] mm [18]. In our study, in which we used a different set of specimens, the average Tb.Sp was higher (mean Tb.Sp = 1.66 mm compared to Krebs’ Tb.Sp = 1.09 mm using fuzzy distance [18]). However, errors from linear regression in our study were very similar with an RMSE of Tb.Sp of 0.032 mm (2.9%) for the UHRnm protocol and 0.037 mm (3.3%) for the UHRdm protocol. In a recent study, Guha et al. [32] compared several in vivo CT modalities for the assessment of bone microstructure in human radii ex vivo. For MSCT, they showed that Tb.Sp could be estimated with a normalized RMSE of 3.54% against gold-standard µCT scans, very similar to our linear regression results (Table 3). The good agreement observed in Tb.Sp, highlighted by the very high r_CCC and the low relative errors against the gold-standard, come at the price of an overestimation of BV/TV (not shown) compared with XtremeCT. As expected, thin trabecular bone structures of the order of 150 µm thickness cannot be individually resolved by the clinical or the photon-counting CT protocols. As can be visually compared in Fig. 2, small separations between very adjacent trabecular structures or even small perforations cannot be resolved individually by the CT protocols but instead are agglomerated into a coarser trabecular structure. This observation is supported by the overestimated Tb.Sp for the 10% percentile using the CT protocols. Nevertheless, PCCT yields a reproducible representation of the trabecular microstructure represented by Tb.Sp and its percentiles. Further refinement of the methods may target other microstructural variables, or in practice, researchers may focus on a few microstructural variables like Tb.Sp in this work, while calibrating BV/TV or other microstructural variables against the gold-standard, e.g. by means of a Bland-Altman analysis. Moreover, the first clinical version of the prototype photon-counting CT used in this study provides even smaller detector pixels with a size of 150 µm in the center of rotation and is equipped with a dedicated iterative reconstruction algorithm [33]. These features might allow for the visualization of thin trabecular structures at a reasonable dose level.

Chen et al. used two Siemens MSCT devices, Flash and Force, to quantify trabecular microstructure in the lower extremities with a delivered dose of 0.17 mSv and 0.05 mSv with each device, respectively. Note that these very low dose levels are due to the peripheral measurement site [9]. In that work, they used the UHR scan modes of the two CT devices. In those modes, a high-frequency comb or grid is placed between the patient and the detector reducing the effective pixel size. Therefore, in such a setting, it is possible to achieve a spatial resolution similar to the UHR mode of the photon-counting detectors. However, the grid behind the patient makes that protocol very inefficient in terms of dose and limits its applicability to extremities only.

In a recent publication of an in vivo study, Pumberger et al. [12] used vertebral biopsies with trabecular bone and compared µCT derived trabecular measurements with those obtained from the pre-operative CT scans of the patients but they did not report correlations between MSCT- and µCT-derived trabecular structure variables. Presumably, this could be explained by a number of factors: they stated that their CT protocol included voxel sizes of 0.5×0.5×0.5 mm³, which were coarser than voxel sizes used in other HR-MSCT studies (0.156×0.156×0.3 mm³) [20]; the volume of the biopsies, although not stated in the mentioned publication, may not have been large enough to yield robust correlations with µCT. HR-MSCT resolution is not yet good enough to resolve individual trabecular elements, thus a large volume of interest is needed to observe correlated measures for example of trabecular separation. According to Chen [9], for a VOI size of 75.8 mm³ (corresponding to a sphere of 5.25 mm diameter) with µCT for trabecular evaluations at the ankle stabilized, reaching a maximum plateau at around r = 0.80. At the central skeleton the, resulting increase in image noise due to surrounding tissue and fat, this minimum requirement for the VOI size must probably be increased. The usage of a non-sharp, standard reconstruction kernel (FC30 from Canon Medical, former Toshiba) may have smoothed trabecular structures in the MSCT volumes of Pumberger et al. A sharp reconstruction kernel could have caused the opposite effect, namely, enhance trabecular structures of the biopsy volumes.

One limitation of our study is the small number of samples used. However, these vertebrae covered a relevant range from osteoporotic to normal values of BMD and microstructural data are based on a large volume of many individual trabeculae, quantified in 3D. Thus, we believe that the proof of principle presented in this work, that PCCT yields a reproducible representation of the trabecular density and microstructure, represented by Tb.Sp, is well documented. While such associations have been shown in earlier MSCT studies, e.g. in experiments performed by Graeff et al., Krebs et al., Chen et al. and Guha et al. [9], [18], [20], [32], the demonstrated dose reduction points to a new direction. Reduced dose levels in future microstructure and bone strength assessments may facilitate actual in vivo scans and patient studies.

Perhaps even more important than new options for assessment of bone structure is the impact on photon-counting CT on clinical assessment of BMD. The reduction of radiation exposure by more than a factor of two without an increase of noise, i.e. without an increase of the precision error, is highly relevant to further increase acceptance of QCT among physicians and patients. Despite proven advantages of using vertebral BMD as measured by QCT for prediction of vertebral fracture risk [34] compared to areal BMD measured by DXA, DXA is still the dominant modality. One reason is the higher radiation exposure of QCT, which for a current standard scan of L1 and L2 is about 1.5 mSv [35]. Thus, with photon-counting technology, the exposure per scan could be reduced from 63% of the natural background radiation (2.4 mSv) to less than 30% which would be a very important achievement.

In summary, at similar dose levels, CT with UHR-PC detectors demonstrated lower image noise and better reproducibility for assessments of bone microstructure than current EICT protocols. Using UHR protocols, BMD and the microstructural variables Tb.Sp and Tb.Sp-IQR were highly repeatable with short-term reproducibility of less than 0.2% for BMD and down to 0.21% (or 1/3 of the EICT error level) for Tb.Sp. For UHRnm, the radiation exposure level could be reduced by a factor of about 2.3 or 56% without deterioration of performance levels in the assessment of bone mineral density and bone microstructure. Our results may support establishing dose-efficient in vivo methods for the assessment of trabecular microstructure at fracture relevant sites like the spine and increased use of QCT for fracture prediction in osteoporotic subjects.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A: Noise, Presampling and MTF. Derivation of Formula 1

We follow reference [27] in the following. Let us assume that the measured projection g(x) is a convolution (*) of the ideal projection f(x) with a presampling function s(x) and an algorithm factor a(x) as

$$\mathrm{g}\left(\mathrm{x}\right)=\mathrm{f}\left(\mathrm{x}\right)\ast \mathrm{s}\left(\mathrm{x}\right)\ast \mathrm{a}(\mathrm{x})$$ (A.1)

In case of an ideal detector, s(x) could be considered a rectangle function and a(x) describes a linear interpolation. The point spread function (PSF) of such a system in spatial domain is

$$\mathrm{p}\mathrm{s}\mathrm{f}\left(\mathrm{x}\right)=\mathrm{s}\left(\mathrm{x}\right)\ast \mathrm{a}(\mathrm{x})$$ (A.2)

The corresponding modulation transfer function (MTF) is thus

$$\mathrm{M}\mathrm{T}\mathrm{F}\left(\mathrm{u}\right)=\mathrm{S}\left(\mathrm{u}\right)\bullet \mathrm{A}(\mathrm{u})$$ (A.3)

where A(u) is the Fourier transform of a(x) and S(u) is the presampling function in frequency domain. Since the MTF is a metric defined in frequency domain, the corresponding variable is u rather than x. Using Rayleigh’s theorem, we find variance σ² as

$${\mathrm{\sigma }}^2\propto \int \mathrm{d}\mathrm{x}{\mathrm{a}}^2\left(\mathrm{x}\right)=\int \mathrm{d}\mathrm{u}{\mathrm{A}}^2\left(\mathrm{u}\right)=\int \mathrm{d}\mathrm{u}\frac{{\mathrm{M}\mathrm{T}\mathrm{F}}^2(\mathrm{u})}{{\mathrm{S}}^2(\mathrm{u})}$$

Thus,

$${\mathrm{\sigma }}^2\propto \int \mathrm{d}\mathrm{u}\frac{{\mathrm{M}\mathrm{T}\mathrm{F}}^2(\mathrm{u})}{{\mathrm{S}}^2(\mathrm{u})}.$$ (A.4)

Let us now consider two detectors A and B. Detector A provides a larger pixel size compared to detector B. In frequency domain, it thus holds that ${\mathrm{S}}_{\mathrm{B}}\left(\mathrm{u}\right)>{\mathrm{S}}_{\mathrm{A}}(\mathrm{u})$ and hence ${\mathrm{\sigma }}_{\mathrm{B}}^2<{\mathrm{\sigma }}_{\mathrm{A}}^2$ assuming that MTF(u) is kept constant in both cases.

Appendix B: Correction of PMMA influence for BMD

In order to obtain accurate BMD results on the embedded vertebral samples used we had to eliminate the artificial bias of the plastic embedding material (PMMA), which features higher attenuation levels compared to typical bone marrow. The density calibration procedure performed on whole body clinical CT scanners is different than the one used by the XtremeCT device (different calibration reference phantoms, different CT acquisition settings, etc.), resulting in an offset in the pure PMMA material for the two approaches. The correction procedure was based on measurements of the average mineral density values in the spongiosa and outside of the vertebrae in the PMMA regions, as depicted in the color VOIs of Fig. 1 (C,D). The following steps were conducted for each sample and CT scan:

• •Initial correction by subtracting the PMMA measured equivalent density from the initially measured BMD at the spongiosa. sBMD_ij = BMD_ij – PMMA_ij for CT scan i and sample j and sBMD_ij the intermediate corrected BMD value at this step.
• •Calculation of a theoretical bone volume fraction (BV/TV^theory) using sBMD_ij divided by the theoretical bone mineralization for healthy bone, i.e. 1200 mgHA/cm³.
• •(BV/TV^theory)_ij = sBMD_ij/1200. This will yield an approximate bone volume fraction for each sample and CT scan. In other words, this BV/TV^theory tells to what extent the PMMA is infiltrating the spongiosa bone. A BV/TV of 0 would mean that there is pure PMMA. Conversely, a BV/TV of 1 will mean there is only bone tissue.
• •Actual correction by subtracting the measured PMMA density weighted by (1 –BV/TV^theory) from the originally measured BMD:

$${\mathrm{c}\mathrm{B}\mathrm{M}\mathrm{D}}_{\mathrm{i}\mathrm{j}}={\mathrm{B}\mathrm{M}\mathrm{D}}_{\mathrm{i}\mathrm{j}}-(1-{\mathrm{B}\mathrm{V}/\mathrm{T}\mathrm{V}}_{\mathrm{i}\mathrm{j}}^{\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{o}\mathrm{r}\mathrm{y}})\bullet {\mathrm{P}\mathrm{M}\mathrm{M}\mathrm{A}}_{\mathrm{i}\mathrm{j}}$$ (B.1)

with cBMD_ij the PMMA-corrected BMD value for scan i and CT scan j. It is the value given in the Results section in Fig. 4.

The same correction procedure was applied to the XtremeCT scans. For XtremeCT, the spongiosal BMD values before and after correction did not differ as a much as for the CT protocols as can be seen in Fig. 4 and Table 3.

Appendix C: Bland-Altman Plots

Bland-Altman plots between XtremeCT and the corresponding CT variables are presented in Fig. C1.

Fig. C1.

Bland-Altman plots with linear regression fit lines for the different variables evaluated. Diff and Avg are the difference and the average values between XtremeCT and CT protocols (photon-counting: UHRnm and UHRdm, EI: energy integrating), respectively. Dashed lines are +/-1 SEM. BMD*: BMD corrected post-hoc for the influence of PMMA.