Mitigation of motion effects in pencil-beam scanning – Impact of repainting on 4D robustly optimized proton treatment plans for hepatocellular carcinoma

Abstract

Proton fields delivered by the active scanning technique can be interfered with the intrafractional motion. This in-silico study seeks to mitigate the dosimetric impacts of motion artifacts, especially its interplay with the time-modulated dose delivery. Here four-dimensional (4d) robust optimization and dose repainting, which is the multiple application of the same field with reduced fluence, were combined. Two types of repainting were considered: layered and volumetric repainting. The time-resolved dose calculation, which is necessary to quantify the interplay effect, was integrated into the treatment planning system and validated. Nine clinical cases of hepatocellular carcinoma (HCC) showing motion in the range of 0.4–1.5 cm were studied. It was found that the repainted delivery of 4D robustly optimized plans reduced the impact of interplay effect as quantified by the homogeneity index within the clinical target volume (CTV) to a tolerable level. Similarly, the fractional over- and underdosage was reduced sufficiently for some HCC cases to achieve the purpose of motion management. This holds true for both investigated types of repainting with small dosimetric advantages of volume repainting over layered repainting. Volume repainting, however, cannot be applied clinically in proton centers with slow energy changes. Thus, it served as a reference in the in-silico evaluation. It is recommended to perform the dynamic dose calculation for individual cases to judge if robust optimization in conjunction with repainting is sufficient to keep the interplay effect within bounds.

1. Introduction

In proton therapy (PT) with pencil-beam scanning (PBS) a narrow beam is magnetically steered across the clinical target while the fluence is being modulated. The fluence modulation of PBS beamlets, so called “spots”, in conjunction with energy switching at the level of the accelerator enables conformal dose distributions. Furthermore, the characteristic dose profile of proton fields facilitates a rather low dose in the entry port and zero dose in the exit port, thereby sparing healthy tissues. Although PBS is now well established in a number of particle therapy centers, it is still subject of development and its clinical use is still in a phase of expansion. This is especially true for targets that are subject to respiratory motion. In addition to the motion management necessary for any external beam modality, the control of the so-called interplay effect requires dedicated measures in PBS-based PT [1], [2], [3], [4], [5], [6]. The interplay effect is caused by the interference of the time-modulated field application and the intrafractional motion that may result in a degradation of the dose distribution.

The 4D dynamical dose distribution (4DDD) in the patient, which is estimated by time-resolved dose calculations based on motion information and the beam delivery dynamics, may guide the motion management at the phase of treatment planning. If the 4DDD does not meet the clinical dose criteria under free breathing conditions or with abdominal compression [7], additional motion mitigation measures, e.g. beam-gating or breath-hold, shall be taken [8], [9]. The current study explores the possibilities of PT for moving targets without the latter mitigation techniques. Lesions in the liver, primarily hepatocellular carcinomas (HCCs), were chosen as the clinical example because this treatment region exhibits less variation of tissue density than in the thorax [10]. This allows the use of a dose engine based on a pencil-beam algorithm as will be outlined in Section 3.3. So far, the majority of clinical PT of liver tumors has been conducted with passively scattered fields [11], [12], [13]. As the ongoing expansion of PT is mainly based on new installations of PBS treatment heads, PBS is expected to gain increasing importance as the treatment modality for moving targets including liver tumors [14]. For instance, Yoo et al. recently reported the clinical outcomes HCC treated by PT of HCC delivered by PBS and passive scattering [15].

The current paper developed on our previous studies [16], [17] by combining the established robustly optimized plans with repeated application of spots of an energy layer with reduced fluence for each proton field, i.e. energy-layered repainting. The current study focused on energy-layered repainting, i.e. the repetition of the delivery of spots, which are grouped within one energy level (“energy layer”). The energy layer is completed before the wedge-based energy selection system downstream of the cyclotron switches to the next energy level. The energy switching time for the used proton machine is around one second. Previous studies indicated that the repainting (sometimes referred to as “rescanning”) effectively reduces the dose distortions of the interplay effect [1], [18], [19], [20], [21], [22]. This is motivated by the averaging effect of the multiple sampling of the dose application per energy layer (Sections 2.4 and 3.2).

Robust optimization generally reduces the sensitivity to the physical uncertainty of the proton range and geometric uncertainties in the treatment setup and the patient anatomy. This is a major concern for intensity-modulated proton therapy (IMPT) used in the current study. 4D robust optimization, by considering all respiratory phases captured in the 4D CT during treatment planning, primarily facilitates to replace the expansion of the target volume (CTV) to the internal target volume (iCTV). Previous studies indicated that the robust optimization accounting for respiration-induced tumor motion and uncertainties related to the proton range and patient setup, is dosimetrically beneficial for the sparing of moving organs-at-risk [16], [17].

In this study, the delivery methods and treatment plan parameters are clinically applied at our center. These concern the layered repainting, field configurations, robust planning, multi-field optimization, and 4D dose calculation within the treatment planning system. The 4DDD evaluation was available in a research version of RayStation 8B (RaySearch Laboratories AB, Stockholm, Sweden) [23] providing the fractional interplay dose distributions. Since this was a new software implementation, a validation was performed. The maximum number of repaintings per energy layer was varied slightly beyond the clinically used values. Additionally, volumetric repainting, i.e. multiple applications of a treatment field with a downscaled spot fluence, was evaluated for benchmarking against layered repainting and comparing with previous studies including volumetric repainting [21], [24], [25].

2. Materials and methods

2.1. Characterization of proton field delivery

A gantry room of the West German Proton Therapy Centre (WPE), which is equipped with a ProteusPlus PT machine (IBA PT, Louvain-la-Neuve/Belgium), was used in PBS delivery mode. The isochronous cyclotron provides a quasi-continuous beam with lateral full-width-at-half-maximum between 7.1 mm and 12.7 mm for proton kinetic energies from 226.7 MeV down to 100.0 MeV which correspond to ranges of 32.2 cm to 7.7 cm in water. For shallow target volumes the proton kinetic energy is degraded below 100.0 MeV by means of a homogeneous range shifter block. The range shifter block is mounted on a linear translation stage at the most downstream part of the treatment head. PBS delivery is characterized by the step-and-shoot principle: After application of a spot at a lateral position defined in the treatment plan, the beam is switched off during the change of the deflection magnets to the subsequent spot position. A spot is typically delivered within a few milliseconds. A parameterization of the delivery rate and the speed of deflection has been established for WPE in Ref. [26]. The field delivery proceeds with one energy layer followed by the next. The energy layer switching time has a random variation, which can be approximated by a truncated normal distribution with a mean value of 1.23 s and a standard deviation of 0.26 s [26]. The normal distribution is truncated to the interval [0.9…2.5] s since no energy switching times are observed outside this interval. The proton fluence per spot MU_spot, described by the number of monitor units (MU), has a dynamic range of 400:1.

The number of repaintings N_Rep is a fixed number per plan acting as a downscaling factor on MU_spot. If MU_spot/N_Rep is below a lower limit of MU per spot MU_spot,min, then the number of repaintings of the spot under consideration is reduced to $N_{\mathrm{Rep}}^{\prime }$ until the MU${}_{\mathrm{spot}}/N_{\mathrm{Rep}}^{\prime }\ge {\mathrm{MU}}_{\mathrm{spot},\min }$ [18]. Such spots, which had been irradiated already $N_{\mathrm{Rep}}^{\prime }$ times within a layer, are left out in subsequent energy layers [18]. Following the concept of Klimpki et al. [27], the actual number of repaintings of a spot was described by the quantity:

$$N_{\mathrm{spot},\mathrm{eff}}=\min \left\{⌊\frac{{\mathrm{MU}}_{\mathrm{spot}}}{{\mathrm{MU}}_{\mathrm{spot},\min }}⌋,N_{\mathrm{Rep}}\right\}$$ (1)

In the following, the effective number of repaintings N_eff is reported. N_eff was computed by averaging N_spot,eff over all spots of a treatment plan.

Layered repainting has been introduced clinically in our facility with typically N_Rep = 4 or N_Rep = 5. The resulting delivery times of the treatment plans (between 4 min and 7 min) were regarded as acceptable. We extended our analyses (Section 2.4) of the interval for N_Rep from three to seven. In modeling the volumetric repainting, the iteration of energy-layers is nested within the loop among (the number of) repaints but otherwise identical to the layered repainting. This study used N_Rep = 5 as the reference value in the volumetric repainting mode for benchmark against layered repainting. Note that volumetric repainting as described here has not been tested at WPE but is in principle feasible as shown in Ref. [28].

2.2. Treatment planning

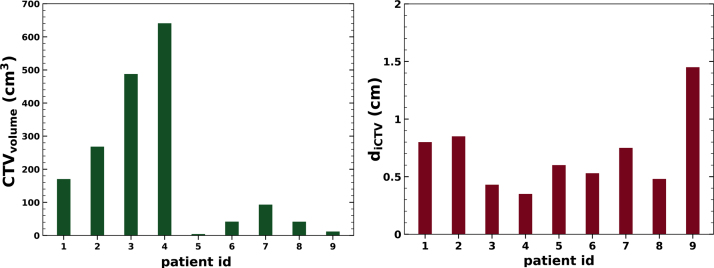
The prescribed dose D_prescr was 63 Gy_RBE, which was normalized to the median dose of the CTV. A generic relative biological effectiveness (RBE) value of 1.1 and a delivery in 15 fractions [29] were assumed. Figure 1 (left) visualizes the volumes of the CTVs, which ranged between 4 cm³ and 640 cm³. The motion amplitudes were between 0.4 cm and 1.5 cm (see Figure 1 right).

Figure 1.

Characteristics of HCC cases: CTV volume (left) and tumor motion amplitude d_iCTV (right). The patient ids 1–9 correspond to patient ids 1, 2, 3, 7, 6, 4, 8a, 8b, 9b of Ref. [16].

The CT corresponding to the 50% breathing phase at the end of end-expiration served as a planning CT and as reference for the computation of the dynamical dose (see Section 2.3). The treatment plans were identical to the plans of Ref. [16]. Each treatment plan comprised two individualized fields employing the ipsilateral and ventral ports. The plan optimization adhered to the procedures established for treatment planning in the WPE, i.e. isocenter location, field angles, couch kicks, and the positioning of range shifters were carefully tuned for the individual cases. Range shifter blocks with typical air gaps of 3 cm to 5 cm were used for the majority of the fields. The spot spacing projected in the isocenter plane was 80% of the energy dependent spot size. The treatment plans for the nine clinical HCC cases were created by (4D) robust optimization [30], [31], which considers in addition to the planning CT the discretized breathing scenarios of the patient anatomy (see Section 2.3). The robust optimization settings in RayStation were chosen to achieve plan robustness against 2 mm setup error and 5% range uncertainty. The range uncertainty comprises a 3.5% uncertainty for the estimation of stopping power and 2 mm measurement uncertainty of the range in water together with the range reproducibility of the proton machine [23]. Note that the clinical treatment planning at WPE includes two extreme CT phases and a set-up uncertainty of 5 mm for abdominal tumors. The current study deviated from the clinical procedure for the sake of facilitating better time resolution in the optimization with ten CT phases. In order to keep the optimization time within practical limits, the set-up robustness parameter was reduced as a countermeasure. Multi-field optimization with single-field doses exceeding the nominal field dose by up to about 30% was performed.

The robustness of each treatment plan was evaluated for all permutations of the following perturbed dose scenarios: a ±2 mm isocenter shift in all cardinal directions, a 5% change of tissue density, and the dose computation on the 0% CT phase and the 50% CT phase. The dose coverage criterion of V₉₅>98% for each perturbed scenario failed only for patient id 9 with a localized cold spot at the boundary to the lung [32]. Eventually, all treatment plans were approved by a medical doctor.

2.3. Dynamic dose calculation

In a previous work a customized software routine was developed that simulates the delivery of a scanned pencil beam to a moving target [26]. It employs description of the dynamic anatomy represented by a 10-phase 4D CT data set with phases CT_i (i = 1 …10). A breathing period of 4 s was assumed. The following steps were performed to predict the fractional dynamic dose, which is the absorbed dose within a treatment session considering the time structure of the PBS field and the patient motion [26]:

• •Using an empirical beam time model of the PT machine, which considers a normal random distribution with a mean of 1.23 s and a standard deviation of 0.26 s for the energy switching, each spot could be assigned to a respiratory phase i described by CT_i.
• •For every phase i the contribution to the fraction dose was calculated yielding d_fx,CTi.
• •Using deformable image registrations d_fx,CTi were mapped to the reference phase yielding $d_{\mathrm{fx},\mathrm{CTi}}^{\mathrm{ref}}$.
• •The fractional interplay dose distribution d_fx was given by ${\sum }_i{d}_{\mathrm{fx},\mathrm{CTi}}^{\mathrm{ref}}$.

We refer to d_fx as the 4DDD and note that summing d_fx over all fractions could be regarded as 4DDD as well. Above processing steps, which had been performed within a Python plug-in module to RayStation in our previous studies [26], [17], were incorporated into the core program of the RayStation research software. The second and the third steps are computationally expensive. Six delivery scenarios with randomly sampled energy switching times were generated, and the start of beam delivery was iterated over all ten phases in the 4DCT. This resulted in a total of 60 evaluation scenarios per treatment plan.

To ease the computational demand with the large number of dose (evaluation) scenarios, the dose distributions were calculated by the pencil-beam algorithm of RayStation [26]. In Section 2.5, the use of the Monte-Carlo dose engine [33] to assess the dosimetric deviations of the pencil-beam dose engine was investigated.

2.4. Data analysis

The amplitude of the target region iCTV was characterized by the average vector length of the deformation vector field (DVF) in-between the CT_ee at the end-expiration phase and the CT_ei at the end-inspiration phase [34], [16]:

$$d_{\mathrm{iCTV}}=\frac{{\sum }_{i=1}^N\sqrt{d_{\mathrm{x},\mathrm{i}}^2+d_{\mathrm{y},\mathrm{i}}^2+d_{\mathrm{z},\mathrm{i}}^2}}{N},$$ (2)

where the internal CTV (iCTV) is created by the union of all CTV contours on the all 4D phases CT_i and the components (d_x,i, d_y,i, d_z,i) of the DVF are considered for voxels i = 1 … N within the iCTV.

In order to quantify the dose coverage of the target volume the two following quantities were evaluated. The first one is the homogeneity index (HI) [35]:

$$\mathrm{HI}[\%]=\left(\frac{D_5-D_{95}}{D_{\mathrm{prescr}}}\right)·100,$$ (3)

where D₅ und D₉₅ refer to the dose covering 5% and 95% of the CTV-volume. The second quantity is the over- and underdosage [34], [16]:

$$V_{107/95}[\%]=V_{107}+(100-V_{95}),$$ (4)

where V₁₀₇ (V₉₅) is the volume percentage of the CTV above (below) D_prescr × 107% (D_prescr × 95%). V_107/95 quantifies hot spots and cold spots in the CTV by combining the underdosage V₉₅ [36], [14] and the overdosage V₁₀₇ [14].

The normal liver tissue, which is the liver contour except the CTV, was evaluated as most relevant organ-at-risk using the mean dose (${\overline{D}}_{\mathrm{L}}$) and the volumes exceeding 42Gy_RBE ($V_{{42\mathrm{Gy}}_{\mathrm{RBE}}}$) and 33Gy_RBE $(V_{{33\mathrm{Gy}}_{\mathrm{RBE}}})$. The liver volume receiving less than 15Gy_RBE (${\mathrm{V}}_{<15{\mathrm{Gy}}_{\mathrm{RBE}}}$) was also evaluated.

In previous studies the relationship between the HI and the number of repaintings was studied based on the idea of statistical averaging [21]. Following these approaches, an empirical relationship was established for the cases under investigation using the following formula

$$\mathrm{HI}(\mathrm{N})[\%]=\frac{a}{\sqrt{N}+b}+c.$$ (5)

Here $1/\sqrt{N}$ describes the averaging over the multiple repainting. The analysis was conducted for N = N_eff and for N = N_Rep. The addend b describes a possible deviation from Poisson statistics. The addend c (c > 0) could account for the non-uniformity of the CTV dose coverage which is not related to motion. A χ² fit was performed for each case in which there was a smooth decline of HI with N_Rep (N_eff).

2.5. Validation of the dynamic dose calculation

The validation of the used software to compute the 4DDD was performed with the following methods:

• 1.One case of Ref. [16] was recomputed and compared to the result of the previous study. In this way the upgraded implementation of 4DDD simulation can be traced back to the validation described in Ref. [26].
• 2.The 4DDD calculation also provides the total delivery time, which has been compared to the measured delivery time of mock treatments of three treatment plans in the gantry room. Because the time model in RayStation (see Section 2.3) does not account for the minimum energy switching time of 0.9 s (see Section 2.1), we expect the computed delivery times to be on average 29% lower than the measurements.
• 3.The impact of possible deficiencies of the pencil-beam algorithm ([10]) was assessed for the nominal delivery and the layered repainting (N_Rep = 5) by recomputing two cases computed with the Monte-Carlo dose engine of RayStation [33]. The target volume of patient id 2 is close to the intestine and in case of patient id 3 it abuts the lung. In both cases one field is traversing a rib. Thus, both cases test proton transport in the presence of density gradients. The statistical uncertainty was set to 0.5%, which is the standard deviation error over all dose voxels exceeding 50% of the maximum dose.
• 4.The impact of simulating a limited population of 60 dose distributions (see Section 2.3) per delivery scenario was evaluated. The standard error of the mean (SEM) was assessed by repeating the simulation of the 4DDD five times for patient id 1 and 4. The SEM of HI and V_107/95 for the nominal delivery and the layered repainting (N_Rep = 5) was evaluated.

3. Results

3.1. Impact of repainting on the interplay effect

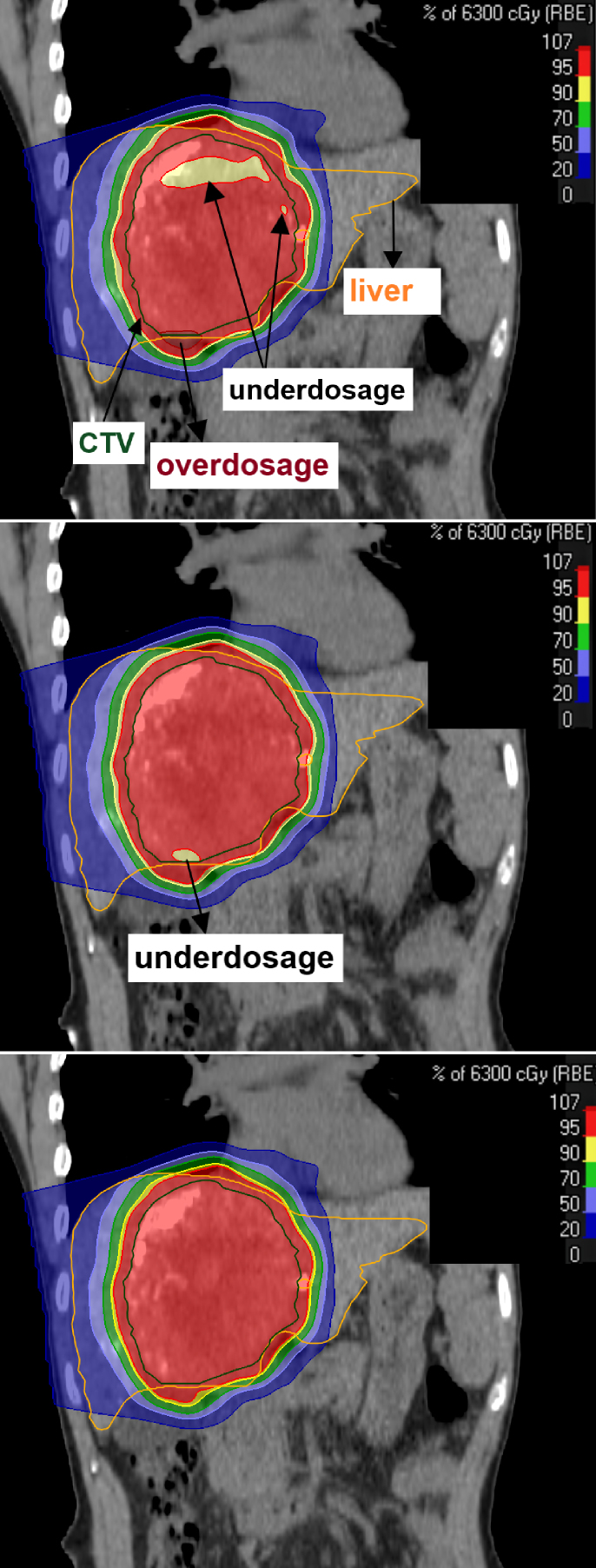
Figure 2 shows the exemplary 4DDDs obtained with and without layered repainting. The effect of interplay between the intrafractional motion and the PBS dynamics can be visualized by patches of underdosage within the CTV that could be effectively recovered by layered repainting with N_Rep = 5 and N_Rep = 7 (middle and bottom, respectively).

Figure 2.

Example of the impact of layered repainting delivery on the dose distribution of patient id 4 in the RayStation treatment planning system (coronar planes). Top: Nominal field deliveries with interplay-effect observed as a partial underdosage in the CTV. Middle: Dose delivery with five repaintings per energy layer. Bottom: Dose delivery with seven repaintings per energy layer.

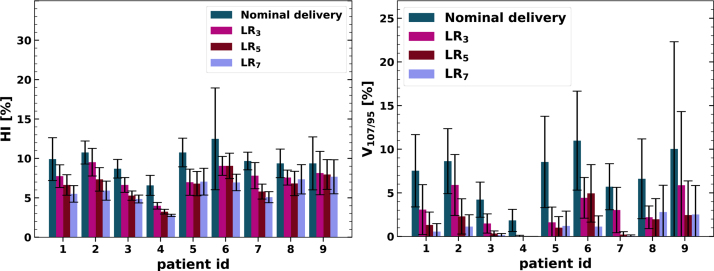
Table 1 lists exact simulation results for two selected patients. Figure 3 depicts the general trend of decreasing HI and V_107/95 with increasing N_Rep. A few exceptions, which were explained by the scatter indicated by the error bars, were observed for patient ids 5-8. The HI, averaged over all cases, was reduced by 23%, 33%, and 39.7% and for V_107/95 by 61%, 81.4%, and 87% with N_Rep = 3, 5, 7, respectively, relative to the nominal delivery without repainting.

Table 1.

Dynamic dose computation with Monte-Carlo (MC) and pencil-beam (PB) algorithm for the example of patient ids 2 and 3. The nominal scenario (index “n”) and layered repainting (N_Rep = 5) have been considered. Resulting values and standard deviations are presented.

Patient id 2
		PBn	MCn	${\mathrm{PB}}_{{\mathrm{LR}}_5}$	${\mathrm{MC}}_{{\mathrm{LR}}_5}$
CTV	HI [%]	10.8 ± 1.5	11.1 ± 1.5	7.3 ± 1.5	7.1 ± 1.1
	V107/95 [%]	8.6 ± 3.7	8.9 ± 3.4	2.3 ± 2.0	2.0 ± 1.8
OAR	$\overline{D_{\mathrm{L}}}[{\mathrm{Gy}}_{\mathrm{RBE}}]$	13.8 ± 0.1	13.8 ± 0.1	13.8 ± 0.1	13.8 ± 0.1
	${{\mathrm{V}}_{42\mathrm{Gy}}}_{\mathrm{RBE}}$ [%]	17.4 ± 0.2	17.2 ± 0.2	17.4 ± 0.1	17.3 ± 0.1
	${{\mathrm{V}}_{33\mathrm{Gy}}}_{\mathrm{RBE}}$ [%]	20.8 ± 0.1	20.7 ± 0.2	20.9 ± 0.1	20.8 ± 0.1
	${\mathrm{V}}_{<15{\mathrm{Gy}}_{\mathrm{RBE}}}$[cm3]	796.8 ± 2.5	795.8 ± 2.5	797.2 ± 1.6	795.6 ± 1.7

Patient id 3
		PBn	MCn	${\mathrm{PB}}_{{\mathrm{LR}}_5}$	${\mathrm{PB}}_{{\mathrm{LR}}_5}$
CTV	HI [%]	8.69 ± 1.18	8.70 ± 0.95	5.28 ± 0.59	5.05 ± 0.57
	OU [%]	4.22 ± 2.01	4.47 ± 1.80	0.34 ± 0.30	0.35 ± 0.37
OAR	$\overline{D_{\mathrm{L}}}[{\mathrm{Gy}}_{\mathrm{RBE}}]$	19.82 ± 0.05	19.96 ± 0.06	19.82 ± 0.02	19.96 ± 0.02
	${{\mathrm{V}}_{42\mathrm{Gy}}}_{\mathrm{RBE}}$ [%]	25.41 ± 0.08	25.43 ± 0.09	25.39 ± 0.04	25.43 ± 0.05
	${{\mathrm{V}}_{33\mathrm{Gy}}}_{\mathrm{RBE}}$ [%]	29.46 ± 0.08	29.54 ± 0.09	29.44 ± 0.25	29.55 ± 0.05
	${\mathrm{V}}_{<15{\mathrm{Gy}}_{\mathrm{RBE}}}$[cm3]	567.36 ± 0.79	564.12 ± 0.81	566.94 ± 0.61	563.84 ± 0.66

Figure 3.

Impact of the number of layered repaintings on the homogeneity index HI (left graph) and on the over- and underdosage V_107/95 (right graph). Indicated are mean values as solid, colored bars and the standard deviation as error bars.

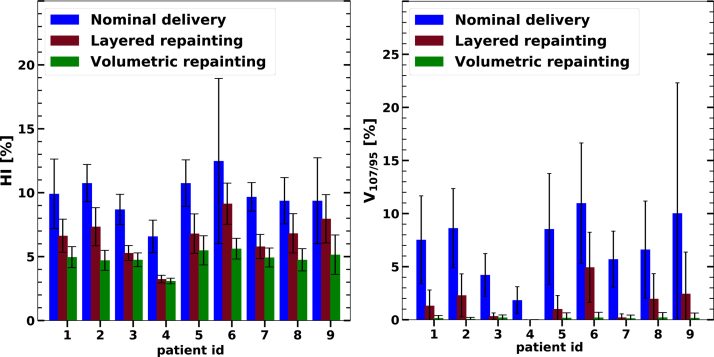
The impact of repainting by the layered option (N_Rep = 5) and the volumetric option, is shown in Figure 4 for the HI (left) and for V_107/95 (right). The reduction of the over-and underdosage was stronger than the reduction of the HI. The relative reduction of V_107/95 for layered (volumetric) repainting ranged between 55% (95%) and 100% (100%) with a mean of 81% (98%). The relative reduction of HI for layered (volumetric) repainting ranged between 15% (45%) and 51% (56%) with a mean of 33% (50%). The large relative reduction is not limited to the mean values of HI and V_107/95 but also to their standard deviation.

Figure 4.

Impact of the volumetric and layered repainting techniques (each spot is revisited up to five times) on the homogeneity index HI and on the over-and underdosage V_107/95 as compared to the nominal delivery of the treatment plan. The standard deviations over the 60 delivery samples are indicated as error bars.

The 4DDD simulations found that the impact of the interplay effect for the normal liver tissue is generally negligible. The change of the mean dose (${\overline{D}}_{\mathrm{L}}$) varies on average by 0.0 Gy_RBE compared to the nominal delivery with a maximum increase of 0.1 Gy_RBE. Similarly, the average (maximum) deviation with respect to the nominal delivery was 0.0%/0.0% (0.2%/0.1%) for $V_{{42\mathrm{Gy}}_{\mathrm{RBE}}}$/$V_{{33\mathrm{Gy}}_{\mathrm{RBE}}}$. For the fact that above dose statistics of the liver are clearly within the tolerances for the nominal delivery [16], this also holds for the repainted dose delivery. Layered repainting reduces ${\mathrm{V}}_{<15{\mathrm{Gy}}_{\mathrm{RBE}}}$, on average, by 0.0%. For a few repainted deliveries, the reduction is on the order of 1 cm³.

3.2. Motion mitigation by repainting interpreted by statistical averaging

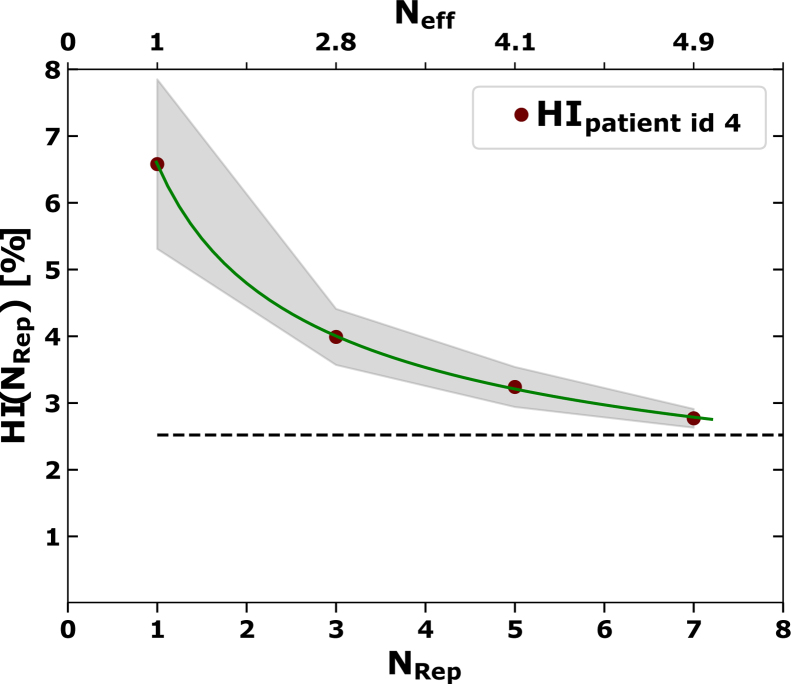
Figure 5 shows the trend of HI with the number of layered repaintings. The solid line indicates that the trend could be described by Eq. (5). The homogeneity index evaluated for a static anatomy, denoted as HI_stat, set the scale of acceptable values for HI. These HI_stat values were calculated in the range of 1.5% and 5.7% among individuals. The plot of Figure 5 shows that for N_Rep = 7 the HI was close to HI_stat. Even for N_Rep = 3, 5 the HI was tolerable. In this example the fit results were a = 6.1%/a = 5.3%, b = 0.0/b = −0.5, and c = 0.5%/c = 0.5% for HI=HI(N_Rep)/HI=HI(N_eff). As the current study did not consider large N_Rep (N_Rep > 7), the extrapolation at large N_Rep was extracted from the model fit (Eq. (5)). In first approximation the offset c is expected to converge towards HI_stat. The fit results show that in five cases the fit parameter c was smaller than 0.5%, which is clearly below HI_stat. Only for one case (patient id 9), featuring the largest motion amplitude (Figure 1), c = 7.0/c = 6.6 was larger than HI_stat = 5.7. The value of b averaged over all cases is 0.6/0.4 for HI=HI(N_Rep)/HI=HI(N_eff).

Figure 5.

Homogeneity index HI as a function of repainted layers N_Rep/N_eff (red solid circles). The standard deviation of HI is indicated by the gray stripe. The green solid line shows the fit function according to Eq. 5. The dashed horizontal line indicates the HI under static conditions (HI_stat).

3.3. Validation of the dynamic dose calculation

Results of the validation test according to the list of Section 2.5 were as follows:

• 1.The relative deviation of HI and V_107/95 between the validated time model of Ref. [26] and the integrated model of the current study is less than 1%. Regarding the organs-at-risk the biggest relative deviation is 1.1% (for ${{\mathrm{V}}_{42\mathrm{Gy}}}_{\mathrm{RBE}}$).
• 2.The delivery time at the machine exceeds the in-silico time by 27.3%, 28.9%, and 19.7% in the three selected cases. The time model (Section 2.3) in RayStation does not account for the clipping of switching times at 0.9 s (Section 2.1). Expecting a mean difference of 29% (see Section 2.5), the calculated and measured delivery times of the first two cases match and deviate for the third case by 13%.
• 3.Table 1 provides the 4DDD evaluation with pencil-beam algorithm and Monte-Carlo dose engine. Differences regarding the organs-at-risk were negligible so are differences regarding the dose in the CTV. The largest absolute difference was found to be 0.32% in V_107/95, corresponding to a relative deviation of 16%.
• 4.The maximum SEM of HI (V_107/95) was 0.2% (0.2%) for the nominal delivery and 0.2% (0.5%) for the layered repainting.

4. Discussion

Our results show that field delivery of 4D robustly optimized plans with five times layered repainting has clear advantages over the nominal field delivery in regards of over- and underdosage and homogeneity. Layered repainting for seven times performed better than five (Figure 3) and approaches the level of volumetric repainting with N_Rep = 5 (Figure 4). Volumetric repainting was regarded as not acceptable in terms of delivery time for a mean energy layer switching time of 1.2 s (see Section 2.1). The choice of layered repainting between four and seven repetitions could be decided on the level of individual patient cases. The evaluation of the dynamical dose in clinical routine planning has not yet been realized. Nevertheless, it appears to be feasible as discussed below. The rather good theoretical interplay mitigation of the volumetric repainting is in line with the study discussed in Ref. [24]. However, it appears to disagree with the others [18], [21] including a simulation study considering liver tumors [21]. Engwall et al. studied 4D robust optimization and repainting for lung tumors but did not consider the random timing of the energy changes [24]. Similar to the current study, they found for lung tumors an improvement of HI and D₉₈ through repainting, whereby the volumetric one was more effective than the layered one. Advantages of the volumetric over the layered repainting option were found to be marginal in our results. They are expected to depend on a number of characteristics, e.g. the dynamics of the beam delivery, the breathing pattern, the tumor size and localization.

According to the 4DDD evaluations, the dose of normal liver tissue is not influenced by the interplay effect (Section 3.1). Regarding the dose distribution in the target volume, the ${\mathrm{HI}}_{{\mathrm{LR}}_{\mathrm{n}}}$ (n = 5–7) approximates the HI under static conditions. The offset c (Eq. (5)), which corresponds to the extrapolation of HI to a large number of repaintings, is even below HI_stat for patient ids 1-8. This could be explained by an overcompensation of the interplay by smoothing of the dose distributions. The offset is only larger than HI_stat for the case with the biggest motion amplitude (patient id 9, Figure 1 right). This implies that the employed motion management technique is at the limit for this case.

The second criterion regarding the CTV, the over- and underdosage V_107/95, must also be met. For a few cases V_107/95 is on a level of 0–2% (N_Rep = 5), which might be regarded as clinically tolerable. For instance, the PTCOG recommendations for the treatment of thoracic tumors with proton PBS provide as example a 3% maximum decrease of V₁₀₀ if the delivery dynamics is included in the dose reconstruction [8], [37]. Pfeiler et al. argue that small underdosed volumes are tolerable in a stereotactic body radiotherapy scheme [16]. Despite the improvements through the incorporation of repainting the energy layers in the 4D robustly optimized plans, the degree of interplay mitigation might still be insufficient [24]. This is indicated by relatively large values of V_107/95 for some evaluated cases, e.g. patient id 6 with V_107/95 = 4.9% ± 3.3% using N_Rep = 5 (see Figure 4 right and Figure 3 right). Whether the additional averaging over fractions would provide a sufficient dose coverage, depends on the fractionation scheme [38]. Following Ref. [24], the corresponding radiobiological assessment (as, e.g. in Ref. [39]) is outside the scope of the current study. One may note that in the current study all breathing phases were sampled as starting point with respect to the start of beam delivery e.g. in Refs. [36], [24], [16], [17]). This can be interpreted as an inherent fractionation [36].

For the example of Figure 5, the results according to Eq. (5) suggests that layered repainting effects in dose averaging. The HI in Figure 5 follows a simple mathematical model with parameters which are consistent with the idea of a fractionation effect. The HI approaches the level of the static HI already with a few repaintings per layer. The presented formula refers to an example. Thus, it should not be used to predict the number of repaintings which are necessary to control the interplay effect for a HCC case. As pointed out above, this has to be checked with 4DDD simulations for individual cases.

There is no clear correlation of V_107/95 for repainted delivery and the motion amplitude. For instance, patient ids 1,2,7, and 9 feature the biggest motion amplitudes (see Figure 1 right) with smaller values of V_107/95 than patient id 6 (Figure 3). Such observation is in line with the findings of the other study of PBS treatment of lungs [40]. Other previous studies about lung [24] and liver [22] treatment assessed repainting to be a viable solution up to motion amplitudes of 10 mm. Inoue et al. found a slight proportionality of the interplay effect with motion amplitude [34]. Generally, the interplay effect is highly case specific [36] and depends on a number of parameters, e.g. tumor size [37]. For example, large tumor volumes (see patient ids 1–4 in Figure 1 left) were associated with low values of V_107/95. The size of our patient cohort, which contains a single patient with a motion amplitude above 1 cm, might be too small to show a clear dependence on a single motion parameter.

The current study only applies to liver tumors. Generally, it would be preferred to identify a class of HCC cases for which robust optimization and layered repainted suffices to keep the interplay effect within tolerable limits. Even if the number of cases is larger than in previous studies of liver tumors (e.g. Ref. [21]), the considered cohort could still be regarded as small as pointed out above. Furthermore, other parameters, e.g. variations of the breathing pattern, have not been considered. The huge parameter space that would need to be navigated in any in-silico study poses practical challenges to fully realize the clinical situation. Instead, the methods of the current paper suggest an evaluation of individual cases [22]. This was realized by the integration of the 4DDD calculation into the treatment planning system. The 4DDD calculation with the pencil-beam algorithm of RayStation proved to be appropriate for the field configurations evaluated in this study. The computational effort to assess the dosimetric impact of motion with a dynamical dose computation is high (Section 2.3) even when using the pencil-beam algorithm. With the advent of GPU-based calculation and other improvements of computer hardware power, the simulation times are expected to decrease in the next few years [41], [42]. As the 4DDD computation was already integrated part of a research build of the TPS based on a validated time model of a commercial PT system, we showed altogether a clear route to future clinical application [43]. The scalability of the 4DDD simulation to include interfractional motion or irregular breathing patterns is possible, should they be the clinical concerns. Simulations of 4DDD could be extended given available verification 4D CTs or cone beam CTs, which are recommended by Refs. [8], [9] for thoracic tumors, combined with breathing patterns derived from surrogate signals, e.g. the motion of the patients surface. We refer to Ref. [44] for an implementation of this concept. A limitation of the current study is the separated evaluations of set-up uncertainties combined with range uncertainties (Section 2.2) and the evaluation of the 4DDD (Section 2.3). The number of scenarios necessary to evaluate the combination of both, as e.g. described in Ref. [45], would entail too large computation times. Reference [46] describes a technical solution to this problem. Another limitation of the current study is the assumption of a fixed breathing period. Reference [22] predicted for layered repainting of liver tumors a very moderate impact on the HI if the breathing follows an irregular pattern.

In the current study, 4D robust optimization was employed for three reasons. Firstly, the clinical treatment planning in WPE generally adheres to the principle of robust optimization regarding the CTV dose coverage. By design, it serves to provide a dose coverage in all respiratory phases. It is, thus, a viable motion management tool even if the artifacts in the time domain are disregarded. Secondly, it was shown in Ref. [16] that 4D robust optimization can accomplish a better sparing of organs-at-risk than single-field uniform dose treatment plans. This applied in particular to e.g. big tumor volumes and small uninvolved liver volumes [16], which are discussed as possible indication for proton beam therapy [47]. Thirdly, we do not expect the time for treatment optimization to be prohibitive on the long-term due do the advances of computation power outlined above. As pointed out in Ref. [8], a 3D robust optimization against set-up and range uncertainties might be sufficient at low motion amplitudes or large number of fractions. In our opinion, however, the inclusion of a few CT phases into the optimization is easier than a case-by-case decision about the adequacy of a 3D robustly optimized plan. The current study does not serve to evaluate the benefits of 3D robust optimization as an interplay mitigation tool, because the robustness parameter for set-up variations is smaller than applied in clinical treatment plan optimization of abdominal tumors (see Section 2.2). In turn, a possible contribution of robust optimization with respect to isocenter shifts on an overall robustness in the time domain is expected to be larger in clinical planning than in the current work. Robust 4D optimization is by design not an interplay mitigation tool [48]. It serves to provide an inherent robustness. This robustness could be provided alternatively by the single-field uniform dose concept as shown in Ref. [22], where also 4DDD simulations of repainted plans with realistic delivery parameters of a commercial PT machine were performed.

In summary, our approach to combine 4D robust optimization and repainted field delivery worked out to mitigate the dose perturbation that would have been caused by the interplay effect. The interpretation of the role of 4D robust optimization for the mitigation of interplay, e.g. a possible synergetic effect with repainting, remains open.

5. Conclusions

With the aims to facilitate the treatment of liver tumors with the proton pencil-beam scanning technique, 4D robust optimization in conjunction with dose delivery by repainting was evaluated in the specific concern of the interplay effect. The feasibility of time-resolved dose calculations for pencil-beam scanning based on ten-phase 4D CTs within a commercial treatment planning system was shown. With the exception of prolonged treatment sessions, the 4D planning and 4D dose evaluation together with layered repainting puts the main workload onto the computational level at the phase of treatment planning. This in-silico study with nine clinical HCC cases showed a clear reduction of the homogeneity index HI. This can be interpreted by a statistical averaging over multiple applications of energy layers. More important, the over- and underdosage V_107/95 decreases from a level of typically 5–10% to about 0–5%, which can clinically be acceptable in some cases.

Conflict of interest statement

C. Bäumer, O. Blanck, M. Chan, S. Plaude, H. Siregar, B. Spaan, B. Timmermann and J. Wulff declare no conflicts of interest. E. Engwall works for RaySearch Laboratories.