Abstract
Machine learning methods are widely used within the medical field. However, the reliability and efficacy of these models is difficult to assess, making it difficult for researchers to identify which machine-learning model to apply to their dataset. We assessed whether variance calculations of model metrics (e.g., AUROC, Sensitivity, Specificity) through bootstrap simulation and SHapely Additive exPlanations (SHAP) could increase model transparency and improve model selection. Data from the England National Health Services Heart Disease Prediction Cohort was used. After comparison of model metrics for XGBoost, Random Forest, Artificial Neural Network, and Adaptive Boosting, XGBoost was used as the machine-learning model of choice in this study. Boost-strap simulation (N = 10,000) was used to empirically derive the distribution of model metrics and covariate Gain statistics. SHapely Additive exPlanations (SHAP) to provide explanations to machine-learning output and simulation to evaluate the variance of model accuracy metrics. For the XGBoost modeling method, we observed (through 10,000 completed simulations) that the AUROC ranged from 0.771 to 0.947, a difference of 0.176, the balanced accuracy ranged from 0.688 to 0.894, a 0.205 difference, the sensitivity ranged from 0.632 to 0.939, a 0.307 difference, and the specificity ranged from 0.595 to 0.944, a 0.394 difference. Among 10,000 simulations completed, we observed that the gain for Angina ranged from 0.225 to 0.456, a difference of 0.231, for Cholesterol ranged from 0.148 to 0.326, a difference of 0.178, for maximum heart rate (MaxHR) ranged from 0.081 to 0.200, a range of 0.119, and for Age ranged from 0.059 to 0.157, difference of 0.098. Use of simulations to empirically evaluate the variability of model metrics and explanatory algorithms to observe if covariates match the literature are necessary for increased transparency, reliability, and utility of machine learning methods. These variance statistics, combined with model accuracy statistics can help researchers identify the best model for a given dataset.
Introduction
Machine learning (ML) algorithms generate predictions from sample data without explicit directions from the user [1–4]. Common ML algorithms (e.g., XGBoost, Random Forest, Neural Networks) have been found to be more accurate than traditional parametric methods (linear regression, logistic regression) [5–8]. It has been hypothesized that this increase in accuracy can be attributed to potential non-linear relationships between the independent and dependent variables and interactions between multiple covariates [9, 10]. However, the increase in ML algorithms compared to traditional parametric methods comes at a significant cost: interpretability [11–15]. Linear regression and logistic regression have clear interpretable output that have been widely studied [16–18]. Machine-learning algorithms are often non-interpretable, leading to their reputation as a “black box” algorithm [10, 19–21]. As a result, the interpretability, reliability, and efficacy of machine-learning models is often difficult to assess [14, 20, 22–24].
Without methods that explain how machine learning algorithms reach their predictions, clinicians will not be able to identify if models are reliable and generalizable or just replicating the biases within the training datasets [11, 13, 25]. Provision of explanations about how model predictions are researched and providing accurate summary statistics for model accuracy metrics (e.g., AUROC, Sensitivity, Specificity, F1, Balanced Accuracy) will increase the transparency of machine learning methods and increase confidence when using their predictions [8, 9, 26, 27]. Potential solutions to these weaknesses in machine learning that have been applied within the field of computer science are SHapely Additive exPlanations (SHAP) for model interpretability and bootstrap simulation for quantifying the statistical distribution of model accuracy metrics [28–30]. However, little is known about the efficacy of SHAP and Bootstrap in evaluating machine-learning methods for medical outcomes such as heart disease. Given these limitations in the literature, with data from the England National Health Services Heart Disease Prediction Cohort, we leveraged SHAP to provide explanations to machine-learning output and bootstrap simulation to evaluate the variance of model accuracy metrics.
Methods
A retrospective, cohort study using the publicly available Heart Disease Prediction cohort (from the England National Health Services database) was conducted. All methods in this research were carried out in accordance with ethical guidelines detailed by the Data Alliance Partnership Board (DAPB) approved national information standards and data collections for use in health and adult social care. The above was approved by the UK Research Ethics Committee (REC). All participants provided written informed consent and their confidentiality was maintained throughout the study.
Independent variables
Demographic covariates of age and sex were collected. Clinical covariates of Resting blood pressure, fasting blood sugar, cholesterol, resting electrocardiogram (ECG), presence of Angina, and maximum heart rate were collected.
Dependent variable
The dependent variable of interest was heart disease, as diagnosed by a clinician.
Model construction and statistical analysis
Descriptive statistics for all patients, patients with heart disease, and patients without heart disease were computed for all covariates and compared using chi-squared tests for categorical variables and t-tests for continuous variables.
Multiple machine-learning methods were evaluated throughout this study (XGBoost, Random Forest, Artificial Neural Network, and Adaptive Boosting). The model metrics were the Area under the Receiver Operator Characteristic Curve (AUROC), Sensitivity, Specificity, Positive Predictive Value, Negative Predictive Value, F1, Accuracy, and Balanced Accuracy. Additionally, the distribution of the Gain statistic, a measure of the percentage contribution of the variable to the model, for each covariate was assessed.
Boost-strap simulation (N = 10,000 simulations) was carried out by varying the train and test sets (70:30), rerunning the model, and assessing model metrics on the test-set. The model metrics from 10,000 simulations were used to construct the distribution for all model metrics and the gain-statistic for all independent covariates. The distribution of each of statistics was evaluated visually through histograms, and analytically through summary statistics (minimum, 5th percentile, 25th percentile, 50th percentile, 75th percentile, 95th percentile, maximum, mean, standard deviation) and the Anderson-Darling test.
The model chosen with best performance would be based upon the median for the distribution of model metrics, not just based upon a singular value (which is what is commonly used in the literature). The model with the highest overall model accuracy would be used to visualize covariates through Shapely Additive Explanations (SHAP). For model explanation, SHAP visualizations were performed for each independent covariate and visualized in figures. These visualizations were evaluated through clinician judgement to evaluate their concordance with understood relationships in cardiology to validate the predictions from the model.
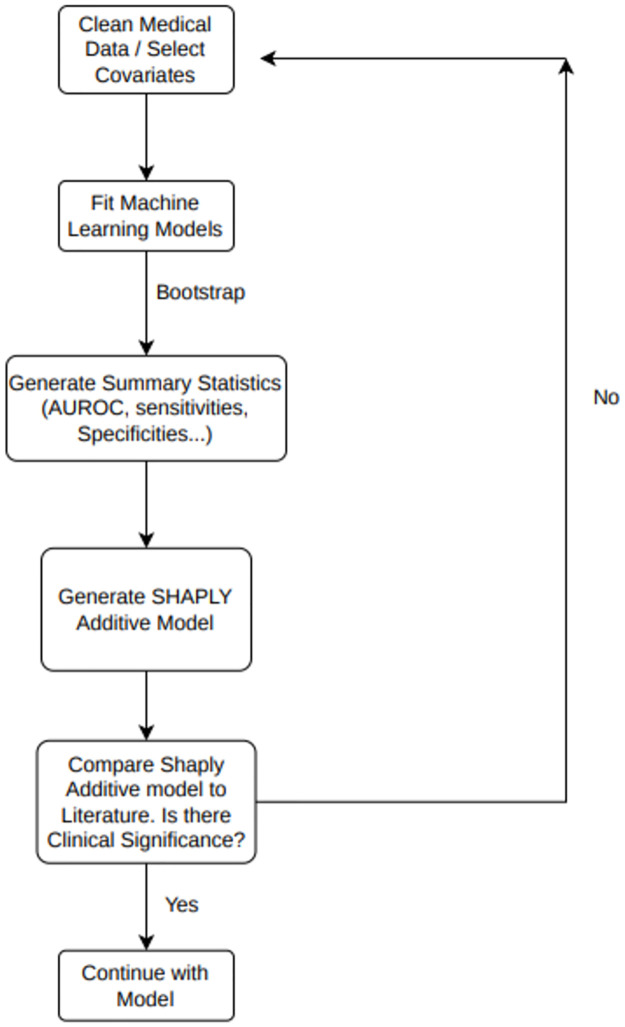
Overall methodology framework is described in Fig 1.
Fig 1. Consort flow diagram of machine learning workflow.
Description of the overall workflow for machine-learning implementation described within study, starting with a cleaned dataset and ending with a final usable model after critical evaluation of model metrics and visualization of the model through SHAP.
Results
Of the 918 patients within the cohort, the mean age was 53.51 (SD = 9.43), with 193 females (21%) and 725 males (79%). The mean Resting Blood Pressure was 132.4 (SD = 19.51), cholesterol was 198.8 (SD = 109.38), 214 (23%) of patients had elevated blood sugar, 188 (20%) of patients had Left Ventricular Hypertrophy (LVH), and 178 (19%) had ST-elevation. The mean heart rate was 136.81 (SD = 25.46) and 371 (40%) patients had Angina. Full demographic information listed in Table 1.
Table 1. Summary of cohort demographics and disease characteristics.
| Heart Disease Category | All Patients | No-Heart Disease | Heart Disease | P Values | |
|---|---|---|---|---|---|
| Patient Count | 918 (100%) | 410 (45%) | 508 (55%) | ||
| Age | 53.51 (SD = 9.43) | 50.55 (SD = 9.44) | 55.9 (SD = 9.73) | p<0.01 | |
| Gender | Female | 192 (21%) | 143 (35%) | 50 (10%) | p<0.01 |
| Male | 725 (79%) | 267 (65%) | 458 (90%) | p<0.01 | |
| Resting Blood Pressure | 132.4 (SD = 18.51) | 130.18 (SD = 16.5) | 134.19 (SD = 19.83) | p<0.01 | |
| Cholesterol | 198.8 (SD = 109.38) | 227.12 (SD = 74.63) | 175.94 (SD = 126.39) | p<0.01 | |
| Fasting Blood Sugar | Elevated | 214 (23%) | 44 (11%) | 170 (33%) | p<0.01 |
| Not Elevated | 704 (77%) | 366 (89%) | 338 (67%) | p<0.01 | |
| Electrocardiogram | LVHa | 188 (20%) | 82 (20%) | 106 (21%) | p<0.01 |
| Normal | 552 (60%) | 267 (65%) | 275 (56%) | p<0.01 | |
| ST elevation | 178 (19%) | 61 (15%) | 117 (23%) | p<0.01 | |
| Maximum Heart Rate | 136.81 (SD = 25.46) | 148.15 (SD = 23.29) | 127.66 (SD = 23.39) | p<0.01 | |
| Angina | No | 547 (60%) | 355 (87%) | 192 (38%) | p<0.01 |
| Yes | 371 (40%) | 55 (13%) | 316 (62%) | p<0.01 | |
aLVH = Left Ventricular Hypertrophy
Compared to patients without heart disease, patients with heart disease have a greater number of males (90% vs 65%, p<0.01), a higher resting blood pressure (134.2 vs 130.2, p<0.01), increased rates of elevated blood sugar (33% vs 11%, p<0.01), increased rates of ST elevation on ECG (23% vs 15%, p<0.01), and increased Angina (62% vs 13%, p<0.01).
Overall performance and variability of the models
Full statistics for model metrics in Table 2. The XGBoost model was observed as the most optimal model for this dataset, with the highest median of all model metrics. We observed that the XGBoost models had strong performance, with median AUROC = 0.87, Balanced Accuracy = 0.79, sensitivity = 0.786, and specificity = 0.785. Among 10,000 simulations completed, we observed that the AUROC ranged from 0.771 to 0.947, a difference of 0.176, the balanced accuracy ranged from 0.688 to 0.894, a 0.205 difference, the sensitivity ranged from 0.632 to 0.939, a 0.307 difference, and the specificity ranged from 0.595 to 0.944, a 0.394 difference.
Table 2. Summary of model metrics for four machine-learning techniques.
| XGBoost | ||||||||||
| Metrics | Minimum | 5th Percentile | 25th Percentile | Median | 75th Percentile | 95th Percentile | Maximum | Mean | Standard Deviation | Range |
| Accuracy | 0.688 | 0.744 | 0.771 | 0.79 | 0.808 | 0.832 | 0.894 | 0.789 | 0.027 | 0.206 |
| F1 | 0.69 | 0.745 | 0.772 | 0.788 | 0.81 | 0.832 | 0.897 | 0.79 | 0.027 | 0.207 |
| Sensitivity | 0.678 | 0.759 | 0.788 | 0.808 | 0.825 | 0.85 | 0.906 | 0.806 | 0.028 | 0.228 |
| Specificity | 0.595 | 0.709 | 0.753 | 0.785 | 0.814 | 0.855 | 0.944 | 0.784 | 0.042 | 0.349 |
| PPV | 0.68 | 0.757 | 0.786 | 0.82 | 0.845 | 0.88 | 0.954 | 0.82 | 0.037 | 0.274 |
| NPV | 0.57 | 0.678 | 0.725 | 0.756 | 0.787 | 0.83 | 0.928 | 0.756 | 0.046 | 0.358 |
| AUROC | 0.771 | 0.828 | 0.853 | 0.87 | 0.885 | 0.906 | 0.947 | 0.869 | 0.023 | 0.176 |
| Random Forest | ||||||||||
| Metrics | Minimum | 5th Percentile | 25th Percentile | Median | 75th Percentile | 95th Percentile | Maximum | Mean | Standard Deviation | Range |
| Accuracy | 0.670 | 0.728 | 0.768 | 0.782 | 0.800 | 0.815 | 0.889 | 0.784 | 0.026 | 0.219 |
| F1 | 0.683 | 0.736 | 0.772 | 0.781 | 0.806 | 0.815 | 0.880 | 0.786 | 0.026 | 0.196 |
| Sensitivity | 0.663 | 0.747 | 0.784 | 0.797 | 0.807 | 0.846 | 0.893 | 0.797 | 0.029 | 0.229 |
| Specificity | 0.584 | 0.708 | 0.743 | 0.784 | 0.807 | 0.845 | 0.925 | 0.774 | 0.042 | 0.340 |
| PPV | 0.673 | 0.741 | 0.778 | 0.808 | 0.842 | 0.862 | 0.947 | 0.806 | 0.041 | 0.274 |
| NPV | 0.551 | 0.658 | 0.716 | 0.740 | 0.769 | 0.829 | 0.911 | 0.754 | 0.042 | 0.360 |
| AUROC | 0.755 | 0.821 | 0.847 | 0.863 | 0.883 | 0.897 | 0.931 | 0.855 | 0.024 | 0.176 |
| Artificial Neural Network | ||||||||||
| Metrics | Minimum | 5th Percentile | 25th Percentile | Median | 75th Percentile | 95th Percentile | Maximum | Mean | Standard Deviation | Range |
| Accuracy | 0.687 | 0.740 | 0.760 | 0.784 | 0.804 | 0.828 | 0.880 | 0.776 | 0.023 | 0.193 |
| F1 | 0.673 | 0.735 | 0.753 | 0.782 | 0.791 | 0.822 | 0.886 | 0.774 | 0.025 | 0.212 |
| Sensitivity | 0.672 | 0.747 | 0.776 | 0.797 | 0.806 | 0.832 | 0.888 | 0.796 | 0.024 | 0.217 |
| Specificity | 0.594 | 0.704 | 0.751 | 0.769 | 0.799 | 0.837 | 0.926 | 0.764 | 0.039 | 0.332 |
| PPV | 0.660 | 0.749 | 0.778 | 0.811 | 0.836 | 0.862 | 0.939 | 0.808 | 0.033 | 0.278 |
| NPV | 0.551 | 0.662 | 0.715 | 0.748 | 0.771 | 0.814 | 0.913 | 0.744 | 0.050 | 0.362 |
| AUROC | 0.752 | 0.819 | 0.838 | 0.862 | 0.882 | 0.889 | 0.946 | 0.851 | 0.025 | 0.194 |
| Adaptive Boosting | ||||||||||
| Metrics | Minimum | 5th Percentile | 25th Percentile | Median | 75th Percentile | 95th Percentile | Maximum | Mean | Standard Deviation | Range |
| Accuracy | 0.687 | 0.732 | 0.759 | 0.79 | 0.793 | 0.82 | 0.886 | 0.776 | 0.028 | 0.199 |
| F1 | 0.67 | 0.743 | 0.758 | 0.769 | 0.806 | 0.826 | 0.892 | 0.775 | 0.025 | 0.221 |
| Sensitivity | 0.674 | 0.752 | 0.781 | 0.808 | 0.812 | 0.835 | 0.89 | 0.796 | 0.023 | 0.216 |
| Specificity | 0.589 | 0.692 | 0.744 | 0.778 | 0.803 | 0.853 | 0.944 | 0.776 | 0.041 | 0.355 |
| PPV | 0.672 | 0.743 | 0.774 | 0.8 | 0.845 | 0.862 | 0.948 | 0.816 | 0.04 | 0.276 |
| NPV | 0.567 | 0.661 | 0.714 | 0.749 | 0.786 | 0.826 | 0.925 | 0.749 | 0.042 | 0.358 |
| AUROC | 0.756 | 0.814 | 0.839 | 0.865 | 0.865 | 0.897 | 0.934 | 0.866 | 0.026 | 0.178 |
Summary of model metrics within the test set for each of the four machine-learning techniques (XGBoost, Random Forest, Artificial Neural Network, and Adaptive Boosting).
Full statistics for model covariate gain statistics in Table 3. We observe that Angina, Cholesterol, Maximum Heart Rate (MaxHR) and age are the most important predictors within the model by the model gain metric. Among 10,000 simulations completed, we observed that the gain for Angina ranged from 0.225 to 0.456, a difference of 0.231, for Cholesterol ranged from 0.148 to 0.326, a difference of 0.178, the MaxHR ranged from 0.081 to 0.200, a range of 0.119, and for Age ranged from 0.059 to 0.157, difference of 0.098.
Table 3. Summary of model gain statistics for each covariate in the XGBoost model.
| Covariates | Minimum | 5th Percentile | 25th Percentile | Median | 75th Percentile | 95th Percentile | Maximum | Mean | Standard Deviation | Range |
|---|---|---|---|---|---|---|---|---|---|---|
| Angina | 0.225 | 0.288 | 0.316 | 0.334 | 0.0353 | 0.383 | 0.456 | 0.335 | 0.029 | 0.231 |
| Cholesterol | 0.148 | 0.209 | 0.228 | 0.24 | 0.252 | 0.269 | 0.326 | 0.24 | 0.018 | 0.178 |
| Maximum Heart Rate | 0.081 | 0.114 | 0.129 | 0.139 | 0.15 | 0.165 | 0.201 | 0.139 | 0.015 | 0.12 |
| Age | 0.059 | 0.082 | 0.095 | 0.103 | 0.112 | 0.124 | 0.156 | 0.103 | 0.013 | 0.097 |
| Resting Blood Pressure | 0.027 | 0.051 | 0.061 | 0.069 | 0.076 | 0.087 | 0.109 | 0.069 | 0.011 | 0.082 |
| Sex | 0.026 | 0.038 | 0.044 | 0.049 | 0.054 | 0.062 | 0.082 | 0.049 | 0.007 | 0.056 |
| Fasting Blood Sugar | 0.007 | 0.029 | 0.037 | 0.043 | 0.05 | 0.063 | 0.142 | 0.044 | 0.011 | 0.135 |
| Resting ECG | 0.003 | 0.012 | 0.017 | 0.02 | 0.024 | 0.029 | 0.043 | 0.02 | 0.005 | 0.04 |
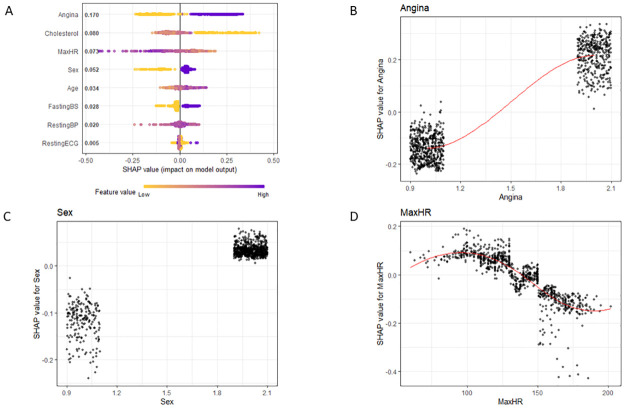
SHAP analysis was completed and visualized for Angina, Sex, and Max Heart Rate in Fig 2. We observe from SHAP that patients who have Angina, who are of Male gender, and with lower maximum heart rates have greater incidence of heart disease, which is concordant with the t-test/chi-squared comparisons that were completed in the Table 1 analysis. All covariates visualized in S1–S5 Figs.
Fig 2. SHAP analysis.
For the XGBoost models A) Overall Model detailing feature importance, with purple values representing High values and yellow values representing low values of each covariate. B) Model effect for Angina (1 –presence of angina) C) Model effect of Sex (1 –Female, 2 –Male) D) model effect for max heart rate (MaxHR).
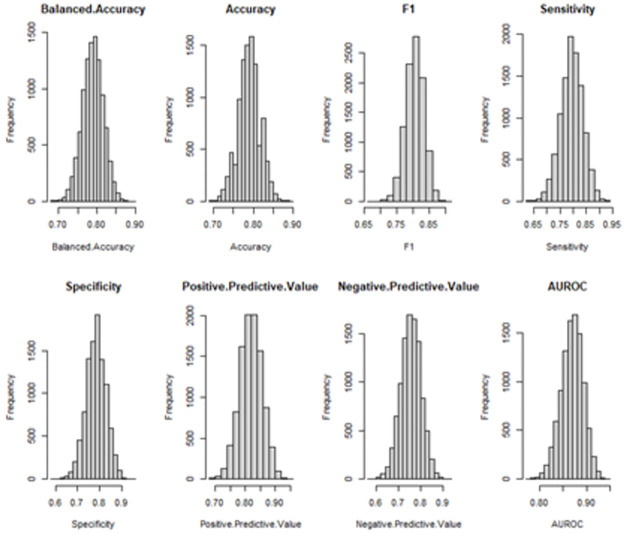
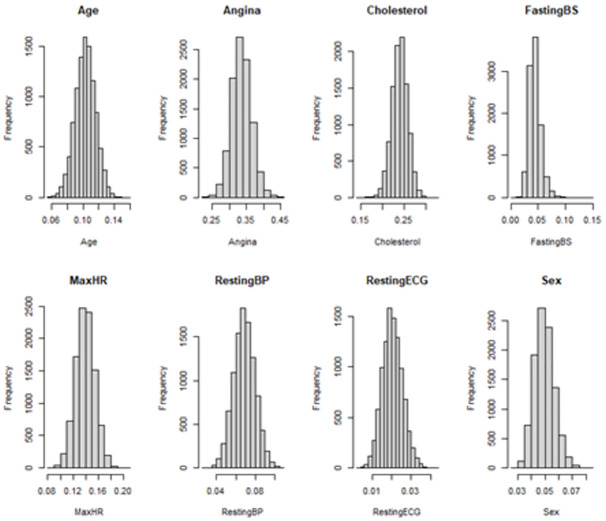
The distributions for all model statistics and the gain statistics for all covariates are in Figs 3 and 4, respectively. The distributions for all model statistics and gain statistics were not significantly different from a normal distribution as ascertained through by the Anderson-Darling Test, using significance of p<0.05 (Table 4).
Fig 3. Model statistics summary.
Balanced accuarcy, Accuracy, F1, Sensitivty, Specificty, Positive Predictive Value, Negative Predictive Value, Area Under the Receiver Operator Characteristic Curve (AUROC) for the XGboost model following bootstrap simulation.
Fig 4. Gain statistics summary.
For the XGBoost models, the distribution of th gain statistic for all covariates: Age, Angina, Cholesterol, Fasting Blood Sugar (Fasting BS), Maximum Heart Rate (MaxHR), Resting Blood Pressure (RestingBP), Resting electrocardiogram (RestingECG), Sex.
Table 4. XGBoost model summaries of anderson darling tests.
| A | B | ||
|---|---|---|---|
| Model Metrics | Anderson Darling P-Value | Model Metrics | Anderson Darling P-Value |
| Balanced Accuracy | 0.53 | Balanced Accuracy | 0.23 |
| Accuracy | 0.44 | Accuracy | 0.46 |
| F1 | 0.46 | F1 | 0.3 |
| Sensitivity | 0.18 | Sensitivity | 0.27 |
| Specificity | 0.36 | Specificity | 0.7 |
| Positive Predictive Value | 0.22 | Positive Predictive Value | 0.18 |
| Negative Predictive Value | 0.97 | Negative Predictive Value | 0.99 |
| AUROC | 0.64 | AUROC | 0.1 |
For the XGBoost models: A) Summary of Anderson Darling Test for Normality for Model Metrics B) Summary of Anderson Darling Test for Normality for Gain Statistics for model covariates.
Discussion
The use of bootstrap simulation generates 10,000 training and test-set combinations and thus also 10,000 model accuracy statistics and covariate gain statistics [31–33]. This method allows for empiric evaluation of the variability in model accuracy to increase the transparency of model efficacy [34–36].
Prior studies have found that machine learning can be an effective tool to predict outcomes in the medical field such as heart failure, postoperative complications, and infection [15, 37–41]. Shi et al. performed the sequence of fitting ML models and utilized SHAP to determine feature importance to predict postoperative malnutrition in children with congenital heart disease and similarly found XGBoost to provide the most accurate predictions [38]. In a separate study, Lu et al. pulled EHR data from UPMC and found XGBoost could predict EF score [15]. Zhou et. Al utilized a similar paradigm of first comparing machine learning models and then utilizing SHAP for model explanation [39].
What our study brings to the literature is a comprehensive framework for machine learning for medical applications. They consist of an initial machine learning selection methodology that utilizes bootstrap simulation to compute confidence intervals of numerous model accuracy statistics, which is not readily done by current studies. Furthermore, this methodology incorporates multiple feature importance statistics for feature selection. Lastly, the clinically relevant features within the model can be visualized accurately using SHAP. This methodology will streamline the reporting of machine learning by first highlighting the variability of machine learning accuracy statistics even when utilizing the same dataset, using feature importance statistics to understand how the model values each feature and finally utilizing SHAP visualization to understand how the model is generating predictions from each covariate.
Overall variability in model accuracy
From simulations, we observed that the AUROC ranged from 0.771 to 0.947, a difference of 0.176. These simulations highlight that for smaller datasets (<10,000 patients), that there may be considerable variation in the classification efficacy of the XGBoost model based upon different training-test set combinations [33, 42, 43]. At the higher end, an AUROC of 0.947 implies near perfect fit, while an AUROC of 0.771, while still significantly more predictive than random chance, provides a much decreased level of confidence in the predictions of the model. This highlights a potential issue in replication of machine-learning methods on similar cohorts [22, 44–47]. Two studies may find vastly different results in the predictive accuracy of machine-learning methods even if they use near identical models, covariates, and model summary statistics just due to the choice of the train-test sets (which are determined strictly by random number generation) [32, 35, 36, 48, 49]. As a result, this study highlights the importance of utilizing multiple different train and test sets when executing machine-learning for prediction of clinical outcomes to accurately represent the variance that is present just in the choice of selection of train and test sets [16, 18, 50]. This will accurately characterize the accuracy of the model and allow for better replications of the study. While the only covariate represented in this discussion session is AUROC, these findings were similar within the other accuracy metrics provided in Table 2.
Overall variability in covariate gain statistics
In addition to capturing the variability in machine-learning methods in model efficacy, there is also significant variability within the gain statistics for each of the covariates. We observed that the gain for Angina ranged from 0.225 to 0.456, a difference of 0.231. Since the gain statistic is a measure of the percentage contribution of the variable to the model, we find that depending on the train and test set, a covariate can have vastly different contributions to the final predictions in the model. This variability in the contribution of each covariate to the final model highlights potential dangers of training-set bias [51, 52]. Depending on which training set is present, a covariate can be twice as important to the final result of the model. This result highlights the need for multiple different “seeds” to be set prior to model training when splitting the training and test sets in order to avoid potential training-set biases and to have the model at least be representative of the cohort it is being trained and tested on (if not representative of the population the cohort is a sample of) [16, 30, 53]. Similar to the model accuracy statistics, this also highlights the difficulty in replication of results in machine-learning models from study to study [1, 54, 55]. Even in our simulation studies with identical cohorts, identical model parameters, and identical covariates, we observed that there was significant variation in which covariates were weighted highly in the final model output. This highlights the need to carefully evaluate the results of the model and not rely on a single seed to set the training and test sets for machine-learning modeling to avoid potential pitfalls that stem from training-test bias [50, 56–61]. While the only covariate represented in this discussion session is Angina, these findings were similar within the other accuracy metrics provided in Table 3.
Utility of SHAP for model explanation and allowing for augmented intelligence
Given the high level of variability in model accuracy metrics as well as covariate importance based upon different combinations of training and test sets, necessity of algorithms to explain the model are necessary to reduce potential for algorithmic bias. After simulations of model accuracy and covariate gain metrics, a seed can be chosen that accurately represents the center of the distribution for model accuracy metrics and covariate gain statistics. Then SHAP may be executed for Model Explanation to allow for interpretation of model covariates [15, 22, 26].
In traditional parametric methods such as linear regression, each covariate can be interpreted clearly (e.g., for each 1 increase in x, we observe 2 increases in y) [17, 49]. However, due to the complexity of the non-parametric algorithms that are common in machine-learning methods, it is impossible for a human to analyze each tree and execute an explanation of how the machine-learning method works [1, 62–65]. Thus, using SHAP allows for a similar covariate interpretation as linear regression even if the exact effect-sizes of the covariates cannot be interpreted the way it can in linear regression [15, 22, 49, 66–68]. Fig 2A highlights the relationship between increasing values of a covariate (purple) and increased odds for heart disease. Additionally, Fig 2B–2D allow for observation of the effect sizes of individual covariates. We observe within these plots that patients with Angina lead to significant increase in risk for heart disease, patients who are Male have an increased chance for heart disease, and patients with greater maximum heart rates have a decreased risk for heart disease. In evaluating these three covariates, a researcher/clinician can make judgment calls on if these are concordant with medical literature (prospective clinical trials, retrospective analyses, physiological mechanisms) to validate the results of the model. If the results of the model are not concordant with the medical literature, either a potentially new interpretation of the covariate should be investigated or continued evaluation of if confounders within the model may be done to rectify these observed discrepancies.
Limitations
This study has several strengths and weaknesses. One weakness is that this study utilizes only one cohort that may not have complete electronic health record data (charts, most labs, diagnoses, or procedural codes) to evaluate model variance. However, since the goal was to evaluate methods to increase transparency in machine-learning instead of developing models for heart disease, this is less of a concern. Furthermore, use of a publicly available dataset already built into an R package allows for increased replicability of this study, which is concordant with the general recommendations within this paper. Another weakness is the need for this methodology to be replicated on other machine-learning methods (neural networks, random-forest) and in other cohorts, both smaller and larger, to get a better understanding of how random chance in selecting training and test sets can significantly impact the perception of model accuracy and the perception of the most important model covariates. Furthermore, this methodology requires a high computational load that would make it difficult to replicate in larger studies with more heterogeneous data. One method to alleviate these issues is pre-selecting covariates that are medically meaningful and have a strong univariable statistical relationship with the outcome. With larger sample sizes, reducing the number of bootstrap simulations can alleviate computational load since a large sample size would naturally decrease variance. Further studies would be needed to utilize this methodology on large heterogeneous electronic health record data.
Conclusion
Machine learning algorithms are a powerful tool for medical prediction. Use of simulations to empirically evaluate variance of model metrics and explanatory algorithms to observe if covariates match the literature are necessary for increased transparency of machine learning methods, helping to detect true signal in the data instead of perpetuating biases within the training datasets.
Supporting information
Each point represents each observation, the red line represents a trend line. X-axis is the covariate of interest, Cholesterol (mg/day). The SHAP value represents the log-odds for heart disease.
(TIF)
Each point represents each observation; the red line represents a trend line. X-axis is the covariate of interest, Age(years). The SHAP value represents the log-odds for heart disease.
(TIF)
Each point represents each observation. X-axis is the covariate of interest, Fasting Blood Sugar. Non-elevated = 1, Elevated = 2. The SHAP value represents the log-odds for heart disease.
(TIF)
Each point represents each observation; the red line represents a trend line. X-axis is the covariate of interest, Resting Blood Pressure (mean arterial pressure). The SHAP value represents the log-odds for heart disease.
(TIF)
Each point represents each observation; the red line represents a trend line. X-axis is the covariate of interest, Resting Electrocardiogram. 1 represents an ST-elevation, 2 represents normal, and 3 represents left ventricular hypertrophy. The SHAP value represents the log-odds for heart disease.
(TIF)
Heart Disease Prediction Cohort from the England National Health Services Database.
(CSV)
Data Availability
All relevant data are within the manuscript and its Supporting information files.
Funding Statement
The authors received no specific funding for this work.
References
- 1.Cau R, Pisu F, Porcu M, Cademartiri F, Montisci R, Bassareo P, et al. Machine learning approach in diagnosing Takotsubo cardiomyopathy: The role of the combined evaluation of atrial and ventricular strain, and parametric mapping. Int J Cardiol. 2022. Epub 20221118. doi: 10.1016/j.ijcard.2022.11.021 . [DOI] [PubMed] [Google Scholar]
- 2.Davies M, Reyes-Figueroa AD, Gurtovenko AA, Frankel D, Karttunen M. Elucidating lipid conformations in the ripple phase: Machine learning reveals four lipid populations. Biophys J. 2022. Epub 20221118. doi: 10.1016/j.bpj.2022.11.024 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Hosseini Sarkhosh SM, Esteghamati A, Hemmatabadi M, Daraei M. Predicting diabetic nephropathy in type 2 diabetic patients using machine learning algorithms. J Diabetes Metab Disord. 2022;21(2):1433–41. Epub 20220726. doi: 10.1007/s40200-022-01076-2 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Kanda E, Suzuki A, Makino M, Tsubota H, Kanemata S, Shirakawa K, et al. Machine learning models for prediction of HF and CKD development in early-stage type 2 diabetes patients. Sci Rep. 2022;12(1):20012. Epub 20221121. doi: 10.1038/s41598-022-24562-2 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Cheng Y, Huang XF, Peng Y, Tang MX, Zhu B, Xia SY, et al. A novel machine learning method for evaluating the impact of emission sources on ozone formation. Environ Pollut. 2022;316(Pt 2):120685. Epub 20221115. doi: 10.1016/j.envpol.2022.120685 . [DOI] [PubMed] [Google Scholar]
- 6.Farajtabar M, Larimi MM, Biglarian M, Sabour D, Miansari M. Machine Learning Identification Framework of Hemodynamics of Blood Flow in Patient-Specific Coronary Arteries with Abnormality. J Cardiovasc Transl Res. 2022. Epub 20221118. doi: 10.1007/s12265-022-10339-5 . [DOI] [PubMed] [Google Scholar]
- 7.Geng EA, Cho BH, Valliani AA, Arvind V, Patel AV, Cho SK, et al. Development of a machine learning algorithm to identify total and reverse shoulder arthroplasty implants from X-ray images. J Orthop. 2023;35:74–8. Epub 20221111. doi: 10.1016/j.jor.2022.11.004 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Orji FA, Vassileva J. Automatic modeling of student characteristics with interaction and physiological data using machine learning: A review. Front Artif Intell. 2022;5:1015660. Epub 20221103. doi: 10.3389/frai.2022.1015660 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Wu CS, Liao SC, Huang WL. Use of machine learning to diagnose somatic symptom disorder: Are the biomarkers beneficial for the diagnosis? World J Biol Psychiatry. 2022:1–36. Epub 20221121. doi: 10.1080/15622975.2022.2149853 . [DOI] [PubMed] [Google Scholar]
- 10.Xu Y, Ye W, Song Q, Shen L, Liu Y, Guo Y, et al. Using machine learning models to predict the duration of the recovery of COVID-19 patients hospitalized in Fangcang shelter hospital during the Omicron BA. 2.2 pandemic. Front Med (Lausanne). 2022;9:1001801. Epub 20221102. doi: 10.3389/fmed.2022.1001801 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Dickinson Q, Meyer JG. Positional SHAP (PoSHAP) for Interpretation of machine learning models trained from biological sequences. PLoS Comput Biol. 2022;18(1):e1009736. Epub 20220128. doi: 10.1371/journal.pcbi.1009736 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Feng M, Zhang J, Zhou X, Mo H, Jia L, Zhang C, et al. Application of an Interpretable Machine Learning Model to Predict Lymph Node Metastasis in Patients with Laryngeal Carcinoma. J Oncol. 2022;2022:6356399. Epub 20221112. doi: 10.1155/2022/6356399 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Hu M, Zhang H, Wu B, Li G, Zhou L. Interpretable predictive model for shield attitude control performance based on XGboost and SHAP. Sci Rep. 2022;12(1):18226. Epub 20221029. doi: 10.1038/s41598-022-22948-w . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Li X, Zhao Y, Zhang D, Kuang L, Huang H, Chen W, et al. Development of an interpretable machine learning model associated with heavy metals’ exposure to identify coronary heart disease among US adults via SHAP: Findings of the US NHANES from 2003 to 2018. Chemosphere. 2023;311(Pt 1):137039. Epub 20221029. doi: 10.1016/j.chemosphere.2022.137039 . [DOI] [PubMed] [Google Scholar]
- 15.Lu S, Chen R, Wei W, Belovsky M, Lu X. Understanding Heart Failure Patients EHR Clinical Features via SHAP Interpretation of Tree-Based Machine Learning Model Predictions. AMIA Annu Symp Proc. 2021;2021:813–22. Epub 20220221. . [PMC free article] [PubMed] [Google Scholar]
- 16.Shi X, Jiang D, Qian W, Liang Y. Application of the Gaussian Process Regression Method Based on a Combined Kernel Function in Engine Performance Prediction. ACS Omega. 2022;7(45):41732–43. Epub 20221103. doi: 10.1021/acsomega.2c05952 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Montero-Diaz M, Chavez-Chong C, Rodriguez-Martinez E, Pita-Rodriguez GM, Lambert-Lamazares B, Basabe-Tuero B, et al. Adjusting Iron Deficiency for Inflammation in Cuban Children Aged Under Five Years: New Approaches Using Quadratic and Quantile Regression. MEDICC Rev. 2022;24(3–4):36–45. Epub 20221031. doi: 10.37757/MR2022.V24.N3-4.1 . [DOI] [PubMed] [Google Scholar]
- 18.Malheiro R, Peleteiro B, Silva G, Lebre A, Paiva JA, Correia S. Hospital context in surgical site infection following colorectal surgery: a multi-level logistic regression analysis. J Hosp Infect. 2022. Epub 20221119. doi: 10.1016/j.jhin.2022.11.004 . [DOI] [PubMed] [Google Scholar]
- 19.Wang Y, Lang J, Zuo JZ, Dong Y, Hu Z, Xu X, et al. The radiomic-clinical model using the SHAP method for assessing the treatment response of whole-brain radiotherapy: a multicentric study. Eur Radiol. 2022. Epub 20220609. doi: 10.1007/s00330-022-08887-0 . [DOI] [PubMed] [Google Scholar]
- 20.Zhang L, Duan S, Qi Q, Li Q, Ren S, Liu S, et al. Noninvasive Prediction of Ki-67 Expression in Hepatocellular Carcinoma Using Machine Learning-Based Ultrasomics: A Multicenter Study. J Ultrasound Med. 2022. Epub 20221122. doi: 10.1002/jum.16126 . [DOI] [PubMed] [Google Scholar]
- 21.Xu M, Sun C, Du Z, Zhu X. Impacts of aquaculture on the area and soil carbon stocks of mangrove: A machine learning study in China. Sci Total Environ. 2022;859(Pt 1):160173. Epub 20221115. doi: 10.1016/j.scitotenv.2022.160173 . [DOI] [PubMed] [Google Scholar]
- 22.Mitchell R, Frank E, Holmes G. GPUTreeShap: massively parallel exact calculation of SHAP scores for tree ensembles. PeerJ Comput Sci. 2022;8:e880. Epub 20220405. doi: 10.7717/peerj-cs.880 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Zhu Y, Wang X, Wang X, Chen L, Wang Z. Commentary: Predicting blood concentration of tacrolimus in patients with autoimmune diseases using machine learning techniques based on real-world evidence. Front Pharmacol. 2022;13:1000476. Epub 20221103. doi: 10.3389/fphar.2022.1000476 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Zarei Ghobadi M, Emamzadeh R, Teymoori-Rad M, Afsaneh E. Exploration of blood-derived coding and non-coding RNA diagnostic immunological panels for COVID-19 through a co-expressed-based machine learning procedure. Front Immunol. 2022;13:1001070. Epub 20221103. doi: 10.3389/fimmu.2022.1001070 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Gramegna A, Giudici P. SHAP and LIME: An Evaluation of Discriminative Power in Credit Risk. Front Artif Intell. 2021;4:752558. Epub 20210917. doi: 10.3389/frai.2021.752558 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Anjum M, Khan K, Ahmad W, Ahmad A, Amin MN, Nafees A. New SHapley Additive ExPlanations (SHAP) Approach to Evaluate the Raw Materials Interactions of Steel-Fiber-Reinforced Concrete. Materials (Basel). 2022;15(18). Epub 20220909. doi: 10.3390/ma15186261 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Oyewola DO, Dada EG, Misra S. Machine learning for optimizing daily COVID-19 vaccine dissemination to combat the pandemic. Health Technol (Berl). 2022;12(6):1277–93. Epub 20221110. doi: 10.1007/s12553-022-00712-4 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Kazmierczak NP, Chew JA, Vander Griend DA. Bootstrap methods for quantifying the uncertainty of binding constants in the hard modeling of spectrophotometric titration data. Anal Chim Acta. 2022;1227:339834. Epub 20220425. doi: 10.1016/j.aca.2022.339834 . [DOI] [PubMed] [Google Scholar]
- 29.Jalali A, Tamimi RM, McPherson SM, Murphy SM. Econometric Issues in Prospective Economic Evaluations Alongside Clinical Trials: Combining the Nonparametric Bootstrap with Methods that Address Missing Data. Epidemiol Rev. 2022. Epub 20220914. doi: 10.1093/epirev/mxac006 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Bhowmik R, Durani F, Sarfraz M, Syed QR, Nasseif G. Does sectoral energy consumption depend on trade, monetary, and fiscal policy uncertainty? Policy recommendations using novel bootstrap ARDL approach. Environ Sci Pollut Res Int. 2022. Epub 20220919. doi: 10.1007/s11356-022-22869-1 . [DOI] [PubMed] [Google Scholar]
- 31.Weber F, Knapp G, Glass A, Kundt G, Ickstadt K. Interval estimation of the overall treatment effect in random-effects meta-analyses: Recommendations from a simulation study comparing frequentist, Bayesian, and bootstrap methods. Res Synth Methods. 2021;12(3):291–315. Epub 20201222. doi: 10.1002/jrsm.1471 . [DOI] [PubMed] [Google Scholar]
- 32.Shultz TD, Hansen CM, Shultz TD. Response to use of bootstrap procedure and monte carlo simulation. J Nutr. 2000;130(10):2619. doi: 10.1093/jn/130.10.2619 . [DOI] [PubMed] [Google Scholar]
- 33.Pareto D, Aguiar P, Pavia J, Gispert JD, Cot A, Falcon C, et al. Assessment of SPM in perfusion brain SPECT studies. A numerical simulation study using bootstrap resampling methods. IEEE Trans Biomed Eng. 2008;55(7):1849–53. doi: 10.1109/TBME.2008.919718 . [DOI] [PubMed] [Google Scholar]
- 34.Thai HT, Mentre F, Holford NH, Veyrat-Follet C, Comets E. Evaluation of bootstrap methods for estimating uncertainty of parameters in nonlinear mixed-effects models: a simulation study in population pharmacokinetics. J Pharmacokinet Pharmacodyn. 2014;41(1):15–33. Epub 20131208. doi: 10.1007/s10928-013-9343-z . [DOI] [PubMed] [Google Scholar]
- 35.Sun J, Chernick MR, LaBudde RA. A bootstrap test for comparing two variances: simulation of size and power in small samples. J Biopharm Stat. 2011;21(6):1079–93. doi: 10.1080/10543406.2011.611082 . [DOI] [PubMed] [Google Scholar]
- 36.Manzato AJ, Tadei WJ, Cordeiro JA. Estimation of population profiles of two strains of the fly Megaselia scalaris (Diptera: Phoridae) by bootstrap simulation. Rev Bras Biol. 2000;60(3):415–24. doi: 10.1590/s0034-71082000000300006 . [DOI] [PubMed] [Google Scholar]
- 37.Dave D, Naik H, Singhal S, Patel P. Explainable AI meets Healthcare: A Study on Heart Disease Dataset. arXiv 2020.
- 38.Shi H, Yang D, Tang K, Hu C, Li L, Zhang L, et al. Explainable machine learning model for predicting the occurrence of postoperative malnutrition in children with congenital heart disease. Clin Nutr. 2022;41(1):202–10. Epub 20211110. doi: 10.1016/j.clnu.2021.11.006 . [DOI] [PubMed] [Google Scholar]
- 39.Zhou Y, Chen S, Rao Z, Yang D, Liu X, Dong N, et al. Prediction of 1-year mortality after heart transplantation using machine learning approaches: A single-center study from China. Int J Cardiol. 2021;339:21–7. Epub 20210713. doi: 10.1016/j.ijcard.2021.07.024 . [DOI] [PubMed] [Google Scholar]
- 40.Zambrano Chaves JM, Chaudhari AS, Wentland AL, Desai AD, Banerjee I, Boutin RD, et al. Opportunistic Assessment of Ischemic Heart Disease Risk Using Abdominopelvic Computed Tomography and Medical Record Data: a Multimodal Explainable Artificial Intelligence Approach. medRxiv. 2021:2021.01.23.21250197. doi: 10.1101/2021.01.23.21250197 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Obaido G, Ogbuokiri B, Swart T, Ayawei N, Kasongo S, Aruleba K, et al. An Interpretable Machine Learning Approach for Hepatitis B Diagnosis. Applied Sciences. 2022. [Google Scholar]
- 42.Kennet-Cohen T, Kleper D, Turvall E. Standard errors and confidence intervals for correlations corrected for indirect range restriction: A simulation study comparing analytic and bootstrap methods. Br J Math Stat Psychol. 2018;71(1):39–59. Epub 20170620. doi: 10.1111/bmsp.12105 . [DOI] [PubMed] [Google Scholar]
- 43.DeBry RW, Olmstead RG. A simulation study of reduced tree-search effort in bootstrap resampling analysis. Syst Biol. 2000;49(1):171–9. . [DOI] [PubMed] [Google Scholar]
- 44.Flynn TN, Peters TJ. Use of the bootstrap in analysing cost data from cluster randomised trials: some simulation results. BMC Health Serv Res. 2004;4(1):33. Epub 20041118. doi: 10.1186/1472-6963-4-33 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Shi Y, Zou Y, Liu J, Wang Y, Chen Y, Sun F, et al. Ultrasound-based radiomics XGBoost model to assess the risk of central cervical lymph node metastasis in patients with papillary thyroid carcinoma: Individual application of SHAP. Front Oncol. 2022;12:897596. Epub 20220826. doi: 10.3389/fonc.2022.897596 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Liu H, Chen X, Liu X. Factors influencing secondary school students’ reading literacy: An analysis based on XGBoost and SHAP methods. Front Psychol. 2022;13:948612. Epub 20220923. doi: 10.3389/fpsyg.2022.948612 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Le TT, Kim H, Kang H, Kim H. Classification and Explanation for Intrusion Detection System Based on Ensemble Trees and SHAP Method. Sensors (Basel). 2022;22(3). Epub 20220203. doi: 10.3390/s22031154 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Tian H, Cheng K, Wang Y, Zhao D, Chai F, Xue Z, et al. Quantitative assessment of variability and uncertainty of hazardous trace element (Cd, Cr, and Pb) contents in Chinese coals by using bootstrap simulation. J Air Waste Manag Assoc. 2011;61(7):755–63. doi: 10.3155/1047-3289.61.7.755 . [DOI] [PubMed] [Google Scholar]
- 49.O’Keefe P, Rodgers JL. A Simulation Study of Bootstrap Approaches to Estimate Confidence Intervals in DeFries-Fulker Regression Models (with Application to the Heritability of BMI Changes in the NLSY). Behav Genet. 2020;50(2):127–38. Epub 20200210. doi: 10.1007/s10519-020-09993-9 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Wei F, Yang X, Pang K, Tang H. Traditional Uses, Chemistry, Pharmacology, Toxicology and Quality Control of Alhagi sparsifolia Shap.: A Review. Front Pharmacol. 2021;12:761811. Epub 20211014. doi: 10.3389/fphar.2021.761811 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Austin PC. Bootstrap model selection had similar performance for selecting authentic and noise variables compared to backward variable elimination: a simulation study. J Clin Epidemiol. 2008;61(10):1009–17 e1. Epub 20080609. doi: 10.1016/j.jclinepi.2007.11.014 . [DOI] [PubMed] [Google Scholar]
- 52.Alfaro ME, Zoller S, Lutzoni F. Bayes or bootstrap? A simulation study comparing the performance of Bayesian Markov chain Monte Carlo sampling and bootstrapping in assessing phylogenetic confidence. Mol Biol Evol. 2003;20(2):255–66. doi: 10.1093/molbev/msg028 . [DOI] [PubMed] [Google Scholar]
- 53.Chan W, Chan DW. Bootstrap standard error and confidence intervals for the correlation corrected for range restriction: a simulation study. Psychol Methods. 2004;9(3):369–85. doi: 10.1037/1082-989X.9.3.369 . [DOI] [PubMed] [Google Scholar]
- 54.Cordes D, Latifi S, Morrison GM. Systematic literature review of the performance characteristics of Chebyshev polynomials in machine learning applications for economic forecasting in low-income communities in sub-Saharan Africa. SN Bus Econ. 2022;2(12):184. Epub 20221110. doi: 10.1007/s43546-022-00328-w . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Ahmadi F, Simchi M, Perry JM, Frenette S, Benali H, Soucy JP, et al. Integrating machine learning and digital microfluidics for screening experimental conditions. Lab Chip. 2022. Epub 20221123. doi: 10.1039/d2lc00764a . [DOI] [PubMed] [Google Scholar]
- 56.Scott-Fordsmand JJ, Amorim MJB. Using Machine Learning to make nanomaterials sustainable. Sci Total Environ. 2022:160303. Epub 20221118. doi: 10.1016/j.scitotenv.2022.160303 . [DOI] [PubMed] [Google Scholar]
- 57.Saleh O, Nozaki K, Matsumura M, Yanaka W, Abdou A, Miura H, et al. Emergence angle: Comprehensive analysis and machine learning prediction for clinical application. J Prosthodont Res. 2022. Epub 20221119. doi: 10.2186/jpr.JPR_D_22_00194 . [DOI] [PubMed] [Google Scholar]
- 58.Peng J, Yang K, Tian H, Lin Y, Hou M, Gao Y, et al. The mechanisms of Qizhu Tangshen formula in the treatment of diabetic kidney disease: Network pharmacology, machine learning, molecular docking and experimental assessment. Phytomedicine. 2022;108:154525. Epub 20221106. doi: 10.1016/j.phymed.2022.154525 . [DOI] [PubMed] [Google Scholar]
- 59.Li J, Zhang Y, Lu T, Liang R, Wu Z, Liu M, et al. Identification of diagnostic genes for both Alzheimer’s disease and Metabolic syndrome by the machine learning algorithm. Front Immunol. 2022;13:1037318. Epub 20221102. doi: 10.3389/fimmu.2022.1037318 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Lee SC, Wang I, Lin GH, Li PC, Lee YC, Chou CY, et al. Development of a Short-Form Stroke Impact Scale Using a Machine Learning Algorithm for Patients at the Subacute Stage. Am J Occup Ther. 2022;76(6). doi: 10.5014/ajot.2022.049136 . [DOI] [PubMed] [Google Scholar]
- 61.Chatterjee A, Pahari N, Prinz A, Riegler M. Machine learning and ontology in eCoaching for personalized activity level monitoring and recommendation generation. Sci Rep. 2022;12(1):19825. Epub 20221118. doi: 10.1038/s41598-022-24118-4 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Smania G, Jonsson EN. Conditional distribution modeling as an alternative method for covariates simulation: Comparison with joint multivariate normal and bootstrap techniques. CPT Pharmacometrics Syst Pharmacol. 2021;10(4):330–9. doi: 10.1002/psp4.12613 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Yang Y, Yuan Y, Han Z, Liu G. Interpretability analysis for thermal sensation machine learning models: An exploration based on the SHAP approach. Indoor Air. 2022;32(2):e12984. Epub 20220119. doi: 10.1111/ina.12984 . [DOI] [PubMed] [Google Scholar]
- 64.Scavuzzo CM, Scavuzzo JM, Campero MN, Anegagrie M, Aramendia AA, Benito A, et al. Feature importance: Opening a soil-transmitted helminth machine learning model via SHAP. Infect Dis Model. 2022;7(1):262–76. Epub 20220203. doi: 10.1016/j.idm.2022.01.004 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Betto I, Hatano R, Nishiyama H. Distraction detection of lectures in e-learning using machine learning based on human facial features and postural information. Artif Life Robot. 2022:1–9. Epub 20221118. doi: 10.1007/s10015-022-00809-z . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Huber DE. Computer simulations of the ROUSE model: an analytic simulation technique and a comparison between the error variance-covariance and bootstrap methods for estimating parameter confidence. Behav Res Methods. 2006;38(4):557–68. doi: 10.3758/bf03193885 . [DOI] [PubMed] [Google Scholar]
- 67.Collins JW, Heyward Hull J, Dumond JB. Comparison of tenofovir plasma and tissue exposure using a population pharmacokinetic model and bootstrap: a simulation study from observed data. J Pharmacokinet Pharmacodyn. 2017;44(6):631–40. Epub 20171108. doi: 10.1007/s10928-017-9554-9 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Nordin N, Zainol Z, Mohd Noor MH, Chan LF. An explainable predictive model for suicide attempt risk using an ensemble learning and Shapley Additive Explanations (SHAP) approach. Asian J Psychiatr. 2022;79:103316. Epub 20221107. doi: 10.1016/j.ajp.2022.103316 . [DOI] [PubMed] [Google Scholar]