Understanding Explosive Sensitivity with Effective Trigger Linkage Kinetics

Abstract

We present a simple linear model for ranking the drop weight impact sensitivity of organic explosives that is based explicitly on chemical kinetics. The model is parameterized to specific heats of explosion, Q, and Arrhenius kinetics for the onset of chemical reactions that are obtained from gas-phase Born-Oppenheimer molecular dynamics simulations for a chemically diverse set of 24 molecules. Reactive molecular dynamics simulations sample all possible decomposition pathways of the molecules with the appropriate probabilities to provide an effective reaction barrier. In addition, the calculations of effective trigger linkage kinetics can be accomplished without prior physical intuition of the most likely decomposition pathways. We found that the specific heat of explosion tends to reduce the effective barrier for decomposition in accordance with the Bell-Evans-Polanyi principle, which accounts naturally for the well-known correlations between explosive performance and sensitivity. Our model indicates that sensitive explosives derive their properties from a combination of weak trigger linkages that react at relatively low temperatures and large specific heats of explosion that further reduce the effective activation energy.

1. Introduction

Correlations between the properties of explosive molecules and materials and their handling sensitivity have been investigated exhaustively over the last 40–50 years.¹ These studies have ultimately sought to augment the slow, trial-and-error development of new explosives with robust guidelines that have been derived from the underlying mechanics and chemistry of energetic materials. The challenge of identifying physically and statistically meaningful trends in the sensitivity of explosives requires us to analyze large amounts of data on a diverse range of molecules. For this reason, the community has tended to rely on the results of drop weight impact tests²⁻⁴ to define explosive sensitivity because they are relatively inexpensive and can be performed quickly on small quantities of material (see, e.g., refs (5)–⁷). Explosive sensitivity in the drop weight impact test is defined as the height, H₅₀, from which a 2.5 kg mass dropped onto a 40 mg sample sandwiched between an anvil and striker, that results in a detectable reaction in 50% of trials. While drop weight impact tests are performed routinely by most laboratories, they involve sub-shock impacts on small amounts of material in a contrived geometry that real explosives are unlikely to experience. Furthermore, the results can exhibit significant variability that depends on site-to-site and operator-to-operator differences in testing protocols and the properties of the explosive.^2,8−10 Nevertheless, sub-shock drop weight impact sensitivity is known to be strongly correlated with small-scale gap test shock sensitivity.^11,12

The pioneering studies of the origins of explosive sensitivity by Wenograd¹³ and Kamlet and Adolph¹⁴ provide what are still among the clearest correlations between the underlying chemistry of the molecules and H₅₀. Wenograd parameterized Arrhenius kinetics models to high temperature time-to-explosion experiments for a small set of explosives and showed that log₁₀(H₅₀) depends linearly on the critical temperature

1

that is required to start a detectable deflagration on the t* ≈ 250 μs duration of the drop weight test. Here, A and E are the pre-exponential factor and the activation enthalpy, respectively, and k_B is Boltzmann’s constant. A similar analysis was performed by Storm et al.¹¹ using Frank-Kamenetskii theory with the Arrhenius kinetics derived by Rogers,¹⁵ which also reported the linear dependence of the logarithm of the shock sensitivity on the critical temperature for reaction. The observations by Wenograd and Storm et al. indicate that certain explosives are less sensitive than others because they require heating to higher temperatures (via the kinetic energy of the drop weight) to start reacting on the time scale of the drop weight impact test. The connection between log₁₀(H₅₀) and T_c was recently confirmed theoretically by our team through the evaluation of the time-to-explosion kinetics of a series of secondary explosives using condensed-phase reactive molecular dynamics (MD) simulations.^16,17

Kamlet and Adolph in the late 1970s showed that within families of closely related explosives, log₁₀(H₅₀) is inversely proportional to the oxygen balance of the molecule.

2

where n_O, n_H, and n_C are the numbers of O, H, and C atoms in the molecule, respectively, and n_COO is the number of carboxyl groups. Molecules with an optimal oxygen balance have an OB₁₀₀ ≈ 0 and form large proportions of product molecules such as H₂O, CO, and CO₂ that are associated with strongly exothermic processes, rather than solid carbon, H₂, or O₂. Hence, the oxygen balance of an explosive, which can be computed just from its chemical formula, is connected with its performance and energy release. The connection between explosive performance and sensitivity inferred by Kamlet has been confirmed, most notably through the body of work from Zeman,^1,18,19 using heats of explosion, Q, directly rather than oxygen balance.²⁰⁻²² In addition, Jensen et al. reported correlations between drop weight impact sensitivity and the temperature of detonation, which is an analogous measure of the energy release during an explosion.²³

Mathieu developed several models that allow explosive sensitivity to be predicted with good accuracy from a parameterized reaction kinetics à la Wenograd²⁴ and by metrics that describe explosive performance, such as the heat of explosion, detonation velocity, detonation pressure, and the Gurney energy (which describes the ability of an explosive to accelerate nearby metals), à la Kamlet.⁶ These models, while empirical, are based firmly on the underlying chemical dynamics of an explosion whereby we require reactions to occur at a sufficiently fast rate and liberate sufficient thermal energy to overcome dissipation to the environment.

In addition to the kinetics and performance-based approaches to understanding and predicting explosive sensitivity, many studies have sought to connect explosive sensitivity to a diverse set of electronic, molecular, vibrational, and material properties.²⁵⁻⁴³ The success of these schemes is likely to be attributed to connections between molecular or solid-state properties to chemical kinetics and performance. The effects on impact sensitivity of crystal structure, crystal packing, and the response of explosives to shear stresses have received considerable attention. These investigations have been motivated primarily by the observation that one of the least impact-sensitive explosives, 2,4,6-trinitrobenzene-1,3,5-triamine (TATB), exhibits a unique crystal structure with extended, parallel, planar layers of molecules with strong in-plane hydrogen bonding.⁴⁴⁻⁴⁸ Nevertheless, a recent series of drop weight impact tests on the β and δ polymorphs of 1,3,5,7-tetranitro-1,3,5,7-tetrazocane (HMX) showed that once differences in particle shape and size are taken into account, any intrinsic differences between the H₅₀ values arising from density, crystal structure, and crystal packing vanish.⁴⁹ Non-linear artificial neural networks and other modern machine learning methods have also been applied successfully to extract correlations within large data sets of impact sensitivities to electronic, molecular, and material descriptors.^7,50−52 Nevertheless, the complexity of these approaches can make it difficult to obtain much physical insight into the origins of explosive sensitivity, and the transferability of the artificial neural networks to molecules that differ significantly from those included in their training data is uncertain.

We report a simple model for the impact sensitivities of a diverse set of organic molecular explosives that transparently combines the dual roles of chemical kinetics and energy release. The contribution from the chemical kinetics is included via the activation enthalpy, E_a, and pre-exponential factor, A, for the rates for breaking the first covalent bonds (which can be thought of as an effective trigger linkage) as a function of temperature, which are obtained from gas-phase reactive MD simulations. The energy release during an explosion is characterized by the heat of explosion, Q, that is estimated using heats of formation, ΔH_f, computed from semi-empirical electronic structure theory. Like Mathieu and Alaime²⁴ and Jensen et al.,²³ we find that combining the contributions from the kinetics and energy release provides a better correlation with experimental drop weight impact data than either when considered independently.

2. Computational Methods

2.1. Reactive Molecular Dynamics

Classical Born-Oppenheimer MD simulations of the time, τ, required for the first bond to break in an explosive molecule were performed using semi-empirical density functional tight binding (DFTB) theory with the lanl31 parameterization.^53,54 The lanl31 DFTB parameterization was fitted to gas-phase density functional theory (DFT) calculations of the atomization energies and interatomic forces in small organic molecules containing C, H, N, and O, and it exhibits good transferability to molecules not included in its training data. We opted to perform MD simulations using DFTB theory rather than at the more accurate DFT level because the former is significantly faster computationally while approaching DFT accuracy.

All of the gas-phase MD calculations reported here were performed in the canonical ensemble with a stochastic Langevin thermostat to control the temperature,⁵⁵ a time step for integration of the equations of motion of δt = 0.25 fs, and a finite electronic temperature corresponding to 0.2 eV to smear the occupancies of the electronic levels in the vicinity of the chemical potential. The Coulombic interactions between atom-centered Mulliken partial charges were evaluated in real space.

An adaptive self-consistent field (SCF) scheme for the electronic degrees of freedom in the DFTB model was developed to reduce the total number of evaluations of the density matrix in each MD trajectory. The adaptive SCF scheme is based on the observation that the highest occupied molecular orbital–lowest unoccupied molecular orbital (HOMO–LUMO) gap shrinks prior to bond breaking events. The extended Lagrangian Born-Oppenheimer MD formalism of Niklasson and co-workers⁵⁶⁻⁵⁹ was used to propagate the electronic degrees of freedom with 1 SCF cycle per time step with linear mixing unless the HOMO–LUMO gap decreased to less than 1 eV, after which the SCF was converged fully at each time step with the Pulay mixing scheme^60,61 to a tolerance of 10^–4 electrons on the Mulliken partial charges. The simulations were returned to linear mixing with 1 SCF per time step if the HOMO–LUMO gap increased to more than 1 eV. This adaptive SCF scheme was found to yield extremely fast calculations and stable trajectories because the extended Lagrangian Born-Oppenheimer MD formalism can be relied upon to provide long-term stability with a minimum number of SCF cycles in the long periods between bond breaking events, but when a bond breaking event is approached, as denoted by the narrowing of the HOMO–LUMO gap, a more robust mixing scheme could be employed to solve for the ground-state electronic structure even when bonds were highly strained.

Thermally activated processes are inherently stochastic at microscopic scales.^62,63 For systems with rates, κ, the probability distribution for the time, t, of first escape of the system from its current state (which in our case corresponds to the breaking of any covalent bond in the molecule) is

3

While eq 3 does not depend on whether the temperature dependence of the rates is described by the Arrhenius form

4

where T is the temperature, in the following discussion we assume that Arrhenius kinetics do describe our systems. If the rates, κ, are large because the activation energy is small with respect to k_BT, we will see a narrow distribution of escape times. Conversely, for systems where the thermal energy is small with respect to the energy barrier, we will expect to see a broad distribution of escape times. In order to extract Arrhenius rates when E_a ≫ k_BT from small MD simulations, we must adequately sample the distribution of escape times. We achieve this by running multiple independent trajectories at the same temperature, T, which use different seeds for the random number generator in the assignment of the initial velocities and in the Langevin thermostat, and then defining an average rate at each temperature

5

where τ_i is the simulation time for the breaking of the first bond in trajectory i and N is the total number of independent MD trajectories.^16,64 The rates presented in Section 3 used N = 100 trajectories at each temperature and evaluated ⟨κ(T)⟩ at between three and six different temperatures.

The simulation time, τ_i, for the breaking of any bond in a trajectory was calculated by the post-processing of a series of snapshots of the atomic positions. The number of fragments within each snap shot was determined using bond distance cutoffs based on 130% of the sum of covalent radii and the corresponding atomic connectivity. The τ_i were taken when more than one molecule (fragment) was detected in the snapshot.

2.2. Heat of Explosion

The specific heat of explosion, Q, is the negative of the change in enthalpy from reactants to products (a large positive value denotes a large energy release during the explosion), which is defined as

6

where ΔH_f is the molar heat of formation, the superscripts r and p denote reactant and product species, respectively, and n_j is the number of moles of product species j derived from the 1 mol of the reactants.⁶⁵ The types and quantities of the product species were calculated according to the oxidation priority established in the literature for detonation reactions.⁶⁶ Oxygen is assumed to first convert all hydrogen to water vapor. Additional oxygen converts all carbon to carbon monoxide, followed by full oxidation to carbon dioxide. Excess oxygen is released as molecular oxygen, O₂. In oxygen-deficient compounds, excess hydrogen and carbon are released in molecular form as H₂ and solid carbon (soot). All nitrogen is released as N₂.

The heat of formation of the reactants, ΔH_f^r, was estimated from total energy calculations with the lanl31 DFTB model and the atom-equivalent energies given in ref (67)

7

where u is the DFTB total energy, η_l the number of atoms in the molecule of type l, and ϵ_l is the corresponding atom equivalent energy. The heat of formation of the product species N₂, H₂O, CO, CO₂, H₂, O₂, and solid carbon were taken from the literature.⁶⁸

3. Results

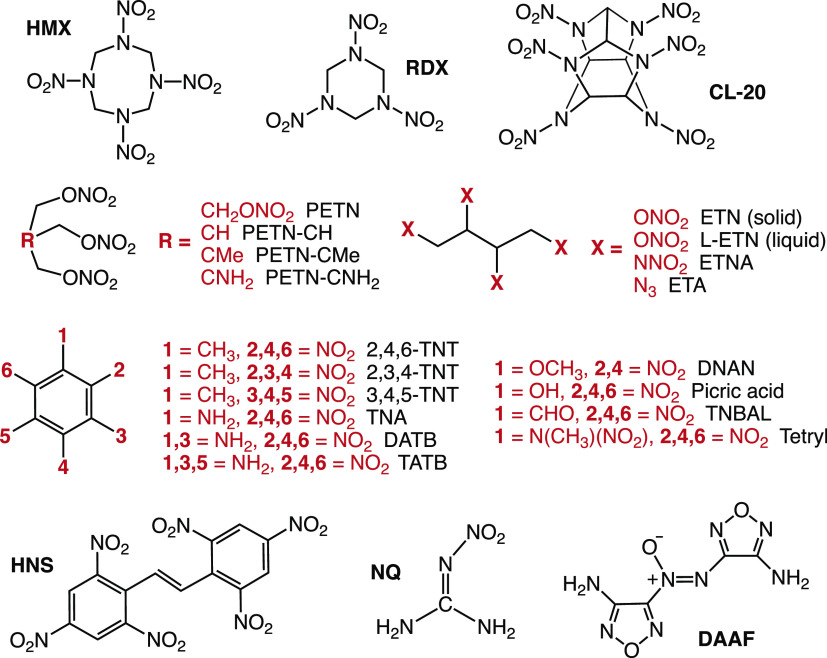
We have computed the rates and specific and molar heats of explosion for a chemically diverse set of 24 organic explosive molecules. The molecules comprise the nitrate ester-based explosives erythritol tetranitrate ([(2R,3S)-1,3,4-trinitrooxybutan-2-yl] nitrate, ETN), its isomer L-ETN,⁶⁹ pentaerythritol tetranitrate ([3-nitrooxy-2,2-bis(nitrooxymethyl)propyl] nitrate, PETN),⁴ and the PETN derivatives 2-((nitrooxy)methyl)propane-1,3-diyl-dinitrate (PETN-CH), 2-methyl-2((nitrooxy)methyl)propane-1,3-diyl-dinitrate (PETN-CMe), and 2,2,2-tris(nitroxymethyl)ethylamine (PETN-CNH₂),⁴² the nitramines cyclotrimethylene trinitramine (1,3,5-trinitro-1,3,5-triazinane, RDX), cyclotetramethylene tetranitramine (HMX),⁴ erythritol tetranitramine (N,N′,N″,N‴-(butane-1,2,3,4-tetrayl)tetranitramide, ETNA),⁷⁰ and hexanitrohexaazaisowurtzitane (2,4,6,8,10,12-hexanitro-2,4,6,8,10,12-hexazatetracyclo[5.5.0.0.^3,110^5,9]dodecane, CL-20),⁷¹ the nitroaromatic molecules diamino trinitrobenzene (2,4,6-trinitrobenzene-1,3-diamine, DATB), triamino trinitrobenzene (TATB),⁴ three isomers of trinitrotoluene (TNT), 2,3,4-TNT, 3,4,5-TNT, and 2,4,6-TNT,¹⁴ 2,4,6-trinitrobenzaldehyde (TNBAL, see Supporting Information), N-Methyl-N,2,4,6-tetranitroaniline (tetryl),⁴ 2,4,6-trinitroaniline (TNA), 2,4,6-trinitrophenol (picric acid), hexanitrostilbene (1,3,5-trinitro-2-[(E)-2-(2,4,6-trinitrophenyl)ethenyl]benzene, HNS), and 2,4-dinitroanisole (1-methoxy-2,4-dinitrobenzene, DNAN), the nitrimine nitroguanidine (1-nitroguanidine, NQ),¹⁴ the azoxyfurazan 3,3′-diamino-4,4′-azoxyfurazan ((4-amino-1,2,5-oxadiazol-3-yl)-[(4-amino-1,2,5-oxadiazol-3-yl)imino]-oxidoazanium, DAAF),⁷² and the azide erythritol tetraazide (1,2,3,4-tetraazidobutane, ETA).⁷⁰ The structures of the 24 molecules are depicted in Figure 1. The drop weight impact sensitivities, H₅₀, were measured using the ERL apparatus, with the Type 12 tool with grit paper for solids and a bare Type 12B tool for liquids, with a 2.5 kg drop weight, and are summarized in Table 1.

Figure 1.

Structures of the 24 explosive molecules.

Table 1. Common and Chemical Names of the Explosive Molecules under Study, the Number of Trigger Linkages per Molecule, N_x, and the Drop Weight Impact Sensitivity (ERL Type 12, 2.5 kg Drop Weight)^a.

common name	chemical name	Nx	H50 (cm)
DAAF	3,3′-diamino-4,4′-azoxyfurazan	2	292b
ETN	erythritol tetranitrate	4	5c
l-ETN	l-erythritol tetranitrate	4	1 (L)c
PETN	pentaerythritol tetranitrate	4	12d
PETN-CH	2-((nitrooxy)methyl)propane-1,3-diyl-dinitrate	3	8 (L), 24e
PETN-CMe	2-methyl-2((nitrooxy)methyl)propane-1,3-diyl-dinitrate	3	12e
PETN-CNH2	2,2,2-tris(nitroxymethyl)ethylamine	3	36 (L)e
RDX	cyclotrimethylene trinitramine	3	19b
HMX	cyclotetramethylene tetranitramine	4	32b
ETNA	erythritol tetranitramine	4	53f
CL-20	hexanitrohexaazaisowurtzitane	6	11g
DATB	diamino trinitrobenzene	2	>320d
TATB	triamino trinitrobenzene	3	>320d
DNAN	2,4-dinitroanisole	1	320g
HNS	hexanitrostilbene	6	54d
2,3,4-TNT	2,3,4-trinitrotoluene	3	56h
3,4,5-TNT	3,4,5-trinitrotoluene	3	107g
2,4,6-TNT	2,4,6-trinitrotoluene	3	220i
TNA	2,4,6-trinitroaniline	1	177h
Tetryl	N-methyl-N,2,4,6-tetranitroaniline	1	38d
Picric acid	2,4,6-trinitrophenol	1	87j
TNBAL	2,4,6-trinitrobenzaldehyde	3	89k
NQ	nitroguanidine	2	320d
ETA	erythritol tetraazide	4	0.7(L)f

^a(L) denotes that the drop weight tests were performed on liquid samples with the bare Type 12B tool.

^bReference (16).

^cReference (69).

^dReference (4).

^eReference (42).

^fReference (70).

^gUnpublished drop weight impact test performed at LANL as in refs (16)(69), and (70).

^hReference (73).

ⁱReference (74).

^jReference (14).

^kSee Supporting Information for details on synthesis and drop weight impact testing.

3.1. Arrhenius Kinetics

We present in Figures 2 and 3 Arrhenius plots derived from the temperature dependence of the time to break the first bond, τ, from our MD simulations. Figure 2 depicts the total rate, ⟨κ⟩, and Figure 3 depicts the rate normalized by the number of trigger linkages per molecule, ⟨κ⟩/N_x. The normalization of the rates allows us to assess the relative strengths of the first bonds to break independently of the size of the molecules. The number of trigger linkages per molecule are listed in Table 1. For most of the molecules listed in Table 1, N_x is equal to the number of energetic moieties. However, by inspection of the MD trajectories, we found that the trigger linkages for DNAN, tetryl, and picric acid are the methoxy, nitramine, and hydroxide groups, respectively, rather than the nitro groups. The amine groups are the trigger linkages for TNA, NQ, DATB, and TATB, leading to N_x = 1, 2, 2, and 3, respectively. The observation that the loss of NH₂ groups are the first reactions in TNA, NQ, DATB, and TATB is unexpected because both DFT calculations and the lanl31 DFTB model used here indicate that the bond dissociation energy for C–NH₂ is significantly larger than that of C–NO₂. We therefore attribute the loss of amines in our high temperature MD simulations to the effects of the thermally induced distortions of the molecules on the activation barrier for the scission of the C–NH₂ bond. This picture is supported by the systematic study by Zhang of bond dissociation energies in nitromethane as a function of molecular distortion.⁷⁵ In addition, recent gas-phase DFT studies of a set of derivatives of picric acid by Wiik et al. highlighted the potential shortcomings of using simple bond dissociation energies to infer explosive sensitivities and reaction mechanisms.⁷⁶

Figure 2.

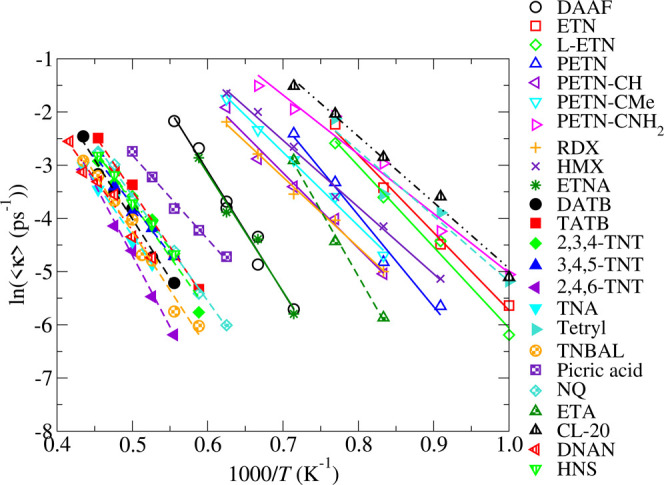
Arrhenius plot for the rate, ⟨κ⟩, of bond breaking from gas-phase MD.

Figure 3.

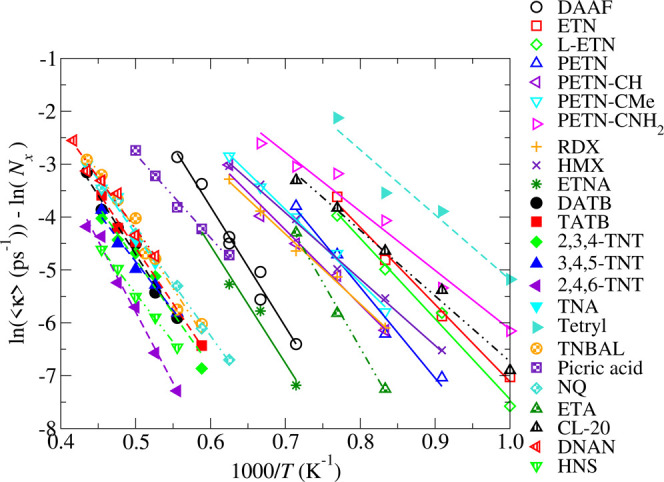
Arrhenius plot for the normalized rate, ⟨κ⟩/N_x, of bond breaking from gas-phase MD.

The Arrhenius plots presented in Figures 2 and 3 provide a considerable amount of insight into the relative stabilities and sensitivities of the set of explosives. For instance, those molecules that lie toward the right of the plot, which include the sensitive explosives ETN, tetryl, and PETN and its derivatives, react at lower temperatures than those that lie toward the left, which include the relatively insensitive explosives 2,4,6-TNT, DATB, TATB, and NQ. In addition, the rates for the nitramine-based explosives RDX, HMX, and ETNA fall at intermediate temperatures, which is consistent with their intermediate handling sensitivities.

Activation enthalpies, E_a, and pre-exponential factors, A, have been obtained from the Arrhenius plot of the rates, ⟨κ⟩ (Figure 3), by linear regression and are presented in Table 2. The normalization of the kinetics by the number of trigger linkages, N_x, affects only the pre-exponential factor, Â = A/N_x, and not the activation enthalpy. The critical temperatures, T_c, for each explosive have been computed using eq 1 using t* = 1 ns, as in refs (16) and (17). We have opted to use a value for t* that is in the range of the time scales accessible to our MD simulations rather than the t* = 250 μs used by Wenograd to mitigate the errors that would arise from the extrapolation of the rates over 5 orders of magnitude in time.

Table 2. Activation Enthalpies, E_a, and Pre-exponential Factors, A, Obtained From the Temperature Dependences of the Rates, Critical Temperatures for Explosion, T_c, and the Specific and Molar Heats of Explosion, Q and Q_m, Respectively, for 25 Gas-phase Explosive Molecules.

	A (ps–1)	Ea (eV)	Tc (t* = 1 ns) (K)	Q (kJ/g)	Qm (kJ/mol)
DAAF	36000	1.96	1303	5.25	1113
ETN	7100	1.26	925	6.03	1822
L-ETN	9600	1.31	947	6.05	1827
PETN	18000	1.48	1028	5.91	1869
PETN-CH	870	1.22	1035	5.42	1308
PETN-CMe	1000	1.19	1000	4.56	1162
PETN-CNH2	460	0.96	855	5.11	1309
CL-20	1700	1.07	989	6.29	2754
RDX	410	1.14	1021	5.17	1149
HMX	520	1.08	953	5.30	1572
ETNA	26000	1.91	1300	4.80	1412
DATB	1200	1.92	1587	3.86	939
TATB	1100	1.81	1508	3.78	976
DNAN	240	1.67	1567	4.29	849
HNS	250	1.58	1475	4.32	1943
2,3,4-TNT	100	1.43	1437	4.66	1058
3,4,5-TNT	230	1.58	11487	4.65	1055
2,4,6-TNT	6200	2.31	1717	4.44	1008
TNA	380	1.78	1597	4.09	933
tetryl	1200	1.06	877	4.57	1313
picric acid	160	1.36	1317	3.63	830
TNBAL	810	1.89	1609	3.88	934
NQ	390	1.62	1462	4.50	469
ETA	2500000	2.13	1145	6.00	1333

3.2. Heat of Explosion

By inspection, the specific and molar heats of explosion presented in Table 2 reveal the well-known correlation between the energy release and sensitivity.^14,19,20,43 Sensitive explosives such as ETA, ETN, CL-20, and PETN have large values of Q, which exceed 6 kJ/g, while the insensitive explosives DATB and TATB exhibit specific heats of explosion less than 4 kJ/g. The nitramine and substituted nitrobenzene explosives, whose sensitivities lie between those of the sensitive nitrate ester-based explosives and insensitive explosives like DATB and TATB, exhibit specific heats of explosion between 4 and 6 kJ/g.

3.3. Correlations with Drop Weight Impact Sensitivity

We have evaluated the extent to which parameters derived from the rates of bond rupture and energy release given in Table 2 are correlated with explosive sensitivity, as characterized by H₅₀. Linear relationships between the logarithm of H₅₀ (or analogous measures of explosive sensitivity) on T_c (eq 1) and Q have been reported by other authors.^11,13,43 This implies that these properties affect the effective activation enthalpy, E_x, for a system to undergo thermal explosion, that is

8

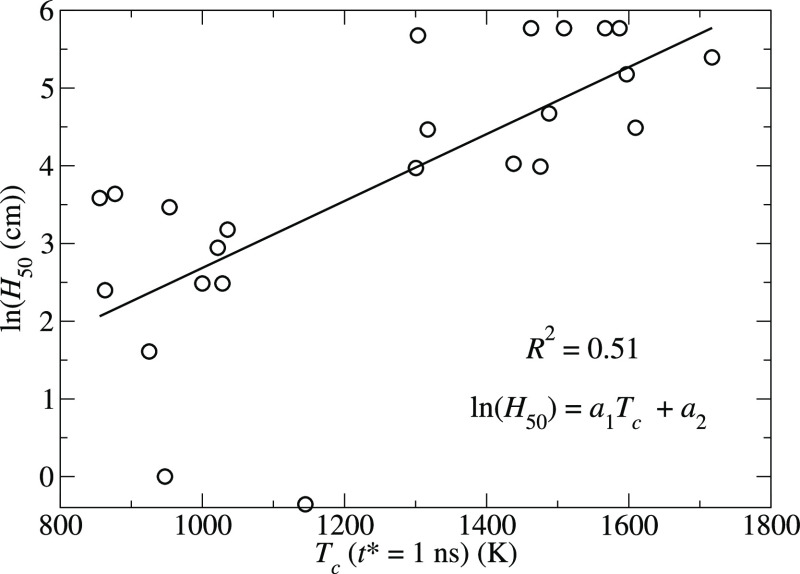
Following Zeman, we first develop separate linear models for the dependence of ln(H₅₀) on T_c and Q

9

and

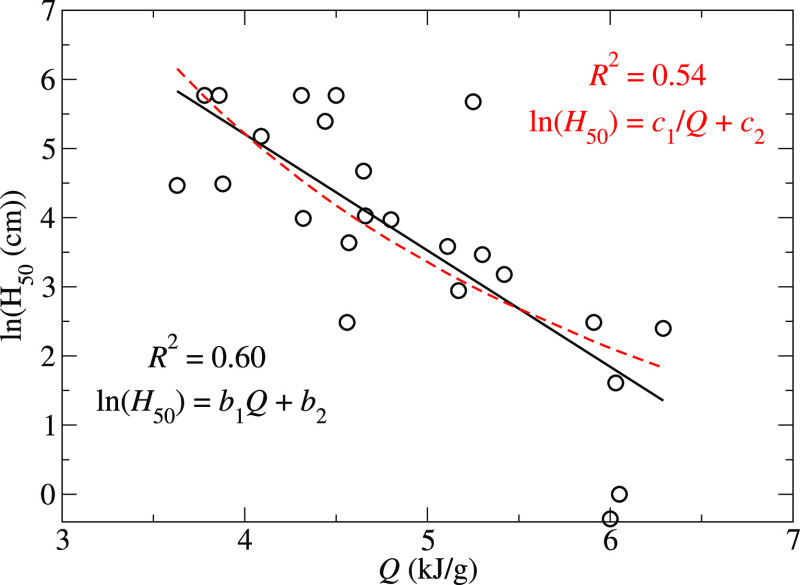
10

where {a} and {b} are adjustable parameters that are determined through linear regression. Wu and Fried,^22,77 Mathieu and Alaime,²⁴ and Jensen et al.²³ proposed models where ln(H₅₀) is inversely proportional to the energy release, and so, in addition we have examined

11

where {c} are adjustable parameters. The results for the models based on the critical temperatures and specific heats of explosion are presented in Figures 4 and 5, respectively. The coefficients of determination, R², obtained from the least-squares fits of eqs 9–11 are 0.51, 0.60, and 0.54, respectively, and the corresponding coefficients are a₁ = 4.3 × 10^–3 K^–1, a₂ = −1.62, b₁ = −1.68 g/kJ, b₂ = 11.94, c₁ = 37.1 kJ/g, and c₂ = −4.07.

Figure 4.

Dependence of ln(H₅₀) on the critical temperature for reaction (eq 1). The solid line represents the linear regression to the data.

Figure 5.

Dependence of ln(H₅₀) on the specific heat of explosion. The solid black line represents the linear regression to the data, and the broken red line represents the least-squares fit of eq 11.

The correlations seen in Figures 4 and 5 are consistent with earlier studies and with eq 8 because i) eq 1 shows that T_c is proportional to the activation enthalpy for breaking the trigger linkages, which is the first step in the cascade of reactions that lead to an explosion, and ii) the Bell-Evans-Polanyi (or Evans-Polanyi-Semenov) principle^78,79 indicates that the effective activation enthalpy, E_x, depends on the enthalpy difference between reactants and products, that is

12

where α is a positive constant because Q > 0, and E₀ is the reference activation enthalpy. While we find that the Bell-Evans-Polanyi principle via eq 10 represents our data better than the models proposed in refs (23) and (24), where ln(H₅₀) ∝ 1/Q, the coefficients of determination are similar and additional experimental data would be required to determine which form is most appropriate. The correlations between H₅₀ and Q are often viewed as being unfortunate since powerful explosives (those with a large specific heat of explosion) will tend to have a small activation enthalpy for initiating reactions, E_x.

Based on the connection between H₅₀ and the effective rate law, eq 8, we have evaluated the dependence of ln(H₅₀) on ln(A), which reveals a weak negative correlation with a coefficient of determination of R² = 0.27 (Figure S1). While the correlation between and ln(A) is relatively weak, its sign is in accordance with what we would expect physically, that is, molecules with the largest pre-exponential factors in their trigger linkage kinetics tend to react on shorter time scales and are more sensitive than the molecules with small pre-exponential factors. The dependence of ln(H₅₀) on the activation energy for breaking the first bonds, E_a, exhibits an even weaker correlation with a coefficient of determination of R² = 0.13 (Figure S2). Nevertheless, despite the large scatter in the data, the dependence of ln(H₅₀) on E_a is in accordance with the physical picture that higher activation energies should be associated with insensitivity.

The dependence of ln(H₅₀) on the kinetics of trigger linkage rupture was assessed by a least-squares fit of

13

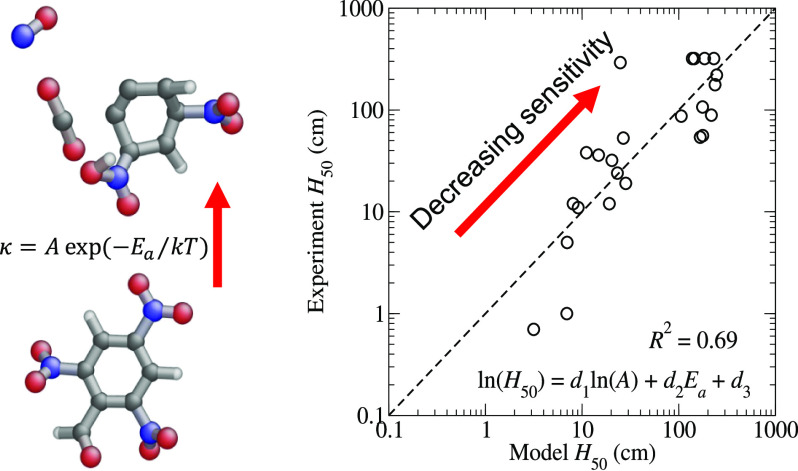
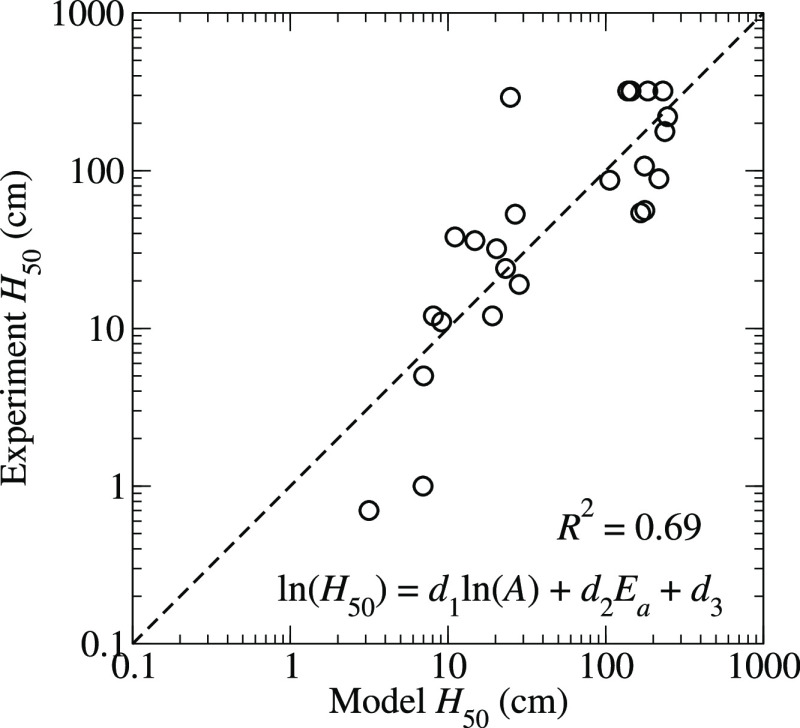
where {d} are adjustable parameters. Figure 6 shows the eq 13 and represents the variation in the ln(H₅₀) data well, with a coefficient of determination of R² = 0.69. The best-fit coefficients are d₁ = −0.63, d₂ = 3.29 eV^–1, and d₃ = 3.39.

Figure 6.

Correlation plot for H₅₀ derived from the model eq 13 for ln(H₅₀).

We have extended our linear model for ln(H₅₀) by explicitly including terms for the activation energy, specific heat of explosion, and the logarithm of the pre-exponential factor,

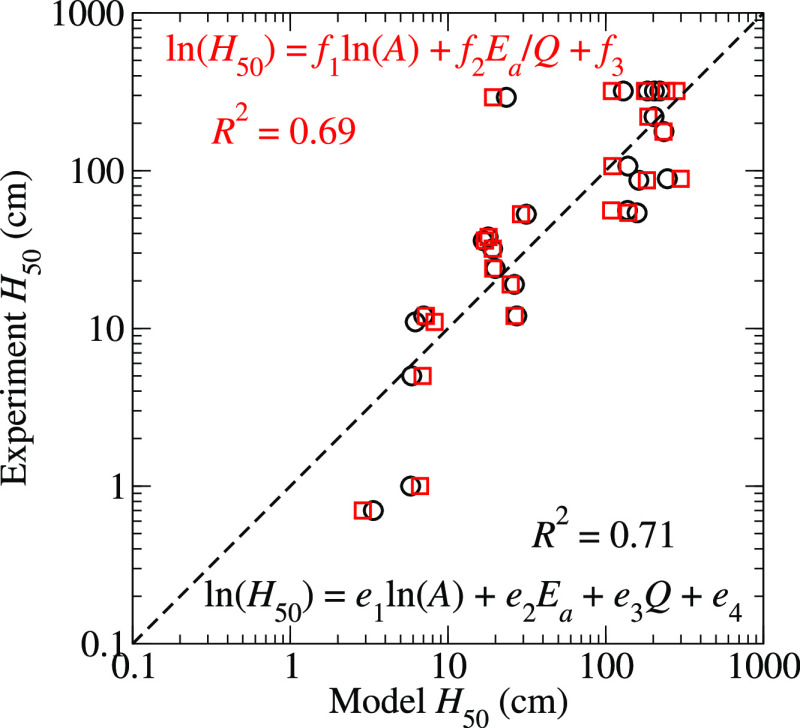
14

where {e} are coefficients determined by a least-squares fit. The ability of the model, eq 14, to reproduce the experimental given in Table 1 is depicted by a correlation plot in Figure 7. The coefficient of determination is R² = 0.71, which is a modest improvement over the linear models in eqs 9, 10, and 13. The best-fit values for the parameters are e₁ = −0.47 × 10² = 2.49 eV^–1, e₃ = −0.53 g/kJ, and e₄ = 6.03. The forms of the parameterized rate laws proposed in refs (23) and (24) have also been studied by performing a least-squares fit of

15

where {f} are adjustable parameters. The fit of eq 15 yields a coefficient of determination of R² = 0.69 and therefore provides little to no improvement over eq 13, which depends only on the Arrhenius kinetics of trigger linkage rupture. The correlation plot is presented in Figure 7, and the best fit parameters are f₁ = −0.41, f₂ = 10.37 kJ/(eV g), and f₃ = 3.40.

Figure 7.

Correlation plots for H₅₀ derived from the model eqs 14 and 15 for ln(H₅₀).

The coefficient of determination reported for Figure 7 implies that the model given in eq 14 accounts for about 71% of the variation in the experimental ln(H₅₀) data. The relatively large R² value is even more encouraging when we note that our recent analysis of hundreds of drop weight impact tests on PETN showed that the H₅₀ values reported in the literature exhibit a variability that is, at best, a multiplicative factor of 1.5 ⁸. Nevertheless, the discrepancies in the H₅₀ values obtained from eq 13, which are provided in the Supporting Information, versus the experimental values presented in Table 1 for several molecules greatly exceed the factor of 1.5 that could be attributable to experimental uncertainties. DAAF is the most significant outlier, with a model H₅₀ of 23 cm versus an experimental value of 292 cm. The critical temperature of DAAF, T_c = 1303 K (which is computed only from the kinetics of trigger linkage rupture), is comparable to those of other explosives with H₅₀ values around 50–100 cm, such as picric acid or 2,3,4-TNT. However, its specific heat of explosion, Q = 5.25 kJ/g, is significantly larger than those of TATB or DATB, and it is more comparable to those of RDX and HMX which leads to a H₅₀ that is smaller than those of the insensitive explosives. Similarly, we propose that the model overestimates the H₅₀ of TNBAL (245 vs 89 cm) and picric acid (162 vs 87 cm) because our scheme yields particularly small values for their specific heats of explosion of Q = 3.88 and 3.63 kJ/g, respectively.

4. Discussion

The so-called trigger linkages in explosive molecules are the first bonds to break when the explosive is subjected to high temperatures. Condensed-phase reactive MD simulations by our team have demonstrated that relatively long incubation times are typically required for the first bonds to break, but once those reactions have occurred, the sequence of reactions that give rise to exothermic runaway and an explosion follow rapidly.^{16,17,42,64,80} The first reactions in explosives tend to form highly reactive species, such as nitrous acid or various radicals, which react promptly with nearby molecules. Hence, the rate-determining step in explosive chemistry is connected intimately with the strength and stability of the molecular trigger linkages because the subsequent reactions tend to follow in quick succession, especially when exothermic processes lead to self-heating.

Trigger linkages in explosive molecules have been investigated using quantum chemical methods and DFT by several groups.^25,26,81,82 For instance, Tsyshevsky, Sharia, and Kuklja computed the energy barriers and pre-exponential factors for the seven most plausible decomposition pathways of PETN with DFT at the PBE0 and wB97XD levels of theory,⁸¹ and Sharia and Kuklja computed decomposition rates for HMX using DFT at the PBE level of theory.⁸³ Our MD-based approach to estimating trigger linkage kinetics differs significantly from the gas-phase DFT performed previously. One of the main challenges in applying traditional gas-phase DFT methods is that one must first identify the most plausible decomposition pathways. For instance, Jensen et al. and Wiik et al. computed–NO₂ bond dissociation energies using gas-phase DFT for a set of explosive molecules to estimate trigger linkage strengths.^23,76 However, based on our work, their focus on −NO₂ loss is likely to be an oversimplification of the first reactions in many explosives because reactions can often start at non-energetic moieties. A properly thermostated MD simulation samples the full potential energy surface of the reactant molecule and will find all possible decomposition pathways with the correct probabilities (which are based on their rates via eq 3) without requiring any prior physical intuition or guidance from the user.⁶³ Hence, the MD framework that we have developed in this work is much better suited to automation than traditional approaches. Since MD simulations sample all possible decomposition paths for a given molecule, we cannot attribute the rates presented in Figures 2 and 3 to specific trigger linkages, but rather to an ensemble of the most probable decomposition pathways. For this reason, we propose that the rates and kinetic models derived from our simulations describe an “effective” rather than a specific trigger linkage for each system.

The pre-exponential factors, A, obtained from the Arrhenius plots (Figures 2 and 3) play a surprisingly prominent role in distinguishing between sensitive and insensitive explosives. For instance, both 2,4,6-TNT and ETA have relatively large activation enthalpies for trigger linkage rupture, E_a, in excess of 2 eV, but their drop weight impact sensitivities differ by more than 200 cm. The pre-exponential factor of ETA is more than 2 orders of magnitude larger than that of 2,4,6-TNT, and up to 4 orders of magnitude larger than those of other molecules, which in part accounts for its relatively high reaction rates and high sensitivity. The pre-exponential factors for gas-phase reactions can be computed using standard atomistic simulation methods from the normal mode frequencies at the transition state, or saddle point,⁸⁴ but this process is somewhat laborious, especially for complex, multi-atom reactions. In contrast, the MD approach to computing trigger linkage kinetics presented here and in ref (17) not only finds the most probable trigger linkages without user input but it also gives the activation enthalpies and otherwise challenging-to-calculate pre-exponential factors essentially “for free” from the resulting Arrhenius plots.

Our results, which show the linear dependence of the logarithm of H₅₀ on critical temperatures, T_c, and the specific heat of explosion, Q, are consistent with those of Zeman, Wenograd, Kamlet, Politzer, and others. These observations imply that the impact sensitivity of explosives is controlled in part by an effective activation enthalpy, E_x, that depends on the underlying chemistry of the molecule via its trigger linkages and its energy release via the Bell-Evans-Polanyi principle. However, our work goes a step further by highlighting the importance of the pre-exponential factor in the kinetics of trigger linkage rupture. Figures 6 and 7 demonstrate that using the rate, κ, rather than just the activation enthalpy, greatly improves the accuracy with which H₅₀ values from experiment can be represented. The model (eq 14) that best describes our data set is consistent with transition state theory, that is

16

Hence, insensitivity (large H₅₀ ) is promoted by a large activation enthalpy for breaking the trigger linkages, E_a, and a small energy release, Q, and pre-exponential factor, A. Equation 16 is a general, physics-based expression for reaction kinetics and we have used a diverse set of explosive molecules, from the primary explosive ETA with H₅₀ = 0.7 cm through to the insensitive secondary explosive TATB, which exhibits H₅₀ > 320 cm, to parameterize eq 13. Hence, we expect the model developed in this article to provide a good representation of any organic explosive.

Using only gas-phase trigger linkage kinetics and the specific heat of explosion, our best models, eqs 14 and 15, account for about 70% of the variation of ln(H₅₀) for our set of 24 explosives. It is likely that the remaining ∼30% of the variation of ln(H₅₀) can be attributed to the condensed-phase properties of the explosives, such as those related to density, crystal structure, and deformation mechanisms, which our simple model neglects completely. For instance, trigger linkage kinetics are likely to differ between gas- and condensed-phase systems because of the effects of neighboring molecules on the molecular conformations, vibrational frequencies, and enthalpic barriers for reaction. Our MD simulations indicate that the C–NH₂ bonds in TNA, NQ, DATB, and TATB are the trigger linkages in these molecules in the gas phase, but the amines may be stabilized by the strong intermolecular hydrogen bonding displayed by these molecules in the condensed phase. It is plausible that the stabilization of the amine trigger linkages by hydrogen bonding decreases the sensitivity of these molecules with respect to other nitrobenzene derivatives, such as 2,4,6-TNT, that cannot form hydrogen bonds. In addition, jetting and melting have been connected with ignition in drop weight impact experiments with transparent anvils,³ such that we might expect to observe a positive correlation between H₅₀ and the specific heat of fusion or melting temperature. Our model predicts RDX to have a slightly larger H₅₀ value than HMX, 26 versus 19 cm, respectively, owing to the slower kinetics and smaller specific heat of explosion of the former. However, experimental measurements consistently show that HMX is less sensitive than RDX, with drop heights about 10–15 cm larger than those of RDX. While the chemistry and heats of explosion of RDX and HMX are very similar, HMX has a significantly higher melting temperature than RDX (247 °C vs 204 °C⁴), which may plausibly inhibit an important ignition mechanism in HMX and account for its decreased sensitivity. The evaluation of these hypotheses will require calculations, simulations, and experiments that are beyond the scope of the gas-phase chemistry considered here.

5. Conclusions

A physically transparent framework for estimating the sensitivity of organic explosives has been developed using the kinetics of trigger linkage rupture and specific heats of explosion, both of which can be estimated from simple, gas-phase MD and total energy calculations. Our results indicate that insensitive explosives, such as TATB and DATB, derive their properties from a combination of both slow kinetics (strong trigger linkages) and a small specific heat of explosion, while the most sensitive explosives, such as ETA, CL-20, and PETN, exhibit both fast kinetics (weak trigger linkages) and large specific heats of explosion. All of the other explosives studied in this work, including the nitramines RDX and HMX, and the various derivatives of trinitrobenzene, exhibit useful combinations of trigger linkage strengths and energy release that establish their handling sensitivities between those of the primary and insensitive explosives. This work also implies that while molecules with large specific heats of explosion will tend to be relatively sensitive, molecules with novel trigger linkage chemistry may still allow for the design of high-performance explosives with reasonable handling sensitivity.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsphyschemau.2c00022.

• Correlation between ln(H₅₀) and ln(A) and E_a, respectively, tabulated H₅₀ values measured experimentally and from the best fit of eq 14 for the 24 explosives , and overview of the synthesis procedure and drop weight impact testing of TNBAL (PDF)

The authors declare no competing financial interest.