The “violin model”: Looking at community networks for dynamic allostery

Abstract

Allosteric regulation of proteins continues to be an engaging research topic for the scientific community. Models describing allosteric communication have evolved from focusing on conformation-based descriptors of protein structural changes to appreciating the role of internal protein dynamics as a mediator of allostery. Here, we explain a “violin model” for allostery as a contemporary method for approaching the Cooper–Dryden model based on redistribution of protein thermal fluctuations. Based on graph theory, the violin model makes use of community network analysis to functionally cluster correlated protein motions obtained from molecular dynamics simulations. This Review provides the theory and workflow of the methodology and explains the application of violin model to unravel the workings of protein kinase A.

SIGNIFICANCE

Studies on dynamics-based descriptions of protein allostery are developing as an exciting frontier. Here, graph theory methods are increasingly being used to understand information flow through protein residue networks. In past few years, we have detailed the use of Girvan–Newman-based community map approach to studying allosteric regulation in protein kinase A. As principles of allostery are applicable to all proteins, we provide here a detailed explanation of our approach called the “violin model”. Foundationally rooted in the Cooper–Dryden model, our approach emphasizes the role of residue motions in mediating biomolecular allostery.

Protein function, especially in the context of signaling enzymes, like protein kinases and phosphatases, is dependent on their “activation” switches.¹ Allostery or allosteric regulation presides over this activation by triggering changes in these proteins through phosphorylation, small molecule binding, and more.² Effectors (including mutations) that enhance a protein’s biological activity are simply allosteric activators and those that decrease a protein’s biological activity are allosteric inhibitors.³ In the natural environment, most, if not all, signaling proteins are regulated by allostery, where certain stimuli allow for manipulating key proteins to elicit a biological response.^4,5 While allostery has been called the “second secret of life”⁶ and has been studied for more than six decades,⁷ the underlying mechanisms of perturbations mediating allosteric regulation remain largely elusive and available explanations continue to be protein specific. The vantage point of describing allostery continues to be its very definition: control from a distance, where the effector site is several angstroms away from the active site.⁸

CONFORMATION-BASED DESCRIPTORS OF ALLOSTERY

The classical view of allostery is cultivated on the seminal works of Monod, Wyman, and Changeux^7,9 and Koshland et al.,¹⁰ who provided the two philosophies of cooperative binding of O₂ to tetrameric hemoglobin (Hb): the concerted/MWC (Monod, Wyman, and Changeux) and sequential/KNF (Koshland, Némethy, and Filmer) models, respectively. Proposed in the 1960s, both models are based on cooperative interaction between the monomers of multimeric proteins when binding a ligand at their active sites. Both models describe two distinct conformations (Fig. 1), viz., a low affinity (tense, T-state) and a high affinity (relaxed, R-state), for the monomers contained in the multimeric protein. In the MWC model, the monomers are defined to coexist in both T- and R-states with an underlying equilibrium that governs their interconversion. The KNF model describes the existence of an intermediate between the T- and R-states such that ligand binding induces a conformational change in the monomers to switch states. In this way, the KNF model predicates that the conformation changes in the protein are in direct proportion to the amount of ligand such that the relaxed/“active” conformation exists only in the presence of the bound ligand. Over time, the simplicity of these structural models¹¹ has allowed research to delve deeper into regulation of oxygen affinity by heterotopic effectors and evolve these models to explain hemoglobin’s structure–function relationship.^12,13

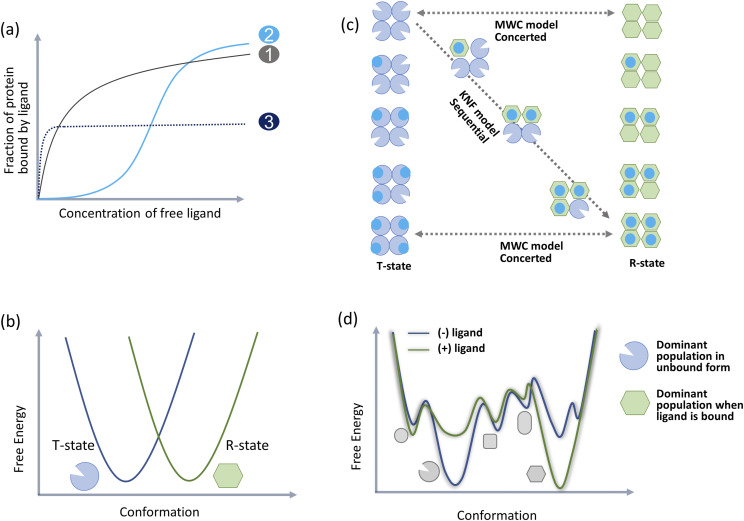
FIG. 1.

Conformation-based description of allostery (a) canonical descriptors of allostery is based on cooperativity seen in multimeric proteins (like hemoglobin) when they bind their ligands. If the active sites of the monomers are independent, ligand binding curves have a hyperbolic shape like those of Michaelis Menten plots (curve 1). In positive cooperativity, the plot flattens at first and then quickly increases to attain maximal signal (curve 2). The MWC formula is an expression for this S-shaped binding function. Negative cooperativity is seen as a steep rise in binding with early flattening of the curve before optimal binding saturation (curve 3). (b) MWC and KNF models of allostery are based on descriptors of two distinct protein conformations that occupy distinct basins in the free energy landscape. Conformation that has low affinity for the ligand is called the tense state (T-state) and the conformation with high affinity for the ligand is the relaxed state (R-state). (c) The MWC model postulates that the two protein conformations coexist in an equilibrium while the KNF model postulates that ligand binding induces conformational switching and converts one conformation to another. (d) The population shift theory postulates that a protein’s free energy landscape includes an ensemble of varying populations of all probable conformations. Allosteric signals (like ligand binding) choose compatible populations to shift the ensemble to a new averaged conformation.

Both the MWC and KNF models have been employed to explain allostery (or classic cooperativity^6,14) in many proteins^15–19 providing a conformation-based description of allostery.^18,20 In both the models, however, cooperativity is defined as an expression for protein-ligand binding functions as it deviates from a hyperbolic curve (Fig. 1). A slow rising sigmoid curve denotes positive cooperativity, while a steeply rising sigmoid curve flattening into a lower saturation value denotes negative cooperativity. Importantly, the shape of the binding function does not provide a view into the free energy landscape of the protein to explain how an averaged conformation is reflected in the Hill coefficient.²¹ Moreover, the coefficient is unable to distinguish competitive, noncompetitive ortho-, iso-, or allosteric mechanisms that may be central to establishing cooperativity. In other words, both MWC and KNF models are phenomenological and attempt to annotate cooperativity emerging from the averaged behavior of protein conformations. Nonetheless, support for the structural view comes from mutation studies,²² evidence of extreme protein conformational changes on ligand binding,²³ and even predictability of protein conformational change from pure structural analysis of unbound or ligand-bound protein forms.^24,25

Since the 1960s, emergence of various biophysical techniques including molecular dynamics simulations and nuclear magnetic resonance (NMR) methods for characterizing protein dynamics changed the way allostery was perceived.^26,27 Relaxing the requirement for symmetric oligomerization coupled to analysis of varied conformations of the protein allowed for a simplified application of the structural view to monomeric proteins.^20,28 This “population shift” model^29–31 recognized that all proteins exist as an ensemble^32,33 of all functional conformations averaged around their native state as defined by their free energy landscape. This ensemble includes all preexisting allowed conformations for the protein (including both ligand-unbound and ligand-bound conformations) as major or minor populations. Allosteric effectors choose and bind their compatible conformations and shift the populations of the ensemble to allow for protein conformation switching (Fig. 1). Consequently, destabilization of the low-populated conformations without affecting the protein’s native structure was used to explain allosteric inhibition.^34,35

However, does the conformation-based view of allostery explain it all? The main limitation of the structural view stems from its vantage point of being tied to the conformation or structure of the protein. However, do structurally similar proteins have similar allosteric footprints? While the view describes distinct unbound–bound protein conformations, it does not define how these conformations are adopted. How do similar proteins that bind a common ligand adopt different conformations?^36,37 The view fails to explain allostery in the absence of conformational change,^38,39 effect of mutations that do not disturb structure but alter protein function,^3,40 role of disordered protein segments,⁴¹ and the most perplexing: agonistic and antagonistic effects mediated from the same effector site.^42,43 Experimental limitations do not allow for exploring all allowed protein conformations as expected from the population shift paradigm, and explanations continue to be specific to the majorly populated one or two conformations in the free energy landscape. Overall, the structural view is so example-specific that it offers no universal understanding to studying proteins or allosteric systems in general.

DYNAMICS-BASED DESCRIPTORS OF ALLOSTERY

In a thermodynamic paradigm, allostery can be thought of as energy transfer or energetic coupling between the effector and active site.¹⁹ This inherently means that energy transfer will be a long-range communication dependent on both enthalpic (structural) and entropic (dynamic fluctuations) components.⁴⁴ In the absence of a change in structure, allosteric communications could, in theory, proceed solely through the entropic component. This defines dynamics-based allostery, as postulated by Cooper and Dryden in the 1980s,⁴⁵ that dispenses with the idea of an overall conformational change. According to the Cooper–Dryden model, binding of an allosteric modulator alters a protein’s conformational entropy through dynamic modulation of the protein’s side chain motions. Hence, an allosteric modulator can affect the properties of the protein’s active site irrespective of its location on the protein surface or ability to change the shape of the protein (Fig. 2).

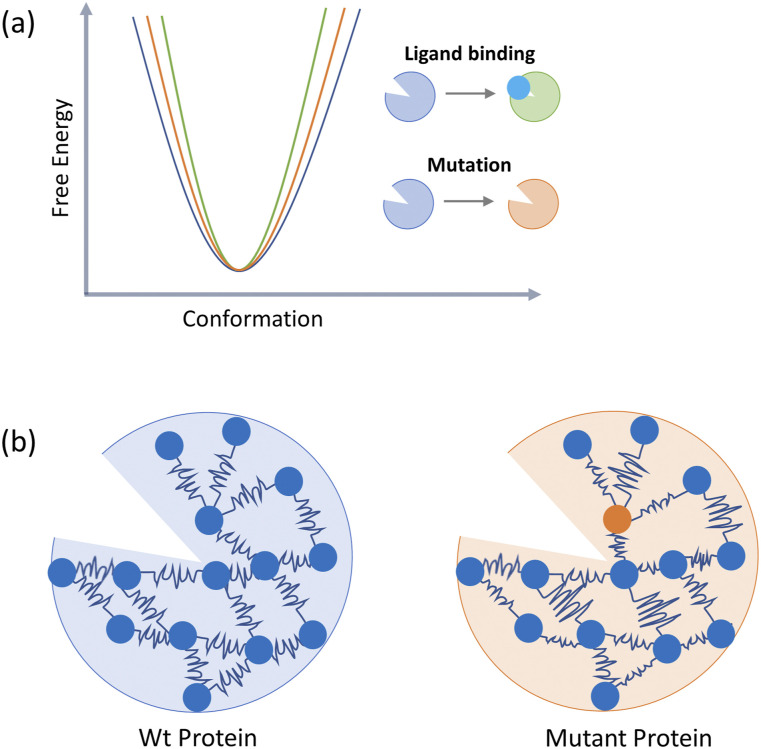
FIG. 2.

Dynamics-based description of allostery (a) The Cooper–Dryden model postulates that reorganization of internal protein motions allows for allosteric communications in proteins in the absence of any major conformational change. (b) The Elastic Network Model reduces a protein into an elastic mass-and-spring network. Allosteric stimuli (like mutations and ligand binding) alter the mass density and moduli of connecting springs.

Unlike protein conformational switching that occurs on the μs-ms time scale, the Cooper–Dryden model emphasizes changes in frequencies and amplitudes of amino acid thermal fluctuations or the redistribution of ps-ns motions in the protein’s interior as the mediator for allostery.⁴⁶ Moreover, as self-organization and dynamics-based folding of a protein are its intrinsic properties,⁴⁷ these correlated ps-ns motions in the interior of the protein would also show distinct patterns in the ligand-unbound states. Here, the structure of the protein would dictate a spatial distribution of amino acid densities and constrain the correlations in their movements to certain regions. This means that while the entropic contribution to allostery is dependent on side chain motions, these motions are nonrandom and are constrained by the inter-residue interactions imposed by the structure of the protein.⁴⁸ This dynamics-based view of allostery is supported by the increased complementary evidence derived from molecular dynamics simulations and protein NMR methods.^49–52

THE “VIOLIN MODEL” OF DYNAMICS-BASED ALLOSTERY

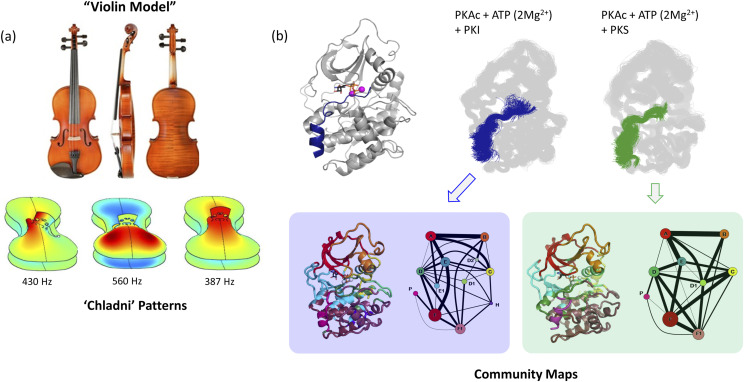
When working on the catalytic domain of protein kinase A (PKA),^{3,44,51,53–57} we explored its dynamics-based allostery based on the Cooper–Dryden model and called it the “violin model.” This was for two reasons: First, the shape of the kinase catalytic domain is a bi-lobal structure that resembles the body of a violin. Second, the physics of a violin based on normal modes and wave-functional approaches^58–61 closely matches the Cooper–Dryden model of allostery in proteins. Acoustics of a violin are determined by the anisotropic elastic properties of its two plates. When the bow is used to excite the strings, a harmonic note is generated as a wave function that disperses through the two plates of the violin.⁶⁰ Depending on the shape, grain of wood, and filing of the plates (parameters that determine its elastic properties), modes played on the violin register a particular resonance pattern on its plates. Named after the physicist who described them, these resonance patterns are called “Chladni patterns”^60–62 and are essentially used as a guide to manufacturing violins. Physically, the presence of Chladni patterns means that certain parts of the violin vibrate together while others synchronously vibrate away from each other at every note (Fig. 3). If a protein (like protein kinase A) is thought to be a violin, it will mean that in every conformational state (note played), there are amino acids in is interior that synchronously either move together or away from each other. Much like the shape and grain of wood for a violin, the elastic properties of the protein will be defined by its amino acid composition and folded structure. Changes in the elasticity of the protein (by mutation or allosteric cues) will change the “Chladni pattern” of the protein without changing its shape. In this way, the violin model will define the founding argument of the Cooper–Dryden model where vibrations/fluctuations/motions in the interior of the protein will define its allosteric communication.⁴⁵ Computationally, the violin model can be approached in two ways: elastic network models^63–66 and community network analysis.^67,68 While both these approaches are explained below, we have used the community network analysis to explore protein kinase A.^{44,51,3,53,57,55,56}

FIG. 3.

Violin model of allostery. (a) Harmonic nodes create a vibrational resonance pattern on the plates of a violin called “Chladni patterns.” At different node frequencies, different parts of the plates are synchronized to vibrate together or against each other. Elastic properties of the plate affect Chladni patterns. Chladni pattern pictures obtained from Ref. 62. (b) If the kinase bi-lobal structure is thought of as a violin, Chladni patterns are reflective of the resonance patterns of internal vibrations/amino acid motions of the protein. Different effectors (like binding of PKI and PKS) generate distinct “community maps” when analyzing dynamics-based amino acid networks.

ELASTIC NETWORK MODELS

In a simplified, low-resolution view of the violin model, a large protein can be thought to be made of several semirigid bodies connected by springs⁶⁹ (Fig. 2). This forms the Elastic Network Model (ENM)⁶⁴ that describes every amino acid as an atomic particle placed in 3D-space in accordance with the structural fold of the protein. These particles in turn are connected to each other by linear Hookean springs in patterns decided by certain rules.^63,70–72 For example, in coarse-grained ENMs, patterns emerge with the use of a distance-based interaction cutoff of ∼10 Å.⁷² If all atomic fluctuations around a reference structure are considered isotropic (independent of the direction of the fluctuation), the overall dynamics of a protein with Nparticles can be described by N-dimensions (only the amplitude of fluctuation and no direction). This forms the Gaussian Network model (GNM) that forms the basis of Normal Mode Analysis (NMA)^71,73–75 used for investigating fluctuations or protein structural transitions. In NMA, protein motion is linearly approximated around an averaged steady state to be decomposed into orthogonal normal modes. Mathematically, this is achieved by solving the eigen problem to linearize the Hessian matrix of the elastic potential energy⁶⁴ such that each eigenvalue points to the frequency of motion in the direction of the corresponding eigenvector. Smaller eigenvalues represent slower, very-low-frequency modes that represent large amplitude motions contributing significantly to protein entropy.^74,76 In the anisotropic model of NMA, atomic functions around the reference structure are considered in three-dimensional space such that the descriptions of protein conformational dynamics are in 3N-dimensions.^65,77

In the most basic application of ENM to study allostery,⁶⁶ mutations in protein are modeled by changing the moduli of the Hookean springs connecting the Cα nodes of the protein. Similarly, allosteric effector binding is modeled with the addition of nodes and local harmonic potentials to the system (Fig. 2). ENM has also been used in combination with other strategies to uncover specifics of allostery in various systems.^78,79 ENM combined with Dynamics Perturbation Analysis (DPA)⁸⁰ and Perturbation Response Scanning (PRS)⁸¹ can detect key residues whose perturbations are coupled to dynamic changes at distal sites. Adaptations of GNM have been used to identify pathways of correlated residues in protein interiors^82,83 and identify allosteric sites on the protein surface.⁸⁴ ENM is now being used in combination with network analysis^83,85 where NMA has been shown to recapitulate linear correlated motions in protein obtained from all-atom molecular dynamics.⁸⁶

COMMUNITY NETWORK ANALYSIS

While ENM provides a compelling global view of protein dynamics, it lacks in its descriptions of amino acid mobility, entropy, or contribution to allostery. Here, graph theory^87,88 based concepts are useful in exploring allosteric communications within the interior of proteins. Sub-microsecond protein motion trajectories as obtained by molecular dynamics simulations are used to assess pairwise amino acid interactions by Dynamic Cross Correlation⁸⁹ or Mutual information.⁹⁰

Dynamic cross correlation is defined by the covariance^89,91 between the motions of two amino acids as denoted by their Cα or side chain atoms. Covariance c(_i,j) is calculated as

$$c\left(i,j\right)=⟨\mathit{\Delta }{r}_i\cdot \mathit{\Delta }{r}_j⟩,$$

where angled brackets denote the average over a trajectory ensemble and Δr_i is the displacement vector of atom i. A Dynamic Cross Correlation Matrix (DCCM) can be generated by calculating the cross-correlation coefficient (or normalized covariance) as

$$C\left(i,j\right)=c\left(i,j\right)/{\left[c\left(i,i\right)c\left(j,j\right)\right]}^{1/2},$$

$$C\left(i,j\right)=⟨\mathrm{\Delta }{r}_i\cdot \mathrm{\Delta }{r}_j⟩/{⟨\mathrm{\Delta }{r}_i^2⟩}^{1/2}{⟨\mathrm{\Delta }{r}_j^2⟩}^{1/2}.$$

Residue pairs with uncorrelated motions intuitively have a cross-correlation coefficient at zero [C(i,j) = 0]. Completely correlated [C(i,j) = 1] or anticorrelated [C(i,j) = −1] motions denote that the motions have the same phase and period. Positive values of [C(i,j) > 0] imply atoms moving in the same direction, while negative values of [C(i,j) > 0] imply atoms moving in opposite directions. When residue pairs move in the same phase and period but their displacements are perpendicular to each other, their cross-correlation coefficient nears zero. This is a limitation of DCCM, where all orthogonal motions disappear as if they were not correlated.⁹²

Mutual information (MI) (though computationally expensive) accounts for pairwise motions in all directions by correlating protein backbone and side chain torsion angles.⁹³ Mutual information simply describes correlations between two observables of a system such that one can measure how much information about observable is gained from the knowledge of another.⁹⁴ Mathematically mutual information I(X;Y) between observables X and Y is defined as difference between sum of the self-entropies of X and Y and the joint entropy of the system comprising X and Y as follows:⁹⁵

I(X;Y) = Σ_x∈_XP(X) ln[P(X)] + Σ_y∈_YP(y) ln[P(y)] − Σ_x∈_XΣ_y∈_YP(x, y) ln[P(x, y)], where P is the probability function. For a protein, these observables are the torsion angles of amino acids such that its conformational (Shannon) entropy can be defined by the equation³

$$\begin{array}{ll}\hfill S_{\mathit{conf}}& =\sum _i^n\underset{0}{\overset{2\pi }{\int }}p\left(\phi \right)\mathrm{I}\mathrm{n}p\left(\phi \right)d{\phi }^{-}\sum _i^n\sum _j^n\underset{0}{\overset{2\pi }{\int }}\underset{0}{\overset{2\pi }{\int }}p\left({\phi }_1,{\phi }_2\right)\mathrm{I}\mathrm{n}\hfill \\ \hfill & \times \frac{p\left({\phi }_1,{\phi }_2\right)}{p\left({\phi }_1\right)p\left({\phi }_2\right)}d{\phi }_1{\phi }_2+\cdots -\cdots ,\hfill \end{array}$$

where i and j denote the amino acid’s torsions summated over n, the total number of torsion angles (φ, ψ, and χ) summated over all the residues of the protein. This equation is an expansion of the protein’s configurational entropy into terms including single, pairwise torsions, etc. to directly use correlated torsions as a measure of thermodynamics. The second-order term in the equation describes the sum of mutual information over each pair of torsion angles. As the fold/packing of a protein determines the degrees of torsions allowed for all amino acid residues, mutual information provides a robust way to measure its correlation and directly compares how the movement in one residue affects the movement in another. One can then calculate a Pearson correlation coefficient r_MI as⁹⁶

$$\left.r_{MI}\left[X,Y\right]=\left[1-\exp \left(-2I\left[X,Y\right]/d\right)\right]\right\},$$

where I is the mutual information between the observables X and Y and d is their dimensionality. The Pearson correlation coefficient r_MI assumes the value of zero for fully uncorrelated motions to reach a value of 1 for fully correlated motions. Hence, unlike the simple covariance measure C(i,j), the Pearson correlation coefficient r_MI does not become zero with the orthogonal movement of pairwise amino acids and efficiently accounts for nonlinear correlated residue-pair motions.

Both the Pearson correlation coefficient r_MI and cross-correlation coefficient C(i,j) can be used to draw the weighted adjacency matrix (A_ij) of proteins to obtain a network graph⁸⁷ of its correlated dynamics (Fig. 4). Simply, a protein of N residues is used to create a graph with N nodes connected by edges that have a certain weight. For any graph weighted by coefficients (edge weights) w_ij, the adjacency matrix is denoted by A_ij = w_ij, if an edge for nodes i and j exists and otherwise by A_ij = 0. The simplest adjacency matrices (A) is a contact map⁹⁷ (as derived from static crystal structures), where two nodes are connected by an edge of weight of 1 when they lie within a set distance cutoff of one another. For analyzing dynamics-based information, two cutoffs are used to provide a robust and maximally converged outcome: distance and percentage.^3,92 A distance cutoff of 3.5–5.5 Å ensures long-range correlation communications are filtered out and only chemically relevant correlations are analyzed. A percentage cutoff is a statistical measure that ensures that measured correlations are present in majority of the simulation frames (75%–85%) and denote effective communications. Edge weights w_ij are obtained from the Pearson correlation coefficient r_MI or cross-correlation coefficient C(i,j) by converting them into communication distances d_ij by a simple negative log transformation. Furthermore, a Laplacian matrix (L_ij) can be derived by taking the difference between the diagonal matrix of degree (D_ij)⁹⁸ and the adjacency matrix (A_ij) of the nodes. This Laplacian matrix (L_ij) when multiplied by a spring constant coincides with the Hessian matrix⁷⁰ of the Gaussian Network model (GNM) of the Elastic Network Models (ENMs) mentioned above.

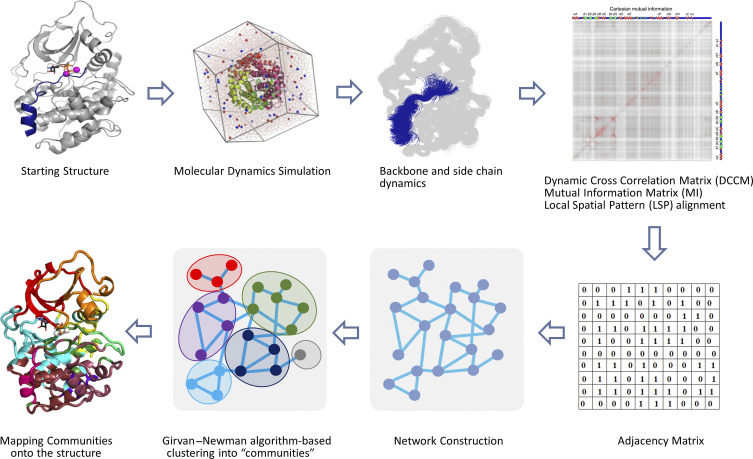
FIG. 4.

Schematic workflow of community map analysis. Amino acid dynamics is obtained by microsecond MD simulations and is assessed for entropic correlations by computing DCCM, MI, or LSP matrices. These matrices, in turn, are used to create an adjacency matrix to reveal a residue network. Girvan–Newman algorithm is used to hierarchically cluster the network into communities based on the property of Edge-Betweenness. Deduced communities are mapped onto the structure to gain a visual assessment of amino acid dynamics.

A dynamic weighted network as obtained from the adjacency matrix provides a digestible visual to the communications in the interior of proteins. Here, residue pairs that are physically associated with each other (within a chemical distance and being present for a major fraction of simulation time) and exchange dynamic information are closer together in the graph when compared to residues that may be physically associated but do not share dynamic information. To reveal the “Chladni” pattern for the protein dynamics, Girvan–Newman algorithm⁸⁸ is used to partition the dynamic weighted networks into “communities” (Fig. 4). Here, a community is defined as a local substructure involving a group of nodes that are densely connected within but sparsely connected to others in the network. Communities are identified on the criterion of Edge-Betweenness (EB) that measures the number of shortest paths through a given edge. Edges with a high EB value have higher information flow through them compared to others. The Girvan–Newman algorithm⁸⁸ iteratively calculates and removes edges in descending order of their betweenness values to reveal a pattern of nonoverlapping subgraphs/community network such that a given node can only be a part of one community. Connections between communities are weighted by the sum of EB values of the pairs of residues connecting any two communities. When defining protein nodes by both amino acid main chain (Cα) and side chain (Cβ) atoms, it is common to get a set of residues wherein their Cα-node is a part of one community and Cβ-node of another.^3,53 These are called “Bridging residues” that physically connect two communities. Optimal partitioning of the network into communities is assessed by calculating the “modularity”^99,100 of the community map. Modularity is a multiplicative constant that defines the number of edges present within a community to the number of edges present in the entire network. Mathematically, modularity Q is defined as⁶⁸

$$\mathrm{Q}={\sum }_{\text{i}}(e_{\mathit{ij}}-a_i^2),$$

where a_i = ∑_j(e_ij) is the fraction of edges that connect nodes within community i and e_ij is the fraction of edges connecting nodes between two given communities i and j. Values of Q range between 0 (entire protein is a single community) and 1 (number of communities is equal to the number of residues), where a higher number is indicative of a better quality of partitioning.⁹⁹ Modularity of community maps obtained from proteins is typically >0.4.^55,99 Optimized community maps when imposed back on the 3D structure of proteins allow for visualizing the protein’s “Chladni pattern” and are a direct reflection of its underlying Cooper–Dryden model of dynamics-based allostery.

To ascertain the residue-wise contribution to the allosteric communications, weighted dynamic networks can be studied for their residue centralities.^57,101,102 The most popular measures of centrality^103,104 include Degree Centrality (DC), Closeness Centrality (CC), Betweenness Centrality (BC), and Eigenvector Centrality (EC). DC assigns a score to a node based on the number of direct physical edges connecting it to other nodes in the network. CC scores nodes based on their closeness with other nodes. Here, shortest paths between all the nodes are calculated using the Floyd–Warshall algorithm¹⁰⁵ and CC score is based on the sum of the shortest paths. Nodes with a higher CC influence the network quicker than nodes with lower CC values. BC is scored based on the presence of a node between the shortest path connecting other nodes and reveals “bridges” of information flow through the network. Finally, EC calculates the extended connections of node and measures a node’s influence on the network. A node connected to other highly connected nodes has a higher EC score and exerts authority over the network. For various protein networks, EC is quickly evolving as a sensitive measure for attributing residue contribution to allostery.^106–108 From the violin model point of view, the central point of communities in protein structures is their behavior as semirigid bodies. It is, thus, logical to suggest that tracking the rotation of residue side chains during molecular dynamics simulation along with their C-α atom displacements can be beneficial for the analysis. Indeed, in our recent work, we demonstrated that Local Spatial Pattern (LSP) alignment (that represents residues as Cα-Cβ vectors) can be efficiently used to weight edges in protein networks.⁵⁷ In the LSP-generated networks, the DC and BC have been significantly more informative in comparison with traditional methods.⁵⁷ Although the LSP-alignment is computationally more expensive, it provides highly convergent results and can be reliably used on trajectories as short as 10 ns. Improving the computational efficiency of the method can open a new opportunity to analyze longer trajectories and large protein complexes. In this review, we summarize our work on protein kinase A and how the violin model has been crucial in explaining its allosteric mechanics.

VIOLIN MODEL EXPLAINS DYNAMICS-BASED ALLOSTERY IN PROTEIN KINASE A (PKA)

Protein kinase A (PKA) was the first eukaryotic kinase to be purified and explored for its biochemical function.¹⁰⁹ In cells, PKA exists as a holoenzyme of two regulatory and two catalytic subunits¹¹⁰ that conceal the activity of the catalytic subunit until a stimuli is received for its function. As signaling events trigger the activation of G-proteins, released 3′,5′-cyclic adenosine monophosphate (cAMP) molecules bind the regulatory subunits of PKA to disrupt the holoenzyme. The catalytic subunit hence freed from holoenzymes becomes available for downstream signaling where it phosphorylates Ser/Thr in the sequence R-R-X-S/T-Y (X is any residue and Y is a hydrophobic residue) in hundreds of cellular substrates.^111,112 This catalytic subunit of PKA serves as the prototype of the Eukaryotic Kinase superfamily of enzymes. It is the first kinase domain to be purified,¹¹³ crystallized,^114,115 and inspected for its structural details.⁵⁴

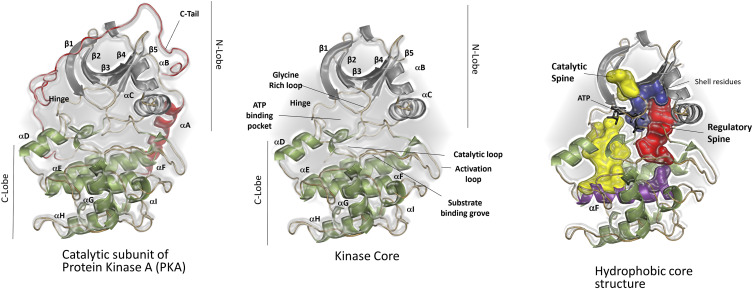
Briefly, the kinase domain is a bean-shaped bi-lobal structure presenting a unique ATP binding pocket sandwiched between the two lobes (Fig. 5). The smaller, N-lobe harbors a glycine-rich loop (G-loop) that assists ATP binding by interacting with its adenine ring,¹¹⁶ the β-strand 3 with the conserved K72,¹¹⁷ and the C-helix with the conserved E91.^117,118 The larger, C-lobe contains elements for binding substrates¹¹⁹ and the regulatory subunits.¹¹⁰ The kinase active site cleft includes the catalytic loop, activation loop, ATP binding pocket, the DFG and HRD (amino acid codes) motifs, all of which are contained in crucial for mediating phosphoryl transfer from ATP to substrate.¹¹⁹ Two divalent metal ions (usually Mg²⁺⁾ stabilize charges in the active site and regulate ADP release through a “lynch pin” mechanism.^120,121 Phosphorylation of the activation loop at T197 is critical for orienting the kinase active site.¹²²

FIG. 5.

The conserved kinase domain. The catalytic domain of protein kinase A (PKA) includes a kinase core flanked by two tails: the N-terminal tail and the C-terminal tail. The kinase core is a signature of the eukaryotic kinase superfamily and has a characteristic bi-lobal structure. ATP binds in the cleft between the two lobes while the substrate peptide binding region is localized to the C-lobe. Two lobes of the kinase core are connected by a network of hydrophobic residues assembled into two “spines.”

Structural data as obtained from crystallography,^119,123 NMR,^51,124,125 and fluorescence¹²⁶ indicate that the kinase domain toggles between open, intermediate, and closed conformations as the kinase circles through its catalytic cycle. Inter-lobal flexibility is important for nucleotide exchange at the active site^127,128 and is mediated by two hydrophobic motifs (called “Spines”) that span the two lobes while resting on the αF-helix of the C-lobe.^129,130 The spine associated with activation of the kinase domain (phosphorylation of T197) is referred to as the regulatory or R-spine, while the spine completed upon ATP binding and committing the kinase to catalysis is called the catalytic or C-spine.¹³¹

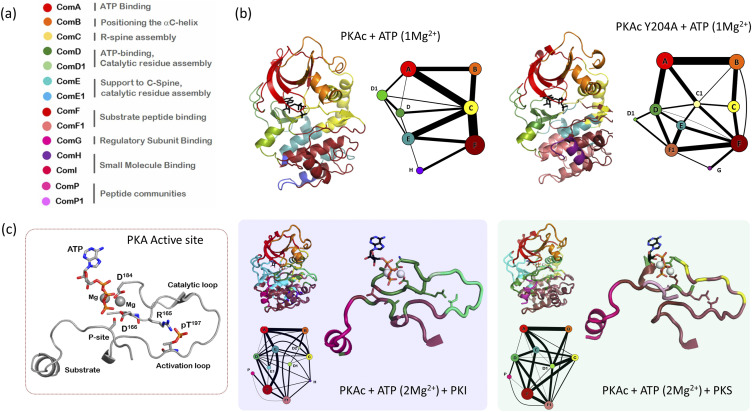
Enzyme function, in general, is dependent on its motion in the ps-μs time scales^132–134 and understanding PKA turnover and catalysis requires an in-depth appreciation for its dynamics-based features.¹³⁵ What role does dynamics play in helping PKA activation,¹³⁶ forming a transition state complex,¹³⁷ or stabilizing the product complex?¹³⁸ Here, the violin model allows us to interpolate the role of dynamics-based allostery in the catalytic workings of PKA. A typical community map of PKA includes about eight communities with 40–60 amino acid residues.^53,55 An expansive repertoire of structural and biochemical data allows for attributing functional features to each community (Figs. 6 and 7).⁵⁵ Community A (and A1) is localized to the N-lobe and includes residues that allow for optimal nucleotide binding. Community B includes residues surrounding the αC helix and the conserved K72-E91 salt bridge that allows for maintaining a folded N-lobe. This includes the FxxF motif of the C-tail of PKA that packs against the tip of the β-sheet of the N-lobe. Community C (and C1) provides support to the assembly of the R-spine and maintains the active conformation of PKA. This includes the cation-π stack provided by W30 in the αA helix to the αC helix. Community D (and D1) and community E (and E1) include residues from the catalytic loop and the C-spine. These stabilize and support substrate cycling at the PKA active site. Community F (and F1) spans majority of the C-lobe including residues from αF helix and the conserved F209-R280 salt bridge. Community F supports substrate binding and its synchronization with ATP for optimal phosphotransferase at the PKA active site. Community G supports protein–protein interactions between the catalytic subunit and regulatory subunits of PKA. Community H and community I form hotspot for small molecule binding.

FIG. 6.

Community map analysis explains the dynamics-based role of inactivating mutations and substrate recognition in PKA. (a) Functional roles assigned to PKA communities based on biochemical/biophysical experiments. (b) Distinct community networks obtained for the Y204A mutation when compared with WT PKA reveals the changing of communities in the C-lobe. Specifically, changes in community E and F explain the loss of synchronization of ATP and peptide at the PKA active site. (b) Community-based segregation of dynamics in the active site of PKA is distinct for an inhibitor peptide (PKI) when compared with a substrate (PKS). PKI tightly binds the kinase (as known by experiments) by engaging with its D and F communities. PKS only engages with community F with all catalytic residues including in the same community. Figure adapted from our earlier manuscripts.^3,53

FIG. 7.

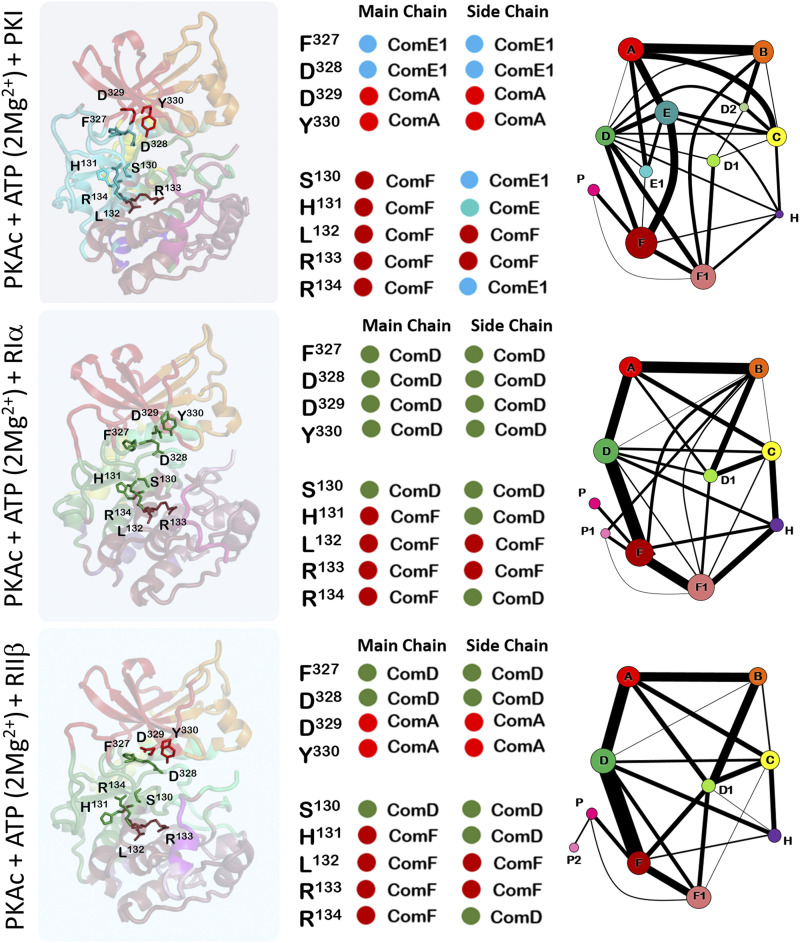
Community map analysis of the ternary complex of PKA:ATP(Mg²⁺):Inhibitor peptide reveals distinct dynamic footprints. Peptides derived from the inhibitory segments of three PKA interacting proteins (PKI, Riα, and RIIβ) break connections between the catalytic residue supporting communities D and E. Community H is strengthened by information flow from associated community C. Figure adapted from our earlier manuscript.⁵³

As PKA progresses through its catalytic cycle, community maps dissect the dynamic network employed to support its function. Comparison of community maps of the Apo and nucleotide-bound forms⁵⁵ of PKA details the role of core communities required for initial steps of the kinase catalytic cycle. Here, community maps are sensitive to capturing the catalytic differences imposed by the presence of a single or two divalent metal ions.^3,55 In the absence of a peptide, major reorganization of communities is limited to the C-lobe with communities A, B, and C on the N-lobe unchanged. Communities D and E that show maximal interaction with metal ions regroup to accommodate the change in active site charges. Community maps of the ternary complexes of PKA:ATP(Mg²⁺):peptide⁵³ demonstrate the PKA’s ability to distinguish between substrate and inhibitor peptides at a dynamics level (Figs. 6 and 7). Allosterically important residues change communities when PKA binds substrate peptides derived from PKS and PLN, product peptides including pPKS and pPLN or inhibitory peptides derived from RIα, RIIβ, and PKI. For example, R133 in the αD helix is a part of community F and is strongly coupled to the bridging residues of community F and the active site. Its neighbor R134 is a critical bridging residue that couples Com F to other communities; R134 connects community F and community E1 in PKA:ATP(Mg²⁺):PKI complex but community F and community D in the PKA:ATP(Mg²⁺):RIα and PKA:ATP(Mg²⁺):RIIβ complexes. In PKA:ATP(Mg²⁺):PKI and PKA:ATP(Mg²⁺):RIIβ complexes, binding of peptides stabilizes R133 such that community F is stabilized. This stabilization is propagated to communities D and E at the active site. However, in the PKA:ATP(Mg²⁺):RIα complex, increase in the distribution of conformations for R133 is associated directly with increased destabilization of community F. These changes in the dynamics-based associations of R133 explain biochemical measurements where the R133A mutation decreases the binding affinity of PKA:ATP(Mg²⁺) binary complex for PKI and RIIβ without affecting its interactions with RIα.¹³⁹ Unique dynamic associations in the PKA:ATP(Mg²⁺):RIα complex is also highlighted by the FDDY motif associating completely with the active site community D (Fig. 7). In contrast, F327 and D328 combine with communities E1 and D in the PKA:ATP(Mg²⁺):PKI and PKA:ATP(Mg²⁺):RIIβ complexes, respectively.

Community analysis can also be used to assess the role of distal mutations on protein catalytic activity. For example, Y204A mutation was identified from a peptide mobility screen and was shown to abolish kinase activity in PKA despite being 8 Å away from the active site.¹⁴⁰ Crystal structure of the Y204A mutant showed no change in the active conformation of PKA.¹⁴¹ Traditional biophysical measurements failed to explain the cause of Y204A inactivity when comparison of community maps of WT PKA and Y204A showed important differences. Specifically, community F (substrate interaction) split into F and F1 while communities C (supporting activation), D, and E (active site) are also affected in Y20A (Fig. 6). Communities responsible for binding the nucleotide (communities A and B in the N-lobe) remain unaltered in Y204A, supporting observations that the mutant binds ATP efficiently. Biochemical assays designed based on information from community maps showed that Y204A had comparable ATP hydrolysis activity to WT PKA and in fact could do a phosphotransfer to water.³ ATP and AMP-PNP binding assays showed that Y204A bound nucleotides almost twice as efficiently compared to the WT protein. Y204A also bound the substrate peptide efficiently such that the Y204A:ATP(Mg²⁺):IP20 complex was thermally more stable than the PKA:ATP(Mg²⁺):IP20 complex in differential scanning fluorimetry assays.³ Finally, we designed a fluorescence polarization-based substrate cooperativity assay to assess if we could biochemically detect uncoupling of nucleotide and substrate peptide at the PKA active site as seen by community map analysis in the Y204A mutation. We showed that while the WT PKA exhibited “positive cooperativity” in binding nucleotide and FAM-IP20, all cooperativity was lost in the Y204A mutation as predicated by the community map analysis.³ PKA bound AMP-PNP with a K_D of ∼40.0 µM in the apo form but showed a three orders enhanced affinity at a K_D of ∼65.0 nM for AMP-PNP binding to the kinase:peptide binary complex. Reciprocally, peptide binding to PKA was enhanced by three orders in the kinase:nucleotide complex as compared to the apo protein. In contrast, Y204A bound AMP-PNP with a K_D of ∼20.0 µM in the apo form, which became slightly worse at K_D of ∼44.0 µM for AMP-PNP binding to the mutant:peptide complex. In conclusion, where traditional approaches failed to provide insights, the violin model was efficient in providing leads to understanding changes in Y204A dynamics that resulted in the loss of its kinase activity.

CONCLUSIONS

Dynamics-based descriptions of protein allostery are crucial in highlighting the workings of signaling proteins, including that of proteins kinases that regulate critical cell functions of growth and division. Often, conformation-based descriptors of allostery are limited in their explanations of protein activation/inhibition and role of mutations and protein–protein interactions. Our violin model-based community map analysis provides an exhaustive method for measuring the role of internal protein motions toward its function.

AUTHOR DECLARATIONS

Conflict of Interest

The authors have no conflicts to disclose.

Author Contributions

L.K.M. has designed and written this manuscript with inputs from C.L.W., A.P.K. and S.S.T.. All authors have read, edited, and approved the initial and revised versions of this manuscript.

Lalima K. Madan: Conceptualization (lead); Visualization (lead); Writing – original draft (lead); Writing – review & editing (lead). Colin L. Welsh: Writing – original draft (supporting); Writing – review & editing (supporting). Alexandr P. Kornev: Writing – review & editing (supporting). Susan S. Taylor: Writing – review & editing (supporting).

DATA AVAILABILITY

Data sharing is not applicable to this article as no new data were created or analyzed in this study. Authors will be available to share details on the computational methods/codes upon reasonable request.